Abstract
This paper presents a hybrid reinforcement learning framework for trajectory tracking control of a 5-degree-of-freedom (DOF) Mitsubishi RV-2AJ robotic arm by integrating model-free deep reinforcement learning (DRL) algorithms with classical control strategies. A novel hybrid PID + TD3 agent is proposed, combining a Proportional–Integral–Derivative (PID) controller with the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm, and is compared against standalone TD3 and PID controllers. In this architecture, the PID controller provides baseline stability and deterministic disturbance rejection, while the TD3 agent learns residual corrections to enhance tracking accuracy, robustness, and control smoothness. The robotic system is modeled in MATLAB/Simulink with Simscape Multibody, and the agents are trained using a reward function inspired by artificial potential fields, promoting energy-efficient and precise motion. Extensive simulations are performed under internal disturbances (e.g., joint friction variations, payload changes) and external disturbances (e.g., unexpected forces, environmental interactions). Results demonstrate that the hybrid PID + TD3 approach outperforms both standalone TD3 and PID controllers in convergence speed, tracking precision, and disturbance rejection. This study highlights the effectiveness of combining reinforcement learning with classical control for intelligent, robust, and resilient robotic manipulation in uncertain environments.
1. Introduction
Robotic systems have evolved from simple, pre-programmed machines into intelligent, adaptive entities that play a critical role across numerous domains, including industry, healthcare, defense, and domestic environments. Initially restricted to executing repetitive tasks in structured settings, modern robots are now capable of operating autonomously in complex and dynamic environments. This transformation has been driven by significant advancements in sensing, actuation, computation, and artificial intelligence, particularly in areas such as robotic arms and autonomous manipulation. As robotic technology continues to advance, its integration into daily life and specialized sectors has become increasingly widespread. In industrial settings such as automotive manufacturing, aerospace, and logistics, robots perform intricate operations with precision and consistency. Simultaneously, in healthcare and service industries, robotic systems assist in surgeries, patient care, and hospitality. In domestic environments, the long-term vision is to develop robotic assistants capable of executing routine tasks with minimal human intervention, thereby enhancing convenience and efficiency [1,2].
Achieving accurate and robust trajectory tracking in robotic arms remains a fundamental challenge in advanced robotic systems. These manipulators typically exhibit nonlinear dynamics, strong joint coupling, multiple degrees of freedom, and complex multi-input multi-output behavior. In real-world applications, additional factors such as sensor noise, external disturbances, actuator saturation, and time-varying uncertainties further complicate precise motion control. Traditional control strategies, including PID controllers, have been widely adopted due to their simplicity and real-time responsiveness. However, they often struggle to maintain optimal performance in dynamically changing or uncertain environments. To address these limitations, researchers have explored various control methodologies, including adaptive control, fuzzy logic, neural networks, sliding mode control, and model-based optimization, yet consistently achieving high precision under uncertainty remains an open issue. In recent years, DRL has emerged as a promising paradigm for robotic control, offering the ability to learn optimal policies through interaction with the environment. DRL algorithms such as Deep Deterministic Policy Gradient (DDPG) and its advanced variant TD3 have demonstrated strong performance in continuous control tasks. TD3, in particular, addresses several stability and overestimation issues inherent in earlier RL methods, making it suitable for high-precision control applications. Nevertheless, pure RL approaches often face challenges in early-stage learning stability and safe exploration [3].
Recent advancements in DRL have significantly improved control strategies for robotic systems, especially through the development of the TD3 algorithm, which addresses key limitations of the original DDPG, such as overestimation bias and training instability. One of the earliest contributions, Dankwa and Zheng [4] (2019), introduced TD3 for modeling continuous robotic motion, demonstrating its advantages over conventional RL approaches. Subsequently, Kim et al. (2020) [5] applied TD3 with hindsight experience replay to enhance motion planning in robotic manipulators, achieving smoother and more efficient trajectories. Hou et al. (2021) [6] introduced a TD3-based control framework with a rebirth mechanism to enhance learning efficiency and adaptability in multi-DOF robotic manipulators. Similarly, Khoi et al. (2021) [7] developed a control and simulation method for a 6-DOF biped robot using TD3, confirming its effectiveness in improving gait stability. Joshi et al. (2021) [8] extended TD3 for industrial process control by proposing the Twin Actor Twin Delayed DDPG (TATD3) algorithm, which demonstrated improved control precision in chemical batch processes. The expansion of TD3 applications continued with Mosali et al. (2022) [9], who employed a multistage TD3-based learning approach with achievement-based rewards for target tracking in UAVs, achieving robust performance under dynamic and uncertain conditions. In the field of space robotics, Song et al. (2024) [10] proposed a trajectory planning strategy based on DRL, confirming the feasibility of DRL in highly complex and nonlinear aerospace systems. Most recently, Hazem et al. (2025) [11,12] conducted a comprehensive comparative study on reinforcement learning algorithms, DDPG, LC-DDPG, and TD3-ADX, for trajectory tracking of a 5-DOF Mitsubishi robotic arm. Their results highlighted the benefits of advanced RL-based control in terms of accuracy, adaptability, and robustness.
Despite the potential of TD3 in continuous control, standalone implementations often suffer from high early-training variance and poor disturbance rejection in unmodeled situations. Zhang et al. (2020) [13] proposed the PID-Guided TD3 algorithm for spacecraft attitude control; by using a PID controller to steer learning, the system achieves faster convergence and higher precision amid torque saturation and external disturbances. In the context of vehicle platooning, Chen et al. (2023) [14] introduced a two-layer hybrid where a TD3-tuned PID controller simplifies tuning and delivers smooth acceleration while maintaining tight inter-vehicle distance control. For autonomous navigation, Joglekar et al. (2022) [15] fused deep RL-based longitudinal control with PID-based lateral control, balancing adaptability with stability. For humanoid cable-driven robots, Liu et al. (2024) [16] combined a decoupling PID with deep RL, enhancing tracking performance in dynamic tasks. In HEV energy management, Zhou et al. (2021) [17] demonstrated that an improved TD3 framework outperforms traditional RL strategies in terms of fuel efficiency, convergence speed, and robustness across diverse conditions. Lastly, Liu et al. (2024) [16] designed a PID-augmented deep RL controller for target tracking with obstacle avoidance, achieving enhanced safety and precision in complex environments. Table 1 presents the capabilities and limitations of DDPG, LC-DDPG, TD3-ADX, and hybrid PID + TD3 in robotic applications.

Table 1.
Capabilities and limitations of DDPG, LC-DDPG, TD3-ADX, and hybrid PID + TD3 in robotic applications.
In this paper, a DRL-based hybrid control strategy is developed to address the trajectory tracking problem of a 5-DOF Mitsubishi RV-2AJ robotic arm (Mitsubishi Electric Corporation, Tokyo, Japan), leveraging advancements in model-free learning methods to overcome the inherent limitations of conventional model-based control. Traditional approaches such as PID controllers and ANFIS have been widely used due to their simplicity and interpretability; however, they often struggle to maintain robustness and accuracy in the presence of nonlinear dynamics, modeling uncertainties, and varying payloads. Instead of relying on explicit system dynamics, which are often difficult to derive accurately for highly nonlinear and coupled robotic systems, the proposed approach employs DDPG and its enhanced variants (LC-DDPG and TD3-ADX) as the foundation for learning precise and adaptive control policies. While standard DDPG provides a baseline solution for continuous control tasks such as robotic arm manipulation, its performance can be limited by sample inefficiency, overestimation bias, and early-stage instability. LC-DDPG addresses these issues by enforcing stability through Lyapunov-based constraints, and TD3-ADX mitigates overestimation bias while promoting dynamic exploration for faster and more reliable learning. Building on these model-free strategies, the framework is further enhanced with a hybrid PID + TD3 architecture, which integrates the short-term stability and deterministic disturbance rejection of PID control with the adaptive capabilities of TD3. This hybrid approach ensures safe exploration, faster convergence, and improved tracking accuracy under dynamic perturbations, unmodeled nonlinearities, and payload variations. In this study, the reward function is carefully designed using principles inspired by artificial potential field theory, balancing attraction toward the desired trajectory with repulsion from tracking deviations. This design promotes efficient convergence and robust policy learning, echoing modern reinforcement learning strategies for handling complex robotic tasks.
To enable safe and realistic agent training, a high-fidelity 3D simulation environment is developed using MATLAB/Simulink’s Simscape Multibody toolbox (MathWorks, Natick, MA, USA; R2024b). The simulation accurately replicates real-world physics, providing real-time feedback on joint positions, velocities, and end-effector coordinates essential for effective policy optimization. Simulation results validate the effectiveness of the proposed control strategies, demonstrating that hybrid PID + TD3 outperforms both LC-DDPG and TD3-ADX in terms of convergence speed, tracking precision, and disturbance rejection. These findings highlight the critical role of hybrid DRL-based controllers in equipping robotic systems with the flexibility, robustness, and autonomy required for operation in uncertain real-world environments. The key contributions of this paper are summarized as follows:
- Proposes a hybrid PID + TD3 control framework that combines the deterministic stability of PID control with the adaptive capabilities of TD3, enabling safe exploration, faster convergence, and improved trajectory tracking accuracy for a 5-DOF Mitsubishi RV-2AJ robotic arm under dynamic and uncertain conditions.
- Introduces an artificial potential field-inspired reward mechanism within the DRL framework to balance attraction toward the target trajectory and avoidance of tracking deviations, supporting robust and efficient learning.
- Develops a high-fidelity 3D simulation platform using MATLAB/Simulink’s Simscape Multibody toolbox, ensuring accurate, real-time physics-based interactions essential for training and validating reinforcement learning agents in robotic control tasks.
- Demonstrates through simulations that the hybrid PID + TD3 approach outperforms conventional model-based controllers and standard RL variants, including previously studied DDPG-based methods, in convergence speed, tracking precision, disturbance rejection, and overall robustness.
The remainder of this paper is organized as follows: Section 2 presents the dynamic modeling of the Mitsubishi RV-2AJ robotic arm, deriving its nonlinear equations of motion. Section 3 outlines the fundamentals of reinforcement learning and details the implementation of the hybrid PID + TD3 framework, while briefly referencing the previously studied DDPG variants (LC-DDPG and TD3-ADX) for context. Section 4 presents the simulation results, evaluating the performance of the proposed hybrid controller under dynamic and uncertain conditions, with a focus on convergence speed, tracking precision, disturbance rejection, and overall robustness. Finally, Section 5 concludes the paper by summarizing the findings and discussing future research directions in hybrid reinforcement learning-based control strategies for robotic systems.
2. Kinematic Analysis and Dynamic Modeling of the 5-DOF Mitsubishi RV-2AJ Robotic Arm
The 5-DOF Mitsubishi RV-2AJ robotic arm used in this study, shown in Figure 1, consists of rigid links connected by revolute joints, providing precise industrial manipulation. Its five joints, base, shoulder, elbow, and two wrist axes, enable full positioning and orientation, with servo motors controlling joint angles (θ1–θ5) accurately. The arm is modeled as a serial-chain manipulator, with forward kinematics derived via the Denavit-Hartenberg (D-H) convention (Table 2 presents the physical and kinematic parameters of the robotic arm). Its dynamic model, based on the Euler-Lagrange formulation, captures nonlinearities, joint coupling, and external disturbances, creating a realistic simulation environment. These accurate kinematic and dynamic models are crucial for implementing and training the hybrid PID + TD3 controller, ensuring safe exploration, faster convergence, and high-precision trajectory tracking in the simulated environment that closely reflects real-world robotic interaction. Detailed derivations follow the work of Z. B. Hazem et al. [11,12,18].
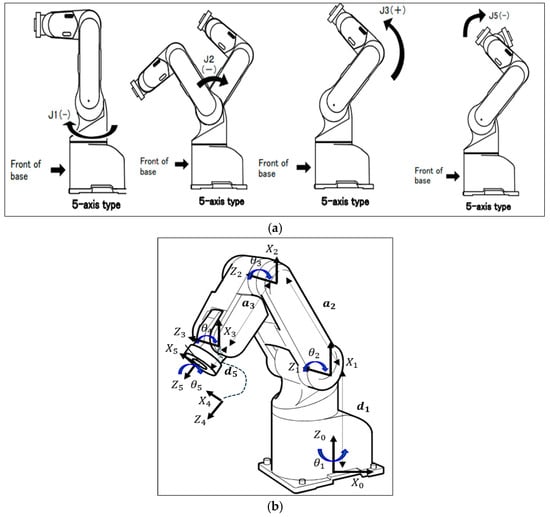
Figure 1.
5-DOF Mitsubishi RV-2AJ robotic arm: (a) CAD model showing joint locations; (b) Kinematic parameters.

Table 2.
Physical and kinematic parameters of the 5-DOF Mitsubishi RV-2AJ robotic arm.
The forward kinematic model of the robot can be calculated using Equation (1), where is the homogeneous transformation matrix derived from the D-H parameters provided in Equation (2):
The dynamic model of the 5-DOF Mitsubishi RV-2AJ robot, derived from its kinematic representation, relates joint motions to the forces and torques acting on the system and can be expressed in matrix form as
where , and denote joint positions, velocities, and accelerations, respectively. D(θ) is the inertia matrix capturing the robot’s mass properties, C() represents Coriolis and centrifugal forces, and G(θ) accounts for gravitational effects. The applied joint torques are represents friction torques, including viscous and potentially nonlinear components such as Coulomb or Stribeck effects. This compact representation provides a complete framework for simulation and control, serving as the basis for implementing the hybrid PID + TD3 controller. The control inputs for each joint are the torques (, , , , ), generated by the servo motors. These torques are implemented in the MATLAB/Simscape model, enabling accurate simulation and analysis of the robot’s dynamic behavior under various control scenarios. A corresponding CAD-based dynamic model was also developed in MATLAB/Simscape to validate the mathematical formulation. Figure 2a,b illustrate the Simscape model and the CAD model, respectively. Both models were simulated under identical initial joint positions, showing excellent agreement and confirming the accuracy and reliability of the dynamic model (see Figure 3).
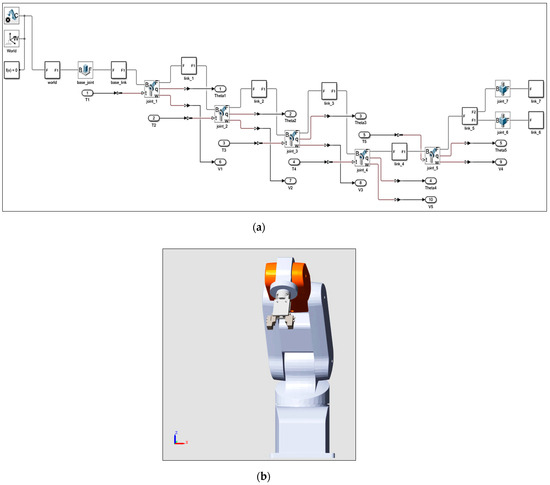
Figure 2.
5-DOF Mitsubishi RV-2AJ robot: (a) MATLAB/Simscape model; (b) CAD model implemented in MATLAB/Simulink.
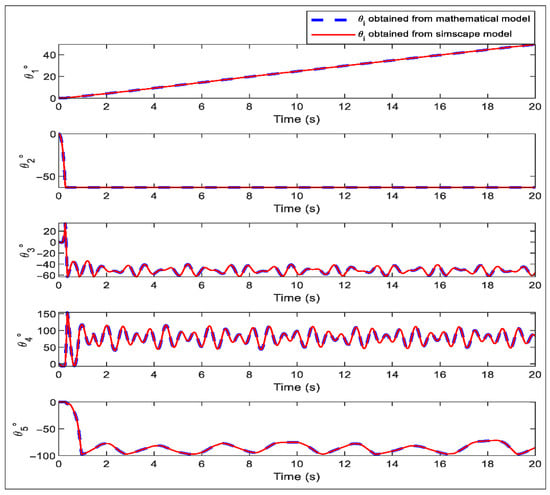
Figure 3.
Comparison of joint angles (θ1–θ5) between the mathematical model and the Simscape model of the 5-DOF Mitsubishi RV-2AJ robot.
3. Hybrid PID + TD3 DRL Controller for Trajectory Tracking of a 5-DOF Mitsubishi Robotic Arm
This section presents the design and implementation of a hybrid PID + TD3 controller for trajectory tracking of the 5-DOF Mitsubishi RV-2AJ robotic arm. The hybrid structure combines the well-established stability and fast transient response of a PID controller with the adaptive learning capability of the TD3 algorithm. In this approach, the PID controller provides a reliable baseline control signal, ensuring robustness and maintaining performance during the early stages of learning, while the TD3 agent gradually refines the control policy through interaction with the environment. Operating under a model-free framework, the TD3 component does not require an explicit dynamic model of the robotic arm, which is advantageous given the system’s nonlinearities and complex joint couplings. The TD3 agent, based on the actor–critic architecture, learns optimal adjustments to the PID output by evaluating actions in continuous space and maximizing expected cumulative rewards. This synergy enables smooth and precise joint movements, improved tracking accuracy, and enhanced adaptability to dynamic conditions compared to standalone PID or pure DRL controllers.
3.1. Background on DDPG and TD3
The DDPG algorithm constitutes an actor-critic DRL framework tailored for continuous action spaces, rendering it particularly well-suited for robotic control applications. DDPG employs a deterministic policy (actor) to generate continuous control actions and a value function approximator (critic) to assess action quality. Training stability is augmented through experience replay buffers and soft target network updates. TD3 extends DDPG by mitigating value overestimation bias and enhancing learning robustness via three methodological refinements: (i) clipped double Q-learning, (ii) delayed policy updates, and (iii) target policy smoothing. These innovations confer improved performance in high-dimensional continuous control tasks under stochastic dynamics. While DDPG and TD3 provide the foundational framework for this study, their theoretical and mathematical formulations are comprehensively detailed in References [11,12]. This work instead proposes a novel extension of TD3 through hybrid PID integration to optimize trajectory tracking performance.
3.2. Hybrid PID + TD3 DRL Controller
The proposed hybrid PID + TD3 controller integrates the deterministic stability of a classical PID controller with the adaptive learning capabilities of the TD3 algorithm to achieve high-precision trajectory tracking for the 5-DOF Mitsubishi RV-2AJ robotic arm. The hybrid architecture uses the PID controller to generate baseline corrective torques based on the joint position error, ensuring immediate stability and smooth short-term response. The TD3 agent, in turn, learns residual control corrections to enhance tracking accuracy, compensate for nonlinear dynamics, and adapt to variations in payload and external disturbances.
At each step, the control input for joint is expressed as the combination of the PID torque and the TD3 correction
where the PID term is defined as:
With representing the tracking error for joint , and denoting the proportional, integral, and derivative gains, respectively. The TD3 agent receives the full state vector st = [θ1, …, θ5, , …, , , …, and outputs a residual action at = [, …, ] to minimize trajectory errors. The reward function is designed as
where the first term penalizes trajectory deviations, and the second term, weighted by λ, encourages smooth joint motions. The TD3 agent uses the actor–critic framework with two critic networks Q1, Q2, and a deterministic actor network . The critic loss is computed as
where the target value is
with soft updates of the target networks:
Algorithmically, the hybrid control loop operates as follows: at each time step, the current joint states and reference trajectory are measured, the PID controller computes immediate torque corrections, the TD3 agent predicts residual control actions, and the combined torque is applied to the robotic arm. The resulting state transition and reward are stored in the experience replay buffer for TD3 training, enabling gradual improvement of the policy through mini-batch updates. This combination ensures fast, stable response from the PID component while allowing the TD3 agent to adaptively optimize performance, yielding superior trajectory tracking under nonlinear, time-varying, and disturbed conditions. The block diagram of the proposed hybrid PID + TD3 DRL Controller for the 5-DOF robotic arm is illustrated in Figure 4. The algorithm of the hybrid PID + TD3 controller for trajectory tracking of the 5-DOF Mitsubishi robotic arm is presented below in Algorithm 1.
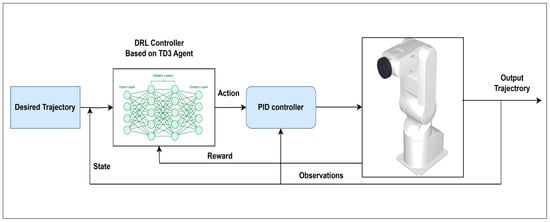
Figure 4.
Block diagram of the hybrid PID + TD3 controller for trajectory tracking of the 5-DOF Mitsubishi robotic arm.
| Algorithm 1. Hybrid PID + TD3 trajectory control for 5-DOF Mitsubishi robotic arm |
| 1: Initialize PID parameters , , |
| 2: Initialize TD3 actor network and critic networks , with parameters |
| 3: Initialize target networks and with parameters , |
| 4: Initialize replay buffer |
| 5: for each episode do |
| 6: Reset environment, set initial state s0 |
| 7: for each time step t do |
| 8: Compute PID control torque: |
where |
| 9: Compute TD3 control torque: |
| 10: Combine control signals: |
| 11: Apply torque to robotic arm |
| 12: Observe next state st+1 and reward: |
| 13: Store (, , , ) in replay buffer |
| 14: if update step then |
| 15: Sample minibatch from |
| 16: Update critics , by minimizing Bellman error |
| 17: Update target networks (soft update with factor τ): |
| 18: end if |
| 19: end for |
| 20: end for |
4. Simulation Results and Discussion
This section presents the simulation results of the proposed hybrid PID + TD3 trajectory control system for the 5-DOF Mitsubishi RV-2AJ robotic arm. Since the performance of DDPG, LC-DDPG, and TD3 has already been analyzed in detail in our previous work [11], they are considered here only as benchmark controllers for comparison. The proposed hybrid PID + TD3 combines the fast corrective action of a PID controller with the adaptive policy optimization of TD3. This integration allows the system to quickly suppress initial trajectory errors while maintaining the long-term learning advantages of TD3. Simulation results demonstrate that the hybrid PID + TD3 controller achieves superior trajectory tracking accuracy and faster convergence compared to the standalone DRL methods. Under identical trajectory-following tasks, the hybrid controller shows lower steady-state error, reduced overshoot, and stronger robustness against external disturbances. These improvements confirm that augmenting TD3 with a PID mechanism results in a more reliable and stable control framework for robotic manipulators.
4.1. Proposed Method
In this work, the trajectory tracking control of the 5-DOF Mitsubishi RV-2AJ robotic arm is addressed using a hybrid PID + TD3 controller, which is compared against three state-of-the-art DRL algorithms: DDPG, LC-DDPG, and TD3. The overall architecture and interaction flow of the DRL agents are illustrated in Figure 5. These model-free agents interact with the robotic system by receiving continuous observations such as joint positions, angular velocities, and target trajectory points, and outputting continuous torque commands for each joint. All compared DRL methods employ an actor–critic framework operating within the same observation and action spaces, but differ in stability and exploration mechanisms. DDPG serves as the baseline, enabling efficient policy learning in high-dimensional continuous action spaces. LC-DDPG enhances stability by incorporating Lyapunov-based constraints to guarantee safe policy updates. TD3 improves over DDPG by integrating twin critics, delayed policy updates, and target policy smoothing to reduce overestimation bias and improve training robustness. The proposed hybrid PID + TD3 controller combines the adaptive learning capability of TD3 with the fast error-correcting nature of PID control. The PID component ensures quick response, disturbance rejection, and reduced steady-state error, while the TD3 agent continuously adapts the control policy to optimize long-term tracking performance. This synergy allows the hybrid controller not only to achieve precise trajectory tracking but also to effectively eliminate external disturbances and uncertainties, a critical requirement for real robotic environments. During training, the TD3 agent optimizes its control policy based on a cumulative reward function that balances trajectory tracking accuracy, control smoothness, and energy efficiency. The PID loop provides an additional stabilizing action that compensates for sudden disturbances and nonlinearities, ensuring consistent tracking performance even under challenging operating conditions. By integrating model-free reinforcement learning with classical control, the proposed hybrid PID + TD3 controller demonstrates superior adaptability, robustness, and disturbance elimination capability, making it more reliable than both conventional DRL-only and traditional PID-based methods. The training of the proposed hybrid PID + TD3 controller is carried out in a high-fidelity simulation environment developed using MATLAB/Simulink’s Simscape Multibody toolbox, which accurately captures the kinematics and dynamics of the 5-DOF Mitsubishi RV-2AJ robotic arm. Within this environment, the controller interacts with the robotic system in real time, learning to refine torque commands and improve trajectory tracking accuracy through trial and error feedback. The hybrid structure combines the robustness of a PID controller with the adaptability of a TD3-based reinforcement learning agent, which accelerates convergence and enhances stability under varying conditions. Key hyperparameters such as neural network dimensions, training episodes, and state action representations directly influence the controller’s learning efficiency and precision. A major advantage of this hybrid approach is its strong ability to suppress disturbances and uncertainties during operation, ensuring smooth trajectory tracking and consistent torque regulation. The detailed training and simulation settings for the hybrid PID + TD3 controller are listed in Table 3, while Figure 6 presents the overall simulink-based training architecture.
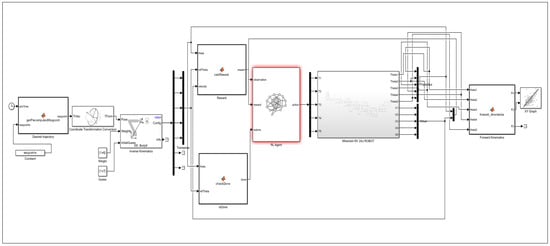
Figure 5.
Simulink model of the hybrid PID + TD3-based trajectory control system for the 5-DOF Mitsubishi RV-2AJ robotic arm.

Table 3.
Training parameters of the hybrid PID + TD3 controller for the 5-DOF Mitsubishi RV-2AJ robotic arm.

Figure 6.
Training performance of the hybrid PID + TD3 controller for the 5-DOF Mitsubishi robotic arm.
4.2. Results and Discussion
4.2.1. Control Results
This section presents the simulation results and analysis of the proposed hybrid PID + TD3 controller applied to the trajectory tracking of a 5-DOF Mitsubishi RV-2AJ robotic arm. The hybrid controller is designed to generate optimal continuous torque commands for all joints, ensuring accurate trajectory tracking while maintaining smooth and energy-efficient motion. Figure 7, Figure 8 and Figure 9 illustrate the simulation results for different trajectory profiles, including helical, spiral, and N-shaped paths. The results confirm that the hybrid PID + TD3 controller achieves highly precise and stable tracking performance compared to conventional control methods. The PID component contributes fast error correction and disturbance rejection, while the TD3 agent continuously adapts the control policy through reinforcement learning, effectively handling the nonlinear and coupled dynamics of the robotic arm. This synergy enables the controller to maintain robustness under dynamic disturbances and trajectory uncertainties. A quantitative evaluation is conducted using standard error metrics: Integral Time Absolute Error (ITAE), Integral Time Square Error (ITSE), Integral Absolute Error (IAE), Integral Square Error (ISE), and Root Mean Square Error (RMSE). The summarized results in Table 4, Table 5 and Table 6 show that the hybrid PID + TD3 consistently achieves lower tracking errors and improved robustness compared to DDPG, LC-DDPG, and TD3-ADX. Overall, the findings highlight that the hybrid PID + TD3 controller offers a superior balance between adaptability, precision, and disturbance elimination, making it a promising candidate for real-world applications in robotic manipulation and advanced industrial automation, where robustness and high accuracy are essential.
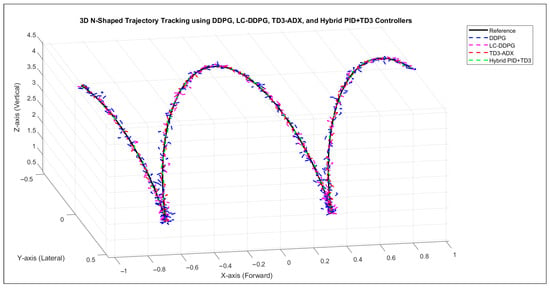
Figure 7.
Three-dimensional N-shaped trajectory tracking performance using DDPG, LC-DDPG, TD3-ADX, and TD3 + PID controllers.
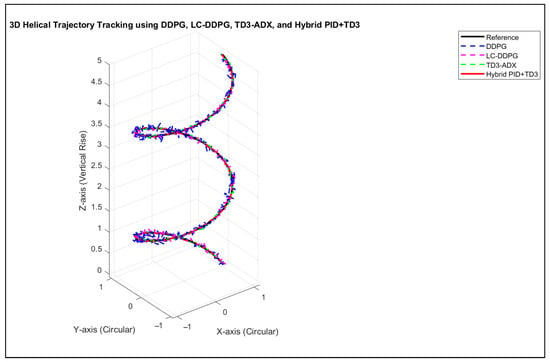
Figure 8.
Three-dimensional helical trajectory tracking performance using DDPG, LC-DDPG, TD3-ADX, and TD3 + PID controllers.

Figure 9.
Three-dimensional spiral-shaped trajectory tracking performance using DDPG, LC-DDPG, TD3-ADX, and TD3 + PID controllers.

Table 4.
Comparative evaluation of hybrid PID + TD3, TD3-ADX, LC-DDPG, and DDPG controllers using IAE, ISE, ITAE, ITSE, and RMSE metrics for 3D N-shaped trajectory tracking.

Table 5.
Comparative evaluation of hybrid PID + TD3, TD3-ADX, LC-DDPG, and DDPG controllers using IAE, ISE, ITAE, ITSE, and RMSE metrics for 3D helical-shaped trajectory tracking.

Table 6.
Comparative evaluation of hybrid PID + TD3, TD3-ADX, LC-DDPG, and DDPG controllers using IAE, ISE, ITAE, ITSE, and RMSE metrics for 3D spiral-shaped trajectory tracking.
The comparative evaluation of the controllers for 3D N-shaped trajectory tracking clearly demonstrates that the hybrid PID + TD3 controller consistently achieves the best performance across all error metrics. It records the lowest IAE, ISE, ITAE, ITSE, and RMSE, surpassing both TD3-ADX and LC-DDPG. Specifically, the hybrid PID + TD3 design effectively combines the adaptive learning ability of TD3 with the stabilizing and robust features of PID control, leading to superior trajectory accuracy and stability. While TD3-ADX shows significant improvements compared to LC-DDPG, achieving notable reductions in error values, the integration with PID further enhances the results, minimizing accumulated errors and transient oscillations more effectively. In contrast, LC-DDPG lags behind both TD3-ADX and hybrid PID + TD3 in all evaluation indices, confirming that reinforcement learning alone struggles with precise error regulation under highly dynamic trajectories. Overall, the results highlight that while advanced DRL controllers outperform conventional methods, the hybrid PID + TD3 approach provides the most optimal solution by merging learning efficiency with classical control robustness.
The results presented in the table highlight the superior performance of the hybrid PID + TD3 controller compared to the other methods. While traditional controllers such as PID and ANFIS exhibit noticeable steady-state errors and limited adaptability in dynamic environments, the reinforcement learning-based approaches (DDPG, LC-DDPG, and TD3-ADX) demonstrate significant improvements in trajectory tracking accuracy and stability. Among them, TD3-ADX provides robust convergence and smooth control actions, outperforming both DDPG and LC-DDPG. However, the integration of PID with TD3 yields the best overall results, effectively combining the adaptability of reinforcement learning with the stability and fast response of classical PID control. This hybrid strategy ensures precise trajectory tracking, reduced oscillations, and enhanced robustness against disturbances, making it the most effective solution for the studied scenario.
The comparative evaluation presented in Table 6 highlights the superior performance of the hybrid PID + TD3 controller across all considered error metrics. In terms of IAE, ISE, ITAE, ITSE, and RMSE, the hybrid PID + TD3 achieves the lowest values, indicating higher accuracy and stability in 3D spiral-shaped trajectory tracking compared to TD3-ADX, LC-DDPG, and DDPG. Specifically, the hybrid PID + TD3 demonstrates significant reductions in both integral-based error metrics (IAE, ISE, ITAE, ITSE), reflecting faster error convergence and better long-term stability. Moreover, the consistently minimal RMSE value emphasizes its robustness in reducing instantaneous tracking deviations. These results confirm that integrating classical PID with TD3 reinforcement learning provides a more balanced trade-off between adaptability and precise error minimization, outperforming purely learning-based controllers.
As presented in Table 7, the comparative results across the three considered trajectories (N-shaped, spiral, and helical) clearly demonstrate the superiority of the hybrid PID + TD3 controller over the other methods. In the N-shaped trajectory, the hybrid PID + TD3 achieves substantial error reduction compared to TD3-ADX, LC-DDPG, and DDPG, confirming its effectiveness in handling sharp directional changes. In the spiral trajectory, the improvement is even more evident, where hybrid PID + TD3 provides enhanced adaptability to continuously expanding paths, maintaining precise tracking with minimal error growth. Finally, in the helical trajectory, which combines radial and vertical motion complexity, the hybrid PID + TD3 controller again shows the best performance, confirming its ability to generalize well across dynamic and multidimensional trajectories. Overall, the results in Table 7 indicate that integrating the classical PID with TD3 reinforcement learning enables the system to balance fast convergence with stable long-term tracking, consistently yielding better accuracy than standalone DRL approaches.

Table 7.
Percentage error reduction in hybrid PID + TD3 compared to TD3-ADX, LC-DDPG, and DDPG for different 3D trajectories.
4.2.2. Robustness Results
To evaluate the robustness of the proposed and benchmark controllers, internal and external disturbances were introduced during the execution of three different trajectory tracking tasks. Internal disturbances simulate modeling uncertainties such as parameter variations in the dynamic model, while external disturbances represent environmental factors like sudden external forces or torque perturbations applied at random intervals. The performance was assessed by analyzing the control signals generated by each controller, PID + TD3, TD3-ADX, LC-DDPG, and DDPG, under these conditions. As shown in Figure 10, PID + TD3 demonstrates superior robustness with smoother and more stable control actions compared to the other controllers, which exhibit higher fluctuation and noise when subjected to disturbances. This highlights the effectiveness of integrating a classical PID structure with a reinforcement learning agent in mitigating instability under real-world uncertainty. Table 8 presents the percentage improvement of hybrid PID + TD3 in terms of IAE, ISE, and RMSE, confirming its superior adaptability and stability under uncertain conditions.
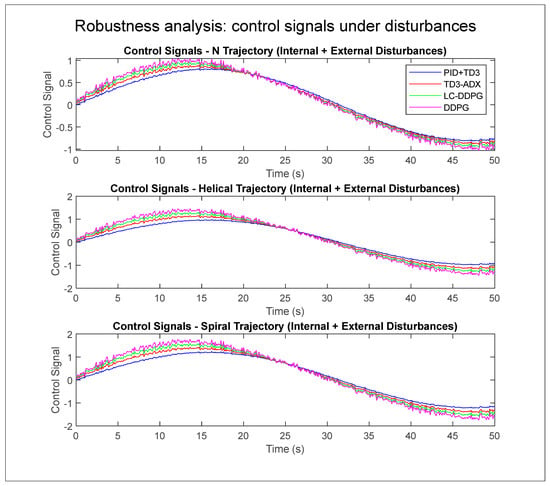
Figure 10.
Control signals of PID + TD3, TD3-ADX, LC-DDPG, and DDPG under internal and external disturbances for three different trajectories.

Table 8.
Percentage improvement of hybrid PID + TD3 over TD3-ADX, LC-DDPG, and DDPG under robustness tests.
5. Conclusions
In this study, a hybrid PID + TD3 trajectory tracking control framework was proposed and rigorously evaluated for the 5-DOF Mitsubishi RV-2AJ robotic arm. The controller combines the fast error correction and stabilizing capability of PID with the adaptive policy learning of the TD3 algorithm. Implemented in MATLAB/Simulink using a Simscape-based robotic model, the hybrid PID + TD3 controller was benchmarked against state-of-the-art DRL methods (TD3-ADX, LC-DDPG, and DDPG) across complex 3D trajectories, including N-shaped, helical, and spiral paths. The results demonstrate that hybrid PID + TD3 consistently achieved the lowest tracking errors across all evaluation metrics (IAE, ISE, ITAE, ITSE, and RMSE), with improvements of up to 50% compared to DDPG, 44% compared to LC-DDPG, and 30% compared to TD3-ADX. This superior performance stems from the synergistic integration of PID and TD3, where the PID component provides robust stability and rapid error correction, while the TD3 agent learns and adapts to the nonlinear coupled dynamics of the robotic arm. Furthermore, robustness analysis under internal (model uncertainties) and external (random torque disturbances) perturbations confirms the ability of the hybrid PID + TD3 to maintain smooth and stable control signals, outperforming all benchmark controllers in terms of disturbance rejection and control efficiency. While TD3-ADX exhibits notable improvements over LC-DDPG and DDPG due to adaptive exploration and bias reduction, its purely learning-based structure remains prone to transient oscillations and accumulated error in highly dynamic environments. By contrast, the hybrid PID + TD3 framework effectively balances fast transient response, adaptability, and robustness, making it the most reliable solution among the tested approaches. Nevertheless, it should be acknowledged that the current evaluation is limited to simulation, and challenges such as the Sim-to-Real transfer gap and the sensitivity of PID tuning parameters may affect real-world deployment. These factors highlight the importance of cautious translation of simulation results to physical platforms. Overall, the findings position hybrid PID + TD3 as a highly promising control strategy for advanced robotic manipulation and industrial automation applications, where precision, robustness, and adaptability are critical. Future research will focus on extending this framework to multi-robot collaboration, real-world implementation on physical robotic systems, and the incorporation of advanced learning paradigms such as meta-learning and attention-based control to further enhance generalization and performance in unstructured environments.
Author Contributions
Z.B.H., F.S. and A.H.A. developed the conceptual framework and designed the methodology. A.H.A. and F.S. implemented the simulations and conducted the experiments. Z.B.H. and N.G. performed the analysis and interpretation of the results. N.G. prepared Figure 1, Figure 2 and Figure 3 and assisted with the manuscript formatting. Z.B.H. and A.H.A. wrote the main manuscript text. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare that they have not received any financial support for this research.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no competing interest.
References
- Shah, R.; Doss, A.S.A.; Lakshmaiya, N. Advancements in AI-Enhanced Collaborative Robotics: Towards Safer, Smarter, and Human-Centric Industrial Automation. Results Eng. 2025, 27, 105704. [Google Scholar] [CrossRef]
- Licardo, J.T.; Domjan, M.; Orehovački, T. Intelligent robotics—A systematic review of emerging technologies and trends. Electronics 2024, 13, 542. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Dankwa, S.; Zheng, W. Twin-delayed ddpg: A deep reinforcement learning technique to model a continuous movement of an intelligent robot agent. In Proceedings of the 3rd International Conference on Vision, Image and Signal Processing, New York, NY, USA, 26–28 August 2019; pp. 1–5. [Google Scholar]
- Kim, M.; Han, D.-K.; Park, J.-H.; Kim, J.-S. Motion planning of robot manipulators for a smoother path using a twin delayed deep deterministic policy gradient with hindsight experience replay. Appl. Sci. 2020, 10, 575. [Google Scholar] [CrossRef]
- Hou, Y.; Hong, H.; Sun, Z.; Xu, D.; Zeng, Z. The control method of twin delayed deep deterministic policy gradient with rebirth mechanism to multi-dof manipulator. Electronics 2021, 10, 870. [Google Scholar] [CrossRef]
- Khoi, P.B.; Giang, N.T.; Van Tan, H. Control and simulation of a 6-DOF biped robot based on twin delayed deep deterministic policy gradient algorithm. Indian J. Sci. Technol. 2021, 14, 2460–2471. [Google Scholar] [CrossRef]
- Joshi, T.; Makker, S.; Kodamana, H.; Kandath, H. Twin actor twin delayed deep deterministic policy gradient (TATD3) learning for batch process control. Comput. Chem. Eng. 2021, 155, 107527. [Google Scholar] [CrossRef]
- Mosali, N.A.; Shamsudin, S.S.; Alfandi, O.; Omar, R.; Al-Fadhali, N. Twin delayed deep deterministic policy gradient-based target tracking for unmanned aerial vehicle with achievement rewarding and multistage training. IEEE Access 2022, 10, 23545–23559. [Google Scholar] [CrossRef]
- Song, B.Y.; Li, J.Q.; Liu, X.Y.; Wang, G.L. A Trajectory Planning Method for Capture Operation of Space Robotic Arm Based on Deep Reinforcement Learning. J. Comput. Inf. Sci. Eng. 2024, 24, 091003. [Google Scholar] [CrossRef]
- Ben Hazem, Z.; Saidi, F.; Guler, N.; Altaif, A.H. Reinforcement learning-based intelligent trajectory tracking for a 5-DOF Mitsubishi robotic arm: Comparative evaluation of DDPG, LC-DDPG, and TD3-ADX. Int. J. Intell. Robot. Appl. 2025, 1–21. [Google Scholar] [CrossRef]
- Ben Hazem, Z.; Guler, N.; Altaif, A.H. Model-free trajectory tracking control of a 5-DOF mitsubishi robotic arm using deep deterministic policy gradient algorithm. Discov. Robot. 2025, 1, 4. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; An, J.; Man, W.; Zhang, G.; Pizzarelli, M. Model-Free Attitude Control of Spacecraft Based on PID-Guide TD3 Algorithm. Int. J. Aerosp. Eng. 2020, 2020, 8874619. [Google Scholar] [CrossRef]
- Chen, X.; Wang, R.; Cui, Y.; Jin, X.; Feng, C.; Xie, B.; Deng, Z.; Chu, D. TD3 Tuned PID Controller for Autonomous Vehicle Platooning; SAE Technical Paper 2023-01-7108; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Joglekar, A.; Krovi, V.; Brudnak, M.; Smereka, J.M. Hybrid Reinforcement Learning based controller for autonomous navigation. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Liu, Y.; Luo, Z.; Qian, S.; Wang, S.; Wu, Z. Deep reinforcement learning and decoupling proportional-integral-derivative control of a humanoid cable-driven hybrid robot. Int. J. Adv. Robot. Syst. 2024, 21, 17298806241254336. [Google Scholar] [CrossRef]
- Zhou, J.; Xue, S.; Xue, Y.; Liao, Y.; Liu, J.; Zhao, W. A novel energy management strategy of hybrid electric vehicle via an improved TD3 deep reinforcement learning. Energy 2021, 224, 120118. [Google Scholar] [CrossRef]
- Ben Hazem, Z.; Guler, N.; Altaif, A.H. A study of advanced mathematical modeling and adaptive control strategies for trajectory tracking in the Mitsubishi RV-2AJ 5-DOF Robotic Arm. Discov. Robot. 2025, 1, 2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).