Modeling and Event-Triggered Output Feedback Control of Input-Affine Polynomial Systems

Abstract

This paper addresses periodic event-triggered output-feedback control (PETOFC) and event-triggered state-feedback control (ETSFC) for polynomial systems modeled by a linear-like representation with state-dependent coefficients. Periodic event-triggering evaluates conditions at fixed intervals, preventing Zeno behavior, while state-feedback control guarantees a minimum inter-event interval. Stability is analyzed using linear matrix inequalities. Under the proposed event-triggered controllers and using the sum-of-squares programming, the asymptotic stability of the closed-loop systems is ensured. Finally, the effectiveness of the proposed controllers are illustrated through two numerical examples.

1. Introduction

Polynomial systems represent a distinct category of nonlinear dynamical frameworks extensively utilized in domains ranging from industrial process regulation to biological system modeling [1,2,3]. Consequently, investigating analytical and synthetic approaches for these systems constitutes a critical research direction in control theory, with particular emphasis on stabilization techniques and optimization strategies. Recent advancements have yielded several effective methodologies. For instance, [4,5,6] developed local stability guarantees through state-feedback synthesis employing quadratic or polynomial Lyapunov functions. Regarding disturbance rejection capabilities, [7] introduced a robust output-feedback controller design, while [8] demonstrated state-feedback approaches accommodating quadratic performance metrics and input constraints. Furthermore, [1] established computational solutions for polynomial matrix problems via sum-of-squares programming. Notably, existing literature shows limited exploration of event-triggered control (ETC) paradigms for polynomial systems.

Recently, several preliminary studies have attempted to address this gap. For example, [9] established fault-tolerant consensus control for linear multi-agent systems with polynomial faults using an event-triggered framework. In addition, [10] introduced a varying-gain event-triggered scheme to enhance security control in polynomial fuzzy systems against DoS attacks. More recently, [11] developed an adaptive control strategy for strict-feedback nonlinear systems with time-varying parameters, incorporating parameter estimators and triggering rules to maintain asymptotic stability while reducing communication load.

ETC represents an innovative digital control approach that has garnered significant research interest in recent years [12,13]. Unlike traditional time-triggered systems with fixed periodic execution intervals, ETC initiates sampling or control updates based on predefined conditions, leading to non-uniform task execution. This paradigm offers notable benefits, including reduced resource usage, lower energy consumption, and mitigated communication congestion. A comprehensive survey on the theoretical developments and applications of dynamic event-triggered control can be found in [14]. A critical theoretical requirement is ensuring positive inter-event intervals to prevent Zeno behavior when continuously verifying triggering conditions. Additionally, periodic event-triggered control (PETC) has emerged as a variant where condition monitoring occurs at regular intervals. Recent literature [15,16,17,18] demonstrates successful applications across diverse systems, such as discrete-time frameworks [19], piecewise-affine systems [20], and linear systems [21]. Despite these advancements, polynomial systems remain an underexplored domain in ETC research, presenting the primary motivation for this study.

The inherent nonconvex nature of polynomial systems presents significant challenges in obtaining feasible solutions. This has made computational methodologies for polynomial systems a crucial research focus in control engineering. While existing approaches like those presented in [22,23] offer potential solutions - including Hamilton-Jacobi inequality-based techniques and state-dependent linear matrix inequality formulations for guaranteed cost state feedback and $H_{\infty }$ performance objectives - these methods occasionally prove ineffective or computationally demanding. Among alternative approaches, sum-of-squares programming stands out as particularly effective due to its ability to efficiently handle positive polynomial systems with reduced conservatism [24]. Consequently, this study employs sum-of-squares programming as the primary solution methodology.

This study develops novel controller synthesis methods for polynomial systems, addressing both periodic event-triggered output-feedback and state-feedback control scenarios. The proposed periodic triggering mechanism employs fixed verification intervals, effectively preventing Zeno phenomena. Key contributions include: derivation of strictly positive inter-event times through continuous condition verification, and computation of control gains via sum-of-squares programming techniques. The framework demonstrates computational efficiency while ensuring solution feasibility.

Compared with previous event-triggered control studies focusing on linear or piecewise-affine systems [20,21], the main novelty of this work lies in extending the event-triggered control framework to polynomial systems modeled in a linear-like representation with state-dependent coefficients. Unlike traditional linear formulations, the proposed approach explicitly handles the nonconvexity inherent in polynomial dynamics by employing sum-of-squares (SOS) programming, enabling tractable stability analysis and controller synthesis. Moreover, both PETOFC and ETSFC are systematically developed within a unified SOS-based framework, ensuring asymptotic stability and preventing Zeno behavior. These contributions collectively establish a generalized and computationally efficient methodology that bridges the gap between polynomial and classical event-triggered control systems.

This paper is structured as follows: Section 1 provides a background of this research. Section 2 details our principal findings regarding PETOFC for polynomial systems. Section 3 presents the state-feedback controller design using the ETC. Section 4 demonstrates numerical validation through concrete examples. Finally, Section 5 concludes with a synthesis of our contributions and their implications.

2. Periodic Event-Triggered Output-Feedback Control

Consider the following polynomial systems expressed by a linear-like representation with state-dependent coefficients:

$$\begin{array}{cc}\hfill \dot{x}& =A\left(x\right)x+Bu,\hfill \\ \hfill y& =Cx,\hfill \end{array}$$

(1)

in which $x\in {\mathbb{R}}^n$ represents the system state, $u\in {\mathbb{R}}^m$ represents the control input, and $y\in {\mathbb{R}}^q$ corresponds to the output signal. The matrix $A\left(x\right)$ is polynomial and dimensionally compatible, while $B\in {\mathbb{R}}^{n\times m}$ and $C\in {\mathbb{R}}^{q\times n}$ are constant matrices.

Assumption 1.

The output matrix C is assumed to have full row rank.

When C possesses full row rank, the result in [25] ensures the existence of nonsingular matrices $\Sigma \in {\mathbb{R}}^{q\times q}$ and $D\in {\mathbb{R}}^{n\times n}$ such that the decomposition $C=\left[\Sigma 0\right]D$ holds.

For the realization of PETC, the output-feedback strategy is defined as:

$$u\left(t\right)=Ky\left(t_{k}h\right),t\in [t_{k}h,t_{k+1}h),k=0,1,2\dots ,$$

(2)

where $K\in {\mathbb{R}}^{m\times q}$ represents the control gain matrix requiring design, h denotes the verification period, i.e., the fixed time interval at which the triggering condition is evaluated. The instant $t_{k}h$ marks the k-th task release instant with $t_k\in \{0,1,2\dots \}$. Consequently, the inter-event interval $T_k=t_{k+1}h-t_{k}h$ maintains the bounded condition $h\le T_k\le mh$, where $m\in \{1,2,3,\dots \}$.

Define the output error

$$e_k\left(t\right)=y\left(t_{k}h\right)-y(t_{k}h+ih),t\in I_i,$$

(3)

where $I_i=[t_{k}h+ih,t_{k}h+(i+1)h),i=0,1,\dots ,m-1$, that is $[t_{k}h,t_{k+1}h)={\bigcup }_{i=0}^{i=m-1}{I}_i$.

Then, the triggering mechanism is specified as

$$\begin{array}{cc}\hfill & {\left[y\left(t_{k}h\right)-y(t_{k}h+ih)\right]}^{\top }{S}_1\left(x\right)\left[y\left(t_{k}h\right)-y(t_{k}h+ih)\right]\hfill \\ \hfill \le & y^{\top }(t_{k}h+ih)S_2\left(x\right)y(t_{k}h+ih),\hfill \end{array}$$

(4)

with $i=0,1,\dots ,m-1$, where $S_1\left(x\right)$ and $S_2\left(x\right)$ denote positive definite polynomial matrices to be determined.

Define $\tau \left(t\right)=t-(t_{k}h+ih),t\in I_i,i=0,1,\dots m-1$, which satisfies $0\le \tau \left(t\right)\le h$. Incorporating Equations (1)–(3) with $\tau \left(t\right)$, the closed-loop dynamic can be equivalently represented as a time-delay system:

$$\begin{array}{cc}\hfill \dot{x}& =A\left(x\right)x+BK{e}_k\left(t\right)+BKy\left(t-\tau \left(t\right)\right),\hfill \\ \hfill y& =Cx.\hfill \end{array}$$

(5)

Accordingly, the PETOFC problem for polynomial systems can be formulated as follows: given a verification period h, the aim is to design both the feedback gain K and the polynomial matrices $S_1\left(x\right)$ and $S_2\left(x\right)$ such that the system Equation (1) governed by the controller Equation (2) under the triggering rule Equation (4) achieves asymptotic stability.

To facilitate our subsequent stability analysis and control synthesis, we first introduce essential mathematical preliminaries including relevant definitions and supporting lemmas. These foundational elements will underpin the key theoretical contributions presented later in this work.

Lemma 1.

(Schur complement, [26]). For a symmetric matrix N partitioned as

$$N=\left[\begin{array}{cc}T& H\\ H^{\top }& R\end{array}\right],$$

with invertible R, the following equivalences hold:

(i) $N>0$ iff $R>0$ and $T-H{R}^{-1}{H}^{\top }>0.$

(ii) if $R>0$, then $N\ge 0$ iff $T-H{R}^{-1}{H}^{\top }\ge 0.$

Definition 1

([27]). A multivariate polynomial $p\left(x\right)$ is said to be a sum-of-squares (SOS) if there exist polynomials $f_1\left(x\right),\dots ,f_m\left(x\right)$ such that:

$$p\left(x\right)=\sum _{i=1}^m{f}_i^2\left(x\right).$$

(6)

Lemma 2

([27]). The polynomial $p\left(x\right)$ satisfies the SOS condition in Equation (6) if and only if there exists a positive semidefinite matrix S such that

$$p\left(x\right)=Z^{\top }\left(x\right)SZ\left(x\right),$$

(7)

where $Z\left(x\right)$ is an appropriately chosen vector of monomial.

Remark 1.

Based on Definition 1 and Lemma 2, we can directly conclude that any SOS polynomial $p\left(x\right)$ satisfies $p\left(x\right)\ge 0$, demonstrating that the SOS property serves as an effective sufficient criterion for verifying polynomial non-negativity.

Building on the preceding analysis, we now present the first result under the assumption that the feedback gain K is predetermined.

To explicitly clarify the scope of the SOS constraints, we note that all SOS conditions in this work are verified over a bounded semialgebraic region of the state space,

$$\Omega =\{x\in {\mathbb{R}}^n:\rho \left(x\right)\ge 0\},$$

(8)

within which the proposed Lyapunov function and SOS-based stability conditions hold. Accordingly, the derived results in Theorems 1–3 should be interpreted as regional asymptotic stability rather than global stability.

Theorem 1.

For a verifying period h and feedback gain K, system Equation (1) with controller Equation (2) and event condition Equation (4) achieves asymptotic stability when there exist symmetric positive definite matrices $P,R,U$, positive polynomial matrices $S_1\left(x\right),S_2\left(x\right)$, matrices X, $L_i(i=1,2,3)$, and polynomial matrices $N\left(x\right)$, $F\left(x\right)$ satisfying:

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(P-{\epsilon }_{1}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(9)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(R-{\epsilon }_{2}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(10)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(U-{\epsilon }_{3}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(11)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(S_1\left(x\right)-{\epsilon }_{4}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(12)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(S_2\left(x\right)-{\epsilon }_{5}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(13)

$${\Omega }_1\left(x\right)=\left[\begin{array}{ccccc}{\Pi }_{11}\left(x\right)& {\Pi }_{12}\left(x\right)& -N_1\left(x\right)& {\Pi }_{14}\left(x\right)& L_{1}BK\\ ★& {\Pi }_{22}\left(x\right)& -N_2\left(x\right)& {\Pi }_{24}& L_{3}BK\\ ★& ★& -R& 0& 0\\ ★& ★& ★& {\Pi }_{44}& L_{2}BK\\ ★& ★& ★& ★& -S_1\left(x\right)\end{array}\right]<0,$$

(14)

$${\Omega }_2\left(x\right)=\left[\begin{array}{cc}X& N\left(x\right)\\ ★& U\end{array}\right]\ge 0,$$

(15)

$${\Omega }_3\left(x\right)=\left[\begin{array}{cc}X& F\left(x\right)\\ ★& U\end{array}\right]\ge 0,$$

(16)

$$X=\left[\begin{array}{cc}{X}_{11}& X_{12}\\ ★& X_{22}\end{array}\right]\ge 0,$$

(17)

where ★ denotes the symmetric block in one symmetric matrix, ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3,{\epsilon }_4,{\epsilon }_5$ are pre-defined scalars, ς denotes the arrays that are independent of x, and

• ${\Pi }_{11}\left(x\right)=Q+F_1\left(x\right)+F_1^{\top }\left(x\right)+L_{1}A\left(x\right)+A^{\top }\left(x\right)L_1^{\top }+h{X}_{11}$,
• ${\Pi }_{12}\left(x\right)=N_1\left(x\right)-F_1\left(x\right)+F_2^{\top }\left(x\right)+L_{1}BKC+A^{\top }\left(x\right)L_3^{\top }+h{X}_{12}$,
• ${\Pi }_{14}\left(x\right)=P-L_1+A^{\top }\left(x\right)L_2^{\top }$,
• ${\Pi }_{22}\left(x\right)=N_2\left(x\right)+N_2^{\top }\left(x\right)-F_2\left(x\right)-F_2^{\top }\left(x\right)+L_{3}BKC+C^{\top }{K}^{\top }{B}^{\top }{L}_3^{\top }+h{X}_{22}+C^{\top }{S}_2\left(x\right)C$,
• ${\Pi }_{24}=-L_3+C^{\top }{K}^{\top }{B}^{\top }{L}_2^{\top }$,
• ${\Pi }_{44}=hU-L_2-L_2^{\top }$,
• $N\left(x\right)={\left[\begin{array}{cc}{N}_1^{\top }\left(x\right)& N_2^{\top }\left(x\right)\end{array}\right]}^{\top }$,
• $F\left(x\right)={\left[\begin{array}{cc}{F}_1^{\top }\left(x\right)& F_2^{\top }\left(x\right)\end{array}\right]}^{\top }$.

Here, G and V are constant design matrices introduced to parameterize the state-feedback and output-feedback gain relationships. This formulation is commonly adopted in SOS-based controller synthesis to linearize the bilinear terms involving the gain matrices [28,29].

Proof. 

Consider the Lyapunov functional defined as:

$$\begin{array}{ccc}\hfill V\left(t\right)& =& x^{\top }\left(t\right)Px\left(t\right)+{\int }_{t-h}^t{x}^{\top }\left(s\right)Rx\left(s\right)\mathrm{d}s+{\int }_{t-h}^t{\int }_s^t{\dot{x}}^{\top }\left(v\right)U\dot{x}\left(v\right)\mathrm{d}v\mathrm{d}s,\hfill \end{array}$$

(18)

where $P,R$ and U represent feasible solutions satisfying conditions Equations (14)–(16).

Taking the Lie derivative of the Lyapunov function $V\left(t\right)$ along the vector field of system Equation (5) leads to the following result:

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& 2x^{\top }\left(t\right)P\dot{x}\left(t\right)+x^{\top }\left(t\right)Rx\left(t\right)-x^{\top }(t-h)Rx(t-h)\hfill \\ \hfill & +h{\dot{x}}^{\top }\left(t\right)U\dot{x}\left(t\right)-\left({\int }_{t-h}^{t-\tau \left(t\right)}{\dot{x}}^{\top }\left(v\right)U\dot{x}\left(v\right)\mathrm{d}v+{\int }_{t-\tau \left(t\right)}^t{\dot{x}}^{\top }\left(v\right)U\dot{x}\left(v\right)\mathrm{d}v\right).\hfill \end{array}$$

(19)

Defining $\overline{x}\left(t\right)={\left[x^{\top }\left(t\right),x^{\top }\left(t-\tau \left(t\right)\right)\right]}^{\top }$ and considering polynomial matrices $N\left(x\right),F\left(x\right)$, we obtain:

$$\begin{array}{cc}\hfill 0=& 2{\overline{x}}^{\top }\left(t\right)N\left(x\right)\left[x\left(t-\tau \left(t\right)\right)-x(t-h)-{\int }_{t-h}^{t-\tau \left(t\right)}\dot{x}\left(s\right)\mathrm{d}s\right],\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill 0=& 2{\overline{x}}^{\top }\left(t\right)F\left(x\right)\left[x\left(t\right)-x\left(t-\tau \left(t\right)\right)-{\int }_{t-\tau \left(t\right)}^t\dot{x}\left(s\right)\mathrm{d}s\right].\hfill \end{array}$$

(21)

Incorporating Equation (5), for appropriately dimensioned matrices $L_i(i=1,2,3)$, we derive:

$$\begin{array}{cc}\hfill 0=& 2\left[x^{\top }\left(t\right)L_1+{\dot{x}}^{\top }\left(t\right)L_2+{\dot{x}}^{\top }\left(t-\tau \left(t\right)\right)L_3\right]\hfill \\ \hfill & \times \left[A\left(x\right)x\left(t\right)+BK{e}_k\left(t\right)+BKy\left(t-\tau \left(t\right)\right)-\dot{x}\left(t\right)\right].\hfill \end{array}$$

(22)

Besides, the following equality

$$\begin{array}{cc}\hfill 0=& h{\overline{x}}^{\top }\left(t\right)X\overline{x}\left(t\right)-{\int }_{t-h}^{t-\tau \left(t\right)}{\overline{x}}^{\top }\left(t\right)X\overline{x}\left(t\right)\mathrm{d}s-{\int }_{t-\tau \left(t\right)}^t{\overline{x}}^{\top }\left(t\right)X\overline{x}\left(t\right)\mathrm{d}s\hfill \end{array}$$

(23)

holds. Furthermore, based on the condition for triggering events Equation (4) and the definition of $e_k\left(t\right)$, we have

$$e_k^{\top }\left(t\right)S_1\left(x\right)e_k\left(t\right)\le x^{\top }\left(t-\tau \left(t\right)\right)C^{\top }{S}_2\left(x\right)Cx\left(t-\tau \left(t\right)\right).$$

(24)

Combining Equations (16)–(24), it follows that

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & z_1^{\top }\left(t\right){\Omega }_1{z}_1\left(t\right)-{\int }_{t-h}^{t-\tau \left(t\right)}{z}_2(t,s){\Omega }_2{z}_2(t,s)\mathrm{d}s\hfill \\ \hfill & -{\int }_{t-\tau \left(t\right)}^t{z}_2^{\top }(t,s){\Omega }_3{z}_2(t,s)\mathrm{d}s,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & z_1\left(t\right)={\left[x^{\top }\left(t\right),x^{\top }\left(t-\tau \left(t\right)\right),x^{\top }(t-h),{\dot{x}}^{\top }\left(t\right),e_k^{\top }\left(t\right)\right]}^{\top },\hfill \\ \hfill & z_2(t,s)={\left[{\overline{x}}^{\top }\left(t\right),{\dot{x}}^{\top }\left(s\right)\right]}^{\top }.\hfill \end{array}$$

The asymptotic stability of system Equation (1) under controller Equation (2) with triggering condition Equation (4) is established, as $\dot{V}\left(t\right)<0$ holds according to Theorem 1. This completes the proof. □

Remark 2.

The Lyapunov functional in Equations (18), together with the introduction of the polynomial matrices $N\left(x\right)$ and $F\left(x\right)$, plays a pivotal role in reducing the conservatism of the stability conditions [29]. Moreover, the adoption of SOS programming enables the efficient treatment of these state-dependent matrices, which would otherwise be intractable under traditional Linear Matrix Inequality (LMI) approaches for polynomial systems.

Building on Theorem 1, which provides SOS-based stability verification under a given feedback gain K, we next present a synthesis method for determining the feedback gain K along with the triggering parameters $S_1\left(x\right)$ and $S_2\left(x\right)$.

Theorem 2.

For a specified verification interval h with positive scalars $\eta >0$ and $\delta >0$, the existence of symmetric positive definite matrices $\overline{P},\overline{R},\overline{U}$, positive polynomial matrices ${\overline{S}}_1\left(x\right),{\overline{S}}_2\left(x\right)$, along with matrices Y, $G_1$, $G_2$, V and polynomial matrices $\overline{N}\left(x\right)$, $\overline{F}\left(x\right)$ must satisfy the subsequent conditions:

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(\overline{P}-{\overline{\epsilon }}_{1}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(25)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(\overline{R}-{\overline{\epsilon }}_{2}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(26)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(\overline{U}-{\overline{\epsilon }}_{3}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(27)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left({\overline{S}}_1\left(x\right)-{\overline{\epsilon }}_{4}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(28)

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left({\overline{S}}_2\left(x\right)-{\overline{\epsilon }}_{5}I\right)\varsigma \mathrm{is}\mathrm{SOS},\end{array}$$

(29)

$$\begin{array}{c}\hfill Y=\left[\begin{array}{cc}{Y}_{11}& Y_{12}\\ ★& Y_{22}\end{array}\right]\ge 0,\end{array}$$

(30)

$${\overline{\Omega }}_1\left(x\right)<0,$$

(31)

$${\overline{\Omega }}_2\left(x\right)=\left[\begin{array}{cc}Y& \overline{N}\left(x\right)\\ ★& \overline{U}\end{array}\right]\ge 0,$$

(32)

$${\overline{\Omega }}_3\left(x\right)=\left[\begin{array}{cc}Y& \overline{F}\left(x\right)\\ ★& \overline{U}\end{array}\right]\ge 0,$$

(33)

where ${\overline{\epsilon }}_1,{\overline{\epsilon }}_2,{\overline{\epsilon }}_3,{\overline{\epsilon }}_4,{\overline{\epsilon }}_5$ are pre-defined scalars, ς denotes the vectors that are independent of x, and

• ${\overline{\Omega }}_1\left(x\right)=\left[\begin{array}{cccccc}{\overline{\Pi }}_{11}\left(x\right)& {\overline{\Pi }}_{12}\left(x\right)& -{\overline{N}}_1\left(x\right)& {\overline{\Pi }}_{14}\left(x\right)& {\overline{\Pi }}_{15}& 0\\ ★& {\overline{\Pi }}_{22}\left(x\right)& -{\overline{N}}_2\left(x\right)& {\overline{\Pi }}_{24}& {\overline{\Pi }}_{25}& \overline{G}{C}^{\top }\\ ★& ★& -\overline{R}& 0& 0& 0\\ ★& ★& ★& {\overline{\Pi }}_{44}& {\overline{\Pi }}_{44}& 0\\ ★& ★& ★& ★& -{\overline{S}}_1\left(x\right)& 0\\ ★& ★& ★& ★& ★& -{\overline{S}}_2\left(x\right)\end{array}\right]$,
• $G=\mathit{diag}\{G_1,G_2\}$,
• $\overline{N}\left(x\right)={\left[\begin{array}{cc}{\overline{N}}_1^{\top }\left(x\right)& {\overline{N}}_2^{\top }\left(x\right)\end{array}\right]}^{\top }$,
• $\overline{F}\left(x\right)={\left[\begin{array}{cc}{\overline{F}}_1^{\top }\left(x\right)& {\overline{F}}_2^{\top }\left(x\right)\end{array}\right]}^{\top }$,
• $\overline{G}=D^{-1}G{\left(D^{-1}\right)}^{\top },\overline{V}=\left[V0\right]$,
• ${\overline{\Pi }}_{11}=\overline{R}+{\overline{F}}_1\left(x\right)+{\overline{F}}_1^{\top }\left(x\right)+\eta A\left(x\right){\overline{G}}^{\top }+\eta \overline{G}{A}^{\top }\left(x\right)+h{Y}_{11}$,
• ${\overline{\Pi }}_{12}={\overline{N}}_1\left(x\right)-{\overline{F}}_1\left(x\right)+{\overline{F}}_2^{\top }\left(x\right)+\eta B\overline{V}{\left(D^{-1}\right)}^{\top }+\delta \overline{G}{A}^{\top }\left(x\right)+h{Y}_{12}$,
• ${\overline{\Pi }}_{14}=\overline{P}-\eta {\overline{G}}^{\top }+\overline{G}{A}^{\top }\left(x\right)$,
• ${\overline{\Pi }}_{15}=\eta B\overline{V}{\left(D^{-1}\right)}^{\top }{C}^{\top }$,
• ${\overline{\Pi }}_{22}={\overline{N}}_2\left(x\right)+{\overline{N}}_2^{\top }\left(x\right)-{\overline{F}}_2\left(x\right)-{\overline{F}}_2^{\top }\left(x\right)+\delta B\overline{V}{\left(D^{-1}\right)}^{\top }+\delta D^{-1}{\overline{V}}^{\top }{B}^{\top }+h{Y}_{22}$,
• ${\overline{\Pi }}_{24}=-\delta {\overline{G}}^{\top }+D^{-1}{\overline{V}}^{\top }{B}^{\top }$,
• ${\overline{\Pi }}_{25}=\delta B\overline{V}{\left(D^{-1}\right)}^{\top }{C}^{\top }$,
• ${\overline{\Pi }}_{44}=h\overline{U}-{\overline{G}}^{\top }-\overline{G}$,
• ${\overline{\Pi }}_{45}=B\overline{V}{\left(D^{-1}\right)}^{\top }{C}^{\top }$,

then the system Equation (1) under the controller Equation (2) and triggering condition Equation (4) is asymptotically stable with $S_1\left(x\right)={\left(C\overline{G}{C}^{\top }\right)}^{-1}{\overline{S}}_1\left(x\right){\left(C{\overline{G}}^{\top }{C}^{\top }\right)}^{-1},S_2\left(x\right)={\overline{S}}_2^{-1}\left(x\right)$ and $K=V{\left(G_1^{\top }\right)}^{-1}{\Sigma }^{-1}$.

Proof. 

The condition ${\overline{\Pi }}_{44}<0$ ensures the non-singularity of both $\overline{G}$ and G. For Equation (14), set $L_1:=\eta {\overline{G}}^{-1}$, $L_2:={\overline{G}}^{-1}$ and $L_3:=\delta {\overline{G}}^{-1}$. Moreover, define $\overline{P}:=\overline{G}P{\overline{G}}^{\top },\overline{R}:=\overline{G}R{\overline{G}}^{\top },\overline{U}:=\overline{G}U{\overline{G}}^{\top },{\overline{N}}_i\left(x\right):=\overline{G}{N}_i\left(x\right){\overline{G}}^{\top },{\overline{F}}_i\left(x\right):=\overline{G}{F}_i\left(x\right){\overline{G}}^{\top }(i=1,2),{\overline{S}}_1\left(x\right):=C\overline{G}{C}^{\top }{S}_1\left(x\right)C{\overline{G}}^{\top }{C}^{\top }\mathrm{and}{\overline{S}}_2\left(x\right):=S_2^{-1}\left(x\right)$. In addition, from feedback gain K, we have

$$\begin{array}{cc}\hfill KC{\overline{G}}^{\top }& =K[\Sigma 0]D{D}^{-1}{G}^{\top }{\left(D^{-1}\right)}^{\top }\hfill \\ \hfill & =K[\Sigma 0]\{G_1^{\top },G_2^{\top }\}{\left(D^{-1}\right)}^{\top }\hfill \\ \hfill & =[K\Sigma G_1^{\top }0]{\left(D^{-1}\right)}^{\top }\hfill \\ \hfill & =\overline{V}{\left(D^{-1}\right)}^{\top }.\hfill \end{array}$$

Define $J=\mathrm{diag}\{\overline{G},\overline{G},\overline{G},\overline{G},C\overline{G}{C}^{\top }\}$. Pre/post-multiplying both sides of Equation (14) by J and $J^{\top }$ and using the Lemma 1, the condition Equation (14) is equivalent to Equation (31).

Define the matrix

$$Y:=\mathrm{diag}\{\overline{G},\overline{G}\}X\mathrm{diag}\{{\overline{G}}^{\top },{\overline{G}}^{\top }\}=\left[\begin{array}{cc}{Y}_{11}& Y_{12}\\ ★& Y_{22}\end{array}\right],$$

with $J_1:=\mathrm{diag}\{\overline{G},\overline{G}\}$. Through analogous operations of pre- and post-multiplying both sides of Equations (15) and (16) by $J_1$ and its transpose, we derive Equatios (32) and (33). Consequently, applying Theorem 1 demonstrates that the system Equation (1) governed by controller Equation (2) with triggeringmechanism Equation (4) achieves asymptotic stability, thereby concluding the proof. □

Remark 3.

For clarity, we emphasize that both Theorem 1 and Theorem 2 pertain to the proposed PETOFC scheme. Theorem 1 gives sufficient SOS conditions to certify asymptotic stability for a pre-specified gain K, whereas Theorem 2 formulates an SOS-based synthesis approach that yields feasible gains and polynomial certificates which satisfy the conditions of Theorem 1.

The steps in the proposed PETOFC design procedure are as follows:

Step 1.

Offline Design:

(a)

Verify system representation, ensure C is full row rank, and decompose $C=\left[\Sigma 0\right]D$.

(b)

Define parameters (h, $\eta$, $\delta$, $ϵ$), formulate SOS constraints from Theorem 2.

(c)

Solve via SOSTOOLS [27] to obtain matrices and compute gain

$$K=V{\left(G^{\top }\right)}^{-1}{\Sigma }^{-1}.$$

(34)

(d)

Derive triggering matrices $S_1\left(x\right),S_2\left(x\right)$ and store all parameters.

Step 2.

Online Execution (during each verification period h):

(a)

Measure the system output $y\left(t_k\right)$, compute error $e_k\left(t\right)$.

(b)

Check trigger:

$$e_k^{\top }{S}_1{e}_k>y^{\top }{S}_{2}y$$

(c)

If triggered, update $u\left(t_k\right)=Ky\left(t_k\right)$ and hold $u\left(t_k\right)$ constant until the next verification instant $t_{k+1}$; else, maintain previous input.

Step 3.

Repeat Step 2 at each subsequent verification instant.

Remark 4.

Small positive constants (e.g., ${\epsilon }_i$, δ) are introduced to ensure strict SOS inequalities and numerical stability, typically chosen within $[{10}^{-4},{10}^{-2}]$. The verification period h directly determines the minimum inter-event time, and thus influences both the average inter-event time and the convergence speed. Within a practical range, a smaller h leads to shorter average inter-event times and faster convergence, while a larger h reduces the triggering frequency but may slow down the response. In most cases, the minimum inter-event time is equal to h. This reflects the trade-off between communication efficiency and control performance.

3. Event-Triggered State-Feedback Control

3.1. Event-Triggered Stabilization

The dynamics of polynomial systems with affine input are captured by the following representation

$$\dot{x}=f\left(x\right)+Bu,f\left(0\right)=0.$$

An equivalent linear-like representation with state-dependent coefficients takes the form:

$$\dot{x}=A\left(x\right)Z\left(x\right)+Bu,$$

(35)

with $x\in {\mathbb{R}}^n$ as the state array and $u\in {\mathbb{R}}^m$ as input signal. The monomial array $Z\left(x\right)\in {\mathbb{R}}^N$ possesses the property $Z\left(x\right)=0\iff x=0$, where $A\left(x\right)$ constitutes a properly dimensioned polynomial matrix and B remains constant.

For system Equation (35), the ETC approach adopts:

$$u=K\widehat{Z}\left(x\right),$$

(36)

wherein $K\in {\mathbb{R}}^{m\times N}$ denotes the control gain matrix requiring computation. The structure of $\widehat{Z}\left(x\right)$ follows:

$$\widehat{Z}\left(x\right)=\left\{\begin{array}{cc}Z\left(x\right),\hfill & if event is triggered,\hfill \\ Z\left(x_{k-1}\right),\hfill & otherwise,\hfill \end{array}\right.$$

where $Z\left(x\right)$ captures real-time state data, whereas $Z\left(x_{k-1}\right)$ preserves the state information from the preceding triggering instance ($k=1,2,\dots$). The error metric $e\left(x\right)$, defined as

$$e\left(x\right)=K\widehat{Z}\left(x\right)-KZ\left(x\right),$$

(37)

which quantifies the discrepancy between the control input at the last triggering instant and the current time. Triggering instants satisfy $e\left(x\right)=0$ due to the inherent property of $\widehat{Z}\left(x\right)$. This formulation explicitly relates the error to temporal control input variations.

By incorporating Equations (36) and (37) into Equation (35), we obtain the reformulated system representation:

$$\dot{x}=A\left(x\right)Z\left(x\right)+BKZ\left(x\right)+Be\left(x\right).$$

(38)

The state update mechanism for $Z\left(x\right)$ is governed by the event-triggered condition

$$\left|\right|e\left(x\right)\left|\right|\le \sigma \left|\right|Z\left(x\right)\left|\right|,$$

(39)

where $\sigma >0$.

These analytical developments lead to the subsequent theoretical proposition.

Theorem 3.

Consider the ETC strategy Equation (39) with a constant $\sigma >0$, where $\left|\right|A\left(x\right)\left|\right|\le ϵ$ and $\left|\right|M\left(x\right)\left|\right|\le \zeta$ hold for $t\in [t_k,t_{k+1})$. Then, the system Equation (35) achieves asymptotic stability under the ETSFC Equation (36) subject to the triggering rule Equation (39), provided that there exist a symmetric positive definite matrix $Q>0$ and an arbitrary matrix W satisfying the inequality:

$$\left[\begin{array}{ccc}\Phi \left(x\right)& M\left(x\right)B& Q\\ B^{\top }{M}^{\top }\left(x\right)& -I& 0\\ Q& 0& -{\sigma }^{2}I\end{array}\right]<0,$$

(40)

where

$$\begin{array}{cc}\hfill \Phi \left(x\right)=& M\left(x\right)A\left(x\right)Q+Q{A}^{\top }\left(x\right)M^{\top }\left(x\right)+M\left(x\right)BW+W^{\top }{B}^{\top }{M}^{\top }\left(x\right),\hfill \end{array}$$

with the controller gain defined as $K=W{Q}^{-1}$ and $M_{ij}\left(x\right)={\displaystyle \frac{\partial Z_i}{\partial x_j}}\left(x\right),i=1,\dots ,N,j=1,\dots ,n.$

Proof. 

To examine the system stability described in Equation (35), we define the Lyapunov function as $V\left(t\right)=Z{\left(x\right)}^{\top }PZ\left(x\right)$. Calculating its time derivative along system Equation (38)’s trajectories yields:

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& 2Z^{\top }\left(x\right)PM\left(x\right)\dot{x}\hfill \\ \hfill =& Z^{\top }\left(x\right)[PM\left(x\right)A\left(x\right)+A^{\top }\left(x\right)M^{\top }\left(x\right)P\hfill \\ \hfill & +PM\left(x\right)BK+K^{\top }{B}^{\top }{M}^{\top }\left(x\right)P]Z\left(x\right)\hfill \\ \hfill & +2Z^{\top }\left(x\right)PM\left(x\right)Be\left(x\right)\hfill \\ \hfill \le & Z^{\top }\left(x\right)[PM\left(x\right)A\left(x\right)+A^{\top }\left(x\right)M^{\top }\left(x\right)P\hfill \\ \hfill & +PM\left(x\right)BK+K^{\top }{B}^{\top }{M}^{\top }\left(x\right)P]Z\left(x\right)\hfill \\ \hfill & +Z^{\top }\left(x\right)\left[PM\left(x\right)B{B}^{\top }{M}^{\top }\left(x\right)P\right]Z\left(x\right)+e^{\top }\left(x\right)e\left(x\right).\hfill \end{array}$$

Using the event condition ${\left|\right|e\left(x\right)\left|\right|}^2\le {\sigma }^2{\left|\right|Z\left(x\right)\left|\right|}^2$, $\dot{V}\left(t\right)$ can be reduced to

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & Z^{\top }\left(x\right)[PM\left(x\right)A\left(x\right)+A^{\top }\left(x\right)M^{\top }\left(x\right)P\hfill \\ \hfill & +PM\left(x\right)BK+K^{\top }{B}^{\top }{M}^{\top }\left(x\right)P]Z\left(x\right)\hfill \\ \hfill & +Z^{\top }\left(x\right)\left[PM\left(x\right)B{B}^{\top }{M}^{\top }\left(x\right)P+{\sigma }^{2}I\right]Z\left(x\right).\hfill \end{array}$$

Applying Lemma 1, Equation (40) is equivalent to

$$\begin{array}{cc}\hfill & M\left(x\right)A\left(x\right)Q+Q{A}^{\top }\left(x\right)M^{\top }\left(x\right)\hfill \\ \hfill & +M\left(x\right)BW+W^{\top }{B}^{\top }\left(x\right)M^{\top }\left(x\right)\hfill \\ \hfill & +M\left(x\right)B{B}^{\top }M\left(x\right)+{\sigma }^{2}QQ<0.\hfill \end{array}$$

(41)

Denote $Q:=P^{-1}$ and $W:=KQ$. Pre/post-multiplying the matrix P on both sides of Equation (41) yields

$$\begin{array}{cc}\hfill & PM\left(x\right)A\left(x\right)+A^{\top }\left(x\right)M^{\top }\left(x\right)P\hfill \\ \hfill & +PM\left(x\right)BK+K^{\top }{B}^{\top }{M}^{\top }\left(x\right)P\hfill \\ \hfill & +PM\left(x\right)B{B}^{\top }{M}^{\top }\left(x\right)P+{\sigma }^{2}I<0.\hfill \end{array}$$

The asymptotic stability of system Equation (35) under controller Equation (36) with triggering condition Equation (39) is demonstrated since $dotV\left(t\right)<0$, thereby concluding the proof. □

Remark 5.

The assumptions imposed on $A\left(x\right)$ and $M\left(x\right)$ in Theorem 3 are not directly utilized in the proof; however, they serve to rule out Zeno behavior by ensuring that the inter-event times $t_{k+1}-t_k$ are bounded below by a strictly positive constant.

3.2. Lower Bound for Inter-Event Times

To demonstrate the applicability of the ETC scheme described earlier, it is necessary to establish that the inter-event time $t_{k+1}-t_k$ possess a positive lower bound:

$$\begin{array}{cc}\hfill t_0& =0,\hfill \\ \hfill t_{k+1}& =\inf \{t:t>t_k,|\left|e\left(x\right)\right||>\sigma |\left|Z\left(x\right)\right||,k\in \mathbb{N}\}.\hfill \end{array}$$

Theorem 4.

The inter-event times $t_{k+1}-t_k,k\in \mathbb{N}$ are guaranteed a positive lower bound $\overline{\tau }$ when two constants ϵ and ζ satisfy $\left|\right|A\left(x\right)\left|\right|\le ϵ$ and $\left|\right|M\left(x\right)\left|\right|\le \zeta$ respectively for $t\in [t_k,t_{k+1})$. This demonstrates temporal separation between events under bounded system dynamics.

Proof. 

Denote $y={\left|\right|e\left(x\right)\left|\right|}^2/{\left|\right|Z\left(x\right)\left|\right|}^2$, taking the time derivative of y

$$\begin{array}{cc}\hfill {\displaystyle \frac{dy}{dt}}& ={\displaystyle \frac{2e^{\top }\left(x\right)\dot{e}\left(x\right)Z^{\top }\left(x\right)Z\left(x\right)-2e^{\top }\left(x\right)e\left(x\right)Z^{\top }\left(x\right)\dot{Z}\left(x\right)}{{\left|\right|Z\left(x\right)\left|\right|}^4}}\hfill \\ \hfill & \le 2{\displaystyle \frac{\left|\right|e\left(x\right)\left|\right|\left|\right|\dot{e}\left(x\right)\left|\right|}{{\left|\right|Z\left(x\right)\left|\right|}^2}}+2{\displaystyle \frac{{\left|\right|e\left(x\right)\left|\right|}^2\left|\right|\dot{Z}\left(x\right)\left|\right|}{{\left|\right|Z\left(x\right)\left|\right|}^3}}\hfill \\ \hfill & =2\left|\right|K\left|\right|{\displaystyle \frac{\left|\right|e\left(x\right)\left|\right|\left|\right|\dot{Z}\left(x\right)\left|\right|}{{\left|\right|Z\left(x\right)\left|\right|}^2}}+2{\displaystyle \frac{{\left|\right|e\left(x\right)\left|\right|}^2\left|\right|\dot{Z}\left(x\right)\left|\right|}{{\left|\right|Z\left(x\right)\left|\right|}^3}}\hfill \\ \hfill & =2\left(\left|\right|K\left|\right|\sqrt{y}+y\right){\displaystyle \frac{\left|\right|\dot{Z}\left(x\right)\left|\right|}{\left|\right|Z\left(x\right)\left|\right|}}.\hfill \end{array}$$

(42)

By the definition of $Z\left(x\right)$, we have

$$\begin{array}{c}\hfill \dot{Z}\left(x\right)=M\left(x\right)\left(\left(A\left(x\right)+BK\right)Z\left(x\right)+Be\left(x\right)\right).\end{array}$$

(43)

Substituting Equation (43) into Equation (42) gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{dy}{dt}}& \le 2\left(\left|\right|K\left|\right|\sqrt{y}+y\right)\left(\left|\right|M\left(x\right)A\left(x\right)+M\left(x\right)BK\left|\right|+\left|\right|M\left(x\right)B\left|\right|\sqrt{y}\right)\hfill \\ \hfill & \le 2\left(\left|\right|K\left|\right|\sqrt{y}+y\right)\left(c+d\sqrt{y}\right)\hfill \\ \hfill & =2a_1\sqrt{y}+2a_{2}y+2a_3{y}^{3/2},\hfill \end{array}$$

(44)

where $c=ϵ\zeta +\zeta \left|\right|BK\left|\right|,d=\zeta \left|\right|B\left|\right|,a_1=\left|\right|K\left|\right|c,a_2=c+\left|\right|K\left|\right|d\mathrm{and}{a}_3=d$.

Based on the comparison principle, the solution $y\left(t\right)$ of Equation (44) with $y\left(0\right)=0$ is upper-bounded by the solution $\varphi \left(t\right)$ of the differential equation $\dot{\varphi }=2a_1\sqrt{\varphi }+2a_2\varphi +2a_3{\varphi }^{3/2}$, where $\varphi \left(0\right)=0$, ensuring $y\left(t\right)\le \varphi \left(t\right)$. From condition Equation $\left(\right)$, the minimum inter-event interval $\widehat{\tau }$ corresponds to the time required for $y\left(t\right)$ to transition from 0 to ${\sigma }^2$. Clearly, $\widehat{\tau }$ is at least as large as the interval $\overline{\tau }$ needed for $\varphi \left(t\right)$ to evolve from 0 to ${\sigma }^2$. The explicit form of $\varphi \left(t\right)$ is:

$$t=\left\{\begin{array}{cc}\left|{\displaystyle \frac{\ln \left|\right|\left|K\right||c\varphi +c|-\ln \left|\right|\left|K\right||d\varphi +c|}{c-\left|\right|K\left|\right|d}}\right|,\hfill & c\ne \left|\right|K\left|\right|d,\hfill \\ {\displaystyle \frac{2}{c+\left|\right|K\left|\right|d}}-{\displaystyle \frac{2}{c+\left|\right|K\left|\right|d+2d\sqrt{\varphi }}},\hfill & c=\left|\right|K\left|\right|d,\hfill \end{array}\right.$$

one has

$$\overline{\tau }=\left\{\begin{array}{cc}\left|{\displaystyle \frac{\ln \left|\right|\left|K\right||c\sigma +c|-\ln \left|\right|\left|K\right||d\sigma +c|}{c-\left|\right|K\left|\right|d}}\right|,\hfill & c\ne \left|\right|K\left|\right|d,\hfill \\ {\displaystyle \frac{2}{c+\left|\right|K\left|\right|d}}-{\displaystyle \frac{2}{c+\left|\right|K\left|\right|d+2d\sqrt{\sigma }}},\hfill & c=\left|\right|K\left|\right|d.\hfill \end{array}\right.$$

Consequently, $\tau \ge \overline{\tau }>0$, which shows that minimum inter-event interval have a strict positive lower bound such that $t_{k+1}-t_k\ge \tau$. This proof is completed. □

Remark 4.

Theorem 4 offers a theoretical guarantee against Zeno behavior by establishing a strictly positive lower bound $\overline{\tau }$ for the inter-event times. This condition is essential for practical implementation of ETC, as it ensures that the system cannot generate an infinite number of events within a finite time, which would be infeasible for a physical digital controller to execute.

Remark 7.

Given the condition $f\left(0\right)=0$, a polynomial matrix $A\left(x\right)$ satisfying $f\left(x\right)=A\left(x\right)x$ can always be constructed. This representation can be alternatively expressed as

$$f\left(x\right)=\left[\begin{array}{cc}A\left(x\right)& 0\end{array}\right]\left[\begin{array}{c}x\\ \overline{Z}\left(x\right)\end{array}\right],$$

where $\overline{Z}\left(x\right)$ comprises higher-degree monomials or polynomials in x. Consequently, the Linear-like representation with state-dependent coefficients Equation (35) is guaranteed to exist, with $Z\left(x\right)$ being non-unique. Furthermore, for a fixed $Z\left(x\right)$, the selection of $A\left(x\right)$ may also lack uniqueness. Specifically, if $A_0\left(x\right)$ yields the representation Equation (35), then $A\left(x\right)=A_0\left(x\right)+N\left(x\right)$ remains valid for any non-zero polynomial matrix $N\left(x\right)$ that satisfies $N\left(x\right)Z\left(x\right)=0$.

The steps in the proposed ETSFC design procedure are as follows:

Step 1.

Offline Design:

(a)

Formulate SOS constraints based on Theorem 3 to ensure asymptotic stability under the triggering condition Equation (39).

(b)

Solve the SOS optimization using SOSTOOLS [27] to obtain matrices $P,Q,W$ and polynomial certificates.

(c)

Compute the controller gain as

$$K=W{Q}^{-1}.$$

(45)

(d)

Verify a positive minimum inter-event time using Theorem 4 to exclude Zeno behavior.

Step 2.

Online Execution (during each verification period h):

(a)

At each verification instant $t_k=kh$, measure the state $x\left(t_k\right)$.

(b)

Evaluate the triggering condition:

$$\left|\right|e\left(x\right)\left|\right|>\sigma \left|\right|Z\left(x\left(t_k\right)\right||.$$

(c)

If the triggering condition is satisfied, update the control input $u\left(t_k\right)=Kx\left(t_k\right)$, and hold it constant until the next verification instant $t_{k+1}$; else, maintain previous input.

Step 3.

Repeat Step 2 at each subsequent verification instant.

Remark 8.

It is worth noting that the structure of system Equation (35) is more general than that of Equation (1) in representing polynomial systems, as the array $Z\left(x\right)$ may include monomials of the state variable x.

Remark 9.

It should be emphasized that the matrix inequalities Equations (31)–(33) and Equation (40) are state-dependent, making them challenging to address using conventional linear matrix inequality techniques. Nevertheless, as demonstrated in this work, these state-dependent inequalities can be efficiently handled through SOS programming.

Remark 10.

The triggering threshold σ plays a similar role. A smaller σ makes the triggering condition more sensitive, leading to a higher triggering rate and a smaller average inter-event time, whereas a larger σ reduces communication frequency but may slow the transient response. Hence, proper selection of σ balances communication load and control responsiveness.

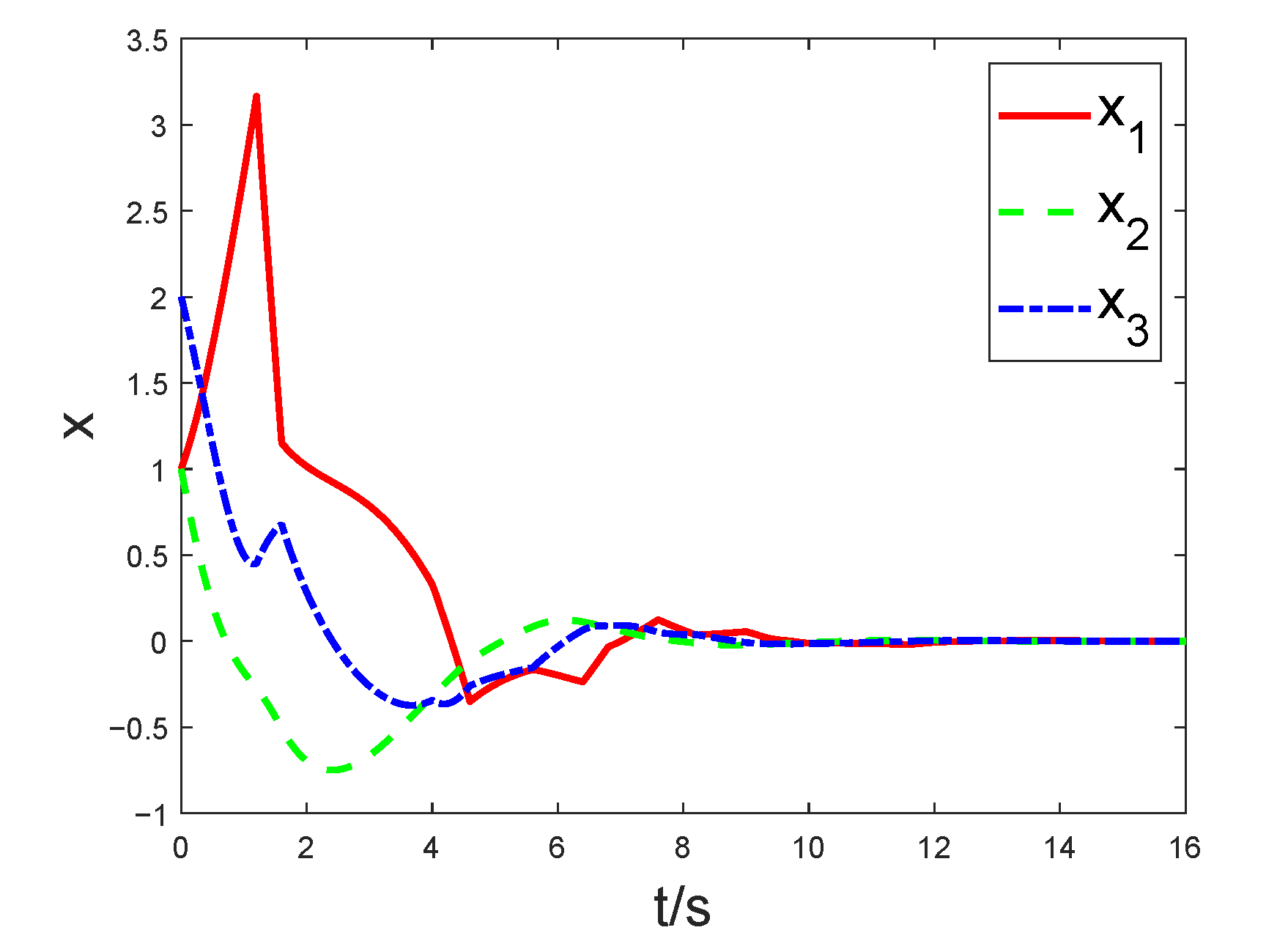
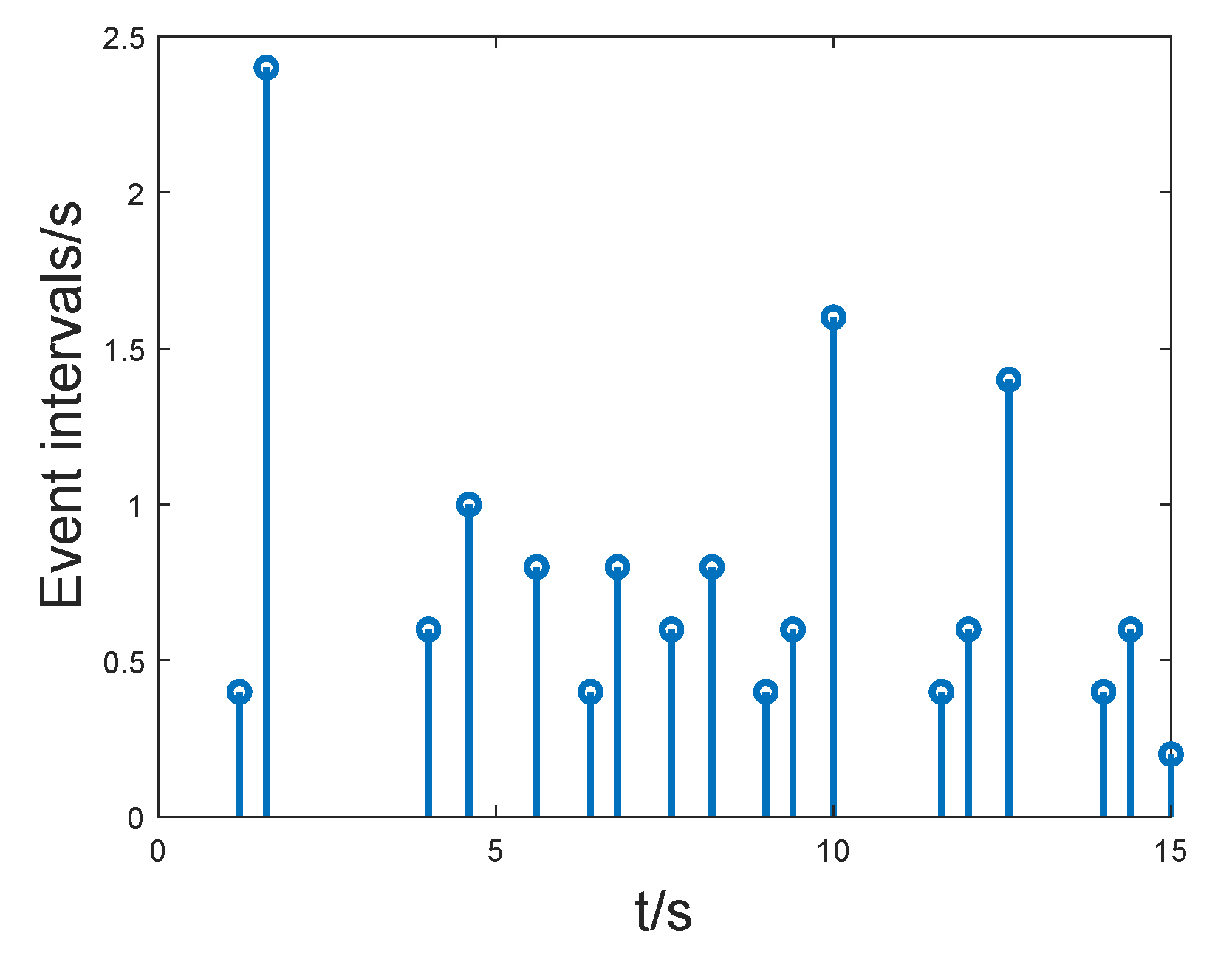
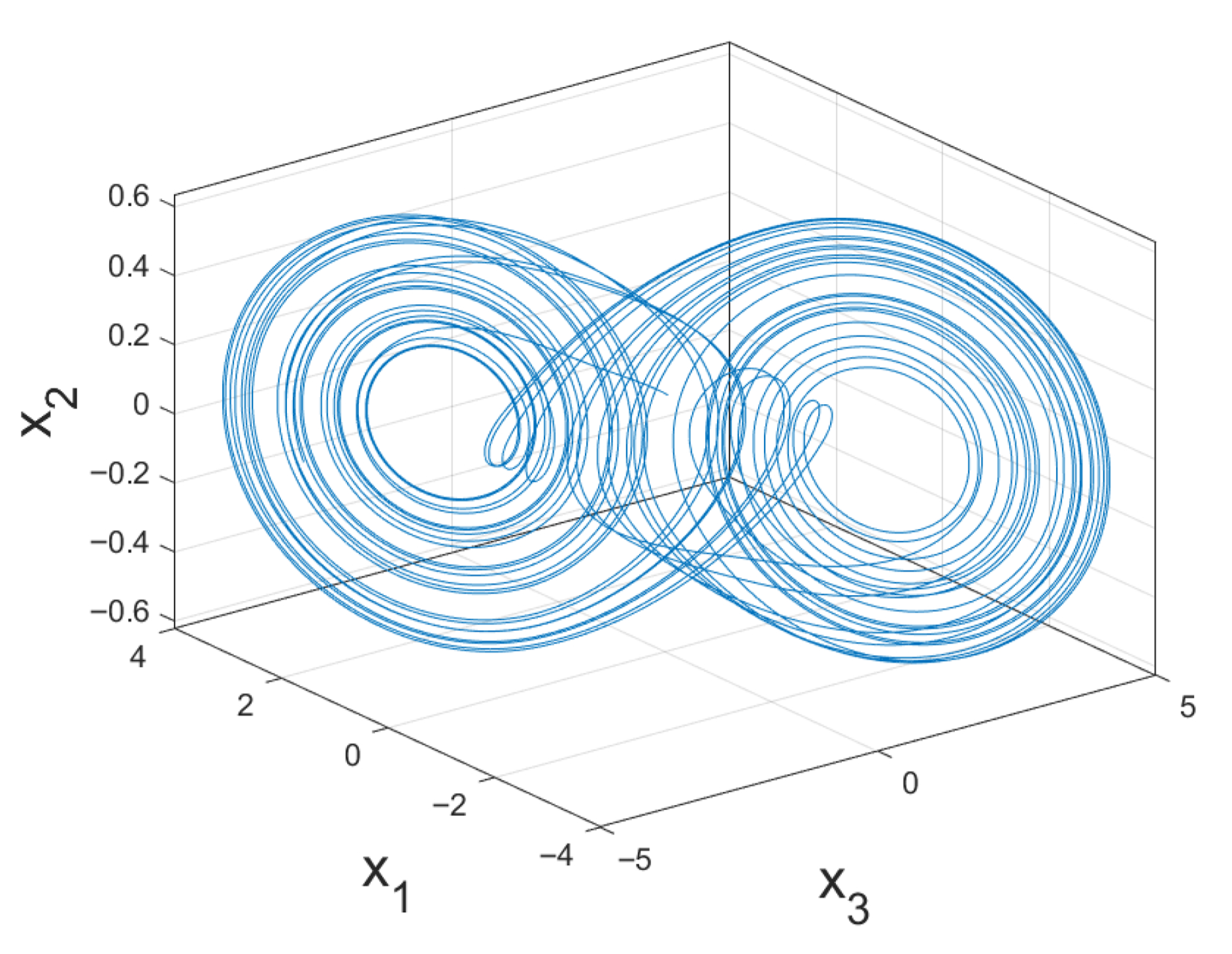
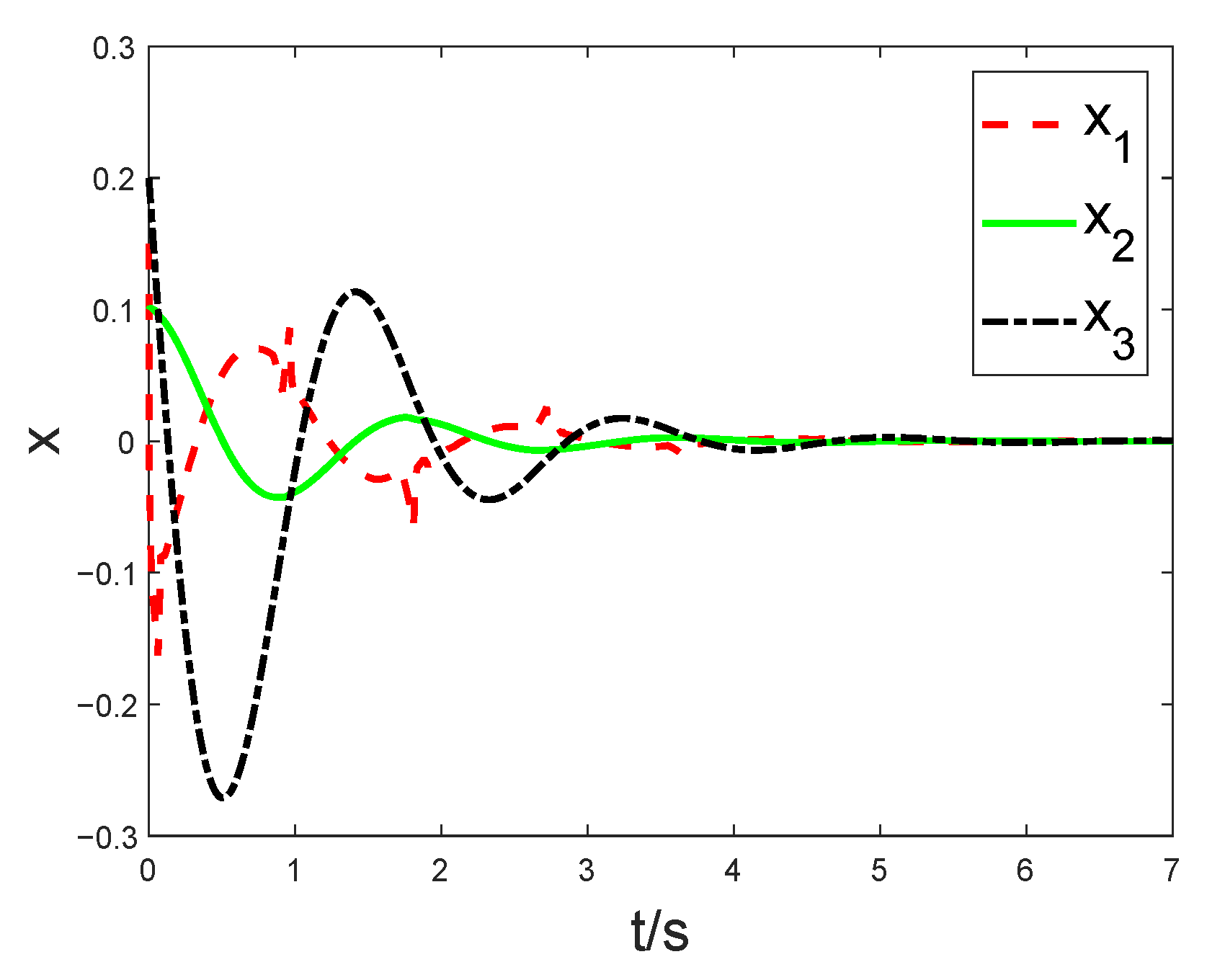
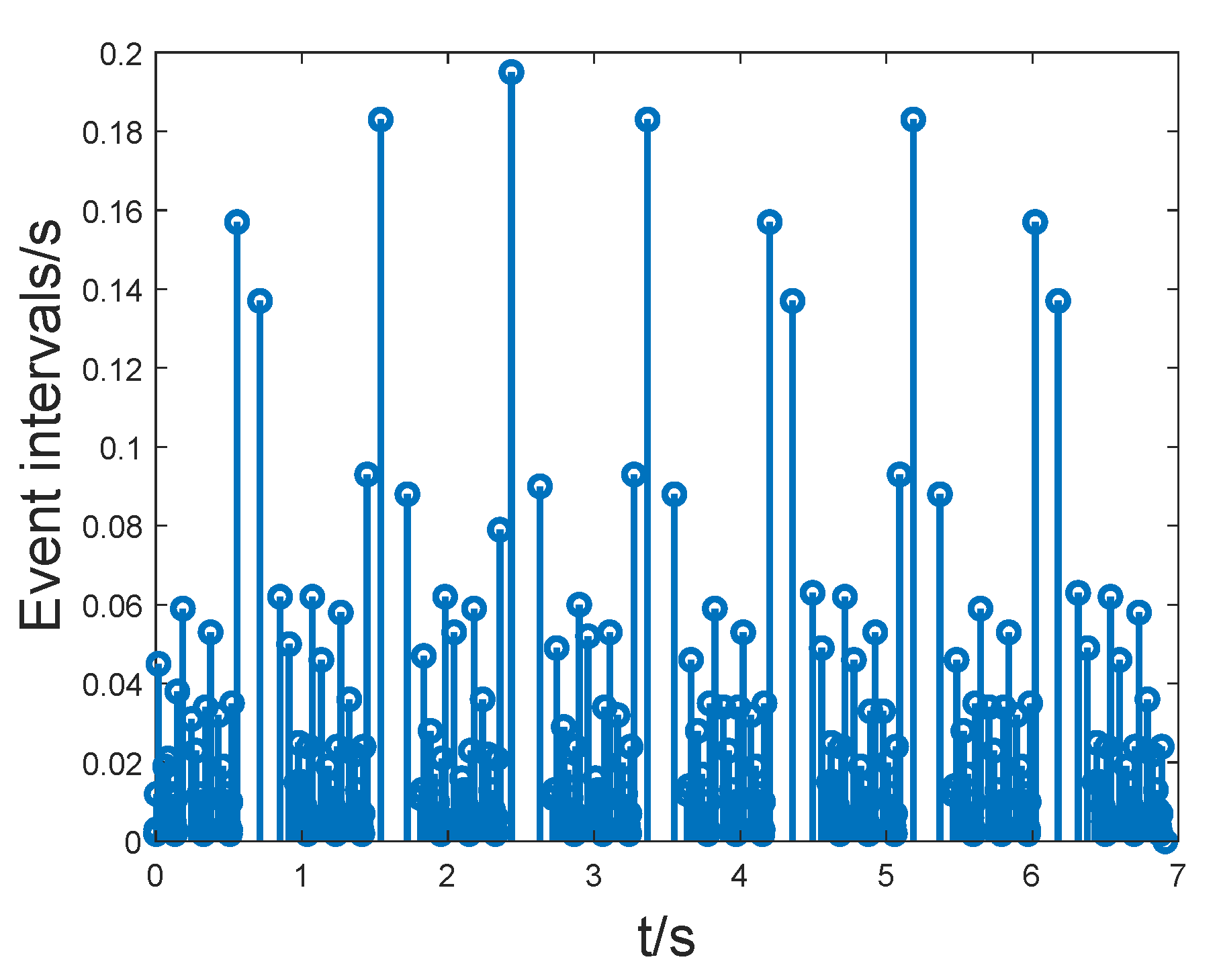
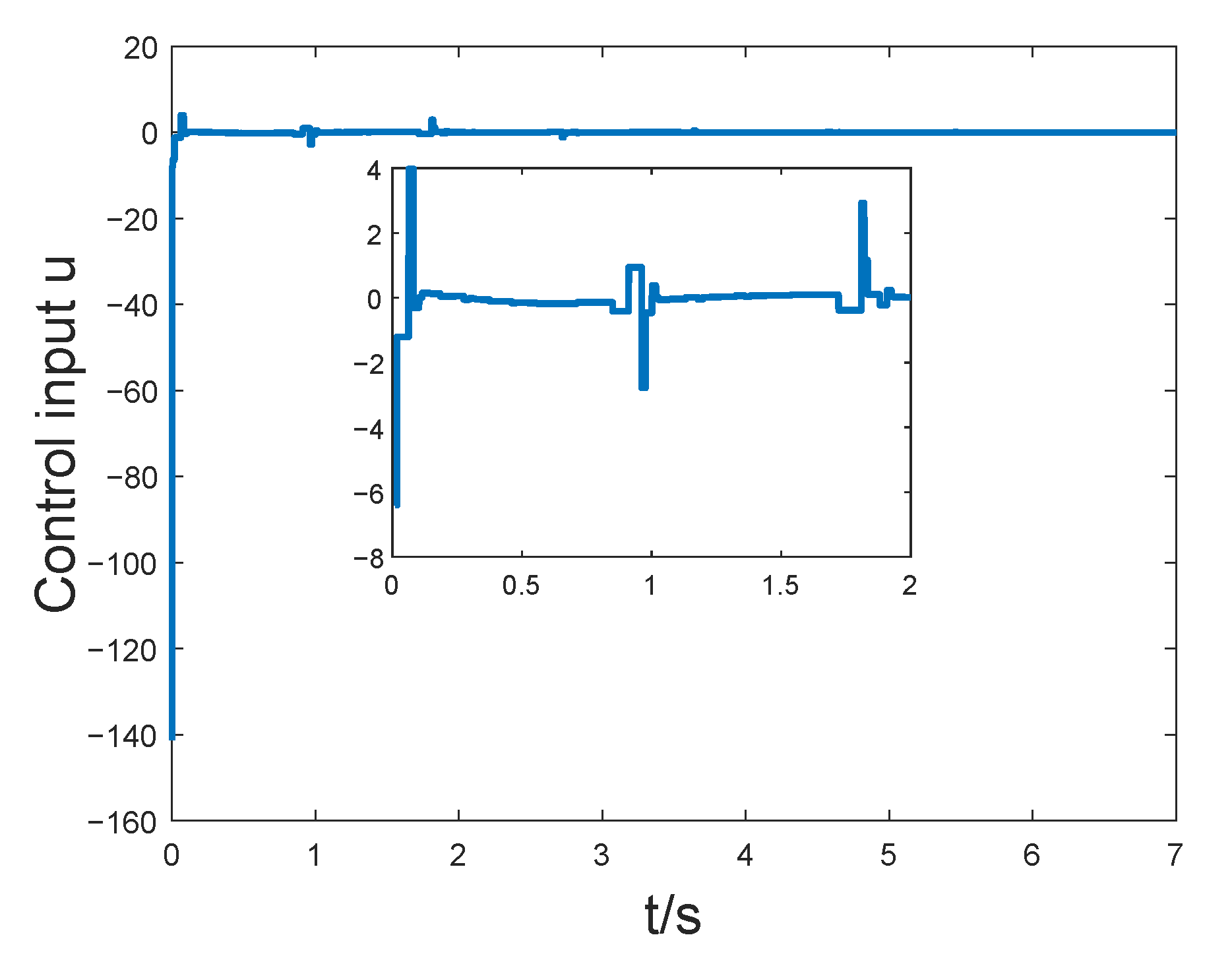
4. Numerical Examples

Two numerical demonstrations validate the theoretical findings from earlier sections, implemented using SOSTOOLS [27], which is a free MATLAB (R2025b) toolbox for formulating and solving sums of squares (SOS) optimization programs.

Remark 11.

The numerical examples were solved using SOSTOOLS (v3.00) [27]. The synthesis problem involves two primary types of constraints: (i) SOS conditions, such as ensuring that ${\varsigma }^{\top }\left(P-{\epsilon }_{1}I\right)\varsigma$ is SOS as in Equations (9)–(13) and Equations (25)–(29), and (ii) state-dependent matrix inequalities, for example, ${\Omega }_1\left(x\right)<0$ in Equation (14) for output-feedback and the LMI in Equation (40) for state-feedback. SOSTOOLS automatically reformulates these matrix inequalities into equivalent SOS constraints, thereby converting the entire problem into a semidefinite programming (SDP) problem. The resulting polynomial matrices (e.g., $S_1\left(x\right)$, $S_2\left(x\right)$) are obtained in a monomial basis. For the sake of simplicity in the example presentation, these matrices are displayed as constant matrices, although their positive definiteness for all x is rigorously guaranteed by the SOS synthesis procedure.

Example 1.

Consider the polynomial system [30] expressed in the Linear-like representation with state-dependent coefficients:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{x}& =A\left(x\right)x+Bu,\hfill \\ \hfill y& =Cx,\hfill \end{array}\end{array}$$

where

$$A\left(x\right)=\left[\begin{array}{ccc}0& -1& 0\\ 0& 0& -1\\ -0.915& 1-0.915x_1^2& -1\end{array}\right],$$

$$B=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 1\end{array}\right],C=\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& 0\\ 1& 1& 0\end{array}\right].$$

Clearly, the matrix C is of full row rank. Consequently, one may choose

$$\Sigma =\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right]\mathrm{and}D=\left[\begin{array}{ccc}1& 0& -1\\ 0& -1& 0\\ 1& 1& 0\end{array}\right].$$

Choose $h=0.2s,\eta =1,\delta =1,{\overline{\epsilon }}_1={\overline{\epsilon }}_2={\overline{\epsilon }}_3={\overline{\epsilon }}_4={\overline{\epsilon }}_5=1\times {10}^{-5}$. By applying Theorem 2, we can obtain a group of feasible solution

$$K=\left[\begin{array}{ccc}-1.9986& 0& 0\\ 0& -0.0026& 0\\ 0& 0& 0.6633\end{array}\right],$$

$$S_1\left(x\right)=\left[\begin{array}{ccc}1687.2& -31.6& 225.6\\ -31.6& 1235.1& 36.1\\ 225.6& 36.1& 1307.7\end{array}\right],$$

$$S_2\left(x\right)=\left[\begin{array}{ccc}1179& 2.8& 1.9\\ 2.8& 1174.9& 0.3\\ 1.9& 0.3& 1175.9\end{array}\right].$$

Figure 1 displays the closed-loop system’s state trajectories, while Figure 2 presents the triggeringinstants and Figure 3 illustrates control input u. In this simulation, the controller triggered a total of 18 events, with an average inter-event time of 0.889 s and a minimum inter-event time of 0.2 s. The system reached steady state within 10.814 s (tolerance = 0.01), confirming that the proposed method achieves asymptotic stability with a remarkably low communication rate. For comparison, a conventional periodic control scheme with a fixed sampling period of h = 0.2 s would require continuous updates, whereas the proposed PETOFC achieves a comparable response with over an order-of-magnitude reduction in communication.

Figure 1. System states under control.

Figure 2. Event-triggering instants.

Figure 3. Control input u.

Example 2.

The Chua’s circuit implementation of a classic chaotic system [31] can be mathematically represented in controlled form as:

$$\begin{array}{cc}\hfill & \dot{x_1}=\alpha (x_2-x_1-f\left(x_1\right))+u,\hfill \\ \hfill & \dot{x_2}=x_1-x_2+x_3,\hfill \\ \hfill & \dot{x_3}=-\beta x_2,\hfill \end{array}$$

(46)

where x denotes the state array, with α and β as system parameters. The control input u influences the system dynamics, where $f\left(z\right)$ characterizes Chua’s diode piecewise-linear behavior:

$$f\left(z\right)=dz+0.5(d-m)\left(\right|z+1|-|z-1\left|\right),$$

where constants d and m satisfy $d<m<0$.

The matrix representation of system Equation (46) corresponds to Equation (35) with:

$$A\left(x\right)=\left[\begin{array}{ccc}-\alpha & \alpha & 0\\ 1& -1& 1\\ 0& -\beta & 0\end{array}\right],Z\left(x\right)=\left[\begin{array}{c}{x}_1+f\left(x_1\right)\\ x_2\\ x_3\end{array}\right],B={[1,0,0]}^{\top }.$$

Figure 4 illustrates the uncontrolled chaotic behavior of the system with parameters α = 9.2156, β = 15.9946, d = −1.24905 and m = −0.75735.

Figure 4. Chaotic attractor in the Chua’s system.

To implement the ETSFC, we selected $\sigma =0.09$ with initial conditions $x_0$=${[0.15,0.1,0.2]}^{\top }$. Considering the piecewise linear nature of Chua’s diode characteristic f, the controller was systematically developed for three distinct operational regions. For the case where $x_1<-1$, Theorem 3 yields the control law u=−30.2781$x_1$−20.1238$x_2$−10.5643$x_3$+50.2735 with the positive definite matrix

$$P=\left[\begin{array}{ccc}1.231& 0.2343& 0.8\\ 0.2343& 0.07234& 0.137\\ 0.8& 0.137& 1.156\end{array}\right]>0.$$

When $|x_1|\le 1$, the controller is designed as $u=-68.5647x_1-60.2567x_2-12.4456x_3$ and

$$P=\left[\begin{array}{ccc}0.0212& 0.008435& 0.04879\\ 0.008435& 0.05367& 0.04678\\ 0.04879& 0.04678& 0.7213\end{array}\right]>0.$$

When $|x_1|>1$, the controller is designed as $u=-30.2781x_1-20.1238x_2-10.5643x_3-50.2735$ and

$$P=\left[\begin{array}{ccc}1.231& 0.2343& 0.8\\ 0.2343& 0.07234& 0.137\\ 0.8& 0.137& 1.156\end{array}\right]>0.$$

The closed-loop system achieves asymptotic stability as all conditions of Theorem 3 are satisfied. Figure 5 displays the state trajectories of system Equation (46), while Figure 6 and Figure 7 illustrate the triggeringinstances and control input u respectively.

Figure 5. System states under control.

Figure 6. Event-triggering instants.

Figure 7. Control input u.

Figure 5 depicts the closed-loop response of the system under the ETSFC strategy, demonstrating rapid convergence and stable performance. In this simulation, the event-triggered controller was implemented with parameters ϵ = 19.1817 and ζ = 1.74081. A total of 286 triggering events occurred, with an average inter-event time of 0.0245 s and a minimum of 0.001 s. The system reached steady state within 3.587 s (tolerance = 0.01), which indicates that the proposed ETSFC approach ensures fast convergence while maintaining a strictly positive inter-event time and effectively avoiding Zeno behavior.

5. Conclusions

This study presents novel solutions for PETOFC and ETSFC in polynomial systems modeled by Linear-like representation with state-dependent coefficients. We developed specialized event-triggering mechanisms and corresponding controllers, demonstrating their efficacy through rigorous stability analysis that guarantees asymptotic stability while preventing Zeno behavior in both control schemes. The proposed approaches were validated through numerical simulations and application to Chua’s system, confirming their practical viability and performance. Despite the promising results, the proposed PETOFC and ETSFC schemes may face scalability and computational challenges in large-scale systems, and experimental validation will be pursued in future work.