Abstract
The integration of artificial intelligence (AI) into intelligent control systems has advanced significantly, enabling improved adaptability, robustness, and performance in nonlinear and uncertain environments. This study conducts a PRISMA-2020-compliant systematic mapping of 188 peer-reviewed articles published between 2000 and 15 January 2025, identified through fully documented Boolean queries across IEEE Xplore, ScienceDirect, SpringerLink, Wiley, and Google Scholar. The screening process applied predefined inclusion–exclusion criteria, deduplication rules, and dual independent review, yielding an inter-rater agreement of κ = 0.87. The resulting synthesis reveals three dominant research directions: (i) control model strategies (36.2%), (ii) parameter optimization methods (45.2%), and (iii) adaptability mechanisms (18.6%). The most frequently adopted approaches include fuzzy logic structures, hybrid neuro-fuzzy controllers, artificial neural networks, evolutionary and swarm-based metaheuristics, model predictive control, and emerging deep reinforcement learning frameworks. Although many studies report enhanced accuracy, disturbance rejection, and energy efficiency, the analysis identifies persistent limitations, including overreliance on simulations, inconsistent reporting of hyperparameters, limited real-world validation, and heterogeneous evaluation criteria. This review consolidates current AI-enabled control technologies, compares methodological trade-offs, and highlights application-specific outcomes across renewable energy, robotics, agriculture, and industrial processes. It also delineates key research gaps related to reproducibility, scalability, computational constraints, and the need for standardized experimental benchmarks. The results aim to provide a rigorous and reproducible foundation for guiding future research and the development of next-generation intelligent control systems.
1. Introduction
Intelligent control systems have evolved substantially in recent decades as industrial processes have become increasingly complex, nonlinear, and subject to uncertainty. Traditional control techniques, while effective in well-defined operating conditions, often struggle in environments characterized by rapid variability, incomplete models, and multivariable interactions. In parallel, advances in artificial intelligence (AI), including fuzzy logic, neural networks, evolutionary computation, and machine learning, have led to new approaches capable of learning from data, adapting to disturbances, and handling complexity beyond the reach of conventional controllers.
Historical developments show a progressive convergence between AI and control theory. Initial AI-inspired methods such as fuzzy inference and early neural models complemented classical PID and state-space control. More recent approaches incorporate hybrid neuro-fuzzy systems, metaheuristic optimization, predictive control architectures, and deep reinforcement learning, significantly expanding the toolbox available for intelligent control design. As a result, the integration of AI-based techniques has become a central research direction for improving robustness, adaptability, fault tolerance, and performance in applications such as renewable energy systems, industrial automation, robotics, power grids, and autonomous systems.
Despite the growing volume of publications in this domain, the existing literature reviews exhibit several limitations. Most lack reproducible methodologies, do not explicitly report Boolean search strategies, and rarely follow PRISMA-2020 guidelines. Many analyses focus on specific techniques—such as fuzzy systems, optimization algorithms, or predictive control—without offering a unified classification or mapping of the field. Furthermore, prior reviews generally do not compare methodological trade-offs among AI-enabled controllers, nor do they assess practical implications such as computational cost, scalability, real-time feasibility, or robustness under industrial conditions. Emerging contributions, including deep reinforcement learning, hybrid metaheuristics, or adaptive neuro-fuzzy architectures, are inconsistently integrated into broader trends.
Research Gap:
The current literature lacks the following:
(1) A standardized, PRISMA-2020-aligned synthesis of intelligent control systems.
(2) A unified taxonomy covering control models, optimization strategies, and adaptive mechanisms.
(3) Comparative analyses addressing real-world trade-offs, scalability, computational constraints, and industrial feasibility.
(4) Integration of emerging hybrid and deep learning-based controllers within the evolution of the field.
(5) Discussion of reproducibility challenges, including incomplete hyperparameter reporting and limited experimental validation.
Objective of This Review:
This study addresses these gaps by providing a systematic mapping of 188 peer-reviewed articles published between 2000 and 15 January 2025. This review employs explicit Boolean queries across multiple databases, dual screening with inter-rater agreement, deduplication procedures, and PRISMA-2020-aligned documentation of the study-selection flow and checklist. It offers a structured classification of intelligent control systems into three main contribution areas, i.e., control model strategies, optimization techniques, and adaptability mechanisms, while integrating emerging approaches such as deep reinforcement learning and hybrid metaheuristics. The analysis provides methodological comparisons, domain-specific insights, and a consolidated overview of challenges and future research directions.
The remainder of this article is organized as follows. Section 2 describes the PRISMA-2020 methodology and search protocol. Section 3 presents systematic mapping results, taxonomy, and comparative analysis. Section 4 discusses trends, practical implications, research opportunities, and limitations. Section 5 concludes with key findings and recommendations for advancing intelligent control systems.
2. Methodology
2.1. Review Design and Reproducibility
This work is designed as a systematic mapping study of AI-based intelligent control systems and follows the PRISMA-2020 recommendations for transparent reporting of systematic mapping. The review process included database selection, construction of Boolean search queries, deduplication, screening by two independent reviewers, eligibility assessment, extraction using a structured form, and synthesis and classification, with a cut-off date of 15 January 2025 for all database searches.
All papers included were published between 2000 and 2025, including early-access and online-first articles. Their status is explicitly indicated in the reference list, Table 1.

Table 1.
Databases and full Boolean search strings used in this review.
2.2. Databases and Full Boolean Search Strings
2.3. Search Execution, Deduplication, and Screening Process
The initial search returned 469 records. Deduplication was performed using Zotero automatic duplicate detection, manual verification of title/DOI, and independent screening by two reviewers. After deduplication, 347 unique records remained. Two independent screeners (Author 1 and Author 2) evaluated all records; conflicts were resolved by discussion, and, when disagreement persisted, a third reviewer resolved the case. The inter-rater agreement was κ = 0.87, indicating strong agreement.
2.4. Inclusion, Exclusion, and Selection Criteria (Standardized Labels)
Inclusion Criteria (ICs):
IC-1: Terms related to intelligent control appear in title or abstract.
IC-2: Publication year between 2000 and 15 January 2025.
IC-3: The study addresses control problems aligned with research questions.
IC-4: The study includes control engineering implementation.
IC-5: Focus on intelligent strategies: fuzzy, ANN, ML, metaheuristics, MPC-hybrid, and hybrid.
IC-6: The study includes evaluation (case study, experiment, simulation, review, survey).
Exclusion Criteria (ECs):
EC-1: Published before 2000.
EC-2: High-level general control discussions with no intelligent methods.
EC-3: Non-research formats (editorials, patents, letters).
EC-4: Studies not written in English.
EC-5: Not related to intelligent controllers.
Selection Criteria (SCs):
SC-1: Apply IC/EC to title and abstract.
SC-2: Read introduction and conclusion to verify alignment.
SC-3: Full-text reading of remaining articles.
SC-4: Classification into one dominant contribution category (mutually exclusive).
SC-5: Papers may map to multiple structures, but classification uses the main contribution only.
2.5. PRISMA-2020 Flow Diagram
The study selection process was documented using the PRISMA-2020 flow diagram. Figure 1 summarizes the flow from 469 identified records to the final set of 188 included studies.
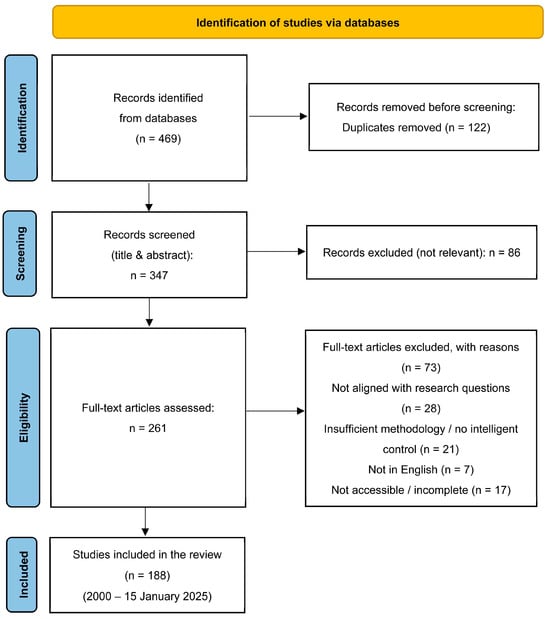
Figure 1.
PRISMA-2020 flow diagram for study selection (source: own elaboration based on systematic mapping).
2.6. Data Extraction
A structured extraction form captured the following:
- Year, authors, and publication type.
- Control structure.
- Intelligent techniques (fuzzy, ANN, ML, MPC, evolutionary, hybrid).
- Optimization method.
- Application domain.
- Type of evaluation (simulation, experiment).
- Reported metrics.
2.7. Research Questions
The research questions guiding this systematic mapping were reorganized into three conceptual categories to improve clarity and better reflect the analytical structure of the study. Each category addresses a specific dimension of intelligent control systems and supports the objectives of systematic mapping.
Category 1: Publication Sources
This category identifies where the scientific community is publishing intelligent control research and helps determine the concentration of knowledge in journals, conferences, and publishers.
Q1. What are the primary publication sources reporting advances in intelligent control systems?
Category 2: Technologies, Methods, and Architectures
This group focuses on the technical core of the review and examines how intelligent control systems are designed, implemented, and optimized. These questions explore the engineering contributions, computational techniques, and the structural features of controllers.
Q2. What types of engineering contributions and applications are reported in the development of intelligent control systems?
Q3. What research approaches and study types characterize intelligent controller designs?
Q4. What control structures and techniques define intelligent control systems in the recent literature?
Q5. Which computational tools and algorithms are most frequently used for the development of intelligent control systems?
Category 3: Trends, Challenges, and Future Directions
This category provides a forward-looking analysis by assessing emerging patterns, unresolved issues, and research opportunities in the field.
Q6. What are the current research trends in intelligent control?
Q7. What challenges and research opportunities remain open for the advancement of intelligent control systems?
Motivation for Research Questions
These seven questions were designed to achieve the following:
- Map the scientific landscape (Q1), identifying dominant publishers, journals, and dissemination channels.
- Characterize the technical evolution of intelligent control (Q2, Q3, Q4, Q5) by examining control structures, AI-driven algorithms, and hybrid architectures.
- Identify trends and gaps in intelligent control research (Q6, Q7), drawing insights into emerging techniques, scalability issues, reproducibility challenges, and future research needs in academic and industrial contexts.
Together, these research questions establish a comprehensive framework for analyzing the state of AI-based intelligent control and ensuring that the systematic mapping captures both technical and methodological perspectives.
2.8. Classification Rules
Classification rules were defined as follows: Tables within Section 3.5.1–Section 3.5.3 include per-node counts (n). Multi-label assignments are allowed at the node level; however, each article is assigned to one dominant contribution category when computing global percentages.
3. Results
From identifying sources of publications on intelligent controllers to assessing research trends and methodological approaches used in this field, this comprehensive analysis provides a detailed view of the current landscape. We analyze the most reported computational tools and algorithms in the literature for the design of these controllers.
3.1. Publication Sources
To complement the global distribution of publishers, Figure 2 shows the temporal evolution of the publication venues where AI-based intelligent control systems have been reported between 2001 and 2025. The stacked bars represent, for each year, the number of articles and conference papers indexed by the main editorial ecosystems, including Elsevier, IEEE Xplore, Springer, Wiley, AJC, JART, and MDPI. This view highlights not only the dominance of Elsevier and IEEE Xplore over the entire period, but also the progressive diversification of publication outlets in recent years, with an increasing presence of Springer proceedings and isolated yet relevant contributions in Wiley, AJC, JART, and MDPI journals and conferences. Overall, the figure confirms that research on AI-enabled intelligent control has intensified and broadened its editorial base, particularly after 2010, following the consolidation of hybrid, learning-based, and optimization-driven control strategies.
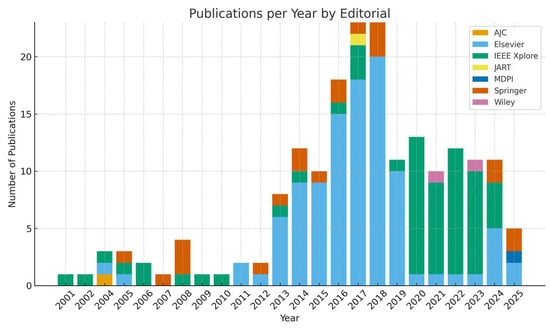
Figure 2.
Number of publications per year is grouped by publisher (source: own elaboration based on systematic mapping).
Table A4 in Appendix D summarizes the main journals and conference proceedings where the included studies were published, ordered by the number of contributions per venue. IFAC and Applied Soft Computing appear as the most frequent outlets, followed by ISA Transactions, Neurocomputing, and Energy Procedia, confirming the strong presence of AI-based intelligent control research in both control engineering and soft computing communities.
The sources of intelligent controller publications reveal a marked predominance of a small group of publishers. Elsevier is the most prominent, representing 54.78% of the 188 articles included in this review, followed by IEEE with 31.91% and Springer with 10.63%. Wiley accounts for 1.06% of the total. MDPI, AJC, and JART each contribute a single article, i.e., 0.54% per venue, together representing about 1.62% of all publications. Percentages are computed over the full set of 188 peer-reviewed articles, each assigned to a single publisher, pooling journal, and conference contributions. This distribution indicates that research on AI-based intelligent controllers is strongly concentrated within a limited set of editorial ecosystems, with Elsevier and IEEE playing a central role in disseminating advances in this area.
We found that the journals published 67.5% of the reviewed articles. Specialized intelligent controller conferences presented the remaining 32.5%. These figures highlight publishers’ significant role in disseminating scientific articles in this domain. Figure 3 summarizes these values.
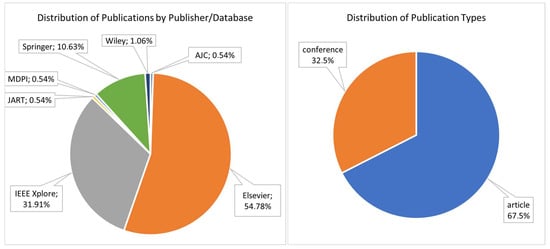
Figure 3.
Distribution of 188 included articles across publisher’s databases and type of publication (source: own elaboration based on systematic mapping).
3.2. Engineering Contributions and Applications in Intelligent Controllers
The review of research types has enabled us to identify and distill three primary areas of contributions in the field of engineering. Firstly, the contribution related to control model strategies stands out, representing 36.2% of the total, which encompasses the development and improvement of new intelligent algorithms for controllers, whether intelligent or conventional, as well as the introduction of new control structures with intelligent algorithms. The category of optimization models constitutes 45.2%, distinguishing itself through the presentation of new intelligent optimization models and the integration of artificial intelligence techniques with other conventional or intelligent ones.
Finally, the contribution of adaptability, with 18.6%, focuses on developing intelligent controllers that exhibit adaptability in their structure to provide control with high-speed response, robustness, and other qualities. These results provide a comprehensive overview of the various engineering contributions and applications in the field of intelligent controllers. Figure 4 presents a summary of the total number of articles according to the contribution made to intelligent controllers.
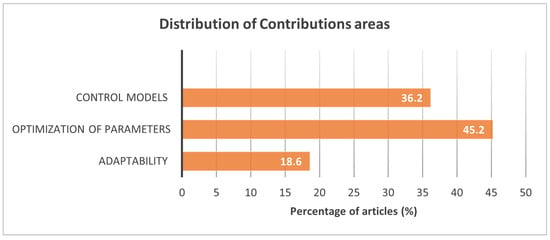
Figure 4.
Distribution of contribution areas in the reviewed studies (source: own elaboration based on systematic mapping).
3.3. Structures and Techniques in Intelligent Controllers
Intelligent controllers use diverse control structures and techniques to optimize efficiency and adaptability across various systems. Artificial neural networks are among the most common structures; they excel at modeling nonlinear behaviors and learning complex patterns. Fuzzy logic and its ability to handle uncertainty offer a crucial option in dynamic environments.
Many specific techniques use meta-heuristics such as particle swarm optimization (PSO) and genetic algorithms (GAs) to fine-tune controller parameters for better performance. Predictive control is particularly good at anticipating and managing changes in a system’s dynamics. Multilayer neural networks (MNNs) have adaptable structures that can model complex systems and learn from data. The adaptive fuzzy tracking algorithm-based control adaptive fuzzy tracking algorithm-based control and fuzzy MIMO control prove how fuzzy logic can adapt to many inputs and outputs in complex systems. In e-learning, dynamic parameter adjustment and grammatical evolution are effective strategies. These techniques show how control engineering is moving toward more adaptable solutions, combining fundamental principles with AI strategies to tackle modern system complexities.
3.4. Most Reported Computational Tools and Algorithms
The results of this study offer information on preferences and trends in algorithms and control structures. This comes from an analysis of scientific articles published from 2000 to early 2025. The most common classifications found are as follows:
- Artificial neural networks: 9.7%;
- Evolutionary or optimization algorithms: 15.0%;
- Fuzzy logic: 19.4%;
- Hybrid methods: 26.6%;
- Iterative learning control: 4.1%;
- Internal model control: 3.1%;
- Machine learning: 1.8%;
- Metaheuristic optimization: 11.4%;
- Model predictive control: 6.0%;
- Others: 2.9%.
Artificial neural networks (ANNs) are widely used in intelligent control due to their ability to approximate nonlinear system dynamics and adapt their internal weights based on error signals. Their layered structure enables learning-based modeling and control without requiring explicit analytical equations, making them effective for processes with significant uncertainty or nonlinearities. ANNs are commonly applied for system identification, predictive modeling, and adaptive control in complex industrial environments [1,2,3].
Evolutionary algorithms (EAs) provide a robust global search mechanism for tuning controller parameters, optimizing rule bases, and solving high-dimensional nonlinear optimization problems. By relying on population-based operators such as selection, crossover, mutation, and survival strategies, EAs efficiently explore complex search spaces where gradient-based methods fail. Common variants such as genetic algorithms, evolution strategies, and genetic programming are widely used for controller tuning, hybrid fuzzy–neural design, and multi-objective optimization in intelligent control [4,5,6].
Fuzzy logic (FL) enables the incorporation of expert knowledge into control systems through rule-based reasoning, handling nonlinear behaviors and uncertainty without requiring mathematical plant models. Its use of graded membership functions and linguistic rules allows smooth decision making in noisy or imprecise environments. FL is widely applied in industrial control, pattern recognition, decision systems, and medical diagnostics due to its interpretability and robustness [7,8,9].
Hybrid methods combine complementary intelligent techniques such as FL with neural networks or evolutionary algorithms to enhance robustness, accuracy, and adaptability. These architectures exploit the strengths of each component, such as neural learning with fuzzy interpretability or evolutionary global search with local refinement. Hybrid solutions are effective in complex control applications, including robotics, mechatronics, economic forecasting, and large-scale optimization [10,11,12].
Iterative learning control (ILC) improves control performance in repetitive operations by refining control actions based on previous execution errors. Through trial-by-trial updates, ILC enhances trajectory tracking and accuracy, making it suitable for robotics, automated manufacturing, additive manufacturing, and precision motion systems. Its learning mechanism allows continuous improvement without requiring explicit model updates [13,14,15].
Internal model control (IMC) employs a model of the plant to predict disturbances and generate corrective actions, resulting in a control strategy that is robust to model uncertainty and external perturbations. IMC’s predictive capability is particularly suitable for chemical processes, thermal systems, and manufacturing environments where disturbances are frequent, and constraints must be respected [16,17,18].
Machine learning (ML) enhances intelligent control by enabling systems to extract patterns from operational data, adapt to changing conditions, and support predictive decision making. ML techniques, i.e., supervised, unsupervised, and reinforcement learning, are used for fault detection, anomaly identification, controller parameter tuning, and modeling complex nonlinear systems in finance, healthcare, autonomous systems, and industrial automation [1,19,20,21].
Metaheuristic optimization (MO) offers a flexible framework for approximating solutions to nonlinear, multidimensional optimization problems where analytical approaches fail. Algorithms inspired by biological and physical processes such as PSO, GWO, ACO, DE, and simulated annealing are widely applied for controller tuning, membership-function optimization, and parameter identification. Their exploration–exploitation balance provides improved global performance in engineering, logistics, bioinformatics, and industrial control [10,22,23,24].
Model predictive control (MPC) optimizes control actions by predicting system behavior over a finite horizon and enforcing constraints in real time. MPC is particularly effective for multivariable and constraint-bound industrial processes, including energy systems, autonomous vehicles, and chemical production. Its integration with ANN or FL models further improves performance under nonlinear or time-varying conditions [25,26,27,28].
3.5. Outcomes of Studies
Appendix A, Appendix B and Appendix C presents a classification of the analyzed 188 articles, specifying the type and focus of research that categorizes them into one of these three topics: the control model, the implementation of techniques for parameter optimization, and adaptive controllers. In addition, the classification is based on the type of contribution, exploring various contributions and engineering applications derived from advances in intelligent controllers, including contributions related to control, optimization, and adaptability models. In addition, the structures and control techniques used to specify and design intelligent controllers are analyzed, encompassing both classical and modern control structures, as well as the artificial intelligence techniques employed, such as neural networks, fuzzy logic, and evolutionary algorithms. Finally, the most widely used computational algorithms in the literature are those for designing and implementing controllers that enhance the efficiency and performance of intelligent controllers in various applications and scenarios.
3.5.1. Result of Contributions: Control Models
The integration of AI techniques into intelligent controllers represents a significant advance in the field of control systems. These new control models combine conventional methods with AI approaches to improve adaptability, accuracy, and efficiency in complex and variable environments. This combination enables the handling of challenges ranging from variability in operating conditions to unforeseen disturbances, opening opportunities to optimize and continuously improve system performance. The reviewed articles present relevant contributions across several categories of intelligent control models, including hybrid controllers, fuzzy logic controllers, predictive controllers, iterative learning controllers, and neural controllers.
Hybrid controllers combine two or more control techniques or algorithms to leverage their strengths and compensate for their weaknesses. They are increasingly popular in industrial, energy, and complex system applications, particularly in contexts involving AI, optimization, and classical control. The reviewed literature reveals advanced control and optimization strategies applied to dynamic, nonlinear, and complex systems. Several works propose hybrid methods that merge techniques such as artificial neural networks (ANNs) and fuzzy logic (FL), often supported by evolutionary algorithms (EAs) for improved model identification, controller design, tuning, and robustness against uncertainties and perturbations. Various architectures integrate ANNs with type-1, type-2, or fractional fuzzy logic for control and compensation tasks in nonlinear and uncertain environments ([29,30,31,32,33,34,35,36,37,38,39]). Additionally, numerous studies employ genetic algorithms, differential evolution, evolutionary strategies, particle swarm optimization, harmony search, cuckoo search, and related heuristics to optimize strategies, parameters, and rule sets in hybrid controllers ([37,38,40,41,42,43,44,45,46,47,48,49]). Other papers incorporate model predictive control (MPC), frequently combined with ANNs or fuzzy logic to accelerate computations or enhance tracking and robustness ([50,51,52,53,54,55,56]). Hybrid schemes that integrate classical control techniques (PI, PID, H∞, deadbeat, sliding mode control) with intelligent components (ANN, FL) demonstrate improved accuracy, adaptability, and robustness, even in systems with incomplete models or operating under changing conditions ([45,57,58,59,60,61,62,63,64]). These approaches are validated in real or simulated systems—including power plants, turbines, robots, chemical processes, hybrid energy systems, irrigation systems, and autonomous vehicles—showing enhanced performance, reduced error, increased robustness, and improved energy efficiency compared to traditional controllers ([45,48,49,52,59,63]).
Fuzzy logic controllers (FLCs) have proven highly effective due to their ability to handle uncertainty and their adaptability to variable operating conditions. Based on IF–THEN rules and fuzzy sets, these controllers are well suited for environments with frequent disturbances or dynamically changing parameters. A Takagi–Sugeno incremental fuzzy state model improves stability and error rejection by integrating an FLC–LQR structure with an optimal observer [65]. In automotive applications, comparisons between PID and fuzzy logic controllers for vehicle stability show that fuzzy logic offers superior robustness, though PID remains easier to implement [66]. In power electronics, a type-2 fuzzy neural controller (T2FNS) outperforms a conventional PI controller in terms of speed, overshoot, and power quality for converter control [67], while a fuzzy controller for DC–DC converters achieve faster responses and better disturbance rejection than traditional PI controllers [68]. In water treatment, a Mamdani FLC achieves greater pH stability and contaminant reduction where classical PIDs fail [39], and in electric motor applications, a Mamdani FLC provides improved tracking and robustness under disturbances compared to PID [69]. In renewable energy, an adaptive FLC enhances wind energy extraction with better dynamic performance than PI control [70], while in agriculture, an efficient FLC regulates greenhouse temperature and humidity with high accuracy under real conditions [71]. For photovoltaic systems, an optimized MPPT fuzzy controller offers faster convergence, improved accuracy, and reduced steady-state oscillations. References [72,73] present the design and experimental validation of a Mamdani-type fuzzy PI controller for liquid-level regulation in an industrial training plant (Festo Didactic MPS® PA Compact Workstation), and the plant is first identified in MATLAB R2022 using the System Identification toolbox, achieving a transfer function model with 98.45% fit and a fuzzy PI controller with five membership functions per input, and a rule base derived from operator knowledge is designed and compared against two PID controllers: one tuned automatically with MATLAB’s PID Tuner and another tuned manually by an experienced operator; simulation results under reference changes and disturbances show that the fuzzy PI achieves faster settling time and better disturbance rejection than both PID configurations, the controller is then implemented on the real plant and tested with different reference profiles (step, ramp, sinusoidal, sawtooth, and square inputs), and quantitative performance indices (mean error, mean absolute error, mean square error, and root mean square error) confirm that the fuzzy PI consistently attains slightly lower tracking errors than the PID controller while preserving stability and robustness. Finally, [74] presents the design and implementation of a fuzzy–Smith compensator for speed control of an induction motor driven by a frequency converter in a networked control system architecture based on Siemens S7-1200 PLCs and PROFINET communication, the plant is first identified in MATLAB, obtaining a first-order model with 96% fit, and a Mamdani fuzzy controller is designed using error and error derivative as inputs, with seven triangular membership functions and 49 rules, to adapt the gain of the Smith predictor and compensate modeling errors and network-induced delays; in simulation, the fuzzy–Smith compensator is compared against two PI/PID controllers (one auto-tuned in MATLAB and one tuned by an experienced operator), showing similar or faster responses with reduced overshoot. Experimental tests on a 1 HP induction motor training kit confirm that the MATLAB-tuned PID becomes oscillatory, while the operator-tuned PID and the fuzzy–Smith compensator remain stable; the fuzzy compensator halves the rise time (2 s vs. 4 s) and maintains overshoot below 5%, achieving the lowest mean, absolute, and root-mean-square tracking errors among all controllers.
Model-based predictive controllers (MPCs) estimate future system outputs through internal models and continuously adjust control actions, making them ideal for scenarios requiring anticipatory behavior. A detailed review of MPC applications in agriculture covers classical, robust, nonlinear, distributed, and stochastic variants, with successful implementations in irrigation, machinery, production, and greenhouse climate control [75]. This review highlights MPC’s superiority over traditional and AI-based controllers in managing multivariable, time-delayed, and nonlinear systems, while acknowledging existing challenges in real-world agricultural applications. A Robust Economic Predictive Control (reMPC) method incorporates stochastic perturbation information for time-invariant linear systems using a tube-based formulation to maintain feasibility and robustness [76]. This method leverages known fault distributions to optimize performance and terminal costs, and its validation in a CSTR reactor demonstrates its advantages over conventional robust MPC approaches.
Iterative learning controllers (ILCs) are effective in applications involving repetitive tasks requiring high precision. These controllers refine the control input based on error information from previous iterations, progressively improving tracking accuracy. A comparison of three Norm-Optimal ILC schemes—standard quadratic ILC (QILC), integrated-estimation ILC (E-QILC), and iteration-domain Kalman ILC (K-ILC)—reveals that while the methods are equivalent under certain conditions, the K-ILC approach offers superior convergence speed and robustness to noise [77], validated through simulations on a mass–spring–damper system. Another robust ILC formulation incorporates performance weighting functions to ensure convergence under plant uncertainty, also validated through simulation studies [78].
Neural controllers (ANNCs) leverage artificial neural networks to learn and adapt to varying conditions by adjusting their internal weights, making them suitable for nonlinear and complex systems. A comprehensive review highlights that data-driven models can replace or complement classical elements within control loops [55], supported by a case study showing that a deep neural network improves autonomous surface vehicle performance and resilience to modeling errors compared to conventional linearizing controllers. Another contribution proposes a robust predictive control scheme using ANNCs in a dual-stage structure—one for plant modeling and one for residual uncertainty—achieving stability and improved robustness in a pneumatic servomechanism validated experimentally [79]. The learning feedback linearization (LFL) approach employs a NARMA-type MLP neural network to learn nonlinear system inverse dynamics, enabling subsequent PI control with successful simulation results [80]. Another controller based on a modified fuzzy cerebellar model combined with a functional link network and sliding mode control demonstrates high robustness in chaotic system synchronization and inverted pendulum control [81]. In motor control applications, an ANNC for three-phase induction motors achieves superior speed tracking and disturbance rejection compared to a fuzzy controller [82]. For electric vehicle-charging systems, an ANN-PMC-based intelligent adaptive controller improves energy management by reducing overshoot and DC bus settling time [72]. Reinforcement learning combined with deep neural networks (RL-DLNN) has been applied to chiller-type HVAC systems, achieving superior adaptation, stability, and tracking performance compared to PID and MPC controllers, especially in highly nonlinear and disturbed MIMO environments [83]. Finally, [84] proposes an adaptive neural network controller for pressure regulation in industrial processes, implemented on a Festo MPS® PA Compact Workstation and compared against conventional PID control, and the controller uses a simple feedforward neural network with sigmoid activation and online weight adaptation based on the Brandt–Lin algorithm from the adaptive interaction theory, which allows learning directly from the pressure error without an explicit training phase or prior plant model. After identifying the plant in MATLAB (67% fit) to build the simulation model, the authors compare the adaptive neural controller with two PIDs (one auto-tuned by MATLAB and one tuned by an experienced operator) in simulation and then implement both the neural controller and the operator-tuned PID on the real plant via a PLC–OPC–Simulink architecture. Experimental tests with step, ramp, square, sinusoidal, sawtooth references, and disturbance inputs show that the adaptive neural controller achieves faster response and better tracking than the PID, with lower mean error (1.28% vs. 5.13%), mean absolute error (4.77% vs. 9.59%), mean square error, and RMSE, demonstrating superior robustness and accuracy for pressure control under varying operating conditions.
Table A1 in Appendix A presents the articles that contributed to control models in control systems-based AI.
The integration of AI techniques into intelligent controllers has led to a diverse set of control-model structures. Based on the 68 studies classified in this category, fuzzy-logic-based controllers constitute the largest group with 28 contributions, confirming their central role in AI-enabled control. Within this family, 12 works employ generic FLC structures without specifying the inference type, while seven studies explicitly implement Mamdani-type controllers, typically in level, flow, or drive-control applications. Two studies adopt Takagi–Sugeno (T–S) models to handle nonlinearities via local linear models, and one work focuses on type-2 fuzzy logic, addressing membership uncertainty in highly disturbed environments. In addition, six contributions fall into the adaptive fuzzy category, including ANFIS-based schemes and self-learning fuzzy controllers capable of updating rules or scaling factors online to cope with changing operating conditions.
Beyond fuzzy controllers, five articles are primarily based on model predictive control (MPC), covering classical, robust, and economic MPC formulations for multivariable processes with constraints. Three studies belong to iterative learning control (ILC), where trajectory tracking is improved across repetitions via norm-optimal or predictive ILC structures. Ten contributions employ artificial neural networks (ANNs) as the core control mechanism, either through direct neural controllers, neural feedback linearization, or dual-network architectures for plant modeling and residual compensation. Finally, 22 studies are categorized as hybrid controllers, in which two or more paradigms (e.g., fuzzy–ANN, fuzzy–PID, ANN–PID, fuzzy–MPC, type-2 FLC + PID, H∞/H2 combined with evolutionary algorithms, or RFCMAC-based schemes) are tightly integrated into a single control law. These hybrid architectures consistently seek to exploit complementary strengths—such as fuzzy interpretability, neural learning capability, and model-based prediction—while mitigating individual limitations. This can be observed in the synthesis of node quantities in Table 2 below.

Table 2.
Control model contribution type groups.
Note: Node counts reflect multi-label assignments within the control-model dimension (68 contributions). Global percentages in Section 3.2 are computed over 188 articles, each assigned to a single dominant category.
In summary, Figure 5 presents a classification of the groups of control models that contribute to the application of AI in control systems.
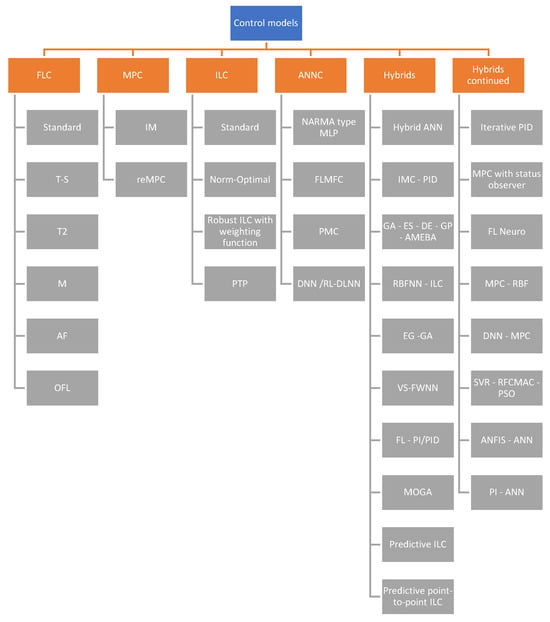
Figure 5.
Control model contribution type groups (source: own elaboration based on systematic mapping).
3.5.2. Result of Contributions: Optimization of Parameters
New AI optimization methods have led to significant improvements in performance, adaptability, and efficiency in the design and implementation of intelligent controllers for control systems. The following articles present contributions to optimization-based control models, grouped by their predominant technique.
Researchers employ artificial neural networks to enhance optimization and learning within controllers, as machine learning facilitates parameter tuning and improves the accuracy of control models in complex systems. ANNs effectively manage nonlinearities, increasing the accuracy and robustness of controllers in diverse environments. They have been applied to the design of PID controllers, offering an advanced method to enhance system response [85]. Support vector machines have been used for excitation control to improve system stability through supervised learning [86], and supervised learning neural networks have been utilized for learning and verification in feedback control systems [87]. Machine learning and predictive control techniques have also been applied in the design of adaptive PID controllers [88].
Evolutionary algorithms, particularly genetic algorithms, play a significant role in optimizing control parameters, especially for systems with uncertainties or nonlinear characteristics. By simulating natural evolutionary processes, these algorithms search for optimal solutions. GAs have been used to refine the rule base of Mamdani fuzzy logic controllers [89], improve modified PID controller performance [90], and enhance the adaptability of self-adjusting PID controllers [91]. Multi-objective GAs are essential for improving controller performance under competing objectives [92], including in fractional-order PID controllers for multivariable systems [93]. GAs have also been used to optimize control structures with a focus on structural adaptation [94], to fine-tune fuzzy controllers for vibration suppression [95], to develop hybrid controllers using Hydra structures optimized with GA-based strategies [96], and to support multi-objective optimization in control systems using the taxi-cab evolutionary algorithm [97].
Metaheuristic optimization algorithms such as particle swarm optimization, gray wolf optimization, gravitational search, and cuckoo optimization are widely employed to adjust parameters in complex controllers, effectively exploring large search spaces to identify optimal solutions. PSO has been applied to tune PID controllers [98], design fuzzy PID controllers for Quasi-Z-Source converters [99], optimize fuzzy-PDC controllers [100], and improve fuzzy controllers for distillation processes [101]. Gray wolf optimization has been used to optimize fuzzy PID controllers for power system frequency regulation [102], while gravitational search algorithms have improved the dynamic response of PID controllers [103]. The cuckoo optimization algorithm has been applied to energy management within fuzzy controllers [104]. Differential evolution algorithms have been used to design fuzzy controllers for wireless sensor networks [105], the Firefly Algorithm has been applied to develop optimized fuzzy PID drivers [106], and the bee colony algorithm has proven effective for designing fuzzy controllers [107].
Several articles focus on fuzzy controllers designed to manage uncertainty and variability in complex systems through fuzzy logic. Fuzzy PID controllers have shown improvements in continuous industrial processes [108], performed effectively as multivariable controllers [109], and have been applied to control underactuated manipulators [110]. A low-cost servo system based on fuzzy control is introduced in [111], while a fuzzy PID controller for BLDC motor control is proposed in [112].
Hybrid techniques combine two or more methods such as fuzzy logic and metaheuristic optimization to capitalize on their strengths and improve controller performance and adaptability. Integrated fuzzy control and optimization approaches have been employed for frequency regulation in electrical networks [113]. Hybrid GWO–SCA structures have been deployed in type-II fuzzy controllers for multi-area frequency control [114], while combinations of harmony search and cuckoo optimization have been applied in fuzzy PID drivers [115]. A hybrid PSO–GSA strategy has also been used in fuzzy sliding-mode controllers for wind power systems [116],
Predictive control techniques, which anticipate system changes and adjust control actions based on future predictions, further enhance controller adaptability and performance in systems with high variability. In this category, SVMs have been integrated into nonlinear predictive controllers to anticipate and correct system behavior multiple steps ahead [117].
Several works explore additional or unique optimization techniques that fall outside the conventional categories. These include optimized PID controllers developed using multi-objective techniques, providing effective methods to manage multiple performance criteria in control systems [118].
Finally, reference [119] presents a generic identification methodology for liquid-level systems in industrial processes based on time-series artificial neural networks, validated on a Festo MPS® PA Compact Workstation. The authors design two identifiers: a nonlinear NARX network trained with Levenberg–Marquardt and a simplified GADALINE network trained with an LMS-based algorithm including normalization and momentum, both implemented for online and offline operation. Experimental tests with different excitation signals (step, pulse train, sinusoidal, and sawtooth) show that both neural identifiers reproduce the real tank dynamics more accurately than a conventional first-order Laplace model, especially under disturbances, with GADALINE achieving the best compromise between accuracy, numerical simplicity, and availability of an explicit discrete transfer function. Using the GADALINE-based model to tune a PI controller yields improved control performance, reducing level-control settling time from 29 s to 25 s (≈13.8%) and slightly decreasing dispersion by 0.9% compared with the PI tuned from the classical identification. This section concludes that NARX and GADALINE time-series neural networks are promising tools for practical system identification in industrial processes, enabling more efficient controller design while keeping implementation complexity moderate
The analysis of optimization-focused contributions shows that metaheuristic algorithms clearly dominate the landscape, with 37 out of 85 studies (43.5%) relying primarily on population-based heuristic methods. This group encompasses a wide variety of nature-inspired optimizers, including PSO, GWO, GSA, DE, ACO, ABC, FA, HS, WOA, BFOA, FOFMO, ICDBO, SOA, and several recent variants. These algorithms are predominantly used to tune PID and fractional-order PID gains, adjust fuzzy membership functions and rule bases, or optimize hybrid controller structures under nonlinear, constrained, or highly coupled dynamics. Their prevalence confirms that global, stochastic search methods have become the default choice for parameter optimization in intelligent control systems.
Evolutionary algorithms represent the second largest family, with 16 studies (18.8%). This category includes classical genetic algorithms, multi-objective evolutionary schemes (MOEA, MOEA-CCG), and problem-specific evolutionary formulations such as taxi-cab evolutionary algorithms. In these works, evolutionary methods are commonly applied to refine controller structures, optimize multi-objective performance indices, or perform structural and parametric tuning of PID and fuzzy controllers. Together, metaheuristics and evolutionary algorithms account for more than 60% of all optimization contributions, underscoring the central role of population-based search strategies in intelligent controller design.
A smaller but relevant subset of works exploits hybrid optimization strategies, where two or more metaheuristics are combined in a single tuning framework. This group comprises 11 studies (12.9%), including, for example, GWO–SCA, PSO–GSA, ZOA–OOA, and hybrid arithmetic–gorilla optimization algorithms. These approaches aim to exploit complementary strengths—such as exploration capability from one algorithm and exploitation/refinement from another—to improve convergence speed, robustness, and solution diversity relative to single-heuristic designs.
In addition, nine studies (10.6%) fall under Fuzzy Optimization, where fuzzy mechanisms themselves (fuzzy predictors, fuzzy adaptation rules, ANFIS-based optimization, or fuzzy coefficient adjustment) are used as the core optimization engine rather than as the structure being optimized. Neural Networks Optimization accounts for six articles (7.1%), in which neural models are explicitly employed to support tuning—either as surrogate models to approximate the cost landscape or as direct learning schemes for controller parameters (e.g., neural network-based FRIT PID tuning). ML-based Optimization contributes five studies (5.9%), including SVM/SVR-based optimizers and reinforcement learning-driven tuning (e.g., DDPG, TD3) that adapt controller gains from performance data.
Finally, only one study (1.2%) remains in the Others/Miscellaneous category, corresponding to a problem-specific tunable-model formulation that does not fit neatly into the previous groups. Overall, these results confirm that parameter optimization in intelligent control is overwhelmingly dominated by metaheuristic and evolutionary methods, while hybrid, fuzzy-based, and machine learning-driven optimization provide complementary alternatives in scenarios where interpretability, online adaptation, or surrogate modeling are particularly important. This can be observed in the synthesis of node quantities in Table 3 below.

Table 3.
Optimization of parameters contribution type groups.
Note: Node counts reflect multi-label assignments within the optimization of parameters dimension (85 contributions). Global percentages in Section 3.2 are computed over 188 articles, each assigned to a single dominant category.
Table A2 in Appendix B presents the articles that have contributed to the optimization of artificial intelligence in control systems.
Figure 6 also presents a classification of the groups of optimization strategies that contribute to the application of AI in control systems.
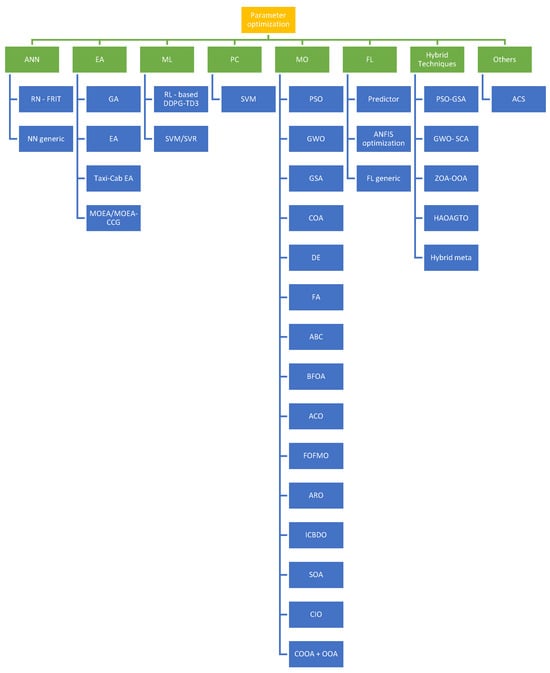
Figure 6.
Optimization contribution groups (source: own elaboration based on systematic mapping).
3.5.3. Result of Contributions: Adaptability
The development of adaptive control strategies has gained significant attention in recent decades due to the increasing complexity of dynamic systems, the presence of nonlinearities, time delays, parametric uncertainties, and external disturbances. In this context, several approaches have been proposed that combine classical control structures such as PID controllers, fuzzy models, and neural networks with modern techniques of adaptation, optimization, and machine learning. The reviewed literature has been organized into different categories according to the predominant control technique, allowing for a clear comparison of the strengths, limitations, and applications of each approach. The main categories include adaptive PID-based controllers, in which the classical PID structure is enhanced through optimization, fuzzy logic, or machine learning; adaptive fuzzy-based controllers (Fuzzy/ANFIS/T–S), which employ fuzzy inference to support decision making and online parameter tuning; adaptive neural network-based controllers, where neural models act as universal approximators to handle uncertain nonlinear dynamics; hybrid adaptive controllers, which synergistically combine fuzzy, neural, robust, or bio-inspired approaches; and optimization and adaptive optimal controllers, where evolutionary algorithms, heuristics, and predictive methods are used to tune parameters of classical or advanced controllers.
Within the domain of adaptive PID-based controllers, numerous studies have introduced significant improvements through optimization and learning techniques. Key contributions include the use of Adaptive Particle Swarm Optimization to tune linear and nonlinear PID controllers, improving stability and convergence speed compared to classical methods [120]; a fuzzy predictor-based adaptive PID controller that enhances online adjustment and tracking accuracy in nonlinear processes [121]; a Model Reference Adaptive System used to tune PID gains for launch vehicles under parameter variations [122]; and a self-adaptive genetic algorithm that optimizes both gains and performance indices for smoother and faster PI/PID responses [123]. Additional contributions include a PLC-implemented fuzzy PID controller for oil pipeline flow regulation [124]; a Kalman-enhanced fuzzy PID controller for liquid-level control in conical tanks, where fuzzy logic adjusts PID gains and Kalman filtering increases robustness against noise [125]; a hybrid OENN–OEANFIS structure to adapt PID parameters through endocrine-inspired neural modeling combined with neuro-fuzzy inference [126]; the use of Self-Adaptive Differential Evolution for dynamic PID tuning [127]; a deep learning-based intelligent PID (CNN–LSTM) for UAVs, predicting parameter adjustments to improve stability and energy efficiency [128]; an AIEM-DDPG algorithm to adapt PI gains in PEM fuel cells, reducing overshoot and enhancing stability [129]; and a TD3-based tuner that adaptively adjusts parameters of PI and lead controllers under uncertainty [130].
In the area of adaptive controllers based on fuzzy logic (Fuzzy/ANFIS/T–S), these methods are widely employed due to their ability to manage uncertainty and variability under changing operating conditions without requiring an exact mathematical model of the system. Notable examples include an adaptive fuzzy controller for MPPT in photovoltaic systems, which adjusts the output scaling factor online to track the maximum power point under varying irradiance and temperature [131]; an ANFIS controller for a PFC boost converter trained online using data from a conventional fuzzy controller to improve voltage regulation [132]; an adaptive fuzzy PI controller for coupled tanks, where Mamdani rules dynamically tune Kp and Ki gains to manage nonlinearities [133]; a T–S adaptive controller with a state observer for nonlinear systems with unknown dead zones, avoiding traditional backstepping complexity [134]; an ANFIS controller with hybrid learning (least squares + backpropagation) for autonomous mobile robot trajectory tracking [135]; a self-learning fuzzy controller based on Autonomous Adaptive Control that generates and updates fuzzy rules online without external supervision [136]; an ANFIS optimized with genetic algorithms for greenhouse climate control, where the GA tunes membership functions and rules to improve robustness and reduce ISE [137]; and a two-level adaptive fuzzy controller for DC motors combining a Mamdani fuzzy controller with an inverse T–S model updated in real time [138].
Regarding adaptive controllers based on bio-inspired or optimal optimization techniques, the literature presents several noteworthy implementations. These include an adaptive fuzzy controller optimized with Adaptive Differential Evolution for synthetic inertia in power systems, where DE dynamically tunes fuzzy membership functions to reduce frequency nadir and enhance stability [139]; an LQR controller optimized with Adaptive Cuckoo Search for vehicle active suspension systems, adjusting Q and R weighting matrices to reduce vertical acceleration and improve ride comfort [140]; and an Adaptive Model Predictive Control scheme employing set-membership identification and tube-based predictions to guarantee constraint satisfaction under parametric uncertainty and disturbances [141].
In the domain of adaptive controllers based on neural networks, several high-impact contributions exist. These include an Initial-Training-Free Online Extreme Learning Machine for adaptive control of nonlinear discrete-time systems with rapidly varying parameters, enabling online identification without prior training data [142]; a multilayer perceptron integrated with integral sliding mode control to compensate for residual and approximation errors in systems with dead-zone nonlinearities [143]; an adaptive Radial Basis Function Neural Network for nonlinear systems with unknown time delays, acting as a universal approximator with Lyapunov-based weight adaptation laws [144]; an adaptive RBFNN combined with second-order sliding mode control to estimate unknown dynamics while eliminating chattering [145]; an RBFNN integrated with backstepping and barrier Lyapunov functions for vibration suppression in flexible string systems with dead-zone effects and output constraints [146]; an RBFNN-based adaptive controller with a neuro-inspired Incentive Actuator Preventor (IAP) mechanism for robotic manipulators under switching constraints [147]; a wavelet neural network observer embedded in an adaptive fuzzy sliding mode stabilizer for multimachine power systems, estimating uncertainties and improving low-frequency oscillation damping [148]; and an adaptive neural network controller for DC–DC converters using online learning to compensate for model uncertainties and improve voltage regulation under dynamic loads [149].
Finally, hybrid adaptive controllers that integrate fuzzy logic, neural networks, robust control, and optimization methods represent some of the most advanced solutions. Representative contributions include a neuro-fuzzy backstepping adaptive controller applied to induction motors with unified nonlinear friction and unknown dynamics, where ANFIS is embedded within a robust backstepping framework to ensure tracking accuracy [150]; a robust adaptive fuzzy neural T–S controller for interconnected nonlinear systems, combining T–S models and neural networks to approximate unknown interconnections while a compensator handles errors [151]; a hybrid adaptive fuzzy navigation controller for mobile manipulators, combining adaptive parameter estimation with T–S fuzzy logic for obstacle avoidance and trajectory tracking in dynamic environments [152]; a robust adaptive controller based on Lyapunov/backstepping to manage strong nonlinearities and uncertainties, ensuring global stability through adaptive update laws [153]; and a fuzzy PID controller hybridized with Ant Colony Optimization for UAV path planning, where fuzzy logic adjusts PID gains in real time and ACO optimizes pheromone updating to generate shorter, smoother trajectories [154].
The adaptability-focused contributions reveal that fuzzy-based adaptive strategies clearly dominate this group. Out of the 35 studies classified under adaptability, 14 articles (40.0%) fall into the Adaptive Fuzzy/ANFIS category. These works rely on Mamdani or Takagi–Sugeno fuzzy controllers, ANFIS architectures, or self-learning fuzzy schemes that adjust rules, membership functions, or scaling factors online. Their primary goal is to handle nonlinearities, parametric uncertainty, and operating-point variations without requiring an exact plant model. Typical applications include coupled-tank processes, greenhouse climate control, photovoltaic MPPT, DC motor drives, and mobile robot trajectory tracking, where fuzzy or neuro-fuzzy controllers continuously retune gains and inference parameters to maintain performance under changing conditions.
Hybrid adaptive controllers constitute the second-largest group, with 11 studies (31.4%). These contributions integrate two or more paradigms such as fuzzy logic with sliding-mode control, fuzzy PID with metaheuristic tuning, neuro-fuzzy backstepping, or PI controllers adjusted by deep reinforcement learning (e.g., DDPG, TD3) into a single adaptive framework. In these architectures, adaptation laws are often derived from Lyapunov-based designs, optimization-driven update rules, or RL policies that update controller parameters online. Hybrid adaptive controllers are particularly prominent in complex nonlinear systems, multi-area power systems, and motion-control problems, where robustness, disturbance rejection, and constraint handling must be addressed simultaneously.
Adaptive neural networks account for five studies (14.3%), in which neural models (e.g., RBFNN, wavelet neural networks, multilayer perceptrons) are used as universal approximators of unknown nonlinear dynamics or time-varying parameters. These controllers typically incorporate adaptive weight-update laws derived from Lyapunov stability analysis, barrier functions, or sliding-mode frameworks, and are applied to systems with dead zones, time delays, flexible structures, or robotic manipulators. Adaptive PID controllers represent three studies (8.6%), where classical PI/PID structures are augmented with online tuning rules—often based on reference-model adaptation, fuzzy predictors, or self-adaptive search strategies—to maintain desired transient and steady-state performance under varying operating conditions.
Only one article (2.9%) is categorized as adaptive MPC, implementing an MPC scheme with adaptive model or constraint updates to cope with parametric uncertainty and disturbances while preserving constraint satisfaction. Another single study (2.9%) is classified as Bio-inspired Adaptive Control, where the adaptation of a model-based controller LQR is governed directly by a bio-inspired optimizer—in this case, an Adaptive Cuckoo Search algorithm—rather than relying solely on analytical update laws. Overall, these results show that adaptability in intelligent control is predominantly addressed through fuzzy/ANFIS architectures and hybrid adaptive schemes, with neural controllers providing additional flexibility in highly nonlinear settings, and with bio-inspired and adaptive MPC approaches emerging as complementary but less frequently explored directions. This can be observed in the synthesis of node quantities in Table 4 below.

Table 4.
Adaptability contribution type groups.
Note: Node counts reflect multi-label assignments within the Adaptability dimension (35 contributions). Global percentages in Section 3.2 are computed over 188 articles, each assigned to a single dominant category.
Table A3 in Appendix C presents a detailed table of the articles that contributed to the adaptability of artificial intelligence in control systems.
In summary, Figure 7 also presents a classification of the groups of adaptability strategies that contribute to the application of AI in control systems.
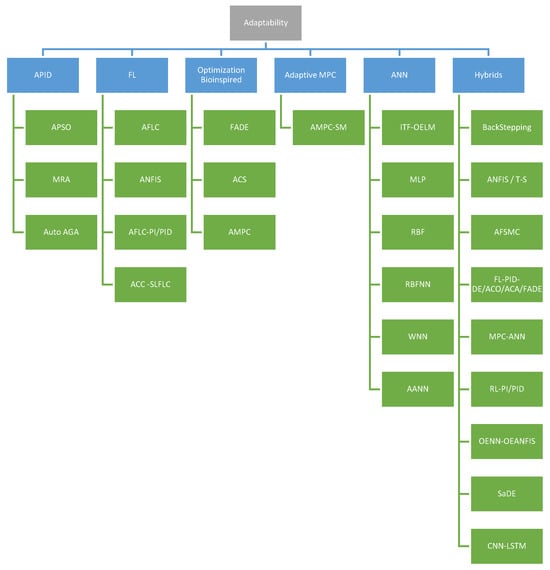
Figure 7.
Adaptability contribution type groups (source: own elaboration based on systematic mapping).
4. Discussion
The systematic mapping reveals a rapidly evolving landscape in AI-enabled control systems, characterized by the emergence of hybrid controllers, metaheuristic optimization frameworks, and advanced adaptive strategies. The analysis consolidates methodological patterns, evaluates practical trade-offs, and highlights critical gaps that must be addressed to translate academic contributions into industrial solutions.
4.1. Comparative Analysis of Control Strategies
Hybrid controllers, particularly neuro-fuzzy systems and ANN-enhanced PID or MPC structures, stand out for their ability to combine interpretability, learning capability, and robustness. They consistently outperform single-technique controllers in nonlinear and highly uncertain environments. Fuzzy controllers provide strong performance in systems where interpretability and tolerance to uncertainty are essential, but they often require rule base optimization to prevent scalability issues. Neural network controllers offer superior adaptability and modeling power but face challenges in explainability, training data dependence, and stability guarantees. Model predictive control remains highly effective for constrained and multivariable systems, yet computational cost limits its deployment in fast real-time applications unless combined with learning-based surrogate models. Metaheuristic approaches, especially PSO, GWO, DE, and hybrid GWO-SCA/PSO-GSA algorithms, demonstrate strong global search efficiency and robustness in tuning controller parameters, but their computational load varies widely and their hyperparameter choices remains inconsistently reported.
Additional experimental evidence from four real-plant studies reinforces these comparative observations. The Mamdani fuzzy PI controller implemented for liquid-level regulation demonstrated a faster settling time and a greater disturbance rejection than both operator-tuned and auto-tuned PID controllers. Likewise, the fuzzy–Smith compensator applied to induction motor control in a networked environment outperformed classical PID under time-delay and packet-latency conditions. Adaptive neural control using the Brandt–Lin algorithm further showed superior transient response and steady-state accuracy compared with PID benchmarking. Together, these results confirm that intelligent controllers offer measurable advantages in robustness, adaptability, and performance when compared directly to conventional techniques.
4.2. Limitations and Threats to Validity
This review presents several limitations and threats to validity that should be considered when interpreting its findings. First, the search strategy relied on a specific set of digital libraries and indexing services; relevant contributions indexed exclusively in other databases or domain-specific repositories may have been omitted. Second, only articles written in English were considered, which introduces a potential language bias and may underrepresent research produced by non-English-speaking communities.
Third, the search queries were formulated around specific combinations of terms related to intelligent controllers, artificial intelligence, adaptation, and optimization. Although the Boolean strings were iteratively refined and piloted, studies that employ substantially different terminology might not have been captured. Fourth, study selection and data extraction, while conducted through double screening with a substantial inter-rater agreement (κ = 0.87), inevitably involve a degree of subjectivity, particularly when assigning each paper to a dominant category within the proposed taxonomy and when handling multi-label cases.
Finally, the review is restricted to peer-reviewed literature and includes four experimental studies authored by the present research group, which may introduce mild publication and self-citation bias. These limitations do not invalidate the overall trends and gaps identified in this work, but they indicate that the results should be interpreted as a structured yet inherently partial view of the rapidly evolving field of AI-based intelligent control systems.
4.3. Validation Gap and Domain-Specific Practical Outcomes
Although AI-based controllers frequently report improvements in accuracy, overshoot reduction, stability, and disturbance rejection, the present mapping shows that the evidence base is still heavily dominated by simulation studies. This imbalance limits the generalizability of results to industrial environments, where measurement noise, actuator nonlinearities, sensor degradation, saturation, and dynamic disturbances are pervasive. For instance, fuzzy-based MPPT controllers routinely achieve faster convergence under irradiance changes in simulation, yet only a small subset of works extends the analysis to real-field variability or environmental noise in grid-connected photovoltaic plants. Similar patterns appear in other domains, where promising control strategies are often validated only under idealized operating conditions.
The mapping also highlights meaningful differences across application domains:
- Renewable energy systems: AI-based controllers improve MPPT tracking, generator stability, and pitch control, but scalability to utility scale plants remains insufficiently validated, and long-term field campaigns are scarce.
- Robotics and autonomous systems: hybrid and learning-based controllers enhance trajectory tracking and disturbance rejection, yet real-time feasibility is often constrained by computational cost and hardware limitations.
- Agriculture and environmental systems: fuzzy and ANFIS controllers provide robust performance under uncertainty; however, few studies quantify energy efficiency, reliability, or maintenance gains with respect to PID baselines in real operating conditions.
- Industrial process control: MPC and hybrid neural controllers demonstrate strong improvements in setpoint tracking and constraint handling, but deployment still requires lightweight implementations and hardware-friendly computation strategies.
By contrast, the relatively small set of experimentally validated studies including adaptive fuzzy PID controllers in oil pipelines, neuro-fuzzy drives for induction motors, adaptive MPC in CSTR reactors, and the four implementations on Festo MPS PA Compact Workstations reviewed here provides valuable evidence that simulation-to-hardware transfer is feasible when robustness to modeling errors, network-induced delays, and actuator limitations is explicitly addressed in the controller design. These works cover level and pressure regulation, motor speed control, and system identification in industrial training plants, and consistently report faster stabilization, lower tracking error, and improved disturbance rejection compared with operator-tuned or auto-tuned PID controllers. They further show that fuzzy PI controllers and ANN-based identification pipelines can enhance robustness in liquid-level processes, adaptive neural controllers can shorten recovery times in pressure regulation, and fuzzy–Smith compensators can effectively mitigate time-delay effects in networked induction-motor drives.
Taken together, the domain-specific analysis and the limited but positive experimental evidence highlight an urgent need for standardized benchmarks and reporting practices that link simulations, hardware-in-the-loop tests, and full plant trials. Future research should systematically document operating conditions, disturbance profiles, implementation details, and computational budgets, enable meaningful cross-domain comparisons, and accelerate the transition of AI-based intelligent controllers from laboratory prototypes to reliable industrial solutions.
4.4. Optimization and Reproducibility Challenges
A critical limitation identified across optimization-based controllers is the absence of reproducible hyperparameter specifications. Many primary studies do not report population sizes, inertia weights, crossover probabilities, search agent counts, or termination criteria for algorithms such as PSO, GA, DE, and GWO. This omission hinders replicability, prevents fair comparisons between optimization strategies, and restricts industrial adoption. While recent hybrid optimizers (OOA, ZOA, ARO, hGWO-CS, NewBAT, MPA) address some limitations of earlier algorithms through improved convergence and exploration–exploitation balance, their performance cannot be independently verified without standardized reporting of hyperparameter settings and computational budget.
The identification results using NARX and GADALINE neural networks highlight additional reproducibility concerns in system identification. The NARX network required careful configuration of time delays and neuron architecture, while the GADALINE estimator depended on learning-rate tuning and momentum scheduling. Although both methods surpassed classical Laplace identification, neither study reports exhaustive hyperparameter settings, training iterations, or computational budgets reflecting a broader reproducibility gap also noted in optimization-based controllers. These observations support the need for standardized reporting protocols that document learning parameters, model complexity, and convergence metrics.
4.5. Integration of Emerging Techniques
Recent contributions increasingly explore DRL, including TD3-, DDPG-, and CNN–LSTM-based adaptive controllers. These techniques significantly enhance adaptability and real-time decision making, offering clear advantages in highly nonlinear or time-varying environments such as HVAC MIMO systems and autonomous vehicles. However, DRL methods introduce new challenges, including sample inefficiency, training instability, safety constraints, and substantial computational requirements factors often overlooked in simulation-based studies. Integrating DRL with classical and fuzzy control structures may help mitigate these issues by leveraging prior knowledge and constraint-aware control laws.
Recent contributions show increasing convergence between intelligent identification and intelligent control. The combination of ANN-based system identification (NARX and GADALINE) with PI control tuning, as demonstrated in one of the reviewed studies, exemplifies the emerging trend of tightly coupling modeling and control. This integration enables data-driven prediction, online learning, and improved adaptation in a unified pipeline. Similarly, adaptive neural controllers leveraging the Brandt–Lin algorithm represent an intermediate step between classical adaptive schemes and deep reinforcement learning, enabling real-time learning without pretraining.
4.6. Reproducibility Issues in Parameter Optimization Methodologies
A critical issue identified across the analyzed literature is the lack of reproducible detail regarding the configuration of meta-heuristic algorithms used for controller parameter optimization. Although numerous studies report the use of optimization techniques such as PSO, GA, GWO, GSA/CGSA, ABC, DE, WOA, GOA, and others, the vast majority do not provide the essential hyperparameter settings required to replicate their optimization processes.
In most cases, the articles mentioned only the algorithm name but omitted key configuration parameters, including population size or number of agents, which fundamentally determines the exploration capability of the algorithm.
Total number of iterations or generations directly affects convergence behaviors.
Internal coefficients are as follows:
- PSO inertia weight and cognitive/social parameters (w, c1, c2);
- GA crossover and mutation probabilities and elite size;
- GWO coefficients (a, A, C);
- GSA/CGSA gravitational constants, decay factors, and chaotic maps;
- ABC abandonment limits and employed/onlooker bee counts;
- GOA adaptive coefficient c.
Parameter search bounds for controller gains (Kp, Ki, Kd), fractional orders, or fuzzy scaling factors.
Additionally, only a small subset of studies specify the following:
- Whether a random seed was used to ensure experimental reproducibility;
- The software platform and version (e.g., MATLAB/Simulink, toolboxes, hardware);
- Stopping criteria, constraint-handling strategies, or performance thresholds;
- Any sensitivity analysis that assesses how hyperparameter changes influence the outcome.
This lack of methodological transparency makes it difficult to achieve the following:
- Replicate published tuning results;
- Compare the effectiveness of different optimization algorithms under consistent conditions;
- Validate the robustness of the control strategies reported in the literature.
Consequently, two studies may claim to use the “same algorithm” (e.g., PSO or GA), while their actual optimization processes and therefore their results differ substantially.
It is therefore recommended that future research adopt more rigorous reporting practices, including detailed hyperparameter tables, explicit description of performance indices and stopping criteria, and, where appropriate, pseudocode or supplementary reproducibility checklists, in line with current international best-practice standards for reproducible computational research.
4.7. Synthesis of Findings
Overall, intelligent control research demonstrates significant progress in addressing nonlinearities, uncertainties, and multi-objective requirements. However, simulation-heavy evaluations, incomplete reporting, high computational burden, and a lack of standardized experimental protocols limit the field’s reproducibility and industrial applicability. Emerging approaches including hybrid learning–optimization frameworks, DRL-based adaptive controllers, and real-time surrogate modeling show promise but require further benchmarking under operational constraints.
Synthesizing across the four experimental contributions, several consistent patterns emerge, i.e., (1) fuzzy-based controllers tend to outperform PID in disturbance-rich nonlinear processes; (2) adaptive neural controllers provide superior transient performance and accuracy, particularly when online learning is enabled; (3) ANN-based identification pipelines significantly enhance controller performance compared with classical identification; and (4) Smith-predictor-based structures benefit substantially from fuzzy compensation to handle time delays. These findings align with the broader literature indicating that hybrid AI-based controllers combine interpretability, learning, and robustness in ways unattainable for traditional methods.
4.8. Implications and Recommendations
To accelerate practical adoption, future research should prioritize the following:
(1) Standardized reporting of optimization hyperparameters and computational budgets.
(2) Experimental validation under diverse and realistic industrial conditions.
(3) Development of lightweight and embedded-oriented AI controllers.
(4) Systematic comparison of controllers across common datasets, benchmarks, and disturbance profiles.
(5) Scalable hybrid architectures combining interpretability and learning efficiency.
(6) Safety-aware DRL and constraint-integrated learning methods.
Building on these priorities, the results of the four reviewed studies suggest that future intelligent controllers should integrate real-time learning mechanisms, simplified and lightweight ANN architectures, and hybrid compensatory structures capable of handling modeling errors, disturbances, and network-induced delays. Models such as GADALINE provide a promising path for embedded implementation due to their low computational demand, while delay-aware intelligent architecture such as fuzzy–Smith compensators demonstrate the need for controllers that combine fuzzy reasoning with predictive capabilities. To maximize reproducibility and industrial applicability, future publications should standardize hyperparameter reporting, dataset availability, tuning methodology, and computational specifications. This consolidated perspective provides a coherent basis for guiding the development of next-generation intelligent control systems capable of achieving robustness, transparency, adaptability, and real-time performance in modern industrial environments.
This review provides a consolidated basis for identifying promising research directions and guiding the development of next-generation intelligent control systems capable of fulfilling industrial requirements for robustness, transparency, and real-time performance.
5. Conclusions
5.1. Main Findings
This PRISMA-2020-aligned systematic mapping analyzed 188 peer-reviewed studies published between 2000 and 15 January 2025 concerning the integration of artificial intelligence (AI) into intelligent control systems. Through a transparent methodology comprising database-specific Boolean queries, deduplication procedures, predefined inclusion–exclusion criteria, dual independent screening, and inter-rater agreement (κ = 0.87), this review provides a reproducible and comprehensive mapping of the field. The analysis identified three dominant contribution areas: (i) control model strategies, (ii) parameter optimization techniques, and (iii) adaptability mechanisms, which collectively reflect the evolution of AI-enabled control toward improved robustness, efficiency, and autonomy.
Hybrid intelligent controllers particularly neuro-fuzzy architectures, ANN-supported PID/MPC designs, and fuzzy–predictive hybrids consistently demonstrate enhanced tracking accuracy, disturbance rejection, and robustness in nonlinear and uncertain systems. Metaheuristic optimization methods remain central for automated tuning, with classical algorithms (PSO, GA, GWO, DE) now complemented by newer hybrid and nature-inspired variants (OOA, ZOA, ARO, NewBAT, hGWO-CS), offering superior convergence behavior. Adaptive controllers, including ANFIS, adaptive MPC, and deep reinforcement learning (DRL) methods such as TD3 and DDPG, further extend adaptability under time-varying conditions.
5.2. Key Trends in Controller Development
The systematic mapping highlights several trends shaping the current and future landscape of intelligent control:
- Hybridization as a dominant paradigm:
- Increasing integration of fuzzy logic, neural networks, predictive control, and evolutionary optimization to leverage complementary strengths.
- 2.
- Integration of deep learning:
- DRL and neural surrogate models are increasingly adopted to improve prediction, adaptation, and autonomous decision making.
- 3.
- Advances in optimization:
- Research is shifting toward hybrid and multi-strategy metaheuristics capable of balancing exploration–exploitation more effectively.
- 4.
- Real-time feasibility and lightweight designs:
- Development of reduced-complexity rule bases, compact neural networks, and embedded-friendly MPC variants to meet industrial real-time constraints.
- 5.
- Multi-objective control design:
- Controllers are now expected to jointly optimize stability, accuracy, energy efficiency, robustness, and computational cost.
- 6.
- Industrial orientation:
- Growing use cases in renewable energy systems, autonomous platforms, process automation, and precision agriculture.
- 7.
- Hybridization of control strategies:
- Controllers increasingly combine fuzzy logic, neural networks, predictive control, and classical methods (e.g., fuzzy–Smith, ANN–PID, neuro-fuzzy).
- 8.
- Movement toward real-time adaptive learning:
- Adaptive neural controllers capable of online learning (e.g., Brandt–Lin ANN) reflect a shift from static to dynamic adaptation.
- 9.
- Integration of identification + control:
- The use of ANN-based identification (NARX, GADALINE) as a basis for control tuning highlights a trend toward tightly coupled modeling–control loops.
- 10.
- Delay-aware intelligent control in NCS:
- Fuzzy–Smith compensators demonstrate the emerging need for intelligent methods capable of handling network delays and distributed industrial systems.
- 11.
- Low-complexity, embedded-friendly AI models:
- GADALINE neural networks exemplify the trend toward lighter architectures suitable for deployment in PLCs, edge devices, and industrial controllers.
- 12.
- Shift from pure simulation to real-plant validation:
- All four contributions provide real-world tests, aligning with an increasingly recognized need for validation beyond MATLAB/Simulink environments.
5.3. Identified Research Gaps
This review reveals several structural gaps that currently limit the industrial deployment and scientific reproducibility of AI-based controllers:
- Validation gap: evidence is still dominated by simulations and short laboratory trials, with relatively few hardware-in-the-loop or plant-scale experiments under realistic noise, disturbances, and hardware nonlinearities.
- Reproducibility gap in optimization and learning pipelines: many studies incompletely report optimization and learning settings (hyperparameters, learning rates, stopping criteria, random seeds, computational budget, and software/hardware stack), making exact replication and fair comparison difficult.
- Lack of standardized benchmarks and metrics: there is no widely accepted set of datasets, disturbance profiles, or performance indices for intelligent controllers, which prevents rigorous cross-study comparisons and meta-analyses.
- Scalability and complexity limitations: most works focus on SISO or small-scale laboratory systems; there is limited analysis of scalability to MIMO plants, microgrids, large-scale industrial processes, or multi-agent settings, and little discussion of the complexity deploy ability trade-off in embedded or PLC-based implementations.
- Safety, robustness, and interpretability deficits: safety constraints, formal stability guarantees, and explainability are only sporadically considered, particularly in DRL-based and deep architectures intended for safety-critical or regulated domains.
- Limited delay- and network-aware design: few contributions explicitly analyze robustness to communication delays, jitter, packet loss, or cyber–physical faults in networked control systems.
- Insufficient characterization of computational cost and real-time feasibility: reporting of sampling times, execution times, memory footprint, and hardware requirements is often superficial, hindering assessment of industrial feasibility.
- Underdeveloped hybrid intelligent model-based frameworks: only a small fraction of works systematically integrate learning-based components (ANN, fuzzy, DRL) with first-principles controllers (e.g., MPC, robust control) within unified identification–control pipelines.
5.4. Contribution of This Study
This review makes the following contributions:
- To the best of our knowledge, few prior reviews have applied PRISMA-2020 to systematically map AI-based intelligent control systems, covering 188 high-quality peer-reviewed studies with a fully reproducible methodology.
- It introduces a unified three-dimensional taxonomy that organizes contributions across control-model structures, optimization strategies, and adaptability mechanisms, explicitly integrating recent developments in deep reinforcement learning and hybrid metaheuristic-based designs.
- It offers a comparative, application-oriented synthesis that highlights trade-offs among robustness, computational cost, interpretability, and real-time feasibility, helping practitioners and researchers to select suitable intelligent controller architecture for specific constraints and industrial requirements.
- It identifies domain-specific outcomes in renewable energy systems, robotics, agriculture, and industrial process control, clarifying where AI-based intelligent controllers have already demonstrated tangible performance gains and where evidence remains mostly simulation-based.
- It systematically highlights major reproducibility barriers such as incomplete reporting of hyperparameters, training protocols, datasets, and computational cost and proposes methodological improvements and reporting guidelines to enhance transparency, comparability, and replicability.
- It synthesizes key technological trends and open research gaps, outlining the evolution of intelligent control and its projected trajectory toward next-generation industrial systems that combine learning, adaptation, and safety-aware decision making.
- It integrates evidence from four real-plant experimental implementations (a Mamdani fuzzy PI level controller, an adaptive neural pressure controller based on the Brandt–Lin algorithm, a fuzzy–Smith compensator for induction motors over networked control systems, and an ANN-based NARX/GADALINE identification scheme), providing concrete case examples that link the high-level mapping with practical industrial deployment of AI-based intelligent controllers.
5.5. Future Work
This review suggests several directions for addressing the above gaps and advancing AI-based intelligent controllers:
- Standardized evaluation frameworks and benchmarks: develop shared benchmark datasets, disturbance scenarios, and hardware-in-the-loop (HIL) protocols, together with agreed-upon performance metrics, to enable fair and reproducible comparison of intelligent controllers in both simulation and experimental settings.
- Reproducibility-oriented reporting and open artifacts: promote explicit reporting of optimization and learning hyperparameters, training procedures, computational budgets, software/hardware platforms, and controller architectures, complemented by open-source implementations and standardized reporting templates.
- Lightweight and embedded AI controllers: design interpretable fuzzy–neural hybrids, compressed neural networks, and efficient MPC formulations that can be executed on PLCs and edge devices under strict real-time and memory constraints, including systematic evaluation of computational cost and embedded feasibility.
- Safety-aware, robust, and hybrid DRL controllers: advance deep reinforcement learning and adaptive schemes with explicit safety and stability guarantees, constraint handling, and safe exploration mechanisms, while integrating DRL agents with fuzzy, ANN, MPC, or robust control structures to balance performance, interpretability, and sample efficiency, including delay-aware and network-robust architectures for Industry 4.0 environments.
- Scalable and distributed control architectures: develop distributed, hierarchical, and multi-agent intelligent controllers for large-scale energy systems, complex industrial automation networks, and cooperative robotics, with explicit treatment of communication constraints, coordination strategies, and fault tolerance.
- Hybrid AI–model-based identification control pipelines: tighten the integration between first-principles models and data-driven learning for both identification and control, aiming at greater transparency, robustness, and extrapolation capability. This includes hybrid identification control pipelines where learned models (e.g., ANN, fuzzy, or surrogate models) are used to initialize, adapt, or supervise model-based controllers online.
- Advanced adaptive learning and identification: extend adaptive learning methods such as Brandt–Lin and GADALINE to multivariable, nonlinear, and strongly coupled processes, while exploring online learning, drift compensation, and cross-domain adaptation to maintain performance over long-term operation.
- Experimental validation and long-term industrial studies: move beyond short-term pilot tests by conducting long-duration experiments on operational industrial plants, systematically documenting reliability, maintainability, and lifecycle performance, and closing the gap between simulation-based results and full-scale industrial adoption.
Author Contributions
Conceptualization, E.R.F.M. and D.P.-R.; methodology, E.R.F.M.; software, E.R.F.M.; validation, E.R.F.M. and D.P.-R.; formal analysis, E.R.F.M. and D.P.-R.; investigation, E.R.F.M.; resources, E.R.F.M.; data curation, E.R.F.M.; writing—original draft preparation, E.R.F.M.; writing—review and editing, E.R.F.M. and D.P.-R.; visualization, E.R.F.M.; supervision, E.R.F.M.; project administration, E.R.F.M.; funding acquisition, not applicable. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. All data supporting the findings of this study are available within the cited literature.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
Only acronyms that are used in the main text are listed below. Each acronym is assigned to a single, non-ambiguous meaning.
| AANN | Adaptive Artificial Neural Network |
| ABC | Artificial Bee Colony |
| AC | Adaptive Control |
| ACA | Ant Colony Algorithm |
| ACO | Ant Colony Optimization |
| ACS | Automatic Control System |
| ACSA | Adaptive Cuckoo Search Algorithm |
| AFL | Adaptive Fuzzy Logic |
| AFSMC | Adaptive Fuzzy Slider Mode Controller |
| AGA | Adaptive Genetic Algorithm |
| AIEM-DDPG | Ambient Intelligence Exploration Multidelay Deep Deterministic Policy Gradient |
| AIGA | Advanced Intelligent Genetic Algorithm |
| ALR | Adaptive Learning Rate |
| AMPC | Adaptive Model Predictive Control |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| ANNC | Artificial Neural Network Controller |
| APID | Adaptive PID |
| APSO | Adaptive Particle Swarm Optimization |
| ARO | Artificial Rabbit Optimization |
| A-WOA | Advanced Whale Optimization Algorithm |
| BCA | Bee Colony Algorithm |
| BFOA | Bacterial Foraging Optimization Algorithm |
| CGSA | Chaotic Gravitational Search Algorithm |
| CIO | Cohort Intelligence Optimization |
| CNN | Convolutional Neural Network |
| COA | Cuckoo optimization Algorithm |
| COOA | Coot Optimization Algorithm |
| CS | Cuckoo Search |
| DDPG | Deep Deterministic Policy Gradient |
| DE | Differential Evolution |
| DEA | Differential Evolution Algorithm |
| DLNN | Deep Learning Neural Network |
| DNN | Deep Neural Network |
| DRL | Deep Reinforcement Learning |
| EA | Evolutionary Algorithms |
| EOM | Extreme Optimization Method |
| E-QILC | Estimation-based Quadratic ILC |
| ES | Evolutionary Strategy |
| FA | Firefly Algorithm |
| FAO | Firefly Algorithm Optimized |
| FFOPI | Fuzzy Fractional Order PI |
| FL | Fuzzy Logic |
| FLC | Fuzzy Logic Controller |
| FLMFC | Fuzzy Cerebellar Model with Functional Link Network |
| FLSC | Fuzzy Logic Smart Controller |
| FOFMO | Fractional Order Fish Migration Optimization Algorithm |
| FOPID | Fractional Order PID |
| FPI | Feedback PI |
| FSMC | Fuzzy Sliding Mode Control |
| FSMC | Fuzzy-based Sliding Mode |
| GA | Genetic Algorithm |
| GADALINE | Generalized ADAptive LINear Element |
| GM | Gray Model |
| GOA | Grasshopper Optimization Algorithm |
| GP | Genetic Programming |
| GPSOFC | Fuzzy Self-Organizing with Gray Prediction |
| GSA | Gravitational Search Algorithm |
| GSA-CW | Enhanced Gravitational Search |
| GWO | Gray Wolf Optimizer |
| HAOAGTO | Arithmetic Optimization Algorithm and Artificial Gorilla Troop’s Optimization |
| HBCC | Hysteresis Band Current Control |
| HFFC | Hybrid Fuse–Fuse Controller |
| HICA | Hybrid Imperialist Competitive Algorithm |
| HIL | Hardware-In-the-Loop |
| HS | Harmony Search |
| IACO | Improved Ant Colony Optimization |
| ICDBO | Improved Chebyshev Dung Beetle Optimizer |
| IFOC | Indirect Field-Orientated Control |
| ILC | Iterative Learning Control |
| ILO | Iterative Learning Observer |
| IMC | Internal Model Control |
| INNEM | Neural Inverse Model |
| IT2FLS | Interval Type-2 Fuzzy Logic System |
| IT2FPID | Range-2 Fuzzy PID |
| IT2FPIDC | Type-2 Fuzzy PID Interval Controller |
| ITFOELM | External online learning without initial training |
| K-ILC | Kalman-based ILC |
| KM | Karnik–Mendel |
| LFC | Load Frequency Control |
| LFL | Learning Feedback Linearization |
| LGA | Lion Group Genetic Algorithm |
| LI-D-FC | Fuzzy with Linear Interpolation |
| LM | Levenberg–Marquardt Algorithm |
| LMAF | Levenberg–Marquardt Activation Function |
| LSE | Least Squares Estimation |
| LSO | Least Squares Optimization |
| LSTM | Long Short-Term Memory Network |
| MDE | Modified Differential Evolution |
| ML | Machine Learning |
| MMAC | Multi-Model Adaptive Control |
| MO | Metaheuristic Optimization |
| MOA | Mayfly Optimization Algorithm |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| MPA | Marine Predator Algorithm |
| MPC | Model Predictive Control |
| MRA | Model Reference Adaptive |
| MT | Tunable Model |
| NARMA | Nonlinear Auto-Regressive Moving Average model |
| NARX | Nonlinear Autoregressive eXogenous |
| NFC | Neuro-Fuzzy Controller |
| NNPC | Predictive-based Neural Networks |
| NOA | Nutcracker Optimization Algorithm |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| OFL | Optimized Fuzzy Logic |
| OOA | Osprey Optimization Algorithm |
| PANN | Propagation artificial neural networks |
| PC | Predictive Control |
| PI | Proportional–Integral Controller |
| PID | Proportional–Integral–Derivative Controller |
| PMC | Predictive Model Controller |
| PSMC | Predictive Sliding Mode Control |
| PSO | Particle Swarm Optimization |
| PTP ILMPC | Point-to-Point Iterative Learning of Predictive Control |
| QILC | Quadratic Iterative Learning Control |
| QOHS | Quasi-Oppositional Harmony Search |
| QP | Quadratic Programming |
| RA | Robust adaptive |
| RBFNN | Radial Basis Function Neural Network |
| reMPC | Robust Economic Model Predictive Control |
| RFCMAC | Recurrent Fuzzy CMAC Network |
| RL | Reinforcement Learning |
| RL-DLNN | Reinforcement Learning–Deep Learning Neural Network |
| RLS | Recursive Least Square |
| SaDE | Self-Adaptive Differential Evolution |
| SCA | Sine Cosine Algorithm |
| SCFNN | Self-Constructing Fuzzy Neural Network Controller |
| SF-FLC | Scaling Factor-based Fuzzy Logic Controller |
| SFL | Standard Fuzzy Logic |
| SIA | Swarm Intelligence Algorithm |
| SLPMM | Sequential Linear Programming Matrix Method |
| SMC | Sliding Mode Control |
| SOA | Seagull Optimization Algorithm |
| SOS | Symbiotic Organism Search |
| SSA | Slap Swarm Algorithm |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| T2FNS | Type-2 Fuzzy Neural System |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient |
| TOSMC | Third Order Sliding Mode Control |
| T-S | Takagi–Sugeno Fuzzy Model |
| VS-FWNN | Fuzzy Wave Neural Network |
| WOA | Whale Optimization Algorithm |
| ZOA | Zebra Optimization Algorithm |
Appendix A. Detailed Classification of Control Models

Table A1.
Results of the classification of the analyzed articles according to the contribution of control models (source: own elaboration based on systematic mapping).
Table A1.
Results of the classification of the analyzed articles according to the contribution of control models (source: own elaboration based on systematic mapping).
| ID | Year | Control Structures | Set Strategies | Algorithms | Ref. |
|---|---|---|---|---|---|
| 1 | 2014 | ANNC | Supervised and unsupervised | Kohonen and the Gradient Descent Method | [32] |
| 2 | 2016 | IMC-PID | Set-point Change Test and FOPDT | LSM | [59] |
| 3 | 2015 | FLC | Linear square diffuse base regulator (FLC-LQR) | Incremental State Model T-S | [65] |
| 4 | 2016 | PID, FLC, PID–FLC, Control with Thresholds | PID incremental, FLC Mamdani | FL | [66] |
| 5 | 2018 | Model-Based Predictive Control, MPC | Predictive Control | Predictive algorithm | [75] |
| 6 | 2016 | Predictive control based on a robust economic model, REMPC | Predictive control using stochastic information | Predictive algorithm | [76] |
| 7 | 2014 | Optimal ILC based on standards, Norm-optimal ILC | Quadratic ILC, Estimation-based QILC, Kalman-based ILC | Optimal iterative learning | [77] |
| 8 | 2015 | PI | Identification of type gray box and black box | Parametric and Structural Evolutionary Algorithms | [42] |
| 9 | 2006 | Widespread IP | IL and ANN | LMI and RBFNN | [155] |
| 10 | 2017 | ANN feedforward | ANN | GE and GA | [44] |
| 11 | 2018 | VS-FWNN | ANN | Gradient descent with adaptive rates | [33] |
| 12 | 2002 | Programmed Gain Control and Fuzzy PI | FL | MOGA | [46] |
| 13 | 2017 | PID and PI Cascading | Cascade control | GA | [45] |
| 14 | 2001 | H infinity | Designing a specified structured | GA | [43] |
| 15 | 2004 | H2 | Feedback control of states and outputs, and control with a fixed structure | SLPMM | [156] |
| 16 | 2018 | MLC, NN | CNN | RBF | [55] |
| 17 | 2016 | Predictive ILC, PILC | IL | Quadratic Cost Function | [157] |
| 18 | 2018 | PTP ILMPC | IL and MPC | ILO and QP | [51] |
| 19 | 2011 | ILC PID | PID-ILC | ILC | [58] |
| 20 | 2014 | Robust ILC | Feedback + ILC | ILC | [78] |
| 21 | 2017 | MPC | MPC | SCESO and QP | [50] |
| 22 | 2015 | NFSS-MPC | Predictive Control | Gradient descent with backpropagation | [52] |
| 23 | 2018 | MPC | INNEM | RBFNN | [53] |
| 24 | 2018 | DNN | LSTM, ANN, and LSTMSNN | NNB | [54] |
| 25 | 2018 | RMPC | MPC-ANN | NNF and MEM | [79] |
| 26 | 2008 | RFCMAC | CMAC | SVR-PSO | [158] |
| 27 | 2016 | Diffuse PID | PID with FL with Mamdani structure | Euler–Lagrange and FL | [34] |
| 28 | 2015 | VOFFLC | Fuzzy variable-order fractional PID with Mamdani structure | Nelder–Mead | [35] |
| 29 | 2004 | PD-ELC | PD | ELC | [159] |
| 30 | 2008 | FC7, ANFIS, ANN | FC7, ANFIS with Sugeno structure, ANN | FL, Gradient Down and Least Squares, backpropagation | [160] |
| 31 | 2018 | ANN | PI-ANN | LM | [36] |
| 32 | 2016 | ANN | NARMA and PI | LFL | [80] |
| 33 | 2014 | IT2F-PID | PID, IT2-FLS | KM and the average of the extremes | [29] |
| 34 | 2018 | FPID and FO-FPID | FOPID and Fuzzy Logic | PSO and DE | [47] |
| 35 | 2019 | Deadbeat Fuzzy Logic Controller | Fuzzy logic | FL | [161] |
| 36 | 2017 | FLMFC | FLC | PI Learning Algorithm | [81] |
| 37 | 2019 | FSMC | SMC | HICA | [40] |
| 38 | 2019 | FNNC | FLC and ANNC | MOPSO | 62 |
| 39 | 2019 | SCFNN | FLC and ANNC | ALR and Lyapunov Stability | [62] |
| 40 | 2017 | FLSC | FLC and MIMO | FL | [63] |
| 41 | 2016 | Predictive FLC | FLC and ANNC | MLP, ART-2, and PNN | [57] |
| 42 | 2019 | FLC-MPPT | FLC | FL Mamdani | [61] |
| 43 | 2017 | T2FNS | FLC and ANNC | Gradient Descent | [67] |
| 44 | 2017 | SF-FLC | FLC | Algorithm QOHS | [41] |
| 45 | 2014 | ANFIS | FLC and Adaptive ANNC | LSE and Backpropagation | [31] |
| 46 | 2014 | FLC | FLC | FL, like Mamdani | [68] |
| 47 | 2015 | Online ANFIS supervised by FL PID | PID, FLC, and Adaptive ANNC | Fuzzy ART, Backpropagation, and RLS | [30] |
| 48 | 2017 | IT2FPIDC | FL and PID Cascading | CS | [37] |
| 49 | 2011 | FLC | FL | Fuzzy logic, like Mamdani | [39] |
| 50 | 2017 | NFC | FL and NN | Fuzzy logic and adaptive learning | [162] |
| 51 | 2017 | ANNC | ANNC | LM | [82] |
| 52 | 2017 | FLC | FL | FL | [69] |
| 53 | 2015 | HFFC | FL | FL | [163] |
| 54 | 2013 | FLC | FL | Adaptive algorithm | [70] |
| 55 | 2017 | FLC-PID | FL and PID | GSA-CW | [164] |
| 56 | 2013 | GPSOFC | FL | GM | [165] |
| 57 | 2013 | LI-D-FC | FL | FL | [64] |
| 58 | 2018 | FLC | FL | FL, like Mamdani | [71] |
| 59 | 2015 | NNPC + FLC P | ANN and FL | LM and T-S type P | [56] |
| 60 | 2019 | FLC | FL | Fuzzy Mamdani-like logic based on a new β (beta) parameter | [72] |
| 61 | 2017 | IT2FPID | PID and FL | GA | [38] |
| 62 | 2024 | ANN-PMC | ANN | LMAF and interaction adaptive | [166] |
| 63 | 2023 | Two-level FNNC | FL and ANN | Improved GA | [48] |
| 64 | 2021 | ANFIS | FL and ANN | Mayfly optimization algorithm, MOA | [49] |
| 65 | 2025 | RL-DLNN | TD3 Agent | Deep Learning Neural Network, DLNN | [83] |
| 66 | 2024 | Fuzzy PI | Five-Member Fuzzy | Mamdani-type | [73] |
| 67 | 2024 | ANN | Adaptive | Brandt–Lin adaptive interaction algorithm | [84] |
| 68 | 2025 | FLC | Seven-Member Fuzzy + Smith Predictor | Mamdani-type | [74] |
Appendix B. Optimization Contribution Details

Table A2.
Results of the article classification according to the optimization contribution (source: own elaboration based on systematic mapping).
Table A2.
Results of the article classification according to the optimization contribution (source: own elaboration based on systematic mapping).
| ID | Year | Control Structures | Optimization Techniques | Algorithms | Ref. |
|---|---|---|---|---|---|
| 1 | 2005 | FLC | FLC Mamdani | GA | [89] |
| 2 | 2017 | PID | GA Online Learning | GA | [90] |
| 3 | 2013 | PID | Discrete FRIT method | ANN | [85] |
| 4 | 2008 | PID | PSO-tuned PID controller | PSO | [98] |
| 5 | 2018 | PID | FLC | Adaptive Fit | [108] |
| 6 | 2006 | Hydra Control Structure | Geno Hydra Hybrid | GA | [96] |
| 7 | 2015 | PID | PID using a gravitational search algorithm | GSA | [103] |
| 8 | 2018 | ANN | Control with advancing neural networks | Feedback Laws | [87] |
| 9 | 2016 | FLC | Adjustment of dynamic parameter | Adaptive bee colony algorithm | [107] |
| 10 | 2016 | PID | Optimized PID with PSO | Objective Function | [118] |
| 11 | 2018 | PID | Optimized PID with APFC | EO | [88] |
| 12 | 2009 | PID | PID with GA base rules | GA | [91] |
| 13 | 2012 | MOEA | MOEA-CCG | CCG | [92] |
| 14 | 2014 | FOPID | GA | [93] | |
| 15 | 2005 | NMPC | Numerical Method SVM | SVM | [117] |
| 16 | 2013 | F-PID | F-PID | FL Predictor | [109] |
| 17 | 2008 | Approximate Model | Numerical Method | SVM | [86] |
| 18 | 2015 | PID-based structures | Optimized Classic Control | EA | [94] |
| 19 | 2013 | SEA Method | Numerical Method | Taxi-Cab | [97] |
| 20 | 2019 | FSMC-based control | PSO-GSA Optimization | PSO-GSA | [116] |
| 21 | 2014 | FLC | Search Algorithm Optimization | CSA | [104] |
| 22 | 2016 | FLC | Vehicle-to-Grid (V2G) | Membership Features and Fuzzy Rules | [113] |
| 23 | 2017 | MTEJ Controller | Fuzzily Tuning with an Additional Integrator | Fuzzy Coefficient Adjustment | [110] |
| 24 | 2013 | FLC | Optimization by an EA | Adjustment Approach Based on EA | [111] |
| 25 | 2017 | PID | Tuned by ANN | ANN | [112] |
| 26 | 2018 | PID Controller | FL | Improved GWO | [102] |
| 27 | 2012 | PID Controller | FL | PSO | [101] |
| 28 | 2018 | PID and FLC | Hybrid Algorithm | Hybrid optimization algorithm | [115] |
| 29 | 2016 | FLC | EA | DE | [105] |
| 30 | 2015 | FLC | Optimized by the SA | PSO | [99] |
| 31 | 2019 | Automatic Generation Control with FL | Hybrid Algorithm | GWO-SCA hyper algorithm | [114] |
| 32 | 2016 | FLC | Fuzzy Rule Tuning | GA | [95] |
| 33 | 2018 | T-S Control | Distributed Parallel Compensation Technique | PSO | [100] |
| 34 | 2016 | PID Controller | FL | FA | [106] |
| 35 | 2019 | PID | ACS tuning via algebraic methods and nonlinear programming | MT | [167] |
| 36 | 2024 | PID | AVR | ARO | [168] |
| 37 | 2024 | NN, NN-PIDD, ELNN-PID | NN, PID | COOA | [169] |
| 38 | 2025 | PI | FPI | GA | [170] |
| 39 | 2024 | FLC | FL | GA | [171] |
| 40 | 2021 | Controller Fuzzy type-1 | FL | GWO | [172] |
| 41 | 2025 | FL-SMC | FL | hGWO-CS | [173] |
| 42 | 2022 | TOSMC | IFOC | GWO | [174] |
| 43 | 2024 | PID | PID | PSO, I-GWO, and NOA | [175] |
| 44 | 2020 | FL | T-S | AIGA | [176] |
| 45 | 2023 | PID | AVR | ZOA-OOA | [177] |
| 46 | 2020 | FL PD | PID | ABC | [178] |
| 47 | 2019 | FLPID | FPID | IACO | [179] |
| 48 | 2021 | PID | PID | DRL | [180] |
| 49 | 2024 | FOPID | PID | ACO | [181] |
| 50 | 2022 | PSMC | PSMC | GWO | [182] |
| 51 | 2023 | FL PID | PID | A-WOA | [183] |
| 52 | 2022 | PID | PID Cascaded | CIO | [184] |
| 53 | 2020 | PID | AGC | MDE | [185] |
| 54 | 2022 | FOPID | OPID | ACO | [186] |
| 55 | 2021 | PID | PID | PSO | [187] |
| 56 | 2021 | LFC-PI | PI | FAO | [188] |
| 57 | 2020 | PID | fuzzy PID | GA | [189] |
| 58 | 2020 | PID | AVR | GSA | [190] |
| 59 | 2023 | PID | PID | DEA | [191] |
| 60 | 2023 | PID | PID | BFOA | [192] |
| 61 | 2022 | PI | PI | PSO, GA, ABC | [193] |
| 62 | 2024 | PID | PID | RL | [194] |
| 63 | 2022 | PID | PID | BFOA | [195] |
| 64 | 2023 | FL PID | FPID | SIA | [196] |
| 65 | 2022 | PID | PID | FL, ANN, GA | [197] |
| 66 | 2023 | LFC | LFC | ANFIS | [198] |
| 67 | 2020 | PID | PID-MPPT | CGSA | [199] |
| 68 | 2022 | PID | PID | NN | [200] |
| 69 | 2020 | FFOPI | AGC | SOS | [201] |
| 70 | 2021 | PID | PID | FOFMO | [202] |
| 71 | 2020 | FPI | PI | GOA | [203] |
| 72 | 2020 | PID | AVR | LGA | [204] |
| 73 | 2020 | FOPID | AVR | HPSGWO | [205] |
| 74 | 2024 | PID | PID | ICDBO | [206] |
| 75 | 2023 | PI | PI | PSO | [207] |
| 76 | 2022 | PID | PID | SOA | [208] |
| 77 | 2020 | PI | PI | BFOA | [209] |
| 78 | 2022 | PID | PID | MPA | [210] |
| 79 | 2021 | P-PI | P-PI | SSA | [49] |
| 80 | 2022 | PI | PI | NSGA-II | [211] |
| 81 | 2021 | PI | PI | GA, SA, RL, TD3 | [212] |
| 82 | 2023 | PID | PID | HAOAGTO | [213] |
| 83 | 2023 | FOPID | PID | NewBAT, CS, FF, GWO, WOA | [214] |
| 84 | 2021 | PID | PID | ABC, ACO, ALO, BA, BHO, CLONALG, CS, CSO, DA, DE, FFA, GA, GBS, GOA, HS, KH, MFO, PSO, SCA, SFL, WOA | [215] |
| 85 | 2025 | ANN-NARX | GADALINE | LM and LMS | [119] |
Appendix C. Adaptability Contribution Details

Table A3.
Results of the article classification according to the contribution of adaptability (source: elaboration based on systematic mapping).
Table A3.
Results of the article classification according to the contribution of adaptability (source: elaboration based on systematic mapping).
| ID | Year | Control Structures | Control Techniques | Algorithms | Ref. |
|---|---|---|---|---|---|
| 1 | 2016 | ANN | MMAC | ITFOELM | [142] |
| 2 | 2018 | PID | PSO-tuned PID controller | PSO | [120] |
| 3 | 2014 | PID | FLC | Adaptive Fit | [121] |
| 4 | 2013 | FL based on back-stepping | Control based on an adaptive fuzzy tracking algorithm | Adaptive algorithm | [134] |
| 5 | 2005 | Multilayer ANN with variable structure | AC-ANN | Adaptive algorithm | [143] |
| 6 | 2018 | ANN | Control with an AANN | Adaptive algorithm applied to the Lyapunov barrier function | [146] |
| 7 | 2004 | PID | Estimating Profit Using a Reference System | Adaptive algorithm | [122] |
| 8 | 2016 | ANN | Robust Adaptive Control | Adaptive algorithm | [144] |
| 9 | 2018 | ANN | RBF | Adaptive algorithm | [145] |
| 10 | 2010 | ANN | FL-ANN | Adaptive algorithm | [151] |
| 11 | 2017 | PID | GA-adjusted PID | GA | [123] |
| 12 | 2007 | FLC | FLC-AAC | AAC | [136] |
| 13 | 2017 | MPC | Tuned MPC with adaptive algorithm | Adaptive Algorithm | [141] |
| 14 | 2017 | PID-Fuzzy | Adaptive fuzzy PID | PFC | [149] |
| 15 | 2017 | MPC | MPC-ANN | ANN | [153] |
| 16 | 2016 | FLC | Control by FLC-ANN | ANN | [150] |
| 17 | 2018 | RBF-NN | Control with hybrid functions | ILAP, SMC | [147] |
| 18 | 2014 | Hybrid Structure | LSO and Propagation Algorithm Back | ANFIS | [135] |
| 19 | 2016 | PID | PID | OENN-OEANFIS | [126] |
| 20 | 2016 | AC with FL | Adaptive Algorithm | FL | [152] |
| 21 | 2017 | AFSMC | Adaptive Law | Lyapunov stability | [148] |
| 22 | 2019 | AFLC | Adaptive Law | DEA | [139] |
| 23 | 2014 | AFLC | Adaptive Adjustment of Fuzzy Rules | Fuzzy rules | [131] |
| 24 | 2017 | ANFIS-HBCC | Adaptive Adjustment | ANFIS | [132] |
| 25 | 2018 | PID Controller | FL Parameter Adjustment | FL and PID Tuning | [124] |
| 26 | 2018 | FL | Adaptation Mechanism | Adaptive Algorithm | [138] |
| 27 | 2017 | FLC | Adaptation Law | Kalman Algorithm | [125] |
| 28 | 2014 | PI Controller | FL | Fuzzy Rules | [133] |
| 29 | 2018 | ANFIS | Adaptive Law | GA | [137] |
| 30 | 2023 | FL PID | PI | ACA | [154] |
| 31 | 2021 | PI | PI | AIEM-DDPG | [129] |
| 32 | 2024 | PID | APID | DRL | [128] |
| 33 | 2020 | LQR | LQR | ACSA | [140] |
| 34 | 2022 | RL and DNN | RL-DNN | TD3 | [130] |
| 35 | 2020 | PID | PID | SADE | [127] |
Appendix D

Table A4.
Editorials and journals/conferences of the included studies, with the number of articles per venue.
Table A4.
Editorials and journals/conferences of the included studies, with the number of articles per venue.
| Editorial | Journal | Quantity |
|---|---|---|
| Elsevier | IFAC | 14 |
| Elsevier | Applied Soft Computing | 10 |
| Elsevier | ISA Transactions | 8 |
| Elsevier | Neurocomputing | 7 |
| Elsevier | Energy Procedia | 5 |
| IEEE Xplore | Access | 5 |
| IEEE Xplore | Chinese Control | 4 |
| IEEE Xplore | Computational Intelligence for Smart Power System and Sustainable Energy | 4 |
| Elsevier | Energy Conversion and Management | 3 |
| Elsevier | Engineering Applications of Artificial Intelligence | 3 |
| Elsevier | Heliyon | 3 |
| Elsevier | ISA Transactions | 3 |
| Elsevier | Ain Shams Engineering Journal | 2 |
| Elsevier | Applied Thermal Engineering | 2 |
| Elsevier | Automatica | 2 |
| Elsevier | Engineering Science and Technology, an International Journal | 2 |
| Elsevier | Procedia Computer Science | 2 |
| Elsevier | Renewable Energy | 2 |
| Elsevier | e-Prime - Advances in Electrical Engineering, Electronics and Energy | 2 |
| IEEE Xplore | Conference on Industrial Electronics and Applications | 2 |
| IEEE Xplore | Electrical Engineering | 2 |
| IEEE Xplore | Intelligent Controller and Computing for Smart Power | 2 |
| Springer | Communication and Computational Technologies | 2 |
| AJC | Asia Journal Control | 1 |
| Elsevier | Advanced Research | 1 |
| Elsevier | Advances in Engineering Software | 1 |
| Elsevier | Ain Shams Engineering | 1 |
| Elsevier | Alexandria Engineering | 1 |
| Elsevier | Applied Energy | 1 |
| Elsevier | Chaos, Solitons and Fractals | 1 |
| Elsevier | Computers and Electrical Engineering | 1 |
| Elsevier | Computers and Electronics in Agriculture | 1 |
| Elsevier | Control Engineering Practice | 1 |
| Elsevier | Electric Power Systems Research | 1 |
| Elsevier | Electrical Power and Energy Systems | 1 |
| Elsevier | Electrical Systems and Information Technology | 1 |
| Elsevier | Energy | 1 |
| Elsevier | Energy Reports | 1 |
| Elsevier | Engineering Applications of Artificial Intelligence | 1 |
| Elsevier | European Journal of Control | 1 |
| Elsevier | Expert Systems With Applications | 1 |
| Elsevier | Flow Measurement and Instrumentation | 1 |
| Elsevier | Franklin Institute | 1 |
| Elsevier | Franklin Open | 1 |
| Elsevier | Fuzzy set and systems | 1 |
| Elsevier | International Journal of Hydrogen Energy | 1 |
| Elsevier | Journal of King Saud University | 1 |
| Elsevier | Knowledge-Based Systems | 1 |
| Elsevier | Measurement | 1 |
| Elsevier | Neural Networks | 1 |
| Elsevier | Procedia Engineering | 1 |
| Elsevier | Procedia Environmental Sciences | 1 |
| Elsevier | Process Control | 1 |
| Elsevier | Results in Engineering | 1 |
| Elsevier | Robotics and Computer–Integrated Manufacturing | 1 |
| Elsevier | Sustainable Energy, Grids and Networks | 1 |
| Elsevier | The Franklin Institute | 1 |
| IEEE Xplore | ANDESCON | 1 |
| IEEE Xplore | Advanced Science and Engineering | 1 |
| IEEE Xplore | Advances in Electrical Engineering and Computer Applications | 1 |
| IEEE Xplore | Advances in Power, Signal, and Information Technology | 1 |
| IEEE Xplore | Algorithms, High Performance Computing and Artificial Intelligence | 1 |
| IEEE Xplore | Applied Machine Intelligence and Informatics | 1 |
| IEEE Xplore | Artificial Intelligence and Intelligent Information Processing | 1 |
| IEEE Xplore | Artificial Intelligence, Robotics and Control | 1 |
| IEEE Xplore | Chinese Control and Decision | 1 |
| IEEE Xplore | Computational Intelligence | 1 |
| IEEE Xplore | Computational Intelligence and Communication Networks | 1 |
| IEEE Xplore | Computer Science, Engineering and Applications | 1 |
| IEEE Xplore | Conference on Power, Energy and Electrical Engineering | 1 |
| IEEE Xplore | Control Applications | 1 |
| IEEE Xplore | Control Systems and Computer Science | 1 |
| IEEE Xplore | Current Research in Engineering and Science Applications | 1 |
| IEEE Xplore | Decision & Control | 1 |
| IEEE Xplore | Decision and Control | 1 |
| IEEE Xplore | Electrical Engineering | 1 |
| IEEE Xplore | Emerging Trends in Industry 4.0 | 1 |
| IEEE Xplore | Energy, Power and Environment: Towards Flexible Green Energy Technologies | 1 |
| IEEE Xplore | Engineering Mechatronics and Automation | 1 |
| IEEE Xplore | Indian Control | 1 |
| IEEE Xplore | Information Science and Control Engineering | 1 |
| IEEE Xplore | Intelligent Computing and Control Systems | 1 |
| IEEE Xplore | International Conference on Control, Automation and Systems | 1 |
| IEEE Xplore | International Symposium on Intelligent Control | 1 |
| IEEE Xplore | Internet of Things, Automation and Artificial Intelligence | 1 |
| IEEE Xplore | Machine Learning and Cybernetics, Guangzhou | 1 |
| IEEE Xplore | Mechatronics and Automation | 1 |
| IEEE Xplore | Natural Computation, Fuzzy Systems and Knowledge Discovery | 1 |
| IEEE Xplore | Power Electronics | 1 |
| IEEE Xplore | Power, Electrical Engineering, Electronics and Control | 1 |
| IEEE Xplore | Recent Advances in Electrical, Electronics, Ubiquitous Communication, and Computational Intelligence | 1 |
| IEEE Xplore | Robotics, Control and Automation | 1 |
| IEEE Xplore | SYSTEMS, MAN, AND CYBERNETICS | 1 |
| IEEE Xplore | Smart Instrumentation, Measurement and Applications | 1 |
| IEEE Xplore | Soft Computing & Machine Intelligence | 1 |
| IEEE Xplore | Symposium on Intelligent Control | 1 |
| IEEE Xplore | Systems and Control | 1 |
| IEEE Xplore | Transactions on Industrial Electronics | 1 |
| JART | Applied Research and Technology | 1 |
| MDPI | Algorithms | 1 |
| Springer | AETA 2017-Recent Advances in Electrical Engineering and Related Sciences | 1 |
| Springer | Applications of Computational Intelligence | 1 |
| Springer | Applied Intelligence | 1 |
| Springer | Artificial Intelligence XXXV | 1 |
| Springer | Artificial Intelligence and Soft Computing | 1 |
| Springer | Artificial Neural Networks and Machine Learning | 1 |
| Springer | Central South University | 1 |
| Springer | Computational Intelligence | 1 |
| Springer | Computer and Systems Sciences International | 1 |
| Springer | Congress on Control, Robotics, and Mechatronic | 1 |
| Springer | Control Theory and Technology | 1 |
| Springer | Evolutionary Multi-Criterion Optimization | 1 |
| Springer | Journal of Control, Automation, and Systems | 1 |
| Springer | Learning and Intelligent Optimization | 1 |
| Springer | Nature-Inspired Computing for Control Systems | 1 |
| Springer | Neural Processing Letters | 1 |
| Springer | Russian Electrical Engineering | 1 |
| Springer | System Assurance Engineering and Management | 1 |
| Wiley | Advance Transportation | 1 |
| Wiley | Optimal Control Applications and Methods | 1 |
References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Fogel, D.B. Evolutionary Computation: Toward a New Philosophy of Machine Intelligence; Wiley-IEEE Press: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Moore, K.L.; Xu, J.X. Iterative Learning Control for Deterministic Systems; Springer: Berlin, Heidelberg, 1997. [Google Scholar]
- Bristow, D.A.; Tharayil, M.; Alleyne, A.G. A Survey of Iterative Learning Control: A Learning-Based Method for High-Performance Tracking Control; IEEE Control Systems Magazine: Piscataway, NJ, USA, 1996. [Google Scholar]
- Amann, N.; Owens, D.H.; Rogers, E. Iterative learning control using optimal feedback and feedforward actions. Int. J. Control 1996, 65, 277–293. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A. Process Dynamics and Control; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Rivera, D.E.; Morari, M.; Skogestad, S. Internal Model Control: PID Controller Design. Ind. Eng. Chem. Process. Des. Dev. 1986, 25, 252–265. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Glover, F.; Kochenberger, G.A. Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Pearson Education: Harlow, UK, 2002. [Google Scholar]
- El-Bardini, M.; El-Nagar, A.M. Interval type-2 fuzzy PID controller for uncertain nonlinear inverted pendulum system. ISA Trans. 2014, 53, 732–743. [Google Scholar] [CrossRef] [PubMed]
- Premkumar, K.; Manikandan, B. Fuzzy PID supervised online ANFIS based speed controller for brushless DC motor. Neurocomputing 2015, 157, 76–90. [Google Scholar] [CrossRef]
- KPremkumar, K.; Manikandan, B. Adaptive Neuro-Fuzzy Inference System based speed controller for brushless DC motor. Neurocomputing 2014, 138, 260–270. [Google Scholar] [CrossRef]
- Ben Nasr, M.; Chtourou, M. Neural network control of nonlinear dynamic systems using hybrid algorithm. Appl. Soft Comput. 2014, 24, 423–431. [Google Scholar] [CrossRef]
- Solgi, Y.; Ganjefar, S. Variable structure fuzzy wavelet neural network controller for complex nonlinear systems. Appl. Soft Comput. 2018, 64, 674–685. [Google Scholar] [CrossRef]
- Londhe, P.S.; Singh, Y.; Santhakumar, M.; Patre, B.M.; Waghmare, L.M. Robust nonlinear PID-like fuzzy logic control of a planar parallel (2PRP-PPR) manipulator. ISA Trans. 2016, 63, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Pan, F.; Xue, D. Variable-order fuzzy fractional PID controller. ISA Trans. 2015, 55, 227–233. [Google Scholar] [CrossRef]
- Sendoya-Losada, D.F.; Vargas-Duque, D.C.; Ávila-Plazas, I.J. Implementation of a neural control system based on PI control for a non-linear process. In Proceedings of the 2018 IEEE 1st Colombian Conference on Applications in Computational Intelligence (ColCACI), Medellín, Colombia, 16–18 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Hamza, M.F.; Yap, H.J.; Choudhury, I.A. Cuckoo search algorithm based design of interval Type-2 Fuzzy PID Controller for Furuta pendulum system. Eng. Appl. Artif. Intell. 2017, 62, 134–151. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, V. Evolving an interval type-2 fuzzy PID controller for the redundant robotic manipulator. Expert Syst. Appl. 2017, 73, 161–177. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L. The Design and Application of Fuzzy Controller in a Novel Plasma Water Treatment System. Procedia Environ. Sci. 2011, 10, 1818–1822. [Google Scholar] [CrossRef][Green Version]
- Chen, Z.H.; Yuan, X.; Yuan, Y.; Lei, X.; Zhang, B. Parameter estimation of fuzzy sliding mode controller for hydraulic turbine regulating system based on HICA algorithm. Renew. Energy 2019, 133, 551–565. [Google Scholar] [CrossRef]
- Mahto, T.; Mukherjee, V. A novel scaling factor based fuzzy logic controller for frequency control of an isolated hybrid power system. Energy 2017, 130, 339–350. [Google Scholar] [CrossRef]
- Corn, M.; Atanasijević-Kunc, M. Designing model and control system using evolutionary algorithms. IFAC-PapersOnLine 2015, 48, 526–531. [Google Scholar] [CrossRef]
- IKitsios, I.; Pimenides, T.; Groumpos, P. A genetic algorithm for designing H/sub/spl infin//structured specified controllers. In Proceedings of the 2001 IEEE International Conference on Control Applications (CCA’01) (Cat. No. 01CH37204), Mexico City, Mexico, 7 September 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 1196–1201. [Google Scholar]
- Kazaryan, D.; Savinkov, A. Grammatical evolution for neural network optimization in the control system synthesis problem. Procedia Comput. Sci. 2017, 103, 14–19. [Google Scholar] [CrossRef]
- Patil, N.A.; Lakhekar, G.V. Design of PID controller for cascade control process using genetic algorithm. In Proceedings of the 2017 International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 15–16 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1089–1095. [Google Scholar]
- Stirrup, R.; Chipperfield, A. Hybrid control and evolutionary decision support within a sustainable environment. In Proceedings of the IEEE International Symposium on Intelligent Control, Vancouver, BC, Canada, 27–30 October 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 526–531. [Google Scholar]
- Asgharnia, A.; Shahnazi, R.; Jamali, A. Performance and robustness of optimal fractional fuzzy PID controllers for pitch control of a wind turbine using chaotic optimization algorithms. ISA Trans. 2018, 79, 27–44. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y. Design of Automatic Control System for Garden Irrigation Based on Artificial Intelligence Algorithm. In Proceedings of the 2023 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 25–27 September 2023; IEEE: Piscataway, NJ, USA; pp. 435–440. [Google Scholar]
- Elsisi, M.; Tran, M.Q.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Robust design of ANFIS-based blade pitch controller for wind energy conversion systems against wind speed fluctuations. IEEE Access 2021, 9, 37894–37904. [Google Scholar] [CrossRef]
- Liu, C.G.; Negenborn, R.R.; Zheng, H.; Chu, X. A state-compensation extended state observer for model predictive control. Eur. J. Control 2017, 36, 1–9. [Google Scholar] [CrossRef]
- Oh, S.K.; Park, B.J.; Lee, J.M. Point-to-point iterative learning model predictive control. Automatica 2018, 89, 135–143. [Google Scholar] [CrossRef]
- Todorov, Y.V.; Terziyska, M.N.; Petrov, M.G. NEO-Fuzzy State-Space Predictive Control. IFAC PapersOnLine 2015, 48, 99–104. [Google Scholar] [CrossRef]
- Stogiannos, M.; Alexandridis, A.; Sarimveis, H. Model predictive control for systems with fast dynamics using inverse neural models. ISA Trans. 2018, 72, 161–177. [Google Scholar] [CrossRef]
- Kumar, S.S.P.; Tulsyan, A.; Gopaluni, B.; Loewen, P. A Deep Learning Architecture for Predictive Control. IFAC PapersOnLine 2018, 51, 512–517. [Google Scholar] [CrossRef]
- Moe, S.; Rustad, A.M.; Hanssen, K.G. Machine learning in control systems: An overview of the state of the art. In Proceedings of the Artificial Intelligence XXXV: 38th SGAI International Conference on Artificial Intelligence, AI 2018, Cambridge, UK, 11–13 December 2018; Proceedings 38. Springer International Publishing: Cham, Switzerland, 2018; pp. 250–265. [Google Scholar]
- Vasičkaninová, A.; Bakošová, M. Control of a heat exchanger using neural network predictive controller combined with auxiliary fuzzy controller. Appl. Therm. Eng. 2015, 89, 1046–1053. [Google Scholar] [CrossRef]
- Bielecki, A.; Bielecka, M.; Ernst, S. Proposal of an intelligent, predictive fuzzy controller for off-grid devices. IFAC PapersOnLine 2016, 49, 523–528. [Google Scholar] [CrossRef]
- Marino, R.; Scalzi, S.; Tomei, P.; Verrelli, C. Generalized PID learning control. IFAC Proc. Vol. 2011, 44, 3629–3634. [Google Scholar] [CrossRef]
- Li, X.F.; Chen, G.; Wang, Y.G. IMC-PID controller design for power control loop based on closed-loop identification in the frequency domain. IFAC PapersOnLine 2016, 49, 79–84. [Google Scholar] [CrossRef]
- Han, H.-G.; Zhang, L.; Liu, H.-X.; Qiao, J.-F. Multiobjective design of fuzzy neural network controller for wastewater treatment process. Appl. Soft Comput. 2018, 67, 467–478. [Google Scholar] [CrossRef]
- Zainal, N.A.; Yusoff, A.R.; Apen, A. Integrated cooling systems and maximum power point tracking of fuzzy logic controller for improving photovoltaic performances. Measurement 2019, 131, 100–108. [Google Scholar] [CrossRef]
- Tavakoli, A.R.; Seifi, A.R.; Arefi, M.M. Designing a self-constructing fuzzy neural network controller for damping power system oscillations. Fuzzy Sets Syst. 2019, 356, 63–76. [Google Scholar] [CrossRef]
- Derrouazin, A.; Aillerie, M.; Mekkakia-Maaza, N.; Charles, J.-P. Multi input-output fuzzy logic smart controller for a residential hybrid solar-wind-storage energy System. Energy Convers. Manag. 2017, 145, 234–245. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, Z.; Sun, Z.; Quan, L. A Linear Interpolation Fuzzy Controller for a Boiler Pressure Control System. IFAC Proc. Vol. 2013, 46, 650–654. [Google Scholar] [CrossRef]
- Al-Hadithi, B.M.; Jiménez, A.; Perez-Oria, J. New incremental Takagi–Sugeno state model for optimal control of multivariable nonlinear time delay systems. Eng. Appl. Artif. Intell. 2015, 45, 259–268. [Google Scholar] [CrossRef]
- Li, H.M.; Wang, X.B.; Song, S.B.; Li, H. Vehicle control strategies analysis based on PID and fuzzy logic control. Procedia Eng. 2016, 137, 234–243. [Google Scholar] [CrossRef]
- Coteli, R.; Acikgoz, H.; Ucar, F.; Dandil, B. Design and implementation of Type-2 fuzzy neural system controller for PWM rectifiers. Int. J. Hydrogen Energy 2017, 42, 20759–20771. [Google Scholar] [CrossRef]
- Saravanan, A.G.; Rajaram, M. Fuzzy controller for dynamic performance improvement of a half-bridge isolated DC–DC converter. Neurocomputing 2014, 140, 283–290. [Google Scholar] [CrossRef]
- Sathishkumar, H.; Parthasarathy, S.S. A novel fuzzy logic controller for vector controlled induction motor drive. Energy Procedia 2017, 138, 686–691. [Google Scholar] [CrossRef]
- Aissaoui, A.G.; Tahour, A.; Abid, M.; Essounbouli, N.; Nollet, F. Power control of wind turbine based on fuzzy controllers. Energy Procedia 2013, 42, 163–172. [Google Scholar] [CrossRef]
- Ben Ali, R.; Bouadila, S.; Mami, A. Development of a Fuzzy Logic Controller applied to an agricultural greenhouse experimentally validated. Appl. Therm. Eng. 2018, 141, 798–810. [Google Scholar] [CrossRef]
- Li, X.S.; Wen, H.Q.; Hu, Y.H.; Jiang, L. A novel beta parameter based fuzzy-logic controller for photovoltaic MPPT application. Renew. Energy 2019, 103, 416–427. [Google Scholar] [CrossRef]
- Núñez, L.C.B.; Chaparro, A.S.V.; Mareco, E.F.; Pinto-Roa, D.P. Design of a Fuzzy Controller Applied to Level Control in Industrial Processes. In Proceedings of the International Conference on Computational Intelligence, Singapore, 13–15 December 2023; Springer Nature: Singapore, 2023; pp. 23–37. [Google Scholar]
- Galeano, V.; González, D.; Mareco, E.F.; Pinto-Roa, D.P. Fuzzy Compensator Design for Induction Motor Control Using a Frequency Converter in Networked Control Systems. In Proceedings of the International Conference on Communication and Computational Technologies, Singapore, 8–9 January 2024; Springer Nature: Singapore, 2024; pp. 431–448. [Google Scholar]
- Ding, Y.; Wang, L.; Li, Y.; Li, D. Model predictive control and its application in agriculture: A review. Comput. Electron. Agric. 2018, 151, 104–117. [Google Scholar] [CrossRef]
- Bayer, F.A.; Lorenzen, M.; Müller, M.A.; Allgöwer, F. Robust economic model predictive control using stochastic information. Automatica 2016, 74, 151–161. [Google Scholar] [CrossRef]
- Degen, N.; Schoellig, A.P. Design of norm-optimal iterative learning controllers: The effect of an iteration-domain Kalman filter for disturbance estimation. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 5–17 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3590–3596. [Google Scholar]
- Doh, T.-Y.; Ryoo, J.R.; Chang, D.E. Robust iterative learning controller design using the performance weighting function of feedback control systems. Int. J. Control Autom. Syst. 2014, 12, 63–70. [Google Scholar] [CrossRef]
- Patan, K. Two stage neural network modelling for robust model predictive control. ISA Trans. 2018, 72, 56–65. [Google Scholar] [CrossRef]
- Şahin, S. Learning feedback linearization using artificial neural networks. Neural Process. Lett. 2016, 44, 625–637. [Google Scholar] [CrossRef]
- Huynh, T.-T.; Lin, C.-M.; Pham, T.-T.T.; Cho, H.-Y.; Le, T.-L. A modified function-link fuzzy cerebellar model articulation controller using a PI-type learning algorithm for nonlinear system synchronization and control. Chaos Solitons Fractals 2019, 118, 65–82. [Google Scholar] [CrossRef]
- Sathishkumar, H.; Parthasarathy, S.S. A novel neural network intelligent controller for vector controlled induction motor drive. Energy Procedia 2017, 138, 692–697. [Google Scholar] [CrossRef]
- Tudoroiu, R.E.; Zaheeruddin, M.; Curiac, D.I.; Radu, M.S.; Tudoroiu, N. Investigations into the Design and Implementation of Reinforcement Learning Using Deep Learning Neural Networks. Algorithms 2025, 18, 170. [Google Scholar] [CrossRef]
- Vera, L.; Benítez, A.; Fernández Mareco, E.; Pinto Roa, D. Design of an Adaptive Neural Controller Applied to Pressure Control in Industrial Processes. In Proceedings of the Congress on Control, Robotics, and Mechatronics, Singapore, 25–26 March 2023; Springer Nature: Singapore, 2023; pp. 621–639. [Google Scholar]
- Ohnishi, Y.; Kitagawa, H.; Mori, S.; Wakitani, S.; Yamamoto, T. Design of Neural Networks Based FRIT PID Controllers and Its Applications. IFAC Proc. Vol. 2013, 46, 355–359. [Google Scholar] [CrossRef]
- Yuan, X.F.; Wang, Y.N.; Li, S.T. A novel excitation controller using support vector machines and approximate models. J. Control Theory Appl. 2008, 6, 239–245. [Google Scholar] [CrossRef]
- Dutta, S.; Jha, S.; Sankaranarayanan, S.; Tiwari, A. Learning and verification of feedback control systems using feedforward neural networks. IFAC PapersOnLine 2018, 51, 151–156. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Du, W. Design of PID controller based on a self-adaptive state-space predictive functional control using extremal optimization method. J. Frankl. Inst. 2018, 355, 2197–2220. [Google Scholar] [CrossRef]
- Belarbi, K.; Titel, F.; Bourebia, W.; Benmahammed, K. Design of Mamdani fuzzy logic controllers with rule base minimisation using genetic algorithm. Eng. Appl. Artif. Intell. 2005, 18, 875–880. [Google Scholar] [CrossRef]
- Jeong, H.H. A study for learning method of modified PID controller with on-line hybrid genetic algorithm. In AETA 2017-Recent Advances in Electrical Engineering and Related Sciences: Theory and Application; Springer International Publishing: Cham, Switzerland, 2018; pp. 488–497. [Google Scholar]
- Fan, L.; Joo, E.M. Design for auto-tuning PID controller based on genetic algorithms. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xian, China, 25–27 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1924–1928. [Google Scholar]
- Sato, H.; Coello, C.A.C.; Aguirre, H.E. Adaptive control of the number of crossed genes in many-objective evolutionary optimization. In Proceedings of the Learning and Intelligent Optimization: 6th International Conference, LION 6, Paris, France, 16–20 January 2012; Revised Selected Papers. Springer: Berlin/Heidelberg, Germany, 2012; pp. 478–484. [Google Scholar]
- Moradi, M. A genetic-multivariable fractional order PID control to multi-input multi-output processes. J. Process. Control. 2014, 24, 336–343. [Google Scholar] [CrossRef]
- Przybył, A.; Szczypła, J.; Wang, L. Optimization of controller structure using evolutionary algorithm. In Proceedings of the Artificial Intelligence and Soft Computing: 14th International Conference, ICAISC 2015, Zakopane, Poland, 14–18 June 2015; Proceedings, Part II. Springer International Publishing: Cham, Switzerland, 2015; pp. 261–271. [Google Scholar]
- Tairidis, G.; Foutsitzi, G.; Koutsianitis, P.; Stavroulakis, G. Fine tuning of a fuzzy controller for vibration suppression of smart plates using genetic algorithms. Adv. Eng. Softw. 2016, 101, 123–135. [Google Scholar] [CrossRef]
- Sanornoi, N.; Wongwai, S.; Areerak, K. A Geno-Hydra Control System: Design and Tuning Hybrid Controller based on Hydra Control Structure by using Genetic Algorithms. In Proceedings of the 2006 1st IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–6. [Google Scholar]
- Moen, H.J.F.; Hansen, N.B.; Hovland, H.; Tørresen, J. Many-objective optimization using taxi-cab surface evolutionary algorithm. In Proceedings of the Evolutionary Multi-Criterion Optimization: 7th International Conference, EMO 2013, Sheffield, UK, 19–22 March 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 128–142. [Google Scholar]
- Oi, A.; Hasegawa, Y.; Ohishi, K. Development of PSO-based PID tuning method. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, Republic of Korea, 14–17 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1917–1920. [Google Scholar]
- Ranjani, M.; Murugesan, P. Optimal fuzzy controller parameters using PSO for speed control of Quasi-Z Source DC/DC converter fed drive. Appl. Soft Comput. 2015, 27, 332–356. [Google Scholar] [CrossRef]
- Pal, D.; Chatterjee, A.; Rakshit, A. Robust-stable quadratic-optimal fuzzy-PDC controllers for systems with parametric uncertainties: A PSO based approach. Eng. Appl. Artif. Intell. 2018, 70, 38–51. [Google Scholar] [CrossRef]
- Dorrah, H.T.; El-Garhy, A.M.; El-Shimy, M.E. PSO based optimized fuzzy controllers for decoupled highly interacted distillation process. Ain Shams Eng. J. 2012, 3, 251–266. [Google Scholar] [CrossRef]
- Sahoo, B.P.; Panda, S. Improved grey wolf optimization technique for fuzzy aided PID controller design for power system frequency control. Sustain. Energy Grids Netw. 2018, 16, 278–299. [Google Scholar] [CrossRef]
- Oliveira, P.d.M.; Pires, E.S.; Novais, P. Design of Posicast PID control systems using a gravitational search algorithm. Neurocomputing 2015, 167, 18–23. [Google Scholar] [CrossRef]
- Berrazouane, S.; Mohammedi, K. Parameter optimization via cuckoo optimization algorithm of fuzzy controller for energy management of a hybrid power system. Energy Convers. Manag. 2014, 78, 652–660. [Google Scholar] [CrossRef]
- Prauzek, M.; Krömer, P.; Rodway, J.; Musilek, P. Differential evolution of fuzzy controller for environmentally-powered wireless sensors. Appl. Soft Comput. 2016, 48, 193–206. [Google Scholar] [CrossRef]
- Pradhan, P.C.; Sahu, R.K.; Panda, S. Firefly algorithm optimized fuzzy PID controller for AGC of multi-area multi-source power systems with UPFC and SMES. Eng. Sci. Technol. Int. J. 2016, 19, 338–354. [Google Scholar] [CrossRef]
- Caraveo, C.; Valdez, F.; Castillo, O. Optimization of fuzzy controller design using a new bee colony algorithm with fuzzy dynamic parameter adaptation. Appl. Soft Comput. 2016, 43, 131–142. [Google Scholar] [CrossRef]
- Rodríguez-Castellanos, J.E.; Grisales-Palacio, V.H.; Cote-Ballesteros, J.E. A tuning proposal for direct fuzzy PID controllers oriented to industrial continuous processes. IFAC PapersOnLine 2018, 51, 657–662. [Google Scholar] [CrossRef]
- Savran, A. A multivariable predictive fuzzy PID control system. Appl. Soft Comput. 2014, 13, 2658–2667. [Google Scholar] [CrossRef]
- Naghibi, S.R.; Pirmohamadi, A.A.; Moosavian, S.A.A. Fuzzy MTEJ controller with integrator for control of underactuated manipulators. Robot. Comput. Manuf. 2017, 48, 93–101. [Google Scholar] [CrossRef]
- Precup, R.-E.; David, R.-C.; Petriu, E.M.; Rădac, M.-B.; Preitl, S.; Fodor, J. Evolutionary optimization-based tuning of low-cost fuzzy controllers for servo systems. Knowledge Based Syst. 2013, 38, 74–84. [Google Scholar] [CrossRef]
- Pongfai, J.; Assawinchaichote, W. Optimal PID parametric auto-adjustment for BLDC motor control systems based on artificial intelligence. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Falahati, S.; Taher, S.A.; Shahidehpour, M. Grid frequency control with electric vehicles by using of an optimized fuzzy controller. Appl. Energy 2016, 178, 918–928. [Google Scholar] [CrossRef]
- Sahu, P.C.; Prusty, R.C.; Panda, S. Approaching hybridized GWO-SCA based type-II fuzzy controller in AGC of diverse energy source multi area power system. J. King Saud Univ. Eng. Sci. 2020, 32, 186–197. [Google Scholar] [CrossRef]
- Gheisarnejad, M. An effective hybrid harmony search and cuckoo optimization algorithm based fuzzy PID controller for load frequency control. Appl. Soft Comput. 2018, 65, 121–138. [Google Scholar] [CrossRef]
- Bounar, N.; Labdai, S.; Boulkroune, A. PSO–GSA based fuzzy sliding mode controller for DFIG-based wind turbine. ISA Trans. 2019, 85, 177–188. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.-M.; Pi, D.-Y.; Sun, Y.-X. Support vector machine based nonlinear model multi-step-ahead optimizing predictive control. J. Central South Univ. Technol. 2005, 12, 591–595. [Google Scholar] [CrossRef]
- Sahib, M.A.; Ahmed, B.S. A new multiobjective performance criterion used in PID tuning optimization algorithms. J. Adv. Res. 2016, 7, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Goiburú, J.; Vera, J.; Mareco, E.F.; Pinto-Roa, D.P. Identification of Liquid-Level Systems in Industrial Processes Through Artificial Neural Networks. In Proceedings of the International Conference on Communication and Computational Technologies, Singapore, 8–9 January 2024; Springer Nature: Singapore, 2024; pp. 411–429. [Google Scholar]
- Valluru, S.K.; Singh, M. Performance investigations of APSO tuned linear and nonlinear PID controllers for a nonlinear dynamical system. J. Electr. Syst. Inf. Technol. 2018, 5, 442–452. [Google Scholar] [CrossRef]
- Savran, A.; Kahraman, G. A fuzzy model based adaptive PID controller design for nonlinear and uncertain processes. ISA Trans. 2014, 53, 280–288. [Google Scholar] [CrossRef]
- Abdallah, Y.M.; Filho, W.C.L. An Adaptive Tuning Strategy of PID Attitude Control System. IFAC Proc. Vol. 2004, 37, 1009–1014. [Google Scholar] [CrossRef]
- Patrascu, M.; Ion, A. Self-Adaptation in Genetic Algorithms for Control Engineering: The Case of Time Delay Systems. In Proceedings of the 2017 21st International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 29–31 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 19–25. [Google Scholar]
- Priyanka, E.B.; Maheswari, C.; Thangavel, S. Online monitoring and control of flow rate in oil pipelines transportation system by using PLC based Fuzzy-PID Controller. Flow Meas. Instrum. 2018, 62, 144–151. [Google Scholar] [CrossRef]
- Tamilselvan, G.M.; Aarthy, P. Online tuning of fuzzy logic controller using Kalman algorithm for conical tank system. J. Appl. Res. Technol. 2017, 15, 492–503. [Google Scholar] [CrossRef]
- Milovanović, M.B.; Antić, D.S.; Milojković, M.T.; Nikolić, S.S.; Perić, S.L.; Spasić, M.D. Adaptive PID control based on orthogonal endocrine neural networks. Neural Networks 2016, 84, 80–90. [Google Scholar] [CrossRef]
- Emami, H.; Sharifi, A.A.; Azarnia, G. Tuning PID Controller using Self-Adaptive Differential Evolution Algorithm. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 4–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Zhao, F.; Wang, S.; Li, S.; Zhao, L.; Zhang, H.; Wang, Y.; Jin, M. Adaptive Flight Control Based on Artificial Intelligence Algorithms. In Proceedings of the 2024 20th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Xian, China, 19–21 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar]
- Li, J.; Yu, T.; Yang, B. Adaptive controller of PEMFC output voltage based on ambient intelligence large-scale deep reinforcement learning. IEEE Access 2021, 9, 6063–6075. [Google Scholar] [CrossRef]
- Detroja, K.P. Parameterized Adaptive Controller Design using Reinforcement Learning and Deep Neural Networks. In Proceedings of the 2022 Eighth Indian Control Conference (ICC), Mumbai, India, 14–16 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 121–126. [Google Scholar]
- Guenounou, O.; Dahhou, B.; Chabour, F. Adaptive fuzzy controller based MPPT for photovoltaic systems. Energy Convers. Manag. 2014, 78, 843–850. [Google Scholar] [CrossRef]
- Benyamina, A.; Moulahoum, S.; Colak, I.; Bayindir, R. Design and real time implementation of adaptive neural-fuzzy inference system controller based unity single phase power factor converter. Electr. Power Syst. Res. 2017, 152, 357–366. [Google Scholar] [CrossRef]
- Mahapatro, S.R.; Subudhi, B.; Ghosh, S. Adaptive fuzzy PI controller design for coupled tank system: An experimental validation. IFAC Proc. Vol. 2014, 47, 878–881. [Google Scholar]
- Wang, R.; Yu, F.S.; Wang, J.Y. Adaptive fuzzy control for a class of uncertain nonlinear systems with unknown nonsymmetric dead-zone input. In Proceedings of the 32nd Chinese Control Conference, Xian, China, 26–28 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 513–518. [Google Scholar]
- Cherroun, L.; Boumehraz, M. Path following behavior for an autonomous mobile robot using neuro-fuzzy controller. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 352–360. [Google Scholar] [CrossRef]
- Karavaev, M.V.; Zhdanov, A.A. Construction of self-learning fuzzy controllers using autonomous adaptive control methodology. J. Comput. Syst. Sci. Int. 2007, 46, 255–261. [Google Scholar] [CrossRef]
- Mohamed, S.; Hameed, I.A. A GA-based adaptive neuro-fuzzy controller for greenhouse climate control system. Alex. Eng. J. 2018, 57, 773–779. [Google Scholar] [CrossRef]
- Zaki, A.M.; El-Bardini, M.; Soliman, F.; Sharaf, M.M. Embedded two level direct adaptive fuzzy controller for DC motor speed control. Ain Shams Eng. J. 2018, 9, 65–75. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Riaño, I.; Gerndt, R.; Zelinka, I.; Gonzalez-Longatt, F.; Sood, V.K. Synthetic inertia control based on fuzzy adaptive differential evolution. Int. J. Electr. Power Energy Syst. 2019, 105, 803–813. [Google Scholar] [CrossRef]
- Chi, X.; Chi, R. Optimal design of linear quadratic regulator controller based on adaptive cuckoo search algorithm. In Proceedings of the 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1981–1986. [Google Scholar]
- Lorenzen, M.; Allgöwer, F.; Cannon, M. Adaptive model predictive control with robust constraint satisfaction. IFAC PapersOnLine 2017, 50, 3313–3318. [Google Scholar] [CrossRef]
- Gao, X.H.; Wong, K.I.; Wong, P.K.; Vong, C.M. Adaptive control of rapidly time-varying discrete-time system using initial-training-free online extreme learning machine. Neurocomputing 2016, 194, 117–125. [Google Scholar] [CrossRef]
- Zhang, T.-P.; Mei, J.-D.; Mao, Y.-Q.; Chen, J. Adaptive neural network control of nonlinear systems with unknown dead-zone model. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1351–1355. [Google Scholar]
- Ma, H.; Wang, Z.; Wang, D.; Liu, D.; Yan, P.; Wei, Q. Neural-network-based distributed adaptive robust control for a class of nonlinear multiagent systems with time delays and external noise. IEEE Trans. Syst. Man, Cybern. Syst. 2015, 46, 750–758. [Google Scholar] [CrossRef]
- Moawad, N.M.; Elawady, W.M.; Sarhan, A.M. Development of an adaptive radial basis function neural network estimator-based continuous sliding mode control for uncertain nonlinear systems. ISA Trans. 2019, 87, 200–216. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, J.; Lan, X.; Wang, X.; Yang, J. Adaptive neural network control of a flexible string system with non-symmetric dead-zone and output constraint. Neurocomputing 2018, 283, 1–8. [Google Scholar] [CrossRef]
- Klecker, S.; Hichri, B.; Plapper, P. Learning-while controlling RBF-NN for robot dynamics approximation in neuro-inspired control of switched nonlinear systems. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Proceedings, Part III. Springer International Publishing: Cham, Switzerland, 2018; pp. 717–727. [Google Scholar]
- Farahani, M.; Ganjefar, S. Intelligent power system stabilizer design using adaptive fuzzy sliding mode controller. Neurocomputing 2017, 226, 135–144. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Q.; Zhang, R. Improved fuzzy PID controller design using predictive functional control structure. ISA Trans. 2017, 71, 354–363. [Google Scholar] [CrossRef]
- Boulkroune, A.; Issaouni, S.; Chekireb, H. Adaptive Neuro-Fuzzy Controller of Induction Machine Drive with Nonlinear Friction. In Nature-Inspired Computing for Control Systems; Springer: Cham, Switzerland, 2016; pp. 169–192. [Google Scholar]
- Zhang, Y.-X. Fuzzy neural network adaptive robust control of a class of nonlinear interconnected systems based on TS fuzzy model. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2561–2564. [Google Scholar]
- Karray, A.; Njah, M.; Feki, M.; Jallouli, M. Intelligent mobile manipulator navigation using hybrid adaptive-fuzzy controller. Comput. Electr. Eng. 2016, 56, 773–783. [Google Scholar] [CrossRef]
- Vatankhah, B.; Farrokhi, M. Nonlinear model-predictive control with disturbance rejection property using adaptive neural networks. J. Frankl. Inst. 2017, 354, 5201–5220. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, J.; Li, Y.; Zhang, Z. UAV oute Planning Based on Fuzzy PID Control Ant Colony Algorithm. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Chengdu, China, 24–28 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4726–4731. [Google Scholar]
- Wang, H.; Afshar, P.; Yue, H. Ilc-based generalised pi control for output pdf of stochastic systems using lmi and rbf neural networks. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 5048–5053. [Google Scholar]
- Lu, L.L.; Xie, L.H.; Cai, W.J. H2 controller design for networked control systems. Asian J. Control 2004, 6, 88–96. [Google Scholar] [CrossRef]
- Wang, L.P.; Freeman, C.T.; Rogers, E. Predictive iterative learning control with experimental validation. Control Eng. Pract. 2016, 53, 24–34. [Google Scholar] [CrossRef][Green Version]
- Lee, Z.-J. A robust learning algorithm based on support vector regression and robust fuzzy cerebellar model articulation controller. Appl. Intell. 2008, 29, 47–55. [Google Scholar] [CrossRef]
- Ouyang, P.; Zhang, W.; Gupta, M. A robust PD-type evolutionary learning control for nonlinear time-varying systems. In Proceedings of the 2004 IEEE International Symposium on Intelligent Control, Taipei, Taiwan, 2–4 September 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 90–95. [Google Scholar]
- Bradai, R.; Shetat, B.; Ladygin, A.N. Increase in the efficiency of the speed controller of an induction machine drive by means of artificial intelligence. Russ. Electr. Eng. 2008, 79, 676–684. [Google Scholar] [CrossRef]
- Rocha-Osorio, C.M.; Solís-Chaves, J.; Rodrigues, L.L.; Puma, J.A.; Filho, A.S. Deadbeat–fuzzy controller for the power control of a Doubly Fed Induction Generator based wind power system. ISA Trans. 2019, 88, 258–267. [Google Scholar] [CrossRef]
- Sathishkumar, H.; Parthasarathy, S. A novel neuro-fuzzy controller for vector controlled induction motor drive. Energy Procedia 2017, 138, 698–703. [Google Scholar] [CrossRef]
- Magzoub, M.A.; Saad, N.B.; Ibrahim, R.B. Efficiency improvement of induction motor variable speed drive using a hybrid fuzzy-fuzzy controller. Energy Procedia 2015, 75, 1529–1535. [Google Scholar] [CrossRef][Green Version]
- Li, C.; Mao, Y.; Zhou, J.; Zhang, N.; An, X. Design of a fuzzy-PID controller for a nonlinear hydraulic turbine governing system by using a novel gravitational search algorithm based on Cauchy mutation and mass weighting. Appl. Soft Comput. 2017, 52, 290–305. [Google Scholar] [CrossRef]
- Lin, J.; Lian, R.-J. Design of a grey-prediction self-organizing fuzzy controller for active suspension systems. Appl. Soft Comput. 2013, 13, 4162–4173. [Google Scholar] [CrossRef]
- Singh, A.P.; Kumar, Y.; Sawle, Y.; Alotaibi, M.A.; Malik, H.; Márquez, F.P.G. Development of artificial Intelligence-Based adaptive vehicle to grid and grid to vehicle controller for electric vehicle charging station. Ain Shams Eng. J. 2024, 15, 102937. [Google Scholar] [CrossRef]
- Lisitsyn, A.N.; Zadorozhnaya, N.M. Adaptive wind turbine PID controller tuner algorithm with elements of artificial intelligence. Procedia Comput. Sci. 2019, 150, 591–596. [Google Scholar] [CrossRef]
- Saravanan, G.; Suresh, K.P.; Pazhanimuthu, C.; Kumar, R.S. Artificial rabbits optimization algorithm based tuning of PID controller parameters for improving voltage profile in AVR system using IoT. e-Prime 2024, 8, 100523. [Google Scholar] [CrossRef]
- Mohamed, M.J.; Oleiwi, B.K.; Azar, A.T.; Hameed, I.A. Coot optimization algorithm-tuned neural network-enhanced PID controllers for robust trajectory tracking of three-link rigid robot manipulator. Heliyon 2024, 10, e32661. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Colak, I.; Yessef, M.; Elbarbary, Z.M.S.; Bizon, N. Feedback action and genetic algorithm-based proportional-integral controller to improve the performance of the direct power control of a variable-speed contra-rotating wind turbine generation system. Energy Rep. 2025, 13, 2153–2173. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; García-Cerezo, A.; García-Martínez, J.R. Fuzzy logic controller for UAV with gains optimized via genetic algorithm. Heliyon 2024, 10, e26363. [Google Scholar] [CrossRef] [PubMed]
- Bojan-Dragos, C.-A.; Precup, R.-E.; Preitl, S.; Roman, R.-C.; Hedrea, E.-L.; Szedlak-Stinean, A.-I. GWO-based optimal tuning of type-1 and type-2 fuzzy controllers for electromagnetic actuated clutch systems. IFAC PapersOnLine 2021, 54, 189–194. [Google Scholar] [CrossRef]
- Bouaddi, A.; Rabeh, R.; Ferfra, M. Load Frequency Control in Autonomous Microgrids using Hybrid Algorithm GWO-CS based Fuzzy logic Sliding Mode Controller. Results Eng. 2025, 25, 104412. [Google Scholar] [CrossRef]
- Terfia, E.-S.; Mendaci, S.; Rezgui, S.E.; Gasmi, H.; Kantas, W. Optimal third-order sliding mode controller for dual star induction motor based on grey wolf optimization algorithm. Heliyon 2024, 10, e32669. [Google Scholar] [CrossRef]
- Shekher, V.; Sisodiya, A.; Sinha, A.K.; Harsh, H.; Soren, N. Optimal tuning of PID controller for V/f control of linear induction motor using artificial biological intelligence. Frankl. Open 2024, 9, 100183. [Google Scholar] [CrossRef]
- Civelek, Z. Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm. Eng. Sci. Technol. Int. J. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Pazhanimuthu, C.; Saravanan, G.; Suresh, K.; Kumar, R.S. Performance analysis of voltage profile improvement in AVR system using zebra optimization algorithms based on PID controller. e-Prime 2023, 6, 100380. [Google Scholar] [CrossRef]
- Arostegui, A.; Benítez, D.S.; Caiza, L. A fuzzy-PD controller optimized by artificial bee colony algorithm applied to a small-scale pasteurization plant. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Chen, G.; Li, Z.; Zhang, Z.; Li, S. An improved ACO algorithm optimized fuzzy pid controller for load frequency control in multi area interconnected power systems. IEEE Access 2019, 8, 6429–6447. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. An intelligent non-integer PID controller-based deep reinforcement learning: Implementation and experimental results. IEEE Trans. Ind. Electron. 2020, 68, 3609–3618. [Google Scholar] [CrossRef]
- Nair, A.A. Ant Colony Optimization-Tuned Fractional Order PID Controller for Speed Regulation In Hybrid Electric Vehicle. In Proceedings of the 2024 International Conference on Recent Advances in Electrical, Electronics, Ubiquitous Communication, and Computational Intelligence (RAEEUCCI), Chennai, India, 17–18 April 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Tian, C.; Ni, S.; Wang, Z.; Zhang, Y. Application of Grey Wolf Optimization Algorithm in Tuning Controller Parameters of Hypersonic Vehicle. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 323–328. [Google Scholar]
- Mohapatra, A.K.; Sahu, P.C.; Mohapatra, S.; Bhatta, S.K.; Debnath, M.K. Artificial Intelligence technique governed robust fuzzy controller for microgrid frequency control. In Proceedings of the 2023 International Conference in Advances in Power, Signal, and Information Technology (APSIT), Power, Signal, 20 April 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 236–241. [Google Scholar]
- Murugesan, D.; Shah, P.; Jagatheesan, K.; Sekhar, R.; Kulkarni, A.J. Cohort intelligence optimization based controller design of isolated and interconnected thermal power system for automatic generation control. In Proceedings of the 2022 Second International Conference on Computer Science, Engineering and Applications (ICCSEA), Gunupur, India, 8 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Pattnaik, R.; Chandak, S.; Rout, P.K.; Routray, S.K.; Sahu, B.K. Design and analysis of automatic generation control of two area power system based on modified differential evolution algorithm. In Proceedings of the the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Odisha, India, 29–31 July 2020; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Ibrahim, E.K.; Gitaffa, S.A.; Issa, A.H. Design of FOPID controller for DC motor speed control using intelligent swarm techniques. In Proceedings of the 2022 4th International Conference on Current Research in Engineering and Science Applications (ICCRESA), Baghdad, Iraq, 20–21 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 40–46. [Google Scholar]
- Xu, J.; Bhattacharyya, S.P. Efficient Tuning of PID Controllers using Swarm-based Optimization Algorithms. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 572–579. [Google Scholar]
- Ranjitha, K.; Sivakumar, P.; Elavarasu, R.; Monica, M.; Rajapandiyan, A. Firefly algorithm optimized load frequency controller for multi-source power system. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Ahmadi, S.; Talami, S.H.; Sahnesaraie, M.A.; Dini, F.; Tahernejadjozam, B.; Ashgevari, Y. FUZZY aided PID controller is optimized by GA algorithm for Load Frequency Control of Multi-Source Power Systems. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 23–25 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 000207–000212. [Google Scholar]
- Ray, N.K.; Mohapatra, S.K.; Dash, S.S. Gravitational Search Algorithm for Optimal Tunning of controller parameters in AVR system. In Proceedings of the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Sambalpur, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Jia, W.; Zhan, Y.; Sun, J.; Zhang, J.; Dai, Y. Grinding Constant Force Control based on PID Controller with Nonlinear Differential Link Optimized by Differential Evolution Algorithm. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Chengdu, China, 24–28 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4298–4303. [Google Scholar]
- Rosnani, A.A.M.; Hadi, M.S.; Jamali, A.; Darus, I.Z.M.; Yatim, H.M.; Ab Talib, M.H. Hub Angle Control of Double Link Flexible Robotic Arm Manipulator Using PID Controller Tuned by Bacterial Foraging Optimization Algorithm. In Proceedings of the 2023 13th International Conference on Power, Energy and Electrical Engineering (CPEEE), Langkawi, Malaysia, 13–15 February 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 144–148. [Google Scholar]
- Guru, N.; Prusty, A.; Pani, S.; Nanda, K.; Barisal, A.K. Intelligent control based level shifted PWM Multilevel Inverter. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Bhubaneswar, India, 15–17 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Zhai, Y.; Zhao, Q.; Han, Y.; Wang, J.; Zeng, W. Intelligent PID Controller Based on Deep Reinforcement Learning. In Proceedings of the 2024 8th International Conference on Robotics, Control and Automation (ICRCA), Sanya, China, 19–21 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 343–348. [Google Scholar]
- Abd Raof, A.I.; Hadi, M.S.; Jamali, A.; Yatim, H.M.; Ab Talib, M.H.; Darus, I.Z.M. Intelligent PID controller tuned by bacterial foraging optimization algorithm for vibration suppression of horizontal flexible structure. In Proceedings of the 2022 IEEE 8th International Conference on Smart Instrumentation, Measurement and Applications (ICSIMA), Kuala Lumpur, Malaysia, 13–15 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 237–241. [Google Scholar]
- Hua, S.; Xu, M.; Li, S.; Han, K.; Xu, Z.; Zhao, Z. Intelligent water and fertilizer control strategy of fuzzy PID optimized by swarm intelligence algorithm. In Proceedings of the 2023 2nd International Conference on Artificial Intelligence and Intelligent Information Processing (AIIIP), Xian, China, 27–29 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 262–267. [Google Scholar]
- Lanker, J.H.; Bhushan, R.; Gupta, N. Load Frequency Control of Multi Area Power System Using Meta-heuristic/Artificial Intelligence Techniques. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Bhubaneswar, India, 15–17 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Saklani, M.; Chhetri, A.; Saini, D.K.; Yadav, M.; Gupta, Y.C. Load frequency control of two area power systems using optimised ANFIS controller. In Proceedings of the 2023 5th International Conference on Energy, Power and Environment: Towards Flexible Green Energy Technologies (ICEPE), Shillong, India, 5–7 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Pattnayak, S.K.; Choudhury, S.; Nayak, N.; Bagarty, D.P.; Biswabandhya, M. Maximum power tracking & harmonic reduction on grid PV system using chaotic gravitational search algorithm based MPPT controller. In Proceedings of the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Sambalpur, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Xu, P. Neural network based self-tuning PID controller. In Proceedings of the 2022 2nd International Conference on Algorithms, High Performance Computing and Artificial Intelligence (AHPCAI), Xian, China, 21–23 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 655–661. [Google Scholar]
- Sahoo, S.; Jena, N.K.; Naik, A.K.; Sahu, B.K.; Debnath, M.K. Optimal design and implementation of fuzzy fractional order PID controller for AGC study. In Proceedings of the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Sambalpur, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Guo, B.; Zhuang, Z.; Pan, J.S.; Chu, S.C. Optimal design and simulation for PID controller using fractional-order fish migration optimization algorithm. IEEE Access 2021, 9, 8808–8819. [Google Scholar] [CrossRef]
- Chen, D.; Li, J. Optimal Design of Speed Controller in PMSM Based on Grasshopper Optimization Algorithm. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 11–14 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Sun, J.; Wu, L.; Yang, X. Optimal Fractional Order PID Controller Design for AVR System Based on Improved Genetic Algorithm. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 25–27 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 351–355. [Google Scholar]
- Oladipo, S.; Sun, Y.; Wang, Z. Optimization of FOPID controller with hybrid Particle Swarm and Grey Wolf optimization for AVR System. In Proceedings of the 2020 12th International Conference on Computational Intelligence and Communication Networks (CICN), Bhimtal, India, 5–7 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 273–279. [Google Scholar]
- Ma, T.; Ma, H.; Xue, J. Optimization of PID Parameter Tuning Based on Improved Dung Beetle Algorithm. In Proceedings of the 2024 6th International Conference on Internet of Things, Automation and Artificial Intelligence (IoTAAI), Xian, China, 19–21 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 515–520. [Google Scholar]
- Rojas-López, A.G.; Villarreal-Cervantes, M.G.; Rodríguez-Molina, A. Optimum online controller tuning through de and pso algorithms: Comparative study with bldc motor and offline controller tuning strategy. In Proceedings of the 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI), Zacatecas, Mexico, 13–15 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 215–221. [Google Scholar]
- You, M.; Wu, Y.; Wang, Y.; Xie, X.; Xu, C. Parameter optimization of PID controller based on improved sine-SOA algorithm. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 12–17. [Google Scholar]
- Ronald, R.H.; Alejandra, A.B.; Jaime, R.C.; Antonio, T.B.J. PI tuning based on Bacterial Foraging Algorithm for flow control. In Proceedings of the 2020 IX International Congress of Mechatronics Engineering and Automation (CIIMA), Mérida, Mexico, 23–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Ghith, E.S.; Tolba, F.A.A. Real-time implementation of an enhanced PID CONTROLLER based on marine predator algorithm (MPA) for micro-robotics system. In Proceedings of the 2022 3rd International Conference on Artificial Intelligence, Robotics and Control (AIRC), Dubai, United Arab Emirates, 23–25 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 40–45. [Google Scholar]
- Hussein, O.M.; Yasin, N.M. Salp Swarm Algorithm-based Position Control of a BLDC Motor. In Proceedings of the 2022 4th International Conference on Advanced Science and Engineering (ICOASE), Duhok, Iraq, 21–22 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 188–193. [Google Scholar]
- Dos Santos, G.F.; Da Silva, W.G.; Júnior, G.D.C. Tuning of pi controllers for electric drives using evolutionary multi-objective optimization algorithm. In Proceedings of the 2022 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Montevideo, Uruguay, 14–18 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Nicola, M.; Nicola, C.I. Tuning of PI speed controller for PMSM control system using computational intelligence. In Proceedings of the 2021 21st International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 18–22 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Güven, A.F.; Mengi, O.Ö. Nature-ınspired algorithms for optimizing fractional order PID controllers in time-delayed systems. Optim. Control. Appl. Methods 2024, 45, 1251–1279. [Google Scholar] [CrossRef]
- Fernando, L.; DM, L.; Garc, F.S.; Hern, N.; Nuria, G. Speed Proportional Integrative Derivative Controller: Optimization Functions in Metaheuristic Algorithms. J. Adv. Transp. 2021, 2021, 5538296. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).