Abstract
Potential applications of quantum dots in the nanotechnology industry make these systems an important field of study in various areas of physics. In particular, thermodynamics has a significant role in technological innovations. With this in mind, we studied some thermodynamic properties in quantum dots, such as entropy and heat capacity, as a function of the magnetic field over a wide range of temperatures. The density of states plays an important role in our analyses. At low temperatures, the variation in the magnetic field induces an oscillatory behavior in all thermodynamic properties. The depopulation of subbands is the trigger for the appearance of the oscillations.
1. Introduction
The study of the two-dimensional electron gas (2DEG) is crucial for understanding physical phenomena in semiconductor materials, offering valuable insights into charge transport [1], high-mobility phenomena [2], and quantum properties in nanostructures [3,4], all pivotal for advancements in electronics and nanotechnological devices [5,6,7]. 2DEG has been used to describe the physics of various mesoscopic models to study the properties of quantum dots [8,9,10,11], quantum rings [12,13,14,15,16], and other effective theories [17,18,19]. Over the years, extensive research has focused on the thermodynamics of a two-dimensional electron gas and its dependence on magnetic fields. Experimental data reveal that equilibrium properties at low temperatures exhibit oscillations depending on the magnetic field strength [20,21,22]. Theoretically, when a magnetic field is applied perpendicular to the 2DEG plane, degenerate energy levels, the Landau levels, are formed [23]. This characteristic is the basis for the oscillatory behavior of all thermodynamic properties, such as the oscillations observed in heat capacity, chemical potential, and de Haas–van Alphen oscillations (dHvA effect) in magnetization [24,25,26,27,28]. Chemical potential plays an important role in understanding oscillations. Hence, importance is given to the study of the dependence of chemical potential on the magnetic field and temperature [29].
The investigation into the thermodynamic properties of semiconductor quantum dots, as pursued in this study, plays an important role in comprehending the behavior of these nanostructures under diverse conditions [30,31,32,33,34,35,36,37]. Exact energy spectra and wave functions are obtained analytically when a parabolic potential models a quantum dot. In contrast to the Landau levels, accidental degenerations occur when the magnetic field varies [38]. This behavior is responsible for much of the new physics uncovered in the quantum dot systems [39]. Determining electronic states, internal energy, magnetization, Helmholtz free energy, specific heat, and entropy contributes to the fundamental understanding required for harnessing these materials in various technological applications. In this work, we offer an alternative approach for exploring thermodynamic properties, relying on density of states (DOS) calculations rather than the grand partition function approach commonly found in the literature (see, e.g., Ref. [40]). We employ the canonical ensemble, where the number of particles in the quantum dot remains fixed while the system exchanges energy with a thermal reservoir. This approach allows us to study temperature-dependent thermodynamic properties without changing the number of electrons in the system.
The structure of our article is presented as follows. In Section 2, we present the model that describes the motion of an electron with effective mass and electric charge confined by a radial potential in the presence of a uniform magnetic field along the z-direction. We derive the Schrödinger equation for the system and determine the eigenvalues of energy and corresponding wave functions. Next, we present the density of the model’s states. Section 3 is dedicated to studying the chemical potential of the system, particularly considering the scenario of a semiconductor quantum dot with multiple electrons. We explore the Fermi energy and its relationship with the physical parameters involved. In Section 4, we examine the magnetization as a function of the magnetic field at different temperatures. Section 5 is dedicated to the study of the system’s entropy. We take the opportunity to present an important physical phenomenon, the magnetocaloric effect, which consists of the variation in temperature as a function of the magnetic field. In Section 6, we study the heat capacity of a two-dimensional electron gas in a quantum dot. Our conclusions are given in Section 7.
2. Description of the Model
In this section, we describe the model of an electron with effective mass and charge e confined by a radial potential and under the influence of a uniform magnetic field along the z-direction. The motion of the particle is governed by the Schrödinger equation with minimal coupling
where is the momentum operator and denotes the vector potential. In this formulation, we adopt the symmetric gauge vector potential given by
where B represents the magnetic field strength. Additionally, the confinement potential is given by [41]
where . This potential has a minimum at . Furthermore, it can be shown that , which defines the strength of the transverse confinement. It is known that any variation in parameters and implies changes in the spatial distribution of the electron. The radial potential is a model for the theoretical definition of a ring of average radius with finite width. However, it can also describe other systems, such as a quantum dot with the condition . The radial potential creates an environment where the electron’s quantum properties are highlighted, giving rise to phenomena such as confinement and discrete energy level structures. Through the model of the interaction of an electron with the magnetic field at a radial potential, we can explore phenomena such as bound-state formation, discrete energy spectra, and spatial confinement effects. These aspects are fundamental for understanding the physics of nanostructured systems and their potential applications in quantum devices.
The energy eigenvalues and wavefunctions of Equation (1) are given, respectively, by
and
where is the effective angular moment, is the radial quantum number, which denotes a subband, is the magnetic quantum number. Also, is the confluent hypergeometric function of the first kind, is the effective cyclotron frequency, is the cyclotron frequency, and is the effective magnetic length.
By using Equation (4), we can show that the minimum energy of a subband is given by
and the separation energy between the bottoms of neighboring subbands is .
In a ring, the number of states at energy E in a subband is given by
where
and is the Heaviside function. From this result, we compute the density of states of a subband:
The density of states of a two-dimensional quantum ring has poles at , which leads to the appearance of Van Hove singularities [42].
In this work, we focus on the case of a quantum dot. So, the density of states of a subband is reduced to
The total density of states takes a ladder-like function. For a quantum dot, the parameter is the number of states in a subband in energy interval . The density of states is of fundamental importance in studies of a 2DEG. This parameter is directly derivable from measurable properties such as magnetization, capacitance, and heat capacity [21,28].
In the subsequent sections, we study the dependence of some thermodynamic properties of quantum dots on temperature and magnetic field. For numerical analysis, we consider a sample made of GaAs with the effective mass of the electron , where is the electron mass. We also consider that there are spinless electrons. The confinement energy parameter used for this purpose is meV [43].
3. Chemical Potential
The Fermi energy corresponds to the energy of the topmost filled level in the N electron system [42]. Furthermore, a subband at the Fermi energy is only partially occupied. With that in mind, we can define the Fermi energy as
In this equation, corresponds to the highest occupied subband at the Fermi energy, and . These parameters are given, respectively, by
where denotes the largest integer less than or equal to x, , and
By using the results above, we can also express the Fermi energy as a function of the parameter and the filling factor as
It is worth noting that an expression for Fermi energy as a function of the square root of number electrons N and the frequencies and was obtained in Ref. [44], where the authors use a geometric approach to study some physical properties of quantum dots. Such a result corresponds to the case when in Equation (14). Comparing Equations (6) and (11), this particular case tells us that the Fermi energy is located at the bottom of the subband, i.e., when the subband is nearly depleted. These are the points at which the model from Ref. [44] coincides with the exact results.
So far, we have considered the ideal case of zero temperature. However, from the density of states, given by Equation (10), we can obtain the chemical potential and magnetization at any temperature. In addition, other thermodynamic properties that depend on temperature can be accessed, such as the heat capacity of electrons and the system’s entropy. In that case, the number of electrons is computed as [22,42]
In this equation, is given by Equation (10), and is the Fermi–Dirac distribution function, given by
where is chemical potential and is the Boltzmann constant. In a system at temperature T containing N electrons, the chemical potential is calculated from Equation (15). In the limit , the chemical potential corresponds to the Fermi energy given by Equation (11).
Figure 1 shows the dependence of the chemical potential on the magnetic field at different temperatures. In Figure 1a, the black and brown lines correspond to the Fermi energy computed from Equation (11) and self-consistently [45], respectively. As we can see, our approach leads to an excellent agreement on the exact result. Nevertheless, our model considers a continuous density of states of a subband, meaning some results are not observed. In Section 4, we will return to this question. The oscillations, consisting of a series of almost parabolas with cusps pointing upward, are attributed to the depopulation of energy subbands when the magnetic field increases. Peaks occur when the Fermi energy is at the bottom of a subband, which, as noted above, occurs with the condition . Thus, Equation (13) provides
which corresponds to the magnetic field values for the oscillations to take maximum value. This result was also obtained in Ref. [44]. Another result that we can obtain from Equation (17) is that increasing the confinement intensity leads to the shift of the peaks to higher magnetic fields. However, there is no increase in the number of oscillations. We can verify this result by noting that the number of oscillations depends on the number of subbands occupied when , which we can obtain from Equation (12). Therefore, increasing the confinement energy leads to a reduction in the magnetic field effects. Increasing the confinement energy also increases the Fermi energy. The shift of peaks to higher magnetic fields also occurs if the number of electrons N increases. In this case, there is also an increase in the number of oscillations. Equation (8) shows that increases with the square of the magnetic fields. The parameter is small for weak magnetic fields, so many occupied subbands are required to accommodate 1400 electrons. Furthermore, the depopulation of subbands is rapid. For strong magnetic fields, it is the opposite; namely, is large such that few occupied subbands are needed, and depopulation occurs over a larger magnetic field range. This explains both the increase in the amplitude and the increased period of the oscillations. Exactly when the subband with is completely depopulated, such that all electrons can be fitted into the subband with . In this case, there are no more oscillations. The quantum dot states tend to the usual Landau quantization in the range of strong magnetic fields.

Figure 1.
(a) The black line corresponds to the chemical potential at computed from Equation (11). To compare with exact results, we also plot the Fermi energy computed self-consistently (line brown). In (b,c), the red and blue lines correspond to the chemical potential at finite temperatures obtained from Equation (15). We plot the chemical potential at (black line) to better visualize the temperature effect. The dashed lines in (a–c) show the position at which subbands with are depopulated. The corresponding magnetic fields are obtained from Equation (17).
For finite temperatures, Figure 1b,c show that the oscillations are softened and washed out. Furthermore, we can observe the decrease in chemical potential at finite temperatures. Indeed, as the number of electrons N must remain constant, the chemical potential must decrease with increasing temperature. In the high-temperature regime, the role played by subband depopulation is less important.
4. Magnetization
At zero temperature, the magnetization of a system containing a fixed number N of electrons is given by , where U is the total internal energy, which is computed from
Since the density of states is independent of the energy range considered, the total internal energy is easily calculated:
Consequently, we can show that the magnetization is given by
where .
For magnetic fields in which only the subband with is occupied, we can show from Equation (20) that the magnetization is given by
For strong magnetic fields, , while . Consequently, the absolute value of magnetization tends to .
The magnetization for non-zero temperatures is given by
where F, the free energy, is computed as
Figure 2 shows the dependence of magnetization on the magnetic field at different temperatures. The oscillations correspond to the dHvA effect. In Figure 2a, the black line corresponds to the magnetization computed from Equation (20). The brown line corresponds to the exact magnetization results. Here, we understand the question raised in Section 3 about the density of states. It is a well-known result in the literature that in addition to dHvA-type oscillations, there is also a second oscillation in the magnetization of low-dimensional systems. These oscillations are associated with crossing states and are defined as AB-type oscillations [43]. For low magnetic fields, where , the AB-type oscillations superimpose on the dHvA-type oscillations. For strong magnetic fields, where , it is the opposite; AB-type oscillations are suppressed by increasing the magnetic field, while the amplitude of dHvA-type oscillations increases. This is precisely the situation presented by the brown line in Figure 2a. In our model, the density of states is a continuous parameter. As a result, AB-type oscillations are not observed. We emphasize the small amplitudes of these oscillations, particularly in the regime of strong magnetic fields. As a consequence, the amplitude of these oscillations decreases at temperatures lower than those shown in Figure 2b,c [16].

Figure 2.
(a) The black line corresponds to the magnetization at computed from Equation (20). We also plot the exact magnetization results (brown line) for comparison. In (b,c), the red and blue lines correspond to the magnetization at finite temperatures obtained from Equation (22). The dashed lines in (a–c) show the position at which subbands with are depopulated. The corresponding magnetic fields are obtained from Equation (17).
5. Entropy
The entropy of the system is computed from . Using F given by Equation (23), we write the entropy as
Figure 3 shows entropy as a function of the magnetic field in different temperatures. From Figure 3a, we can see that the entropy oscillations are almost perfectly sawtoothlike for lower temperatures. The vertical dashed lines, which correspond to the B values given by Equation (17), show that at each dHvA period, the entropy is pinned to its value at zero magnetic fields. Entropy is assigned to the states of a subband within an energy range of the chemical potential that can be thermally excited to higher levels. Far from the bottom of a subband, in the ranges of magnetic fields where the chemical potential is equivalent to the Fermi energy, the entropy is approximately given by [46].
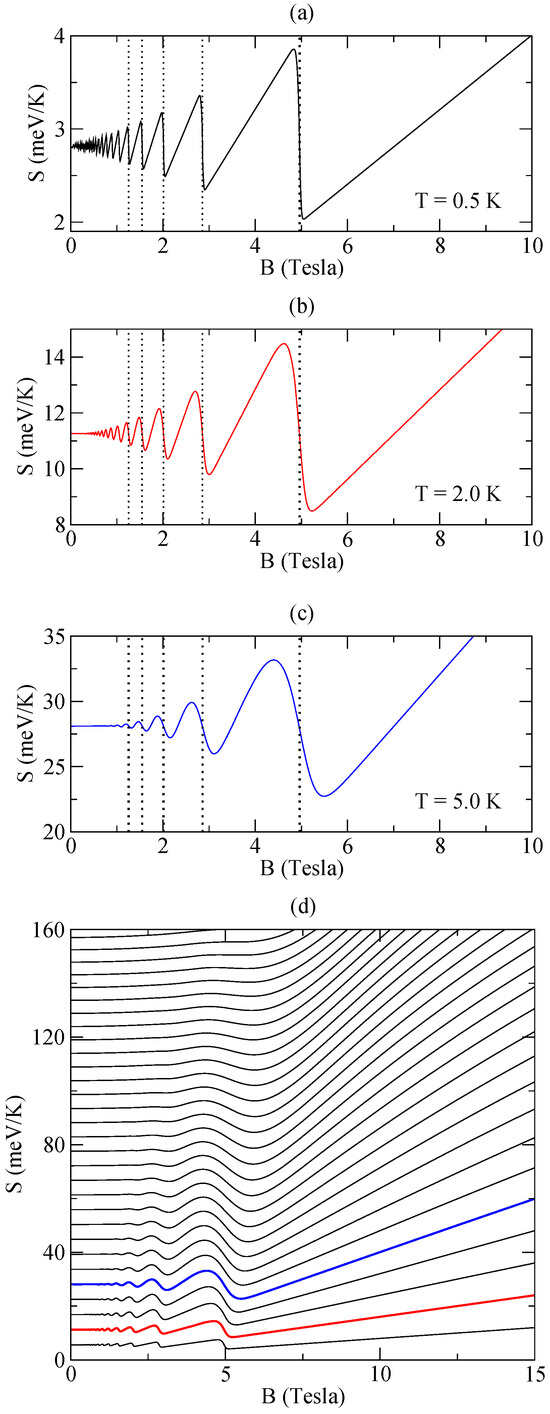
Figure 3.
Entropy (Equation (24)) as a function of the magnetic field in a wide range of temperatures. The dashed lines in (a–c) show the position at which subbands with are depopulated. The corresponding magnetic fields are obtained from Equation (17). In (d), temperatures vary from K to K, with a range of K. The curves highlighted in red and blue correspond to temperatures of K and K, respectively.
As , , in accordance with the third law of thermodynamics. On the other hand, near the bottom of a subband, the contribution of thermally excited states of the subband that is being depopulated decreases, which implies a reduction in the system’s entropy. When the contribution from the lower subbands prevails, the entropy increases again with the increase in the magnetic field. Although entropy is an increasing function of temperature, the dependence is not always linear. For example, in strong magnetic fields, the rate of entropy change is high at low temperatures; at high temperatures, it is the opposite. This result can be seen in Figure 3c.
In a thermally isolated system, there is no exchange of energy, and any process that occurs must be carried out adiabatically, i.e., the entropy must remain constant. As described above, entropy presents a complex pattern as a function of the magnetic field in different temperature regimes. In this context, for entropy to remain constant for all magnetic field values, the temperature must be a function of the magnetic field; this is the definition of the magnetocaloric effect [25,35]. The magnetocaloric effect is said to be normal when the temperature increases with the magnetic field. Figure 4 shows that this scenario occurs when the chemical potential is close to the bottom of a subband. On the other hand, when the temperature decreases with an increase in the magnetic field, we have the inverse magnetocaloric effect. Figure 4 shows that this scenario occurs when the chemical potential is far from the bottom of a subband. In particular, the inverse magnetocaloric effect occurs in the range of strong magnetic fields occupied by a single subband. This is also the case when the initial temperature is very high, as we can infer from Figure 3c. In Refs. [47,48], Reis addressed the connection of oscillations found in thermodynamic quantities of diamagnetic materials with potential applications due to its inverse and normal magnetocaloric effect at low temperatures. Furthermore, quantum dots stimulate theoretical and experimental research, given the variety of applicability of these heterostructures. This information reinforces our results as a basis for future applications.

Figure 4.
Temperature as a function of the magnetic field. The dashed lines in (a,b) show the position at which subbands with are depopulated. The corresponding magnetic fields are obtained from Equation (17).
6. Heat Capacity
The heat capacity of the electron gas is given in general as
Following the same procedures as in Ref. [25], we can show that the heat capacity can be written as
where we define the parameter as
Figure 5 exhibits the effect of the interplay between temperature and magnetic fields on the heat capacity. Figure 5a shows that, in the low-temperature regime, heat capacity has a similar pattern to entropy, as we can see by comparing Figure 3a and Figure 5a. Indeed, at low temperatures, , with S given by Equation (25). Therefore, we recover the results from the literature, namely, the heat capacity is proportional to both the density of states and the temperature [42]. However, we can see that additional oscillations appear when a subband is depopulated. Figure 5b,c show this behavior more clearly. Oh et al. also observed this oscillatory behavior when studying the heat capacity of quantum wires and spherical dots [31]. In a subband, the excited states in a thickness below the chemical potential and the upper levels above the chemical potential contribute separately to the heat capacity. When the chemical potential approaches the bottom of a subband, there is a reduction in the number of states below the chemical potential, which implies a decrease in heat capacity. In this process, the number of available states above the chemical potential does not decrease. Consequently, as soon as the contribution of these states prevails, the heat capacity increases again. However, as the magnetic field increases and the chemical potential moves away from the bottom of a subband, the number of available states above the chemical potential also decreases. This, again, leads to a decrease in heat capacity.
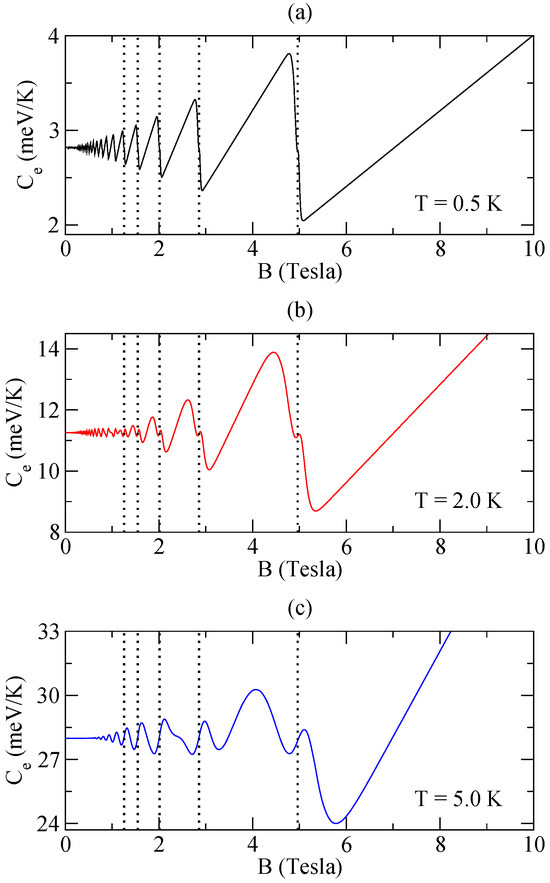

Figure 5.
Heat capacity (Equation (27)) as a function of the magnetic field in a wide range of temperatures. The dashed lines in (a–c) show the position at which subbands with are depopulated. The corresponding magnetic fields are obtained from Equation (17). In (d), temperatures vary from K to K, with a range of K. The curves highlighted in red and blue correspond to temperatures of K and K, respectively.
As the temperature increases, Figure 5d shows another very interesting behavior in the heat capacity of quantum dots in the range of strong magnetic fields, namely, the heat capacity presents a bump followed by a decrease until an apparent saturation value. The saturation value corresponds to , where N is the number of electrons in the sample. At lower temperatures, the saturation value is reached in very strong magnetic fields. On the other hand, for a fixed magnetic field value, we also verified (although not shown here) that at very high temperatures, the heat capacity tends to the value . Therefore, there is a competition between the magnetic field and temperature. This behavior is in agreement with what has been found in Ref. [35], where the authors use the partition function to explore the thermodynamic properties of quantum dots as a temperature function for different magnetic field values.
7. Conclusions
In this study, we have developed a model from which we extract the density of states of a 2DEG confined in a quantum dot. To test the model’s validity, we compared our approach with known results from the literature and verified great accuracy.
One of the key observations of this study is the richness of phenomena observed in the thermodynamic properties of the quantum dot. We found that the presence of a magnetic field leads to distinct oscillations in the system’s chemical potential, magnetization, entropy, and heat capacity, resulting from the depopulation of energy subbands as the magnetic field is increased. These oscillations reveal important information about the system’s energy structure and are crucial for understanding the physics of nanostructured systems.
Furthermore, we observed that temperature plays a significant role in the thermodynamic properties of the system. Temperature variation influences the distribution of electrons in different energy subbands, directly affecting the entropy and heat capacity of the system. We observed phenomena such as the magnetocaloric effect, where the applied magnetic field modulates the system’s temperature. In addition, two interesting aspects are observed in the heat capacity. First is the appearance of additional oscillations as the temperature increases. The second is the behavior of the heat capacity of a quantum dot when subjected to strong magnetic fields. These aspects suggest complex behaviors in the distribution of energy of confined electrons.
In summary, this study provides valuable insights into the effects of temperature and magnetic field on the thermodynamic properties of quantum dots. Additionally, the observations and results obtained here may be useful for developing new technologies in quantum devices and for the fundamental understanding of the physics of nanostructured systems.
Author Contributions
L.F.C.P.: conceptualization, methodology, preparation, writing—review and editing, software, supervision; E.O.S.: conceptualization, methodology, software, supervision, writing—original draft preparation, writing—review and editing, project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Brazilian agencies CAPES, CNPq, and FAPEMA. E. O. Silva acknowledges CNPq Grant 306308/2022-3, FAPEMA Grants UNIVERSAL-06395/22 and APP-12256/22. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank A. Queiroz, S. Queiroz and V. Queiroz for their comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sawa, Y.; Yokoyama, T.; Tanaka, Y. Charge transport in 2DEG/s-wave superconductor junction with Dresselhaus-type spin–orbit coupling. J. Magn. Magn. Mater. 2007, 310, 2277–2279. [Google Scholar] [CrossRef]
- Wang, Z.T.; Hilke, M.; Fong, N.; Austing, D.G.; Studenikin, S.A.; West, K.W.; Pfeiffer, L.N. Nonlinear transport phenomena and current-induced hydrodynamics in ultrahigh mobility two-dimensional electron gas. Phys. Rev. B 2023, 107, 195406. [Google Scholar] [CrossRef]
- Dini, K.; Kibis, O.V.; Shelykh, I.A. Magnetic properties of a two-dimensional electron gas strongly coupled to light. Phys. Rev. B 2016, 93, 235411. [Google Scholar] [CrossRef]
- Beenakker, C.; van Houten, H. Quantum Transport in Semiconductor Nanostructures. In Semiconductor Heterostructures and Nanostructures; Solid State Physics; Ehrenreich, H., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1991; Volume 44, pp. 1–228. [Google Scholar] [CrossRef]
- Wong, K.Y.; Tang, W.; Lau, K.M.; Chen, K.J. Two-dimensional electron gas (2DEG) IDT SAW devices on AlGaN/GaN heterostructure. In Proceedings of the 2007 7th IEEE Conference on Nanotechnology (IEEE NANO), Hong Kong, China, 2–5 August 2007; pp. 1041–1044. [Google Scholar] [CrossRef]
- Casparis, L.; Connolly, M.R.; Kjaergaard, M.; Pearson, N.J.; Kringhøj, A.; Larsen, T.W.; Kuemmeth, F.; Wang, T.; Thomas, C.; Gronin, S.; et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotechnol. 2018, 13, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.T.; Fischer, I.A.; Tang, J.; Wang, C.Y.; Yu, G.; Fan, Y.; Murata, K.; Nie, T.; Oehme, M.; Schulze, J.; et al. Electrical detection of spin transport in Si two-dimensional electron gas systems. Nanotechnology 2016, 27, 365701. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, V.; Mughnetsyan, V.; Abdullah, N.R.; Tang, C.S.; Moldoveanu, V.; Manolescu, A. Unified approach to cyclotron and plasmon resonances in a periodic two-dimensional GaAs electron gas hosting the Hofstadter butterfly. Phys. Rev. B 2022, 105, 155302. [Google Scholar] [CrossRef]
- Mickelsen, D.L.; Carruzzo, H.M.; Coppersmith, S.N.; Yu, C.C. Effects of temperature fluctuations on charge noise in quantum dot qubits. Phys. Rev. B 2023, 108, 075303. [Google Scholar] [CrossRef]
- Filgueiras, C.; Rojas, M.; Aciole, G.; Silva, E.O. Landau quantization, Aharonov–Bohm effect and two-dimensional pseudoharmonic quantum dot around a screw dislocation. Phys. Lett. A 2016, 380, 3847–3853. [Google Scholar] [CrossRef]
- Wang, Q.; ten Haaf, S.L.D.; Kulesh, I.; Xiao, D.; Thomas, C.; Manfra, M.J.; Goswami, S. Triplet correlations in Cooper pair splitters realized in a two-dimensional electron gas. Nat. Commun. 2023, 14, 4876. [Google Scholar] [CrossRef]
- Lima, D.F.; dos S. Azevedo, F.; Pereira, L.F.C.; Filgueiras, C.; Silva, E.O. Optical and electronic properties of a two-dimensional quantum ring under rotating effects. Ann. Phys. 2023, 459, 169547. [Google Scholar] [CrossRef]
- Pereira, L.F.C.; Silva, E.O. Modification of Landau Levels in a 2D Ring Due to Rotation Effects and Edge States. Annalen der Physik 2023, 535, 2200371. [Google Scholar] [CrossRef]
- Pereira, L.F.C.; Andrade, F.M.; Filgueiras, C.; Silva, E.O. Effects of Curvature on the Electronic States of a Two-Dimensional Mesoscopic Ring. Few-Body Syst. 2022, 63, 64. [Google Scholar] [CrossRef]
- Pereira, L.F.C.; Cunha, M.M.; Silva, E.O. 1D Quantum ring: A Toy Model Describing Noninertial Effects on Electronic States, Persistent Current and Magnetization. Few-Body Syst. 2022, 63, 58. [Google Scholar] [CrossRef]
- Pereira, L.F.C.; Andrade, F.M.; Filgueiras, C.; Silva, E.O. Study of electronic properties, magnetization and persistent currents in a mesoscopic ring by controlled curvature. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 132, 114760. [Google Scholar] [CrossRef]
- Souza, P.H.; Silva, E.O.; Rojas, M.; Filgueiras, C. A Curved Noninteracting 2D Electron Gas with Anisotropic Mass. Ann. Phys. 2018, 530, 1800112. [Google Scholar] [CrossRef]
- Filgueiras, C.; Silva, E.O. 2DEG on a cylindrical shell with a screw dislocation. Phys. Lett. A 2015, 379, 2110–2115. [Google Scholar] [CrossRef]
- da Silva Leite, L.; Filgueiras, C.; Cogollo, D.; Silva, E.O. Influence of spatially varying pseudo-magnetic field on a 2D electron gas in graphene. Phys. Lett. A 2015, 379, 907–911. [Google Scholar] [CrossRef]
- Gornik, E.; Lassnig, R.; Strasser, G.; Störmer, H.L.; Gossard, A.C.; Wiegmann, W. Specific Heat of Two-Dimensional Electrons in GaAs-GaAlAs Multilayers. Phys. Rev. Lett. 1985, 54, 1820–1823. [Google Scholar] [CrossRef]
- Wang, J.K.; Tsui, D.C.; Santos, M.; Shayegan, M. Heat-capacity study of two-dimensional electrons in GaAs/AlxGa1−xAs multiple-quantum-well structures in high magnetic fields: Spin-split Landau levels. Phys. Rev. B 1992, 45, 4384–4389. [Google Scholar] [CrossRef]
- Schwarz, M.P.; Wilde, M.A.; Groth, S.; Grundler, D.; Heyn, C.; Heitmann, D. Sawtoothlike de Haas–van Alphen oscillations of a two-dimensional electron system. Phys. Rev. B 2002, 65, 245315. [Google Scholar] [CrossRef]
- Heinzel, T. Mesoscopic Electronics in Solid State Nanostructures; John Wiley & Sons: Weinheim, Germany, 2006. [Google Scholar]
- Vagner, I.D.; Maniv, T.; Ehrenfreund, E. Ideally Conducting Phases in Quasi Two-Dimensional Conductors. Phys. Rev. Lett. 1983, 51, 1700–1703. [Google Scholar] [CrossRef]
- Zawadzki, W.; Lassnig, R. Specific heat and magneto-thermal oscillations of two-dimensional electron gas in a magnetic field. Solid State Commun. 1984, 50, 537–539. [Google Scholar] [CrossRef]
- Gammag, R.; Villagonzalo, C. The interplay of Landau level broadening and temperature on two-dimensional electron systems. Solid State Commun. 2008, 146, 487–490. [Google Scholar] [CrossRef]
- Fezai, I.; Jaziri, S. Thermodynamic properties of Landau levels in InSb two-dimensional electron gas. Superlattices Microstruct. 2013, 59, 60–65. [Google Scholar] [CrossRef]
- Hidalgo, M.A. Equilibrium properties of 2D electron systems in quantum wells and graphene. Eur. Phys. J. Plus 2023, 138, 983. [Google Scholar] [CrossRef]
- Vagner, I.D. Thermodynamics of two-dimensional electrons on Landau levels. HIT J. Sci. Eng. A 2006, 3, 102–152. [Google Scholar]
- De Groote, J.J.S.; Hornos, J.E.M.; Chaplik, A.V. Thermodynamic properties of quantum dots in a magnetic field. Phys. Rev. B 1992, 46, 12773–12776. [Google Scholar] [CrossRef]
- Oh, J.; Chang, K.J.; Ihm, G.; Lee, S. Electronic heat-capacity in quantum wires and dots under magnetic-fields. J. Korean Phys. Soc. 1995, 28, 132–135. [Google Scholar]
- Nguyen, N.T.T.; Peeters, F.M. Magnetic field dependence of the many-electron states in a magnetic quantum dot: The ferromagnetic-antiferromagnetic transition. Phys. Rev. B 2008, 78, 045321. [Google Scholar] [CrossRef]
- Boyacioglu, B.; Chatterjee, A. Heat capacity and entropy of a GaAs quantum dot with Gaussian confinement. J. Appl. Phys. 2012, 112, 083514. [Google Scholar] [CrossRef]
- Castaño-Yepes, J.; Ramirez-Gutierrez, C.; Correa-Gallego, H.; Gómez, E.A. A comparative study on heat capacity, magnetization and magnetic susceptibility for a GaAs quantum dot with asymmetric confinement. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 103, 464–470. [Google Scholar] [CrossRef]
- Negrete, O.; Peña, F.; Florez, J.; Vargas, P. Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem" and Its Extension to Quantum Dots. Entropy 2018, 20, 557. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; Negrete, O.; Alvarado Barrios, G.; Zambrano, D.; González, A.; Nunez, A.S.; Orellana, P.A.; Vargas, P. Magnetic Otto Engine for an Electron in a Quantum Dot: Classical and Quantum Approach. Entropy 2019, 21, 512. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.F.C.; Andrade, F.M.; Filgueiras, C.; Silva, E.O. Modifications of Electron States, Magnetization, and Persistent Current in a Quantum Dot by Controlled Curvature. Ann. Phys. 2019, 531, 1900254. [Google Scholar] [CrossRef]
- Reimann, S.M.; Manninen, M. Electronic structure of quantum dots. Rev. Mod. Phys. 2002, 74, 1283. [Google Scholar] [CrossRef]
- Kushwaha, M.S. Plasmons and magnetoplasmons in semiconductor heterostructures. Surf. Sci. Rep. 2001, 41, 1–416. [Google Scholar] [CrossRef]
- Meir, Y.; Entin-Wohlman, O.; Gefen, Y. Magnetic-field and spin-orbit interaction in restricted geometries: Solvable models. Phys. Rev. B 1990, 42, 8351–8360. [Google Scholar] [CrossRef]
- Tan, W.; Inkson, J. Electron states in a two-dimensional ring-an exactly soluble model. Semicond. Sci. Technol. 1996, 11, 1635. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Tan, W.C.; Inkson, J.C. Magnetization, persistent currents, and their relation in quantum rings and dots. Phys. Rev. B 1999, 60, 5626–5635. [Google Scholar] [CrossRef]
- de Lira, F.A.; Silva, E.O. Theoretical approach for the description of a single quantum dot using geometry. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 147, 115617. [Google Scholar] [CrossRef]
- Kushwaha, M.S. Magneto-optical absorption in semiconducting spherical quantum dots: Influence of the dot-size, confining potential, and magnetic field. AIP Adv. 2014, 4, 127151. [Google Scholar] [CrossRef]
- Dense Gases – Ideal Gases at Low Temperature. In Statistical Physics: An Introduction; Springer: Berlin/Heidelberg, Germany, 2007; pp. 147–181. [CrossRef]
- Reis, M.S. Oscillating magnetocaloric effect. Appl. Phys. Lett. 2011, 99, 052511. [Google Scholar] [CrossRef]
- Reis, M. Oscillating adiabatic temperature change of diamagnetic materials. Solid State Commun. 2012, 152, 921–923. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).