Abstract
The purpose of this study is to investigate the uncertainty of the design variables of a front suspension lower control arm under fatigue-loading circumstances to estimate a reliable and robust product. This study offers a method for systematic uncertainty quantification (UQ), and the following steps were taken to achieve this: First, a finite element model was built to predict the fatigue life of the control arm under bump-loading conditions. Second, a sensitivity scheme, based on one of the global analyses, was developed to identify the model’s most and least significant design input variables. Third, physics-based and data-driven uncertainty quantification schemes were employed to quantify the model’s input parameter uncertainties via a Monte Carlo simulation. The simulations were conducted using 10,000 samples of material properties and geometrical uncertainty variables, with the coefficients of variation ranging from 1 to 3%. Finally, the confidence interval results show a deviation of about 21.74% from the mean (the baseline). As a result, by applying systematic UQ, a more reliable and robust automobile suspension control arm can be designed during the early stages of design to produce a more efficient and better approximation of fatigue life under uncertain conditions.
1. Introduction
Over the past few decades, structural optimization has become increasingly significant in the automobile sector. The suspension system is one of the car’s most crucial subsystems; it is responsible for protecting the vehicle’s chassis and other components from road shocks, as well as for ensuring stability, comfort, and safety. The suspension system supports the weight of the entire vehicle. One of the independent suspension system designs used in vehicles is the double wishbone suspension system, which employs lower and upper control arms. Forces are transferred from the automobile wheels to the control arm via the ball joint assembly to the wheel as the vehicle crosses over bumps, speed bumps, and other obstacles. Control arms can bend or break when driving over major potholes or can become worn out due to brushing, indicating that the multiaxial loadings associated with many sources of uncertainty are applied to the control arms.
Understanding and managing uncertainty has become increasingly important in the automotive sector to progress the design process, optimize manufacturing procedures, and improve day-to-day technical operations. Areas where uncertainty exists include data collection, processing and interpretation, system modeling, production processes, and operational settings. On the other hand, modern systems require more sophisticated and critical designs that must operate with great dependability, tight safety margins, and high performance. Design approaches for analyzing uncertainty have become more popular as a result and are now being applied in the context of interdisciplinary design [1,2].
The stimulation frequencies of road bumps or speed breakers can cause fatigue damage and dynamic amplification to the suspension’s control arm structure. To ensure service life, it is crucial to take into account the uncertainty in models and parameters. Fatigue damage calculations contain several parameters and combinations of conditions to account for realistic operating scenarios. Although accounting for the variability of some characteristics, such as material qualities and model geometry, is standard practice in the industry, other parameters are typically treated as constants despite data suggesting they may fluctuate dramatically [3]. To understand their significance in terms of the structural response and dependability of the suspension control arm, it is necessary to study these variables. Therefore, the sensitivity of the variables must be addressed before the uncertainty quantification analysis.
The need to identify the most influential factors in the design of support structures, such as suspension control arms, has made sensitivity analysis a popular area of interest in mechanical components. However, determining such values can be challenging due to the complexity of structural design, which includes design requirements, intricate nonlinear models, and numerous input model parameters, all of which significantly increase the uncertainty of the sensitivity results. Researchers from various fields recommend using global sensitivity analysis to account for model uncertainties and nonlinearities in the sensitivity results [4]. Global sensitivity analysis examines the individual and combined effects of the uncertainty of each input parameter on the total variance of the response to determine the most relevant input model parameters. Consequently, a comprehensive examination of the design space that considers interactions between input model parameters can be carried out, providing more reliable sensitivity indices [5]. Global sensitivity analysis has been widely used in the field of structural design due to its advantages. However, previous studies have not provided clear conclusions on which factors to either discard or prioritize (known as model reduction and prioritizing) [6,7] due to the inconsistent selection of input model parameters and the lack of unambiguous convergence metrics. To address this problem, it has been suggested to use multiple global sensitivity analysis methods. For example, rank regression and the Morris methodology, also known as types of elementary effects approaches, have been used with good agreement [4]. However, these methods are not robust enough to identify the most crucial characteristics, and they are limited as researchers will use them before adopting more advanced techniques [5]. Sobol indices, a type of analysis of variance approach, have been successfully used in models with uncorrelated inputs, and are frequently used as a baseline for alternative sensitivity approaches [4,8]. They are able to distinguish between influential and non-influential characteristics, as well as the impacts of their interactions. However, they are computationally expensive and cannot be used for complex models with numerous input parameters as their accuracy highly depends on the number of simulations needed to reach convergence [9].
In order to improve the effectiveness of Sobol’s approach, additional sampling methods and metamodels (surrogate models) have been suggested. Furthermore, the use of metamodels in conjunction with Monte Carlo (MC) simulation has been shown to produce more accurate results than those found in their sampling counterparts [4]. Even though metamodels have been extensively used to quantify uncertainty in mechanical component structures, they have not yet been used in combination with Sobol’s global sensitivity analysis to assist in the design of suspension control arms under fatigue stresses. Therefore, it is necessary to develop sensitivity schemes that enhance the effectiveness and decision making of current sensitivity analyses in the design for fatigue resistance.
Therefore, it is crucial to compute how uncertainties affect model predictions. This study suggested an uncertainty propagation and sensitivity analyses platform in order to measure the variability in fatigue responses of the front-lower suspension control arm. For the sensitivity analysis of the suspension control arm, the Sobol indices approach was suggested, and a Morris one-step-at-a-time (MOAT) parameter screening method [10] was applied for comparison. Surrogate models were compared to replace the computationally expensive finite-element analysis in COMSOL Multiphysics version 6.1 by generating a training sample data using Latin hypercubes (LHCs). A surrogate-based Monte Carlo simulation was then performed to determine the suspension’s lower control arm fatigue life uncertainty. Finally, confidence intervals were computed to quantify the uncertainty in the fatigue life of the lower control arm of the automobile suspension.
The remaining parts of this study are organized as follows: Section 2 explains the details of uncertainty in the fatigue for suspension control arms. Section 3 presents the study methodology, which includes the computational method, fatigue life prediction model, sensitivity analysis scheme, uncertainty propagation model, and surrogate model formulation. The results and discussion are provided in Section 4. Finally, Section 5 provides the study’s conclusion.
2. Uncertainties in Fatigue
Fatigue failure is a common problem in engineering practice, and it can occur randomly. It is particularly challenging to ensure the fatigue resistance of engineering components under specific loading regimes since service conditions and material qualities often fluctuate [11,12,13,14]. Conventional strain-life or stress-life curves that represent only the average response of interest have been shown to be inadequate by [15]. Therefore, probabilistic approaches that take these uncertainties into account are used in practical engineering. In this analysis, probabilistic fatigue modeling is carried out by integrating FE analysis with the Latin hypercube sampling (LHS) technique, which considers the material properties of variability and geometrical uncertainty as capable of producing statistical properties.
The structural engineer is particularly interested in a material’s modulus of elasticity since its value is essential for instability failure scenarios. Even in research that deals with mechanical property variability, Young’s modulus is frequently considered deterministically. However, Galambos and Ravindra [16] addressed the diversity in elastic modulus values and presented important research in this field. For both the tension and compression elastic modulus behavior, they proposed a coefficient of variation (COV) of 0.06 based on the available data at the time. Mansour et al. [17] also researched the variability of Young’s modulus and proposed a COV of 0.031. However, they agreed that the distribution should be normal. Therefore, the COV for this study was set to 0.03 in order to examine fatigue uncertainty within the smaller variability of Young’s modulus under the assumption of a normal distribution; the same COV was also applied to Poisson’s ratio.
Furthermore, the geometrical tolerances between actual and design dimensions are unavoidable due to manufacturing processes or design margins [18,19]. This geometrical tolerance, also known as dimensional tolerance, must be controlled within an authorized range to maintain the interchangeability and assembly of engineering components. As Hu et al. [20] noted, even a small change in dimensional parameters can have a significant impact on how real components respond to stress and strain, thus affecting how well they withstand fatigue.
This study considers geometrical uncertainty when determining the sizes of the suspension control arm. The sampling of dimensions was done in accordance with design margins or manufacturing faults by establishing the tolerance range of each measurement. Following that, the sampled dimensions were used for geometric modeling, and model updates were carried out using finite element (FE) modeling in COMSOL. A few common control arm dimensions were chosen as the geometrical uncertainty inputs from the design and deformation failure analysis perspectives, as shown in Figure 1. In engineering practice, a normal distribution is typically used to model dimensional tolerance [21]. According to DIN EN ISO 286-1 [22], the geometrical tolerances of these dimensions are considered to be ±0.1% changes from the planned size based on the tolerance requirements. Moreover, for this study, the COV for each dimension was considered to be 0.1%, as shown in Table 1.
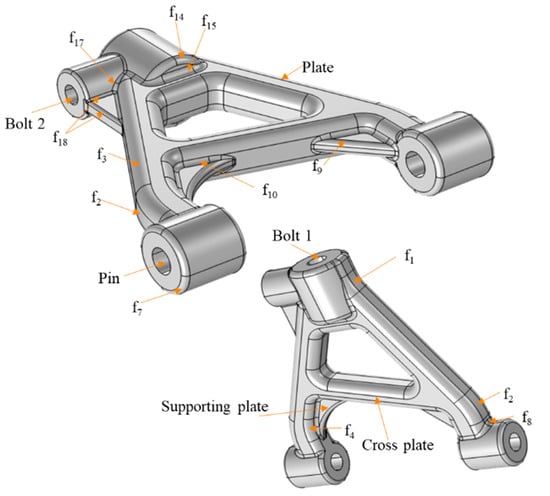
Figure 1.
Geometrical parameters.

Table 1.
Uncertain variables of the front lower suspension control arm.
3. Methodology
In this study, a computational model and an uncertainty quantification framework were developed to investigate the uncertainty of the design variables of a front suspension lower control arm under fatigue-loading conditions. The principal methodology is depicted in Figure 2. The remainder of this section is allocated as follows: computation modeling, sensitivity analysis, probabilistic modeling, and specification of the analysis. These are the main proposed methods of this study.
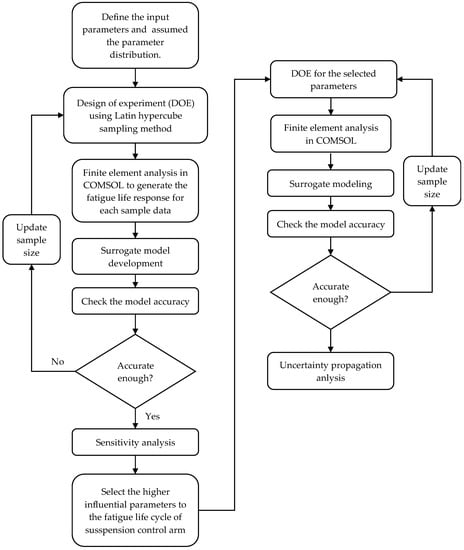
Figure 2.
Schematic representation of the general methodology of analysis employed to quantify the fatigue load uncertainty.
3.1. Computational Modeling of the Control Arm
The stresses and deformations caused by mechanical loads can be computed using structural analysis, which helps ascertain how loads affect the physical structure. Since the lower control arm is connected to the wheel and chassis of a car, it is subject to several loads that cause deformation. Failure of the lower control arm is caused by deformation and cyclic stresses, so it is necessary to determine the stresses acting on the lower arm before it is manufactured. Once the stresses for various loads have been computed using structural analysis, fatigue analysis can be performed based on the stress value after the maximum and minimum stresses have been determined.
For this study, the suspension lower control arm model was prepared in COMSOL, and finite element analysis was performed using COMSOL 6.1 software with the structural mechanics module. Figure 3 illustrates the arrangement of the finite elements used for the front suspension lower control arm in this study. In the design process, the appropriate design variables for the parts involves considering the stress distribution (von Mises stress value). In static analysis, the maximum von Mises stress was considered, and fatigue analysis was conducted via the stress-life approach. To achieve the design objective, it is essential to understand the loads assigned to the suspension control arm. For example, as shown in Figure 3a, the forces acting on a vehicle’s tires can be measured in the x, y, and z directions, where x signifies the longitudinal force, y represents the lateral force, and z is the vertical force. The longitudinal force is caused by rolling resistance and traction–compression cycles, which are caused by braking, while the lateral force is produced by camber and toe angles. In this study, the significant force is the vertical force, which is initiated due to the vehicle’s weight and bumping cycles caused by the road bump.
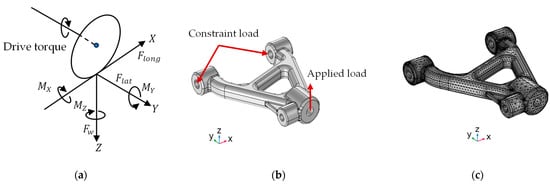
Figure 3.
Suspension control arm: (a) forces acting on vehicle tires; (b) 3D model and boundary conditions; and (c) geometry mesh.
The model is highly dependent on loading and boundary conditions. As previously noted, this study considers a vertical force to be a constant amplitude imposed at the bushing that connects to the tire, while the other two bushings that connect to the body of the car are considered constrained. A tetrahedral mesh was used to approximate the surface contour more accurately, as seen in Figure 3b. To reduce the computational time and to ensure that the FE analysis results were not affected by the mesh size changes, a mesh convergence study was conducted, and the least number of meshes with the highest accuracy was selected.
The mesh in COMSOL Multiphysics always defaults to a physics-controlled mesh with a specified parameter set when you create a model. The predetermined element size parameters are as follows: maximum element size (maxE), minimum element size (minE), maximum element growth rate (maxGR), curvature factor (cf), and the resolution of narrow regions (rnr). The mesh convergency was conducted in a range of extra coarse and extra fine mesh sizes. After the convergency test, the maximum von Mises stress values did not change significantly after the normal mesh size configuration; as such, this study used a fine mesh size (maxE = 8.3 mm, minE = 1.035 mm, maxGR = 1.45, cf = 0.6, and rnr = 0.5) near the necks of the two bushings since these areas are critical for fatigue, and the other part was meshed using the normal mesh size setting (maxE = 10.35 mm, minE = 1.865 mm, maxGR = 1.5, cf = 0.5, and rnr = 0.6) to reduce the computational time.
3.2. Fatigue Life Prediction
Low-cycle fatigue (LCF) and high-cycle fatigue (HCF) are two distinct phases of fatigue characteristics [23]. LCF is typically referred to as “strain-life/strain-based” because strain rather than stress is the most significant descriptive measure of LCF. However, strain is also applicable for damage in HCF, but since HCF occurs in the elastic phase, both stress and strain can be used as the factor. HCF is also regarded as “stress-life/stress-based” since stress is used for practical and historical purposes. The number of cycles determined in this case (suspension control arm) corresponds to an HCF paradigm, which is typically defined as a number of cycles counts needed until reaching a fatigue of more than 104 [24,25].
The type of load pattern applied to a structure under constant load cycles can also have an impact on its performance. The load can be classified as either proportional or non-proportional. In proportional loading, the primary loads and strains remain oriented throughout the load cycle. Another method to distinguish between these two scenarios is to consider the characteristics of the external load. The structural response to a single external load source is represented by a stress tensor, whose components undergo phase changes. If the external load is applied multiple times or, if it is a traveling load, the components of the stress tensor may shift out of phase. Different methods of fatigue evaluation are required for these two distinct types of load cycles [26,27,28,29].
In this research, it was assumed that the load was sinusoidal, which denotes a proportional load. Stress-life models can assess fatigue under proportional loading via the S-N curve model (Wöhler curve model) [30] or Basquin model [31,32]. The S-N curve model (Wöhler curve model) was employed in this study since it is one of the oldest and simplest models for fatigue prediction, and it demonstrates a clear relationship between fatigue life and applied stress. The fatigue properties of the suspension control arm material are summarized in Figure 4. This material has an endurance limit of 110 MPa.
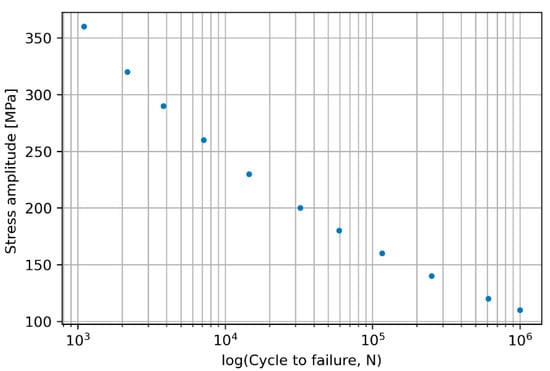
Figure 4.
S-N curve.
Considering that the suspension arm may have a rough surface due to poor cleanliness or fairly large inclusions, this could affect the value of the endurance limit. For instance, the large inclusions can shorten the lifetime. To ensure safety, the S-N curve data should be modified, and one possible modification is to adjust the amplitude stress as follows [33].
where is the stress amplitude, which is determined from the difference between the peak stresses and the mean stress ; is the number of the fatigue lifetime cycle; is the modification factor; and is the S-N curve. Based on past experience, the modification factor caused by the production process of machining can be set between 0.6 and 0.8 [34].
In fatigue evaluation when using the S-N curve model, the amplitude stress can be modified to account for the mean stress. The mean stress is defined as the average of the minimum and maximum stresses during a load cycle. There are three kinds of mean stress correction methods: as per Gerber [35], Goodman [36], and Soderberg [37]. The Gerber and Goodman methods predict failure when the mean stress is at the ultimate tensile stress, whereas the Soderberg method predicts failure when the mean stress is at the yield limit. This study used a yield limit, so we used the Soderberg method. Based on the Soderberg method, the amplitude stress is modified using the mean stress as
where is a yield stress that you need to specify. Figure 5 presents COMSOL’s simulation results for fatigue life, with the mean values of the design variables listed in Table 1. The results indicate that the minimum life cycle occurs around the necks of the two bushings.
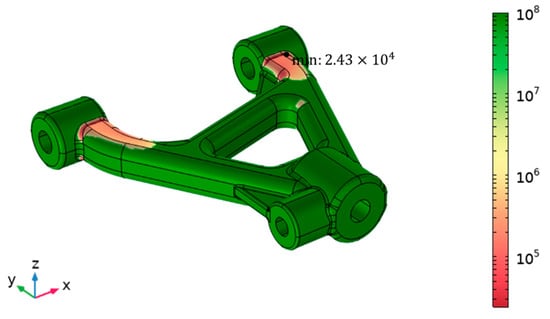
Figure 5.
Fatigue life prediction result at the mean design variables.
3.3. Sensitivity Analysis Model
Sensitivity analysis can identify the parameter or set of parameters that has the greatest impact on the model’s response. As a result, it provides valuable insight into which model input has the most influence on the unpredictability of the model’s response [38]. It is also a useful tool for model developers and users to verify the model’s uncertainty around input parameters, and to provide feedback for model refinement to increase confidence. The results of the sensitivity analysis can help model builders focus on the essential variables that influence the model’s response, especially in the case of a very complex model. As mentioned in the introduction, there are two types of sensitivity analysis: local and global sensitivity analysis. Local sensitivity analysis evaluates variations in the model’s response with respect to variations in a single parameter input [39,40]. In global sensitivity analysis, all parameters are altered simultaneously across the entire parameter space, allowing for the evaluation of both the relative contributions of each individual parameter and the interactions between parameters with respect to the variance of the model’s response.
A variety of global sensitivity methods are available for systems application models, including multiparametric sensitivity analysis, Fourier amplitude sensitivity analysis, the partial rank correlation coefficient, and Sobol’s approach. Zhang et al. [41] attempted to compile the benefits and drawbacks of these approaches, and they concluded that the variance decomposition-based Sobol sensitivity analysis is currently one of the most effective approaches for conducting global sensitivity analysis.
The Sobol method examines the complete input parameter distribution and decomposes the variance of the response into contributions from the input parameters and their interactions. The effects of the parameters are calculated based on the model assessment data. The number of terms in the Sobol indices of the variance of the response with input parameters grows as . To manage this, it is customary to compute only the first-order effects (first-order Sobol indices) and the total effects (total Sobol indices). The first-order index shows the contribution of the parameter to the response variance without interaction. The total effect indices show the overall contribution of a parameter to the response variance, including interaction.
Given a scalar response that is defined as , the variance-based first-order Sobol index is defined as [42]
where indicates the th input parameter and represents all parameters except . The inner expectation value means that the mean of is calculated over all possible values of while is fixed. Then, the outer variance is calculated over all possible values.
The total Sobol index is defined as [42]
which measures the summation of the first-order effect and the interactions with other parameters of the th input parameter. The second term in the equation can be seen as the first-order effect of all parameters except for the th parameter. Therefore, subtracting the second term from one yields the contribution of all terms related to .
In this study, the Sobol indices were computed for the fatigue response of the front lower suspension control arm. With the help of the uncertainty quantification module in COMSOL, there are two different ways through which to compute the Sobol indices. One method is to use the post-processing of a polynomial chaos expansion (PCE) model. The contributions from each input parameter and their interactions can be easily separated given the PCE’s specification. As a result, the Sobol indices can be calculated using the PCE-trained coefficients. In an earlier study from Blatman and Sudret [43], more information on the computation of Sobol indices based on the PCE model was provided. The alternative method for calculating the Sobol indices is the Monte Carlo approach. In this kind of study, a Gaussian process is provided as a surrogate model because performing Monte Carlo simulation directly with model evaluation is computationally expensive. The approach adheres to the recommended method of computing the first and total Sobol indices simultaneously, which was also discussed in Saltelli et al. [5].
3.4. Uncertainty Propagation
Studying the uncertainty propagation of a model is equivalent to approximating the probability density function (PDF) of the response. To construct an accurate PDF of the response, a large number of samples are required. However, this operation is very expensive, so the analysis uses a surrogate model instead. To approximate the PDF, the kernel density estimation (KDE) method is used. This method formulates density in terms of the known kernel functions, which have the following form [44]:
where is a specified symmetric PDF. This study assumed that the kernel function is given as the standard normal distribution, and is a smoothing parameter, which is termed the bandwidth. Silverman’s rule was also applied for the smoothing parameter . More details related to the KDE can be found in Sheather [44].
To evaluate the uncertainty propagation, a confidence interval was used. A confidence interval gives us an indication of the degree of uncertainty in an estimated probability distribution. In statistics, a probability distribution describes all the possible values that a random variable can take within a range. This range is bound to be within certain minimum and maximum possible values, but precisely where the possible value is likely to be plotted on the probability distribution depends on a number of factors. These factors include the distribution’s mean, standard deviation, and skewness. The most common expression for the mean of a statistical distribution with a discrete random variable is the mathematical average of all the terms. To calculate it, add up the values of all the terms and then divide them by the number of terms. The mean of a statistical distribution with a continuous random variable, also called the expected value, is obtained by integrating the product of the variable with its probability, as defined by the distribution. A greater standard error will result in a wider interval; the wider the interval, the less precise the estimate is. Detailed information on confidence intervals can be found in Dekking et al. [45].
In this study, uncertainty propagation was performed by conducting a number of model evaluations while using Latin hypercube sampling data with the selected parameters after conducting sensitivity analysis. These data were used to create surrogate models by using PCE and the GP model in COMSOL. Next, a Monte Carlo analysis was performed using the surrogate model to make predictions. A KDE was generated with the sampled data to produce an estimation of the probability density for each response. The suggested surrogate models for both sensitivity analysis and uncertainty propagation in this study will be discussed in the next section.
3.5. Surrogate Models
Surrogate models are mathematical models that estimate the computationally expensive simulation models, and they are based on the desired design of experiment samples. In this section, the two most commonly used approaches for surrogate modeling are explained along with their adaptive methods, which are also used for sensitivity analysis and uncertainty propagation analysis in this study.
3.5.1. Polynomial Chaos Expansion
To reduce the computational time, a surrogate model based on PCE was extensively implemented in the statistical analysis of various engineering applications. The main idea behind PCE is to provide a polynomial surrogate for the computational model. In this regard, the polynomial chaos expansion that establishes a relationship between the system response () and the independent input parameters of the n-dimensional is given as follows [46]:
where is a multidimensional index that indicates the degree of the polynomial in each of the input variables, denotes the multivariate polynomials, and denotes the unknown coefficients to be determined. The multivariate polynomials are formed by the tensor products of the univariate orthogonal polynomials, which are as follows:
where is the univariate orthogonal polynomial in the ith variable of degree α. The probability distribution of the input parameters is taken into consideration when selecting the univariate orthogonal polynomials. Some commonly used classical univariate polynomials with orthonormal distributions can be obtained in [47]. For example, if the input data distribution is uniform or normal, the suggested univariate polynomials are Legendre and Hermite, respectively. If the input parameters do not have a distribution, such as that which is suggested in Xiu and Karniadakis [48], the algorithm defines an isoprobabilistic transformation to a uniform distribution, and then constructs the PCE using the transformed input parameter.
Based on Equation (5), PCE provides an infinite polynomial series, which means it needs to be truncated to a finite sum for computational purposes, resulting in a truncation error. According to the definition of PCE, truncation is defined as the total degree of all polynomials being less than or equal to . Additionally, the polynomial expansions are further truncated using a hyperbolic truncation method that utilizes a parametric q-norm, . The truncation method truncates all polynomials with total degrees that are less than when . For , hyperbolic truncation retains all high-degree terms in each input parameter but discards the equivalent high-order interaction terms. The truncation method truncates all the interaction terms between the input parameters when .
A sparse representation of PCE refers to a sparsely selected polynomial basis from all the truncated polynomial expansions. An adaptive algorithm based on the least-angle regression method is used to select the significant sparse coefficients from all the truncated polynomial expansions. During the iterative process, the algorithm only adds new polynomial bases that are mostly correlated with the residuals that are built using the existing polynomial basis. The sparse representation is used for reducing the computational cost and, more importantly, for avoiding overfitting. Here, the leave-one-out cross-validation error estimation is defined with a correction factor that considers overfitting to ensure that the generalization error estimate is not underestimated. The generalization error refers to the error for the sample points with unknown model evaluations. Additional details on the sparse PCE representation and error estimation can be found in [43,48].
3.5.2. Gaussian Process
The Gaussian process, commonly referred to as the Kriging model, is one of the most popular surrogate models that provide an estimation of the responses. A Gaussian process model is a probabilistic model that specifies a distribution over functions and evaluates the variance of the estimation at each sample point in the input parameter space. The Gaussian process’s mean, often referred to as the trend, and covariance function, also known as a kernel or correlation function, are used to define it. While the Gaussian process model is being trained, the mean and covariance hyperparameters are tuned. Consequently, the Gaussian process model may be written as follows (considering as the input parameters and the responses as vector y):
where f(x) denotes a Gaussian process with zero mean and covariance , and m(x) is the mean function. Here, denotes the covariance function’s hyperparameters. The joint distribution of the calculated data and the estimated data can then be expressed as [49]
where , is the calculated response, and and are the testing input parameters and estimated response, respectively.
The posterior distribution of the Gaussian process is given as [49]
where and are the covariance and mean of the model, respectively:
Covariance functions are an essential component of Gaussian processes that control the prior and posterior shapes of the model. They encode prior domain knowledge about . These functions, instinctively, allow the model to be generalized by correlating new input data () to the existing observation data (). COMSOL provides three commonly used kernel functions: the spectral exponential kernel, and the Marten kernel, where and . The spectral exponential kernel function is given as [49]
where each is the length scale parameter for dimension . The Marten kernel also functions when given as [50]
where is given as function of and :
Further details about the covariance function and the Gaussian process can be found in Williams and Rasmussen [49].
The kernel function also describes the prior on the types of functions that might be represented in the observed data; for instance, it can convey expectations for smoothness or periodicity. The hyperparameters in the parametric kernels influence this prior and, in turn, the posterior prediction. These kernel hyperparameters can be modified in accordance with a dataset’s characteristics to define a prior value over the functions that are suitable for the situation. To maximize the Gaussian process’s marginal likelihood, , the kernel hyperparameters are often trained using the gradient-based optimization of [50]
where is a nugget factor, and here is an additional hyperparameter, which is used while training the Gaussian process model.
In regard to adapting the Gaussian processes, the Gaussian process is created adaptively by incorporating a new input parameter point at the position of the maximum entropy while it is applied to sensitivity analysis or uncertainty propagation. The Gaussian process is trained to accurately replicate the underlying model in the whole input parameter space for sensitivity analysis or uncertainty propagation. The entropy is expressed here as the standard deviation of the Gaussian process model.
Each adaptation phase involves solving a global optimization problem to determine the position corresponding to the maximum entropy or the maximum expected feasibility function in order to explore the region in the input parameter space and to take advantage of the most recently constructed Gaussian process. There are two different categories of global optimization techniques in COMSOL: the Monte Carlo approach and the dividing rectangles method [51]. The Monte Carlo approach was used in this investigation. It should be noted that adaptive Gaussian process models need adequate initial model assessments for the adaptation approach to find good adaptation points that can raise the model’s accuracy. The unsearched region may not be effectively explored given an initial dataset with too few sample points. Adding extra samples is one technique to solve this issue, so this study applied a sequential optimal Latin hypercube sampling, where the ideal LHS samples randomly cover the entire input parameter space.
4. Results and Discussion
Section 3 describes how uncertainty propagation is used to perform computational fatigue damage modeling and the subsequent design assessment. Model sensitivity analysis is first carried out to eliminate the unnecessary factors from statistical calibration as it would be costly to explore uncertainty propagation by using all design variables. The fatigue analysis data are then used in uncertainty propagation to statistically infer the model’s most important parameters. Finally, the calibrated model with measured uncertainty is used to make predictions about the fatigue strength of the material in the specified loaded stress state.
4.1. Sensitivity Analysis of the Model Input Parameters
4.1.1. Polynomial Chaos Expansion
To begin with, Table 2 describes the validation results of the developed surrogate model for the fatigue life prediction described in Table 1. While we are developing the surrogate model, 400 instances of sample data were generated for the training data via the Latin hypercube sampling method. From the statistics, the comparison between the four types of surrogate models are shown. The root-mean-square error (RMSE) shows the adaptive sparse polynomial chaos expansion, and it shows less errors than the others; thus, for sensitivity analysis, the adaptive sparse polynomial chaos expansion was chosen in this study to proceed with.

Table 2.
Surrogate model comparison for sensitivity analysis.
4.1.2. Sensitivity Analysis
The results of the influence of the car front suspension lower control arm input parameters, which were based on the Sobol method (also known as the variance-based sensitivity analysis method scheme for fatigue life), are depicted in Figure 6a,b. As can be seen from the figure, there are two different types of Sobol indices: the first-order index and total index. As mentioned in Section 2, the first-order index of a parameter shows the sensitivity by varying this parameter alone. As shown in Figure 6b, the first-order index result demonstrates that the control arm thickness () and width () individually had a significant influence on fatigue life. The total index shows how much a parameter contributes to the overall sensitivity. As shown in the figure, for all parameters, the first and total indices were equal, which indicates there is very little or no interaction between the parameters. The Sobol indices and MOAT plots also show that the thickness () of the control arm presents the higher sensitivities, and this is followed by the control arm plate width (); meanwhile, the Young’s modulus () had the third largest contribution in the third, and fillt-3 () had the fourth largest contribution. As a result, small variations in and can significantly increase/decrease the stress concentration of the suspension control arm, which—in turn—increases/decreases the accumulated structural damage (fatigue life) during the suspension control arm operational life. The parameters and also presented slight contributions to the response, particularly . The small variance of the other parameters seems to not have any significant effect on the fatigue life of the control arm. In summary, the most influential parameters, in contrast, were found to be , and ; thus, to reduce the variance of the response, it is recommended to collect more data and conduct more sophisticated simulations to reduce the uncertainty of those parameters.
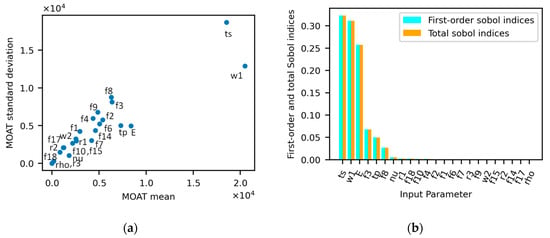
Figure 6.
Parameter sensitivity plots: (a) MOAT method; (b) Sobol method.
4.2. Uncertainty Propagation
The uncertainty quantification used in the fatigue life cycle is described and the model input PDFs are presented; in addition, the confidence interval for the fatigue life cycle response was computed. First, Table 3 presents the selected six parameters (, and ) of the twenty-two used in the sensitivity analysis, along with their probability distributions and coefficients of variation.

Table 3.
Chosen parameters for the uncertainty propagation.
Then, the surrogate model was developed by generating 300 instances of sample data while using LHS for the chosen parameters. Table 4 also describes the validation results of the developed surrogate model for the fatigue life prediction. Based on the RMSE result, the adaptive Gaussian process surrogate model showed less errors than the others. A Monte Carlo analysis was then conducted, using an adaptive Gaussian process surrogate model, to evaluate the uncertainty propagation.

Table 4.
Surrogate model comparison for uncertainty propagation.
Based on the uncertainty quantification study, a kernel density estimation (KDE) plot is shown in Figure 7, along with the corresponding confidence interval information in Table 5. In the uncertainty propagation study, kernel density estimation is computed. Alternatively, you can think of the KDE as a smoothed version of a histogram, which provides an estimate of the probability density function of the quantity of interest based on the input parameters. Based on the confidence interval table and plot of the quantity of interest, we can see that the mean number of cycles is around 22,902.4 with a standard deviation of 4979.2 or 21.74% deviation from the mean. This is achieved as a result of the small variability of input parameters, i.e., a large deviation from the mean (baseline).
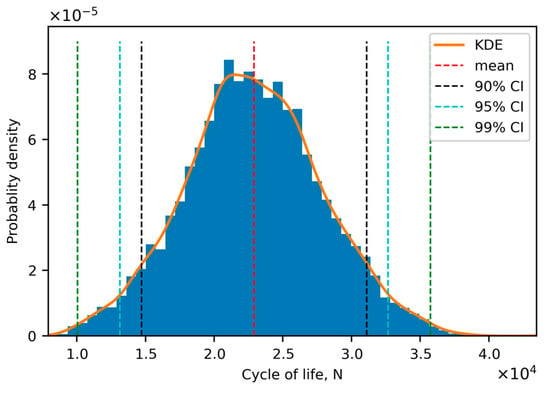
Figure 7.
PDF of the fatigue life response.

Table 5.
Quantity of the interest confidence intervals.
5. Conclusions
In this study, we developed a surrogate-based fatigue uncertainty quantification framework that combines FE analysis with the LHS technique. The objective was to investigate how geometrical uncertainty and material variability affect the fatigue life for a front suspension lower control arm. We compared the fatigue life and examined the failure probability under these uncertainties, along with a sensitivity analysis. For the sensitivity analysis, we used the Sobol method with an adaptive polynomial chaos expansion surrogate model to rank the influential random variables in the fatigue analysis of the front suspension lower control arm. It was found that, out of twenty-two parameters, five geometrical uncertainties and young modulus variabilities had the highest impact on fatigue life and failure probability. We then performed a Monte Carlo analysis using the adaptive Gaussian process surrogate model to examine the uncertainty propagation according to the variability of the selected six parameters.
The uncertainty effect is expressed in terms of fluctuations from the mean value, probability distributions, and percentage deviations from the mean (baseline). We observed a COV of 21.74% as a result of this parameter uncertainty, indicating that uncertainty in parameters has an impact on fatigue life cycle. In this study, the results are based on COV assumptions. However, the outcome of this research clearly illustrates the need to incorporate the uncertainties in car suspension control arm performance analysis for the design and manufacturing process. In the future, researchers can explore more realistic probability distribution functions other than normal distribution functions for uncertainty analysis, and they can use the current results as a benchmark.
Author Contributions
Conceptualization, M.A. and B.K.; methodology, M.A. and B.K.; software, M.A.; validation, M.A.; formal analysis, M.A.; investigation, M.A. and B.K.; resources, B.K.; data curation, M.A.; writing—original draft preparation, M.A.; writing—review and editing, B.K.; visualization, M.A.; supervision, B.K.; project administration, B.K.; funding acquisition, B.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant of the Korean government (No. NRF-2021R1I1A3042226), and by the Korea Institute for Advancement of Technology (KIAT) grant, which was funded by the Korean Government (MOTIE) (P0012769, The Competency Development Program for Industry Specialist).
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mosch, L.; Adolph, S.; Betz, R.; Eckhardt, J.; Tizi, A.; Mathias, J.; Bohn, A.; Ulbrich, S.; Habermehl, K. Control of uncertainties within an interdisciplinary design approach of a robust high heel. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 597–603. [Google Scholar] [CrossRef]
- Zang, T.A. Needs and Opportunities for Uncertainty-Based Multidisciplinary Design Methods for Aerospace Vehicles; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- de Rocquigny, E.; Devictor, N.; Tarantola, S. Uncertainty in Industrial Practice: A Guide to Quantitative Uncertainty Management; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Pang, Z.; O’Neill, Z.; Li, Y.; Niu, F. The role of sensitivity analysis in the building performance analysis: A critical review. Energy Build. 2020, 209, 109659. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Kala, Z. Global sensitivity analysis of reliability of structural bridge system. Eng. Struct. 2019, 194, 36–45. [Google Scholar] [CrossRef]
- Domyancic, L.; Millwater, H. Sensitivity Analysis for Risk Assessment of an Aircraft Fatigue Critical Location. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1855. [Google Scholar]
- Kala, Z. New importance measures based on failure probability in global sensitivity analysis of reliability. Mathematics 2021, 9, 2425. [Google Scholar] [CrossRef]
- Hübler, C.; Gebhardt, C.G.; Rolfes, R. Hierarchical four-step global sensitivity analysis of offshore wind turbines based on aeroelastic time domain simulations. Renew. Energ. 2017, 111, 878–891. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Liao, D.; Niu, X.P. Probabilistic fatigue assessment of notched components under size effect using critical distance theory. Eng. Fract. Mech. 2020, 235, 107150. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Zhang, M.; Wang, Y.; Wang, X. Prediction of material fatigue parameters for low alloy forged steels considering error circle. Int. J. Fatigue 2019, 121, 135–145. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.P.; Keshtegar, B.; Qian, G.; Wang, Q. Probabilistic framework for fatigue life assessment of notched components under size effects. Int. J. Mech. Sci. 2020, 181, 105685. [Google Scholar] [CrossRef]
- Han, J.; Wang, L.; Ma, F.; Ge, Z.; Wang, D.; Li, X. Sensitivity analysis of geometric error for a novel slide grinder based on improved Sobol method and its application. Int. J. Adv. Manuf. Technol. 2022, 121, 6661–6684. [Google Scholar] [CrossRef]
- Lin, Y.C.; Zhao, C.Y.; Chen, M.S.; Chen, D.D. A novel constitutive model for hot deformation behaviors of Ti–6Al–4V alloy based on probabilistic method. Appl. Phys. A 2016, 122, 716. [Google Scholar] [CrossRef]
- Galambos, T.V.; Ravindra, M.K. Properties of Steel for Use in LRFD. J. Struct. Div. 1978, 104, 1459–1468. [Google Scholar] [CrossRef]
- Mansour, A.E.; Jan, H.Y.; Zigelman, C.I.; Chen, Y.N.; Harding, S.J. Implementation of reliability methods to marine structures. Trans.-Soc. Nav. Archit. Mar. Eng. 1984, 92, 353–382. [Google Scholar]
- Zhan, H.J.; Zhao, W.S.; Wang, G. Manufacturing turbine blisks. Aircr. Eng. Aerosp. 2000, 72, 247–252. [Google Scholar] [CrossRef]
- Song, Y.; Yin, M.; Lei, P.; Huang, S.; Yin, G.; Du, Y. Predicting the fatigue life of machined specimen based on its surface integrity parameters. Int. J. Adv. Manuf. Technol. 2022, 119, 8159–8171. [Google Scholar] [CrossRef]
- Hu, D.; Su, X.; Liu, X.; Mao, J.; Shan, X.; Wang, R. Bayesian-based probabilistic fatigue crack growth evaluation combined with machine-learning-assisted GPR. Eng. Fract. Mech. 2020, 229, 106933. [Google Scholar] [CrossRef]
- Mao, J.; Hu, D.; Li, D.; Wang, R.; Song, J. Novel adaptive surrogate model based on LRPIM for probabilistic analysis of turbine disc. Aerosp. Sci. Technol. 2017, 70, 76–87. [Google Scholar] [CrossRef]
- ISO 286-1:2010-04; Geometrical Product Specifications (GPS): ISO Code System for Tolerances on Linear Sizes—Part 1: Basis of Tolerances, Deviations and Fits. International Organization for Standardization (ISO): Geneva, Switzerland, 2010.
- Lee, Y.L.; Pan, J.; Hathaway, R.; Barkey, M. Fatigue Testing and Analysis: Theory and Practice; Elsevier Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Marines, I.; Bin, X.; Bathias, C. An understanding of very high cycle fatigue of metals. Int. J. Fatigue 2003, 25, 1101–1107. [Google Scholar] [CrossRef]
- Lawrence, B.D.; Henry, T.C.; Phillips, F.; Riddick, J.; Kudzal, A. High-cycle tension-tension fatigue performance of additively manufactured 17–4 PH stainless steel. Int. J. Adv. Manuf. Technol. 2023, 126, 777–786. [Google Scholar] [CrossRef]
- Reza Kashyzadeh, K. Effects of axial and multiaxial variable amplitude loading conditions on the fatigue life assessment of automotive steering knuckle. J. Fail. Anal. Prev. 2020, 20, 455–463. [Google Scholar] [CrossRef]
- Kunla, N.; Jearsiripongkul, T.; Keawsawasvong, S.; Thongchom, C.; Lawongkerd, J.; Saffari, P.R.; Refahati, N. Identification of crack location in metallic biomaterial cantilever beam subjected to moving load base on central difference approximation. Curved Layer. Struct. 2023, 10, 20220196. [Google Scholar] [CrossRef]
- Kashyzadeh, K.R.; Ghorbani, S. Comparison of some selected time-domain fatigue failure criteria dedicated for multi input random non-proportional loading conditions in industrial components. Eng. Fail. Anal. 2023, 143, 106907. [Google Scholar] [CrossRef]
- Lu, C.; Mo, J.; Sun, R.; Wu, Y.; Fan, Z. Investigation into multiaxial character of thermomechanical fatigue damage on high-speed railway brake disc. Vehicles 2021, 3, 287–299. [Google Scholar] [CrossRef]
- Wöhler, A. Ueber die Festigkeits-Versuche mit Eisen und Stahl; Ernst & Korn: Berlin, Germany, 1870; pp. 74–106. [Google Scholar]
- Basquin, O.H. The exponential law of endurance test. ASTM STP 1910, 10, 625–630. [Google Scholar]
- Reza Kashyzadeh, K.; Souri, K.; Gharehsheikh Bayat, A.; Safavi Jabalbarez, R.; Ahmad, M. Fatigue life analysis of automotive cast iron knuckle under constant and variable amplitude loading conditions. Appl. Mech. 2022, 3, 517–532. [Google Scholar] [CrossRef]
- COMSOL Fatigue Module User’s Guide, Version: COMSOL 6.1. pp. 60–63. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.fatigue/FatigueModuleUsersGuide.pdf (accessed on 13 July 2023).
- Noll, G.C.; Lipson, C. Allowable working stresses. Soc. Exp. Stress Anal. 1946, 3, 29. [Google Scholar]
- Gerber, W.Z. Bestimmung der zulassigen Spannungen in Eisen-Constructionen. [Calculation of the allowable stresses in iron structures]. Z Bayer Arch. Ing. Ver. 1874, 6, 101–110. [Google Scholar]
- Goodman, J. Mechanics Applied to Engineering, 1st ed.; Longmans, Green and Co.: London, UK, 1899. [Google Scholar]
- Soderberg, C.R. Factor of safety and working stress. Trans. Am. Soc. Test Matls. 1930, 52, 13–28. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis: Wiley Series in Probability and Statistics; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Wolkenhauer, O.; Wellstead, P.; Cho, K.H.; Ingalls, B. Sensitivity analysis: From model parameters to system behavior. Essays Biochem. 2008, 45, 177–194. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol sensitivity analysis: A tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Soboĺ, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407. [Google Scholar]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Sheather, S.J. Density estimation. Stat. Sci. 2004, 19, 588–597. [Google Scholar] [CrossRef]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics: Understanding Why and How; Springer: London, UK, 2005; Volume 488. [Google Scholar]
- Crestaux, T.; Le Maıtre, O.; Martinez, J.M. Polynomial chaos expansion for sensitivity analysis. Reliab. Eng. Syst. Saf. 2009, 94, 1161–1172. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Marinescu, M.; Olivares, A.; Staffetti, E.; Sun, J. Polynomial Chaos Expansion-Based Enhanced Gaussian Process Regression for Wind Velocity Field Estimation from Aircraft-Derived Data. Mathematics 2023, 11, 1018. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2, p. 4. [Google Scholar]
- MacDonald, B.; Ranjan, P.; Chipman, H. GPfit: An R package for fitting a Gaussian process model to deterministic simulator outputs. J. Stat. Softw. 2015, 64, 1–23. [Google Scholar] [CrossRef]
- Finkel, D.E.; Kelley, C.T. Additive scaling and the DIRECT algorithm. J. Glob. Optim. 2006, 36, 597–608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).