Fast and Robust Simulation of Atmospheric Phase Screen by Zernike Polynomials with Recursive Radial Formulas
Abstract
1. Introduction
2. Theory and Problems
2.1. Atmospheric Phase Screen with Zernike Polynomial Method
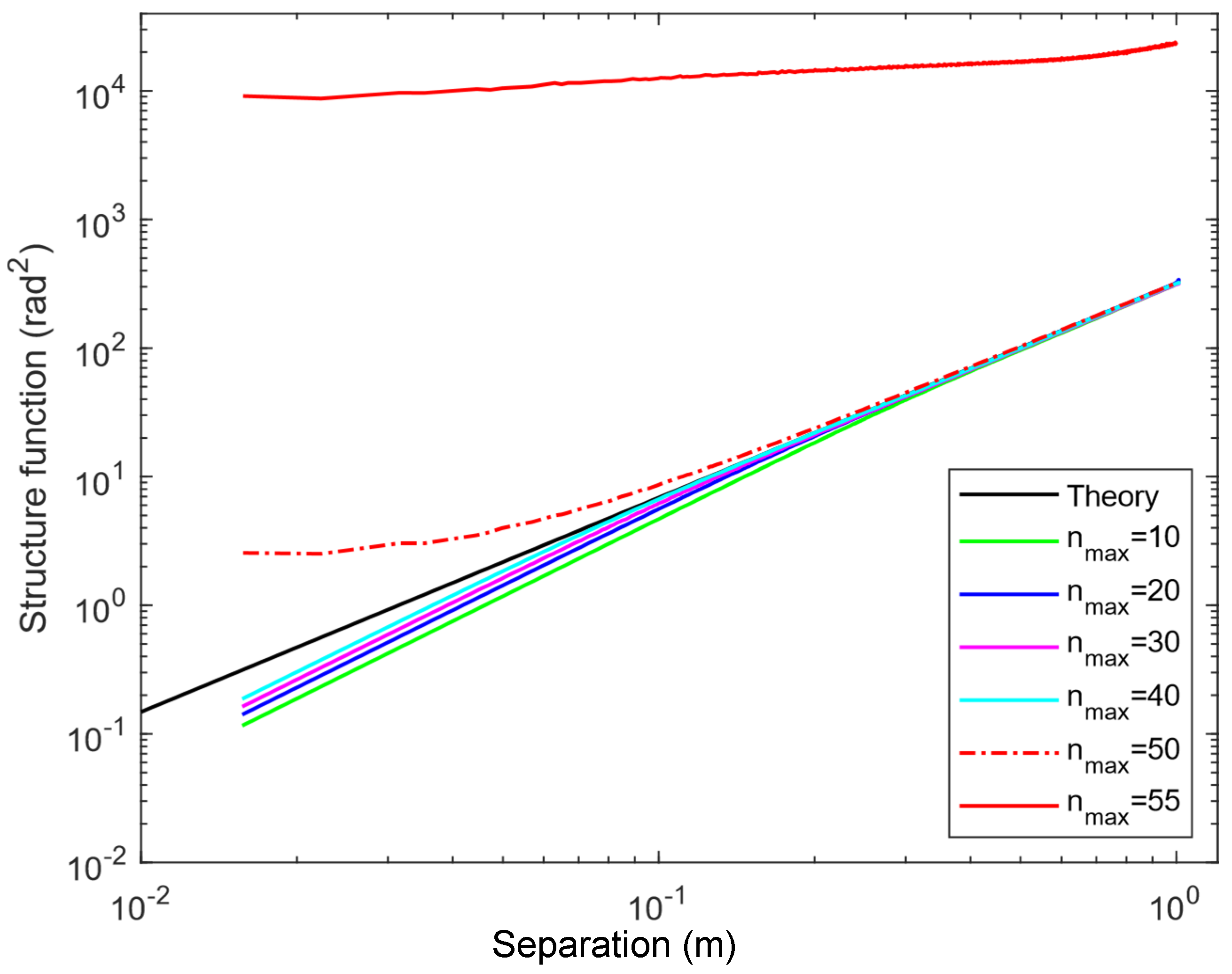
2.2. Evaluation of the Generated Phase Screens
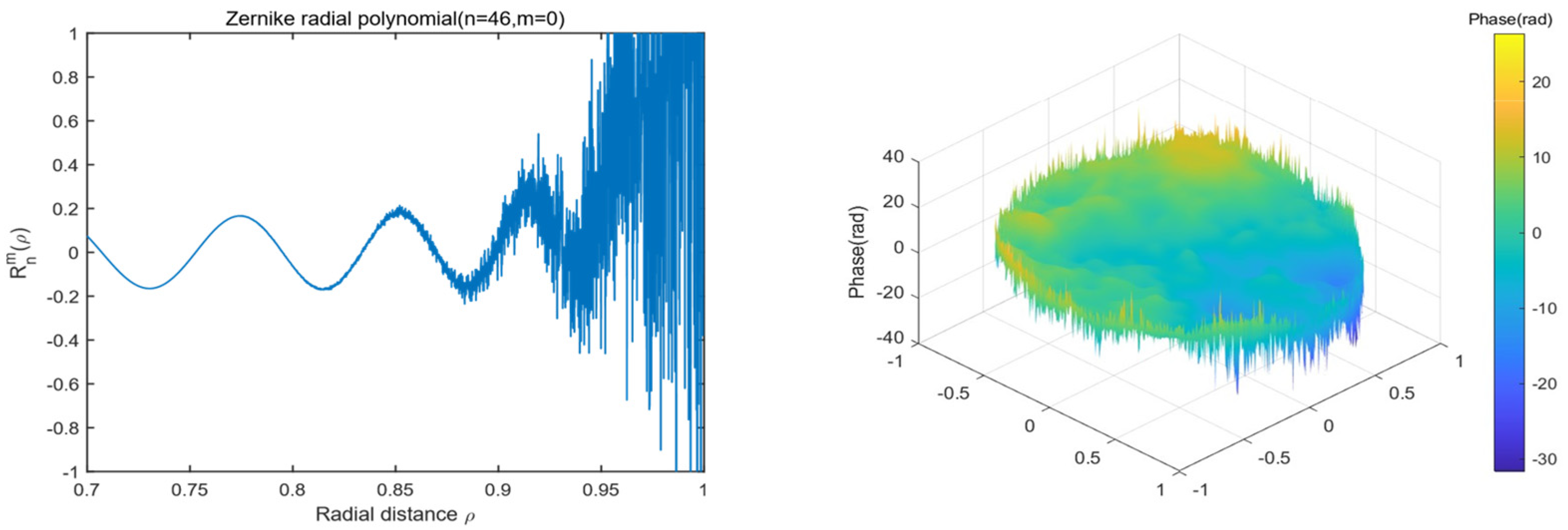
2.3. Challenges in Computational Efficiency and Numerical Stability
3. Recursive Methods for Zernike Radial Polynomials
3.1. Barmak’s Method
3.2. q-Recursive Method
3.3. Prata’s Method
3.4. Kintner’s Method
4. Performance and Discussion
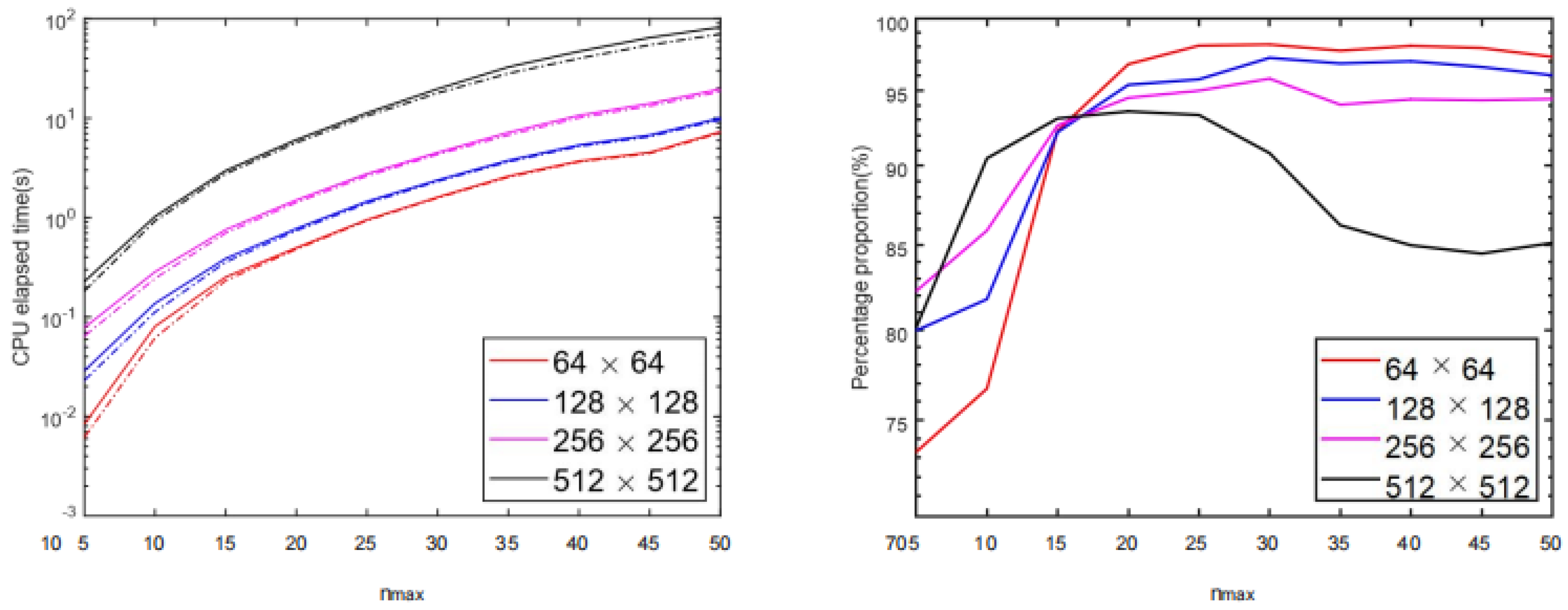
4.1. Computational Efficiency of Phase Screen Generation with Different Recursive Methods
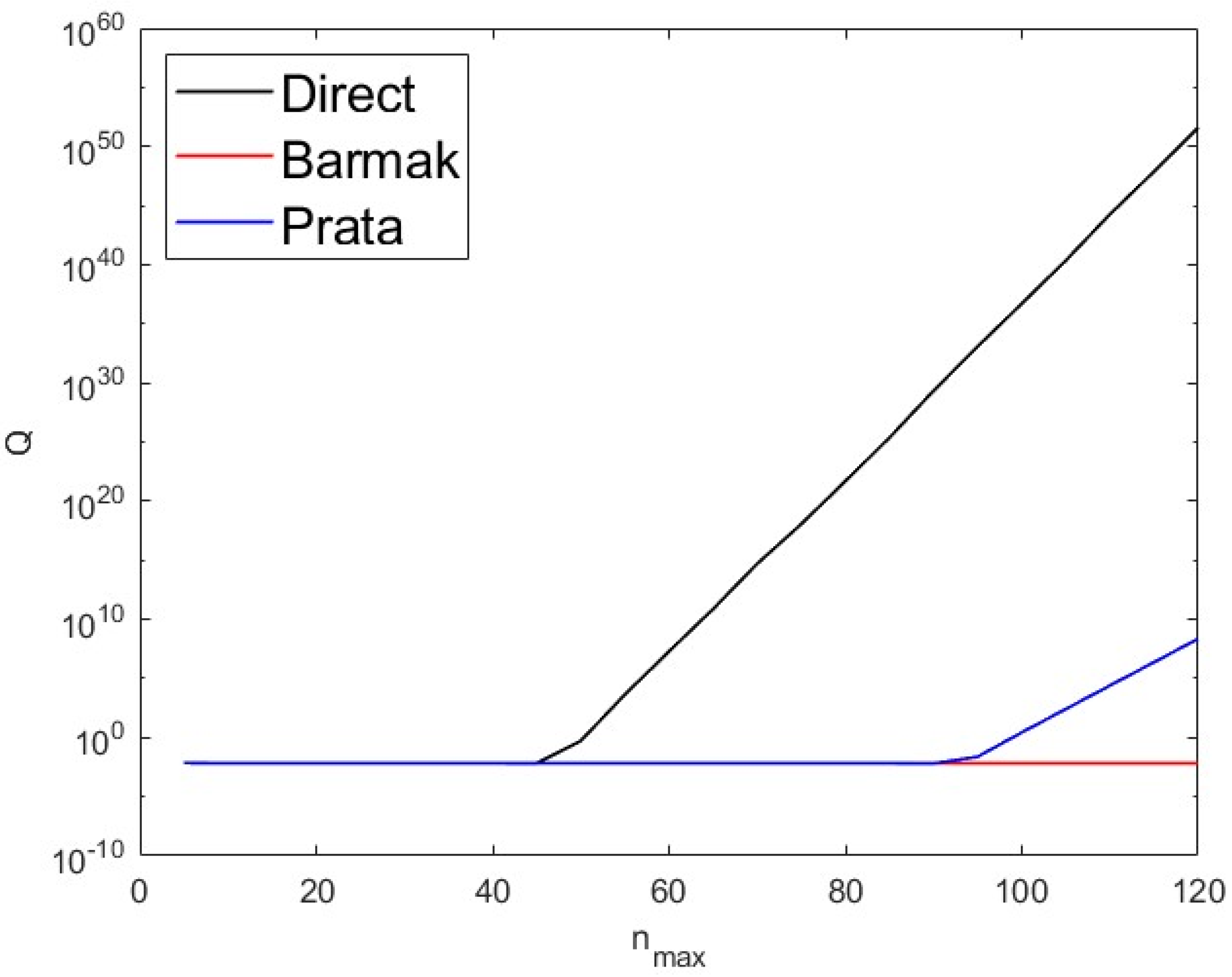
4.2. Numerical Stability of Different Recursive Methods
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tyson, R.K. Principles of Adaptive Optics; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. A Math. Phys. Eng. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Jia, P.; Cai, D.; Wang, D.; Basden, A. Simulation of atmospheric turbulence phase screen for large telescope and optical interferometer. Mon. Not. R. Astron. Soc. 2015, 447, 3467–3474. [Google Scholar] [CrossRef]
- Thomas, S. A simple turbulence simulator for adaptive optics. SPIE Proceed. 2004, 5490, 766–773. [Google Scholar] [CrossRef]
- Jia, P.; Wang, W.; Ning, R.; Xue, X. Digital twin of atmospheric turbulence phase screens based on deep neural networks. Opt. Express 2022, 30, 21362–21376. [Google Scholar] [CrossRef]
- Xu, Q.-W.; Wang, P.-P.; Zeng, Z.-J.; Huang, Z.-B.; Zhou, X.-X.; Liu, J.-M.; Li, Y.; Chen, S.-Q.; Fan, D.-Y. Extracting atmospheric turbulence phase using deep convolutional neural network. Acta Phys. Sin. 2020, 69, 014209. [Google Scholar] [CrossRef]
- Zhao, S.M.; Leach, J.; Gong, L.Y.; Ding, J.; Zheng, B.Y. Aberration corrections for free-space optical communications in atmosphere turbulence using orbital angular momentum states. Opt. Express 2012, 20, 452–461. [Google Scholar] [CrossRef]
- McGlamery, B.L. Computer simulation studies of compensation of turbulence degraded images. SPIE Proceed. 1976, 74, 225–233. [Google Scholar] [CrossRef]
- Zhai, H.; Wang, B.; Zhang, J.; Dang, A. Fractal phase screen generation algorithm for atmospheric turbulence. Appl. Opt. 2015, 54, 4023–4032. [Google Scholar] [CrossRef]
- Roddier, N.A. Atmospheric wavefront simulation using Zernike polynomials. Opt. Engin. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]
- Carbillet, M.; Riccardi, A. Numerical modeling of atmospherically perturbed phase screens: New solutions for classical fast Fourier transform and Zernike methods. Appl. Opt. 2010, 49, G47–G52. [Google Scholar] [CrossRef]
- Chimitt, N.; Chan, S.H. Simulating anisoplanatic turbulence by sampling intermodal and spatially correlated Zernike coefficients. Opt. Eng. 2020, 59, 083101. [Google Scholar] [CrossRef]
- Wilcox, C.C.; Santiago, F.; Martinez, T.; Andrews, J.R.; Restaino, S.R.; Teare, S.W. Performance of a flexible optical aberration generator. Opt. Eng. 2011, 50, 116601. [Google Scholar] [CrossRef]
- Anzuola, E.; Gladysz, S. Modeling dynamic atmospheric turbulence using temporal spectra and Karhunen–Loève decomposition. Opt. Eng. 2017, 56, 071508. [Google Scholar] [CrossRef]
- Forbes, G.W. Robust and fast computation for the polynomials of optics. Opt. Express 2010, 18, 13851. [Google Scholar] [CrossRef] [PubMed]
- Niu, K.; Tian, C. Zernike polynomials and their applications. J. Opt. 2022, 24, 123001. [Google Scholar] [CrossRef]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207. [Google Scholar] [CrossRef]
- Al-Rawi, M.S. Numerical stability quality-factor for orthogonal polynomials: Zernike radial polynomials case study. In Image Analysis and Recognition; Kamel, M., Campilho, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 676–686. [Google Scholar] [CrossRef]
- Chong, C.-W.; Raveendran, P.; Mukundan, R. A comparative analysis of algorithms for fast computation of Zernike moments. Pattern Recognit. 2003, 36, 731–742. [Google Scholar] [CrossRef]
- Shakibaei, B.H.; Paramesran, R. Recursive formula to compute Zernike radial polynomials. Opt. Lett. 2013, 38, 2487–2489. [Google Scholar] [CrossRef]
- Prata, A., Jr.; Rusch, W.V.T. Algorithm for computation of Zernike polynomials expansion coefficients. Appl. Opt. 1989, 28, 749–754. [Google Scholar] [CrossRef]
- Kintner, E.C. On the mathematical properties of the Zernike polynomials. Opt. Acta Int. J Opt. 1976, 23, 679–680. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Boutalis, Y.S.; Papaodysseus, C.N.; Fragoulis, D.K. Numerical error analysis in Zernike moments computation. Image Vis. Comput. 2006, 24, 960–969. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Boutalis, Y.S.; Papaodysseus, C.N.; Fragoulis, D.K. Numerical stability of fast computation algorithms of Zernike moments. Appl. Math. Comput. 2008, 195, 326–345. [Google Scholar] [CrossRef]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE Press: Bellingham, WA, USA, 2010; pp. 76–77. [Google Scholar] [CrossRef]
- Harding, C.M.; Johnston, R.A.; Lane, R.G. Fast simulation of a Kolmogorov phase screen. Appl. Opt. 1999, 38, 2161–2170. [Google Scholar] [CrossRef] [PubMed]
| nmax | Barmak’s | q-Recursive | Prata’s | Kintner’s |
|---|---|---|---|---|
| Method | Method | Method | Method | |
| (a) 64 × 64 resolution | ||||
| 20 | 0.0188 | 0.0287 | 0.0142 | 0.0295 |
| 40 | 0.0959 | 0.1469 | 0.0883 | 0.1559 |
| 60 | 0.3556 | 0.4786 | 0.3474 | 0.5001 |
| 80 | 0.9323 | 1.1018 | 0.9153 | 1.1492 |
| 100 | 2.0232 | 2.2256 | 1.9924 | 2.3105 |
| (b) 128 × 128 resolution | ||||
| 20 | 0.0881 | 0.0902 | 0.0757 | 0.0980 |
| 40 | 0.3095 | 0.3356 | 0.2916 | 0.3723 |
| 60 | 0.7716 | 0.8674 | 0.7956 | 0.9589 |
| 80 | 1.9233 | 2.0885 | 2.0042 | 2.2449 |
| 100 | 4.1382 | 4.3408 | 4.2708 | 4.6017 |
| (c) 264 × 264 resolution | ||||
| 20 | 0.2909 | 0.2907 | 0.2858 | 0.3028 |
| 40 | 1.1555 | 1.1232 | 1.0904 | 1.1513 |
| 60 | 2.8843 | 2.7611 | 2.7011 | 2.8290 |
| 80 | 5.5887 | 5.3755 | 5.2905 | 5.4948 |
| 100 | 9.8839 | 9.5431 | 9.4223 | 9.7540 |
| (d) 512 × 512 resolution | ||||
| 20 | 1.6054 | 1.6578 | 1.5208 | 1.5549 |
| 40 | 6.5728 | 6.1043 | 5.5739 | 5.5705 |
| 60 | 15.6108 | 13.6742 | 12.7198 | 12.6816 |
| 80 | 28.6644 | 24.4980 | 22.9985 | 22.8596 |
| 100 | 51.4420 | 44.4752 | 42.0310 | 41.8682 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lu, B.; Xue, H.; Wang, N.; Cai, D. Fast and Robust Simulation of Atmospheric Phase Screen by Zernike Polynomials with Recursive Radial Formulas. Physics 2025, 7, 58. https://doi.org/10.3390/physics7040058
Li Y, Lu B, Xue H, Wang N, Cai D. Fast and Robust Simulation of Atmospheric Phase Screen by Zernike Polynomials with Recursive Radial Formulas. Physics. 2025; 7(4):58. https://doi.org/10.3390/physics7040058
Chicago/Turabian StyleLi, Yuefeng, Benchu Lu, Huijie Xue, Ning Wang, and Dongmei Cai. 2025. "Fast and Robust Simulation of Atmospheric Phase Screen by Zernike Polynomials with Recursive Radial Formulas" Physics 7, no. 4: 58. https://doi.org/10.3390/physics7040058
APA StyleLi, Y., Lu, B., Xue, H., Wang, N., & Cai, D. (2025). Fast and Robust Simulation of Atmospheric Phase Screen by Zernike Polynomials with Recursive Radial Formulas. Physics, 7(4), 58. https://doi.org/10.3390/physics7040058




