Multiplicity Distributions and the Frontier Between Soft and Hard Physics

Abstract

The multiplicity distributions measured in proton–proton collisions at the LHC exhibit appealing new features. One of them is the appearance of a substructure—the so-called “shoulder”—at relatively large multiplicities. The most natural interpretation of this behavior is the existence of two particle-production mechanisms. The final result is then a superposition of two distributions. In our recent paper, we assumed that the two production mechanisms are soft and semihard partonics scatterings. In this paper, we further discuss this assumption, and, in particular, we study the dependence of the results on the scale that separates soft from hard events.

1. Introduction

Particle production at high energies is a complex phenomenon. It is believed to be understood within quantum chromodynamics (QCD), but the understanding is still to be reached. QCD describes particle production at high momentum transfer (of a few GeV, so-called “hard” reactions), but still to address the production of particles at low (less than 1–2 GeV) momentum transfer (“soft” reactions). In the former case, the theory is in the perturbative regime (pQCD), and reliable calculations can be performed, which have been shown to describe the experimental data quite well.

It is expected that, at increasing energies, the perturbative domain is entered, and, at asymptotically high energies, all processes to be described almost exclusively by pQCD. The question is when pQCD starts to dominate.

Generally, pQCD is applied to events of a hard energy scale (of the order of dozens of GeVs), such as jet events. However, it was shown [1] that parton–parton scatterings with a momentum transfer of a few GeV may be explored and it was realized that pQCD calculations are reliable even in that regime, which was called “semihard”. A few years later, the word “minijet” was coined [2] to describe the same type of (semihard) processes, and nowadays two terms are considered synonyms. Fourty years ago, it was proposed [3] that in proton–proton collisions in the TeV center-of-mass collision energy region, the effects of pQCD to be well pronounced. A two-component model has been built in which the cross-section was explained [3] as the the sum of a soft and a semihard components. The soft ingredient has been assumed to be energy-independent, and the semihard component has been calculated within pQCD. It was assumed that the so-called “minimum-bias” proton–proton collisions to be quite well described by strong energy-dependent pQCD minijets supplemented by quite a weakly depending on energy soft component. In the late 1980s, the accelerators started to be explored in the TeV collision energy region, and certain changes started to be obtained in global inclusive observables, such as transverse momentum and multiplicity distribution. These were considered manifestations of the onset of the QCD perturbative dynamics. The first results were promising. In a subsequent study [4], this two-component model was able to reproduce the measured multiplicity distribution, giving a natural explanation to its double-hump structure. The calculations included integrals over the transverse momentum of the produced partons, which were infrared divergent and needed to be cut at a minimum value, $p_{T\min }$. Apart from regularizing the integrals, this infrared cutoff defines the frontier between soft (below $p_{T\min }$) and semihard (above $p_{T\min }$) physics. In Ref. [3], $1<p_{T\min }<2$ GeV was used for collisions at $\sqrt{s}\approx 1$ TeV. This kind of minijet model was further developed in Ref. [5], where $p_{T\min }\approx 3$ GeV was found to lead to the best agreement with the data. In spite of its initial appropriate description, the two-component models based on additive total cross-sections, i.e., ${\sigma }_{\mathrm{tot}}={\sigma }_{\mathrm{soft}}+{\sigma }_{\mathrm{semihard}}$, and on the infrared cutoff $p_{T\min }$ had two significant problems: first, the dependence of the cross-sections on $p_{T\min }$ was obtained to be quite strong; second, the cross-sections to grow considerably fast with the energy, violating the unitarity bounds [6]. These complications were circumvented by the eikonalized minijet models (see [7] and references therein).

About twenty years later, a new solution for these problems has been suggested. The advance of the studies of the quantum evolution of parton scattering amplitudes led to the theory of the Color Glass Condensate (CGC) [8]. In the CGC approach, an intrinsic energy scale of the theory—the saturation scale $Q_s$—emerges and at the same times regularizes the theory and tames the growth of the parton distributions with the energy. However, this formalism was not able to explain some of the most inclusive observables, such as the total proton–proton cross-section, which, even at the highest energies, seems to contain non-perturbative physics (not directly included in the CGC). Therefore, the development of multi-component models remained relevant. In Ref. [9], a three-component model was proposed to describe the dependence of the proton–proton total cross-section with the energy. Three energy ranges were defined: $0<p_T<{\Lambda }_{\mathrm{QCD}}$, ${\Lambda }_{\mathrm{QCD}}<p_T<Q_s$, with ${\Lambda }_{\mathrm{QCD}}$ the QCD energy scale, and $Q_s<p_T$. It has to be noted that for most cases of practical interest, the saturation scale is small (below 1 GeV) and cannot play the role of separation scale, marking the onset of the perturbative regime. However, the saturation scale has another remarkable effect: it changes the integrand in the cross-section formulas, making it less singular at low $p_T$s. Therefore, it is expected that in CGC-based models, the separation between two regimes becomes less sensitive to the choice of the separating cutoff.

The soft and semihard hysics can be considered to be disentangled using experimental data. In Ref. [10], a thorough analysis of the $p_T$ spectra measured in high-energy proton–proton collisions was performed by correlating the $p_T$ spectra with the corresponding rapidity densities. It was found that there are features common to all observables in hadronic collisions. This may be a manifestation of the dominance of soft interactions. However, at $p_T\approx 0.6$ GeV, significant deviations of the common trend start to occur. This was attributed to semihard interactions. Although this $p_T$ value may seem to appear quite small and its connection to the inputs of real calculations may seem unclear, it is an indication that the transition to the semihard regime starts at transverse momentumof the order of about 1 GeV, rather than at 5 GeV or 10 GeV. Other analyses such as those in Refs. [11,12] address the separation between the soft and semihard physics using experimental data. In these papers, connections between the multiplicity and transverse momentum distributions was derived as well asthe separation scale was set to be related to the effective temperature, which can be inferred from experimental data.

From a more phenomenological point of view, the attempts to understand data with two-component models were quite promissing. In the case of multiplicity distributions, a modified version of the study presented in Ref. [4] was proposed in Refs. [13,14,15] and further developed in Ref. [16]. In these papers, fits were performed to the available multiplicity distributions with a double negative binomial distribution (DNBD). This kind of fit was also adopted by the experimental collaborations when presenting their results, as in Refs. [17,18,19]. In all these studies, the individual distributions considered to come from same type of mechanism or source. It should be mentioned that the double source approach can be further extended to three sources and, consequently, to the use of three negative binomial distributions (TNBDs). Indeed, it was shown in Ref. [20] that in the TNBD approach, it is possible to obtain close enough fits of the data and, in spite of the larger number of parameters, still obtain insights on the data, especially the low-multiplicity region.

Although the motivation for the DNBD was the separation between the soft and semihard components, the formulas had no connections to QCD. Very recently [21], we performed a new DNBD fit but this time calculating the soft and semihard mean multiplicities, with the $k_T$ factorization formula with $k_T$ the parton transverse momentum. In our formalism, not only a straightforward connection to QCD is made, but also this connection introduces new constraints and reduces the number of free parameters. In that our study, we had to use an energy scale $\Lambda$ (which is $p_{T\min }$) to separate soft and semihard processes. We used one single representative value, which, in view of the above discussion, was chosen to be $\Lambda =1.4$ GeV. In the present study, we repeat the procedure and the fits, changing the value of $\Lambda$ in order to test the sensitivity of our results to this cutoff.

2. A Two-Component Model with $k_T$ Factorization

In the $k_T$ factorization approach, the inclusive production cross-section of particle production process in the collisions of two objects (protons) is given by [21,22]

$$E{\displaystyle \frac{d\sigma }{d^{3}p}}=K{\displaystyle \frac{4\pi N_c}{N_c^2-1}}{\alpha }_s\left(Q^2\right){\displaystyle \frac{1}{p_{\perp }^2}}{\int }^{p_{\perp }}d{k}_{\perp }^2{\phi }_1(x_1,k_{\perp }^2){\phi }_2(x_2,{(p-k)}_{\perp }^2),$$

(1)

where $p_{\perp }$ represent the gluon transverse momentum, p, E and y are the produced particle momentum, energy and rapidity, respectively; $Q^2$ is the momentum transfer squared, ${\alpha }_s$ is the strong coupling constant, $x_{1,2}={\displaystyle \frac{p_{\perp }}{\sqrt{s}}}exp(\pm y)$ with $\sqrt{s}$ the center-of-mass energy; $N_c$ is the number of colors, and K is a normalization factor that describes the conversion of partons to hadrons. $\phi$ is the unintegrated gluon distribution (UGD) of each proton, related to the gluon density G by

$$xG(x,{\mu }^2)={\int }^{{\mu }^2}d{k}_{\perp }^2\phi (x,k_{\perp }^2).$$

(2)

Integrating Equation (1) over $p_{\perp }$, one obtains the multiplicity per unit of rapidity:

$${\displaystyle \frac{dN}{dy}}={\displaystyle \frac{1}{S}}{\int }_{p_{\perp \min }}^{p_{\perp \max }}{d}^2{p}_{\perp }E{\displaystyle \frac{d\sigma }{d^{3}p}},$$

(3)

where S is a typical interaction area, and the minimum and maximum values of $p_{\perp }$ are determined by the experimental acceptance. Using Equation (2) and the approximation described in Ref. [21], Equation (3) reads

$$\begin{array}{cc}\hfill {\displaystyle \frac{dN}{dy}}& ={\displaystyle \frac{K}{S}}{\displaystyle \frac{4\pi N_c}{N_c^2-1}}{\int }_{p_{\perp \min }}^{p_{\perp \max }}{\displaystyle \frac{d{p}_{\perp }^2}{p_{\perp }^4}}{\alpha }_s\left(Q^2\right)x{G}_2(x_2,p_{\perp }^2)x{G}_1(x_1,p_{\perp }^2).\hfill \end{array}$$

(4)

The multiplicative constants K and S can be considered a single parameter, which is fixed by fitting the available pseudorapidity distributions. For the UGD, we adopt the one from the GBW model (see [21] for details and discussion). For the purposes of our calculations, the GBW model is particularly appropriate because it reproduces remarkedly well the DIS data on $F_2$ at particularly low scales, which are consistent with the relatively low transverse momenta of the bulk of produced particles at the LHC.

In the expressions (1) and (4), one gluon with $p_{\perp }$ is produced from the fusion of a gluon with $k_{\perp }$ and another gluon with ($p_{\perp }-k_{\perp }$). Therefore, the momentum $p_{\perp }$ is, to a good approximation, the minimum value of the momentum flowing in the three gluon vertex, i.e., the one to be used in the running coupling constant. For $p_{\perp }$ larger than a few GeV, the coupling ${\alpha }_s\left(Q^2\right)$ becomes sufficiently smaller than 1, and then the calculations are performed in the perturbative domain. Following the reasoning given in Section 1, such events are called “semihard”. The events with the lower values of $p_{\perp }$ we call “soft”. The total multiplicity per unit of rapidity is the sum of the contributions from the soft and semihard events. The separation is achieved by introducing a cutoff $\Lambda$ in the integral over $p_{\perp }$, which defines the two contributions:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dN}{dy}}& =& {\displaystyle \frac{K}{S}}{\displaystyle \frac{4\pi N_c}{N_c^2-1}}\left[{\int }_{p_{\perp \min }}^{\Lambda }{\displaystyle \frac{d{p}_{\perp }^2}{p_{\perp }^4}}{\alpha }_s{x}_2{G}_2\left(p_{\perp }^2\right)x_1{G}_1\left(p_{\perp }^2\right)+{\int }_{\Lambda }^{p_{\perp \max }}{\displaystyle \frac{d{p}_{\perp }^2}{p_{\perp }^4}}{\alpha }_s{x}_2{G}_2\left(p_{\perp }^2\right)x_1{G}_1\left(p_{\perp }^2\right)\right]\hfill \\ \hfill & =& {\displaystyle \frac{d{N}_{\mathrm{s}}}{dy}}+{\displaystyle \frac{d{N}_{\mathrm{sh}}}{dy}}.\hfill \end{array}$$

(5)

where $N_{\mathrm{s}}$ and $N_{\mathrm{sh}}$ are the soft and semihard components, respectively. Integrating Equation (5) over the pseudorapidity, one obtains the average multiplicity

$$N=N_{\mathrm{s}}+N_{\mathrm{sh}}.$$

(6)

The only free parameter in Equation (5) is the constant $K/S$, and it is determined in Ref. [21] by using Equation (5) to fit the measured pseudorapidity distributions. In this fitting procedure, we identified the number of produced gluons with the number of measured charged particles (“parton-hadron duality”). As discussed in Ref. [21], for the purposes of the current study, this is a suitable approximation.

At this point, the following remark is in order. Actually, this formalism is only valid for high-energy scales and is valid for the perturbative domain of QCD. In Equation (5), the rapidity distribution depends on the functions G, which in turn are obtained from the UGDs $\phi$, which to be solutions of QCD evolution equations derived in the perturbative regime. In calculations, since the evolution equations are highly complicated, a QCD-inspired ansatz mostly is used for $\phi$, which contains parameters. These parameters are fixed by fitting data of deep inelastic scattering. Part of these data is taken at low $Q^2$ ($Q^2<1{\mathrm{GeV}}^2$) and surely contain essential non-perturbative effects. Thanks to this procedure, the obtained UGDs are appropriate to describe other data that include non-perturbative physics, such as transverse momentum distributions of particles measured in minimum-bias events. Examples of quite a good description of data can be found in Refs. [23,24]. In brief, Equation (5) was derived to study data dominated by perturbative physics (the semihard component as defined here). When it is extrapolated to lower-energy scales (the soft component), it becomes a model, which has to provide with appropriate results because its parameters were fixed by fitting other data in the soft regime domain.

3. Double-Negative Binomial Fits and $\Lambda$-Dependence

The DNBD is expressed as follows:

$$P\left(n\right)=\lambda [\alpha P(n,{⟨n⟩}_s,k_{\mathrm{s}})+(1-\alpha )P(n,{⟨n⟩}_{\mathrm{sh}},k_{\mathrm{sh}})],$$

(7)

where

$$P(n,⟨n⟩,k)={\displaystyle \frac{\Gamma (k+n)}{\Gamma \left(k\right)\Gamma (n+1)}}{\displaystyle \frac{{⟨n⟩}^n{k}^k}{{(⟨n⟩+k)}^{n+k}}}.$$

(8)

The parameter $\alpha$ represents the fraction of soft events; consequently, $(1-\alpha )$ denotes the fraction of semihard events; ${⟨n⟩}_s$ and ${⟨n⟩}_{\mathrm{sh}}$ are the mean multiplicities $k_{\mathrm{s}}$ and $k_{\mathrm{sh}}$ are the negative binomial parameters of the soft and semihard components, respectively. The first few bins in the multiplicity distribution cannot be reproduced by any NBDand are related to a different production mechanism not included in our formalism. Therefore, these bins are removed from the fitting procedure. To account for this, a normalization factor $\lambda$ was introduced in Ref. [17]. The average multiplicity obtained from Equation (7) then reads

$$⟨n⟩=\lambda [\alpha {⟨n⟩}_s+(1-\alpha ){⟨n⟩}_{\mathrm{sh}}].$$

(9)

Comparing the expressions (9) and (6), and recalling that $N=⟨n⟩$, one concludes to

$$\begin{array}{ccc}\hfill \lambda \alpha {⟨n⟩}_s& =& N_{\mathrm{s}},\hfill \\ \hfill \lambda (1-\alpha ){⟨n⟩}_{\mathrm{sh}}& =& N_{\mathrm{sh}}.\hfill \end{array}$$

(10)

Since $N_{\mathrm{s}}$ and $N_{\mathrm{sh}}$ are known from measurements, system (10) reduces the number of free parameters from six to four: $\alpha$, $\lambda$, $k_{\mathrm{s}}$, and $k_{\mathrm{sh}}$.

4. Results and Discussion

In Ref. [21], we used Equation (7) to fit all the available multiplicity distributions measured at the LHC. The fit was of high enough quality, and we were able to determine the energy and rapidity interval dependence of the main parameters. Before going further, let us review the findings of Ref. [21]. First, we used Equation (4) to fit the measured pseudorapidity distributions, thereby fixing the parameter $K/S$, which turned out to be, within the uncertainties, independent of the energy. This behavior is reasonable, given the interpretation of K (as a correction factor accounting for the parton–hadron conversion) and of S (as a typical hadron–hadron interaction area). The next step was to perform a DNBD fit of the available multiplicity distributions, determining the values of $\lambda$, $\alpha$, $k_{\mathrm{s}}$, and $k_{\mathrm{sh}}$. Having obtained these parameters, we used Equation (10) to determine ${⟨n⟩}_s$ and ${⟨n⟩}_{\mathrm{sh}}$. As can be seen in Figure 1 and also in the Figures in Ref [21], the dependence of the fitting parameters with the energy is smooth, and the points can be fitted by some elementary function, allowing us to make some predictions for higher energies. In what follows, we briefly comment on the results of the DNBD fits we applied and compare them with DNBD fits by others.

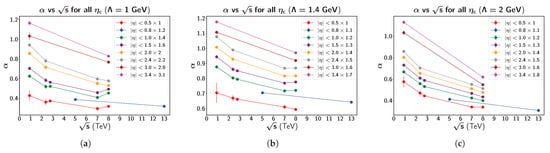
Figure 1. Parameter $\alpha$ as a function of the prorton–proton center-of-mass energy $\sqrt{s}$ for different pseudorapidity intervals. The results (points)) are obtained from fitting the data and are multiplied by certain different factors (as indicated) for a better visualization. The lines are just to guide the eye. The different pseudorapidity intervals $-{\eta }_c<\eta <+{\eta }_c$ are considered and the value of the cutoff $\Lambda$ is fixed, as indicated. See text for details. (a) $\Lambda =1.0$ GeV; (b) $\Lambda =1.4$ GeV; (c) $\Lambda =2.0$ GeV.

4.1. $\lambda$

Within the uncertainties, the $\lambda$ parameter is is found to be quite close to 1 for all energies and all rapidity intervals. This indicates that the removal of the first bins does not sensibly change the normalization of the multiplicity distributions. A similar result was obtained in Ref. [17].

4.2. $\alpha$

The behavior of $\alpha$ is shown in Figure 1. The parameter decreases with the energy for all rapidity intervals. This is the key conclusion of Ref. [21] and is corroborated in the present study, as discussed in Section 4.4 below. On the contrary, in the DNBD fit made in Ref. [17], the opposite trend was observed: the value of $\alpha$ was found to increase with energy. Moreover, the present study finds that $\alpha$ remains constant, within uncertainties, when the pseudorapidity interval size varies. On the contrary, the parameter $\alpha$ obtained in Ref. [17] increases as pseudorapidity interval is widened.

4.3. $k_{\mathrm{s}}$ and $k_{\mathrm{sh}}$

The results obtained here show that the values of the parameters $k_{\mathrm{s}}$ and $k_{\mathrm{sh}}$ decrease with the collision energy in all rapidity intervals, except $\left|\eta \right|<1$, where the velaues of $k_{\mathrm{s}}$ and $k_{\mathrm{sh}}$ are found to be energy independent. This feature and the finding that KNO scaling is obtained only in the narrower intervals (see Section 4.6), steadly suggest that there is a change of dynamics when one moves from one region to another what challenges the understanding.

For comparison, the parameter $k_{\mathrm{s}}$ found in Ref. [17] decreases with the energy for all pseudorapidity intervals. The behavior of $k_{\mathrm{sh}}$ in Ref. [17] is complicated to determine and less consistent.

Fixing the energy and analyzing the variation with the rapidity interval, in Ref. [21], $k_{\mathrm{s}}$ increases when the pseudorapidity intrval is widenning, while in Ref. [17], a decrease was observed. On the other hand, in both studies, $k_{\mathrm{sh}}$ is fonnd to increase as the pseudorapidity interval is widenning.

4.4. ${⟨n⟩}_s$ and ${⟨n⟩}_{\mathrm{sh}}$

The parameters ${⟨n⟩}_s$ and ${⟨n⟩}_{\mathrm{sh}}$ follow the same pattern in both analyses—here and in Ref. [21]—that is, the parameters increase with energy and with the size of pseudorapidity interval.

The main advantage of our approach compared to the DNBD fits is that we obtain a more consistent and physical behavior for the parameters, especially for the parameter $\alpha$. In general, a fitting algorithm always looks for for the best values to describe the data, which may actually lead to a non-physical behavior. We observe that by including the $k_T$ factorization for the determination of the DNBD parameters, one obtains a straightforward and more physical understanding of the proportion of soft and semihard events. Furthermore, our approach naturally leads to a reduction in the number of free parameters and to a consistent behavior of $\alpha$ with energy across the analyzed pseudorapidity intervals, favoring its predictability.

4.5. $\Lambda$

In Ref. [21], the cutoff was fixed to $\Lambda =1.4$ GeV. In view of the discussion in Section 1, this seems a reasonable value. However, to complete the discussion, it is necessary to know how the results change when the value of $\Lambda$ changes. Actually, this is the main goal of the present study. It is straightforward to redo all the fits for different cutoffs. $\Lambda =1$, $1.4$, and 2 GeV are considered here. The results are shown in Figure 2. As can be seen, the three choices of $\Lambda$ lead to fits of similar quality. This statement can be made quantitative by computing the corresponding ${\chi }^2$-test, which is shown in Table 1 and which is small in all cases. One may conclude that the lower cutoff is disfavored by data, but no firm conclusion can be drawn. For conciseness, only the results obtained for $\sqrt{s}=7$ TeV are shown. We have checked that similar conclusions are obtained at the other energies.

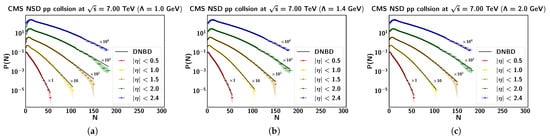
Figure 2. Multiplicity distributions measured in proto–proton collisions at $\sqrt{s}=7$ TeV (points) [25]. The measuremets are fitted by Equation (7) (lines) for different values of the cutoff $\Lambda$ and various rapidity intervals, as indicated. (a) $\Lambda =1.0$ GeV; (b) $\Lambda =1.4$ GeV; (c) $\Lambda =2.0$ GeV.

Table 1. Parameters fitted to adjust Equation (7) to the multiplicity distributions measured in proton–proton collisions at $\sqrt{s}=7$ TeV [25]. See text for details.

$\mathbf{\Lambda }$ (GeV)	${\mathit{\eta }}_{\mathit{c}}$	$\mathit{\alpha }$	${⟨\mathit{n}⟩}_{\mathbf{s}}$	${⟨\mathit{n}⟩}_{\mathbf{sh}}$	${\mathit{\chi }}^2$ / dof
1	0.5	0.294 ± 0.020	2.390 ± 0.227	8.448 ± 0.474	0.502
	1.0	0.291 ± 0.013	4.912 ± 0.318	16.879 ± 0.636	0.495
	1.5	0.285 ± 0.010	7.706 ± 0.406	25.415 ± 0.764	0.568
	2.0	0.275 ± 0.009	10.956 ± 0.501	34.049 ± 0.859	0.492
	2.4	0.271 ± 0.008	13.473 ± 0.572	40.700 ± 0.936	0.442
1.4	0.5	0.610 ± 0.012	3.376 ± 0.182	11.214 ± 0.711	0.102
	1.0	0.598 ± 0.008	6.994 ± 0.267	21.978 ± 0.943	0.113
	1.5	0.591 ± 0.007	10.723 ± 0.347	32.745 ± 1.153	0.188
	2.0	0.583 ± 0.006	14.731 ± 0.447	43.493 ± 1.400	0.310
	2.4	0.578 ± 0.006	17.846 ± 0.504	51.731 ± 1.520	0.411
2.0	0.5	0.341 ± 0.011	11.798 ± 0.299	3.601 ± 0.117	0.093
	1.0	0.354 ± 0.007	23.035 ± 0.452	7.469 ± 0.200	0.106
	1.5	0.360 ± 0.006	34.274 ± 0.601	11.456 ± 0.287	0.182
	2.0	0.365 ± 0.006	45.537 ± 0.776	15.733 ± 0.386	0.313
	2.4	0.367 ± 0.005	54.243 ± 0.911	19.093 ± 0.456	0.420

In Ref. [21], the principal conclusion was that the parameter $\alpha$ (the fraction of soft events) decreases with the collision energy $\sqrt{s}$, as expected, but, quite unexpectedly, the parameter was found to decrease with $\sqrt{s}$ for all rapidity intervals considered. From Figure 1, one can see that this decreasing trend remains valid for the three values of $\Lambda$. In Figure 1c, the two upper lines seem to decrease faster than the others, but this may be due just to the lack of points. From this analysis, one concludes that the precise choice of the “frontier” between soft and semihard physics is not crucial, and it is possible to fit the data with several values of the separating scale $\Lambda$. Moreover, the results obtained confirm the earlier obtained decreasing of the parameter $\alpha$ with the collision energy. This relative insensitivity demonstrates the robustness of the fitting procedure applied.

4.6. KNO Scaling

An intriguing property of multiplicity distributions is the KNO scaling, according to which, at considerably high collisions energies, the multiplicity distribution $P\left(n\right)$, when multiplied by $⟨n⟩$ and plotted as a function of the variable $z=n/⟨n⟩$, becomes an energy-independent function. KNO scaling was shown to be valid for high-energy jets [26,27], which suggests that it is a consequence of perturbative QCD. Ultimately, the scaling emerges asymptotically as a consequence of the cascading nature of parton multiplication [15]. However, KNO scaling was also observed [17] in other experimental scenarios dominated by non-perturbative physics, such as minimum-bias events, where it has a non-trivial behavior. Indeed, it has been observed [17,18] that KNO scaling holds for central and narrow pseudorapidity interval. $\left|\eta \right|<0.5$, but is indeed violated for $\left|\eta \right|>1.0$.

5. Conclusions

In our recent study, [21], using a weighted superposition (7) of two negative binomial distributions we fitted all the available multiplicity distributions measured at the LHC. The fit was of high enough quality, and we were able to determine the collision-energy and rapidity-interval dependences of the key parameters. The separation between soft and semihard processes was made via the introduction of an energy scale $\Lambda$. In Ref. [21], $\Lambda =1.4$ GeV was set fixed. In the present paper, we performed the study, considering different values of $\Lambda$. The behavior of the key parameters with the collisions energy and the size of the rapidity interval remains similar to those in our earlier stiudies. From this we conclude that the precise choice of the “frontier” between soft and semihard physics is not crucial, and it is possible to describe the data using different values of the separating scale $\Lambda$. Moreover, our analysis suggests that there is no correlation between the dominance of soft (or semihard) processes and the KNO scaling. The rapidity dependence of the KNO scaling violations suggests, in addition, that the central and forward pseudorapidity regions are governed by different aspects of QCD, probably related to the composition of the central source (mostly gluons) and the source in the fragmentation region (mostly, valence quark remnants), as pointed out already quite some time [28]. Alternatively, the pseudorapidity-interval size dependence of the KNO scaling may be connected to the multiplicity scaling proposed in Ref. [29]. Further studies are needed.