On Cavitons Generated by the Nonlinear Plasma Waves in HF Heating Experiments at HAARP

Abstract

Analysis of nonlinear plasma waves, formulated and applied for ionospheric HF heating experiments, indicates that Langmuir/upper hybrid waves excited by parametric instabilities can evolve into traveling solitary waves accompanied by self-induced cavitons. To explore these cavitons, a digisonde operating in fast mode was utilized. Significant results were observed in ionograms recorded two minutes after the activation of the O-mode heater. These ionograms displayed two distinct bumps in the virtual height spread, located slightly below both the HF reflection height and the upper hybrid resonance height. It is notable that these heights are also slightly below the excitation regions where Langmuir/upper hybrid Parametric Decay Instabilities (PDIs) are typically generated by an O-mode HF heater. These observations correlate with the theory and provide valuable insights into the dynamics of nonlinear plasma waves and their interaction with the ionosphere during HF heating experiments.

1. Introduction

For many years, active wave–ionosphere interaction has been a significant area of research. This involves transmitting high-power HF waves from ground heating facilities, such as Arecibo [1] in Puerto Rico, USA, EISCAT [2] in Tromso, Norway, and HAARP [3] in Gakona, Alaska, USA, to the ionosphere. These HF heaters initiate linear and nonlinear wave-plasma interactions, which are crucial for revealing the properties of ionospheric plasma [4]. To optimize this interaction, HF waves are transmitted with right-hand (RH) circular polarization (L-mode in a downward magnetic field) at a frequency below foF2 (the maximum plasma frequency of the ionosphere). This allows the HF waves to convert to O-mode before being reflected in the F-region on the bottom-side of the ionosphere. In this region, parametric instabilities [5,6] are exciting, rapidly converting the O-mode HF waves into electrostatic (ES) plasma waves. Consequently, these waves energize electron plasma, enhance airglow [7,8], generate ionization layers [9,10,11,12,13], introduce anomalous heating, and form nonlinear waves. The anomalous heating can form field-aligned density ducts [14], lead to a large region of spread-F [15], and enhance plasma density [16,17,18].

UHF/VHF radars have been utilized to monitor HFPLs and HFILs [2,19,20,21,22], which indicate the parametric excitation of Langmuir and ion acoustic waves by HF heaters. This radar detects return signals that are backscattered by electron and ion plasma waves, provided they satisfy the imposed Bragg backscattering conditions. However, a limitation of backscatter UHF/VHF radars is its inability to detect magnetic field-aligned waves (i.e., their wavefronts are parallel to the magnetic field), such as upper and lower hybrid waves, as these waves do not meet the Bragg backscattering conditions. In an over-dense ionosphere, the O-mode heater passes through the upper hybrid resonance layer before reaching the HF reflection height. Theoretical studies by Lennart Stenflo and colleagues [23,24,25] has demonstrated that the HF heater can parametrically excite upper hybrid instability. When intense Langmuir/upper hybrid waves evolve into nonlinear waves [26], they can form periodic and solitary envelopes [27]. Solitary Langmuir/upper hybrid waves are particularly noteworthy as they become trapped in self-induced density cavities. The feature of electrostatic solitary structures is also of research interest in space plasmas [28]. In multi-dimensional scenarios, solitons can become unstable and collapse [29,30,31,32] if their variance identities [27] become negative. Dynamical variation in background plasma can also instigate soliton collapse [33,34].

The current study investigates nonlinear waves generated by Langmuir/upper hybrid parametric instabilities, with experimental observations made using a digisonde [35,36]. The presence of plasma density irregularities is indicated by the HF enhanced virtual height-spread observed around and below the HF reflection height/upper hybrid resonance region. Further analysis suggests the manifestation of density cavities due to apparent bumps in the virtual height spread [37,38]. Section 2 details the derivation of coupled nonlinear equations for low/high-frequency electrostatic plasma waves. Section 3 provides a detailed derivation and analysis of the nonlinear envelope equations for Langmuir/upper hybrid waves. This involves converting the coupled nonlinear equations from Section 2 into envelope equations by removing the high-frequency wave carriers. When low-frequency responses are baseband (without carrier frequencies), these coupled envelope equations are integrated under specific conditions into a single nonlinear envelope equation for high-frequency plasma waves. The solutions to this equation demonstrate the formation of cavities or density irregularities. Section 4 presents observations from an experiment conducted on 16 and 20 November 2009, with the results being applied to substantiate the proposed theory. A comprehensive summary of this study is provided in Section 5.

2. Derivation of Coupled Nonlinear Equations for Low-Frequency and High-Frequency Electrostatic Plasma Waves

In this Section, the formulation of the governing equation for low-frequency plasma density perturbations, $n_{\mathrm{s}}\left(x,z,t\right),$ is presented. These perturbations, which encompass density irregularities, ion acoustic waves, and lower hybrid waves, are driven by ponderomotive forces. These forces are induced by high-frequency electrostatic electron plasma wave fields through the nonlinearity of the plasma.

In this formulation, “s” is introduced in the subscripts of the relatively low-frequency physical quantities to distinguish them from the background and [comparably] high-frequency physical quantities; the perturbations are considered quasi-neutral, meaning $n_{s\mathrm{e}}= n_{\mathrm{s}\mathrm{i}}=n_{\mathrm{s}}$, because electrons can follow ion motion closely to shield induced wave field ${\mathbf{E}}_{\mathrm{s}}$. Additionally, collision effects are neglected. The background magnetic field ${\mathbf{B}}_0={-B}_0\widehat{\mathbf{z}}$ is set in the negative z direction.

The continuity and momentum equations for electron ($n_{\mathrm{s}\mathrm{e}}, {\mathbf{v}}_{\mathrm{s}\mathrm{e}})$ and ion ($n_{\mathrm{s}\mathrm{i}}, {\mathbf{v}}_{\mathrm{s}\mathrm{i}})$

$${\partial }_t{n}_{\mathrm{s}\mathrm{e}}+n_0\nabla ·{\mathbf{v}}_{\mathrm{s}\mathrm{e}}+\nabla · ⟨{\delta n_{\mathrm{e}}\mathbf{v}}_{\mathrm{e}}⟩=0={\partial }_t{n}_{\mathrm{s}\mathrm{i}}+n_0\nabla ·{\mathbf{v}}_{\mathrm{s}\mathrm{i}},$$

(1)

$${\partial }_t{\mathbf{v}}_{\mathrm{s}\mathrm{e}}+⟨{\mathbf{v}}_{\mathrm{e}}·\nabla {\mathbf{v}}_{\mathrm{e}}⟩=-{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\nabla {\displaystyle \frac{n_{\mathrm{s}\mathrm{e}}}{n_0}}-{\displaystyle \frac{e}{m_{\mathrm{e}}}}{\mathbf{E}}_s+{\Omega }_{\mathrm{e}}{\mathbf{v}}_{\mathrm{s}\mathrm{e}}\times \widehat{\mathbf{z}},$$

(2)

$${\partial }_t{\mathbf{v}}_{\mathrm{s}\mathrm{i}}=-3{\mathrm{v}}_{\mathrm{t}\mathrm{i}}^2\nabla {\displaystyle \frac{n_{\mathrm{s}\mathrm{i}}}{n_0}}+{\displaystyle \frac{e}{m_{\mathrm{i}}}}{\mathbf{E}}_{\mathrm{s}}-{\Omega }_{\mathrm{i}}{\mathbf{v}}_{\mathrm{s}\mathrm{i}}\times \widehat{\mathbf{z}},$$

(3)

where ${\mathrm{v}}_{\mathrm{t}\mathrm{e},\mathrm{i}} ={\left(T_{\mathrm{e},\mathrm{i}}/m_{\mathrm{e},\mathrm{i}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ are the electron/ion thermal speeds with $T_{\mathrm{e}}$ and $T_{\mathrm{i}}$ the temperatures if electrons and ions, respectively, $\delta n_{\mathrm{e}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{v}}_{\mathrm{e}}$ are the electron density and velocity perturbations associated with the high-frequency plasma waves, ${\Omega }_{\mathrm{e},\mathrm{i}}=e{B}_0/m_{\mathrm{e},\mathrm{i}}$ are the electron/ion cyclotron frequencies, e denotes the electron charge, $m_{\mathrm{e}}$ and $m_{\mathrm{i}}$ are the electron and ion masses, respectively, ${\partial }_a\equiv \partial /\partial a,$ and ⟨ ⟩ operates as a mode type filter. The products of low-frequency physical quantities, such as $\nabla ·{n_{\mathrm{s}}\mathbf{v}}_{\mathrm{s}\mathrm{e}}$ and $\nabla ·{n_{\mathrm{s}}\mathbf{v}}_{\mathrm{s}\mathrm{i}}$ terms in the electron/ion continuity Equation (1) and ${\mathbf{v}}_{\mathrm{s}\mathrm{e}}·\nabla {\mathbf{v}}_{\mathrm{s}\mathrm{e}}$ and ${\mathbf{v}}_{\mathrm{s}\mathrm{i}}·\nabla {\mathbf{v}}_{\mathrm{s}\mathrm{i}}$ in the electron/ion momentum Equations (2) and (3), are excluded. The reasons for this exclusion are threefold: (i) $n_{\mathrm{s}}/n_0\ll 1$; (ii) the ambipolar effect, which describes the tendency of electrons and ions to move together in the perturbation, minimizes the velocity responses; and (iii) in this study, relatively high-frequency waves are considered the primary drivers of the comparably low-frequency response.

It is noted that the nonlinear ion term $⟨\delta n_{\mathrm{i}}{\mathbf{v}}_{\mathrm{i}}⟩$ in Equation (1) is zero (i.e., $\delta n_{\mathrm{i}}=0$). This is because ions are too heavy to respond to high-frequency wave oscillations. Due to the large mass ratio, ions respond adiabatically to low-frequency wave fields, while electrons are isothermal. Consequently, the pressure terms (the first term on the RHS) of Equations (2) and (3) have different factors of 1 and 3, respectively.

Applying quasi-neutral assumption, Equations (2) and (3) are combined to one fluid equation

$${\partial }_t{\mathbf{v}}_{\mathrm{s}\mathrm{i}}+C_{\mathrm{s}}^2\nabla {\displaystyle \frac{n_{\mathrm{s}}}{n_0}}-{\Omega }_i\left({\mathbf{v}}_{\mathrm{s}\mathrm{e}}-{\mathbf{v}}_{\mathrm{s}\mathrm{i}}\right)\times \widehat{\mathbf{z}}=-{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}⟨{\mathbf{v}}_{\mathrm{e}}·\nabla {\mathbf{v}}_{\mathrm{e}}⟩ ,$$

(4)

where $C_{\mathrm{s}} = {\left[\left(T_{\mathrm{e}}+3T_{\mathrm{i}}\right)/m_{\mathrm{i}}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ is the ion acoustic speed; variable function ${\mathbf{E}}_{\mathrm{s}}$ is removed from the system (1)–(4).

With the aid of Equation (4), the time derivative of the ion continuity equation in Equation (1) gives

$$\left({\partial }_t^2{-C}_{\mathrm{s}}^2{\nabla }^2\right)n_{\mathrm{s}}+n_0{\Omega }_{\mathrm{i}}\nabla · \left({\mathbf{v}}_{\mathrm{s}\mathrm{e}}-{\mathbf{v}}_{\mathrm{s}\mathrm{i}}\right)\times \widehat{\mathbf{z}}=n_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}\nabla · ⟨{\mathbf{v}}_{\mathrm{e}}·\nabla {\mathbf{v}}_{\mathrm{e}}⟩ .$$

(5)

Regarding the Equations (1)–(5), the derivative on y-coordinate is zero because two-dimensional spatial variation is considered, for example, $n_{\mathrm{s}}= n_{\mathrm{s}}\left(x,z,t\right)$. Let us now move forward with removing the other two function variables: ${\mathbf{v}}_{\mathrm{s}\mathrm{e}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{v}}_{\mathrm{s}\mathrm{i}}$. This step enables the second term on the left-hand side (LHS) of Equation (5) to be explicitly expressed using derivatives of the density perturbation $n_{\mathrm{s}}$. A detailed formulation of this process is provided in Appendix A.

Therefore, a nonlinear equation for the low-frequency plasma density perturbation reads

$$\begin{array}{c}\hfill \left[\left({\partial }_t^2{-C}_{\mathrm{s}}^2{\nabla }^2\right)\left({{\partial }_t^2\nabla }_{\perp }^2+{\Omega }_{\mathrm{e}}^2{\partial }_z^2\right)+{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}{{\partial }_t^2\nabla }_{\perp }^2\right]n_{\mathrm{s}}\hfill \\ \hfill =n_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}\left[{\partial }_t^2{\nabla }_{\perp }^2\left({\partial }_x⟨{\mathrm{v}}_{\mathrm{e}z}{\partial }_z{\mathrm{v}}_{\mathrm{e}x}⟩+{\partial }_x^2⟨{\displaystyle \frac{{\mathrm{v}}_{\mathrm{e}x}^2}{2}}⟩\right)+{{\Omega }_{\mathrm{e}}^2\nabla }^2\left({\partial }_z^2⟨{\displaystyle \frac{{\mathrm{v}}_{\mathrm{e}z}^2}{2}}⟩+{\partial }_z⟨{\mathrm{v}}_{\mathrm{e}x}{\partial }_x{\mathrm{v}}_{\mathrm{e}z}⟩\right)\right]\hfill \\ -{\Omega }_{\mathrm{i}}{\partial }_t{\nabla }_{\perp }^2\left({\Omega }_{\mathrm{e}}\nabla · ⟨{\delta n_e\mathbf{v}}_{\mathrm{e}}⟩-n_0{\partial }_x⟨{\mathbf{v}}_{\mathrm{e}}·{\nabla \mathrm{v}}_{\mathrm{e}y}⟩\right) .\hfill \end{array}$$

(6)

The LHS of Equation (6) represents a mode equation for low-frequency plasma waves. Conversely, the right-hand side (RHS) of the same equation describes the ponderomotive force, which is generated by quite large-amplitude, high-frequency electrostatic electron plasma waves. Examples of such waves include Langmuir waves and upper hybrid waves. If one removes the nonlinear coupling by setting the RHS of Equation (6) to zero, Equation (6) simplifies to a linear mode equation. This linear equation implies two key modes:

1. Ion acoustic mode deduced from the dispersion equation: $\left({\partial }_t^2{-\mathrm{C}}_{\mathrm{s}}^2{\partial }_z^2\right)n_{\mathrm{s}}\left(z,t\right)=0$.

2. Lower hybrid mode deduced from the dispersion equation $\left({\partial }_t^2-C_{\mathrm{s}}^2{\nabla }_{\perp }^2+{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}\right)n_{\mathrm{s}}\left(x,t\right)=0$ for ${\omega }_{\mathrm{p}}^2\gg {\Omega }_{\mathrm{e}}^2$, where ${\omega }_{\mathrm{p}}$ denotes the electron plasma (radian) frequency.

Regarding the high-frequency plasma wave, it is worthy to note that only electrons effectively respond to the wave field at these frequencies. Therefore, the formulations for these waves must exclusively utilize electron fluid equations. These equations can then be integrated to form a nonlinear equation specifically for the electrostatic electron plasma wave field ${\mathbf{E}}_h$.

The continuity and momentum equations, along with Poisson’s equation, for the electron density and velocity perturbations, and the electrostatic wave field, $\delta n_e, {\mathbf{v}}_e, \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{E}}_h$, are as follows:

$${\partial }_t\delta n_{\mathrm{e}}+\nabla ·{n_{\mathrm{e}}\mathbf{v}}_{\mathrm{e}}=0,$$

(7)

$${\partial }_t\left({n_{\mathrm{e}}\mathbf{v}}_{\mathrm{e}}\right)=-3{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\nabla \delta n_{\mathrm{e}}-{\displaystyle \frac{e}{m_{\mathrm{e}}}}{n_e\mathbf{E}}_h+{\Omega }_{\mathrm{e}}{n_{\mathrm{e}}\mathbf{v}}_{\mathrm{e}}\times \widehat{\mathbf{z}},$$

(8)

$$\nabla ·{\mathbf{E}}_h=-e \delta n_{\mathrm{e}}/{ϵ}_0,$$

(9)

where $n_{\mathrm{e}}=n_0+n_{\mathrm{s}\mathrm{e}}+\delta n_{\mathrm{e}}$ is the total electron density, a sum of the background density and density perturbations affiliated, respectively, to the low-frequency and high-frequency waves; in the momentum Equation (8), the convective term is neglected, this term is relatively small and primarily contributes to harmonic wave generation; electron response to the wave field is adiabatic. ${ϵ}_0$ denotes the permittivity of a vacuum.

Let us now combine Equations (7) and (8), by substituting (8) into the equation from the time derivative of Equation (7), it gives

$$\left({\partial }_t^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2+{\omega }_{\mathrm{p}}^2\right)\delta n_{\mathrm{e}}+{\Omega }_{\mathrm{e}}{\nabla ·{(n}_{\mathrm{e}}\mathbf{v}}_{\mathrm{e}}\times \widehat{\mathbf{z}})={\displaystyle \frac{e}{m_{\mathrm{e}}}}{{\nabla ·(n}_{\mathrm{s}}\mathbf{E}}_h),$$

(10)

where ${\omega }_{\mathrm{p}}={\left({\displaystyle \frac{n_0{e}^2}{m_{\mathrm{e}}{ϵ}_0}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ is the electron plasma frequency. We are proceeding with the removal of the other two function variables: $\delta n_{\mathrm{e}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{v}}_{\mathrm{e}}$ by utilizing derivatives of the wave field ${\mathbf{E}}_h$. As detailed in Appendix B, the curl term on the LHS of Equation (10) is explicitly expressed using these derivatives. By applying Poisson’s equation (9) to express $\delta n_{\mathrm{e}}$ in terms of the derivative of ${\mathbf{E}}_h$, one can derive a nonlinear equation for the high-frequency plasma wave field ${\mathbf{E}}_h$:

$$\begin{array}{c}\hfill \left({\partial }_t^2+{\Omega }_{\mathrm{e}}^2\right)\left({\partial }_t^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2+{\omega }_{\mathrm{p}}^2\right){\partial }_z{\mathrm{E}}_{hz}+{\partial }_t^2\left({\partial }_t^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2\right){\partial }_x{\mathrm{E}}_{hx} \hfill \\ =-{\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{n_0}}\left[\left({\partial }_t^2+{\Omega }_{\mathrm{e}}^2\right){\partial }_z\left(n_{\mathrm{s}}{\mathrm{E}}_{hz}\right)+{\partial }_t^2{\partial }_x\left(n_{\mathrm{s}}{\mathrm{E}}_{hx}\right)\right] .\hfill \end{array}$$

(11)

The LHS of Equation (11) models a mode equation specifically for considerably high-frequency plasma waves. Conversely, the RHS of Equation (11) is dedicated to describing the nonlinear feedback mechanisms within the system.

If the scenario is simplified by setting the nonlinear effect to zero—considering the RHS of Equation (11) is disregarded—Equation (11) reduces to a linear mode equation. This simplified linear equation is crucial as it allows us to derive the dispersion relations for quite high-frequency electrostatic electron plasma waves. This linear equation implies two key modes:

1. Electron plasma (Langmuir) mode deduced from the dispersion equation: $\left({\partial }_t^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2+{\omega }_{\mathrm{p}}^2\right){\mathrm{E}}_{lz}\left(z,t\right)=0$, where the subscript $l$ signifies Langmuir wave.

2. Upper hybrid mode deduced from the dispersion equation $\left({\partial }_t^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2\right){\mathrm{E}}_{ux}\left(x,t\right)=0$, where the subscript $u$ signifies upper hybrid wave.

It is worth noting that the formulation of Equations (6) and (11) is rigorous for electrostatic modes, i.e., $\nabla \times \mathbf{E}=0$ in uniform magneto plasma with ${\Omega }_{\mathrm{e}}^2/{\omega }_{\mathrm{p}}^2\ll 1$. However, magnetoplasma also supports hybrid modes, i.e., $\nabla \times \mathbf{E}\ne 0$, where the wave field is a mix of electrostatic (ES) and electromagnetic (EM) components. Equations (6) and (11) remain applicable as long as the magnitude of the electromagnetic component is much smaller than that of the electrostatic component.

3. Nonlinear Envelope Equation for High-Frequency Plasma Waves

In the absence of the plasma nonlinearity, Equations (6) and (11) simplify to the dispersion equations for low-frequency and high-frequency electrostatic plasma modes, respectively. Replacing ${\partial }_t$ by $-i\omega$ and $\nabla$ by $i\mathbf{k}$ in the dispersion equations, where $\omega$ denotes the wave frequency and $\mathbf{k}$ denotes the wave vector, the dispersion relations of the lower hybrid mode ${\omega }_{\mathrm{s}\mathrm{L}}={\left({\Omega }_{\mathrm{e}}{\Omega }_{\mathrm{i}}+k^2{\mathrm{C}}_{\mathrm{s}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, ion acoustic mode ${\omega }_{\mathrm{s}\mathrm{I}}=k{C}_{\mathrm{s}}$, Langmuir mode ${\omega }_{h\mathrm{L}}={\left({\omega }_{\mathrm{p}}^2+3k^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, and upper hybrid mode ${\omega }_{h\mathrm{U}}={\left({\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2+{3k^2\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ are obtained.

Set ${\mathbf{E}}_h=\left[\widehat{\mathbf{x}}{\epsilon }_{hx}(x,z,t)+\widehat{\mathbf{z}}{\epsilon }_{hz}(x,z,t)\right]\exp \left(-i\omega t\right)+\mathrm{c}.\mathrm{c}.$, where $\omega ={\omega }_h$ is the carrier frequency and “c.c.” stands for complex conjugate; thus, the electron linear velocity and density responses to the wave field are evaluated to be

$${\mathbf{v}}_e=-i{\displaystyle \frac{e}{m_{\mathrm{e}}}}\left[\left(\widehat{\mathbf{x}}-i{\displaystyle \frac{{\Omega }_{\mathrm{e}}}{\omega }}\widehat{\mathbf{y}}\right){\displaystyle \frac{\omega }{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\epsilon }_{hx}(x,z,t)+\widehat{\mathbf{z}} {\displaystyle \frac{1}{\omega }}{\epsilon }_{hz}(x,z,t)\right]\exp \left(-i\omega t\right)+\mathrm{c}.\mathrm{c}.,$$

and

$$\delta n_{\mathrm{e}}=-{\displaystyle \frac{{ϵ}_0}{e}}\left[{\partial }_x{\epsilon }_{hx}\left(x,z,t\right)+{\partial }_z{\epsilon }_{hz}\left(x,z,t\right)\right]\exp \left(-i\omega t\right)+\mathrm{c}.\mathrm{c}.,$$

where the convective term and pressure term in the electron momentum equation are neglected because the electron quiver velocity and thermal velocity are much smaller than the phase velocity of the wave. ${\epsilon }_{hx}\left(x,z,t\right) and {\epsilon }_{hz}\left(x,z,t\right)$ are related as ${\partial }_z{\epsilon }_{hx}\left(x,z,t\right)={\partial }_x{\epsilon }_{hz}(x,z,t)$ ascribing to $\nabla \times {\mathbf{E}}_h=0.$ In Appendix C, the RHS terms of Equation (6) are converted to the forms in terms of the derivatives of the high-frequency plasma wave field, it leads Equation (6) to be

$$\begin{gathered} \left[\left({\partial }_t^2{-C}_{\mathrm{s}}^2{\nabla }^2\right)\left({{\partial }_t^2\nabla }_{\perp }^2+{\Omega }_{\mathrm{e}}^2{\partial }_z^2\right)+{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}{{\partial }_t^2\nabla }_{\perp }^2\right]n_{\mathrm{s}} \\ =n_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}}}\right)}^2\left({\displaystyle \frac{1}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\partial }_t^2{\nabla }_{\perp }^2{\partial }_x^2+{\displaystyle \frac{{\Omega }_{\mathrm{e}}^2}{{\omega }^2}}{\nabla }^2{\partial }_z^2\right)\left[{\displaystyle \frac{{\omega }^2}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\left|{\epsilon }_{hx}\right|}^2\left(x,z,t\right)+{\left|{\epsilon }_{hz}\right|}^2\left(x,z,t\right)\right] . \end{gathered}$$

(12)

Regarding the conversion of Equation (11) to a single-mode type envelope equation, the second time derivative can be neglected on the envelope. This is because the time variation of the high-frequency wave envelope is significantly slower compared to its carrier.

After removing the carrier, Equation (11) then reads

$$\begin{gathered} \left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2\right){\partial }_z{\epsilon }_{hz}+{\displaystyle \frac{{\omega }^2}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}\left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_e^2-{3v}_{\mathrm{t}\mathrm{e}}^2{\nabla }^2\right){\partial }_x{\epsilon }_{hx} \\ =-{\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{n_0}}\left[{\partial }_z\left(n_{\mathrm{s}\mathrm{e}}{\epsilon }_{hz}\right)+{\displaystyle \frac{{\omega }^2}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\partial }_x\left(n_{\mathrm{s}\mathrm{e}}{\epsilon }_{hx}\right)\right]. \end{gathered}$$

(13)

We are currently studying the propagation and envelope evolution of relatively high-frequency electrostatic plasma waves in self-induced, non-oscillatory plasma density irregularities $n_{\mathrm{s}}(x,z,t)$. In this context, the temporal variation is relatively slow.

3.1. Parallel-Propagating Langmuir Wave

Set ${\nabla }_{\perp }⟶ 0 \mathrm{a}\mathrm{n}\mathrm{d} {\epsilon }_{hx}=0$; Equations (12) and (13) reduce to

$$n_{\mathrm{s}}={-n}_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2{\displaystyle \frac{1}{{\omega }^2}}{\left|{\epsilon }_{hz}\right|}^2\left(z,t\right)$$

(14)

and

$$\left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_z^2\right){\epsilon }_{hz}={\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{{\omega }^2}}{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2{{\left|{\epsilon }_{hz}\right|}^2\epsilon }_{hz} ,$$

(15)

respectively.

Let us now set ${\epsilon }_{hz}\left(z, t\right)={\tilde{\epsilon }}_L\left(z,t\right)e^{ikz}$ in Equation (15), where ${\tilde{\epsilon }}_L\left(z,t\right)$ is the envelope of the Langmuir wave packet, and k is the wave number of the carrier and related to the carrier frequency through the dispersion relation $\omega ={\left({\omega }_{\mathrm{p}}^2+3k^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, then, Equation (15) becomes

$$\left[-i\left({\partial }_t+{\mathrm{v}}_{g\mathcal{l}}{\partial }_z\right)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }_{\mathcal{l}}{\partial }_z^2\right]{\tilde{\epsilon }}_L={\alpha }_{\mathcal{l}}{\left|{\tilde{\epsilon }}_L\right|}^2{\tilde{\epsilon }}_L,$$

(16)

where ${\mathrm{v}}_{g\mathcal{l}}={3k\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2/\omega ={\partial }_k\omega$ is the group velocity of the wave packet, ${\alpha }_{\mathcal{l}}={\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{{2\omega }^3}}{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2$, and ${\beta }_{\mathcal{l}}={3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2/\omega$. In a moving frame at a velocity ${\mathrm{V}}_z={\mathrm{v}}_{g\mathcal{l}}={\partial }_k\omega$, Equation (16) converts to a conventional cubic nonlinear Schrodinger equation: $i{\varphi }_{\tau }+{\varphi }_{xx}+2{\left|\varphi \right|}^2\varphi =0$, where $\varphi \left(x,\tau \right)=\sqrt{{\displaystyle \frac{{\alpha }_{\mathcal{l}}}{2}}}{\tilde{\epsilon }}_L\left(z,t\right); \tau =t \mathrm{a}\mathrm{n}\mathrm{d} x=\sqrt{{\displaystyle \frac{2}{{\beta }_{\mathcal{l}}}}}\left(z-{\mathrm{v}}_{g\mathcal{l}}t\right).$ This equation is solved via $\mathrm{B}\ddot{\mathrm{a}}\mathrm{c}\mathrm{k}\mathrm{l}\mathrm{u}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{s}$ to give a traveling solitary wave solution [39]:

$${\tilde{\epsilon }}_L\left(z,t\right)=-\sqrt{{\displaystyle \frac{{\beta }_{\mathcal{l}}}{{\alpha }_{\mathcal{l}}}}}{A}_{\mathcal{l}}\mathrm{sech}{A}_{\mathcal{l}}\left(z-{\mathrm{v}}_{g\mathcal{l}}t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\displaystyle \frac{A_{\mathcal{l}}^2{\beta }_{\mathcal{l}}}{2}}t \right),$$

(17)

where the amplitude $A_{\mathcal{l}}$ is given by the initial condition. From Equation (14), the induced caviton is given to be

$$n_{\mathrm{s}\mathrm{L}}\left(z,t\right)={-6n}_0{\displaystyle \frac{A_{\mathcal{l}}^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2}{{\omega }_{\mathrm{p}}^2}}{\mathrm{sech}}^2{A}_{\mathcal{l}}\left(z-v_{g\mathcal{l}}t\right) .$$

(18)

3.2. Perpendicular-Propagating Upper Hybrid Wave

Set ${\partial }_z⟶ 0 \mathrm{a}\mathrm{n}\mathrm{d} {\epsilon }_{hz}=0$, Equations (12) and (13) become

$$\left({{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}-C}_{\mathrm{s}}^2{\partial }_x^2\right)n_{\mathrm{s}}=n_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_e}}\right)}^2{\left({\displaystyle \frac{\omega }{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}\right)}^2{{\partial }_x^2\left|{\epsilon }_{hx}\right|}^2\left(x,z,t\right),$$

(19)

and

$$\left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_x^2\right){\epsilon }_{hx}=-{\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{n_0}}\left(n_{\mathrm{s}}{\epsilon }_{hx}\right) ,$$

(20)

respectively.

3.2.1. Short-Scale Density Irregularities

For short-scale density irregularities, i.e., ${\left|{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}\right|\ll C}_{\mathrm{s}}^2\left|{\partial }_x^2\right|$, Equation (20) becomes

$$\left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_x^2\right){\epsilon }_{hx}={\left({\displaystyle \frac{\omega {\omega }_{\mathrm{p}}}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}\right)}^2{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2{{\left|{\epsilon }_{hx}\right|}^2\epsilon }_{hx} .$$

(21)

By applying a similar procedure by setting ${\epsilon }_{hx}\left(x, t\right)={\tilde{\epsilon }}_U\left(x,t\right)e^{ikx}$ in Equation (21), where ${\tilde{\epsilon }}_U\left(x,t\right)$ is the envelope of the upper hybrid wave packet, and k is the wave number of the carrier and related to the carrier frequency through the dispersion relation $\omega ={\left({\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2+3k^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, then Equation (21) in a moving frame at a velocity ${\mathrm{V}}_x={\mathrm{v}}_{gu}={\partial }_k\omega$, ${\tilde{\epsilon }}_U\left(x,t\right)={ℇ}_u\left(\xi ,t\right)$, where $\xi =x-{\mathrm{v}}_{gu}t$, becomes

$$-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }_u{\partial }_{\xi }^2{\mathrm{ℇ}}_u-{\alpha }_u{\left|{\mathrm{ℇ}}_u\right|}^2{\mathrm{ℇ}}_u=i{\partial }_t{ℇ}_u,$$

(22)

where ${\alpha }_u={\displaystyle \frac{\omega }{2}}{\left({\displaystyle \frac{{\omega }_{\mathrm{p}}}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}\right)}^2{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2$, and ${\beta }_u={3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2/\omega$. Equation (22) has a solution like Equation (17), except that the initial amplitude needs to be enormously large for quite a short pulse.

3.2.2. Large-Scale Density Irregularities

For large-scale density irregularities, i.e., ${\left|{\Omega }_{\mathrm{i}}{\Omega }_{\mathrm{e}}\right|\gg C}_{\mathrm{s}}^2\left|{\partial }_x^2\right|$, Equation (20) becomes

$$\left({-2i\omega \partial }_t-{\omega }^2+{\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_x^2\right){\epsilon }_{ux}=-{\left[{\displaystyle \frac{\omega {\omega }_{\mathrm{p}}}{{\Omega }_{\mathrm{e}}\left({\omega }^2-{\Omega }_{\mathrm{e}}^2\right)}}\right]}^2{\left({\displaystyle \frac{e}{m_{\mathrm{e}}}}\right)}^2{\epsilon }_{ux}{\partial }_x^2{\left|{\epsilon }_{ux}\right|}^2 .$$

(23)

Applying the same moving frame transform from Section 3.2.1, the result is

$$-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }_{\mathrm{u}}{\partial }_{\xi }^2{\mathrm{ℇ}}_{\mathrm{u}}+{\mathrm{\gamma }}_{\mathrm{u}}{\mathrm{ℇ}}_{\mathrm{u}}{\partial }_{\xi }^2{\left|{\mathrm{ℇ}}_{\mathrm{u}}\right|}^2=i{\partial }_{\mathrm{t}}{\mathrm{ℇ}}_{\mathrm{u}},$$

(24)

where ${\mathrm{\gamma }}_u={\displaystyle \frac{\omega }{2}}{\left[{\displaystyle \frac{{\omega }_{\mathrm{p}}}{{\Omega }_{\mathrm{e}}\left({\omega }^2-{\Omega }_{\mathrm{e}}^2\right)}}\right]}^2{\left({\displaystyle \frac{e}{m_{\mathrm{e}}}}\right)}^2.$ Equation (24) does not have a solitary solution.

3.3. Slightly Oblique-Propagating Upper Hybrid Wave, i.e., $\left|{\partial }_z^2\right|\ll \left|{\partial }_x^2\right|,\left|{\partial }_t^2\right|\ll \left|C_s^2{\nabla }^2\right|$

Set ${\epsilon }_{hx}\left(x,z, t\right)={\tilde{\epsilon }}_{Ux}\left(z,t\right)e^{i\left(k_{x}x+k_{z}z\right)}$ and ${\epsilon }_{hz}\left(x,z, t\right)={\tilde{\epsilon }}_{Uz}\left(z,t\right)e^{i\left(k_{x}x+k_{z}z\right)}$, where $\left|k_z\right|\ll \left|k_x\right| \mathrm{a}\mathrm{n}\mathrm{d} k \mathrm{a}\mathrm{n}\mathrm{d} \omega$ are related through the dispersion relation: $\omega ={\left({\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2+3k^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$; ${\partial }_z{\epsilon }_{hx}={\partial }_x{\epsilon }_{hz},$ gives ${\tilde{\epsilon }}_{Ux}\cong \left({\displaystyle \frac{k_x}{k_z}}\right){\tilde{\epsilon }}_{Uz};$ thus, $\left|{\tilde{\epsilon }}_{Ux}\right|\gg \left|{\tilde{\epsilon }}_{Uz}\right|$, Equations (12) and (13) become

$$n_{\mathrm{s}}\cong {-n}_0{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2{\displaystyle \frac{1}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\left|{\tilde{\epsilon }}_U\right|}^2 ,$$

(25)

and

$$\left({-2i\omega \partial }_t-6i{\mathrm{k}}_z{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_z-{3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2{\partial }_z^2\right){\tilde{\epsilon }}_U={\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_s}}\right)}^2{\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{{\omega }^2-{\Omega }_{\mathrm{e}}^2}}{\left|{ \tilde{\epsilon }}_U\right|}^2 ,$$

(26)

respectively, where ${\tilde{\epsilon }}_{Ux}\approx {\tilde{\epsilon }}_U$ is applied. Like Equation (15), Equation (26) has a traveling solitary wave solution,

$${\tilde{\epsilon }}_U\left(z,t\right)=-\sqrt{{\displaystyle \frac{\beta }{\alpha }}}{A}_u\mathrm{sech}{A}_u\left(z-{\mathrm{v}}_{guz}t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\displaystyle \frac{A_u^2\beta }{2}}t \right) ,$$

(27)

where $\alpha ={\displaystyle \frac{{\omega }_{\mathrm{p}}^2}{2\omega \left({\omega }^2-{\Omega }_{\mathrm{e}}^2\right)}}{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\left({\displaystyle \frac{e}{m_{\mathrm{e}}{C}_{\mathrm{s}}}}\right)}^2$, $\beta ={3\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2/\omega$, and ${\mathrm{v}}_{guz}={3\mathrm{k}}_z{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2/\omega ={\partial }_{k_z}\omega$. The induced caviton is given by Equation (14) as

$$n_{\mathrm{s}\mathrm{U}}(z,t)={-6n}_0{\displaystyle \frac{A_u^2{\mathrm{v}}_{\mathrm{t}\mathrm{e}}^2}{{\omega }_{\mathrm{p}}^2}}{\mathrm{sech}}^2{A}_u\left(z-{\mathrm{v}}_{guz}t\right) .$$

(28)

4. Experimental Observations

This experimental study outlines the use of Digisonde, an HF radar, to investigate the effects of HF heating experiments conducted at the High-frequency Active Auroral Research Program (HAARP) transmitter facility. Digisonde probes the electron density distribution in the bottomside of the ionosphere by transmitting O-mode and X-mode sounding pulses with carrier frequencies swept from 1 to 10 MHz, recording sounding echoes in an ionogram. A sounding echo represents a backscatter signal from an ionospheric layer. In a stable, unperturbed ionosphere, these echoes form a smooth trace, indicating the virtual height distribution of the ionospheric plasma, which can then be converted to a true height distribution using an inverse ray tracing technique [35,36].

However, the presence of an F1 layer in the ionosphere causes a virtual height “bump” in the sounding echo trace at frequencies near foF1. The true height profile exhibits a density ledge (or cusp) at foF1, which retards the propagation of sounding signals with frequencies close to foF1. This phenomenon suggests that Digisonde could indirectly explore solitons through the co-products of cavitons. The experiments examined in this study were conducted on 16 November 2009, from 21:00 to 22:36 UTC (12:00–13:36 local time) and on 20 November 2009, from 21:10 to 23:00 UTC (12:10 to14:00 local time) [5,15,16]. During these experiments, the HAARP Digisonde operated in its normal mode, radiating within a 30° (3 dB) half-cone angle. The backscattered signals were recorded as ionogram echoes [35,36], with the Digisonde receiver acquiring ionograms every 30 s (at the minute and 30 s after the minute). Each recording took less than 14 s, and the ionograms ranged from 1.0 to 7.0 MHz.

The HF heating experiments utilized the HAARP transmitter at full power (3.6 MW), with the HF heater transmitting at ${\mathrm{f}}_0=3.2 \mathrm{M}\mathrm{H}\mathrm{z}$ directed along the geomagnetic zenith. The heater operated in 2-min “on” and 2-min “off” cycles. During the “on” periods, the polarization of the heating wave alternated between O-mode and X-mode. Since the Sun remained above the HAARP horizon throughout the experiment, there was no precondition on the background plasma for each O/X-mode heating period. To analyze the impact of the HF heater, we will compare an ionogram acquired the moment the O-mode heater turned off (which still displayed ionospheric effects of the HF heater) with an ionogram acquired before the next O-mode heater turned on. The latter ionogram represents the recovered background, as the X-mode HF heater has no impact on the ionosphere. The difference between these two ionograms reveals heater-induced changes in the background plasma density and the presence of density irregularities and likely nonlinear waves. The cutoff frequency of the X-mode wave ${\omega }_{cx}={\Omega }_{\mathrm{e}}/2+{\left({\omega }_{\mathrm{p}}^2+{\Omega }_{\mathrm{e}}^2/4\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, where Langmuir and upper hybrid wave frequencies are considerably lower than the X-mode heater wave frequency. As a result, PDI cannot be excited because the frequency matching condition cannot be satisfied.

In the November 16 experiments, Langmuir Parametric Decay Instability (PDI) was the primary process, as illustrated in Figure 1a,b, recorded at 21:42 and 21:43 UT. Figure 1a, taken two minutes after the O-mode heater was activated, shows a significant virtual height spread and a distinct virtual height “bump” below 3.2 MHz (the HF reflection height). In contrast, Figure 1b, which represents the background plasma, exhibits minimal echo spread and very low HF wave absorption by the lower ionosphere, as indicated by the second hop echoes ascribing to the rebound of the sounding echoes from the ground. Moreover, after overlapping the echo traces of two ionograms, it further shows that the virtual height spread in the region from 2.1 to 2.9 MHz is downward, rather than upward as observed in a natural spread-F case. It is known that natural spread-F is caused by large-scale field-aligned plasma density irregularities that can appear in the disturbing ionosphere. These density irregularities delay the echo return by modifying the propagation path, which leads to a wideband upward echo spread in the ionogram. Conversely, a downward echo spread indicates the presence of downward-propagating nonlinear periodic waves. These waves can directly backscatter sounding signals, thereby shortening echoes’ return time.

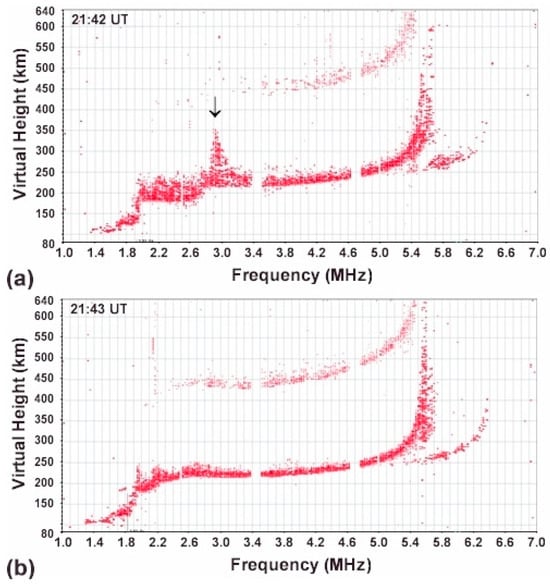
Figure 1. Two contrasting ionograms, acquired at 21:42 and 21:43 UT from 16 November experiments, show the impact of the O-mode HF heater on the ionosphere: (a) recorded at the moment the O-mode heater turns off after being on for 2 min, and (b) recorded after the O-mode heater turns off for 60 s, which is an ionogram of the recovered background. The ionogram (a) shows a significant downward virtual height spread in the region from 2.1 MHz to 2.9 MHz; a mark-arrow points to a distinct virtual height “bump” below 3.2 MHz (the HF reflection height).

For the 20 November experiments, upper hybrid PDI was the dominant phenomenon, as shown in the ionograms in Figure 2 and Figure 3. Specifically, Figure 2a,b were recorded at 21:52 and 21:56 UT, respectively, while Figure 3a,b were recorded at 22:40 and 22:44 UT, respectively. However, Langmuir PDI was also present in the early stages, as evidenced by Figure 2a, which was recorded shortly after the O-mode heater was activated for two minutes.

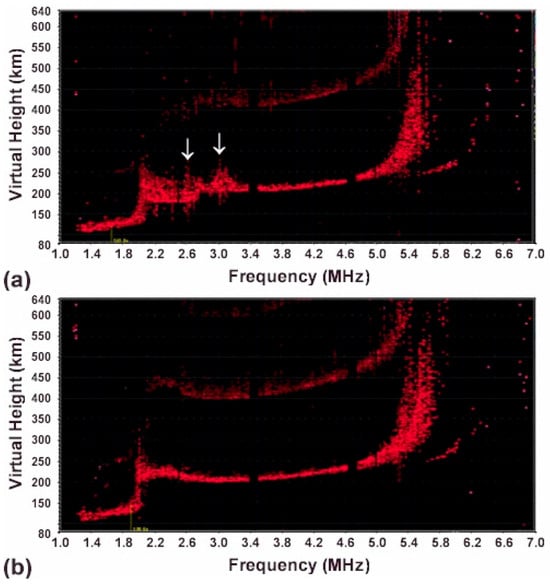
Figure 2. Two contrasting ionograms, acquired at 21:52 and 21:56 UT from 20 November experiments, show (a) the impact of the O-mode HF heater on the ionosphere and (b) the recovered background. Two distinct virtual height “bumps” are indicated by two mark-arrows (a): one below 3.2 MHz (the HF reflection height) and another below 2.88 MHz (the upper hybrid resonance height). A notable downward virtual height spread is displayed in the regions from 2.1 to 2.6 MHz. The bump located near $\mathrm{f}\mathrm{o}\mathrm{F}1\approx 2 \mathrm{M}\mathrm{H}\mathrm{z}$ (a,b) is attributed to the natural plasma density cusp.

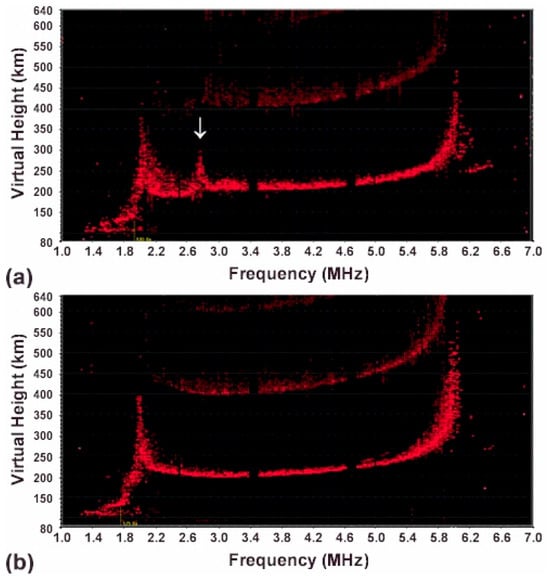
Figure 3. Two contrasting ionograms, acquired at 22:40 and 22:44 UT from 20 November experiments, show (a) the impact of the O-mode HF heater on the ionosphere and (b) the recovered background. A distinct virtual height “bump,” indicated by a mark-arrow (a), is located below 2.88 MHz (the upper hybrid resonance height). Additionally, there is a notable downward virtual height spread in the regions from 2.1 to 2.7 MHz. The bump located near $\mathrm{f}\mathrm{o}\mathrm{F}1\approx 2 \mathrm{M}\mathrm{H}\mathrm{z}$ in both figures is attributed to the natural plasma density cusp.

This ionogram shows two distinct virtual height “bumps” below 3.2 MHz (the HF reflection height) and 2.88 MHz (the upper hybrid resonance height). Figure 2b represents background plasma. In contrast, only one distinct virtual height “bump” below 2.88 MHz appears in Figure 3a. When compared to the background ionograms in Figure 2b and Figure 3b, a notable downward virtual height spread in the regions from 2.1 to 2.6 MHz and 2.1 to 2.7 MHz, respectively, is also visible in Figure 2a and Figure 3a.

These heating-induced bumps are analogous to the virtual height bump observed at foF1 when an F1 layer is present. This suggests the formation of two types of heater-stimulated plasma density cavities, located below the HF reflection height and the upper hybrid resonance height, which explain the observed bumps. These cavities are likely formed by the ponderomotive forces of Langmuir and upper hybrid waves. These plasma waves are excited by the HF heater wave through parametric instabilities in their corresponding matching regions.

Regarding the 20 November experiments, we consistently observed two distinct bumps in the heater-modified ionograms during the early part of the experiments, as illustrated in Figure 2a. However, in the ionograms recorded during the later period, exemplified by Figure 3a, only a single bump was visible. This solitary bump was consistently located below the upper hybrid resonance height. This suggests that in the later phase of the experiments, Langmuir PDI was suppressed. We hypothesize that this suppression was caused by upper hybrid PDI, which effectively drained heater energy in the upper hybrid resonance region before the HF heater could adequately reach the Langmuir PDI region. This insight could be significant for understanding energy distribution in these experiments.

5. Summary

The theoretical predictions and experimental observations of Langmuir PDI excitation in HF heating experiments have been confirmed by UHF/VHF backscatter radars. While upper hybrid PDI has been theoretically predicted, it cannot be directly monitored by these radars. However, its impact may be observable in digisonde ionograms. The distinct excitation regions of Langmuir PDI and upper hybrid PDI are primarily imposed by the frequency matching condition. Due to the difference in the dispersion relations, the upper hybrid PDI excitation region is located at a lower altitude than that of Langmuir PDI. In the experiments, with an HF heater frequency of 3.2 MHz, the Langmuir PDI excitation region is slightly below 3.2 MHz, while the upper hybrid PDI excitation region is slightly below 2.88 MHz. As the HF heater propagates upward, it will first encounter the upper hybrid PDI excitation region before reaching the Langmuir PDI excitation region.

Due to reflection (cutoff of propagation), the HF heater wave field is amplified in the Langmuir PDI excitation region by a swelling effect. This effect, attributed to total reflection at cutoff and the slowing down of wave energy flow, leads to a favorable initial excitation of Langmuir PDI. However, under certain ionospheric conditions, upper hybrid PDI may later become dominant, draining significant heater wave power and potentially suppressing Langmuir PDI.

As HF heater power increases and favorable ionospheric conditions (such as minimum D region absorption and low ionosphere) are present, the excited plasma waves intensify and nonlinearly evolve, modifying their spectral distributions. As discussed in Section 3, these spectral waves condense into wave packages, their envelopes governed by a cubic nonlinear Schrödinger equation, which has traveling solitary wave solutions. Each solitary wave is accompanied by an induced caviton. This caviton forms when intense electron plasma waves nonlinearly evolve into a solitary wave, trapping it and essentially acting as a self-induced structure for pressure balance. Naturally occurring density irregularities in the ionosphere cause the spread of virtual height echoes recorded in ionograms. When an F1 layer is present, a natural bump of virtual height echoes appears in the background ionogram near frequencies close to foF1. This bump is attributed to a density cusp at the E–F2 layer transition, which causes retardation of sounding pulses as the frequency ratio: $\mathrm{f}/\mathrm{f}\mathrm{o}\mathrm{F}1$ approaches one, as well as density depletion in the cusp region. This phenomenon is demonstrated in Figure 3b.

In this study, we explore the appearance and detection of cavitons in HF heating experiments. Ionosondes (digisondes) are instrumental in this detection, as the presence of a caviton is indicated by a discernible bump in the virtual height echoes within an ionogram. Specifically, the bumps observed in Figure 1a and Figure 3a both signify the appearance of a caviton. It is worthy to note, however, that these cavitons manifest at distinct locations: the one in Figure 1a appears slightly below the HF reflection height, while the one in Figure 3a is located somewhat below the upper hybrid resonance region. Furthermore, Figure 2a illustrates two bumps of virtual height echoes in the HF heater modified ionogram, suggesting the simultaneous formation of two cavitons associated with Langmuir and upper hybrid solitons.