Abstract
The production rate of charm quarks in strongly interacting matter is investigated under various conditions, employing the effective quasiparticle framework. This phenomenological approach treats quarks and gluons as quasiparticles with dynamically generated self-energies linked to the medium. This paper studies thermal production of charm quarks in hot deconfined matter when those quarks are treated as impurities with a constant mass or as dynamical quarks dressed by the effective mass. When charm quarks are considered quasiparticles, their large (compared to the bare value) mass generates a significant decrease in the production rate in the crossover region. Various initial conditions for the evolution of the system are applied, showing that lower initial temperature leads to the continual suppression of the charm quark production rate, which appears in line with the previously reported estimate at certain values of the initial parameters.
1. Introduction
For several decades, observables related to heavy quarks, in particular to charm c-quarks, have been considered exceptional probes of the phenomena occurring in heavy ion collisions; for a recent comprehensive review, see [1]. The physics of heavy quarks has been extensively studied both experimentally [2,3,4] and theoretically [5,6,7,8,9,10].
This paper analyzes the thermal production rate of charm quarks in strongly interacting matter with various quark contents. Alongside the commonly used description of the quark–gluon plasma (QGP) with the number of quark flavors (of two light quarks and the strange quark), additionally a system with equilibrated charm quarks, i.e., the case, is investigated. The calculations are performed in the well-grounded quasiparticle model (QPM), which allows one to investigate the dynamical properties of hot QCD matter with thermodynamics obtained from the state-of-the-art lattice quantum chromodynamics (lQCD). The QPM effectively connects perturbative and non-perturbative QCD regimes, therefore allowing for calculation of various QGP parameters in a wide range of temperatures. Previous successes of the considered model include, among others, the computation of transport coefficients, such as shear or bulk viscosities, which appeared in line with the results obtained from other formalisms [11,12,13].
Various characteristics of heavy quarks have been recently explored in the alternative quasiparticle approaches [14,15], including the extension of the system to quark flavors. However, the production rate of charm quasiquarks has not been discussed in the literature so far. Moreover, although the effective models [11,14,15] are based on the same concept, their main features, such as the quasiparticle masses or coupling, are defined differently, and this study additionally illustrates the influence of the model assumptions.
The structure of the paper is as follows. Section 2 introduces the basic components of the QPM, focusing on the differences between the effective running coupling and the quasiparticle masses in the and cases. Section 3 presents the production rate of charm quarks in the QGP with different quark contents. It additionally discusses how the production rate depends on the initial conditions of the one-dimensional expansion of the ideal fluid by comparing the results obtained earlier from a different quasiparticle framework [16]. The conclusions are given in Section 4.
2. Quasiparticle Model
The QPM is based on the assumption that the QGP consists of quasiparticles, i.e., dynamical quarks and gluons, which are characterized by their effective masses [11]
with denoting quasigluons, light (degenerate up and down), strange, and charm quarks, respectively, and their current masses. Here, MeV, MeV, and GeV are used, while bare gluons are naturally massless, . Note that the c-quarks are treated as quasiparticles in the case of only, while in the case, the charm quarks retain their current mass.
The effective masses are acquired through the dynamically generated self-energies emerging from strong interactions within the deconfined medium [17],
where is the effective running coupling and T is the temperature. In Equations (2) and (3), the self-energies are defined at vanishing chemical potential, and in Equation (2) equals 3 or 4, depending on whether the c-quarks are treated as impurities or as quasiparticles, on a par with other QGP constituents.
Figure 1 shows the effective running coupling deduced from the lQCD results for the entropy density of the QGP with [18] and [19] quark flavors. The uncertainties are transferred from the original errors of the lattice data. The charm quarks start to contribute to the equation of state for MeV [19]. Therefore, at lower temperatures, the couplings for different overlap due to the identical entropy densities of the systems. At high temperatures, one observes that in the presence of dynamical charm quarks, the decreases compared to the running coupling for .
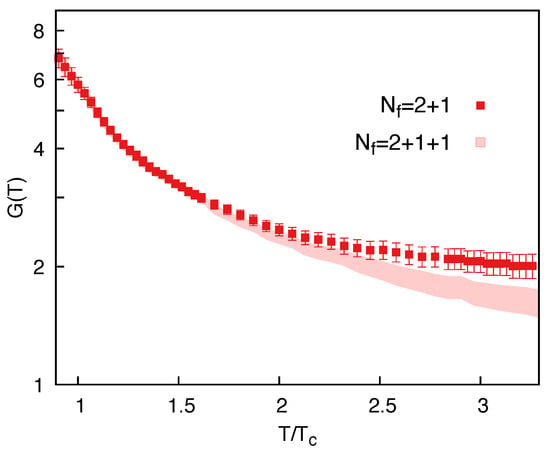
Figure 1.
Effective running coupling , as a function of temperature T scaled by the pseudocritical value MeV, for systems with different numbers of quark flavors (see text for details).
Figure 2 compares the dynamical masses of the quasiparticles in the QGP with different quark contents. In the case of , c-quarks enter the system as impurities of constant mass GeV, with no contribution to the QGP thermodynamics. Alongside, a full quasiparticle picture is considered in which all the QGP constituents, including charm quarks, are treated as dynamical degrees of freedom in thermal equilibrium. Note that such a description is more consistent since it properly accounts for strong interactions transferred from the lQCD results to the QPM through the effective coupling and the medium-dependent masses of all quasiparticle species.
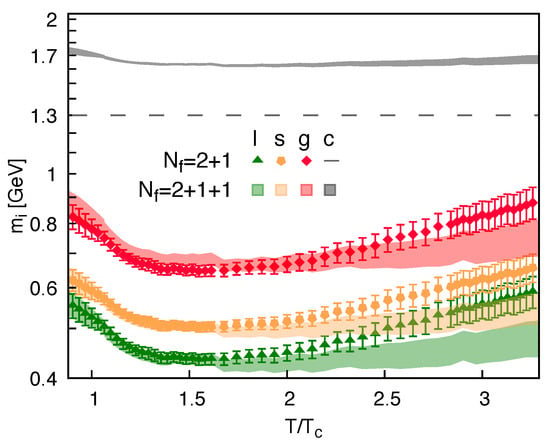
Figure 2.
The quasiparticle masses , as functions of temperature T scaled by the pseudocritical value MeV, for systems with different numbers of quark flavors. In the scenario, GeV, as indicated, while in the , all masses are temperature-dependent (see text for details).
The temperature dependence of the presented masses is defined by Equations (1)–(3). Apart from charm quarks, whose bare mass in the scenario considerably dominates the dynamical part of , one observes that the self-energy provides dominant contributions to the effective masses of the quasiparticles. Also, similar to the behavior of the coupling, the most pronounced difference in the and cases is observed for temperatures above 300 MeV, at which charm quarks enter the QGP equation of state [19].
3. Charm Quark Evolution
Thermal production of particles can be explored in kinetic theory by solving the differential rate equation [20,21,22]
where is the out-of-equilibrium number density of charm quarks, is the flow four-velocity, and is the partial derivative. The rate equation describes the evolution of with time (or with temperature, when is known) as a result of the microscopic interactions within the QGP. The thermal-averaged cross sections correspond to the scatterings producing the pairs from various quasiparticle species that are described by the equilibrium number densities,
which correspond to the Fermi–Dirac (with ‘+’ sign for quarks) or Bose–Einstein (‘−’ sign for gluons) statistics; are the degeneracy factors that include possible color and spin configurations: . The dispersion relation reads , with the momentum p and the effective quasiparticle mass (1).
Note that as charm quarks become equilibrated, i.e., as reaches its equilibrium value , the right-hand side of the Equation (5) vanishes. The numerical pre-factors in Equation (4) are responsible for the appropriate counting of quark and gluon degrees of freedom [22] and are missing in the previous study [23].
This investigation focuses on the square bracket of Equation (4) known as the thermal production rate of the pairs [16,20,21,24],
The thermal-averaged cross sections are computed from the total cross sections according to the following prescription [25,26]:
where are Bessel functions of the first (second) kind; is the total energy of the scattering, bound from below by . In the QPM under consideration, the total cross sections are calculated at tree level, accounting for massive propagators of the on-shell quasiparticles [11]. Note that the Bessel functions in the expression (7) appear from the assumption that in the studied temperature range, the quasiparticles are heavy enough to be described just as well by the classical Boltzmann statistics.
The temperature dependence of the production rate of charm quarks in has been reported earlier in Ref. [22], where the QPM results were juxtaposed to the alternative studies performed in Refs. [14,21].
To analyze the time dependence of the charm quark production rate, let us consider the QGP as a boost-invariant ideal fluid propagating longitudinally. These assumptions are associated with the so-called Bjorken flow; thus the evolution of the system is described by the Bjorken scaling solution [27]
where and describe the initial state of the QGP evolution, for which the parameters (a) MeVand fm [23]. To illustrate the dependence of (6) on the initial conditions, the following values of the parameters (b) MeV and fm are adopted as employed in Ref. [16].
It should be pointed out that for the set (a), the system reaches the pseudocritical temperature at fm, while for the set (b) this happens at fm. Such quite a long QGP lifetime is rather disfavored by the current analyses of the experimental data [28,29,30,31], in which the freeze-out of the fireball takes place at around 10–15 fm, i.e., as in the case (a).
Figure 3 shows the production rate of charm quarks (6) as a function of time computed with the initial parameter cases (a) and (b) for the QGP with different numbers of quark flavors. In the case (b), following the assumptions from Ref. [16], a smaller constituent mass of charm quark is used, GeV, which remains constant in the case or becomes dressed according to Equation (1) in the scenario.
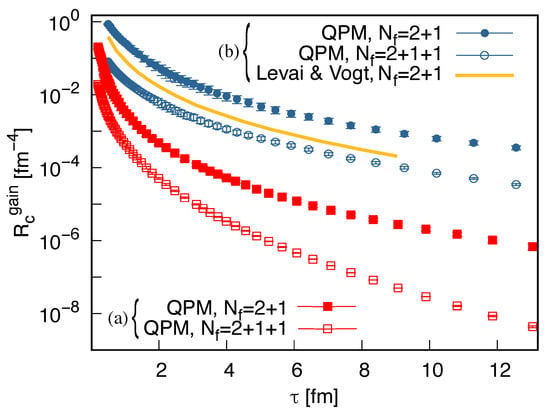
Figure 3.
QPM-computed production rate of charm quarks as a function of time for different numbers of quark flavors and the two sets of initial condition parameters: (a) MeV, fm, GeV and (b) MeV, fm, GeV, see text for details. The result presented in Ref. [16] for PbPb collisions at LHC is also reproduced (marked ‘Levai & Vogt’).
For both sets of the initial parameters, one observes that the production rate of charm quasiquarks in the case is suppressed compared to the scenario, where charm quarks are treated as impurities of constant mass. For the condition (a), a substantial difference (of approximately two orders of magnitude) appears in the crossover region, illustrating that the charm quark mass has quite an impact on the production rate computed within the QPM. The production rate is suppressed by the larger charm quark mass in the description, which was also observed earlier for various constant masses of c-quarks employed in the dynamical quasiparticle model with [24].
Comparing the results obtained for the initial parameters (b), earlier used in Ref. [16] for a parton gas of massive quasiparticles, an overall quantitative agreement is observed, since both studies employ the quasiparticle framework with quark flavors. A numerical discrepancy between the studies arises from the quantitative differences of the applied couplings. Using the employed in Ref. [16], the result of the latter is reproduced as shown in Figure 3. All the numerical results obtained with the set (b exceed the results computed with the set (a) due to a higher initial temperature, which reflects the sensitivity of the production rate to the choice of the initial parameters and .
For the initial condition (a), the discrepancy between the two curves suggests the importance of the formulation of the quasiparticle approach with properly included charm quarks, i.e., as quasiparticles. A lower value of (6) leads to a smaller number of thermally produced pairs. Thus, the result obtained for is expected to provide a better quantitative agreement with the experimental data, since the analysis of the charm yield performed within the Statistical Hadronization Model (SHM) [5] suggests that the number of charm quarks produced at the earlier stage of the heavy-ion collisions stays approximately the same after the QGP phase. A direct comparison with the experimental data requires Equation (4) to be solved, which is considered to be given elsewhere [32].
4. Conclusions
In this paper, the production rate of charm quarks has been explored by employing the quasiparticle model with various microscopic descriptions of strongly interacting matter: versus quark flavors. Moreover, different initial conditions have been tested for the evolution of the QGP described as an ideal fluid propagating in the longitudinal direction. The results obtained reveal that as soon as the charm quarks are treated as effectively dressed quasiparticles (), their thermal production rate significantly diminishes in the vicinity of the crossover, compared to the scenario in which charm quarks are treated as impurities of constant mass. The observed difference suggests that the incorporation of heavy flavors as dynamical degrees of freedom might be essential in order to appropriately capture the properties of heavy flavor in the QGP described in the effective quasiparticle approaches. A closer agreement with the experimental data for the charm quark yield is expected for charm quarks considered as quasiparticles that affect the QGP thermodynamics. One also notices a continual suppression of the production rate for lower initial temperature of the QGP. Furthermore, for a certain initial condition, the obtained results appear in line with the production rate of charm quarks studied earlier in the alternative quasiparticle framework with [16].
Funding
This research was funded by the Polish National Science Center (NCN) under the PRELUDIUM 20 Grant No. UMO-2021/41/N/ST2/02615.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The author would like to thank Pasi Huovinen, Chihiro Sasaki and Krzysztof Redlich for inspiring discussions and useful comments.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Das, S.K.; Torres-Rincon, J.M.; Rapp, R. Charm and bottom hadrons in hot hadronic matter. Phys. Rep. 2025, 1129–1131, 1–53. [Google Scholar] [CrossRef]
- Adam, J. et al. [STAR Collaboration] Centrality and transverse momentum dependence of D0-meson production at mid-rapidity in Au + Au collisions at = 200 GeV. Phys. Rev. C 2019, 99, 034908. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] The ALICE experiment: A journey through QCD. Eur. Phys. J. C 2024, 84, 813. [Google Scholar] [CrossRef]
- Tumasyan, A. et al. [The CMS Collaboration] Study of charm hadronization with prompt baryons in proton–proton and lead–lead collisions at = 5.02 TeV. J. High Energy Phys. 2024, 2024, 128. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Köhler, M.K.; Mazeliauskas, A.; Redlich, K.; Stachel, J.; Vislavicius, V. The multiple-charm hierarchy in the statistical hadronization model. J. High Energy Phys. 2021, 2021, 35. [Google Scholar] [CrossRef]
- Apolinário, L.; Lee, Y.-J.; Winn, M. Heavy quarks and jets as probes of the QGP. Prog. Part. Nucl. Phys. 2022, 127, 103990. [Google Scholar] [CrossRef]
- Capellino, F.; Dubla, A.; Floerchinger, S.; Grossi, E.; Kirchner, A.; Masciocchi, S. Fluid dynamics of charm quarks in the quark–gluon plasma. Phys. Rev. D 2023, 108, 116011. [Google Scholar] [CrossRef]
- Zhao, J.; Aichelin, J.; Gossiaux, P.B.; Beraudo, A.; Cao, S.; Fan, W.; He, M.; Minissale, V.; Song, T.; Vitev, I.; et al. Hadronization of heavy quarks. Phys. Rev. C 2024, 109, 054912. [Google Scholar] [CrossRef]
- Altenkort, L. et al. [HotQCD Collaboration] Quark mass dependence of heavy quark diffusion coefficient from lattice QCD. Phys. Rev. Lett. 2024, 132, 051902. [Google Scholar] [CrossRef]
- Andronic, A.; Gossiaux, P.B.; Petreczky, P.; Rapp, R.; Strickland, M.; Blaizot, J.P.; Brambilla, N.; Braun-Munzinger, P.; Chen, B.; Delorme, S.; et al. Comparative study of quarkonium transport in hot QCD matter. Eur. Phys. J. A 2024, 60, 88. [Google Scholar] [CrossRef]
- Mykhaylova, V.; Bluhm, M.; Redlich, K.; Sasaki, C. Quark-flavor dependence of the shear viscosity in a quasiparticle model. Phys. Rev. D 2019, 100, 034002. [Google Scholar] [CrossRef]
- Mykhaylova, V.; Sasaki, C. Impact of quark quasiparticles on transport coefficients in hot QCD. Phys. Rev. D 2021, 103, 014007. [Google Scholar] [CrossRef]
- Auvinen, J.; Eskola, K.J.; Huovinen, P.; Niemi, H.; Paatelainen, R.; Petreczky, P. Temperature dependence of η/s of strongly interacting matter: Effects of the equation of state and the parametric form of (η/s)(T). Phys. Rev. C 2020, 102, 044911. [Google Scholar] [CrossRef]
- Song, T.; Grishmanovskii, I.; Soloveva, O.; Bratkovskaya, E. Thermal production of charm quarks in relativistic heavy-ion collisions. Phys. Rev. C 2024, 110, 034906. [Google Scholar] [CrossRef]
- Sambataro, M.L.; Greco, V.; Parisi, G.; Plumari, S. Quasi particle model vs lattice QCD thermodynamics: Extension to Nf = 2 + 1 + 1 flavors and momentum dependent quark masses. Eur. Phys. J. C 2024, 84, 881. [Google Scholar] [CrossRef]
- Levai, P.; Vogt, R. Thermal charm production by massive gluons and quarks. Phys. Rev. C 1997, 56, 2707–2717. [Google Scholar] [CrossRef][Green Version]
- Pisarski, R.D. Renormalized fermion propagator in hot gauge theories. Nucl. Phys. A 1989, 498, 423c–428c. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabó, K.K. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef]
- Biró, T.S.; van Doorn, E.; Müller, B.; Thoma, M.H.; Wang, X.-N. Parton equilibration in relativistic heavy ion collisions. Phys. Rev. C 1993, 48, 1275–1284. [Google Scholar] [CrossRef]
- Zhang, B.-W.; Ko, C.M.; Liu, W. Thermal charm production in a quark–gluon plasma in Pb–Pb collisions at = 5.5 TeV. Phys. Rev. C 2008, 77, 024901. [Google Scholar] [CrossRef]
- Mykhaylova, V. Reviewing the production rate of charm quarks in effective kinetic theory. J. Subat. Part. Cosmol. 2025, 3, 100031. [Google Scholar] [CrossRef]
- Mykhaylova, V. Production rate of charm quarks in the quasiparticle approach. Acta Phys. Polon. Suppl. 2024, 17, 6-A10. [Google Scholar] [CrossRef]
- Song, T.; Zhao, J.; Grishmanovskii, I. Heavy quark potential and thermal charm production in heavy-ion collisions. arXiv 2024, arXiv:2411.07383. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Redlich, K. Charmonium production from the secondary collisions at LHC energy. Eur. Phys. J. C 2000, 16, 519–525. [Google Scholar] [CrossRef]
- Kadam, G.P.; Mishra, H. Dissipative properties of hot and dense hadronic matter in an excluded-volume hadron resonance gas model. Phys. Rev. C 2015, 92, 035203. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly relativistic nucleus–nucleus collisions: The central rapidity region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Shou, Q.-Y.; Ma, Y.-G.; Zhang, S.; Zhu, J.-H.; Mao, Y.-X.; Pei, H.; Yin, Z.-B.; Zhang, X.-M.; Zhou, D.-C.; Peng, X.-Y.; et al. Properties of QCD matter: A review of selected results from ALICE experiment. Nucl. Sci. Tech. 2024, 35, 219. [Google Scholar] [CrossRef]
- Sinyukov, Y.M.; Shapoval, V.; Adzhymambetov, M. Space–time structure of particle emission and femtoscopy scales in ultrarelativistic heavy-ion collisions. Universe 2023, 9, 433. [Google Scholar] [CrossRef]
- Kasza, G.; Csörgő, T. Lifetime estimations from RHIC Au + Au data. Int. J. Mod. Phys. A 2019, 34, 1950147. [Google Scholar] [CrossRef]
- Cimerman, J.; Karpenko, I.; Tomášik, B.; Huovinen, P. Next-generation multifluid hydrodynamic model for nuclear collisions at from a few GeV to a hundred GeV. Phys. Rev. C 2023, 107, 044902. [Google Scholar] [CrossRef]
- Mykhaylova, V.; Redlich, K.; Sasaki, C. Charm Quark Kinetics in Heavy-Ion Collisions. Unpublished work. 2025. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).