Abstract
We consider a multi-species mixture of interacting bosons, bosons of mass , bosons of mass , and bosons of mass , in a harmonic trap with frequency . The corresponding intra-species interaction strengths are , , and , and the inter-species interaction strengths are , , and . When the shape of all interactions is harmonic, the system corresponds to the generic multi-species harmonic-interaction model, which is exactly solvable. We start by solving the many-particle Hamiltonian and concisely discussing the ground-state wavefunction and energy in explicit forms as functions of all parameters, the masses, numbers of particles, and the intra-species and inter-species interaction strengths. We then explicitly compute the reduced one-particle density matrices for all the species and diagonalize them, thus generalizing the treatment by the authors earlier. The respective eigenvalues determine the degree of fragmentation of each species. As an application, we focus on phenomena that do not arise in the corresponding single-species or two-species systems. For instance, we consider a mixture of two kinds of bosons in a bath made by a third kind, controlling the fragmentation of the former by coupling to the latter. Another example exploits the possibility of different connectivities (i.e., which species interacts with which species) in the mixture, and demonstrates how the fragmentation of species 3 can be manipulated by the interaction between species 1 and species 2, when species 3 and 1 do not interact with each other. We highlight the properties of fragmentation that only appear in the multi-species mixture. Further applications are briefly discussed.
1. Introduction
Fragmentation of Bose–Einstein condensates draws much attention already for more than six decades [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Here, “fragmentation” refers to the macroscopic occupation of more than a single eigenvalue of the one-particle reduced density matrix [23,24]. Generally, the more complex the underlying bosonic system is, the more intricate its fragmentation can be. When dealing with bosonic mixtures, a natural question is how inter-species interactions govern the fragmentation of individual species. In multi-species mixtures, this latter question is further enriched, which is the topic of the present paper.
Mixtures of two types of indistinguishable bosons have drawn much interest and exhibit a wealth of fascinating phenomena, such as demixing, inter-species entanglement, and induced interactions, to name a few; see Refs. [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. Multi-species bosonic mixtures have been attracting growing interest [46,47,48,49,50,51,52,53,54,55,56,57,58,59], where, apparently, their ground states are even richer than those of two-species mixtures. Yet, treating them numerically at the many-body level of theory is rapidly becoming complicated, especially when the number of particles in each species increases or the interactions between particles grow stronger. To surpass this complication, we refer to a solvable many-body model, which allows analytically expressing the one-particle reduced density matrices and their eigenvalues as functions of the masses, numbers of bosons, and various intra-species and inter-species interactions in a generic multi-species bosonic mixture. Harmonic-interaction models have been extensively applied, covering various setups that include distinguishable and identical particles; see, e.g., [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86]. In this respect, the present study addresses the generic multi-species harmonic-interaction model for an imbalanced bosonic mixture. We add a new facet to the family of exactly solvable many-particle models in nonhomogeneous environments, i.e., in traps. The main results of the present investigation are, first, the analytical evaluation and subsequent diagonalization of one-particle reduced density matrices in a generic trapped mixture of three kinds of identical bosons. Second, the study and demonstration of fragmentation control in scenarios that occur only in multi-species mixtures, like when a two-species mixture is embedded in a third species that serves as a bath.
The structure of the paper is as follows. In Section 2, we present the theoretical framework, in particular, the many-body Hamiltonian is diagonalized and the reduced one-particle density matrices of the different species are evaluated explicitly, thus generalizing the study in [56]. In Section 3, illustrative examples are worked out, demonstrating intricate control of fragmentations in multi-species mixtures. In Section 4, a summary and outlook are put forward. Finally, the three appendices collect supplementary information. Appendix A discusses limiting cases of the frequency matrix associated with the center-of-mass degrees of freedom. Appendix B presents a concise account of the mean-field solution of the multi-species bosonic mixture, and Appendix C presents further details of the derivation of the all-particle density matrix.
2. Theoretical Framework
We treat an imbalanced mixture of three distinct bosonic species, i.e., the smallest generic multi-species mixture. The Hamiltonian is given by
Here, , denote the space coordinates for each species, for example, for the jth boson of species 1, , , and are the numbers of bosons of each species, , , and are their masses, , , and are their intra-species interaction strengths, and , , and are the respective inter-species interaction strengths. We set the reduced Planck constant . It is instructive to define the interaction parameters , , , and , , , , , , which are to be used from now on. The interaction parameters , , , and , , , , , are also referred to as mean-field parameters since they appear in the mean-field theory; see Appendix B. In the so-called infinite-particle-number limit (not treated in this paper; see, e.g., [56,78,87,88,89,90,91]), the interaction parameters are kept fixed as the numbers of bosons tend to infinity. Finally, all bosons are trapped in a three-dimensional isotropic harmonic potential of frequency .
To diagonalize the Hamiltonian (1), we employ a set of Jacobi coordinates for each of the species,
The first set of coordinates in each line is referred to as the relative-motion Jacobi coordinates, and the last coordinate in each line is called the center-of-mass Jacobi coordinate. Transforming to Jacobi coordinates and later back to the laboratory frame is required for the various steps in evaluating quantities.
It is instrumental to define the geometric-mean mass , and, thereafter, to rescale the center-of-mass Jacobi coordinates
The transformation (3) definitely obeys .
Then, the Hamiltonian may be written as a sum of two Hamiltonians:
The Hamiltonian of the relative motions is
where the intra-species relative-motion frequencies are
One sees that, for example, the frequency depends on the interactions of species 1 with species 2 and 3, but not on the inter-species interaction between the latter two. We come back to this issue below in Section 3; see also Appendix B.
The center-of-mass Hamiltonian reads
The frequencies’ matrix governs the coupling of the center-of-mass coordinates and is expressed as a function of all inter-species interaction parameters, , , , , , and , for convenience. It is, certainly, symmetric.
Diagonalizing , the frequencies of the center-of-mass Hamiltonian are
where
The structure of the frequencies is worth a discussion. K is referred to as the two-body part, and G is referred to as the three-body part, which naturally cannot exist in a mixture with two species. We look into the impact of the latter below in Section 3. Finally, as all species are trapped in the same harmonic potential, the center-of-mass frequency is .
Summing all together, the ground-state energy of the generic three-species mixture is given by
where
and
Surely, the frequencies , , , , and must all be positive for the three-species mixture to be bound. This sets five simultaneous restrictions on the interaction parameters:
As a result, the energy (10) is bound from below by the frequency of the trap but is not bound from above. Physically, the lower bounds (13) mean that the overall repulsion between the bosons cannot be too strong. In Section 3, we present an example and emerging effects at the edge of stability of the mixture.
The ground-state wavefunction then takes on the separable form
where the (orthonormal) eigenvectors of the center-of-mass Hamiltonian are denoted as
The explicit expressions for the are depicted in Equation (16) just below.
The components of the two relative center-of-mass coordinates, and , for the case of general nondegenerate roots (8), read
where are the normalizations. Definitely, the components of the relative center-of-mass coordinates depend on the inter-species interaction strengths, unlike the corresponding relative coordinate in the two-species mixture or the relative coordinates for the specific case of a balanced multi-species mixture [56].
In all cases of a three-species mixture, the components of the center-of-mass coordinate are, definitely,
which do not depend on the interaction strengths.
When using the general expressions (16) and (17) explicitly, specific cases and limits to be noted are discussed separately; to not interrupt ongoing discussion, these cases are collected and analyzed in Appendix A.
To proceed and explicitly calculate the one-particle reduced density matrices of species 1, 2, and 3, we work in the representation of the wavefunction that uses the Jacobi coordinates of each species:
where, recall, . The various coefficients of the center-of-mass part are
Then, the all-particle density matrix expressed using the species’ Jacobi coordinates is just
where normalization to unity is employed; see Appendix C. The all-particle density matrix (20) contains the correlations in the ground state to all orders, and contracting it—by integrating over selected degrees of freedom—expresses these correlations in terms of reduced density matrices.
The integration scheme for the one-particle reduced density matrix of species 1 starts by eliminating the relative-motion Jacobi coordinates of species 3 and 2, and then proceeds over the center-of-mass of species 3, , and that of species 2, , yielding
Hence, one sees how the center of mass of the remaining species 1 is dressed by the centers of mass of the other species. Expression (21) generalizes the respective one in Ref. [56] obtained for the balanced three-species mixture. Furthermore, by performing the last integration over the center of mass of species 1, , and keeping in mind that the normalizations of the wavefunctions (14) and (18) are alike, one arrives at a helpful relation between all coefficients:
The relation (22) is instrumental in simplifying the reduced one-particle density matrices; see Equation (31) below.
The resulting expression for the -particle reduced density matrix of species 1 in the three-species mixture is given by
with
where, to recall, and the other coefficients and are collected in Equation (19).
Hence, the one-particle reduced density matrix of species 1 is integrated from Equations (23)–(24) and is given by
The one-particle reduced density matrix (25) in the generic multi-species mixture has the same structure as in relatively simpler cases [56,65,78], albeit with more complex explicit coefficients; also see Equation (31) below. The diagonal, , is just the density of species 1. The corresponding expressions for the one-particle reduced density matrices of species 2 and 3 are obtained in the same way and, thus, relate to Equation (25) by the appropriate interchanges of quantities or indices:
and
where and , and and are the one-particle densities of species 2 and 3, respectively. For completeness, the resulting expressions for the -particle reduced density matrix of species 2 and the -particle reduced density matrix of species 3 in the three-species mixture are obtained analogously to Equation (23) by the corresponding index interchanges.
To compute the depletion of each species, we perform a diagonalization of the one-particle reduced density matrices (25)–(27) using Mehler’s formula [56,62,73,80] in three spatial dimensions,
and are the Hermite polynomials.
Thus, the eigenvalues of each of the reduced one-particle density matrices are generated by the respective parameter appearing in Mehler’s formula (28). The first few occupation numbers per particle, as they are often called, are
Correspondingly, the fraction of depleted bosons, i.e., bosons residing in all the natural orbitals but the first (lowest), is
where is computed hereafter explicitly for each of the species. In what follows, we investigate the fragmentation and depletion of species 1, 2, and 3. Following the relations (29) and (30), we use the terms fragmentation and depletion interchangeably. For species 1, one finds explicitly
where Equation (22) is used. Equation (31) is one of the main results of the present study and describes the fragmentation of species 1 as an explicit function of all parameters in the mixture—the masses, number of particles, intra-species and inter-species interactions in the Hamiltonian (1)—that is, altogether, twelve different parameters. The multi-species result (31) generalizes the two-species expression [82]. Conceptually, there are not only more coefficients in the former, but, as one saw above, the relative center-of-mass coefficients (16) are interaction-dependent, unlike in the two-species mixture, which can support richer fragmentation scenarios. The respective expressions for the fragmentations of species 2 and 3 are obtained analogously and, hence, relate to Equation (31) by the appropriate interchanges of indexes:
and
Finally, the corresponding scalings of the natural orbitals (see Mehler’s formula (28) above) for the different species are , , and . In Section 3, we investigate the depletion of the three species under various conditions.
3. Illustrative Examples
What governs fragmentation in a trapped multi-species bosonic mixture? To answer this question, in the present paper, we explore some answers using the Hamiltonian (1). Let us remove the intra-species interactions completely, i.e., . In this case, in the absence of inter-species interactions, the three non-interacting bosonic species are, certainly, fully condensed. In what follows, we look into how inter-species interactions alone govern fragmentation, focusing on scenarios that go beyond two-species mixtures and that definitely do not exist for single-species bosons in a trap.
Two examples are put forward and investigated. In the first example, we take a two-species bosonic system (species 1 and 3) and embed it in a third species, which serves as a bath (species 2). We fix the interaction within the two-species system and only alter the couplings to the bath. Control of the fragmentation of all species, the system and the bath, is demonstrated and discussed. In the second case, we explore and exploit matters of connectivity, namely, which species interacts with which species, and illustrate that the fragmentation of a species can be controlled by changing the interaction between the other two species. Concretely, we consider a mixture where species 1 interacts only with species 2, which by itself also interacts with species 3 (the interaction between species 2 and 3 is kept fixed). We show that changing the way species 1 interacts with species 2 can drive the fragmentation of species 3 despite the latter not interacting directly with the former.
It is informative to examine the widths of the densities of species 1, 2, and 3, which are given by
and, analogously, by and , respectively. Since all densities are Gaussian-shaped, the width is just that of a Gaussian, . As done throughout this study, the width of the many-boson density (34) for species 1 is given by an analytical closed-form expression in terms of all parameters of the multi-species bosonic mixture. Apparently, this also holds for the other species.
Figure 1 collects the results of the first example. We also present a comparison for different masses of the bath bosons, which is found to be appealing (see below). The respective parameters are chosen to differ one from another to emphasize the treatment of a generic, imbalanced mixture. The corresponding inter-species interactions between species 1 and 3—the system—are kept constant, while jointly and proportionally increasing the couplings of species 1 and 3 to the bath—species 2—by varying the coefficient . The intra-species interactions, as defined above in the beginning of this Section, vanish in the examples considered.
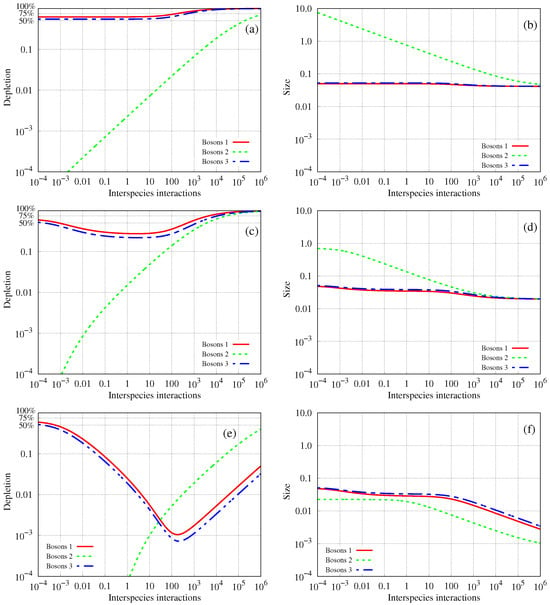
Figure 1.
Fragmentation of a three-species bosonic mixture: the depletion (left) and the size (right) (both quantities are dimensionless) of the two-species system coupled to a third-species bath of bosons. Investigated is a mixture of species 1 and species 3 bosons (the system) and species 2 bosons (the bath) as a function of the inter-species interaction strengths: is kept fixed and and are increasing linearly ( is the common abscissa in the plots). The intra-species interactions of all species are set to zero. The masses used are , , and (a,b), 1 (c,d), and 1000 (e,f). See the text for more details.
Before proceeding further, it is instructive to quantify the strength of the interactions in the multi-species mixture. This is particularly needed whenever there are several interactions involved, and one inquires whether their combined effect on a particular species is considerably weak, intermediate, or strong. Surely, in the absence of interactions, all species are fully condensed. When the inter-species interactions are non-zero, the degree of fragmentation of each species may vary in a non-trivial manner; see below. Thus, to be consistent, one needs to quantify the combined effect of interactions on a specific species by its degree of fragmentation (depletion). Qualitatively, when the fragmentation is relatively weak, the combined interactions acting on a given species are said to be weak, and likewise when the fragmentation is intermediate or strong. We note that the degree of fragmentation is bounded between and .
To be quantitative, further definitions are introduced. The discussion just below is kept brief, with a more detailed exposition given in [84]. We treat species 1 explicitly, but the same analysis holds for any of the species. We rewrite the reduced one-particle density matrix as . From which, the Glauber’s normalized first-order correlation function [92,93] can be analytically computed, . One can now compare two length scales, the off-diagonal decay of the first-order correlation function given by and the decay of the diagonal of the reduced one-particle density matrix given by (basically, the size of the condensate). Their ratio defines the dimensionless coherence length, which quantifies the strength of correlations and is related to the degree of fragmentation [84],
The dimensionless coherence length (35) goes to infinity for a fully condensed system and to zero for a fully depleted system. In other words, when the length scale for the decay of correlations is (much) larger than the size of the species, that is, , the system is said to be weakly correlated, and when the length scale is (much) smaller, , it is said to be strongly correlated. It is natural to set the border of intermediate correlations at , thus separating the regimes of weak and strong correlations. Solving for the inverse relation of (35) and using Equation (30) for the depletion, one finds at this border. In summary, using the dimensionless coherence length (35), the combined effect of all interactions in the multi-species mixtures on a particular species can be consistently quantified as weak, intermediate, or strong.
In the absence of couplings to the bath, the fragmentations of species 1 and 3 are, respectively, and (no rounding here and hereafter). Correspondingly, the sizes of their densities are and . Here and hereafter, we use the size and width of a density interchangeably. Overall (see Figure 1), an intriguing dependence of the depletion values on both the interactions with the bath and the mass of the bosons comprising the bath is found. Generally, increasing the couplings between the two-species system and the bath increases the fragmentation of the bath monotonously. Yet, the fragmentations of species 1 and 3 behave in a non-monotonous manner. Here, the larger the mass of the bath, the stronger the variation in the system’s fragmentation, which first decreases and increases again only at stronger couplings. Interestingly, the depletion of the bath is non-monotonous with the mass of the bath, i.e., given the interactions between the system and the bath, there is an optimal mass for the maximal depletion of the bath. Such behavior of the bath’s fragmentation is not observed in the corresponding two-species mixture [82].
An accompanying analysis of the respective sizes of the three bosonic clouds is instrumental. Here, generally, increasing the couplings to the bath decreases its size as well as that of the system’s species; see Figure 1. Yet, when the mass of the bath is larger, the sizes of species 1 and 3 are more affected by species 2 upon enlarging the interactions. Correspondingly, when the size of the bath is significantly larger than that of the system, enlarging the couplings essentially leads to an increase in the system’s fragmentation. When the mass of the bath is increased, the size of the bath naturally decreases, and the effect on the system is to first reduce its fragmentation and later increase it, as discussed above in this Section. Altogether, the changes in the sizes of the system and the bath are much more involved in the three-species mixture than in the two-species mixture [82]. We emphasize that all results are expressed explicitly in analytical closed form.
Figure 2 depicts the results of the second case.
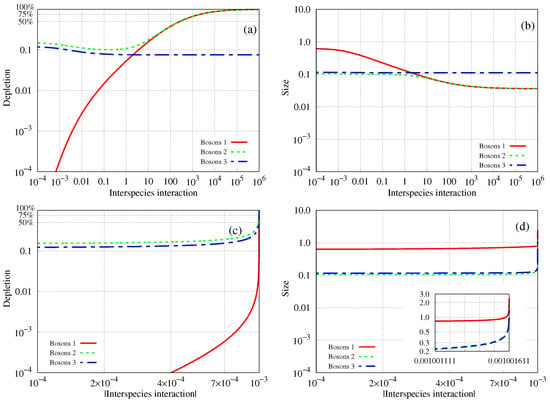
Figure 2.
Fragmentation of a three-species bosonic mixture: effect of connectivity. The depletion (left) and the size (right) (both quantities are dimensionless) of bosons in a mixture of species 1, species 2, and species 3 bosons as a function of the inter-species interaction strength ( is the abscissa in the plots), where is kept fixed and , for the attractive (a,b) and repulsive (c,d) branches. The intra-species interactions of all species are considered zero. The masses used are , , and . See the text for more details.
In the absence of interaction between species 1 and 2, the depletion values of species 2 and 3 are, correspondingly, and . The respective sizes are and . The fragmentation and size of each bosonic cloud are computed in the present example for both attractive and repulsive inter-species interactions, , while the mixture is still bound; see below.
Since the sign of is positive on the attractive branch and negative on the repulsive branch, to avoid confusion, increasing the interaction implies increasing the magnitude of the interaction. An intriguing dependence of the depletion values and sizes on the interaction is found; see Figure 2. Again, all results are obtained analytically and expressed explicitly using the theory derived in Section 2.
On the attractive branch(Figure 2a,b), increasing the inter-species interaction between species 1 and 2 eventually leads to a common growth of their fragmentation and to a joint decrease, followed by a tendency toward saturation, of their sizes. Species 3, which ‘grows apart’ from species 2 when the interaction is enlarged, exhibits a small reduction in its depletion and quite a mild decrease in its size, both tending toward saturation.
On the repulsive branch (Figure 2c,d), the picture differs qualitatively. Enlarging the repulsion between species 1 and 2 leads to a steady increase in the fragmentations of all species and growth of their sizes. In particular, as the system approaches the border of stability, the increase in the depletion and size of all species ‘accelerates’ and tends to their limiting values of unity and infinity, respectively. Thus, species 3 becomes more and more fragmented because species 1 ‘pushes’ species 2, which is coupled to species 3.
Consider the interaction strength , where the mixture is just about to become unbound. Here, the fragmentations are already , , and . The corresponding widths are , , and , compare to their respective values for [, , and ]. How close the findings are to the border of stability, i.e., when at least one of the frequencies (6) and (8) becomes zero (see also the restrictions (13)), for ? The intra-species relative-motion frequencies are found to be , , and , i.e., they are not the reason for approaching the border of stability. On the other end, examining the relative-motion center-of-mass frequencies, it is found that, whereas , then . Hence, for the example studied here, approaching the border of stability is governed by the softening of a relative-motion center-of-mass coordinate. Finally, we note that for , the mixture is already unbound. Overall, altering the interaction between species 1 and 2 crucially impacts the properties of species 3, despite having fixed interaction with species 2 and no interaction with species 1.
4. Summary and Outlook
In the current paper, we investigated the fragmentation of a multi-species bosonic mixture within the framework of an exactly solvable many-particle model. Such models for multi-species trapped bosons are rather rare, making the solution presented here of particular aesthetic and of interest on its own. The present many-body model of interacting multi-species bosons in a trap, where the interparticle interactions are harmonic, is not a substitute for more realistic interactions. Rather, because the model provides exact results that are seldom obtainable with other interactions, its purpose is to deduce intriguing and fundamental consequences, stimulate further investigations, and promote additional explorations of more realistic setups.
We solved the many-particle Hamiltonian and investigated the structure of the ground-state wavefunction and energy, and their dependencies on all parameters, the masses, numbers of particles, and the intra-species and inter-species interaction strengths. Tools to integrate the reduced one-particle density matrices for all the species were put forward, and the explicit expressions as functions of all parameters in the mixture were prescribed and analyzed. As illustrative examples, we focused on scenarios that go beyond the respective single-species and two-species systems, and highlighted the intricate fragmentation properties of the species that only occur in the multi-species mixture.
As an outlook, we touch upon the flexibilities and opportunities offered by the generic multi-species harmonic-interaction model. These include systems with impurities, induced interactions between mutually non-interacting species coupled to another species, and, further down the road, out-of-equilibrium dynamics, all from the perspective of analytical many-body results. We also believe that more insights into the connections and differences between the many-body and mean-field solutions are achievable beyond [56], i.e., benefiting from the imbalance between species. Methodologically, further tools to handle various reduced-density matrices would be instrumental. Another facet that can be anticipated involves using the plethora of analytical results to assess the regimes of validity of numerical approaches. Also, extensions of the model for different harmonic trappings of each species and distinct positions of their minima might prove practical. Finally, applications to bosons in cavities, whether multi-species bosons in a single-mode cavity or the other way around, in the spirit of [84], could be foreseen. Furthermore, extensions to multi-species bosons in open-system setups, like those discussed in Refs. [94,95,96], are challenging directions worth pursuing.
Author Contributions
Methodology, O.E.A. and L.S.C.; Formal analysis, O.E.A. and L.S.C.; Writing—original draft, O.E.A. and L.S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Israel Science Foundation (Grant No. 1516/19).
Data Availability Statement
The data presented in the study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Limiting and Specific Cases of the Frequencies’ Matrix and Its Eigenvectors and Eigenvalues
In the following, we denote the eigenvectors (16) and (17) of the frequencies’ matrix as and enlist and discuss several possibilities.
- A1.
- Generally, the three inter-species interactions , , and , are nonzero and couple the three species. We then have a generic three-species mixture where the relative-motion center-of-mass coordinates (16) depend on the inter-species interactions, and the frequencies are non-degenerate. Quite rarely, the explicit expression for a relative-motion center-of-mass coordinate in (16) may have an accidental vanishing point; for instance, when , and , , , we have for numbers , , and of bosons. In such case, its value at the accidental vanishing point is determined as a limit, specifically, for instance, . The result, which certainly recovers that obtained directly by diagonalizing the frequency matrix at this point is . Interestingly, it does not depend on , the number of bosons of species 3.
- A2.
- If one inter-species interaction is zero, the interaction between species 1 and species 3 is chosen to vanish, i.e., . Correspondingly, the above expressions for K and G (9) somewhat simplify. Indeed, substituting into the three-body part G, the latter does not vanish; namely, we still have a three-species mixture, the relative-motion center-of-mass coordinates depend on the inter-species interactions, and the frequencies are non-degenerate.
- A3.
- If two inter-species interactions are zero, for instance, and , then the three-body part vanishes, , and consequently, degenerates with the trap frequency . Physically, the system boils down to a mixture of two species, 1 and 3, and one individual species, 2; therefore, the expressions for the two-species mixtures [78] plus one individual species are to be used. Explicitly, for the three species: , , and . Indeed, taking , with , and for , Equation (16) becomes and , respectively, and is just taken from Equation (17). Thus, the (remaining) relative-motion center-of-mass coordinate now becomes interaction-independent. Then, taking a linear combination of eigenvectors associated with the degenerate eigenvalue , and , gives the remaining physical center-of-mass coordinates and . Overall, the frequencies are .
- A4.
- If all three inter-species interactions are zero, then . Actually, one deals with three individual species, where the frequencies’ matrix (7) is diagonal and its eigenvectors trivial, , , and , i.e., all coordinates become the species’ center-of-mass coordinates. To recover the limit of three individual species from the generic solution, the scenario A3 is performed first, i.e., one starts with a mixture of species 1 and 3 for which and , and the individual species 2. Then, taking designates that degenerates with the trap frequency as well, implying that one can mix and to obtain the physical center-of-mass coordinates and . In sum, the limit of a non-interacting mixture whose frequencies are three-fold degenerate, , is readily obtained from the generic three-species expressions (16) and (17).
- A5.
- The two relative-motion center-of-mass roots become degenerate in the specific case of a mass-balanced and interaction-balanced three-species mixture. The numbers of bosons , , and need not be equal, but when they are, one has quite a specific case of a balanced three-species mixture, which is dealt with in Ref. [56]. Denoting all masses by m and all inter-species interaction strengths by , one has . The respective eigenvectors do not depend on the interactions and are and along with the center-of-mass coordinate . Now, in the expressions (16) and (17), substituting m for all masses, and setting , for , and taking the limit , one recovers , , and for the eigenvectors of the center-of-mass Hamiltonian. Note that the degenerate frequencies depend on the sum of all bosons only, and one might suspect that the mixture behaves as a single-species mixture. This is not the case. As can be seen, the fragmentations of the species do depend on the individual numbers of bosons , , and .
Appendix B. The Mean-Field Solution of the Generic Multi-Species Mixture
The mean-field solution of the three-species mixture is as follows. The generalization to any number of species P is straightforward. The ansatz for the Gross–Pitaevskii wavefunction is the separable product state
where all bosons of the same type reside in the same normalized orbital. Sandwiching the Hamiltonian (1) with the ansatz (A1) and minimizing the resulting energy functional with respect to the shapes of the orbitals , , and , the three coupled Gross–Pitaevskii equations of the mixture are derived:
where the intra-species , , and inter-species , , , , , interaction parameters are the same as in the many-body theory, and are the chemical potentials of the species. The solution to the three coupled non-linear Equations (A2) is given by
One finds that the density of each species, , , and , is dressed by the inter-species interactions with the other two species, but does not depend on the mutual interaction between the other two species. Naturally, the frequencies , , and have to be positive for the three-species mixture to be bound at the mean-field level. This implies three simultaneous restrictions on the interaction parameters:
for comparison, see the restrictions (13) in the many-body case. For completeness, the chemical potentials read
Finally, the Gross–Pitaevskii energy per particle of the three-species mixture reads
Then, it is the natural starting point for comparing the many-body and mean-field solutions of the multi-species mixture, both for finite systems and in the infinite-particle-number limit.
Appendix C. Further Details of the Derivation of the All-Particle Density Matrix
Since the Hamiltonian can be written as a sum of two terms, (4), the wavefunction (14) can be expressed accordingly as , where
Similarly, the all-particle density matrix (20) can be written as the product , where
and
Equation (A8) is already in the form that is contained in Equation (20). To proceed, we substitute the scaled center-of-mass Jacobi coordinates (3) into Equation (15) and take the square, which gives
Finally, substituting (A10) into (A9) and using definitions (19), one arrives at
Then, combining Equations (A8) and (A11) gives the all-particle density matrix (20).
References
- Girardeau, M. Simple and generalized condensation in many-boson systems. Phys. Fluids 1962, 5, 1468–1478. [Google Scholar] [CrossRef]
- Pollock, F. Quantization of circulation in a non-ideal Bose gas. Phys. Fluids 1967, 10, 473–478. [Google Scholar] [CrossRef]
- Noziéres, P.; Saint James, D. Particle vs. pair condensation in attractive Bose liquids. J. Phys. France 1982, 43, 1133–1148. [Google Scholar] [CrossRef]
- Noziéres, P. Some comments on Bose–Einstein condensation. In Bose–Einstein Condensation; Griffin, A., Snoke, D.W., Stringari, S., Eds.; Cambridge University Press: Cambridge, UK, 1996; pp. 15–30. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Sipe, J.E. Spatial fragmentation of a Bose–Einstein condensate in a double-well potential. Phys. Rev. A 1999, 59, 3868–3877. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Cederbaum, L.S.; Moiseyev, N. Ground-state fragmentation of repulsive Bose–Einstein condensates in double-trap potentials. Phys. Rev. A 2004, 70, 053607. [Google Scholar] [CrossRef]
- Mueller, E.J.; Ho, T.-L.; Ueda, M.; Baym, G. Fragmentation of Bose–Einstein condensates. Phys. Rev. A 2006, 74, 033612. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Pathway from condensation via fragmentation to fermionization of cold bosonic systems. Phys. Rev. Lett. 2005, 95, 140402. [Google Scholar] [CrossRef]
- Bader, P.; Fischer, U.R. Fragmented many-body ground states for scalar bosons in a single trap. Phys. Rev. Lett. 2009, 103, 060402. [Google Scholar] [CrossRef]
- Zhou, Q.; Cui, X. Fate of a Bose–Einstein condensate in the presence of spin-orbit coupling. Phys. Rev. Lett. 2013, 110, 140407. [Google Scholar] [CrossRef]
- Kawaguchi, Y. Goldstone-mode instability leading to fragmentation in a spinor Bose–Einstein condensate. Phys. Rev. A 2014, 89, 033627. [Google Scholar] [CrossRef]
- Song, S.-W.; Zhang, Y.-C.; Zhao, H.; Wang, X.; Liu, W.-M. Fragmentation of spin-orbit-coupled spinor Bose–Einstein condensates. Phys. Rev. A 2014, 89, 063613. [Google Scholar] [CrossRef]
- Kang, M.-K.; Fischer, U.R. Revealing single-trap condensate fragmentation by Measuring density–density correlations after time of flight. Phys. Rev. Lett. 2014, 113, 140404. [Google Scholar] [CrossRef]
- Jen, H.H.; Yip, S.-K. Fragmented many-body states of a spin-2 Bose gas. Phys. Rev. A 2015, 91, 063603. [Google Scholar] [CrossRef]
- Fischer, U.R.; Lode, A.U.J.; Chatterjee, B. Condensate fragmentation as a sensitive measure of the quantum many-body behavior of bosons with long-range interactions. Phys. Rev. A 2015, 91, 063621. [Google Scholar] [CrossRef]
- Lode, A.U.J. Multiconfigurational time-dependent Hartree method for bosons with internal degrees of freedom: Theory and composite fragmentation of multicomponent Bose–Einstein condensates. Phys. Rev. A 2016, 93, 063601. [Google Scholar] [CrossRef]
- Kolovsky, A.R. Bogoliubov depletion of the fragmented condensate in the bosonic flux ladder. Phys. Rev. A 2017, 95, 033622. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Fragmented superradiance of a Bose–Einstein condensate in an optical cavity. Phys. Rev. Lett. 2017, 118, 013603. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Diorico, F.S.; Wu, R.; Molignini, P.; Papariello, L.; Lin, R.; Lévêque, C.; Exl, L.; Tsatsos, M.C.; Chitra, R.; et al. Many-body physics in two-component Bose–Einstein condensates in a cavity: Fragmented superradiance and polarization. New J. Phys. 2018, 20, 055006. [Google Scholar] [CrossRef]
- Tomchenko, M. On a fragmented condensate in a uniform Bose system. J. Low Temp. Phys. 2020, 198, 100–121. [Google Scholar] [CrossRef]
- Lee, J.; Michelangeli, A. On the characterisation of fragmented Bose–Einstein condensation and its emergent effective evolution. Nonlinearity 2023, 36, 6364–6402. [Google Scholar] [CrossRef]
- Bhowmik, A.; Alon, O.E. Interference of longitudinal and transversal fragmentations in the Josephson tunneling dynamics of Bose–Einstein condensates. New J. Phys. 2024, 26, 123035. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys. Rev. 1955, 97, 1474–1489. [Google Scholar] [CrossRef]
- Coleman, A.J.; Yukalov, V.I. Reduced Density Matrices: Coulson’s Challenge; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ho, T.-L.; Shenoy, V.B. Binary mixtures of Bose Condensates of alkali atoms. Phys. Rev. Lett. 1996, 77, 3276–3279. [Google Scholar] [CrossRef] [PubMed]
- Esry, B.D.; Greene, C.H.; Burke, J.P., Jr.; Bohn, J.L. Hartree–Fock theory for double condensates. Phys. Rev. Lett. 1997, 78, 3594–3597. [Google Scholar] [CrossRef]
- Myatt, C.J.; Burt, E.A.; Ghrist, R.W.; Cornell, E.A.; Wieman, C.E. Production of two overlapping Bose–Einstein condensates by sympathetic cooling. Phys. Rev. Lett. 1997, 78, 586–589. [Google Scholar] [CrossRef]
- Stamper-Kurn, D.M.; Andrews, M.R.; Chikkatur, A.P.; Inouye, S.; Miesner, H.-J.; Stenger, J.; Ketterle, W. Optical confinement of a Bose–Einstein condensate. Phys. Rev. Lett. 1998, 80, 2027–2030. [Google Scholar] [CrossRef]
- Pu, H.; Bigelow, N.P. Properties of two-species Bose condensates. Phys. Rev. Lett. 1998, 80, 1130–1133. [Google Scholar] [CrossRef]
- Timmermans, E. Phase separation of Bose–Einstein condensates. Phys. Rev. Lett. 1998, 81, 5718–5721. [Google Scholar] [CrossRef]
- Eckardt, A.; Weiss, C.; Holthaus, M. Ground-state energy and depletions for a dilute binary Bose gas. Phys. Rev. A 2004, 70, 043615. [Google Scholar] [CrossRef][Green Version]
- Sakhel, A.R.; DuBois, J.L.; Glyde, H.R. Condensate depletion in two-species Bose gases: A variational quantum Monte Carlo study. Phys. Rev. A 2008, 77, 043627. [Google Scholar] [CrossRef][Green Version]
- Zöllner, S.; Meyer, H.; Schmelcher, P. Composite fermionization of one-dimensional Bose–Bose mixtures. Phys. Rev. A 2008, 78, 013629. [Google Scholar] [CrossRef]
- Oleś, B.; Sacha, K. N-conserving Bogoliubov vacuum of a two-component Bose–Einstein condensate: Density fluctuations close to a phase-separation condition. J. Phys. A Math. Theor. 2008, 41, 145005. [Google Scholar] [CrossRef]
- Girardeau, M.D. Pairing, off-diagonal long-range order, and quantum phase transition in strongly attracting ultracold Bose gas mixtures in tight waveguides. Phys. Rev. Lett. 2009, 102, 245303. [Google Scholar] [CrossRef] [PubMed]
- Girardeau, M.D.; Astrakharchik, G.E. Ground state of a mixture of two bosonic Calogero–Sutherland gases with strong odd-wave interspecies attraction. Phys. Rev. A 2010, 81, 043601. [Google Scholar] [CrossRef]
- Gautam, S.; Angom, D. Ground state geometry of binary condensates in axissymmetric traps. J. Phys. B. At. Mol. Opt. Phys. 2010, 43, 095302. [Google Scholar] [CrossRef]
- García-March, M.; Busch, T. Quantum gas mixtures in different correlation regimes. Phys. Rev. A 2013, 87, 063633. [Google Scholar] [CrossRef]
- Ardila, L.A.P.; Giorgini, S. Impurity in a Bose–Einstein condensate: Study of the attractive and repulsive branch using quantum Monte Carlo methods. Phys. Rev. A 2015, 92, 033612. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose–Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Schurer, J.M.; Negretti, A.; Schmelcher, P. Unraveling the structure of ultracold mesoscopic collinear molecular ions. Phys. Rev. Lett. 2017, 119, 063001. [Google Scholar] [CrossRef]
- Chen, J.; Schurer, J.M.; Schmelcher, P. Entanglement induced interactions in binary mixtures. Phys. Rev. Lett. 2018, 121, 043401. [Google Scholar] [CrossRef]
- Sowiński, T.; García-March, M. One-dimensional mixtures of several ultracold atoms: A review. Rep. Prog. Phys. 2019, 82, 104401. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Volosniev, A.G.; Schmelcher, P. Induced correlations between impurities in a one-dimensional quenched Bose gas. Phys. Rev. Res. 2020, 2, 023154. [Google Scholar] [CrossRef]
- Andriati, A.; Brito, L.; Tomio, L.; Gammal, A. Stability of a Bose condensed mixture on a bubble trap. Phys. Rev. A 2021, 104, 033318. [Google Scholar] [CrossRef]
- Roberts, D.C.; Ueda, M. Stability analysis for n-component Bose–Einstein condensate. Phys. Rev. A 2006, 73, 053611. [Google Scholar] [CrossRef]
- Krönke, S.; Cao, L.; Vendrell, O.; Schmelcher, P. Non-equilibrium quantum dynamics of ultra-cold atomic mixtures: The multi-layer multi-configuration time-dependent Hartree method for bosons. New J. Phys. 2013, 15, 063018. [Google Scholar] [CrossRef]
- Mason, P.; Gardiner, S.A. Number-conserving approaches to n-component Bose–Einstein condensates. Phys. Rev. A 2014, 89, 043617. [Google Scholar] [CrossRef]
- Barman, A.; Basu, S. Phase diagram of multi-component bosonic mixtures: Emergence of mixed superfluid and insulating phases. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 055301. [Google Scholar] [CrossRef]
- Eto, Y.; Takahashi, M.; Nabeta, K.; Okada, R.; Kunimi, M.; Saito, H.; Hirano, T. Bouncing motion and penetration dynamics in multicomponent Bose–Einstein condensates. Phys. Rev. A 2016, 93, 033615. [Google Scholar] [CrossRef]
- He, Y.Z.; Liu, Y.M.; Bao, C.G. Spin-structures of the Bose–Einstein condensates with three kinds of spin-1 atoms. Sci. Rep. 2020, 10, 2727. [Google Scholar] [CrossRef]
- Jimbo, K.; Saito, H. Surfactant behavior in three-component Bose–Einstein condensates. Phys. Rev. A 2021, 103, 063323. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, C.; Cui, X. Borromean droplet in three-component ultracold Bose gases. Phys. Rev. Lett. 2021, 127, 043002. [Google Scholar] [CrossRef]
- Liu, C.; Chen, P.; He, L.; Xu, F. Ground-state properties of multicomponent bosonic mixtures: A Gutzwiller mean-field study. Phys. Rev. A 2023, 108, 013309. [Google Scholar] [CrossRef]
- Saboo, A.; Halder, S.; Das, S.; Majumder, S. Rayleigh–Taylor instability in a phase-separated three-component Bose–Einstein condensate. Phys. Rev. A 2023, 108, 013320. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Properties of a trapped multiple-species bosonic mixture at the infinite-particle-number limit: A solvable model. J. Chem. Phys. 2024, 161, 184307. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Ho, T.-L.; Cui, X. Shell-shaped quantum droplet in a three-component ultracold Bose gas. Phys. Rev. Lett. 2025, 134, 043402. [Google Scholar] [CrossRef] [PubMed]
- Anh-Tai, T.D.; García-March, M.A.; Busch, T.; Fogarty, T. Quantum correlations and spatial localization in trapped one-dimensional ultra-cold Bose–Bose–Bose mixtures. New J. Phys. 2025, 27, 073201. [Google Scholar] [CrossRef]
- Theel, F.; Mistakidis, S.I.; Schmelcher, P. Effective approaches to the dynamical properties of two distinguishable Bose polarons. Phys. Rev. A 2025, 111, 013306. [Google Scholar] [CrossRef]
- Pruski, S.; Maćkowiak, J.; Missuno, O. Reduced density matrices of a system of N coupled oscillators. 2. Eigenstructure of the 1-particle matrix for the canonical ensemble. Rep. Math. Phys. 1972, 3, 227–233. [Google Scholar] [CrossRef]
- Pruski, S.; Maćkowiak, J.; Missuno, O. Reduced density matrices of a system of N coupled oscillators. 3. The eigenstructure of the p-particle matrix for the ground state. Rep. Math. Phys. 1972, 3, 241–246. [Google Scholar] [CrossRef]
- Robinson, P.D. Coupled oscillator natural orbitals. J. Chem. Phys. 1977, 66, 3307–3308. [Google Scholar] [CrossRef]
- Hall, R.L. Some exact solutions to the translation-invariant N-body problem. J. Phys. A Math. Gen. 1978, 11, 1227–1233. [Google Scholar] [CrossRef]
- Hall, R.L. Exact solutions of Schrödinger’s equation for translation-invariant harmonic matter. J. Phys. A Math. Gen. 1978, 11, 1235–1240. [Google Scholar] [CrossRef]
- Cohen, L.; Lee, C. Exact reduced density matrices for a model problem. J. Math. Phys. 1985, 26, 3105–3108. [Google Scholar] [CrossRef]
- Osadchii, M.S.; Muraktanov, V.V. The System of harmonically interacting particles: An exact solution of the quantum-mechanical problem. Int. J. Quant. Chem. 1991, 39, 173–181. [Google Scholar] [CrossRef]
- Załuska-Kotur, M.A.; Gajda, M.; Orłowski, A.; Mostowski, J. Soluble model of many interacting quantum particles in a trap. Phys. Rev. A 2000, 61, 033613. [Google Scholar] [CrossRef]
- Yan, J. Harmonic interaction model and its applications in Bose–Einstein condensation. J. Stat. Phys. 2003, 113, 623–634. [Google Scholar] [CrossRef]
- Gajda, M. Criterion for Bose–Einstein condensation in a harmonic trap in the case with attractive interactions. Phys. Rev. A 2006, 73, 023603. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Zinner, N.T.; Fedorov, D.V.; Jensen, A.S. Analytic harmonic approach to the N-body problem. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 055303. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Zinner, N.T.; Fedorov, D.V.; Jensen, A.S. Virial expansion coefficients in the harmonic approximation. Phys. Rev. E 2012, 86, 021115. [Google Scholar] [CrossRef]
- Kościk, P.; Okopińska, A. Correlation effects in the Moshinsky model. Few-Body Syst. 2013, 54, 1637–1640. [Google Scholar] [CrossRef]
- Schilling, C. Natural orbitals and occupation numbers for harmonium: Fermions versus bosons. Phys. Rev. A 2013, 88, 042105. [Google Scholar] [CrossRef]
- Bouvrie, P.A.; Majtey, A.P.; Tichy, M.C.; Dehesa, J.S.; Plastino, A.R. Entanglement and the Born–Oppenheimer approximation in an exactly solvable quantum many-body system. Eur. Phys. J. D 2014, 68, 346. [Google Scholar] [CrossRef]
- Benavides-Riveros, C.L.; Toranzo, I.V.; Dehesa, J.S. Entanglement in N-harmonium: Bosons and fermions. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 195503. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Volosniev, A.G.; Fedorov, D.V.; Jensen, A.S.; Zinner, N.T. Analytic solutions of topologically disjoint systems. J. Phys. A Math. Theor. 2015, 48, 085301. [Google Scholar] [CrossRef]
- Schilling, C.; Schilling, R. Number-parity effect for confined fermions in one dimension. Phys. Rev. A 2016, 93, 021601. [Google Scholar] [CrossRef]
- Alon, O.E. Solvable model of a generic trapped mixture of interacting bosons: Reduced density matrices and proof of Bose–Einstein condensation. J. Phys. A Math. Theor. 2017, 50, 295002. [Google Scholar] [CrossRef]
- Alon, O.E. Solvable model of a generic driven mixture of trapped Bose–Einstein condensates and properties of a many-boson floquet state at the limit of an infinite number of particles. Entropy 2020, 22, 1342. [Google Scholar] [CrossRef]
- Alon, O.E. Fragmentation of identical and distinguishable bosons’ pairs and natural geminals of a trapped bosonic mixture. Atoms 2021, 9, 92. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Effects beyond center-of-mass separability in a trapped bosonic mixture: Exact results. J. Phys. Conf. Ser. 2022, 2249, 012011. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Fragmentation of a trapped bosonic mixture. J. Phys. Conf. Ser. 2023, 2494, 012014. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Correlation effects in a trapped Bose–Fermi mixture: Exact results. J. Phys. Conf. Ser. 2024, 2894, 012012. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Entanglement and correlations in an exactly-solvable model of a Bose–Einstein condensate in a cavity. J. Phys. A Math. Theor. 2024, 57, 295305. [Google Scholar] [CrossRef]
- Jiménez, M.D.; Díaz, W.J.; Cuestas, E.; Valdés-Hernández, A.; Majtey, A.P. Spatial correlations and entanglement in a hybrid system of N fermion pairs with harmonic interaction. J. Phys. A Math. Theor. 2025, 58, 225303. [Google Scholar] [CrossRef]
- Kuroś, A.; Pieprzycki, A.; Gawin, E.; Kościk, P. Exact collective occupancies of the Moshinsky model in two-dimensional geometry. Sci. Rep. 2025, 15, 29466. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R.; Yngvason, J. Bosons in a trap: A rigorous derivation of the Gross–Pitaevskii energy functional. Phys. Rev. A 2000, 61, 043602. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R. Proof of Bose–Einstein condensation for dilute trapped gases. Phys. Rev. Lett. 2002, 88, 170409. [Google Scholar] [CrossRef]
- Cederbaum, L.S. Exact many-body wave function and properties of trapped bosons in the infinite-particle limit. Phys. Rev. A 2017, 96, 013615. [Google Scholar] [CrossRef]
- Anapolitanos, I.; Hott, M.; Hundertmark, D. Derivation of the Hartree equation for compound Bose gases in the mean field limit. Rev. Math. Phys. 2017, 29, 1750022. [Google Scholar] [CrossRef]
- Lee, J. Rate of convergence toward Hartree type equations for mixture condensates with factorized initial data. J. Math. Phys. 2021, 62, 091901. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Naraschewski, M.; Glauber, R.J. Spatial coherence and density correlations of trapped Bose gases. Phys. Rev. A 1999, 59, 4595–4606. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Shen, H.Z.; Yang, J.F.; Yi, X.X. Unconventional photon blockade with non-Markovian effects in driven dissipative coupled cavities. Phys. Rev. A 2024, 109, 043714. [Google Scholar] [CrossRef]
- Zhou, Y.-H.; Liu, T.; Su, Q.-P.; Zhang, X.-Y.; Wu, Q.-C.; Chen, D.-X.; Shi, Z.-C.; Shen, H.Z.; Yang, C.-P. Universal photon blockade. Phys. Rev. Lett. 2025, 134, 183601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).