Techniques for Background Identification in the Search for Rare Processes with Crystal Scintillators

Abstract

In astroparticle, nuclear and subnuclear physics, low-counting experiments play an increasingly important role in the investigation of rare processes such as dark matter, double beta decay, some neutrino processes and low-background spectrometry. Extremely low-background features are more and more required to produce detectors and apparata of suitable sensitivity. Over time, a great deal of interest and attention in developing experimental techniques suitable to improve, verify and maintain the radiopurity of these detectors has arisen. In this paper, the characterization of inorganic crystal scintillators (such as, e.g., NaI(Tl), ZnWO${}_4$ and CdWO${}_4$) using $\alpha$, $\beta$ and $\gamma$ radioactive sources and the main experimental techniques applied in the field to quantitatively identify the radioactive contaminants are highlighted; in particular, we focus on inorganic crystal scintillators, widely used in rare processes investigation, considering their applications at noncryogenic temperatures in the framework of the DAMA experiment activities at the Gran Sasso National Laboratory of the INFN (National Institute for Nuclear Physics, INFN).

1. Introduction

The search for rare processes such as dark matter (DM), double beta decay and some neutrino processes requires low-counting experiments conducted in deep underground laboratories. Radioactive contaminants with natural, cosmogenic or anthropogenic origin are present in all of the parts of the experimental apparata. For decades, many efforts have been dedicated to developing techniques and procedures to improve the radiopurity levels of the setups. The detectors, their components, the nearby environment and the shields have been designed, developed and put in operation after a careful screening of all the materials because they can be source of possible background, a limiting factor for the achievable sensitivity of the experiments.

The sources of background can vary in different experiments. The contamination can be different, even in batches of the same material with different geological or chemical history because of differences in chemical composition of ores. Thus, the adopted solutions for reaching high levels of radiopurity can be different. Indeed, they depend also on the energy range of interest for the searched process. For example, it is of the order of the keV for DM and of the order of the MeV for double beta decay.

The sensitivity of an experiment dedicated to a rare event search is roughly inversely proportional to the square root of the background rate. A wide set of requirements have to be satisfied to achieve the highest sensitivity in ultralow level detection: primarily, the choice of a suitable underground laboratory that allows a reduction of the cosmic rays induced background by several orders of magnitude. The laboratory must also ensure the availability of facilities and infrastructures, important to operate in a clean and not polluted environment.

Apparata in underground laboratories must be shielded from the environmental radioactivity, mainly gammas, neutrons and radon gas. Different applications and objectives support passive or active shields. Advantages and drawbacks of both are discussed in the literature [1]. A continuous flushing of high purity (HP) gas (typically nitrogen) allows preventing the detectors from radon contamination.

A setup can use one or more crystal scintillator(s), eventually equipped with light guides, and photomultipliers. The presence of multiple detectors offers the advantage to identify the event patterns and to discriminate between the background events and the searched signal. The light guides can be useful when the photomultipliers have a poorer radiopurity with respect to the detectors. In this case, the detector response must be optimized to have an advantageous compromise between the reachable radiopurity and the loss in energy resolution and light yield.

Finally, the way to obtain the highest sensitivities is closely related to the achievement of an extreme and ultimate radiopurity, a process that can be slow and challenging. For a long time, possible sources of background radiations have been deeply investigated, classified and extensively documented in the literature [1]. The measurement of radioactive contaminants in crystal scintillators is mainly driven by the sensitivity required by the low-background application. In general, indirect methods can be pursued, measuring the corresponding chemical element or derivatives. Inductively coupled plasma mass spectrometry (ICP-MS) [2,3], atomic absorption spectroscopy (AAS) [4], the X-ray fluorescence method [5], electron microscope measurements [6], and the neutron activation technique [7] are mainly used. However, when possible, direct methods are also applied [8] and, in this case, the contamination of an isotope is directly identified by its emitted radiation or by that of its decay products. Direct methods (such as, e.g., measurements by ultralow-background (ULB) HP Ge $\gamma$ detectors) generally have higher sensitivity with respect to indirect methods when the presence of nonprimordial nuclides is investigated. Moreover, direct methods can also be used to determine whether U and Th decay chains are at equilibrium or not. Even more, when the crystal scintillators are operated as detectors in a low-background configuration, the highest sensitivity can be achieved. These measurements give an ultimate information on the complete detector construction. In this paper, the characterization of inorganic crystal scintillators (such as, e.g., NaI(Tl), ZnWO${}_4$ and CdWO${}_4$) using $\alpha$, $\beta$ and $\gamma$ radioactive sources and the main experimental techniques applied in the field to quantitatively identify the radioactive contaminants will be outlined. Moreover, some of the measurements performed in the framework of the DAMA experiment activities at the Gran Sasso National Laboratory of the INFN will be used as practical examples of application of the discussed techniques. Similar methods of background identification are applied also by other experiments working in the field of rare events investigation. For details, we refer to the wide literature in the field, see e.g., refs. [9,10,11,12,13].

In Section 2, a characterization of the response of crystal scintillators to $\alpha$, $\beta$ and $\gamma$ radiations and to heavy particles will be given. Then, Section 3 will review the main steps in the development of radiopure crystal scintillators. And finally, in Section 4, the main experimental techniques to quantitatively identify the radioactive contaminants, applied to the case of inorganic crystal scintillators at non-cryogenic temperature, will be focused (see also [14,15,16,17]).

2. Low-Background Measurements and the Detector Response

In the framework of low-background measurements with crystal scintillators, the highest sensitivity to the presence of contaminants is favored by the optimal detection efficiency for $\alpha$ and $\beta$ particles assured by the source–detector approach.

A focal point to interpret the background measured by a crystal scintillator is the characterization of its response to $\alpha$, $\beta$ and $\gamma$ radiations. The crystal detector response depends on the properties of the crystal and, therefore, on the parameters of the growth process such as temperature and rate of growth, surface structure, temperature gradient, etc. [18,19,20,21,22,23,24,25]. Indeed, the presence of impurities, homogeneity, inclusions and structural perfection, among other aspects, can modify the response of the crystal. Other factors that influence the detector response are the crystal machining, the crystal surface treatment, the used reflecting materials, the purity of components, additives and dopants, the form and size of the crystal and its bond with the photoreceiver. The protocols for the detector assembling have to be optimized as well as the used equipment and the environment. Finally, to the previously mentioned features, all the requirements specifically needed for low-background measurements in rare events investigation have to be taken into account. Calibrations to determine the energy scale, the energy resolution, the time and energy response of the crystals can be pursued with external suitable radioactive sources or internal contaminants of well-known decay features. An important quantity in the evaluation of the response of a scintillator to heavy ionizing particles, such as $\alpha$ particles and nuclear recoils, is the quenching factor. It is defined as the ratio between the detected energy of the heavy ionizing particle, in the energy scale measured with $\gamma$ sources, and its kinetic energy. The quenching factor in the case of $\alpha$ particles is often named the $\alpha /\gamma$ ratio. It is worth noting that the light yield of scintillating materials depends not only on the amount of energy deposited by the interacting particle but also on the magnitude of its stopping power. This latter effect is negligible for particles with low stopping power (as fast electrons), but it is important for highly ionizing particles as $\alpha$’s and nuclear recoils [26,27]. For these particles, the quenching factor also depends on their stopping power and, consequently, on their energy [28].

2.1. Response to $\gamma$ and $\beta$ Radiation

Sources in a wide energy interval from a few keV (5.9 keV Mn K X-rays from ${}^{55}$Fe) up to 2615 keV ($\gamma$ quanta of ${}^{208}$Tl) can be used to study the response to $\gamma$ quanta, the linearity of the energy scale and the energy resolution of the crystal. Internal calibration is also possible in presence of specific contaminants. With suitable high quality inorganic crystals, optimal performance in the linearity of the energy scale can be achieved (see, e.g., [29]).

Scintillation signals for $\gamma$ quanta can sometimes be quenched in comparison to $\beta$ particles. This typically happens in organic liquid scintillators, but it can be present in some specific crystal scintillators as well. A similar behavior of scintillation light-efficiency quenching is observed in the CdWO${}_4$ scintillator for $\gamma$ quanta in comparison to electrons; that resulted in a higher estimate of the total energy released ($Q_{\beta }$) in the $\beta$ decay of ${}^{113}$Cd: $Q_{\beta }$ = 337 keV and $Q_{\beta }$ = 345 keV [30,31], respectively. These values are substantially larger than the table value $Q_{\beta }$ = 323.83(27) keV. This quenching has been explained by the nonproportionality in the scintillation response of CdWO${}_4$ crystal scintillators, with a significant effect for energies below about 0.1 MeV [32].

2.2. Response to $\alpha$ Radiation

Sources are typically in the energy region from about 5.3 to about 8.8 MeV (${}^{228}$Th, ${}^{241}$Am, ${}^{244}$Cm, ${}^{252}$Cf). Calibrations with $\alpha$ particles are difficult with external sources; they are commonly used to identify internal contaminants. In the case of external sources, the presence of absorbers allows the calibration at lower energies. The $\alpha$/$\gamma$ ratio is affected by the quenching of the scintillation light caused by $\alpha$ particles and due to their higher ionization density. For a detailed review on $\alpha$/$\gamma$ ratio in different scintillators, see, e.g., [33].

In some scintillation crystals, the $\alpha$/$\gamma$ ratio can depend on the direction of $\alpha$ particles relatively to crystal axes. This happens in anisotropic scintillators. This effect was observed both in organic (such as stilbene and anthracene [26,34,35]) and inorganic crystal scintillators (such as CdWO${}_4$ [36], ZnWO${}_4$ [37] and MgWO${}_4$ [38]). Measurements on ZnWO${}_4$ are discussed in [39].

The presence of $\alpha$ peaks from internal contaminants allows checking calibration measurements by external sources and represents the only practical method to measure the response to $\alpha$ particles in the case of encapsulated scintillation detectors (such as those that are highly hygroscopic), such as NaI(Tl), LaCl${}_3$(Ce) and LaBr${}_3$, among others.

2.3. Response to Heavy Particles

As far as for $\alpha$ particles, the quenching of scintillation light is also present for heavy particles, such as low-energy nuclear recoils, of interest for direct investigation of some DM candidates. Nuclear recoils can be studied using a neutron generator and neutron detectors to tag the scattered neutrons at suitable angles. This defines the energy and the direction of the recoiling nucleus, whereas the detected energy in the crystal scintillator, measured in keV electron equivalent (keVee), allows the determination of the corresponding quenching factor. These measurements are difficult and always affected by significant experimental uncertainties. Moreover, it is to be noted that the quenching factors are a property of the specific detector and not a general property of the scintillation crystal material, particularly in the very low energy range. They depend on the adopted growing procedures, on the dopant concentration and uniformity in the detector and on the specific additives always used by companies to strengthen the performance of the detectors, among other aspects. A comparison between the quenching factors measured with different crystals made of the same scintillation material is reported, e.g., in [28,40,41]. All these aspects are always relevant sources of uncertainties for example when comparing results in terms of DM candidates inducing nuclear recoils. In summary, different quenching factors values imply that the same energy in keV electron equivalent corresponds to different recoil energies in the different experiments.

In anisotropic crystals, such as, e.g., ZnWO${}_4$, the light response and the pulse shape of such scintillators depend on the impinging direction both for the $\alpha$ particles and heavy particles, with respect to the crystal axes. A possible favored direction of the excitons propagation in the crystal lattice, affecting the scintillation mechanism’s dynamic, can explain such an anisotropic effect [26,42,43,44,45,46,47,48]. The anisotropic response of these scintillators could be exploited to study the directionality signature as proposed for the first time in [49] and revisited in [50], where the case of an anthracene detector was preliminarily analyzed. A possibility to use anisotropic properties of a ZnWO${}_4$ scintillator to search for diurnal variation of the DM counting rate and, therefore, to explore the directionality was pointed out for the first time in [37]. Recently, measurements have shown that the ZnWO${}_4$ is a promising scintillator in this field and R&D are in progress (ADAMO project: Anisotropic detectors for DArk Matter Observation [39,51,52,53,54,55]).

Finally, in crystal scintillators, the possibility of channeling has also been deeply discussed and can be found in literature (see e.g., [56,57,58] and references therein), being of interest in the direct investigation of some DM candidates.

3. Development of Radiopure Crystal Scintillators

The goal of reaching a high radiopurity requires long and difficult work. The reachable ultimate radiopurity levels depend on the initial impurity concentrations and on the adopted methods and protocols. In particular, the development of radiopure crystal scintillators involves several subsequent steps. It starts with the selection and screening of the powder samples by different techniques, followed by the chemical/physical purification of the selected materials. As regards the crystal production, the best growing processes have to be selected as well as the used additives. The crystallization process can represent a possible further purification step of the powders residual contaminants. It is the case of the ULB NaI(Tl) crystals of DAMA/LIBRA, grown with the Kyropoulos method using selected platinum crucibles (see [29] for details).

The tools and abrasives used for crystal cutting and polishing should be carefully selected. In particular, after the ingots production, all the materials used for the detector production and assembling have to be selected for radiopurity and their number should be minimized. Moreover, all the operations on the bare crystals require selected and controlled environment and procedures, in order to avoid possible surface pollution. As it can be seen, many of these prescriptions, such as those described in the previous sections, also determine the performances in terms of response of the crystal detector.

The main sources of radioactive contamination in inorganic scintillation materials are natural radionuclides from ${}^{232}$Th, ${}^{238}$U and ${}^{235}$U families and ${}^{40}$K, but other cosmogenic and/or anthropogenic radionuclides can also be present. In some cases, radioactive isotopes are present in the scintillator material itself, as ${}^{113}$Cd in CdWO${}_4$ or ${}^{138}$La in LaCl${}_3$ and LaBr${}_3$, and so on [15].

Radioactive contaminations into inorganic crystal scintillators span in a broad range. For example, the standard contaminants in inorganic crystal scintillators developed for low-background measurements such as NaI(Tl), CaF${}_2$(Eu), CsI(Tl), ZnWO${}_4$, CdWO${}_4$ and Li${}_2$MoO${}_4$ can vary in the range 0.01–1 mBq/kg. Some of the best results achieved in terms of radiopurity are reported in [15], where the data on radioactive contamination of different scintillators are presented.

Slight differences in the residual contaminants of detectors may be present even if the same production procedures are applied. In fact, during the growth and handling procedures, some casual pollution may be possible due to the industrial environment of the production systems. Differences may also depend on the selected part of the boule/ingot used to build the detector (a possible nonuniformity of contaminant distribution can play a role). Anyway, adopting safe protocols and reliable procedures, the spread in the contaminants levels and in the performances can be limited.

Generally, ULB HP-Ge detectors are used to measure gamma emitting radioactive contaminants in samples of materials used in crystals or nearby the detectors (sensitivity at level of mBq/kg for isotopes from ${}^{232}$Th, ${}^{238}$U and ${}^{235}$U chains and for ${}^{40}$K). Analytical methods of analysis are also applied, such as AAS and ICP-MS. Both of the methods require pretreatment of the samples. In case of the AAS, the wavelengths of light absorbed by the different elements are used to evaluate their concentrations in the solutions, and a good sensitivity (at the ppb and sub-ppb levels) can be reached. An even better sensitivity at ppb-ppm and ppq-ppt level can be obtained with ICP-MS. In this technique, the mass-to-charge ratio ($m/e$) is used to identify the isotopes of an element. Each peak in the mass spectrum has an intensity proportional to the isotope concentration.

However, only a final low-background measurement where a scintillator is operating as a detector can assure the highest sensitivity to the identification of the internal contaminants in the crystal, and it is essential to complete the information on the chosen configuration. In this phase, the radioactive contaminants can be identified by exploiting many different techniques, as discussed in the following section. This kind of determination gives an ultimate information on the complete assembled detector configuration.

4. Techniques for Background Identification with Crystal Scintillators

The main experimental techniques to quantitatively identify the radioactive contaminants in the case of inorganic crystal scintillators at noncryogenic temperature are discussed in the following. In particular, pulse shape discrimination [59,60], energy spectrum analysis [29], time–amplitude analysis [61,62], Bi-Po analysis [29,36,63], coincidence analysis [29] and a possible background modeling (see, e.g., [64]) will be described. Some examples will be also considered and applied to specific detectors.

4.1. Pulse Shape Discrimination

This approach is particularly useful to estimate the $\alpha$ active nuclides, and different methods can be exploited. For example, it is possible to use the first moment of the time distribution of each scintillation pulse (recorded by a transient digitizer, TD) $\tau =\frac{{\mathsf{\Sigma }}_i{h}_i{t}_i}{{\mathsf{\Sigma }}_i{h}_i}$, where $h_i$ is the pulse height at the time $t_i$ and the sum is over a suitable time interval after the starting of the pulse [29,65,66,67,68]. An interesting application of this technique is given by the highly radiopure NaI(Tl) detectors of DAMA/LIBRA [29], an apparatus of ≃250 kg made of 25 NaI(Tl) highly radiopure detectors. The experiment has been taking data up to the MeV scale despite the optimization of the lowest energy region. The DAMA/LIBRA detectors and all the details on the project, the implementation, the protocols applied over time and the radiopurity obtained are exhaustively discussed in [29]. The $\alpha /\beta$ pulse shape discrimination in NaI(Tl), which has practically 100% effectiveness in the MeV range, allows us to evaluate the internal $\alpha$ particles produced by U and Th chains and, therefore, a preliminary estimate of their residual contamination (see the next section). In Figure 1, the calculated $\tau$ values are reported as a function of energy for four detectors of the DAMA/LIBRA setup. The sum is over 600 ns after the pulse starting point.

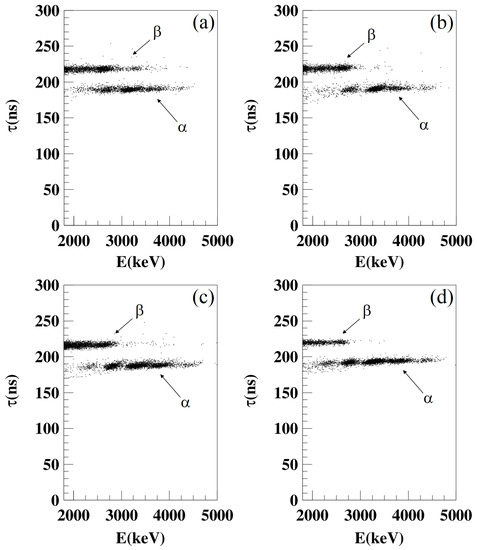
Figure 1. Distribution of the first moment, $\tau$, as a function of the energy (in keV electron equivalent, keVee) for scintillation pulses measured by four DAMA/LIBRA detectors (a–d). The averaging time is 600 ns. Two clearly separated populations are visible; they are due to $\gamma$($\beta$) and $\alpha$ events. Several spots are visible in the $\alpha$ population; they are due to $\alpha$ particles produced by decays of different nuclides (see text for details). Reprinted with permission from [29]. Copyright 2008 Elsevier.

The two populations—$\gamma$($\beta$) and $\alpha$—are clearly separated; the $\alpha$ particles have shorter $\tau$ values. The measured $\alpha$ yield in the DAMA/LIBRA detectors ranges from 7 to some tens $\alpha$/kg/day. The distributions of parameters $\tau$ for $\alpha$ and $\gamma$($\beta$) signals are also well described by Gaussian functions. Therefore, a figure of merit (FOM):

$$FOM=\frac{|{\tau }_{\alpha }-{\tau }_{\gamma }|}{\sqrt{{\sigma }_{\alpha }^2+{\sigma }_{\gamma }^2}},$$

can be used to estimate the efficiency of the method.

Another approach often used is the optimal filter method proposed by Gatti and De Martini [59], hence developed for CdWO${}_4$ crystal scintillators [60], and then successfully applied to many scintillators (see, e.g., [36,37,38,68,69,70,71,72]). In the optimal filter method, a pulse shape numerical characteristic, named shape indicator (SI), can be calculated for each scintillation event produced by a scintillator using the following formula:

$$SI=\frac{\mathsf{\Sigma }f\left(t_k\right)\times P\left(t_k\right)}{\mathsf{\Sigma }f\left(t_k\right)},$$

where the sum is over time channels k from the origin of the pulse up to a certain time and f($t_k$) is a digitized amplitude of a signal at the time channel $t_k$; P($t_k$) is a weight function defined as

$$P\left(t_k\right)=\frac{|f_{\alpha }\left(t\right)-f_{\gamma }\left(t\right)|}{f_{\alpha }\left(t\right)+f_{\gamma }\left(t\right)},$$

where $f_{\alpha }$(t) and $f_{\gamma }$(t) are digitized amplitudes of reference $\alpha$ and $\gamma$($\beta$) signals, respectively. The distributions of the SI have a Gaussian shape. Therefore, in this case, the FOM is a measure of the discrimination ability and can be calculated using the expression proposed in [59]:

$$FOM=\frac{|S{I}_{\alpha }-S{I}_{\gamma }|}{\sqrt{{\sigma }_{\alpha }^2+{\sigma }_{\gamma }^2}}.$$

Scatter plots of the SI versus energy for some ZnWO${}_4$ crystal scintillators developed by the R&D campaign within the ADAMO project [55] are shown in Figure 2.

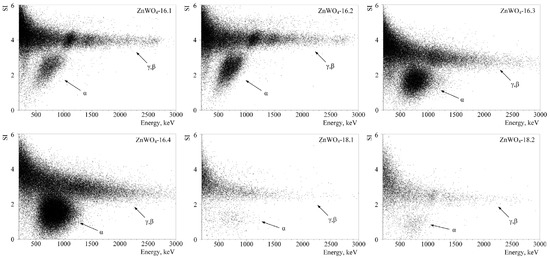
Figure 2. SI versus energy for the background data measured with some ZnWO${}_4$ crystal scintillators developed by the R&D campaign within the ADAMO project [55]. The populations of the $\alpha$ and $\gamma$($\beta$) events are noted by arrows. Reprinted with permission from [55]. Copyright 2019 Elsevier.

The data are separated into two populations, corresponding to the $\alpha$ and $\gamma$($\beta$) events, respectively. The dependence of the SI on energy for $\gamma$($\beta$) signals was confirmed by the pulse shape analysis of the calibration measurements with a ${}^{228}$Th $\gamma$ source. The position of the $\alpha$ populations in the energy scale is much lower than the real energy of the $\alpha$ particles because of the quenching of the light emission in the crystals due to $\alpha$ particles in comparison with the case of $\gamma$ quanta [55].

4.2. The Study of the Energy Distribution of $\alpha$ Particles

The case of the highly radiopure NaI(Tl) detectors of DAMA/LIBRA has offered a clear example in order to study the energy distribution of $\alpha$ particles. This distribution can be easily obtained in detectors as NaI(Tl) scintillators, where the $\alpha$/$\beta$ pulse shape discrimination has practically 100% effectiveness in the MeV range see previous section. The study of the $\alpha$ energy distribution can, in principle, be used to determine the different contributions due to the ${}^{238}$U and ${}^{232}$Th subchains. Indeed, the equilibrium of the ${}^{238}$U and ${}^{232}$Th chains in all the materials is usually assumed to be broken. In fact, due to physical or chemical processes utilized in the material production, the secular equilibrium in the ${}^{232}$Th and ${}^{238}$U decay chains is typically broken in almost all of the materials [15,73,74]. However, they can be split into subchains that can be considered in equilibrium.

The energy distributions of $\alpha$ particles from ${}^{238}$U and ${}^{232}$Th chains measured by four NaI(Tl) crystals of the DAMA/LIBRA setup are shown in Figure 3.

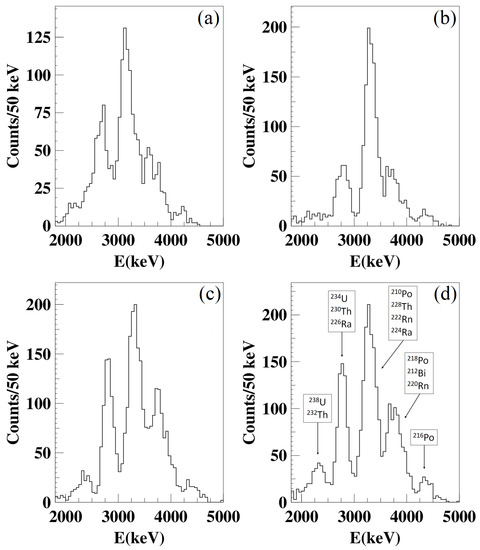
Figure 3. The $\alpha$ energy distributions in four NaI(Tl) crystals of the DAMA/LIBRA setup (a–d), corresponding to a live time of 570 h. As an example, arrows with the indication of the $\alpha$ origin have been included in case (d) for each of the five peaks. The energy is given in keV electron equivalent, keVee. Reprinted with permission from [29]. Copyright 2008 Elsevier.

Five $\alpha$ peaks can be recognized in the energy distributions of Figure 3. Starting from the left, they can be associated with (the total energies released in the $\alpha$ decays, $Q_{\alpha }$, are also given):

(1)

${}^{232}$Th ($Q_{\alpha }=4.08$ MeV) + ${}^{238}$U (4.27 MeV);

(2)

${}^{234}$U (4.86 MeV) + ${}^{230}$Th (4.77 MeV) + ${}^{226}$Ra (4.87 MeV);

(3)

${}^{210}$Po (5.41 MeV) + ${}^{228}$Th (5.52 MeV) + ${}^{222}$Rn (5.59 MeV) + ${}^{224}$Ra (5.79 MeV);

(4)

${}^{218}$Po (6.12 MeV) + ${}^{212}$Bi (6.21 MeV) + ${}^{220}$Rn (6.41 MeV) and

(5)

${}^{216}$Po (6.91 MeV).

It is worth noting that the events due to $\alpha$ decays of ${}^{212}$Po and of ${}^{214}$Po are not present in the shown energy distributions because they belong to a Bi-Po event and they are mainly vetoed by the acquisition system.

A model of the $\alpha$ energy distribution can be obtained assuming the ${}^{238}$U radioactive chain split into five segments (${}^{238}$U →${}^{234}$U →${}^{230}$Th →${}^{226}$Ra →${}^{210}$Pb →${}^{206}$Pb) and the ${}^{232}$Th chain at equilibrium. The activities of the five ${}^{238}$U subchains and of the ${}^{232}$Th chain can be determined by fitting the experimental energy spectra with the model. The results obtained by DAMA confirmed the hypotheses that the ${}^{238}$U chain is broken in these NaI(Tl) crystals. As an example in the detector (d) of Figure 1 and Figure 3, the ${}^{232}$Th and ${}^{238}$U contents obtained by the fit were:

• $(8.5\pm 0.5)$$\mu$Bq/kg of ${}^{232}$Th;
• $(4.4\pm 0.7)$$\mu$Bq/kg for ${}^{238}$U →${}^{234}$U decay subchain;
• $(15.8\pm 1.6)$$\mu$Bq/kg for ${}^{234}$U →${}^{230}$Th + ${}^{230}$Th →${}^{226}$Ra decay subchains (they all contribute to the same peak);
• $(21.7\pm 1.1)$$\mu$Bq/kg for ${}^{226}$Ra →${}^{210}$Pb decay subchain and
• $(24.2\pm 1.6)$$\mu$Bq/kg for ${}^{210}$Pb →${}^{206}$Pb decay subchain.

The energy distributions reported in Figure 3 were measured with NaI(Tl) crystals grown with the same selection of materials, purification processes and protocols. Nevertheless, the obtained spectra are not the same. This shows that the residual contaminants may be slightly different even among crystals grown with the same procedures, for the reasons already discussed in the previous sections. For example, in the case of the DAMA/LIBRA setup, the $\alpha$ activities measured for the 25 NaI(Tl) detectors range in the interval from 7 to some tens $\alpha$/kg/day. In general, differences can be present both in the bulk and surface contaminations. In the case of surface contamination, the energy of the $\alpha$ particles is only partially collected and it gives rise to a continuum distribution in the spectrum. Instead, for bulk contamination, a Gaussian shape is expected for each emitted $\alpha$ particle, with an energy resolution that is well compatible with that measured for $\gamma$ quanta, as shown by the results of the time amplitude analysis in Figure 4.

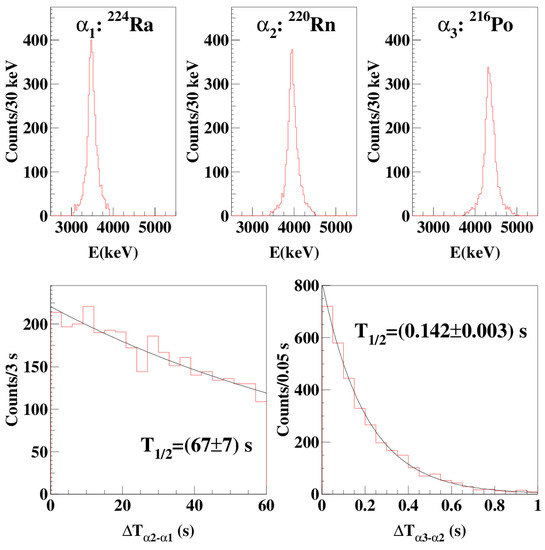
Figure 4. Results of the time–amplitude analysis applied to the data collected with a detector of the DAMA/LIBRA setup (exposure of 8100 kg × day). Top: $\alpha$ peaks obtained for ${}^{224}$Ra, ${}^{220}$Rn and ${}^{216}$Po decays; their energy resolutions ($\sigma =$ 75, 83 and 90 keV) are well compatible with those measured with $\gamma$’s calibrations. Bottom: distributions of the time intervals between the ${}^{224}$Ra and ${}^{220}$Rn $\alpha$ decays (left) and between the ${}^{220}$Rn and ${}^{216}$Po $\alpha$ decays (right). The fitted half-lives for ${}^{220}$Rn: $(67\pm 7)$ s, and for ${}^{216}$Po: $(0.142\pm 0.003)$ s, are in agreement with the table values (55.6 s and 0.145 s, respectively [75]). Reprinted with permission from [29]. Copyright 2008 Elsevier.

4.3. The Time–Amplitude Method

The activities of ${}^{228}$Th (${}^{232}$Th family), ${}^{227}$Ac (${}^{235}$U) and ${}^{226}$Ra (${}^{238}$U) can be determined with the help of the time–amplitude method. In particular, the energy and arrival time of the acquired events can be used to select fast decay chains from the ${}^{232}$Th, ${}^{235}$U and ${}^{238}$U families. The method of time–amplitude analysis is widely described (see, e.g., [29,61,62,71]).

In the case of the ${}^{232}$Th family, the following sequence of $\alpha$ decays can be pointed out ($Q_{\alpha }$ and half-life values, $T_{1/2}$, are also given): ${}^{224}$Ra ($Q_{\alpha }$ = 5789 keV; $T_{1/2}$ = 3.66 d) → ${}^{220}$Rn ($Q_{\alpha }$ = 6405 keV; $T_{1/2}$ = 55.6 s) → ${}^{216}$Po ($Q_{\alpha }$ = 6906 keV; $T_{1/2}$ = 144 ms) → ${}^{212}$Pb. These radionuclides are in equilibrium with ${}^{228}$Th ($T_{1/2}$ = 1.912 year, subchain in the ${}^{232}$Th family).

In the case of ${}^{235}$U family, another short chain can be identified with this approach: ${}^{223}$Ra ($Q_{\alpha }$ = 5979 keV; $T_{1/2}$ = 11.43 d) → ${}^{219}$Rn ($Q_{\alpha }$ = 6946 keV; $T_{1/2}$ = 3.96 s) → ${}^{215}$Po ($Q_{\alpha }$ = 7526 keV; $T_{1/2}$ = 1.781 ms)→ ${}^{211}$Pb. The radionuclide ${}^{223}$Ra can be considered in equilibrium with ${}^{227}$Ac ($T_{1/2}$ = 21.772 year, subchain in the ${}^{235}$U family; see, e.g., [15,62]).

In the case of ${}^{238}$U family, the following sequence of $\beta$ and $\alpha$ decays can be used: ${}^{214}$Bi ($Q_{\beta }$ = 3270 keV; $T_{1/2}$ = 19.9 m) → ${}^{214}$Po ($Q_{\alpha }$ = 7833 keV; $T_{1/2}$ = 163.6 $\mathsf{\mu }$s) → ${}^{210}$Pb. These radionuclides are in equilibrium with ${}^{226}$Ra ($T_{1/2}$ = 1600 year, subchain in the ${}^{238}$U family). For this latter very fast sequence, the sensitivity of the method can be rather low because of the comparatively large minimal time between signals that the data acquisition system is able to record separately (typically of the order of few ms). An alternative approach to search for this sequence is described in the following section.

In the case of the highly radiopure NaI(Tl) detectors of DAMA/LIBRA, the time–amplitude method was used to determine the activity of the ${}^{228}$Th subchain. Figure 4 shows an example of the achieved results for the detector (d) of Figure 1.

Fast sequences of $\alpha$ decays started by ${}^{224}$Ra decay were identified in the detector data searching for triple delayed coincidences:

(1)

an events in the energy interval 3050–3900 keV,

(2)

followed within 60 s by another event in the energy interval 3400–4500 keV,

(3)

still followed within 1 s by another event in the energy interval 3650–5100 keV.

The distributions of the energies and of the time intervals obtained for the events from the selected sequences were in good agreement with those expected for the searched subchain: ${}^{224}$Ra →${}^{220}$Rn →${}^{216}$Po →${}^{212}$Pb. The position of the $\alpha$ peaks measured on an energy scale calibrated with $\gamma$ sources was used to determine the $\alpha /\gamma$ light ratio of the detector used: $\alpha /\gamma =0.467\left(6\right)+0.0257\left(10\right)\times E_{\alpha }$, where $E_{\alpha }$ is the energy of the $\alpha$ particle in MeV. Moreover, given the number of identified sequences, the exposure and the calculated detection efficiency, it was possible to determine the ${}^{228}$Th activity for the considered crystal as $(9.0\pm 0.4)$$\mathsf{\mu }$Bq/kg. Repeating the same analysis for all the crystals of the DAMA/LIBRA apparatus, a ${}^{228}$Th activity ranging from 2 to about 30 $\mathsf{\mu }$Bq/kg was obtained, depending on the crystal.

4.4. The Bi-Po Events

The activities of ${}^{228}$Th (${}^{232}$Th family) and ${}^{226}$Ra (${}^{238}$U) can be determined also with the analysis of the Bi-Po events. The Bi-Po events from ${}^{232}$Th chain is given by the $\beta$ decay of ${}^{212}$Bi into ${}^{212}$Po followed by the ${}^{212}$Po $\alpha$ decay ($Q_{\alpha }$ = 8954 keV; $T_{1/2}$ = 299 ns) to ${}^{208}$Pb. As already mentioned, the ${}^{238}$U chain produces Bi-Po events, due to ${}^{214}$Bi $\beta$ decay to ${}^{214}$Po and to the subsequent ${}^{214}$Po $\alpha$ decay ($Q_{\alpha }$ = 7833 keV; $T_{1/2}$ = 163.6 $\mathsf{\mu }$s) to ${}^{210}$Pb. Similar events can be identified by studying the pulse information recorded by a TD.

It is worth noting that the Bi-Po analysis provides a second independent approach to measure the ${}^{228}$Th contamination and its result can be compared with that obtained using the time–amplitude method. For example, the activity for ${}^{228}$Th decay subchain obtained with Bi-Po analysis for the DAMA/LIBRA detector (d) of Figure 1 was $(9.4\pm 1.5)$$\mathsf{\mu }$Bq/kg, well compatible with the determination obtained with the time–amplitude method (see previous section and [29]).

An example of Bi-Po analysis is reported in [76] where it was used to determine ${}^{228}$Th and ${}^{226}$Ra contaminations in a BaF${}_2$ crystal scintillator.

Figure 5a shows the typical pulse shape of a Bi-Po event as recorded by the TD of the BaF${}_2$ detector in this experiment [76]; $\Delta$t is the measured delay time between the $\beta$ and $\alpha$ pulses. Figure 5b shows the energy distribution (in keVee) of the $\alpha$ particles in the Bi-Po events. The peak at higher energy is due to the ${}^{212}$Po $\alpha$ decays (E${}_{\alpha }$ = 8785 keV). The peak at lower energy corresponds instead to $\alpha$ particles from the ${}^{214}$Po decays (E${}_{\alpha }$ = 7687 keV) occurring within the TD time window (since the used time window was 3125 ns, Bi-Po events from ${}^{232}$Th chain were mostly recorded). From the distributions in Figure 5b, the $\alpha /\gamma$ light ratio in the used BaF${}_2$ detector was estimated to be $0.41\pm 0.01$ for $\alpha$ particles with energy in the range of about 7.7–8.8 MeV. Finally, the measured $\Delta$t distribution of the Bi-Po events from ${}^{212}$Bi is shown in Figure 5c; here, Bi-Po events from ${}^{212}$Bi were selected applying a suitable energy window on the associated $\alpha$ particles. The measured half-life of the ${}^{212}$Po $\alpha$ decay, ($297\pm 1$) ns is in agreement with the value available in literature.

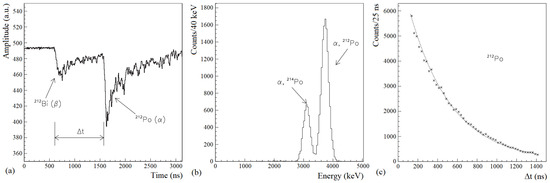
Figure 5. Bi-Po events collected with a BaF${}_2$ crystal scintillator [76]: (a) typical pulse shape of a Bi-Po event as recorded by the TD; (b) energy distribution of the $\alpha$ particles from the ${}^{212}$Po (peak at higher energy) and from the ${}^{214}$Po (peak at lower energy) decays (as evident, here, keV is keVee); (c) measured $\Delta$t distribution of the Bi-Po events from ${}^{212}$Bi. Reprinted with permission from [76]. Copyright 2004 Elsevier.

Another clear example is given in the framework of the AURORA experiment [63], performed to investigate the double beta decay of ${}^{116}$Cd with radio-pure ${}^{116}$CdWO${}_4$ crystals (enriched at 82% in ${}^{116}$Cd). The front-edge analysis was developed to reject the fast subchain of Bi-Po decays. A rise time for each signal was calculated as time between the signal origin and the time where signal reach 0.7 of its maximal value. The distributions of SI versus rise time for the background events acquired with the ${}^{116}$CdWO${}_4$ detector No. 2 over 26,831 h are shown in Figure 6. Two energy intervals are considered: (0.6–1.3) MeV and (1.7–4.0) MeV (Figure 6 left and right, respectively). The latter interval includes the expected sum energy released in the ${}^{212}$Bi-${}^{212}$Po decay: around (1.8–4.4) MeV; these events are characterized by a longer rise time. The green events in Figure 6 (labeled as “LS signals pile-ups”) were identified and rejected as pile-ups of the ${}^{116}$CdWO${}_4$ pulses with the signals coming from the liquid scintillator surrounding the ${}^{116}$CdWO${}_4$ crystals [63]. The front-edge analysis allowed the rejection of these events thanks to a shorter rise time (less than 38 ns) of the liquid scintillator pulses.

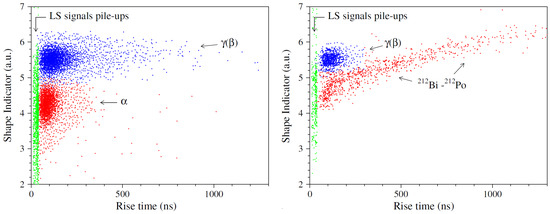
Figure 6. Distribution of SI versus rise time for the background events acquired with the ${}^{116}$CdWO${}_4$ detector No. 2 over 26,831 h in the energy intervals (0.6–1.3) MeV (left) and (1.7–4.0) MeV (right). Reprinted with permission from [63]. Copyright 2018 American Physical Society.

The sum energy spectrum collected with two ${}^{116}$CdWO${}_4$ detectors and its $\gamma$($\beta$), $\alpha$ and ${}^{212}$Bi-${}^{212}$Po components are reported in Figure 7.

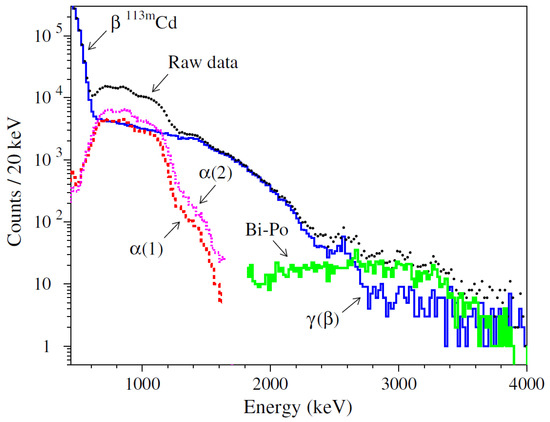
Figure 7. The sum energy spectrum acquired with two ${}^{116}$CdWO${}_4$ detectors over 26,831 h (raw data) and spectra of $\gamma$($\beta$), $\alpha$ and ${}^{212}$Bi-${}^{212}$Po events (Bi-Po) selected by the pulse shape and the front-edge analyses described in the text. The label (1) and (2) refers to the detectors No. 1 and No. 2, respectively. Reprinted with permission from [63]. Copyright 2018 American Physical Society.

The ${}^{212}$Bi-${}^{212}$Po events, selected by the front-edge analysis, are part of the ${}^{228}$Th subchain. Its activity was determined to be 0.018(2) mBq/kg and 0.027(3) mBq/kg for the crystals No. 1 and No. 2, respectively, in good agreement with the result of the time–amplitude analysis. As shown in Figure 7 the Bi-Po events contribute to the 2.7–2.9 MeV energy region, where the signal of the $0\nu 2{\beta }^{-}$ decay of ${}^{116}$Cd is expected, so that their removal allowed the reduction of the background counting rate by a factor of about 1.5 for this decay mode.

4.5. The Coincidence Analysis

In setups equipped with multiple detectors, it is possible to identify (and/or exclude) background sources with the coincidence analysis. In the direct search for DM particles, for example, events with multiplicity greater than one can be discarded since the DM multiscattering probability is negligible. For some rare processes, the best signal-to-background ratio is obtained searching for multiple coincidences induced by the process searched for, e.g., a rare nuclear decay involving the excited levels of the daughter nucleus, a $\beta \beta$ decay with positrons emission and a cluster decay, among others. In the following, some examples of coincidence analysis used to identify background sources contained in the detectors or in the surrounding environment will be described.

4.5.1. Identification of Internal Contamination

In a setup with multiple detectors working at a very low energy threshold (∼keV level), it is possible to measure the internal contamination of ${}^{40}$K searching for double coincidences. The ${}^{40}$K (0.0117% of natural potassium, ${}^{\mathrm{nat}}$K) is a naturally occurring radioactive isotope with $T_{1/2}=1.248\times {10}^9$ year and its origins are primordial. It decays by electronic capture (EC) to the 1461 keV level of ${}^{40}$Ar with probability 10.67%. The X-rays/Auger electrons emitted after EC are detected by the crystal where the decay take place, hereafter A, with efficiency ∼1. The 1461 keV de-excitation $\gamma$ can instead escape from detector A and hit another one, giving rise to a double coincidence. In the case of EC from shell K of ${}^{40}$Ar, the detected X-rays/Auger electrons produce a peak at 3.2 keV in crystal A. In particular, an electron from shell K ($E_K=$ 3.2 keV) is involved in the process in the 76.1% of the cases, an electron from shell L ($E_L=$ 0.3 keV) in the 21.1% and an electron from upper shells in 2.77%.

An example of measurement of the potassium content is present in the analysis of the data of the DAMA/LIBRA-phase1 set-up, where the presence of these peculiar double coincidences was investigated over a large exposure.

Figure 8 shows, as an example, a scatter plot of the energies detected in a given detector A as a function of the energy detected in the other crystals involved in the double coincidence. It is evident that a spot that correlates the 1461 keV events in the other crystals with the 3.2 keV peak in crystal A. The detection efficiency for such coincidences was evaluated for each crystal by Monte Carlo code. The analysis gave for the ${}^{\mathrm{nat}}$K content in the NaI(Tl) crystals values not exceeding about 20 ppb.

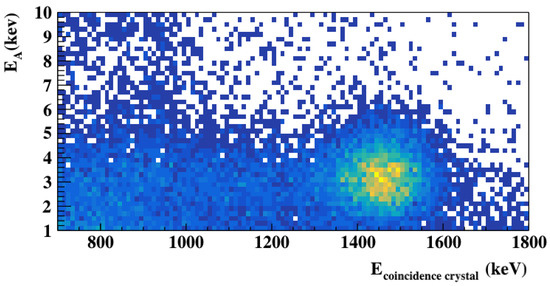
Figure 8. Scatter plot of the energies detected in a given detector A of DAMA/LIBRA-phase1 set-up as a function of the energy detected in the other crystals involved in the double coincidence. A spot is evident and correlates the 1461 keV events in the other crystals with the 3.2 keV peak in crystal A. These double coincidences can be used to study the ${}^{\mathrm{nat}}$K contamination in the detector A.

The coincidence analysis can be used also to measure the contamination of other radioactive isotopes, specific of the used scintillators, as, e.g., the isotopes produced by cosmogenic activation in the period between the crystal production and its transportation in the underground laboratory. For example, in NaI(Tl), one of the isotopes produced by cosmogenic activation that can be investigated with this technique is ${}^{22}$Na. It has $T_{1/2}$ = 2.6 year and its calculated maximum rate level is ≃100 cpd/kg at sea level [29]. An estimate of the ${}^{22}$Na activity in the NaI(Tl) crystals can be obtained by studying multiple coincidences produced by the ${\beta }^{+}$ decay of ${}^{22}$Na followed by 1274.6 keV de-excitation $\gamma$ (b.r. 90.33%). In setups with multiple detectors, this decay can give rise to triple or quadruple coincidence events, where the positron release all its energy in the source detector, while the two 511 keV annihilation $\gamma$’s and the 1274.6 keV $\gamma$ can hit other two or three detectors. The pattern with the highest sensitivity can be chosen, taking into account the competing background events and the coincidence efficiency calculated with Monte Carlo code.

4.5.2. Identification of External Background Sources

The coincidence analysis can also be used to measure the possible presence of radon gas traces in the space between the used detectors. This space is normally kept in HP nitrogen atmosphere, flushing HP nitrogen gas in a sealed box containing the detectors. The possible presence of radon trace can be investigated by searching for the double coincidences of the gamma rays (602 keV and 1120 keV) emitted by the ${}^{214}$Bi radon daughter. The DAMA/LIBRA-phase1 experiment, for example, with the help of this technique, obtained an upper limit <5.8 $\times {10}^{-2}$ Bq/m${}^3$ (90% C.L. (confidence level)) on the radon concentration in the HP nitrogen atmosphere inside the Cu box, that contains its 25 NaI(Tl) detectors. This upper limit was then used to calculate that roughly <2.5 $\times {10}^{-5}$ cpd/kg/keV can be expected from this background source in the lowest energy bins of single-hit events in DAMA/LIBRA-phase1 region of interest for DM detection [77].

In some cases, the residual components of the neutron flux surviving the setup shielding can be studied using the coincidence analysis. Two examples can be taken again from the DAMA/LIBRA experiment, which studied the residual thermal and fast neutron fluxes surviving the setup shielding. Regarding the thermal neutrons, the neutron capture reactions ${}^{23}$Na(n,$\gamma$)${}^{24}$Na with 0.1 barn cross-section and the reaction ${}^{23}$Na(n,$\gamma$)${}^{24m}$Na with 0.43 barn cross-section, can be investigated in experiments using multiple NaI(Tl) detectors, as DAMA/LIBRA. The ${}^{24}$Na isotope is a $\beta$-emitter ($Q_{\beta }$ = 5515 keV; $T_{1/2}$ = 14.997 h). In 99.855% of events, it decays to 4123 keV excited level of ${}^{24}$Mg ($\beta$ endpoint equal to 1393 keV) with two prompt associated $\gamma$ particles with energies: 2754 keV and 1369 keV (see Figure 9).

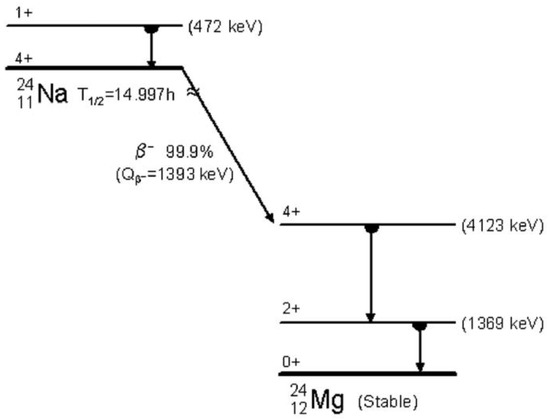
Figure 9. Decay scheme of ${}^{24}$Na produced as a consequence of thermal neutron capture of ${}^{23}$Na in a NaI(Tl) detector (see text). Reprinted with permission from [78]. Copyright 2005 Springer Nature.

The ${}^{24m}$Na isotope decays 100% of the times in ${}^{24}$Na by internal transition with a $\gamma$ of 472 keV. Thus, the presence of ${}^{24}$Na in the NaI(Tl) crystals gives information about the thermal neutron flux surviving the DAMA/LIBRA shielding and impinging on the DAMA/LIBRA detectors. The decay of ${}^{24}$Na can give rise to triple coincidences where the $\beta$ (with energy E1) and the two $\gamma$ particles (E2, E3) are detected in adjacent detectors. These coincidences were investigated with high sensitivity in DAMA/LIBRA considering: (i) the [0.57, 1.3] MeV interval for E1 and (ii) E2, E3 in the energy region within $\pm 1\sigma$ from the photopeak positions. Taking into account the detection efficiency of the process, an upper limit was obtained for the ${}^{24}$Na activity: <0.26 $\mathsf{\mu }$Bq/kg (90% C.L.). The latter can be used to calculate an upper limit on the capture rate due to a steady thermal neutron flux: <0.022 captures/day/kg and finally on the thermal neutron flux surviving the DAMA/LIBRA shield: <1.2 $\times {10}^{-7}$ cm${}^{-2}$s${}^{-1}$ (90% C.L.).

A similar procedure was also used to study the flux of fast neutrons surviving the setup shielding. In this case, the inelastic reaction ${}^{23}$Na(n,n’)${}^{23}$Na*(2076 keV) was taken into account. As a result of this reaction, two $\gamma$ particles in coincidence with energies 1636 keV and 440 keV are produced. From the study of the coincidences induced by these gammas in the DAMA/LIBRA setup, an upper limit <2.2 $\times {10}^{-7}$ n cm${}^{-2}$ s${}^{-1}$ (90% C.L.) was obtained for the flux of these particles, well compatible with the value measured at LNGS.

4.6. Possible Model of the Background

The previous methods increase the comprehension of the backgrounds and are useful tools in the reduction of the background caused, e.g., by $\alpha$ events in the detector coming from the residual contamination in ${}^{232}$Th and ${}^{238}$U. Moreover, as mentioned, further reduction of the background counting rate (mainly in the MeV region) can be achieved by exploiting the anticoincidence among the detectors. Anyway, additional specific contaminants, peculiar of the considered detectors, can play a significant role in the background spectrum.

Partial contributions to the measured background due to “internal” (radioactive contamination of the crystal) and “external” (radioactive contamination of the setup details) sources can be estimated with Monte Carlo simulation. The weight of each contribution can be constrained only when the activity of the related contaminant is known from previous measurements or analyses. In the other cases, only a hypothesis can be made on the nature and origin of the contamination. In detectors with good energy resolution, the presence of peaks or structures in the energy spectrum can be used to recognize and quantify a specific contaminant and its internal or external origin. However, many contaminants do not produce peculiar or identifiable structures in the energy spectrum (the $\beta$ active nuclides are an example) and their contributions cannot be distinguished from each other without a certain degree of ambiguity. This is especially true for detectors with poor energy resolution. These difficulties give rise to uncertainties in the construction of the background model, which must be taken into account in the analysis of the rare processes searched for. Moreover, in the case of DM investigation or in the search for rare processes in the keV energy region, a precise modeling of background is always rather prohibitive because of the limitation of Monte Carlo simulations at very low energies. In general, other sources of uncertainties for a background model are: (i) the fact that often just upper limits for residual contaminants are available (and thus the real amount is unknown); (ii) the unknown location of each residual contaminant in each component of the setup; (iii) the possible presence of nonstandard contaminants, generally unaccounted, and more. They have to be taken into account in the evaluation of the systematics of the obtained result, and it is generally not done.

As an example of background model, here, the case of analysis of data accumulated in a low-background experiment to search for 2$\beta$ decay of ${}^{106}$Cd is considered. The setup consists of an enriched ${}^{106}$CdWO${}_4$ detector (enriched in ${}^{106}$Cd at 66%) placed between two CdWO${}_4$ scintillation counters (with natural Cd composition) in a close geometry [64]. Several background components were simulated, including internal (in the ${}^{106}$CdWO${}_4$ crystal scintillator) and external sources. In particular, the activities of internal ${}^{226}$Ra → ${}^{210}$Pb, ${}^{210}$Pb →${}^{206}$Pb, ${}^{228}$Ra →${}^{228}$Th, ${}^{228}$Th →${}^{208}$Pb and ${}^{40}$K were taken from those measured in the previous stages of the experiment [79,80]. Moreover, the contribution of internal $\alpha$ particles from ${}^{232}$Th and ${}^{238}$U decay chains not discarded by the pulse shape analysis and of internal $2\nu 2{\beta }^{-}$ decay of ${}^{116}$Cd with $T_{1/2}$ = 2.63 × 10${}^{19}$ year [63] were taken into account. Regarding the external background sources, ${}^{226}$Ra →${}^{210}$Pb, ${}^{228}$Ra →${}^{228}$Th, ${}^{228}$Th → ${}^{208}$Pb and ${}^{40}$K were simulated in the internal and external copper details, in the PbWO${}_4$ crystal light-guide, in the quartz light guides and in the PMTs. Moreover, the contribution of ${}^{56}$Co and ${}^{60}$Co in the internal copper bricks, ${}^{226}$Ra →${}^{210}$Pb and ${}^{228}$Th → ${}^{208}$Pb in the CdWO${}_4$ crystal scintillators and ${}^{210}$Pb → ${}^{206}$Pb in the PbWO${}_4$ crystal light-guide were taken into account. Few peaks due to high intensity $\gamma$ rays from external contaminants are well visible in the measured energy spectrum reported in Figure 10a: the peaks at 1764 keV and 2204 keV due to external ${}^{214}$Bi and the peak at 2615 keV produced by external ${}^{208}$Tl. Recently, in the new stage of the experiment, the background induced by external contaminants has been reduced by a factor ≈2 in the energy interval 1200–3500 keV, thanks to the use of ultraradiopure PMTs, longer quartz light-guides for the CdWO${}_4$ counters and a more powerful passive shield of the detector system. The simulations were performed with the EGSnrc package and the DECAY0 event generator [81] (update 5 December 2018) while the residual spectrum of $\alpha$ particles was derived from the experimental data using the pulse shape analysis. The obtained background models were used to fit the measured spectra for $\gamma$ and $\beta$ events in configurations that were of interest for the study of the ${}^{106}$Cd double beta decay modes. In particular, the anticoincidence spectrum with the CdWO${}_4$ counters was fitted in the energy intervals (940–4000) keV, whereas the spectrum obtained in coincidence with event(s) in at least one of the CdWO${}_4$ counters in the energy window $E=$ (511 ± 2$\sigma$) keV was fitted in the energy interval (240–3940) keV. The fit quality is reasonable (${\chi }^2$ = 457 for 235 degrees of freedom). Figure 10 shows the results of the fit and the main components of the background.

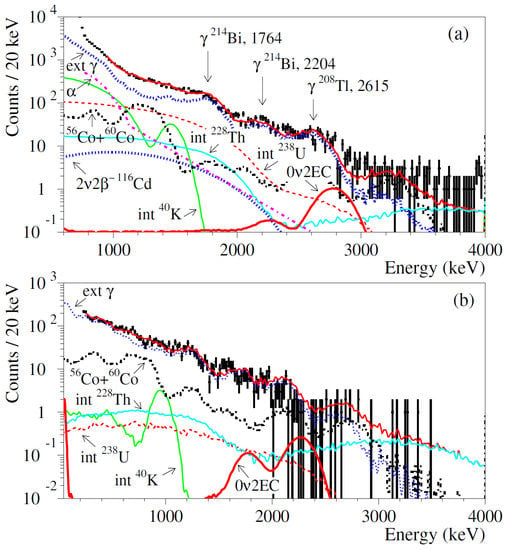
Figure 10. The $\gamma$ and $\beta$ energy spectra acquired in 26033 h by the ${}^{106}$CdWO${}_4$ scintillation detector in anticoincidence with the two CdWO${}_4$ counters (a) and in coincidence with the 511 keV annihilation $\gamma$ quanta in at least one of the two CdWO${}_4$ counters (b) (points). The background model (red line) is superimposed: the distributions of internal contaminations (int ${}^{40}$K, int ${}^{232}$Th, and int ${}^{238}$U) and external $\gamma$ quanta (ext $\gamma$), residual $\alpha$ particles in the ${}^{106}$CdWO${}_4$ crystal ($\alpha$), cosmogenic ${}^{56}$Co and ${}^{60}$Co in the copper shield details and the 2$\nu$2$\beta$ decay of ${}^{116}$Cd are shown. The excluded distributions of the 0$\nu$2EC decay of ${}^{106}$Cd to the ground state of ${}^{106}$Pd with the half-life $T_{1/2}$ = 6.8 × 10${}^{20}$ year are drawn by red solid line. Reprinted with permission from [64]. Creative Commons License CC BY 4.0.

5. Conclusions

Main arguments on the development of radiopure inorganic crystal scintillators, on their response to different kind of particles and on low-background analysis techniques in rare event investigations have been underlined. In particular, the pulse shape discrimination, the energy spectra analysis, the time–amplitude analysis, the Bi-Po analysis, the coincidence analysis and the background modeling have been reviewed and some examples of their application have been given in the case of specific detectors. These techniques allow the identification, in some cases even with very good precision, of many internal and external background sources. However, the systematics of the background modeling must always be properly considered in the search for rare processes.

Large efforts are in progress all over the world to improve the low-background technology, so fundamental in the ultimate frontier of investigation of rare processes with a challenge in developing advanced low-background techniques on both fronts of measurements and analysis. In particular, the development of radiopure crystal scintillators is in continue evolution and the research on innovative materials and purification techniques is leading to a wide set of inorganic scintillators for the investigation of rare processes [14,15]. The radiopurity of the surrounding materials is important as well. In fact, in many recent low-background experiments (see, e.g., Figure 10) the predominant background contribution is attributed by the authors to external contamination and not to intrinsic contaminants of the detectors. The techniques discussed in this paper also represent a useful tool to identify the best step for further improvements of the overall background level.