Abstract
High-multiplicity proton-proton (pp) collisions at the Large Hadron Collider (LHC) energies have created a new domain of research to look for a possible formation of quark–gluon plasma in these events. In this paper, we estimate various thermal properties of the matter formed in pp collisions at the LHC energies, such as mean free path, isobaric expansivity, thermal pressure, and heat capacity using a thermodynamically consistent Tsallis distribution function. Particle species-dependent mean free path and isobaric expansivity are studied as functions of final state charged particle multiplicity for pp collisions at the center-of-mass energy = 7 TeV. The effects of degree of non-extensivity, baryochemical potential, and temperature on these thermal properties are studied. The findings are compared with the theoretical expectations.
1. Introduction
One of the many astounding revelations of 20th century physics is the relatively new state of matter called quark–gluon plasma (QGP), expected to be formed in ultra-relativistic heavy-ion collisions. The temperature in such collisions reaches up to a few hundred MeV. For a better grasp of this temperature, consider the temperature at the core of the Sun: the temperature at the core of the Sun is around times less than that produced in heavy-ion collisions at Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). At such high temperatures, the normal baryonic matter with hadrons as their degrees of freedom goes through a cross-over phase transition to produce QGP, which has quarks and gluons as its degrees of freedom. Earlier, the general understanding was that only high-energy heavy-ion collisions can produce QGP while proton-proton (pp) collisions were taken as baseline measurements to understand medium formation in nuclear collisions. However, recent advances in high-energy pp collisions have shown us that there is a possibility to form QGP droplets, hopefully in high-multiplicity pp collisions in view of the observed heavy-ion-like signatures in such collisions [1,2]. Perturbative QCD (pQCD)-based Monte Carlo event generators like PYTHIA8 model in their advanced tunes such as multipartonic interactions, color reconnection, and rope hadronization have been successful in explaining some of the features in small collision systems [3]. These include color reconnections bringing out flow-like features in small systems [4], which is in principle a macroscopic hydrodynamic feature with a possible microstate dynamics responsible for thermalization, and rope hadronization explaining the enhancement of multi-strange particles with respect to pions [5]. Although there is no built-in thermalization in PYTHIA8, it is successful in mimicking the macroscopic flow features in pp collisions. In contrast to PYTHIA8, the energy conserving quantum mechanical multiple scattering approach, based on partons (parton ladders), off-shell remnants, and Splitting of parton ladders EPOS Monte Carlo model also describes the heavy-ion-like features in small collision systems [6]. It includes event-by-event 3+1-dimensional hydrodynamic evolution of the system produced in high-energy collisions [6,7,8]. The description of hard sectors for PYTHIA8 and EPOS generator is similar; however, the key difference in the EPOS model is that it includes a hydrodynamical description of the underlying mechanisms for generating collectivity instead of the color reconnection mechanism in PYTHIA8. Therefore, unlike PYTHIA8, EPOS includes the thermalization of a core (bulk) part of the system.
In view of these, there is a need to obtain a deeper understanding of high-multiplicity pp events to obtain a better understanding of the produced systems, possible associated thermodynamics, particle production dynamics, and freeze-out. There have been attempts to study these events using event topology, which separates jetty (pQCD-based hard scattering events) from isotropic (dominated by soft processes) events [9,10,11,12,13,14]. Using the temperature, T, and Tsallis non-extensive parameter, q, extracted from the transverse momentum -spectra, various thermodynamical quantities are estimated in order to characterize the system created in pp [15] and heavy-ion collisions [16]. In line with these explorations from various fronts, in the present study, we make an attempt to understand some of the thermodynamic features of pp collisions using experimentally motivated Tsallis non-extensive distribution, which describes the particle spectra [17,18]. In our study, we consider a cosmological expansion scenario, where the fireball produced in high-energy hadronic and nuclear collisions cools down during its spacetime expansion following a temperature profile with time [13]. The final state particles decouple from the system following a differential freeze-out scenario, with heavier particles coming out of the system early in time, which corresponds to higher decoupling temperatures. These decoupling points also depend on the interaction of cross section of individual particles with the produced system.
To understand the behavior of the matter formed in high-energy collisions at ultra-relativistic energies, we need to obtain an overall idea about its thermodynamical properties. The mean free path of a system gives the average distance that a particle has to travel before it collides with another particle in the system. It can give us an idea about the state of the system under consideration. One of the important thermodynamic properties of a system to study is isobaric expansivity, . The tendency of matter to change its shape, area, or volume is known as thermal expansion of that matter. The relative expansion per change in temperature at constant pressure is called the matter’s coefficient of thermal expansion or isobaric expansivity [19]. The study of isobaric expansivity of the matter formed in high-energy collisions tells us about the key features in such systems. Thermal pressure, , is nothing but the ratio of isobaric expansivity and isothermal compressibility. It tells us how much the pressure of the system increases with an increase in temperature at constant volume. The heat capacity, , of the system is the amount of heat energy that is required to raise the temperature of the system by one unit at constant volume. It tells us how the entropy, S, of the system changes with the change in temperature: . Entropy being directly related to the experimentally measured midrapidity charged particle density in pseudorapidity, , is an important observable when studying the QCD phase transition [20]. This makes the study of more interesting.
In high-energy collisions, a large number of final state particles are produced, which encourage us to take a statistical approach to describe such systems. The transverse momentum of the produced particles are expected to follow a thermalized Boltzmann–Gibbs (BG) distribution function. However, there have been observations of a finite degree of deviation from the equilibrium statistical description of identified particle -spectra in experiments at RHIC [21,22] and LHC [23,24,25,26]. This deviations are a result of a higher contribution of pQCD processes and can be better described by a combination of Boltzmann-type distribution functions along with a pQCD inspired power-law function [27]. Tsallis non-extensive statistical distribution has been found to be very accurate in explaining the -spectra of hadronic collisions and is used to obtain particle multiplicities in experimental measurements [21,22,23,24]. Whereas Tsallis distribution function fits the -spectra very well in the midrapidity region, there are other types of distribution functions in the literature that can fit the -spectra away from zero rapidity very well [28]. As a Boltzmann-type distribution, which is isotropic in transverse and longitudinal momenta, cannot explain the whole -spectra, in the present study, we use a thermodynamically consistent Tsallis distribution function to describe the -spectra in pp collisions [29]. The parameter q in Tsallis distribution function denotes the degree of deviation from the equilibrium, and q = 1 corresponds to the equilibrium condition (BG scenario). At higher charged particle multiplicities in heavy-ion collisions, the value of q tends towards 1, which signifies that the system has obtained thermodynamic equilibrium. From the Tsallis distribution fit to the -spectra of pp collisions at the centre-of-mass energy = 7 TeV, we extracted thermodynamical parameters such as temperature, T, and the non-extensive parameter, q, which were then used to find the particle species-dependent mean free path and isobaric expansivity of the hadronic system formed in pp collisions.
2. Formulation
As the identified particle -spectra for pp collisions are well-described by a Tsallis non-extensive distribution function, we estimated various thermal properties of the produced fireball using a thermodynamically consistent Tsallis distribution function, which is given as follows [29,30,31,32]:
where T and are the temperature and the chemical potential, respectively, with as the baryochemical potential, as the chemical potential related to the electric charge and as the chemical potential related to the strangeness quantum number. Here, is the energy, with p being the momentum and m being the mass of the particle under study. The thermodynamical quantities in non-extensive statistics are given by
where n, , P, and g are the number density, energy density, pressure, and degeneracy, respectively. This formulation gives a thermodynamically consistent description, meaning the basic thermodynamic relationships are satisfied:
Furthermore, the variable T, used in the above expressions, obeys the thermodynamic relation:
Hence, it could be termed as the temperature even though the system follows Tsallis non-extensive statistics. Here, U is the internal energy of the system. It is noteworthy to mention here that there are various forms of Tsallis distribution functions available in the literature [33,34]. However, the form used in this work is thermodynamically consistent and, hence, gives a scope to deal with various thermodynamic variables to characterize the created fireball.
Going ahead with the above prescription, in view of thermodynamic consistency and Tsallis non-extensive statistics, the expressions for the discussed thermodynamic observables could be written as follows. The general expression of mean free path is given by
Here is the scattering cross section. Using Equation (2), the expression for mean free path for the hadron gas becomes
where is the energy of the ath particle and can be taken as 11.3 mb considering a hard core hadron radius, = 0.3 fm, and using [35,36]. The choice of an average value of hard core hadron radius, = 0.3 fm, seems to be a good choice in the estimation of viscosity of the system [35] while giving proper estimation of hadron yields in a statistical hadron gas model [36]. A change in in the calculation of hadron scattering cross section may induce a change in the absolute values of . However, we have checked it explicitly that, this will have no impact on the trend of of the particles when it is studied as a function of temperature, final state multiplicity, q-parameter, or the baryochemical potential of a system.
From thermodynamics, the expression of isobaric expansivity is given as [19]:
As the exact freeze-out volume for identified charged particles is not very well measurable, Equation (11) can be rewritten in terms of particle number density, n as follows:
Using Equation (2), one obtains
The thermal pressure is given by (see Equation (4))
The heat capacity or the specific heat at constant volume is defined as
and, using Equation (3), this is given by
In all of the above equations, we have taken , assuming exact charge and strangeness conservation in the system. In the present study, we took a particle mass cutoff of 1.5 GeV to include all the hadrons in the Review of Particle Physics [37] in all of our theoretical estimations. In LHC pp collisions, the baryochemical potential is assumed to be zero because of the baryon-antibaryon symmetry. Therefore, in our calculations, we took = 0 except when we study the effect of baryochemical potential on various thermal observables. There are recent developments [38], where is extracted as a fit parameter from the Tsallis fit to the transverse momentum spectra, while this is beyond the scope of the present study.
3. Results and Discussion
To calculate the mean free path, we used Equation (10). In Figure 1, we plot the mean free path, , of a hadron gas system as a function of temperature for different values of q-parameter. One observes that, for low temperature, the mean free path of the system is very high and suddenly decreases, becoming minimum at the high temperature region, which usually corresponds to freeze-out temperatures in high energy hadronic and nuclear collisions [39]. One also notices that the mean free path is highly sensitive to the q parameter in the low temperature regime, whereas the dependency decreases at higher temperatures becoming almost negligible. These trends are expected because, at low temperature, the number density in the system is less, which results in a high . As the temperature increases, the number density also increases drastically between a short temperature range before becoming almost constant at very high temperatures. In the low temperature regime, at a given temperature, the mean free path decreases when the system slowly moves away from equilibrium. For an expanding fireball, initially, the system volume is low and, hence, for a given number of particles, the mean free path is smaller. The constituents of the system go through mutual collisions as a part of the process of equilibration, while the system is still expanding, resulting in a higher mean free path. Below the expected kinetic freeze-out temperature, the fireball volume becomes much higher and the mean free path becomes higher than the system volume.
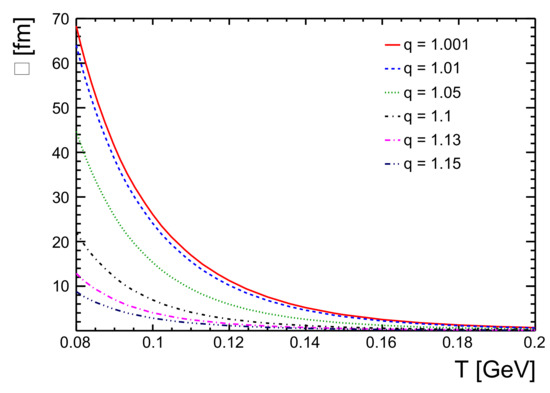
Figure 1.
Mean free path, , as a function of temperature, T, for a hadron gas for different values of non-extensive parameter, q, for baryochemical potential, = 0.
This means that, at this point and beyond, the momentum spectra are frozen because the constituent particles hardly collide with each other.
Figure 2 shows the mean free path of a hadron gas as a function of temperature for different values of baryochemical potentials. For this study, we took five different baryochemical potentials; = 0, 0.025, 0.200, 0.436, and 0.600 GeV, which correspond to, respectively, LHC energies, RHIC at = 200 GeV and 19.6 GeV, RHIC/FAIR at = 7.7 GeV, and NICA at = 3 GeV [40,41,42,43]. Here, we took the non-extensive parameter, q = 1.001, which corresponds to a near equilibrium state. One observes that, when is zero, the trend of the mean free path of the system mimics the trend which we get from Figure 1. However, as we go on increasing the value of , which happens when one moves down in collision energy, the mean free path of the system at a given temperature becomes lower. The dependence on baryochemical potential on the mean free path is clearly visible in the low temperature regime. There is universality in the decreasing nature of the mean free path as a function of temperature for various values. This is due to the fact that, with an increase in baryon chemical potential, the number density of the system will increase, resulting in a lower mean free path. Similarly, one expects to produce more particles at higher system temperatures, making the number density in the system higher. This makes the mean free path decrease with temperature irrespective of the baryochemical potential of the system. This is clearly evident from Figure 2.
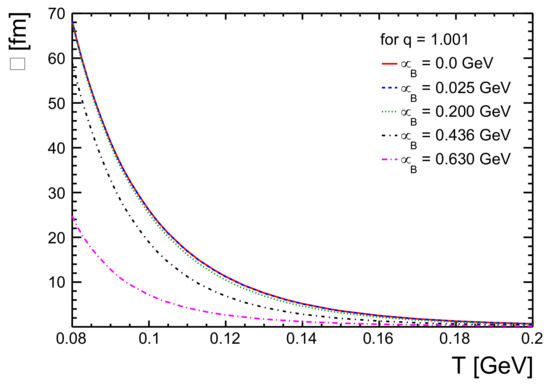
Figure 2.
Mean free path, , as a function of temperature, T, for a hadron gas for different values of baryochemical potential, .
Beyond these studies on the dependencies of mean free path on the , T, and q parameters of the system for a hadron gas, one must be curious to look into the behaviour of mean free path as a function of final state event multiplicity for pp collisions at LHC energies for different identified particles. In order to do that, we took the multiplicity-dependent identified particle -spectra for pp collisions at = 7 TeV, and using the discussed Tsallis non-extensive statistics, we obtained the T and q parameters [44]. Taking these as inputs, we estimated as a function of final state event multiplicity, which is shown in Figure 3. The definition of event class through final state multiplicity was taken from the ALICE experiment [1]. The hardening of -spectra with event multiplicity for pp collisions at = 7 TeV has been seen recently [1]. This points to an increase in system temperature with event multiplicity. Hence, in Figure 3, the x-axis becomes a replica of temperature although the explicit functionality with event multiplicity is not known. In view of this, the experimental behavior of particle mean free path assuming a common cross section for all particle species [35] as a function of temperature agrees with the theoretical expectations [45] for and , as shown in Figure 1 and Figure 2. After a threshold of (10–15), the mean free path becomes independent of particle species, and for higher event multiplicities, it attains a lower asymptotic value between (1–10) fm.
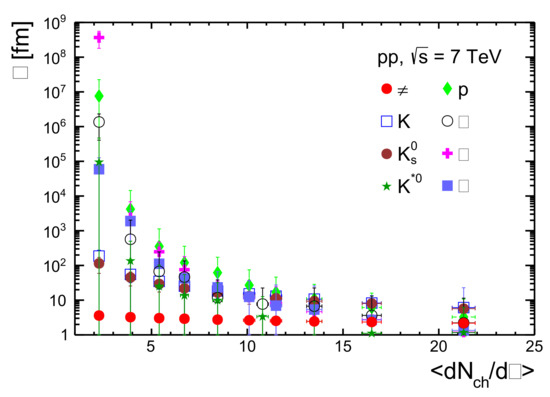
Figure 3.
Mean free path, , as a function of final state charged particle mean multiplicity density in pseudorapidity, (which is a centrality classifier), for different identified particles in pp collisions at = 7 TeV. The values of the mean free path are estimated by using Equation (10) by taking the values from the Tsallis distribution fitting to the experimental transverse momentum spectra of identified particles.
We use Equation (13) to calculate the isobaric expansivity of a hadron gas. Figure 4 shows the isobaric expansivity as a function of temperature for different values of the non-extensive parameter q. One observes that, for lower temperatures, the system shows lower values and that, as the temperature increases slowly, increases rapidly and the trend becomes almost flat for higher values of temperature, 180 MeV. One can also see that the isobaric expansivity is highly dependent on q at low temperatures. For 1, which is for an equilibrated system, is the lowest in the high temperature regime. For high temperature, the value of increases as q increases, i.e., as the system stays away from the equilibrium. The expansivity of the system is thus found to be correlated with the degree of non-extensivity of the system.
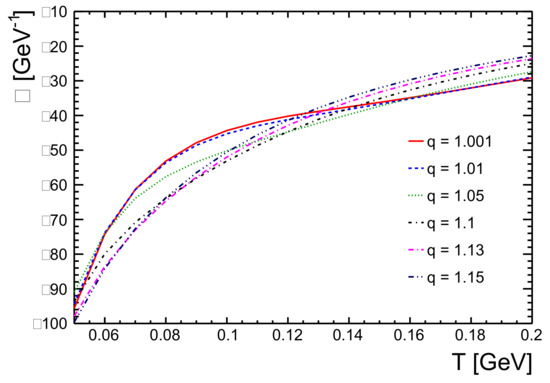
Figure 4.
Isobaric expansivity, , as a function of temperature, T, for different values of non-extensive parameter, q, for hadron gas for baryochemical potential, = 0.
The isobaric expansivity of hadron gas as a function of temperature for different values of baryochemical potential, , is shown in Figure 5. Here, we take the non-extensive parameter q = 1.001 and estimated for different values. For = 0 (the case at the LHC energies), we obtain a similar trend as we got for the case of q = 1.001, shown in Figure 4. A correlation between and the expansivity of the system can be observed from Figure 5. At high temperature, the expansivity of the hadron gas is lower for = 0 and it becomes higher for high values. The reason for negative expansivity can be due to different physical processes such as transverse vibrational modes, rigid unit modes, and phase transitions [46]. However, in our case, considering an expanding fireball scenario, we know that, at higher temperatures, the system volume is smaller. As the temperature decreases, the volume of the system increases. Thus, we infer that, when we increase the temperature of the expanding fireball at a given point in time, its volume becomes smaller—as if it would appear to contract. This is the reason why we get a negative expansivity for a hadron gas.
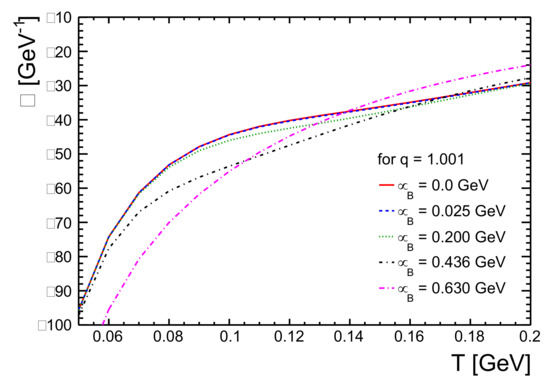
Figure 5.
Isobaric expansivity, , as a function of temperature, T, for different values of baryochemical potential, for hadron gas.
Figure 6 shows the isobaric expansivity of the hadron gas system formed in LHC pp collisions at = 7 TeV as a function of final state-charged particle multiplicity, which is an event classifier in pp collisions. We took the temperature and q values from the Tsallis fit to the -spectra of the identified particles produced in LHC pp collisions at = 7 TeV [47] to estimate the isobaric expansivity of the system for different identified particles [44]. At the LHC energies, the baryochemical potential of the system is almost zero, and for our studies, we use = 0. One observes an increasing trend in the expansivity of the system as the final state charged particle multiplicity increases. For lower , the expansivity of identified particles are different and mostly follow a mass ordering, with massive particle having lower than lighter particles. This is a consequence of the fact that, in the hadronic phase, the number density of the lighter particles are higher than that of the massive particles—statistical production of particles in the multi-particle production process. When we increase the temperature, the number density of all the particles increases. The given temperature can be translated into the kinetic energy of the particles in the system. Taking the solid state and gaseous phase analogy, for a denser system, the increase in temperature makes a small increase in the volume of the system, whereas for a less dense system, the change is very high. However, after a certain charged particle multiplicity = 10, we observe that all the hadronic species in the system have almost the same isobaric expansivity. This suggests a change in the dynamics of the system at higher than 10 [48].
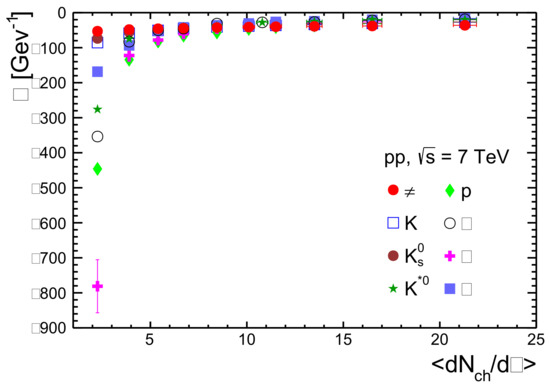
Figure 6.
Isobaric expansivity, , as a function of final state charged particle mean multiplicity density in pseudorapidity, , for pp collisions at = 7 TeV for identified charged particles. The values of isobaric expansivity are estimated by using Equation (13) by taking the values from the Tsallis distribution fitting to the experimental transverse momentum spectra of identified particles at the midrapidity.
It is known that water has a negative expansivity from 0 C to 4 C. However, with the increase in temperature, it gains positive expansivity. At 30 C, water has an isobaric expansivity of about [49]. This comparison is made to obtain a physical realization of the system produced in high-energy collisions.
We use Equation (14) to estimate , the thermal pressure of the produced system. Figure 7 shows the variation in as a function of temperature for different values of the non-extensive parameter q. One observes that for low temperatures, the thermal pressure is lower for the system, but as the temperature increases, the thermal pressure also increases. One also can see that, when the system is near equilibrium, gets the lowest value. For higher q values, increases, meaning that, as the degree of non-extensivity of the system increases, the thermal pressure also increases at any given temperature. Hence, the thermal pressure is responsible for the degree of non-equilibration of the system. In addition, at lower temperatures, the number density of the system would be smaller (as the volume of the system increases). With a small change in temperature, the change in pressure of the system would be smaller in comparison to the case of higher temperature regimes, where the number density of the system would be much higher, which contributes to a higher thermal pressure.
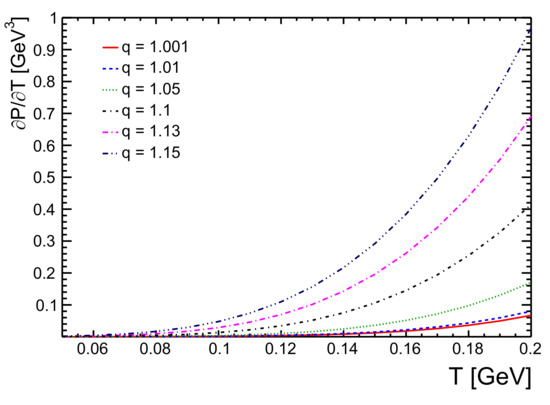
Figure 7.
The thermal pressure, , of the system as a function of temperature, T, for hadron gas for different q values for baryochemical potential, = 0.
We calculate the specific heat at constant volume for a system with hadrons as the constituents using Equation (16). Figure 8 shows the variation in as a function of temperature. One sees that, for low temperatures, the specific heat of the system is low while it increases gradually as the temperature increases. One also observes that, for q = 1.001, i.e., when the system is near equilibrium, the specific heat of the system gets the lowest value. This is expected, as for an equilibrated system, the degree of change in the internal energy of the system is less. For higher q values, becomes higher at any given temperature. From Figure 9, one observes that the baryochemical potential plays a big role in the outcome of . For all values, the of the system shows an increase. The higher the values, the higher the values of specific heat at all temperatures.
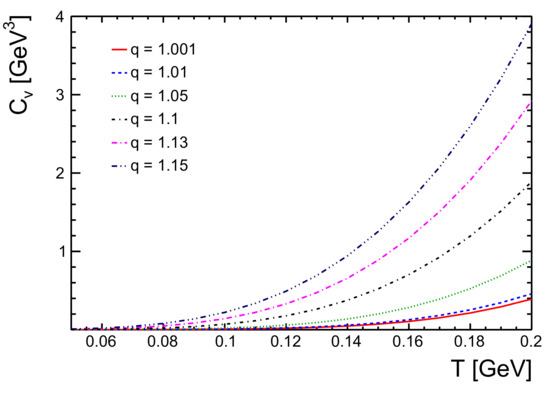
Figure 8.
The specific heat at constant volume, , as a function of temperature, T, for hadron gas for different q-values for baryochemical potential, = 0.
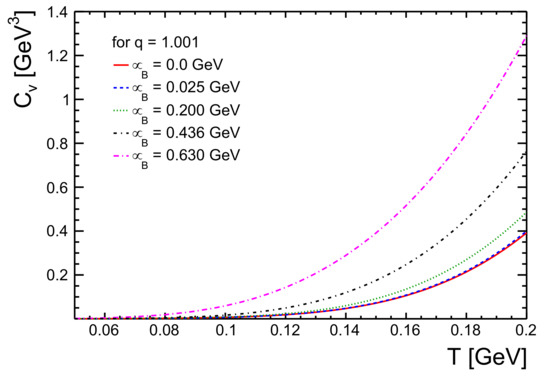
Figure 9.
The specific heat at constant volume, , as a function of temperature, T, for hadron gas for different baryochemical potential values, .
4. Summary and Conclusions
The observations of heavy-ion-like features in high-multiplicity proton-proton (pp) collisions at the Large Hadron Collider energies and the corresponding explanations using different tunes in pQCD-inspired Monte Carlo model such as PYTHIA8 have warranted a deeper look into these events. In the present study, we estimated various thermal properties of the matter formed in high-energy proton-proton collisions, such as mean free path, , isobaric expansivity, , thermal pressure, , and heat capacity, , using a thermodynamically consistent Tsallis distribution function. The effect of the non-extensive parameter, q, baryochemical potential, , and temperature, T, on these thermal properties are studied. Some of these observables such as mean free path and isobaric expansivity are studied as a function of final state charged particle multiplicity for pp collisions at the center-of-mass energy = 7 TeV, and the findings are compared to the theoretical expectations. The important results are summarized below.
- The mean free path is found to be highly sensitive to the equilibration parameter q at lower temperatures. In the domain of high temperature, it is found to be almost independent from the q parameter. The higher the baryochemical potential, the lower the mean free path of the system at a certain temperature. For all values of baryochemical potential, the spectra show a decreasing trend with temperature.
- The mean free path is then studied for identified particles with the () inputs from the experimental transverse momentum spectra. The midrapidity charged particle pseudorapidity density (10–15) is found to be a threshold in the final state event multiplicity, after which the mean free path becomes independent of particle species. For higher event multiplicities, the mean free path seems to attain a lower asymptotic value between (1–10) fm.
- A negative isobaric expansivity of the hadron gas system is observed. The isobaric expansivity is highly sensitive to the q parameter. In a higher temperature region, the expansivity is higher for a system away from equilibrium. Similarly, for high values, we observe a higher expansivity of the system in the high temperature region.
- For the isobaric expansivity of the identified particles, we observed a threshold midrapidity charged particle pseudorapidity density, 10, after which the isobaric expansivity almost converged to the same value. This may indicate a change in the dynamics of the system.
- The thermal pressure was found to be weakly dependent on the q parameter at lower temperatures, but the dependency became stronger with the increase in temperature. As expected, at lower temperatures, the thermal pressure in the system is lower, which goes up, as the temperature of the system increases. The thermal pressure is found to be positively correlated with the degree of non-extensivity of a physical system.
- The specific heat at constant volume is weakly dependent on the equilibration parameter q at lower temperatures and highly dependent on q in the higher temperature region. As the temperature increases, we observed an increase in the specific heat of the system. We also studied the effect of baryochemical potential on the specific heat and observed that, for a baryon-rich environment, the specific heat becomes higher for high baryochemical potential.
- Although in this paper a theoretical estimation of various important thermodynamic quantities was made as a function of final state multiplicity keeping pp collisions in mind in order to carry out a systematic study, the physical interpretation of the thermodynamic properties of the systems corresponding to low-multiplicities must be performed with caution.
Author Contributions
All authors of this paper have made contributions to conceptualization, formal analysis, paper writing and agree to the published version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is carried out under DAE-BRNS Project No. 58/14/29/2019-BRNS of Government of India.
Acknowledgments
D.S. acknowledges the initial discussions with Golam Sarwar and Sushanta Tripathy. Some help from Vaibhav Lohia and Archita Rani Dash on these studies are highly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ALICE Collaboration. Enhanced production of multi-strange hadrons in high-multiplicity proton–proton collisions. Nature Phys. 2017, 13, 535. [Google Scholar] [CrossRef]
- Velicanu, D. (for CMS Collaboration). Ridge correlation structure in high-multiplicity pp collisions with CMS. J. Phys. G 2011, 38, 124051. [Google Scholar] [CrossRef]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. PYTHIA 6.4 physics and manual. JHEP 2006, 05, 026. [Google Scholar]
- Ortiz Velasquez, A.; Christiansen, P.; Flores, E.C.; Cervantes, I.M.; Paić, G. Color reconnection and flowlike patterns in pp collisions. Phys. Rev. Lett. 2013, 111, 042001. [Google Scholar] [CrossRef] [PubMed]
- Nayak, R.; Pal, S.; Dash, S. Effect of rope hadronization on strangeness enhancement in p-p collisions at LHC energies. Phys. Rev. D 2019, 100, 074023. [Google Scholar] [CrossRef]
- Werner, K.; Guiot, B.; Karpenko, I.; Pierog, T. Analysing radial flow features in p-Pb and p-p collisions at several TeV by studying identified particle production in EPOS3. Phys. Rev. C 2014, 89, 064903. [Google Scholar] [CrossRef]
- Werner, K.; Karpenko, I.; Pierog, T.; Bleicher, M.; Mikhailov, K. Event-by-event simulation of the three-dimensional hydrodynamic evolution from flux tube initial conditions in ultrarelativistic heavy ion collisions. Phys. Rev. C 2010, 82, 044904. [Google Scholar] [CrossRef]
- Drescher, H.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton based Gribov-Regge theory. Phys. Rept. 2001, 350, 93. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Charged-particle production as a function of multiplicity and transverse spherocity in pp collisions at =5.02 and 13 TeV. Eur. Phys. J. C 2019, 79, 857. [Google Scholar] [CrossRef]
- Khatun, A.; Thakur, D.; Deb, S.; Sahoo, R. J/ψ Production dynamics: Event shape, multiplicity and rapidity dependence in proton+proton collisions at LHC energies using PYTHIA8. J. Phys. G 2020, 47, 055110. [Google Scholar] [CrossRef]
- Ortiz, A.; Paić, G.; Cuautle, E. Mid-rapidity charged hadron transverse spherocity in pp collisions simulated with Pythia. Nucl. Phys. A 2015, 941, 78. [Google Scholar] [CrossRef]
- Rath, R.; Khuntia, A.; Tripathy, S.; Sahoo, R. A Baseline study of the event-shape and multiplicity dependence of chemical freeze-out parameters in proton-proton collisions at = 13 TeV using PYTHIA8. Physics 2020, 2, 40. [Google Scholar] [CrossRef]
- Tripathy, S.; Bisht, A.; Sahoo, R.; Khuntia, A.; Malavika, P.S. Event shape and multiplicity dependence of freeze-out scenario and system thermodynamics in proton+proton collisions at = 13 TeV Using PYTHIA8. Adv. High Energy Phys. 2021, 2021, 8822524. [Google Scholar] [CrossRef]
- Khuntia, A.; Tripathy, S.; Bisht, A.; Sahoo, R. Event shape engineering and multiplicity dependent study of identified particle production in proton+proton collisions at = 13 TeV using PYTHIA. J. Phys. G 2021, 48, 035102. [Google Scholar] [CrossRef]
- Deb, S.; Sarwar, G.; Sahoo, R.; Alam, J.-E. Study of QCD dynamics using small systems. arXiv 2019, arXiv:1909.02837. [Google Scholar]
- Azmi, M.; Bhattacharyya, T.; Cleymans, J.; Paradza, M. Energy density at kinetic freeze-out in Pb–Pb collisions at the LHC using the Tsallis distribution. J. Phys. G 2020, 47, 045001. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Marques, L.; Mogliacci, S.; Paradza, M.W. On the precise determination of the Tsallis parameters in proton–proton collisions at LHC energies. J. Phys. G 2018, 45, 055001. [Google Scholar] [CrossRef]
- Khuntia, A.; Tripathy, S.; Sahoo, R.; Cleymans, J. Multiplicity dependence of non-extensive parameters for strange and multi-strange particles in proton-proton collisions at = 7 TeV at the LHC. Eur. Phys. J. A 2017, 53, 103. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics; John Wiley: New York, NY, USA, 1987. [Google Scholar]
- Kharzeev, D.E.; Levin, E.M. Deep inelastic scattering as a probe of entanglement. Phys. Rev. D 2017, 95, 114008. [Google Scholar] [CrossRef]
- Abelev, B.I.; Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Anderson, M.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; et al. Strange particle production in p+p collisions at = 200 GeV. Phys. Rev. C 2007, 75, 064901. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitan, N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; et al. Identified charged hadron production in p+p collisions at =200 and 62.4 GeV. Phys. Rev. C 2011, 83, 064903. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Quintana, A.A.; Abramyan, A.; Adamova, D.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; et al. Production of pions, kaons and protons in pp collisions at =900 GeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1655. [Google Scholar] [CrossRef]
- Abelev, B.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; Ahammed, Z.; et al. Neutral pion and η meson production in proton-proton collisions at s=0.9 TeV and =7 TeV. Phys. Lett. B 2012, 717, 162. [Google Scholar] [CrossRef]
- ALICE Collaboration. Multi-strange baryon production in pp collisions at =7 TeV with ALICE. Phys. Lett. B 2012, 712, 309. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Study of the inclusive production of charged pions, kaons, and protons in pp collisions at =0.9, 2.76, and 7 TeV. Eur. Phys. J. C 2012, 72, 2164. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Khuntia, A.; Pareek, P.; Sahoo, R. Radial flow in non-extensive thermodynamics and study of particle spectra at LHC in the limit of small (q-1). Eur. Phys. J. A. 2016, 52, 30. [Google Scholar] [CrossRef]
- Pirner, H.J.; Reygers, K. Light-cone QCD plasma. Phys. Rev. D 2012, 86, 034005. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution in proton-proton collisions at = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic thermodynamics: transverse momentum distributions in high-energy physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Deppman, A. Self-consistency in non-extensive thermodynamics of highly excited hadronic states. Physica A 2012, 391, 6380. [Google Scholar] [CrossRef]
- Deppman, A. Properties of hadronic systems according to the nonextensive self-consistent thermodynamics. J. Phys. G Nucl. Part. Phys. 2014, 41, 055108. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S. Tsallis-thermometer: A QGP indicator for large and small collisional systems. arXiv 2020, arXiv:2003.03278. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E.; Menezes, D.P.; Frederico, T. Fractal structure and non extensive statistics. Entropy 2018, 20, 633. [Google Scholar] [CrossRef] [PubMed]
- Kadam, G.P.; Mishra, H. Dissipative properties of hot and dense hadronic matter in an excluded-volume hadron resonance gas model. Phys. Rev. C 2015, 92, 035203. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Oliinychenko, D.R.; Sorin, A.S.; Zinovjev, G.M. Simple solution to the strangeness horn description puzzle. Eur. Phys. J. A 2013, 49, 30. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. (Particle Data Group), Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Cleymans, J.; Paradza, M.W. Tsallis statistics in high energy physics: Chemical and thermal freeze-outs. Physics 2020, 2, 38. [Google Scholar] [CrossRef]
- Kraus, I.; Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Chemical equilibrium in collisions of small systems. Phys. Rev. C 2007, 76, 064903. [Google Scholar] [CrossRef]
- Tawfik, N.A.; Abou-Salem, L.I.; Shalaby, A.G.; Hanafy, M.; Sorin, A.; Rogachevsky, O.; Scheinast, W. Particle production and chemical freezeout from the hybrid UrQMD approach at NICA energies. Eur. Phys. J. A 2016, 52, 324. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Magestro, D.; Redlich, K.; Stachel, J. Hadron production in Au-Au collisions at RHIC. Phys. Lett. B 2001, 518, 41. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Khuntia, A.; Tiwari, S.K.; Sharma, P.; Sahoo, R.; Nayak, T.K. Effect of Hagedorn states on isothermal compressibility of hadronic matter formed in heavy-ion collisions: From NICA to LHC energies. Phys. Rev. C 2019, 100, 014910. [Google Scholar] [CrossRef]
- Khuntia, A.; Sharma, H.; Tiwari, S.K.; Sahoo, R.; Cleymans, J. Radial flow and differential freeze-out in proton-proton collisions at =7 TeV at the LHC. Eur. Phys. J. A 2019, 55, 3. [Google Scholar] [CrossRef]
- Sarkar, N.; Ghosh, P. Thermalization in a small hadron gas system and high-multiplicity pp events. Phys. Rev. C 2017, 96, 04490. [Google Scholar] [CrossRef]
- Fisher, D.J. Negative Thermal Expansion Materials; Materials Research Forum LLC: Millersville, PA, USA, 2018. [Google Scholar]
- ALICE Collaboration. Multiplicity dependence of light-flavor hadron production in pp collisions at = 7 TeV. Phys. Rev. C 2019, 99, 024906. [Google Scholar] [CrossRef]
- Sahu, D.; Tripathy, S.; Pradhan, G.S.; Sahoo, R. Role of event multiplicity on hadronic phase lifetime and QCD phase boundary in ultrarelativistic collisions at energies available at the BNL Relativistic Heavy Ion Collider and CERN Large Hadron Collider. Phys. Rev. C 2020, 101, 014902. [Google Scholar] [CrossRef]
- Kell, G.S. Density, thermal expansivity, and compressibility of liquid water from 0. deg. to 150. deg.. Correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. J. Chem. Eng. Data 1975, 20, 97. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).