Abstract
Modern network intrusion detection systems (NIDSs) rely on complex deep learning models. However, the “black-box” nature of deep learning methods hinders transparency and trust in predictions, preventing the timely implementation of countermeasures against intrusion attacks. Although explainable AI (XAI) methods provide a solution to this problem by providing insights into the reasons behind the predictions, the explanations provided by the majority of them cannot be trivially converted into actionable countermeasures. In this work, we propose a novel tabular diffusion-based counterfactual explanation framework that can provide actionable explanations for network intrusion attacks. We evaluated our proposed algorithm against several other publicly available counterfactual explanation algorithms on three modern network intrusion datasets. To the best of our knowledge, this work also presents the first comparative analysis of the existing counterfactual explanation algorithms within the context of NIDSs. Our proposed method provides plausible and diverse counterfactual explanations more efficiently than the tested counterfactual algorithms, reducing the time required to generate explanations. We also demonstrate how the proposed method can provide actionable explanations for NIDSs by summarizing them into a set of actionable global counterfactual rules, which effectively filter out incoming attack queries. This ability of the rules is crucial for efficient intrusion detection and defense mechanisms. We have made our implementation publicly available on GitHub.
1. Introduction
Deep learning-based network intrusion detection systems (NIDSs) play a crucial role in the modern cybersecurity landscape, mainly due to the generalizability and scalability of deep learning models for high-dimensional network telemetry data [1,2]. Nonetheless, the opaque nature of these deep learning models presents a significant challenge for human analysts at security operation centers (SoCs) to determine the root causes of threats and formulate appropriate countermeasures against intrusion attempts. Explainable AI (XAI) techniques are generally proposed as an effective solution to address the issue of opaqueness across various application domains. In the context of NIDSs, feature attribution methods such as Shapley Additive Explanations (SHAPs) and Local Interpretable Model-Agnostic Explanations (LIMEs) are frequently used to explain decisions made by NIDSs [3]. Feature attribution methods usually provide a ranking of features based on a certain type of feature score. The feature score is derived based on the model’s outputs (i.e., predictions) for a data point or a group of data points. For example, Shapley values provide feature scores as a measurement of the contribution of each feature to the prediction of a black-box model [4]. LIMEs also calculate a feature importance score based on a simple surrogate model, such as a logistic regression model trained on synthetically sampled instances around a data point that needs to be explained.
However, a major shortcoming of the existing feature attribution methods is that they do not provide any actionable recourse for human analysts to work on. Feature attribution methods primarily help human analysts to identify important features related to NIDS decisions. Analysts would then use these explanations to identify the type of threat and design appropriate defense mechanisms using their domain expertise. This entire process can consume a substantial amount of time, which is crucial for acting against the threat and ensuring normal operations without incurring losses. On the other hand, emerging paradigms such as “Zero-touch Networks” demand the ability to automate the process of defense against intrusion attacks without having to rely on the expertise of human analysts [5]. Counterfactual (CF) explanations provide actionable explanations that can alleviate the challenges posed by the existing feature attribution-based XAI methods used in NIDSs. Despite this advantage, the utility of these explanations is still underexplored in the network intrusion detection domain. Our proposed method seeks to take the initial step toward addressing this gap in the literature.
CF explanations bear the advantages of feature attribution methods as well as the potential to provide actionable countermeasures within the explanations. The traditional definition of CF explanations describes that they should produce an alternate data point that has a different (or preferred) prediction from the black-box model, with minimal changes to the original data point that needs to be explained [6]. As a prevalent example taken from the finance domain, a CF explanation provided for a user who applied for a loan could be ‘if the user had increased their income and paid existing credit balances, the loan would have been approved’ [6]. In the context of NIDSs, for a data point that has classified a certain network activity as an intrusion, a CF explanation would be a new data instance that is classified as a normal (non-intrusion) activity by the black-box NIDS. This explanation would highlight the minimal set of feature modifications required to alter the original prediction, thereby revealing both the influential features contributing to the model’s original decision and the specific value adjustments necessary to change the original decision. These value adjustments can then be converted to actions against the attack.
A diverse range of CF explanation methods have been proposed in the literature for algorithmic recourse, mainly concerning the financial domain (e.g., loan application scenarios) or recidivism as real-world applications [7,8,9]. This multitude of counterfactual algorithms also provides different approaches to generate CF explanations with distinct properties. For instance, sparsity (minimal changes) in CF explanations has generally been preferred, while certain types of algorithms prefer plausibility (explanations following the underlying distribution of the original data) over sparsity [10]. This difference in qualities can be observed across domains. For example, the finance or recidivism domains would prioritize fairness and plausibility of CF explanations more often, while CF explanations for debugging applications would prioritize other qualities, such as sparsity [11].
Based on these observations, we propose an efficient generative counterfactual approach for NIDSs inspired by diffusion models from the tabular data synthesis domain [12] (further details provided in Section 3). In addition, we aim to explore the utility of counterfactual generation in the NIDS domain and quantitatively evaluate several counterfactual methods. Overall, our main contributions in this work are listed below.
- We propose a novel tabular diffusion-based algorithm to generate CF explanations for network intrusion detection applications. This proposed method is devised based on a technique borrowed from the diffusion-based tabular data synthesis literature. We provide empirical evidence for the utility of the proposed method compared to several existing publicly available counterfactual algorithms.
- To the best of our knowledge, the quantitative comparison of the existing counterfactual methods presented in this work provides the first analysis of its kind in the NIDS domain.
- Finally, we propose global counterfactual rules to summarize the CF explanations generated by the proposed method. These rules are derived using a simple yet effective technique based on decision trees. They summarize the important features for a cohort of attack data points and the associated value bounds that separate them from benign data. Hence, these rules can be used in actionable defense measures against network intrusion attacks, which is a novel utility of CF explanations in the NIDS domain.
In this study, we constrain the downstream task to a supervised binary classification setting, focusing on generating CF explanations for data instances that are classified as attacks. The rest of this paper is organized as follows: Section 2 reviews the related work from the counterfactual and NIDS literature; Section 3 provides background details on CF explanations for NIDSs, including the generative CF explanation methods considered in this work; Section 4 provides details regarding the proposed methodology; Section 5 presents the experimental results; Section 6 offers an in-depth discussion; and Section 7 concludes the paper with a summary of its contributions and directions for future research. We have released our code on GitHub (https://github.com/VinuraD/Counterfactuals-for-NIDS, accessed on 30 August 2025).
2. Related Work
CF explanations have recently gained traction among practitioners, mainly due to their ability to provide actionable explanations. The inherent qualities of these explanations can vary depending on the algorithmic approach employed for their generation [7]. For example, a list of the types of model-agnostic algorithms is presented, where each type of approach offers different qualities of CF explanations [13]. A few recent attempts show how certain algorithms impact the quality of the generated explanations [14,15]. Owing to the impact of AI regulatory frameworks [16] and the early literature [6], most of the research in this domain revolves around domains such as finance and criminal justice [6]. Nevertheless, CF explanations have also been utilized in other domains/data modalities, such as time-series data and images, and use cases such as model debugging and knowledge extraction.
The NIDS literature has recently focused more on providing explainability along with intrusion detection. Among the plethora of proposals for integrating XAI into NIDSs, feature importance methods have been of particular interest [17]. A combination of three feature attribution methods (SHAPs, LIMEs, and RuleFit) is proposed for NIDSs in the Internet of Things (IoT) domain [3]. These feature importance methods provide the most critical features that affect each decision either locally or globally. LIMEs and SHAPs are again used in IoT NIDSs, and the generated explanations show that the proposed model is aware of the protocol-specific features for the classification of each attack [18]. In addition to popularly used LIME and SHAP methods, partial dependence plots and individual conditional expectation plots have also been utilized [19]. A comprehensive survey regarding the utility of XAI for NIDSs in the IoT domain is presented by Moustafa et al. [20], and a number of similar feature-based explanation frameworks can be found in the literature [21,22,23]. Following along this direction, proposals of unifying evaluation benchmarks for feature attribution-based methods and the evaluation of the consistency among such methods have also been undertaken [24,25].
Although feature attribution methods have frequently been used to produce explanations, CF explanations have only been sparingly considered in the NIDS domain. As the earliest related attempt to use CF explanations, a method for generating adversarial examples is presented to provide explanations for misclassified network activities [26]. This closely aligns with the concept of CF explanations; however, the adversarial example approach lacks the provision of meaningful or actionable alternatives that human analysts can effectively interpret and implement. Moreover, their approach is limited as an analysis tool for known misclassified samples. The nearest CF explanations are used to provide counterexamples for the botnet domain generation algorithm detection task [27]. However, they do not conduct an in-depth analysis of counterfactual methods, instead focusing on a novel ‘second-opinion’ explanation method. Counterfactual inference (not explanations) has been used to identify different Distributed Denial of Service (DDoS) attack types [28]. There, counterfactual inference is used to determine the anomalous features that a specific DDoS attack type could have caused. In one study, different types of feature attribution methods and CF explanations are briefly compared against each other for IoT NIDSs [29]. However, they dismiss the diversity aspect and limit the analysis to one type of algorithm. We show that the diversity aspect will be helpful to provide multiple different explanations for an incoming attack data point. They mainly focus on using SHAP feature attribution values calculated using nearest CF explanation (CF-SHAP), which can be computationally inefficient as well. More recently, a novel approach for generating CF explanations based on an energy minimization concept has been proposed, with a focus on NIDSs in the IoT domain [30]. The method involves finding minimally perturbed instances around a local neighborhood of the classifier function, which is approximated by a Taylor expansion of the local decision boundary. They also conduct a robustness analysis of the proposed method. However, their work lacks a comparative analysis involving commonly used counterfactual evaluation metrics and methods. In contrast, this work provides a comparison between several publicly available counterfactual methods in terms of multiple evaluation metrics.
3. Counterfactual Explanations for Network Intrusion Detection
As observed in the existing literature, CF explanations can possess different properties or qualities, such as sparsity, validity, and plausibility. Hence, it is imperative to identify different qualities expected by these explanations for NIDSs. We propose a list of qualities that would be desired for NIDSs, along with initial justifications for them, as presented below.
- Efficiency—Modern cybersecurity operation centers are fast-paced and handle dynamic threat landscapes. Such an environment requires efficient explanation generation in order to quickly identify threats and design countermeasures.
- Validity—The generated explanations are required to be valid (reside in the intended target class), which would otherwise reduce the utility of generated explanations for defense measures.
- Diversity—Intrusion attacks generally comprise multiple attack queries (e.g., malformed HTTP requests in a Denial of Service (DoS) attack). Generating multiple explanations per query can offer different perspectives on attacks than one explanation per query. Later, we use this quality to aggregate and produce global rules using diverse explanations.
- Sparsity and plausibility—Sparsity ensures minimal changes to the original, and plausibility ensures that the generated CF explanations are realistic. These two qualities can provide human analysts with explanations that are easier to analyze and utilize for countermeasures against threats.
In the following section, we identify and describe types of existing CF explanation algorithms that fulfill these qualities. We identify certain existing types of CF explanation algorithms, such as ‘in-training’ methods, which are better suited for NIDSs [31]. Diffusion models have recently emerged as a more efficient and flexible type of generative model for tabular datasets compared to other prevalent generative models, such as variational auto-encoders and generative adversarial networks [12]. Hence, we utilize tabular diffusion models in our proposed CF explanation algorithm.
3.1. Counterfactual Algorithms for Intrusion Detection
Based on the recent literature on CF explanation methods, we identify that generative counterfactual methods—specifically the class of explanation generation algorithms named ‘in-training’ methods as potential candidates for the NIDS domain. These methods can efficiently sample plausible CF explanations from learned distributions while maintaining good validity [31,32]. Simply described, in-training methods refer to training the counterfactual generation algorithm with the knowledge of the decision boundary of the classifier model. VCNet [31] is one of the two in-training counterfactual methods available in the literature, where a conditional variational auto-encoder (CVAE) is trained in tandem with a classifier model. The other approach utilizes a simple feed-forward neural network instead of a CVAE [32]. However, this would not be scalable for complex datasets used in domains such as NIDSs.
More recently, diffusion models have been incorporated in tabular (structured) data domains due to their success in the image generation domain [33]. Structured Counterfactual Diffuser (SCD) is presented as a CF explanation method for tabular data and has shown promising results in efficiently generating diverse CF explanations for simple tabular datasets [34]. Inspired by this, we propose a novel improved version of a tabular diffusion-based CF explanation method for network intrusion detection by adapting the TabDDPM [12]—a method originally proposed for tabular data synthesis. This proposed, improved version handles the heterogeneous features in the tabular network intrusion datasets without transforming them into a continuous latent space using lookup embeddings compared to SCD [34], which empirically exhibits better performance. The proposed model is then further improved using ‘progressive distillation’ [35]. This distillation step primarily reduces the time to generate CF explanations by reducing the number of diffusion steps required. This distillation step yields improvements in the sparsity of the explanations as well. In this work, we reduce the number of diffusion steps by tenfold, which is explained further in the succeeding subsection (Section 3.2.2).
3.2. Guided Diffusion-Based Counterfactual Explanations for Network Intrusion Detection
SCD utilizes diffusion guidance to generate CF explanations. This approach is similar to in-training methods to a certain extent, where the knowledge of the decision boundary is used to train the CF explanation generation method. In contrast to SCD’s utilization of a shared embedding layer to encode both continuous and categorical types of features, we treat numerical and categorical features separately in our proposed model. This approach leads to better performance with our proposed approach, as presented later in the results (Section 5). We provide an overview of the theoretical background for the VCNet model and the guided diffusion model proposed in this work in the following section.
3.2.1. VCNet Model
VCNet model, an ‘in-training’ CF explanation algorithm, utilizes a conditional variational auto-encoder (CVAE) to learn the conditional data distributions during the training phase. The classifier (black-box model) is also trained alongside the CVAE, and the classifier’s prediction outputs are fed to the CVAE as a conditional signal. This feedback path is used for generating explanations during the inference stage. The CF explanation () for an input data instance x is generated using the trained CVAE with the help of the target label information. This is mathematically represented by Equation (1).
is the target label, and y denotes the original label. denotes the trained CVAE decoder, which takes a latent representation () conditioned on the target label as the input. This latent representation is the output of the trained CVAE encoder. denotes the output of the encoder , and z denotes the latent representation of the input x, obtained using the trained encoder. The latent representations are sampled from the encoder’s learned distribution (), which typically follows a normal distribution conditioned on x and y.
In our experiments, we replace the simple unit Gaussian prior of the CVAE with a mixture of Gaussians. This is due to our initial findings, which showed that a mixture of Gaussians can improve the validity of the produced explanations without hindering other performance metrics.
3.2.2. Guided Diffusion Models
Denoising diffusion probabilistic models (DDPMs) are built on the concept of diffusion—gradually (stepwise) destroying the structure of an input data distribution until it takes the form of a known prior distribution, such as the isotropic Gaussian [36]. This process is referred to as the forward diffusion process. During sampling, a reverse diffusion process replaces the forward diffusion process. This is executed by taking samples from the known prior distribution. In the context of CF explanations for tabular datasets, we propose using separate diffusion processes for numerical and categorical features, inspired by the TabDDPM [12]. These separate diffusion processes ensure that numerical features are diffused using Gaussian noise, while the categorical features are diffused using categorical noise. For a tabular dataset D with numerical features and categorical features, the forward diffusion process for numerical features is formulated as
Here, denotes the original numerical features of the input and , which is the noise sampled from a unit Gaussian distribution (). represents a scaling parameter, and represents the added noise to the original input, which yields the final diffused representation (). This mathematical expression analytically provides the diffused representation of the input at any timestep t () [36]. The number of diffusion timesteps is limited to a maximum value of T, which can be set appropriately. We set T to 2500 in our proposed models.
Forward diffusion process for categorical features [37] is represented as
where represents a multinomial distribution described by the parameters within the parentheses. is the categories of feature i and . The terms and are calculated similarly to the forward diffusion process for numerical features (Equation (2)). Unlike for numerical features, each categorical feature is treated separately (forward and reverse diffusion) following the algorithm of the TabDDPM [12].
During sampling (reverse diffusion), CF explanations are generated using the guidance from a classifier model, which was trained using the outputs of the trained diffusion model. The classifier guidance is in the form of a gradient value, which is calculated as the gradient of an explanation loss function (Equation (4)) with respect to the intermediate outputs of the diffusion model during the reverse diffusion process. In our method, we modify the counterfactual loss function proposed in SCD to a simpler version.
Here, t denotes the diffusion steps, which are followed in reverse order (from T to 0). The term inside the square brackets denotes the binary cross-entropy loss calculated with respect to the target prediction of the CF explanation. and x denote the target prediction of the explanation and the original query, respectively. A distance-measuring function is denoted by d, which penalizes explanations generated far away from the original query. L1-norm is used for d in our proposed method. The CF explanation generation process is carried out by first obtaining an instance randomly drawn from the known prior distribution—the unit Gaussian distribution. The original input is added to this noisy sample, creating a noisy version of the original input. Then, the reverse diffusion process is applied on this noisy sample using classifier guidance (Equation (5)) until an explanation is reached. In other words, is generated at the end of the reverse diffusion process. The classifier guidance in Equation (5) simply guides the intermediate representations () toward the explanation () using the scaled gradient of the loss function (Equation (4)) with respect to . The scalar value () can be set arbitrarily, or fine-tuned such that .
The proposed diffusion methods and SCD inherently provide the capability of obtaining multiple explanations during the generation process (‘diverse’ CF explanations). These diverse explanations are then utilized to generate global counterfactual rules, as shown later in results (Section 5). This ability of diffusion models stands out as they can efficiently generate multiple explanations at a time.
Afterward, we further refine the diffusion model through ‘progressive distillation’, which reduces the number of diffusion steps required to generate explanations [35]. We were able to reduce the number of steps by tenfold (2500 to 250), as shown in the results (Section 5) using progressive distillation. Although further reduction is possible, we adopted a tenfold reduction due to the trade-off observed between computational time and plausibility of explanations. Theoretical background regarding the distillation method is presented in Appendix A.
4. Methodology
We consider the downstream classification task as a binary classification task (benign vs. attack) and generate CF explanations for a randomly selected pool of attack queries from the test dataset during the explanation generation stage. An average of the evaluation metrics across 5 such random pools was obtained. This approach allowed fair comparison among different CF explanation methods within feasible resource and time constraints. These random pools were kept consistent for all the evaluated methods and the experiments. The variability of the results across 5 different attack pools was recorded in terms of the standard deviation. We ensured that the results were reproducible by using the same five attack pools across all experiments. Quantitative evaluations are carried out for increasing amounts of the random pool, and the maximum size of a random pool is limited to 4000 data points due to resource and time constraints. All the experiments were carried out on a system containing a single NVIDIA-RTX-2080 GPU with 12 GB of memory.
4.1. Datasets
Three popular network intrusion detection datasets are selected: UNSW-NB15 [38], CIC-IDS-2017 [39], and CIC-DDoS-2019 [40]. Each dataset comprises benign and attack queries, derived based on network flow data, and multiple categories of attack queries. The datasets are preprocessed by removing highly correlated features. This step ensures that the performance of the black-box classifier is improved, and the generated explanations are more compact. A ‘K-Bins Discretizer’ is used for scaling the numerical features for the SCD model (following the original work), and ‘Quantile Transformer’ for the rest of the models. This was selected following the approach used in the TabDDPM. A One-Hot Encoder is used to preprocess the categorical features. An overview of the dataset statistics after preprocessing is provided in Table 1. We use the dataset files of these intrusion detection datasets publicly available on Kaggle (https://www.kaggle.com/dhoogla/datasets, accessed on 20 January 2025).

Table 1.
Summary of the three datasets used in experiments.
4.2. Baseline Counterfactual Methods
We use publicly available implementations of Wachter [6], DiCE [41], FACE [42], and CCHVAE [43]. These implementations were adopted from the CF explanation benchmarking tool ‘CARLA’ [44]. VCNet and SCD models were implemented on our own as there were no publicly available implementations. Due to the fact that the CF explanation literature is still at its inception for the NIDS domain, we take the aforementioned generic CF explanation methods from other domains (e.g., finance) in our evaluations. As our primary focus is on evaluating the performance of CF explanations, we exclude other feature attribution methods from our quantitative evaluations. A feed-forward neural network was selected as the black-box classifier model for all the experiments. The same architecture was used for the black-box classifier models across all the CF explanation generation methods. For VCNet, we stick with a slightly different architecture (i.e., different hidden layers and layer sizes) based on our initial experimental runs. Additional details about the black-box classifiers are provided in Appendix B.
4.3. Evaluation Metrics
We pick the following evaluation metrics to evaluate the performance of generated explanations by each method: k-validity, 1-validity, sparsity, Local Outlier Factor (LOF), and time to generate. These evaluation metrics were selected based on the prior work in the counterfactual recourse domain [44,45,46] and also considering requirements such as efficiency for the NIDS domain. k-validity measures the average number of valid explanations generated from a pool of generated explanations (denoted by k (e.g., k = 10)) for an attack query. This metric is then only applicable to CF explanation methods that are capable of generating multiple (diverse) explanations (further elaborated on in results (Section 5)). Further, 1-validity measures the ability of a method to generate at least one valid explanation for each of the original queries. This is also calculated as an average across the dataset. Sparsity measures the average number of feature changes (L0 norm), and LOF measures the plausibility of the generated explanations. Time to generate measures either the number of seconds taken to generate one explanation or a group of explanations (if it is allowed by the CF explanation method).
5. Results
Table 2 shows the results obtained for the UNSW-NB15 dataset. The Acc./F1 column depicts the performance of the black-box classifier model for each CF explanation method. We omit the FACE method results for the other two datasets, as well as larger attack pools, as it took a long time (>5 min per explanation) to generate explanations for an attack pool of 1000 instances from the UNSW-NB15 dataset. The k-validity values are omitted for FACE and VCNet as they are unable to generate multiple (diverse) explanations by design. CCHVAE is also limited to generating a single explanation for a query. Although the authors of CCHVAE claim that it can be extended to achieve diversity in the generated explanations [43], we were unable to test it since that was not implemented in CARLA. Similarly, Table 3 and Table 4 show the results for the CIC-DDoS-2019 and CIC-IDS-2017 datasets. The line plots in Figure 1 depict the performance of the same metrics on increasing sizes of attack pools. The results from CCHVAE for the last two datasets (Table 3 and Table 4) were also omitted as it failed to return explanations for the attack queries within a reasonable amount of time. The proposed methods (TabDiff and TabDiff-distill.) consistently provide explanations with high validity across all the datasets. The VCNet model provides the best efficiency (in terms of the time to generate explanations). The distilled version of the diffusion model (TabDiff-distill.) provides the second-best efficiency across the three datasets. However, VCNet lags in terms of sparsity, as observed for the UNSW-NB15 dataset, in addition to being limited to a single explanation per query. This is clearly shown in Figure 2a, where TabDiff-distill. shows better sparsity, and in Table 2, Table 3 and Table 4, where the VCNet model does not carry k-validity values. Moreover, the proposed methods produce plausible explanations, as reflected by the comparatively low log-LOF values. The scatter plots in Figure 2 illustrate the performance differences regarding the CF explanation methods from Table 2, Table 3 and Table 4 when the sparsity, efficiency, and validity metrics are combined. Table 5 shows a few samples of the explanations generated for the CIC-DDoS-2019 dataset.

Table 2.
Results for UNSW-NB15 dataset with 1000 attack queries. The arrow directions alongside each metric denote the preferred direction (low/high) for the metric to behave in order to obtain better explanations. The proposed methods are in bold font. Each evaluated metric contains its standard deviation (std.) across the 5 multiple runs (, in small font) alongside its mean value. Zero std. values denote that the evaluated metric is consistent across the 5 attack pools. For example, validity of the proposed method TabDiff-distill. is consistently 1 across all the attack pools. stands for std. . The proposed methods provide plausible CF explanations with high validity, efficiency, and sparsity.

Table 3.
Results for CIC-DDoS-2019 dataset with 1000 attack queries. Each evaluated metric contains its standard deviation (std.) across the 5 multiple runs (, in small font). The proposed methods provide plausible CF explanations with high validity, efficiency, and sparsity. While VCNet shows comparably good performance by providing sparse and valid explanations, it fails to do so across all the datasets consistently.

Table 4.
Results for CIC-IDS-2017 dataset with 1000 attack queries. Each evaluated metric contains its standard deviation (std.) across the 5 multiple runs (, in small font). TabDiff-distill. provides highly valid and efficient CF explanations. Although maximally sparse results with high validity are provided by DiCE, this behavior was not consistent across other datasets. The values of the sparsity metric of TabDiff models are similar to other datasets when considered as a ratio to the total number of features.
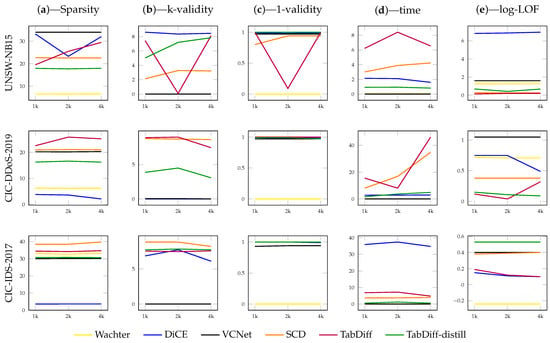
Figure 1.
Comparison of the evaluated metrics of the CF explanations with increasing attack pool sizes. Each row of figures depicts the results for UNSW-NB15, CIC-DDoS-2019, and CIC-IDS-2017, respectively. The x-axis of each plot corresponds to the size of the attack pool (1k, 2k, and 4k). Each column of figures is dedicated to each of the evaluation metrics, and their values are represented in the y-axis in each plot. The preferred direction of each evaluation metric is the same direction indicated by arrows in Table 2, Table 3 and Table 4. Simple methods such as Wachter remain non-performative, while generative methods, specifically the proposed method (TabDiff-distill.), show consistent performance in terms of validity, plausibility, and efficiency.
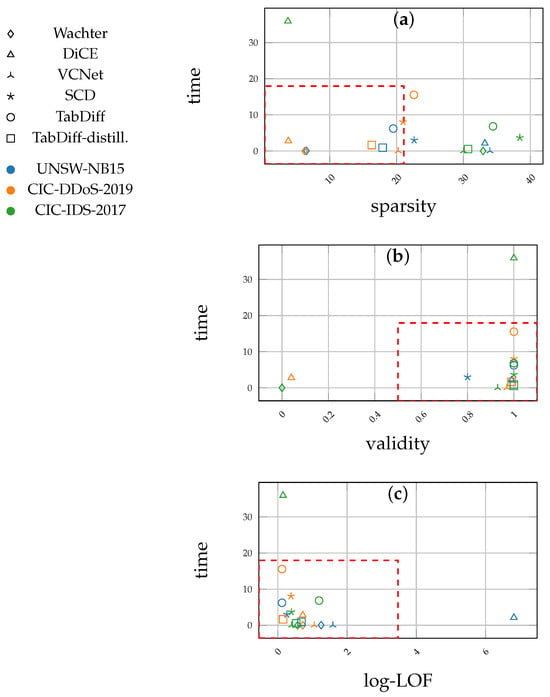
Figure 2.
Scatter plots representing the behavior of selected evaluation metrics against time: sparsity–time (a), validity–time (b), and log-LOF–time (c) (extracted from Table 2, Table 3 and Table 4). For each plot, points inside the rectangular box marked by red dashed lines are preferred in terms of performance ((a) low left corner; (b) low right corner; (c) low left corner). The shapes refer to each CF explanation algorithm tested, and the colors denote each dataset. Proposed methods, especially TabDiff-distill, fall close to these regions. Shapes = CF explanation methods; colors = datasets.

Table 5.
Combined features and predictions for generated CF explanations.
Global Counterfactual Rules
The above results present a holistic view of the generated CF explanations across different methods in terms of quantitative metrics. We then look at how these explanations can be utilized for identifying and drawing countermeasures against attacks. A trivial approach would be to compare the feature values of the queries and their respective CF explanations. As an alternative approach, we propose a simple counterfactual rule approach. First, we extract a set of specific attack data points from the training set and create a new version of the original training set without the specific attack. This step ensures that the specific attack was not seen during the model training phase. These extracted attack data points can be regarded as an unknown (or ‘zero-day’) attack.
As example use cases, we consider two attacks. The first one is the ‘Analysis’ attack from the UNSW-NB15 dataset, and the second one is the ‘LDAP DDoS’ attack from the CIC-DDoS-2019 dataset (these two attacks were picked based on the performance of the classifier model for them). We first evaluate the performance of the black-box classifier on the unseen attack to confirm that it is at an acceptable level (for the ‘Analysis’ attack, we obtain an accuracy of 81.81%). Explanations are then generated for this specific attack’s test set using the proposed diffusion method. Finally, global counterfactual rules are extracted using a simple decision tree (the algorithm for extracting the rules is presented as pseudo-code in Algorithm 1). A simple decision tree is employed regarding the benign data points (CF explanations generated) and their respective attack queries as inputs. The decision tree is created with default parameters and with no restrictions on the tree depth.
A few such extracted rules for the ‘Analysis’ attack are presented below. Each rule provides a set of value bounds (appear with equality signs) for a set of essential features picked by the rule extraction algorithm. Each of these value bounds combined with an ‘AND’ operator defines the benign data points that are closest to the group of ‘Analysis’ attack data points. For example, data points that have a connection state value (state) less than 2, protocol code (proto) between 46 and 0, and destination jitter (djit) less than or equal to 91,402.99 should be benign data points that are the closest to the ‘Analysis’ attack (as per the first rule provided below).
- ‘state < 2’, ‘proto ≤ 46’, ‘djit ≤ 91,402.99’, ‘proto > 0’
- ‘state ≥ 1’, ‘trans_depth ≤ 1.0’, ‘dload ≤ 2,579,956.5’, ‘state < 7’, ‘proto > 25’, ‘proto < 27’
Each rule defines bounds on a set of important intrusion-related features, filtering benign data from attack data [38]. We further compare these rules against rules obtained by replacing the CF explanations with randomly sampled benign data from the training dataset (Figure 3b). Evidently, the rules presented by the training data can differ in terms of features compared to the rules derived using CF explanations. In other words, rules derived using training data pick common features across different attacks, such as ‘response_body_len’ and ‘is_ftp_login’, which can be relevant to different types of attacks.
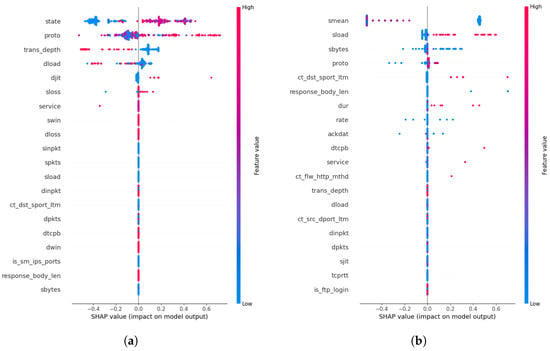
Figure 3.
SHAP feature importance plot obtained using generated (a) CF explanations, and (b) using training data for the ‘Analysis’ attack. The SHAP values show a ranking of how each feature contributes towards the average model prediction across the dataset. For example, certain feature values in the ‘state’ feature negatively contribute to the model prediction (blue), and positively contribute (red) to the average model prediction.
- dur ≤ 15.34, sload ≤ 72,363,628.0, response_body_len ≤ 141.5, ct_flw_http_mthd ≤ 2.5, dtcpb ≤ 4,201,986,176.0, ct_dst_sport_ltm ≤ 3.5, is_ftp_login ≤ 2.5
| Algorithm 1 Simple Rule Extraction |
function rule extraction()
end function |
The rules extracted from the CF explanations, followed by the rules extracted from training data for the ‘LDAP DDoS’ attack (CIC-DDoS-2019 dataset), are shown below. With CF explanations,
- ‘Fwd Header Length’ ≤ 205.00, ‘ACK Flag Count’ > 0, ‘Protocol’ ≤ 11, ‘CWE Flag Count’ < 1, ‘Protocol’ > 3, ‘Idle Std’ ≤ 31137002.0
- ‘Fwd Header Length’ ≤ 205.00, ‘ACK Flag Count’ > 0.5, ‘Protocol’ ≤ 11, ‘CWE Flag Count’ > 0, ‘RST Flag Count’ < 1, ‘Fwd PSH Flags’ > 0, ‘SYN Flag Count’ > 0’
With training data (only a single rule is available),
- ‘Flow IAT Mean’ > 0.625, ‘Fwd Packet Length Min’ ≤ 1148.498’
Moreover, we conduct a simple evaluation to assess the capability of the derived global rules to act as countermeasures against attacks using the CIC-DDoS-2019 dataset. In this experiment, the extracted rules are applied to the datasets: the separated attack set (LDAP DDoS) and the test set (consisting of benign data and other attack data, which is not LDAP DDoS). The percentages of the remaining data points after this filtration step are presented in Table 6.

Table 6.
Using global rules as countermeasures. The filtered dataset refers to the dataset that was filtered using the extracted rules shown in the ‘Rules’ column. The counterfactual-based rules (associated with CF) filter the unseen attack data points more efficiently than rules extracted using actual training data (associated with Tr). This demonstrates the actionability of the CF explanations and the rules derived.
6. Discussion
The results reveal that the proposed diffusion-based methods, specifically the TabDiff-distill. version, offer the best CF explanations in terms of sparsity, plausibility, validity, and efficiency for the UNSW-NB15 and CIC-DDoS-2019 datasets. It can also be observed that TabDiff-distill. trades off the improvements in sparsity and efficiency from the vanilla TabDiff model with the anomaly score. This behavior can be attributed to the trade-off between generation quality and efficiency (by reducing the number of diffusion steps) of progressive distillation [35]. The DiCE method provides the best explanation in terms of sparsity for the CIC-IDS-2017 dataset with good plausibility. This behavior contradicts its behavior for the other two datasets, which return explanations with high anomaly scores (high log-LOF). DiCE returning anomalous explanations can be expected because of the nature of the algorithm, which utilizes random perturbations. The behavior of CIC-IDS-2017 can be attributed to DiCE’s ability to generate CF explanations that are close to the data manifold and with minimal modifications through random perturbations. However, this behavior is not consistent across all the datasets.
Although the performance is not consistent, VCNet provides plausible and valid CF explanations for two datasets. The inconsistent behavior can be attributed to the lack of an explicit optimization method available for VCNet (i.e., VCNet resorts to conditional sampling from the CVAE model but does not perform any optimization in the latent space). Generative methods such as VCNet and TabDiff tend to generate explanations in the form of real data samples, which is evident from their plausibility and the nature of their sparsity, while random perturbation methods aim at generating explanations with minimal modifications to the original. These random perturbations may not be consistently successful in all instances, as observed in the UNSW-NB15 and CIC-DDoS-2019 datasets. On the other hand, while simple algorithms such as Wachter are unsuccessful at producing explanations, more advanced methods such as FACE and CCHVAE also fail to do so. This raises the concern that not all available CF explanation methods that are primarily focused on algorithmic recourse would be suitable for a complex domain such as NIDSs.
It was observed that the global counterfactual rules extracted from the training data contain features such as ‘Flow IAT Mean’ and ‘Fwd Packet Length Min’, which are general to all types of DDoS attacks [40], whereas rules extracted from CF explanations contain protocol-specific rules. The difference between the manner of deriving rules (i.e., using CF explanations versus training data) is more pronounced for the ‘LDAP DDoS’ attack. As seen in Table 5, the diversity of the generated explanations provides different explanations that act as different viewpoints. For example, changing ‘CWE Flag Count’ to 1 or keeping it 0 and increasing ‘Fwd Packet Length Std’ or keeping it the same are two options when generating CF explanations (in rows 2 and 4). In addition, these global rules can be generated even with a small number of attack queries since the diversity of CF explanations provides multiple benign samples for each attack query.
As seen in Table 6, the rules extracted from the CF explanations filter the unseen attack data points more efficiently than (0% vs. 4.9%) the only rule available with the training data. It is also imperative that the extracted rules function well on other types of attack data points and do not disrupt benign data. It can be observed that the counterfactual-based rules show this capability, similar to the rules obtained from the benign data.
The global rules derived from CF explanations provide further insights into the nature of the ‘Analysis’ attack. Features such as ‘djit’ (destination jitter), ‘dload’ (destination load), and ‘trans_depth’ (transaction depth) can be abnormal for the ‘Analysis’ attack as an attacker sends probing packets to target devices with high variations and abrupt connections (e.g., prematurely ending an HTTP connection). Moreover, the proposed technique of obtaining such rules using CF explanations eliminates the need to access the training data to derive explanations and rules. In addition, using training data to derive such rules can present more generic rules, whereas CF explanation-based rules can be more specific. This can be observed from the features present in the training data-based rules, which contain ‘response_body_len’ (length of the response body), potentially more common to different types of attacks. Another example is ‘is_ftp_login’ (FTP login attempt), which can be common to other attack types. However, one shortcoming of this rule derivation is that the supervised approach requires an acceptable classifier performance of the black-box classifier on unseen attacks to derive valid explanations and rules. A straightforward utility of the derived rules provides actionable explanations that can act as countermeasures against incoming attacks by filtering out packets based on the identified features and their value bounds. We only evaluate the efficacy of the filtering capability of the rules using a simple experiment (Table 6). The results of this experiment show that global rules derived from CF explanations are more specialized toward the selected unseen attack data points, and also efficient on benign data points and other types of attack data points. Some counterfactual-based rules might slightly disrupt the benign data and leave a small amount of other attack data points behind (e.g., -1 in Table 6). This behavior is expected for some rules as they are more specialized toward the unseen attack set and not generalized to all the attack types and benign data. However, the availability of multiple rules can provide a workaround by allowing the user to select the most effective rule as needed.
Moreover, we compare the SHAP plots obtained for the Analysis attack and the features highlighted by the corresponding global counterfactual rules (Figure 3a,b). It is observed that the derived global rules can provide value bounds that can filter benign data from attack data while also being consistent with the important features identified by the SHAP explanations. This can be noted as an advantage of CF explanations, where users can obtain actionable explanations from CF explanations instead of being limited to feature importances provided by SHAPs. The SHAP plot and the corresponding rules for LDAP DDoS attacks show that the features identified using the CF explanations are more informative than the rules derived using training data (Figure 4a,b).
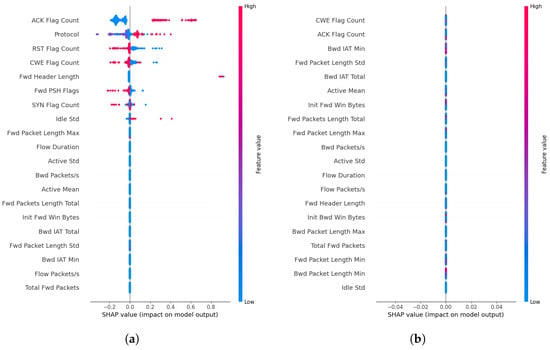
Figure 4.
SHAP feature importance plot obtained (a) using generated CF explanation, and (b) using training data for the ‘DDoS LDAP’ attack.
Although the proposed methodologies are based on binary classification (which is prominent in NIDSs), they can also be extended to a multiclass classification scenario given datasets of sufficient quality and quantity that facilitate supervised learning of multiple classes of intrusions. In a multiclass setting, the CF explanations would be generated toward a desired target class (or a predefined set of target classes) for each predicted data point, allowing human analysts to gain insights into important features, potential countermeasures, and even how novel attacks can be similar to known attacks.
7. Conclusions
We carried out an empirical evaluation of several existing CF explanation algorithms for NIDSs and proposed novel diffusion-based CF explanation generation approaches. The proposed methods can efficiently generate valid, diverse, and plausible CF explanations for network intrusion datasets. In addition, we presented a simple approach to obtain global counterfactual rules that can potentially act as countermeasures against incoming intrusion attacks. We anticipate that this work will stimulate further discussions regarding applications of CF explanations within the domain of NIDSs, which is largely overlooked at present. Evaluating the efficacy of derived global rules in different practical scenarios, evaluating the proposed methods on other NIDS datasets, and extending the proposed methodologies to multiclass classification scenarios remain as future work. In addition, a comprehensive comparison of CF explanations with existing feature attribution methods in terms of assessing their utility and robustness against adversarial attacks is a promising future research avenue.
Author Contributions
Conceptualization, V.G.; methodology, V.G.; software, V.G.; validation, V.G.; formal analysis, V.G.; writing—original draft preparation, V.G.; conceptualization, J.S.; writing—review and editing, J.S.; supervision, J.S.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Natural Sciences and Engineering Research Council of Canada (NSERC) (grant number: RGPIN-2017-04755).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data derived from public domain resources. https://www.kaggle.com/dhoogla/datasets, accessed on 20 January 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NIDS | Network Intrusion Detection System |
| XAI | Explainable Artificial Intelligence |
| CF | Counterfactual |
| CVAE | Conditional Variational Auto-Encoder |
| DDPM | Denoising Diffusion Probabilistic Model |
Appendix A. Theoretical Details
Progressive Distillation of DDPM
We adopt the progressive distillation method proposed by Salimans et al. [35]. As per their findings, we reformulate the conventional diffusion processes in DDPM with ‘v-diffusion’ first. v-diffusion is a angular reparameterization of the original diffusion process and can be represented mathematically as in Equation (A1).
where
Then, the goal of the diffusion model becomes approximating the v-value (Equation (A3)).
This reformulation is carried out as it has been shown that progressive distillation technique works better with v-diffusion [35]. The distillation starts with the original diffusion model (with 2500 steps) and iteratively attempts to approximate 2 consecutive diffusion steps with 1 step. This process is carried out until the student model (distilled model) can approximate 2500 steps with 250 steps.
Appendix B. Details of the Classifier Models and Other Hyperparameters
Black-Box Classifier
The black-box classifier (feed-forward neural network) contains the below architecture and hyperparameter choices. A different number of epochs was used for the CIC-IDS-2017 dataset, which is indicated in Table A1.

Table A1.
Architecture and the hyperparameters used for the black-box classifier models.
Table A1.
Architecture and the hyperparameters used for the black-box classifier models.
| Parameter | Value |
|---|---|
| No. of Hidden Units | 1,286,432 |
| Optimizer and lr. | Adam, |
| Epochs | 600, (300—CIC-IDS-2017) |
References
- Gamage, S.; Samarabandu, J. Deep learning methods in network intrusion detection: A survey and an objective comparison. J. Netw. Comput. Appl. 2020, 169, 102767. [Google Scholar] [CrossRef]
- Chinnasamy, R.; Subramanian, M.; Easwaramoorthy, S.V.; Cho, J. Deep learning-driven methods for network-based intrusion detection systems: A systematic review. ICT Express 2025, 11, 181–215. [Google Scholar] [CrossRef]
- Houda, Z.A.E.; Brik, B.; Khoukhi, L. “Why Should I Trust Your IDS?”: An Explainable Deep Learning Framework for Intrusion Detection Systems in Internet of Things Networks. IEEE Open J. Commun. Soc. 2022, 3, 1164–1176. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Benzaid, C.; Taleb, T. AI-Driven Zero Touch Network and Service Management in 5G and Beyond: Challenges and Research Directions. IEEE Netw. 2020, 34, 186–194. [Google Scholar] [CrossRef]
- Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual Explanations without Opening the Black Box: Automated Decisions and the GDPR. arXiv 2018, arXiv:1711.00399. [Google Scholar] [CrossRef]
- Guidotti, R. Counterfactual explanations and how to find them: Literature review and benchmarking. Data Min. Knowl. Discov. 2022, 38, 2770–2824. [Google Scholar] [CrossRef]
- Verma, S.; Dickerson, J.P.; Hines, K. Counterfactual Explanations for Machine Learning: A Review. arXiv 2020, arXiv:2010.10596. [Google Scholar]
- Stepin, I.; Alonso, J.M.; Catala, A.; Pereira-Farina, M. A Survey of Contrastive and Counterfactual Explanation Generation Methods for Explainable Artificial Intelligence. IEEE Access 2021, 9, 11974–12001. [Google Scholar] [CrossRef]
- Pawelczyk, M.; Broelemann, K.; Kasneci, G. On Counterfactual Explanations under Predictive Multiplicity. In Proceedings of the 36th Conference on Uncertainty in Artificial Intelligence (UAI), PMLR, Virtual, 3–6 August 2020; pp. 809–818. [Google Scholar]
- Gupta, V.; Nokhiz, P.; Roy, C.D.; Venkatasubramanian, S. Equalizing Recourse across Groups. arXiv 2019, arXiv:1909.03166. [Google Scholar] [CrossRef]
- Kotelnikov, A.; Baranchuk, D.; Rubachev, I.; Babenko, A. TabDDPM: Modelling Tabular Data with Diffusion Models. In Proceedings of the 40th International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., Scarlett, J., Eds.; Volume 202, pp. 17564–17579. [Google Scholar]
- Chou, Y.L.; Moreira, C.; Bruza, P.; Ouyang, C.; Jorge, J. Counterfactuals and causability in explainable artificial intelligence: Theory, algorithms, and applications. Inf. Fusion 2022, 81, 59–83. [Google Scholar] [CrossRef]
- Leemann, T.; Pawelczyk, M.; Prenkaj, B.; Kasneci, G. Towards Non-Adversarial Algorithmic Recourse. arXiv 2024, arXiv:2403.10330. [Google Scholar] [CrossRef]
- Ferry, J.; Aïvodji, U.; Gambs, S.; Huguet, M.J.; Siala, M. Taming the Triangle: On the Interplays Between Fairness, Interpretability, and Privacy in Machine Learning. Comput. Intell. 2025, 41, e70113. [Google Scholar] [CrossRef]
- General Data Protection Regulation (GDPR)–Legal Text—gdpr-info.eu. Available online: https://gdpr-info.eu/ (accessed on 16 August 2025).
- Zhang, Z.; Hamadi, H.A.; Damiani, E.; Yeun, C.Y.; Taher, F. Explainable Artificial Intelligence Applications in Cyber Security: State-of-the-Art in Research. IEEE Access 2022, 10, 93104–93139. [Google Scholar] [CrossRef]
- Krishnan, D.; Singh, S.; Sugumaran, V. Explainable AI for Zero-Day Attack Detection in IoT Networks Using Attention Fusion Model. Discov. Internet Things 2025, 5, 83. [Google Scholar] [CrossRef]
- Keshk, M.; Koroniotis, N.; Pham, N.; Moustafa, N.; Turnbull, B.; Zomaya, A.Y. An explainable deep learning-enabled intrusion detection framework in IoT networks. Inf. Sci. 2023, 639, 119000. [Google Scholar] [CrossRef]
- Moustafa, N.; Koroniotis, N.; Keshk, M.; Zomaya, A.Y.; Tari, Z. Explainable Intrusion Detection for Cyber Defences in the Internet of Things: Opportunities and Solutions. IEEE Commun. Surv. Tutor. 2023, 25, 1775–1807. [Google Scholar] [CrossRef]
- Barnard, P.; Marchetti, N.; DaSilva, L.A. Robust Network Intrusion Detection Through Explainable Artificial Intelligence (XAI). IEEE Netw. Lett. 2022, 4, 167–171. [Google Scholar] [CrossRef]
- Kalakoti, R.; Vaarandi, R.; Bahsi, H.; Nõmm, S. Evaluating Explainable AI for Deep Learning-Based Network Intrusion Detection System Alert Classification. arXiv 2025, arXiv:2506.07882. [Google Scholar] [CrossRef]
- Naif Alatawi, M. Enhancing Intrusion Detection Systems with Advanced Machine Learning Techniques: An Ensemble and Explainable Artificial Intelligence (AI) Approach. Secur. Priv. 2025, 8, e496. [Google Scholar] [CrossRef]
- Arreche, O.; Guntur, T.R.; Roberts, J.W.; Abdallah, M. E-XAI: Evaluating Black-Box Explainable AI Frameworks for Network Intrusion Detection. IEEE Access 2024, 12, 23954–23988. [Google Scholar] [CrossRef]
- Dietz, K.; Hajizadeh, M.; Schleicher, J.; Wehner, N.; Geißler, S.; Casas, P.; Seufert, M.; Hoßfeld, T. Agree to Disagree: Exploring Consensus of XAI Methods for ML-based NIDS. In Proceedings of the 2024 20th International Conference on Network and Service Management (CNSM), Prague, Czech Republic, 28–31 October 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Marino, D.L.; Wickramasinghe, C.S.; Manic, M. An Adversarial Approach for Explainable AI in Intrusion Detection Systems. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 3237–3243. [Google Scholar] [CrossRef]
- Suryotrisongko, H.; Musashi, Y.; Tsuneda, A.; Sugitani, K. Robust Botnet DGA Detection: Blending XAI and OSINT for Cyber Threat Intelligence Sharing. IEEE Access 2022, 10, 34613–34624. [Google Scholar] [CrossRef]
- Zeng, Z.; Peng, W.; Zeng, D.; Zeng, C.; Chen, Y. Intrusion detection framework based on causal reasoning for DDoS. J. Inf. Secur. Appl. 2022, 65, 103124. [Google Scholar] [CrossRef]
- Gyawali, S.; Huang, J.; Jiang, Y. Leveraging Explainable AI for Actionable Insights in IoT Intrusion Detection. In Proceedings of the 2024 19th Annual System of Systems Engineering Conference (SoSE), Tacoma, WA, USA, 23–26 June 2024; pp. 92–97. [Google Scholar] [CrossRef]
- Evangelatos, S.; Veroni, E.; Efthymiou, V.; Nikolopoulos, C.; Papadopoulos, G.T.; Sarigiannidis, P. Exploring Energy Landscapes for Minimal Counterfactual Explanations: Applications in Cybersecurity and Beyond. arXiv 2025, arXiv:2503.18185. [Google Scholar] [CrossRef]
- Guyomard, V.; Fessant, F.; Guyet, T.; Bouadi, T.; Termier, A. VCNet: A Self-explaining Model for Realistic Counterfactual Generation. In Proceedings of the Machine Learning and Knowledge Discovery in Databases, Grenoble, France, 19–23 September 2022; Amini, M.R., Canu, S., Fischer, A., Guns, T., Kralj Novak, P., Tsoumakas, G., Eds.; Springer: Cham, Switzerland, 2023; pp. 437–453. [Google Scholar]
- Guo, H.; Nguyen, T.H.; Yadav, A. CounterNet: End-to-End Training of Prediction Aware Counterfactual Explanations. In Proceedings of the KDD ’23: 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 577–589. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion Models Beat GANs on Image Synthesis. arXiv 2021, arXiv:2105.05233. [Google Scholar] [CrossRef]
- Madaan, N.; Bedathur, S. Navigating the Structured What-If Spaces: Counterfactual Generation via Structured Diffusion. arXiv 2023, arXiv:2312.13616. [Google Scholar] [CrossRef]
- Salimans, T.; Ho, J. Progressive Distillation for Fast Sampling of Diffusion Models. In Proceedings of the The Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, 25–29 April 2022. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H.T., Eds.; Curran Associates, Inc.: New York, NY, USA, 2020; Volume 33, pp. 6840–6851. [Google Scholar]
- Hoogeboom, E.; Nielsen, D.; Jaini, P.; Forré, P.; Welling, M. Argmax Flows and Multinomial Diffusion: Learning Categorical Distributions. In Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P.S., Vaughan, J.W., Eds.; Curran Associates, Inc.: New York, NY, USA, 2021; Volume 34, pp. 12454–12465. [Google Scholar]
- Moustafa, N.; Slay, J. UNSW-NB15: A comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In Proceedings of the 2015 Military Communications and Information Systems Conference (MilCIS), Canberra, Australia, 10–12 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sharafaldin, I.; Habibi Lashkari, A.; Ghorbani, A.A. Toward Generating a New Intrusion Detection Dataset and Intrusion Traffic Characterization. In Proceedings of the 4th International Conference on Information Systems Security and Privacy, Funchal, Madeira, Portugal, 22–24 January 2018; pp. 108–116. [Google Scholar] [CrossRef]
- Sharafaldin, I.; Lashkari, A.H.; Hakak, S.; Ghorbani, A.A. Developing Realistic Distributed Denial of Service (DDoS) Attack Dataset and Taxonomy. In Proceedings of the 2019 International Carnahan Conference on Security Technology (ICCST), Chennai, India, 1–3 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Mothilal, R.K.; Sharma, A.; Tan, C. Explaining Machine Learning Classifiers through Diverse Counterfactual Explanations. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 607–617. [Google Scholar] [CrossRef]
- Poyiadzi, R.; Sokol, K.; Santos-Rodriguez, R.; De Bie, T.; Flach, P. FACE: Feasible and Actionable Counterfactual Explanations. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, Barcelona, Spain, 27–30 January 2020; pp. 344–350. [Google Scholar] [CrossRef]
- Pawelczyk, M.; Broelemann, K.; Kasneci, G. Learning Model-Agnostic Counterfactual Explanations for Tabular Data. In Proceedings of the WWW ’20: The Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 3126–3132. [Google Scholar] [CrossRef]
- Pawelczyk, M.; Bielawski, S.; den Heuvel, J.V.; Richter, T.; Kasneci, G. CARLA: A Python Library to Benchmark Algorithmic Recourse and Counterfactual Explanation Algorithms. In Proceedings of the Thirty-Fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 1), Virtual, 6–14 December 2021. [Google Scholar]
- Moreira, C.; Chou, Y.L.; Hsieh, C.; Ouyang, C.; Pereira, J.; Jorge, J. Benchmarking Instance-Centric Counterfactual Algorithms for XAI: From White Box to Black Box. Acm Comput. Surv. 2024, 57, 145. [Google Scholar] [CrossRef]
- Bayrak, B.; Bach, K. Evaluation of Instance-Based Explanations: An In-Depth Analysis of Counterfactual Evaluation Metrics, Challenges, and the CEval Toolkit. IEEE Access 2024, 12, 137683–137695. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).