Cotton Yield Map Prediction Using Sentinel-2 Satellite Imagery in the Brazilian Cerrado Production System
Abstract
1. Introduction
2. Materials and Methods
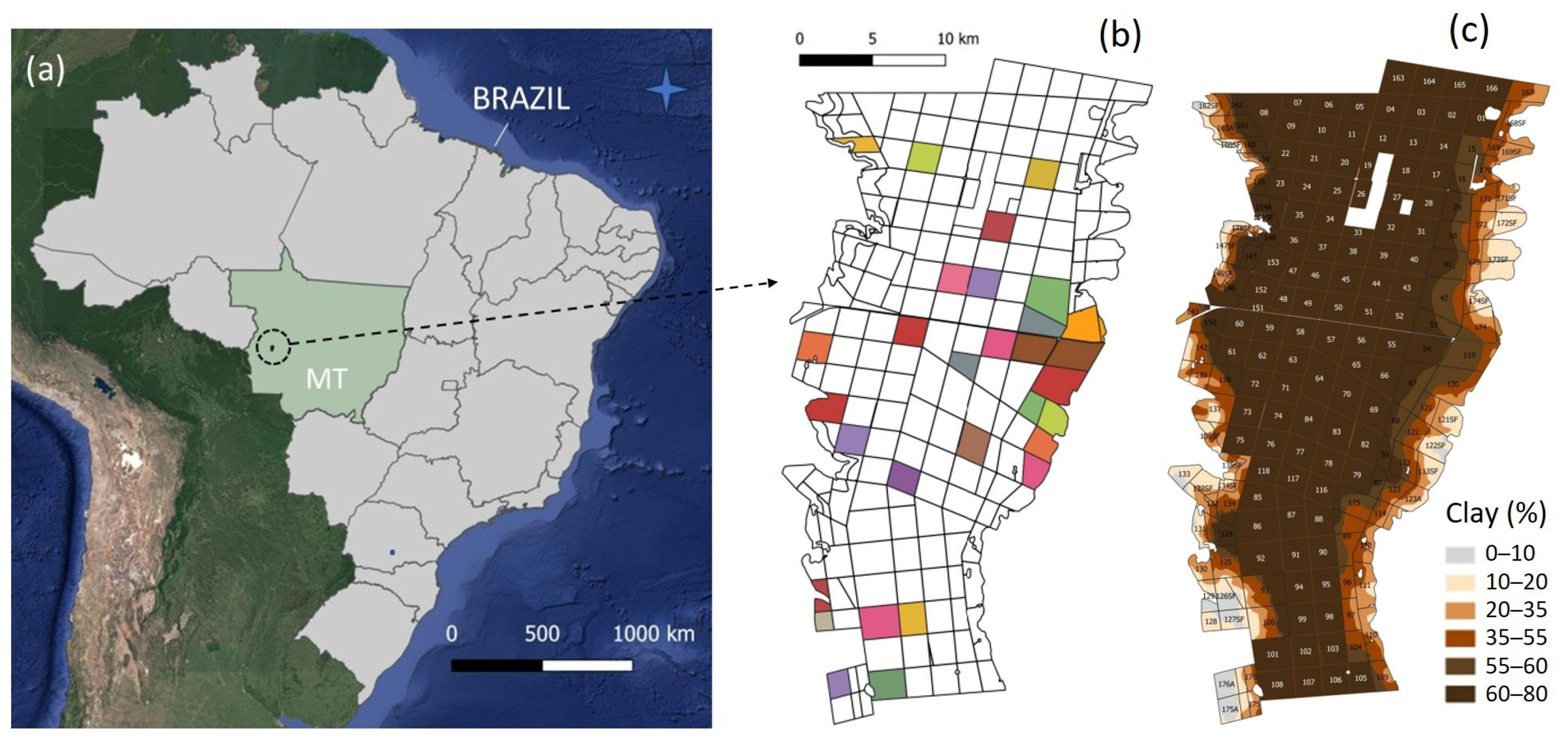
2.1. Experimental Area
2.2. Satellite Data and Processing
2.3. Yield Mapping Data from Combine Harvesters
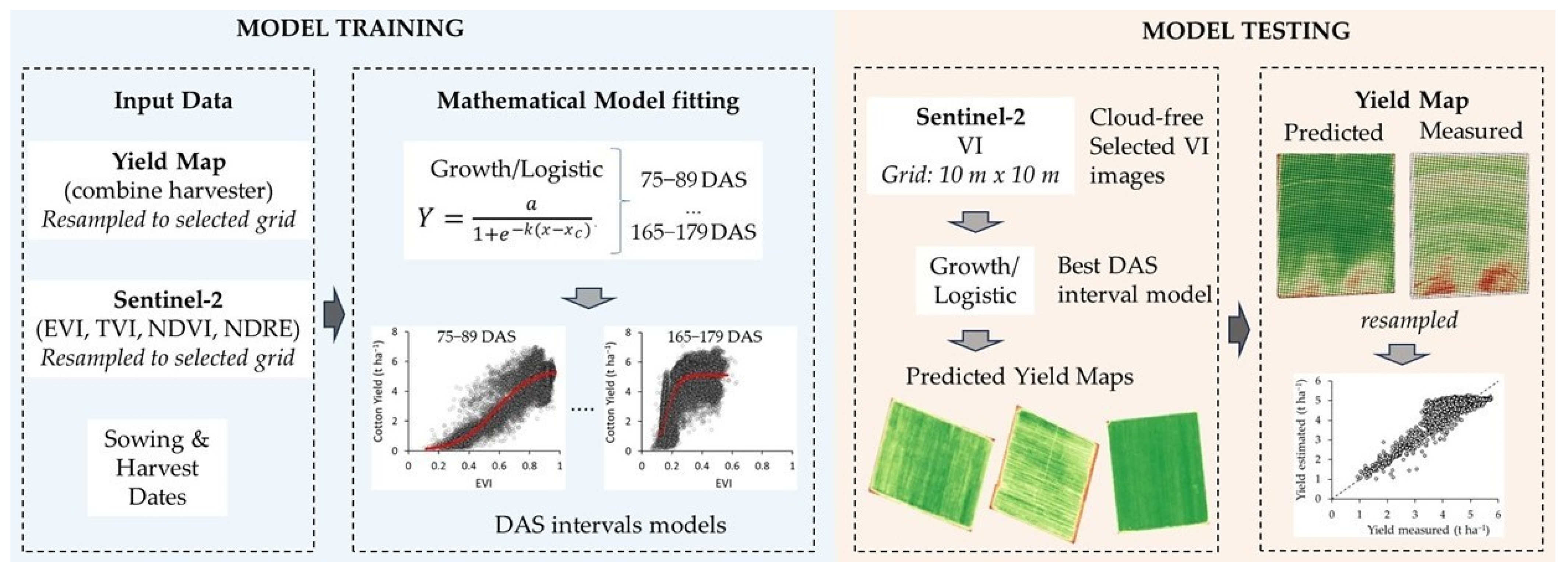
2.4. Regression Modeling Approach
3. Results and Discussion
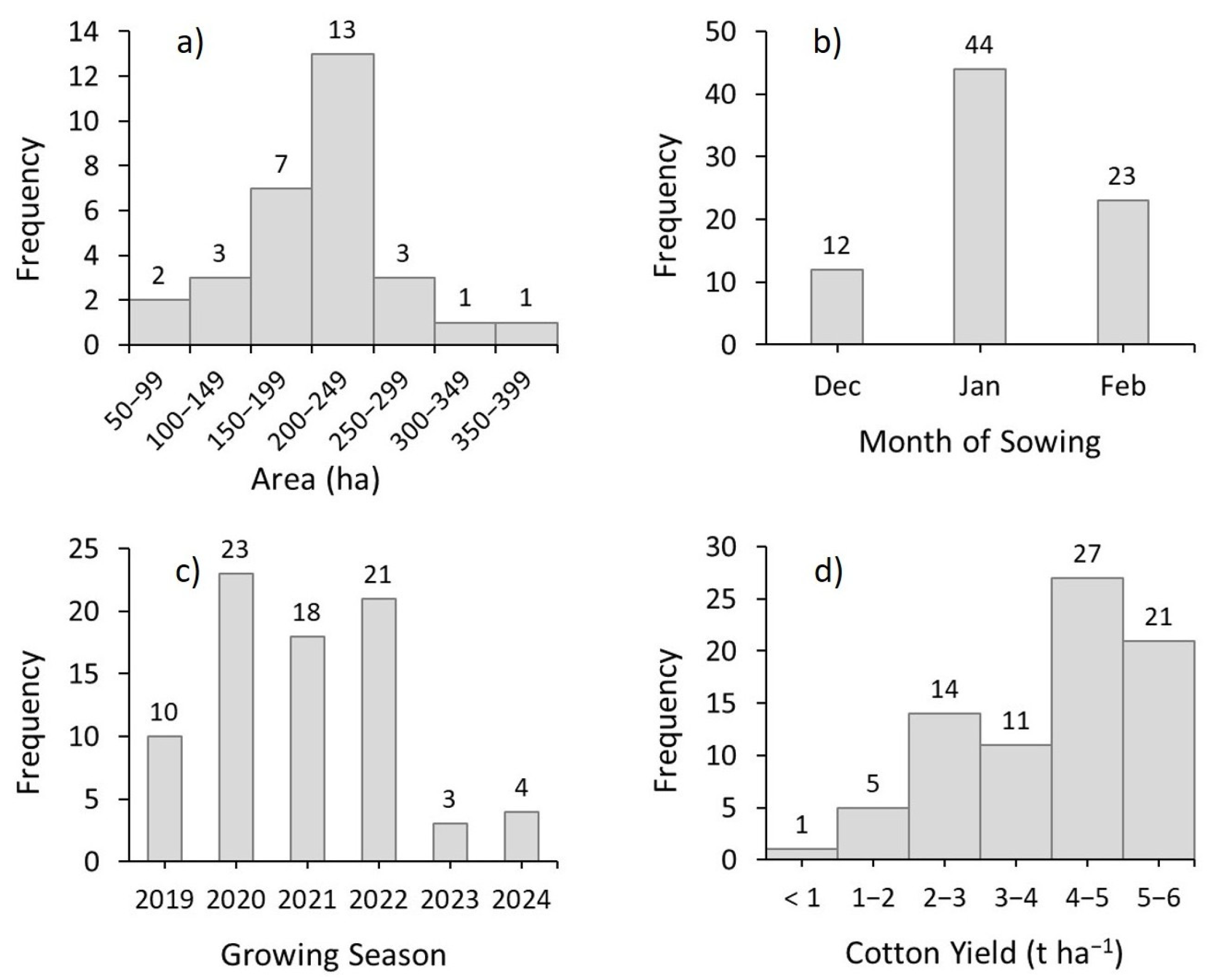
3.1. Dataset Evaluation
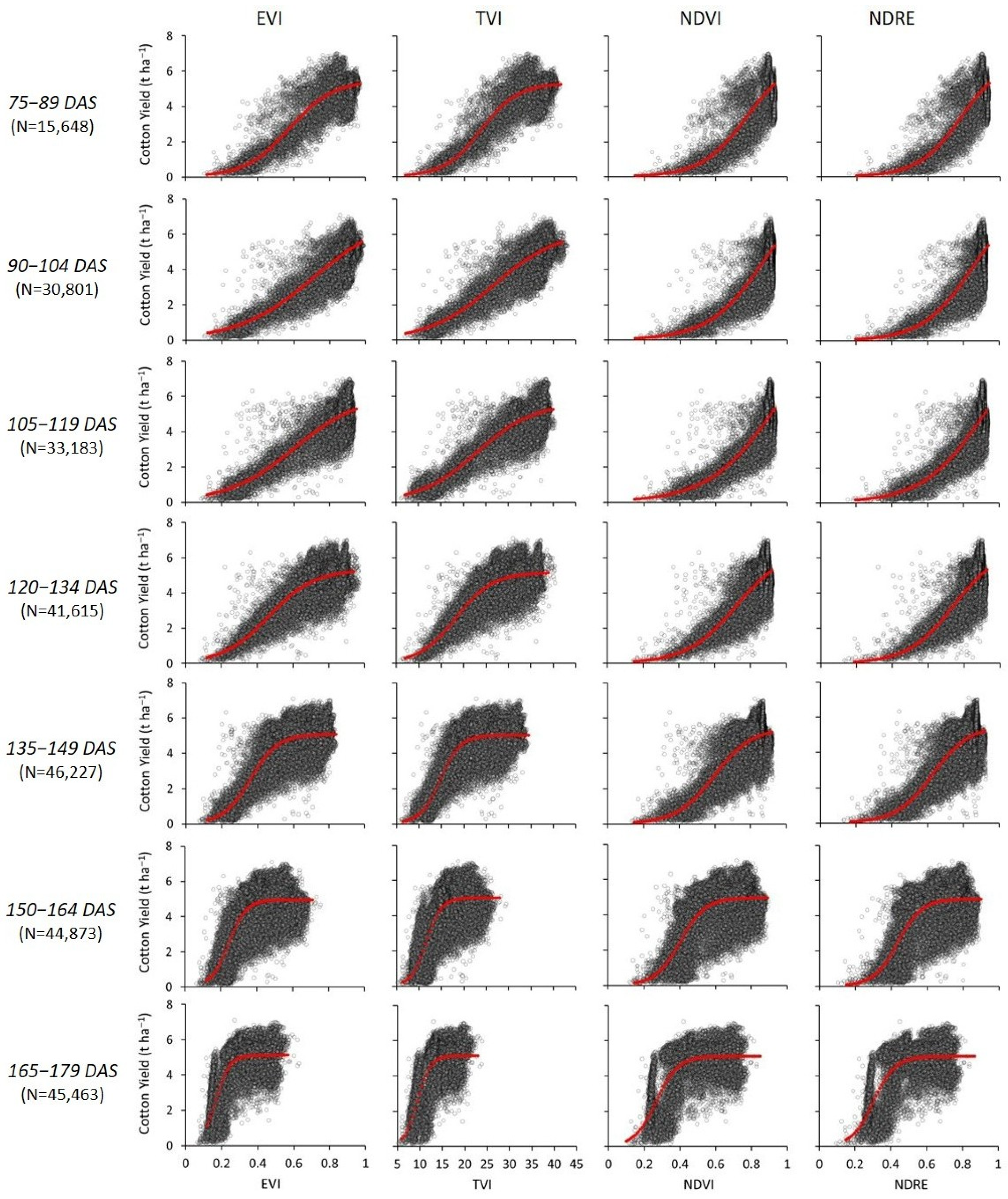
3.2. Cloud-Free VI Images Evaluation
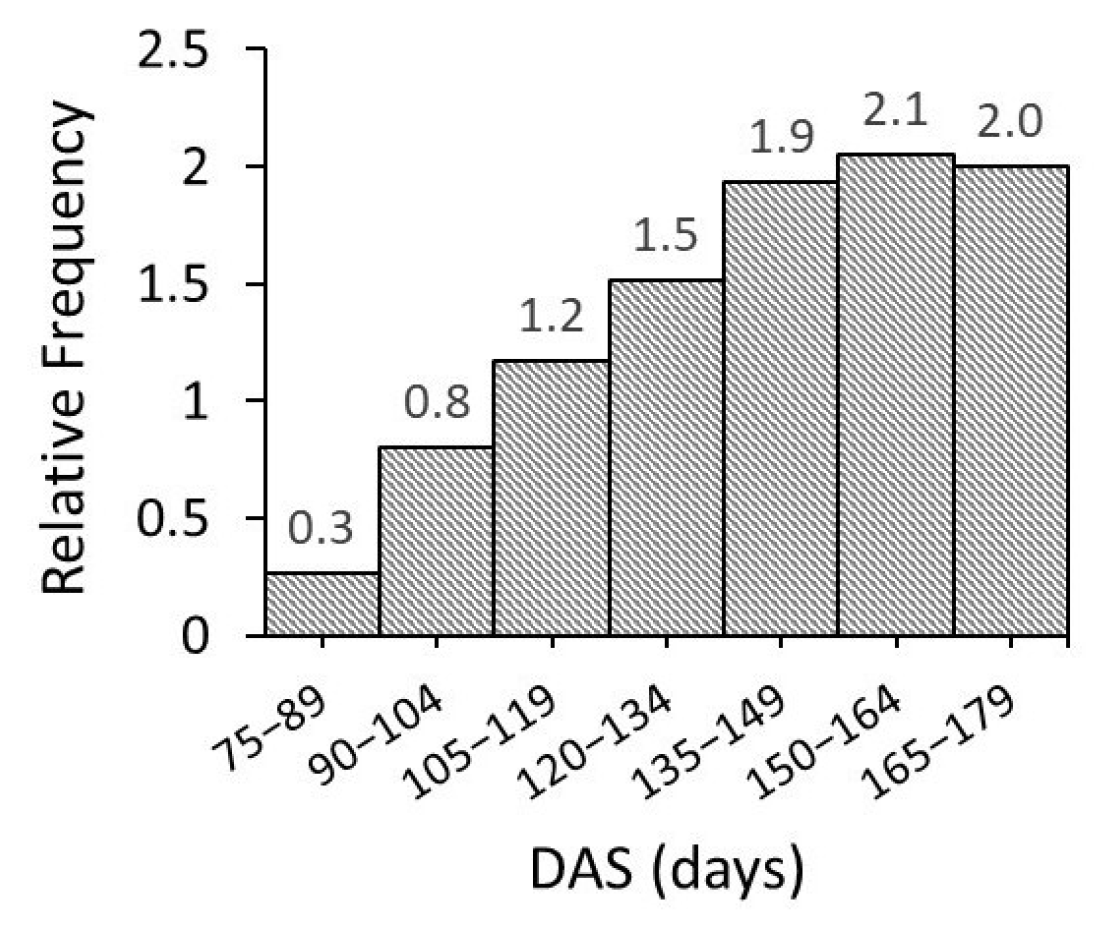
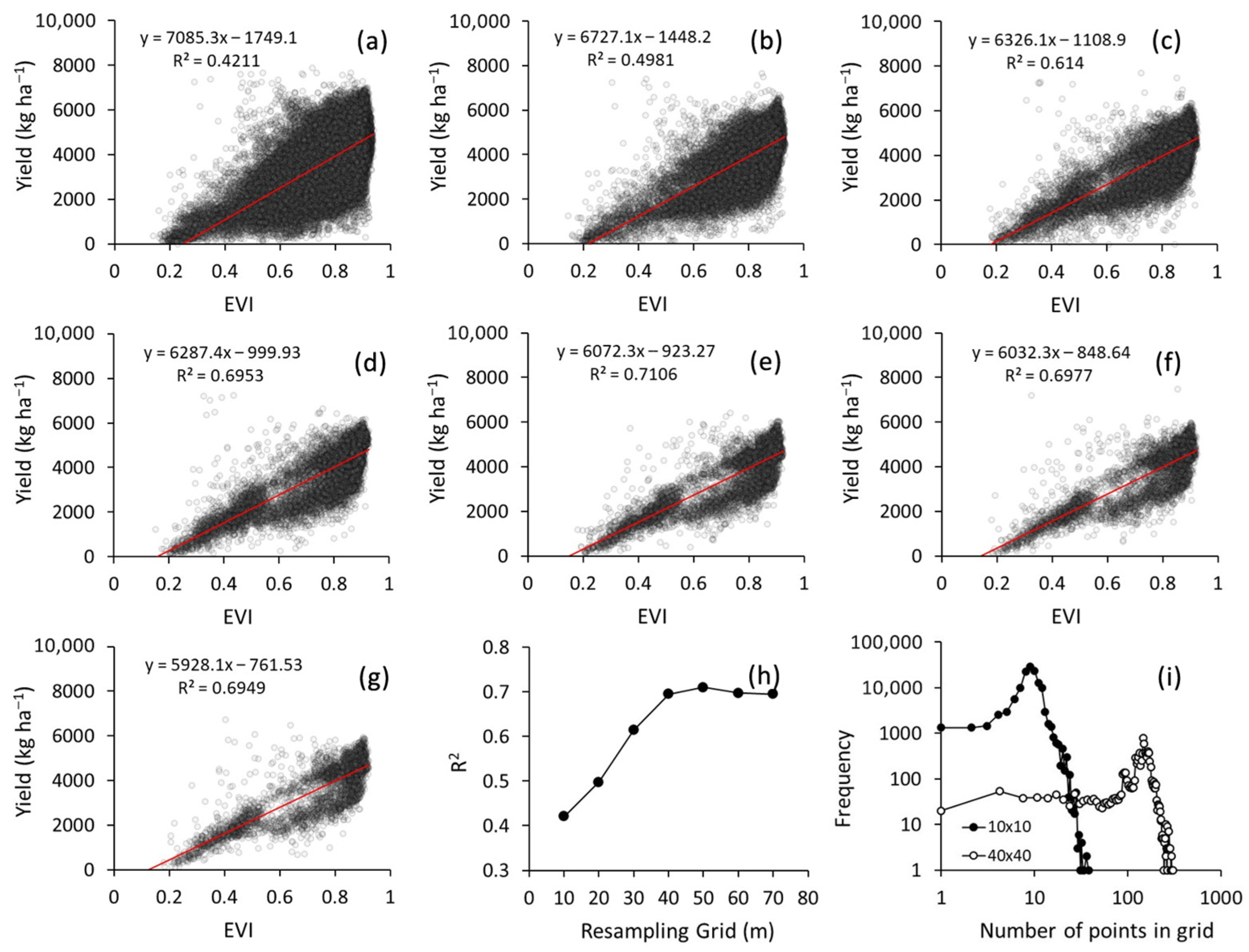
3.3. Resampling Grid for Yield and VI Maps
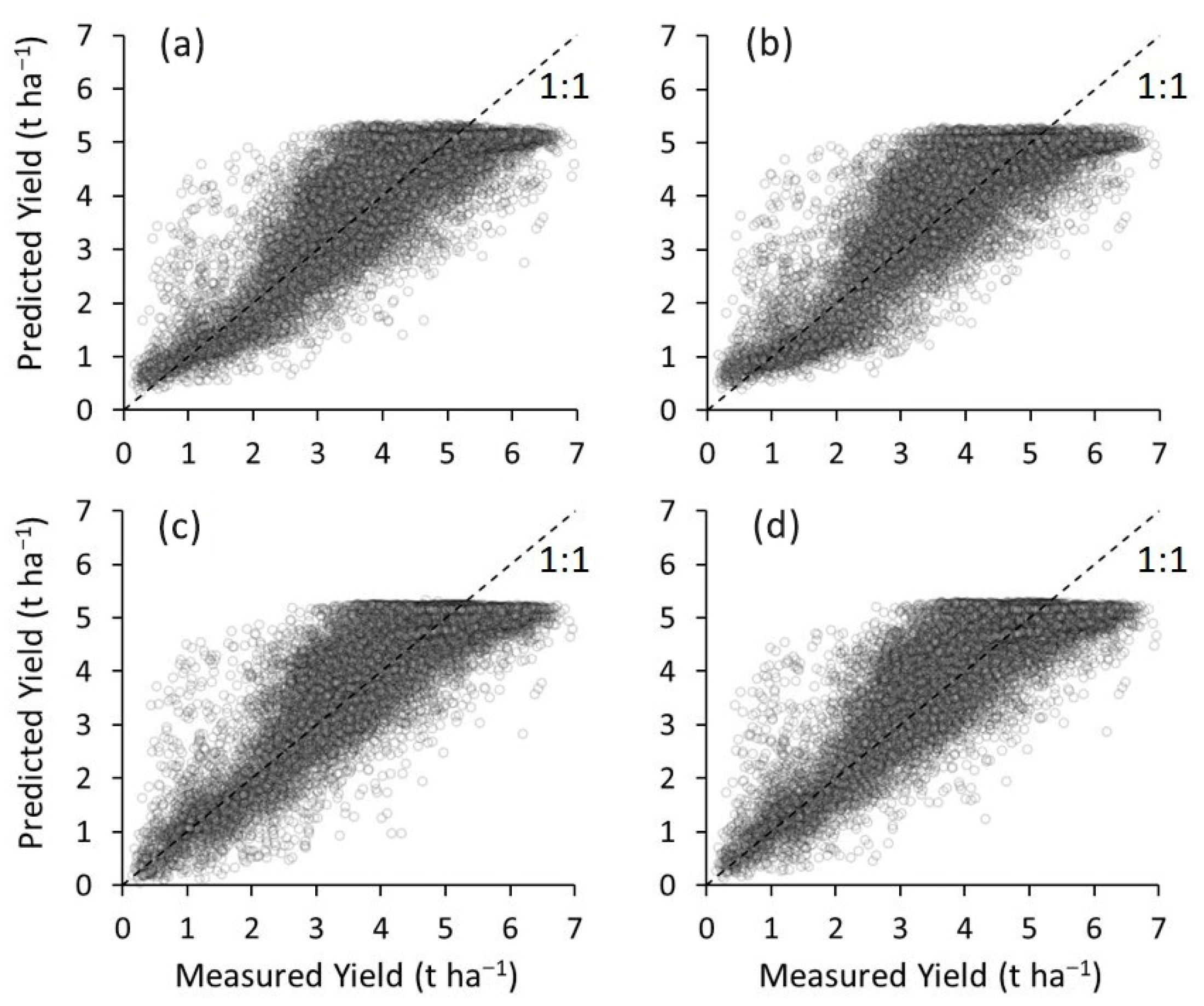
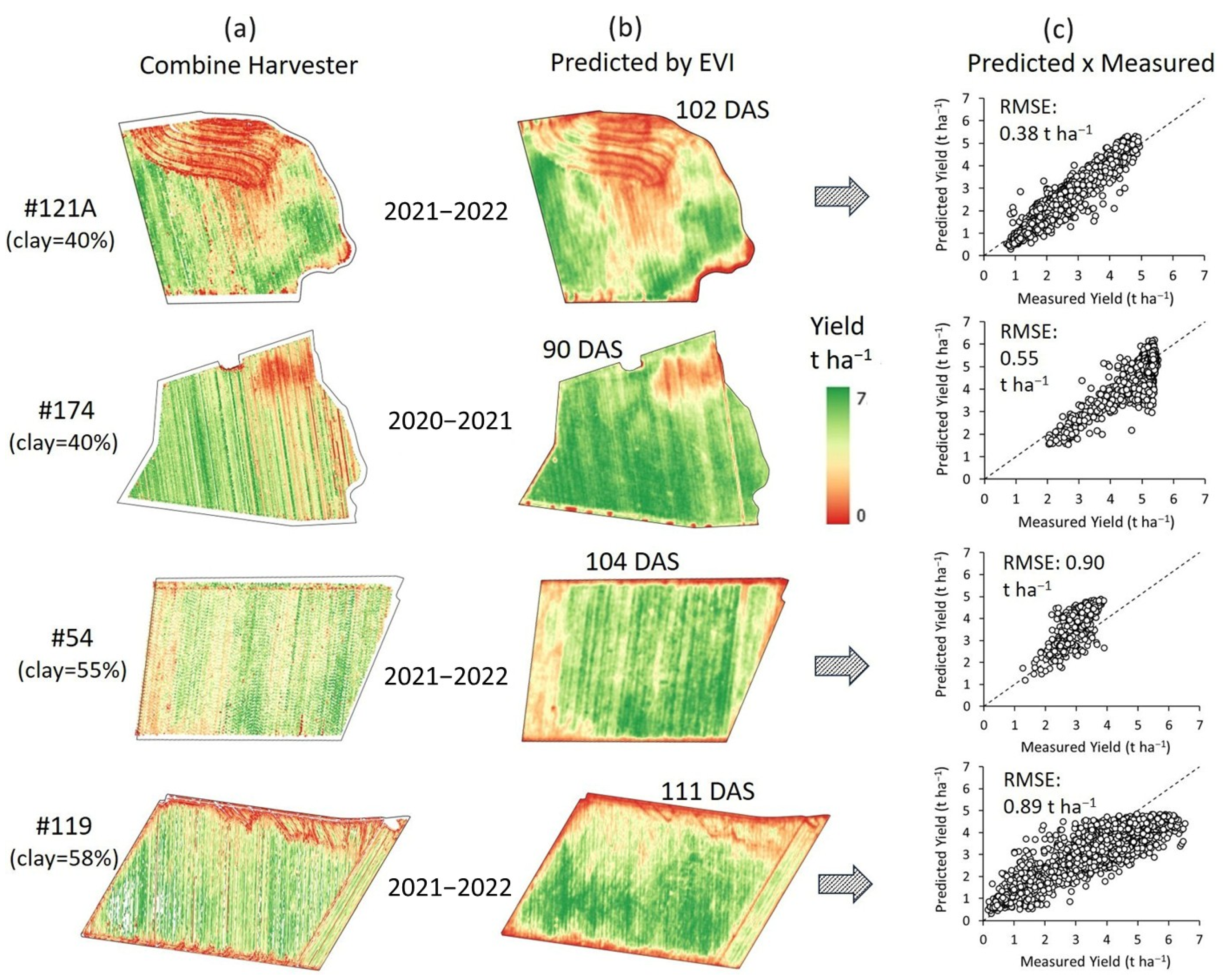
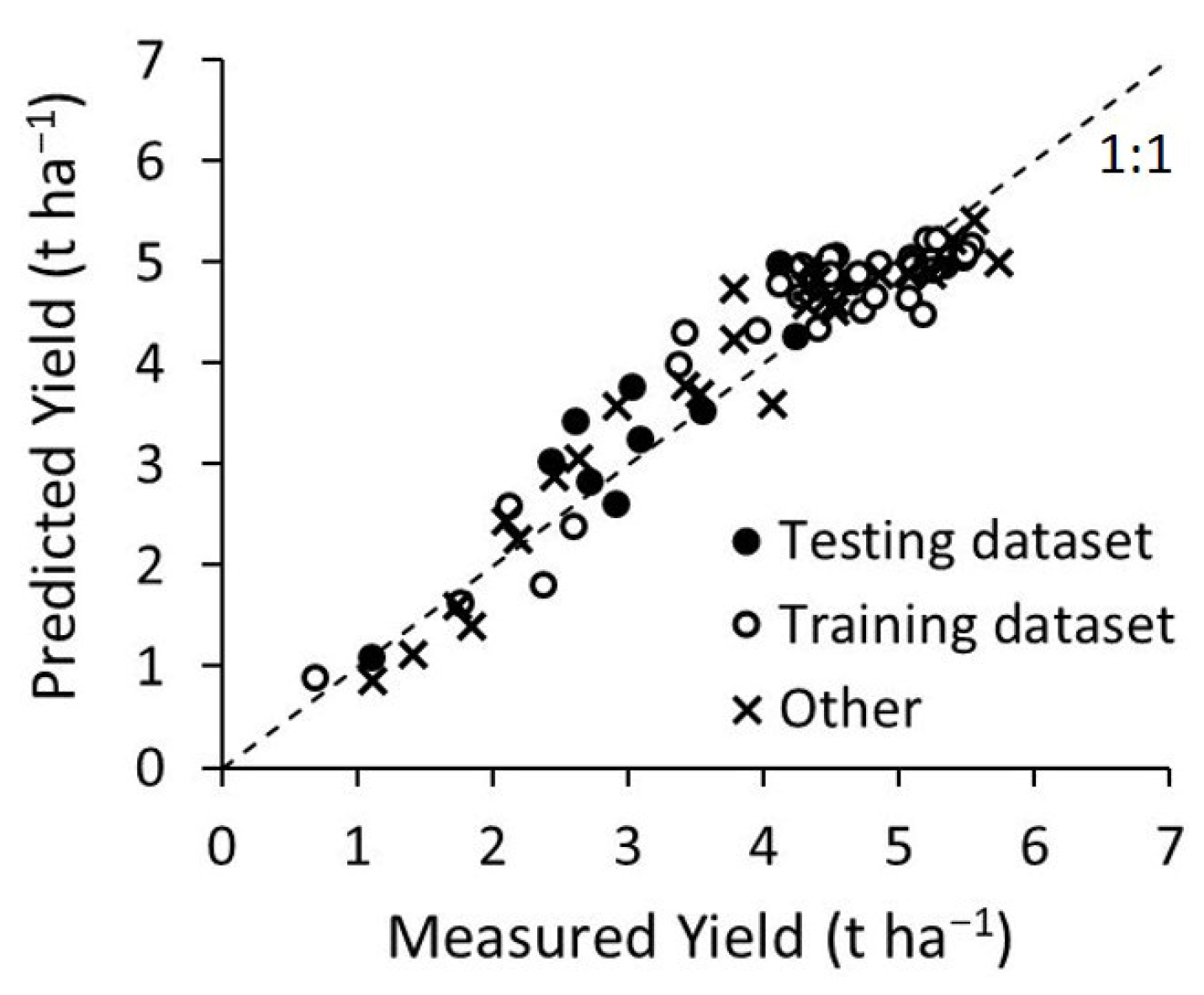
3.4. Model Training and Testing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blackmore, S.; Godwin, R.J.; Fountas, S. The analysis of spatial and temporal trends in yield map data over six years. Biosyst. Eng. 2003, 84, 455. [Google Scholar] [CrossRef]
- Grisso, R.D.; Alley, M.M.; Thomason, W.E.; Holshouser, D.L.; Roberson, G.T. Precision Farming Tools: Variable-Rate Application; Virginia Cooperative Extension: Blacksburg, VA, USA, 2011; 16p. [Google Scholar]
- Adhikari, K.; Smith, D.R.; Hajda, C.; Kharel, T.P. Within-field yield stability and gross margin variations across corn fields and implications for precision conservation. Precis. Agric. 2023, 24, 1401–1416. [Google Scholar] [CrossRef]
- Speranza, E.A.; Naime, J.M.; Vaz, C.M.P.; dos Santos, J.C.F.; Inamasu, R.Y.; Lopes, I.O.N.; Queirós, L.R.; Rabello, L.M.; Jorge, L.A.C.; Chagas, S.; et al. Delineating management zones with different yield potentials in soybean-corn and soybean-cotton production systems. AgriEngineering 2023, 5, 1481–1497. [Google Scholar] [CrossRef]
- Machado, S.; Bynum, E.D.; Archer, T.L.; Lascano, R.J.; Wilson, L.T.; Bordovsky, J.; Segarra, E.; Bronson, K.; Nesmith, D.M.; Xu, W. Spatial and temporal variability of corn growth and grain yield: Implications for site-specific farming. Crop Sci. 2002, 42, 1564–1576. [Google Scholar] [CrossRef]
- Blackmore, S. The interpretation of trends from multiple yield maps. Comput. Electron. Agric. 2000, 26, 37–51. [Google Scholar] [CrossRef]
- Gauci, A.A.; Fulton, J.P.; Lindsey, A.; Shearer, S.A.; Barker, D.; Hawkins, E.M. Precision of grain yield monitors for use in on—Farm research strip trials. Precis. Agric. 2024, 25, 771–784. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, M.; Zeng, H.; Tian, F.; Potgieter, A.B.; Qin, X.; Yan, N.; Chang, S.; Zhao, Y.; Dong, Q.; et al. Challenges and opportunities in remote sensing-based crop monitoring: A review. Natl. Sci. Rev. 2023, 10, nwac290. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Zhang, X. Mapping Crop Phenology in near real-time using satellite remote sensing: Challenges and opportunities. J. Remote Sens. 2021, 2021, 8379391. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 data for land cover/use mapping: A review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Li, J.; Chen, B. Global revisit interval analysis of Landsat-8/9 and Sentinel-2A/2B data for terrestrial monitoring. Sensors 2020, 20, 6631. [Google Scholar] [CrossRef] [PubMed]
- Sano, E.E.; Ferreira, L.G.; Asner, G.P.; Steinke, E.T. Spatial and temporal probabilities of obtaining cloud-free Landsat images over the Brazilian tropical savanna. Int. J. Remote Sens. 2007, 28, 2739–2752. [Google Scholar] [CrossRef]
- Lang, P.; Zhang, L.; Huang, C.; Chen, J.; Kang, X.; Zhang, Z.; Tong, Q. Integrating environmental and satellite data to estimate county-level cotton yield in Xinjiang Province. Front. Plant Sci. 2023, 13, 1048479. [Google Scholar] [CrossRef] [PubMed]
- de Siqueira, D.A.B.; Vaz, C.M.P.; da Silva, F.S.; Ferreira, E.J.; Speranza, E.A.; Franchini, J.C.; Galbieri, R.; Belot, J.L.; de Souza, M.; Perina, F.J.; et al. Estimating cotton yield in the Brazilian Cerrado using linear regression models from MODIS vegetation index time series. AgriEngineering 2024, 6, 947–961. [Google Scholar] [CrossRef]
- Johnson, D.M.; Rosales, A.; Mueller, R.; Reynolds, C.; Frantz, R.; Anyamba, A.; Pak, E.; Tucker, C. USA crop yield estimation with MODIS NDVI: Are remotely sensed models better than simple trend analyses? Remote Sens. 2021, 13, 4227. [Google Scholar] [CrossRef]
- He, L.; Mostovoy, G. Cotton yield estimate using Sentinel-2 data and an ecosystem model over the southern US. Remote Sens. 2019, 11, 2000. [Google Scholar] [CrossRef]
- Amin, E.; Pipia, L.; Belda, S.; Perich, G.; Graf, L.V.; Aasen, H.; Wittenberghe, S.V.; Moreno, M.; Verrelst, J. In-season forecasting of within-field grain yield from Sentinel-2 time series data. Int. J. Appl. Earth Obs. Geoinf. 2024, 126, 103636. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Wu, B.; Hammer, G.L. Predicting wheat yield at the field scale by combining high-resolution sentinel-2 satellite imagery and crop modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Kayad, A.; Sozzi, M.; Gatto, S.; Marinello, F.; Pirotti, F. Monitoring within-field variability of corn yield using sentinel-2 and machine learning techniques. Remote Sens. 2019, 11, 2873. [Google Scholar] [CrossRef]
- Perich, G.; Turkoglu, M.O.; Graf, L.V.; Wegner, J.D.; Aasen, H.; Walter, A.; Liebisch, F. Pixel-based yield mapping and prediction from Sentinel-2 using spectral indices and neural networks. Field Crops Res. 2023, 292, 108824. [Google Scholar] [CrossRef]
- Batistella, D.; Modolo, A.J.; Campos, J.R.R.; Lima, V.A. Comparative analysis of orbital sensors in soybean yield estimation by the random forest algorithm. Ciênc. Agrotec. 2023, 47, e002423. [Google Scholar] [CrossRef]
- Amankulova, K.; Farmonov, N.; Mucsi, L. Time-series analysis of Sentinel-2 satellite images for sunflower yield estimation. Smart Agr. Technol. 2023, 3, 100098. [Google Scholar] [CrossRef]
- Shuai, G.; Basso, B. Subfield maize yield prediction improves when in-season crop water deficit is included in remote sensing imagery-based models. Remote Sens. Environ. 2022, 272, 112938. [Google Scholar] [CrossRef]
- Crusiol, L.G.T.; Nanni, M.R.; Sibaldelli, R.N.R.; Sun, L.; Furlanetto, R.H.; Gonçalves, S.L.; Neumaier, M.; Farias, J.R.B. Early modeling of the upcoming Landsat next constellation for soybean yield prediction under varying levels of water availability. Remote Sens. 2024, 16, 4184. [Google Scholar] [CrossRef]
- Peralta, N.R.; Assefa, Y.; Du, J.; Barden, C.J.; Ciampitti, I.A. Mid-season high-resolution satellite imagery for forecasting site-specific corn yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef]
- Skakun, S.; Kalecinski, N.I.; Brown, M.G.L.; Johnson, D.M.; Vermote, E.F.; Roger, J.C.; Belen, F. Assessing within-field corn and soybean yield variability from WorldView-3, Planet, Sentinel-2, and Landsat 8 satellite imagery. Remote Sens. 2021, 13, 872. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Rouse, J.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium—Volume I: Technical Presentations, NASA SP-351. Washington, DC, USA, 1 January 1974; pp. 309–317. [Google Scholar]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground-based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Lorençone, J.A.; Lorençone, P.A.; Aparecido, L.E.O.; Torsoni, G.B.; Rolim, G.S.; Macedo, F.G. The future of cotton in Brazil: Agroclimatic suitability and climate change impacts. AgriEngineering 2025, 7, 198. [Google Scholar] [CrossRef]
- dos Santos, A.; Matos, E.S.; Freddi, O.S.; Galbieri, R.; Lal, R. Cotton production systems in the Brazilian Cerrado: The impact of soil attributes on field-scale yield. Eur. J. Agron. 2020, 118, 126090. [Google Scholar] [CrossRef]
- Ghansah, B.; Landivar Scott, J.L.; Zhao, L.; Starek, M.J.; Foster, J.; Landivar, J.; Bhandari, M. Satellite vs. uncrewed aircraft Systems (UAS): Combining high-resolution SkySat and UAS images for cotton yield estimation. Comput. Electron. Agric. 2025, 234, 110280. [Google Scholar] [CrossRef]
- Alshihabi, O.; Persson, K.; Söderström, M. Easy yield mapping for precision agriculture. Acta Agric. Scand. B 2024, 74, 2411950. [Google Scholar] [CrossRef]
- Fita, D.; Rubio, C.; Franch, B.; Castiñeira-Ibáñez, S.; Tarrazó-Serrano, D.; San Bautista, A. Improving harvester yield maps postprocessing leveraging remote sensing data in rice crop. Precis. Agric. 2025, 26, 33. [Google Scholar] [CrossRef]
- Lyle, G.; Bryan, B.; Ostendorf, B. Post-processing methods to eliminate erroneous grain yield measurements: Review and directions for future development. Precis. Agric. 2014, 15, 377–402. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A Comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Kawano, T.; Wallbridge, N.; Plummer, C. Logistic models for simulating the growth of plants by defining the maximum plant size as the limit of information flow. Plant Signal. Behav. 2020, 15, e1709718. [Google Scholar] [CrossRef]
- Eberhardt, I.D.R.; Schultz, B.; Rizzi, R.; Sanches, I.D.; Formaggio, A.R.; Atzberger, C.; Mello, M.P.; Immitzer, M.; Trabaquini, K.; Foschiera, W.; et al. Cloud cover assessment for operational crop monitoring systems in tropical areas. Remote Sens. 2016, 8, 219. [Google Scholar] [CrossRef]
- Echer, F.R.; Galdi, L.V.; Silva, G.R.A.; Santos, J.W.S.; Rocha, C.H.; Cagna, C.P.; Tormena, C.A.; Silva, I.F.; Atarassi, R. Components of high-yielding cotton grown in rain-fed conditions in the Brazilian Cerrado. Agronomy 2024, 14, 2920. [Google Scholar] [CrossRef]
- Oosterhuis, D.M. Growth and development of the cotton plant. In Nitrogen Nutrition in Cotton: Practical Issues; Miley, W.N., Oosterhuis, D.M., Eds.; American Society of Agronomy: Madison, WI, USA, 1990; pp. 1–24. [Google Scholar]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Leo, S.; De Antoni Migliorati, M.; Grace, P.R. Predicting within-field cotton yields using publicly available datasets and machine learning. Agron. J. 2021, 113, 1150–1163. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Gite, S.; Chakraborty, S. Remote-sensing data and deep-learning techniques in crop mapping and yield prediction: A systematic review. Remote Sens. 2023, 15, 2014. [Google Scholar] [CrossRef]
- Wang, H.; Dai, Y.; Yao, Q.; Ma, L.; Zhang, Z.; Lv, X. Multi-task learning model driven by climate and remote sensing data collaboration for mid-season cotton yield prediction. Field Crops Res. 2025, 333, 110070. [Google Scholar] [CrossRef]
- Singh, R.; Kaur, S.; Joshi, D.R.; Iboyi, J.; Dar, E.; Sharma, L.K.; Singh, H. Estimating cotton biomass and nitrogen content using high-resolution satellite and UAV data fusion with machine learning. Smart Agric. Technol. 2025, 12, 101191. [Google Scholar] [CrossRef]
- Kharel, T.P.; Swink, S.N.; Maresma, Á.; Youngerman, C.; Kharel, D.; Czymmek, K.J.; Ketterings, Q.M. Yield monitor data cleaning is essential for accurate corn grain and silage yield determination. Agron. J. 2019, 111, 509–516. [Google Scholar] [CrossRef]
- José, J.V.; Freitas, K.C.d.S.; Costa, J.d.O.; Quiloango-Chimarro, C.A.; Bonfim-Silva, E.M.; Silva, T.J.d.A. Caracterização do cultivo de algodão: Considerações espaço-temporais para o estado de Mato Grosso. Rev. Bras. Eng. Biossistemas 2022, 16, e1097. [Google Scholar]
- Ge, Y.; Thomasson, J.A.; Sui, R.; Morgan, C.L.S. A module-specific post-processing calibration method to improve cotton yield mapping. Comput. Electron. Agric. 2009, 68, 161–167. [Google Scholar] [CrossRef]
- Vellidis, G.; Perry, C.D.; Rains, G.C.; Thomas, D.L.; Wells, N.; Kvien, C.K. Simultaneous assessment of cotton yield monitors. Appl. Eng. Agric. 2003, 19, 259–272. [Google Scholar] [CrossRef]
- Maldaner, L.F.; Molin, J.P.; Spekken, M. Methodology to filter out outliers in high spatial density data to improve maps reliability. Sci. Agric. 2022, 79, e20200178. [Google Scholar] [CrossRef]
| Vegetation Index | Formula | Ref. |
|---|---|---|
| Enhanced Vegetation Index (EVI) | EVI = 2.5 × (NIR − R) / (1 + NIR + 6 × R − 7.5 × B) | [29] |
| Triangular Chlorophyll Absorption Ratio Index (TVI) | TVI = 60 × NIR – G − 100 × (R − G) | [30] |
| Normalized Difference Vegetation Index (NDVI) | NDVI = (NIR − R) / (NIR + R) | [31] |
| Normalized Difference Red Edge Index (NDRE) | NDRE = (NIR − RE) / (NIR + RE) | [32] |
| DAS | VI | a (95% CI) | xc (95% CI) | k (95% CI) | R2 | N |
|---|---|---|---|---|---|---|
| 75–89 | EVI | 5.480 (5.436–5.523) | 0.579 (0.572–0.586) | 8.116 (7.917–8.507) | 0.80 | 15,648 |
| 90–104 | 7.131 (7.003–7.260) | 0.715 (0.698–0.733) | 4.757 (4.655–4.958) | 0.82 | 30,801 | |
| 105–119 | 6.111 (6.042–6.180) | 0.606 (0.594–0.617) | 5.379 (5.270–5.592) | 0.79 | 33,183 | |
| 120–134 | 5.333 (5.310–5.356) | 0.466 (0.462–0.470) | 7.844 (7.707–8.112) | 0.67 | 41,615 | |
| 135–149 | 5.067 (5.056–5.079) | 0.362 (0.359–0.364) | 12.99 (12.79–13.38) | 0.68 | 46,227 | |
| 75–89 | TVI | 5.313 (5.285–5.342) | 23.82 (23.62–24.01) | 0.242 (0.237–0.252) | 0.83 | 15,648 |
| 90–104 | 6.216 (6.157–6.275) | 26.79 (26.42–27.16) | 0.138 (0.136–0.143) | 0.83 | 30,801 | |
| 105–119 | 5.581 (5.546–5.616) | 22.90 (22.62–23.15) | 0.159 (0.156–0.165) | 0.8 | 33,183 | |
| 120–134 | 5.143 (5.127–5.158) | 18.33 (18.20–18.45) | 0.246 (0.242–0.254) | 0.67 | 41,615 | |
| 135–149 | 4.998 (4.988–5.008) | 14.78 (14.71–14.86) | 0.447 (0.440–0.461) | 0.67 | 46,227 | |
| 75–89 | NDVI | 6.828 (6.613–7.043) | 0.775 (0.756–0.794) | 7.825 (7.518–8.426) | 0.75 | 15,648 |
| 90–104 | 9.126 (8.686–9.565) | 0.875 (0.845–0.906) | 6.419 (6.211–6.826) | 0.76 | 30,801 | |
| 105–119 | 10.92 (10.13–11.71) | 0.942 (0.891–0.993) | 5.306 (5.125–5.661) | 0.76 | 33,183 | |
| 120–134 | 6.491 (6.480–6.503) | 0.720 (0.709–0.731) | 7.276 (7.071–7.677) | 0.62 | 41,615 | |
| 135–149 | 5.457 (5.424–5.490) | 0.600 (0.596–0.604) | 9.277 (9.090–9.644) | 0.65 | 46,227 | |
| 75–89 | NDRE | 6.839 (6.628–7.050) | 0.787 (0.769–0.804) | 8.209 (7.895–8.827) | 0.75 | 15,648 |
| 90–104 | 8.380 (8.053–8.706) | 0.855 (0.831–0.878) | 7.093 (6.874–7.522) | 0.76 | 30,801 | |
| 105–119 | 10.036 (9.421–10.65) | 0.916 (0.875–0.956) | 5.829 (5.636–7.522) | 0.76 | 33,183 | |
| 120–134 | 6.551 (6.431–6.671) | 0.744 (0.733–0.755) | 7.817 (7.595–8.251) | 0.62 | 41,615 | |
| 135–149 | 5.511 (5.475–5.546) | 0.630 (0.626–0.634) | 9.734 (9.537–10–12) | 0.66 | 46,227 |
| VI | RMSE | MAE | Bias | R2 |
|---|---|---|---|---|
| t ha−1 | ||||
| EVI | 0.695 | 0.542 | 0.03 | 0.78 |
| TVI | 0.705 | 0.550 | 0.03 | 0.76 |
| NDVI | 0.722 | 0.569 | 0.05 | 0.77 |
| NDRE | 0.707 | 0.555 | 0.08 | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaz, C.M.P.; Ferreira, E.J.; Speranza, E.A.; Franchini, J.C.; Naime, J.d.M.; Inamasu, R.Y.; Lopes, I.d.O.N.; das Chagas, S.; Schelp, M.X.; Vecchi, L.; et al. Cotton Yield Map Prediction Using Sentinel-2 Satellite Imagery in the Brazilian Cerrado Production System. AgriEngineering 2025, 7, 390. https://doi.org/10.3390/agriengineering7110390
Vaz CMP, Ferreira EJ, Speranza EA, Franchini JC, Naime JdM, Inamasu RY, Lopes IdON, das Chagas S, Schelp MX, Vecchi L, et al. Cotton Yield Map Prediction Using Sentinel-2 Satellite Imagery in the Brazilian Cerrado Production System. AgriEngineering. 2025; 7(11):390. https://doi.org/10.3390/agriengineering7110390
Chicago/Turabian StyleVaz, Carlos Manoel Pedro, Ednaldo José Ferreira, Eduardo Antônio Speranza, Júlio César Franchini, João de Mendonça Naime, Ricardo Yassushi Inamasu, Ivani de Oliveira Negrão Lopes, Sérgio das Chagas, Mathias Xavier Schelp, Leonardo Vecchi, and et al. 2025. "Cotton Yield Map Prediction Using Sentinel-2 Satellite Imagery in the Brazilian Cerrado Production System" AgriEngineering 7, no. 11: 390. https://doi.org/10.3390/agriengineering7110390
APA StyleVaz, C. M. P., Ferreira, E. J., Speranza, E. A., Franchini, J. C., Naime, J. d. M., Inamasu, R. Y., Lopes, I. d. O. N., das Chagas, S., Schelp, M. X., Vecchi, L., & Galbieri, R. (2025). Cotton Yield Map Prediction Using Sentinel-2 Satellite Imagery in the Brazilian Cerrado Production System. AgriEngineering, 7(11), 390. https://doi.org/10.3390/agriengineering7110390








