A Dynamic Empirical Bayes Signal Model for Attribute Defect Detection

Abstract

This study evaluates Empirical Bayes (EB) c-charts for monitoring count-type data under precautionary (PLF) and logarithmic (LLF) loss functions. By assuming an exponential prior for the Poisson mean, the EB framework enables the construction of predictive densities for future observations. Simulation studies and a real-world dataset on missing rivets in large aircraft were used to compare the methods’ ability to detect out-of-control conditions. The results show that EB–LLF charts exhibit high sensitivity for small and moderate process shifts, and both EB approaches outperform the classical c-chart by integrating prior information to detect shifts earlier while controlling false alarms. These findings highlight the importance of loss function choice and demonstrate the effectiveness of EB charts for robust process monitoring.

1. Introduction

Statistical Process Control (SPC) serves as a cornerstone in ensuring process stability and maintaining product and service quality. It provides a systematic and data-driven framework for identifying unexpected deviations or shifts in process performance, enabling timely corrective actions before nonconformities escalate. Beyond its traditional applications in industrial manufacturing, SPC has found relevance in numerous modern domains—such as healthcare [1,2,3], finance [4,5], information systems and network monitoring [6,7], and energy and environmental monitoring [8,9,10]—where the early detection of abnormal patterns plays a vital role in minimizing risk and improving operational efficiency.

Within the diverse family of SPC tools, the c-chart is one of the most widely adopted methods for monitoring attribute-type data, specifically the number of defects or nonconformities in inspection units of fixed size. It is grounded in the Poisson distribution, making it suitable for situations where defect occurrences are independent and rare. Practical examples include detecting surface imperfections on materials, counting assembly errors, or recording missing components in production lines. By visualizing defect counts over time within upper and lower control limits, the c-chart enables practitioners to distinguish between natural fluctuations in the process and statistically significant shifts that may indicate underlying process deterioration [11,12,13,14]. Consequently, the c-chart helps maintain process reliability by separating common cause from special cause variation, ensuring that interventions are both justified and effective.

Despite its long-standing usefulness, the traditional c-chart is often limited by its reliance on fixed parameters derived from classical estimation methods. Such fixed parameter designs become less reliable in uncertain or dynamically changing production environments, where defect rates may evolve over time and the assumption of process stationarity no longer holds. These conventional approaches also lack mechanisms to formally incorporate prior information or quantify uncertainty, resulting in delayed detection, increased false alarms, and reduced robustness when the process exhibits parameter drift.

To address this limitation, Bayesian inference has been increasingly utilized in SPC due to its inherent capacity to incorporate prior information, handle uncertainty, and adapt to sequential decision-making scenarios. As highlighted by Bayarri and Garcia-Donato [15], Bayesian approaches provide more flexible and coherent inferential structures than classical techniques. Several studies have demonstrated that Bayesian-based control charts outperform traditional methods in adjusting sampling frequencies, determining control limits, and optimizing decision rules through posterior probability updating [16,17]. Moreover, Bayesian principles have been successfully applied to construct control charts for monitoring the mean and variance in both normally [18] and non-normally distributed processes [19,20,21,22], as well as in developing Bayesian charts under various loss functions for process monitoring frameworks [23,24,25]. Furthermore, a variety of loss functions within the Bayesian framework—ranging from the conventional and weighted squared error loss to more recent formulations such as the K-loss, DeGroot loss, and precautionary loss—have been investigated in both estimation studies [26] and control chart design [27]. Comparative findings consistently show that Bayesian charts constructed under precautionary and K-loss functions exhibit superior sensitivity to out-of-control conditions relative to their classical counterparts [27,28,29,30,31], highlighting the importance of loss function choice in enhancing detection capability. Building on these developments, our study introduces an Adaptive Empirical Bayes framework to address the practical challenges of monitoring count-type data under evolving process conditions and uncertainty.

Building on the expanding role of Bayesian and loss function-based approaches in SPC, another promising direction is the Empirical Bayes (EB) framework. When prior distribution parameters are not explicitly known but estimated directly from observed data, the approach is termed Empirical Bayes (EB). This hybrid methodology combines the strengths of Bayesian and frequentist paradigms by using empirical data to refine prior information. The Empirical Bayes method has demonstrated strong potential for estimation and classification problems, and its applications in SPC have improved adaptability and accuracy in control chart design [32,33,34]. Recent research has shown that EB-based SPC techniques offer advantages in dynamically updating control limits and enhancing robustness under model uncertainty [35]. Furthermore, studies incorporating non-informative priors, such as the Jeffreys prior, have demonstrated significant improvements in key performance indicators, including the Average Run Length (ARL) and the Standard Deviation of Run Length (SDRL) [36], compared to the classical approach [37].

A recent study by Supharakonsakun [38] further advanced the Bayesian c-chart by employing the gamma prior to derive posterior predictive control limits. This modification resulted in higher ARLs and lower false alarm rates than conventional methods, confirming the superiority of Bayesian frameworks for process monitoring. However, the effectiveness of such models depends strongly on the choice of hyperparameters, suggesting that data-driven adjustment mechanisms are essential for optimal performance. The Empirical Bayes approach provides an attractive alternative, allowing for adaptive estimation of these hyperparameters directly from process observations.

Motivated by these developments, the present research focuses on evaluating the signal detection performance of a Bayesian-based attribute control chart constructed under the Empirical Bayes framework. In particular, this study explores parameter estimation using the precautionary loss function, which accounts for asymmetric decision risks, and compares its performance with the conventional squared error loss function and the classical c-chart. This work explicitly extends an earlier study [35], which introduced the use of Empirical Bayes methods for constructing c-charts within a single loss function framework. Building on this foundation, the present study broadens the analysis by incorporating and comparing two additional loss functions—the Precautionary Loss Function (PLF) and the Logarithmic Loss Function (LLF)—to provide a more comprehensive evaluation of how different Bayesian decision criteria influence chart performance. This extension provides deeper insights into the role of loss function selection in EB-based attribute control charts and enhances the generalizability of the previous findings.

The remainder of this article is structured as follows: Section 2 introduces the Empirical Bayes framework for constructing c-charts under different loss functions; Section 3 presents simulation studies assessing chart performance across various process shifts and sample sizes; Section 4 applies the proposed methodology to a real dataset on missing rivets in large aircraft; and Section 5 provides the discussion and conclusions, summarizing insights and implications for practical process monitoring. The aim is to assess the chart’s efficiency in detecting process shifts and improving decision robustness under uncertainty, thereby introducing a novel and adaptive framework for attribute defect monitoring.

2. Empirical Bayes for the c-Chart Under Loss Function Frameworks

The c-chart is widely used in situations where defect occurrences follow a Poisson distribution, such as monitoring surface imperfections in materials, identifying missing components in assembly processes, or detecting errors in printed circuit boards. By continuously plotting the number of detected defects against statistically derived control limits, the c-chart allows practitioners to recognize unusual increases in defect counts, signaling potential disturbances that warrant investigation and corrective measures [39].

The traditional control limits, determined under the assumption that the process mean $\mu$ represents the average number of defects per inspection unit, are calculated as follows:

$$\begin{array}{cc}\hfill UCL=& \mu +3\sqrt{\mu },\hfill \\ \hfill CL=& \mu ,\hfill \\ \hfill LCL=& \mu -3\sqrt{\mu }.\hfill \end{array}$$

(1)

When inspection units are independently and uniformly sampled over time, the count of nonconformities detected in the i^th observation is modeled as a Poisson process with parameter $\mu$, the expected number of defects per inspection interval. The probability mass function can thus be expressed as

$$f\left(x_i|\mu \right)={\displaystyle \frac{e^{-\mu }{\mu }^{x_i}}{x_i!}},\hspace{0.17em}{x}_i=0,1,2,\dots \hspace{0.17em}\hspace{0.17em},i=1,\dots ,n;\hspace{0.17em}\mu >0$$

(2)

However, the traditional control limits are derived under fixed parameter assumptions and often neglect process uncertainty or prior information regarding the defect generation mechanism. In practical scenarios, such assumptions may lead to biased assessments of process stability and delayed identification of abnormal variations. To overcome these limitations, Bayesian approaches have been proposed that integrate prior knowledge with observed data to establish posterior-based predictive control limits that dynamically adapt to changing process conditions.

Furthermore, when the prior parameters are unknown and estimated directly from observed data, the Empirical Bayes (EB) approach provides a more data-driven alternative. This method bridges the gap between full Bayesian inference and classical estimation by refining the prior distributions through empirical evidence. As a result, Empirical Bayes estimation enhances the flexibility and robustness of the c-chart, thereby improving its sensitivity to subtle process shifts or deviations.

In this study, an informative prior is employed within the Bayesian framework.

Let the random variable follow an exponential distribution with parameter $\lambda$, denoted as $\mu$∼ Exp($\lambda$), which is a special case of the Gamma distribution with the shape parameter equal to 1.

The probability density function (PDF) of the exponential distribution is given by

$$\pi \left(\mu \right)=\lambda e^{-\lambda \mu };\hspace{0.17em}\mu ,\lambda >0.$$

(3)

Supharakonsakun and Jampachasri [40] proposed an Empirical Bayes estimator for $\mu$ by estimating the hyperparameter $\lambda$ using the maximum likelihood estimator (MLE) derived from the marginal posterior distribution (see [41]). The MLE of the hyperparameter $\lambda$ is obtained as

$$\widehat{\lambda }={\displaystyle \frac{n}{{\displaystyle \sum _{i=1}^n{x}_i}}}{\displaystyle \frac{1}{\overline{x}}}.$$

(4)

where $\overline{x}$ denotes the sample mean, calculated as the average of the observed count data collected across all inspection units.

In this study, the Empirical Bayes framework adopts this MLE-based estimate ($\widehat{\lambda }=1/{\displaystyle \frac{1}{\overline{x}}}$) across all simulation experiments and real-world applications. This specification ensures a fully data-driven prior that is coherent with the predictive density formulation used in conjunction with the PLF and LLF.

The posterior distribution of $\mu$ can be obtained by combining the prior information with the likelihood function derived from the observed data. By applying Bayes’ theorem, the posterior distribution can be explicitly expressed, providing a complete probabilistic description of $\mu$ that incorporates both prior knowledge and observed evidence, as follows:

$$\begin{gathered} h(\mu |X)=\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{f\left(\underset{\_}{x}|\mu \right)\pi \left(\mu \right)}{{\displaystyle \underset{0}{\overset{\infty }{\int }}f\left(\underset{\_}{x}|\mu \right)\pi \left(\mu \right)d\mu }}} \\ =\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\frac{\widehat{\lambda }{e}^{-\left(n+\widehat{\lambda }\right)\mu }{\mu }^{{\displaystyle \sum _{i=1}^n{x}_i}}}{{\displaystyle \prod _{i=1}^n{x}_i!}}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{\widehat{\lambda }{e}^{-\left(n+\widehat{\lambda }\right)\mu }{\mu }^{{\displaystyle \sum _{i=1}^n{x}_i}}}{{\displaystyle \prod _{i=1}^n{x}_i!}}d\mu }}} \\ =\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\widehat{\lambda }{e}^{-\left(n+\widehat{\lambda }\right)\mu }{\mu }^{{\displaystyle \sum _{i=1}^n{x}_i}}}{{\displaystyle \prod _{i=1}^n{x}_i!}}}\cdot {\displaystyle \frac{{\left(n+\widehat{\lambda }\right)}^{{\displaystyle \sum _{i=1}^n{x}_i}+1}{\displaystyle \prod _{i=1}^n{x}_i!}}{\widehat{\lambda }\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{x}_i}+1\right)}} \end{gathered}$$

Specifically, it can be shown that the posterior distribution of $\mu$ follows a gamma distribution with shape parameter ${\displaystyle \sum _{i=1}^n{x}_i}+1$ and rate parameter $n+\widehat{\lambda }$, which can be expressed as

$$h(\mu |X)=\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\left(n+\widehat{\lambda }\right)}^{{\displaystyle \sum _{i=1}^n{x}_i+1}}}{\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{x}_i+1}\right)}}{e}^{-\left(n+\widehat{\lambda }\right)\mu }{\mu }^{{\displaystyle \sum _{i=1}^n{x}_i+1-1}}.$$

(5)

In this formulation, Y denotes the number of nonconformities observed within an inspection unit. The above expression can be further reformulated into a predictive density function, as shown below (see [18]):

$$f\left(Y|X\right)={\displaystyle \frac{{\left(n+\widehat{\lambda }\right)}^{{\displaystyle \sum _{i=1}^n{X}_i+1}}\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{X}_i+Y+1}\right)}{Y!\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{X}_i+1}\right){\left(n+\widehat{\lambda }+1\right)}^{{\displaystyle \sum _{i=1}^n{X}_i+Y}+1}}}.$$

(6)

By simplifying the expression, the predictive density can be written as

$$f\left(Y|X\right)={\displaystyle \frac{\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{X}_i+Y+1}\right)}{\mathrm{\Gamma }\left(Y+1\right)\mathrm{\Gamma }\left({\displaystyle \sum _{i=1}^n{X}_i+1}\right)}}{\left({\displaystyle \frac{n+\widehat{\lambda }}{n+\widehat{\lambda }+1}}\right)}^{{\displaystyle \sum _{i=1}^n{X}_i+1}}{\left({\displaystyle \frac{1}{n+\widehat{\lambda }+1}}\right)}^Y.$$

(7)

Hence, the predictive density follows a negative binomial distribution, which can be denoted as

$$Y~BN\left({\displaystyle \sum _{i=1}^n{X}_i+1,\frac{n+\widehat{\lambda }}{n+\widehat{\lambda }+1}}\right).$$

(8)

These advantages become particularly evident when the estimation process is examined under different loss function frameworks, such as the squared error loss function (SELF) and the precautionary loss function (PLF). Each of these frameworks provides a distinct lens for evaluating estimation accuracy and decision-making sensitivity.

In statistical inference, a loss function is a quantitative measure that penalizes the discrepancy between an estimated value and the true, unknown parameter. The choice of a loss function directly influences the nature of the resulting estimator, reflecting the emphasis placed on underestimation or overestimation errors. Accordingly, selecting an appropriate loss function is crucial for aligning the estimation process with practical objectives and risk preferences in quality control and process monitoring.

Among various alternatives, the squared error loss function (SELF) has been the most commonly adopted criterion due to its mathematical simplicity and symmetric treatment of estimation errors. It penalizes deviations from the true value equally in both directions, yielding estimators that are optimal for minimizing the expected squared deviation. The SELF framework also provides a convenient analytical foundation for Bayesian estimation, where the optimal estimator is the posterior mean.

2.1. Squared Error Loss Function (SELF)

The squared error loss function (SELF) is one of the most widely used and fundamental loss functions in statistical estimation theory. Originally introduced by Legendre [42] in the context of the method of least squares and later formalized by Gauss [43], the SELF provides a symmetric and analytically convenient criterion for evaluating the accuracy of parameter estimates.

Let $\mu$ denote the unknown parameter associated with a study variable Y, and let $\widehat{\mu }$ represent an estimator of μ that minimizes the expected posterior loss. The SELF measures the discrepancy between the estimator and the true parameter value and is defined as

$$L\left(\mu ,\widehat{\mu }\right)={\left(\widehat{\mu }-\mu \right)}^2.$$

(9)

Under this loss function, the Bayes estimator is obtained by minimizing the posterior expected loss. It can be shown that the resulting estimator corresponds to the posterior predictive mean, expressed as

$${\widehat{\mu }}_{SELF}=E\left(Y|X\right).$$

(10)

For the exponential Empirical Bayes (EB) prior, the detailed derivation and proof of the Bayes estimator under the squared error loss function are provided in [43]. The resulting form of the estimator can be expressed as follows:

$${\widehat{\mu }}_{SELF}={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{X}_i+1}}{n+\widehat{\lambda }}},$$

(11)

which highlights the estimator’s dependence on the posterior expectation of the parameter, given the likelihood of the observed data.

This property makes the SELF particularly attractive in Bayesian analysis, as it is simple, symmetric, and directly interpretable as a measure of estimation accuracy.

2.2. Precautionary Loss Function (PLF)

The precautionary loss function (PLF) employed in Bayesian estimation is a symmetric, continuous, and differentiable function of both the true parameter, denoted by $\mu$, and its estimator, $\widehat{\mu }$. This function is particularly appropriate in decision-making environments where the consequences of overestimation and underestimation are equally undesirable. Unlike asymmetric loss functions that assign different penalties depending on the estimation direction, the PLF treats both types of estimation errors equally, thereby promoting more stable and conservative inferential decisions.

The formal definition of the precautionary loss function has been established in the literature [44,45,46], as follows:

$$L\left(\mu ;\widehat{\mu }\right)={\displaystyle \frac{{\left(\mu -\widehat{\mu }\right)}^2}{\widehat{\mu }}}=\sqrt{E\left(Y^2|X\right)}.$$

(12)

In Bayesian inference, the precautionary loss function serves as a decision-theoretic foundation for deriving estimators that minimize expected posterior loss. Specifically, the Bayesian estimator under the PLF is obtained by minimizing the posterior expected value of the loss function, conditional on the observed data. This process incorporates both the posterior predictive distribution and the uncertainty associated with the underlying model parameters:

$$E\left(Y^2|X\right)=Var\left(Y|X\right)+E{\left(Y|X\right)}^2.$$

(13)

To initiate this derivation, the posterior predictive variance must first be determined, as it plays a central role in defining the expected loss and, consequently, the optimal estimator. For an informative prior, particularly an exponential Empirical Bayes (EB) prior, the variance of the posterior predictive distribution can be expressed as

$$Var\left(Y|X\right)={\displaystyle \frac{\left({\displaystyle \sum _{i=1}^n{X}_i+1}\right)\left(n+\widehat{\lambda }+1\right)}{{\left(n+\widehat{\lambda }\right)}^2}}.$$

(14)

Using this result, the Empirical Bayes estimator of the Poisson parameter under the precautionary loss function—based on the posterior predictive density derived from the exponential prior—is formulated by minimizing Equation (11). The intermediate steps of this derivation can be presented as follows:

$$E\left(Y^2|X\right)={\displaystyle \frac{\left({\displaystyle \sum _{i=1}^n{X}_i+1}\right)\left({\displaystyle \sum _{i=1}^n{X}_i+n+\widehat{\lambda }+2}\right)}{{\left(n+\widehat{\lambda }\right)}^2}}.$$

(15)

Accordingly, the Bayesian estimator for the posterior predictive density under the precautionary loss function with exponential Empirical Bayes prior is obtained as

$${\widehat{\mu }}_{PLF}={\displaystyle \frac{\sqrt{\left({\displaystyle \sum _{i=1}^n{X}_i+1}\right)\left({\displaystyle \sum _{i=1}^n{X}_i+n+\widehat{\lambda }+2}\right)}}{n+\widehat{\lambda }}}.$$

(16)

2.3. Logarithmic Loss Function (LLF)

The logarithmic (mode-based) loss function employed in Bayesian estimation is particularly suitable for discrete count data, such as the number of nonconformities monitored using a c-chart. Unlike symmetric loss functions that minimize mean or squared deviations, the mode-based loss focuses on the mode of the posterior predictive distribution, making it appropriate when the most likely outcome is of primary interest.

In the literature, the formal definition of the logarithmic loss function was provided by Brown (1968) [47] as follows:

$$L\left(\mu ;\widehat{\mu }\right)=\left|\ln {\displaystyle \frac{\widehat{\mu }}{\mu }}\right|.$$

(17)

The Bayesian estimator under this loss function, commonly referred to as the mode-based Bayes estimator, is defined as the mode of the posterior predictive distribution conditional on the observed data:

$${\widehat{\mu }}_{LLF}=\mathrm{Mode}\left(Y|X\right).$$

(18)

For the negative binomial posterior predictive distribution derived from an Empirical Bayes (EB) approach from Equation (8), the mode of predictive density of Y can be explicitly expressed as

$${\widehat{\mu }}_{LLF}=\left({\displaystyle \sum _{i=1}^n{X}_i+1-1}\right)\left({\displaystyle \frac{1}{n+\widehat{\lambda }+1}}\right)\left({\displaystyle \frac{n+\widehat{\lambda }+1}{n+\widehat{\lambda }}}\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{X}_i}}{n+\widehat{\lambda }}}.$$

(19)

The resulting estimate represents the most likely number of nonconformities in a future inspection unit, taking into account both the information from the observed data—namely, the total number of defects across inspected units—and the prior knowledge, reflected in the sample size and the prior hyperparameter estimate. By adopting the mode as the estimator, practitioners obtain a stable, practical value that highlights the most probable outcome rather than the average, which is especially advantageous when working with discrete count data and when process monitoring is intended to capture the typical pattern of defect occurrences.

The Empirical Bayes (EB) estimators derived from the exponential prior under both the squared error loss function (SELF), the precautionary loss function (PLF), and the logarithmic loss function (LLF) are subsequently employed to establish control limits for the c-chart. These limits are then compared with those obtained from the traditional estimator used in the classical c-chart framework. The comparative evaluation aims to determine the degree to which the EB-based approaches enhance sensitivity and stability in process monitoring.

The proposed EB predictive approach is inherently adaptive, as it updates parameter estimates and the resulting control limits according to the selected loss function. This adaptive feature enables the control chart to respond with varying sensitivities to process shifts, reflecting different risk attitudes and enhancing the overall effectiveness of monitoring.

The effectiveness and efficiency of the proposed control chart procedures are primarily assessed using the Average Run Length (ARL) criterion, which measures the expected number of samples taken before an out-of-control signal is triggered. To provide a more comprehensive performance evaluation, two supplementary metrics—namely, the Average Extra Quadratic Loss (AEQL) and the Performance Comparison Index (PCI) introduced by Alevizakos et al. [48]—are also incorporated into the analysis.

The AEQL quantifies the average deviation between the estimated and true process conditions, thereby serving as an indicator of estimation accuracy and signal responsiveness. It is defined as follows:

$$\mathrm{AEQL}={\displaystyle \frac{1}{\Delta }}{\displaystyle \sum _{\delta }{\delta }^2\times \mathrm{ARL}}.$$

(20)

Here, δ represents the magnitude of process change, reflecting the incremental shift between the in-control and out-of-control states. In this study, a value of δ = 10 is adopted to represent a meaningful and practically observable level of process variation. Control charts yielding smaller AEQL values are considered to demonstrate superior detection capability and more reliable estimation accuracy.

To facilitate a direct comparison of AEQL performance across different charting methods, the Performance Comparison Index (PCI) is employed. This index expresses the efficiency of each control chart relative to the chart exhibiting the lowest AEQL value, thus serving as a standardized efficiency measure:

$$\mathrm{PCI}={\displaystyle \frac{\mathrm{AEQL}}{{\mathrm{AEQL}}_{lowest}}}.$$

(21)

A PCI value of 1 indicates the most efficient control chart design, while values exceeding 1 indicate comparatively lower efficiency relative to the benchmark chart.

The simulation results, including the ARL-based performance assessment and the comparative analysis of AEQL and PCI across various methods, are presented and discussed in the following section.

3. Simulation Studies

The simulation study, conducted in R, compared the Empirical Bayes (EB) and frequentist approaches for detecting shifts in the process mean ($\mu$ set to 10, 5, 20, and 25). The EB method was evaluated under three loss functions: squared error (SELF), precautionary (PLF), and logarithmic (LLF).

The study covered a wide range of shift magnitudes (δ = 0.01 to 10.0) and inspection unit sizes (20, 30, and 50), with the in-control Average Run Length (ARL₀) fixed at 370. Performance was judged by minimizing the out-of-control ARL₁, SDRL₁, and AEQL; a control structure with a PCI of 1.0000 was designated as superior, indicating faster, more consistent, and cost-efficient detection.

Table 1 presents the ARL and SDRL values obtained from both classical and Empirical Bayes (EB) methods for inspection unit sizes of 20, 30, and 50 with $\mu$ = 10. The EB method using the proposed LLF consistently provides lower ARL1 and SDRL₁ values across all shift magnitudes and inspection unit sizes. In addition, the AEQL and PCI values confirm the superior performance of the EB-LLF method, achieving the lowest AEQL and a PCI of 1.0000, demonstrating its high effectiveness in detecting process shifts.

Table 1. Comparative ARL, SDRL, AEQL, and PCI for μ = 10 across different δ and sample sizes (n = 20, 30, 50).

n	δ	Classical		SELF		PLF		LLF
		ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	ADRL
20	0.00	368.9767	368.4764	371.3061	370.8058	368.5627	368.0624	368.9323	368.4320
	0.01	366.0527	365.5523	368.4012	367.9008	367.2476	366.7473	366.0152	365.5149
	0.05	353.0520	352.5517	355.7032	355.2028	356.7016	356.2012	353.0066	352.5063
	0.10	335.9875	335.4871	338.704	338.2037	344.6514	344.151	335.9383	335.4379
	0.50	231.7346	231.2341	235.075	234.5745	255.1630	254.6626	231.7060	231.2055
	1.00	145.2664	144.7655	147.6289	147.1280	168.5420	168.0413	145.2483	144.7474
	2.00	60.9055	60.4034	61.9621	61.4601	73.3615	72.8597	60.8958	60.3937
	3.00	28.8954	28.3910	29.3695	28.8652	34.5128	34.0091	28.8906	28.3862
	5.00	9.1344	8.6199	9.2518	8.7375	10.5021	9.9896	9.1329	8.6184
	10.0	1.9673	1.3795	1.9792	1.3922	2.0930	1.5125	1.9671	1.3793
AEQL		113.6250		115.2100		131.2621		113.6084
PCI		1.0001		1.0141		1.1554		1.0000
30	0.00	375.0978	374.5975	374.7203	374.2200	370.9942	370.4939	372.0921	371.5917
	0.01	369.5463	369.0459	369.8422	369.3418	368.7656	368.2653	366.6556	366.1553
	0.05	355.5141	355.0138	356.0419	355.5415	358.5976	358.0973	352.6435	352.1432
	0.10	338.3618	337.8614	339.2413	338.7409	345.7828	345.2824	335.6287	335.1283
	0.50	224.6680	224.1675	226.8117	226.3112	250.4513	249.9508	222.9427	222.4421
	1.00	139.3808	138.8799	141.1208	140.6199	162.4423	161.9415	138.3321	137.8312
	2.00	58.5011	57.9989	59.30007	58.7979	69.30863	68.8068	58.0808	57.5786
	3.00	28.0610	27.5564	28.3952	27.8907	32.7395	32.2356	27.8699	27.3653
	5.00	9.02361	8.5089	9.1089	8.5944	10.1653	9.6523	8.9702	8.4554
	10.0	1.9654	1.3775	1.9731	1.3856	2.0704	1.4887	1.9596	1.3713
AEQL		110.8541		111.9933		126.2509		110.1710
PCI		1.0062		1.0165		1.1460		1.0000
50	0.00	373.7736	373.2733	372.869	372.3687	371.2053	370.7049	372.2023	371.7020
	0.01	369.9825	369.4822	369.1394	368.6391	369.2369	368.7365	368.3220	367.8217
	0.05	353.6270	353.1266	352.7805	352.2802	357.6939	357.1936	352.0816	351.5813
	0.10	336.8294	336.3290	336.0218	335.5214	344.3732	343.8729	335.3304	334.8301
	0.50	221.5347	221.0342	221.2796	220.7790	245.782	245.2815	220.5333	220.0327
	1.00	135.8372	135.3363	135.7785	135.2776	157.1769	156.6761	135.3177	134.8167
	2.00	57.0898	56.5876	57.0866	56.5844	66.6111	66.1092	56.9144	56.4122
	3.00	27.5378	27.0331	27.5375	27.0329	31.6708	31.1668	27.4665	26.9618
	5.00	8.9547	8.4399	8.9547	8.4399	9.9803	9.4671	8.9388	8.4240
	10.0	1.9674	1.3795	1.9674	1.3795	2.0656	1.4837	1.9661	1.3782
AEQL		109.2317		109.2169		123.0546		108.9657
PCI		1.0024		1.0023		1.1293		1.0000

Table 2 summarizes the results for $\mu$ = 15. For an inspection unit size of n = 20, the EB method under the SELF yields lower ARL₁ and SDRL₁ values for shift sizes δ ≤ 0.1. However, for larger shifts (δ = 0.5 − 10.0), both the classical and EB methods under the LLF perform better. When n = 30, the EB method under the SELF continues to show lower ARL₁ and SDRL₁ values for several shift magnitudes, with performance similar to the classical approach in some cases. For n = 50, the EB method under the SELF again provides smaller ARL₁ and SDRL₁ for δ ≤ 1.0, while the EB method under the LLF performs better for larger shifts (δ ≥ 2.0). Moreover, the EB-LLF method achieves the minimum AEQL and a PCI of 1.0000, reinforcing its high detection efficiency.

Table 2. Comparative ARL, SDRL, AEQL, and PCI for μ = 15 across different δ and sample sizes (n = 20, 30, 50).

n	δ	Classical		SELF		PLF		LLF
		ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	ADRL
20	0.00	370.5513	370.0509	369.8393	369.3390	370.6831	370.1828	370.5513	370.0509
	0.01	368.8153	368.3150	368.1009	367.6005	368.6579	368.1575	368.8153	368.3150
	0.05	358.3686	357.8683	358.1409	357.6405	362.7802	362.2799	358.3686	357.8683
	0.10	347.3638	346.8635	347.3592	346.8589	354.8880	354.3876	347.3638	346.8635
	0.50	266.9993	266.4988	269.0063	268.5058	294.356	293.8555	266.9993	266.4988
	1.00	187.6703	187.1697	189.9637	189.4630	220.0157	219.5151	187.6703	187.1697
	2.00	92.8014	92.3001	94.3951	93.8938	115.1271	114.6260	92.8014	92.3001
	3.00	47.9768	47.4742	48.7783	48.2757	59.7134	59.2112	47.9768	47.4742
	5.00	15.9889	15.4808	16.2109	15.7029	19.2252	18.7185	15.9889	15.4808
	10.0	2.9645	2.4133	2.9867	2.4359	3.2710	2.7255	2.9645	2.4133
AEQL		175.7996		178.2149		210.3756		175.7996
PCI		1.0000		1.0137		1.1967		1.0000
30	0.00	371.9941	370.4938	373.0860	372.585	371.4364	370.9361	371.0646	370.5642
	0.01	369.6530	369.1527	371.1669	370.6666	370.0204	369.5201	369.6530	369.1527
	0.05	358.5652	358.0648	360.4643	359.9639	363.2604	362.7600	358.5652	358.0648
	0.10	347.1349	346.6346	349.2883	348.7879	354.6086	354.1083	347.1286	346.6282
	0.50	260.1515	259.6511	262.7648	262.2643	286.0635	285.5630	260.1321	259.6317
	1.00	179.6576	179.1569	182.0079	181.5072	208.9943	208.4937	179.6524	179.1517
	2.00	87.4304	86.9289	88.6934	88.1920	105.2861	104.7849	87.4304	86.9289
	3.00	45.5722	45.0694	46.1449	45.6422	54.67914	54.1768	45.5720	45.0692
	5.00	15.4034	14.8950	15.5675	15.0592	17.9335	17.4263	15.4034	14.8950
	10.0	2.9318	2.3798	2.9477	2.3961	3.1799	2.6329	2.9318	2.3798
AEQL		168.7237		170.6165		196.4586		168.7225
PCI		1.0000		1.0112		1.1644		1.0000
50	0.00	372.1788	371.6784	370.2538	369.7535	370.7635	370.2632	371.2827	370.7823
	0.01	369.3755	368.8751	367.6731	367.1728	368.9055	368.4051	368.6190	368.1187
	0.05	357.9255	357.4251	356.2715	355.7711	360.7977	360.2974	357.1486	356.6482
	0.10	344.8732	344.3728	343.3357	342.8353	351.0863	350.5859	344.1632	343.6628
	0.50	254.5093	254.0088	253.8017	253.3012	277.8729	277.3724	254.1346	253.6341
	1.00	173.9633	173.4626	173.7365	173.2358	199.9993	199.4986	173.7691	173.2684
	2.00	84.0606	83.5591	84.0367	83.5352	99.3770	98.8757	83.9938	83.4923
	3.00	43.8923	43.3894	43.8893	43.3864	51.5847	51.0822	43.8703	43.3674
	5.00	15.1251	14.6165	15.1250	14.6165	17.2786	16.7711	15.1189	14.6103
	10.0	2.9123	2.3599	2.91232	2.3599	3.1267	2.5787	2.9116	2.3592
AEQL		164.2602		164.2055		188.0323		164.1615
PCI		1.0006		1.0003		1.1454		1.0000

Table 3 presents the results for $\mu$ = 20. The EB method with the proposed LLF consistently achieves lower ARL₁ and SDRL₁ values across all shift magnitudes and inspection unit sizes. Similarly, the AEQL and PCI results confirm the superior performance of the EB-LLF method, with the lowest AEQL and a PCI of 1.0000, indicating strong detection capability and robustness.

Table 3. Comparative ARL, SDRL, AEQL, and PCI for μ = 20 across different δ and sample sizes (n = 20, 30, 50).

n	δ	Classical		SELF		PLF		LLF
		ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	ADRL
20	0.00	374.1135	373.6131	375.703	375.2027	374.8274	374.3271	374.1104	373.6101
	0.01	371.8283	371.3279	373.4414	372.9411	372.7648	372.2645	371.8226	371.3222
	0.05	364.7591	364.2587	366.1449	365.6446	368.3870	367.8867	364.7506	364.2503
	0.10	356.5772	356.0769	358.2591	357.7588	362.1955	361.6951	356.5741	356.0737
	0.50	292.4373	291.9369	295.2417	294.7412	313.1581	312.6577	292.4338	291.9333
	1.00	221.5976	221.0970	224.4144	223.9138	250.7054	250.2049	221.5975	221.0969
	2.00	122.8515	122.3505	124.8676	124.3666	148.1849	147.6840	122.8412	122.3401
	3.00	68.0310	67.5291	69.1943	68.6925	83.5208	83.0193	68.0271	67.5253
	5.00	24.1108	23.6055	24.4665	23.9613	28.9878	28.4835	24.1107	23.6055
	10.0	4.2591	3.7257	4.2947	3.7616	4.7540	4.2245	4.2591	3.7257
AEQL		243.1587		246.6112		287.8097		243.1507
PCI		1.0000		1.0142		1.1837		1.0000
30	0.00	373.3011	372.8008	373.4056	372.9052	372.3616	371.8613	372.8030	372.3026
	0.01	371.0034	370.5030	371.1343	370.6339	370.7784	370.2781	370.5182	370.0179
	0.05	363.5448	363.0444	363.8059	363.3055	365.4480	363.3055	363.0416	362.5413
	0.10	353.9103	353.4099	354.3354	353.8350	358.8225	358.3221	353.4381	352.9377
	0.50	284.7108	284.2104	285.7609	285.2605	304.3808	303.8804	284.3282	283.8277
	1.00	211.7901	211.2895	213.2383	212.7377	238.4740	237.9735	211.5327	211.0322
	2.00	114.1172	113.6161	115.2015	114.7004	135.2194	134.7185	113.9932	113.4921
	3.00	63.4419	62.9399	64.04702	63.5450	75.5310	75.0294	63.3708	62.8688
	5.00	22.9709	22.4654	23.1535	22.6480	26.7479	26.2432	22.9499	22.4443
	10.0	4.1577	3.6233	4.1778	3.6436	4.5564	4.0255	4.1541	3.6198
AEQL		230.4941		232.3015		266.4102		230.2561
PCI		1.0010		1.0089		1.1570		1.0000
50	0.00	370.5382	370.0378	371.499	370.9986	370.7643	370.2640	370.4832	369.9829
	0.01	368.8154	368.3151	369.7235	369.2231	369.8948	369.3945	368.7524	368.2521
	0.05	360.5681	360.0677	361.7505	361.2502	363.8851	363.3847	360.5134	360.0130
	0.10	350.8075	350.3072	351.8739	351.3735	356.8128	356.3124	350.7501	350.2498
	0.50	276.6224	276.1219	277.7813	277.2808	297.9958	297.4954	276.5907	276.0903
	1.00	202.7101	202.2095	203.7874	203.2867	228.3659	227.8654	202.6996	202.1990
	2.00	108.0139	107.512	108.6426	108.1414	126.2137	125.7128	108.0108	107.5097
	3.00	60.1163	59.6142	60.4509	59.9488	70.2389	69.7371	60.1157	59.6136
	5.00	22.0265	21.5207	22.1278	21.6221	25.1608	24.6558	22.0265	21.5207
	10.0	4.0826	3.5476	4.0946	3.5597	4.4248	3.8928	4.0826	3.5476
AEQL		220.8337		221.8976		251.5885		220.8300
PCI		1.0000		1.0048		1.1393		1.0000

Table 4 reports the findings for $\mu$ = 25. The EB method with the LLF again provides lower ARL₁ and SDRL₁ values for inspection unit sizes of n = 20 and 30 across all shift magnitudes. For n = 50, the EB method under the SELF performs the best for smaller shifts (δ ≤ 0.1); meanwhile, for larger shifts (δ = 0.5 − 10.0), both the classical and EB methods under the LLF outperform the others. For n = 30, the EB method under the SELF still yields smaller ARL₁ and SDRL₁ values across several shift magnitudes, with results comparable to those of the classical approach.

Table 4. Comparative ARL, SDRL, AEQL, and PCI for μ = 25 across different δ and sample sizes (n = 20, 30, 50).

n	δ	Classical		SELF		PLF		LLF
		ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	ADRL
20	0.00	369.2062	368.7059	369.9639	369.4635	368.4157	367.9153	369.1618	368.6614
	0.01	368.4303	367.9300	369.2082	368.7079	368.4620	367.9617	368.3884	367.8881
	0.05	363.0985	362.5981	363.9534	363.4531	364.2134	363.7130	363.0619	362.5615
	0.10	356.5014	356.0011	357.3377	356.8374	357.3377	359.6573	356.4657	355.9653
	0.50	303.2351	302.7347	304.8576	304.3572	320.4020	319.9016	303.2178	302.7173
	1.00	241.7294	241.2289	243.8805	243.3800	267.7462	267.2457	241.7222	241.2216
	2.00	144.8330	144.3321	146.6523	146.1514	170.9531	170.4524	144.8316	144.3307
	3.00	85.8482	85.3468	87.0538	86.5524	103.6527	103.1515	85.8480	85.3465
	5.00	32.5164	32.0124	32.9737	32.4699	38.9071	38.4038	32.5163	32.0124
	10.0	5.7371	5.2132	5.7893	5.2656	6.4424	5.9213	5.7371	5.2132
AEQL		306.0634		309.7981		358.5972	306.0612	306.0634	309.7981
PCI		1.0000		1.0122		1.1717		1.0000
30	0.00	371.3556	370.8552	371.3852	370.8849	370.8655	370.3652	370.4918	369.9915
	0.01	369.5937	369.0933	369.5063	369.0060	369.5429	369.0426	368.6895	368.1891
	0.05	364.8866	364.3862	364.7629	364.2626	366.0358	365.5355	363.9399	363.4396
	0.10	363.4396	354.1488	355.0976	354.5973	359.7188	359.2184	353.8330	353.3331
	0.50	297.3034	296.8029	298.6462	298.1458	315.8952	315.3948	296.6654	296.1650
	1.00	232.6323	232.1318	234.4433	233.9428	258.9842	258.4837	232.2883	231.7878
	2.00	136.2089	135.7080	137.7224	137.2215	159.9698	159.4690	136.1269	135.6260
	3.00	80.0030	79.5014	80.9858	80.4843	95.1778	94.6765	79.9887	79.4871
	5.00	30.5202	30.0160	30.8613	30.3572	35.8552	35.3517	30.5197	30.0155
	10.0	5.5706	5.0459	5.6136	5.0891	6.1802	5.6581	5.5706	5.0459
AEQL		289.6469		292.6259		335.3387		289.5398
PCI		1.0004		1.0107		1.1582		1.0000
50	0.00	371.7764	371.2761	371.1620	370.6617	372.0659	371.5656	371.7764	371.5656
	0.01	370.2104	369.7100	369.5696	369.0692	370.4222	369.9219	370.2104	369.7100
	0.05	363.8776	363.3772	363.3036	362.8032	365.9906	365.4902	363.8776	363.3772
	0.10	355.0944	354.5941	354.4788	353.9784	360.1442	359.6439	355.0944	354.5941
	0.50	292.6509	292.1505	292.7261	292.2257	310.0448	309.5444	292.6509	292.1505
	1.00	224.6695	224.1689	225.1262	224.6256	248.1750	247.6745	224.6695	224.1689
	2.00	129.5630	129.0620	130.0806	129.5797	149.3590	148.8581	129.5630	129.0620
	3.00	75.8967	75.3950	76.2072	75.7055	88.1706	87.6692	75.8967	75.3950
	5.00	29.3891	28.8848	29.4939	28.9895	33.6462	33.1424	29.3891	28.8848
	10.0	5.4601	4.934	5.4715	4.946	5.9552	5.4323	5.4601	4.9348
AEQL		278.4390		279.3482		315.7886		278.4390
PCI		1.0000		1.0033		1.1341		1.0000

In addition, the AEQL and PCI results confirm the superior performance of the EB-LLF method, which achieves the lowest AEQL and a PCI of 1.0000, demonstrating consistency and high effectiveness in detecting process shifts.

4. Application

In this section, a performance comparison is conducted between the traditional c-chart and Empirical Bayes (EB) c-charts constructed under three loss function frameworks: the squared error, precautionary, and logarithmic loss functions. To demonstrate their applicability, a real dataset concerning the inspection of missing rivets on large aircraft is analyzed. The dataset consists of 26 successive observations, each corresponding to the number of missing rivets identified per aircraft. Because these defects are presumed to occur randomly and independently throughout the aircraft structure, the count of nonconformities in each sample is modeled using a Poisson distribution [49]. Although this dataset does not include specification limits typical of manufacturing processes, it provides a practical example to illustrate the applicability and comparative performance of the traditional and EB c-charts.

This dataset provides a practical setting for examining how effectively each charting approach can identify shifts in the process mean. The Poisson mean parameter was separately estimated using the classical technique and three EB estimation procedures, each derived from a distinct loss function. These parameter estimates were subsequently used to define the control limits for tracking changes in the average number of defects. A constant control width of three standard deviations was adopted across all charting schemes. The comparative outcomes of the four control charting strategies are illustrated in Figure 1, Figure 2, Figure 3 and Figure 4.

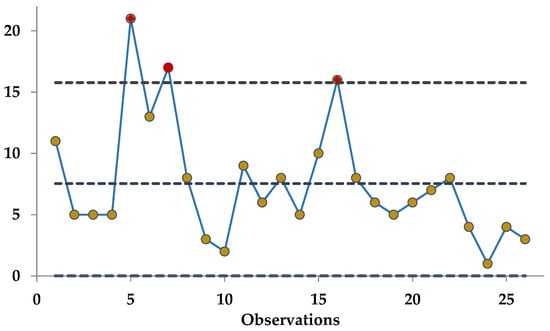
Figure 1. Classical c-chart for monitoring missing rivet counts.

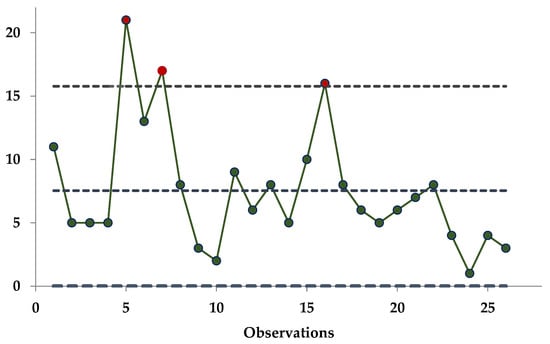
Figure 2. EB c-chart under the squared error loss function (SELF).

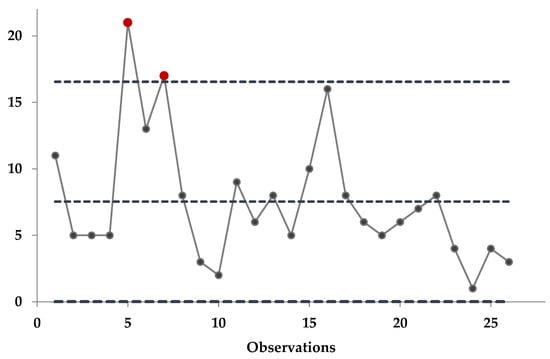
Figure 3. EB c-chart under the precautionary loss function (PLF).

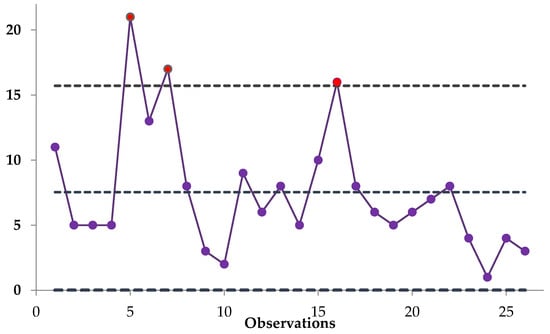
Figure 4. EB c-chart under the logarithmic loss function (LLF).

Figure 1 depicts the traditional c-chart constructed from the actual dataset. The chart indicates that the process went out of control at the 5th, 7th, and 16th observations. The delayed recognition of these abnormal points reveals the limited responsiveness of the conventional method, particularly in detecting gradual or minor process deviations. This drawback underscores the need for more flexible monitoring strategies, such as Empirical Bayes (EB)-based approaches, especially in industries that require high sensitivity to quality variation.

Figure 2 presents the results of the EB c-chart formulated under the squared error loss function. Using this approach, abnormal conditions are identified at the 5th, 7th, and 16th observations. Compared with the classical chart, this EB version responds more rapidly to process irregularities. The earlier detection of these variations demonstrates its higher sensitivity, which can be highly beneficial in manufacturing contexts where timely identification of defects supports waste reduction and consistent quality control.

Figure 3 presents the EB c-chart derived from the precautionary loss function. Unlike the other EB approaches, this chart detects out-of-control signals only at the 5th and 7th samples. The limited number of detections suggests that the precautionary loss function is less responsive in identifying process mean shifts. Consequently, its effectiveness appears lower than that of the EB charts based on the squared error and logarithmic loss functions.

Figure 4 illustrates the EB c-chart developed using the logarithmic loss function. This method also identifies out-of-control signals at the 5th, 7th, and 16th data points, reflecting the same pattern observed in the other EB configurations. The uniformity of the results across all EB charts demonstrates the stability and robustness of the Bayesian framework, regardless of the chosen loss function.

Overall, the empirical results indicate that the EB c-chart based on the precautionary loss function exhibits comparatively lower sensitivity in detecting process mean shifts. Unlike the other EB variations, this chart identified only two out-of-control points—at the 5th and 7th observations—suggesting a more conservative detection behavior. While its performance is less responsive, the method may still offer advantages in processes where excessive false alarms must be avoided or where only significant deviations are of concern.

5. Discussion and Conclusions

The comparative evaluation of the Empirical Bayes (EB) control charts shows that the choice of loss function plays a crucial role in monitoring performance. The EB chart based on the logarithmic loss function (LLF) consistently exhibited the highest sensitivity to process mean shifts in both simulation studies and real rivet inspection data. Its ability to detect small deviations early while maintaining stable false alarm rates indicates a well-balanced and robust detection mechanism, making it particularly suitable for industrial and environmental applications where rapid anomaly identification is essential.

In contrast, the EB chart using the precautionary loss function (PLF) behaved more conservatively, detecting fewer out-of-control points and yielding higher ARL₁ and SDRL₁ values across several scenarios. Although less sensitive than the LLF-based chart, the PLF approach offers greater resistance to overreaction due to minor random fluctuations, making it appropriate for processes where operational stability and false alarm avoidance are prioritized. Overall, while both EB methods outperform the classical c-chart by incorporating prior information and adapting control limits to the observed data, the LLF provides the best balance between early detection and reliability.

A key limitation of this study is the assumption of an exponential prior for the Poisson mean. While this assumption facilitates analytic tractability within the EB framework, it may not adequately represent processes with highly variable or multi-modal defect patterns. Future work could explore more flexible prior distributions, such as Gamma or mixture priors, to improve the model’s generalizability. Additionally, the proposed EB c-charts rely on Poisson-based count data, which may not fully capture dispersion characteristics in processes exhibiting overdispersion, zero inflation, or dependence among defect occurrences. Extending the framework to accommodate these complexities further strengthens its practical applicability.

Future work may investigate hybrid or adaptive loss functions and explore alternative modeling perspectives—such as modeling inter-occurrence times via exponential distributions—to enhance the sensitivity and stability of EB-based control charts, particularly in settings where time-to-defect information provides additional insight into process behavior.