Beyond the Standard Model with Six-Dimensional Spinors
Abstract
1. Introduction
A Review of Various Grand Unification Models
2. Three Mass Generations from 6D Spacetime
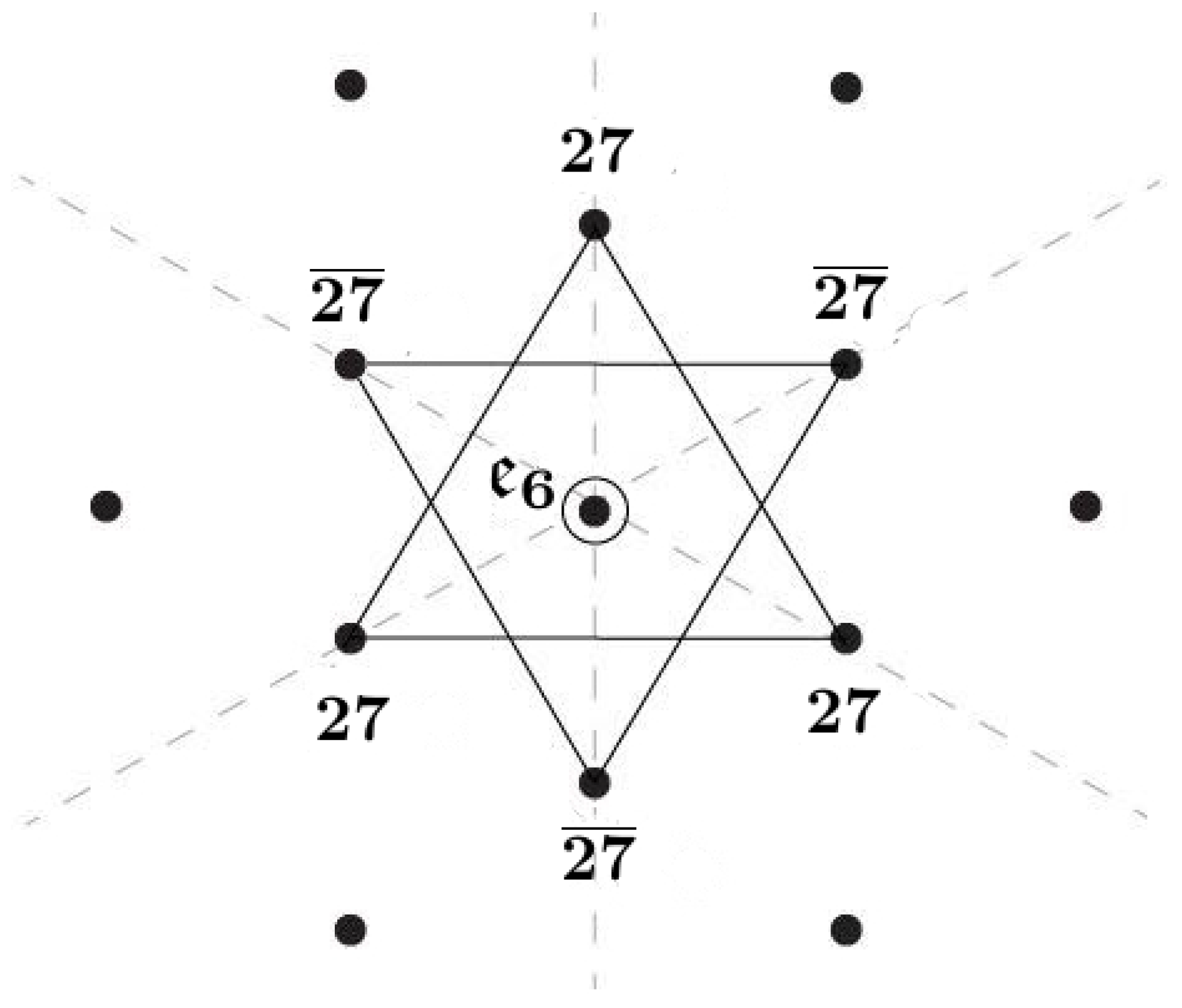
2.1. Intuition from the Magic Star of
2.2. Three Momenta with Different Mass
3. High Energy Theories from Four Spacelike Dimensions
3.1. From to GUT with Spacetime: A Threefold Way
3.2. From to Pati–Salam GUT with Spacetime: A Twofold Way
3.3. From to GUT with Spacetime: A Threefold Way
4. High Energy Theories from Four Timelike Dimensions
4.1. An Attempt for
4.2. Spacetime from
4.3. Branes and GUT Symmetry Breaking: A Glance to the Geometric Perspective
5. Summary and Conclusions
5.1. Summary
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SM | standard model |
| GUT | grand unified theory |
| dofs | degrees of freedom |
| EP | exceptional periodicity |
References
- Pati, J.C.; Salam, A. Lepton number as the fourth “color”. Phys. Rev. D 1974, 10, 275, Erratum in Phys. Rev. D 1975, 11, 703. [Google Scholar]
- Pati, J.C. Probing Grand Unification Through Neutrino Oscillations, Leptogenesis, and Proton Decay. Int. J. Mod. Phys. A 2003, 18, 4135. [Google Scholar] [CrossRef]
- Hartmann, F.; Kilian, W.; Schnitter, K. Multiple scales in Pati-Salam unification models. J. High Energy Phys. 2014, 5, 64. [Google Scholar] [CrossRef]
- Saad, S. Fermion masses and mixings, Leptogenesis and Baryon number violation in Pati-Salam model. Nucl. Phys. B 2019, 943, 114630. [Google Scholar] [CrossRef]
- Molinaro, E.; Sannino, F.; Wang, Z.W. Asymptotically safe Pati-Salam theory. Phys. Rev. D 2018, 98, 115007. [Google Scholar] [CrossRef]
- Li, T.; Mansha, A.; Sun, R. Revisiting the supersymmetric Pati–Salam models from intersecting D6-branes. Eur. Phys. J. C 2021, 81, 82. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unity of all elementary-particle forces. Phys. Rev. Lett. 1974, 32, 438. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Georgi, H. Softly broken supersymmetry and SU (5). Nucl. Phys. B 1981, 193, 150–162. [Google Scholar] [CrossRef]
- Ibáñez, L. Locally supersymmetric SU (5) grand unification. Phys. Lett. B 1982, 118, 73–78. [Google Scholar] [CrossRef]
- Buchmüller, W.; Wyler, D. Constraints on SU (5)-type leptoquarks. Phys. Lett. B 1986, 177, 377–382. [Google Scholar] [CrossRef]
- Giveon, A.; Hall, L.J.; Sarid, U. SU (5) unification revisited. Phys. Lett. B 1991, 271, 138–144. [Google Scholar] [CrossRef]
- Arnowitt, R.; Nath, P. Supersymmetric mass spectrum in SU (5) supergravity grand unification. Phys. Rev. Lett. 1992, 69, 725. [Google Scholar] [CrossRef]
- Nath, P.; Arnowitt, R. Predictions in SU (5) supergravity grand unification with proton stability and relic density constraints. Phys. Rev. Lett. 1993, 70, 3696. [Google Scholar] [CrossRef]
- Altarelli, G.; Feruglio, F. SU (5) grand unification in extra dimensions and proton decay. Phys. Lett. B 2001, 511, 257–264. [Google Scholar] [CrossRef]
- Georgi, H. The State of the Art—Gauge Theories. AIP Conf. Proc. 1975, 23, 575. [Google Scholar]
- Fritzsch, H.; Minkowski, P. Unified interactions of leptons and hadrons. Ann. Phys. 1975, 93, 193–266. [Google Scholar] [CrossRef]
- Del Aguila, F.; Ibanez, L.E. Higgs bosons in SO (10) and partial unification. Nucl. Phys. B 1981, 177, 60–86. [Google Scholar] [CrossRef]
- Aulakh, C.S.; Mohapatra, R.N. Implications of supersymmetric SO (10) grand unification. Phys. Rev. D 1983, 28, 217. [Google Scholar] [CrossRef]
- Babu, K.S.; Mohapatra, R.N. Predictive neutrino spectrum in minimal SO (10) grand unification. Phys. Rev. Lett. 1993, 70, 2845. [Google Scholar] [CrossRef] [PubMed]
- Chamseddine, A.H.; Fröhlich, J. SO (10) unification in noncommutative geometry. Phys. Rev. D 1994, 50, 2893. [Google Scholar] [CrossRef]
- Hall, L.J.; Rattazzi, R.; Sarid, U. Top quark mass in supersymmetric SO (10) unification. Phys. Rev. D 1994, 50, 7048. [Google Scholar] [CrossRef] [PubMed]
- Barr, S.M.; Raby, S. Minimal SO (10) unification. Phys. Rev. Lett. 1997, 79, 4748. [Google Scholar] [CrossRef]
- Lykken, J.; Montroy, T.; Willenbrock, S. Group-theoretic evidence for SO (10) grand unification. Phys. Lett. B 1998, 418, 141–144. [Google Scholar] [CrossRef]
- Plümacher, M. Baryon asymmetry, neutrino mixing and supersymmetric SO (10) unification. arXiv 1998, arXiv:hep-ph/9807557. [Google Scholar] [CrossRef]
- Blažek, T.; Dermíšek, R.; Raby, S. Yukawa unification in SO (10). Phys. Rev. D 2002, 65, 115004. [Google Scholar] [CrossRef]
- Özer, A.D. SO(10)-Grand Unification and Fermion Masses. Ph.D. Thesis, LMU München, Munich, Germany, 2005. [Google Scholar]
- King, S.F.; Malinský, M. Towards a complete theory of fermion masses and mixings with SO (3) family symmetry and 5D SO (10) unification. J. High Energy Phys. 2006, 2006, 071. [Google Scholar] [CrossRef][Green Version]
- Bertolini, S.; Di Luzio, L.; Malinský, M. Intermediate mass scales in the nonsupersymmetric SO (10) grand unification: A reappraisal. Phys. Rev. D 2009, 80, 015013. [Google Scholar] [CrossRef]
- Feruglio, F.; Patel, K.M.; Vicino, D. A realistic pattern of fermion masses from a five-dimensional SO (10) model. J. High Energy Phys. 2015, 2015, 1–30. [Google Scholar] [CrossRef]
- Babu, K.S.; Bajc, B.; Saad, S. Yukawa sector of minimal SO (10) unification. J. High Energy Phys. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- de Anda, F.J.; King, S.F.; Perdomo, E. SO (10)× S4 grand unified theory of flavour and leptogenesis. J. High Energy Phys. 2017, 2017, 1–30. [Google Scholar] [CrossRef]
- Gürsey, F. First Workshop on Grand Unification: New England Center University of New Hampshire 10–12 April 1980; Birkhäuser: Boston, MA, USA, 1980; pp. 39–55. [Google Scholar]
- Barbieri, R.; Nanopoulos, D.V. An exceptional model for grand unification. Phys. Lett. B 1980, 91, 369–375. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Mohapatra, R.N.; Pal, P.B. Implications of E 6 grand unification. Phys. Rev. D 1986, 33, 2010. [Google Scholar] [CrossRef] [PubMed]
- Hall, L.; Nomura, Y.; Okui, T.; Smith, D. SO (10) unified theories in six dimensions. Phys. Rev. D 2002, 65, 035008. [Google Scholar] [CrossRef]
- Ito, M.; Kuwakino, S.; Maekawa, N.; Moriyama, S.; Takahashi, K.; Takei, K.; Teraguchi, S.; Yamashita, T. E 6 grand unified theory with three generations from heterotic string theory. Phys. Rev. D 2011, 83, 091703. [Google Scholar] [CrossRef]
- Chiang, C.-W.; Nomura, T.; Sato, J. Gauge-Higgs Unification Models in Six Dimensions with Extra Space and GUT Gauge Symmetry. Adv. High Energy Phys. 2012, 2012, 260848. [Google Scholar] [CrossRef]
- Benli, S.; Dereli, T. Masses and Mixing of Neutral Leptons in a Grand Unified E6 Model with Intermediate Pati-Salam Symmetry. Int. J. Theor. Phys. 2018, 57, 2343–2358. [Google Scholar] [CrossRef]
- Schwichtenberg, J.; Tremper, P.; Ziegler, R. A grand-unified Nelson–Barr model. Eur. Phys. J. C 2018, 78, 1–11. [Google Scholar] [CrossRef]
- Gürsey, F. New Pathways in High-Energy Physics I: Magnetic Charge and Other Fundamental Approaches; Springer: Boston, MA, USA, 1976; pp. 231–248. [Google Scholar]
- Lednický, R.; Tzeitlin, V. Neutral currents in the E7 theory. Phys. Lett. B 1979, 88, 302–305. [Google Scholar] [CrossRef]
- Kugo, T.; Yanagida, T. Unification of families based on a coset space E7/SU (5)× SU (3)× U (1). Phys. Lett. B 1984, 134, 313–317. [Google Scholar] [CrossRef]
- Bars, I. Group Theoretical Methods in Physics; Springer: Berlin/Heidelberg, Germany, 1980; pp. 560–566. [Google Scholar]
- Baaklini, N.S. Supergrand unification in E8. Phys. Lett. B 1980, 91, 376–378. [Google Scholar] [CrossRef]
- Konshtein, S.E.; Fradkin, E.S. Asymptotically supersymmetrical model of a single interaction based on E8. Pisma Zh. Eksp. Teor. Fiz. 1980, 32, 575. [Google Scholar]
- Koca, M. On tumbling E8. Phys. Lett. B 1981, 107, 73–76. [Google Scholar] [CrossRef]
- Ong, C.L. Supersymmetric models for quarks and leptons with nonlinearly realized E 8 symmetry. Phys. Rev. D 1985, 31, 3271. [Google Scholar] [CrossRef]
- Itoh, K.; Kugo, T.; Kunitomo, H. Supersymmetric Non-Linear Lagrangians of Kählerian Coset Spaces G/H: G= E 6, E 7 and E 8. Prog. Theor. Phys. 1986, 75, 386–426. [Google Scholar] [CrossRef]
- Buchmüller, W.; Napoly, O. Exceptional coset spaces and the spectrum of quarks and leptons. Phys. Lett. B 1985, 163, 161–166. [Google Scholar] [CrossRef]
- Barr, S.M. E 8 family unification, mirror fermions, and new low-energy physics. Phys. Rev. D 1988, 37, 204. [Google Scholar] [CrossRef]
- Mahapatra, S.; Deo, B.B. Supergravity-induced E 8 gauge hierarchies. Phys. Rev. D 1988, 38, 3554. [Google Scholar] [CrossRef] [PubMed]
- Ellwanger, U. Dynamical electroweak, GUT and family symmetry breaking in an E8 SUSY sigma model. Nucl. Phys. B 1991, 356, 46–68. [Google Scholar] [CrossRef]
- Adler, S.L. Should E8 SUSY Yang–Mills be reconsidered as a family unification model? Phys. Lett. B 2002, 533, 121–125. [Google Scholar] [CrossRef]
- Adler, S.L. Further thoughts on supersymmetric E8 as a family and grand unification theory. arXiv 2004, arXiv:0401212. [Google Scholar]
- Lisi, A.G. An Exceptionally Simple Theory of Everything. arXiv 2007, arXiv:0711.0770. [Google Scholar]
- Pavšič, M. A novel view on the physical origin of E8. J. Phys. A Math. Theor. 2008, 41, 332001. [Google Scholar] [CrossRef]
- Castro Perelman, C. The Exceptional E8 geometry of clifford (16) superspace and conformal gravity yang–mills grand unification. Int. J. Geom. Methods Mod. Phys. 2009, 6, 385–417. [Google Scholar] [CrossRef]
- Lisi, A.G. An Explicit Embedding of Gravity and the Standard Model in E8. arXiv 2010, arXiv:1006.4908. [Google Scholar]
- Castro, C. A Clifford algebra-based grand unification program of gravity and the Standard Model: A review study. Can. J. Phys. 2014, 92, 1501–1527. [Google Scholar] [CrossRef]
- Douglas, A.; Repka, J. The GraviGUT algebra is not a subalgebra of E8, but E8 does contain an extended GraviGUT algebra. SIGMA 2014, 10, 072. [Google Scholar]
- Lisi, A.G. Lie Group Cosmology. arXiv 2015, arXiv:1506.08073. [Google Scholar]
- Green, M.B.; Schwarz, J.H. Anomaly cancellations in supersymmetric D= 10 gauge theory and superstring theory. Phys. Lett. B 1984, 149, 117–122. [Google Scholar] [CrossRef]
- Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. Vacuum configurations for superstrings. Nucl. Phys. B 1985, 258, 46–74. [Google Scholar] [CrossRef]
- Dixon, L.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on orbifolds. Nucl. Phys. B 1985, 261, 678–686. [Google Scholar] [CrossRef]
- Dixon, L.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on orbifolds (II). Nucl. Phys. B 1986, 274, 285–314. [Google Scholar] [CrossRef]
- Greene, B.R. Superstrings: Topology, Geometry and Phenomenology and Astrophysical Implications of Supersymmetric Models. Ph.D. Thesis, University of Oxford, Oxford, UK, 1986. [Google Scholar]
- Damour, T.; Henneaux, M.; Nicolai, H. E 10 and a small tension expansion of M theory. Phys. Rev. Lett. 2002, 89, 221601. [Google Scholar] [CrossRef]
- Kleinschmidt, A.; Nicolai, H.; Palmkvist, J. K (E9) from K (E10). J. High Energy Phys. 2007, 2007, 051. [Google Scholar] [CrossRef]
- Kleinschmidt, A.; Nicolai, H. Maximal supergravities and the E10 model. J. Phys. Conf. Ser. 2006, 33, 150. [Google Scholar] [CrossRef]
- Houart, L. Kac-Moody algebras in gravity and M-theories. AIP Conf. Proc. 2006, 841, 298. [Google Scholar]
- Palmkvis, J. Exceptional Lie algebras and M-theory. arXiv 2009, arXiv:0912.1612. [Google Scholar]
- West, P. E11 and M theory. Class. Quantum Gravity 2001, 18, 4443. [Google Scholar] [CrossRef]
- de Buyl, S. Kac-Moody Algebras in M-theory. arXiv 2006, arXiv:0608161. [Google Scholar]
- Bossard, G.; Kleinschmidt, A.; Sezgin, E. On supersymmetric E11 exceptional field theory. J. High Energy Phys. 2019, 10, 165. [Google Scholar] [CrossRef]
- Cheung, C.; O’Connell, D. Amplitudes and spinor-helicity in six dimensions. J. High Energy Phys. 2009, 2009, 075. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.; Dennen, T.; Huang, Y.T.; Ita, H. Generalized unitarity and six-dimensional helicity. Phys. Rev. D 2011, 83, 085022. [Google Scholar] [CrossRef]
- Chester, D. Bern-Carrasco-Johansson relations for one-loop QCD integral coefficients. Phys. Rev. D 2016, 93, 065047. [Google Scholar] [CrossRef]
- Babu, K.S.; Barr, S.M.; Kyae, B. Family unification in five and six dimensions. Phys. Rev. D 2002, 65, 115008. [Google Scholar] [CrossRef]
- Kojima, K.; Takenaga, K.; Yamashita, T. The standard model gauge symmetry from higher-rank unified groups in grand gauge-Higgs unification models. J. High Energy Phys. 2017, 2017, 1–35. [Google Scholar] [CrossRef]
- Sezgin, E. Super Yang-Mills in (11, 3) dimensions. Phys. Lett. B 1997, 403, 265–272. [Google Scholar] [CrossRef]
- Bars, I. A case for 14 dimensions. Phys. Lett. B 1997, 403, 257–264. [Google Scholar] [CrossRef]
- Nesti, F.; Percacci, R. Gravi-weak unification. J. Phys. A Math. Theor. 2008, 41, 075405. [Google Scholar] [CrossRef]
- Alexander, S.H. Isogravity: Toward an electroweak and gravitational unification. arXiv 2007, arXiv:0706.4481. [Google Scholar]
- Percacci, R. Mixing internal and spacetime transformations: Some examples and counterexamples. J. Phys. A Math. Theor. 2008, 41, 335403. [Google Scholar] [CrossRef]
- Das, C.R.; Laperashvili, L.V.; Tureanu, A. Graviweak unification, invisible universe and dark energy. Int. J. Mod. Phys. A 2013, 28, 1350085. [Google Scholar] [CrossRef]
- Froggatt, C.D.; Das, C.R.; Laperashvili, L.V.; Nielsen, H.B.; Tureanu, A. Gravi-weak unification and multiple point principle. arXiv 2013, arXiv:1311.4413. [Google Scholar]
- Das, C.R.; Laperashvili, L.V. Graviweak unification in the visible and invisible universe and inflation from the Higgs field false vacuum. arXiv 2014, arXiv:1409.1115. [Google Scholar]
- Laperashvili, L.V.; Nielsen, H.B.; Tureanu, A. Standard model and graviweak unification with (super) renormalizable gravity. Part I: Visible and invisible sectors of the universe. Int. J. Mod. Phys. A 2015, 30, 1550044. [Google Scholar] [CrossRef]
- Laperashvili, L.V.; Nielsen, H.B.; Sidharth, B.G. Planck scale physics, gravi-weak unification and the Higgs inflation. arXiv 2015, arXiv:1503.03911. [Google Scholar]
- Das, C.R.; Laperashvili, L.V. False vacuum Higgs inflation and the graviweak unification. arXiv 2015, arXiv:1506.08366. [Google Scholar]
- Sidharth, B.G.; Das, C.R.; Laperashvili, L.V.; Nielsen, H.B. Gravi-weak unification and the black-hole-hedgehog’s solution with magnetic field contribution. Int. J. Mod. Phys. A 2018, 33, 1850188. [Google Scholar] [CrossRef]
- Nesti, F.; Percacci, R. Chirality in unified theories of gravity. Phys. Rev. D 2010, 81, 025010. [Google Scholar] [CrossRef]
- Percacci, R. Gravity from a particle physicists’ perspective. arXiv 2009, arXiv:0910.5167. [Google Scholar]
- Lisi, A.G.; Smolin, L.; Speziale, S. Unification of gravity, gauge fields and Higgs bosons. J. Phys. A Math. Theor. 2010, 43, 445401. [Google Scholar] [CrossRef]
- Rios, M.; Marrani, A.; Chester, D. Geometry of exceptional super Yang-Mills theories. Phys. Rev. D 2019, 99, 046004. [Google Scholar] [CrossRef]
- Rios, M.; Marrani, A.; Chester, D. Exceptional super Yang-Mills in 27+ 3 and worldvolume M-theory. Phys. Lett. B 2020, 808, 135674. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.M.; Johansson, H. New relations for gauge-theory amplitudes. Phys. Rev. D 2008, 78, 085011. [Google Scholar] [CrossRef]
- Bern, Z.; Dennen, T.; Huang, Y.T.; Kiermaier, M. Gravity as the square of gauge theory. Phys. Rev. D 2010, 82, 065003. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.M.; Dixon, L.J.; Johansson, H.; Roiban, R. Simplifying multiloop integrands and ultraviolet divergences of gauge theory and gravity amplitudes. Phys. Rev. D 2012, 85, 105014. [Google Scholar] [CrossRef]
- Bern, Z.; Davies, S.; Dennen, T.; Huang, Y.T.; Nohle, J. Color-kinematics duality for pure Yang-Mills and gravity at one and two loops. Phys. Rev. D 2015, 92, 045041. [Google Scholar] [CrossRef]
- Bern, Z.; Davies, S.; Nohle, J. Double-copy constructions and unitarity cuts. Phys. Rev. D 2016, 93, 105015. [Google Scholar] [CrossRef]
- Monteiro, R.; O’Connell, D.; White, C.D. Black holes and the double copy. J. High Energy Phys. 2014, 2014, 1–23. [Google Scholar] [CrossRef]
- Ridgway, A.K.; Wise, M.B. Static Spherically Symmetric Kerr-Schild Metrics and Implications for the Classical Double Copy. arXiv 2015, arXiv:1512.02243. [Google Scholar] [CrossRef]
- Chester, D. Radiative double copy for Einstein-Yang-Mills theory. Phys. Rev. D 2018, 97, 084025. [Google Scholar] [CrossRef]
- Chiodaroli, M.; Günaydin, M.; Johansson, H.; Roiban, R. Gauged supergravities and spontaneous supersymmetry breaking from the double copy construction. Phys. Rev. Lett. 2018, 120, 171601. [Google Scholar] [CrossRef]
- Azevedo, T.; Chiodaroli, M.; Johansson, H.; Schlotterer, O. Heterotic and bosonic string amplitudes via field theory. J. High Energy Phys. 2018, 2018, 1–42. [Google Scholar] [CrossRef]
- Cho, W.; Lee, K. Heterotic Kerr-Schild double field theory and classical double copy. J. High Energy Phys. 2019, 2019, 1–30. [Google Scholar] [CrossRef]
- Rudychev, I.; Sezgin, E. Superparticles in D> 11. Phys. Lett. 1997, B415, 363. [Google Scholar] [CrossRef]
- Rudychev, I.; Sezgin, E.; Sundell, P. Supersymmetry in dimensions beyond eleven. Nucl. Phys. B 1998, 68, 285–294. [Google Scholar] [CrossRef]
- Popławski, N.J. Nonsingular Dirac particles in spacetime with torsion. Phys. Lett. B 2010, 690, 73. [Google Scholar] [CrossRef]
- Popławski, N. Noncommutative momentum and torsional regularization. Found. Phys. 2020, 50, 900–923. [Google Scholar] [CrossRef]
- Popławski, N. Torsional regularization of vertex function. arXiv 2018, arXiv:1807.07068. [Google Scholar]
- Bern, Z.; Chi, H.H.; Dixon, L.; Edison, A. Two-loop renormalization of quantum gravity simplified. Phys. Rev. D 2017, 95, 046013. [Google Scholar] [CrossRef]
- MacDowell, S.W.; Mansouri, F. Unified geometric theory of gravity and supergravity. Phys. Rev. Lett. 1977, 38, 739. [Google Scholar] [CrossRef]
- Wise, D.K. MacDowell–Mansouri gravity and Cartan geometry. Class. Quantum Gravity 2010, 27, 155010. [Google Scholar] [CrossRef]
- Bjorken, J. Darkness: What comprises empty space? Annalen der Physik 2013, 525, A67–A79. [Google Scholar] [CrossRef]
- Aydemir, U. A scale at 10 MeV, gravitational topological vacuum, and large extra dimensions. Universe 2018, 4, 80. [Google Scholar] [CrossRef]
- Krasnov, K.; Percacci, R. Gravity and unification: A review. Class. Quantum Gravity 2018, 35, 143001. [Google Scholar] [CrossRef]
- Distler, J.; Garibaldi, S. There is no “theory of everything” inside E8. Commun. Math. Phys. 2010, 298, 419–436. [Google Scholar] [CrossRef]
- Maalampi, J.; Roos, M. Physics of mirror fermions. Phys. Rep. 1990, 186, 53–96. [Google Scholar] [CrossRef]
- Mukai, S. Simple Lie algebra and Legendre variety. Nagoya Sūri Forum 1996, 3, 1–12. [Google Scholar]
- Truini, P. Exceptional Lie algebras, SU (3), and Jordan pairs. Pac. J. Math. 2012, 260, 227–243. [Google Scholar] [CrossRef]
- Marrani, A.; Truini, P. Exceptional lie algebras at the very foundations of space and time. P-Adic Numbers Ultrametric Anal. Appl. 2016, 8, 68–86. [Google Scholar] [CrossRef][Green Version]
- Slansky, R. Group theory for unified model building. Phys. Rep. 1981, 79, 1–128. [Google Scholar] [CrossRef]
- Baez, J.; Huerta, J. The algebra of grand unified theories. Bull. Am. Math. Soc. 2010, 47, 483–552. [Google Scholar] [CrossRef]
- Barr, S.M. A new symmetry breaking pattern for SO (10) and proton decay. Phys. Lett. B 1982, 112, 219–222. [Google Scholar] [CrossRef]
- Derendinger, J.P.; Kim, J.E.; Nanopoulos, D.V. Anti-su (5). Phys. Lett. B 1984, 139, 170–176. [Google Scholar] [CrossRef]
- Antoniadis, I.; Ellis, J.; Hagelin, J.S.; Nanopoulos, D.V. Supersymmetric flipped SU (5) revitalized. Phys. Lett. B 1987, 194, 231–235. [Google Scholar] [CrossRef]
- Tamvakis, K. Flipped so (10). Phys. Lett. B 1988, 201, 95–100. [Google Scholar] [CrossRef]
- Antoniadis, I.; Ellis, J.R.; Hagelin, J.S.; Nanopoulos, D.V. The flipped SU (5) x U (1) string model revamped. Phys. Lett. B 1989, 231, 65–74. [Google Scholar] [CrossRef]
- Lopez, J.L.; Nanopoulos, D.V. Flipped SU(5): Origins and Recent Developments. arXiv 1991, arXiv:9110036. [Google Scholar]
- Huang, C.S.; Li, T.; Liu, C.; Shock, J.P.; Wu, F.; Wu, Y.L. Embedding flipped SU (5) into SO (10). J. High Energy Phys. 2006, 2006, 035. [Google Scholar] [CrossRef]
- Chen, C.M.; Chung, Y.C. Flipped SU (5) GUTs from E 8 singularities in F-theory. J. High Energy Phys. 2011, 2011, 49. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.; Nagata, N.; Nanopoulos, D.V.; Olive, K.A. Symmetry breaking and reheating after inflation in no-scale flipped SU (5). J. Cosmol. Astropart. Phys. 2019, 2019, 9. [Google Scholar] [CrossRef]
- Croon, D.; Gonzalo, T.E.; Graf, L.; Košnik, N.; White, G. GUT physics in the era of the LHC. Front. Phys. 2019, 7, 76. [Google Scholar] [CrossRef]
- Maekawa, N.; Yamashita, T. Flipped SO (10) model. Phys. Lett. B 2003, 567, 330–338. [Google Scholar] [CrossRef]
- Bertolini, S.; Di Luzio, L.; Malinský, M. Minimal flipped S O (10) U (1) supersymmetric Higgs model. Phys. Rev. D 2011, 83, 035002. [Google Scholar] [CrossRef]
- Dubois-Violette, M. Exceptional quantum geometry and particle physics. Nucl. Phys. B 2016, 912, 426–449. [Google Scholar] [CrossRef]
- Todorov, I.; Dubois-Violette, M. Deducing the symmetry of the standard model from the automorphism and structure groups of the exceptional Jordan algebra. Int. J. Mod. Phys. A 2018, 33, 1850118. [Google Scholar] [CrossRef]
- Dubois-Violette, M.; Todorov, I. Exceptional quantum geometry and particle physics II. Nucl. Phys. B 2019, 938, 751–761. [Google Scholar] [CrossRef]
- Schwichtenberg, J. Dark matter in E6 Grand unification. J. High Energy Phys. 2018, 2018, 1–25. [Google Scholar] [CrossRef]
- de Rujula, A.; Georg, H.; Glashow, S.L. Fifth Workshop on Grand Unification; Kang, K., Fried, H., Frampton, F., Eds.; World Scientific: Singapore, 1984. [Google Scholar]
- Babu, K.S.; He, X.G.; Pakvasa, S. Neutrino masses and proton decay modes in SU (3)× SU (3)× SU (3) trinification. Phys. Rev. D 1986, 33, 763. [Google Scholar] [CrossRef]
- Lazarides, G.; Panagiotakopoulos, C. MSSM from SUSY trinification. Phys. Lett. B 1994, 336, 190–193. [Google Scholar] [CrossRef][Green Version]
- Lazarides, G.; Panagiotakopoulos, C. Minimal supersymmetric standard model and large tan from SUSY trinification. Phys. Rev. D 1995, 51, 2486. [Google Scholar] [CrossRef]
- Kim, J.E. Z3 orbifold construction of SU (3) 3 GUT with sin2W0= 38. Phys. Lett. B 2003, 564, 35–41. [Google Scholar] [CrossRef]
- Willenbrock, S. Triplicated trinification. Phys. Lett. B 2003, 561, 130–134. [Google Scholar] [CrossRef][Green Version]
- Carone, C.D.; Conroy, J.M. Higgsless grand unified theory breaking and trinification. Phys. Rev. D 2004, 70, 075013. [Google Scholar] [CrossRef]
- Hetzel, J. Phenomenology of a left-right-symmetric model inspired by the trinification model. arXiv 2015, arXiv:1504.06739. [Google Scholar]
- Camargo-Molina, J.E.; Morais, A.P.; Pasechnik, R.; Wessén, J. On a radiative origin of the Standard Model from Trinification. J. High Energy Phys. 2016, 2016, 1–40. [Google Scholar] [CrossRef]
- Babu, K.S.; Bajc, B.; Nemevšek, M.; Tavartkiladze, Z. Trinification at the TeV scale. AIP Conf. Proc. 2017, 1900, 020002. [Google Scholar]
- Fukugita, M.; Yanagida, T.; Yoshimura, M. NN oscillation without left-right symmetry. Phys. Lett. B 1982, 109, 369–372. [Google Scholar] [CrossRef]
- Majumdar, P. NN oscillations in an SU (6) GUT: With and without supersymmetry. Phys. Lett. B 1983, 121, 25–29. [Google Scholar] [CrossRef]
- Tabata, K.; Umemura, I.; Yamamoto, K. A realistic SU (6) GUT with dynamical generation of gauge hierarchy. Prog. Theor. Phys. 1984, 71, 615–632. [Google Scholar] [CrossRef]
- Hartanto, A.; Handoko, L.T. Grand unified theory based on the SU (6) symmetry. Phys. Rev. D 2005, 71, 095013. [Google Scholar] [CrossRef]
- Huang, C.S.; Li, W.J.; Wu, X.H. E6 GUT through effects of dimension-5 operators. J. Phys. Commun. 2017, 1, 055025. [Google Scholar] [CrossRef]
- Kawase, H.; Maekawa, N. Flavor structure of E 6 GUT models. Prog. Theor. Phys. 2010, 123, 941–955. [Google Scholar] [CrossRef]
- Truini, P.; Rios, M.; Marrani, A. The Magic Star of Exceptional Periodicity. arXiv 2017, arXiv:1711.07881. [Google Scholar]
- McCrimmon, K. A Taste of Jordan Algebras; Springer: New York, NY, USA, 2004. [Google Scholar]
- Wilczek, F.; Zee, A. Families from spinors. Phys. Rev. D 1982, 25, 553. [Google Scholar] [CrossRef]
- BenTov, Y.; Zee, A. Origin of families and S O (18) grand unification. Phys. Rev. D 2016, 93, 065036. [Google Scholar] [CrossRef]
- Reig, M.; Valle, J.W.; Vaquera-Araujo, C.A.; Wilczek, F. A model of comprehensive unification. Phys. Lett. B 2017, 774, 667–670. [Google Scholar] [CrossRef]
- Reig, M.; Valle, J.W.; Wilczek, F. SO (3) family symmetry and axions. Phys. Rev. D 2018, 98, 095008. [Google Scholar] [CrossRef]
- De Graaf, W.A.; Marrani, A. Real forms of embeddings of maximal reductive subalgebras of the complex simple Lie algebras of rank up to 8. J. Phys. A Math. Theor. 2020, 53, 155203. [Google Scholar] [CrossRef]
- Floerchinger, S. Real Clifford algebras and their spinors for relativistic fermions. Universe 2021, 7, 168. [Google Scholar] [CrossRef]
- King, S.F. Predicting neutrino parameters from SO (3) family symmetry and quark-lepton unification. J. High Energy Phys. 2005, 2005, 105. [Google Scholar] [CrossRef]
- Wilson, R.A. Subgroups of Clifford algebras. arXiv 2020, arXiv:2011.05171. [Google Scholar]
- Wilson, R.A.; Dray, T.E.V.I.A.N.; Manogue, C.A. An octonionic construction of E8 and the Lie algebra magic square. arXiv 2022, arXiv:2204.04996. [Google Scholar]
- Manogue, C.A.; Dray, T.; Wilson, R.A. Octions: An E8 description of the Standard Model. arXiv 2022, arXiv:2204.05310. [Google Scholar] [CrossRef]
- Gogberashvili, M.; Sakhelashvili, O. Geometrical Applications of Split Octonions. arXiv 2015, arXiv:1506.01012. [Google Scholar] [CrossRef]
- Marrani, A.; Corradetti, D.; Chester, D.; Aschheim, R.; Irwin, K. A magic approach to octonionic Rosenfeld spaces. arXiv 2022, arXiv:2212.06426. [Google Scholar]
- Ivanov, E.A.; Niederle, J. Gauge formulation of gravitation theories. I. The Poincaré, de Sitter, and conformal cases. Phys. Rev. D 1982, 25, 976. [Google Scholar] [CrossRef]
- Günaydin, M.; Sierra, G.; Townsend, P.K. Exceptional supergravity theories and the magic square. Phys. Lett. B 1983, 133, 72–76. [Google Scholar] [CrossRef]
- Günaydin, M.; Sierra, G.; Townsend, P.K. The geometry of N = 2 Maxwell-Einstein supergravity and Jordan algebras. Nucl. Phys. B 1984, 242, 244–268. [Google Scholar]
- Kawai, H.; Lewellen, D.C.; Tye, S.H. A relation between tree amplitudes of closed and open strings. Nucl. Phys. B 1986, 26, 1–23. [Google Scholar] [CrossRef]
- Cheung, C.; Remmen, G.N. Twofold symmetries of the pure gravity action. J. High Energy Phys. 2017, 2017, 1–22. [Google Scholar] [CrossRef]
- Cheung, C.; Remmen, G.N. Hidden simplicity of the gravity action. J. High Energy Phys. 2017, 2017, 1–18. [Google Scholar] [CrossRef]
- Chu, C.S.; Giataganas, D. AdS/dS CFT correspondence. Phys. Rev. D 2016, 94, 106013. [Google Scholar] [CrossRef]
- Langacker, P. Grand unified theories and proton decay. Phys. Rep. 1981, 72, 185–385. [Google Scholar] [CrossRef]
- Chisholm, J.S.R.; Farwell, R.S. Clifford Algebras and Their Applications in Mathematical Physics: Proceedings of Second Workshop Held at Montpellier, France, 1989; Springer: Dordrecht, The Netherlands, 1992; pp. 363–370. [Google Scholar]
- Krasnov, K. Spontaneous symmetry breaking and gravity. Phys. Rev. D 2012, 85, 125023. [Google Scholar] [CrossRef]
- Das, S.; Faizal, M. Dimensional reduction via a novel Higgs mechanism. Gen. Relativ. Gravit. 2018, 50, 87. [Google Scholar] [CrossRef]
- Goldberger, W.D.; Grinstein, B.; Skiba, W. Distinguishing the Higgs boson from the dilaton at the Large Hadron Collider. Phys. Rev. Lett. 2008, 100, 111802. [Google Scholar] [CrossRef] [PubMed]
- Dijkgraaf, R.; Verlinde, E.; Verlinde, H. BPS quantization of the five-brane. Nucl. Phys. B 1997, 486, 89–113. [Google Scholar] [CrossRef][Green Version]
- Hestenes, D. Space-time structure of weak and electromagnetic interactions. Found. Phys. 1982, 12, 153–168. [Google Scholar] [CrossRef]
- Chisholm, J.S.R.; Farwell, R.S. Electroweak spin gauge theories and the frame field. J. Phys. A Math. Gen. 1987, 20, 6561. [Google Scholar] [CrossRef]
- Trayling, G.; Baylis, W.E. A geometric basis for the standard-model gauge group. J. Phys. A Math. Gen. 2001, 34, 3309. [Google Scholar] [CrossRef]
- Hestenes, D. Gauge gravity and electroweak theory. In Proceedings of the Eleventh Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, Berlin, Germany, 23–29 July 2008. [Google Scholar]
- Sugamoto, A. 4d gauge theory and gravity generated from 3d gauge theory and gravity at high energy. Prog. Theor. Phys. 2002, 107, 793–804. [Google Scholar] [CrossRef]
- Todorov, I.; Drenska, S. Octonions, Exceptional Jordan Algebra and The Role of The Group F4 in Particle Physics. Adv. Appl. Clifford Algebr. 2018, 28, 82. [Google Scholar] [CrossRef]
- Krasnov, K. SO (9) characterization of the standard model gauge group. J. Math. Phys. 2021, 62, 021703. [Google Scholar] [CrossRef]
- Furey, C. Three generations, two unbroken gauge symmetries, and one eight-dimensional algebra. Phys. Lett. B 2018, 785, 84–89. [Google Scholar] [CrossRef]
- Todorov, I. Exceptional Quantum Algebra for the Standard Model of Particle Physics. Springer Proc. Math. Stat. 2019, 335, 29–52. [Google Scholar]
- Bern, Z.; Carrasco, J.J.M.; Johansson, H. Perturbative quantum gravity as a double copy of gauge theory. Phys. Rev. Lett. 2010, 105, 061602. [Google Scholar] [CrossRef] [PubMed]
- Baez, J.C.; Huerta, J. Division algebras and supersymmetry I. Proc. Symp. Pure Maths. 2010, 81, 65. [Google Scholar]
- Truini, P.; Marrani, A.; Rios, M. Magic star and exceptional periodicity: An approach to quantum gravity. J. Phys. Conf. Ser. 2019, 1194, 012106. [Google Scholar] [CrossRef]
- Vafa, C. Evidence for F-theory. Nucl. Phys. B 1996, 469, 403–415. [Google Scholar] [CrossRef]
- Bars, I. S theory. Phys. Rev. 1997, D55, 2373. [Google Scholar]
- Bars, I.; Kuo, Y.C. Super Yang-Mills theory in 10+ 2 dimensions, The 2T-physics Source for N= 4 SYM and M (atrix) Theory. arXiv 2010, arXiv:1008.4761. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chester, D.; Marrani, A.; Rios, M. Beyond the Standard Model with Six-Dimensional Spinors. Particles 2023, 6, 144-172. https://doi.org/10.3390/particles6010008
Chester D, Marrani A, Rios M. Beyond the Standard Model with Six-Dimensional Spinors. Particles. 2023; 6(1):144-172. https://doi.org/10.3390/particles6010008
Chicago/Turabian StyleChester, David, Alessio Marrani, and Michael Rios. 2023. "Beyond the Standard Model with Six-Dimensional Spinors" Particles 6, no. 1: 144-172. https://doi.org/10.3390/particles6010008
APA StyleChester, D., Marrani, A., & Rios, M. (2023). Beyond the Standard Model with Six-Dimensional Spinors. Particles, 6(1), 144-172. https://doi.org/10.3390/particles6010008





