Situational Awareness for Oil Storage Tank Accidents Based on Complex Networks and Evidence Theory
Abstract
1. Introduction
2. Methods
2.1. Complex Network Node Assessment Metrics
2.2. Cloud Model Theory
- (1)
- The calculation method for is shown in Equation (6):
- (2)
- The calculation method for is shown in Equation (7):
- (3)
- The calculation method for is shown in Equation (8):where is an empirically determined value based on expert judgment. To keep the uncertainty within an acceptable range during the identification of risk threshold intervals, the hyper-entropy value is set to 0.05.
2.3. Dempster-Shafer Evidence Theory
3. Results
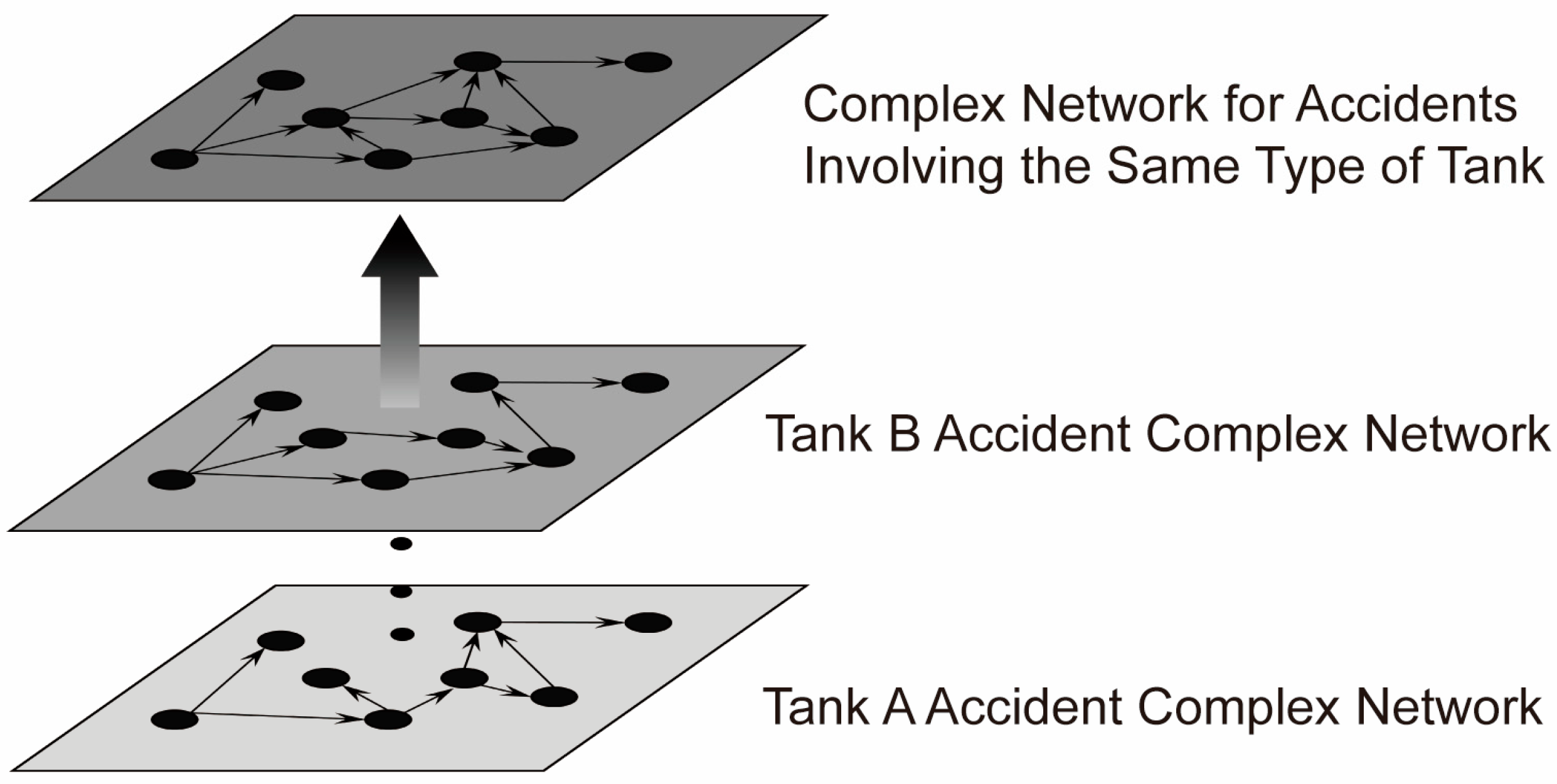
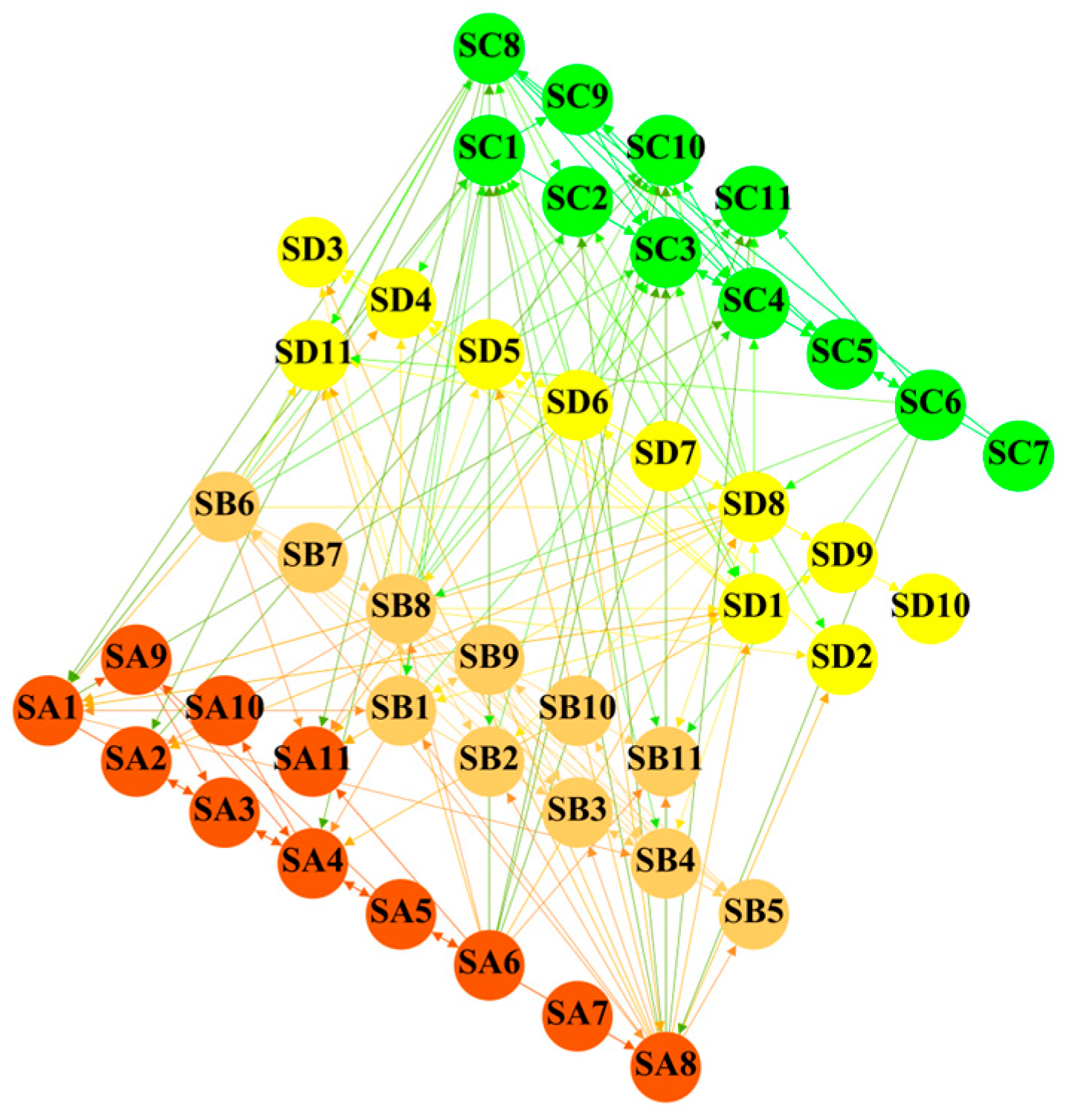
3.1. Constructing a Multi-Layer Network Model of Oil Storage Tank Accident Chains
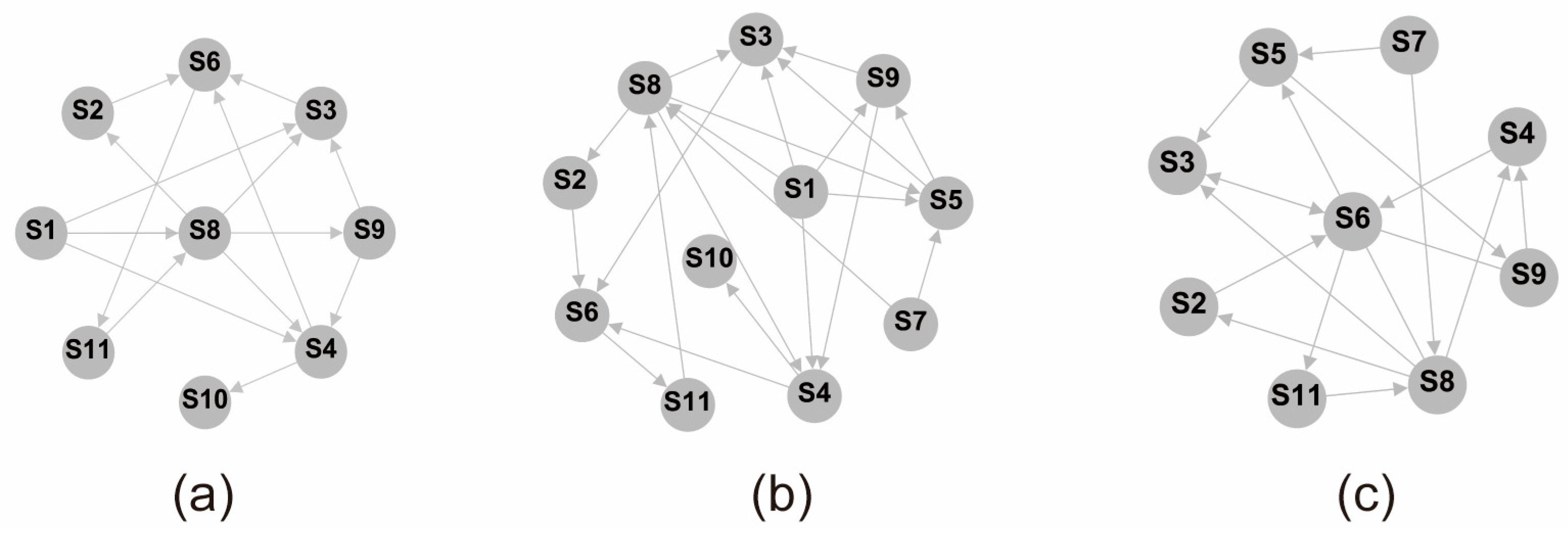
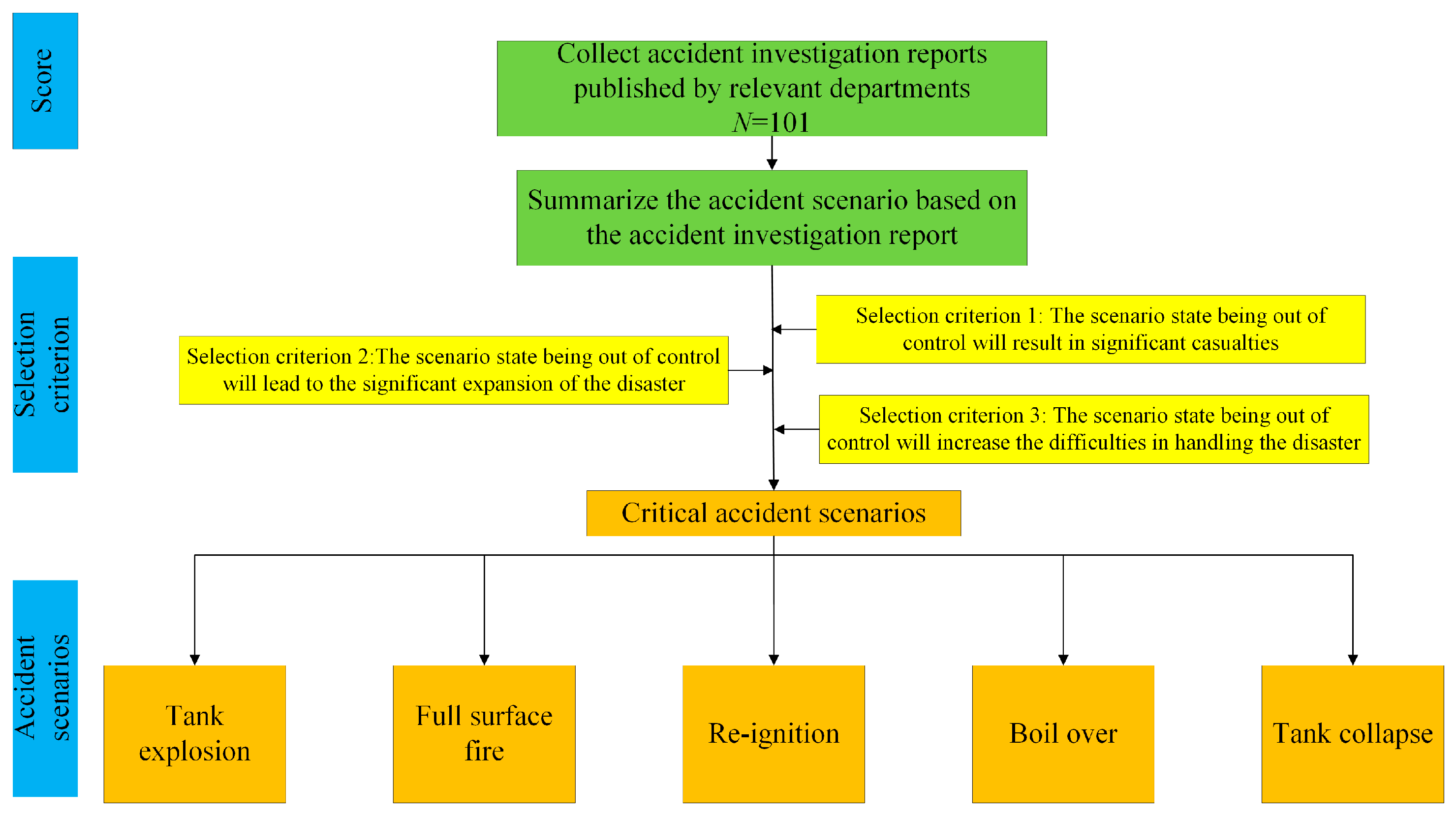
3.1.1. Identification of Oil Storage Tank Accident Scenarios
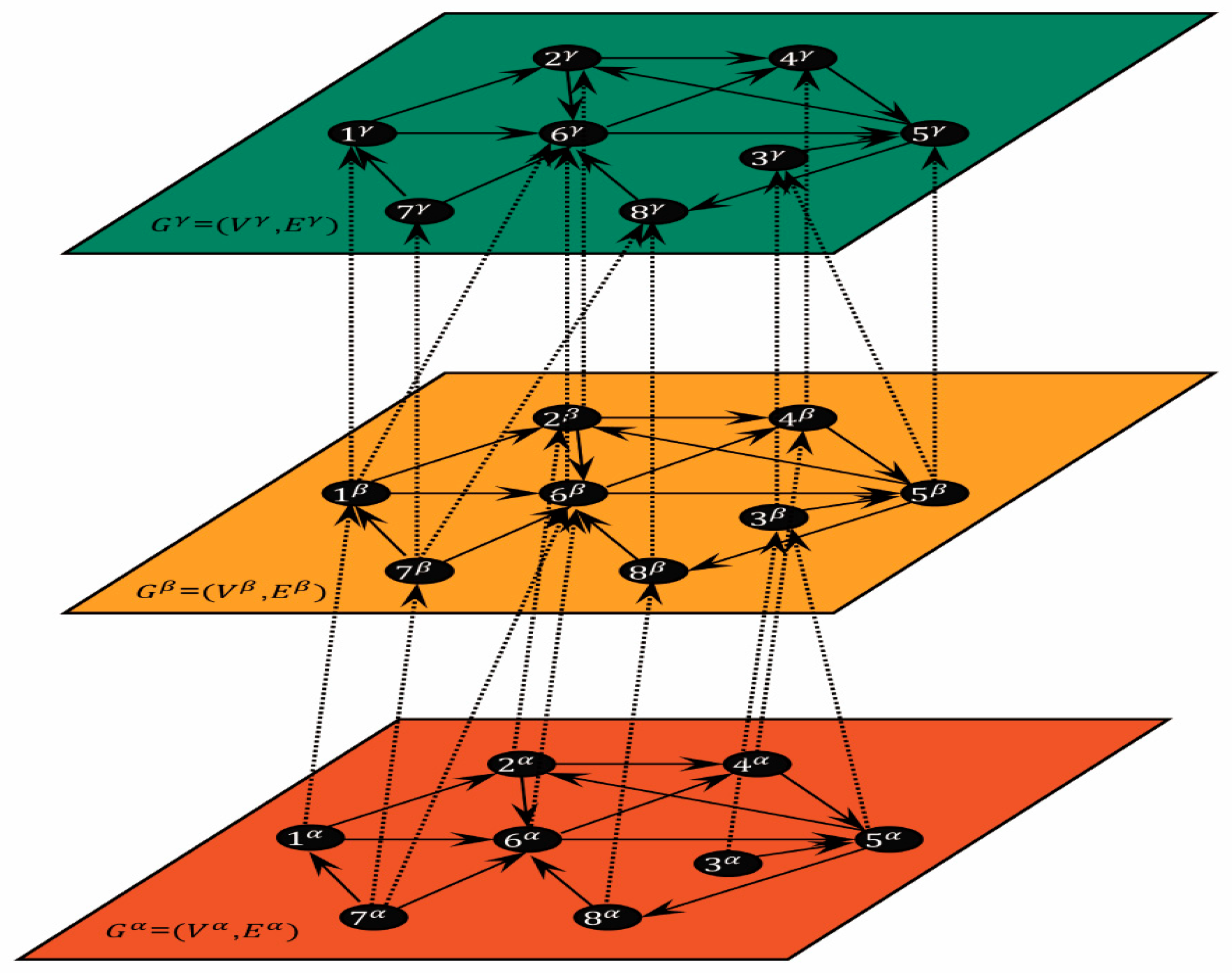
3.1.2. Multi-Layer Network Construction for Oil Storage Tanks
3.2. Information Interpretation and Situational Awareness for Major Accidents in Oil Storage Tank Areas
3.2.1. Identification of Key Scenarios and Associated Information Parameters
- Loss of control over the scenario state leads to significant casualties;
- Loss of control over the scenario state contributes to the escalation of the disaster;
- Loss of control over the scenario state significantly increases difficulties in handling the disaster.
3.2.2. Determination of Threshold Intervals for Information Parameters
3.2.3. Data Fusion and Situational Awareness Process
- (1)
- First, the key accident scenarios that require focused attention are identified and the risk parameters that are highly relevant to these scenarios are determined, as detailed in Section 3.2.1.
- (2)
- Second, based on existing accident research findings, national industry standards, and practical feedback from frontline emergency responders, risk threshold intervals are established for the key parameters. These intervals are used to effectively match observed parameter values with predefined hazard levels, thereby enabling an initial classification of risk levels (Section 3.2.2).
- (3)
- After defining the threshold intervals for each key parameter across different risk levels, the cloud model is applied to process the multi-source data obtained from sensors. Specifically, Equations (6)–(8) are used to calculate the numerical characteristics of each parameter—namely, , , and —to represent their statistical behavior across different risk levels. Based on these computed characteristics, the corresponding parameter values for each critical accident scenario are evaluated to determine their membership degrees to different risk levels. These membership degrees are then used as the BPAs under the established recognition framework. The relevant computational formulas are presented as follows.where represents the BPA value of the parameter information at a specific risk level, represents the BPA value under uncertainty, refers to the numerical value of the parameter, is a random value between 0 and 1, and denotes the number of cloud drops.
- (4)
- Finally, the BPAs are dynamically fused using D-S evidence theory to produce a real-time, integrated interpretation of the incident scene. This approach determines quantifiable confidence levels for each key scenario under different risk grades, thus supporting a comprehensive understanding of evolving situations in large-scale oil storage tank accidents.
4. Case Study
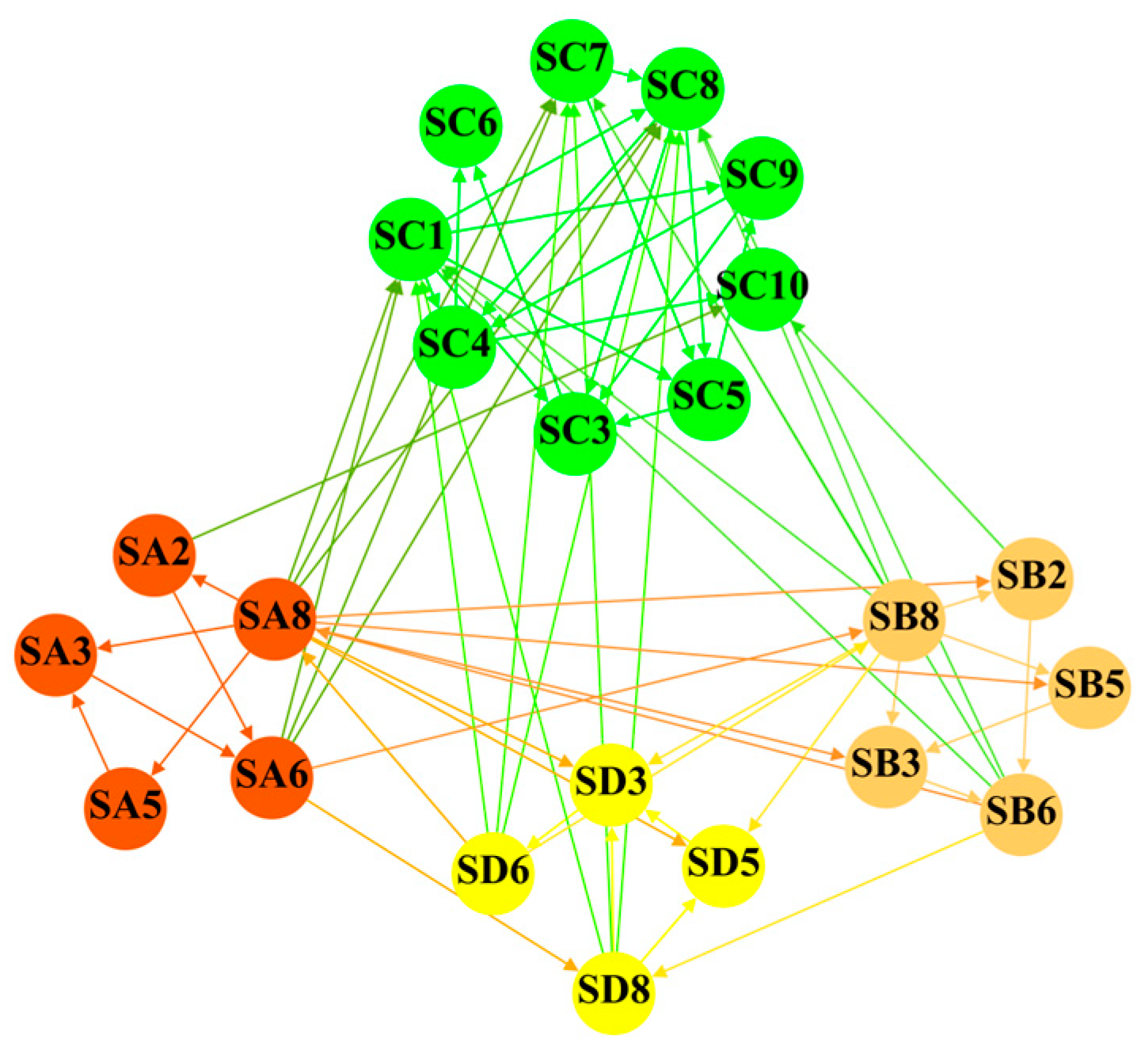
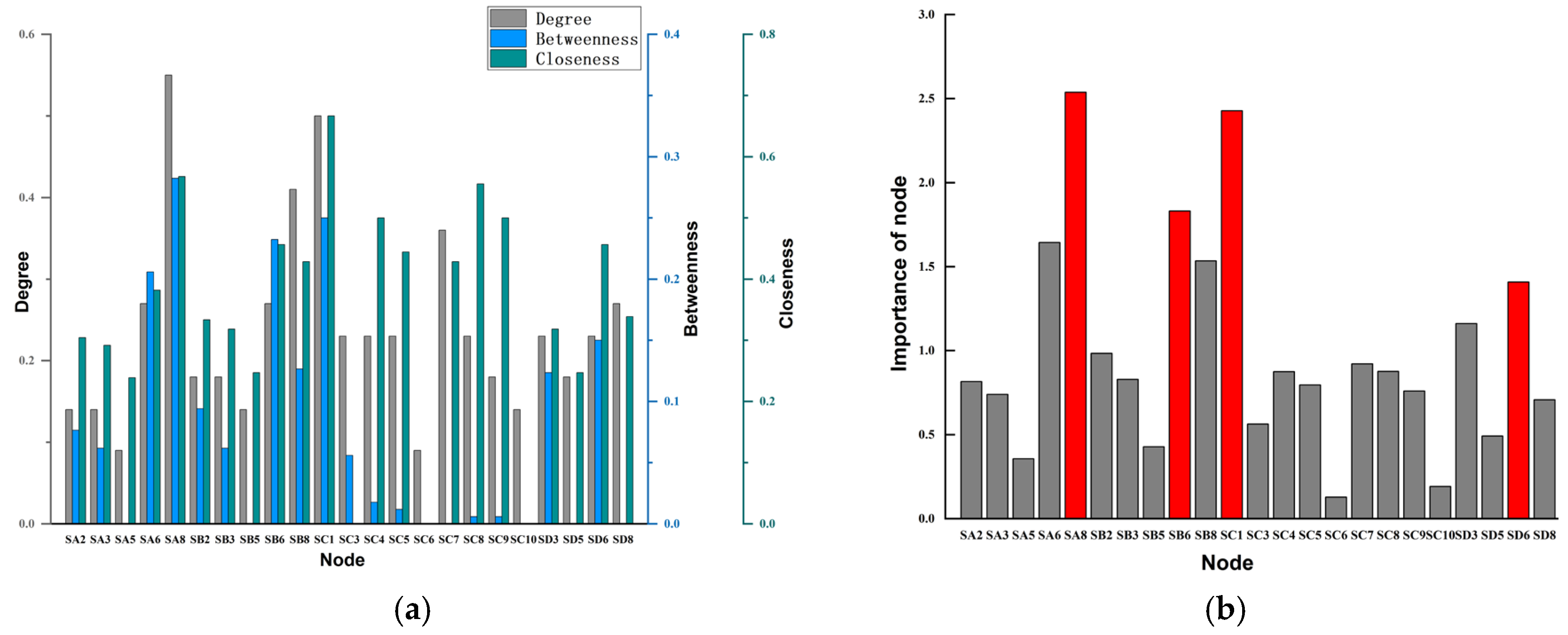
4.1. Situation Awareness of Oil Storage Tanks Based on Complex Networks
4.2. Refined Situational Perception of Oil Storage Tanks Using Reconnaissance Information
5. Conclusions
- (1)
- Single-layer network models for fixed roof, inner floating roof, and outer floating roof tanks were first established based on complex network theory. Building on these models, a multi-layer fire propagation framework was developed by incorporating the logical relationships among different accident scenarios across tanks. By integrating degree, betweenness, and closeness centrality, the analysis identified high-risk nodes within accident chains. The results provide preliminary references for firefighters in the early stage of fire response, particularly when real-time fire data are not yet available.
- (2)
- Through a comprehensive review of the literature, historical accident cases, and frontline firefighter experience, five critical accident scenarios in oil storage tank areas—namely tank explosion, boil over, tank collapse, re-ignition, and full surface fire—were identified and their associated parameters were analyzed. On this basis, a multi-source information fusion mechanism was constructed by integrating cloud models and D-S evidence theory, which enables the fusion of reconnaissance data collected by firefighters upon arrival at a scene. This mechanism not only provides a useful reference for processing on-site information but also enhances the accuracy of emergency decision-making.
- (3)
- The proposed method is primarily based on historical oil storage tank accidents, which may limit its generalizability to other industrial scenarios. In addition, uncertainties in multi-source data, the static nature of the constructed networks, and limitations of evidence theory may affect the accuracy of situational awareness. Future work will focus on extending the framework to other accident types, enhancing dynamic network updates, improving evidence theory-based fusion, and leveraging advanced technologies such as big data analytics and artificial intelligence to strengthen data integration.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The 4th (2024) Petrochemical Storage & Transportation Tank Farm Technical Conference, Featuring over 500 Attendees and over 60 Technical Reports. Available online: https://www.sohu.com/a/754250518_121856153 (accessed on 8 July 2025).
- Jiang, H.; Ding, L.; Ji, J.; Zhu, J. Building reliability of risk assessment of domino effects in chemical tank farm through an improved uncertainty analysis method. Reliab. Eng. Syst. Saf. 2024, 252, 110388. [Google Scholar] [CrossRef]
- Zeng, T.; Wei, L.; Reniers, G.; Chen, G. A comprehensive study for probability prediction of domino effects considering synergistic effects. Reliab. Eng. Syst. Saf. 2024, 251, 110318. [Google Scholar] [CrossRef]
- Petrochina 7.16 Dalian Oil Pipeline Explosion Accident. Available online: http://en.dxpd.com/index.php?c=show&id=57 (accessed on 8 July 2025).
- Oil Tank on Fire in Dongxing Industrial Zone, Nandagang Industrial Park, Cangzhou, Hebei Province, No Casualties. Available online: https://equalocean.com/briefing/20210601230050220 (accessed on 8 July 2025).
- Heydari, P.; Babamiri, M.; Tapak, L.; Golmohammadi, R.; Kalatpour, O. Weighing and prioritization of individual factors affecting the performance of industries firefighters. Fire Saf. J. 2022, 127, 103512. [Google Scholar] [CrossRef]
- Smith, T.D.; Eldridge, F.; DeJoy, D.M. Safety-specific transformational and passive leadership influences on firefighter safety climate perceptions and safety behavior outcomes. Saf. Sci. 2016, 86, 92–97. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, G.; Li, X.; Men, J.; Xu, Q.; Zhou, L.; Zhao, J. A novel unmanned aerial vehicle driven real-time situation awareness for fire accidents in chemical tank farms. J. Loss Prev. Process Ind. 2024, 91, 105357. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, G.; Gao, X. An event-driven modeling methodology of situation awareness: Towards emergency response process in fire-induced domino scenario. J. Loss Prev. Process Ind. 2025, 96, 105618. [Google Scholar] [CrossRef]
- Naderpour, M.; Lu, J.; Zhang, G. A situation risk awareness approach for process systems safety. Saf. Sci. 2014, 64, 173–189. [Google Scholar] [CrossRef]
- Dos Santos, V.; Son, C. Identifying firefighters’ situation awareness requirements for fire and non-fire emergencies using a goal-directed task analysis. Appl. Ergon. 2024, 114, 104136. [Google Scholar] [CrossRef] [PubMed]
- Luokkala, P.; Virrantaus, K. Developing information systems to support situational awareness and interaction in time-pressuring crisis situations. Saf. Sci. 2014, 63, 191–203. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, M.; Pan, W. Dynamic probability analysis on accident chain of atmospheric tank farm based on bayesian network. Process Saf. Environ. Prot. 2022, 158, 146–158. [Google Scholar] [CrossRef]
- Malik, A.A.; Nasif, M.S.; Arshad, U.; Mokhtar, A.A.; Tohir, M.Z.M.; Al-Waked, R. Predictive modelling of wind-influenced dynamic fire spread probability in tank farm due to domino effect by integrating numerical simulation with ANN. Fire 2023, 6, 85. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Z. Analysis of uncertainty propagation path of fire-induced domino effect based on an approach of layered fuzzy petri nets. Chem. Eng. Sci. 2023, 268, 118410. [Google Scholar] [CrossRef]
- Sarebanzadeh, K.; Hasheminejad, N.; Alimohammadlou, M.; Es’haghi, M. Using fuzzy cognitive map in bow tie method for dynamic risk assessment of spherical storage tanks: A case study. Heliyon 2024, 10, e2680. [Google Scholar] [CrossRef]
- Zhong, W.; Wang, S.; Wu, T.; Gao, X.; Liang, T. Optimized machine learning model for fire consequence prediction. Fire 2024, 7, 114. [Google Scholar] [CrossRef]
- Feng, J.R.; Zhao, M.; Lu, S. Accident spread and risk propagation mechanism in complex industrial system network. Reliab. Eng. Syst. Saf. 2024, 244, 109940. [Google Scholar] [CrossRef]
- Li, J.; Xu, X.; Liu, X. Complex Network Analysis on Fire Risk Evolution of Hazardous Chemical Tanks. In Proceedings of the 8th Annual Meeting of Risk Analysis Council of China Association for Disaster Prevention (RAC 2018), Xi’an, China, 20–21 October 2018. [Google Scholar]
- Liu, Z.; Zhou, J.; Reniers, G. Association analysis of accident factors in petrochemical storage tank farms. J. Loss Prev. Process Ind. 2023, 84, 105124. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Zhou, L.; Zhao, Y.; Xu, Q.; Zhao, J. Complex network analysis for accident causes modelling to enhance process safety in chemical enterprises. Can. J. Chem. Eng. 2025, 103, 679–696. [Google Scholar] [CrossRef]
- Yang, J.; Wang, P.; Liu, X.; Bian, M.; Chen, L.; Lv, S.; Tao, J.; Suo, G.; Xuan, S.; Li, R.; et al. Analysis on causes of chemical industry accident from 2015 to 2020 in chinese mainland: A complex network theory approach. J. Loss Prev. Process Ind. 2023, 83, 105061. [Google Scholar] [CrossRef]
- Gangadhari, R.K.; Khanzode, V.; Murthy, S. Application of rough set theory and machine learning algorithms in predicting accident outcomes in the Indian petroleum industry. Concurr. Comput. Pract. Exp. 2022, 34, e7277. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Zhou, N.; Yuan, X. Probability analysis of hazardous chemicals storage tank leakage accident based on neural network and fuzzy dynamic fault tree. Appl. Sci. 2025, 15, 3504. [Google Scholar] [CrossRef]
- Qiao, S.; Fan, Y.; Wang, G.; Zhang, H. Multi-sensor data fusion method based on improved evidence theory. J. Mar. Sci. Eng. 2023, 11, 1142. [Google Scholar] [CrossRef]
- Durukan, O.; Akyuz, E.; Destanoğlu, O.; Arslanoğlu, Y.; Sezer, S.I. Quantitive HAZOP and D-S evidence theory-fault tree analysis approach to predict fire and explosion risk in inert gas system on-board tanker ship. Ocean Eng. 2024, 308, 118274. [Google Scholar] [CrossRef]
- Xia, D.; Chen, C.; Zheng, C.; Xin, J.; Zhu, Y. Research on sequential decision-making of major accidents with incomplete information. Fire 2024, 7, 49. [Google Scholar] [CrossRef]
- Niu, Q.; Yuan, Q.; Wang, Y.; Hu, Y. Fire risk assessment of urban utility tunnels based on improved cloud model and evidence theory. Appl. Sci. 2023, 13, 2204. [Google Scholar] [CrossRef]
- Wang, H.; Shi, Y.; Chen, L.; Zhang, X. A tunnel fire detection method based on an improved Dempster-Shafer evidence theory. Sensors 2024, 24, 6455. [Google Scholar] [CrossRef]
- Fu, L.; Yang, Q.; Liu, Z.; Liu, X.; Wang, Z. Risk identification of major infectious disease epidemics based on complex network theory. Int. J. Disaster Risk Reduct. 2022, 78, 103155. [Google Scholar] [CrossRef]
- Ding, R. The complex network Theory-based urban land-use and transport interaction studies. Complexity 2019, 2019, 4180890. [Google Scholar] [CrossRef]
- Xie, S.; Dong, S.; Chen, Y.; Peng, Y.; Li, X. A novel risk evaluation method for fire and explosion accidents in oil depots using bow-tie analysis and risk matrix analysis method based on cloud model theory. Reliab. Eng. Syst. Saf. 2021, 215, 107791. [Google Scholar] [CrossRef]
- Shen, S.; Lin, S.; Zhou, A. A cloud model-based approach for risk analysis of excavation system. Reliab. Eng. Syst. Saf. 2023, 231, 108984. [Google Scholar] [CrossRef]
- Xiang, X.; Li, K.; Huang, B.; Cao, Y. A multi-sensor data-fusion method based on cloud model and improved evidence theory. Sensors 2022, 22, 5902. [Google Scholar] [CrossRef]
- Xia, D.; Li, C.; Xin, J.; Zhu, Y. A method for emergency response alternative decision-making under uncertainty. J. Control Decis. 2021, 8, 422–430. [Google Scholar] [CrossRef]
- GB50183-2004; Code for Fire Protection Design of Petroleumand Natural Gas Engineering. China Planning Press: Beijing, China, 2004.
| Node ID | Scenario Node | Node ID | Scenario Node |
|---|---|---|---|
| S1 | Tank explosion | S7 | Sealing ring fire |
| S2 | Boil over | S8 | Full surface fire |
| S3 | Tank collapse | S9 | Enclosed combustion |
| S4 | Tank rupture | S10 | Torch fire |
| S5 | Floating roof failure | S11 | Re-ignition |
| S6 | Flowing fire |
| Code | Key Accident Scenario |
|---|---|
| Y1 | Tank explosion |
| Y2 | Boil over |
| Y3 | Full surface fire |
| Y4 | Tank collapse |
| Y5 | Re-ignition |
| Code | Key Parameter |
|---|---|
| X1 | Combustible gas concentration |
| X2 | Pressure |
| X3 | Temperature |
| X4 | Foam coverage ratio |
| X5 | Liquid-level-to-tank-height ratio |
| X6 | Water content |
| X7 | Wind speed in downwind direction |
| X8 | Time exposed to heat radiation |
| X9 | Heat radiation |
| Combustible Gas Concentration | Pressure | Temperature | Foam Coverage Ratio | Liquid-Level -to-Tank -Height Ratio | Water Content | Wind Speed in Downwind Direction | Time Exposed to Heat Radiation | Heat Radiation | |
|---|---|---|---|---|---|---|---|---|---|
| Tank explosion | √ | √ | √ | ||||||
| Boil over | √ | √ | √ | ||||||
| Full surface fire | √ | √ | √ | ||||||
| Tank collapse | √ | √ | |||||||
| Re-ignition | √ | √ |
| Key Accident Scenario | Grade | Low | Medium | High | |
|---|---|---|---|---|---|
| Information Parameters | |||||
| Tank explosion | Gauge pressure at tank top (°C) | [0.20, 2.10) | [2.10, 5.52) | [5.52, 6.90] | |
| Tank top temperature (°C) | [40, 60) | [60, 80) | [80, 100] | ||
| Gasoline vapor concentration (%) | [0, 1.9) | [1.9, 3.8) | [3.8, 7.6] | ||
| Diesel vapor concentration (%) | [0, 1.88) | [1.88, 3.75) | [3.75, 7.50] | ||
| Boil over | Liquid-level-to-tank-height ratio | [0, 0.5) | [0.5, 0.8) | [0.8, 1] | |
| Water layer temperature (°C) | [20, 64) | [64, 80) | [80, 100] | ||
| Water content (%) | [0, 0.66) | [0.66, 1.32) | [1.32, 2] | ||
| Full surface fire | Downwind wind speed (m/s) | [0, 4) | [4, 6) | [6, 8] | |
| Duration of thermal radiation exposure (min) | [0, 10) | [10, 20) | [20, 30] | ||
| Intensity of received thermal radiation (kW/m2) | [0, 5) | [5, 10) | [10, 15] | ||
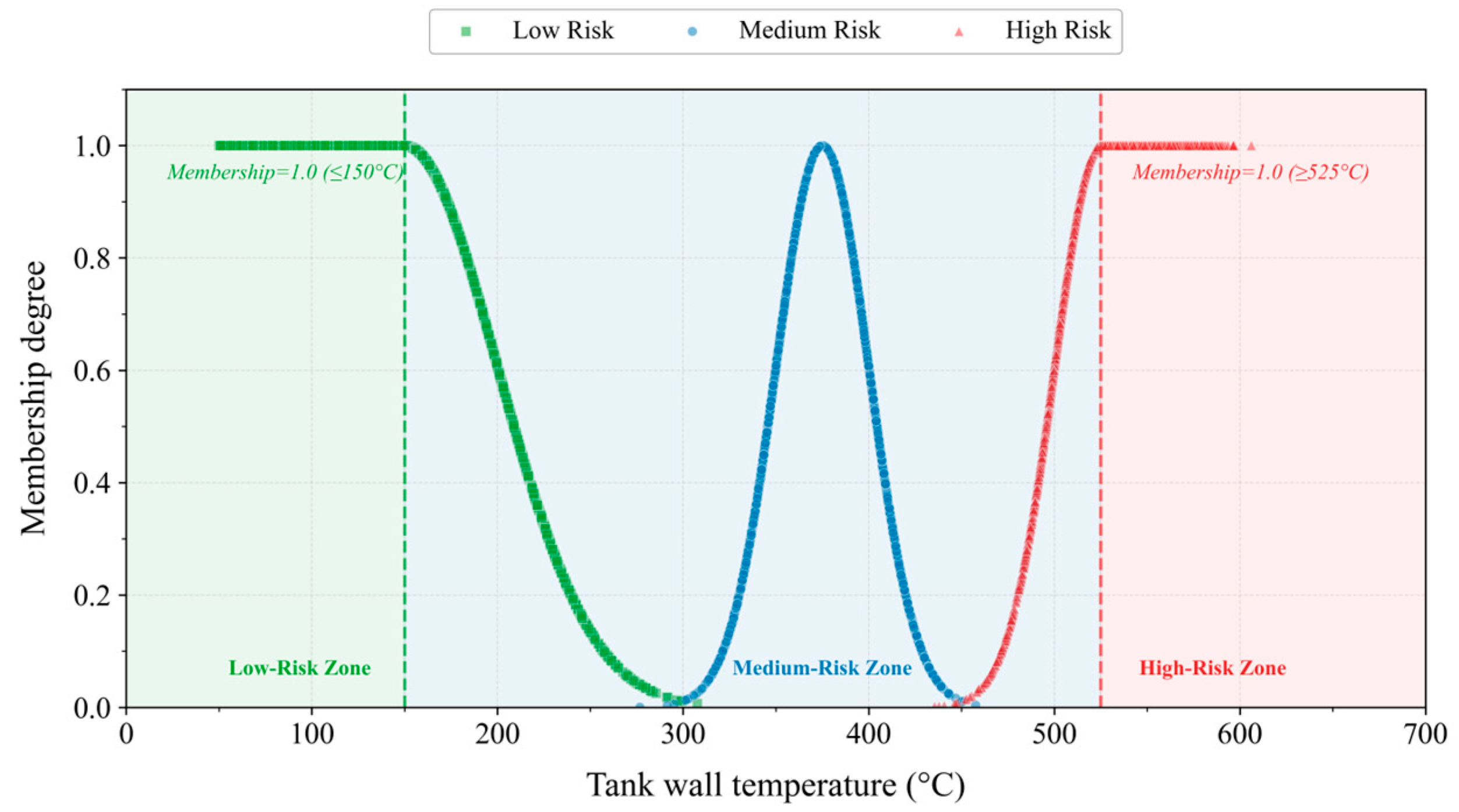
| Tank collapse | Tank wall temperature (°C) | [0, 300) | [300, 450) | [450, 600] | |
| Liquid-level-to-tank-height ratio | [0.8, 1) | [0.5, 0.8) | [0, 0.5] | ||
| Re-ignition | Foam coverage ratio (%) | [90, 100) | [70, 90) | [0, 70] | |
| Oil surface temperature (°C) | [20, 40) | [40, 60) | [60, 80] | ||
| Key Accident Scenarios | Grade | Low | Medium | High | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Information Parameters | |||||||||||
| Tank explosion | Gauge pressure at tank top (°C) | 1.15 | 0.32 | 0.05 | 3.81 | 0.57 | 0.05 | 6.21 | 0.23 | 0.05 | |
| Tank top temperature (°C) | 50 | 3.33 | 0.05 | 70 | 3.33 | 0.05 | 90 | 3.33 | 0.05 | ||
| Gasoline vapor concentration (%) | 0.95 | 0.32 | 0.05 | 2.85 | 0.32 | 0.05 | 5.70 | 0.63 | 0.05 | ||
| Diesel vapor concentration (%) | 0.94 | 0.31 | 0.05 | 2.82 | 0.31 | 0.05 | 5.63 | 0.63 | 0.05 | ||
| Boil over | Liquid-level-to-tank-height ratio | 0.25 | 0.08 | 0.05 | 0.65 | 0.05 | 0.05 | 0.90 | 0.03 | 0.05 | |
| Water layer temperature (°C) | 42 | 7.33 | 0.05 | 72 | 2.67 | 0.05 | 90 | 3.33 | 0.05 | ||
| Water content (%) | 0.33 | 0.11 | 0.05 | 0.99 | 0.11 | 0.05 | 1.66 | 0.11 | 0.05 | ||
| Full surface fire | Downwind wind speed (m/s) | 2 | 0.67 | 0.05 | 5 | 0.33 | 0.05 | 7 | 0.33 | 0.05 | |
| Duration of thermal radiation exposure (min) | 5 | 1.67 | 0.05 | 15 | 1.67 | 0.05 | 25 | 1.67 | 0.05 | ||
| Intensity of received thermal radiation (kW/m2) | 2.5 | 0.83 | 0.05 | 7.5 | 0.83 | 0.05 | 12.5 | 0.83 | 0.05 | ||
| Tank collapse | Tank wall temperature (°C) | 150 | 50 | 0.05 | 375 | 25 | 0.05 | 525 | 25 | 0.05 | |
| Liquid-level-to-tank-height ratio | 0.90 | 0.03 | 0.05 | 0.65 | 0.05 | 0.05 | 0.25 | 0.08 | 0.05 | ||
| Re-ignition | Foam coverage ratio (%) | 95 | 1.67 | 0.05 | 80 | 3.33 | 0.05 | 35 | 11.67 | 0.05 | |
| Oil surface temperature (°C) | 30 | 3.33 | 0.05 | 50 | 3.33 | 0.05 | 70 | 3.33 | 0.05 | ||
| Low | Medium | High | Uncertain | ||
|---|---|---|---|---|---|
| Tank collapse | Liquid-level-to-tank-height ratio | 0.0000 | 0.0007 | 0.5670 | 0.4323 |
| Tank wall temperature (°C) | 0.0000 | 0.0000 | 0.6065 | 0.3935 | |
| Fusion | 0.0000 | 0.0003 | 0.8295 | 0.1702 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Shi, J.; Xun, C.; Kong, B.; Chen, C.; Zhu, Y.; Xia, D. Situational Awareness for Oil Storage Tank Accidents Based on Complex Networks and Evidence Theory. Fire 2025, 8, 353. https://doi.org/10.3390/fire8090353
Xia Y, Shi J, Xun C, Kong B, Chen C, Zhu Y, Xia D. Situational Awareness for Oil Storage Tank Accidents Based on Complex Networks and Evidence Theory. Fire. 2025; 8(9):353. https://doi.org/10.3390/fire8090353
Chicago/Turabian StyleXia, Yunlong, Junmei Shi, Cheng Xun, Bo Kong, Changlin Chen, Yi Zhu, and Dengyou Xia. 2025. "Situational Awareness for Oil Storage Tank Accidents Based on Complex Networks and Evidence Theory" Fire 8, no. 9: 353. https://doi.org/10.3390/fire8090353
APA StyleXia, Y., Shi, J., Xun, C., Kong, B., Chen, C., Zhu, Y., & Xia, D. (2025). Situational Awareness for Oil Storage Tank Accidents Based on Complex Networks and Evidence Theory. Fire, 8(9), 353. https://doi.org/10.3390/fire8090353





