Quantifying the Lagged Teleconnection Between the Southern Oscillation Index (SOI) and the Bushfire Danger Index

Abstract

To improve preparedness and minimise losses, this paper presents the development of artificial intelligence (AI)-based forecasting models using a large-scale climate index for Victoria (Australia), which is known to be one of the most fire-prone areas in the country. Using an Artificial Neural Network (ANN) approach, this study investigates the nonlinear relationships between SOI and the Forest Fire Danger Index (FFDI) to develop a robust predictive model. Levenberg–Marquardt optimisation through the backpropagation method was employed to train the ANN models. Based on local climate data, FFDI values were calculated for eight locations within southeast Australia, and SOI values of earlier months were correlated with the FFDI values of the later months. A total of 55 years (1965–2019) of monthly SOI and FFDI values were used to train, validate, and test the developed ANN models. The findings show that the developed models can predict future FFDI values, having correlation coefficients ranging 0.71~0.96, 0.70~0.95, and 0.75~0.93 for 1-month, 2-month, and 3-month lagged periods, respectively. As is obvious, one-month-ahead predictions were more accurate than two/three-month-ahead predictions. In general, the stations located in the eastern parts are attributed to higher prediction accuracy than stations located in the western regions, possibly due to their closer proximity to the location from where SOI originates (i.e., southern Pacific). These variations between the stations located in the eastern and western parts may partly exhibit the applicability of FFDI to different vegetation types. However, the outcomes hold potential for informing stakeholders, improving resource allocation for fire preparedness, and mitigating the devastating impacts of bushfires on communities and ecosystems.

1. Introduction

Bushfires are a natural and recurring phenomenon in Australia, damaging properties, lives, and ecosystems, especially eucalyptus-dominated forests in the east. In recent decades, these fires have become increasingly frequent and severe due to changing climatic and meteorological conditions, particularly in southeastern Australia [1,2,3]. Since 1851, bushfires have claimed approximately 800 lives and devastated billions of animals. The 2019–2020 fire season alone saw over 7.3 million hectares burned, 33 human fatalities, and thousands of homes destroyed or damaged [4,5]. Recent analyses describe the 2019/20 “Black Summer” fires as the most catastrophic in recorded history, burning nearly 19 million hectares, destroying over 3000 homes, and causing an estimated AUD 40 billion economic loss [6]. These unprecedented fires reaffirm the accelerating intensity of fire seasons in New South Wales and Victoria and highlight the increasing impact of climatic extremes on ecosystems, air quality, and biodiversity [6,7].

Australia is one of the most fire-prone continents in the world, with diverse climate systems heavily influenced by surrounding oceans. The country’s fire weather is significantly modulated by large-scale climate variability associated with phenomena, such as the El Niño–Southern Oscillation (ENSO), Indian Ocean Dipole (IOD), and Southern Annular Mode (SAM), which have the potential to affect rainfall, temperature, and humidity patterns [8,9]. These processes are frequently condensed through indices, such as the Southern Oscillation Index (SOI), which serve as statistical indicators of the state of the underlying complex physical systems and processes. For example, negative SOI values (<−7), typically associated with El Niño events, correspond to drier conditions and elevated fire danger, while positive SOI values (> +7), linked to La Niña phases, are generally associated with wetter conditions and intensified vegetation growth that can contribute to increased fuel future loads [8]. Marshall et al. [10] further highlight the role of the Madden–Julian Oscillation (MJO) in modulating Australian springtime temperatures and extreme heat events, particularly across southern and southeastern regions. The MJO is, therefore, increasingly recognised as a sub-seasonal predictor of fire weather variability in operational forecast systems [10].

The Indian Ocean Dipole, particularly in its positive phase (pIOD), leads to warmer western Indian Ocean temperatures and cooler waters near Australia, contributing to decreased rainfall and higher temperatures in southeastern regions. This exacerbates fire weather, with research showing that pIOD events often precede major Victorian bushfires [11]. Cai et al. [11] investigated the relationship between bushfires and IOD across Victoria following identification of 21 significant bushfire events. During the study period (1950 to 2009), there were 16 pIOD, 2 nIOD, and 3 neutral years. Of the 21 major fire events analysed, more than 76% occurred following positive IOD years, underscoring its effects and role in bushfire risk.

More recent findings by Taylor et al. [12] further demonstrate that the IOD, together with ENSO and SAM, substantially contributes to the predictability of extreme fire danger episodes at two- to three-week lead times across Australia. This integrated assessment using the Australian Fire Behaviour Index (FBI) identified the complementary influences of multiple climate drivers in modulating regional fire risk during critical periods [12]. To assess and forecast fire danger, the Forest Fire Danger Index (FFDI), developed in the 1960s, has long served as the standard metric. It integrates temperature, relative humidity, wind speed, and drought factors to estimate daily fire risk [1]. In recent years, Australia has transitioned to the Australian Fire Danger Rating System (AFDRS), a nationally consistent framework that builds upon the legacy of FFDI by incorporating a wider range of vegetation types and improved fire-behaviour modelling [13,14]. While AFDRS is now operationally adopted nationwide, FFDI remains critical for research applications and long-term analyses due to its extensive historical record and widespread use in climatological datasets.

Despite these advancements, limitations persist in operational forecasting systems such as ACCESS-S2 and AFDRS, which often underestimate the spatial extent and frequency of extreme fire danger events [12,15]. These gaps underscore the need for complementary modelling frameworks that integrate statistical and dynamical approaches to improve accuracy and warning lead time [15].

Numerous studies have explored how climate drivers influence bushfire risk in Australia. Williams and Karoly [16] found that ENSO phases strongly affect fire severity and frequency, with El Niño years increasing seasonal fire danger. Fuller and Murphy [17] observed significant correlations between SOI and fire activity in Southeast Asia, identifying lag effects that offer forecasting potential. Similarly, Mason et al. [18] highlighted that in the U.S., ENSO influences spatial and seasonal patterns of fire potential, with increased fire risk during La Niña in certain regions. These findings underscore the global impact of climate oscillations on fire behaviour. More recently, Taylor et al. [15] showed that forecasting models integrating climate driver signals such as ENSO, IOD, and SAM can successfully predict extreme FBI conditions up to three weeks in advance, though statistical models may overestimate risk while dynamical models tend to underestimate it. Their findings reinforce the importance of multi-model and AI-based systems to balance forecast accuracy and false-alarm rates.

In Australia, van Oldenborgh et al. [19] linked rising fire danger to anthropogenic climate change, noting that extreme 2019 fire weather conditions were at least four times more likely due to global warming compared to 1900. The observed trend in the Fire Weather Index has surpassed model predictions, suggesting that the current risk assessments may underestimate future danger under continued warming [19]. Together, these findings underscore that fire danger in southeastern Australia is now driven by both anthropogenic warming and interacting climate oscillations such as ENSO, IOD, SAM, and MJO [12,15].

Despite these insights, the existing research has largely focused on the individual effects of climate indices or their short-term impacts. The combined and lagged relationships between ENSO, SOI, IOD, and FFDI are still not comprehensively modelled, limiting the effectiveness of early warning systems. Mariani et al. [20] found a persistent relationship between ENSO and southeast Australian fire activity, while Cowan and Cai [11] emphasised the role of IOD in shaping interannual fire risk. However, more work is needed to capture these complex interactions holistically. Emerging studies advocate for integrating dynamical and statistical forecasts with machine learning methods such as Artificial Neural Networks (ANNs) to better capture the nonlinear and lagged effects of multiple climate drivers on fire danger indices [15].

Taylor et al. [15] compared the predictive abilities of the ACCESS-S2 dynamical model with a newly developed statistical model in forecasting extreme Fire Behaviour Index (FBI). ACCESS-S2 generally captured broad fire danger patterns but significantly underestimated extreme events. Conversely, the statistical model responded better to climate drivers but produced high false alarm ratios, raising concerns about overwarning and misallocated resources [15]. These findings highlight the ongoing challenge of balancing prediction accuracy and community preparedness. Considering these developments, ANN-based approaches offer a promising alternative by learning complex, nonlinear patterns from climate indices without requiring explicit statistical assumptions, thus bridging the gap between data-driven and physical forecasting methods [2,15,21].

To overcome the limitations of conventional models, this study adopts Artificial Neural Networks (ANNs) to simulate the complex, nonlinear relationships between the lagged climate index, SOI and FFDI. ANNs have proven effective in environmental and hydrological modelling due to their ability to learn patterns from noisy, nonlinear datasets without assuming explicit relationships [2,21]. Their flexibility allows for adaptation to local variability, improving generalisation and robustness, which are key factors in designing region-specific fire danger forecasting tools. This study builds on recent advances that combine climate predictor information with machine learning frameworks to enhance seasonal fire danger forecast skill in southeastern Australia [12,15].

Recent studies have emphasised the need for models that integrate climate data with machine learning algorithms to improve prediction accuracy [2,21]. These techniques can capture synergistic effects which traditional statistical approaches may overlook, offering valuable insights into bushfire potential at lead times suitable for operational planning. Ultimately, this research aims to fill existing gaps by using ANN-based models to forecast FFDI from multiple lagged climate indices. Once accomplished, it will contribute to a more reliable and comprehensive early warning system, which is essential for managing bushfire risk in an evolving climatic condition. The ability to model these complex relationships supports a proactive approach to disaster preparedness, benefiting emergency responders, policymakers, and vulnerable communities alike.

Table 1 summarises some key previous studies that investigated the influence of large-scale climate drivers on Australian fire weather through statistical or dynamical approaches. However, most did not explore lagged, nonlinear relationships at a regional scale. The present study addresses this gap by developing an ANN-based predictive model linking the Southern Oscillation Index (SOI) and the Forest Fire Danger Index (FFDI) across multiple Victorian stations.

Table 1. Summary of recent studies on climate drivers and bushfire/fire danger prediction in Australia.

Study (Year)	Region/Data Used	Methodology	Climate Drivers/Variables	Main Findings	Gap/Limitation Addressed by This Study
Taylor et al. (2024) [12]	Australia; Fire Behaviour Index (AFDRS) data	Statistical and dynamical forecasting (ACCESS-S2)	ENSO, IOD, SAM, MJO, STRH	Demonstrated strong relationships between large-scale climate drivers and extreme FBI; hybrid approach improves early-warning capability.	National-scale statistical model; lacks station-level nonlinear (ANN) prediction using lagged SOI–FFDI relationships.
Marshall et al. (2023) [10]	Australia; spring–summer fire weather records	Subseasonal-to-seasonal driver evaluation	MJO and related atmospheric indices	Identified MJO’s influence on extreme fire weather and forecast skill.	Focused on MJO; no lagged SOI-based predictive analysis for FFDI.
Dowdy (2020) [22]	Australia; seasonal prediction context	Statistical–climatological framework	ENSO, IOD, SAM	Highlighted the potential of climate drivers for seasonal bushfire prediction.	Conceptual and national in scope; no predictive ANN model linking SOI to FFDI.
Dowdy et al. (2017) [1]	Southeastern Australia; Black Saturday (2009) event	Observational analysis (lightning, radar, MODIS)	Fire–atmosphere coupling, instability indices	Demonstrated feedback between convection and lightning ignition during extreme fire events.	Event-specific case study; not a climate-index-based predictive approach.

2. Materials and Methods

2.1. Study Area

Southeastern Australia, encompassing parts of New South Wales (NSW), Victoria, and the Australian Capital Territory (ACT), is a region highly prone to bushfires. The most specific factor is perhaps the temperate climate, generally characterised by extremely hot and dry summers that offer extremely favourable conditions for bushfires. Its vegetation type is dominated by highly flammable vegetation classes, which include eucalyptus forests, grasslands, and shrublands that are an abundance of fuel for fires. The southeastern part of Australia, within its diverse landscape and different climate zones, has some of the most fire-prone areas in the world. This study particularly focuses on the state of Victoria, in southeastern Australia, which has experienced devastating bushfires such as the Black Saturday fires of 2009, the catastrophic 2019–2020 “Black Summer” fires, and more recently, the 2023–2024 Victorian bushfires in Gippsland and the Grampians, all of which occurred under extreme fire weather conditions. The topography of Victoria varies from a coastline to mountainous terrain; besides having a temperate climate, it is very prone to extreme fire weather conditions. The vegetation cover in Victoria ranges from thick eucalyptus forests to grasslands, adding to the tendency for bushfires.

Although the 2009 Black Saturday fires were one of the most devastating events in Victoria’s history, the region has continued to experience severe bushfire activity in more recent years. During the 2019–2020 “Black Summer” season, Victoria recorded over 1.5 million hectares burned, with catastrophic losses of homes and wildlife [6]. More recently, in early 2023, several districts in western and northeastern Victoria faced destructive grass and forest fires under extreme temperature and wind conditions, prompting widespread emergency warnings issued by the Bureau of Meteorology (BOM) and State Emergency Services. These events underscore that, despite advancements in fire management and mitigation strategies, southeastern Australia remains highly vulnerable to climate-driven fire weather extremes.

In the following analysis of the relationship between the Southern Oscillation Index and the Forest Fire Danger Index, data are used from eight selected weather stations across Victoria (Figure 1). Details of the selected stations are outlined in Table 2. These stations were chosen based on the availability of historical meteorological data and to ensure geographic representativeness, covering various districts across the state. By including stations from inland, coastal, and transitional zones, this research aims to capture the diverse climatic conditions that influence fire weather patterns across Victoria. The selection of these stations underscores an effort to represent the entire state and provides insights into the spatial dynamics of bushfire risk.

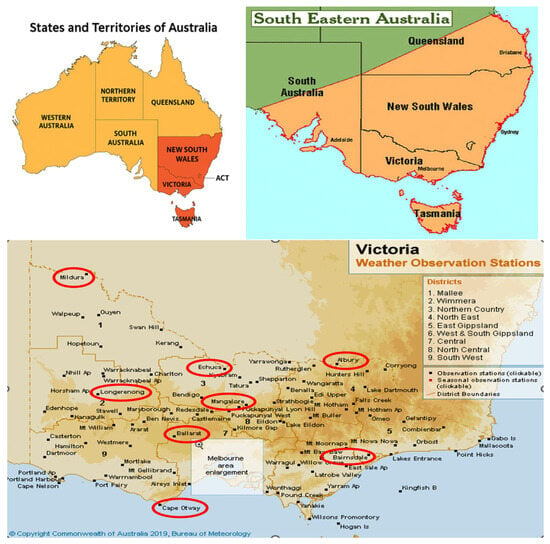
Figure 1. Locations of weather stations in Victoria used in this study [23,24,25].

Table 2. Overview of the selected weather stations used in this study, showing their regional distribution, geographic coordinates, and elevation.

Station Number	Station Name	Region	Latitude	Longitude	Elevation
76031	Mildura Airport	Mallee	34.24° S	142.09° E	50 m
072160	Albury Airport AWS	Mallee	36.07° S	146.95° E	164 m
80015	Echuca Aerodrome	Northern	36.16° S	144.76° E	96 m
88109	Mangalore Airport	Northern	36.89° S	145.19° E	141 m
89002	Ballarat Aerodrome	Central	37.51° S	143.79° E	435 m
90015	Cape Otway Lighthouse	Southwest	38.86° S	143.51° E	80 m
79028	Longerenong	Wimmera	36.67° S	142.30° E	133 m
085279	Bairnsdale Airport	Northeast	37.88° S	147.57° E	49 m

2.2. Data Collection and Pre-Processing

The input dataset comprises 55 years (1965–2019) of monthly SOI values. SOI was selected due to its established influence on climatic variability in the region. The output dataset consists of corresponding monthly FFDI values for 8 different stations across Victoria for the same period. While the Grassland Fire Danger Index (GFDI) would be more representative of grassland fuels, the necessary input variables (e.g., curing percentage or specific grass fuel parameters) were not consistently available for all the selected sites and time periods. Consequently, this study focuses on FFDI, which continues to be the most widely used fire danger across Australia and forms the basis for historical fire danger trend analyses.

It is also important to note that since 2022, the Australasian Fire and Emergency Services Authorities Council (AFAC) and Australian fire agencies have implemented the Australian Fire Danger Rating System (AFDRS) to substitute the commonly adopted FFDI for operational use. The AFDRS implemented the influence of multiple vegetation types to better represent fire behaviour potential across Australia’s diverse landscapes. Although this study relies on FFDI due to the availability of a long historical record and data stability, future analyses will integrate AFDRS-based indices to improve the representativeness of fire danger across distinctive vegetation classes.

The FFDI values are calculated based on Equation (1), consistent with the formulation by Noble et al. [26]. FFDI is based on earlier research that established the empirical relationships between fuel moisture, wind speed, and fire behaviour by McArthur [27]. The calculator, thus, represents a practical implementation of those foundational studies. The data were obtained from the Australian BOM Climate Data Online portal (https://www.bom.gov.au/climate/data/ accessed on 30 June 2025). For this study, only the key fire-season months (October to February) were considered.

All the datasets were verified against the published BOM archives to ensure consistency, and missing monthly values, where present, were linearly interpolated prior to analysis.

$$FFDI=2\times \exp \left(-0.45+0.987lnDF+0.0338T-0.0345RH+0.0234U\right)$$

(1)

where ‘T’ is temperature (°C), ‘RH’ is relative humidity (%), ‘U’ is wind speed (km/h) and ‘DF’ is drought factor as outlined below (Equation (2)).

$$DF={\displaystyle \frac{7\times {FMC}_a}{FMC}}$$

(2)

where ‘FMC_a’ is the influence of the air on fuel moisture content, and ‘FMC’ is fuel moisture content, as explained below.

Equations for FMC_a and FMC are as follows:

$${FMC}_a=10-{\displaystyle \frac{\left(T-RH\right)}{4}}$$

(3)

$$FMC=5.658+0.04651RH+3.151\times {10}^{-4}{RH}^3{T}^{-1}-0.1854T^{0.77}$$

(4)

where the variables ‘T’ and ‘RH’ are defined earlier.

As the established relationships between SOI and FFDI are expected to be used for forecasting, the aim was to establish lagged relationships, i.e., the SOI values in earlier months to be correlated with the FFDI values in the later months, especially within the dry months. For this purpose, three lag periods were considered: 1-month, 2-month, and 3-month.

In the study, SOI was taken as the sole climate predictor due to its pre-established relation with Australian weather conditions [28]. Although some other climate indices (IOD, SAM) may have an impact on Victorian bushfires [29], being a preliminary study, only SOI was considered. The relevant SOI data were extracted from the Bureau of Meteorology (BOM) website (https://www.bom.gov.au/climate/enso/soi/ accessed on 30 June 2025). The data were pre-processed for optimal performance of the ANN through normalisation; the input and output data were normalised within the range of [0, 1] to enhance convergence during model training. As usual for ANN architecture, the dataset was split (randomly) into training (70%), validation (15%), and testing (15%) subsets to ensure sound model evaluation.

Less than 2% of the data points were missing; the FFDI values were imputed using the mean of the adjacent monthly values for continuity. Herein, standard Australian definition seasons are used, namely the following: summer—December to February, and spring—September to November. This approach ensures the analysis captures seasonal variations critical to bushfire risk assessment.

2.3. Model Development and Evaluation

The ANN approach was employed for establishing relationships between the FFDI values and SOI values. The ANN methodology allows for the inclusion of nonlinearities and complex interdependencies, making it a more suitable choice for this research. ANNs are known to be strong nonlinear modelling tools with a higher capacity for capturing the most complex data relationships. Therefore, in this study, a feedforward ANN was used to establish the relationship between input (SOI) and output (FFDI) variables using the Levenberg–Marquardt algorithm for backpropagation [30,31]. MATLAB’s (version R2024b) in-built function was used to establish the relationships. To account for the delayed climatic influence of large-scale oceanic drivers on fire weather, the SOI input data were lagged by one, two, and three months relative to the corresponding FFDI targets. This lagged-input analysis enables the model to capture the temporal response of fire danger to preceding climate signals and reflects the real-world delay between atmospheric anomalies and their surface fire impacts. Each lag configuration (1-, 2-, and 3-month) was trained and evaluated independently to ensure reproducibility and comparability across all the scenarios.

2.3.1. Artificial Neural Network ANN

Artificial Neural Networks (ANNs) are well-regarded for their ability to model complex and nonlinear patterns within data. In this research, a feedforward ANN structure was employed to map the connection between input and target variables, using the Levenberg–Marquardt optimisation method for training through backpropagation.

Each neuron in the hidden layer transforms its inputs by applying a nonlinear activation function, commonly a sigmoid or hyperbolic tangent, to a weighted sum of the inputs, as illustrated in Equation (5) [30].

$$h_j=f\left(\sum _{i=1}^n{\omega }_{ij}^{\left(1\right)}{x}_i+b_j^{\left(1\right)}\right)$$

(5)

In this equation, $h_j$ represents the output of the hidden neuron, $x_i$ is the input signal, ${\omega }_{ij}^{\left(1\right)}$ denotes the weight linking the input $x_i$ to the hidden neuron $h_j$, and $b_j^{\left(1\right)}$ is the bias associated with the hidden neuron. The output layer consists of a single node that calculates the final predicted value $\widehat{y} ,$ as shown in Equation (6) [30].

$$\widehat{y}=f\left(\sum _{j=1}^m{\omega }_j^{\left(2\right)}+b^{\left(2\right)}\right)$$

(6)

Here, ${\omega }_j^{\left(2\right)}$ represents the weights connecting the hidden layer neurons to the output node, and $b^{\left(2\right)}$ denotes the bias term for the output layer.

Figure 2 illustrates the basic feedforward ANN architecture used in this study. The left diagram shows the internal configuration of the network with one input layer, a single hidden layer containing multiple neurons, and one output layer. Each neuron receives weighted inputs (W), applies a bias (b), and passes the summed signal through an activation function to introduce nonlinearity. The right schematic conceptually demonstrates the flow of information—forward propagation from input (SOI) to output (FFDI) and backward propagation during training, where errors are minimised by adjusting the weights and biases. This structure forms the foundation of the model used to learn and generalise the nonlinear relationships between SOI and FFDI. It is worth noting that the ANN has the potential to provide strong predictive performance, but it is subject to some limitations involving high data requirements, potential overfitting, and limited interpretability.

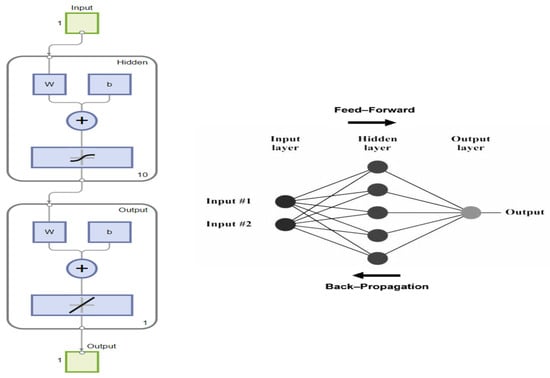
Figure 2. AINN structure schematic.

2.3.2. Data Pre-Processing

The data were pre-processed for optimal performance of the ANN by performing the following:

(i)

Normalisation: The input and output data were normalised within the range of [0, 1] using min–max normalisation, implemented through MATLAB’s mapminmax function, to scale each variable linearly according to Equation (7):

$$x^{\prime }={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(7)

where x′ is the normalised value, x is the original value, and x_min and x_max are the minimum and maximum of the dataset, respectively.

This normalisation ensures uniform feature scaling and faster convergence during training [32,33].

(ii)

Data Splitting: The dataset was divided into training (70%), validation (15%), and testing (15%) subsets. The data partitioning was performed using MATLAB’s “dividerand” function, which divides the dataset randomly rather than sequentially by time. This ensures that each subset contains representative samples across the full range of SOI–FFDI variability. Such random partitioning helps the ANN learn generalizable patterns rather than being influenced by specific time-based sequences.

(iii)

Handling Missing Values: Any occasional missing monthly entries were estimated using linear interpolation to maintain data continuity prior to training.

2.3.3. ANN Architecture

• Type of Network: Feedforward Multilayer Perceptron (MLP) neural network, where the information flows in one direction from the input layer to the output layer via a single hidden layer without feedback connections.
• Hidden Layers: The model architecture was optimised by adjusting the number of neurons in the hidden layer to achieve the best correlation between the predicted and observed FFDI values. As a single hidden layer with an adequate number of neurons can effectively balance model complexity and performance, the network size was varied iteratively until an optimal configuration was achieved. This tuning process identified the structure that produced the highest correlation (R-value) and the lowest mean squared error, ensuring an effective trade-off between simplicity and predictive accuracy.
• Activating Functions: Sigmoid is the activating function in the neurons of the hidden layer, which presents nonlinearity. Similarly, a linear activation function may be used in an output layer.
• Because the model operates as a black box system, its internal weight interactions cannot be directly interpreted; therefore, the evaluation relied on statistical performance metrics (MAE, MSE, R) to quantify prediction accuracy.

2.3.4. Training Algorithm

In this study, the Levenberg–Marquardt (L-M) variant of the backpropagation algorithm was employed due to its efficiency and suitability for solving nonlinear optimisation problems. Even though this approach allows rapid convergence, the method has the potential for early termination in certain circumstances. To evaluate the steadiness of the solution, training was repeated with numerous randomised initial weights and the consistent performance metrics were observed across runs. However, some vulnerability to local minima remains possible, which is common for L-M-based training of nonlinear systems. This algorithm iteratively adjusts the weights and biases of the network to minimise the difference between the predicted and observed values. The training process used a gradient-based approach, with the mean squared error (MSE), defined in Equation (8), serving as the loss function. Early stopping through validation monitoring was employed during training to prevent overfitting, ensuring that model learning ceased once validation performance no longer improved.

2.3.5. Performance Evaluation

The performance of the ANN was evaluated using the following metrics:

• Mean Squared Error: To measure overall error between the observed and predicted values.

$$MSE={\displaystyle \frac{1}{N}}\sum _{k=1}^N{\left(y_k-{\widehat{y}}_k\right)}^2$$

(8)

• Correlation Coefficient (R-value): To measure the strength of the relationship between the predicted and observed values. The Pearson correlation coefficient R is calculated as shown in Equation (9):

$$R={\displaystyle \frac{{\sum }_{k=1}^N(y_k-\overline{y}\left)\right({\widehat{y}}_k-\overline{\widehat{y}})}{\sqrt{{\sum }_{k=1}^N{(y_k-\overline{y})}^2{\sum }_{k=1}^N{({\widehat{y}}_k-\widehat{\overline{y}})}^2}}}$$

(9)

• Mean Absolute Error (MAE): To assess the average absolute deviation of predictions from observed values. The MAE is calculated as shown in Equation (10):

$$MAE={\displaystyle \frac{1}{N}}\sum _{k=1}^N\left|y_k-{\widehat{y}}_k\right|$$

(10)

In this context, ${\mathrm{y}}_{\mathrm{k}}$ and ${\widehat{\mathrm{y}}}_{\mathrm{k}}$ represent the observed and predicted FFDI values for instance k, respectively, and N is the total number of observations. The gradients of the error function with respect to each weight were calculated using the chain rule and propagated backward through the network, as described in Equation (11) [28]. To improve convergence speed and stability, the Levenberg–Marquardt (LM) algorithm was utilised, which updates the weights w by solving the following equation:

$$w_{t+1}=w_t-{(J^{t}J+\lambda I)}^{-1}{J}^{t}e$$

(11)

In the above formulation, J denotes the Jacobian matrix containing the partial derivatives of the network errors with respect to the weights, e is the vector of residual errors, λ is the damping parameter, and i is the identity matrix. The Levenberg–Marquardt algorithm thus blends the rapid convergence of the Gauss–Newton method with the robustness of gradient descent, a combination that has proven effective in hydrological applications. To guard against overfitting, early-stopping criteria and weight regularisation were incorporated during training. For each lag scenario (1-month, 2-month, and 3-month), separate SOI–FFDI dataset pairs were created, where each SOI value corresponded to FFDI of the following month(s). Both input and output data were updated accordingly, and each lag configuration was trained and tested independently using the same ANN architecture and training settings to maintain consistency across scenarios. The hidden-layer size was adjusted iteratively across a wide range of neuron counts to identify the configuration that achieved the highest correlation (R-value) and the lowest error (MSE and MAE), ensuring an optimal balance between model complexity and predictive performance.

3. Results

Correlation analyses were conducted to explore the relationships between the climate index and the bushfire risk indicator. Analyses were performed for the eight selected weather stations. Individual climate index (SOI) was analysed to explore its correlation with bushfire risk, FFDI during summer and spring at the selected stations: Mildura, Ballarat, Longerenong, Echuca, Cape Otway, Mangalore, Albury, and Bairnsdale. The findings from these analyses are presented in Table 2, Table 3, Table 4, Table 5 and Table 6.

Table 3. Pearson correlation (R) of 1-month lagged SOI with FFDI.

Climate Index	Weather Station
	Mildura Airport	Longerenong	Cape Otway	Mangalore Airport	Echuca Aerodrome	Ballarat Aerodrome	Albury	Bairnsdale
SOI-OCT	0.88	0.80	0.87	0.81	0.74	0.96	0.81	0.88
SOI-NOV	0.93	0.85	0.85	0.74	0.90	0.85	0.82	0.82
SOI-DEC	0.80	0.71	0.88	0.86	0.79	0.80	0.73	0.78
SOI-JAN	0.81	0.95	0.87	0.78	0.71	0.73	0.95	0.95

Table 4. Pearson correlation (R) of 2-month lagged SOI with FFDI.

Climate Index	Weather Station
	Mildura Airport	Longerenong	Cape Otway	Mangalore Airport	Echuca Aerodrome	Ballarat Aerodrome	Albury	Bairnsdale
SOI-OCT	0.86	0.81	0.85	0.77	0.83	0.77	0.95	0.91
SOI-NOV	0.74	0.84	0.94	0.77	0.83	0.72	0.86	0.80
SOI-DEC	0.73	0.70	0.83	0.82	0.81	0.77	0.71	0.82

Table 5. Performances of the 2-month lagged model for training, validation, and testing periods.

Region	Station	Model	Training Period			Validation Period			Testing Period
			R	MSE	MAE	R	MSE	MAE	R	MSE	MAE
Eastern Victoria	Albury Airport	SOI-OCT	0.45	67.1	6.6	0.22	121.2	10.1	0.95	2.3	0.7
		SOI-NOV	−0.03	167.0	9.3	0.33	73.6	6.8	0.86	44.6	5.6
		SOI-DEC	−0.13	111.5	8.2	0.10	34.5	4.5	0.71	47.0	6.4
	Bairnsdale Airport	SOI-OCT	0.71	1.6	0.9	0.35	2.0	1.1	0.91	2.0	1.1
		SOI-NOV	0.77	2.2	1.1	−0.33	12.6	3.0	0.80	7.7	2.3
		SOI-DEC	0.31	7.4	1.9	−0.58	10.4	3.0	0.82	3.7	1.5
Central Victoria	Echuca Aerodrome	SOI-OCT	0.29	20.9	4.6	−0.00	21.4	4.6	0.83	11.2	3.4
		SOI-NOV	0.56	14.3	3.8	−0.38	44.7	6.7	0.83	6.1	2.5
		SOI-DEC	0.81	6.4	2.5	−0.22	35.5	6.0	0.81	12.2	3.5
	Ballarat Aerodrome	SOI-OCT	0.88	3.5	1.9	0.40	14.9	3.9	0.77	5.4	2.3
		SOI-NOV	0.73	9.9	3.2	−0.37	71.1	8.4	0.72	25.5	5.1
		SOI-DEC	0.57	15.5	3.9	0.06	37.5	6.1	0.77	8.9	3.0
	Mangalore Airport	SOI-OCT	0.65	12.7	3.6	0.20	35.8	6.0	0.77	16.3	4.0
		SOI-NOV	0.68	16.1	4.0	0.61	35.5	6.0	0.77	6.1	2.5
		SOI-DEC	0.74	8.9	3.0	−0.24	73.6	8.6	0.82	60.3	7.8
Western Victoria	Mildura Airport	SOI-OCT	0.47	25.6	5.1	−0.11	61.7	7.9	0.86	17.6	4.2
		SOI-NOV	0.44	31.1	5.6	0.12	24.6	5.0	0.74	28.7	5.4
		SOI-DEC	0.41	18.6	4.3	0.10	64.1	8.0	0.73	48.5	7.0
	Longerenong	SOI-OCT	0.60	12.5	3.5	0.46	74.8	8.7	0.81	14.1	3.8
		SOI-NOV	0.26	27.0	5.2	−0.52	37.8	6.1	0.84	29.4	5.4
		SOI-DEC FFDIFEB	0.72	9.1	3.0	0.46	21.7	4.7	0.70	24.6	5.0
	Cape Otway	SOI-OCT	0.44	2.1	1.0	0.69	0.2	0.2	0.85	1.8	1.0
		SOI-NOV	0.00	17.6	3.0	0.64	7.7	1.5	0.94	11.8	2.4
		SOI-DEC	0.62	9.3	2.5	0.24	11.9	2.5	0.83	4.4	1.8

Table 6. Pearson correlation (R) of 3-month lagged SOI with FFDI.

Climate Index	Weather Station
	Mildura Airport	Longerenong	Cape Otway	Mangalore Airport	Echuca Aerodrome	Ballarat Aerodrome	Albury	Bairnsdale
SOI-OCT	0.84	0.93	0.79	0.75	0.91	0.80	0.81	0.87
SOI-NOV	0.87	0.82	0.86	0.75	0.88	0.78	0.80	0.92

3.1. Correlation Analysis of One-Month Lagged SOI with FFDI

Table 3 presents the Pearson correlation coefficients (R) for the relationship between the one-month lagged SOI values and the Forest Fire Danger Index (FFDI) across eight weather stations in southeastern Australia. The presented ‘R’ values are for the testing period of the ANN models. The SOI values for October, November, December, and January were analysed to capture their influence on the FFDI one-month-ahead prediction. The results show consistent positive correlations between SOI and FFDI across all the stations, with variations in the strength of the relationship depending on the month and station. It is found that for 36 scenarios covering all the stations and four prediction months, the achieved correlations were more than 0.8, except for 8 cases where the correlations varied from 0.71 to 0.79. The highest correlation achieved was 0.96 for Ballarat, predicting the November FFDI value using the October SOI value. Also, for six stations, the correlations achieved were higher than 0.9 for at least one of the prediction months. This ascertains models’ capability of predicting bushfire potential one month in advance using the SOI value in the earlier month. Nonetheless, the highest correlation value for all the locations may not happen in the same month when predicting for the following month.

Regarding spatial variability, there is no clear trend in the correlation strengths based on geographical location. Very good correlations (>0.9) were achieved in far-east (Albury and Bairnsdale), central (Echuca and Ballarat), and far-west (Mildura and Longerenong) locations.

The temporal variation in correlation strength suggests that the influence of SOI on FFDI evolves throughout the fire season, with October, November, and January often showing higher correlations at multiple stations. This aligns with the seasonal dynamics of southeastern Australia, where spring SOI anomalies set the stage for heightened bushfire risk in summer.

3.2. Correlation Analysis of Two-Month Lagged SOI with FFDI

Table 4 summarises the Pearson correlation coefficients (R) between the two-month lagged SOI values and the FFDI values for the selected stations across southeastern Australia. Examining these lagged relationships provides insight into the extent to which SOI anomalies influence fire danger conditions in the following months. The results show clear spatial and temporal differences in correlation strength. The SOI values for October, November and December were analysed to capture their influence on the FFDI two-month-ahead prediction. Among the relationships, Albury showed the highest correlation (R = 0.95) for the October SOI value predicting the December FFDI value. Also, for predicting the January FFDI values, the correlation coefficient with the November SOI values is 0.86. The second-highest correlation (R = 0.94) was observed at Cape Otway for the November SOI value predicting the January FFDI value. For this station, the average correlation value for predicting FFDI values for all three months (December, January, and February) with the SOI values of the earlier months was 0.87. The third-highest correlated station was Bairnsdale, where a correlation coefficient of 0.91 was observed for the October SOI value predicting the December FFDI value. For this station, the average correlation value for predicting the FFDI values for all three months (December, January, and February) with the SOI values of the earlier months was 0.84. In general, the achieved correlation values for the two-month lag models were inferior to the achieved correlation values for the one-month lagged models; the correlation values achieved for one-month lagged models varied from 0.71 to 0.96 (average 0.83), whereas the correlation values achieved for two-month lagged models varied from 0.71 to 0.95 (average 0.81). Such outcomes from the models are reasonable, as the influences of the climate indices (SOI in this instance) are likely to become weaker with longer lag periods.

Table 5 presents the correlation values for the developed models for all the model stages (i.e., training, validation, and testing) grouped into different regions (eastern, central, and western). In general, correlation values during training and validation periods were much inferior to the corresponding correlation values in the testing period. It is to be noted that for such modelling tasks, the accuracy of the testing period results is the most crucial. The table also presents the MSE and MAE values for all the simulations.

Regarding spatial variations, it was observed that the accuracies of the eastern region’s predictions were more accurate compared to the prediction accuracies of the central and western regions’. The average ‘R’ value from all the simulations for the eastern region was 0.84, whereas the similar average ‘R’ values for the central and western regions were 0.79 and 0.81, respectively. Similarly, the average MAE value from all the simulations for the eastern region was 2.93, whereas the similar average MAE values for the central and western regions were 3.79 and 4.0, respectively. In terms of mean squared error (MSE), the eastern region recorded the lowest average value of 8.92, indicating smaller overall variance between the predicted and observed FFDI values. The central and western regions exhibited slightly higher MSEs (10.75 and 11.43, respectively), reflecting larger deviations in model predictions. The combination of lower MAE and MSE values in the east signifies that the ANN model achieved both higher accuracy and greater consistency in that region. Such variations from east to west are justified, i.e., due to the proximity of the SOI origin (i.e., the South Pacific) towards the eastern region, locations in the eastern region are likely to exhibit stronger correlations compared to the locations in the western region. This spatial gradient underscores the influence of large-scale ocean–atmosphere interactions on bushfire potential, validating the regional differentiation in predictive performance.

3.3. Correlation Analysis of Three-Month Lagged SOI with FFDI

Table 6 summarises the Pearson correlation coefficients (R) for the 3-month lagged SOI values with FFDI values across the studied weather stations. The highest correlation (0.93) was achieved for Longerenong when predicting January FFDI from the October SOI. The second-highest correlation (0.92) was observed for Bairnsdale, predicting February FFDI using November SOI values, followed by Echuca (0.91) for predicting January FFDI using October SOI values.

The achieved correlation values for the three-month lag models varied from 0.75 to 0.93 (average 0.84). The maximum correlation value (0.93) was slightly lower than the corresponding peak correlations for the one-month and two-month lagged models (0.96 and 0.95, respectively). This gradual decline in correlation with increasing lag reflects the weakening influence of SOI anomalies over longer lead times, which is physically consistent with seasonal memory decay in ocean–atmosphere coupling.

Alongside correlation, the mean absolute error (MAE) and mean squared error (MSE) were evaluated to better quantify model precision. The average MAE values across the eastern, central, and western regions were 2.75, 3.15, and 3.42, respectively, while the average MSEs were 7.56, 9.89, and 10.42. These relatively low error magnitudes indicate that the ANN predictions deviated only slightly from the observed FFDI, supporting the model’s reliability even with a three-month lag.

Table 7 presents the correlation values for the developed models for all the model stages (i.e., training, validation, and testing) grouped into different regions (eastern, central, and western). In general, as with the two-month lag simulations, correlation values during training and validation were somewhat lower than those during the testing phase.

Table 7. Performances of the 3-month lagged model for training, validation, and testing periods.

Region	Station	Model	Training Period			Validation Period			Testing Period
			R	MSE	MAE	R	MSE	MAE	R	MSE	MAE
Eastern Victoria	Albury Airport AWS	SOI-OCT	0.59	20.7	3.2	−0.05	75.1	7.3	0.81	16.8	3.1
		SOI-NOV	0.71	15.1	2.7	0.29	27.3	4.0	0.80	25.6	4.7
	Bairnsdale Airport	SOI-OC	0.53	3.6	1.6	−0.12	2.2	1.2	0.87	3.1	1.5
		SOI-NOV	0.22	8.7	2.2	0.30	2.0	1.3	0.92	9.7	1.7
Central Victoria	Echuca Aerodrome	SOI-OCT	0.43	19.8	3.0	−0.02	13.0	3.1	0.91	2.9	1.3
		SOI-NOV	0.85	5.0	1.5	0.03	20.7	3.7	0.88	7.8	2.1
	Ballarat Aerodrome	SOI-OCT	0.68	11.9	3.5	0.07	44.9	6.7	0.80	29.9	5.5
		SOI-NOV	0.69	11.8	3.4	0.66	6.8	2.6	0.78	9.3	3.1
	Mangalore Airport	SOI-OCT	0.82	7.9	2.8	0.08	99.3	1.0	0.75	17.9	4.2
		SOI-NOV	0.73	10.6	3.3	0.22	44.5	6.7	0.75	7.3	2.7
Western Victoria	Mildura Airport	SOI-OCT	0.47	28.2	3.8	0.77	28.7	3.7	0.84	12.9	3.0
		SOI-NOV	0.37	30.1	4.0	0.24	28.7	4.5	0.87	33.1	4.7
	Longerenong	SOI-OCT	0.41	31.5	5.6	−0.05	52.6	7.3	0.93	7.1	2.7
		SOI-NOV	0.82	6.4	2.5	0.41	22.2	4.7	0.82	37.7	6.1
	Cape Otway	SOI-OCT	0.64	3.0	1.2	0.30	7.2	2.2	0.79	4.9	2.0
		SOI-NOV	0.40	5.1	1.4	0.36	2.0	1.3	0.86	5.5	2.0

Regarding spatial variations, considering only R-values, the average R for the eastern, central, and western regions were 0.85, 0.81, and 0.85, respectively. Similarly, the average MAE values were 2.75, 3.15, and 3.42. The eastern region again exhibited the lowest MSE and MAE, confirming stronger SOI–FFDI coupling and better predictive skill closer to the South Pacific source of the SOI signal. The progressive rise in MSE and MAE from east to west highlights increasing climatic variability and reduced teleconnection strength toward inland Victoria. As mentioned earlier, such variations from east to west are justified by the proximity of SOI’s origin (i.e., the South Pacific) toward the eastern region.

3.4. Graphical Comparisons of the Results

Figure 3 shows the scatter plots of the actual versus predicted FFDI values for the testing periods. To avoid the volume of graphs, the comparisons are shown for a few selected stations and selected lag periods. Figures also show the ideal (i.e., 45⁰) line on each diagram. From the figures it is evident that most of the scatter points lie close to the respective ideal line, which ascertains the accuracy of the models’ predictions with an unknown dataset (i.e., testing period). The scatter plot for the projected versus estimated fire danger values (Figure 3) exhibits the inherent variability in the data rather than uncertainty of the model training.

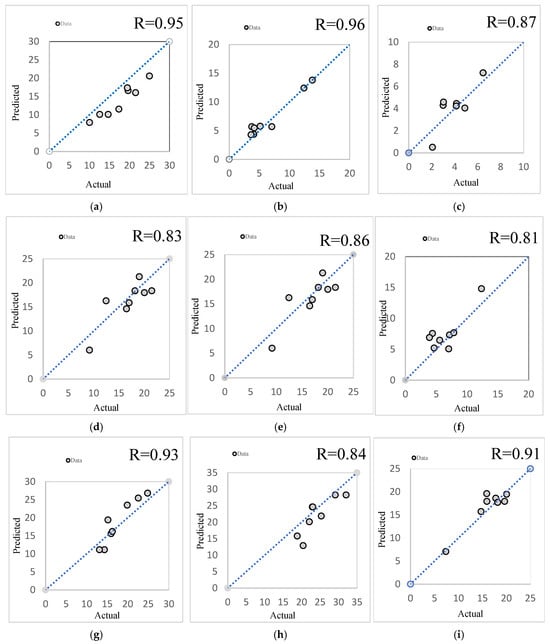
Figure 3. Scatter plots of the observed vs. predicted bushfire risk during the testing: For a 1-month lag for (a) Albury, (b) Ballarat and (c) Cape Otway. For a 2-month lag for (d) Echuca, (e) Albury, and (f) Bairnsdale. For a 3-month lag for (g) Longerenong, (h) Mildura, and (i) Echuca.

To interpret the results in detail, Figure 4, Figure 5 and Figure 6 present the time series plots showing comparisons of the predicted and actual FFDI values for the whole simulation period. For demonstration, one station was selected from each region. Figure 4 shows for Albury (eastern region), Figure 5 shows for Echuca (central region) and Figure 5 shows for Mildura (western region). Each figure shows the two lagged periods, 1-month and 3-month. From the figures it is evident that the models can simulate the actual FFDI values with good accuracy. It is to be noted that in some instances, the models’ results vary from the actual values, which might be due to some other local factors involved in evolving the FFDI values. Ideally, SOI values are not the sole driver for the evolution of FFDI values.

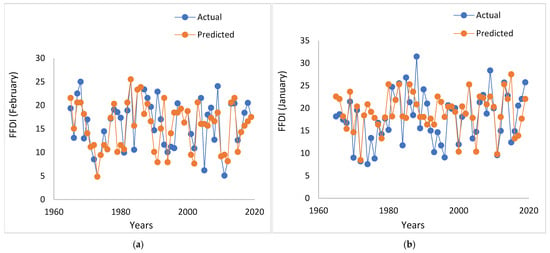
Figure 4. Time series comparison between the observed and predicted bushfire risk for Albury Airport: (a) 1-month lag, (b) 3-month lag.

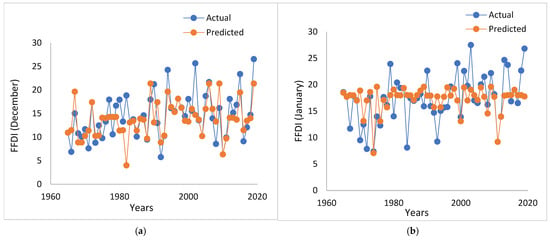
Figure 5. Time series comparison between the observed and predicted bushfire risk for Echuca Aerodrome: (a) 1-month lag, (b) 3-month lag.

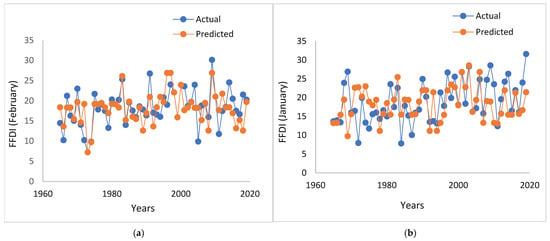
Figure 6. Time series comparison between the observed and predicted bushfire risk for Mildura Airport: (a) 1-month lag and (b) 3-month lag.

4. Discussion

This study examined the predictive relationship between SOI and FFDI across southeastern Australia using ANNs. While this research adopted Artificial Neural Networks (ANNs) to model the associations between climate indices and FFDI, other AI techniques, such as support vector machines, decision trees, random forests, and fuzzy logic systems, present complementary frameworks for pattern recognition and uncertainty modelling. Hybrid methods (e.g., fuzzy neural networks) may further enhance predictive performance and interpretability and represent a valuable avenue for future work.

The models successfully captured meaningful correlations between lagged SOI and FFDI values, demonstrating that large-scale climate variability plays a measurable role in influencing regional fire danger. The results confirm that lagged SOI values—particularly at one- to three-month intervals—carry predictive significance, supporting the potential use of climate precursors for short-term bushfire forecasting and preparedness planning.

Across all the testing periods, the ANN models achieved high predictive accuracy, with correlation coefficients (R) ranging from 0.71 to 0.96. The mean absolute error (MAE) values generally remained below 3.5, while the mean squared error (MSE) values were typically under 20, indicating low residual deviations between the predicted and observed FFDI. These results demonstrate that the ANN models were able to reproduce the observed fire danger trends with reasonable precision, validating their ability to learn complex nonlinear relationships between SOI fluctuations and fire weather response. In particular, eastern stations such as Albury Airport and Bairnsdale achieved the lowest error values (MAE ≈ 1.5–2.0; MSE < 5), highlighting strong model generalisation and minimal bias during testing.

Regional differences were evident. The eastern region consistently achieved higher correlations (average R ≈ 0.84) and lower errors (MAE ≈ 2.9) compared with the central (R ≈ 0.79, MAE ≈ 3.8) and western regions (R ≈ 0.81, MAE ≈ 4.0). This spatial trend aligns with the climatic influence of the South Pacific, as eastern locations are more directly affected by SOI-driven atmospheric variations. The central region displayed stable but moderate performance, while western coastal sites such as Cape Otway showed delayed but notable predictive relationships (R ≈ 0.94 for a 2-month lag), possibly due to maritime buffering or topographic influences.

The findings suggest that no universal lag period applies across all regions; instead, the SOI–FFDI linkage is region- and time-specific. Generally, predictive accuracy declined with increasing lag, as local meteorological variability and shorter-term weather systems began to dominate. Overall, the combination of high correlation coefficients and low error metrics confirms that the ANN models effectively captured the dynamic yet lagged relationships between SOI and FFDI, providing a scientifically robust basis for short-term bushfire danger forecasting.

The connections between large-scale climate indices and fire danger metrics, e.g., FFDI, are essentially nonlinear and often include temporal lags with many climate drivers. While the approaches used in this study capture general associations, they do not explicitly model delayed responses of multiple climate indices or higher-order connections. As such, high correlation values should be interpreted carefully, as they do not inevitably reveal predictive precision under extreme or unseen conditions. Similar observations were obtained for other climatic parameters, e.g., rainfall prediction [34,35,36]. Therefore, Khastagir et al. [3] adopted a probability distribution in determining bushfire potential in Victoria. Incorporating multiple lagged predictors or dynamic modelling frameworks would likely improve the robustness of future analyses.

Although the ANN model showed good forecasting capability for fire danger prediction, several constraints should be acknowledged. The model’s performance relies deeply on the characteristics and representativeness of the data input, which may change within stations and vegetation types.

5. Conclusions

Using ANN, this work assessed the predictive link between SOI and FFDI to better understand climate–fire interactions in southeastern Australia. The results demonstrate that SOI exerts a measurable influence on fire weather conditions, with the ANN model capturing key lagged relationships between SOI and FFDI. Among the tested scenarios, the one-month lag exhibited the strongest predictive association, indicating its potential relevance for short-term fire risk forecasting, while the two- and three-month lags provided insights into longer-term seasonal variability.

The model’s performance across multiple stations suggests that lag-based ANN frameworks can complement the existing fire-danger assessments by offering an additional perspective on how large-scale climate signals translate into local fire weather responses. The best predictive performance was observed for the SOI values during October–November in relation to the FFDI peaks from November to February, which broadly aligns with the regional fire season in Victoria.

Despite these encouraging results, the models did not fully capture some extreme FFDI values, likely due to influences from local meteorological factors such as temperature anomalies, wind variability, and humidity. The observed overestimation during periods like the ‘Millennium Drought’ further indicates that SOI alone cannot explain all variations in bushfire risk. Incorporating additional climate indices and localised variables could therefore improve predictive accuracy.

Methodologically, ANN models require large, high-quality datasets and remain limited by their “Blackbox” nature, which constrains interpretability and reproducibility. They are also sensitive to parameter selection and data division methods. Future research should address these challenges through ensemble approaches, systematic cross-validation, and integration with physically based or hybrid statistical models to enhance robustness and transparency.

Overall, this research provides an initial framework for linking large-scale climate drivers with regional bushfire danger. While preliminary, the findings highlight the potential for developing climate-informed early-warning tools that support preparedness and fire-management strategies in southeastern Australia.