Deployable and Habitable Architectural Robot Customized to Individual Behavioral Habits
Abstract
1. Introduction
- (1)
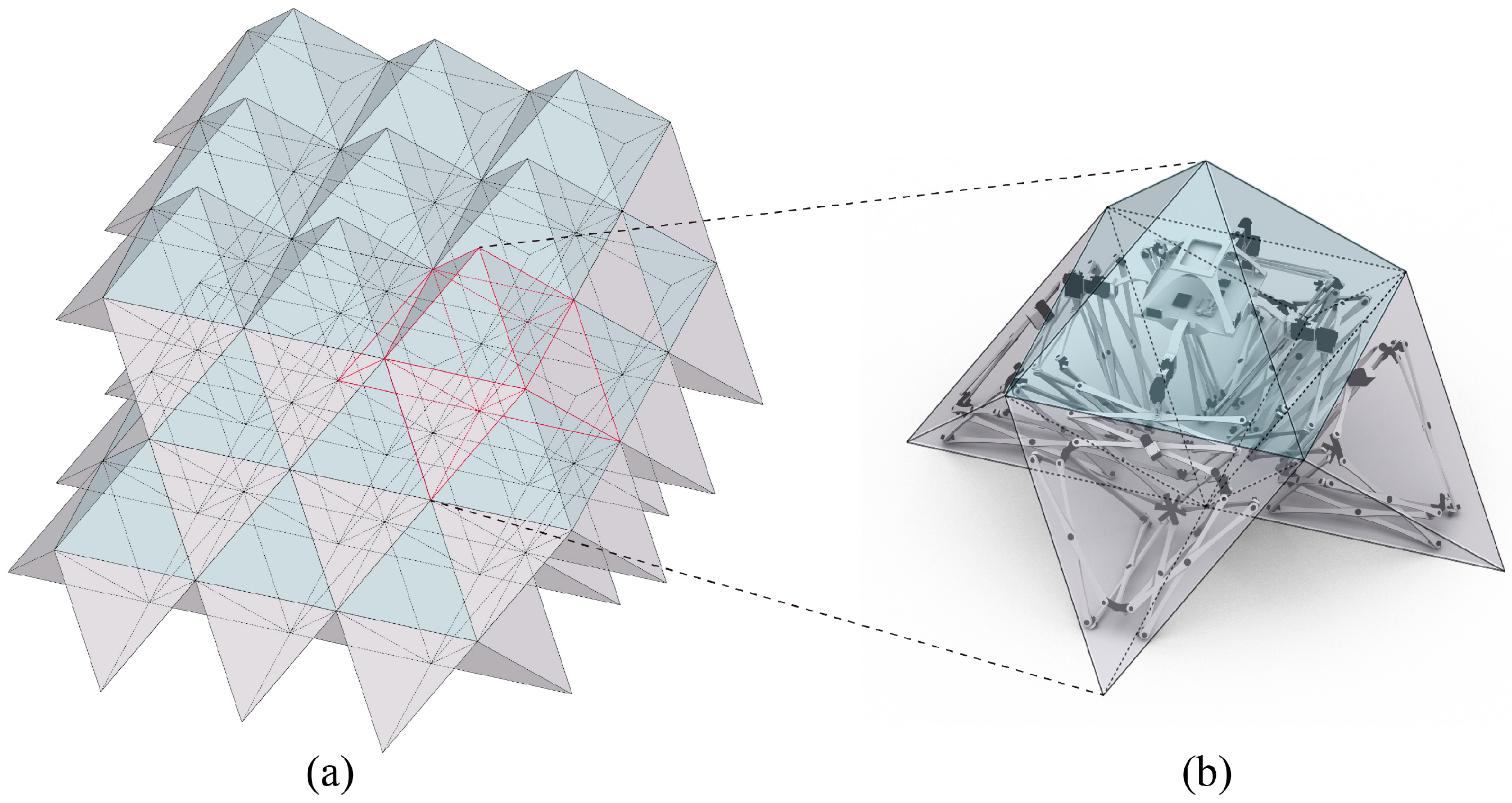
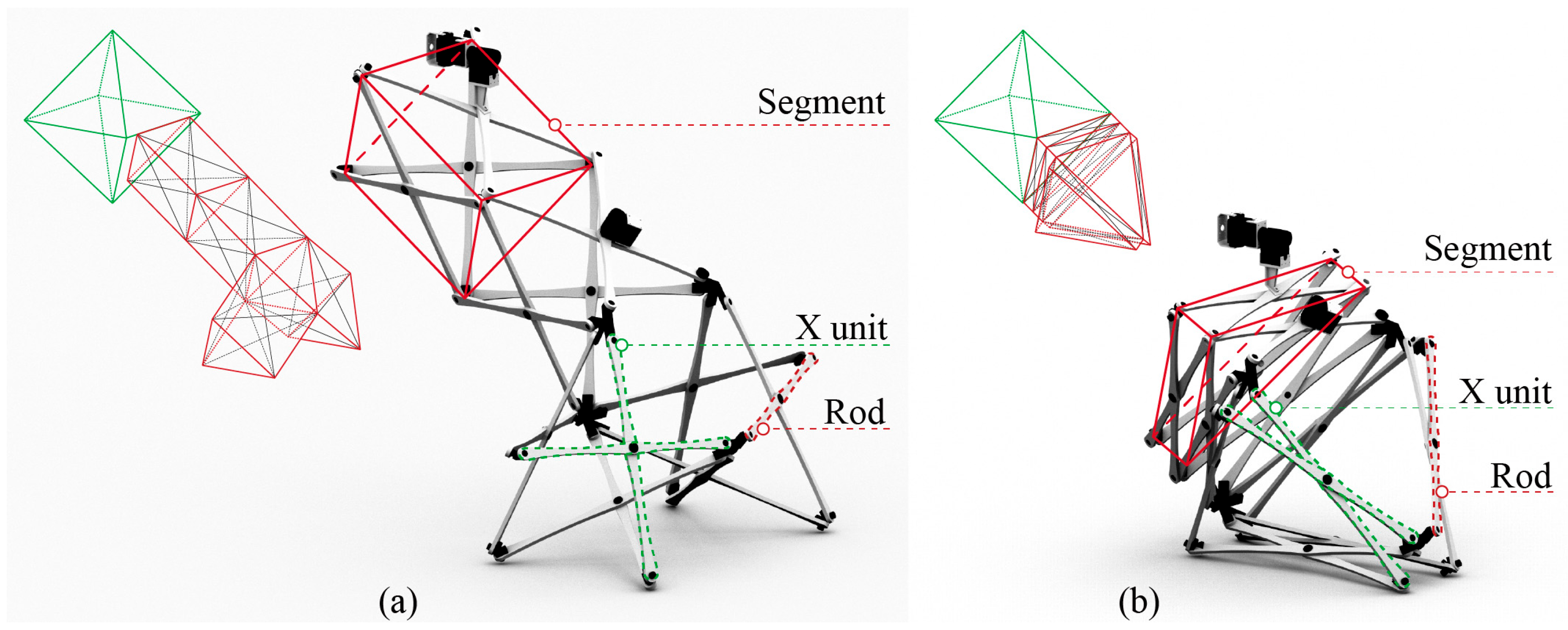
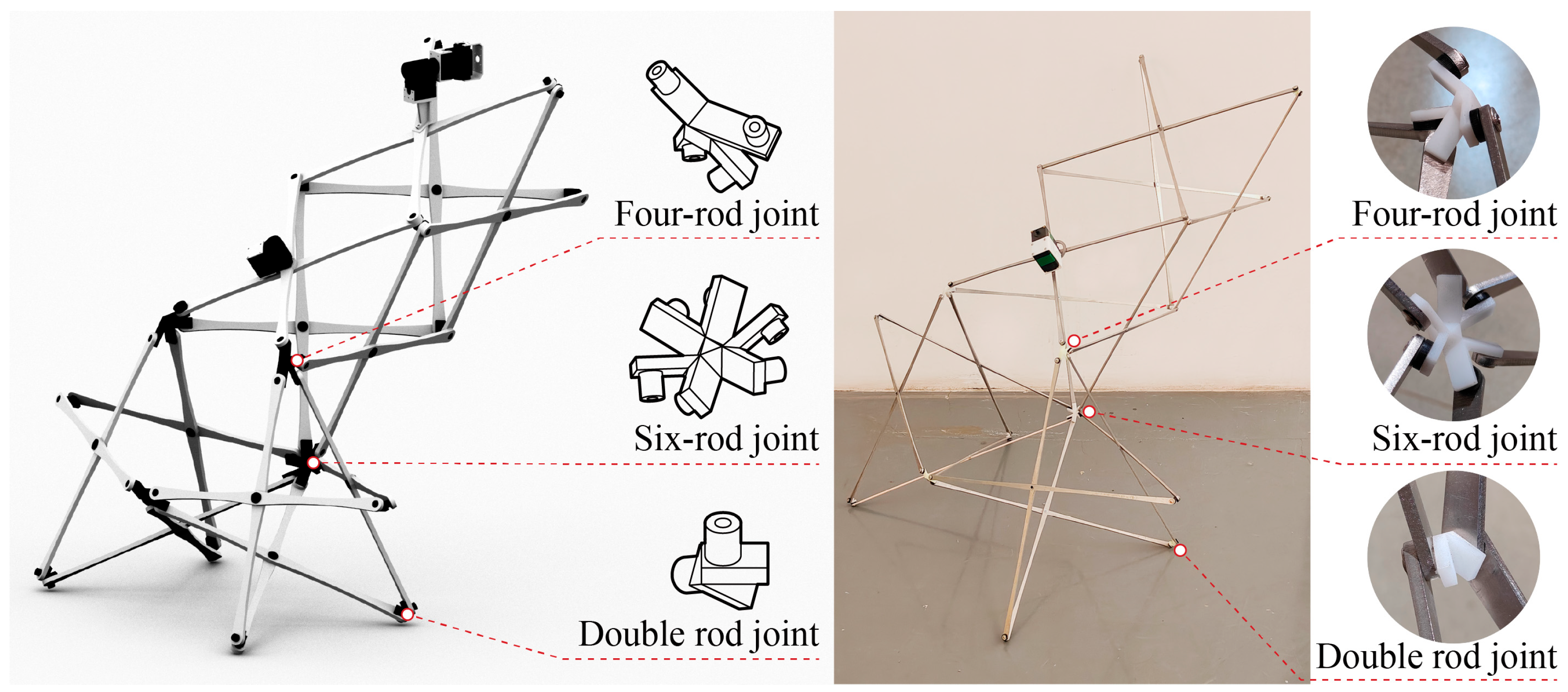
- A foldable robotic prototype based on scissor mechanisms is designed. When folded, multiple robots are arranged in a tessellated layout for efficient bulk storage and transport. When deployed as living space, the device rapidly unfolds to form a compact area supporting basic user activities.
- (2)
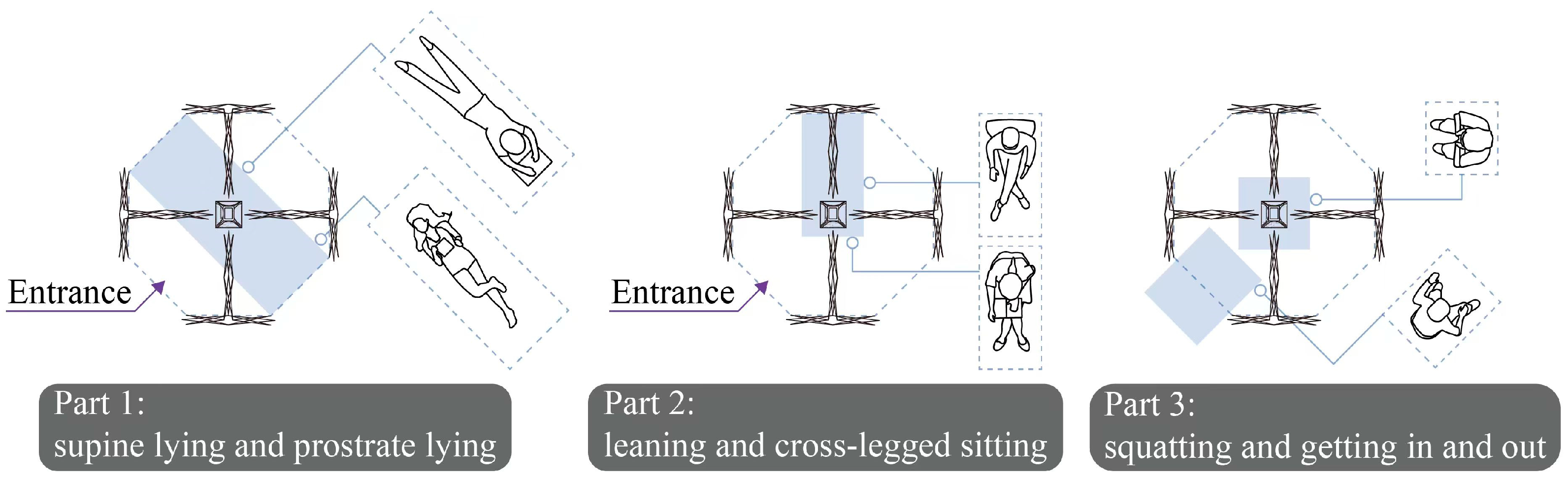
- A user-oriented design system is built by linking spatial modulation with individual living habits. The customizable system allows users to design an individualized architectural robot depending on their body features, behavioral habits, and personal tastes. The system is user-friendly, with an easy-to-use interface that facilitates real-time interaction.
- (3)
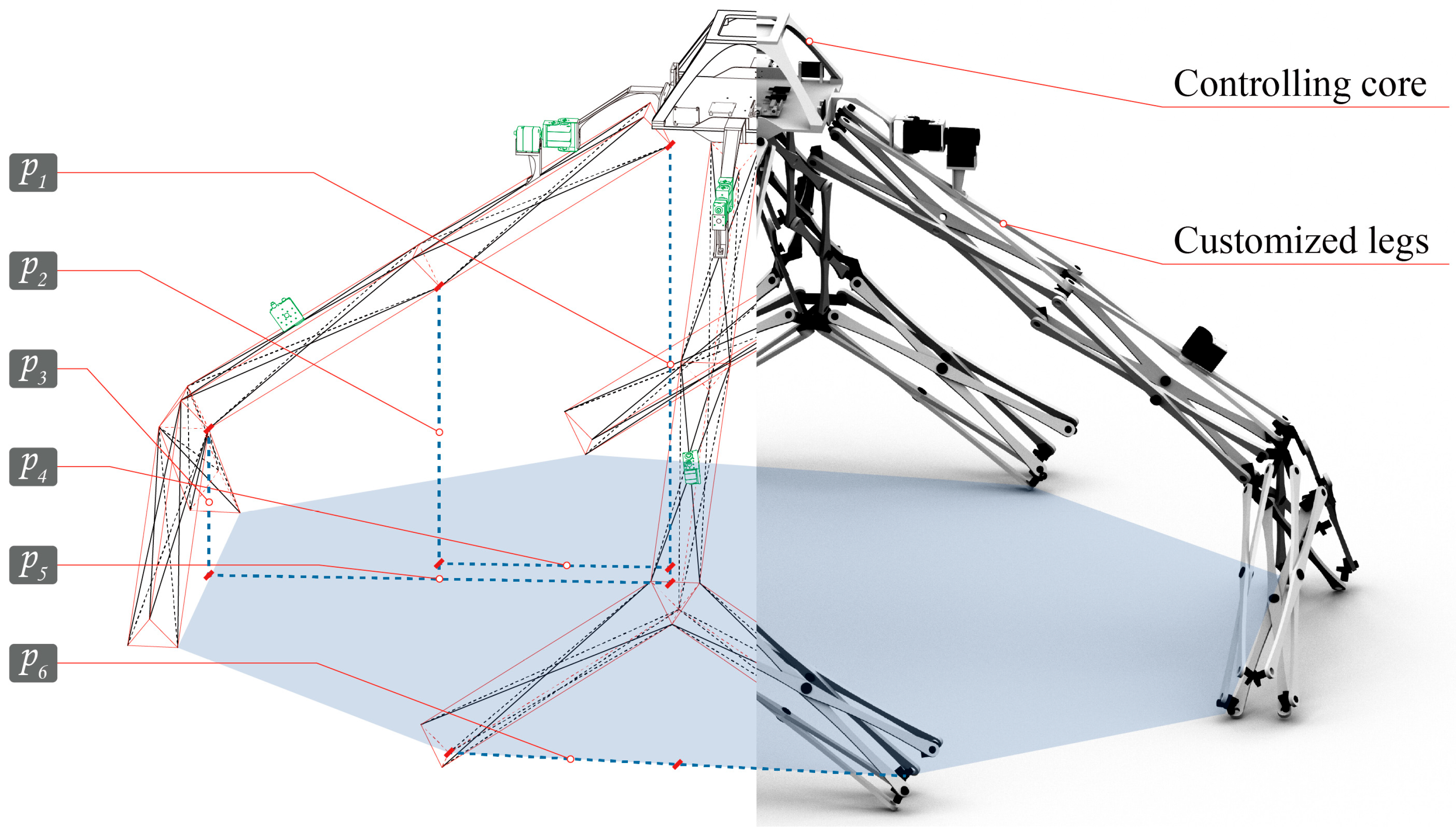
- A moving method that allows the architectural robot to follow its owner is developed. We designed the gait pattern of the architectural robot by referring to the locomotion of quadruped animals. With a self-developed script, the user is able to control when the robot starts and stops moving.
- (4)
- An example of such an architectural robot was constructed to demonstrate the feasibility of the method. The “Design–Optimization–Fabrication” workflow of the experiment is illustrated, and the specific fabrication data is presented.
2. Background and Related Works
3. Methodology
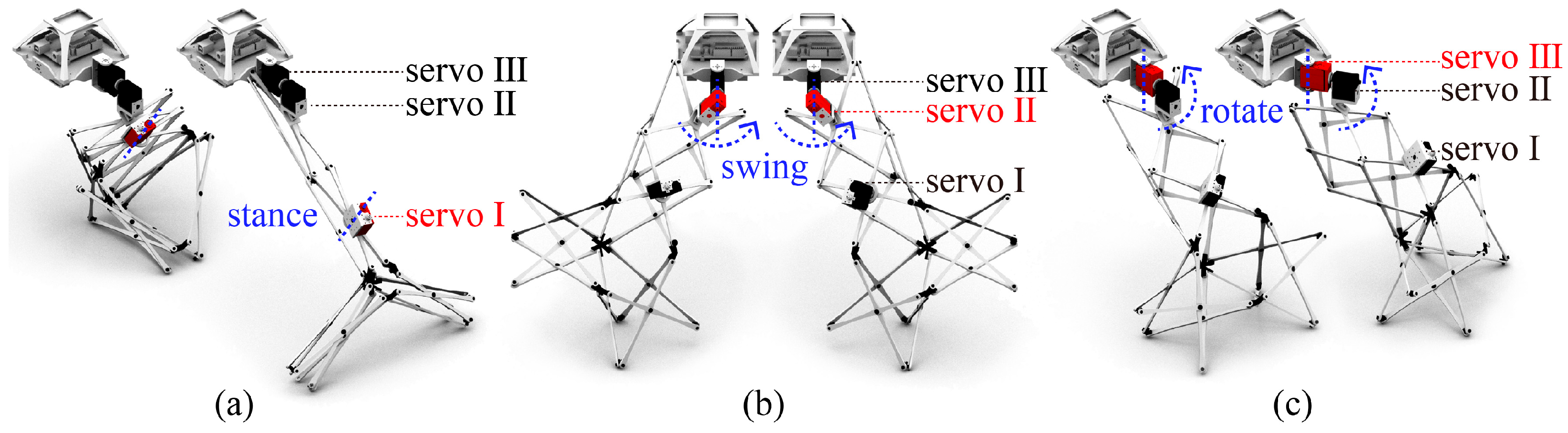
3.1. Portability: Develop a Deployable and Inhabitable Robot Prototype
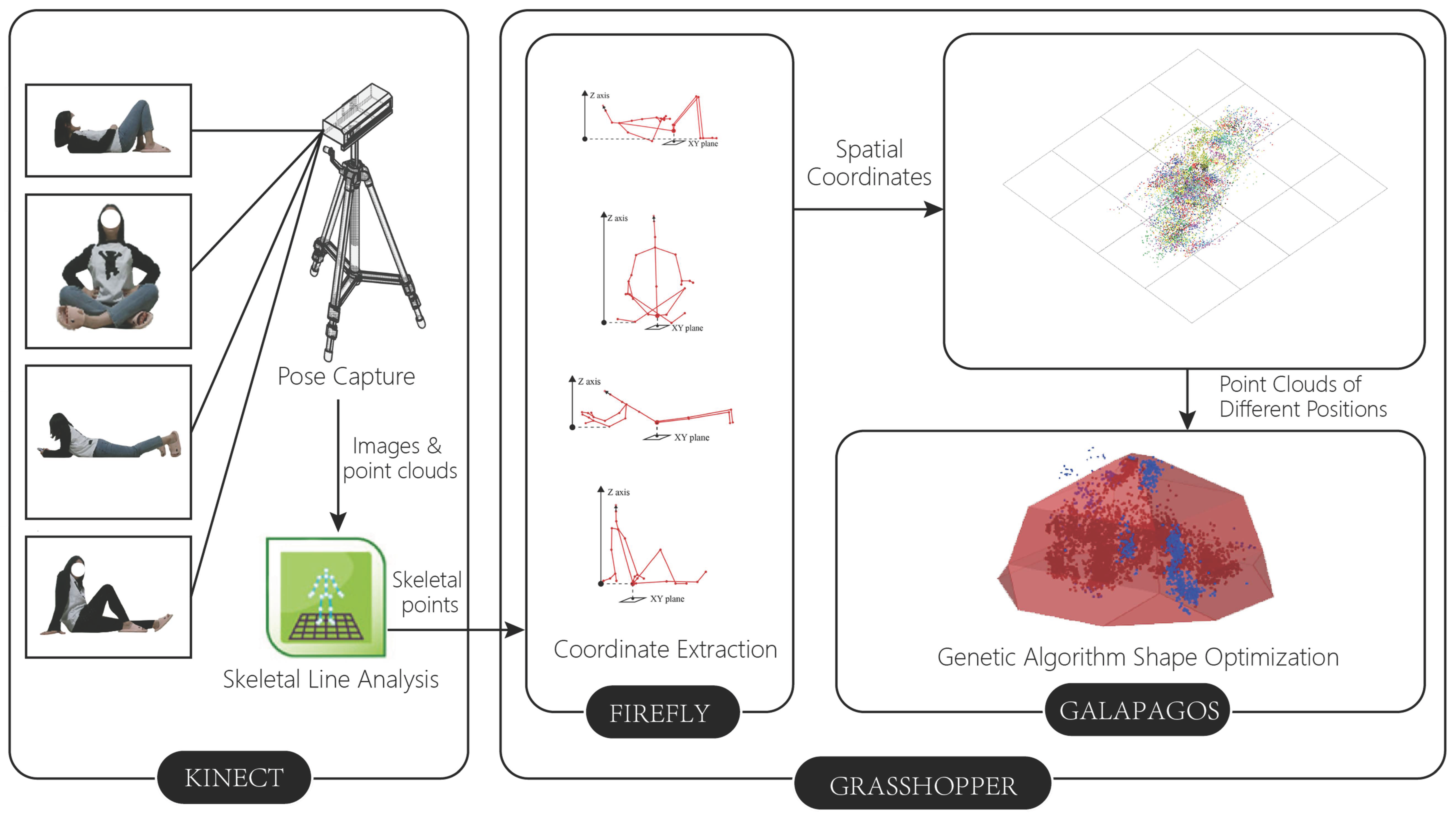
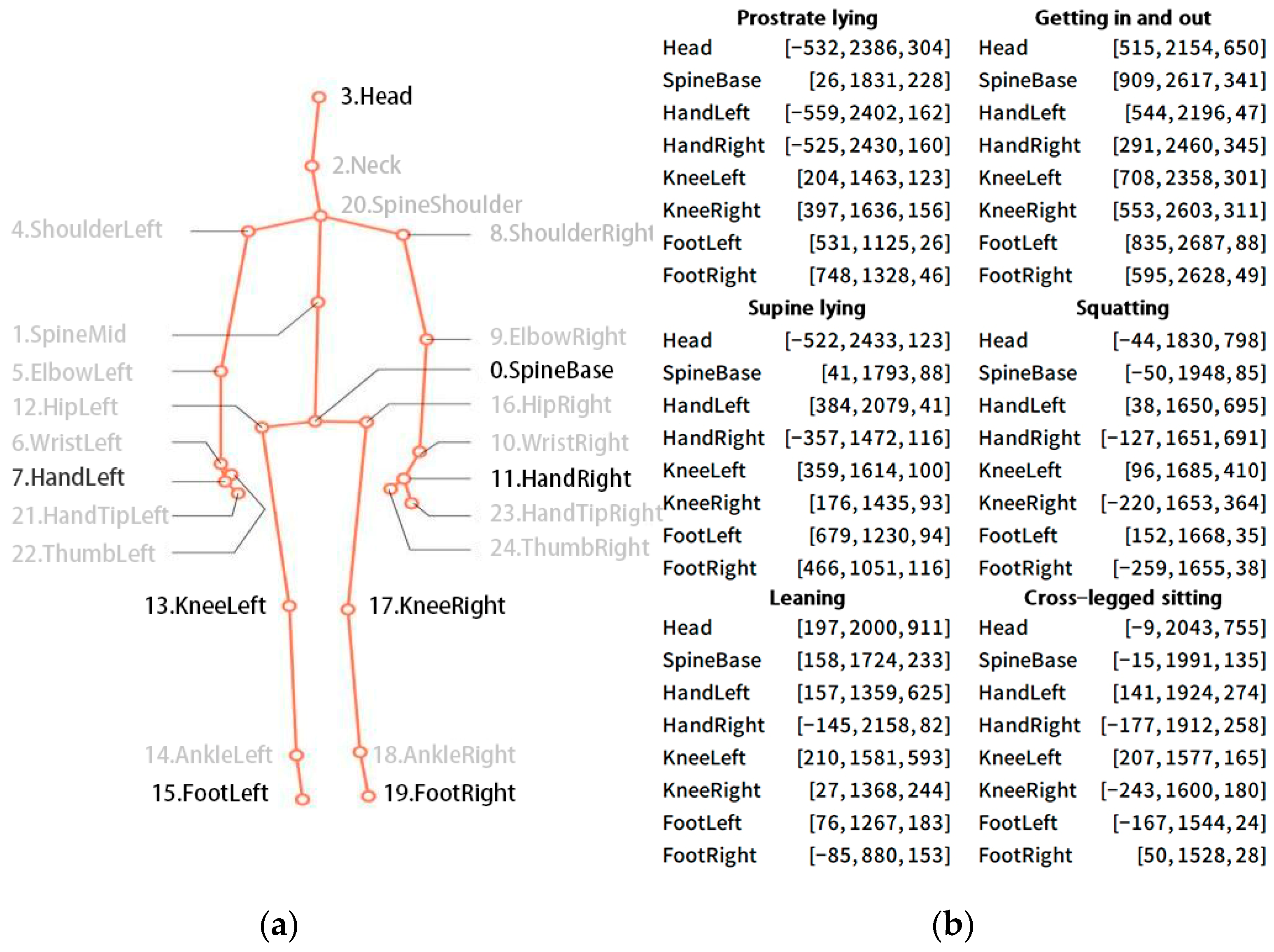
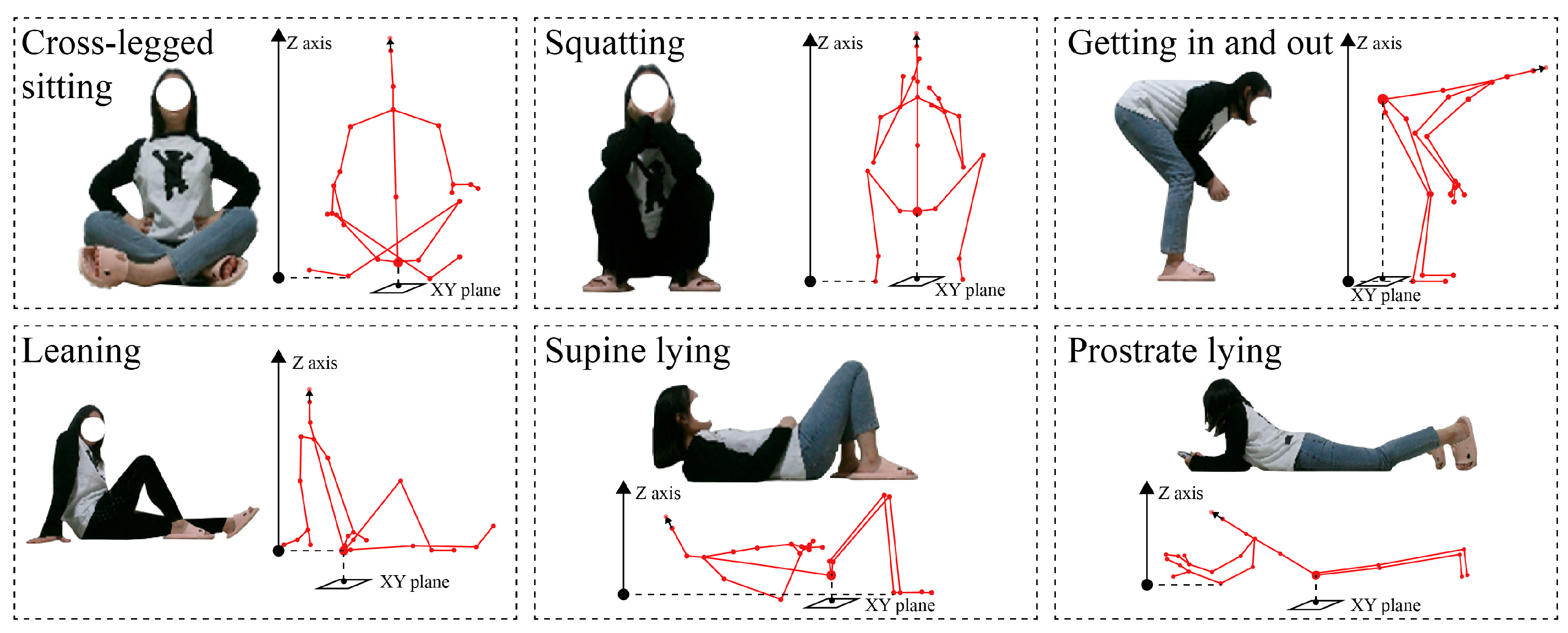
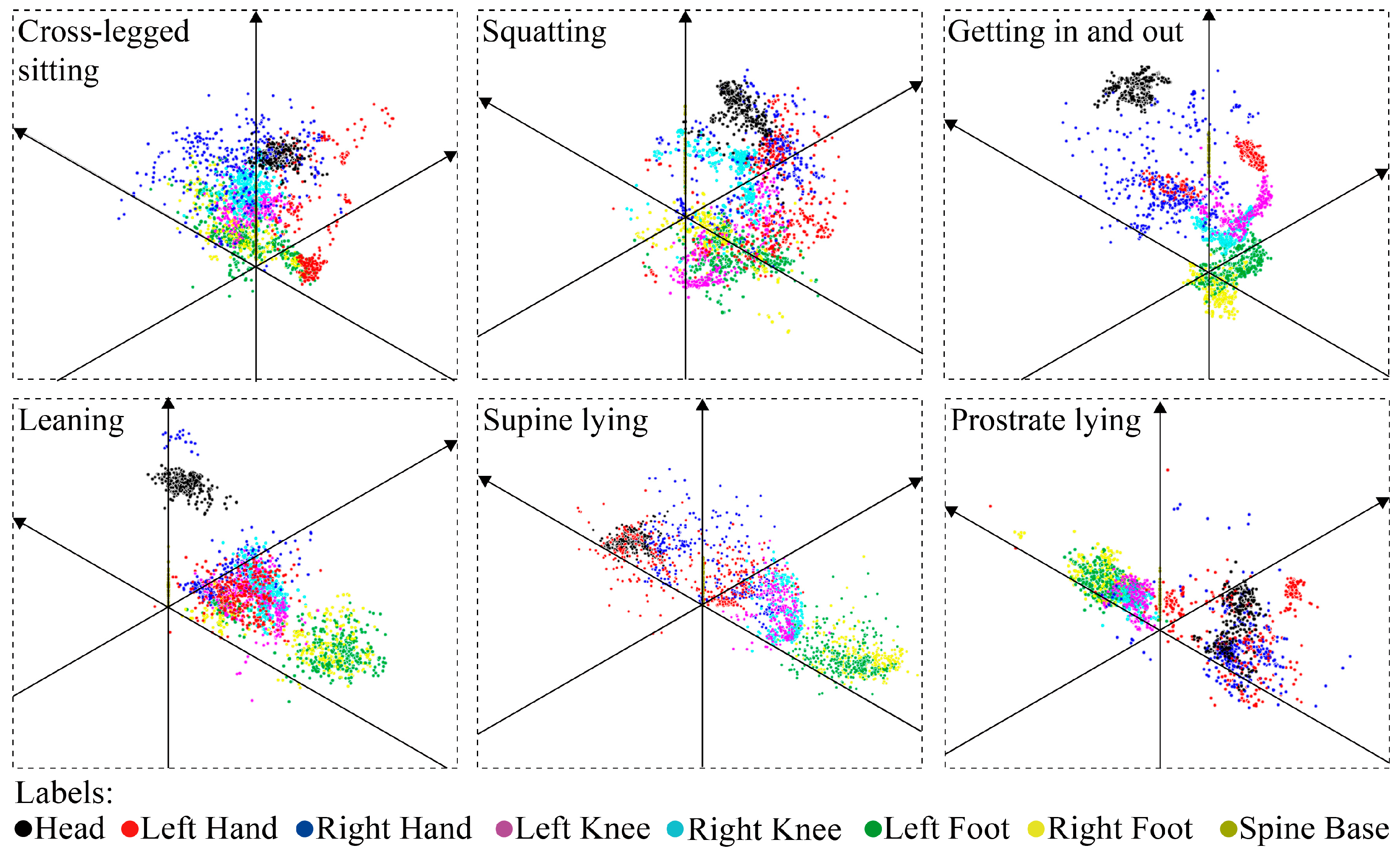
3.2. Customizability: Developing a User-Oriented Customizable Design System
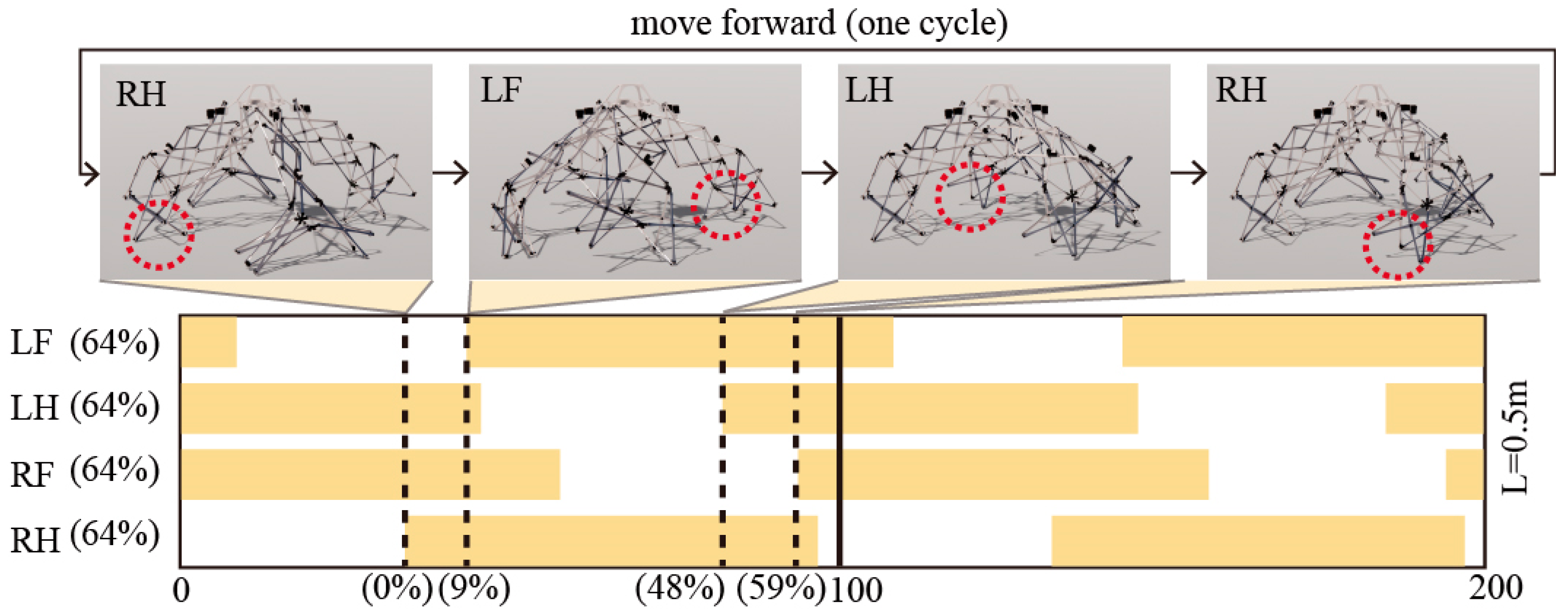
3.3. Mobility: The Architectural Robots Can Follow Their Owners Like Puppies
4. Experimental Results and Discussion
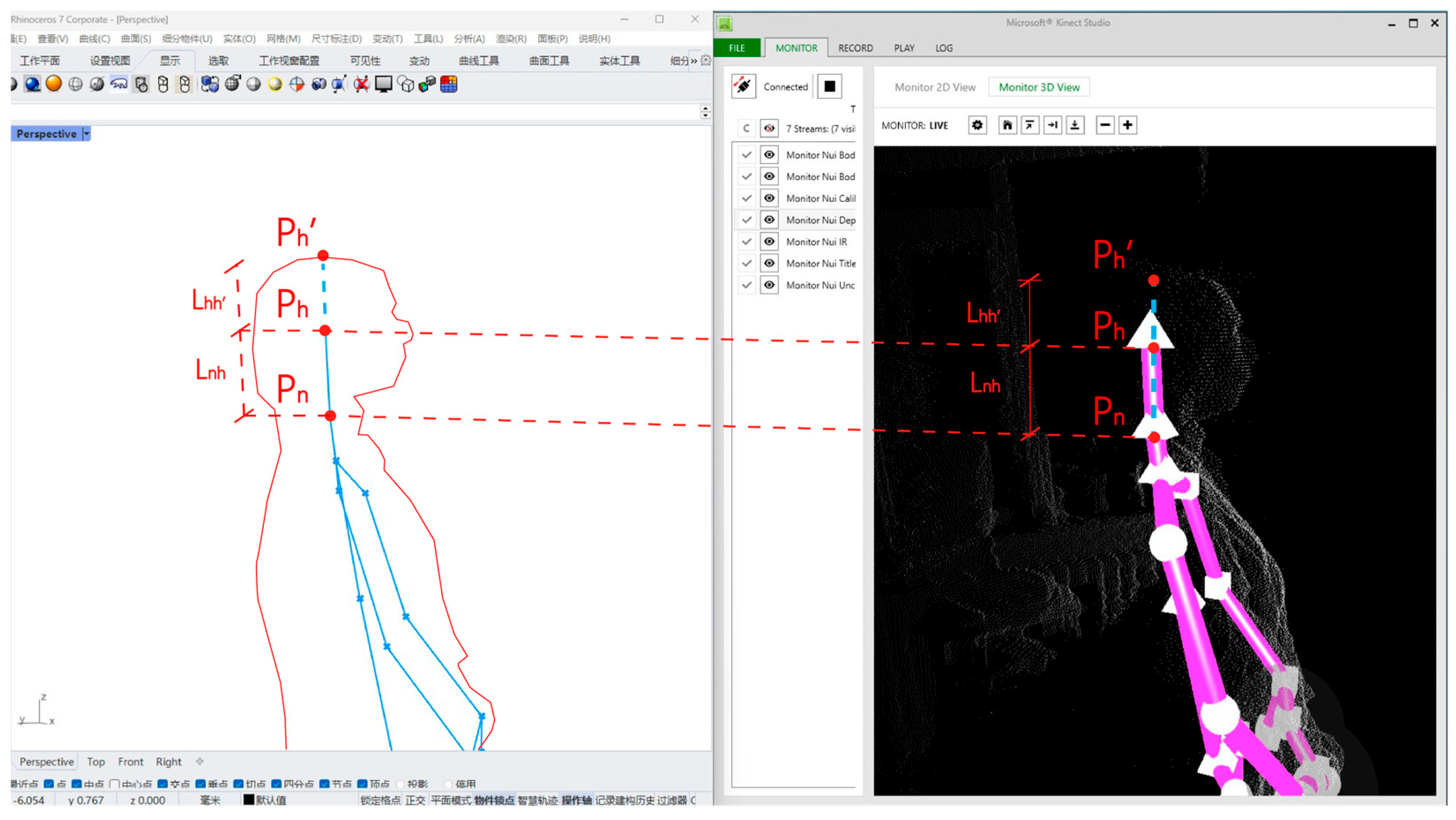
4.1. “Scan–Generation–Fabrication” of an Experimental Architectural Robot
4.2. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gross, M.D.; Green, K.E. Architectural robotics, inevitably. Interactions 2012, 19, 28–33. [Google Scholar] [CrossRef]
- Dinevari, N.F.; Shahbazi, Y.; Maden, F. Geometric and analytical design of angulated scissor structures. Mech. Mach. Theory 2021, 164, 104402. [Google Scholar] [CrossRef]
- Huang, W.; Wu, C.; Hu, J.; Gao, W. Weaving structure: A bending-active gridshell for freeform fabrication. Autom. Constr. 2022, 136, 104184. [Google Scholar] [CrossRef]
- Duarte, J.P. A discursive grammar for customizing mass housing: The case of Siza’s houses at Malagueira. Autom. Constr. 2005, 14, 265–275. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Z.; Zheng, H.; Li, Z.; Yuan, P.F. Automated architectural spatial composition via multi-agent deep reinforcement learning for building renovation. Autom. Constr. 2024, 167, 105702. [Google Scholar] [CrossRef]
- Price, C. The fun palace. Drama Rev. TDR 1968, 12, 127–134. [Google Scholar] [CrossRef]
- Maierhofer, M.; Soana, V.; Yablonina, M.; Suzuki, S.; Koerner, A.; Knippers, J.; Menges, A. Self-choreographing network: Towards cyberphysical design and operation processes of adaptive and interactive bending-active systems. In Proceedings of the 39th Annual Conference of the Association for Computer Aided Design in Architecture (ACADIA), Austin, TX, USA, 21–26 October 2019. [Google Scholar] [CrossRef]
- Deyong, S. Companion to the History of Architecture; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 1–12. [Google Scholar] [CrossRef]
- Eastman, C.M. Adaptive Conditional Architecture. Institute of Physical Planning, Carnegie-Mellon University: Pittsburgh, PA, USA, 1972. [Google Scholar]
- Negroponte, N. Soft Architecture Machines; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Sterk, T.E. Building upon Negroponte: A hybridized model of control suitable for responsive architecture. Autom. Constr. 2005, 14, 225–232. [Google Scholar] [CrossRef]
- Kroner, W.M. An intelligent and responsive architecture. Autom. Constr. 1997, 6, 381–393. [Google Scholar] [CrossRef]
- Attia, S. Evaluation of adaptive facades: The case study of Al Bahr Towers in the UAE. QSci. Connect 2017, 2017, 6. [Google Scholar] [CrossRef]
- Wigginton, M.; Harris, J. Intelligent Skins; Routledge: Oxford, UK, 2013; pp. 173–178. [Google Scholar]
- Droege, P.; Porta, S.; Salingaros, N. Intelligent Environments: Spatial Aspects of the Information Revolution; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Oosterhuis, K. Programmable Architecture; L’Arcaedizione: Milan, Italy, 2002. [Google Scholar]
- Oosterhuis, K. Towards a New Kind of Building: Tag, Make, Move, Evolve; NAi: Rotterdam, The Netherlands, 2011. [Google Scholar]
- Bullivant, L. Jason Bruges: Light and space explorer. Archit. Des. 2005, 75, 79–81. [Google Scholar] [CrossRef]
- Floreano, D.; Nosengo, N. Tales from a Robotic World: How Intelligent Machines Will Shape Our Future; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar] [CrossRef]
- Gray, J.; Hoffman, G.; Adalgeirsson, S.O.; Berlin, M.; Breazeal, C. Expressive, Interactive Robots: Tools, Techniques, and Insights Based on Collaborations. In Proceedings of the HRI 2010 Workshop “What Do Collaborations with the Arts Have to Say About HRI?”, Osaka, Japan, 2–5 March 2010. [Google Scholar]
- Green, K.E. Architectural Robotics: Ecosystems of Bits, Bytes, and Biology; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- De Aguiar, C.H.; Fateminasab, R.; Frazelle, C.G.; Scott, R.; Wang, Y.; Wooten, M.B.; Green, K.E.; Walker, I.D. The networked, robotic home+ furniture suite: A distributed, assistive technology facilitating aging in place. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016. [Google Scholar] [CrossRef]
- Oosterhuis, K. Hyperbodies: Towards an E-motive Architecture; Birkhäuser: Basel, Switzerland, 2003. [Google Scholar]
- Bier, H.H. Robotic buildings(s). Next Gener. Build. 2014, 1, 83–92. [Google Scholar] [CrossRef]
- Kilian, A. The flexing room architectural robot: An actuated active-bending robotic structure using human feedback. In Proceedings of the 38th Annual Conference of the Association for Computer Aided Design in Architecture, Mexico City, Mexico, 18–20 October 2018. [Google Scholar] [CrossRef]
- Grasshopper. Available online: https://www.grasshopper3d.com/ (accessed on 3 December 2024).
- Shotton, J.; Girshick, R.; Fitzgibbon, A.; Sharp, T.; Cook, M.; Finocchio, M.; Moore, R.; Kohli, P.; Criminisi, A.; Kipman, A.; et al. Efficient human pose estimation from single depth images. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 2821–2840. [Google Scholar] [CrossRef] [PubMed]
- Kinect v2 Sensor. Available online: https://learn.microsoft.com/zh-cn/shows/visual-studio-connect-event-2014/716 (accessed on 3 December 2024).
- Firefly. Available online: https://www.food4rhino.com/en/app/firefly (accessed on 3 December 2024).
- ISO 7250-1:2008; Basic Human Body Measurements for Technological Design. ISO: Geneva, Switzerland, 2008.
- Galapagos. Available online: https://www.grasshopper3d.com/group/galapagos (accessed on 3 December 2024).
- Hoyt, D.F.; Taylor, C.R. Gait and the energetics of locomotion in horses. Nature 1981, 292, 239–240. [Google Scholar] [CrossRef]
- Muybridge, E. Animal Locomotion: The Muybridge Work at the University of Pennsylvania, the Method and the Result; JB Lippincott Company: New York, NY, USA, 1888. [Google Scholar]
- Hildebrand, M. Symmetrical Gaits of Horses: Gaits can be expressed numerically and analyzed graphically to reveal their nature and relationships. Science 1965, 150, 701–708. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, M. Symmetrical gaits of primates. Am. J. Phys. Anthropol. 1967, 26, 119–130. [Google Scholar] [CrossRef]
- Hildebrand, M. Symmetrical gaits of dogs in relation to body build. J. Morphol. 1968, 124, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Cartmill, M.; Lemelin, P.; Schmitt, D. Support polygons and symmetrical gaits in mammals. Zool. J. Linn. Soc. 2002, 136, 401–420. [Google Scholar] [CrossRef]
- Patrick, S.K.; Noah, J.A.; Yang, J.F. Interlimb Coordination in Human Crawling Reveals Similarities in Development and Neural Control With Quadrupeds. J. Neurophysiol. 2009, 101, 603–613. [Google Scholar] [CrossRef] [PubMed]
- Owaki, D.; Kano, T.; Nagasawa, K.; Tero, A.; Ishiguro, A. Simple robot suggests physical interlimb communication is essential for quadruped walking. J. R. Soc. Interface 2013, 10, 20120669. [Google Scholar] [CrossRef] [PubMed]







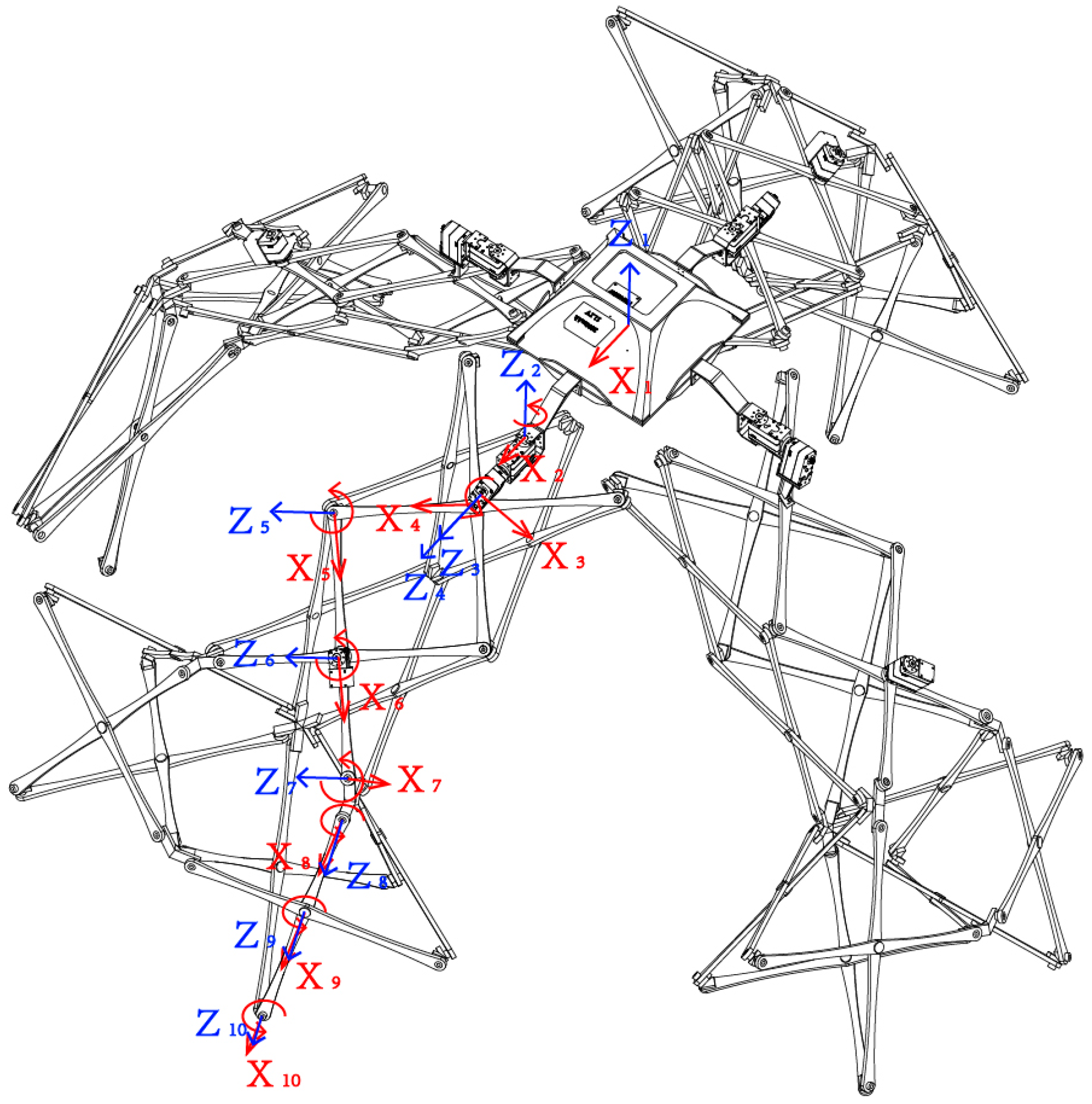






| Frame_from | Frame_to | α | a | d | θ |
|---|---|---|---|---|---|
| joint 1 | joint 2 | 0 | 290 | −48 | 0 |
| joint 2 | joint 3 | 141 | 166 | 166 | −176 |
| joint 3 | joint 4 | −54 | 0 | −130 | −135 |
| joint 4 | joint 5 | 0 | 250 | 0 | 90 |
| joint 5 | joint 6 | 0 | 250 | 0 | 0 |
| joint 6 | joint 7 | 0 | 212 | −143 | 76 |
| joint 7 | joint 8 | 33 | 0 | 135 | −103 |
| joint 8 | joint 9 | 0 | 212 | 0 | 0 |
| joint 9 | joint 10 | 0 | 250 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ren, P.; Wang, H.; Cui, Y.; Xu, Z. Deployable and Habitable Architectural Robot Customized to Individual Behavioral Habits. Appl. Syst. Innov. 2025, 8, 169. https://doi.org/10.3390/asi8060169
Zhang Y, Ren P, Wang H, Cui Y, Xu Z. Deployable and Habitable Architectural Robot Customized to Individual Behavioral Habits. Applied System Innovation. 2025; 8(6):169. https://doi.org/10.3390/asi8060169
Chicago/Turabian StyleZhang, Ye, Penghua Ren, Haoyi Wang, Yu Cui, and Zhen Xu. 2025. "Deployable and Habitable Architectural Robot Customized to Individual Behavioral Habits" Applied System Innovation 8, no. 6: 169. https://doi.org/10.3390/asi8060169
APA StyleZhang, Y., Ren, P., Wang, H., Cui, Y., & Xu, Z. (2025). Deployable and Habitable Architectural Robot Customized to Individual Behavioral Habits. Applied System Innovation, 8(6), 169. https://doi.org/10.3390/asi8060169







