Abstract
Identifying similar network structures is key to capturing graph isomorphisms and learning representations that exploit structural information encoded in graph data. This work shows that ego networks can produce a structural encoding scheme for arbitrary graphs with greater expressivity than the Weisfeiler–Lehman (1-WL) test. We introduce , a preprocessing step to produce features that augment node representations by encoding ego networks into sparse vectors that enrich message passing (MP) graph neural networks (GNNs) beyond 1-WL expressivity. We formally describe the relation between and 1-WL, and characterize its expressive power and limitations. Experiments show that matches the empirical expressivity of state-of-the-art methods on isomorphism detection while improving performance on nine GNN architectures and six graph machine learning tasks.
1. Introduction
Novel approaches for representation learning on graph-structured data have appeared in recent years []. Graph neural networks can efficiently learn representations that depend both on the graph structure and node and edge features from large-scale graph data sets. The most popular choice of architecture is the message passing graph neural network (MP-GNN). MP-GNNs represent nodes by repeatedly aggregating feature ‘messages’ from their neighbors.
Despite being successfully applied in a wide variety of domains [,,,,], there is a limit on the representational power of MP-GNNs provided by the computationally efficient Weisfeiler–Lehman (1-WL) test [] for checking graph isomorphisms [,]. Establishing this connection has lead to a better theoretical understanding of the performance of MP-GNNs and many possible generalizations at the price of additional computational cost [,,,,].
To improve the expressivity of MP-GNNs, recent methods have extended the vanilla message passing mechanism is various ways. For example, using higher order k-vertex tuples [] leading to k-WL generalizations, introducing relative positioning information for network vertices [], propagating messages beyond direct neighborhoods [], using concepts from algebraic topology [], or combining subgraph information in different ways [,,,,,,]. Similarly, provably powerful graph networks (PPGN) [] have been proposed as an architecture with 3-WL expressivity guarantees, at the cost of quadratic memory and cubic time complexities with respect to the number of nodes. More recently, Balcilar et al. [] proposed a novel MP-GNN with linear time and memory complexity, but theoretically more powerful than the 1-WL test, and experimentally as powerful as 3-WL by leveraging a preprocessing, spectral decomposition step, with cubic worst-case time complexity. All aforementioned approaches improve expressivity by extending MP-GNN architectures, often evaluating on standarized benchmarks [,,]. However, identifying the optimal approach on novel domains requires costly architecture searches.
In this work, we show that a simple encoding of local ego networks is a possible solution to these shortcomings. We present Igel, an Inductive Graph Encoding of Local ego network subgraphs allowing MP-GNN and deep neural network (DNN) models to go beyond 1-WL expressivity without modifying existing model architectures. produces inductive representations that can be introduced into MP-GNN models. reframes capturing 1-WL information irrespective of model architecture as a preprocessing step that simply extends node/edge attributes. Our main contributions in this paper are:
- C1
- We present a novel structural encoding scheme for graphs, describing its relationship with existing graph representations and MP-GNNs.
- C2
- We formally show that the proposed encoding has more expressive power than the 1-WL test, and identify expressivity upper bounds for graphs that match subgraph GNN state-of-the-art methods.
- C3
- We experimentally assess the performance of nine model architectures enriched with our proposed method on six tasks and thirteen graph data sets and find that it consistently improves downstream model performance.
We structure the paper as follows: In Section 2, we introduce our notation and the required background, including relevant works extending MP-GNNs beyond 1-WL. Then, we describe in Section 3. We analyze ’s expressivity in Section 4 and evaluate its performance experimentally in Section 5. Finally, we discuss our findings and summarize our results in Section 6.
2. Notation and Related Work
Given a graph , we define and , is the degree of a node v in and is the maximum degree. For , is their shortest distance, and is the diameter of G. Double brackets denote a lexicographically-ordered multi-set, is the -depth ego network centered on v, and is the set of neighbors of v in G up to distance , i.e., .
2.1. Message Passing Graph Neural Networks
Graph neural networks are deep learning architectures for learning representations on graphs. The most popular choice of architecture is the message passing graph neural network (MP-GNN). In MP-GNNs, there is a direct correspondence between the connectivity of network layers and the structure of the input graph. Because of this, the representation (embedding) of each node depends directly on its neighbors and only indirectly on more distant nodes.
Each layer of an MP-GNN computes an embedding for a node by iteratively aggregating its attributes and the attributes of their neighboring nodes. Aggregation is expressed via two parametrized functions: , which represents the computation of joint information for a vertex and a given neighbor, and , a pooling operation over messages that produces a vertex representation. Let denote an initial w-dimensional feature vector associated with . Each i-th GNN layer computes the i-th message passing step, such that is the multi-set of messages received by v:
and is the output of a permutation-invariant function over the message multi-set and the previous vertex state:
For machine learning tasks that require graph-level embeddings, an additional parameterized function dubbed produces a graph-level representation , pooling all vertex representations at step i:
The functions , , and are differentiable with respect to their parameters, which are optimized during learning via gradient descent. The choice of functions gives rise to a broad variety of GNN architectures [,,,,]. However, it has been shown that all MP-GNNs defined by , , and are at most as expressive as the 1-WL test when distinguishing non-isomorphic graphs [].
2.2. Expressivity of Weisfeiler–Lehman and
The classic Weisfeiler–Lehman algorithm (1-WL), also known as color refinement, is shown in Algorithm 1. The algorithm starts with an initial color assignment to each vertex according to their degree and proceeds updating the assignment at each iteration.
| Algorithm 1 1-WL (Color refinement). |
|
The update aggregates, for each node v, its color and the colors of its neigbors , then hashes this multi-set of colors, mapping it into a new color to be used in the next iteration . The algorithm converges to a stable color assignment, which can be used to test graphs for isomorphism. Note that neighbor aggregation in 1-WL can be understood as a message passing step, with the operation being analogous to Update steps in MP-GNNs.
Two graphs, , , are not isomorphic if they are distinguishable (that is, their stable color assignments do not match). However, if they are not distinguishable (that is, their stable color assignments match), they are likely to be isomorphic []. To reduce the likelihood of false positives when color assignments match, one can consider k-tuples of vertices instead of single vertices, leading to higher order variants of the WL test (denoted k-WL) which assign colors to k-vertex tuples. In this case, and are said to be k-WL equivalent, denoted , if their stable assignments are not distinguishable. For more details on the algorithm, we refer to [,]. k-WL tests are more expressive than their -WL counterparts for , with the exception of 2-WL, which is known to be as expressive as the 1-WL color refinement test [].
Among the various characterizations of k-WL expressivity, the relationship with matrix query languages defined by Matlang [] has also found applications for graph representation learning []. Matlang is a language of operations on matrices, where sentences are formed by sequences of operations. There exists a subset of Matlang——that is as expressive as the 1-WL test. Another subset——is strictly more expressive than the 1-WL test but less expressive than the 3-WL test. Finally, there exists another subset that is as expressive as the 3-WL test []. We provide additional technical details on Matlang and its sub-languages in Appendix E, where we analyze the relation between and Matlang.
2.3. Graph Neural Networks beyond 1-WL
Recently, approaches have been proposed for improving the expressivity of MP-GNNs. Here, we focus on subgraph and substructure GNNs, which are most closely related to . For an overview on augmented message passing methods, see [] and Appendix I.
k-hop MP-GNNs (k-hop) [] propagate messages beyond immediate vertex neighbors, effectively using ego network information in the vertex representation. Neighborhood subgraphs are extracted, and message passing occurs on each subgraph, with an exponential cost on the number of hops k both at preprocessing and at each iteration (epoch). In contrast, only requires a preprocessing step that can be cached once computed.
Distance encoding GNNs (DE-GNN) [] also propose to improve MP-GNN by using extra node features by encoding distances to a subset of p nodes. The features obtained by DE-GNN are similar to IGEL when conditioning the subset to size and using a distance encoding function with . However, these features are not strictly equivalent to , as node degrees within the ego network can be smaller than in the full graph.
Graph Substructure networks (GSNs) [] incorporate topological features by counting local substructures (such as the presence of cliques or cycles). GSNs require expert knowledge on what features are relevant for a given task with modifications to MP-GNN architectures. In contrast, reaches comparable performance using a general encoding for ego networks and without altering the original message passing mechanism.
GNNML3 [] performs message passing in spectral domain with a custom frequency profile. While this approach achieves good performance on graph classification, it requires an expensive preprocessing step for computing the eigendecomposition of the graph Laplacian and -order tensors to achieve k-WL expressiveness with cubic time complexity.
More recently, a series of methods formulate the problem of representing vertices or graphs as aggregations over subgraphs. The subgraph information is pooled or introduced during message passing at an additional cost that varies depending on each architecture. Consequently, they require generating the subgraphs (or effectively replicating the nodes of every subgraph of interest) and pay an additional overhead due to the aggregation.
These approaches include identity-aware GNNs (ID-GNNs) [], which embed each node while incorporating identity information in the GNN and apply rounds of heterogeneous message passing; nested GNNs (NGNNs) [], which perform a two-level GNN using rooted subgraphs and consider a graph as a bag of subgraphs; GNN-as-Kernel (GNN-AK) [], which follows a similar idea but introduces additional positional and contextual embeddings during aggregation; equivariant subgraph aggregation networks (ESAN) [] encode graphs as bags of subgraphs and show that such an encoding can lead to a better expressive power; shortest-path neural networks (SPNNs) [], which represent nodes by aggregating over sets of neighbors at the same distance; and subgraph union networks (SUN) [], which unify and generalize previous subgraph GNN architectures and connect them to invariant graph networks []. Compared to all these methods, only relies on an initial preprocessing step based on distances and degrees without having to run additional message passing iterations or modify the architecture of the GNN.
Interestingly, recent work [] showed that the implicit encoding of the pairwise distance between nodes plus the degree information which can be extracted via aggregation are fundamental to provide a theoretical justification of ESAN. Furthermore, the work on SUN [] showed that node-based subgraph GNNs are provably as powerful as the 3-WL test. This result is aligned with recent analyses on the hierarchies of model expressivity [].
In this work, we directly consider distances and degrees in the ego network, explicitly providing the structural information encoded by more expressive GNN architectures. In contrast to previous work, aims to be a minimal yet expressive representation of network structures without learning that is amenable to formal analysis, as shown in Section 4. This connects ego network properties to subgraph GNNs, corroborating the 3-WL upper bound of SUN and the expressivity analysis of ESAN—to which is strongly related in its ego networks policy (EGO+). Furthermore, these relationships may explain the comparable empirical performance of to the state of the art, as shown in Section 5.
3. Local Ego-Network Encodings
The idea behind the encoding is to represent each vertex v by compactly encoding its corresponding ego network at depth . The choice of encoding consists of a histogram of vertex degrees at distance , for each vertex in . Essentially, runs a breadth-first traversal up to depth , counting the number of times the same degree appears at distance . We postulate that such a simple encoding is sufficiently expressive and at the same time computationally tractable to be considered as vertex features.
Figure 1 shows an illustrative example for . In this example, the green node is encoded using a (sparse) vector of size , since the maximum degree at depth 2 is 5 and there are three distances considered: . The ego network contains six nodes, and all (distance, degree) pairs occur once, except for degree 3 at distance 2, which occurs twice. Algorithm 2 describes the steps to produce the encoding iteratively.
| Algorithm 2 Encoding. |
|
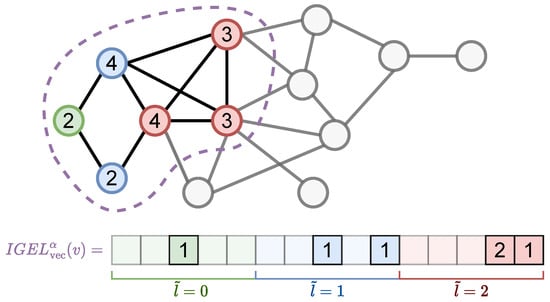
Figure 1.
encoding of the green vertex. Dashed region denotes . The green vertex is at distance 0, blue vertices at 1, and red vertices at 2. Labels show degrees in . The frequency of distance degree tuples forming is: .
Similarly to 1-WL, information of the neighbors of each vertex is aggregated at each iteration. However, 1-WL does not preserve distance information in the encoding due to the hashing step. Instead of hashing the degrees into equivalence classes, keeps track of the distance at which a degree is found, generating a more expressive encoding.
The cost of such additional expressiveness is a computational complexity that grows exponentially in the number of iterations. More precisely, the time complexity follows , with when . In Appendix F, we provide a possible breadth-first search (BFS) implementation that is embarrassingly parallel and thus can be computed over p processors following time complexity.
The encoding produced by Algorithm 1 can be described as a multi-set of path length and degree pairs in the -depth ego graph of v, :
which also results in exponential space complexity. However, can be represented as a (sparse) vector , where the i-th index contains the frequency of path length and degree pairs , as shown in Figure 1:
which has linear space complexity , conservatively assuming every node requires parameters at every depth from the center of the ego network, where in the worst case when a vertex is fully connected. Note that in practice, we may normalize raw counts by, e.g., applying log1p-normalization, and for real-world graphs, , where the probability of larger degrees often decays exponentially []). Finally, complexity can be further reduced by making use of sparse vector implementations.
We finish this section with two remarks. First, the produced encodings can differ only for values of , since otherwise the ego network is the same for all nodes, , and thus the resulting encodings, i.e., for . Second, the sparse formulation in Equation (5) can be understood as an inductive analogue of Weisfeiler–Lehman graph kernels [], as we explore in Appendix B.
4. Which Graphs Are -Distinguishable?
We now present results about the expressive power of , extending previous preliminary results on 1-WL that had been presented in []. We discuss the increased expressivity of with respect to 1-WL, and identify upper-bounds on the expressivity on graphs that are also indistinguishable under Matlang and the 3-WL test. We assess expressivity by studying whether two graphs can be distinguished by comparing the encodings obtained by the k-WL test and the encodings for a given value of . Similarly to the definition of k-WL equivalence, we say that and are -equivalent if the sorted multi-set of node representations is the same for and :
4.1. Distinguishability on 1-WL Equivalent Graphs
We first show is more powerful than 1-WL, following Lemmas 1 and 2:
Lemma 1.
is at least as expressive as 1-WL. For two graphs, , , which are distinguished by 1-WL in k iterations () it also holds that for . If does not distinguish two graphs and , 1-WL also does not distinguish them: .
Lemma 2.
There exist at least two non-isomorphic graphs, , that can distinguish but that 1-WL cannot distinguish; i.e., while .
First, we formally prove Lemma 1, i.e., that is at least as expressive as 1-WL. For this, we consider a variant of 1-WL which removes the hashing step. This modification can only increase the expressive power of 1-WL and makes it possible to directly compare such (possibly more expressive) 1-WL encodings with the encodings generated by . Intuitively, after k color refinement iterations, 1-WL considers nodes at k hops from each node, which is equivalent to running with , i.e., using ego networks that include information of all nodes that 1-WL would visit.
Proof of Lemma 1.
For convenience, let be a recursive definition of Algorithm 1 where hashing is removed and . Since the hash is no longer computed, the nested multi-sets contain strictly the same or more information as in the traditional 1-WL algorithm.
For to be less expressive than 1-WL, it must hold that there exist two graphs and such that while .
Let k be the minimum number of color refinement iterations such that and . We define an equally or more expressive variant of the 1-WL test 1-WL* where hashing is removed, such that , nested up to depth k. To avoid nesting, the multi-set of nested degree multi-sets can be rewritten as the union of degree multi-sets by introducing an indicator variable for the iteration number where a degree is found:
At each step i, we introduce information about nodes up to distance i of . Furthermore, by construction, nodes will be visited on every subsequent iteration—i.e., for , we will observe exactly times, as all its neighbors encode the degree of in . The flattened representation provided by 1-WL* is still equally or more expressive than 1-WL, as it removes hashing and keeps track of the iteration at which a degree is found.
Let be a less expressive version of that does not include edges between nodes at hops of the ego network root. Now, consider the case in which from 1-WL*, and let so that considers degrees by counting edges found at k to hops of and . Assume that . By construction, this means that . This implies that all degrees and iteration counts match as per the distance indicator variable at which the degrees are found, so which contradicts the assumption and therefore implies that also . Thus, for and also . Therefore, by extension is at least as expressive as 1-WL. □
To prove Lemma 2, we show graphs that can distinguish despite being undistinguishable by 1-WL and the Matlang sub-languages and . In Section 4.1.1, we provide an example where distinguishes 1-WL/ equivalent graphs, while Section 4.1.2 shows that also distinguishes graphs that are known to be distinguishable in the strictly more expressive language.
4.1.1. /1-WL Expressivity: Decalin and Bicyclopentyl
Decalin and Bycyclopentyl (in Figure 2) are two molecules whose graph representations are not distinguishable by 1-WL despite their simplicity. The graphs are non-isomorphic, but 1-WL identifies 3 equivalence classes in both graphs: central nodes with degree 3 (purple), their neighbors (blue), and peripheral nodes farthest from the center (green).
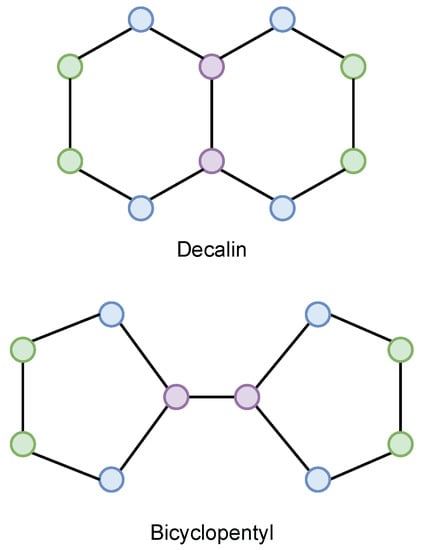
Figure 2.
Decalin (top) and Bicyclopentyl (bottom). 1-WL (Algorithm 1) produces equivalent colorings in both graphs; hence, they are 1-WL equivalent. The colorings match between central nodes (purple), their immediate neighbors (blue), and peripheral nodes farthest from the center (green).
Figure 2 shows the resulting encoding for the central node (in purple) using (top) and (bottom). For , the encoding field of is too narrow to identify substructures that distinguish the two graphs (Figure 3, top). However, for the representations of central nodes differ between the two graphs (Figure 3, bottom). In this example, any value of can distinguish between the graphs.
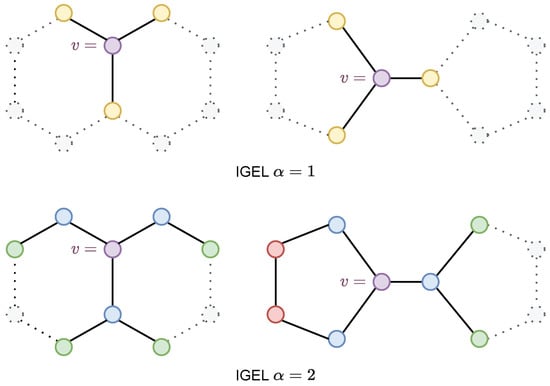
Figure 3.
encodings () for Decalin and Bicyclopentyl computed for purple vertices (v). Dotted sections are not encoded. Colors denote different tuples. distinguishes the graphs since Decalin nodes at distance 2 from v have degree 1 (green) while their Bicyclopentyl counterparts have degrees 1 (green) and 2 (red).
4.1.2. Expressivity: Cospectral 4-Regular Graphs
can also distinguish -equivalent graphs. Recall that is strictly more expressive than 1-WL, as described in Section 2.2. It is known that d-regular graphs of the same cardinality are indistinguishable by the 1-WL test in Algorithm 1 and that co-spectral graphs cannot be distinguished in :
Definition 1.
is d-regular with if .
Remark 1.
For any pair of n-vertex d-regular graphs and , (see [], Example 3.5.2, p. 81).
Definition 2.
Two graphs and are co-spectral if their adjacency matrices have the same multi-set of eigenvalues.
Remark 2.
For any pair of n-vertex co-spectral graphs and , (see [], Proposition 5.1).
In contrast to 1-WL, we can find examples of non-isomorphic d-regular graphs that can distinguish, as the generated encodings will differ for any pair of graphs whose sets of sorted degree sequences do not match at any path length less than . Furthermore, we can find examples of co-spectral graphs that can be distinguished by encodings. In both cases, the intuition is that the ego network encoding generated by discards the edges that connect nodes beyond the subgraph. Consequently, the generated encoding will depend on the actual connectivity at the boundary of the ego network and provide with increased expressivity compared to other methods.
Figure 4 shows two co-spectral 4-regular graphs taken from [], and the structures obtained using encodings with on each graph. The 1-WL test assigns a single color to all nodes and stabilizes after one iteration. Likewise, any sentences executed as operations on the adjacency matrices of both graphs produce equal results. However, identifies four different structures (denoted a, b, c, d). Since the encodings between both graphs do not match, they are distinguishable. This is the case for any value of .
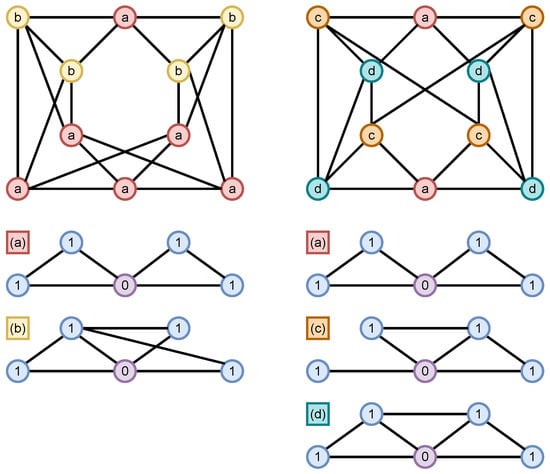
Figure 4.
encodings for two co-spectral 4-regular graphs from []. distinguishes 4 kinds of structures within the graphs (associated with every node as a, b, c, and d). The two graphs can be distinguished since the encoded structures and their frequencies do not match.
4.2. Indistinguishability on Strongly Regular Graphs
We identify an upper bound on the expressive power of : non-isomorphic Strongly Regular Graphs with equal parameters. In this case, two non-isomorphic graphs are not indistinguishable by .
Definition 3.
A n-vertex d-regular graph is strongly regular—denoted —if all adjacent vertices have λ vertices in common and all non-adjacent vertices have γ vertices in common.
Remark 3.
For any , [].
Theorem 1.
cannot distinguish two SRGs when n, d, and λ are the same, and between any value of γ (equal or not).
Formally, given , :
- —
- ;
- —
- ;
- —
- no values of γ can be distinguished by or .
Proof.
Recall that for any graph G, encodings are equal for all and per Remark 3, SRGs have diameters of two or less. Let , only produce different encodings for nodes of G. By construction, in G, v has encoding , so the encoding of G is . Furthermore, only encodes n, d, and , and only encodes n and d by expanding in Algorithm 2:
- -
- Let : . Since G is d-regular, v is the center of , and has d-neighbors. By definition, d neighbors of v have shared neighbors with v each, plus an edge with v, and does not include edges beyond its neighbors. Thus, for SRGs where , , and , where
- -
- Let : as when . G is d-regular, so . Thus, for any SRGs s.t. and , where
Thus, with can only distinguish between different values of n, d and . □
4.3. Expressivity Implications
As expected from Theorem 1, cannot distinguish the Shrikhande and Rook graphs (shown in Figure 5), which are known to be -equivalent graphs [,] with parameters despite not being isomorphic.
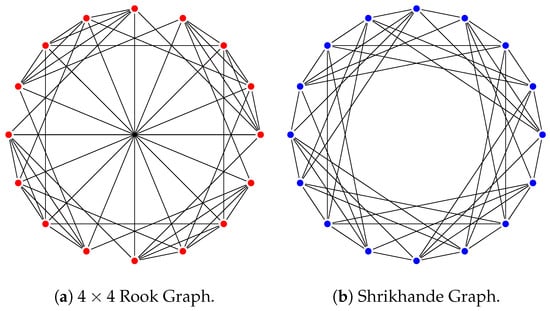
Figure 5.
3-WL equivalent Rook ((a), red) and Shrikhande ((b), blue) graphs are indistinguishable by as they are non-isomorphic SRGs with parameters .
Our findings show that is a powerful permutation-equivariant representation (see Lemma A1), capable of distinguishing 1-WL equivalent graphs such as Figure 4—which as cospectral graphs are known to be expressable in strictly more powerful Matlang sub-languages than 1-WL []. Furthermore, in Appendix D, we connect to SPNNs [] and show that is strictly more expressive than SPNNs on unattributed graphs. Finally, we note that the upper bound on strongly regular graphs is a hard ceiling on expressivity since SRGs are commonly known to be indistinguishable by 3-WL [,,,,].
formally reaches an expressivity upper bound on SRGs, distinguishing SRGs with different values of n, d, and . These results are similar with subgraph methods implemented within MP-GNN architectures, such as nested GNNs [] and GNN-AK [], which are known to be not less powerful than 3-WL, and the ESAN framework when leveraging ego networks with root-node flags as a subgraph sampling policy (EGO+), which is as powerful as 3-WL on SRGs []. However, in contrast to these methods, cannot distinguish graphs with different values of . Furthermore, in Section 5, we study in a series of empirical tasks, finding that the expressivity difference that exhibits on SRGs does not have significant implications in downstream tasks.
Summarizing, distinguishes non-isomorphic graphs that are undistinguishable by the 1-WL test. Furthermore, Lemma 2 shows that can distinguish any graphs that 1-WL can distinguish. We derive a precise expressivity upper bound for on SRGs, showing that cannot distinguish SRGs with equal parameters or between values of . Overall, the expressive power of on SRGs is similar to other state-of-the-art methods, including k-hop GNNs [], GSNs [], NGNNs [], GNN-AK [], and ESAN [].
5. Empirical Validation
We evaluate as a sparse local ego network encoding following Equation (5), extending vertex/edge attributes on six experimental tasks: graph classification, graph isomorphism detection, graphlet counting, graph regression, link prediction, and vertex classification. With our experiments, we seek to evaluate the following empirical questions:
- Q1.
- Does improve MP-GNN performance on standard graph-level tasks?
- Q2.
- Can we empirically validate our results on the expressive power of compared to 1-WL?
- Q3.
- Are encodings appropriate features to learn on unattributed graphs?
- Q4.
- How do GNN models compare with more traditional neural network models when they are enriched with features?
5.1. Overview of the Experiments
For graph classification, isomorphism detection, and graphlet counting, we reproduce the benchmark proposed by [] on eight graph data sets. For each task and data set, we introduce as vertex/edge attributes, and compare the performance of including or excluding on several GNN architectures—including linear and MLP baselines (without message passing), GCNs [], GATs [], GINs [], Chebnets [], and GNNML3 []. We measure whether improves inductive MP-GNN performance while validating our theoretical expressivity analysis (Q1 and Q2). We also evaluate on the Zinc-12K and Pattern data sets from benchmarking GNNs [] to test on larger, real-world data sets.
For link prediction, we experiment on two unattributed social network graphs. We train self-supervised embeddings on encodings and compare them against standard transductive vertex embeddings. Transductive methods require that all nodes in the graph are known at training and inference time, while inductive methods can be applied to unseen nodes, edges, and graphs. Inductive methods may be applied in transductive settings but not vice-versa. Since is label and permutation invariant, its output is an inductive representation. We detail the self-supervised embedding approach in Appendix H. We compare our results against strong vertex embedding models, namely DeepWalk [] and Node2Vec [], seeking to validate as a theoretically grounded structural feature extractor in unattributed graphs (Q3).
For vertex classification, we train using encodings and vertex attributes as inputs on DNN models without message passing on an inductive protein-to-protein interaction (PPI) multi-label classification problem. We evaluate the impact of introducing on top of vertex attributes and compare the performance of -inclusive models with MP-GNNs (Q4).
5.2. Experimental Methodology
On graph-level tasks, we introduce encodings concatenated to existing vertex features, and also introduce as edge-level features representing an edge as the element-wise product of node-level encodings at each end of the edge into the best performing model configurations found by [] without any hyper-parameter tuning (e.g., number of layers, hidden units, choice pooling and activation functions). We evaluate performance differences with and without on each task, data set and model on 10 independent runs, measuring statistical significance of the differences through paired t-tests. On benchmark data sets, we reuse the best reported GIN-AK+ baseline from [] and simply introduce as additional node features with , with no hyper-parameter changes.
On vertex and edge-level tasks, we report best performing configurations after hyper-parameter search. Each configuration is evaluated on five independent runs. Our results are compared against strong standard baselines from the literature, and we provide a breakdown of the best-performing hyper-parameters found in Appendix A.
5.3. Results and Notation
The following formatting denotes significant (as per paired t-tests) positive (in bold), negative (in italic), and insignificant differences (no formatting) after introducing , with the best results per task/data set underlined.
5.4. Graph Classification: TU Graphs
Table 1 shows graph classification results for TU molecule data sets []. In each data set, nodes represent atoms and edges represent their atomic bonds. The graphs contain no edge features while, node features are a one-hot encoded vector of the atom represented by that node. We evaluate differences in mean accuracies with and without through paired t-tests, denoting significance intervals of as * and as ⋄.

Table 1.
Per-model classification accuracy metrics on TU data sets. Each cell shows the average accuracy of the model and data set in that row and column, with (left) and without (right).
Our results show that in the Mutag and Proteins data sets improves the performance of all MP-GNN models, including GNNML3, contributing to answer Q1. By introducing in those data sets, MP-GNN models reach similar performance to GNNML3. Introducing achieves this at preprocessing costs compared to worst-case eigen-decomposition costs associated with GNNML3’s spectral supports.
Additionally, since is an inductive method, the worst-case when cost is only required when the graph is first processed. Afterwards, encodings can be reused, recomputing them for nodes neighboring new nodes or updated edges as given by . This contrasts with GNNML3’s spectral supports, which are computed on the adjacency matrix and would require a full recalculation when nodes or edges change.
On the Enzymes and PTC data sets, results are mixed: for all models other than GNNML3, either significantly improves accuracy (on MLPNet, GCN, and GIN on Enzymes), or does not have a negative impact on performance. GAT outperforms GNNML3 in PTC, while GNNML3 is the best performing model on Enzymes. Additionally, GNNML3 performance degrades when is introduced on the Enzymes and PTC data sets. We believe this degradation may be caused by overfitting due to a lack of additional parameter tuning, as GNNML3 models are deeper in Enzymes and PTC (four GNNML3 layers) when compared Mutag and Proteins (three and two GNNML3 layers respectively). It may be possible to improve GNNML3 performance with by re-tuning model parameters, but due to computational constraints we do not test this hypothesis. Nevertheless, we observe that all models improve in at least two different data sets after introducing without hyper-parameter tuning, which we believe indicates our results are a conservative lower-bound on model performance.
We also compare the best results from Table 1 with state-of-the-art methods improving expressivity. Table 2 summarizes the reported results for k-hop GNNs [], GSNs [], nested GNNs [], ID-GNNs [], GNN-AK [], and ESAN []. When we compare and the best performing baseline for every data set, none of the differences are statistically significant () except for ID-GNN in Proteins (where ).

Table 2.
Mean ± stddev of best configuration and state-of-the-art results reported on [,,,,,] with best performing baselines underlined.
Overall, our results show that incorporating the encodings in a vanilla GNN yields comparable performance to state-of-the-art methods (Q2).
5.5. Graph Isomorphism Detection
Table 3 shows isomorphism detection results on two data sets: Graph8c (as described in Appendix A), and EXP []). On the Graph8c data set, we identify isomorphisms by counting the number of graph pairs for which randomly initialized MP-GNN models produce equivalent outputs. Equivalence is measured by the Manhattan distance between graph on 100 independent initialization runs further described in Appendix A. The EXP data set contains 1-WL equivalent pairs of graph, and the objective is to identify whether they are isomorphic or not. We report model accuracies on the binary classification task of distinguishing non-isomorphic graphs that are 1-WL equivalent.

Table 3.
Graph isomorphism detection results. The column denotes whether is used or not in the configuration. For Graph8c, we describe graph pairs erroneously detected as isomorphic. For EXP classify, we show the accuracy of distinguishing non-isomorphic graphs in a binary classification task.
On Graph8c, introducing significantly reduces the amount of graph pairs erroneously identified as isomorphic for all MP-GNN models. Furthermore, allows a linear baseline employing a sum readout over input feature vectors, then projecting onto a 10-component space to identify all but 1571 non-isomorphic pairs compared to GCNs (4196 errors) or GATs (1827 errors) that can be identified without .
We also find that all Graph8c graphs can be distinguished if the encodings for and are concatenated. We do not study the expressivity of concatenating combinations of in this work, but based on our results we hypothesize it produces strictly more expressive representations.
On EXP, introducing is sufficient to correctly identify all non-isomorphic graphs for all standard MP-GNN models, as well as the MLP baseline. Furthermore, the linear baseline can reach 97.25% classification accuracy with despite only computing a global sum readout before a single-output fully connected layer. Results on Graph8c and EXP validate our theoretical claims that is more expressive than 1-WL and can distinguish graphs that would be indistinguishable under 1-WL, answering Q2.
We also evaluate on the SR25 data set (described in Appendix A), which contains 15 strongly regular 25 vertex non-isomorphic graphs known to be indistinguishable by 3-WL where we can empirically validate Theorem 1. In [], it was shown that all models in our benchmark are unable to distinguish any of the 105 non-isomorphic graph pairs in SR25. Introducing does not improve distinguishability—as expected from Theorem 1.
5.6. Graphlet Counting
We evaluate on a graphlet counting regression task, training a model to minimize mean squared error (MSE) on the normalized graphlet counts. Counts are normalized by the standard deviation of counts in the training set, as in [].
In Table 4, we show the results of introducing in five graphlet counting tasks on the RandomGraph data set []. We identify 3-stars, triangles, tailed triangles and 4-cycle graphlets, as shown in Figure 6, plus a custom structure with 1-WL expressiveness proposed in [] to evaluate GNNML3. We highlight statistically significant differences when introducing ().

Table 4.
Graphlet counting results. On every cell, we show mean test set MSE error (lower is better), with stat. sig () results highlighted and best results per task underlined. For comparison, we also report strong literature results from two subgraph GNNs: GNN-AK+ using a GIN base [] and SUN [].
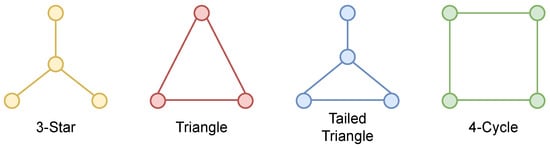
Figure 6.
Graphlet types in the counting task.
Introducing improves the ability of 1-WL GNNs to recognize triangles, tailed triangles, and custom 1-WL graphlets from []. Stars can be identified by all baselines, and introducing only produces statistically significant differences on the linear baseline. Interestingly, on the linear model produces results outperforming MP-GNNs without for star, triangle, tailed triangle, and custom 1-WL graphlets.
By introducing on the MLP baseline, it obtains the best performance (lower MSE) on the triangle, tailed-triangle, and custom 1-WL graphlets, even when compared to GNNML3 and subgraph GNNs—including when encodings are input to GNNML3.
Results on linear and MLP baselines are interesting as neither baseline uses message passing, indicating that raw encodings may be sufficient to identify certain graph structures in simple linear models. For all graphlets except 4-cycles, introducing outperforms or matches GNNML3 performance at lower preprocessing and model training/inference costs—without the need for costly eigen decomposition or message passing, answering Q1 and Q2. moderately improves performance counting 4-cycle graphlets, but the results are not competitive when compared to GNNML3.
5.7. Benchmark Results with Subgraph GNNs
Given the favorable performance of compared to related subgraph aware methods such as NGNN and ESAN, as shown in Table 2, we also explore introducing on a subgraph GNN, namely GNN-AK proposed by []. We follow a similar experimental approach as in previous experiments, reproducing the results of GNN-AK using GINs [] with edge-feature support [] (GINs are the best performing base model in three out of the four data sets, as reported in []) as the base GNN on two real-world benchmark data sets: Zinc-12K (as a graph regression task minimizing mean squared error ↓, where lower is better) and Pattern (as a graph classification task, where higher accuracy ↑ is better) from benchmarking GNNs [].
Without performing any additional hyper-parameter tuning or architecture search, we evaluate the impact of introducing with on the best performing model configuration and code published by the authors of GNN-AK []. Furthermore, we also evaluate the setting in which subgraph information is not used to assess whether can provide comparable performance to GNN-AK without changes to the network architecture. Table 5 summarizes our results.

Table 5.
Mean and standard deviations of the evaluation metrics on the real-world benchmark data sets in combination with GNN-AK [], highlighting positive and negative stat. sig, () results when is added with best per-data set results underlined.
maintains or improves performance in both cases when introduced on a GIN, but only in the case of Pattern we find a statistically significant difference (). When introducing on a GIN-AK model, we find statistically significant improvements on Zinc-12K. Introducing on GIN-AK+ in Pattern produces unstable losses on the validation set, with model performance showing larger variations across epochs. We believe that this instability might explain the loss in performance and that further hyper-parameter tuning and regularization (e.g., tuning dropout to avoid overfitting on specific features) could result in improved model performance.
Finally, we note that despite our constrained setup, introducing is also interesting from a runtime and memory standpoint. In particular, introducing on a GIN for Pattern yields performance only −0.2% worse than its GNN-AK (86.711 vs. 86.877), while executing 3.87 times faster (62.21 s vs. 240.91 s per iteration) and requiring 20.51 times less memory (26.2 GB vs. 1.3 GB). This is in line with our theoretical analysis in Section 3, as can be computed once as a preprocessing step and then introduces a negligible cost on the input size of the first layer, which is amortized in multi-layer GNNs. Together with our results on graph classification, isomorphism detection, and graphlet counting, our experiments show that is also an efficient way of introducing subgraph information without architecture modifications in large real-world data sets.
5.8. Link Prediction
We also test on a link prediction task, following the approach of [] to compare with well-known transductive node embedding methods on the Facebook and ArXiv AstroPhysics data sets []. We mode the task as follows: for each graph, we generate negative examples (non-existing edges) by sampling random unconnected node pairs. Positive examples (existing edges) are obtained by removing half of the edges, keeping the pruned graph connected after edge removals. Both sets of vertex pairs are chosen to have the same cardinality. Note that keeping the graph connected is not required for —it is required by transductive methods, which fail to learn meaningful representations on disconnected graph components. We learn self-supervised embeddings with a DeepWalk [] approach (described in Appendix H) and model the link prediction task as a logistic regression problem whose input is the representation of an edge—as the element-wise product of embeddings of vertices at each end of an edge without fine-tuning, which is the best edge representation reported by [].
In Table 6, we report AUC results averaged on five independent executions and compared against previous reported baselines. In this case, we perform hyper-parameter search, with results described on Appendix A. We provide additional details on the unsupervised parameters in our code repositories also referenced in Appendix A.

Table 6.
Area under the ROC curve (AUROC) link prediction results on Facebook and AP-arXiv. Embeddings learned on encodings outperform transductive methods. stddevs .
with significantly outperforms standard transductive methods on both data sets. This is despite the fact that we compare against methods that are aware of node identities and that several vertices can share the same encodings. Furthermore, is an inductive method that may be used on unseen nodes and edges, unlike transductive methods DeepWalk or node2vec. We do not explore the inductive setting as it would unfairly favor and cannot be directly applied to DeepWalk or Node2vec.
Additionally, significantly underperforms when . We believe this might be caused by the fact that when , it is not possible for the model to assess whether two vertices are neighbors based on their representation. Overall, our link prediction results show that encodings can be used as a potentially inductive feature generation approach in unattributed networks, without degrading performance when compared to standard vertex embedding methods—answering Q3.
5.9. Vertex Classification
In light of our graph-level results on graphlet counting, we evaluate to which extent a vertex classification task can be solved by leveraging structural features without message passing (Q4). We introduce in a DNN model and evaluate against several MP-GNN baselines. Our comparison includes supervised baselines proposed by GraphSAGE [], LCGL [], and GAT [] on a multi-label classification task in a protein-to-protein interaction (PPI) [] data set. The aim is to predict 121 binary labels, given graph data where every vertex has 50 attributes. We tune the parameters of a multi-layer perceptron (MLP) whose input features are either , vertex attributes, or both through randomized grid search—and we provide a detailed description of the grid-search parameters in Appendix A.
Table 7 shows Micro-F1 scores averaged over five independent runs. Introducing alongside vertex attributes in an MLP can outperform standard MP-GNNs like GraphSAGE or LGCL despite not using message passing—and thus only having access to the attributes of a vertex without additional context from its neighbors, answering Q4. Furthermore, even though underperforms when compared with GAT, the results reported by [] use a three-layer GAT model propagating messages through 3-hops, while we observe the best performance with . We believe that the structural information at 1-hop captured by might be sufficient to improve performance on tasks where local information is critical, potentially reducing the hops required by downstream models (e.g., GATs).

Table 7.
Multi-label class. Micro-F1 scores on PPI. plus node features as input for an MLP outperforms LGCL and GraphSAGE. stddevs .
6. Discussion and Conclusions
is a novel and simple vertex representation algorithm that increases the expressive power of MP-GNNs beyond the 1-WL test. Empirically, we found can be used as a vertex/edge feature extractor on graph-, edge-, and node-level settings. On four different graph-level tasks, significantly improves the performance of nine graph representation models without requiring architectural modifications—including Linear and MLP baselines, GCNs [], GATs [], GINs [], ChebNets [], GNNML3 [], and GNN-AK []. We introduce without performing hyper-parameter search on an existing baseline, which suggests that encodings are informative and can be introduced in a model without costly architecture search.
Although structure-aware message passing [,,,], substructure counts [], identity [], and subgraph pooling [] may also be combined with existing MP-GNN architectures, reaches comparable performance as related models while simply augmenting the set of vertex-level feature without tuning model hyper-parameters. consistently improves performance on five data sets for graph classification: one data set for graph regression, two data sets for isomorphism detection, and five different graphlet structures in a graphlet counting task. Furthermore, even though MP-GNNs with learnable subgraph representations are expected to be more expressive since they can freely learn structural characteristics according to optimization objectives, our results show that introducing produces comparable results on three different domains and improves the performance of a strong GNN-AK+ baseline on Zinc-12K. Additionally, introducing on a GIN model in the Pattern data set achieves 99.8% of the performance of a strong GIN-AK+ baseline at 3.87 times lower memory costs. The computational efficiency is a key benefit of as it only requires a single preprocessing step that extends vertex/edge attributes and can be cached during training and inference.
On link prediction tasks evaluated in two different graph data sets, -based DeepWalk [] embeddings outperformed transductive methods based on embedding node identities such as DeepWalk [] and Node2vec []. Finally, with outperformed certain MP-GNN architectures like GraphSAGE [] on a protein–protein interaction node-classification task despite being used as an additional input to a DNN without message passing. More powerful MP-GNNs—namely a three-layer GAT []—outperformed the -enriched DNN model, albeit at potentially higher computational costs due to the increased depth of the model.
A fundamental aspect in our analysis of the expressivity of is that the connectivity of nodes is different depending on whether they are analyzed as part of the subgraph (ego network) or within the entire input graph. In particular, edges at the boundary of the ego network are a subset of the edges in the input graph. exploits this idea in combination with a simple encoding based on frequencies of degrees and distances. This is a novel idea, which allows us to connect the expressive power of with other analyses like the 1-WL test, as well as Weisfeiler–Lehman kernels (see Appendix B), shortest-path neural networks (see Appendix D), and (see Appendix E). Furthermore, the ego network formulation allows us to identify an upper-bound on expressivity in strongly regular graphs—matching recent findings on the expressivity of subgraph GNNs.
Although we have presented on unattributed graphs, the principle underlying its encoding can be also applied to labelled or attributed graphs. Appendix G outlines possible extensions in this direction. In Appendix G.3, we also connect with k-hop GNNs and GNN-AK—drawing a direct link between subgraph GNNs and our proposed encoding.
Overall, our results show that can be efficiently used to enrich network representations on a variety of tasks and data sets, which we believe is an attractive baseline in expressivity-related tasks. This opens up interesting future research directions by showing that explicit network encodings like can perform competitively compared to more complex learnable representations while being more computationally efficient.
Author Contributions
N.A.-G.: Conceptualization, Methodology, Software, Investigation, Formal analysis, Writing—Original Draft; A.K.: Validation, Supervision, Writing—Review & Editing; V.G.: Resources, Validation, Supervision, Writing—Review & Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been co-funded by MCIN/AEI/10.13039/501100011033 under the Maria de Maeztu Units of Excellence Programme (CEX2021-001195-M). This publication is part of the action CNS2022-136178 financed by MCIN/AEI/10.13039/501100011033 and by the European Union Next Generation EU/PRTR.
Institutional Review Board Statement
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed Consent Statement
Not applicable.
Data Availability Statement
This work uses publicly available graph data sets. We produced no new data sets, and access the data sets in our empirical evaluation through open-source libraries. We provide dataset details and links to code repositories and artifacts in Appendix A.1 in Appendix A.
Acknowledgments
We thank the anonymous reviewers of the MAKE journal and the First Learning on Graphs Conference (LoG 2022) for their comments that helped improve the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Additional Settings and Results
Appendix A.1. Data Set Details
We summarize all graph data sets used in the experimental validation of in Table A4. To provide an overview of each data set and its usage, we indicate the average cardinality of the graphs in the data set (Avg. n), the average number of edges per graph (Avg. m), and the total number of graphs per data set. We describe the task, loosely grouped in graph classification, non-isomorphism detection, graph regression, link prediction and vertex classification. We also provide the shape of the output for every problem and describe the split regime for training/validation/test sets when relevant.
Reproducibility—We provide three code repositories with our code and changes to the original benchmarks, including our modeling scripts, metadata, and experimental results: https://github.com/nur-ag/IGEL, https://github.com/nur-ag/gnn-matlang and https://github.com/nur-ag/IGEL-GNN-AK (all accessed on 16 September 2023).
Appendix A.2. Hyper-Parameters and Experiment Details
Graph Level Experiments. We reproduce the benchmark of [] without modifying model hyper-parameters for the tasks of graph classification, graph isomorphism detection, and graphlet counting. For classification tasks, the six models in Table 2 are trained on binary/categorical cross-entropy objectives depending on the task. For Graph isomorphism detection, we train GNNs as binary classification models on the binary classification task on EXP [], and identify isomorphisms by counting the number of graph pairs for which randomly initialized MP-GNN models produce equivalent outputs on Graph8c—Simple 8 vertices graphs from: http://users.cecs.anu.edu.au/~bdm/data/graphs.html (accessed on 16 September 2023). This evaluation procedure means models are not trained but simply initialized, following the approach of []. We also evaluate on the SR25 dataset and find encodings cannot distinguish the 105 Strongly Regular graph pairs with parameters from: http://users.cecs.anu.edu.au/~bdm/data/graphs.html (accessed on 16 September 2023). For the graphlet counting regression task on the RandomGraph data set [], we train models to minimize mean squared error (MSE) on the normalized graphlet counts for five types of graphlets.
On all tasks, we experiment with and optionally introduce a preliminary linear transformation layer to reduce the dimensionality of encodings. For every setup, we execute the same configuration 10 times with different seeds and compare runs introducing or not by measuring whether differences on the target metric (e.g., accuracy or MSE) are statistically significant, as shown in Table 1 and Table 2. In Table A1, we provide the value of that was used in our experimental results. Our results show that the choice of depends on both the task and model type. We believe these results may be applicable to subgraph-based MP-GNNs, and will explore how different settings, graph sizes, and downstream models interact with in future work.

Table A1.
Values of used when introducing in the best reported configuration for graphlet counting and graph classification tasks. The table is broken down by graphlet types (upper section) and graph classification tasks on the TU data sets (bottom section).
Table A1.
Values of used when introducing in the best reported configuration for graphlet counting and graph classification tasks. The table is broken down by graphlet types (upper section) and graph classification tasks on the TU data sets (bottom section).
| Chebnet | GAT | GCN | GIN | GNNML3 | Linear | MLP | |
|---|---|---|---|---|---|---|---|
| Star | 2 | 1 | 2 | 1 | 1 | 2 | 1 |
| Tailed Triangle | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
| Triangle | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4-Cycle | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| Custom Graphlet | 2 | 1 | 1 | 1 | 2 | 2 | 2 |
| Enzymes | 1 | 2 | 2 | 1 | 2 | 2 | 2 |
| Mutag | 1 | 1 | 1 | 1 | 1 | 1 | 2 |
| Proteins | 2 | 2 | 2 | 1 | 2 | 1 | 1 |
| PTC | 1 | 1 | 2 | 1 | 1 | 2 | 2 |
Vertex and Edge-level Experiments. In this section we break down the best performing hyper-parameters on the edge- (link prediction) and vertex-level (node classification) experiments.
Link Prediction—The best performing hyperparameter configuration on the Facebook graph including , learning component vectors with walks per node, each of length and negative samples per positive for the self-supervised negative sampling. Respectively, on the arXiv citation graph, we find the best configuration at , , , and .
Node Classification—In the node classification experiment, we analyze both encoding distances . Other hyper-parameters are fixed after a small greedy search based on the best configurations in the link prediction experiments. For the MLP model, we perform a greedy architecture search, including number of hidden units, activation functions and depth. Our results show scores averaged over five different seeded runs with the same configuration obtained from hyperparameter search.
The best performing hyperparameter configuration on the node classification is found with on length embedding vectors, concatenated with node features as the input layer for 1000 epochs in a three-layer MLP using ELU activations with a learning rate of 0.005. Additionally, we apply 100 epoch patience for early stopping, monitoring the F1 score on the validation set.
Reproducibility—We provide a replication folder in the code repository for the exact configurations used to run the experiments.
Appendix B. Relationship to Weisfeiler–Lehman Graph Kernels
The Weisfeiler–Lehman algorithm has inspired the design of graph kernels for graph classification, as proposed by [,]. In particular, Weisfeiler–Lehman graph kernels [] produce representations of graphs based on the labels resulting of evaluating several iterations of the 1-WL test described in Algorithm 1. The resulting vector representation resembles encodings, particularly in vector form—. In the case of WL kernels, the function maps sorted label multi-sets in terms of their position in lexicographic order within the iteration. An iteration of the algorithm is illustrated in Figure A1.
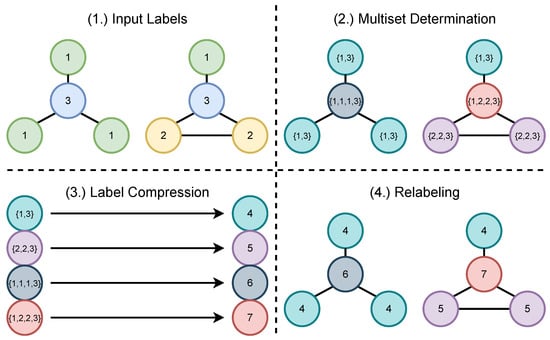
Figure A1.
One iteration of the Weisfeiler–Lehman graph kernel where input labels are node degrees. Given an input labeling, one iteration of the kernel computes a new set of labels based on the sorted multi-sets produced by aggregating the labels of each node’s neighbors.
After k iterations, graphs are represented by counting the frequency of distinct labels that were observed at each iteration . The resulting vector representation can be used to compare whether two graphs are similar and as an input to graph classification models.
However, WL graph kernels can suffer from generalization problems, as the label compression step assigns different labels to multi-sets that differ on a single element within the multi-set. If a given graph contains a previously unseen label, each iteration will produce previously unseen multi-sets, propagating at each iteration step and potentially harming model performance. Recent works generalize certain iteration steps of WL graph kernels to address these limitations, introducing topological information [] or Wasserstein distances between node attribute to derive labels []. can be understood as another work in that direction, removing the hashing step altogether and simply relying on target structural features—path length and distance tuples—that can be inductively computed in unseen or mutating graphs.
Appendix C. IGEL Is Permutation Equivariant
Lemma A1.
Given any for and given a permuted graph of G produced by a permutation of node labels such that , .
The representation is permutation equivariant at the graph level
The representation is permutation invariant at the node level
Proof.
Note that in Algorithm 2 can be expressed recursively as
Since only relies on node distances and degree nodes , and both and are permutation invariant (and the node level) and equivariant (at the graph level) functions, the representation is permutation equivariant at the graph level, and permutation invariant at the node level. □
Appendix D. Connecting IGEL and SPNNs
In this section, we connect with the shortest-path neural network (SPNN) model [] and show that is strictly more expressive than SPNNs.
Proposition A1.
is strictly more expressive than SPNNs on unattributed graphs.
Proof.
First, we show that encodings contain at least the same the information as SPNNs in unattributed graphs. Let be the nodes in G exactly at distance k of v. In [], the embedding of v at layer () in a k-depth SPNN is defined based on the following aggregation over the -distance neighborhoods:
where and are learnable parameters that modulate aggregation of node embeddings for node v and node embeddings for nodes at a distance i, respectively.
For unattributed graphs, the information captured by Equation (A1) is equivalent to counting the frequency of all node distances to node v in . This can be written as a reduced representation following Equation (4):
This representation captures an encoding that only considers distances. While can be used to compute the degree of in the entire graph G, it does not capture the degree of any node u only within the ego network . Thus, by definition, the encoding of Equation (4), contains at least all the necessary information to construct Equation (A2)—showing that is at least as expensive as SPNNs in unattributed graphs.
Second, we show that there exist unattributed graphs that can distinguish but that cannot be distinguished by SPNNs. Figure A2 shows an example. Thus, is strictly more expressive than SPNNs. □
Figure A2.
encodings for two SPNN-indistinguishable graphs [] from [] (top). with distinguishes both graphs (bottom) as all ego networks form tailed triangles on the right graph and stars on the left. However, SPNNs (as well as 1-WL) fail to distinguish them as all ego network roots (purple) have three adjacent nodes (blue) and two non-adjacent nodes at 2-hops (dotted).
Appendix E. IGEL and MATLANG
A natural question is to explore how relates to —whether can be expressed in , , or , and whether certain operations (and hence languages containing them) can be reduced to . We focus on the former to evaluate whether can be computed for a given node as an expression in .
Appendix E.1. MATLANG Sub-Languages
As introduced in Section 1, Matlang is a language of operations on matrices. Matlang sentences are formed by sequences of operations containing matrix multiplication (·), addition (+), transpose (), element-wise multiplication (⊙), column vector of ones (), vector diagonalization (), matrix trace (), scalar-matrix/vector multiplication (×), and element-wise function application (f). Given Matlang’s operations , [] shows that a language containing is as powerful as the 1-WL test, is strictly more expressive than the 1-WL test, but less expressive than the 3-WL test, and is as powerful as the 3-WL test. For , enriching the language with has no impact on expressivity.
Appendix E.2. Can IGEL Be Represented in MATLANG?
Let be the adjacency matrix of where . Our objective is to find a sequence of operations in such that when applied to A, we can express the same information as for all . To compute the encoding of v for a given , we must write sentences to compute:
- (a)
- , the ego network of v in G at depth .
- (b)
- The degrees of every node in .
- (c)
- The shortest path lengths from every node in to v.
Let denote the adjacency matrix of . Provided we can compute from A, computing the degree is a trivial operation in as we only need to compute the matrix-vector product (·) of with the vector of ones (). Recall that is the degree of vertex , and let denote the i-th index in the resulting vector:
Furthermore, if we can find , it is also possible to find . Thus, we can compute the distance of every node to v by progressively expanding k, mapping the degrees of nodes to the value of k being processed by means of unary function application (f), and then computing the minimum value. Let denote a distance vector containing entries for all vertices found at distance k of v:
where
The distance between a given node u to v in can then be computed in terms of operations that may be applied recursively:
where is a unary function that retrieves the minimum length from having computed :
Thus, computing the distance is also possible in given . However, in order to compute , we must be able to extract a subset of V contained in . Following the approach of [] (see Proposition 7.2), we may leverage a node indicator vector for where when and 0 otherwise. We can then compute via a diagonal mask matrix such that when , and when , computed as . Finding involves
It follows from Equation (A3) that if we are provided M, it is possible to compute in . However, since indicator vectors are not part of , it is not possible to extract the ego subgraph for a given node v. As such cannot be expressed within unless indicator vectors are introduced.
A natural question is whether it is possible to express with an operator that requires no knowledge of unlike indicator vectors, which require computing beforehand. One possible approach is to only allow indicator vectors for single vertices, encoding any only if . We denote single-vertex indicator vectors as —an operation that represents the one-hot encoding of v. Note that for any , its indicator vector can be computed as the sum of one-hot encoding vectors: . Thus, introducing is as expressive as introducing indicator vectors.
We now express in terms of the operation. Consider the following expression where :
For , we obtain an indicator vector containing the neighbors of v—matching —which is binarized (mapping non-zero values to 1—e.g., applying returns 0 when x is 0, and 1 otherwise). Furthermore, when computed recursively for steps, matches the indicator vector of , which can trivially be used to compute . We can then find M as used in Equation (A3)
Appendix F. Implementing IGEL through Breadth-First Search
The idea behind the encoding is to represent each vertex v by compactly encoding its corresponding ego network at depth . The choice of encoding consists of a histogram of vertex degrees at distance , for each vertex in . Essentially, runs a breadth-first traversal up to depth , counting the number of times the same degree appears at distance .
The algorithm shown in Algorithm 2 showcases and its relationship to the 1-WL test. However, in a practical setting, it might be preferable to implement through breadth-first search (BFS). In Algorithm A1, we show one such implementation that fits the time and space complexity described in Section 3.
| Algorithm A1 Encoding (BFS). |
|
Due to how we structure BFS to count degrees and distances in a single pass, each edge is processed twice—once for each node at end of the edge. It must be noted that when processing every , the time complexity is . However, the BFS implementation is also embarrassingly parallel, which means that, as noted in Section 3, it can be distributed over p processors with time complexity.
Appendix G. Extending IGEL beyond Unattributed Graphs
In this appendix, we explore extensions to beyond unattributed graphs. In particular, we describe how minor modifications would allow to leverage label and attribute information, connecting with state-of-the-art MP-GNN representations.
Appendix G.1. Application to Labelled Graphs
Labeled graphs are defined given , where is a mapping function assigning a label to each vertex. A standard way of applying the 1-WL test to labeled graphs is to replace in the first step of Algorithm 1 with , such that the initial coloring is given by node labels. Since retains a similar structure, the same modification can be introduced in Equation (4). Some applications might require both degree and label information, achievable through a mapping that combines and given a label indexing function :
Applying or only requires adjusting the shape of the vector representation, whose cardinality will depend on the size of the label set (e.g., ), or the combination of degrees and given by .
Appendix G.2. Application to Attributed Graphs
can also be applied to attributed graphs of the form , where . Following Algorithm 2, relies on two discrete functions to represent structural features—the path length between vertices and vertex degrees . However, in an attributed graph, it may be desirable to consider the attributes of a node besides degree to represent it with respect to its attributes and the attributes of its neighbors. To extend the representation to node attributes, may be replaced by a bucketed similarity function applicable for v and any , whose output is discretized into buckets . A straightforward implementation of is to compute the cosine similarity () between attribute vectors and remaps the interval to discrete buckets by rounding:
- is a generalization over the structural representation function in Algorithm 2 to take also source vertex v. Thus, unattributed and unlabeled can be understood as the case in which , such that .
Furthermore, by introducing the bucketing transformation in -, we are de-facto providing a simple mechanism to control the size of encoding vectors. By implementing or introducing non-linear transformations such as with , it is possible to compress into the denser components of a t-dimensional vector.
Appendix G.3. IGEL and Subgraph MP-GNNs
Another natural extension is to apply the distance-based aggregation schema to message passing GNNs. This can be achieved by expressing message passing in terms not just of immediate neighbors of v but from nodes at every distance . Equation (1) then becomes
The update step will need to pool over the messages passed onto v:
This formulation matches the general form of k-hop GNNs [] presented in Section 2.3. Furthermore, introducing distance and degree signals in the message passing can yield models analogous to GNN-AK []—which explicitly embed the distance of a neighboring node when representing the ego network root during message passing. As such, directly connects the expressivity of k-hop GNNs with the 1-WL algorithm and provides a formal framework to explore the expressivity of higher order MP-GNN architectures.
Appendix H. Self-Supervised IGEL
We provide additional context for the application of as a representational input for methods such as DeepWalk []. This section describes in detail how self-supervised embeddings are learned. We also provide a qualitative analysis of in the self-supervised setting using networks that are amenable for visualization. We focus on analyzing how influences the learned representations.
IGEL & Self-Supervised Node Representations
can be easily incorporated in standard node representation methods like DeepWalk [] or node2vec []. Due to its relative simplicity, integrating only requires replacing the input to the embedding method so that encodings are used rather than node identities. We provide an overview of the process of generating embeddings through DeepWalk, which involves (a) sampling random walks to capture the relationships between nodes and (b) training a negative-sampling based embedding model in the style of word2vec [] on the random walks to embed random walk information in a compact latent space.
Distributional Sampling through Random Walks— First, we sample random walks from each vertex in the graph. Walks are generated by selecting the next vertex uniformly from the neighbors of the current vertex. Figure A3 illustrates a possible random walk of length 9 in the graph of Figure 1. By randomly sampling walks, we obtain traversed node sequences to use as inputs for the following negative sampling optimization objective.
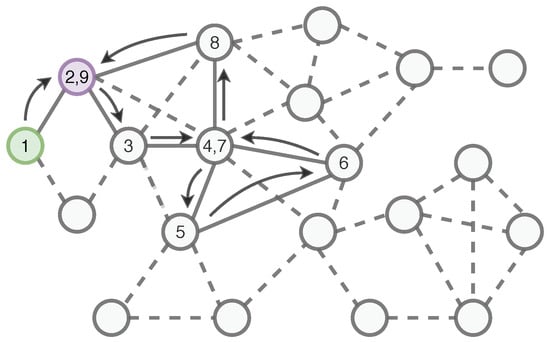
Figure A3.
Example of random walk starting on the green node and finishing on the purple node. Nodes contain the time-step when they were visited. The context of a given vertex will be any nodes whose time-steps are within the context window of that node.
Negative Sampling Optimization Objective— Given a random walk , defined as a sequence of nodes of length s, we define the context associated with the occurrence of vertex v in as the the sub-sequence in containing the nodes that appear close to v, including repetitions. Closeness is determined by p, the size of the positive context window, i.e., the context contains all nodes that appear at most p steps before/after the node within . In DeepWalk, a skip-gram negative sampling objective learns to represent vertices appearing in similar contexts within random walks.
Given a node in random walk , our task is to learn embeddings that assign high probability for nodes appearing in the context and lower probability for nodes not appearing in the context. Let denote the logistic function. As we focus on the learned representation capturing these symmetric relationships, the probability of being in is given by
Table A2 summarizes the hyper-parameters of DeepWalk. Our global objective function is the following negative sampling log-likelihood. For each of the random walks and each vertex at the center of a context in the random walk, we sum the term corresponding to the positive cases for vertices found in the context and the expectation over z negative, randomly sampled vertices.

Table A2.
DeepWalk hyper-parameters.
Table A2.
DeepWalk hyper-parameters.
| Param. | Description |
|---|---|
| Random walks per node | |
| Steps per random walk | |
| # of neg. samples | |
| Context window size |
Let be a noise distribution from which the z negative samples are drawn; our task is to maximize (A4) through gradient ascent:
Defining the -DeepWalk embedding function— In DeepWalk, for every vertex , there is a corresponding t-dimensional embedding vector . As such, one can represent the embedding function as a product between a one-hot encoded vector corresponding to the index of the vertex where and an embedding matrix :
Introducing requires modifying the shape of to account for the shape of -dimensional encoding vectors dependent on and , so that embeddings are computed as a weighted sum of embeddings corresponding to each (path length, degree) pair. Let define a structural embedding matrix with one embedding per (path length, degree) pair; a linear can be defined as:
Since the definition of is differentiable, it can be used as a drop-in replacement of in Equation (A4).
Appendix I. Comparison of Existing Methods
In this section, we provide a summarized overview of the existing work presented in Section 2, including an overview of the main methods that exemplify distance-aware, subgraph, structural, and spectral approaches most related to our theoretical and practical work. Table A3 summarizes the main model architectures, the extensions they introduce within the message passing mechanism, and the limitations associated with each approach.
In contrast with existing methods, Igel is capable of boosting the expressivity of underlying MP-GNN architectures as additional features concatenated to node/edge attributes—that is, without requiring any modification to the design of the downstream model.

Table A3.
Comparison of state-of-the-art methods most closely related to Igel. We provide an overview of the four families of approaches that extend the expressivity of GNNs beyond 1-WL, summarizing key model architectures, the message passing extensions that they introduce in the learning process, and the common limitations for each approach.
Table A3.
Comparison of state-of-the-art methods most closely related to Igel. We provide an overview of the four families of approaches that extend the expressivity of GNNs beyond 1-WL, summarizing key model architectures, the message passing extensions that they introduce in the learning process, and the common limitations for each approach.
| Approach | Model Architectures | Message Passing Extensions | Limitations |
|---|---|---|---|
| Distance-Aware | PGNNs [] DE-GNNs [] SPNNs [] | Introduce distance to target nodes, ego network roots as an encoded variables, or as the explicit distance as part of the message passing mechanism. | Considers a fixed set of target nodes or requires architecture modifications to introduce permutation equivariant distance signals. |
| subgraph | k-hop GNNs [] Nested-GNNs [] ESAN [] GNN-AK [] SUN [] | Propagate information through subgraphs around k-hops, either applying GNNs on the subgraphs, pooling subgraphs, and introducing distance/context signals within the subgraph. | Requires learning over subgraphs with an increased time and memory cost and architecture modifications to propagate messages across subgraphs (incl. distance, context, and node attribute information). |
| Structural | SMP [] GSNs [] | Explicitly introduce structural information in the message passing mechanism, e.g., counts of cycles or stars where a node appears. | Requires identifying and introducing structural features (e.g., node roles in the network) during message passing through architecture modifications. |
| Spectral | GNN-ML3 [] | Introduce features from the spectral domain of the graph in the message passing mechanism. | Requires cubic-time eigenvalue decomposition to construct spectral features and architecture modifications to introduce them during message passing. |

Table A4.
Overview of the graphs used in the experiments. We show the average number of vertices (Avg. n), edges (Avg. m), number of graphs, target task, output shape, and splits (when applicable).
Table A4.
Overview of the graphs used in the experiments. We show the average number of vertices (Avg. n), edges (Avg. m), number of graphs, target task, output shape, and splits (when applicable).
| Avg. n | Avg. m | Num. Graphs | Task | Output Shape | Splits (Train/Valid/Test) | |
|---|---|---|---|---|---|---|
| Enzymes | 32.63 | 62.14 | 600 | Multi-class Graph Class. | 6 (multi-class probabilities) | 9-fold/1 fold (Graphs, Train/Eval) |
| Mutag | 17.93 | 39.58 | 188 | Binary Graph Class. | 2 (binary class probabilities) | 9-fold/1 fold (Graphs, Train/Eval) |
| Proteins | 39.06 | 72.82 | 1113 | Binary Graph Class. | 2 (binary class probabilities) | 9-fold/1 fold (Graphs, Train/Eval) |
| PTC | 25.55 | 51.92 | 344 | Binary Graph Class. | 2 (binary class probabilities) | 9-fold/1 fold (Graphs, Train/Eval) |
| Graph8c | 8.0 | 28.82 | 11,117 | Non-isomorphism Detection | N/A | N/A |
| EXP Classify | 44.44 | 111.21 | 600 | Binary Class. (pairwise graph distinguishability) | 1 (non-isomorphic graph pair probability) | Graph pairs 400/100/100 |
| SR25 | 25 | 300 | 15 | Non-isomorphism Detection | N/A | N/A |
| RandomGraph | 18.8 | 62.67 | 5000 | Regression (Graphlet Counting) | 1 (graphlet counts) | Graphs 1500/1000/2500 |
| ZINC-12K | 23.1 | 49.8 | 12,000 | Molecular prop. regression | 1 | Graphs 10,000/1000/1000 |
| PATTERN | 118.9 | 6079.8 | 14,000 | Recognize subgraphs | 2 | Graphs 10,000/2000/2000 |
| ArXiv ASTRO-PH | 18,722 | 198,110 | 1 | Binary Class. (Link Prediction) | 1 (edge probability) | Randomly sampled edges 50% train/50% test |
| 4039 | 88,234 | 1 | Binary Class. (Link Prediction) | 1 (edge probability) | Randomly sampled edges 50% train/50% test | |
| PPI | 2373 | 68,342.4 | 24 | Multi-label Vertex Class. | 121 (binary class probabilities) | Graphs 20/2/2 |
References
- Bronstein, M.M.; Bruna, J.; Cohen, T.; Veličković, P. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Duvenaud, D.K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Samanta, B.; De, A.; Jana, G.; Gómez, V.; Chattaraj, P.; Ganguly, N.; Gomez-Rodriguez, M. NEVAE: A Deep Generative Model for Molecular Graphs. J. Mach. Learn. Res. 2020, 21, 1–33. [Google Scholar] [CrossRef]
- Battaglia, P.; Pascanu, R.; Lai, M.; Jimenez Rezende, D.; Kavukcuoglu, K. Interaction Networks for Learning about Objects, Relations and Physics. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Weisfeiler, B.; Leman, A. The Reduction of a Graph to Canonical Form and the Algebra which Appears Therein. Nauchno-Tech. Inf. 1968, 2, 12–16. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the 7th International Conference on Learning Representations ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Morris, C.; Ritzert, M.; Fey, M.; Hamilton, W.L.; Lenssen, J.E.; Rattan, G.; Grohe, M. Weisfeiler and Leman Go Neural: Higher-Order Graph Neural Networks. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI-19), Honolulu, HI, USA, 27 January–1 February 2019; 2019; 33, pp. 4602–4609. [Google Scholar]
- Grohe, M. Descriptive Complexity, Canonisation, and Definable Graph Structure Theory; Lecture Notes in Logic; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Brijder, R.; Geerts, F.; Bussche, J.V.D.; Weerwag, T. On the Expressive Power of Query Languages for Matrices. ACM Trans. Database Syst. 2019, 44, 1–31. [Google Scholar] [CrossRef]
- Barceló, P.; Kostylev, E.V.; Monet, M.; Pérez, J.; Reutter, J.; Silva, J.P. The Logical Expressiveness of Graph Neural Networks. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 26 April–1 May 2020. [Google Scholar]
- Geerts, F. On the Expressive Power of Linear Algebra on Graphs. Theory Comput. Syst. 2021, 65, 1–61. [Google Scholar] [CrossRef]
- Morris, C.; Lipman, Y.; Maron, H.; Rieck, B.; Kriege, N.M.; Grohe, M.; Fey, M.; Borgwardt, K. Weisfeiler and Leman go machine learning: The story so far. arXiv 2021, arXiv:2112.09992. [Google Scholar]
- You, J.; Ying, R.; Leskovec, J. Position-aware Graph Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 7134–7143. [Google Scholar]
- Nikolentzos, G.; Dasoulas, G.; Vazirgiannis, M. k-hop graph neural networks. Neural Netw. 2020, 130, 195–205. [Google Scholar] [CrossRef] [PubMed]
- Bodnar, C.; Frasca, F.; Otter, N.; Wang, Y.; Liò, P.; Montufar, G.F.; Bronstein, M. Weisfeiler and Lehman Go Cellular: CW Networks. Adv. Neural Inf. Process. Syst. 2021, 34, 2625–2640. [Google Scholar]
- Vignac, C.; Loukas, A.; Frossard, P. Building powerful and equivariant graph neural networks with structural message-passing. Adv. Neural Inf. Process. Syst. 2020, 33, 14143–14155. [Google Scholar]
- Bouritsas, G.; Frasca, F.; Zafeiriou, S.; Bronstein, M.M. Improving Graph Neural Network Expressivity via Subgraph Isomorphism Counting. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 657–668. [Google Scholar] [CrossRef]
- Zhang, M.; Li, P. Nested graph neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 15734–15747. [Google Scholar]
- Zhao, L.; Jin, W.; Akoglu, L.; Shah, N. From Stars to Subgraphs: Uplifting Any GNN with Local Structure Awareness. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 25–29 April 2022. [Google Scholar]
- Bevilacqua, B.; Frasca, F.; Lim, D.; Srinivasan, B.; Cai, C.; Balamurugan, G.; Bronstein, M.M.; Maron, H. Equivariant Subgraph Aggregation Networks. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 25–29 April 2022. [Google Scholar]
- Frasca, F.; Bevilacqua, B.; Bronstein, M.M.; Maron, H. Understanding and Extending Subgraph GNNs by Rethinking Their Symmetries. In Proceedings of the Advances in Neural Information Processing Systems, Virtual/New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Michel, G.; Nikolentzos, G.; Lutzeyer, J.; Vazirgiannis, M. Path Neural Networks: Expressive and Accurate Graph Neural Networks. In Proceedings of the 40th International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Maron, H.; Ben-Hamu, H.; Serviansky, H.; Lipman, Y. Provably Powerful Graph Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Balcilar, M.; Héroux, P.; Gaüzère, B.; Vasseur, P.; Adam, S.; Honeine, P. Breaking the Limits of Message Passing Graph Neural Networks. In Proceedings of the 38th International Conference on Machine Learning (ICML), Virtual conference, 18–24 July 2021. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open Graph Benchmark: Datasets for Machine Learning on Graphs. In Proceedings of the Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Virtual conference, 6–12 December 2020; Volume 33. [Google Scholar]
- Morris, C.; Kriege, N.M.; Bause, F.; Kersting, K.; Mutzel, P.; Neumann, M. TUDataset: A collection of benchmark datasets for learning with graphs. In Proceedings of the ICML 2020 Workshop on Graph Representation Learning and Beyond (GRL+ 2020), Virtual conference, 12–18 July 2020. [Google Scholar]
- You, J.; Ying, Z.; Leskovec, J. Design Space for Graph Neural Networks. Adv. Neural Inf. Process. Syst. 2020, 33, 17009–17021. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, USA, 4–9 December 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, Canada, 30 April–3 May 2018. [Google Scholar]
- Gao, H.; Wang, Z.; Ji, S. Large-Scale Learnable Graph Convolutional Networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1416–1424. [Google Scholar]
- Babai, L.; Kucera, L. Canonical labelling of graphs in linear average time. In Proceedings of the 20th Annual Symposium on Foundations of Computer Science (sfcs 1979), San Juan, PR, USA, 29–31 October 1979; pp. 39–46. [Google Scholar] [CrossRef]
- Huang, N.T.; Villar, S. A Short Tutorial on The Weisfeiler–Lehman Test And Its Variants. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 8533–8537. [Google Scholar]
- Veličković, P. Message passing all the way up. In Proceedings of the Workshop on Geometrical and Topological Representation Learning, International Conference on Learning Representations, Virtual Conference, 25–29 April 2022. [Google Scholar]
- Li, P.; Wang, Y.; Wang, H.; Leskovec, J. Distance Encoding: Design Provably More Powerful Neural Networks for Graph Representation Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 4465–4478. [Google Scholar]
- You, J.; Gomes-Selman, J.M.; Ying, R.; Leskovec, J. Identity-aware graph neural networks. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21), Virtual conference, 2–9 February 2021; 2021; 35, pp. 10737–10745. [Google Scholar]
- Abboud, R.; Dimitrov, R.; Ceylan, İ.İ. Shortest Path Networks for Graph Property Prediction. In Proceedings of the First Learning on Graphs Conference (LoG), Virtual Conference, 9–12 December 2022. [Google Scholar]
- Maron, H.; Ben-Hamu, H.; Shamir, N.; Lipman, Y. Invariant and Equivariant Graph Networks. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhang, B.; Luo, S.; Wang, L.; He, D. Rethinking the Expressive Power of GNNs via Graph Biconnectivity. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Papp, P.A.; Wattenhofer, R. A Theoretical Comparison of Graph Neural Network Extensions. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; 162, pp. 17323–17345. [Google Scholar]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Shervashidze, N.; Schweitzer, P.; Jan, E.; Leeuwen, V.; Mehlhorn, K.; Borgwardt, K. Weisfeiler–Lehman Graph Kernels. J. Mach. Learn. Res. 2010, 1, 1–48. [Google Scholar]
- Alvarez-Gonzalez, N.; Kaltenbrunner, A.; Gómez, V. Beyond 1-WL with Local Ego-Network Encodings. In Proceedings of the First Learning on Graphs Conference (LoG), Virtual Conference, 9–12 December 2022. Non-archival Extended Abstract track. [Google Scholar]
- Van Dam, E.R.; Haemers, W.H. Which Graphs Are Determined by Their Spectrum? Linear Algebra Its Appl. 2003, 373, 241–272. [Google Scholar] [CrossRef]
- Brouwer, A.E. and Van Maldeghem, Hendrik. Strongly Regular Graphs; Cambridge University Press: Cambridge, UK, 2022; Volume 182, p. 462. [Google Scholar]
- Arvind, V.; Fuhlbrück, F.; Köbler, J.; Verbitsky, O. On Weisfeiler-Leman invariance: Subgraph counts and related graph properties. J. Comput. Syst. Sci. 2020, 113, 42–59. [Google Scholar] [CrossRef]
- Dwivedi, V.P.; Joshi, C.K.; Laurent, T.; Bengio, Y.; Bresson, X. Benchmarking Graph Neural Networks. arXiv 2020, arXiv:2003.00982. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online Learning of Social Representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. Node2Vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Abboud, R.; Ceylan, I.I.; Grohe, M.; Lukasiewicz, T. The Surprising Power of Graph Neural Networks with Random Node Initialization. In Proceedings of the International Joint Conferences on Artificial Intelligence Organization, Virtual Conference, 19–26 August 2021; pp. 2112–2118. [Google Scholar]
- Chen, Z.; Chen, L.; Villar, S.; Bruna, J. Can Graph Neural Networks Count Substructures? Adv. Neural Inf. Process. Syst. 2020, 33, 10383–10395. [Google Scholar]
- Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.; Leskovec, J. Strategies for Pre-training Graph Neural Networks. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 26 April–1 May 2020. [Google Scholar]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. 2014. Available online: https://snap.stanford.edu/data/index.html (accessed on 16 September 2023).
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 2014–2023. [Google Scholar]
- Shervashidze, N.; Borgwardt, K. Fast subtree kernels on graphs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 7–12 December 2009; Volume 22. [Google Scholar]
- Rieck, B.; Bock, C.; Borgwardt, K. A Persistent Weisfeiler–Lehman Procedure for Graph Classification. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; 2019; Volume 97, pp. 5448–5458. [Google Scholar]
- Togninalli, M.; Ghisu, E.; Llinares-López, F.; Rieck, B.; Borgwardt, K. Wasserstein Weisfeiler–Lehman Graph Kernels. Adv. Neural Inf. Process. Syst. 2019, 32, 6436–6446. [Google Scholar]
- Kriege, N.M.; Morris, C.; Rey, A.; Sohler, C. A Property Testing Framework for the Theoretical Expressivity of Graph Kernels. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden, 13–19 July 2018; 2018; Volume 7, pp. 2348–2354. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.; Dean, J. Distributed Representations of Words and Phrases and Their Compositionality. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, USA, 5–10 December 2013; Volume 2, pp. 3111–3119. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).