Accurate Closed-Form Solutions for the Free Vibration and Supersonic Flutter of Laminated Circular Cylindrical Shells

Abstract

According to the Donnell–Mushtari shell theory, this work presents a closed-form solution procedure for free vibration of open laminated circular cylindrical shells with arbitrary homogeneous boundary conditions (BCs). The governing differential equations of free vibration are derived from the Rayleigh quotient and solved by the iterative separation-of-variable (iSOV) method. In addition, considering axial aerodynamic pressure, simulated by the linear piston theory, the exact eigensolutions for the flutter of open laminated cylindrical shells with simply supported circumferential edges and closed laminated cylindrical shells are also achieved. The governing differential equations of cylindrical shell flutter are derived from the Hamilton variational principle and solved by the separation-of-variable (SOV) method. The influence of circumferential dimension on flutter speed is investigated for open cylindrical shells, which reveals that the number of circumferential waves in critical flutter mode increases with circumferential length, and there exists an infimum for flutter speed that is an invariant independent of circumferential length. The present results agree well with those obtained by the Galerkin method, the finite element method, and other analytical methods.

1. Introduction

As an important structural component, cylindrical laminated shells have a widespread application in diverse engineering fields, such as civil, mechanical, aerospace, marine, and offshore engineering, which can be attributed to their high stiffness-to-weight and strength-to-weight ratios and flexibility in design, wherein free vibration and flutter are two important issues that are related to structural safety and integrity. How to achieve the analytical solutions for these two eigenvalue problems of cylindrical laminated shells has long been a topic of interest for scholars.

Engineers need to understand the vibration behaviors of shell structures for more reliable and cost-effective designs [1]. The frequency of free vibration is an intrinsic quality for structural components, and calculating free vibration characteristics for cylindrical shells intrigues numerous engineers and scientists. The exact frequencies of cylindrical shells with simply supported conditions (also called shear diaphragm conditions [2,3]) on all edges are accessible by the inverse method [2,3,4], which can be considered a natural extension of the Naiver solutions. As for more complex conditions, wherein closed cylindrical shells have arbitrary homogeneous boundary conditions (BCs) on axial edges or open cylindrical shells have two opposite edges simply supported, the semi-inverse method can be used to obtain the Levy type of solutions. Without assumptions or simplifications beyond those underlying governing differential equations, Forsberg [5] obtained the exact frequencies of closed cylindrical shells with different axial boundaries. Following Forsberg’s work, the natural frequencies of clamped cylindrical shells were presented by Smith and Haft [6]. However, as pointed out by Smith and Half themselves, care must be taken to monitor the roots of the characteristic equation to ensure that the assumed form of solutions is preserved. Vronay and Smith [7] overcame this disadvantage by carrying all complex quantities as complex through the solution process. In order to decrease the effort required to solve for the coefficients of modal functions, Callahan and Baruh [8] developed a systematic procedure for obtaining closed-form solutions for thin circular cylindrical shell vibration; there, the obtained coefficients of modal functions were numerically determined. By using exact expressions for modal coefficients instead of calculating the coefficients through numerical methods, Xing and Liu et al. [2,3] obtained the exact solutions for the free vibration of isotropic and orthotropic closed and open circular cylindrical shells. In addition, the exact solutions for the free vibration of closed cylindrical shells with elastic restraints were attained by Zhong et al. [9]. To shorten the length of this article, the free vibration solutions obtained by numerical methods, such as the Galerkin method, the finite element method, the Rayleigh–Ritz method, etc., are not reviewed here. Relevant achievements can be found in the reviews presented by Liew et al. [10] and Qatu et al. [11,12,13].

Flutter is a self-excited oscillation caused by the coupling of elastic, inertial, and aerodynamic forces [14]. Since the first observation of panel flutter in World War II [14], panel flutter has been a popular subject of research on the aerodynamic behavior of aircraft structures, and plentiful research results have been achieved. The early theoretical and experimental studies were reviewed by Dowell [15] in 1970 and Mei et al. [16] in 1999, respectively, wherein flutter models are divided into five categories. Within the author’s knowledge, the up-to-date review for panel flutter was presented by Chai et al. [17] in 2021, wherein the state-of-the-art developments in panel flutter were summarized in detail from the perspectives of flutter mechanism, flutter model, flutter control, solving method, and the outlook on future investigations. In general, the theoretical analysis of panel flutter consists of solving flutter differential equations by using different structural dynamics theories and aerodynamic theories.

The calculation of aerodynamic pressure is an important part of panel flutter analysis. The aerodynamic theories used in panel flutter analysis mainly include the piston theory [18,19], the potential flow theory [20], and the theories based on Navier–Stokes equations [21,22], wherein the linear piston theory has a widespread application due to its concise expression for aerodynamic pressure. The piston theory was proposed by Lighthill [18], and its application scope has been investigated [16,20]. Meng [23,24] explained the physical meaning of high-order terms in the piston theory. When applied to a cylindrical shell, a more accurate version of linear piston theory was presented by Krumhaar [25], wherein the effect of curvature was taken into account.

Based on Donnell’s shell theory, Olson and Fung [26,27] compared the results obtained by the piston theory, potential theory, and experiment for simply supported cylindrical shells, indicating that results obtained by the piston theory appear to correspond more closely to the experiment. Motivated by the circumferentially traveling waves observed in the experiment [26], a nonlinear flutter analysis for simply supported cylindrical shells was performed by Evensen and Olson [28], which revealed that the circumferentially traveling wave flutter can be predicted through a nonlinear analysis. Using an improved structural and aerodynamic model, Amabili and Pellicano [29,30] reinvestigated the nonlinear stability of simply supported circular cylindrical shells in supersonic axial airflow. Except for the classical shell theory, the geometrical model of a shallow shell can also be constructed by a plate with initial deformation, as Amirzadegan and Dowell [31,32] performed. In their work, the instability and post-stability limit cycle oscillations of shallow shells in a supersonic gas flow were studied by the Galerkin method, which can be viewed as a sequel to Dowell’s earlier work [33]. Note that the flutter differential equations used in [27,28,29,30,31,32,33] were solved by the Galerkin method.

Since the trial functions used in the Galerkin method need to change as BCs and panel models change, the finite element method (FEM) is more convenient than the Galerkin method to solve complicated panel flutter models. Singha and Mandal [34] studied the supersonic flutter behaviors of laminated cylindrical shells using isoparametric degenerated shell elements. According to the Sander shell theory, Sabri and Lakis [35] investigated the influence of internal pressure and axial loading on the flutter characteristics of cylindrical shells by a hybrid FEM, and the results predicted by the FEM agreed with the experiment [26]. Based on the semi-analytical FEM, Mahmoudkhani [36] illustrated the effects of imperfections on the aero-thermoelastic behavior of functionally graded cylindrical shells. With the variable stiffness composite laminates (VSCLs) and the Love shell theory, Cachulo et al. [37] analyzed the aeroelastic stability of a VSCL cylindrical shell under supersonic airflow by the $p$-version FEM. Bochkarev et al. [38] investigated the aeroelastic stability of shallow cylindrical shells stiffened with stringers by the FEM. Except for the Galerkin method and the finite element method, the Rayleigh–Ritz method [39] is also a common discrete method in flutter analysis for cylindrical shells.

From the above review, one can see that there are few analytical solutions of free vibration for open cylindrical shells. As for shell flutter, the analytical solutions of cylindrical shells are scarcer than those of beams [40,41] and flat panels [42,43,44], since the governing differential equations of cylindrical shell flutter are more complex than those of beams and flat plates.

In this context, according to the Donnell shell theory, this work obtains the closed-form analytical solutions of free vibration for open cylindrical shells with arbitrary combinations of homogeneous BCs by the iterative separation-of-variable (iSOV) method [45]. In addition, considering the axial aerodynamic pressure calculated by the linear piston theory, the exact solutions of open cylindrical shell flutter with simply supported circumferential edges and closed cylindrical shell flutter are also presented in this work. The effect of the circumferential dimension of the open cylindrical shell on flutter characteristics is investigated. The present results are compared with those obtained by the FEM, the Galerkin method, and other analytical methods.

The rest of this paper is organized as follows: Section 2 and Section 3 give the derivation of the basic equations for free vibration and flutter, respectively. Section 4 introduces the solving method. Section 5 presents the results of free vibration and flutter and compares them with those of other methods. Finally, the conclusions are drawn in Section 6.

2. Basic Equations of Free Vibration

An open circular cylindrical shell with thickness $h$, axial length $2a$, and circumferential length $2b$ is shown in Figure 1. The cylindrical coordinate system with axial coordinate $\alpha$, circumferential coordinate $\beta$, and normal coordinate $\gamma$ is set in the middle surface, and the origin $O$ is located at the center of the middle surface. The cylindrical shell consists of five layers of homogeneous orthotropic sheets in the ply stacking sequence of $0^{°}/{90}^{°}/0^{°}/{90}^{°}/0^{°}$. Each layer with identical thickness uses the same orthotropic material with the density $\rho$, the Young’s modulus $E_1,E_2$, the shear modulus $G_{12}$, and the Poisson’s ratio $v_{12},v_{21}$.

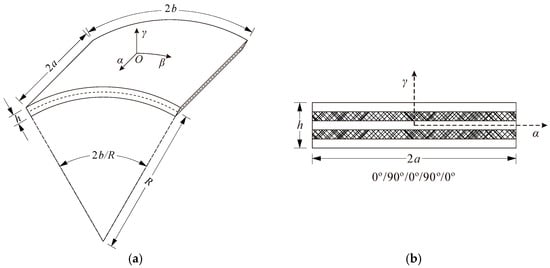
Figure 1. An open laminated circular cylindrical shell and coordinates. (a) Open circular cylindrical shell. (b) Ply stacking sequence.

2.1. Expressions of Energy

According to the Donnell shell theory, the displacements of the cylindrical shell have the forms as follows:

$$\begin{array}{l}\widehat{u}\left(\alpha ,\beta ,\gamma ,t\right)=u\left(\alpha ,\beta ,t\right)-\gamma {\displaystyle \frac{\partial w}{\partial \alpha }}\\ \widehat{v}\left(\alpha ,\beta ,\gamma ,t\right)=v\left(\alpha ,\beta ,t\right)-\gamma {\displaystyle \frac{\partial w}{\partial \beta }}\\ \widehat{w}\left(\alpha ,\beta ,\gamma ,t\right)=w\left(\alpha ,\beta ,t\right)\end{array}$$

(1)

where $\widehat{u},\widehat{v},\widehat{w}$ are the displacements of an arbitrary point in the cylindrical shell along the $\alpha ,\beta ,\gamma$ directions, $u,v,w$ are the displacements of the middle surface along the $\alpha , \beta ,\gamma$ directions, and $t$ is the time variable. The kinetic energy $T$ can be expressed as follows:

$$T={\displaystyle \frac{1}{2}}{\displaystyle \underset{-b}{\overset{b}{\int }}{\displaystyle \underset{-a}{\overset{a}{\int }}\rho h\left[{\left(\frac{\partial u}{\partial t}\right)}^2+{\left(\frac{\partial v}{\partial t}\right)}^2+{\left(\frac{\partial w}{\partial t}\right)}^2\right]\mathrm{d}\alpha \mathrm{d}\beta }}$$

(2)

The potential energy is as follows:

$$U=U_{\mathrm{m}}+U_{\mathrm{d}}$$

(3)

wherein $U_{\mathrm{m}}$ and $U_{\mathrm{d}}$ represent the membrane and bending energy, respectively, which have the following forms [46]:

$$U_{\mathrm{m}}={\displaystyle \frac{1}{2}}{\displaystyle \underset{-b}{\overset{b}{\int }}{\displaystyle \underset{-a}{\overset{a}{\int }}\left[A_{11}{\left(\frac{\partial u}{\partial \alpha }\right)}^2+A_{22}{\left(\frac{\partial v}{\partial \beta }+\frac{w}{R}\right)}^2+2A_{12}\frac{\partial u}{\partial \alpha }\left(\frac{\partial v}{\partial \beta }+\frac{w}{R}\right)+A_{66}{\left(\frac{\partial u}{\partial \beta }+\frac{\partial v}{\partial \alpha }\right)}^2\right]\mathrm{d}\alpha \mathrm{d}\beta }}$$

(4)

$$U_{\mathrm{d}}={\displaystyle \frac{1}{2}}{\displaystyle \underset{-b}{\overset{b}{\int }}{\displaystyle \underset{-a}{\overset{a}{\int }}\left[D_{11}{\left(\frac{{\partial }^{2}w}{\partial {\alpha }^2}\right)}^2+D_{22}{\left(\frac{{\partial }^{2}w}{\partial {\beta }^2}\right)}^2+2D_{12}\frac{{\partial }^{2}w}{\partial {\alpha }^2}\frac{{\partial }^{2}w}{\partial {\beta }^2}+4D_{66}{\left(\frac{{\partial }^{2}w}{\partial \alpha \partial \beta }\right)}^2\right]\mathrm{d}\alpha \mathrm{d}\beta }}$$

(5)

where $A_{ij}$ and $D_{ij}$ denote the membrane and bending stiffness, respectively. Considering the ply stacking sequence $0^{°}/{90}^{°}/0^{°}/{90}^{°}/0^{°}$, the expressions of $A_{ij}$ and $D_{ij}$ are as follows:

$$\begin{array}{l}{D}_{11}={\displaystyle \frac{33}{500}}{Q}_{11}{h}^3+{\displaystyle \frac{13}{750}}{Q}_{22}{h}^3\hspace{1em}\hspace{0.33em},\hspace{1em}{D}_{12}={\displaystyle \frac{1}{12}}\hspace{0.33em}{Q}_{12}{h}^3\hspace{0.33em}\\ D_{22}={\displaystyle \frac{33}{500}}{Q}_{22}{h}^3+{\displaystyle \frac{13}{750}}{Q}_{11}{h}^3\hspace{1em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{D}_{66}={\displaystyle \frac{1}{12}}\hspace{0.33em}{Q}_{66}{h}^3\\ A_{11}=\hspace{0.33em}{\displaystyle \frac{3}{5}}h{Q}_{11}+{\displaystyle \frac{2}{5}}h{Q}_{22}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em},\hspace{1em} \hspace{0.33em}{A}_{12}\hspace{0.33em}=\hspace{0.33em}h{Q}_{12}\\ A_{22}={\displaystyle \frac{3}{5}}h{Q}_{22}+{\displaystyle \frac{2}{5}}h{Q}_{11}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} A_{66}=h{Q}_{66}\end{array}$$

(6)

where

$$Q_{11}={\displaystyle \frac{E_1}{1-v_{12}{v}_{21}}}\hspace{1em};\hspace{1em}{Q}_{12}={\displaystyle \frac{v_{12}{E}_2}{1-v_{12}{v}_{21}}}={\displaystyle \frac{v_{21}{E}_1}{1-v_{12}{v}_{21}}}\hspace{1em};\hspace{1em}{Q}_{22}={\displaystyle \frac{E_2}{1-v_{12}{v}_{21}}}\hspace{1em};\hspace{1em}{Q}_{66}=G_{12}$$

(7)

For convenience, the dimensionless coordinates $\xi =\alpha /a, \eta =\beta /b$ are used in the following equations. Assume that the displacements of the middle surface can be written in the separation-of-variable form as follows:

$$u={\varphi }_1\left(\xi \right){\phi }_1\left(\eta \right)e^{i{\omega }_{d}t}\hspace{1em},\hspace{1em}v={\varphi }_2\left(\xi \right){\phi }_2\left(\eta \right)e^{i{\omega }_{d}t}\hspace{1em},\hspace{1em}w={\varphi }_3\left(\xi \right){\phi }_3\left(\eta \right)e^{i{\omega }_{d}t}$$

(8)

where ${\omega }_{\mathrm{d}}$ represents the dimensional frequency for free vibration and $\mathrm{i}=\sqrt{-1}$. Substituting Equation (8) into Equation (2) obtains the amplitude $T_{\mathrm{a}\mathrm{m}\mathrm{p}}={\omega }_{\mathrm{d}}^2{T}_0$ of the kinetic energy, where the referenced kinetic energy $T_0$ is as follows:

$$T_0={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}{\displaystyle \underset{-1}{\overset{1}{\int }}\rho h\left[{\left({\varphi }_1{\phi }_1\right)}^2+{\left({\varphi }_2{\phi }_2\right)}^2+{\left({\varphi }_3{\phi }_3\right)}^2\right]\mathrm{d}\xi \mathrm{d}\eta }}$$

(9)

Introducing Equation (8) into Equations (4) and (5) yields the amplitude of the potential energy, as follows:

$$U_{\mathrm{amp}}=U_{\mathrm{ma}}+U_{\mathrm{ba}}$$

(10)

where

$$U_{\mathrm{ma}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{A_{11}}{a^2}{\left(\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }{\phi }_1\right)}^2+\frac{A_{22}}{b^2}{\left({\varphi }_2\frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }+\frac{b}{R}{\varphi }_3{\phi }_3\right)}^2+\\ 2\frac{A_{12}}{ab}\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }{\phi }_1\left({\varphi }_2\frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }+\frac{b}{R}{\varphi }_3{\phi }_3\right)+A_{66}{\left(\frac{1}{b}{\varphi }_1\frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }+\frac{1}{a}\frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }{\phi }_2\right)}^2\end{array}\right]\mathrm{d}\xi \mathrm{d}\eta }}$$

(11)

$$U_{\mathrm{ba}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{D_{11}}{a^4}{\left(\frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}{\phi }_3\right)}^2+\frac{D_{22}}{b^4}{\left({\varphi }_3\frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}\right)}^2+\\ 2\frac{D_{12}}{a^2{b}^2}\left(\frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}{\phi }_3\right)\left({\varphi }_3\frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}\right)+4\frac{D_{66}}{a^2{b}^2}{\left(\frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }\frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }\right)}^2\end{array}\right]\mathrm{d}\xi \mathrm{d}\eta }}$$

(12)

In the following, the governing differential equations in the $\xi$ and $\eta$ directions are derived from the Rayleigh quotient.

$${\omega }_{\mathrm{d}}^2=\mathrm{st}{\displaystyle \frac{U_{\mathrm{amp}}}{T_0}} \mathrm{or} \delta U_{\mathrm{amp}}={\omega }_{\mathrm{d}}^2\delta T_0$$

(13)

where ‘st’ stands for ${\omega }_{\mathrm{d}}^2$ as the stationary value of the quotient $U_{\mathrm{a}\mathrm{m}\mathrm{p}}/T_0$, and $\mathsf{\delta }$ represents variation calculus.

2.2. Basic Equations in the $\xi$ Direction

In order to obtain the governing differential equations about the mode functions ${\varphi }_1~{\varphi }_3$, assume that ${\phi }_1~{\phi }_3$ are known. Hence, Equations (9)–(12) can be simplified as follows:

$$\begin{array}{l}{T}_0={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}\rho h\left[S_{1010}{\varphi }_1^2+S_{2020}{\varphi }_2^2+S_{3030}{\varphi }_3^2\right]\mathrm{d}\xi }\\ U_{\mathrm{ma}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{A_{11}}{a^2}{S}_{1010}{\left(\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }\right)}^2+\frac{A_{22}}{b^2}\left(S_{2121}{\varphi }_2^2+\frac{b^2}{R^2}{S}_{3030}{\varphi }_3^2+2\frac{b}{R}{S}_{2130}{\varphi }_2{\varphi }_3\right)+\\ 2\frac{A_{12}}{ab}\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }\left(S_{1021}{\varphi }_2+\frac{b}{R}{S}_{1030}{\varphi }_3\right)+\\ \frac{A_{66}}{b^2}{S}_{1111}{\varphi }_1^2+\frac{A_{66}}{a^2}{S}_{2020}{\left(\frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }\right)}^2+2\frac{A_{66}}{ab}{S}_{1120}{\varphi }_1\frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }\end{array}\right]\mathrm{d}\xi }\\ U_{\mathrm{ba}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{D_{11}}{a^4}{S}_{3030}{\left(\frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}\right)}^2+\frac{D_{22}}{b^4}{S}_{3232}{\varphi }_3^2+\\ 2\frac{D_{12}}{a^2{b}^2}{S}_{3032}{\varphi }_3\frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}+4\frac{D_{66}}{a^2{b}^2}{S}_{3131}{\left(\frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }\right)}^2\end{array}\right]\mathrm{d}\xi }\end{array}$$

(14)

where the integral parameter $S_{mnrs}$ has the following form:

$$S_{mnrs}={\displaystyle \underset{-1}{\overset{1}{\int }}\frac{{\mathrm{d}}^n{\phi }_m}{\mathrm{d}{\eta }^n}\frac{{\mathrm{d}}^s{\phi }_r}{\mathrm{d}{\eta }^s}}\mathrm{d}\eta$$

(15)

Substituting Equation (14) into the Rayleigh quotient (13) and performing variation operations, we can obtain the governing differential equations for ${\varphi }_1~{\varphi }_3$ as follows:

$$\begin{array}{l}{k}_1{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_1}{\mathrm{d}{\xi }^2}}+r_1{\varphi }_1+m{\displaystyle \frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }}+l{\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}=0\\ -m{\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}+k_2{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_2}{\mathrm{d}{\xi }^2}}+r_2{\varphi }_2+n{\varphi }_3=0\\ l{\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}-n{\varphi }_2+{\displaystyle \frac{{\mathrm{d}}^4{\varphi }_3}{\mathrm{d}{\xi }^4}}+k_3{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}}+r_3{\varphi }_3=0\end{array}$$

(16)

where

$$\begin{array}{l}{k}_1={\displaystyle \frac{S_{1010}}{S_{3030}}}{\displaystyle \frac{a^2{A}_{11}}{D_{11}}}\hspace{1em},\hspace{1em}{r}_1={\displaystyle \frac{S_{1010}}{S_{3030}}}{\omega }^2-{\displaystyle \frac{S_{1111}}{S_{3030}}}{\displaystyle \frac{a^4{A}_{66}}{b^2{D}_{11}}}\\ k_2={\displaystyle \frac{S_{2020}}{S_{3030}}}{\displaystyle \frac{a^2{A}_{66}}{D_{11}}}\hspace{1em},\hspace{1em}{r}_2={\displaystyle \frac{S_{2020}}{S_{3030}}}{\omega }^2-{\displaystyle \frac{S_{2121}}{S_{3030}}}{\displaystyle \frac{a^4{A}_{22}}{b^2{D}_{11}}}\\ k_3=2{\displaystyle \frac{S_{3032}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}-4{\displaystyle \frac{S_{3131}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{66}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}{r}_3=-{\omega }^2+{\displaystyle \frac{S_{3232}}{S_{3030}}}{\displaystyle \frac{a^4{D}_{22}}{b^4{D}_{11}}}+{\displaystyle \frac{a^4{A}_{22}}{R^2{D}_{11}}}\\ l={\displaystyle \frac{S_{1030}}{S_{3030}}}{\displaystyle \frac{a^3{A}_{12}}{R{D}_{11}}}\hspace{1em},\hspace{1em}m={\displaystyle \frac{S_{1021}}{S_{3030}}}{\displaystyle \frac{a^3{A}_{12}}{b{D}_{11}}}-{\displaystyle \frac{S_{1120}}{S_{3030}}}{\displaystyle \frac{a^3{A}_{66}}{b{D}_{11}}}\hspace{1em},\hspace{1em}n=-{\displaystyle \frac{S_{2130}}{S_{3030}}}{\displaystyle \frac{a^4{A}_{22}}{bR{D}_{11}}}\end{array}$$

(17)

where the dimensionless frequency $\omega$ is defined as follows:

$$\omega ={\omega }_{\mathrm{d}}{a}^2\sqrt{{\displaystyle \frac{\rho h}{D_{11}}}}$$

(18)

The resultant BCs can also be obtained as follows:

$$\begin{array}{l}{\left.\left({\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}+{\displaystyle \frac{S_{1021}}{S_{1010}}}{\displaystyle \frac{a{A}_{12}}{b{A}_{11}}}{\varphi }_2+{\displaystyle \frac{S_{1030}}{S_{1010}}}{\displaystyle \frac{a{A}_{12}}{R{A}_{11}}}{\varphi }_3\right)\delta {\varphi }_1\right|}_{-1}^1=0\\ {\left.\left({\displaystyle \frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }}+{\displaystyle \frac{S_{1120}}{S_{2020}}}{\displaystyle \frac{a}{b}}{\varphi }_1\right)\delta {\varphi }_2\right|}_{-1}^1=0\\ {\left.\left[{\displaystyle \frac{{\mathrm{d}}^3{\varphi }_3}{\mathrm{d}{\xi }^3}}+\left({\displaystyle \frac{S_{3032}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}-4{\displaystyle \frac{S_{3131}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{66}}{b^2{D}_{11}}}\right){\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}\right]\delta {\varphi }_3\right|}_{-1}^1=0\\ {\left.\left({\displaystyle \frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}}+{\displaystyle \frac{S_{3032}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}{\varphi }_3\right)\delta \left({\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}\right)\right|}_{-1}^1=0\end{array}$$

(19)

According to Equation (19), the simply supported (S), clamped (C), and free (F) BCs of the edges of $\xi =\pm 1$ are shown in Table 1, wherein the superscripts ‘n’ and ‘t’ represent the normal and tangential directions of edges, respectively.

Table 1. The homogeneous boundary conditions of the edges of $\xi =\pm 1$.

BCs	${\varphi }_1$	${\varphi }_2$	${\varphi }_3$	${\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}$	$F_{\xi }^n$	$F_{\xi }^t$	$F_{\xi }$	$M_{\xi }$
S		0	0		0			0
C	0	0	0	0
F					0	0	0	0
$\begin{array}{l}{F}_{\xi }^n={\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}+{\displaystyle \frac{S_{1021}}{S_{1010}}}{\displaystyle \frac{a{A}_{12}}{b{A}_{11}}}{\varphi }_2+{\displaystyle \frac{S_{1030}}{S_{1010}}}{\displaystyle \frac{a{A}_{12}}{R{A}_{11}}}{\varphi }_3\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{F}_{\xi }^t={\displaystyle \frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }}+{\displaystyle \frac{S_{1120}}{S_{2020}}}{\displaystyle \frac{a}{b}}{\varphi }_1\\ F_{\xi }={\displaystyle \frac{{\mathrm{d}}^3{\varphi }_3}{\mathrm{d}{\xi }^3}}+\left({\displaystyle \frac{S_{3032}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}-4{\displaystyle \frac{S_{3131}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{66}}{b^2{D}_{11}}}\right){\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{M}_{\xi }={\displaystyle \frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}}+{\displaystyle \frac{S_{3032}}{S_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}{\varphi }_3\end{array}$

Eliminating any two functions of ${\varphi }_1$, ${\varphi }_2$, and ${\varphi }_3$ from Equation (16) generates the following equation:

$$T_8{\displaystyle \frac{{\mathrm{d}}^8{\varphi }_i}{\mathrm{d}{\xi }^8}}+T_6{\displaystyle \frac{{\mathrm{d}}^6{\varphi }_i}{\mathrm{d}{\xi }^6}}+T_4{\displaystyle \frac{{\mathrm{d}}^4{\varphi }_i}{\mathrm{d}{\xi }^4}}+T_2{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_i}{\mathrm{d}{\xi }^2}}+T_0{\varphi }_i=0\left(i=1,2,3\right)$$

(20)

where the coefficients are as follows:

$$\begin{array}{l}{T}_8=k_1{k}_2\hspace{0.33em}\hspace{0.33em}\\ T_6=k_1{k}_2{k}_3+k_1{r}_2+k_2{r}_1+m^2\\ T_4=k_1{k}_2{r}_3+k_1{k}_3{r}_2+k_2{k}_3{r}_1+r_1{r}_2-l^2{k}_2+m^2{k}_3\\ T_2=k_1{r}_2{r}_3+k_2{r}_1{r}_3+k_3{r}_1{r}_2-l^2{r}_2+m^2{r}_3+n^2{k}_1+2lmn\\ T_0=r_1{r}_2{r}_3+n^2{r}_1\end{array}$$

(21)

Substituting the solution ${\varphi }_i=A{e}^{\lambda \xi }$, where $\lambda$ is the spatial eigenvalue in the $\xi$ direction, into Equation (20) yields the following characteristic equation:

$$T_8{\lambda }^8+T_6{\lambda }^6+T_4{\lambda }^4+T_2{\lambda }^2+T_0=0$$

(22)

It can be seen from Equations (17) and (21) that the coefficients $T_8~T_0$ are functions of $\omega$, so $\lambda$ is also a function of $\omega$. Given a $\omega$, the eight roots of ${\lambda }_1~{\lambda }_8$ can be obtained by the Ferrari formula. Letting ${\lambda }_{\mathrm{1,2}}=\pm {\alpha }_1, { \lambda }_{\mathrm{3,4}}=\pm {\alpha }_2, {\lambda }_{\mathrm{4,5}}=\pm {\alpha }_3, {\lambda }_{\mathrm{6,7}}=\pm {\alpha }_4,$ then ${\varphi }_1, {\varphi }_2,{\varphi }_3$ can be expressed as follows:

$$\begin{array}{l}{\varphi }_1={\displaystyle \sum _{k=1}^4\left(E_k\cosh {\alpha }_k\xi +F_k\sinh {\alpha }_k\xi \right)}\\ {\varphi }_2={\displaystyle \sum _{k=1}^4\left(M_k\cosh {\alpha }_k\xi +N_k\sinh {\alpha }_k\xi \right)}\\ {\varphi }_3={\displaystyle \sum _{k=1}^4\left(A_k\cosh {\alpha }_k\xi +B_k\sinh {\alpha }_k\xi \right)}\end{array}$$

(23)

where $A_k,B_k, E_k,F_k,M_k,N_k$ are unknown constants. Substituting Equation (23) into Equation (16), the relations between these constant coefficients can be found as follows:

$$\begin{array}{l}{E}_k=P_k{B}_k\hspace{1em},\hspace{1em}{F}_k=P_k{A}_k\hspace{1em} ,\hspace{1em}{P}_k=-{\displaystyle \frac{l{\alpha }_k\left(k_2{\alpha }_k^2+r_2\right)-mn{\alpha }_k}{\left(k_1{\alpha }_k^2+r_1\right)\left(k_2{\alpha }_k^2+r_2\right)+m^2{\alpha }_k^2}}\\ M_k=Q_k{A}_k\hspace{1em},\hspace{1em}{N}_k=Q_k{B}_k\hspace{1em},\hspace{1em}{Q}_k=-{\displaystyle \frac{n\left(k_1{\alpha }_k^2+r_1\right)+lm{\alpha }_k^2}{\left(k_1{\alpha }_k^2+r_1\right)\left(k_2{\alpha }_k^2+r_2\right)+m^2{\alpha }_k^2}}\end{array}$$

(24)

It can be seen from Equation (24) that there are eight unknowns, $A_k, B_k \left(k=1, 2, 3, 4\right)$, which can be determined via the BCs of the edges $\xi =\pm 1$ as shown in Table 1.

Substituting Equation (23) into the BCs of the edges $\xi =\pm 1$ yields eight homogeneous linear equations for $A_k,B_k$, as follows:

$${\mathit{\Lambda }}_{\xi }{\mathit{q}}_{\xi }=0$$

(25)

where ${\mathit{\Lambda }}_{\xi }$ is a matrix of $8\times 8$ and

$${\mathit{q}}_{\xi }^{\mathrm{T}}=[A_1,A_2,A_3,A_4,B_1,B_2,B_3,B_4]$$

(26)

The existence of nontrivial solutions for $A_k$ and $B_k$ requires that the determinant of the coefficient matrix ${\mathit{\Lambda }}_{\xi }$ must be zero, i.e.,

$$\det \left({\mathit{\Lambda }}_{\xi }\right)=0$$

(27)

which is a transcendental equation with respect to $\omega$. After solving for $\omega$, $A_k$ and $B_k$ can then be obtained from Equation (25).

2.3. Basic Equations in the $\eta$ Direction

Similar to the derivation performed in Section 2.2, the basic equations in the $\eta$ direction can be obtained by assuming ${\varphi }_1~{\varphi }_3$ are known. In this case, the amplitudes of the kinetic and potential energy shown in Equations (9)–(12) change to the following:

$$\begin{array}{l}{T}_0={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}\rho h\left(H_{1010}{\phi }_1^2+H_{2020}{\phi }_2^2+H_{3030}{\phi }_3^2\right)\mathrm{d}\eta }\\ U_{\mathrm{ma}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{A_{11}}{a^2}{H}_{1111}{\phi }_1^2+2\frac{A_{12}}{ab}{\phi }_1\left(H_{1120}\frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }+\frac{b}{R}{H}_{1130}{\phi }_3\right)+\\ \frac{A_{22}}{b^2}{H}_{2020}{\left(\frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }\right)}^2+\frac{A_{22}}{R^2}{H}_{3030}{\phi }_3^2+2\frac{A_{22}}{bR}{H}_{2030}\frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }{\phi }_3+\\ \frac{A_{66}}{b^2}{H}_{1010}{\left(\frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }\right)}^2+\frac{A_{66}}{a^2}{H}_{2121}{\phi }_2^2+\frac{2A_{66}}{ab}{H}_{1021}\frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }{\phi }_2\end{array}\right]\mathrm{d}\eta }\\ U_{\mathrm{ba}}={\displaystyle \frac{1}{2}}ab{\displaystyle \underset{-1}{\overset{1}{\int }}{\displaystyle \underset{-1}{\overset{1}{\int }}\left[\begin{array}{l}\frac{D_{11}}{a^4}{H}_{3232}{\phi }_3^2+\frac{D_{22}}{b^4}{H}_{3030}{\left(\frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}\right)}^2+\\ \frac{2D_{12}}{a^2{b}^2}{H}_{3032}{\phi }_3\frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}+\frac{4D_{66}}{a^2{b}^2}{H}_{3131}{\left(\frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }\right)}^2\end{array}\right]\mathrm{d}\eta }}\end{array}$$

(28)

where the integral coefficient $H_{mnrs}$ is defined as follows:

$$H_{mnrs}={\displaystyle \underset{-1}{\overset{1}{\int }}\frac{{\mathrm{d}}^n{\varphi }_m}{\mathrm{d}{\xi }^n}\frac{{\mathrm{d}}^s{\varphi }_r}{\mathrm{d}{\xi }^s}\mathrm{d}\xi }$$

(29)

Substituting Equation (28) into the Rayleigh quotient (13) generates the following governing differential equations about ${\phi }_1~{\phi }_3$:

$$\begin{array}{l}{\widehat{k}}_2{\displaystyle \frac{{\mathrm{d}}^2{\phi }_2}{\mathrm{d}{\eta }^2}}+{\widehat{r}}_2{\phi }_2+\widehat{m}{\displaystyle \frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }}+\widehat{l}{\displaystyle \frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }}=0\\ -\widehat{m}{\displaystyle \frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }}+{\widehat{k}}_1{\displaystyle \frac{{\mathrm{d}}^2{\phi }_1}{\mathrm{d}{\eta }^2}}+{\widehat{r}}_1{\phi }_1+\widehat{n}{\phi }_3=0\\ \widehat{l}{\displaystyle \frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }}-\widehat{n}{\phi }_1+{\widehat{k}}_D{\displaystyle \frac{{\mathrm{d}}^4{\phi }_3}{\mathrm{d}{\eta }^4}}+{\widehat{k}}_3{\displaystyle \frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}}+{\widehat{r}}_3{\phi }_3=0\end{array}$$

(30)

where

$$\begin{array}{l}{\widehat{k}}_2={\displaystyle \frac{H_{2020}}{H_{3030}}}{\displaystyle \frac{a^4{A}_{22}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}{\widehat{r}}_2=\left({\displaystyle \frac{H_{2020}}{T_{3030}}}{\omega }^2-{\displaystyle \frac{H_{2121}}{T_{3030}}}{\displaystyle \frac{a^2{A}_{66}}{D_{11}}}\right)\\ {\widehat{k}}_1={\displaystyle \frac{H_{1010}}{H_{3030}}}{\displaystyle \frac{a^4{A}_{66}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}{\widehat{r}}_1=\left({\displaystyle \frac{H_{1010}}{H_{3030}}}{\omega }^2-{\displaystyle \frac{H_{1111}}{H_{3030}}}{\displaystyle \frac{a^2{A}_{11}}{D_{11}}}\right)\\ {\widehat{k}}_3=2{\displaystyle \frac{H_{3032}}{T_{3030}}}{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}-4{\displaystyle \frac{H_{3131}}{H_{3030}}}{\displaystyle \frac{a^2{D}_{66}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}{\widehat{r}}_3=-{\omega }^2+{\displaystyle \frac{a^4{A}_{22}}{R^2{D}_{11}}}+{\displaystyle \frac{H_{3232}}{H_{3030}}}\hspace{1em},\hspace{1em}{\widehat{k}}_D={\displaystyle \frac{a^4{D}_{22}}{b^4{D}_{11}}}\\ \widehat{l}={\displaystyle \frac{H_{2030}}{H_{3030}}}{\displaystyle \frac{a^4{A}_{22}}{bR{D}_{11}}}\hspace{1em},\hspace{1em}\widehat{m}=\left({\displaystyle \frac{H_{1120}}{H_{3030}}}{\displaystyle \frac{a^3{A}_{12}}{b{D}_{11}}}-{\displaystyle \frac{H_{1021}}{H_{3030}}}{\displaystyle \frac{a^3{A}_{66}}{b{D}_{11}}}\right)\hspace{1em},\hspace{1em}\widehat{n}=-{\displaystyle \frac{H_{1130}}{H_{3030}}}{\displaystyle \frac{a^3{A}_{12}}{R{D}_{11}}}\end{array}$$

(31)

The obtained BCs for the edges of $\eta =\pm 1$ are as follows:

$$\begin{array}{l}{\left.\left({\displaystyle \frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }}+{\displaystyle \frac{T_{1021}}{T_{1010}}}{\displaystyle \frac{b}{a}}{\phi }_2\right)\delta {\phi }_1\right|}_{-1}^1=0\\ {\left.\left({\displaystyle \frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }}+{\displaystyle \frac{T_{1120}}{T_{2020}}}{\displaystyle \frac{b{A}_{12}}{a{A}_{22}}}{\phi }_1+{\displaystyle \frac{T_{2030}}{T_{2020}}}{\displaystyle \frac{b}{R}}{\phi }_3\right)\delta {\phi }_2\right|}_{-1}^1=0\\ {\left.\left[{\displaystyle \frac{{\mathrm{d}}^3{\phi }_3}{\mathrm{d}{\eta }^3}}+\left({\displaystyle \frac{T_{3032}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}-4{\displaystyle \frac{T_{3131}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{66}}{a^2{D}_{22}}}\right){\displaystyle \frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }}\right]\delta {\phi }_3\right|}_{-1}^1=0\\ {\left.\left({\displaystyle \frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}}+{\displaystyle \frac{T_{3032}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}{\phi }_3\right)\delta \left({\displaystyle \frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }}\right)\right|}_{-1}^1=0\end{array}$$

(32)

which are shown in Table 2 for the simply supported, clamped, and free BCs.

Table 2. The homogeneous boundary conditions of the edges $\mathit{\eta }=\pm 1$.

BCs	${\varphi }_1$	${\varphi }_2$	${\varphi }_3$	${\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}$	$F_{\eta }^t$	$F_{\eta }^n$	$F_{\eta }$	$M_{\eta }$
S	0		0			0		0
C	0	0	0	0
F					0	0	0	0
$\begin{array}{l}{F}_{\eta }^n={\displaystyle \frac{\mathrm{d}{\phi }_2}{\mathrm{d}\eta }}+{\displaystyle \frac{T_{1120}}{T_{2020}}}{\displaystyle \frac{b{A}_{12}}{a{A}_{22}}}{\phi }_1+{\displaystyle \frac{T_{2030}}{T_{2020}}}{\displaystyle \frac{b}{R}}{\phi }_3\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{F}_{\eta }^t={\displaystyle \frac{\mathrm{d}{\phi }_1}{\mathrm{d}\eta }}+{\displaystyle \frac{T_{1021}}{T_{1010}}}{\displaystyle \frac{b}{a}}{\phi }_2\hspace{0.33em}\\ F_{\eta }={\displaystyle \frac{{\mathrm{d}}^3{\phi }_3}{\mathrm{d}{\eta }^3}}+\left({\displaystyle \frac{T_{3032}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}-4{\displaystyle \frac{T_{3131}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{66}}{a^2{D}_{22}}}\right){\displaystyle \frac{\mathrm{d}{\phi }_3}{\mathrm{d}\eta }}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{M}_{\eta }={\displaystyle \frac{{\mathrm{d}}^2{\phi }_3}{\mathrm{d}{\eta }^2}}+{\displaystyle \frac{T_{3032}}{T_{3030}}}{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}{\phi }_3\end{array}$

From Equation (30), we obtain the following:

$$L_8{\displaystyle \frac{{\mathrm{d}}^8{\phi }_i}{\mathrm{d}{\eta }^8}}+L_6{\displaystyle \frac{{\mathrm{d}}^6{\phi }_i}{\mathrm{d}{\eta }^6}}+L_4{\displaystyle \frac{{\mathrm{d}}^4{\phi }_i}{\mathrm{d}{\eta }^4}}+L_2{\displaystyle \frac{{\mathrm{d}}^2{\phi }_i}{\mathrm{d}{\eta }^2}}+L_0{\phi }_i=0\left(i=1,2,3\right)$$

(33)

where the coefficients $L_8~L_0$ are as follows:

$$\begin{array}{l}{L}_8={\widehat{k}}_D{\widehat{k}}_1{\widehat{k}}_2\\ L_6={\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3+{\widehat{k}}_D{\widehat{k}}_1{\widehat{r}}_2+{\widehat{k}}_D{\widehat{k}}_2{\widehat{r}}_1+{\widehat{k}}_D{\widehat{m}}^2\\ L_4={\widehat{k}}_1{\widehat{k}}_2{\widehat{r}}_3+{\widehat{k}}_1{\widehat{k}}_3{\widehat{r}}_2+{\widehat{k}}_2{\widehat{k}}_3{\widehat{r}}_1+{\widehat{k}}_D{\widehat{r}}_1{\widehat{r}}_2-{\widehat{l}}^2{\widehat{k}}_1+{\widehat{m}}^2{\widehat{k}}_3\\ L_2={\widehat{k}}_1{\widehat{r}}_2{\widehat{r}}_3+{\widehat{k}}_2{\widehat{r}}_1{\widehat{r}}_3+{\widehat{k}}_3{\widehat{r}}_1{\widehat{r}}_2-{\widehat{l}}^2{\widehat{r}}_1+{\widehat{m}}^2{\widehat{r}}_3+n^2{\widehat{k}}_2+2\widehat{l}\widehat{m}\widehat{n}\\ L_0={\widehat{r}}_1{\widehat{r}}_2{\widehat{r}}_3+{\widehat{n}}^2{\widehat{r}}_2\end{array}$$

(34)

The characteristic equation of Equation (33) has the following form:

$$L_8{\mu }^8+L_6{\mu }^6+L_4{\mu }^4+L_2{\mu }^2+L_0=0$$

(35)

According to Equations (31) and (34), the coefficients $L_8~L_0$ are functions of frequency $\omega$. With a specific frequency $\omega$, the eight roots, ${\mu }_{\mathrm{1,2}}=\pm {\beta }_1, {\mu }_{\mathrm{3,4}}=\pm {\beta }_2, {\mu }_{\mathrm{5,6}}=\pm {\beta }_3, {\mu }_{\mathrm{7,8}}=\pm {\beta }_4$, can be obtained from the Ferrari formula, and the general solutions of the mode function ${\phi }_1~{\phi }_3$ can be expressed as follows:

$$\begin{array}{l}{\phi }_1={\displaystyle \sum _{k=1}^4\left({\widehat{E}}_k\cosh {\beta }_k\eta +{\widehat{F}}_k\sinh {\beta }_k\eta \right)}\\ {\phi }_2={\displaystyle \sum _{k=1}^4\left({\widehat{M}}_k\cosh {\beta }_k\eta +{\widehat{N}}_k\sinh {\beta }_k\eta \right)}\\ {\phi }_3={\displaystyle \sum _{k=1}^4\left({\widehat{A}}_k\cosh {\beta }_k\eta +{\widehat{B}}_k\sinh {\beta }_k\eta \right)}\end{array}$$

(36)

where ${\widehat{E}}_k, {\widehat{F}}_k, {\widehat{M}}_k, {\widehat{N}}_k$,${\widehat{A}}_k, {\widehat{B}}_k$ are unknown coefficients that are determined by boundary conditions in edges $\eta =\pm 1$. Introducing Equation (36) into Equation (30) yields the following:

$$\begin{array}{l}{\widehat{E}}_k={\widehat{P}}_k{A}_k ,\hspace{1em}{\widehat{F}}_k={\widehat{P}}_k{B}_k ,\hspace{1em}{\widehat{P}}_k=-{\displaystyle \frac{\widehat{n}\left({\widehat{k}}_2{\beta }_k^2+{\widehat{r}}_2\right)+\widehat{l}\widehat{m}{\beta }_k^2}{\left({\widehat{k}}_1{\beta }_k^2+{\widehat{r}}_1\right)\left({\widehat{k}}_2{\beta }_k^2+{\widehat{r}}_2\right)+{\widehat{m}}^2{\beta }_k^2}}\\ {\widehat{M}}_k={\widehat{Q}}_k{\widehat{B}}_k,\hspace{1em}{N}_k={\widehat{Q}}_k{\widehat{A}}_k,\hspace{1em}{\widehat{Q}}_k=-{\displaystyle \frac{{\beta }_k\widehat{l}\left({\widehat{k}}_1{\beta }_k^2+{\widehat{r}}_1\right)-\widehat{m}\widehat{n}{\beta }_k}{\left({\widehat{k}}_1{\beta }_k^2+{\widehat{r}}_1\right)\left({\widehat{k}}_2{\beta }_k^2+{\widehat{r}}_2\right)+{\widehat{m}}^2{\beta }_k^2}}\end{array}$$

(37)

In order to achieve the solutions of coefficients ${\widehat{A}}_k$ and ${\widehat{B}}_k$, substituting Equations (36) and (37) into the boundary conditions in edges $\eta =\pm 1$ as shown in Table 2 leads to eight homogeneous linear equations for the coefficients ${\widehat{A}}_k,{\widehat{B}}_k$, i.e.,

$${\mathit{\Lambda }}_{\eta }{\mathit{q}}_{\eta }=0$$

(38)

where ${\mathit{\Lambda }}_{\eta }$ is a matrix of size $8\times 8$ and

$${\mathit{q}}_{\eta }^T=\left[{\widehat{A}}_1,{\widehat{A}}_2,{\widehat{A}}_3,{\widehat{A}}_4,{\widehat{B}}_1,{\widehat{B}}_2,{\widehat{B}}_3,{\widehat{B}}_4\right]$$

(39)

For a nontrivial solution of ${\mathit{q}}_{\eta }$, a transcendental equation with respect to the frequency $\omega$ is generated by requiring the determinant of ${\mathit{\Lambda }}_{\eta }$ to be zero, i.e.,

$$\det \left({\mathit{\Lambda }}_{\eta }\right)=0$$

(40)

and with a specific frequency $\omega$, the nonzero ${\widehat{A}}_k$ and ${\widehat{B}}_k$ can also be obtained from Equation (38).

3. Basic Equations of Flutter

Consider an open and a closed circular cylindrical shell subjected to axial airflow with velocity $V$ as shown in Figure 2. The dimension, material, and coordinate system of the cylindrical shells defined in Section 2 are also used here. In the following, the governing differential equation for the cylindrical shells under aerodynamic load is derived from the general form of the Hamilton principle, and then the equation is solved using the SOV method.

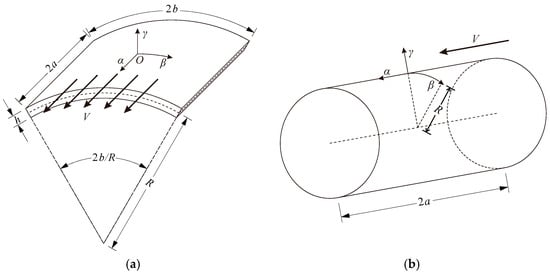
Figure 2. Cylindrical shell under aerodynamic pressure. (a) Open cylindrical shell. (b) Middle surface of a closed cylindrical shell.

The general form of the Hamilton principle is as follows:

$${\displaystyle \underset{t_1}{\overset{t_2}{\int }}\mathsf{\delta }\left(T-U\right)\mathrm{d}t}+{\displaystyle \underset{t_1}{\overset{t_2}{\int }}\mathsf{\delta }{W}_P\mathrm{d}t}=0$$

(41)

where $t_1$ and $t_2$ are two time points, the kinetic energy $T$ and the potential energy $U$ are given in Equations (2)–(5), and the integration of the external virtual work ${\mathsf{\delta }W}_P$ has the following form:

$${\displaystyle \underset{t_1}{\overset{t_2}{\int }}\mathsf{\delta }{W}_P\mathrm{d}t}={\displaystyle \underset{t_1}{\overset{t_2}{\int }}{\displaystyle \underset{-a}{\overset{a}{\int }}{\displaystyle \underset{-b}{\overset{b}{\int }}P\mathsf{\delta }w\mathrm{d}\alpha \mathrm{d}\beta \mathrm{d}t}}}$$

(42)

where the aerodynamic pressure P is determined by the first-order piston theory and has the following form [29,35]:

$$P=-{\displaystyle \frac{{\gamma }_{\infty }{p}_{\infty }{M}^2}{\sqrt{M^2-1}}}\left({\displaystyle \frac{\partial w}{\partial \alpha }}+{\displaystyle \frac{M^2-2}{M^2-1}}{\displaystyle \frac{1}{V}}{\displaystyle \frac{\partial w}{\partial t}}-{\displaystyle \frac{1}{2R\sqrt{M^2-1}}}w\right)$$

(43)

where $M=V/a_{\infty }, a_{\infty }, p_{\infty }$, and ${\gamma }_{\infty }$ are the Mach number, the sound speed, the freestream static pressure, and the adiabatic exponent of the airflow, respectively. For sufficiently high Mach numbers, a different version of Equation (43), which was derived by Krumhaar [25], is as follows:

$$P=-{\rho }_{\infty }{a}_{\infty }\left(V{\displaystyle \frac{\partial w}{\partial \alpha }}+{\displaystyle \frac{\partial w}{\partial t}}-{\displaystyle \frac{a_{\infty }}{2R}}w\right)$$

(44)

where ${\rho }_{\infty }$ is the density of the airflow.

By substituting Equations (2)–(5) and Equation (42) into Equation (41) and then performing partial integration of $\mathsf{\delta }U$ and $\mathsf{\delta }T$ with respect to time $t$ and spatial variable $\alpha ,\beta$, respectively, one can obtain the following governing differential equations for $u,v,w:$

$$\begin{array}{l}{\displaystyle \frac{A_{11}}{a^2}}{\displaystyle \frac{{\partial }^{2}u}{\partial {\xi }^2}}+\left({\displaystyle \frac{A_{12}}{ab}}{\displaystyle \frac{{\partial }^{2}v}{\partial \xi \partial \eta }}+{\displaystyle \frac{A_{12}}{aR}}{\displaystyle \frac{\partial w}{\partial \xi }}\right)+\left({\displaystyle \frac{A_{66}}{b^2}}{\displaystyle \frac{{\partial }^{2}u}{\partial {\eta }^2}}+{\displaystyle \frac{A_{66}}{ab}}{\displaystyle \frac{{\partial }^{2}v}{\partial \xi \partial \eta }}\right)=\rho h{\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}\\ \left({\displaystyle \frac{A_{22}}{b^2}}{\displaystyle \frac{{\partial }^{2}v}{\partial {\eta }^2}}+{\displaystyle \frac{A_{22}}{bR}}{\displaystyle \frac{\partial w}{\partial \eta }}\right)+{\displaystyle \frac{A_{21}}{ab}}{\displaystyle \frac{{\partial }^{2}u}{\partial \xi \partial \eta }}+\left({\displaystyle \frac{A_{66}}{ab}}{\displaystyle \frac{{\partial }^{2}u}{\partial \xi \partial \eta }}+{\displaystyle \frac{A_{66}}{a^2}}{\displaystyle \frac{{\partial }^{2}v}{\partial {\xi }^2}}\right)=\rho h{\displaystyle \frac{{\partial }^{2}v}{\partial t^2}}\\ \left[{\displaystyle \frac{D_{11}}{a^4}}{\displaystyle \frac{{\partial }^{4}w}{\partial {\xi }^4}}+{\displaystyle \frac{D_{22}}{b^4}}{\displaystyle \frac{{\partial }^{4}w}{\partial {\eta }^4}}+\left({\displaystyle \frac{2D_{12}}{a^2{b}^2}}+{\displaystyle \frac{4D_{66}}{a^2{b}^2}}\right){\displaystyle \frac{{\partial }^{4}w}{\partial {\xi }^2\partial {\eta }^2}}\right]+\left({\displaystyle \frac{A_{22}}{bR}}{\displaystyle \frac{\partial v}{\partial \eta }}+{\displaystyle \frac{A_{22}}{R^2}}w+{\displaystyle \frac{A_{21}}{aR}}{\displaystyle \frac{\partial u}{\partial \xi }}\right)\\ +{\displaystyle \frac{{\gamma }_{\infty }{p}_{\infty }{M}^2}{\sqrt{M^2-1}}}\left({\displaystyle \frac{1}{a}}{\displaystyle \frac{\partial w}{\partial \xi }}+{\displaystyle \frac{M^2-2}{M^2-1}}{\displaystyle \frac{1}{V}}{\displaystyle \frac{\partial w}{\partial t}}-{\displaystyle \frac{1}{2R\sqrt{M^2-1}}}w\right)=-\rho h{\displaystyle \frac{{\partial }^{2}w}{\partial t^2}}\end{array}$$

(45)

The obtained BCs for the edges of $\xi =\pm 1$ and $\eta =\pm 1$ are as follows:

$$\begin{array}{l}{\left.\left[{\displaystyle \frac{\partial u}{\partial \xi }}+{\displaystyle \frac{a{A}_{12}}{b{A}_{11}}}\left({\displaystyle \frac{\partial v}{\partial \eta }}+{\displaystyle \frac{b}{R}}w\right)\right]\delta u\right|}_{\xi =-1}^{\xi =1}=0\hspace{1em}\hspace{1em}\hspace{1em},\hspace{1em}{\left.\left({\displaystyle \frac{\partial v}{\partial \xi }}+{\displaystyle \frac{a}{b}}{\displaystyle \frac{\partial u}{\partial \eta }}\right)\delta v\right|}_{\xi =-1}^{\xi =1}=0\\ {\left.\left[{\displaystyle \frac{{\partial }^{3}w}{\partial {\xi }^3}}+{\displaystyle \frac{a^2\left(D_{12}+4D_{66}\right)}{b^2{D}_{11}}}{\displaystyle \frac{{\partial }^{3}w}{\partial \xi \partial {\eta }^2}}\right]\delta w\right|}_{\xi =-1}^{\xi =1}=0\hspace{1em},\hspace{1em}{\left.\left({\displaystyle \frac{{\partial }^{2}w}{\partial {\xi }^2}}+{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\eta }^2}}\right)\delta \left({\displaystyle \frac{\partial w}{\partial \xi }}\right)\right|}_{\xi -1}^{\xi =1}=0\end{array}$$

(46)

$$\begin{array}{l}{\left.\left({\displaystyle \frac{\partial v}{\partial \eta }}+{\displaystyle \frac{b}{R}}w+{\displaystyle \frac{b{A}_{12}}{a{A}_{22}}}{\displaystyle \frac{\partial u}{\partial \xi }}\right)\delta v\right|}_{\eta =-1}^{\eta =1}=0{\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em},\hspace{1em}\left({\displaystyle \frac{\partial u}{\partial \eta }}+{\displaystyle \frac{b}{a}}{\displaystyle \frac{\partial v}{\partial \xi }}\right)\delta u\right|}_{\eta =-1}^{\eta =1}=0\\ {\left.\left[{\displaystyle \frac{{\partial }^{3}w}{\partial {\eta }^3}}+{\displaystyle \frac{b^2\left(D_{12}+4D_{66}\right)}{a^2{D}_{22}}}{\displaystyle \frac{{\partial }^{3}w}{\partial {\xi }^2\partial \eta }}\right]\delta w\right|}_{\eta =-1}^{\eta =1}=0\hspace{1em},\hspace{1em}{\left.\left({\displaystyle \frac{{\partial }^{2}w}{\partial {\eta }^2}}+{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\xi }^2}}\right)\delta \left({\displaystyle \frac{\partial w}{\partial \eta }}\right)\right|}_{\eta =-1}^{\eta =1}=0\end{array}$$

(47)

The obtained BCs at four corners are as follows:

$${\left.\left({\left.{\displaystyle \frac{{\partial }^{2}w}{\partial \xi \partial \eta }}\delta w\right|}_{\xi =-1}^{\xi =1}\right)\right|}_{\eta =-1}^{\eta =1}=0$$

(48)

The simply supported BCs at the edges $\eta =\pm 1$ have the following forms:

$${\left(u\right)}_{\eta =\pm 1}=0\hspace{1em},\hspace{1em}{\left(F_{\eta }^t\right)}_{\eta =\pm 1}=0\hspace{1em},\hspace{1em}{\left(w\right)}_{\eta =\pm 1}=0\hspace{1em},\hspace{1em}{\left(M_{\eta }\right)}_{\eta =\pm 1}=0$$

(49)

where

$$F_{\eta }^t={\displaystyle \frac{\partial v}{\partial \eta }}+{\displaystyle \frac{b}{R}}w+{\displaystyle \frac{b{A}_{12}}{a{A}_{22}}}{\displaystyle \frac{\partial u}{\partial \xi }}\hspace{1em},\hspace{1em}{M}_{\eta }={\displaystyle \frac{{\partial }^{2}w}{\partial {\eta }^2}}+{\displaystyle \frac{b^2{D}_{12}}{a^2{D}_{22}}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\xi }^2}}$$

(50)

As far as the open cylindrical shell with simply supported BCs at the edges $\eta =\pm 1$ is concerned, the Levy type of solution for Equation (45) has the following forms:

$$\begin{array}{l}u\left(\xi ,\eta \right)={\varphi }_1\left(\xi \right)\sin \left(n\pi {\displaystyle \frac{1+\eta }{2}}\right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\\ v\left(\xi ,\eta \right)={\varphi }_2\left(\xi \right)\cos \left(n\pi {\displaystyle \frac{1+\eta }{2}}\right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\\ w\left(\xi ,\eta \right)={\varphi }_3\left(\xi \right)\sin \left(n\pi {\displaystyle \frac{1+\eta }{2}}\right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\end{array}$$

(51)

where ${\Omega }_{\mathrm{d}}$ is a complex eigenvalue and $n=1, 2, 3,\dots$. It is obvious that Equation (51) satisfies the simply supported boundary conditions in edges $\eta =\pm 1$ and the corner boundary condition naturally. As for the closed cylindrical shell, the BCs of edges $\eta =\pm 1$ are replaced by periodical continuity conditions, and the solution has the following form:

$$\begin{array}{l}u\left(\xi ,\eta \right)={\varphi }_1\left(\xi \right)\sin \left(n\pi \eta \right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\\ v\left(\xi ,\eta \right)={\varphi }_2\left(\xi \right)\cos \left(n\pi \eta \right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\\ w\left(\xi ,\eta \right)={\varphi }_3\left(\xi \right)\sin \left(n\pi \eta \right){\mathrm{e}}^{{\Omega }_{\mathrm{d}}t}\end{array}$$

(52)

According to Equation (46), the homogeneous BCs of edges $\xi =\pm 1$ for the open and closed cylindrical shells are given in Table 3.

Table 3. The homogeneous boundary conditions of axial edges $\mathit{\xi }=\pm 1$.

BCs	$u$	$v$	$w$	${\displaystyle \frac{\partial w}{\partial \xi }}$	$F_{\xi }^n$	$F_{\xi }^t$	$F_{\xi }$	$M_{\xi }$
S		0	0		0			0
C	0	0	0	0
F					0	0	0	0
$\begin{array}{l}{F}_{\xi }^n={\displaystyle \frac{\partial u}{\partial \xi }}+{\displaystyle \frac{a{A}_{12}}{b{A}_{11}}}\left({\displaystyle \frac{\partial v}{\partial \eta }}+{\displaystyle \frac{b}{R}}w\right)\hspace{1em}\hspace{1em}\hspace{1em},\hspace{1em}{F}_{\xi }^t={\displaystyle \frac{\partial v}{\partial \xi }}+{\displaystyle \frac{a}{b}}{\displaystyle \frac{\partial u}{\partial \eta }}\\ F_{\xi }={\displaystyle \frac{{\partial }^{3}w}{\partial {\xi }^3}}+{\displaystyle \frac{a^2\left(D_{12}+4D_{66}\right)}{b^2{D}_{11}}}{\displaystyle \frac{{\partial }^{3}w}{\partial \xi \partial {\eta }^2}}\hspace{1em},\hspace{1em}{M}_{\xi }={\displaystyle \frac{{\partial }^{2}w}{\partial {\xi }^2}}+{\displaystyle \frac{a^2{D}_{12}}{b^2{D}_{11}}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\eta }^2}}\end{array}$

Substituting Equation (51) into Equation (45) yields the ordinary differential governing equations for ${\varphi }_1,{\varphi }_2$, and ${\varphi }_3$ as follows:

$$\begin{array}{l}{\tilde{k}}_1{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_1}{\mathrm{d}{\xi }^2}}+{\tilde{r}}_1{\varphi }_1+\tilde{m}{\displaystyle \frac{\mathrm{d}{\varphi }_2}{\mathrm{d}\xi }}+\tilde{l}{\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}=0\\ -\tilde{m}{\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}+{\tilde{k}}_2{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_2}{\mathrm{d}{\xi }^2}}+{\tilde{r}}_2{\varphi }_2+\tilde{n}{\varphi }_3=0\\ \tilde{l}{\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\xi }}-\tilde{n}{\varphi }_2+{\displaystyle \frac{{\mathrm{d}}^4{\varphi }_3}{\mathrm{d}{\xi }^4}}+{\tilde{k}}_3{\displaystyle \frac{{\mathrm{d}}^2{\varphi }_3}{\mathrm{d}{\xi }^2}}+p_s{\displaystyle \frac{\mathrm{d}{\varphi }_3}{\mathrm{d}\xi }}+{\tilde{r}}_3{\varphi }_3=0\end{array}$$

(53)

where the dimensionless parameters are defined as follows:

$$\begin{array}{l}{\tilde{k}}_1={\displaystyle \frac{a^2{A}_{11}}{D_{11}}}\hspace{1em},\hspace{1em}{\tilde{r}}_1=-{\Omega }^2-{\chi }^2{\displaystyle \frac{a^4{A}_{66}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}\chi ={\displaystyle \frac{n\pi }{2}}\\ {\tilde{k}}_2={\displaystyle \frac{a^2{A}_{66}}{D_{11}}}\hspace{1em},\hspace{1em}{\tilde{r}}_2=-{\Omega }^2-{\chi }^2{\displaystyle \frac{a^4{A}_{22}}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}\Omega =a^2\sqrt{{\displaystyle \frac{\rho h}{D_{11}}}}{\Omega }_{ \mathrm{d}}\\ {\tilde{k}}_3=-{\chi }^2{\displaystyle \frac{a^2\left(2D_{12}+4D_{66}\right)}{b^2{D}_{11}}}\hspace{1em},\hspace{1em}{\tilde{r}}_3={\Omega }^2+p_d\Omega -p_c+{\chi }^4{\displaystyle \frac{a^4{D}_{22}}{b^4{D}_{11}}}+{\displaystyle \frac{a^4{A}_{22}}{R^2{D}_{11}}}\\ \tilde{l}={\displaystyle \frac{a^3{A}_{12}}{R{D}_{11}}}\hspace{1em},\hspace{1em}\tilde{m}=-\chi {\displaystyle \frac{a^3\left(A_{12}+A_{66}\right)}{b{D}_{11}}}\hspace{1em},\hspace{1em}\tilde{n}=\chi {\displaystyle \frac{a^4{A}_{22}}{bR{D}_{11}}}\end{array}$$

(54)

and the dimensionless aerodynamic parameters are as follows:

$$p_s={\displaystyle \frac{{\gamma }_{\infty }{p}_{\infty }{M}^2}{\sqrt{M^2-1}}}{\displaystyle \frac{a^3}{D_{11}}} , p_d={\displaystyle \frac{{\gamma }_{\infty }{p}_{\infty }{M}^2}{V\sqrt{M^2-1}}}{\displaystyle \frac{M^2-2}{M^2-1}}{\displaystyle \frac{a^2}{\sqrt{\rho h{D}_{11}}}} , p_c={\displaystyle \frac{{\gamma }_{\infty }{p}_{\infty }{M}^2}{M^2-1}}{\displaystyle \frac{a^4}{2R{D}_{11}}}$$

(55)

where $p_s, p_d$, and $p_c$ denote the aerodynamic stiffness, aerodynamic damping, and curvature correction, respectively. When the aerodynamic pressure is calculated by Equation (44), the aerodynamic parameters in Equation (55) can be simplified as follows:

$$p_s={\displaystyle \frac{{\rho }_{\infty }{a}_{\infty }{a}^3}{D_{11}}}V\hspace{1em},\hspace{1em}{p}_d={\displaystyle \frac{{\rho }_{\infty }{a}_{\infty }{a}^2}{\sqrt{\rho h{D}_{11}}}}\hspace{1em},\hspace{1em}{p}_c={\displaystyle \frac{a^4{a}_{\infty }^2{\rho }_{\infty }}{2R{D}_{11}}}$$

(56)

For closed circular cylindrical shells, one just needs to replace $\chi =n\pi /2$ with $\chi =n\pi$ in Equation (54).

Eliminating any two functions of ${\varphi }_1$, ${\varphi }_2$, and ${\varphi }_3$ from Equation (53) yields the following:

$${\displaystyle \sum _{k=1}^8{G}_k\frac{{\mathrm{d}}^k{\varphi }_i}{\mathrm{d}{\xi }^k}}+G_0{\varphi }_i=0\left(i=1,2,3\right)$$

(57)

where the coefficients $G_0~G_8$ are as follows:

$$\begin{array}{l}{G}_8={\tilde{k}}_1{\tilde{k}}_2\hspace{0.33em}\hspace{0.33em}\hspace{1em},\hspace{1em}{G}_7=0\\ G_6={\tilde{k}}_1{\tilde{k}}_2{\tilde{k}}_3+{\tilde{k}}_1{r}_2+{\tilde{k}}_2{\tilde{r}}_1+{\tilde{m}}^2\\ G_5=p_s{\tilde{k}}_1{\tilde{k}}_2\\ G_4={\tilde{k}}_1{\tilde{k}}_2{\tilde{r}}_3+{\tilde{k}}_1{\tilde{k}}_3{\tilde{r}}_2+{\tilde{k}}_2{\tilde{k}}_3{\tilde{r}}_1-{\tilde{k}}_2{\tilde{l}}^2+{\tilde{k}}_3{\tilde{m}}^2+{\tilde{r}}_1{\tilde{r}}_2\\ G_3=p_s\left({\tilde{k}}_1{\tilde{r}}_2+{\tilde{k}}_2{\tilde{r}}_1+{\tilde{m}}^2\right)\\ G_2={\tilde{k}}_1{\tilde{r}}_2{\tilde{r}}_3+{\tilde{k}}_2{\tilde{r}}_1{\tilde{r}}_3+{\tilde{k}}_3{\tilde{r}}_1{\tilde{r}}_2-{\tilde{l}}^2{\tilde{r}}_2+{\tilde{m}}^2{\tilde{r}}_3+{\tilde{k}}_1{\tilde{n}}^2+2\tilde{l}\tilde{m}\tilde{n}\\ G_1=p_s{\tilde{r}}_1{\tilde{r}}_2\hspace{1em},\hspace{1em}{G}_0={\tilde{r}}_1{\tilde{r}}_2{\tilde{r}}_3+{\tilde{n}}^2{\tilde{r}}_1\end{array}$$

(58)

The characteristic equation of Equation (57) can be expressed as follows:

$${\displaystyle \sum _{k=1}^8{G}_k{\lambda }^k}+G_0=0$$

(59)

Since the coefficients $G_0~G_8$ are functions of $\Omega$, the spatial eigenvalue $\lambda$ can be obtained by numerical methods for a specific $\Omega$. With the eight eigenvalues, ${\lambda }_1~{\lambda }_8$, the general solution of Equation (57) can be written as follows:

$${\varphi }_1\left(\xi \right)={\displaystyle \sum _{k=1}^8{\tilde{A}}_k{\mathrm{e}}^{{\lambda }_k\xi }}\hspace{1em},\hspace{1em}{\varphi }_2\left(\xi \right)={\displaystyle \sum _{k=1}^8{\tilde{B}}_k{\mathrm{e}}^{{\lambda }_k\xi }}\hspace{1em},\hspace{1em}{\varphi }_3\left(\xi \right)={\displaystyle \sum _{k=1}^8{\tilde{C}}_k{\mathrm{e}}^{{\lambda }_k\xi }}$$

(60)

Substituting Equation (60) into Equation (53) yields the relations among ${\tilde{A}}_k,{\tilde{B}}_k,{\tilde{C}}_k$ as follows:

$$\begin{array}{l}{\tilde{A}}_k={\tilde{P}}_k{\tilde{C}}_k\hspace{1em},\hspace{1em}{\tilde{P}}_k=-{\displaystyle \frac{\tilde{l}{\lambda }_k\left({\tilde{k}}_2{\lambda }_k^2+{\tilde{r}}_2\right)-\tilde{m}\tilde{n}{\lambda }_k}{\left({\tilde{k}}_1{\lambda }_k^2+{\tilde{r}}_1\right)\left({\tilde{k}}_2{\lambda }_k^2+{\tilde{r}}_2\right)+{\tilde{m}}^2{\lambda }_k^2}}\\ {\tilde{B}}_k={\tilde{Q}}_k{\tilde{C}}_k\hspace{1em},\hspace{1em}{\tilde{Q}}_k=-{\displaystyle \frac{\tilde{n}\left({\tilde{k}}_1{\lambda }_k^2+{\tilde{r}}_1\right)+\tilde{l}\tilde{m}{\lambda }_k^2}{\left({\tilde{k}}_1{\lambda }_k^2+{\tilde{r}}_1\right)\left({\tilde{k}}_2{\lambda }_k^2+r_2\right)+{\tilde{m}}^2{\lambda }_k^2}}\end{array}$$

(61)

where ${\tilde{C}}_1~{\tilde{C}}_8$ can be determined by the BCs of edges $\xi =\pm 1$. By substituting Equation (60) into the BCs shown in Table 3, one can obtain eight homogeneous linear equations for ${\tilde{C}}_1~{\tilde{C}}_8$, as follows:

$$\mathit{\Lambda }\mathit{q}=0$$

(62)

where $\mathit{\Lambda }$ is a matrix with the size of $8\times 8$ and

$$q={\left[{\tilde{C}}_1,{\tilde{C}}_2,\cdots {\tilde{C}}_8\right]}^T$$

(63)

The existence of nontrivial solutions for ${\tilde{C}}_1~{\tilde{C}}_8$ requires the following:

$$\det \left(\mathit{\Lambda }\right)=0$$

(64)

which leads to a transcendental equation with respect to $\Omega$. For an obtained $\Omega$, the nonzero ${\tilde{C}}_k$ can be obtained from Equation (62).

4. Solution Procedures

For free vibration, the open cylindrical shell with arbitrary combinations of homogeneous BCs is considered, and the transcendental equations about the natural frequency $\omega$ in the $\xi$ direction and the $\eta$ direction are Equation (27) and Equation (40), respectively.

As for the flutter, the open cylindrical shell with simply supported circumferential edges and the closed cylindrical shell are taken into account, and the transcendental equation about the flutter eigenvalue $\Omega$ is Equation (64).

This section aims to find $\omega$ satisfying both Equation (27) and Equation (40) and $\Omega$ satisfying Equation (64).

4.1. Solving Method for Free Vibration

Using the iSOV method [45], the procedure for solving the natural frequency $\omega$ is presented as follows:

• Assume that ${\phi }_1={\phi }_{10},{\phi }_2={\phi }_{20},{\phi }_3={\phi }_{30}$, wherein ${\phi }_{10},{\phi }_{20},{\phi }_{30}$ are given initial values.
• Substituting ${\phi }_1~{\phi }_3$ into $S_{mnsr}$ or Equation (15), the root ${\omega }_{\xi }$ of Equation (27) can be obtained by the Newton–Raphson method or the bisection method. With a specific frequency ${\omega }_{\xi }$, solving ${\mathit{\Lambda }}_{\mathsf{\xi }}{\mathit{q}}_{\xi }=0$ or Equation (25) yields the mode functions ${\varphi }_1~{\varphi }_3$.
• Since ${\varphi }_1~{\varphi }_3$ are solved, the root ${\omega }_{\eta }$ of equation $\det \left({\mathit{\Lambda }}_{\eta }\right)=0$ or Equation (40) can be achieved by the Newton–Raphson method or the bisection method. With a specific frequency ${\omega }_{\eta }$, solving ${\mathit{\Lambda }}_{\eta }{\mathit{q}}_{\eta }=0$ or Equation (38) yields the mode functions ${\phi }_1~{\phi }_3$.
• If $\left|{\omega }_{\xi }-{\omega }_{\eta }\right|/\left|{\omega }_{\xi }\right|<\epsilon$, wherein $\epsilon =1\times {10}^{-8}$ is satisfied, then the iteration stops. Otherwise, update ${\phi }_1~{\phi }_3$ using the results obtained in Step (3) and go back to Step (2).

Generally, the exact mode function for simply supported BCs at the edges $\eta =\pm 1$ can be chosen as the initial mode functions ${\phi }_{10},{\phi }_{20},{\phi }_{30}$, i.e.,

$${\phi }_{10}=\sin \left({\displaystyle \frac{n\mathsf{\pi }}{2}}\left(\eta +1\right)\right) , {\phi }_{20}=\sin \left({\displaystyle \frac{n\mathsf{\pi }}{2}}\left(\eta +1\right)\right) , {\phi }_{30}=\cos \left({\displaystyle \frac{n\mathsf{\pi }}{2}}\left(\eta +1\right)\right) , \left(n=1,2,3,\cdots \right)$$

(65)

4.2. Solving Method for Flutter

Assuming $\Omega =\upsilon +\mathrm{i}\omega$, wherein the real number $\upsilon$ denotes the variation in amplitude and the real number $\omega$ represents the frequency, substituting $\Omega =\upsilon +\mathrm{i}\omega$ into Equation (64) yields the following equation:

$$\det \left(\mathit{\Lambda }\right)=f_1\left(\upsilon ,\omega \right)+{\mathit{if}}_2\left(\upsilon ,\omega \right)=0$$

(66)

Equation (66) is equivalent to the following:

$$\begin{array}{c}{f}_1\left(\upsilon ,\omega \right)=0\\ f_2\left(\upsilon ,\omega \right)=0\end{array}$$

(67)

The expressions of $f_1\left(\upsilon ,\omega \right)$ and $f_2\left(\upsilon ,\omega \right)$ are implicit. But if $\upsilon$ and $\omega$ are given, one can attain the values of $f_1\left(\upsilon ,\omega \right)$ and $f_2\left(\upsilon ,\omega \right)$ so that the Newton–Raphson method, in which local derivatives are approximated by numerical differences, can be used to solve Equation (67). If $‖{\Omega }_{k+1}-{\Omega }_k‖/‖{\Omega }_k‖<\epsilon$, where $\epsilon =1\times {10}^{-8}$, wherein k is the iteration times, then the iteration stops.

5. Numerical Results

The numerical results of the free vibration and flutter of circular cylindrical shells are presented and discussed in this section. The subscript $mn$ is used to distinguish different $\omega$ and $\Omega$, i.e., ${\omega }_{mn}$ and ${\Omega }_{mn}$, where $m$ and $n$ denote the “mth” mode in the $\alpha$ direction and the “nth” mode in the $\beta$ direction, respectively. In addition, $\widehat{n}$ denotes the order of a frequency from lower to higher. The cylindrical shells are stated by specifying the support type for the edges, starting with edge $\xi =-1$ and proceeding in the counterclockwise direction by looking down to the upper surface of the shell from above; refer to Figure 1. For instance, CSFS defines an open cylindrical shell with the clamped (C) edge $\xi =-1$, the simply supported (S) edge $\eta =-1$, the free (F) edge $\xi =1$, and the simply supported (S) edge $\eta =1$. In addition, SF represents a closed cylindrical shell with a simply supported edge $\xi =-1$ and a free edge $\xi =1$.

Unless otherwise specified, the parameters of the shell and airflow are defined as ${\rho }_{\infty }=1.205 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$ and $a_{\infty }=340 \mathrm{m}/\mathrm{s}$, respectively, and the aerodynamic pressure is calculated by Equation (44): $2a/R=1, 2b/R=\pi /3, h/R=0.005, R=1 \mathrm{m}$. The physical parameters of the orthotropic material (unidirectional carbon-fiber composite) are listed in Table 4.

Table 4. The material property of unidirectional carbon-fiber composite.

Material	$\rho$ $\left(\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\right)$	$E_1$ $\left(\mathrm{G}\mathrm{P}\mathrm{a}\right)$	$E_2$ $\left(\mathrm{G}\mathrm{P}\mathrm{a}\right)$	$G_{12}$ $\left(\mathrm{G}\mathrm{P}\mathrm{a}\right)$	$v_{12}$
AS4/3501-6	1580	126	11	6.6	0.28

5.1. Numerical Results for Free Vibration

Considering the CCCC and CFCF circular cylindrical shells, Table 5 compares the present frequencies with the FEM’s results obtained by Nastran with a mesh of $200\times 200$, and the shell elements are used to model the cylindrical shell structure. The present results agree well with those of the FEM, with a relative difference of less than $2\%$, but the present frequencies are slightly larger. The principal reason for this phenomenon is the present assumption that the mode functions have a separation-of-variable form. Moreover, the different shell theories used in the present work and the FEM also contribute to the difference. In addition, the present transverse deflection modes are validated by comparing them with those of the FEM, as shown in Figure 3 and Figure 4.

Table 5. The natural frequencies of the CCCC and CFCF laminated cylindrical shells (Hz).

$\widehat{n}$	CCCC				CFCF
	Present		FEM		Present		FEM
	$m=1$	$m=2$	$m=1$	$m=2$	$m=1$	$m=2$	$m=1$	$m=2$
1	181.34	290.18	180.43	289.24	77.673	161.08	77.579	160.28
2	198.59	298.48	197.32	297.25	77.866	162.08	77.676	161.34
3	290.74	377.15	289.46	375.51	160.31	265.56	159.40	263.89
4	305.45	423.37	304.24	421.22	167.35	285.23	166.81	284.14
5	434.05	541.87	432.23	539.79	218.31	329.09	217.32	326.04
6	544.79	580.77	543.83	579.24	292.23	356.97	291.91	355.83
7	713.72	752.33	712.74	749.94	308.98	460.77	307.77	459.53
8	840.98	861.92	840.22	860.98	422.54	535.09	421.40	530.77
9	967.74	980.54	967.30	980.32	557.46	589.80	556.22	588.47
10	1081.0	1107.1	1079.9	1105.1	712.56	741.14	711.20	739.65

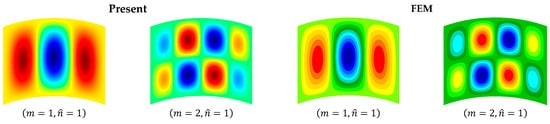
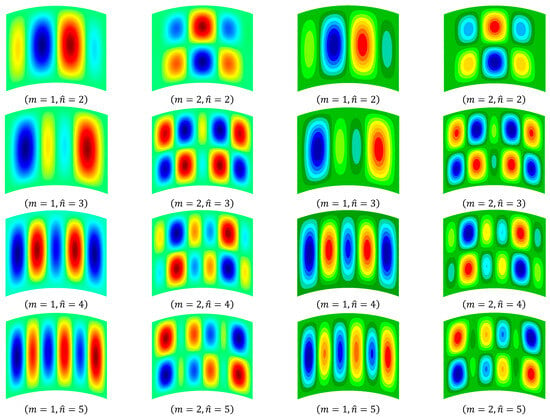
Figure 3. The transverse deflection modes of the CCCC laminated cylindrical shell.

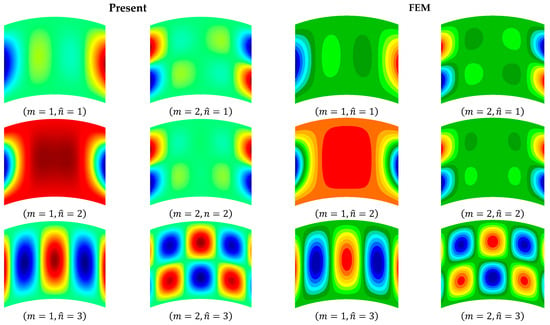
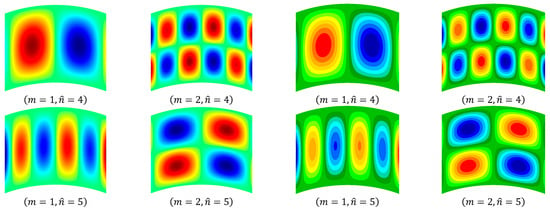
Figure 4. The transverse deflection modes of the CFCF laminated cylindrical shell.

Preparing for the flutter analysis of cylindrical shells, the dimensionless natural frequencies $\omega ={\omega }_{\mathrm{d}}{a}^2\sqrt{\rho h/D_{11}}$ of the SSSS, SCSC, and CSFS cylindrical shells are presented in Table 6 and Table 7. Note that the exact frequencies of the SSSS cylindrical shell shown in Table 6 are obtained by the solution procedure presented in [2]. It follows that the present results for the SSSS shell are also exact, and the FEM’s frequencies are a little smaller.

Table 6. The natural frequencies $\omega ={\omega }_{\mathrm{d}}{a}^2\sqrt{\rho h/D_{11}}$ of the SSSS laminated cylindrical shell.

$n$	Exact		Present		FEM
	$m=1$	$m=2$	$m=1$	$m=2$	$m=1$	$m=2$
1	40.409	73.529	40.409	73.529	40.408	73.528
2	20.704	43.388	20.704	43.388	20.665	43.366
3	17.271	32.576	17.271	32.576	17.165	32.512
4	23.107	32.339	23.107	32.339	22.967	32.228
5	34.011	39.716	34.011	39.716	33.864	39.577
6	48.192	52.218	48.192	52.218	48.044	52.066
7	65.191	68.409	65.191	68.409	65.042	68.251
8	84.884	87.682	84.884	87.682	84.734	87.520
9	107.23	109.80	107.23	109.80	107.08	109.63

Table 7. The natural frequencies $\omega ={\omega }_{\mathrm{d}}{a}^2\sqrt{\rho h/D_{11}}$ of the CSCS and CSFS laminated cylindrical shells.

$n$	CSCS				CSFS
	Present		FEM		Present		FEM
	$m=1$	$m=2$	$m=1$	$m=2$	$m=1$	$m=2$	$m=1$	$m=2$
1	42.166	75.231	42.165	75.228	20.410	57.214	20.404	57.213
2	23.888	46.231	23.856	46.209	10.672	30.426	10.600	30.395
3	20.265	36.093	20.176	36.033	13.035	23.342	12.900	23.255
4	24.933	35.720	24.804	35.616	21.433	26.558	21.288	26.427
5	35.049	42.436	34.907	42.302	33.098	36.182	32.952	36.036
6	48.838	54.296	48.691	54.147	47.517	49.814	47.371	49.662
7	65.636	70.020	65.487	69.862	64.600	66.550	64.453	66.396
8	85.217	88.973	85.067	88.809	84.326	86.100	84.179	85.943
9	107.50	110.86	107.35	110.69	106.69	108.36	106.54	108.20

In addition, the transverse deflection modes of the SCSC and CSFS cylindrical shells are plotted in Figure 5 and Figure 6, respectively. The present results are in good agreement with those of the FEM.

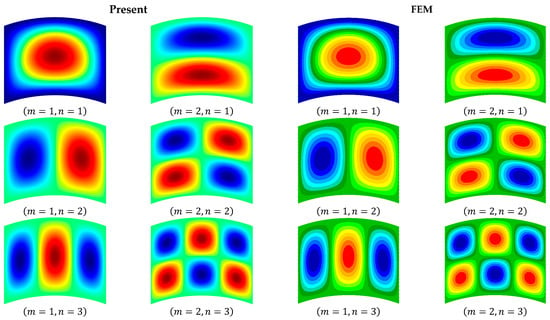
Figure 5. The transverse deflection modes of the CSCS laminated cylindrical shell.

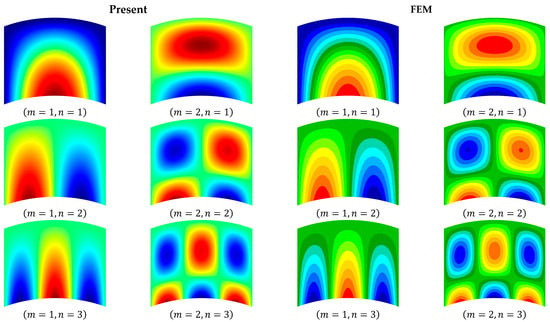
Figure 6. The transverse deflection modes of the CSFS laminated cylindrical shell.

In order to further validate the present work, an isotropic shell is also considered, and the material parameters and the size of the shell are $2b/R=\mathsf{\pi },h/R=0.01,E_1=E_2=E,v_{12}=v_{21}=v=0.3,G_{12}=G=E/2\left(1+v\right)$. The present results for the SCSC and SFSF cylindrical shells are compared with the exact results [2] and those of the FEM in Table 8 and Figure 7, respectively. In general, the present results are consistent with the exact results. In fact, when the open cylindrical shell has simply supported opposite edges, the iSOV method used in this work yields the Levy type of exact solutions [47]. But for the SFSF shell, the difference between the present results and the exact ones is more obvious, which is caused by the difference between the free BCs used in this work and those in [2].

Table 8. The natural frequencies $\tilde{\omega }$ of the SCSC and SFSF isotropic cylindrical shells ($\tilde{\omega }={\omega }_d{R}^2\sqrt{\rho h/D_{11}}, m=1$).

${\displaystyle \frac{2a}{R}}$	$\widehat{n}$	SCSC			SFSF
		Exact (Ref. [2])	FEM	Present	Exact (Ref. [2])	Present
5	1	21.107	20.416	21.111	5.4792	5.4862
	2	23.261	22.611	23.261	5.5826	5.5898
	3	35.213	34.638	35.213	14.974	14.970
	4	39.540	38.703	39.540	17.935	17.929
10	1	12.975	12.352	12.975	2.4371	2.4405
	2	16.547	15.791	16.547	2.7917	2.7953
	3	28.890	28.054	28.890	7.0714	7.0684
	4	33.323	32.843	33.323	9.8732	9.8696

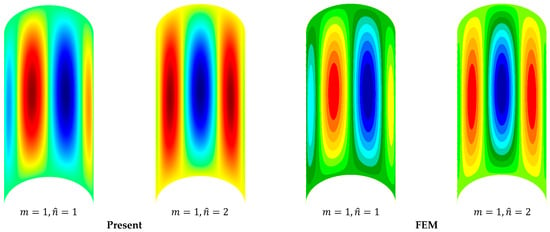
Figure 7. The transverse deflection modes of the SCSC isotropic cylindrical shell ($2a/R=5$).

5.2. Numerical Results for Flutter

For flat panels, flutter is generally caused by lower frequencies coalescing. However, due to the existence of curvature, higher frequency coalescing is liable to lower flutter speed for cylindrical shells. In addition, the modes with more waves for a flat panel usually correspond to higher frequencies, but this rule fails for cylindrical shells. For instance, Table 6 presents the natural frequencies of the SSSS cylindrical shell, from which one can see that the natural frequencies first decrease with the number of the circumferential waves $n$ and then increase.

(1)

The case of the SSSS open laminated cylindrical shell

Considering the SSSS laminated cylindrical shell under the aerodynamic load, the relationships between the complex eigenvalue $\Omega$ and the aerodynamic stiffness $p_s$ are shown in Figure 8 and Figure 9, wherein “Im” and “Re” represent the imaginary and the real part, respectively. ‘Re($\Omega$)’ denotes the variation in amplitude, and ‘Im($\Omega$)’ represents the frequency. Figure 8 indicates that Im(${\Omega }_{1n}$) and Im(${\Omega }_{2n}$) tend to coalesce with the increase in $p_s$, caused by the axial airflow, and for different $n$, Im(${\Omega }_{16}$) and Im(${\Omega }_{26}$) coalesce earlier than other eigenvalues.

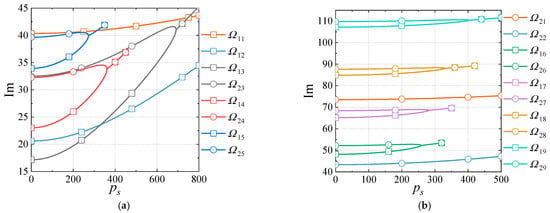
Figure 8. Relationships between ${\mathit{\Omega }}_{\mathit{m}\mathit{n}}$ and ${\mathit{p}}_{\mathit{s}}$ for the SSSS laminated cylindrical shell ($m=1, 2$ and $n=1~9$). (a) The imaginary parts of $\Omega$. (b) The imaginary parts of $\Omega$.

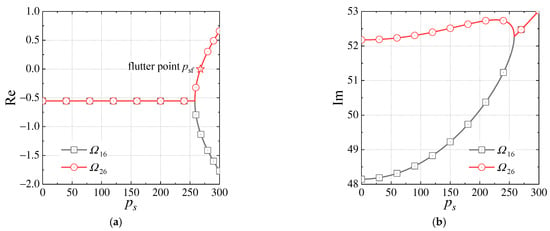
Figure 9. Relationships between ${\mathit{\Omega }}_{16}, {\mathit{\Omega }}_{26}$, and ${\mathit{p}}_{\mathit{s}}$ for the SSSS laminated cylindrical shell. (a) The real parts of ${\Omega }_{16}$ and ${\Omega }_{26}$, where ‘☆’ denotes the flutter point. (b) The imaginary parts of ${\Omega }_{16}$ and ${\Omega }_{26}$.

In order to present more detail about the variations in $\Omega$, the variations in ${\Omega }_{16}$ and ${\Omega }_{26}$ are plotted again in Figure 9. It can be seen that $\mathrm{I}\mathrm{m}\left({\Omega }_{16}\right)$ increases with $p_s$, but $\mathrm{I}\mathrm{m}\left({\Omega }_{26}\right)$ first increases with $p_s$ and then decreases, gradually approaching $\mathrm{I}\mathrm{m}\left({\Omega }_{16}\right)$; when $p_s$ is small, $\mathrm{R}\mathrm{e}\left({\Omega }_{16}\right)$ and $\mathrm{R}\mathrm{e}\left({\Omega }_{26}\right)$ are constants less than zero, implying that vibration is decaying before flutter. When $\mathrm{I}\mathrm{m}\left({\Omega }_{16}\right)$ and $\mathrm{I}\mathrm{m}\left({\Omega }_{26}\right)$ coincide, $\mathrm{R}\mathrm{e}\left({\Omega }_{16}\right)$ and $\mathrm{R}\mathrm{e}\left({\Omega }_{26}\right)$ change dramatically in reverse directions. If $\mathrm{R}\mathrm{e}\left(\Omega \right)$ is greater than 0, flutter occurs, and $p_s$ corresponding to $\mathrm{R}\mathrm{e}\left(\Omega \right)=0$ is the flutter point, denoted as $p_{\mathrm{s}\mathrm{f}}\approx 267.6$.

Figure 10 shows the transverse deflection flutter mode ${\varphi }_3\left(\xi \right)$ corresponding to $\Omega =52.4312\mathrm{i}$ in $p_s=267.6$ and $\Omega =0.6605+53.0237\mathrm{i}$ in $p_s=300$. The peaks of ${\varphi }_3$ are postponed by the airflow. There are numerous sets of ${\tilde{C}}_1~{\tilde{C}}_8$, but ${\tilde{C}}_1~{\tilde{C}}_8$ is normalized by dividing ${\tilde{C}}_1~{\tilde{C}}_8$ by ${\varphi }_3\left(0\right)$ to make ${\varphi }_3\left(0\right)=1$ in Figure 10.

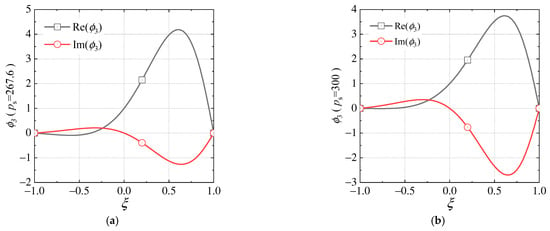
Figure 10. Flutter modes for the SSSS laminated cylindrical shell. (a) ${\varphi }_3\left(\xi \right)$ corresponding to $\Omega =52.4312\mathrm{i}$ and $p_s=267.6$. (b) ${\varphi }_3\left(\xi \right)$ corresponding to $\Omega =0.6605+53.0237\mathrm{i}$ and $p_s=300$.

Moreover, also for the SSSS cylindrical shell, the relationships between the dimensionless circumferential length $2b/R$ and the flutter points $p_{\mathrm{s}\mathrm{f}}$ caused by the different coalescing of ${\Omega }_{1n}$ and ${\Omega }_{2n}$ ($n=3~17$) are depicted in Figure 11. For a specific $n$, $p_{\mathrm{s}\mathrm{f}}$ first decreases with $2b/R$ and then increases, inducing the phenomenon that the $n$ corresponding to the minimum flutter point (also called the critical flutter point) increases with $2b/R$. Only retaining the minimum flutter points, the relationships between $p_{\mathrm{s}\mathrm{f}}$ and $2b/R$ are replotted in Figure 12. Notably, the minimum flutter points have an infimum $p_{\mathrm{s}\mathrm{d}}=265.69$, independent of $2b/R$.

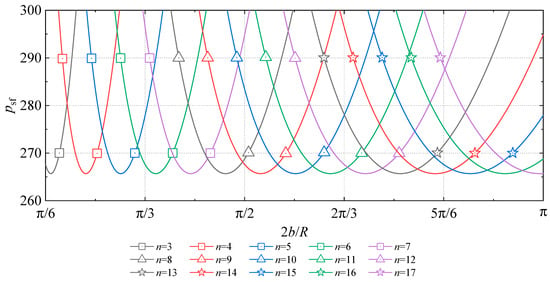
Figure 11. The flutter points $p_{\mathrm{s}\mathrm{f}}$ caused by ${\Omega }_{1n}$ and ${\Omega }_{2n}$ ($2a/R=1,h/R=0.005$ and n = 3~17).

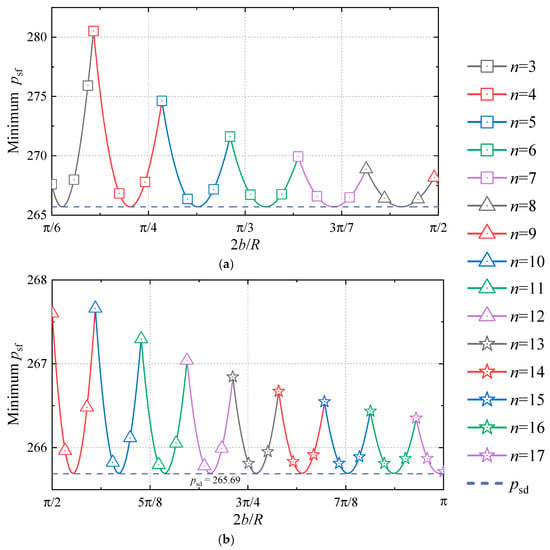
Figure 12. The minimum flutter points $p_{\mathrm{s}\mathrm{f}}$ caused by ${\Omega }_{1n}$ and ${\Omega }_{2n}$ with different $2b/R$ ($2a/R=1,h/R=0.005$ and $n=3~17$). (a) $\mathsf{\pi }/6\le 2b/R\le \mathsf{\pi }/2$. (b) $\mathsf{\pi }/2\le 2b/R\le \mathsf{\pi }$.

(2)

The case of the CSCS and CSFS open laminated cylindrical shells

For the CSCS and CSFS laminated cylindrical shells, the natural frequencies are given in Table 7. Considering the aerodynamic load, the relationships between $\Omega$ and $p_s$ are shown in Figure 13, wherein Im(${\Omega }_{16}), \mathrm{I}\mathrm{m}({\Omega }_{26})$ for CSCS and Im(${\Omega }_{15}),\mathrm{I}\mathrm{m}({\Omega }_{25})$ for CSFS coalesce earlier. The detailed variations in ${\Omega }_{16}, {\Omega }_{26}$ for CSCS and ${\Omega }_{15}, {\Omega }_{25}$ for CSFS are all given in Figure 14.

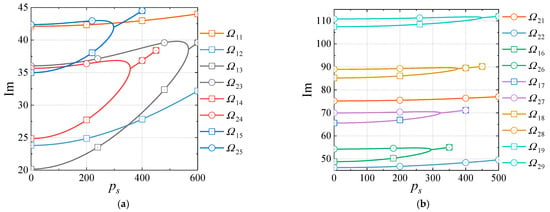
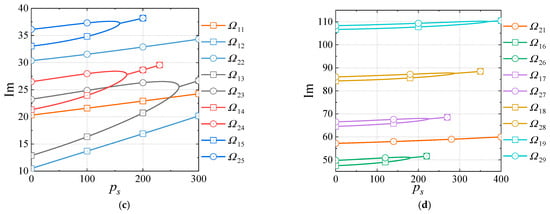
Figure 13. Relationships between $\Omega$ and $p_s$ for the CSCS and CSFS cylindrical shells. (a) CSCS. (b) CSCS. (c) CSFS. (d) CSFS.

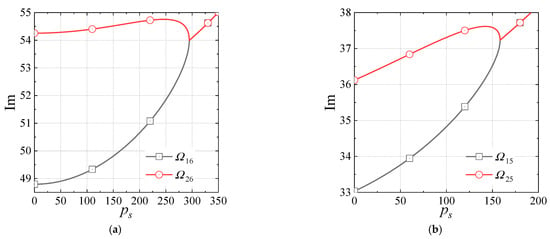
Figure 14. Variations in the pairs of coalescing frequencies with minimum $p_s$ for the CSCS and CSFS cylindrical shells. (a) CSCS. (b) CSFS.

(3)

The case of the SS, CC, and SF closed isotropic cylindrical shells

The closed cylindrical shell with arbitrary combinations of homogeneous BCs can also be handled by the formulae derived in Section 3. The parameters defined in [29,35] for a closed isotropic cylindrical shell are used below. The material properties of the shell are as follows:

$$E_1=E_2=E=16\times {10}^6 \mathrm{l}\mathrm{b}/{\mathrm{i}\mathrm{n}}^2=110.32 \mathrm{G}\mathrm{P}\mathrm{a},v_{12}=v_{21}=v=0.35,$$

$${ G}_{12}=\mathrm{G}=E/2\left(1+v\right)$$

The dimensions of the shell are as follows:

$$2a=15.4 \mathrm{i}\mathrm{n}=0.39116 \mathrm{m},R=8 \mathrm{i}\mathrm{n}=0.2032 \mathrm{m},R/h=2000,$$

$$\rho =8905.37 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$$

And $M=3,{\mathsf{\gamma }}_{\mathrm{\infty }}=1.4,a_{\infty }=8400 \mathrm{i}\mathrm{n}/\mathrm{s}=213.36 \mathrm{m}/\mathrm{s}$ for the airstream.

The comparison of the natural frequency and the flutter point is shown in Table 9; the natural modes are given in Figure 15, and the variations in $\Omega$ with $p_{\infty }$ are presented in Figure 16. Note that, to compare with the results in [35], Equation (43) is also used here. In addition, the present natural frequencies in Table 9 are obtained by neglecting the aerodynamic force, i.e., $p_s=p_c=p_c=0$. The present frequencies are slightly less than the results in [35], whereas they are slightly larger than the results of the FEM. In addition, the present flutter points as marked by ‘☆’ in Figure 16 are larger than those in [35]. This is because the present shell theory differs from those in [35] and the FEM. In general, the present results are in good agreement with those of the referenced results.

Table 9. The natural frequency and flutter point for the SS cylindrical shell ($n=25$).

	${\omega }_{mn}$(Hz) of the SS Shell				The Flutter Point$p_{\mathrm{s}\mathrm{f}}$
	$m=1$	$m=2$	$m=3$	$m=4$	SS	CC	SF
Ref. [35]	268.047	274.899	294.742	334.912	3592	4791	2668
Present	266.654	273.706	293.620	333.452	3734	4892	2827
FEM	266.205	273.161	292.954	332.701	---	----	----
Difference	$\le 1\%$	$\le 1\%$	$\le 1\%$	$\le 1\%$	$\le 4\%$	$\le 3\%$	$\le 6\%$

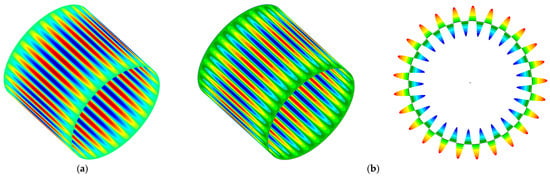
Figure 15. The transverse deflection natural modes of the SS isotropic cylindrical shell with $m=1,n=25.$ (a) Present. (b) FEM.

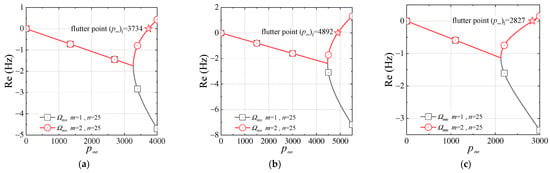
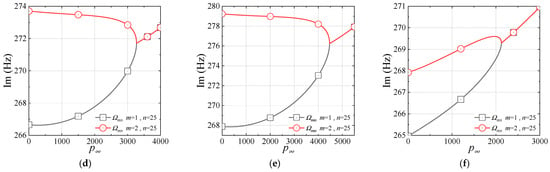
Figure 16. The relationships between $\Omega$ and $p_{\infty }$ for the closed cylindrical shell. (a) $\mathrm{R}\mathrm{e}\left(\Omega \right)$ of the SS shell, where ‘☆’ denotes the flutter point. (b) $\mathrm{R}\mathrm{e}\left(\Omega \right)$ of the CC shell, where ‘☆’ denotes the flutter point. (c) $\mathrm{R}\mathrm{e}\left(\Omega \right)$ of the SF shell, where ‘☆’ denotes the flutter point. (d) $\mathrm{I}\mathrm{m}\left(\Omega \right)$ of the SS shell. (e) $\mathrm{I}\mathrm{m}\left(\Omega \right)$ of the CC shell. (f) $\mathrm{I}\mathrm{m}\left(\Omega \right)$ of the SF shell.

(4)

The results of the Galerkin method

The Galerkin method has been widely used in panel flutter analysis. In order to further verify the present results, Figure 17 and Figure 18 compare the present ${\Omega }_{16}$ and ${\Omega }_{26}$ for the SSSS and CSCS laminated cylindrical shells with those of the Galerkin method, wherein the free vibration modes $\left(m=1~N,n=6\right)$ are taken as the trial functions. The formulation of the Galerkin method can be found in Appendix A. Figure 19 compares the present ${\Omega }_{15}$ and ${\Omega }_{25}$ of the CSFS cylindrical shell with those of the Galerkin method, in which the free vibration modes $\left(m=1~N,n=5\right)$ are used as the trial functions. The Galerkin method taking $N=9$ for the SSSS and CSCS shells agrees well with the present method, validating the accuracy of the present results. As for the CSFS shell, the Galerkin method with $N=5$ is accurate enough. According to Figure 17, Figure 18 and Figure 19, it follows that the frequencies coalescing in the Galerkin method is later than the present results when $N$ is odd, while it is earlier than the present results when $N$ is even.

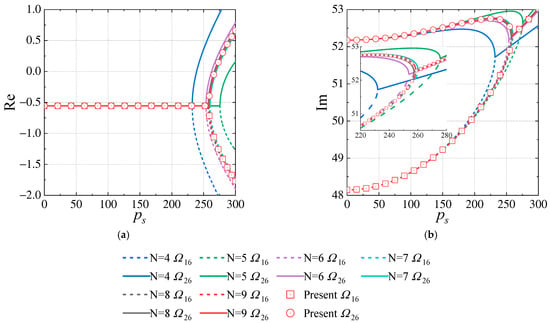
Figure 17. Comparison of the present method and the Galerkin method for the SSSS laminated cylindrical shell (the free vibration modes with $m=1~N,n=6$ are taken as the trial functions). (a) The real parts of ${\Omega }_{16}$ and ${\Omega }_{26}$. (b) The imaginary parts of ${\Omega }_{16}$ and ${\Omega }_{26}$.

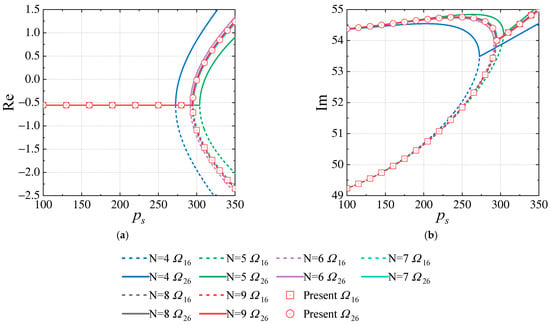
Figure 18. Comparison of the present method and the Galerkin method for the CSCS laminated cylindrical shell (the free vibration modes with $m=1~N,n=6$ are taken as the trial functions). (a) The real parts of ${\Omega }_{16}$ and ${\Omega }_{26}$. (b) The imaginary parts of ${\Omega }_{16}$ and ${\Omega }_{26}$.

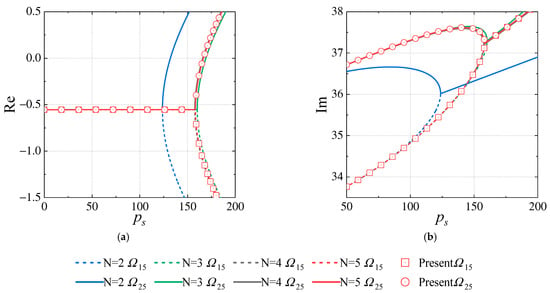
Figure 19. Comparison of the present method and the Galerkin method for the CSFS cylindrical shell (the free vibration modes with $m=1~N,n=5$ are taken as the trial functions). (a) The real parts of ${\Omega }_{15}$ and ${\Omega }_{25}$. (b) The imaginary parts of ${\Omega }_{15}$ and ${\Omega }_{25}$.

6. Conclusions

This work presented a closed-form analytical solution procedure for the free vibration of open circular cylindrical Donnell–Mushtari laminated shells. The governing differential equations were derived by the Rayleigh quotient and solved by the iterative separation-of-variable (iSOV) method. The free vibration problem of the open cylindrical shell with arbitrary combinations of homogeneous boundary conditions can be dealt with by the present method.

In addition, the exact solutions for the flutter of the laminated cylindrical shell were also obtained here. The governing differential equations of flutter were achieved by the Hamilton variational principle and solved by the SOV method. The axial aerodynamic pressure was calculated by the linear piston theory. The present method is applicable to closed cylindrical shells with arbitrary homogeneous boundary conditions and open cylindrical shells with simply supported circumferential edges and arbitrary axial edges.

The influence of the circumferential dimension on flutter characteristics was investigated for the SSSS cylindrical shell. The numerical results manifested that the number of circumferential waves in the critical flutter modes increases with circumferential length; moreover, there exists an infimum for flutter points that is independent of the circumferential length.

In order to verify the present exact solutions of the cylindrical shell flutter, the Galerkin method using the free vibration modes as trial functions was presented. It was concluded that the frequencies coalescing in the Galerkin method is later than the present results when the number of the trial functions is odd, while it is earlier than the present results when the number of the trial functions is even. The present results were also validated through comparison with the results of the finite element method, the Galerkin method, and the available literature. This work fills the gap in the research on the closed-form analytical solutions for the free vibration and flutter of the circular cylindrical shell and provides a benchmark for examining approximation methods.