Improving Prediction Accuracy and Robustness in Injection Mechanism Based on Simplified Pareto and Updated Training Set Hybrid Metamodel
Abstract
1. Introduction
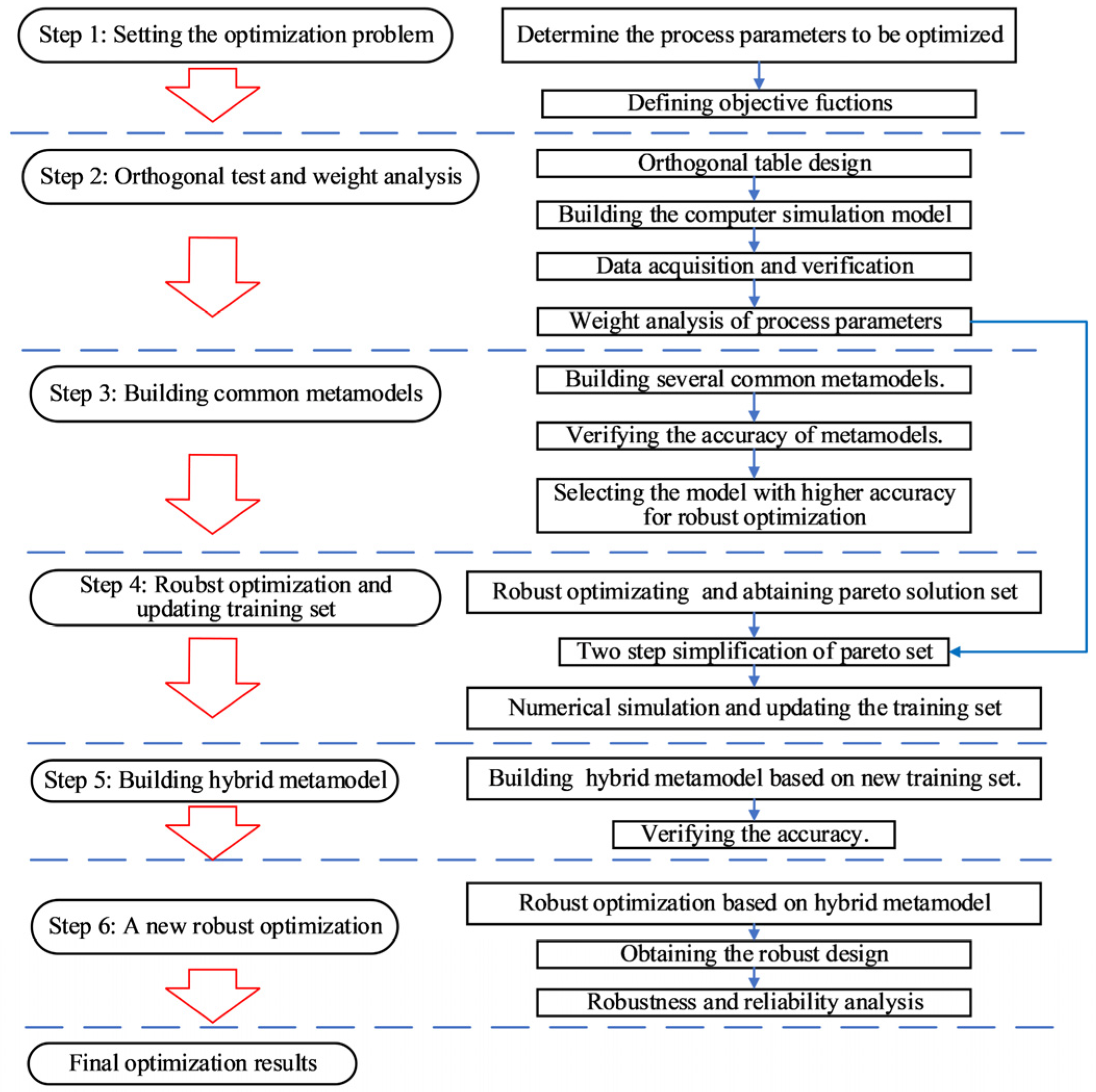
2. Methodology
2.1. Parameter Weight Analysis and SPUTS
- (1)
- Pareto solutions close to the sample points in the training set of the previous step are deleted. The shortest spatial distance is used to determine the closeness between a Pareto solution and sample point and is calculated for Equation (3).
- (2)
- The spatial distance is used as the evaluation criterion for K-means clustering of the Pareto solutions to obtain representative and evenly distributed sample points. The obtained cluster centroids are numerically simulated and are used to update the training set. The K-means clustering includes the following steps: initialize k points in the design space as the centroid of the initial class, assign each solution to the nearest centroid in the space and divide them into k classes, and recalculate the centroids of the k classes. The solution assignment and centroid recalculation are then repeated until the centroids converge or no longer move.
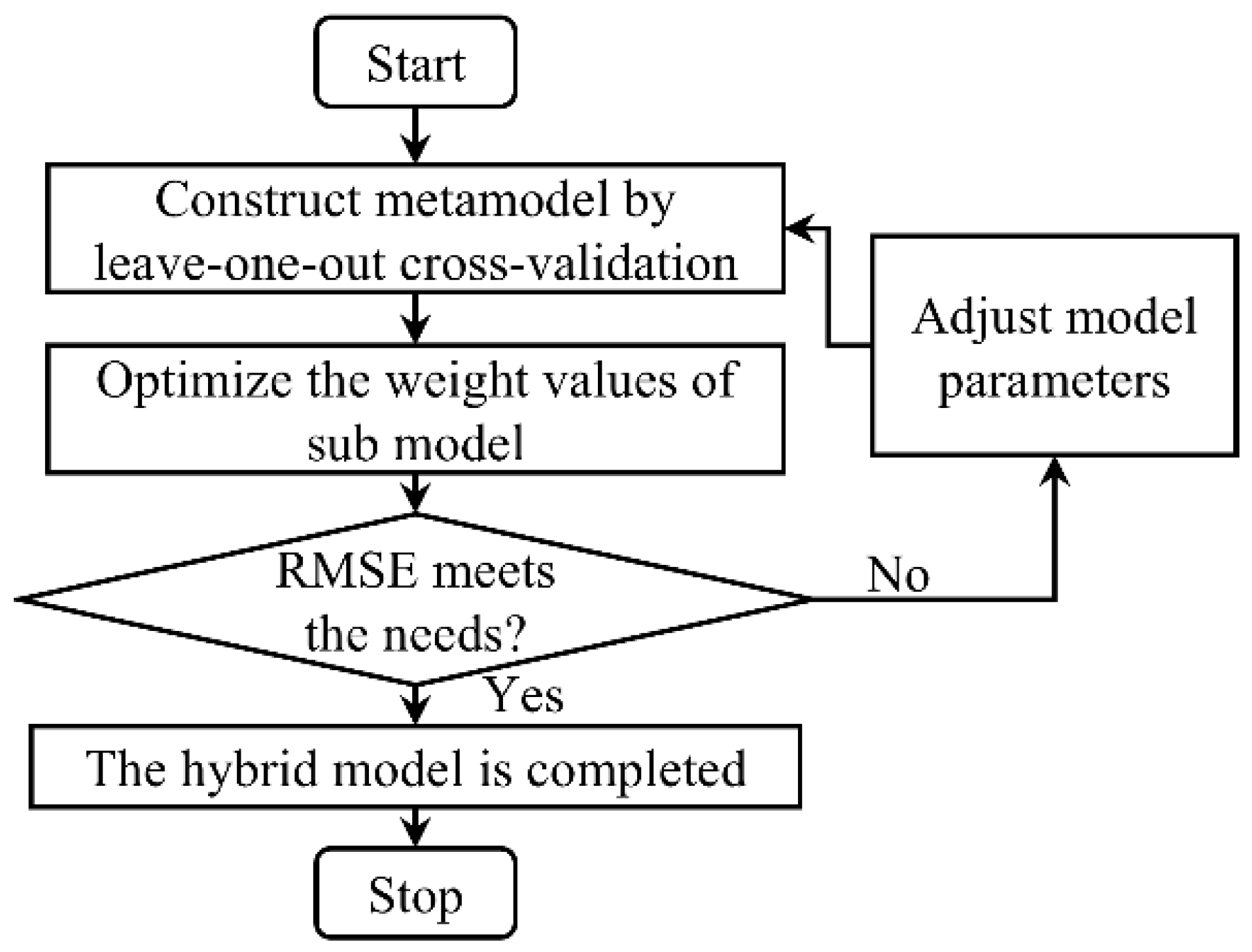
2.2. Hybrid K-R Metamodel
2.3. 6σ Robust Optimization
3. Validation and Application
3.1. Design Variables and Target Response
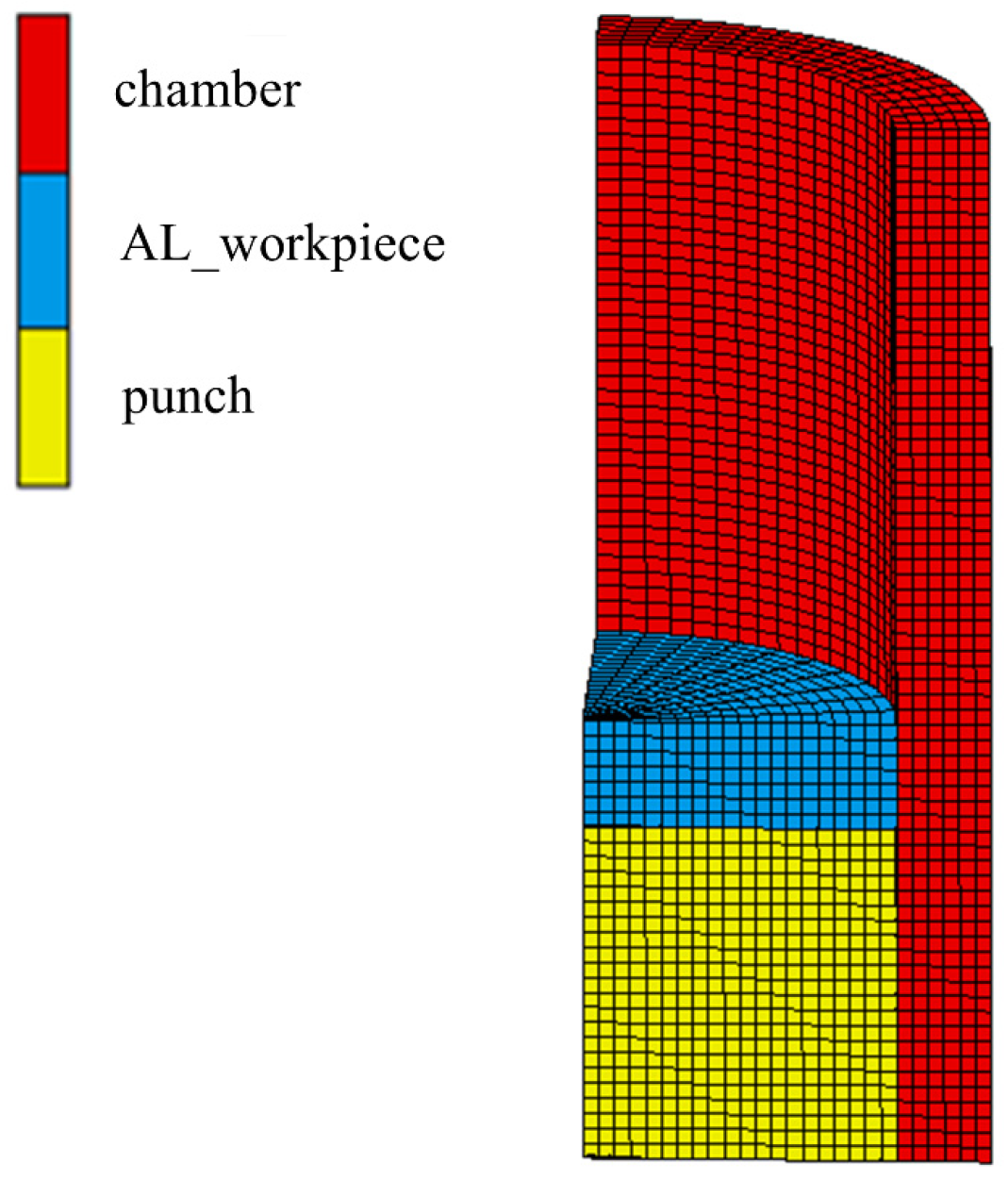
3.2. Experiment and FE Simulation of Injection Mechanism
4. Results and Discussions
4.1. Parameter Weight Analysis
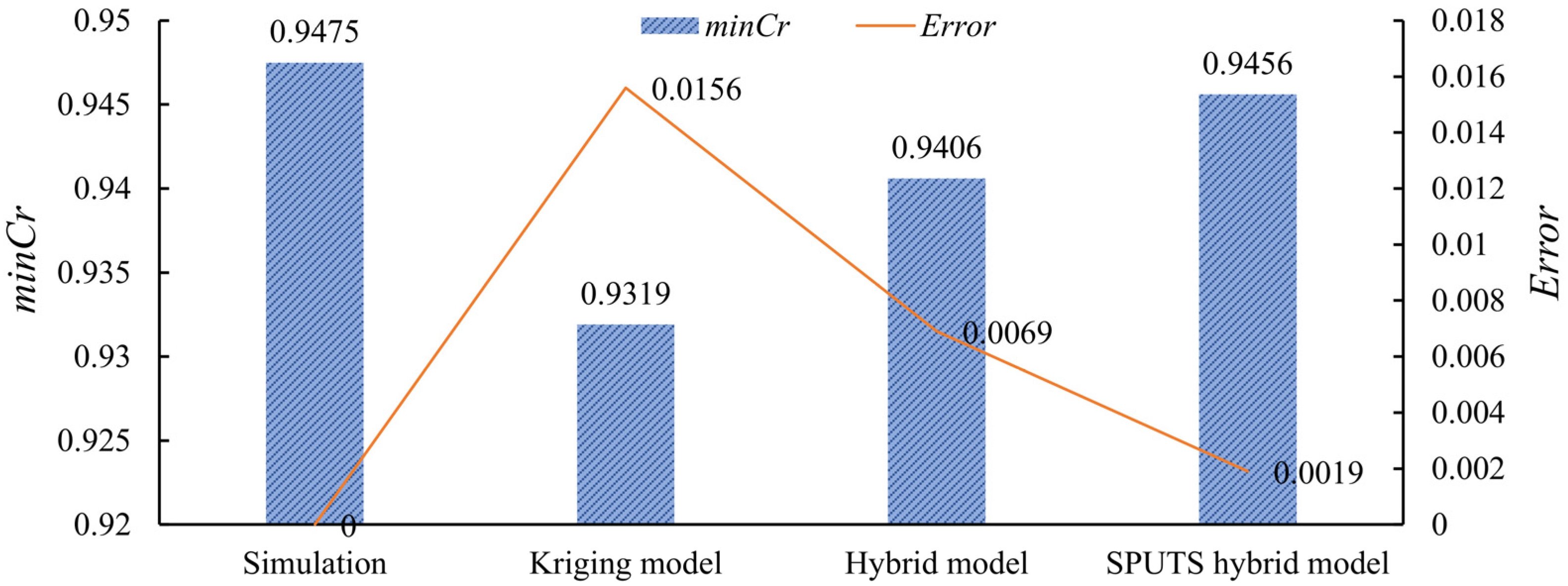
4.2. Original Metamodel and First Robust Optimization
4.3. Robust Optimization of Design
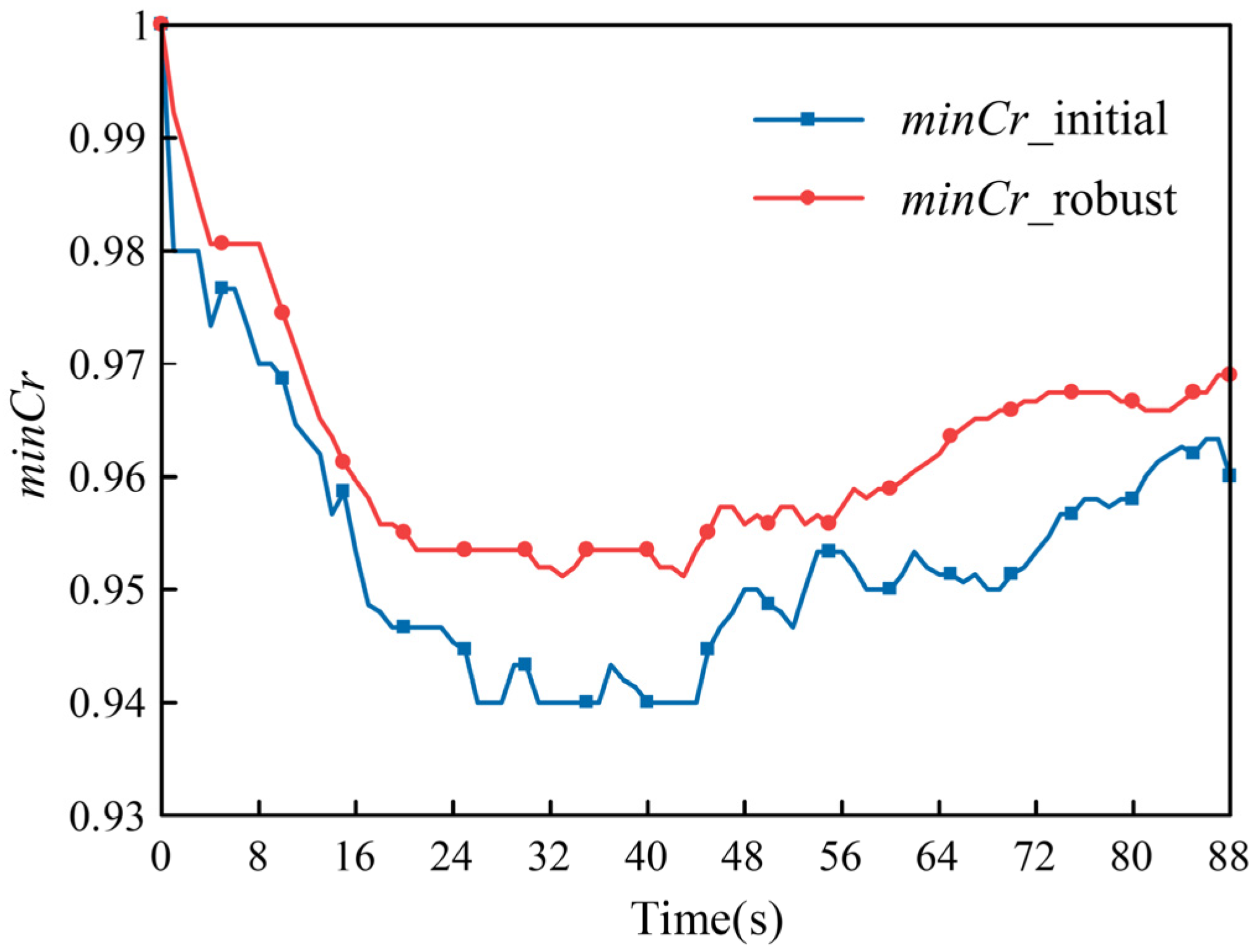
4.4. Comparison of Experimental Results
5. Conclusions
- (1)
- The hybrid metamodel, requiring only a small number of additional sample points, reduced the test set prediction error by 33.33% and the optimized design prediction error by 87.82% compared to the ordinary Kriging model.
- (2)
- The optimized design increased the system’s σ level to 4.87 times that of the initial design, indicating a substantial improvement in reliability. It also reduced the RMSE by 14.32% and increased the response mean by 1.58%, demonstrating enhanced robustness.
- (3)
- Experimental results showed that the optimized design achieved a higher clearance rate throughout the injection process, with a minimum clearance rate 1.2% greater than the initial design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lelièvre, N.; Beaurepaire, P.; Mattrand, C.; Gayton, N.; Otsmane, A. On the consideration of uncertainty in design: Optimization-reliability-robustness. Struct. Multidiscip. Optim. 2016, 54, 1423–1437. [Google Scholar] [CrossRef]
- Nie, J.; Zhong, S. Distributionally Robust Optimization with Polynomial Robust Constraints. J. Glob. Optim. 2025, 92, 509–534. [Google Scholar] [CrossRef]
- Wei, N.; Zhang, P. Adjustability in robust linear optimization. Math. Program. 2024, 208, 581–628. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J.; Ding, X.; Wang, H.; Wang, S. Six sigma robust optimization method based on a pseudo single-loop strategy and RFR-DBN with insufficient samples. Comput. Struct. 2021, 257, 106653. [Google Scholar] [CrossRef]
- Nejlaoui, M.; Alghafis, A.; Sadig, H. Six sigma robust multi-objective design optimization of flat plate collector system under uncertain design parameters. Energy 2022, 239, 121883. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Y.; Zheng, R.; Wang, P. Robust optimization for suspension parameters of suspended monorail vehicle using Taguchi method and kriging surrogate model. J. Chin. Soc. Mech. Eng. 2019, 40, 481–489. [Google Scholar]
- Wang, P.; Yang, Y.; Yi, B.; Zeng, W.; Wang, T. Robust optimization of high-speed rail vehicle suspension parameters based on vertical running stability. J. Chin. Soc. Mech. Eng. 2019, 40, 583–593. [Google Scholar]
- Du, Y.; Gu, J.; Zhang, H.; Hua, W. Reliability-based robust optimization of high-speed PM synchronous machine with local surrogate model Strategy. IEEE Trans. Transp. Electrif. 2024, 10, 9679–9690. [Google Scholar] [CrossRef]
- Xiong, N.; Tao, Y.; Lin, J.; Liu, X.Q. Multi-levels Kriging surrogate model-based robust aerodynamics optimization design method. Int. J. Mod. Phys. B 2020, 34, 2040115. [Google Scholar] [CrossRef]
- Xue, D.; Li, Y.; Zhang, H.; Tong, X.; Gao, B.; Yu, J. Reliability-based robust optimization design for tolerance of aerospace thin-walled components based on surrogate model. Adv. Eng. Inform. 2024, 62, 102754. [Google Scholar] [CrossRef]
- Georgakis, C. Dynamic data-driven models for complex pharmaceutical reactions—The dynamic response surface methodology. Curr. Opin. Chem. Eng. 2024, 45, 101045. [Google Scholar] [CrossRef]
- Haodong, L.I.U.; Jiang, H.; Sujun, D.O.N.G.; Longxian, X.U.E.; Yongji, L.I.U.; Jianjun, W.U. Simulation of an aircraft thermal management system based on vapor cycle response surface model. Chin. J. Aeronaut. 2024, 37, 64–77. [Google Scholar] [CrossRef]
- He, Y.; Tan, K.; Fu, C.; Luo, J. An efficient gradient-enhanced kriging modeling method assisted by fast kriging for high-dimension problems. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 3967–3993. [Google Scholar] [CrossRef]
- Appriou, T.; Rullière, D.; Gaudrie, D. High-dimensional Bayesian Optimization with a Combination of Kriging models. Struct. Multidiscip. Optim. 2024, 67, 196. [Google Scholar] [CrossRef]
- Yamanaka, Y.; Matsubara, S.; Hirayama, N.; Moriguchi, S.; Terada, K. Surrogate modeling for the homogenization of elastoplastic composites based on RBF interpolation. Comput. Methods Appl. Mech. Eng. 2023, 415, 116282. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Zhao, J.; Jiang, W. A novel active learning method based on matrix-operation RBF model for high-dimensional reliability analysis. Comput. Methods Appl. Mech. Eng. 2024, 432, 117434. [Google Scholar] [CrossRef]
- Qosja, A.; Georges, D.; Gjika, E.; Nikolla, L.; Cela, A. A novel approach to electricity demand forecasting: An optimized Kalman filter-based RBF model. Int. J. Dyn. Control. 2025, 13, 165. [Google Scholar] [CrossRef]
- Jin, R.; Du, X.; Chen, W. The use of metamodeling techniques for optimization under uncertainty. Struct. Multidiscip. Optim. 2003, 25, 99–116. [Google Scholar] [CrossRef]
- Yondo, R.; Andrés, E.; Valero, E. A review on design of experiments and surrogate models in aircraft real-time and many-query aerodynamic analyses. Prog. Aerosp. Sci. 2018, 96, 23–61. [Google Scholar] [CrossRef]
- Liu, X.; Hu, C.; Li, X.; Gao, J.; Huang, S. An online data-driven multi-objective optimization of a permanent magnet linear synchronous motor. IEEE Trans. Magn. 2021, 57, 8204804. [Google Scholar] [CrossRef]
- Xie, G.; Zhao, C.; Li, H.; Du, W.; Liu, J.; Wang, Y.; Wang, H. A combination of extended finite element method and the Kriging model based crack identification method. Phys. Scr. 2023, 98, 115109. [Google Scholar] [CrossRef]
- Li, S.; Wen, J.; Wang, J.; Liu, W.; Yuan, S. A high-precision surrogate modeling method based on parallel multipoint expected improvement point infill criteria for complex simulation problems. Mathematics 2022, 10, 3088. [Google Scholar] [CrossRef]
- Gu, D.; Han, W.; Guo, J.; Guo, H.; Gao, S.; Liu, X. A Kriging-based adaptive adding point strategy for structural reliability analysis. Probabilistic Eng. Mech. 2023, 74, 103514. [Google Scholar] [CrossRef]
- Chen, H.; Xu, C.; Li, Y.; Xu, C.; Su, H.; Guo, Y. An adding-points strategy surrogate model for well control optimization based on radial basis function neural network. Can. J. Chem. Eng. 2024, 102, 3514–3531. [Google Scholar] [CrossRef]
- Wang, J.; Xia, G.; Li, R.; Ma, D.; Zhou, W.; Wang, J. Numerical simulation and microchannels parameters optimization for thermal management of GaN HEMT devices. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2841–2861. [Google Scholar] [CrossRef]
- Vural, N.; Yilmazer Hitit, Z.; Ertunç, S. Multi-objective optimization of drying conditions for the Olea europaea L. Leaves with NSGA-II. J. Food Process. Preserv. 2021, 45, e15625. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, F. A two-stage hybrid optimization for honeycomb-type cellular structures under out-of-plane dynamic impact. Appl. Math. Model. 2020, 80, 755–770. [Google Scholar] [CrossRef]
- Fang, Z.; Tang, Z. Pareto equilibrium solution algorithm based on the metrics planning method and its application to multi-objective aerospace optimization. AIP Adv. 2025, 15, 035145. [Google Scholar] [CrossRef]
- Lee, K.H.; Jeong, G.I.; Lee, S.H. An approximate optimization strategy using refined hybrid metamodel. Comput. Intell. 2020, 36, 35–54. [Google Scholar] [CrossRef]
- Long, J.; Liao, Y.; Yu, P. Multi-response weighted adaptive sampling approach based on hybrid surrogate model. IEEE Access 2021, 9, 45441–45453. [Google Scholar] [CrossRef]
- Lv, Y.; Lin, L.; Guo, H.; Tong, C.; Liu, Y.; Zhang, S.; Suo, S. An adaptive hybrid surrogate model for FEA of telescopic boom of rock drilling jumbo. Eng. Appl. Artif. Intell. 2024, 130, 107710. [Google Scholar] [CrossRef]
- Srivastava, N.; Anas, M. An investigative review of squeeze casting: Processing effects & impact on properties. Mater. Today Proc. 2020, 26, 1914–1920. [Google Scholar]
- Ghomashchi, M.R.; Vikhrov, A. Squeeze casting: An overview. J. Mater. Process. Technol. 2000, 101, 1–9. [Google Scholar] [CrossRef]
- Yuanyuan, L.; Weiwen, Z.; Haidong, Z.; Dongdong, Y.; Datong, Z.; Ming, S.; Wen, Z. Research progress on squeeze casting in China. China Foundry 2014, 11, 239–246. [Google Scholar]
- You, D.; Wang, X.; Cheng, X.; Jiang, X. Friction modeling and analysis of injection process in squeeze casting. J. Mater. Process. Technol. 2017, 239, 42–51. [Google Scholar] [CrossRef]
- You, D.; Pang, W.; Li, F.; Zhu, Q. Thermohydrodynamic lubrication-based friction mechanism modeling and integrated simulation of dynamic coordination for squeeze casting processes. Int. J. Adv. Manuf. Technol. 2022, 120, 6481–6495. [Google Scholar] [CrossRef]
- You, D.; Luo, X.; Zhu, Y.; Deng, J. Robust Optimization of Dynamic Fit Parameters for Injection Mechanism in Squeeze Casting Based on Six-sigma Frame and Bayesian Kriging Metamodel. Int. J. Met. 2023, 17, 124–142. [Google Scholar] [CrossRef]
- Dargusch, M.S.; Hamasaiid, A.; Dour, G. An inverse model to determine the heat transfer coefficient and its evolution with time during solidification of light alloys. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9, 275–282. [Google Scholar] [CrossRef][Green Version]
- Javidani, M.; Larouche, D. Application of cast Al–Si alloys in internal combustion engine components. Int. Mater. Rev. 2014, 59, 132–158. [Google Scholar] [CrossRef]



| Tc (°C) | Tm (°C) | V (mm/s) | C0 (mm) | |
|---|---|---|---|---|
| Lower limit | 700 | 100 | 40 | 0.05 |
| Upper limit | 760 | 400 | 76 | 0.17 |
| Material Properties | Punch | Shot Sleeve | Casting |
|---|---|---|---|
| Density (kg/m3) | 7060 | 7800 | 2700 |
| Young’s modulus (GPa) | 169 | 210 | - |
| Poisson’s ratio | 0.257 | 0.3 | - |
| Thermal conductivity (W/m·k) | 24.5–32.2 | 25.0–34.2 | 60–160 |
| Specific heat (J/kg·k) | 560–856 | 460–520 | 963–1082 |
| Linear expansion coefficient (10−5/K) | 1.3 | 1.15 | - |
| Mesh Size (mm) | Number of Elements | Maximum Relative Error (%) |
|---|---|---|
| 5 | 13,960 | 0 |
| 2.5 | 111,680 | 1.21 |
| 1.25 | 893,440 | 1.45 |
| 1 | 1,745,000 | 1.53 |
| Tc | Tm | V | C0 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 2 |
| 1 | 3 | 3 | 3 |
| 2 | 1 | 2 | 3 |
| 2 | 2 | 3 | 1 |
| 2 | 3 | 1 | 2 |
| 3 | 1 | 3 | 2 |
| 3 | 2 | 1 | 3 |
| 3 | 3 | 2 | 1 |
| Level | Tc | Tm | V | C0 |
|---|---|---|---|---|
| 1 | 0.8813 | 0.8526 | 0.8811 | 0.8102 |
| 2 | 0.8926 | 0.8905 | 0.9006 | 0.9128 |
| 3 | 0.8923 | 0.9196 | 0.8846 | 0.9433 |
| Weight | 0.0541 | 0.2682 | 0.0880 | 0.5897 |
| Parameter | Initial | Optimized | ||
|---|---|---|---|---|
| Value | σ Level | Value | σ Level | |
| Tc | 720 | 8 | 712 | 8 |
| Tm | 220 | 8 | 377.1 | 8 |
| C0 | 0.15 | 1.6954 | 0.1290 | 2.9352 |
| V | 40 | 0.6745 | 43.4 | 8 |
| System | - | 0.6028 | - | 2.9352 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, D.; Zheng, S.; Li, F.; Luo, X. Improving Prediction Accuracy and Robustness in Injection Mechanism Based on Simplified Pareto and Updated Training Set Hybrid Metamodel. J. Manuf. Mater. Process. 2025, 9, 358. https://doi.org/10.3390/jmmp9110358
You D, Zheng S, Li F, Luo X. Improving Prediction Accuracy and Robustness in Injection Mechanism Based on Simplified Pareto and Updated Training Set Hybrid Metamodel. Journal of Manufacturing and Materials Processing. 2025; 9(11):358. https://doi.org/10.3390/jmmp9110358
Chicago/Turabian StyleYou, Dongdong, Shiwen Zheng, Fenglei Li, and Xiao Luo. 2025. "Improving Prediction Accuracy and Robustness in Injection Mechanism Based on Simplified Pareto and Updated Training Set Hybrid Metamodel" Journal of Manufacturing and Materials Processing 9, no. 11: 358. https://doi.org/10.3390/jmmp9110358
APA StyleYou, D., Zheng, S., Li, F., & Luo, X. (2025). Improving Prediction Accuracy and Robustness in Injection Mechanism Based on Simplified Pareto and Updated Training Set Hybrid Metamodel. Journal of Manufacturing and Materials Processing, 9(11), 358. https://doi.org/10.3390/jmmp9110358






