Abstract
The electro-discharge (ED) drilling of precision boreholes in difficult-to-machine materials, particularly with respect to the cost-effectiveness of the overall process, is still a challenge. Flushing is one key factor for the precise machining of boreholes, especially with high aspect ratios. Therefore, the influence of internal and external flushing geometries for six types of brass tool electrodes with a diameter of 3 mm with and without a helical groove was analyzed experimentally and numerically. Using this helical external flushing channel, drilling experiments in X170CrVMo18-3-1 (Elmax Superclean) with an aspect ratio of five revealed a material removal rate (MRR) that was increased by 112% compared with a rod electrode, increased by 28% for a single-channel tool electrode and decreased by 8% for a multi-channel tool electrode. Signal analyses complemented these findings and highlighted correlations between classified discharge event types and the experimental target parameters. Amongst others, it was verified that the arcing frequency ratio drove the electrode wear rate and the beneficial frequency ratio correlated with the MRR and the surface roughness Ra. Sophisticated 3D computational fluid dynamics (CFD) models of the liquid phase were introduced and evaluated in great detail to demonstrate the validity and further elucidate the effect of the external flushing channel on the evacuation capability of debris and gas bubbles. The presented methods and models were found to be suitable for obtaining in-depth knowledge about the flushing conditions in the ED drilling working gap.
1. Introduction
Electrical discharge machining (EDM) is an established manufacturing process for machining metal and electrically conductive ceramic materials. It enables the manufacturing of precise holes with high surface quality and small tolerances, independent of the hardness and strength of the material. However, in addition to the physical limitation of the minimum electrical conductivity of σ > 0.01 S/cm of the material [1] (p. 3), the production of high aspect ratios, which refer to the ratio of machining depth dm to hole diameter dh, is a limiting factor in electro-discharge (ED) drilling [2]. With the decreasing diameter of the tool electrode, the maximum achievable aspect ratio of the hole and the material removal rate (MRR) decrease and the electrode wear rate (EWR) increases [3,4,5]. This is caused by the deterioration of the process conditions in the working gap between the electrodes with increasing machining depth since removed particles can no longer be efficiently evacuated [6,7]. Today, it is generally agreed that the EWR is primarily associated with the material properties. However, both the EWR and the MRR result from overlapping discharge crater geometries and increase with an increased discharge energy We [8]. The latter is generally influenced by the generator that acts as a source of charge carriers and its main parameters, which depend on the generator type. More theoretically, at the micro level, the system of tool and workpiece electrode and dielectric fluid can be interpreted as a capacitor. Its energy depends on the capacity and voltage applied, resulting in an electric field strength that influences the energy density in a quadratic manner or the surface charge density in a linear manner, respectively [9]. This is why one can say that the process target parameters of MRR and EWR are directly connected to the process parameters of open-circuit voltage ûi and discharge capacity Ce by means of the surface charge density σS. Other process parameters, such as the charge current iL and the pulse duration ti or the pulse interval time t0, instead affect the charging process of the capacitor or the time interval available for flushing. Apart from the electrical parameters and the charge carrier source, the dielectric itself also contributes to increasing the energy density by constricting the discharge channel [10].
The flushing conditions therefore play a decisive role, but in practice are often underrated regarding improved process stability and the removal of debris particles, and hence, an increased MRR and a decreased machining time and EWR. The dielectric can be supplied or removed either by positive or negative pressure in one or more flushing channels of the tool or workpiece electrode or by lateral flushing from the outside by means of an articulated hose. Flushing holes in the tool or workpiece electrode allow for direct flushing of the discharge area between the electrodes. Amongst others, Uhlmann et al. gave an overview of different flushing approaches, like the inverted pressure flushing, an external automated flushing unit, a multi-fluidic spindle, oscillating tool electrode segments and alternative dielectric fluids, as well as a first introduction of the tool electrodes with external flushing channels discussed in detail in the present work [11]. Rod and tube electrodes as single- or multi-channel electrodes are predominantly used in ED drilling. However, previous studies mainly focused on drastically simplified numerical models and single aspects of the flushing conditions. Generally, improvement of the material removal characteristics can be observed when as little dielectric as possible flows in the working gap. However, if the volume flow rate is too low, the material removal process comes to a standstill because removal products are no longer removed from the gap [10] (p. 42).
The aim of this study was to comprehensively investigate the influence of flushing conditions during ED drilling using tool electrodes with different internal and external geometries, as well as their interactions. The authors intended to address the research question of whether the improvements in process target parameters accomplished by several authors are actually due to the provision of additional space for the evacuation of debris and gas bubbles in the form of external flushing channels and what impact superimposed active flushing has. In comparison with the literature on similar topics, active flushing is not only considered but also given a special focus, as it promises further process improvements. Also, sophisticated transient numerical calculations are presented that go beyond steady-state results. From a numerical point of view, no holistically generated insights are available. Existing publications on this topic by the same authors will be considerably extended by much more detailed explanations of the numerical modeling approaches, with the objective of enabling accurate comprehensibility and reproducibility, as well as by a considerably improved and more elaborate discussion of the signal analyses [11,12,13,14]. The fluid mechanical phenomena in the working gap, the effects on the process target parameters and the process stability with increasing machining depth were analyzed. Figure 1 illustrates the overall investigation approach to maintain the process stability at high aspect ratios due to improved flushing conditions.
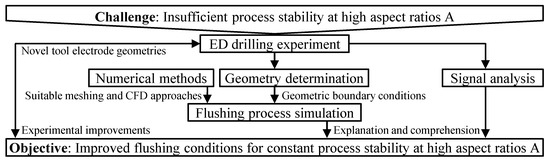
Figure 1.
Overall approach of improving the flushing conditions by use of tool electrodes with external flushing channels.
Following a state-of-the-art discussion in Section 2 and a detailed description of the materials and methods in Section 3, this paper presents the processing results of the ED drilling in Section 4.1, as well as corresponding numerical results of the fluid flow field for novel tool electrode geometries based on the standard tool rod (R), single-channel (1C) and multi-channel (4C) electrodes without and with a helical external flushing channel (prefix H, i.e., HR, H1C and H4C). In this way, commonly used tool electrode types, like 1C and 4C, can serve as references. In Section 4.2, a generic, numerical computational fluid dynamics (CFD) model created with ANSYS Fluent 2020R1 from ANSYS Inc., Canonsburg, PA, USA, with sufficient complexity was used to compare different meshing techniques and to find the trade-off between the mesh resolution and the accuracy of the solution. A complex 3D CFD model was developed on the basis of these findings to enable detailed numerical investigations of the fluid flow within the working gap in general and an evaluation of the external flushing channel’s influence on the flow field in particular in Section 4.3. This was done for all six types of tool electrodes with and without internal and external flushing channels, respectively. In addition, signal analyses of the gap voltage u and current i are used for evaluation in Section 4.4, utilizing a signal analysis system combining sophisticated measurement hardware and a Raspberry Pi 4 single-board computer from the Raspberry Pi Foundation, Cambridge, UK [15]. Performance-enhancing algorithms for the event classification using vector calculations, multithreading and multiprocessing techniques enabled a substantial reduction in the runtime and are also presented. Finally, the Supplementary Materials not only contain detailed experimental and numerical data of this work but also additional flow visualizations in the form of transient multi-phase CFD simulation animations.
2. State of the Art
An intuitive approach to avoid destabilization of the process conditions is the use of partially electrically insulated tool electrodes applying coatings or oxidation to drill holes with high aspect ratios. This, however, implies persisting challenges regarding delamination and fracturing of the insulation layers, as well as a loss of strength or deviations in straightness [11] (p. 628) and [16,17]. Nevertheless, Ferraris et al. improved the shape quality and the achievable aspect ratio by 30% to a maximum of A = 126 in micro-ED drilling [17]. Major improvements of the process characteristics or at least maintaining decent process stability while increasing the aspect ratio are prevalently assured by influencing the flushing conditions.
Takeuchi and Kunieda verified relations between an analytically obtained debris concentration and the measured frontal working gap width sF under given working conditions and for different volume flow rates. They found that the frontal working gap width sF is reduced by an increasing volume flow rate but increases with increasing debris concentration in the gap. However, the authors also state that these findings might differ for other discharge energies We or frontal areas Ae of the tool electrodes since both affect the probability of discharges or particle size. Nevertheless, universally it was found that electrophoresis plays a neglectable role, and the average velocities of the dielectric and the debris particles are the same [18,19].
Kliuev et al. supplemented contradictory works by Yilmaz and Okka and Bozdana and Ulutas by investigating the use of multi-channel tool electrodes and stated that the flushing efficiency is dependent on the tool electrode length and geometry, the machining depth and the flushing pressure [20,21,22]. Kliuev et al. also used experimental and numerical calculations of the volume flow rates and the flow field for comparative purposes. They concluded that single-channel tool electrodes provide the best flushing efficiency and also reduce the recast layer thickness, which is important in ED drilling applications in aerospace [20].
Beyond internal geometries, other authors investigated external geometric modifications of tool electrodes in ED drilling, like D-shaped or elliptic tool electrodes [23,24], rotating graphite tool electrodes with eight different cross sections [25], a stirrer-shaped tool electrode [26], internal or external inclined pathways through rod tool electrodes [27,28,29], eccentric micro-slots in tool electrode tips [30], a rectangular tool electrode cross-section [31], or radially arranged straight and helical slots [7,32,33,34,35]. Yadav et al., Nastasi and Koshy, and Natsu et al. compared straight-slotted and helical external flushing channels with cylindrical or rod tool electrodes in near-dry or conventional ED drilling, and all achieved improvements in the process target parameters but with different rankings of the tool electrodes. In the case without active flushing, single deep-slot or multi-slot tool electrodes performed better than helical external geometries, which in turn were better than the standard rods [7], whereas the performance ranking was different with active flushing of a glycerin-air mist [33]. In micro-ED drilling using deionized water, all geometrical adaptions led to an improvement by a factor of 2.8 in terms of the achievable depth [34]. The process improvements observed in all these works were mainly attributed to the additional space as a result of the geometric modifications, as well as the evacuation of gas bubbles and debris directly along the modified geometry features reducing the hydrodynamic resistance of the working gap and, therefore, increasing the volume flow rate [36].
Tools with external helical geometries in general are almost without exception used in conventional drilling or milling, e.g., twist drill geometries or axial slots for chip flow. In the field of EDM, however, only a few works dedicated to the use of helical external geometries exist so far [2,7,27,33,37,38,39]. In addition, the so-called helical electrodes have found their way into research on electrochemical machining (ECM) [40,41,42,43], as well as hybrid processes [44,45]. All of these research activities followed the objective of providing additional space in the lateral working gap for the evacuation of debris and gas bubbles with the aid of the external flushing channels. Actually, the use of tool electrodes with external flushing channels, especially with external helical geometries, shows great potential for improving the flushing conditions in ED drilling [12]. Plaza et al. conducted an experimental study with helical electrodes for machining the titanium alloy Ti6Al4V. They investigated the influence of helix geometries on the evacuation of particles removed in the case of micro-bores with high aspect ratios. Using a rotational speed of n = 40 min−1, they were able to confirm that helical grooves help to improve the flushing conditions. The optimal combination of pitch and groove depth led to a reduction in the machining time of 37% compared with conventional rod electrodes. However, process instabilities occurred above the aspect ratio of A = 5.6. Tip regenerations following the primary hole helped to compensate for the loss of helix geometry at the tip of the tool electrode due to wear and to increase the achievable aspect ratio by 60% [2]. Nastasi and Koshy used external flushing channels to improve the removal of particles during the machining of the aluminum alloy 6061. They optimized the geometries of the flushing channels of copper tool electrodes with outer diameters of do = 15.8 mm. With a single, deep groove, they were able to achieve a 300% higher MRR compared with conventional rod electrodes and a 38% higher MRR compared with the equal-area quadruple-grooved tool electrode. Numerical simulations showed that for helical electrodes, the evacuation and supply of fluid occur through the helical groove and the lateral working gap separately, while for axially grooved electrodes, both the evacuation and the supply of fluid occur within the vertical groove [7]. Wang et al. investigated the use of tool electrodes with outer diameters of do = 0.07 mm with axial and double helical grooves in the area of micro-ED drilling in steel 1.0503. They observed slightly reduced hole diameters and increased process stability with the double helix electrode. Applying a rotational speed of n = 300 min−1, the maximum aspect ratio achieved with the double helix was A = 13, which was about 30% higher than that of the bore produced with the axially grooved tool electrode. The numerical investigations showed that the fluid undergoes vertical convection movements within the helices and has opposite inflow or outflow areas in the case of helical electrodes, while the vertical fluid movement is absent with axially grooved electrodes [37]. Wang et al. used helical electrodes with increased rotational speeds of 1000 min−1 ≤ n ≤ 8000 min−1 to machine the titanium alloy Ti6Al4V. Increasing the rotational speed resulted in an increase in the MRR by 75% to 95% depending on the direction of rotation and reductions in the EWR by at least 60% and taper or hole conicity α by up to 50% [38]. Kumar and Singh also confirmed the advantages of helical electrodes in the same material. Amongst others, a groove or flute angle of αg = 60° led to the helix-induced evacuation of the particles removed in such a way that according to the authors, active flushing can be omitted. With multiple grooved electrodes, it was possible to increase the maximum aspect ratio by 300% [27]. Hu et al. conducted very similar but more in-depth studies than Uhlmann et al., and like the works discussed so far, they did not apply active flushing. Both author groups found a groove or flute angle of αg = 60° to be optimal in intervals of 30° ≤ αg ≤ 75° or 15° ≤ αg ≤ 60°, respectively [12,39]. Hu et al. stated that in most cases, the larger groove width and groove depth allow for higher machining speeds and lower EWR while avoiding severe bore shape and surface defects. However, basic numerical simulations using a rather simple mesh without dissolving the boundary layer and no further information about the model or software used led to the conclusion that the dielectric is sucked into the helical groove at the bottom of the bore and moves upward in a spiral path [39]. Uhlmann et al., however, more generally pointed out that minimum groove depths dg ≥ 0.3 mm and groove angles αg ≥ 45° are needed for tool electrodes with an outer diameter of do = 3 mm to improve the ED drilling process. Similar to Plaza et al., this is explained by a loss of the helical geometry at the tool electrode tips but, furthermore, with the possibility of clogging of the groove geometry with removed and re-solidified tool and workpiece material [13] (p. 17). Using rod tool electrodes, with the deepest groove of dg = 1.0 mm, they reduced the machining time by 39% in MAR-M247 or by 64% in X170CrVMo18-3-1 with a groove depth of dg = 0.5 mm [11,12,13].
Tool electrodes with external flushing channels were also successfully used in ECM, where electrolysis was used as the fundamental working principle [10]. The renewal of the electrolyte is critical for improving the process stability and dissolution rate and reducing form defects at high aspect ratios [43]. Increasing the rotational speed of the rotating helical tool electrode had a reducing effect on the working gap in both electrochemical micro-drilling [12] and electrochemical contouring, allowing for precise manufacturing of gap contours in quartz glass with an aspect ratio of A = 6.8 [43] and complex structures in steel 1.4301 [42]. Studies by Tsui et al. showed that the use of helical electrodes resulted in a significant reduction in the hole conicity by 42.4% compared with conventional cylindrical electrodes [40]. Hung et al. were able to achieve a significant reduction in the hole diameter by 45.6% using helical tool electrodes with insulating layers of epoxy and ceramic [41]. Supposedly as the first, Hung et al. specifically investigated the influence of helical external geometries on the process target parameters of a material removal process, in this case, a hybrid process of ED drilling and ultrasonic-assisted ED sinking. Using specially manufactured helical tungsten carbide tool electrodes, they were able to manufacture holes with a maximum aspect ratio of A = 10, achieving a reduction in machining time, working gap and roughness characteristics [44].
The literature focuses on manufacturing aspects when using helical tool electrodes, but usually excludes detailed considerations of the fluid mechanical processes in the working gap. On the other hand, the numerical fluid simulations performed are mostly single-phase and steady-state. Hinduja and Kunieda gave a major and in-depth overview of the phenomena and several corresponding models to simulate these different phenomena occurring during EDM but also ECM, and they introduced a generalized model for EDM processes [46].
Generally, numerical simulations, especially fluid mechanical analyses using CFD, have contributed to improving the understanding of the phenomena in the working gap. The increased possibilities in terms of available hardware and modeling approaches have made a decisive contribution to this. The extremely fast physical processes in the working gap, the severely limited optical accessibility due to the very small dimensions, and challenges with flow visualization make CFD an indispensable tool and is especially helpful for the investigation of multi-phase interactions, as well as for compressible phenomena, like in the case of dry-ED milling or drilling [44,47,48].
While in the beginning, in-house codes or the first CFD software, like Star-CD from CD adapco group, Melville, NY, USA, were used [6,49], today only a few authors do this, e.g., in order to exploit the potentials of fully resolved particle simulations that accurately resolve all relevant fluid scales and the fluid flow around each debris particle [50,51]. Today, only the use of so-called supercomputers allows for the fully resolved simulation of the two-phase flow of particles and fluid, e.g., as performed by Brito Gadeschi et al. [51] based on the method by Schneiders et al. [52], or even three-phase flow including gas bubbles. Various authors analyzed the flushing conditions during ED processes using Reynolds-averaged Navier–Stokes (RANS) approaches within commercial software, such as CFX [7,38,48,53,54] or Fluent [37,40,55,56,57,58,59,60,61], both by ANSYS, Inc., Canonsburg, PA, USA, but also COMSOL Multiphysics by COMSOL, Inc., Burlington, VT, USA [35,62,63,64,65], or STAR-CCM+ by Siemens Industry Software Inc., Plano, TX, USA [66]. The degrees of complexity of the RANS modeling approaches are equally crucial but quite different in the existing works. Detailed information on the boundary conditions, meshing or models used can be found in a minority of works. It can be assumed that many numerical analyses are greatly simplified calculations, e.g., by neglecting a resolution of the wall boundary layer by so-called inflation layers.
For the purpose of closing the gap between the averaged results from ED drilling experiments and insights into the fluid mechanic processes within the working gap using sophisticated CFD simulations, the analysis of voltage and current signals over the entire machining depth of a borehole is a well-established method. Experimentally validated CFD models allow researchers to match directions or absolute values of physical properties, like the velocity, the fluid flow or turbulence characteristics, from the local or global flow field with process target parameters, which are typically single, averaged values representing a specific case based on three experiments for statistical validation. These kinds of process target parameters, like the MRR or EWR, are strongly affected by the type of appearing discharges [67]. In addition to the process-averaged quantities, signal analyses possess a temporal component since measurements, and thus, event classifications are possible over the entire machining depth or parts of it. This allows for online control, as well as global and time-dependent evaluations of the process stability to be made [67,68]. Dauw et al. already developed a pulse discriminator, not just for the basic four pulse type classification of normal sparks, short circuits, arcs and open circuits but also for the subdivision of fifteen pulse types, e.g., ignition-delay-free discharges or less effective normal spark discharges [67]. Other authors used thresholds [15,69,70,71,72,73,74], discharge-energy-based approaches [68,75] or field programmable gate arrays (FPGAs) for real-time signal processing [76,77]. Nirala and Saha observed the distribution of energy in micro-ED drilling while studying online responses, such as the pulse frequency and the pulse type density, as well as offline responses, such as the MRR or volume removal per discharge. They defined the share of effective discharges in the removal as the discharge energy and state where the effective discharges have 50% of the discharge energy of the normal discharges. Therefore, they defined the number of effective discharges as the number of normals plus half of the number of effectives and noted that the number of effective discharges increases, whereas the number of normals decreases with the drilling depth [69] (p. 11). The evaluation of the process stability is determined by the decrease in volume per discharge over the drilling depth [69] (p. 15). Yeo et al. applied a similar approach, also for micro-EDM signals based on RC generators, but used the fixed pulse cycle time as one discrimination parameter and counted the number of current peaks in it to distinguish between short circuits and groups of arcs. The comparison of the peak current enabled them to detect normal and delayed discharges [73]. Chu et al. used FPGA logical circuits with adjustable thresholds for the discrimination of normal, short-circuit and open-circuit pulses, and finally improved the machining efficiency and the feed rate stability in wire EDM [78]. The same authors later used this classification method to evaluate the discharge statistics during the visual observation of ED drilling on an inclined surface [79]. Amongst others, Schneider investigated the energy input in the continuous erosion process and, therefore, also applied an FPGA-based real-time signal processing that was originally developed by Schwade and later evolved for the realization of online process monitoring by Küpper et al. [76,77,80,81].
3. Materials and Methods
The materials and methods used to accomplish the results presented in Section 4 are deliberately described in great detail in the following. In particular, the descriptions of numerical models often lack information and are not well or not at all suited to be fully understood, adapted, or replicated by other researchers or research groups. These numerical models are mostly regarded as tools for obtaining evaluable numerical results without clearly demonstrating their validity and origins, although sophisticated numerical models themselves should be considered as results of development processes. In particular, Section 3.2, Section 3.3 and Section 3.4 are intended to go beyond the content of other literature to facilitate replication and allow others to build on these methods as part of the results. This is especially the case, as the numerical models presented here enqueue in a history of experimentally validated CFD modeling ([11,47], [48] (pp. 16–17)).
3.1. Experimental Setup for ED Drilling
For the purpose of machining blind holes to a machining depth of dm = 15 mm and with a process-dependent hole diameter of dh > 3 mm, the die-sinking machine tool AGIETRON compact 1 from GF Machining Solutions, Losone, Switzerland, was used, offering a generator that is capable of generating both transistor and resistance–capacitance (RC)-type pulses (Figure 2). The process parameters given in Table 1 were selected based on preliminary experiments with capacitor discharges. The latter generally not only allows for very low discharge energies We ≤ 0.1 µJ in micro-EDM but also enables levels of the discharge current ie that exceed those of static discharges on the same machine tool. The spindle that enabled rotation was the Jet Injektion-H.S.2000 from Schleinkofer GmbH, Rödermark, Germany, allowing for a rotational speed 0 min−1 ≤ n ≤ 2000 min−1 with an age-related run-out error of er ≤ 0.016 mm.

Figure 2.
Experimental setup on the machine tool AGIETRON compact 1.

Table 1.
Process parameters used for the experiments.
Following Equation (1), the selected parameters led to high theoretical discharge energies of We ≤ 21.4 mJ and adverse process conditions in the form of a high particle load in the working gap due to the short pulse interval time t0 = 2.4 µs and high discharge currents ie < 125 A. This helps to emphasize the effects of the lateral working gap that might result from improved flushing conditions.
We = 0.5 × Ce × ûi2
Brass tool electrodes in the form of rod, single-channel and multi-channel electrodes manufactured by EDM-Deutschland, Kahl am Main, Germany, were used as tool electrodes for the ED drilling process. In addition to these, tool electrodes with helical external flushing channels were prepared with a groove angle of αg = 60° and a groove depth of dg = 0.5 mm using an automatic CNC lathe Cincom B12E by Citizen Machinery Europe GmbH, Esslingen, Germany [12]. Figure 3 visualizes the tool electrode variants that were manufactured and their geometrical specifications, as well as a comparison of the flushing conditions with the established internal flushing and an additional external flushing channel in the form of schematic diagrams.
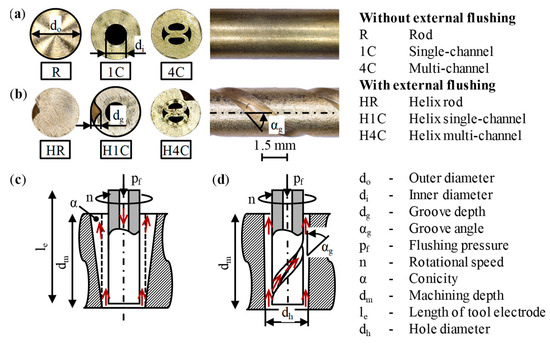
Figure 3.
Tool electrodes used for the ED drilling experiments: (a) without external flushing channel; (b) with external flushing channel; (c) schematic of conventional flushing with internal flushing; (d) schematic of flushing with additional external flushing channel.
All tool electrodes had a nominal outer diameter of do = 3 mm and a length of le = 60 mm, resulting in a total of six different tool electrodes that were analyzed with three experiments each in a workpiece made of the powder-metallurgy-based high-performance steel web from Uddeholms AB, Hagfors, Sweden. In cases of internal flushing, the dielectric IME63 from oelheld GmbH, Stuttgart, Germany, was supplied with an average flushing pressure pf = 2 MPa. The combination of this relatively high flushing pressure pf and internal flushing cross-sections of Af,1C = 1.07 mm2 for the 1C type and Af,4C = 0.74 mm2 for the 4C type led to volume flow rates = 0.69 L/min and 4C = 0.58 L/min. With a displacement volume of VHP = 0.0092 L for one double stroke, these flow rates could hardly be supplied by the M22 DVE double-acting high-pressure piston pump from Maximator GmbH, Nordhausen, Germany, in a constant manner. This was why the double stroke led to flushing pressure fluctuations in the range pf = 1.6 MPa to pf = 2.2 MPa.
3.2. Geometry Determination for Sophisticated 3D CFD Model
Then, in order to accurately simulate the internal and external flushing process, it was obligatory to determine the final tool and workpiece geometries subsequent to the ED drilling experiments. By cutting the bores in half using wire EDM and measuring the contour polygons of the bores and the associated tool electrodes using an InfiniteFocus G4 digital microscope from Alicona Imaging GmbH, Raaba, Austria, it was possible to design a digital representation of the tool and workpiece geometries and, therefore, gain the geometric boundary conditions after the ED drilling experiments for the six types of tool electrodes defined in Figure 3a,b. Figure 4 visualizes this sequence of the geometry determination. In Figure 4c, the sliding mesh approach, which split the working gap in two, is shown and is explained in the following section.
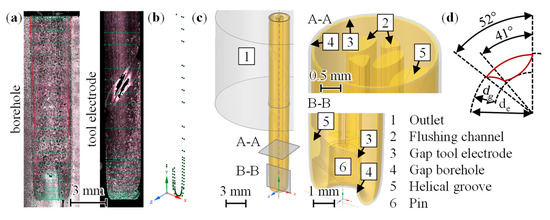
Figure 4.
Sequence of geometry determination, which was exemplary for the H4C tool electrode as a multi-channel tool electrode with helical external flushing channel: (a) images obtained using digital microscope, including measurement lines (green); (b) contour polygons of bore and associated tool electrode; (c) 3D fluid domain in ANSYS SpaceClaim 2022R2 with details from sectional views; (d) design of the helical groove in top view. Table S1 contains all original data.
3.3. Generic Numerical Model and Approaches for Rotating Asymmetric Domains
Preliminary investigations focused on determining suitable meshing approaches, as well as a trade-off between the accuracy of the solution and the resolution of the wall boundary layer. For this purpose, as discussed in Section 4.2, the number of inflation layers nIL and the height of the first layer h1L were studied and three methods to model the rotating fluid domain, namely, counter-rotating wall (CRW), sliding mesh (SM) and overset mesh (OM), were compared. This section introduces these three meshing approaches, gives the theoretical background and motivates the settings. From here on, specific software or numeric-related terms are written in italics to clarify and highlight related terminology. Figure 5 shows the basic generic model that was used for the mesh analyses, as well as the three generic models derived from it to model the rotation of the asymmetric tool electrode geometry. It can be seen that the latter three encompassed a straight slot that worked as a simplified groove with a groove length lg = 8 mm, a groove depth dg = 0.5 mm and a groove width of wg = 0.5 mm. All four models shared the same geometrical specifications, which included an outer diameter do = 3 mm and a length le = 12 mm of the tool electrode, an inner diameter di = 1 mm and a hole diameter dh = 3.2 mm, resulting in a working gap width s = 0.1 mm and a machining depth dm = 6 mm, giving an aspect ratio A = 2, as well as physical boundary conditions, namely, a rotational speed n = 500 min−1 and a flushing pressure pf = 2 MPa. All radii were to R1 = 0.1 mm, except the bottom radius inside the borehole, which was R2 = 0.2 mm.
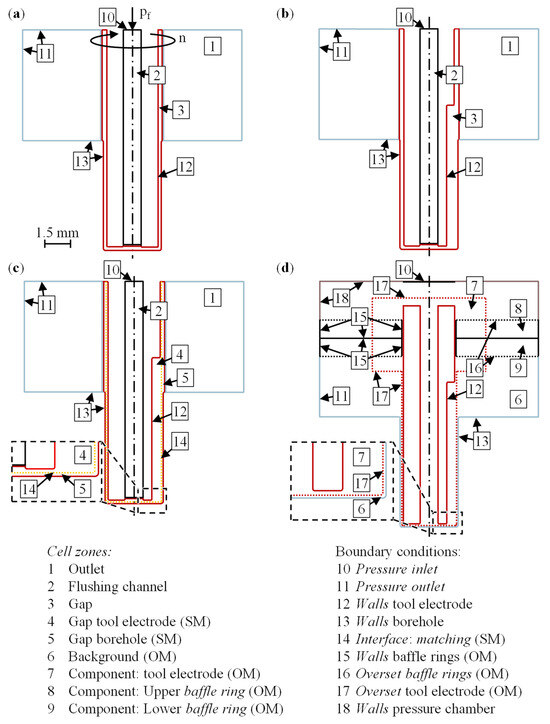
Figure 5.
Cell zones and boundary conditions of the generic models: (a) basic model for mesh analyses; (b) counter-rotating wall; (c) sliding mesh (SM); (d) overset mesh (OM).
With the help of the generic model given in Figure 5a, relevant mesh parameters of the inflation layer at the walls were varied with the objective of correctly resolving the wall boundary layer. Across a discrete span, the distances of the wall parallel prism cells were steadily increased in the normal direction to the wall to resolve the usually high gradients of any fluid mechanic property. The most important example is the velocity |c|, which is |c| = 0 m/s at any wall with a no-slip boundary condition. Regions that are outside of the wall’s influence are meshed with selected cell types, like ted-, hex- or polyelements.
In addition, the global mesh was divided into three cell zones with the option share topology in ANSYS SpaceClaim for the basic model in Figure 5a. These cell zones were linked with each other at their contact areas, which acted as interfaces, as they were set to internal. In this way, the generation of conformal meshes in ANSYS Fluent with individual element sizes for each cell zone was possible, increasing the control over the mesh resolution at relevant locations, like the working gap. The theory of wall boundary layers uses dimensionless parameters, like the dimensionless wall distance y+ and the dimensionless velocity u+, to describe fluid mechanical quantities; see Equations (2)–(4):
with y being the coordinate normal to the wall, ν the kinematic viscosity, ρ the density, the average wall-parallel velocity and uτ the friction velocity as the characteristic velocity for turbulent flows with given shear stress . This notation arises from the examination of the Couette flow, whose velocity distribution is of a universal character, especially for large Reynolds numbers, and results in the logarithmic law of the wall [82]. The velocity distribution u+(y+) is divided in the three regions viscous sublayer for y+ < 5 with the approximation u+ = y+, the buffer layer for 5 < y+ < 70, and the log law region for y+ > 70 with u+ = 1/κ × ln y+ + C+, κ = 0.41 and C+ = 5.0 [82]. The influence of the dynamic viscosity µ is dominant in the viscous sublayer but drastically decreases toward the log law region, which is nearly fully turbulent. The aforementioned wall functions are usually applied with turbulence models, like the k-ε turbulence model, on meshes with distances of y+ ≥ 30 to the cell closest to the wall. This is only acceptable for cases where the turbulence production k and the dissipation ε are in balance but not for cases with strongly three-dimensional flow structure; tangential upstream oriented pressure gradients; or missing far away flow, like in the case of narrow gaps [83]. As a solution, low-Re turbulence models help to describe the transition from the fully turbulent core flow to the boundary layer by introducing damping functions to correct the turbulence production k and dissipation ε. Unfortunately, this advantage comes with the necessity of a higher mesh resolution and increased numerical effort, which results from the recommendation of applying a dimensionless wall distance in the order of y+ = 1 for the cell closest to the wall [83]. This is why, in common cases of free external flows, like the flow around airfoils, the viscous sublayer and the buffer layer of the boundary layer are to be resolved with several inflation layers nIL ≥ 10 [83,84].
The enhanced wall treatment method within ANSYS Fluent is a direct consequence and combines a classical two-layer model with enhanced wall functions to determine the dissipation ε and the turbulent viscosity µt. Therefore, the whole fluid domain is divided into a fully turbulent and a viscous region, which are delimited by a characteristic Reynolds number Rey:
where y is the wall-normal distance to the respective cell centers. In fully turbulent regions with Rey ≥ 200, the standard k-ε turbulence model is used, whereas in the viscous layer, the turbulent viscosity µt is derived with a turbulent length scale lµ. A blend function is then used to determine the turbulent viscosity μt as a function of the characteristic Reynolds number Rey [84]. For the sake of completeness, it should be noted that a y+-insensitive wall treatment is used by default in the case of turbulence models based on the ω-equation for the specific rate of dissipation ω.
As a result of these considerations, the number of inflation layers nIL and the height of the first layer h1L were varied according to Table 2. First, the number of inflation layers nIL was analyzed with a fixed height of the first layer h1L = 2.0 µm regarding the axial velocity profiles and an inspection of the mesh elements, which were colored with the corresponding values of the wall-parallel velocity. Afterward, the most appropriate number of inflation layers nIL was used to vary the height of the first layer h1L and analyze it accordingly.

Table 2.
Relevant parameters of the boundary layer that were varied.
As mentioned before, the recommendation of applying a dimensionless wall distance in the order of y+ = 1 comes with increased numerical effort. For transient calculations, this also may result in a very small time step Δt. Additional objectives for the inflation layer analyses were as follows:
- NV = 5 volume cells between opposite inflation layers across a gap, amongst others, was a necessary condition for the overset mesh approach;
- The inflation layer volume fraction amounted to about 50% of the working gap;
- The total number of cells NC needed to be as low as possible to enable a transfer of the meshing parameters to the even bigger mesh of the full numerical model;
- The dimensionless wall distance of the first cell should be in the order of y+ = 1.
For all these numerical calculations, a global mesh using poly-hexcore elements, two peel layers, a transition ratio between the last inflation layer cell and the first volume cell of TR = 0.4, and an inflation gap factor of IGF = 1 were applied and the option keep layer height was activated. The inflation gap factor ensured that the cells between both inflation layers and the inner volume cells had the same volume ratio as the inflation layers on both sides. The pressure-based SIMPLE solver was selected for the sequential pressure–velocity coupling, as it is recommended for steady-state incompressible flows. The PISO solver should be used for transient calculations, especially with skewed meshes. A coupled scheme includes the advantages of robust and efficient solutions of steady-state flows and the use of a large time step Δt, in conjunction with meshes of low quality for transient calculations [85]. To study the mesh, in addition to the standard SIMPLE algorithm, a first-order upwind method was used to discretize the momentum equation, and the warped-face gradient correction was activated to improve the accuracy of the gradient. The latter is recommended for three-dimensional simulations on poly-hexcore meshes, as these do not have perfectly planar faces [85].
The counter-rotating wall (CRW) approach shown in Figure 5b is the simplest way to model the rotation of the asymmetric tool electrode geometry. This approach works based on the assumption of a change in the reference position, originating from the stationary workpiece to the rotating tool electrode. As seen from this moving reference point, the tool electrode is at rest and the wall of the workpiece electrode moves in the direction opposite to the actual direction of rotation. The volume forces on the fluid are generated by the rotation of the whole fluid domain or cell zone respectively by applying frame motion on the cell zone ‘gap’ with a rotational speed of n = 500 min−1 (see Figure 5). The walls of the ‘electrode’ are walls moving relative to an adjacent cell zone, whereas the walls of the ‘borehole’ are absolute moving walls, both with a rotational speed of n = 0 min−1. The difference between these definitions becomes apparent when the proximity to a stationary or rotating cell zone is considered. The aforementioned relative specification implies a resting wall in the moving reference frame and, at the same time, a moving wall in the absolute reference frame. The absolute specification means that the wall rests in the absolute reference frame and moves in the opposite direction in the moving reference frame. Frame motion only allows for capturing steady-state flow phenomena within the CRW approach. The steady-state solution is reached after a number of iterations of nI = 1000 iterations. A transient calculation would need a mesh motion or dynamic mesh approach instead and a respective interface to the stationary domain. This is exactly what a sliding mesh offers.
The sliding mesh (SM) approach, as shown in Figure 5c, allows for calculating even transient behavior of at least two cell zones that move relative to each other. In other words, during the simulation, one cell zone slides along the connecting surface within a discrete time step Δt. The former cell zone ‘gap’ is now split into a moving cell zone ‘gap tool electrode’ and a stationary cell zone ‘gap borehole’, which are connected via a mesh interface with the option matching, which tries to match the element nodes on both sides of the interface to reduce the oscillations of the solution. A reason for this might lie in the interpolation of the mass flow from the interface to the sliding surfaces that might locally influence the mass balance. The meshes of the rotating and stationary parts are created separately and brought back together inside the setup of ANSYS Fluent 2020R1 via append case. The interface boundary conditions of both sides will be merged and interpreted again as internal. The PISO solver is used because, in the long run, multiple rotations of the tool electrode are supposed to be considered, and hence, a bigger time step Δt is needed but also supported by that algorithm. When using frame motion for the rotating cell zones during the steady-state calculation, a number of iterations of nI = 1000 was again computed for comparability reasons. This solution acts as the initial solution or flow field for the transient calculation, now using mesh motion. Bounded second-order implicit was selected for the time integration since this allowed for improved accuracy and stability compared with the standard settings by maintaining limits regarding the time discretization of the variables [85]. The transient calculation was performed with a fixed time step of Δt = 0.0015 s, which corresponded to an incremental angle passed of β = 4.5° as the result of the rotational speed of n = 500 min−1. In the center of the working gap in the tangential direction, this equaled a swept arc with an arc length of about la = 0.12 mm. By specifying the number of time steps nΔt = 160 and the number of iterations nI/Δt = 20 per time step Δt, a maximum of nI = 3200 iterations were calculated. During this period, the tool electrode performed two full rotations.
The overset mesh (OM) approach has the advantage of allowing for arbitrary movements of the component meshes on the background mesh and, therefore, translation movements of the tool electrode are possible. This is visualized in Figure 5c and involves additional boundary conditions. The background and component geometries have to be designed and meshed independently. Merging of those overset regions happens during the initialization of the flow field within the setup and is not only highly complex and numerically expensive but also subject to numerous and strict requirements [85]:
- Component meshes of an overset interface may overlap arbitrarily, allowing them to be combined into a complex object, provided that physical boundary conditions, such as walls, an inlet or an outlet, do not intersect;
- However, component and background meshes can be placed in such a way that the physical boundary conditions lie on top of each other, and thus, e.g., wall boundary conditions can be coincident with each other;
- Overset boundary conditions, on the other hand, can intersect other overset boundary conditions, as well as physical boundary conditions;
- The calculation has to be performed with double precision;
- The time step selection for dynamic meshes must be based on the relative mesh motion per time step Δt, which should be below the smallest volume cell size lc of the overset interface.
The merging process includes the following steps (see Figure 6) [85]:
- Hole cutting: The process of marking mesh elements as dead cells that are outside of the fluid domain of interest, e.g., on the inside of bodies. Excessive overlap of component meshes and the background mesh is numerically inefficient. The transition of both meshes ideally occurs in areas with similar resolution. Large deviations between the overlapping meshes influence the interpolation, and thus, impair the quality of the solution.
- Overlap minimization: The process of converting solve cells to receptor cells, as well as unnecessary receptor cells in dead cells, between component meshes and the background mesh. A solve cell is converted into a receptor cell if a suitable donor cell with a higher donor quality can be found for this cell. The specification of a donor priority method influences this cell replacement procedure depending on the local mesh resolution.
- Donor search: A solve cell containing the centroid of a receptor cell of the overlapping mesh is used together with the adjacent solve cells as a donor for the selected receptor. Within the search, each receptor cell must be associated with at least one eligible donor or solve cell. Four or more cells must be present in the overlap zone of both meshes to ensure a successful donor search. Orphan cells are generated during initialization wherever this routine fails.
The avoidance of orphan cells is the major challenge when using the OM approach because even fairly simple geometry configurations involve numerous potentially problematic combinations and overlaps of boundary conditions and components, especially with additional use of the bodies of influence meshing method or other auxiliary bodies.
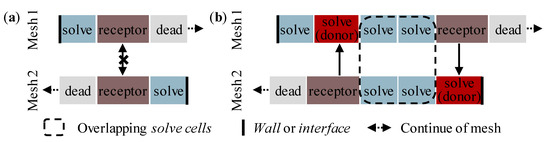
Figure 6.
Overlapping of two meshes to form an overset interface: (a) invalid overlap creating orphan cells; (b) valid overlap with sufficient cells in the overlap zone [85].
The specific third requirement for the donor search motivates the first objective concerning the inflation layer analyses below Table 2. The OM approach was already introduced for CFD simulations in the field of ED drilling without internal flushing, also providing detailed visual insights into modeling, meshing and merging [14]. In addition, Figure 7a shows the overset mesh for the present case with internal flushing, which was generated with the procedure described above and on the basis of Figure 5d. The working gap was successfully resolved with a number of cells of NC = 18, which was divided into NV = 6 volume cells between the two inflation layers. The little detail of an inlet, which could not be placed at the boundary of the mesh (see the first OM requirement), led to the necessity of adding some kind of pressure chamber domain around the tool electrode’s top pressure inlet and sealing this chamber on the outside walls of the tool electrode to prevent perpendicular bypass fluid flows. This fact resulted in many additional geometries for the implementation of baffle walls (Figure 7a) or collar grids (Figure 7b), which, in turn, caused the heavy occurrence of orphan cells and, therefore, diverging solutions. These additional geometries were also multiplied by additional auxiliary bodies, namely, the bodies of influence, for the purpose of local mesh refinements because the latter cannot be set up by the cell sizes inside the cell zones in the case of the OM approach. The idea of applying a hollow ring instead of the two baffle rings holds the advantage of generating more dead cells and, therefore, reducing the numerical effort. Nevertheless, additional components with respective meshes have to be generated and increase the complexity, not only for the user but also for the merging algorithm. During initialization, the flood filling of dead cells in areas where no fluid is supposed to be starts with placing seed cells. Complexities in the topology or mesh resolution issues can cause the algorithm to unintentionally identify seed cells inside fluid regions and end up marking entire fluid regions or cell zones as dead. Different variants and arrangements of component meshes led to incorrectly identified seed cells and, as a consequence, dead regions, which is why the approach of using baffle walls is preferred.
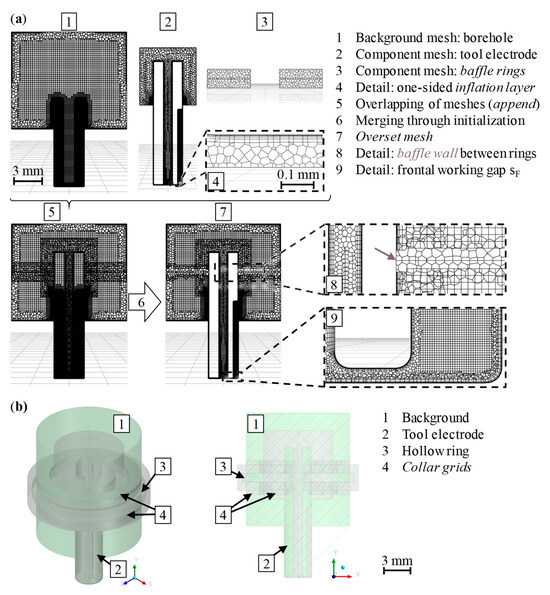
Figure 7.
Creation of the overset mesh by overlapping and merging different components: (a) final OM domain with baffle walls; (b) geometries of overlapped background and components for the use of collar grids.
Identical transient settings were used compared with the SM approach and were supplemented by a frozen flux formulation for the implicit discretization of the convective terms to improve convergence. The underlying steady-state solution with frame motion was achieved with a number of iterations of nI = 500 this time because the coupled scheme used accelerated convergence. Table 3 summarizes the most significant models and solver settings of the three generic models for reproduction purposes.

Table 3.
Models, solver settings and mesh characteristics of the generic models.
The most accurate and effective meshing approach and respective CFD setup were identified by means of the generic models described here (see upcoming Section 4.2). Using the resulting recommendations and the realistic geometric boundary conditions obtained as described in the previous Section 3.2, the fluid flow in the working gap was simulated on those realistic, greater domains, as introduced in the following Section 3.4. The numerical results gained with these sophisticated models of all six tool electrode types finally allowed for deriving analogies to the experimental results of Section 4.1.
3.4. Sophisticated 3D CFD Model
Fluid simulations of the tool electrodes introduced in Figure 3 were carried out with ANSYS Fluent 2020R1 in the case of R, HR, 1C and H1C, as well as ANSYS Fluent 2022R2 in the case of 4C and H4C from ANSYS Inc., Canonsburg, PA, USA. Rod, single-channel and multi-channel electrodes were compared with their equivalent helix geometries to examine the influences of the internal and external flushing channels. Figure 8 exemplarily shows both fluid domains for the R types. A sliding mesh approach was used to model the rotation of the tool electrodes, dividing the working gap into a moving and a stationary domain via a sliding interface.
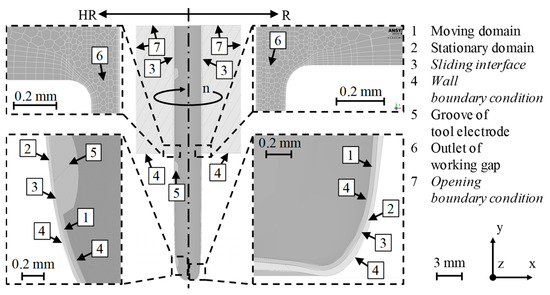
Figure 8.
Numerical model, exemplary for the type R and HR tool electrodes, with details of the mesh and the sliding mesh approach.
This model was built using measured contour polygons of the bores and the associated tool electrodes as depicted in Figure 4 ensuring realistic values of the frontal and lateral working gap width sF and sL. The groove geometry, as well as an enlarged hole conicity α, increased the number of polyhedral cells NC, especially orthogonally across the lateral working gap (see the hole entrance areas in Figure 8).
The fluid properties for all CFD simulations that are presented in this paper can be found in Table 4. Data for the dielectric IME63 was taken from the manufacturer oelheld GmbH. The properties of air were needed for the supplemental multi-phase simulations, as mentioned at the end of Section 4.3 and linked in the Supplementary Materials section.

Table 4.
Material properties for CFD simulations.
The most important boundary conditions, as well as assumptions and additional details, supplemental to the information in Table 5, are listed hereafter:
- 50% of the cells across the working gap were volume cells;
- RANS modeling for the single-phase flow;
- Reference and operating pressure: pref = 0 MPa, pop = 0.1 MPa;
- Inlet pressure equaled the flushing pressure pf = 1.9 MPa;
- Moving domains rotated with rotational speed n = 400 min−1;
- Liquid only: neglected the presence of debris and gas bubbles;
- Steady-state solution after a number of iterations nI = 1000 iterations was followed by nR = 11 transient revolutions being calculated;
- Adaptive time step Δt for the first revolution to ensure CFL ≤ 1 (see Section 4.2);
- Last ten revolutions: fixed time step Δt = 0.00375 s; incremental angle passed: β = 9°; simulation durations tsim = 35 h for HR and tsim = 96 h for H1C.
It has to be stated that ANSYS Fluent internally uses a subtraction of the absolute pressure pabs and the operating pressure pop to avoid roundoff errors [85]. The result following Equation (6), namely, the gauge pressure pgauge, is what is manually specified within the software; this is why the gauge pressure needs to be set to pgauge = 1.9 MPa to ensure a flushing pressure of pf = 2.0 MPa at the pressure inlet:
pabs = pop + pgauge.
Schematic sketches of the rod and single-channel geometries are illustrated in Figure 9, which also details positions P1 to P7 for later evaluations. The multi-channel geometries are equivalent to Figure 9b, except for the internal channels. The geometrical and physical parameters of all fluid flow simulations are consistent with the experiments and correspond to an aspect ratio of A = 5.
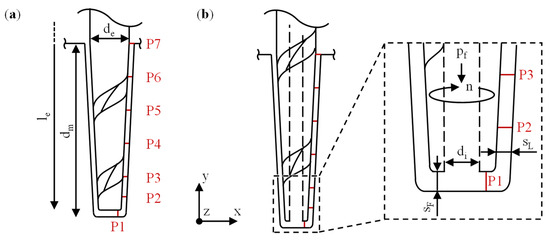
Figure 9.
Schematic sketch of the tool electrodes and definition of evaluation positions and velocity components: (a) R and HR types; (b) 1C, H1C, 4C and H4C types.

Table 5.
Models, solver settings and mesh characteristics of the sophisticated models.
Table 5.
Models, solver settings and mesh characteristics of the sophisticated models.
| Mesh Characteristic | Value or Setting |
| Type of mesh | Poly-hexcore |
| Cell size in working gap | 20 µm ≤ lc ≤ 30 µm |
| Number of inflation layers | nIL = 6 |
| Height of the first layer | 0.5 µm ≤ h1L ≤ 10.0 µm |
| Total number of cells | 9.33 mil. ≤ NC ≤ 11.65 mil. |
| Model/Setting | Value or Setting |
| Turbulence | Realizable k-ε model, enhanced wall treatment |
| Pressure–velocity coupling | R, HR: SIMPLE; 1C, H1C, 4C, H4C: coupled |
| Spatial discretization | |
| Gradients | Least squares cell-based with warped-face gradient correction |
| Pressure | Second order |
| Momentum | Second-order upwind |
| Turbulent kinetic energy | First-order upwind |
| Turbulent dissipation rate | First-order upwind |
| Transient formulation | Steady: pseudo-time method global Transient: bounded second-order implicit |
| Time step | Δt = 0.00375 s |
| Iterations per time step | nI/Δt = 20 |
The qualitative and quantitative evaluations in Section 4.3 were based on these evaluation positions, which are further specified in Table 6.

Table 6.
Geometrical parameters and evaluation positions for simulated tool electrodes.
Comparative quantitative and qualitative evaluations and analyses of results gained by using CFD simulations are usually based on common tools like streamlines, vector plots or contour plots of the parameters of interest. One advantage of numerical results besides an infinite spatial resolution arises from the possibility of calculating nearly any physical or non-physical parameter and, by using it, its average value or sum on auxiliary geometries or any other mathematical construct with it for explanatory approaches. In 3D CFD simulations, the components of the velocity vector c in the global Cartesian coordinate system are frequently used to reveal local flow field characteristics. Figure 10 visualizes and defines the velocity vector c on cross-sectional views of the H1C type tool electrode for the cases of a global Cartesian coordinate system and a slightly rotated coordinate system, marked with apostrophes, where the radial velocity vector crad is the vector resulting from the velocity components cx’ and cz’ being perpendicular to the vector of the axial velocity cax. The latter in this work will always be aligned in the main flow direction. Vector quantities are written in bold. The evaluation positions and velocity components defined this way are used in Section 4 for the detailed evaluation of the calculated 3D flow fields.
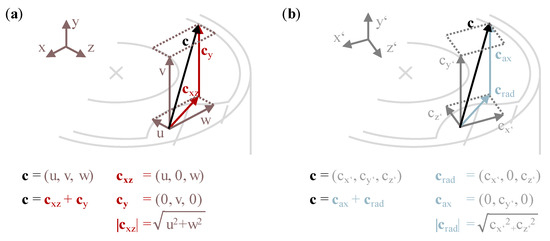
Figure 10.
Visualization and vector quantities of the velocity in the example of the H1C-type tool electrode in a cross-sectional view: (a) stationary, global Cartesian coordinate system; (b) moving consideration with the vectors cax and crad giving the axial and radial components of the main flow, respectively.
3.5. Signal Analysis
In order to ensure a good EDM process, discharge conditions must be created in the working gap that largely exclude the occurrence of short-circuit, false discharge and open-circuit pulses. A short-circuit pulse in this context occurs when the electrodes are touching or when bridging takes place due to removed particles [10] (p. 12). The task of the feed control is, therefore, to feed the tool electrode according to the material removal, the wear and the respective gap conditions [10] (p. 41). A detailed signal analysis of the current i and gap voltage u by detecting rising and falling flanks allowed for explanations and further quantification of the influence of internal and external flushing geometries on the process stability. The general approach of using rising and falling flanks in combination with threshold crossing points was inspired by the pulse classification algorithms proposed by Zhou et al., Janardhan and Samuel, and Nirala et al. [69,70,71,72]. Janardhan and Samuel described a method to detect rising and falling signal flanks by detecting and storing the sampling data points just before and after a voltage or current threshold is crossed [71]. Nirala et al. solely used voltage thresholds for the pulse discrimination and rightly stated that the corresponding threshold values should be determined empirically (Table 7). Therefore, they are hardly transferable from one parameter setting to another. This is why the thresholds have to be adapted to every machine tool and generator type. They also measured the current signal and utilized this additional information to calculate the average energy to further obtain an implication of the process stability. This was based on the understanding that an early discharge originates from a locally increased electrical conductivity σ, e.g., as a consequence of process residues, like debris or a too-small working gap. Due to those early discharges, only partially charged capacitors are ignited and contribute a maximum of half of the discharge energy We per pulse to the material removal process, following their thresholds and Equation (1) [69,70].

Table 7.
Thresholds for differentiation of discharge event types following Nirala et al. [70].
Other authors utilized the ignition delay time for classification purposes. Since the ignition delay time is the time from the voltage pulse being applied until the ignition of the discharge, i.e., until the current rises, this is only possible for static pulse generators [10]. For RC generators, switching on the voltage pulse does not necessarily initiate the ignition of the discharge, but instead the charging of the capacitor first, necessitating other strategies for event classification.
The basis of the signal analysis for the purpose of a classification of discharges proposed in this work is a semi-automated software tool written in the Python programming language and utilizing the Qt toolkit for the graphical user interface (GUI). It was introduced as the first version in prior work, enabling data acquisition and signal analysis based on lists and nested loop iterations to perform classification [15,86]. In this way, the classification was very slow and the raw data had to be split 50 times to achieve an improvement of more than 90% in runtime and disk space. Nevertheless, the time to be spent on signal analysis was in the order of hours rather than minutes for each case and parameter setting, thus hindering the search for an adequate benchmark of the signal analysis parameters. As stated above, this empirical determination of thresholds implies a user-dependent character and threshold evaluation at random that both led to a general underestimation of events by nearly 40%, mainly short circuits, compared with previous results [11].
For performance reasons, these algorithms have now been further enhanced and the discharge energy We can be used as an additional indicator for a sophisticated threshold determination. In particular, the implementation of vector calculations with Numpy, in combination with multithreading and multiprocessing techniques enabled a substantial reduction of the runtime. By substituting the use of loops and entirely adopting Numpy-based computations, the runtime could thus be reduced from 200 times the machining time down to just 0.1 times the machining time of an actual drilling process. These combined methods now allow for real-time signal analysis in principle [68]. Table 8 specifies the thresholds for the gap voltage u that were manually adapted to the signals resulting from the process parameters given in Table 1 and were finally used for the offline signal analysis. The classification algorithm implemented not only utilized the gap voltage u but also the current i for the detection and characterization of discharge events. The combination with edge detection whenever a certain voltage threshold uth = 0.16×ûi = 28.8 V was undercut (falling edge) allowed for the discrimination between different types of events and their assignment to any interval of the pulse cycle time tp. If a falling voltage edge fell from above a gap voltage u = 0.85×ûi to below the voltage threshold uth in close temporal proximity to a rising current edge that exceeded the current threshold ith = 5.9 A, this event was registered as normal. In the same way, the classification of the event types effective and arcing was enabled, only using different voltage thresholds. Current edges occurring at voltage values u < uth were counted as short circuiting.

Table 8.
Adapted thresholds for the differentiation of discharge event types.
Figure 11 details the classification algorithm for the analysis of static, as well as capacitor-based process signals of the gap voltage u and the current i. In this work, capacitor-based process signals were analyzed, which is why the focus was on these data.
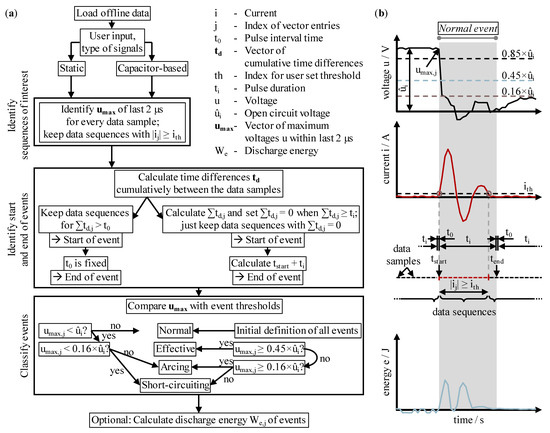
Figure 11.
General algorithm to identify and classify discharge events: (a) flow chart; (b) visualization of the data analysis on the example of a capacitor-based normal event.
The measurement system for signal acquisition involved a TT-HV 150 high-voltage probe from Testec Elektronik GmbH, Frankfurt, Germany, and a TCP303 current probe in combination with a TCPA300 current probe amplifier from Tektronix, Inc., Beaverton, OR, USA, which were both connected to a PicoScope 3405D USB-oscilloscope from Pico Technology, Cambridgeshire, UK. The data were recorded using a Raspberry Pi 4 single-board computer from Raspberry Pi Foundation, Cambridge, UK. Considering the times for buffering tb, transfer tt and saving ts of each data file, a measurement ratio of around rmeas = 0.65 of the ED drilling process was captured for every type of tool electrode within the machining depth 12 mm ≤ dm ≤ 15 mm. The sampling frequency was set to fS = 1 MHz; the number of data points was set to ndp = 250,000 for each data file; and scaling factors of Fu = 100 and Fi = 50 were used for the voltage and current signals, respectively. The first two parameters resulted in a continuous measuring period of tm = 0.25 s for each data file. This period, as well as the internal processing time, for the data handling between two measurement intervals directly affected the measurement ratio rmeas [15], following Equation (8), and the measuring duration tmeas by multiplying it with the number of recorded data files nDF, as seen in Equation (7):
tmeas = nDF × tm
rmeas = tm/(tm + tb + tt + ts)
In addition to the absolute values of the classification results, the event pulse frequency, which is the number of discharge events of a certain type occurring in the working gap per unit time, and the frequency ratio λ, which is calculated as the ratio with the pulse frequency fp, were used for the process evaluations in Section 4.4 [10]. The combination of sophisticated numerical modeling and signal analyses allowed for explanations and to attest to the improved process stability when using helical external flushing channels.
4. Results and Discussion
4.1. Experimental Results
Figure 12 presents the machining results, comparing the process target parameters of MRR, EWR, surface roughness Ra and hole conicity α for the six types of tool electrodes, which are further referred to with the abbreviations given in Figure 3. The standard deviation sD gives the statistical error. The surface roughness Ra represents the surface quality on the hole’s lateral surfaces. Table 9 summarizes in detail all comparisons of interest between the six types of tool electrodes, e.g., the sum of the internal and external flushing channels cross-sectional areas and the flushing cross-sections Af. In addition to Figure 12, the changes in the frontal area Ae, which resulted from the subtraction of the internal and external flushing channels, as well as the machining time tm, are given. These seemingly minor geometric differences were also taken into account for the calculations of the MRR and EWR.
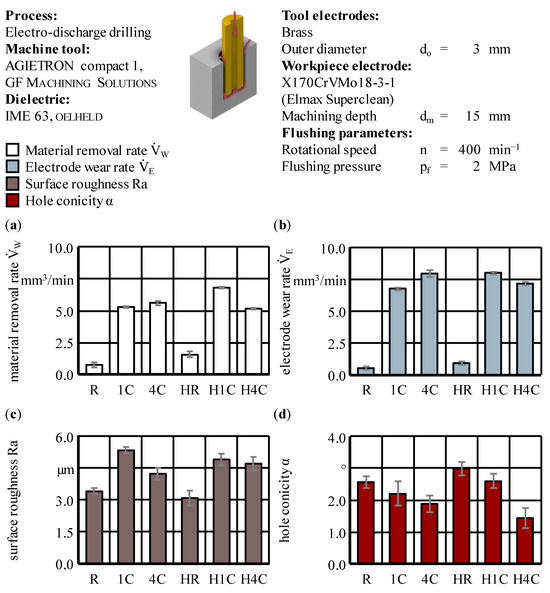

Table 9.
Numeral comparison of process target parameters of the tool electrode types studied [11].
In general, the common target parameters of the EDM process cannot be influenced independently of each other. The results presented in Figure 12 and Table 9 mirror the complex correlations between the target parameters and the fact that they cannot all be improved together.
The influence of the external flushing channel with respect to the MRR and EWR was most obvious for the comparison of the rods. Due to the improved debris removal from the frontal working gap, the MRR and EWR were increased by 112% and 75%, respectively. The latter results from the flushing through the external flushing channel greatly decreasing the machining time tm by 64% by increasing the volume per unit time that was eroded from both electrodes. In fact, the absolute value for the relative linear wear of ϑl = 71.2% for the HR type showed only a minor difference compared with the R type with ϑl = 75.5%. Generally, the additional external flushing channel favored improvements in terms of MRR and surface roughness Ra, but deteriorations of the EWR and the conicity α for the R and 1C types. Surprisingly, it was the complete opposite for the 4C types.
The vastly increased values of the MRR and EWR when using single- and multi-channel tool electrodes instead of one of the rod types resulted from the application of pressure flushing through the internal channels and the direct evacuation of the process residues. The activation of pressure flushing in all cases led to an increase in the surface roughness Ra and a stepwise decrease in the conicity α, as well as the lateral working gap width sL, when comparing R, 1C and 4C or HR, H1C and H4C. In contrast, adding the additional helical flushing channel increased the hole conicity α when comparing R and HR or 1C and H1C. Nonetheless, when comparing 4C and H4C, an improvement of 24% could be stated for the hole conicity α.
Further advancements resulting from the supplementary space for debris and gas bubbles within the external flushing channel could be stated in terms of the MRR with the 1C type, as well as the EWR with the 4C type. In the case of H1C, an improvement of 28% from = 5.3 mm3/min to = 6.8 mm3/min could be stated, but the helical groove caused a slight increase in the relative linear wear from ϑl = 138.7% to ϑl = 144.5%, corresponding to an increase in the EWR by 19%. A similar behavior could be found for the 4C electrodes, where the values were ϑl = 155.0% for 4C and ϑl = 164.3% for H4C, indicating an increase. Nevertheless, the EWR dropped by 10%, which underlines the need to take the geometries of the boreholes and the tool electrodes into account in a precise and detailed manner. The process-effective frontal areas Ae of the tool electrodes were decreased by the inner diameter di of the tool electrodes, as well as the cross-section of the external flushing channel or groove, in terms of the variants with additional passive flushing. Therefore, simplified methods for determining the values of the MRR and EWR, like using the aspired machining depth dm of the holes and the linear wear of the tool electrode ΔlE alone, were not applicable for systematical analyses of the influence of internal and external flushing geometries.
The theoretical effect that a reduced effective cross-section due to subtraction of those geometries led to a decrease in the MRR and an increase in the EWR for reaching a specified machining depth dm of the holes was superseded by the effects of fluid mechanics and thermodynamics when using a flushing pressure and a rotational speed.
When applying an external flushing channel with the particular groove geometry chosen for these experiments, the frontal areas Ae of the tool electrodes were decreased by 7% to 9%. The utilization of internal flushing channels reduced the frontal area Ae by 12% to 20%, resulting in pins with a diameter dp in the order of dp = di − 2s that remained in the blind holes. In the cases of 1C and H1C, the pin kept its full pin height of hp = 15 mm and the pin diameters were dp,1C = 1.00 mm and dp,H1C = 1.05 mm, respectively. Also, in the cases of 4C and H4C, a small pin remained, with pin heights of hp,4C = 3.04 mm and hp,H4C = 2.19 mm and pin diameters of dp,4C = 1.19 mm and dp,H4C = 1.17 mm, respectively. These different pin geometries helped to explain the counterintuitive comparison between 1C and 4C, showing an increase in the MRR, EWR and machining time. Risto et al. already stated that changes in the tool electrodes cross-section combined with the pin formation reduces the effective flushing cross-section Af, hence resulting in increased hydraulic resistance and a decreased volume flow rate for constant flushing pressures pf [36]. Yilmaz and Okka did not explicitly discuss pin formation issues, but just like Bozdana and Ulutas, applied brass multi-channel tool electrodes whose flushing cross-sections Af, unlike in the present study, exceeded those of the single-channel tool electrodes by up to 144% and 34%, respectively. These investigations led to contradictory results concerning a considerable reduction or increase in the MRR but an increased EWR in both cases [21,22]. These results, which are partly contradictory to the present study and each other, underline the fact that generalized findings on internal flushing channels are difficult to deduce and are always case and geometry dependent. Consequentially, the same applies to external flushing channels.
Figure 13 shows the electrode tips on the scanning electron microscope (SEM) images, which were measured using an SEM of type JCM-5000 NeoScope from Jeol Ltd., Akishima, Japan. In the case of the rod electrodes without internal flushing, a small cavity evolved at the tips of R and HR. Only for negatively polarized tool electrodes, as in the present case, Li et al. revealed similar concave contours of the electrode tip and explained this fact with the skin effect and a decreased discharge probability in the center [87]. The authors did not attribute this concavity to the ejection of debris, but from their SEM images, it can be supposed that the center concavity deepened as a result of the increasing rotational speed [87] (p. 9). It can therefore be further concluded that the concave tip contour was also a consequence of accumulated debris in the frontal working gap due to the absence of pressure flushing, supporting the formation of a stationary vortex. The helical geometry of HR reduced this effect, but instead led to an increased relative edge wear ϑIK and, therefore, a more conical tip, relocating the beginning of the groove upward (see Figure 13b,c). The unevenly distributed areas of discharge craters with predominant directions on the lateral surfaces were probably caused by a combination of spindle run-out and pressure flushing, resulting in fluctuating lateral low-pressure regions, with both leading to vibrations of the tool electrode and promoting those irregularities (see Ferraris et al. [17] (p. 193)).
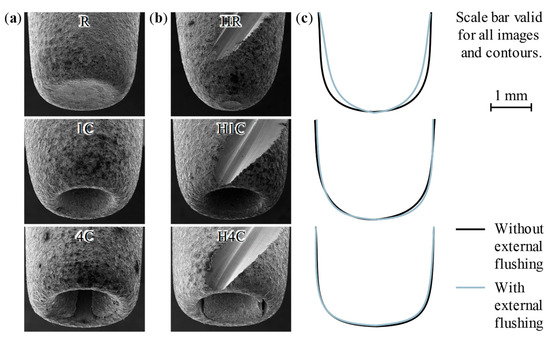
Figure 13.
SEM images and contours of worn tool electrode tips: (a) without external flushing; (b) with external flushing; (c) comparison of contours [11].
The contours of the tool electrodes shown in Figure 13, as well as the bores that were drilled with them, were digitized by using the digital microscope mentioned in Section 3.2. The data obtained in this way enabled fluid dynamic simulations with geometries and working gap dimensions as close as possible to realistic conditions of the ED drilling process, providing explanatory approaches for the process behavior discussed.
Section summary:
- The additional external flushing channel geometry applied favored improvements in terms of MRR and surface roughness, but deteriorations in the EWR and the conicity for the R and 1C types while exhibiting the opposite behavior for the 4C types.
- The MRR increased by 112% when adding an external flushing channel to the R type, by 28% when adding it to the 1C type, but decreased by 8% in the case of the 4C type.
- Due to the relative frontal wear ϑIF, the beginning of the groove, and thus, its beneficial effect, were shifted upward for the HR type. Nevertheless, the bubble-flushing effect most probably generated sufficient additional lift from the tool electrode tip to push and pull removal products in the impact area of the groove.
- A precise comparison of the MRR and EWR between the six tool electrode types necessitated considering geometric differences in the greatest possible detail.
- The resulting pin geometries explained the comparison between 1C and 4C.
- Nevertheless, the effects of the altered frontal areas and flushing cross-sections on the process target parameters were superseded by the effects of cooling and direct ejection of the removal products as a result of the active high-pressure flushing.
4.2. Preliminary Numerical Results with the Generic Models
With the objective of maximizing the numerical robustness and physical validity and likewise minimizing the numerical effort, a generic model with all characteristic properties of the liquid domain of an ED drilling process was introduced, as described in Section 3.3. Figure 14 and Figure 15 show the results of the inflation layer analyses for the number of inflation layers nIL with a fixed height of the first layer h1L and vice versa (see Table 2).
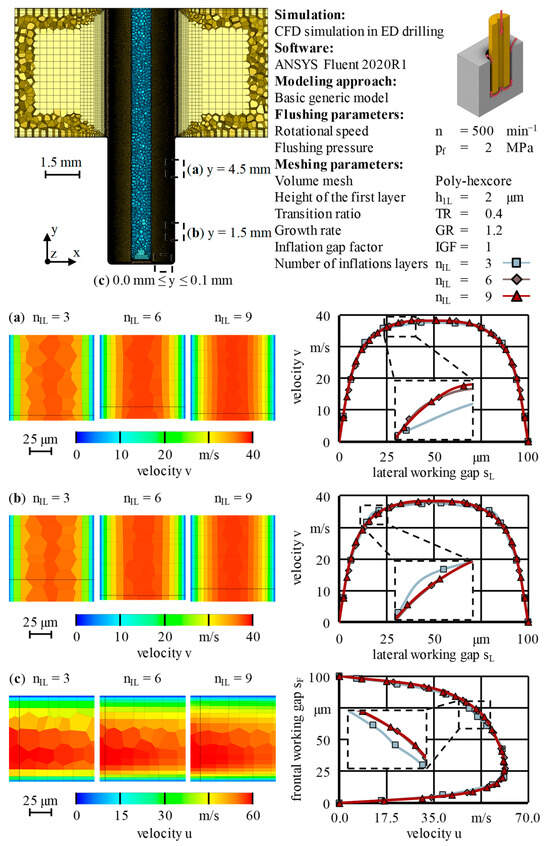
Figure 14.
Variation in the number of inflation layers nIL with fixed height of the first layer h1L = 2 µm. Cells of the mesh are colored according to the velocity downstream of the respective velocity profiles on the right side. Positions: (a) y = 4.5 mm; (b) y = 1.5 mm; (c) 0.0 mm ≤ y ≤ 0.1 mm. Basic generic model, see Figure 5.
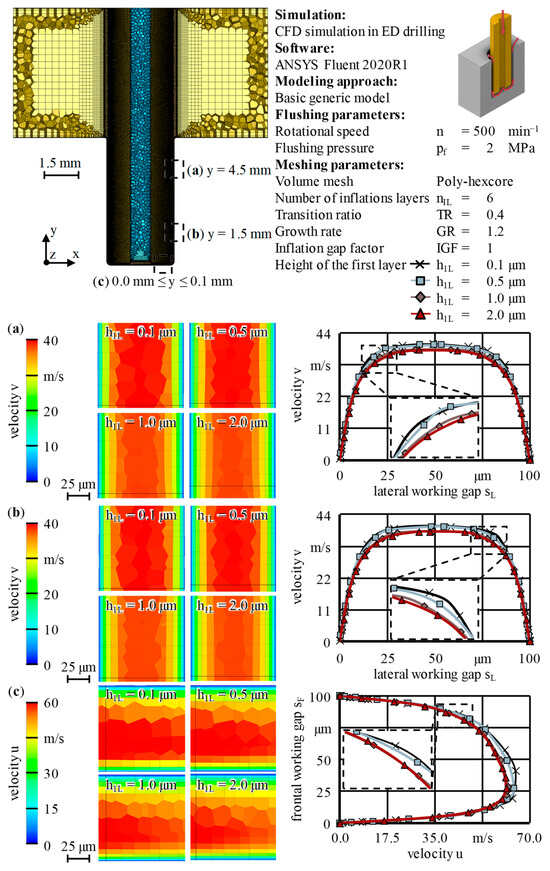
Figure 15.
Variation in the height of the first layer h1L with fixed number of inflation layers nIL = 6. Cells of the mesh colored according to the velocity downstream of the respective velocity profiles on the right side. Positions: (a) y = 4.5 mm; (b) y = 1.5 mm; (c) 0.0 mm ≤ y ≤ 0.1 mm. Basic generic model, see Figure 5.
The velocity profiles with nIL = 3 differed from those with nIL = 6 or nIL = 9, which were nearly identical. This also indicates that a further increase in the number of inflation layers nIL would bring no benefit. For both of the latter, when looking at those cells that were colored according to the dominant velocity component, it can be seen that nearly the full gradients in the direction orthogonal to the wall occurred inside the inflation layer. In contrast, a number of inflation layers nIL = 3 was not capable of resolving the velocity gradients. This is also suggested by the fact that in the last inflation layer, the velocity u or v amounted to just 50% to 70% of its maximum value. Finally, the total number of cells generated was strongly influenced by the number of inflation layers nIL (see Table 10). Based on the first three objectives for the inflation layer analyses below Table 2, nIL = 6 was set for all further analyses.

Table 10.
Total number of cells NC for varying the number of inflation layers nIL and maximum values of y+ in dependence of the height of the first layer h1L.
The variation in the height of the first layer h1L with a fixed number of inflation layers nIL = 6 revealed that the velocity profiles on the right side of Figure 15 showed similar and almost congruent curves for the values below and above h1L = 1 µm. When using heights of the first layer of h1L = 0.1 µm and h1L = 0.5 µm, the maximum velocity was increased by about Δu = 4 m/s in the frontal working gap and about Δv = 2 m/s in the lateral working gap. The colored cells on the left side of Figure 15 highlight these differences. These findings apply to all three positions in Figure 15 and might be explained by the values of the dimensionless wall distance y+, which is related to the height of the first layer h1L in the form of the wall-normal distance y to the first node, following Equation (2). Up to h1L = 0.5 µm, five polyhedral volume cells were placed between the inflation layers on both sides of the working gap with a total share of more than 50%. An increase in the height of the first layer h1L led to a considerable thickening of the inflation layers and, therefore, a decrease in the volume cell percentage between them. Table 10 lists the strong increase in the total number of cells NC for increments of the number of inflation layers nIL, as well as the maximum values of y+ for increasing heights of the first layer h1L. Bearing in mind that values of about y+ = 1 are recommended to properly model turbulence with the near-wall model used and in accordance with the objectives for the inflation layer analyses expressed below Table 2, a height of the first layer of h1L = 0.5 µm was selected for all further studies.
Minimizing the numerical effort is closely related to a minimization of the total number of cells NC but also to the selection of the modeling approach, like CRW, SM or OM, as well as wall functions, solvers, additional algorithms concerning stability and robustness and physical validity of the solution. Using the mesh settings developed so far, the three generic models applying CRW, SM and OM to model the rotation of an asymmetric tool electrode geometry with one straight groove as depicted in Figure 5b–d are compared in Figure 16 and Figure 17. A steady-state solution was first generated and used as the starting solution of the transient calculation of two tool electrode rotations, provided that the respective approach fulfilled the prerequisites for this.
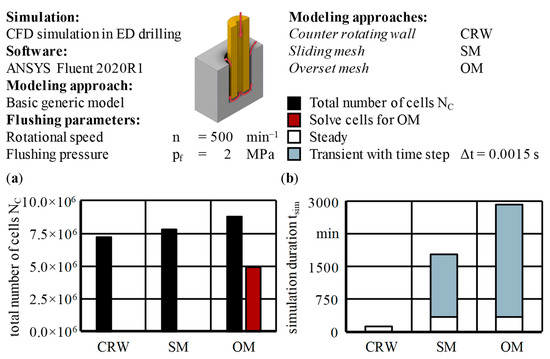
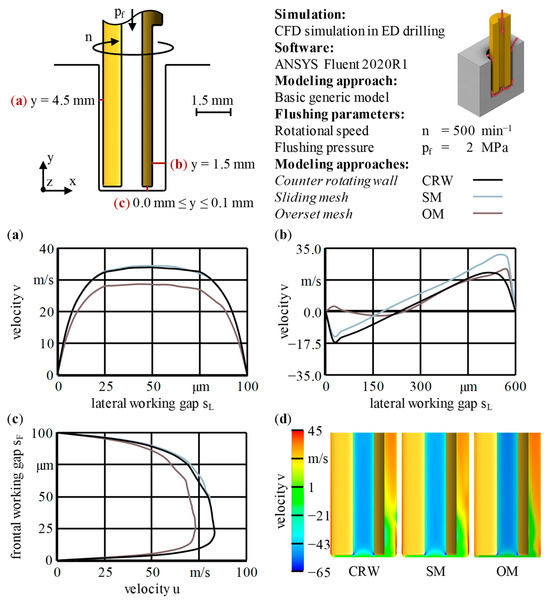
Figure 17.
Comparison of modeling approaches CRW, SM and OM concerning the resulting flow field after two rotations in the form of velocity profiles at positions (a) y = 4.5 mm, (b) y = 1.5 mm and (c) 0.0 mm ≤ y ≤ 0.1 mm. (d) Contour plots. Basic generic model, see Figure 5.
The initially motivated objective to describe the effects of an asymmetric, rotating tool electrode without a numerically expensive mesh motion could not be achieved with the CRW approach because only a steady-state flow condition is generated by means of frame motion. Even in the case of a transient calculation, the steady-state solution remains. This fact makes the CRW approach unattractive for detailed analyses of the influence of external flushing channels. Nonetheless, CRW might be a means to analyze high numbers of simulations, like the variation in input parameters or other considerations where transient effects are of minor interest.
The total number of cells NC increased with the complexity of the modeling. In the case of OM, the merging algorithm and the utilization of bodies of influence for local mesh refinements significantly reduced the total number of cells, as described in Section 3.3 and visualized in Figure 7a. The number of solve cells NS = 4.9 mil. amounted to just 44% of the total number of cells NC before the merging process. Nevertheless, the simulation duration tsim = 48.6 h was the highest for OM by far. The simulation duration tsim = 5.6 h of the steady-state solution was comparable to that of the SM approach but only half of the number of iterations nI = 500 were necessary by applying the coupled scheme in the case of OM. Thus, it can be stated that among other things, settings such as the coupled scheme versus the PISO scheme could lead to a doubling of the simulation duration tsim. The required simulation durations tsim of the transient calculations were additionally driven by the fact that the overset interface must be recreated at the beginning of each time step Δt, meaning that all steps of the merging process have to be repeated over and over again. In conclusion, even in the present simple extension of a steady-state solution of only a generic model, the calculation time increased by a factor of 4.2 or 7.8 for the SM or OM approaches, respectively, when switching to transient modeling.
Figure 17 shows the resulting flow field for the three modeling approaches CRW, SM and OM. Generally, reduced magnitudes of the velocity u or v were calculated for OM compared with CRW and SM, up to a maximum of 20% for Figure 17a. The velocity profiles of the velocities u or v of CRW and SM deviated from each other by about 3 m/s. With an almost linear profile, when crossing from negative to positive velocities v, they indicate a backflow or dead water zone inside the straight groove, whereas the velocity profile for OM hardly reached negative values and assumed a smooth curved profile on the inside of the groove. The backflow area was caused by the very high velocities around u = 75 m/s in the bottom area of the borehole that induced a low-pressure region inside the groove and hindered the ability of the flow to stay attached to the walls. In the case of SM, it can be stated that no unsteady behavior or jump in the velocity profile was generated across the sliding mesh interface. The contour plots in Figure 17d exhibit perceptible differences, especially in the lower half of the groove where the backflow area was of qualitatively different character. Within the steady-state solution of CRW, the upward flow inside the groove was interrupted by a small region of decreased velocity v < 10 m/s, whereas both flow fields of SM and OM directly pointed upward at the outside wall of the borehole with velocities v > 20 m/s. In the case of OM, the flow reattached to the inside wall within the groove considerably later than in the case of SM. The general lack of measured values or observations only allowed for relative benchmarks of the velocity profiles and contour plots. However, the relative comparisons suggest that the OM, in addition to the greatest numerical effort, also ran the risk of leading to distorted flow fields due to numerical diffusion as a result of superimposed interpolations between the different meshes, especially in narrow gaps with strong gradients of the flow variables.
Based on the Courant–Friedrichs–Lewy condition shown in Equation (9), the underlying discretization of the time-dependent partial differential equations can be evaluated concerning stability.
The so-called von Neumann stability requirement is met as long as CFL ≤ 1, where CFL is the Courant number [88]. In this way, the Courant number CFL serves as a stability condition that establishes a relationship between the mesh resolution Δx, the occurring velocities c and the time step Δt, as shown in Equation (10):
Therefore, it indicates the maximum number of cells by which a quantity under consideration moves per time step Δt. For explicit formulations, the Courant number should be below CFL = 1, as mentioned; implicit formulations of the first and second order also remain stable for higher values, like 10 ≤ CFL ≤ 1000, with the exact value depending on the solution method and the complexity of the flow problem. With the given time step of Δt = 0.0015 s for SM and OM, the Courant number is well within the three-digit range in transient areas of the flow field, meaning that theoretically, the time step Δt was supposed to be smaller or the mesh resolution Δx in the form of the volume cell size lc was supposed to be greater. The comparison of the field variable CFL indicates that SM tended to allow for a greater time step Δt than OM. As the calculation of SM was stable and converged with a time step of Δt = 0.0015 s and the global boundary conditions enforced a minimal mesh resolution Δx inside the working gap, there was very limited scope for CFL adaptions.
For the following detailed analyses of the influence of internal and external flushing channels, the SM approach was preferred, especially because of the possibility to use a greater time step Δt, as well as a decreased simulation duration tsim compared with the OM approach.
Section summary:
- Based on a basic 3D generic numerical model, the number of inflation layers and the height of the first layer were identified to be nIL = 6 and h1L = 0.5 µm to assure maximized numerical robustness and physical validity. These findings led to three more generic models to model the rotation of the asymmetric tool electrode geometry.
- The sliding mesh (SM) approach is the best trade-off between the mesh resolution and the accuracy of the solution based on generic numerical CFD models and compared against the two other techniques counter-rotating wall and overset mesh (OM). It holds the possibility to perform transient calculations and use greater time steps with less computation time.
4.3. Numerical Investigations of External Flushing Channels
The simulation results for all tool electrode types R, HR, 1C, H1C, 4C and H4C were obtained by applying the numerical model introduced in Section 3.4 and are visualized in Figure 18. The absolute velocity |c| gave a general insight into the velocity magnitudes inside the internal flushing channels, as well as the frontal and lateral working gaps (Figure 18a). In Figure 18b,c, the component in the vertical y-direction, namely, the velocity v, was considered alone because it was assumed to be mainly responsible for the removal of the debris and gas bubbles (see also Figure 10).
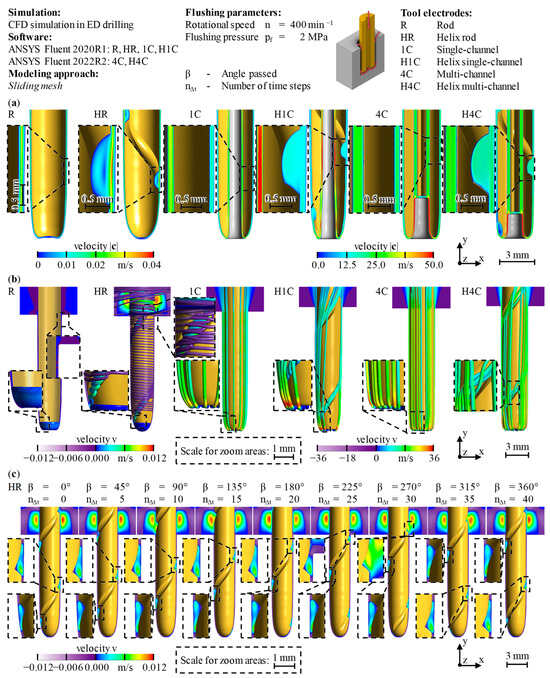
Figure 18.
Quantitative and qualitative visualization of the single-phase fluid flow for all tool electrode types in the form of contour plots and streamlines: (a) absolute velocity |c|; (b) vertical velocity v; (c) transient fluid transport without pressure flushing for the HR type [11], also animated in Video S1. Sliding mesh approach, see Figure 8.
At a constant density ρ of the fluid, the conservation of mass results in an increase or decrease in the velocity magnitudes due to a decrease or increase in the area passed by the fluid. Hence, the differences in velocity magnitudes in the working gaps toward the inner pins, as well as the lateral working gaps, of all six types were direct consequences of the flushing cross-sections Af specified in Table 9 at constant pressure inlet conditions.
This dependency can specifically be seen inside the internal flushing channels of the H1C, 4C and H4C types. Deviations in the contour polygons resulted in slightly variable working gap widths s toward the inner pin, but also, the transition areas from the internal flushing channels toward the remaining pin itself affected the cross-sections and, therefore, increased the velocity |c| to global maxima. In the lateral working gap, the velocities |c| reached values of around |c| = 15 m/s for the 1C and H1C types and around |c| = 25 m/s for the 4C and H4C types, but were below |c| = 0.05 m/s for the R and HR types.
Without pressure flushing, the flow in the working gap only resulted from the electrode rotation. The streamlines in Figure 18b consequently only wrapped around the tool electrode tip for the R type. The color bars helped to separate positive and negative values of the velocity v. Hence, contaminated dielectric fluid mainly circulated in the frontal and lateral working gap, respectively. In addition, the coloring emphasized that there were hardly any velocities v in the axial direction. In contrast, complex vortices formed inside the groove of the HR type. The streamlines shown, as well as the transient observation of the HR tool electrode in Figure 18c for one full rotation, corresponding to an angle passed of β = 360°, indicate an upward transport of the dielectric fluid. For this full rotation, a number of time steps nΔt = 40 was calculated with a time step of Δt = 0.00375 s, ensuring CFL < 5 throughout the domain. It can be seen that the fluid followed a vortex only inside the groove, starting where the groove developed from the tool electrode tip in the positive y-direction. Due to relative frontal wear ϑIF, the beginning of the groove, and thus, its beneficial effect was shifted upward for the HR type, as seen in the SEM images in Figure 13b. Similar vortices within the grooves were also shown by Machida and Natsu in parallel rectangular grooves for tool electrodes with outer diameters of do = 0.09 mm [35].
On the other hand, counter-rotating streamlines with considerably smaller velocities v were downward oriented inside the groove and allowed for fresh dielectric to enter the frontal and lateral working gaps. Nevertheless, the main inward flow passed and circulated along the lateral surface of the HR tool electrode [14]. In comparison, the influence of the helical grooves on the flow fields was much lower for the 1C and 4C types. Most of the dielectric was directly and straight flushed out of the borehole with high vertical velocities of 15 m/s ≤ v ≤ 30 m/s and maxima at the tool electrode tips, showing the dominance of the relatively high flushing pressure pf = 2 MPa over the rotational speed n = 400 min−1. For the H1C and H4C types, the streamlines were not as evenly distributed as with the 1C and 4C types and showed radial and tangential deflections. As with the HR type, there were streamlines following the circumferential groove, but seemed to be pulled out of the groove near the hole outlet and were additionally much less twisted.
This insight was further emphasized by the visual observation that the lateral surfaces of the tool electrodes of type H1C and H4C exhibited asymmetrical distributions of discharge craters, which may have resulted from this flow pattern, as characterized by the deflected streamlines in Figure 18b. This band of discharge craters that developed noticeably wound radially and exactly parallel to the groove of the tool electrodes, indicating an increased amount of lateral discharges in this region. This observation not only supported the numerical results above but also the conclusion that each combination of groove angle and groove depth was related to an optimal combination of the fluid mechanic parameters of flushing pressure and rotational speed. This is supported by observations that the dielectric and debris particles have the same velocities on average [18,19]. Therefore, the assumption that the particles predominantly perfectly follow the fluid and vice versa was justified, showing that findings based on single-phase simulations are sufficient for these kinds of insights. For this reason, the fluid mechanic parameters probably have to be set in such a way that the ratio of the axial to the radial components of the main flow cax/crad decreases so that gas bubbles and debris are pulled into the grooves while being evacuated upward.
Using the evaluation positions given in Figure 9 and Table 6, as well as the definitions in Figure 10, the detailed influence of the helical groove on the flow field could be evaluated (Figure 19 and Figure 20). In all cases, the additional external flushing channel clearly increased the upward oriented volume flow rate as a consequence of the constant flushing pressure pf and the additional flushing cross-section Af (Figure 19a). The differences in the extended flushing cross-sections Af around the lateral working gaps were, however, rather driven by lateral material removal, leading to hole conicity α on the workpiece electrode, as well as relative lateral wear ϑlL on the tool electrode side, resulting in varying lateral working gap widths sL. This explains the steadily rising graphs in Figure 19b and the deceleration for the H1C and H4C types from P3 in Figure 19c. The increased volume flow rates when comparing the 1C and 4C or H1C and H4C types follow from the much higher velocities |c| in the bottom area of the pin (see Figure 18a). In Figure 19c, the ratio of the axial velocity |cax| to the radial velocity |crad| is an indicator of the vertical pull effect. The ratio decreased for all tool electrode types from evaluation position P1 to P2 because of higher radial velocities crad in the bottom area where the fluid must follow the conical contour of the electrode tips. Nevertheless, comparing the pull effects, especially for the additional external flushing channels in that particular area at P2 where particles and gas bubbles originated, the helical groove led to an increase in the velocity ratio by 52% for H1C compared with 1C to a value of |cax|/|crad| = 3.0 and by 1635% for HR compared with R to a value of |cax|/|crad| = 0.04. However, the ratio was reduced by 15% for H4C compared with 4C to a value of |cax|/|crad| = 3.4. These qualitative velocity ratio tendencies coincided very well with the experimental material removals quantified in Figure 12 and Table 9 in terms of the MRR and EWR. Also, the 98% increase in the velocity ratio to a value of |cax|/|crad| = 4.0 for the 4C type compared with the 1C type is in good agreement, not only with the upward volume flow rate but also with the experimental data. This difference between both types persisted at P3 and P4.
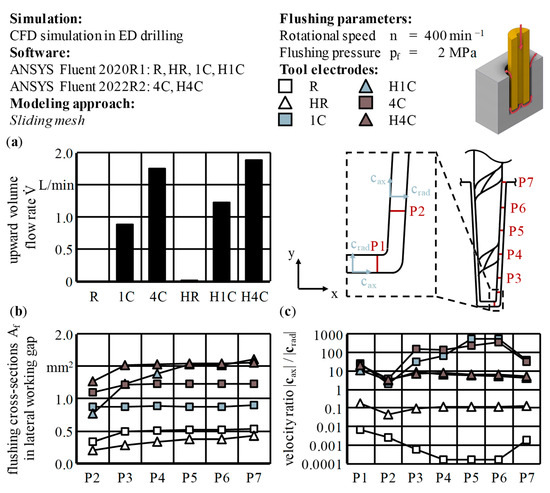
Figure 19.
Quantitative evaluations of the single-phase fluid flow for all tool electrode types: (a) upward-oriented volume flow rate ; (b) development of the flushing cross-sections Af along the lateral working gap; (c) calculated velocity ratio of absolute axial to radial velocity |cax|/|crad|. Sliding mesh approach, see Figure 8. Table S4 contains all original data.
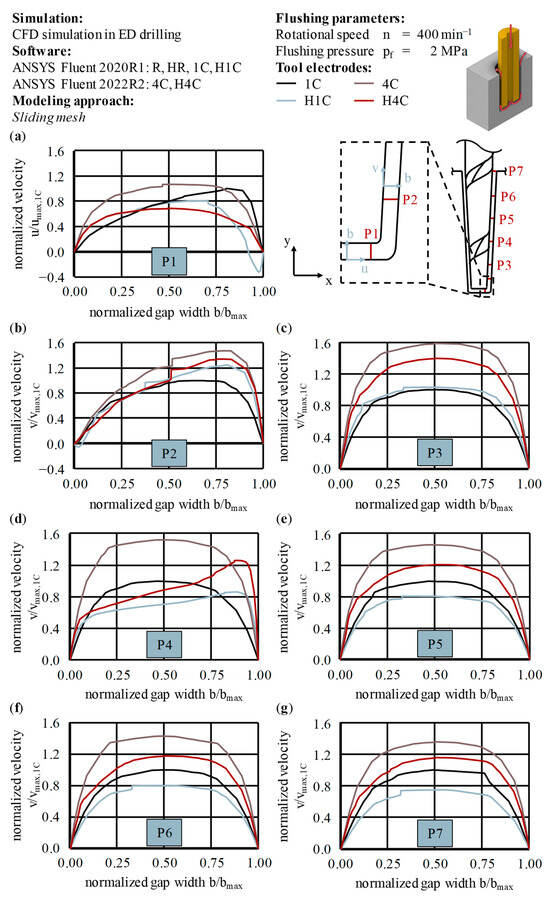
However, for the two rod types R and HR, the ratio shows the transformation of pure radial to a considerable axial movement of the dielectric as a result of the external flushing channel. The proportion of the axial velocity |cax| increased by up to three orders of magnitude for P4 to P6, from 0.015% to over 10%. Even though the R type has a reduced relevance for industrial applications, its detailed consideration allows for separately analyzing the influence of an external flushing channel without superposed pressure flushing.
The external flushing channel entails an increased flushing cross-section Af by 39% in the case of the 1C types and, therefore, resulted in an enhanced volume flow rate by the same amount (Figure 19a,b). The additional circumferential components of the H1C and H4C types steadily increased with growing distance in the y-direction and reduced the velocity ratio |cax|/|crad| by one to two orders of magnitude from P3 upward compared with 1C and 4C. As a result, the residence time tr of the dielectric in the working gap was prolonged, increasing the probability of fault discharges but also of shearing and scattering of gas bubbles and particle clusters. The residence time tr between P3 and P7 was naturally minimal for 1C and 4C, as the radial velocities crad were of negligible relevance compared with the axial velocities cax. Less contamination was the natural consequence.
The velocity profiles of all four tool electrode types with active flushing, normalized with the maximal velocity of the reference 1C type umax,1C or vmax,1C at any given position, further elucidated the velocity magnitudes across the normalized gap width b, as indicators for the flushing efficiency If (see Figure 20). The flushing efficiency If can be assumed to be the product of density ρ and velocity |c|, with area-based mean velocity values suggested in the present case [47]. The R and HR types were omitted from the comparison due to their very low axial velocity values. Step-like jumps in some graphs, as in Figure 20b, originated from the sliding mesh interface, but represent only local discontinuities in the velocity profiles (see also Figure 5c, no. 14).
It can be seen that the velocity profiles of 1C and H1C were asymmetrically deformed toward the tool electrode wall at P1, as are all profiles toward the borehole wall at P2, indicating increased flushing efficiencies If for b > 0.5×bmax. Only the H1C type produced a local backflow in the area of P1 with a velocity of u = −12.5 m/s, which developed negligibly further when following the electrode contour to P2. This fluid flow detachment happened in close vicinity to the tool electrode wall at a distance of b ≥ 0.9 bmax at P1 or b ≤ 0.1×bmax at P2. Generally, from P3 to P7, all velocity profiles resembled the well-known profiles of a Poiseuille flow and declined along the lateral working gap. While the H4C type exhibited the highest volume flow rate in the working gap, the 4C type, with v ≤ 1.6×vmax,1C, had the consistently highest velocities v in the fluid domain, still ahead of the H4C type with v ≤ 1.4×vmax,1C. The highest upward volume flow rates and velocity ratios |cax|/|crad| correlated with the conicity α (see Figure 12). Above P3, the velocities v of the H1C type decreased to more than 20% below those of the reference 1C type. This was because the H1C type experienced the greatest increase in the flushing cross-section Af along the lateral working gap (Figure 19b). This kind of abrupt area increase also accompanied the region around the helical groove at P4 (Figure 20d). Generally, the fluid was noticeably decelerated inside the external flushing channel within a normalized gap width b/bmax ≤ 0.75 and exhibited velocity peaks in the area of the lateral working gap for b/bmax > 0.8 in the order of the preceding velocity magnitudes at P3.
The velocity profiles of the H1C and H4C types show the influence of the groove geometry, and it, therefore, seems reasonable to evaluate the capabilities of evacuating debris and gas bubbles, not only by means of the velocity profiles at this point P4 but also to try to influence these local profiles specifically by varying the fluid mechanical parameters of rotational speed n and flushing pressure pf. The objective of this could be the generation of a pressure gradient through greater velocities within the helical groove in order to pull the removal products into the groove already in the bottom area of the borehole instead of them being transported vertically through the lateral working gap due to the velocity peaks there, and thus, increasing the probability of fault discharges. Figure 21, therefore, shows the influences of the fluid mechanical parameters of rotational speed n and flushing pressure pf on the velocity ratio |cax|/|crad| and the corresponding velocity profiles at the evaluation position P4 of the H1C type. All cases were calculated in ANSYS Fluent 2023R2.
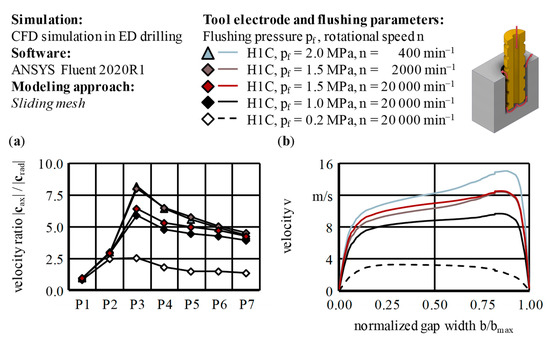
Figure 21.
Influences of the fluid mechanical parameters flushing pressure and rotational speed on (a) the velocity ratio |cax|/|crad| and (b) the velocity profile at evaluation position P4. Sliding mesh approach, see Figure 8. Table S6 contains all original data and Video S2 visualizes the gas evacuation capabilities for three distinct cases in 3D.
As discussed above for the H1C and H4C types in Figure 18, the dielectric was mostly directly and straight flushed out of the borehole as a consequence of the dominance of the flushing pressure pf = 2 MPa from the rotational speed n = 400 min−1. Gradually decreasing the flushing pressure but at the same time increasing the rotational speed shifted the velocity profile downward, maintaining its qualitative shape (Figure 21b). Despite the pressure reduction, axial velocity components |cax| were generated and the corresponding ratio was increased (brown diamonds) compared with the reference case (blue triangles) (Figure 21a). Further increasing the rotational speed ten times while keeping the flushing pressure constant considerably lowered the velocity ratios |cax|/|crad| along the whole lateral working gap (red diamonds) because of the high radial velocity components |crad|. The respective velocity profile at P4 did not alter very much. Nevertheless, the vertical velocity v was visibly increased for b/bmax < 0.75, enhancing the evacuation capabilities of the groove itself. Keeping the rotational speed constant at a value of n = 20 000 min−1 and further decreasing the flushing pressure down by 33% to pf = 1.0 MPa (black diamonds) and by 87% to pf = 0.2 MPa (white diamonds) significantly but not linearly reduced both the velocity profiles, as well as the velocity ratios. However, the latter still exhibited velocity ratios of around |cax|/|crad| = 1.5. Qualitatively, the velocity profile resulting from the lowest flushing pressure analyzed nearly corresponded to the Poiseuille profile (see Figure 20e–g), but this time with a perceptibly shifted peak from the outer to the inner side of the lateral working gap, displaying a 21% difference between b/bmax =0.7 and b/bmax = 0.3. This shows the theoretical possibility of even manipulating the velocity profiles so that the vertical velocity v inside the groove is higher than in the lateral working gap.
Additional multi-phase simulations were carried out to even better illustrate the effects of the different combinations of fluid mechanical parameters of Figure 21 in 3D, over time and in interaction with a gaseous phase. These results are given in Video S2 as a kind of preview to future work but are not meant to be the main focus of the present paper. A time step of Δt = 0.00375 s and a surface tension coefficient of γ = 30 N/m were utilized, with both being a factor 1000 higher than physically reasonable but facilitating an appropriate simulation duration tsim, as well as sharp phase boundaries. The corresponding fluid properties are given in Table 4.
Section summary:
- A complex 3D CFD model using the SM approach ensured detailed numerical investigations of the fluid flow within the working gap in general and evaluations of the external flushing channel’s influence on the flow field for all six types of tool electrodes in particular.
- For the two rod types, the ratio of the axial to the radial velocity components showed the transformation of pure radial to a considerable upward-oriented axial movement of the dielectric as a result of the additional external flushing channel. Inside the groove, a downward-oriented fluid flow allowed fresh dielectric to enter the borehole.
- In the cases of the 1C and 4C types, most of the dielectric was directly and straight flushed out of the borehole with high vertical velocities, showing the dominance of the high flushing pressure over the rotational speed. In contrast, for the H1C and H4C types, the residence time of the dielectric in the working gap was prolonged, increasing the probability of fault discharges but also of the probably positive effect of shearing and scattering of gas bubbles and particle clusters.
- All types with an external flushing channel exhibited increased upward volume flow rates, as well as streamlines that followed the circumferential groove. However, some streamlines of the H1C and H4C types were pulled out of the groove, suggesting continuous spillover of fluid along the whole groove edge. Therefore, the need for adaptions of the fluid mechanical parameters specifically for each combination of groove angle and groove depth became evident. This has to be done in a way that means the ratio of the axial to the radial components of the main flow decreases so that gas bubbles and debris are pulled into the groove while being evacuated upwards.
- This is why the possibility of manipulating the velocity profiles on purpose was shown.
- An additional external flushing channel improved the pull effects in the area where particles and gas bubbles originated. The revealed tendencies coincided very well with the quantified experimental data in terms of the MRR and EWR. Also, the increase in the corresponding velocity ratio for the 4C compared with the 1C type was in good agreement, not only with the quantified upward volume flow rate but also with the experimental data.
4.4. Signal Analysis Results
Utilizing the software and classification algorithm described in Section 3.5, the ED drilling process was captured and analyzed for all types of tool electrodes at the machining depth 12 mm ≤ dm ≤ 15 mm because the process influencing flushing conditions was assumed to be increasingly effective with proceeding machining depth dm. The relatively short pulse duration ti = 18 µs led to a staircase-like charging of the capacitor. With this high duty factor of τ = 0.88, four loading cycles of the capacitor were necessary to provide the full theoretical discharge energy We ≤ 21.4 mJ and reach the open circuit voltage ûi. The very short pulse interval time t0 = 2.4 µs furthermore favored high loads of debris and gas bubbles, as well as consecutive discharges. This can lead to a high MRR and low EWR, provided that the electrical conductivity σ of the dielectric does not increase too much [10] (p. 39). The latter is related to the breakdown resistance ED, which is influenced by the frontal or lateral working gap, as well as by contamination, such as debris. Increasing the charge current iL will increase the effective pulse frequency fe of capacitor discharges within the set pulse cycle time tp, given that the latter is sufficiently long to allow for more than one discharge. If the working gap is too small or the dielectric strength of the process medium is too low, the capacitors, which are not yet fully charged, will discharge early [10,53]. It is not to be forgotten that any discharge event statistics obtained in the manner presented here also include lateral discharges. Thißen et al. presented an approach to distinguish between discharges that occur in the frontal or lateral working gap [86]. There, the same tool electrode geometries but different fluid mechanic parameters and a prolonged pulse cycle time tp were used to include the whole capacitor charging phase. Amongst others, the authors found that as the machining depth dm increased, the number of detrimental events gradually decreased for the H1C type in the lower workpiece half, but remained the same for the H4C type [86]. This supports the assumption of deteriorating effects of turbulences when using multi-channel tool electrodes.
Figure 22 shows exemplary parts of the signal waveforms, as well as the associated classification result, arranged according to their discharge energy We. During the discharges as a consequence of fully loaded capacitors, discharge currents ie < 125 A flow through the working gap, resulting in average discharge currents e < 20 A for one discharge event that is classified as normal. With e ≈ 17 µs, the actual average discharge duration perfectly fit in the pulse cycle time tp = 20.4 µs.
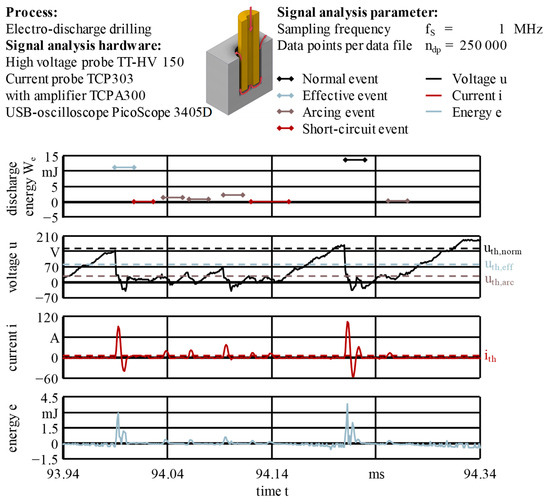
Figure 22.
Exemplary classification results plotted against the events discharge energy We on the basis of the thresholds chosen, as well as excerpts of the waveforms of voltage u, current i and energy e. For process parameters, see Table 1.
The evaluation of the process performance on the basis of the discharge energies We contributed by the respective event types in Figure 23 revealed quantitative measures for the mean discharge energies of normal events with We,norm = 14.31 mJ, effective events being about half of that with We,eff = 6.49 mJ and arcing events with We,arc = 1.62 mJ. These average values were all nearly constant across the six tool electrode types and featured very low standard deviations 0.62% ≤ sD ≤ 2.34% for the 1C, 4C, H1C and H4C types (see Figure 23a). Nevertheless, for the R and HR types, the slightly reduced mean values, as well as the standard deviations 7% ≤ sD ≤ 10%, for all three event types indicate frequent early discharges with releases of smaller amounts of the stored capacitor energies during the process. It can be assumed that accumulated particles frequently bridged the working gap due to poor flushing conditions. In general, with no current flow, open-circuit events had no more energetic contribution to any material removal than the short-circuiting events, which arose from the aforementioned bridging and whose mean discharge energies of We,short = 0.1 µJ were six orders of magnitude lower than those of normal events. This merely computational energy amount resulted from the signal noise of the voltage around the value u = 0 V. This is why these energetic inputs could be neglected.
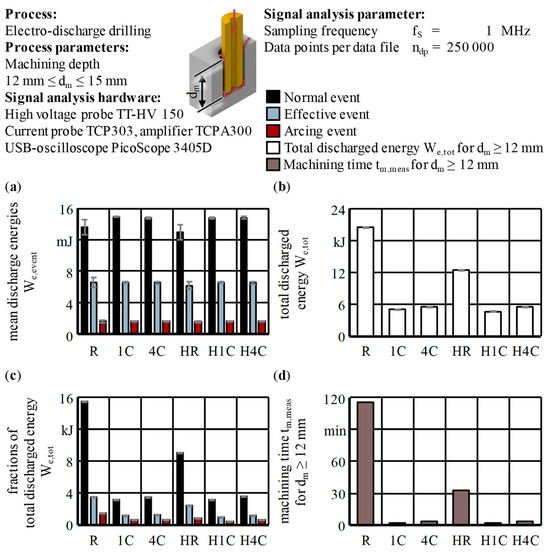
Figure 23.
Evaluation of process performance on the basis of discharge energies We contributed by the respective event types: (a) mean discharge energy We,event per event type; (b) total discharge energy We,tot for the entire machining depth 12 mm ≤ dm ≤ 15 mm; (c) total discharge energy We,tot, split into its fractions; (d) machining time tm,meas for the machining depth 12 mm ≤ dm ≤ 15 mm. For process parameters, see Table 1. Table S7 contains all original data.
The total discharged energy We,tot in Figure 23c and the fractions of it for every event type in Figure 23b correlated very well with the machining time tm,meas for the drilling process during the signal data acquisition in Figure 23d for all tool electrode types. The fact that the highest values of the total discharged energy We,tot during drilling was related to the longest machining times tm,meas or lowest MRR was misleading. The causality was the other way around, where an unstable, and thus, long drilling process resulted in significantly more discharge events in absolute terms, and thus, higher cumulative or total discharge energies We,tot. In addition, it is necessary to recall that neither the total nor always the same amount of discharge energy We is available for material removal at both ends of the plasma channel. Thus, the location-dependent amounts of heat and, hence, energy losses in the form of heat conduction, convection and radiation, as well as the local transient temperature field resulting from the numerous discharges, all together lead to variable percentage shares of the real energy input into the workpiece that is available for material removal [76,89,90]. These variable percentage shares were hence especially affected by the varying velocity gradients within the flow fields of the six different tool electrode geometries considered. Thus, similar discharge phenomena had different effects for different types of tool electrodes.
Data from the literature on the relative energy amounts transferred to the workpiece vary between 1% and 40% and apparently depend on the process boundary conditions [76,89]. For steel in a hydrocarbon-based dielectric, as well as for pulse durations in the order applied in the present study, values in the range of or below 20% are mentioned, as well as the fact that a usually much larger proportion of the energy than 20% dissipates into the dielectric [76,89]. The flushing efficiency If in this context is one major factor that directly influences the convective energy dissipation into the dielectric as a result of forced convection. The so-called Richardson number characterizes mixed convection problems. From the absolute velocity |c| inside the frontal and lateral working gaps in Figure 18a, it must be concluded that the 1C, 4C, H1C and H4C types exhibited very small Richardson numbers, indicating flows dominated by forced convection. In contrast, the R and HR types, with velocities three orders of magnitude lower, were presumably dominated by free convection. When calculating the energy distribution in continuous sinking EDM processes from measured temperature curves, Oßwald et al. verified the crucial influence of flushing on the temperature field of the electrodes by increasing the forced convection through a higher flushing jump frequency. The fifth of the pause between electrode jumps cut the electrodes’ absolute heat Q by more than half. Also, they illustrated a vast decrease in heat transfers to the workpiece and tool electrodes over the machining process, down to less than 1% at the end of the process, whereas heat transfers into the dielectric and machine tank increased from 35% to 55% and from 7% to 13% [89] (p. 7).
The preceding paragraph emphasizes that it is not possible to draw direct, let alone linear, connections from the discharge energies calculated by means of signal analysis to the process target parameters, such as the MRR, EWR, surface roughness Ra or hole conicity α. Nevertheless, the classification and quantification of the discharge event types allow for conclusions regarding their frequencies, and thus, the process stability, which is further motivated by the comparison of the classification results and waveforms of the HR and the 4C type tool electrodes in Figure 24.
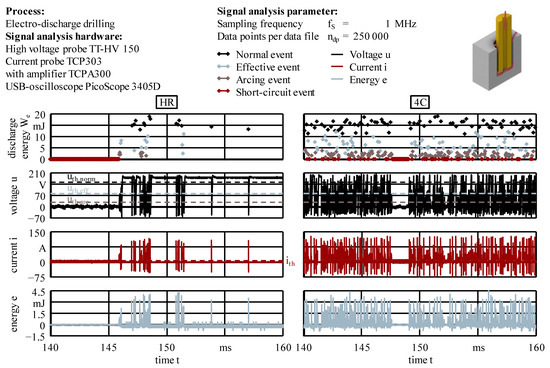
Figure 24.
Comparison of classification results and the waveforms of voltage u, current i and energy e of the HR and 4C type tool electrodes as examples for tool electrodes without and with active flushing. For process parameters, see Table 1.
Qualitatively similar results were obtained for the R type or the 1C, H1C and H4C types as for the HR type or 4C type. For this reason, the latter two were considered representative. Their waveforms and classification results directly illustrate and explain the major differences between the target parameters of those tool electrodes without or with active flushing in Figure 12. Without active flushing, the process signals show numerous long sequences of open-circuit events, as well as detrimental discharge events, such as short-circuiting. In particular, the numerous short circuits result in frequent retraction movements of the feed axis, and thus, not necessarily an increased frequency but an increased absolute number of open-circuit periods, as well as a longer machining time tm or decreased MRR. Li et al. observed this halt in the feed motion within micro-bores and highlighted the occurrence of discharges only between the tool and the dielectric particle mixture [91]. The absolute values for the machining time during the signal analysis tm,meas in minutes or percentage, as well as for the event distribution, verify this conclusion (Table 11).

Table 11.
Detailed qualitative and quantitative information on the signal analysis with absolute values for the classification results.
Figure 25d–g show the signal analysis results for all six types of tool electrodes by differentiating discharge events in the categories of full capacitor discharges (normal), early capacitor discharges (effective), arcing and short circuiting. These categories were merged into beneficial and detrimental events in Figure 25a,b, which summed up to 100%, together with those events without any contribution (open circuit) during the capacitor charging cycles or retraction movements of the feed axis (Figure 25c). Open-circuit events beyond the charging cycles originating from retraction movements could be identified by calculating the ratio of open circuits to beneficials. With the given process parameters and for a perfect series of normals and effectives, that ratio would be three to four. However, it equals 70 and 29 for the R and HR types, but only 10 for the 4C and H4C types, as well as 7 for the 1C and H1C types. This underlines the different frequencies of retraction movements of the feed axis, as well as the machining times tm,meas in Figure 23d.
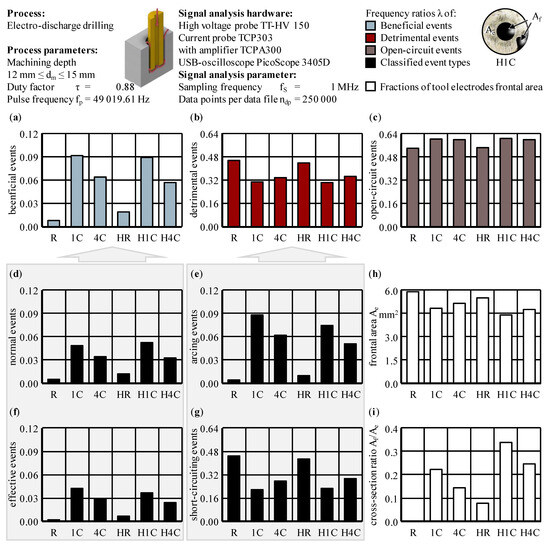
Figure 25.
Signal analysis results for all six types of tool electrodes. Contributions of (a) beneficial discharge events λben; (b) detrimental discharge events λmal; (c) open-circuit events λopen; (d) normal events λnorm; (e) arcing events λarc; (f) effective events λeff; (g) short-circuiting events λshort. Tool electrode frontal areas: (h) frontal area Ae; (i) ratio of flushing cross-sections to frontal areas Af/Ae. For process parameters, see Table 1. Table S8 contains all original data.
For all these bar diagrams, the frequency ratio λ was used because it divides those categories according to percentage fractions and, therefore, mirrors the relative event distribution. In this way, implications are given concerning the process stability in the following way. A high share of beneficial events is an indicator of increased process stability and, vice versa, a high share of detrimental events indicates low process stability. Additionally, Figure 25h,i display the absolute frontal area Ae and the relative flushing cross-section Af/Ae available for flushing for all tool electrode types. Haas et al. used a classification that detected events with and without ignition delay time td, as well as open circuits and also utilized the frequency ratio λ for the evaluation of gap flushing in deep hole drilling by establishing relationships between the volume flow rate and the event types or the MRR and EWR [92].
The most relevant conclusions and relationships to be drawn from Figure 25 are as follows:
- The R and HR types led to the lowest frequencies and frequency ratios of beneficials (see figure parts (a), (d) and (f)).
- Open circuits were driven by normals and effectives because of the corresponding charging cycles of fully or nearly full charged capacitors (see figure part (c)).
- The beneficial frequency ratio λben correlated with the MRR and the surface roughness Ra (see figure part (a) and Figure 12).
- The arcing frequency ratio λarc drove the EWR, in addition to the high energetic normal discharges (see figure part (e) and Figure 12).
- The normal frequency ratio λnorm correlated with the use of internal flushing and the flushing cross-section ratio Af/Ae (see figure parts (d) and (i)).
- The short-circuit frequency ratio λshort was slightly favored as a consequence of turbulences or radial velocity components |crad|, which were both primarily induced by multi-channel tool electrodes (1C → H1C, 4C → H4C) (see figure part (g) and Table 9). Furthermore, the streamlines for the H1C and H4C types in Figure 18b suggest continuous spillover of some fluid along the whole grooves edge as another reason for the systematic triggering of short circuits.
- The probability of detrimental events correlated with greater frontal areas Ae or smaller flushing cross-sections Af (see figure parts (b), (h) and (i)).
Figure 26 allowed for similar conclusions to be drawn, but highlights the evolution of the discharge distribution over the entire last machining depth dm = 3 mm of the boreholes. For this purpose, the relative event distributions in Figure 26a, as well as the amounts of the discharge energies We classified per data file and summed up according to the event types in Figure 26b are shown. The open-circuit fractions were not considered here, and thus, the 100% in Figure 26a refers to the total amount of all actually occurring discharge events. Each symbol in the scatter plots represents the integral information of an event type out of one data file containing a continuous measuring period of tm = 0.25 s each. It can be seen that the scattered points for the relative event distributions, as well as for the discharge energies We, generally homogenized as a result of an external flushing channel (R → HR, 1C → H1C, 4C → H4C). The scatter of the points thus decreased verifiably. Also, the slight increase of the mean short-circuit fractions when comparing 1C and H1C or 4C and H4C, as well as the increase in the mean energy fractions of the normal events when comparing R and HR or 1C and H1C, are important to highlight. Looking at the gradients or slopes of the average percentage event distributions from Figure 26a over the whole machining depth from dm = 12 mm to dm = 15 mm, it can be found that conventional internal flushing continued to drive increases in the beneficial events by 0.7 and 0.4 absolute percentage points on average for the 1C and 4C types, respectively. The additional external flushing channel when compared with the H1C and H4C types resulted in a reduction in beneficials by 1.6 percentage points for H1C but an increase by 1.4 percentage points for H4C (see Figure 27).
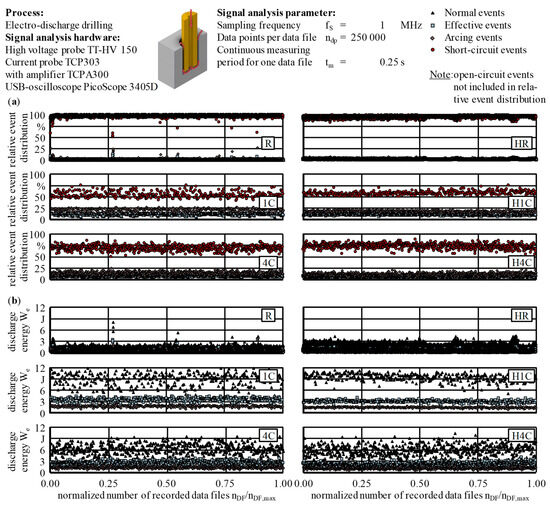
Figure 26.
Signal analysis results for all six types of tool electrodes over machining time tm,meas or the normalized number of recorded data files nDF/nDF,max: (a) relative event distribution excluding open circuits; (b) discharge energy We for each data file, split into the event fractions. For process parameters, see Table 1.
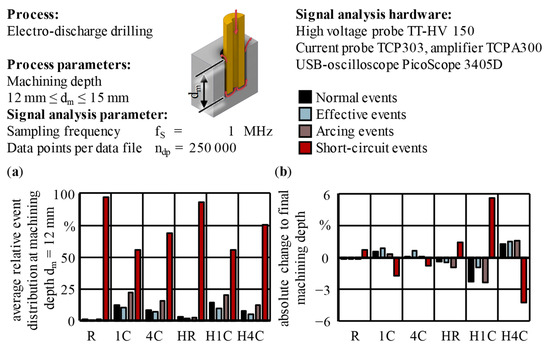
Figure 27.
Quantitative evaluations of the relative event distributions and their changes over the last fifth of drilling: (a) average relative event distributions at the beginning of the signal analysis; (b) changes in absolute percentage points up to a machining depth of dm = 3 mm. For process parameters, see Table 1.
However, the initial level must always be taken into account since H1C had 14.5% normals and 10% effectives after dm = 12 mm, whereas H4C had only 7.5% and 5.4%, respectively. The HR type very slowly converged to the R type as the machining depth increased. The initially 2 to 3 times higher percentage shares of beneficials and arcs decreased by averages of 0.4 and 1 percentage points, respectively, and the 93% initially lower share of shorts increased twice as fast as for the R type. Despite these converging trends, it can be assumed that even for further-increasing machining depths, the positive effects of the HR type remained and the induced positive vertical velocities v as depicted in Figure 19c amplified the bubble flushing effect that was described in detail by Li et al. [65]. Additionally, gas bubbles were most probably sheared off by the rotating groove and, therefore, reduced in size, as well as partly ejected through the groove. In contrast, following the findings of Li et al., the R-type particles in particular behaved as colloidal particles, and thus, formed flakes and clusters that tended to accumulate. Also, the bubble-flushing effect faded for increasing aspect ratios A ≥ 3.3 and, as a consequence, the process conditions deteriorated and the feed rate was decreased for the R type in particular [65]. The latter could also be seen for similar aspect ratios in [12] (p. 2).
Starting at the same level, short-circuit events steadily decreased by 1.7 percentage points for the 1C type but grew by 5.6 percentage points for the H1C type. The percentage of shorts of the H4C type was expected to fall below that of the 4C electrode at a machining depth of dm = 16 mm if the trend remained unchanged.
Section summary:
- Signal analyses of the gap voltage and current within the machining depth 12 mm ≤ dm ≤ 15 mm capturing 65% of all events allowed for a detailed event classification based on the edge detection and thresholds.
- Using performance-enhancing algorithms and techniques, the classification runtime could be reduced from 200 times the machining time down to 0.1 times the machining time of the actual drilling process, allowing for real-time signal analyses in principle.
- The R and HR types exhibited frequent early discharges as a result of accumulated particles that were bridging the working gap due to poor flushing conditions.
- Among other things, it was shown that the arcing frequency ratio defined the EWR, and the beneficial frequency ratio correlated with the MRR and the surface roughness.
- The short-circuit frequency ratio was favored as a consequence of turbulences or radial velocity components, like when using 4C or H4C tool electrodes or adding the additional external flushing channel.
- The probability of detrimental events correlated with greater frontal areas or smaller flushing cross-sections.
- The abstinence of active flushing led to numerous long sequences of open-circuit events as a result of frequent retraction movements of the feed axis.
- The frequencies of feed axis retractions as a result of arcing or short circuiting were calculated directly from the data of the signal analysis, revealing excellent agreement with the corresponding machining time over all types of tool electrodes.
- The causalities of an unstable process, and therefore, long machining time or low MRR with high values of the cumulative discharged energy were explained in light of the variable percentage shares of the real energy input being available for material removal, as well as the fact that the removal effects of distinguished discharge event types were influenced by the flow field’s gradients.
5. Conclusions and Outlook
In this study, the influence of flushing conditions during ED drilling using tool electrodes with different internal and external geometries, as well as their interactions, were investigated. For this purpose, the processing results of ED drilling with tool electrode geometries based on the standard tool rod (R), single-channel (1C) and multi-channel (4C) electrodes, each without and with a helical external flushing channel (prefix H), were presented, as well as corresponding numerical results of the single-phase fluid flow field based on the measured geometry contours. Steady-state solutions were complemented with sophisticated transient numerical calculations. Hence, in contrast with the literature, not only passive flushing but also the impact of superimposed active flushing was considered. A special focus was given to detailed explanations of the numerical modeling approaches to ensure comprehensibility and reproducibility. Further explanatory approaches were given by results of the signal analyses, with substantially reduced runtimes by using vector calculations in combination with multithreading and multiprocessing techniques, as well as related elaborate discussions. These experimental and numerical methods and models summed up to an overall suitable approach to maintain the process stability at high aspect ratios due to improved flushing conditions on the basis of in-depth knowledge about the complex processes inside the working gap.
Concerning the research question, it was concluded that causal relationships existed between the variables analyzed, namely, the improvements in process target parameters, the additional spaces in the form of external flushing channels and the additional active flushing applied. The main findings of this study were as follows:
- The additional external flushing channel geometry applied favored improvements in terms of the MRR and surface roughness, but deteriorations in the EWR and the conicity for the R and 1C types while exhibiting opposite behavior for the 4C types.
- The MRR increased by 112% when adding an external flushing channel to the R type and by 28% when adding it to the 1C type, but decreased by 8% in the case of the 4C type.
- The experimental results, especially when compared with the literature, underline the fact that generalized findings on internal flushing channels are difficult to deduce and are very case and geometry dependent. Consequentially, the same applies to external flushing channels and interdependencies with any kind of internal flushing.
- Single-phase simulations were sufficient for basic insights into the already complex flow field inside the working gap.
- Steady-state simulations were also sufficient for most basic analyses, like parameter studies on fluid mechanic parameters. Nevertheless, transient calculations were indispensable for the examination of transient effects, like multi-phase flow and phase interactions. However, transient calculations came with a vastly increased numerical cost, especially when performing parameter studies or two-way coupled two- or even three-phase calculations.
- However, the possibilities to explain any detail of the experimental results were, of course, limited. The major reasons for this were not only the imperfections of real experiments, like pressure fluctuations, spindle run-out errors, and the resulting low-pressure regions or tool electrode vibrations, but also the well-known limits and idealizations of numerical models, namely, perfect symmetry and constant boundary conditions, missing multi-phase considerations or the always limited validity of the models applied at any level, e.g., RANS approaches.
- It was not possible to draw direct, let alone linear, connections from the discharge energies to the process target parameters, such as the MRR, EWR, surface roughness or hole conicity. However, the classification and quantification of the discharge event types allowed for conclusions regarding their frequencies, and thus, the process stability.
- Amongst others, it was verified that the arcing frequency ratio drove the EWR and the beneficial frequency ratio correlated with the MRR and the surface roughness.
- External flushing channels verifiably led to convergence and reduced scattering of the relative event distributions
The experimental results reveal the possibility of major improvements with regard to the process target parameters by applying external flushing channels, even without pressure flushing, e.g., for the purpose of avoiding blind hole pins. The numerical evaluation of the flushing conditions indicated an inadequate operating point concerning the combination of flushing pressure and rotational speed. The idea of ejecting the gas bubbles and debris particles mainly through the groove alone most likely is not very promising. Nevertheless, the approach of optimizing the fluid mechanical parameters in a way to generate low pressure within the groove was found to be attainable.
In order to actually assume constant flushing pressure, and thus, flushing conditions, it was necessary to reduce the pressure fluctuations of the high-pressure piston pump from minus 20% and plus 10% in the present case to values below 5% and eliminate the run-out error of the spindle that enabled rotation. Steady-state single-phase simulations are to be used to find optimal combinations of the fluid mechanic parameters, with the objective of increasing the probability of gas bubbles and debris pulled into the grooves while being evacuated upward. Supplementary experiments with varying fluid mechanic parameters will allow for a confirmation of that optimal combination, as well as insights into their influences on the process target parameters. In addition, for a further increased understanding of the processes in the working gap, transient multi-phase simulations are necessary, including experimental validation of the numerical results using, e.g., pressure measurements and fluid flow visualizations. The developed sophisticated single-phase CFD model laid the basis for these future transient multi-phase investigations, considering the interactions of gas bubbles, debris particles and the dielectric liquid phase in the vicinity of an external flushing channel. Animations that extend the content of this work by visualizing the gas evacuation capabilities of the H1C type can be found in Supplementary Video S2. The provided possibility to perform real-time signal analyses using enhanced algorithms now calls for data acquisition in streaming mode to ensure a measurement ratio of 100% rather than measuring single files in block mode. Finally, additional experiments using an approach to distinguish between discharges occurring in the frontal or lateral working gap would further increase the value of the signal analyses.
Supplementary Materials
The following supporting information can be downloaded from the DepositOnce Repository of the Technische Universität Berlin, available online via the respective DOI: https://depositonce.tu-berlin.de (accessed on 30 November 2023). Table S1: Supplementary table to Figure 4 containing the original images and contour polygons (DOI: https://doi.org/10.14279/depositonce-19003), Table S2: Supplementary table to Figure 12 containing the original experimental data (DOI: https://doi.org/10.14279/depositonce-19006), Table S3: Supplementary table to Figure 16 with the original comparison data of the modeling approaches (DOI: https://doi.org/10.14279/depositonce-19007), Table S4: Supplementary table to Figure 19 containing the original data of the quantitative evaluations of the single-phase fluid flow for all tool electrode types (DOI: https://doi.org/10.14279/depositonce-19017), Table S5: Supplementary table to Figure 20 containing the original velocity profiles data from inside the lateral working gaps (DOI: https://doi.org/10.14279/depositonce-19018), Table S6: Supplementary table to Figure 21 containing the original data of the influences of the fluid mechanical parameters flushing pressure and rotational speed (DOI: https://doi.org/10.14279/depositonce-19019), Table S7: Supplementary table to Figure 23 containing the original data of the discharge energies We contributed by the respective event types (DOI: https://doi.org/10.14279/depositonce-19008), Table S8: Supplementary table to Figure 25 containing the original data of the signal analysis results for all six types of tool electrodes (DOI: https://doi.org/10.14279/depositonce-19009) and Video S1: Supplementary animation to Figure 18c visualizing the transient fluid transport for the HR type (DOI: https://doi.org/10.14279/depositonce-19118). The animations of transient two-phase CFD results contained in Video S2: Supplementary animation to Figure 21 with transient two-phase CFD results (DOI: https://doi.org/10.14279/depositonce-19124) go beyond the main content of this work by visualizing the gas evacuation capabilities for three cases in Figure 21 showing the example of the H1C type of tool electrode.
Author Contributions
Conceptualization, S.Y. and M.P.; methodology, S.Y., N.G. and E.S.; software, W.P. and K.T.; validation, S.Y., N.G., E.S., K.T. and W.P.; formal analysis, S.Y., N.G. and E.S.; investigation, S.Y., N.G., E.S. and K.T.; resources, E.U. and M.P.; data curation, S.Y., N.G. and E.S.; writing—original draft preparation, S.Y. and N.G.; writing—review and editing, S.Y., K.T., W.P. and M.P.; visualization, S.Y., N.G. and E.S.; supervision, E.U. and M.P.; project administration, S.Y.; funding acquisition, E.U., M.P. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 431706863. We acknowledge support from the Open Access Publication Fund of TU Berlin.
Data Availability Statement
Data supporting the reported results including links to publicly archived datasets analyzed or generated during the study can be found in the DepositOnce Repository of Technische Universität Berlin (see the Supplementary Materials section).
Acknowledgments
The authors acknowledge the technical support of CADFEM Germany GmbH concerning the implementation of the overset mesh approach soon after the release and before the revision of this technique in later software versions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- König, W.; Dauw, D.F.; Levy, G.; Panten, U. EDM-Future Steps towards the Machining of Ceramics. CIRP Ann. 1988, 37, 623–631. [Google Scholar] [CrossRef]
- Plaza, S.; Sanchez, J.A.; Perez, E.; Gil, R.; Izquierdo, B.; Ortega, N.; Pombo, I. Experimental study on micro EDM-drilling of Ti6Al4V using helical electrode. Precis. Eng. 2014, 38, 821–827. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Rajurkar, K.P.; Shen, H. High Aspect Ratio and Complex Shaped Blind Micro Holes by Micro EDM. CIRP Ann. 2002, 51, 359–362. [Google Scholar] [CrossRef]
- Yu, Z.; Rajurkar, K.P.; Narasimhan, J. Effect of Machining Parameters on Machining Performance of Micro EDM and Surface Integrity. In Proceedings of the 18th Annual ASPE Meeting, Portland, OR, USA, 26–31 October 2003. [Google Scholar]
- Tsai, Y.-Y.; Masuzawa, T. An index to evaluate the wear resistance of the electrode in micro-EDM. J. Mater. Proc. Technol. 2004, 149, 304–309. [Google Scholar] [CrossRef]
- Cetin, S.; Okada, A.; Uno, Y. Effect of Debris Distribution on Wall Concavity in Deep-Hole EDM. JSME Int. J. Ser. C 2004, 47, 553–559. [Google Scholar] [CrossRef]
- Nastasi, R.; Koshy, P. Analysis and performance of slotted tools in electrical discharge drilling. CIRP Ann. 2014, 63, 205–208. [Google Scholar] [CrossRef]
- Jahan, M.P. Micro-Electrical Discharge Machining. In Nontraditional Machining Processes. Research Advances; Davim, J.P., Ed.; Springer: London, UK, 2013; pp. 111–151. [Google Scholar] [CrossRef]
- Flegel, G.; Birnstiel, K.; Nerreter, W.; Borcherding, H.; Meier, U. Elektrotechnik für Maschinenbau und Mechatronik, 10th ed.; Hanser: München, Germany, 2016. [Google Scholar]
- Klocke, F.; König, W. Fertigungsverfahren 3—Abtragen, Generieren Lasermaterialbearbeitung, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Uhlmann, E.; Polte, M.; Yabroudi, S. Novel Advances in Machine Tools, Tool Electrodes and Processes for High-Performance and High-Precision EDM. Procedia CIRP 2022, 113, 611–635. [Google Scholar] [CrossRef]
- Uhlmann, E.; Yabroudi, S.; Perfilov, I.; Schweitzer, L.; Polte, M. Helical electrodes for improved flushing conditions in drilling EDM of MAR-M247. In Proceedings of the 18th International Conference & Exhibition, Venice, Italy, 4–8 June 2018; Euspen: Bedford, UK, 2018; pp. 415–417. [Google Scholar]
- Yabroudi, S. Von ultrafein bis makro: Alternative Dielektrika sowie Elektrodenformen und -werkstoffe für das funkenerosive Bohren. In Proceedings of the 12th Fachtagung Funkenerosion, Aachen, Germany, 26–28 November 2019. [Google Scholar] [CrossRef]
- Yabroudi, S. Einsatzbewertung neuartiger Werkzeugelektroden mit außenliegenden Spülkanälen beim funkenerosiven Bohren mittels CFD Simulationen. In Proceedings of the 37th CADFEM ANSYS Simulation Conference, Kassel, Germany, 15–17 October 2019. [Google Scholar] [CrossRef]
- Thißen, K.; Streckenbach, J.; Koref, I.S.; Polte, M. Signal analysis on a single board computer for process characterisation in sinking electrical discharge machining. In Production at the Leading Edge of Technology; Behrens, B.A., Brosius, A., Drossel, W.G., Hintze, W., Ihlenfeldt, S., Nyhuis, P., Eds.; WGP 2021, Lecture Notes in Production Engineering; Springer: Cham, Switzerland, 2021; pp. 169–176. [Google Scholar] [CrossRef]
- Uhlmann, E.; Polte, J.; Streckenbach, J.; Dinh, N.C.; Yabroudi, S.; Polte, M.; Börnstein, J. High-Performance Electro-Discharge Drilling with a Novel Type of Oxidized Tool Electrode. J. Manuf. Mater. Proc. 2022, 6, 113. [Google Scholar] [CrossRef]
- Ferraris, E.; Castiglioni, V.; Ceyssens, F.; Annoni, M.; Lauwers, B.; Reynaerts, D. EDM drilling of ultra-high aspect ratio micro holes with insulated tools. CIRP Ann. 2013, 62, 191–194. [Google Scholar] [CrossRef]
- Takeuchi, H.; Kunieda, M. Relation between Debris Concentration and Discharge Gap Width in EDM Process. J. JSEME 2007, 41–98, 156–162. [Google Scholar] [CrossRef][Green Version]
- Takeuchi, H.; Kunieda, M. Relation between Debris Concentration and Discharge Gap Width in EDM Process. IJEM 2007, 12, 17–22. [Google Scholar]
- Kliuev, M.; Baumgart, C.; Wegener, K. Fluid Dynamics in Electrode Flushing Channel and Electrode-Workpiece Gap During EDM Drilling. Procedia CIRP 2018, 68, 254–259. [Google Scholar] [CrossRef]
- Yilmaz, O.; Okka, M.A. Effect of single and multi-channel electrodes application on EDM fast hole drilling performance. Int. J. Adv. Manuf. Technol. 2010, 51, 185–194. [Google Scholar] [CrossRef]
- Bozdana, A.T.; Ulutas, T. The Effectiveness of Multichannel Electrodes on Drilling Blind Holes on Inconel 718 by EDM Process. Mater. Manuf. Proc. 2016, 31, 504–513. [Google Scholar] [CrossRef]
- Bozdana, A.T.; Al-Kharkhi, N.K. Comparative Experimental and Numerical Investigation on Electrical Discharge Drilling of AISI 304 using Circular and Elliptical Electrodes. J. Mech. Eng. 2018, 64, 269–279. [Google Scholar] [CrossRef]
- Yan, B.H.; Huang, F.Y.; Chow, H.M.; Tsai, J.Y. Micro-hole machining of carbide by electric discharge machining. J. Mater. Proc. Technol. 1999, 87, 139–145. [Google Scholar] [CrossRef]
- Goiogana, M.; Elkaseer, A. Self-Flushing in EDM Drilling of Ti6Al4V Using Rotating Shaped Electrodes. Materials 2019, 12, 989. [Google Scholar] [CrossRef]
- Hirao, A.; Gotoh, H.; Tani, T. Effect of Electrode Shape on High Aspect Ratio Deep Hole Drilling by EDM. Procedia CIRP 2022, 113, 262–266. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, I. Productivity improvement of micro EDM process by improvised tool. Prec Eng. 2018, 51, 529–535. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, I. A modified electrode design for improving process performance of electric discharge drilling. J. Mater. Proc. Technol. 2019, 264, 211–219. [Google Scholar] [CrossRef]
- Manikandaprabu, P.; Kumar Thakur, D.; Sathish Kumar, M.; Sivanesh Prabhu, M.; Ramesh Kumar, A. Study and analysis of various inclination pathway electrode tool in electrical discharge drilling. Mater. Today Proc. 2021, 43, 1215–1219. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, I. Blind Hole Fabrication in Aerospace Material Ti6Al4V Using Electric Discharge Drilling: A Tool Design Approach. J. Mater. Eng. Perform. 2021, 30, 8677–8685. [Google Scholar] [CrossRef]
- Nguyen, D.; Volgin, V.; Lyubimov, V. Modeling Electrical Discharge Machining of Deep Micro-Holes by Rotating Tool-Electrode. In Proceedings of the 6th International Conference on Industrial Engineering (ICIE 2020), Sochi, Russia, 18-22 May 2021; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 171–179. [Google Scholar] [CrossRef]
- Takezawa, H.; Toyoda, H.; Yuasa, K. Effects of Thin Pipe Electrodes with Grooves in Small Deep Hole EDM. IJEM 2021, 26, 46–53. [Google Scholar] [CrossRef]
- Yadav, V.K.; Singh, R.; Kumar, P.; Dvivedi, A. Performance enhancement of rotary tool near-dry EDM process through tool modification. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 72. [Google Scholar] [CrossRef]
- Natsu, W.; Miyamoto, T.; Li, S. Clarification and Solution of Depth-dependent Tool Wear and Removal Rate in Micro Electrical Discharge Drilling. In Proceedings of the 13th International Conference of the EUSPEN, Berlin, Germany, 27–31 May 2013; EUSPEN: Bedford, UK, 2013; pp. 149–153. [Google Scholar]
- Machida, M.; Natsu, W. Flow analysis of working fluid in micro electrical discharge drilling process. In Proceedings of the 14th euspen International Conference & Exhibition, Dubrovnik, Croatia, 2–6 June 2014; EUSPEN: Bedford, UK, 2014; pp. 107–111. [Google Scholar]
- Risto, M.; Munz, M.; Haas, R.; Abdolahi, A. Securing a robust electrical discharge drilling process by means of flow rate control. In Proceedings of the 20th International ESAFORM Conference on Material Forming, Dublin, Ireland, 26–28 April 2017; p. 050007. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, H.; Fang, F. Micro hole machining using double helix electrodes in electro discharge machining. J. Cent. South Univ. (Sci. Technol.) 2015, 46, 2857–2862. [Google Scholar]
- Wang, K.; Zhang, Q.; Zhu, G.; Liu, Q.; Huang, Y. Experimental study on micro electrical discharge machining with helical electrode. Int. J. Adv. Manuf. Technol. 2017, 93, 2639–2645. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, H.; Wang, Z. Influence of helical electrode and its structure on EDM small hole machining. Int. J. Adv. Manuf. Technol. 2022, 123, 3437–3453. [Google Scholar] [CrossRef]
- Tsui, H.-P.; Hung, J.-C.; You, J.-C.; Yan, B.-H. Improvement of Electrochemical Microdrilling Accuracy Using Helical Tool. Mater. Manuf. Proc. 2008, 23, 499–505. [Google Scholar] [CrossRef]
- Hung, J.; Liu, H.; Chang, Y.; Hung, K.; Liu, S. Development of Helical Electrode Insulation Layer for Electrochemical Microdrilling. Procedia CIRP 2013, 6, 373–377. [Google Scholar] [CrossRef][Green Version]
- Fang, X.; Zhang, P.; Zeng, Y.; Qu, N.; Zhu, D. Enhancement of performance of wire electrochemical micromachining using a rotary helical electrode. J. Mater. Proc. Technol. 2016, 227, 129–137. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Z.; Wang, M.; Zhang, J. Experimental investigation of micro wire electrochemical discharge machining by using a rotating helical tool. J. Manuf. Proc. 2017, 29, 265–271. [Google Scholar] [CrossRef]
- Hung, J.-C.; Lin, J.-K.; Yan, B.-H.; Liu, H.-S.; Ho, P.-H. Using a helical micro-tool in micro-EDM combined with ultrasonic vibration for micro-hole machining. J. Micromech. Microeng. 2006, 16, 2705–2713. [Google Scholar] [CrossRef]
- Hsue, A.W.-J.; Chang, Y.-F. Toward synchronous hybrid micro-EDM grinding of micro-holes using helical taper tools formed by Ni-Co/diamond Co-deposition. J. Mater. Proc. Technol. 2016, 234, 368–382. [Google Scholar] [CrossRef]
- Hinduja, S.; Kunieda, M. Modelling of ECM and EDM processes. CIRP Ann. 2013, 62, 775–797. [Google Scholar] [CrossRef]
- Uhlmann, E.; Perfilov, I.; Yabroudi, S.; Mevert, R.; Polte, M. Dry-ED milling of micro-scale contours with high-speed rotating tungsten tube electrodes. Procedia CIRP 2020, 95, 533–538. [Google Scholar] [CrossRef]
- Yabroudi, S. CFD-Simulation in Mikrospülkanälen beim funkenerosiven Feinbohren mit flüssigen und gasförmigen Dielektrika. In Proceedings of the 35th CADFEM ANSYS Simulation Conference, Koblenz, Germany, 15–17 November 2017. [Google Scholar] [CrossRef]
- Uhlmann, E.; Frost, T.; Piltz, S.; Szulczynski, H. Strömungssimulation von Bearbeitungsprozessen. Neue Potentiale für die Fertigungstechnik von morgen. Wt Werkstattstech. Online 2001, 91, 320–324. [Google Scholar] [CrossRef]
- Brito Gadeschi, G.; Schneider, S.; Mohammadnejad, M.; Meinke, M.; Klink, A.; Schröder, W.; Klocke, F. Numerical Analysis of Flushing-Induced Thermal Cooling Including Debris Transport in Electrical Discharge Machining (EDM). Procedia CIRP 2017, 58, 116–121. [Google Scholar] [CrossRef]
- Brito Gadeschi, G.; Schneiders, L.; Meinke, M.H.; Schroeder, W. Direct particle-fluid simulation of flushing in die-sink electrical-discharge machining. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017; p. 3619. [Google Scholar] [CrossRef]
- Schneiders, L.; Meinke, M.; Schröder, W. Direct particle–fluid simulation of Kolmogorov-length-scale size particles in decaying isotropic turbulence. J. Fluid. Mech. 2017, 819, 188–227. [Google Scholar] [CrossRef]
- Langmack, M. Laserwendel-und funkenerosives Mikrobohren. Ph.D. Thesis, TU Berlin, Berlin, Germany, 11 July 2014. [Google Scholar]
- Kliuev, M.; Baumgart, C.; Büttner, H.; Wegener, K. Flushing Velocity Observations and Analysis during EDM Drilling. Procedia CIRP 2018, 77, 590–593. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Cao, M.R.; Yang, S.Q.; Li, W.H. Numerical Simulation of Liquid-Solid Two-Phase Flow Field in Discharge Gap of High-Speed Small Hole EDM Drilling. AMR 2008, 53–54, 409–414. [Google Scholar] [CrossRef]
- Pontelandolfo, P.; Haas, P.; Perez, R. Particle Hydrodynamics of the Electrical Discharge Machining Process. Part 2: Die Sinking Process. Procedia CIRP 2013, 6, 47–52. [Google Scholar] [CrossRef][Green Version]
- Wang, D. Simulation of Particles Movement in Powder Mixed EDM. AMR 2010, 97–101, 4150–4153. [Google Scholar] [CrossRef]
- Wang, J.; Han, F. Simulation model of debris and bubble movement in electrode jump of electrical discharge machining. Int. J. Adv. Manuf. Technol. 2014, 74, 591–598. [Google Scholar] [CrossRef]
- Wang, J.; Han, F. Simulation model of debris and bubble movement in consecutive-pulse discharge of electrical discharge machining. Int. J. Mach. Tools Manuf. 2014, 77, 56–65. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, W.; Liu, Y.; Ma, F.; Su, C.; Sha, Z. Study on the Gap Flow Simulation in EDM Small Hole Machining with Ti Alloy. Adv. Mater. Sci. Eng. 2017, 2017, 8408793. [Google Scholar] [CrossRef]
- Wang, Z.; Tong, H.; Li, Y.; Li, C. Dielectric flushing optimization of fast hole EDM drilling based on debris status analysis. Int. J. Adv. Manuf. Technol. 2018, 97, 2409–2417. [Google Scholar] [CrossRef]
- Klocke, F.; Herrig, T.; Zeis, M.; Klink, A. Modeling and simulation of the fluid flow in wire electrochemical machining with rotating tool (wire ECM). In Proceedings of the 20th International ESAFORM Conference on Material Forming, Dublin, Ireland, 26–28 April 2017; p. 50014. [Google Scholar] [CrossRef]
- Klocke, F.; Zeis, M.; Heidemanns, L. Fluid structure interaction of thin graphite electrodes during flushing movements in sinking electrical discharge machining. CIRP J. Manuf. Sci. Technol. 2018, 20, 23–28. [Google Scholar] [CrossRef]
- Xia, W.; Zhang, Y.; Chen, M.; Zhao, W. Study on Gap Phenomena Before and After the Breakout Event of Fast Electrical Discharge Machining Drilling. J. Manuf. Sci. Eng. 2020, 142, 041004. [Google Scholar] [CrossRef]
- Li, G.; Natsu, W.; Yu, Z. Elucidation of the mechanism of the deteriorating interelectrode environment in micro EDM drilling. Int. J. Mach. Tools Manuf. 2021, 167, 103747. [Google Scholar] [CrossRef]
- Izquierdo, B.; Wang, J.; Sánchez, J.A.; Ayesta, I. Study of particle size and position on debris evacuation during Wire EDM operations. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 12022. [Google Scholar] [CrossRef]
- Dauw, D.F.; Snoeys, R.; Dekeyser, W. Advanced Pulse Discriminating System for EDM Process Analysis and Control. CIRP Ann. 1983, 32, 541–549. [Google Scholar] [CrossRef]
- Uhlmann, E.; Polte, M.; Yabroudi, S.; Thißen, K.; Penske, W. Real-time energy monitoring in electrical discharge machining. Wt Werkstattstech. Online 2023, 113, 304–310. [Google Scholar] [CrossRef]
- Nirala, C.K.; Saha, P. Evaluation of μEDM-drilling and μEDM-dressing performances based on online monitoring of discharge gap conditions. Int. J. Adv. Manuf. Technol. 2016, 85, 1995–2012. [Google Scholar] [CrossRef]
- Nirala, C.K.; Unune, D.R.; Sankhla, H.K. Virtual Signal-Based Pulse Discrimination in Micro-Electro-Discharge Machining. J. Manuf. Sci. Eng. 2017, 139, 094501. [Google Scholar] [CrossRef]
- Janardhan, V.; Samuel, G.L. Pulse train data analysis to investigate the effect of machining parameters on the performance of wire electro discharge turning (WEDT) process. Int. J. Mach. Tools Manuf. 2010, 50, 775–788. [Google Scholar] [CrossRef]
- Zhou, M.; Han, F.; Soichiro, I. A time-varied predictive model for EDM process. Int. J. Mach. Tools Manuf. 2008, 48, 1668–1677. [Google Scholar] [CrossRef]
- Yeo, S.H.; Aligiri, E.; Tan, P.C.; Zarepour, H. A New Pulse Discriminating System for Micro-EDM. Mater. Manuf. Proc. 2009, 24, 1297–1305. [Google Scholar] [CrossRef]
- Bellotti, M.; Qian, J.; Reynaerts, D. Breakthrough phenomena in drilling micro holes by EDM. Int. J. Mach. Tools Manuf. 2019, 146, 103436. [Google Scholar] [CrossRef]
- Petersen, T.; Küpper, U.; Klink, A.; Herrig, T.; Bergs, T. Discharge energy based optimisation of sinking EDM of cemented carbides. Procedia CIRP 2022, 108, 734–739. [Google Scholar] [CrossRef]
- Schneider, S. Modellierung der Energiedissipation in der Funkenerosion. Ph.D. Thesis, RWTH, Aachen, Germany, 7 July 2021. [Google Scholar]
- Küpper, U.; Herrig, T.; Klink, A.; Welling, D.; Bergs, T. Evaluation of the Process Performance in Wire EDM Based on an Online Process Monitoring System. Procedia CIRP 2020, 95, 360–365. [Google Scholar] [CrossRef]
- Chu, H.-Y.; Li, Z.-L.; Xi, X.-C.; Zhao, W.-S. Study on Adaptive Servo Control Strategy of WEDM Based on Discharge State Detector. Procedia CIRP 2020, 95, 354–359. [Google Scholar] [CrossRef]
- Chu, H.-Y.; Zhang, M.; Xi, X.-C.; Li, Z.-L.; Zhao, W.-S. Observation of molten material and recast layer distribution of fast EDM drilling on inclined surface. Procedia CIRP 2022, 113, 250–255. [Google Scholar] [CrossRef]
- Schwade, M. Fundamental Analysis of High Frequent Electrical Process Signals for Advanced Technology Developments in W-EDM. Procedia CIRP 2014, 14, 436–441. [Google Scholar] [CrossRef][Green Version]
- Schwade, M. Automatisierte Analyse hochfrequenter Prozesssignale bei der funkenerosiven Bearbeitung von Magnesium für die Medizintechnik. Ph.D. Thesis, RWTH, Aachen, Germany, 20 April 2017. [Google Scholar]
- Schlichting, H.; Gersten, K. Grenzschicht-Theorie, 10th ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 517–524. [Google Scholar]
- Schwarze, R. CFD-Modellierung, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 134–155. [Google Scholar]
- ANSYS Inc. ANSYS Fluent Theory Guide, 2020R1 ed.; Ansys Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- ANSYS Inc. ANSYS Fluent User’s Guide, 2020R1 ed.; Ansys Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Thißen, K.; Yabroudi, S.; Uhlmann, E. Localization of discharges in drilling EDM through segmented workpiece electrodes. In Production at the Leading Edge of Technology; Liewald, M., Verl, A., Bauernhansl, T., Möhring, H.C., Eds.; WGP 2022. Lecture Notes in Production Engineering; Springer: Cham, Switzerland, 2022; pp. 209–218. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Liu, Y.; Zhao, F. Research on Shape Changes in Cylinder Electrodes Incident to Micro-EDM. Adv. Mater. Sci. Eng. 2019, 2019, 8087462. [Google Scholar] [CrossRef]
- Tu, J.; Liu, C.; Yeoh, G.H. Computational Fluid Dynamics. A practical Approach, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 220–222. [Google Scholar] [CrossRef]
- Oßwald, K.; Schneider, S.; Hensgen, L.; Klink, A.; Klocke, F. Experimental investigation of energy distribution in continuous sinking EDM. CIRP J. Man. Sci. Technol. 2017, 19, 36–43. [Google Scholar] [CrossRef]
- Kunieda, M.; Lauwers, B.; Rajurkar, K.P.; Schumacher, B.M. Advancing EDM through Fundamental Insight into the Process. CIRP Ann. 2005, 54, 64–87. [Google Scholar] [CrossRef]
- Li, G.; Natsu, W.; Yu, Z. Observation of phenomena in gap area during micro hole drilling with micro EDM. In Proceedings of the 17th International Conference & Exhibition, Hannover, Germany, 29 May–2 June 2017; EUSPEN: Bedford, UK, 2017; pp. 195–196. [Google Scholar]
- Haas, R.; Munz, M.; Huber, M.; Knabe, R. Adequate Gap Flushing in High Speed EDM Drilling of Deep Small Holes in Moulds and Dies. In Proceedings of the 7th International Conference on High Speed Machining (CIRP), Darmstadt, Germany, 28–29 May 2008; Abele, E., Ed.; Meisenbach Verlag: Bamberg, Germany, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).