Information Theoretic Objective Function for Genetic Software Clustering ^†

Abstract

Software clustering is usually used for program comprehension. Since it is considered to be the most crucial NP-complete problem, several genetic algorithms have been proposed to solve this problem. In the literature, there exist some objective functions (i.e., fitness functions) which are used by genetic algorithms for clustering. These objective functions determine the quality of each clustering obtained in the evolutionary process of the genetic algorithm in terms of cohesion and coupling. The major drawbacks of these objective functions are the inability to (1) consider utility artifacts, and (2) to apply to another software graph such as artifact feature dependency graph. To overcome the existing objective functions’ limitations, this paper presents a new objective function. The new objective function is based on information theory, aiming to produce a clustering in which information loss is minimized. For applying the new proposed objective function, we have developed a genetic algorithm aiming to maximize the proposed objective function. The proposed genetic algorithm, named ILOF, has been compared to that of some other well-known genetic algorithms. The results obtained confirm the high performance of the proposed algorithm in solving nine software systems. The performance achieved is quite satisfactory and promising for the tested benchmarks.

1. Introduction

Comprehending the code of a large and complicated program is hard and sometimes impossible. Program understanding is an essential activity for application development and maintenance [1]. Software clustering is an effective method to improve the comprehensibility of the software architecture and to discover the software structure [1]. In [2,3], the impact of software clustering on software understanding and software evolution has been investigated. The software architecture extracting aims to use clustering algorithms to partition an application from the source code into meaningful and understandable segments [1]. In fact, this assists to understand the application in the software maintenance process.

Most search-based software clustering algorithms use the Artifact Dependency Graph (ADG) (or Module Dependency Graph) for modeling a software system [4,5,6,7,8,9,10,11]. It is used for modeling the relationship between artifacts (e.g., calling dependency between artifacts) and provides an abstract view of software structure. In these graphs, the software system’s artifacts (such as class, function, file, etc.) are presented as nodes and their connections as edges. The end of software clustering is to locate the artifacts within clusters, so that cohesion (i.e., connections between the artifacts of the same cluster) is maximized and coupling (i.e., connections between artifacts of two different clusters) is minimized [1,4,5]. Since the problem of finding the best clustering for a software system is an NP-hard problem [5], genetic-based algorithms are applied to obtain a good clustering [5]. Figure 1 depicts an ADG for an example software system that comprises six program files, namely a–f, and two utility files, namely g and h, and Figure 2 and Figure 3 show two different clusterings of it.

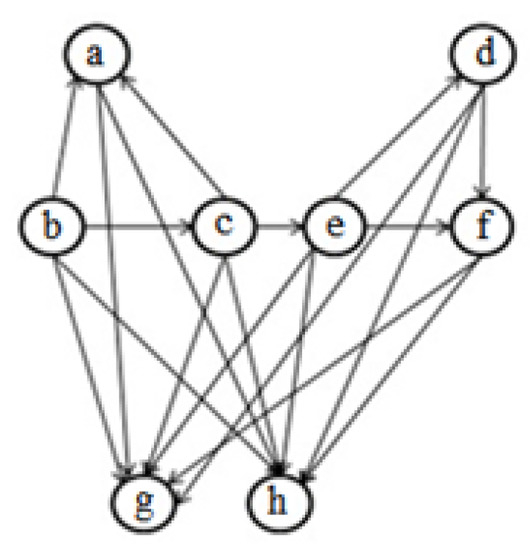
Figure 1. A sample Artifact Dependency Graph (ADG).

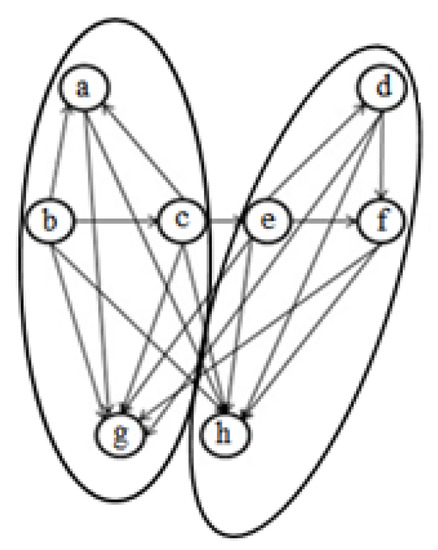
Figure 2. An obtained clustering for Figure 1.

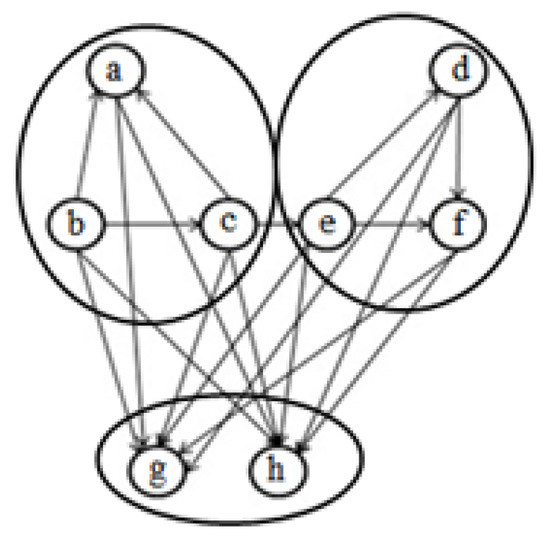
Figure 3. Another clustering for Figure 1.

Libraries and drivers are examples of utility artifacts. Libraries provide services to many of the other artifacts, and drivers consume the services of many of the other artifacts. These files should be isolated in one cluster in the clustering process because they tend to obfuscate the software’s structure [11].

Several genetic algorithms have been developed to solve the software clustering problem. One of the operators that largely affect the performance of a genetic algorithm in finding the appropriate clustering is the objective function (other names are: fitness function or quality function). As the aim of the genetic algorithm is to optimize the objective function. Several objective functions have been developed in the literature for software clustering so that the existing evolutionary algorithms in this context use these objective functions for clustering. Maximizing cohesion and minimizing coupling is the overall goal of these functions. However, these objective functions have disadvantages in which clustering found are not so acceptable. These disadvantages are: (1) There is no reason for a software developer to use principles of maximum cohesion and minimum coupling in the development of a software application; (2) almost there are a number of utility in every system that are not necessarily dependent on each other; therefore, the existing objective functions in each different clustering locate them in different clusters and thus they obscure the system’s structure; (3) objective functions available are used only on graphs that have been created by relationship between artifacts, such as calling operations, and cannot perform the clustering on other graphs that can be extracted from a program, such as semantic graphs, or the graphs used in hierarchical clustering algorithms.

In this paper, using information theory and the concept of entropy, a new objective function is proposed, which can solve the problems mentioned in the existing objective functions and improves the quality of clustering. The aim is to propose a new objective function that an evolutionary algorithm (e.g., genetic algorithm) can use to put artifacts with the minimum information loss into the same cluster.

The rest of this paper is organized as follows. Section 2 addresses the existing objective functions. Section 3 describes the proposed objective function based on information theory. To validate the performance of the proposed objective function, a genetic algorithm is adopted to optimize it in this section. Section 4 compares the proposed algorithm. Finally, the conclusions and future work are presented in Section 5.

2. Related Work

Software clustering (or software modularization) algorithms can be categorized into hierarchical (e.g., see [12,13]) and non-hierarchical (including search-based methods and greedy algorithms) categories.

In search-based clustering methods, the problem of clustering is counted as a search problem. Since the software clustering problem is an NP-hard problem, evolutionary approaches such as genetic algorithms are utilized to find the more qualified clustering. Most search-based algorithms aims to find a modularization with maximum cohesion and minimum coupling. Objective functions in search-based software clustering algorithms guide optimization algorithms to find a good clustering for a software system. The two most popular objective functions are BasicMQ and TurboMQ [4]. If $A_i$ is an internal connection (internal edges) for a cluster and $E_{ij}$ represents connection level between two clusters $“i”$ and $“j”$, then having a program graph divided to $“k”$ clusters, BasicMQ is defined as follows:

$$BasicMQ=\frac{1}{k}\sum A_i-\frac{1}{\frac{k(k-1)}{2}}\sum E_{ij}$$

(1)

The BasicMQ has five shortcomings, as follows:

• The execution time of BasicMQ is high, which restricts its application to small systems,
• unable to handle the ADGs with weighted edges,
• only considers cohesion and coupling in the calculation of the clustering quality,
• unable to handle the non-structural features,
• unable to detect utility artifacts.

Let the internal relationships of a cluster and relationships between two clusters are respectively denoted by ${\mu }_i$ and ${\epsilon }_{i,j}$, TurboMQ is computed as follows:

$$TurboMQ=\sum _{i=1}^{k}C{F}_i$$

(2)

$$C{F}_i=\frac{2{\mu }_i}{2{\mu }_i+\sum _{j=1}^k({\epsilon }_{i,j}+{\epsilon }_{j,i})}$$

(3)

The TurboMQ has three drawbacks, as follows:

• Only considers cohesion and coupling in the calculation of the clustering quality,
• unable to handle the non-structural features,
• unable to detect utility artifacts.

Most search-based software clustering algorithms use BasicMQ and TurboMQ as objective function such as E-CDGM [6], EDA [7], Bunch [4,8], DAGC [9], SAHC [8], NAHC [8], HC+Bunch [5], modified firefly algorithm [14], MAEA-SMCP [15] and GAKH [16]. The limitations of using these objective functions are mentioned before. In addition, there are a number of objective functions that we will discuss below.

In [17], two multi-objective functions, namely MCA and ECA, are proposed for clustering. The objectives used in MCA include “maximizing the sum of intra-edges of all clusters”, “minimizing the sum of inter-edges of all clusters”, “maximizing the number of clusters”, “maximizing TurboMQ”, “minimizing the number of isolated clusters”; and the objectives used in ECA are the same as the MCA, with the difference that instead of the last one, the “difference between the maximum and minimum number of modules in a cluster (minimizing)”, has been used. These two objective functions also suffer from the same TurboMQ drawbacks.

Huang and Liu in [18] stated that the BasicMQ does not take into account utility artifacts and edge directions between two obtained clusters. Therefore, they proposed an objective function, to overcome these limitations of BasicMQ. To evaluate the performance of the proposed objective function, they developed three algorithms named hill-climbing algorithm (HC-SMCP), genetic algorithm (GA-SMCP), and multi-agent evolutionary algorithm (MAEA-SMCP).

In [19], a PSO-based algorithm, named PSOMC, was proposed for software clustering. The objectives used in PSOMC for clustering are the “intracluster dependency”, “intercluster dependency”, “number of clusters”, and “number of module per cluster”.

In [20], a Harmony search-based algorithm, named HSBRA, was proposed for object-oriented software systems clustering. The objectives used in HSBRA for clustering are “cohesion”, “coupling”, “package count index”, and “package size index”.

3. Entropy-Based Objective Function

We use Figure 1 to illustrate how to calculate the new objective function. The corresponding data table matrix for this graph is shown in Table 1. Rows of this matrix indicate the artifacts that will be clustered and the columns indicate the number of features that characterize these artifacts. An entry, if equal to “1” indicates the dependency between two artifacts and if equal to “0” indicates no relation between them.

Table 1. Data table for Figure 1.

	a	b	c	d	e	f	g	h
a	0	1	1	0	0	0	1	1
b	1	0	1	0	0	0	1	1
c	1	1	0	0	1	0	1	1
d	0	0	0	0	1	1	1	1
e	0	0	1	1	0	1	1	1
f	0	0	0	1	1	0	1	1
g	1	1	1	1	1	1	0	0
h	1	1	1	1	1	1	0	0

To use the concepts of information theory [21] in the software clustering context, the data table matrix should be normalized so that the elements of each row sum up to one. Let A be a random variable that gains its values from the artifacts set $\{a_1,a_2,...,a_n\}$ and F represents a random variable that gets its values from feature set $\{f_1,f_2,...,f_m\}$. Suppose M indicates a data table matrix, this matrix can be normalized using Equation (4).

$$p\left(f_j\right|a_i)=\frac{M[a_i,f_j]}{{\sum }_{f\in F}M[a_i,f]}$$

(4)

The normalized matrix for Table 1 is shown in Table 2. Each row of a normalized matrix represents a feature vector for an artifact, which equals to the conditional probability: $p\left(F\right|A=a_i)$. In information theory, the mutual information (MI) of two random variables measures how much one random variable tells us about another. More specifically, it quantifies the “amount of information" obtained about one random variable, through the other random variable. MI between two random variables is computed as follow:

$$MI(A,F)=\sum _{a_i,f}p(a_i,f)log\frac{p(a_i,f)}{p\left(a_i\right)p\left(f\right)}$$

(5)

Table 2. Normalized matrix for Table 1.

	a	b	c	d	e	f	g	h
a	0	1/4	1/4	0	0	0	1/4	1/4
b	1/4	0	1/4	0	0	0	1/4	1/4
c	1/5	1/5	0	0	1/5	0	1/5	1/5
d	0	0	0	0	1/4	1/4	1/4	1/4
e	0	0	1/5	1/5	0	1/5	1/5	1/5
f	0	0	0	1/4	1/4	0	1/4	1/4
g	1/6	1/6	1/6	1/6	1/6	1/6	0	0
h	1/6	1/6	1/6	1/6	1/6	1/6	0	0

In information theory, higher entropy reflects more uncertainty; in contrast, lower entropy represents more certainty. In the clustering problem, lower entropy is preferred. In the clustering of software, it is ideal that the selection probability of each feature of an artifact is the same before and after clustering.

Assume $a_i$ and $a_j$ are two artifacts before clustering and $a_i\cup a_j$ represents merging them after clustering. Our aim will be to calculate the distance between $a_i$ and $a_j$ with $a_i\cup a_j$ (actually to know how much information is lost). Let $a_i=p\left(f\right|a_i)$, $a_j=p\left(f\right|a_j)$, so we define:

$$\begin{array}{cc}\hfill {\displaystyle \overline{p}}\left(f\right)=& a_i\cup a_j=p\left(f\right|a_i\cup a_j)=\frac{1}{2}p\left(f\right|a_i)+\frac{1}{2}p\left(f\right|a_j),f\in F\hfill \end{array}$$

(6)

Using Equations (4)–(6), the information loss between $a_i$ and $a_j$, $\delta I(a_i,a_j)$, is computed as follows:

$$\begin{array}{cc}\hfill \delta I(a_i,a_j)& ={\sum }_{f\in F}[\frac{1}{2}p\left(f\right|a_i)log\frac{p\left(f\right|a_i)}{p\left(f\right)}+\frac{1}{2}p\left(f\right|a_j)log\frac{p\left(f\right|a_j)}{p\left(f\right)}]-{\sum }_{f\in F}p\left(f\right|a_i\cup a_j)log\frac{p\left(f\right|a_i\cup a_j)}{p\left(f\right)}\end{array}$$

(7)

By substituting $\overline{p}\left(f\right)$ (i.e., $p\left(f\right|a_i\cup a_j)$) in Equation (7), $\delta I(a_i,a_j)$ is calculated as follows:

$$\begin{array}{cc}\hfill \delta I(a_i,a_j)& =\frac{1}{2}{\sum }_{f\in F}p\left(f\right|a_i)log\frac{p\left(f\right|a_i)}{\overline{p}\left(f\right)}+\frac{1}{2}{\sum }_{f\in F}p\left(f\right|a_j)log\frac{p\left(f\right|a_j)}{\overline{p}\left(f\right)}\end{array}$$

(8)

$\delta I(a_i,a_j)$ means that after clustering of $a_i$ and $a_j$, what is the possibility to identify their features. We used information theory to determine the distance between $a_i$, $a_j$ with $a_i\cup a_j$. In the following we define information loss respectively for two artifacts, a cluster and a clustering.

Definition 1. 

Divergence for a cluster (denoted by DM)—for cluster k with nodes $\{1,2,···,n\}$ is computed as follows:

$$D{M}_k=\frac{{\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^n\delta I(a_i,a_j)}{n}$$

(9)

where n denotes the number of artifacts in a cluster.

Definition 2. 

Divergence for a clustering (denoted by MQ)—for an obtained clustering, it is computed as follows:

$$MQ=\sum _{i=1}^{k}D{M}_i$$

(10)

The lower MQ indicates that less information is lost, so a proper clustering is obtained. We need to convert this minimization problem to maximization one (see Equation (11)).

Definition 3. 

Objective Function (denoted by O.F.)—we define our new objective function as follows:

$$O.F.=\sum _{i=1}^n\sum _{j=1}^n\delta I(a_i,a_j)-MQ$$

(11)

where n is the number of artifacts.

To illustrate, Figure 2 and Figure 3 represent the clusterings created by the Bunch algorithm and our algorithm, respectively. As it can be seen, our objective function identifies the utilities and isolate them while TurboMQ used in Bunch cannot identify them.

Genetic Algorithm

In the standard genetic algorithm, initially, a set of all solutions (known as the chromosomes) is produced and then the chromosomes are assessed utilizing an objective function (fitness function). Then until the end condition is satisfied, chromosomes are chosen and crossover and mutation operators are done on them respectively and the previous solutions are replaced by the new solutions. In our proposed genetic algorithm, the initial population (i.e., the set of all solutions) is generated randomly. We employ the encoding method used in the Bunch algorithm [4,8]. In this method, the number of gens in each chromosome is equal to the number of artifacts. The content of each gene represents the cluster number that the artifact has to allocate to it. This value ranges between one and the number of artifacts. For example, Figure 4 illustrates a sample encoding and Figure 5 shows obtained clustering for that.

Figure 4. The chromosome structure for a sample ADG.

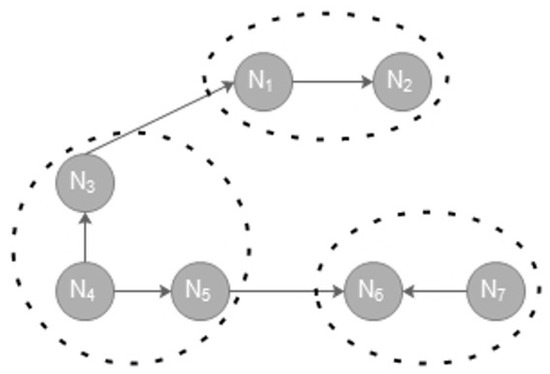
Figure 5. Obtained clustering for a sample string S = 1122233.

The objective function. The objective function has a great impact on the performance of the genetic algorithm to find a suitable solution. The objective function measures the quality of each clustering achieved during the evolutionary process of the genetic algorithm. To calculate an obtained clustering quality, we use Equation (11). The designed genetic algorithm aims to maximize the proposed quality function.

4. Results

For evaluating and comparing the effect of the proposed objective function, we choose nine real-world applications. The descriptions concerning these applications are presented in Table 3.

Table 3. The description of tested software systems.

Software System	Description	#Artifacts	#Links
compiler	A small compiler developed at the University of Toronto	13	32
nos	A file system	16	52
boxer	Graph drawing tool	18	29
ispell	Spelling and typographical error correction software	24	103
ciald	Program dependency analysis tool	26	64
cia	Program dependency graph generator for C programs	38	87
grappa	Genome Rearrangements Analyzer	86	295
acqCIGNA	An industrial software	114	188
cia++	Dependency graph generator for C++ programs	124	369

For evaluating the achieved clustering by an algorithm, internal metrics are employed [1]. Internal metrics measure how well the clusters are separated. We use the silhouette coefficient, denoted by SC, and separation criteria for internal evaluation [1]. Let n denotes the number of artifacts, Table 4 gives the parameter tuning for the experiments. In a genetic algorithm, the number of generations is usually greater than the population size. Therefore, we have followed this principle in the proposed algorithm, and we also considered this value linearly and a coefficient of the number of artifacts.

Table 4. The parameter setting for experiments.

Parameters	Value
Population size	10n
Generation	200n
P${}_c$ (crossover rate)	0.8
P${}_m$ (mutation rate)	0.05
Selection operator	Roulette wheel selection
Crossover operation	One-point
Mutation operation	randomly changed a gene

In Table 5, the proposed algorithm, named ILOF, is compared on nine software systems with five algorithms in terms of SC and Separation. We chose the mean of results for each algorithm over 20 independent runs. The results demonstrate that the clustering achieved with ILOF are higher quality than those achieved with other algorithms for all the ADGs in terms of SC and separation. According to the definition of SC and Separation, their values should be as high as possible (close to one). In all of these cases, it appears that the proposed algorithm is better able to separate the clusters with the new objective function.

Table 5. Comparing the proposed algorithm against five search-based algorithms.

Algorithms	Bunch		DAGC		EDA		ECA		GA-SMCP		ILOF
Software Systems	SC	Separation	SC	Separation	SC	Separation	SC	Separation	SC	Separation	SC	Separation
Compiler	0.204	0.487	0.204	0.487	0.204	0.487	0.204	0.487	0.201	0.406	0.405	0.821
nos	0.14	0.574	0.069	0.459	0.14	0510	0.291	0.628	0.13	0.566	0.433	0.690
boxer	0.205	0.550	0.095	0.431	0.205	0.550	0.205	0.550	0.221	0.558	0.358	0.610
ispell	0.051	0.441	0.063	0.487	0.161	0.491	0.91	0.610	0.050	0.398	0.333	0.872
ciald	0.217	0.545	0.087	0.434	0.217	0.512	0.321	0.573	0.217	0.521	0.364	0.750
cia	−0.004	0.577	−0.194	0.460	0.003	0.464	0.005	0.600	0.008	0.581	0.28	0.831
grappa	0.082	0.554	0.245	0.786	0.082	0.563	0.422	0.536	0.082	0.494	0.249	0.590
acqCIGNA	−0.167	0.525	−0.329	0.435	0.001	0.510	0.031	0.530	−0.209	0.369	0.049	0.590
cia++	−0.012	0.544	−0.323	0.450	0.002	0.610	0.012	0.534	0.002	0.508	0.049	0.621

5. Conclusions

This paper presents a new objective function based on information theory. Like other objective functions (such as TurboMQ), the proposed objective function can be used by evolutionary approaches for software clustering. To use the proposed objective function, we have developed a genetic algorithm that can maximize the proposed objective function. The results showed that the results of the proposed objective function are very promising.

The following suggestions are made for future work:

• Evaluating the presented objective function on other real-world applications with differing sizes from various fields.
• Use of other formulas of entropy as an objective function and addressing the obtained results.