Abstract
Using the newly introduced, by the author, basic complex and hybrid complex rheologic models of the fractional type, the dynamics of a series of mechanical rheologic discrete dynamical systems of the fractional type (RDDSFT) of rheologic oscillators (ROFTs) or creepers (RCFTs), with corresponding independent generalized coordinates (IGCs) and external (IGCEDF) and internal (IGCIGF) degrees of freedom of movement, were studied. Laplace transformations of solutions for independent generalized coordinates (IGCs), as well as external (IGCEDFs) and internal (IGCIDF) degrees of freedom of system dynamics, were determined. On the studied specimens, it was shown that rheologic complex models of the fractional type introduce internal degrees of freedom into the dynamics of rheologic discrete dynamical systems. New challenges appear for mathematicians, such as translating the Laplace transformations of solutions for independent generalized coordinates (LTIGCs) into the time domain. A number of translations of Laplace transformations of solutions into the time domain were performed by the author of this paper. A series of characteristic surfaces of elongations of Laplace transformations of independent generalized coordinates (IGCs) of the dynamics of rheologic discrete dynamic systems of the rheologic oscillator type, i.e., the rheologic creeper type, is shown as a function of fractional order differentiation exponent and Laplace transformation parameter. This manuscript presents the scientific results of theoretical research on the dynamics of rheologic discrete dynamic systems of the fractional type that was conducted using new models and a rigorous mathematical analytical analysis with fractional-order differential equations (DEFOs) and Laplace transformations (LTs). These results can contribute to new experimental research and materials technologies. A separate section presents the theoretical foundations of the methods and methodologies used in this research, without the details that can be found in the author’s previously published works.
Keywords:
Newton’s ideally viscous fluid flow of the fractional type (NIVFFT); new rheologic discrete dynamic systems of the fractional type (RDDSFTs); internal degrees of freedom (IDFs) of movement; rheological creeper (RCFT); Laplace transformations; surfaces of elongations of Laplace transformation (SELTs) MSC:
34A08; 74B05; 74A20; 74-xx; 74hXX
1. Introduction
New scientific research results on the impact of dynamics on a series of non-conservative fractional type systems are presented herein. These rheological discrete dynamic systems, of the fractional type (RDDSFT-NCs), both those with self-dynamics and those with forced dynamics, are described.
All RDDSFT-NCs of this class are dissipative. The energy dissipation of these RDDSFTs is the result of the energy dissipation caused by Newtonian fluid elements of the fractional type [1,2], one or more of which are contained in the SLRCM FTs that connect rigid bodies in RDDSFTs. For each of these systems, we can determine a generalized energy dissipation function of the fractional type (GEDFFT) as a function of the fractional type velocity of the IGC, the external degrees of freedom of motion dynamics, and the corresponding number of internal degrees of freedom of movement of the system (for details see reference [3]).
In a new study [2] published in 2025, a complete overview of the new class of RCMMPEFTs with differential constitutive relations of the fractional order (DCRFO) is presented. Using these DCRFOs, the normal stress and axial dilatation relationships, the mechanical elastoplastic (EV) or viscoelastic (VE) properties of the material models of a larger number of RCMFT materials with electrical polarization properties, and the coupled electrical polarization phenomena of the Faraday rheological piezoelectric element (RFPE) have been analyzed. In this paper, this analysis, presented in reference [2], is the basis for the formation of standard lightweight rheological complex elements (SLREFTs) of the connections between the rigid objects (bodies or material points) of RDDSs.
This class of non-conservative RDDS has two subclasses: rheological discrete oscillators of the fractional type (RDOFTs) and rheological discrete creepers of the fractional type (RDCFTs).
Note that there are also classes of hereditary discrete and/or hereditary continuous systems, which have the property of memory. The dynamics of these classes of hereditary systems with memory are described by ordinary or partial integro-differential equations. Characteristic of these systems is the possession of a relaxation core and a rheology core, which are determined experimentally (for details see references [4,5,6,7]).
The author reviewed a large number of the available publications, which were published by many publishers of scientific literature and, based on that, came to the following conclusions:
a* That most of the papers on DDSs are related to classical DDSs with holonomic or non-holonomic constrains between their rigid bodies (see references [8,9,10,11]);
b* That there are very few papers on the dynamics of RDDSFTs. In the papers on the dynamics of RDDSs, the dynamics of systems with one degree of freedom of movement are mainly analyzed, and light rheological classical connection models are mainly used. For example, in references [12,13], yarn dynamics in the textile industry are studied using the classical linear complex Burgers yarn model, which is also applied to the dynamics of cotton and a combination of wool and cotton. In published works [14,15,16,17], the dynamics of structures and constructions were studied using classical rheological models from a civil engineering standpoint. In article [18], torsional oscillations of the trunk and crown of a young tree were presented.
The use of fractional order differential equations to describe the non-conservative dynamics of biosystems and biomaterials, as well as bio-oscillators and bio-creepers, is described in references [19,20,21,22]. The propagation of fractional-type waves in a continuum is studied using the general mathematical theory of the continuum with fractional properties in the publications [23,24,25].
The author had two goals in forming the manuscript. One is to be comprehensive and to contain new scientific results in one integral article and to include a presentation of the dynamics of basic rheological discrete models of dynamic systems, as well as complex rheological discrete models of dynamic systems. To this end, the author repeatedly shortened the original manuscript and especially compiled a comparative table that provides readers with a clear understanding and possible future research, inspired by this work. The author set the second goal of this mathematical manuscript to stimulate the interest of younger researchers in numerical and experimental research on the dynamics of rheological discrete dynamic systems of the oscillator or creeper fractional type and formed a comparative table of the studied rheological discrete dynamic systems, which can be used in this new, both theoretical and numerical, and experimental research.
2. Elements of Mathematical Phenomenology and the Method of Studying the Dynamics of RDDSFT
The basic elements of mathematical phenomenology (for details see References [26,27,28]) in the study of the dynamics of RDDSFT are necessary to determine the generalized coordinates of degrees of freedom of motion, as well as the differential constitutive relations of the fractional order for each individual element in conjunction with the connective rheological complex models with rigid bodies in the RDDSFT. Then, systems of inhomogeneous ordinary SODFFO should be compiled, which describe the dynamics of the RDDSFT.
In these SDEFOs, a differential operator appears to be the differentiation of the fractional order (for details see References [29,30,31,32]). Solving such systems of DEFO is realized by applying Laplace transform (for details see References [33,34,35]), which leads to a system of inhomogeneous algebraic equations (IAEs), from which we determined the Laplace transforms of IGC, which correspond to the external, as well as internal, degrees of freedom of motion of the RDDSFO. Then, we determine the inverse Laplace transforms from the LTIGC of IDEFO in the time domain, if possible. And, often, this is not possible at this level of mathematical knowledge.
Then, we help ourselves by visualizing the LTIGC, which corresponds to the RDDFT. This visualization of LTIGC is drawn using certain analytical expressions and displayed as space surfaces in the coordinate systems of LT with the following coordinate axes: Laplace transformation elongation , Laplace transformation parameter , and fractional order differentiation exponent in the interval .
Let us continue with basic information about the differentiation of fractional order.
As it is known, differentiation of the FO, although it appeared in the scientific communications of Leibniz and the Marquis L’Hospital, has only recently gained wider application in various fields of science and technology. In scientific publications [36,37,38,39], a short history of fractional calculus is presented. The different definitions of differentiating a FO are known. We accept that there are different definitions of differentiating the fractional order (for more details see References [40,41]). We use the so-called Caputo’s definition, which we called the differential operator of fractional order (DOFO) and which we used in our previously published articles with applications of non-integer order leads in mechanics, analogies of mechanical and electric rheologic oscillators, as well as in rheologic biodynamics of fractional-type systems, and for details see previously cited references.
This means that we use Caputo’s definition of the derivative of the FO over the differential operator of the FO, in the following form:
where , is the exponent of fractional order differentiation, and is the special Gamma function defined in the form of an integral (see References [42,43,44,45]):
In the second form, in the general case of the function of the variable , this special Gamma function is in the following form:
Different numerical methods for fractional calculus are presented in the following publications [46,47]. An evaluation of generalized Mittag–Leffler functions based on the real line and computation of the Mittag–Leffler function and its derivatives are contents of References [48,49]. Some results of the extended beta and extended hypergeometric functions are given in article [50].
The analysis of DEFO is given in a series of publications as [51,52,53].
An introduction for physicists in the area of FC is presented in article [54]. In Reference [55], usefully, the Mathematica Book is presented.
In this paper, we use the so-called Laplace operator in the following form:
The Laplace operator applied to the potential time function given the following expression:
The Laplace operator applied to the potential time function given the following expression:
First, it is necessary to explain how these DEFOs of dynamics of the structure of basic and complex RDDSFOs are compiled. Then, we assumed that the resulting dynamics are obtained as the sum of component element motion in RE connected in parallel or in serial. We also show, through the decomposition of RDDSFT into the component elements with corresponding displacements and velocities, as well as interaction forces caused by external and internal degrees of the system, of the fractional type, how to compose SODEFO.
Considering that the previously published papers by the author [3,56], as well as two [2,57] in this Journal “Fractals and Fractional”, which are in the list of references, contain detailed descriptions of the methods and methodology, the author did not consider it necessary to describe them separately here. The author includes necessary descriptions of individual elements of the methodology in the corresponding part in manuscript.
For further research and testing the usefulness of other methods, it is useful to examine some transformation methods. In this paper, the Laplace transform was used. However, it is advisable to investigate the generalization of this method to a more universal transformation that includes well-known transformations such as the Laplace and Fourier transforms, presented in the complex reference [58,59].
3. Rheological Newton Viscous Fluid Element Fractional Type
In the previous published article [2], we listed the basic mechanical properties of ideal bodies, the basic properties of the materials from which they are most often made.
In this paper, we intend to apply one more ideal model based on its characteristics. The first new model is a generalization of the rheologic Newton’s ideally viscous fluid material based on the differential constitutive relationship between the normal stress and the velocity fractional order, by introducing a differential operator (1). For this element, the differential constitute relation is in the form , in which normal stress is determined by DCRFO, where is an exponent, in the interval between zero and one, . It is a generalization of the viscous dissipative element and includes it.
Such a rheological element of basic ideal materials with pure ideal properties can be combined into hybrid rheological complex models, where one pair of elements of basic materials can be connected in two ways.
a* serial–in a series, which is indicated by a horizontal line “-” between the elements; see the example of a rheological basic complex, Maxwell’s model;
and
b* parallel, which is indicated by a vertical line “/” between the elements; see the example of a rheological basic complex, Kelvin–Voigt’s model; for details, see Reference [2].
4. Rheological Discrete Dynamic Systems, Fractional Type Oscillators or Crawlers (Creepers) Fractional Type
In this part of the article, we present the results of the study of the dynamics and properties, as well as the analysis of the dynamics of RDDSFO with one external degree of freedom of movement, which are bound by SLRCMFT. The SLRCMFT contains the light structure of one of the RCMFT material models, presented in Reference [2], for which the properties and differential constitutive relations, the fractional order, were defined in one of the previous published papers (for some details see Reference [2]) and for which we assumed negligible masses. We also assumed that they have the properties (elasticity and viscosity) of the basic rheologic elements that modeled the corresponding structure. For each of the elements that make up the SLRCMFO, we assume that it has negligible mass, but that it has the appropriate properties: ideal elasticity, i.e., ideal fluid viscosity, fractional type, i.e., the ability of ideal plastic weaving.
The term “standard lightweight rheological model” denotes one of the rheological basic or hybrid complex models of ideal materials (presented in Reference [2]), for which we have introduced the assumption of a negligibly small mass. Such “standard lightweight rheological models (SLRCMFO)” have properties of elasticity and mechanical energy dissipation, which depend on their structure and the number of rheological elements that are connected in order, in parallel, and in combination. SLRCMFO serves as a connection between rigid bodies (or material points) so that they are an integral part of an RDDSFO. The dynamics of an RDDSFO depend on the character and properties of the SLRCMFO that connects rigid bodies to each other in an RDDSFO.
The SLRCMFO has a potential energy and an energy-dissipation function, but due to the introduced assumption of negligible mass, it has negligible kinetic energy.
Thus, we define the following, that the SLRCMFO poses potential energy and a fractional type of the energy dissipation:
- *
- The SLRCMFO Kelvin–Voigt model, without an internal degree of freedom of the motion;
- *
- The SLRCMFO Maxwell model with one internal degree of freedom of the motion;
- *
- The SLRCMFO Bingham model, with one internal degree of freedom of the motion;
- *
- The SLRCMFO Lethersich model, with one internal degree of freedom of the motion;
- *
- The SLRCMFO Jeffrys model, with one internal degree of freedom of the motion;
- *
- The SLRCMFO Burgers model, with two internal degrees of freedom of the motion.
It is possible to define numerous other types of SLRCMFOs, depending on the placed and assembled structures, from light basic elements.
Each of those SLRCMFOs, depending on the basic rheological elements in the structure, introduce ideal elasticity, ideal viscosity of the fractional type, or the composition of the plastic properties into the model.
For example, the SLRCMFO Kelvin–Voigt model has the property of sustainable elasticity, which we showed in published Reference [2]. This SLRCMFO Kelvin–Voigt model has the property of the accumulation of potential energy (deformation work) due to the deformation of the Hooke element and also the energy-dissipation property of the fractional type, when Newton’s viscous element, of the fractional type, is in the state of the property of the fractional type dilation velocity. This model does not have any degree of internal freedom of movement.
For example, the SLRCMFO Maxwell model has the property of normal stress relaxation, which we showed in published Reference [2]. This SLRCMFO Maxwell model has the property of accumulating potential energy (deformation work) due to deformation of Hooke’s element, but with the property of normal stress relaxation, the accumulation of potential energy (deformation work) tends to zero with time and also has the property of energy dissipation of the fractional type, when the Newton viscous element, of the fractional type, is in the state of the property of the velocity (rate) of dilation of the fractional type. This model has one internal degree of freedom of movement.
For example, the SLRCMFO Burgers model, has the property of normal stress relaxation, which we showed in published Reference [2]. This SLRCMFO Burgers model has the property of accumulating potential energy (deformation work) due to deformation of two Hooke’s elements, but with the property of stress relaxation, the accumulation of potential energy (deformation work) tends to zero with time, and also has the property of energy dissipation of the fractional type, when two Newton viscous elements, of the fractional type, are in the dilation velocity property fractional type. This Burgers model has two internal degrees of freedom of movement.
Here, it is only emphasized that the parallel connection of rheologic basic elements in the structure of SLRCMFO does not introduce a single, so the RDDSFT is an oscillator with the property of the fractional type dissipation of energy. However, each regular-serial connection of the basic rheological elements in the structure of SLRCMFO introduces one internal degree of freedom of movement, and the property of the dynamics of the RDDSFO, whether it is a rheologic creeper or an rheologic oscillator, must be analyzed in particular. If the regular-serial connection of the basic Newton fluid elements is “external”, then it is an RDDSFO always of the creeper type. In the event that the parallel connection of basic Newton fluid elements or groups of elements is “external”, then it is an RDDSFO always of the rheologic oscillator type with fractional type dissipation of the system.
4.1. Dynamics of a Fractional Type Rheologic Discrete Kelvin–Voigt Fractional Type Oscillator, with One External Degree of Freedom of Oscillation
A fractional type rheologic discrete Kelvin–Voigt oscillator (RD-KV-OFT) with one external degree of freedom of oscillation is bound by one standard light Kelvin–Voigt of the fractional type, model (SLRBC-KV-FTM), with the property of subsequent elasticity (SE).
In Figure 1a, two material points (rigid bodies), mass and , are bound by a standard light rheologic basic complex of Kelvin–Voigt’s model of the fractional type (SLBC-KV-MFT), stiffness and , as a rheologic discrete dynamics system (RDDS) with two degrees of freedom of movement, and one degree of freedom of rheologic oscillations, one material point (rigid body) in relation to the other, subjected to the action of single frequency force , and for which are the positions are determined by independent generalized coordinates and .
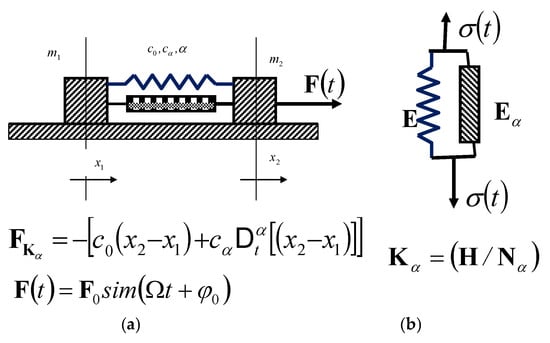
Figure 1.
Rheological discrete dynamic system (a) of two material points, mass and , bound by a standard light rheological basic complex of the Kelvin–Voigt model, fractional type, stiffness and , as a RDDSFO with two degrees of freedom of movement, and one degree of freedom of oscillation, one material particle in relation to the second, for which positions are determined by IGC and ; (b) structure of an SLRBC-KV-FTM.
Figure 1b shows the structure of a standard lightly rheological basic complex of the Kelvin–Voigt model, fractional type (SLRBC-KV-FT).
The system of ordinary differential equations of the fractional order (SODEFO) of the dynamics of the rheological discrete dynamical system (RDDSFT), from Figure 1a, when action of the active single frequency force is acting, is as follows (for more details see Reference [56]):
If we now multiply the first ODEFO (10) by and the second (11) by and then subtract the first from the second, we get one ODEFO of the following form:
And if we add them up, we get the following equation:
which, through integration, gives , from which we conclude that for the entire RDDSFT, both masses move with a constant amount (linear momentum) of movement.
In the first ODEFO form (10), we introduce the following symbols, and , and we introduce a new IGC , which represents the relative displacement of one material particle in relation to another. Now, we can write the first ODFFO of form (11) in the following form:
The system of ordinary inhomogeneous differential equations, of fractional order, of the dynamics of the discrete dynamics system from Figure 1a, is as follows (for details see Reference [56]):
If we now multiply the first inhomogeneous fractional differential Equation (110) by and the second (11) by and then subtract the first from the second, we get an IODSFO of the following form:
And if we add this up, we get
which gives, through integration,
from which we conclude that for the entire rheological discrete dynamic system, both masses move harmonically with an oscillatory amount of movement (harmonically oscillatory impulse-linear momentum).
In the first previously obtained IODEFO form (18), introduce symbols , and , and we introduce a new independent generalized coordinate , which represents the relative displacement of one material point in relation to another. Now, we can write the first previously obtained ordinary inhomogeneous differential equation, of fractional order, of the form (13) in the following form:
And this completely represents a relatively forced rheological oscillation, of the fractional type, of one material point in relation to another, of the fractional type system.
For borderline cases when and , we get simple classical cases, the solutions of which are known (see Reference [56]).
The ODEFO, (14), when the exponent of the fractional order differentiation is a rational number from the interval , can be solved using Laplace transforms (LTs). Let us introduce the notation for the Laplace transform , which is defined by the definite integral in the form (4) in which is a parameter, which can be a complex number.
It is also the following:
because we believe that the initial conditions are .
Based on the previous expressions (4) and (17) and applying the Laplace transformation to the ODEFO (10), we obtain the following:
The solution of the previous algebraic Equation (18) represents the Laplace transformation of the solution by an IGC and the form is as follows:
Now, we write the previous solution (19) for the Laplace transform in the following form:
and we rewrite the previous solution in the Laplace transform (20) in series by the degrees of parameter in the following form (for details see References [3,23,56]):
i.e., in the following form:
Given that the Laplace transform of this degree function of , as well as its inverse, is the inverse Laplace transform of , it is as follows:
we translate the Laplace transform (21), using expression (23), into the time domain.
Now, through the inverse Laplace transformation of the previous solution , we obtain the required approximate analytical solution of the ordinary homogeneous differential equation, of fractional order (16), in an analytical approximate form:
or in the following form (see References [3,23,56]):
Special cases are obtained for and they are as follows: a* for and ; b* for and .
For the case that the coefficient is equal to zero and the fractional differentiation exponent is from the interval , it follows that
Then, for the analytical approximate solution of the homogeneous ordinary differential Equation (16), of fractional order (14), for the case that the coefficient , is equal to zero, as well as , we now get the following:
By analyzing the previous expression (27), for the analytical approximate generalized solution, , we come to the conclusion that we can divide it into two own-eigen modes -“likecos” and -“likesin”, which we define based on the following analytical approximate summation forms (for details see References [3,56]):
We gave them these names, for -“likecos” and for -“likesin”, because naturally they are equal to cosine and sine, when for the case when the exponent of fractional order differentiation , and , the expressions are defined by and :
We also applied the Laplace transform over the functions and , in the following form, which we need in the further solution:
Based on the previous analytical approximate expressions (24), (29), and (30), as well as (18) and (33), and applying Laplace transformations to the IODEFO (16), we obtain the following:
The solution of the previous inhomogeneous algebraic Equation (34) represents the Laplace transformation of an IGC in the following form:
Now, we write the previous analytical approximate solution (35) for the Laplace transform in the form
i.e., we write the previous expression (36) in the recognizable form of the second term for the convolution integral in the form of the product of two Laplace transforms of the functions, one of which is the Laplace transform of the “likesin” mode (30) of the fractional type eigen mod of rheologic oscillators, , and the other is the Laplace transform transformation of a single frequency force , that is in the following form:
or decomposed into terms corresponding to eigen rheological modes of free rheological oscillations and forced rheological mode:
As we analyzed the first two terms and of the previous approximate analytical solution (31) via the Laplace transformation in the previous part, as an approximate analytical solution of the autonomous ordinary differential equation, fractional order (14), it is as follows:
that is, by applying the inverse of the Laplace transform, we obtain an expression for those terms in the time domain in the free regime of rheologic fractional type oscillations:
in which and are how we determined them in the previous part with expressions (29) and (30).
Now, we only have to determine the particular approximate analytical solution, in the time domain, using the third term from the approximate analytical solution (40), now in the following form:
We see that we have written the Laplace transform of the forced mode, a particular analytical approximate solution of an ordinary inhomogeneous differential equation, fractional order, (16) in the form of the product of two Laplace transforms and of two functions in convolution with the third. This leads us to use the properties of the three functions, which are in convolution.
The Laplace transform of the product of two functions , which are in convolution with the third, is equal to the product of the individual Laplace transforms of those functions and .
Now, we use the previous property of the Laplace transforms of those functions and and apply it to expression (41) in which is the approximate analytical particular solution of the function in convolution with the functions and . Now, based on the property of the functions and being in convolution, we wrote the following:
or
or
And let us recall the convolution theorem, which says that three functions, , , and , are in convolution (denoted by the symbol) if they satisfy the following relation:
For these three functions, , , and , which are in convolution, it is valid that the Laplace transform is equal to the product of the Laplace transforms of the two functions and , with which it is in convolution: .
- The Graphs of Free and Forced Modes, the Fractional Type, of the Dynamics of a Kelvin–Voigt Oscillator, of the Fractional Type, with Subsequent Elasticity
a.1. An analytically approximate expression (29) for the fractional type eigenmode, of a fractional type rheologic Kelvin–Voigt oscillator, of free oscillations, “likecos” is of the form , Figure 2a. For , the eigrn mode is purely harmonic, because it is a linear differential equation with one of the particular solutions of the following form: and . The expressions of boundary lines of the fractional type eigen surface of the rheologic Kelvin–Voigt oscillator, of free oscillations, “lkecos” are as follows: and . See Figure 2a.
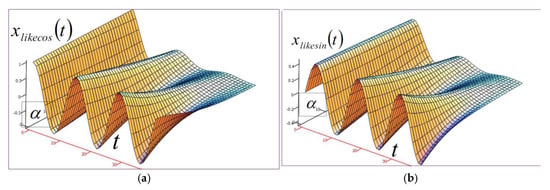
Figure 2.
(a) The graph of the numerical experiment over the analytical approximate expression (29) for the fractional type eigen rheological mode of the rheological Kelvin–Voigt discrete dynamical system of the fractional type for free oscillations, “likecos”, which is of the approximate analytical form: in the form of the surface in the coordinate system: elongation of the fractional type “likecos” mode, time , and exponent of a fractional order derivative in interval from zero to one, ; the expressions for boundary lines are as follows: and . (b) The graph of the numerical experiment over the analytical approximate expression (30) for the fractional type eigen rheological mode of the rheologic Kelvin–Voigt discrete dynamical system of fractional type free oscillations, “likesin” form in the form of the surface in coordinate system: elongation “likesin” fractional type mode, time and exponent of fractional order derivative in the interval from zero to one, ; expressions for boundary lines are as follows: “likesin”, which is of the approximate analytical form: in the form of the surface in the coordinate system: elongation of the fractional type “likesin” mode, time , and exponent of fractional order derivative in the interval from zero to one, ; the expressions for boundary lines are as follows: and .
b.1. An analytically approximate expression (30) of a fractional type rheological Kelvin–Voigt oscillator, of free rheological oscillations, for the eigen rheological mode “likesin” is of the form , Figure 2b. For , the eigrn mode is purely harmonic, because it is a linear differential equation with one of the particular solutions of the following form: and . The expressions of boundary lines of the fractional type eigen surface of the rheological Kelvin–Voigt oscillator, of free oscillations, “likesin” are as follows: and .
c.1. The graph of the forced rheologic mode, fractional type, of the dynamics of a fractional type rheologic Kelvin–Voigt discrete oscillator, with the property of subsequent elasticity.
In this part, we show a graphic representation of the surface of the forced main rheologic mode, of the fractional type (43), of the rheologic oscillatory dynamics of the rheologic dynamical Kelvin–Voigt oscillatory DDSFT based on the analytical approximate expression (45) of a particular solution in the form , for different values of the parameters and , and of the frequency , that is, of the circular frequency of the external single frequency force. This single frequency force, which acts on the rheologic Kelvin–Voigt DDSFT oscillator, has one degree of freedom of rheological oscillation, as well as for their various relationships .
The graphic is in the form of the space surface in the coordinate system of forced mode elongation, fractional type, , time and exponent of fractional order of differentiation, for interval .
A numerical experiment under the approximate analytical expression of a particular solution in the form indicates that the series was performed with 40 (60) terms of the power series at time , and it was shown that the series for forced modes, of the fractional type, converges to the exact solution. To check the criteria of the convergence, we used the criterion that for the limit value on the graphs of the space surfaces of rheologic forced main modes of the fractional type, the limit (boundary) line is a line graph of a sinusoidal, basically cosine function, in areas far from the resonant value of the circular frequency , for the linear case, and in areas close to the resonant value of the circular frequency becomes associated with large elongations and amplitudes (for details of the complex numerical experiment, see References [3,56]).
In the following, only a characteristic graphical contribution is shown for some discrete values of the frequency , , that is, the circular frequency of the external excitation of the single frequency force.
A graphical representation of the space surface of the particular solution of the OIDEFO (43) is presented in Figure 3. This space surface is shown in Figure 3 and describes the elongation of the FRMFT of the dynamics of the rheological Kelvin–Voigt DDSFO forced rheologic oscillations under the action of a single frequency force, in the CS: elongation of the forced rheological mode, time , and exponent in , for an external force circular frequency .
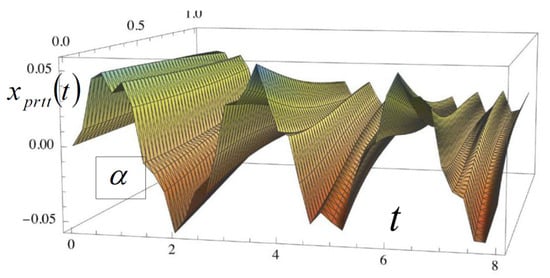
Figure 3.
Graphical representation of the space surface of the particular solution of the OIDEFO (16), which describes the elongation of the forced rheological mode, fractional type, of the rheological Kelvin–Voigt DDSFO-forced rheological oscillations under the action of a single frequency force, in the coordinate system: elongation of the FRMFT, time , and exponent in , and for the external force circular frequency .
From the numerical experiment, we see that for the selected parameters of the rheological Kelvin–Voigt DDSFO oscillatory system, of the fractional type, and with one degree of freedom of forced oscillation, the particular integral, around the value of the frequency , has a characteristic shape in relation to the cases with lower and higher frequencies, and in the same interval times. In the same time interval, for frequency values around , it has the smallest number of whole oscillations, while for lower, as well as higher, frequencies, the external forcing oscillator has a larger number of whole waves.
4.2. Dynamics of a Rheological Maxwell Discrete Dynamic System-A Fractional Type Creeper, with One External and One Internal Degree of Freedom of Movement
A rheologic Maxwell discrete dynamic system-a fractional type crawler (creeper), with one external and one internal degree of freedom of movement is with stress relaxation.
Figure 4 shows the rheological discrete dynamic Maxwell system, the fractional type (RDDS-M-FT) of one material point (rigid body in translator motion), and mass , bound by a standard light basic complex Maxwell model of the fractional type (SLRBC-M-MFT), with properties of normal stress relaxation (NSR), stiffness and , as a system with one external and one internal degree freedom of movement, for which the positions are determined by independent generalized coordinates (IGCs) and in two variants in the upper part and in the lower part of Figure 4, with the reverse order connection of rheological elements in (SLRBC-M-MFT). In the left part of Figure 4, the SLRBC-M-MFT Maxwell model with stress relaxation is shown.
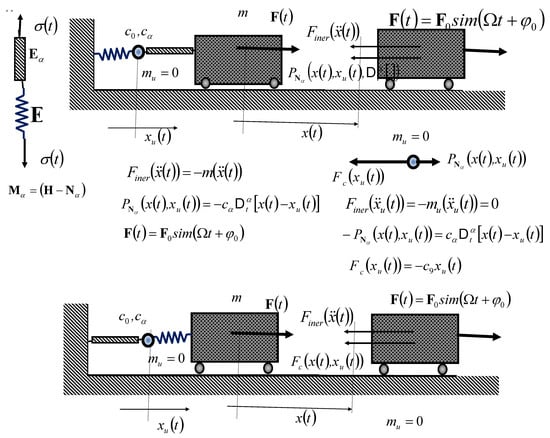
Figure 4.
Rheological Maxwell discrete dynamic system fractional type (RDD-M-SFT), from one material point (rigid body in translation), mass bound by a standard light basic complex Maxwell model of the fractional type (SLRCB-M-MFT), with the property of normal stress relaxation (NSR), stiffness and , as a rheological discrete dynamic system (RDDSFO) with one external and one internal degree of freedom of movement, for which the positions are determined by IGC and ; in the left part of Figure 4, structure of the SLRBC-M-MFT; in upper part and drawn part of Figure 4, two variants of RDD-M-SFO with the reverse of the binding structure of SLRBC-M-MF.
The rheologic discrete dynamical Maxwell’s system (RDD-M-SFT), shown in the upper part of Figure 4, has one external degree of freedom of movement and one internal degree of freedom of movement, introduced within the standard light basic complex Maxwell model of fractional type (SLRBC-M-MFT). is IGC, which corresponds to the external, and is IGC, which corresponds to the internal degree of freedom of SLRBC-M-MFT. In the point of internal coupling of rheological simple elements of the structure of the SLRBC-M-MFT, let us set one fictitious material point of mass equal to zero, that is, .
Now, let us set up a system of IODEFO, when we will assume that the basic mass of that RDD-M-SFT is , which describes the dynamics of the RDD-M-SFT for the case of binding the structure of the SLRBC-M-MFT, from the upper part of Figure 4, and is in the following form:
For the second case of binding the structure of the SLRBC-M-MFT, from the other dawn part in Figure 4, the system of IODEFO, which describes the dynamics of that RDD-M-SFT, is of the following form:
Now, let us introduce the following denotations:
and we rewrite the previous systems (47) and (48) of IDEFO in the following forms:
* The first case of the binding structure of the SLRBC-M-MF system of IDEFO is in the following form:
* The second case of binding the structure of the SLRBC-M-MF system of IDEFO is in the following form:
Now, let us apply Laplace’s transformation to both previous systems of IODEFO:
* For the first system of IODEFO:
And, respectively,
That is, from the second equation of the previous algebra system (51), it is as follows:
From the previous equations, we get the Laplace transformation of the IGC of the external degree of freedom independent in the following form:
First, it is necessary to determine the invert Laplace transformation of the IGC of the external degree of freedom , for free self-creeps, and move to the time domain.
And then, use the convolution integral and individual inverse Laplace transformations and determine the IGC of external degree of freedom , for forced creeping movement , for forced creep motion, and move to the time domain.
We can, then, determine the IGC displacement point of the order connection of Hooke’s ideally elastic element and Newton’s ideally viscous element, fractional type, in SLRBC-M-MFT in the following form:
Doing so, we keep in mind that when the three functions , , and are in convolution, then the Laplace transform can be written as a product of the Laplace transforms of those two functions and .
Now, for the second case of binding the structure of the SLRBC-M-MFT, presented in the lower part in Figure 4, let us apply Laplace’s transformation to both ODEFOs, of the second system (49). That is, from the second algebra equation, it is
which replaces the first one, and from the previous equations, we get the Laplace transformation IGC , of the external degree of freedom:
Now, it is necessary to determine the invert Laplace transformation of the IGC .
First, it is necessary to determine the invert Laplace transformation of the IGC , of the external degree of freedom, for free self-creep motion and move to the time domain.
We can, then, determine the IGC of the displacement of the point of order connection of two basic elements, of the fractional type, in SLRBC-M-MFT in the following form:
The three functions , , and are in convolution. In doing so, we keep in mind that when the three functions are in convolution, then the Laplace transform can be written as a product of the Laplace transforms of those two functions.
Theorem and Three Collearies
By comparing the obtained expressions, we see that the way of predicting the structure of SLRBC-M-MFT has a greater influence on the resulting movement of RDD-M-SFT.
Theorem of a difference between two RDD-M-SFT a rheologic oscillator and/or a rheologic creeper in free and forced regime of motion. The structural scheme of a SLRBCMFT, which represents a link within an RDDSFT, can be seen as a character of the dynamics of RDDSFT.
Colleary 1.
If at least one of the fluid elements, of the fractional type, is regularly-serially connected in the structure independently, and is not in a parallel connection or not within a parallel connection with any of ideally elastic elements, then it is also about viscoelastic creeper of RDDCSFT.
Colleary 2.
If each of Newton’s elements is connected in a parallel or intra-parallel connection with one of Hooke’s c elements, DDSFT is with elastoviscous damped oscillations.
Colleary 3.
Each regular-serial connection of one of the fluid elements and ideally elastic element introduces one internal degree of freedom of movement of RDDSFT, before the external degrees of freedom, which contains SLRBCMFT as binding elements.
4.3. Dynamics of a Rheological Lethersich Discrete Dynamic System of the Fractional Type Creeper
The dynamics of a rheological Lethersich discrete dynamic system is of the fractional type (RDD-l-SFT) creeper (or crawler), with one external and one internal degree of freedom of movement, which is bound by one Lethersich SLRC-L-MFT, with normal stress relaxation (NSR).
Figure 5 shows two rheologic discrete dynamic Lethersich’s systems of the fractional type (RDD-L-SFT), containing one material point (rigid body), mass , bound by the standard light structure of an SLRC-L-MFT composed, in a regular connection, of the SLRC-KV-MFT, with the properties of subsequent elasticity, and the basic Newton’s ideal viscous fluid element, of the fractional type, stiffness , , and , as a system with one external and one internal degree of freedom of movement, for which the positions are determined by IGC and . The left part of Figure 5 shows the structure of an SLRC-L-MFT. Figure 5 in the upper and dawn parts shows two cases of RDD-L-SFT with a reversed sequence of the elements of the SLRC-L-MFT in a system with a material particle (rigid body), mass .
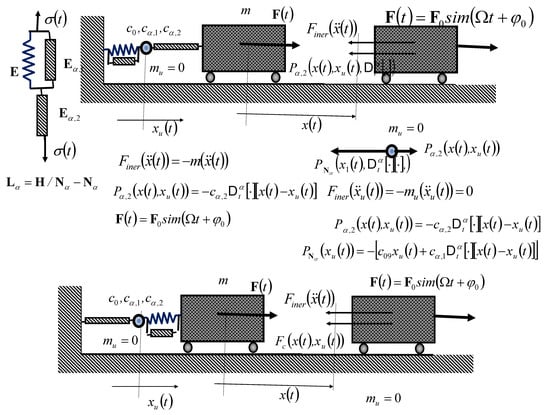
Figure 5.
Rheologic Lethersich’s discrete dynamic system of the fractional type (RDD-L-SFT) bound a standard light rheologic complex of Lethersich’s model of the fractional type (SLRC-L-MFR), ideal visco-elastic fluid, stiffness , , and , as a rheological discrete dynamical system (RSSDFT) with one external and one internal degree of freedom of movement, for which the positions are determined by IGCs and ; in the left part of Figure 5 is the structure of a standard SLRC-L-MFR; in upper and dawn parts of Figure 5 are two cases of RDD-L-SFT with the reverse of the binding order of the elements of the SLRC-L-MFR.
The RDD-L-SFT, shown in the upper part in Figure 5, has one external degree of freedom of movement-creep and one internal degree of freedom of movement within itself.
Let us denote by , the IGC, which corresponds to the external degree of freedom of movement, and by , the IGC, which corresponds to the internal degree of freedom of movement of the RDD-L-SFT.
At the point of the internal series coupling of the SLRC-KV-MFT elements of the structure of the SLRC-L-MFT, we set one fictitious material point of the mass equal to zero, that is , while we set the system of ODEFO, assuming that the basic material particle of the RDD system is mass . The system of ODEFO for describing the dynamics of the RDD-L-SFT presented in the upper part of Figure 5, is in the following form:
For the second case, the reverse order of binding of the order of the elements of the structure of the SLRC-L-MFT, presented in the lower part of Figure 5, the system of ODEFO is of the following form:
Now, let us introduce the following denotations:
and, the previous systems (58) and (59) of the ODEFO are rewritten in the following forms:
*For another system of ODE, for describing the dynamics of the RDD-L-SFT, presented in the lower part of Figure 5:
For another system of ODE, for describing the dynamics of the RDD-L-SFT, presented in the lower part of Figure 5, it is in the following form:
Now, let us apply the Laplace transformation to both previous systems (61) and (62) of ODEFO, so it is as follows:
*First, for the first system (61), application of the Laplace transformation gives the following:
and, that is the algebra system with two algebra equations along two the Laplace transformations and of IGCs, and , one of an external and one of an internal degree of freedom motion, in the following form:
That is, from the second algebra equation of the system (64) the Laplace transformation IGC e of an internal degree of freedom, is in the following form:
and substituting expression (65) of the Laplace transformation into the first algebra equation of the previous system (64), gives the Laplace transformation of IGC in the following form:
The last Equation (66) gives the Laplace transform of the IGC , of the external degree of freedom, and now, it is necessary to determine the inverse Laplace transform of this IGC , and it is necessary to move to the time domain.
First, determine the inverse transformation from the Laplace transformation of the IGC , for the free self-creep motion of the RDD-L-SFT, and move to the time domain.
And then, the individual invert transforms of the two expressions
and , determine the IGC , for forced creep (crawler) dynamics, and move to the time domain.
We can, then, determine the IGC of displacement of the point of the order–series of an ideally elastic element and ideal element, into SLRC-L-MFT
using the property of the three functions, , , and in convolution.
The second model of RDD-L-SFT is with the reversed order of the elements of the SLRC-L-MFT, in the system (see the dawn part of Figure 5). For the second RDD-L-SFT, with the reversed order of the elements of the SLRC-L-MFT, which is shown in the lower part of the Figure 5, the system of ODEFO is in the form (63).
Now, let us apply the Laplace transformation to the system (63) of differential equations, of the fractional order, so it is as follows:
And through substitution of the second expression of the previous system (68) into the first algebra equation, it gives the Laplace transform of the IGC in the following form:
Now, of IGC , and move to the time domain.
First, of IGC , for the free self-creep of the RDD-L-SFT, which is shown in the lower part of Figure 5, and move to the time domain.
And then, inverse transform two expressions and determine the IGC for forced dynamic process-forced creep (crawler), and move to the time domain.
We can, then, determine IGC of the displacement of the point of the order–series coupled to a basic ideally elastic element and ideally viscous element, into standard light Maxwell’s basic complex rheologic element, of the fractional type, in the following form:
using the property of the three functions, , , and that they are in convolution.
Theorem and Theory
Theorem 1.
In forced crawler (creeper) movements, when a periodic single frequency force acts on the RDD-L-SFT, which is shown in the upper and the lower part of Figure 5, it is characteristic that instead of crawling, which is characteristic of the free movement of crawlers, pulsations occur during crawling under the action of external single frequency periodic force.
Colleary 4.
By comparing the obtained analytical expressions for both free forced modes of the particle (rigid body), for two cases of order in a series of elements, we see that the sequence orders of the basic elements of the structure of the SLRC-L-MFT have a great influence on the resulting movement dynamics of RDD-L-SFT.
It is a characteristic of RDD-L-SFT that they can perform decreasing, damped creeping, with yielding and self-free creep (crawler-yielding), or forced pulsating creeping “oscillations” in creep (crawler-yielding) under the action of periodic forces of certain frequencies.
4.4. Dynamics of a Rheological Jeffrys’ Discrete Dynamic System of the Fractional Type Creeper
The dynamics of a rheological Jeffrys’ discrete dynamic system of the fractional type (RDD-J-SFT) are the rheologic creeper (crawler) fractional type, with one external and one internal degree of freedom of movement, which is bound by one standard light rheological complex Jeffrys’ model of the fractional type (SLRC-J-MFT), with the property of normal stress relaxation (NSR).
In Figure 6, Rheologic Jeffrys’ discrete dynamic system, of the fractional type, of one material point, mass bound by a standard light rheologic complex Jeffrys’ model of the fractional type, stiffnesses , , and , as a RDDS-J-FT with one external and one internal degree of freedom of movement, for which the positions are determined by IGC and ; in the left part of Figure 6, the structure of standard light rheologic complex Jeffrys’ model of the fractional type; in the upper and lower parts, Figure 6 shows two cases of Jeffrys’ RDDS-J-FT of the reversed sequence of rheologic elements of a SLCJMFT in a RDDS-J-FT. Jeffrys’ RDDS-J-FT is composed, in parallel connection, of the rheologic basic complex Maxwell model, with the property of normal stress relaxation, and basic Newton’s ideal viscous fluid, fractional type element, stiffness , , and , as a system with one external and one internal degree of freedom of movement, for which the positions are determined by independent generalized coordinates and .
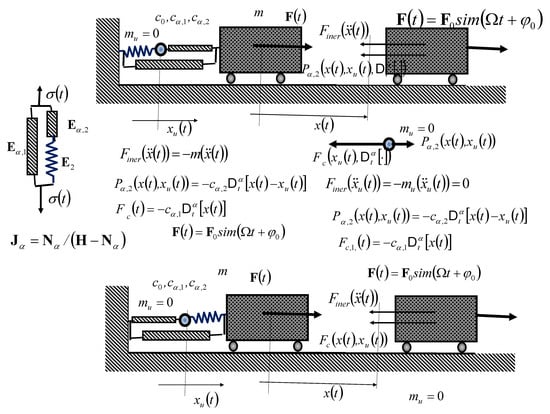
Figure 6.
Rheologic Jeffrys’ discrete dynamic system, of the fractional type, of one material point, mass bound by a Jeffrys’ SLRCJMFT , stiffnesses , , and , as a RDDS-J-FT with one external and one internal degree of freedom of movement, for which the positions are determined by IGC and ; in the left part of Figure 6, the structure of SLRCJMFT Jeffrys’ model; in the upper and lower parts, Figure 6 shows two cases of Jeffrys’ RDDS-J-FT, of the reversed sequence of Jeffrys’s SLRCJMFT in a Jeffrys’ RDDS-J-FT.
Figure 6, in the left part, shows the structure of a standard light rheologic complex Jeffrys’ model of the fractional type. Figure 6, in the upper and lower part, shows two cases of Jeffrys’ RDDS-J-FT, of the reversed sequence of rheologic elements of a SLRCJMFT Jeffrys’ model in a Jeffrys’ creeper system.
The rheologic Jeffrys’ discrete dynamic system, shown in the upper part in Figure 6, with the basic property of creep, (crawler) has one external creep-yielding degree of freedom and one internal creep degree of freedom, within the standard light rheologic complex Jeffrys’ model of the fractional type itself. Let us denote the independent generalized coordinate , which corresponds to the external degree of freedom of creep or yielding flow, and , the independent generalized coordinate, which corresponds to the internal degree of freedom of movement of the attachment point of the structure elements of the modified standard light rheologic complex Jeffrys’ model of the fractional type of this standard light model.
At the point of the internal series-order coupling of the elements of the structure of the standard light rheologic Maxwell model of the fractional type, models of the substructure of the standard light rheologic Jeffrys’ model of the fractional type, let us set one fictitious material point of mass equal to zero, that is, , while we set a system of ordinary differential equations, of fractional order, assuming that the basic material particle of the system is with mass . The system of the ordinary differential equation, of fractional order describing the dynamics of rheological Jeffrys’ discrete dynamic system, shown in the upper part in Figure 5, is in the following form:
For the binding order of the elements of the sub structure of SLRC-J-MFT, from the lower part of Figure 6, the system of ODEFO is
Now, let us introduce the following denotations:
We rewrite the previous systems (71) and (72) of ODEFO in the following form:
* For the first RDD-J-SFT and the first order of elements in the structure of the SLRC-J-MFT, from the upper part of Figure 6, the system of ODEFO is in the following form:
For the second RDD-J-SFT and the reverse order, from the previous one, of the elements in the structure of the SLRC-J-MFT, from the lower part of Figure 6, the system of ODEFO is in the following form:
Now, let us apply the Laplace transformation to both previous systems (74) and (75) of ODEFO.
We get of the IGC , of the external degree of freedom movement, in the following form:
First, determine of IGC , for free own self-flows-creeping, and move to the time domain.
We can, then, determine the IGC of displacement of the point of order connection in the substructure of basic ideally elastic and ideally viscous elements, in SLRBC-M-MFT, in the following:
The second order of connecting the rheologic elements of the structure of the SLRC-J-MFT in the RDD-J-SFT, presented in the lower part of Figure 6, described by the other system (75) of ODEFO in the form (75), gives the Laplace transform of IGC of the external degree of freedom:
First, of the IGC, of the external degree of freedom, for self-free creep (crawler) motion must be determined, and move to the time domain.
And then, determine IGC , of the external degree of freedom for forced creep (crawler) dissipative motion in the creep (crawler-yielding) regime under the action of single-frequency periodic forces of certain frequencies, and move to the time domain.
Then, we can also determine the IGC , of the internal degree of freedom of the displacement of the point of order promise of basic Hooke’s element and Newton’s element, in the structure of the SLRBC-M-MFT, in the following:
From the obtained analytical expressions for both natural and forced creeping modes of the main particle (rigid body), we see that the order of the sequence of the basic elements in the substructure of SLRC-J-MFT has a great influence on the resulting creeping dynamics of the RDD-J-SFT.
4.5. Dynamics of a Rheologic Jeffrys’-H2 Discrete Dynamic System, the Fractional Type Rheologic Oscillator
A rheologic Jeffrys’-H2 discrete dynamic system of the fractional type (RDD-JH2-SFT) is a rheologic oscillator (ROFT), with one external and one internal degree of freedom of movement, which is bound by one standard light rheological complex Jeffrys-H’s model of fractional type model (SLRC-JH2-MFT). RDD-JH2-SFT and SLRC-JH2-MFT are with the property of SE and internal NSR.
Figure 7 shows the RDD-JH2-SFT of one material point (rigid body in translator morion), mass , bound by SLRC-JH2-MFT, composed, in a parallel connection, of the Maxwell RCB-M-MFT, with the internal property of normal stress relaxation, and a basic Hooke’s ideal elastic, stiffnesses , , and , as a system with one external and one internal degree of freedom of oscillatory movement, for which the positions are determined by IGC and .
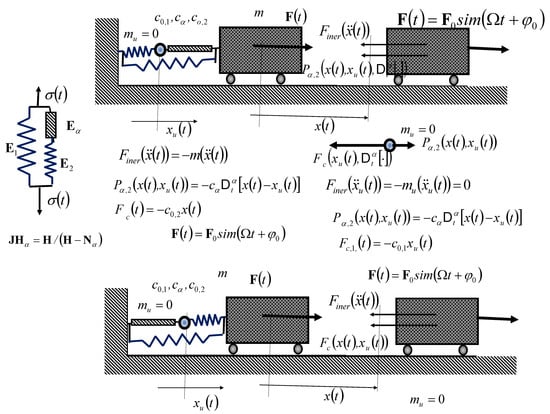
Figure 7.
Rheologic Jeffrys-H’s discrete dynamic system of the fractional type (RDD-JH2-SFT), of one material point, mass bound by a standard light rheologic complex Jeffrys-H’s model of the fractional type (SLRC-JH2-MFT), stiffnesses , , and , as a rheologic Jeffrys-H’s discrete dynamic system, of the fractional type (SLRC-JH2-MFT), with one external and one internal degree of freedom of oscillatory movement, for which the positions are determined by independent generalized coordinates and ; Figure 7, in the left part, contains the structure of standard light complex Jeffrys-H’ model of the fractional type (SLRC-JH2-MFT); Figure 7, in the upper part and in lower part, contains two cases of the RDD-JH2-SFT with the reverse order of binding elements of the SLRC-JH2-MFT.
Figure 7, in the left part, shows the structure of an SLRC-JH2-MFT. Figure 7, in the upper part and in the lower part, shows two cases of RDD-JH2-SFT, with a reversed sequence of rheologic elements of the structure of the SLRC-JH2-MFT in an RDD-JH2-SFT with a main material point (rigid body) mass .
The RDD-JH2-SFT is a rheological Jeffrys-H2’s discrete dynamic oscillatory system, shown in the upper part of Figure 7, and has one external oscillating degree of freedom and one internal oscillating degree of freedom within the SLRC-JH2-MFT .
Denote by the IGC, which corresponds to the external degree of freedom of rheological oscillation, and by , the IGC, which corresponds to the internal degree of freedom of SLRC-JH2-MFT .
At the point of the internal series coupling of the RCB-M-MFT of structure of the SLRC-JH2-MFT, let us set one fictitious material point of mass equal to zero, that is, , while we set the system of ODEFO, assuming that the basic mass of the RDD-JH2-SFT is .
The system of ODEFO of the RDD-JH2-SFT describing the dynamics of the RDD-JH2-SFT, presented in upper part of Figure 7, is in the following form:
For the second case of binding of SLRC-JH2-MFT, from the lower part of Figure 7, the system of ODEFO, describing the dynamics of RDD-JH2-SFT, is as follows:
Now, let us introduce the following denotations:
We rewrite the previous systems (80) and (81) of ODEFO in the new following forms:
For the first RDD-JH2-SFT and the first order of elements in the structure of the SLRC-JH2-MFT, from the upper part of Figure 7, the system of ODEFO, describing the dynamics of the RDD-JH2-SFT, is in the following form:
For the second RDD-JH2-SFT and the reverse order, from the previous one, of the elements in the structure of the SLRC-JH2-MFT, from the lower part of Figure 7, the system of ODEFO, describing dynamics of the RDD-JH2-SFT, is in the following form:
Now, let us apply the Laplace transformation to both previous systems (83) and (84) of ODEFO.
Now, we apply the Laplace transformation to the first (83) and second (84) of the previous two systems of ODEFO (83) and (84) and write two algebra systems along two corresponding Laplace transformations of IFCs describing the dynamics of RDD-JH2-SFT, presented in the upper and in lower parts in Figure 7, then, from the corresponding algebra system:
* For the first RDD-JH2-SFT, we get the Laplace transform of IGC of the dynamics of RDD-JH2-SFT, the model presented in the upper part in Figure 7, in the following:
and
*For the second RDD-JH2-SFT, the Laplace transform of the IGC , of the dynamics of RDD-JH2-SFT, presented in the lower part in Figure 7, from the second algebra equation of the system (84), is
4.6. Dynamics of a Rheologic Burgers Discrete Dynamic System, the Fractional Type, and Creeper (Crawler, Yielding)
A rheologic Burgers discrete dynamic system, of the fractional type (RDD-B-SFT,) is a rheologic creeper (crawler, yielding) type (RCFT). RDD-B-SFT is with one external and two internal degrees of freedom of movement. RDD-B-SFT is bound by Burgers SLRC-B-MFT of normal stress relaxation (NSR) and subsequent elasticity (SE).
In Figure 8, two models of RDD-B-SFT with the reversed binding order of the structural elements of SLRC-B-MFT, with a main material mass point (rigid body), mass , are presented in the upper part and lower part of Figure 8. RDD-B-SFT bound by an SLRC-B-MFT, stiffnesses , , , and , and is with one external and two internal degrees of freedom, for which the positions are determined by three IGCs , , and . The structure of SLRC-B-MFT is visible in the left part of Figure 8. Reverse the order-series of binding elements of SLRC-B-MFT in the RDD-B-SFT, as a second model is shown, in the lower part of Figure 8.
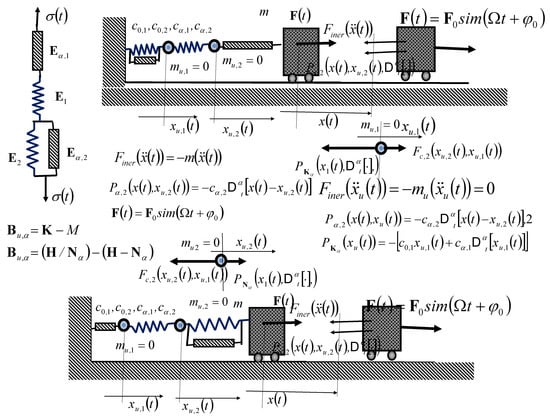
Figure 8.
Two models of the Burgers rheologic discrete dynamic system (RDD-B-SFT) with reversed binding order of the structural elements of the standard light rheologic Burgers model, of the fractional type (SLRC-B-MFT), with a main material mass point, mass ; RDD-B-SFT of one material point, mass , bound by an SLRC-B-MFT, stiffnesses , , , and , as a rheologic Burgers discrete system with one external and two internal degrees of freedom of movement, for which the positions are determined by independent generalized coordinates , , and ; in the left part of Figure 8, SLRC-B-MFT; in the upper part and in the lower part of Figure 8, two cases of RDD-B-SFT with the reverse order of binding elements of the SLRC-B-MFT.
RDD-B-SFT consists of one material mass point (rigid body), mass , which moves along a smooth horizontal plane, and which is bound by the SLRC-B-MFT, stiffnesses , , , and . The SLRC-B-MFT consists of two rheologic basic complex and regularly sequential connected models, the Kelvin–Voigt’s and Maxwell’s models, and both models are of the fractional type. SLRBC-KV-MFT possesses the property of subsequent elasticity (SE), and SLRBC-M-MFT possesses the property of normal stress relaxation (NSR) (for details and a large explanation, see References [2,18,56]). Each sequential connection of elements introduces one internal degree of freedom into the model, as well as in RDDS.
RDD-B-SFT, shown in Figure 8, has one external degree of freedom of creeping motion and two internal degrees of freedom of creeping motion introduced within the SLRC-B-MFT. Denote this by IGC, which corresponds to the external degree of freedom of creep-flow and by and , the IGC, which correspond to the internal degrees of freedom inside of the SLRC-B-MFT.
In the points of the internal series connection of Kelvin–Voigt RBCKVMFT and Maxwell RBCMMFT, of SLRC-B-MFT, place one fictitious material point, each, with mass equal to zero, that is, and , while we set up a system of ODEFO, and it will be that the system is with mass , in the following form:
* For the first order of binding of standard light rheologic basic complex models, SLRBC-KV-MFT and SLRBC-M-MFT, in the structure of the SLRC-B-MFT, included in the RDD-B-SFT, shown in the upper part of the Figure 8, the system of ODEFO contains three differential equations of fractional order, describing the dynamics of that system and is in the following form:
In the first RDD-B-SFT, presented in the upper part of Figure 8, the SLRC-B-MF, is set so that the Maxwell part of the structure is related to the material point mass , and the Kelvin–Voight’s part of the structure is attached to a fixed wall.
For the second order of binding of the light rheologic substructure, the Burgers RDD-B-SFT, shown in the lower part of Figure 8, in the structure of SLRC-B-MFT, the system of ODEFO also contains three ordinary differential equations of the fractional order, describing the dynamics of RDD-B-SFT, and is in the following form:
In the second RDD-B-SFT, presented in the lower part of Figure 8, the SLRC-B-MFT is set so that the Maxwell part of the structure is related to a fixed wall, and the Kelvin–Voigt’s part of the structure is attached to the material point mass .
Now, let us introduce the following denotation:
and the previous system (87) of ordinary differential equations, of fractional order, describing the dynamics of RDD-B-SFT, presented in the upper part of Figure 8, the first order of the bonding substructure of rheological basic complex models, is rewritten in the following form:
The second system (88) of ODEFO, describing the dynamics of RDD-B-SFT, presented in the lower part of Figure 8, the second reverse order of the binding substructure of rheological models, is rewritten in the following form:
Then, applying this to both previous systems of three differential equations, (90) and (91), we obtain two systems of algebraic equations in terms of the unknown Laplace transforms of IGC.
Solving these systems of algebraic equations in terms of the unknown Laplace transforms, we obtain the following:
* The , and , of IGC, one corresponding to the external degree of freedom and two, and , corresponding to the internal degrees of freedom, of the dynamics of RDD-B-SFT, for the model shown in the upper part of Figure 8, are as follows:
* The Laplace transforms , , and , of the IGC, one corresponding to the external degree of freedom and two, and , corresponding to the internal degrees of freedom of motion, of the dynamics of RDD-B-SFT, for the model shown in the dawn part of Figure 8, are as follows:
5. Energy Analysis of the Dynamics of Rheologic Discrete Dynamic Systems
In this part, we will state the expressions for the potential energy and the generalized function of the fractional type of energy dissipation (for details, see References [5,7,8]) for the dynamics of each RDDSFT, which we described by the systems of IDEFO.
The total potential energy of dynamics of the studied RDDSFT in the previous sections depends on the number of rheologic Hooke ideally elastic elements, contained in the corresponding SLRCM of the rigid body attachment, their axial deformations, and the order of attachment to the rigid body and the immovable wall. The total potential energy is equal to the sum of the individual potential energies of all the potential energies of Hooke’s ideally elastic elements due to the deformation work of each of them.
The generalized function of the fractional-type dissipation, the total energy of the dynamics of the studied rheologic discrete dynamic systems in the previous sections, depends on the number of rheological Newton’s viscous elements, the fractional type, contained in the corresponding standard light rheologic complex model of solid body binding, their fractional type axial velocities, and the order of weaving for a rigid body and a stationary wall.
The total generalized function, the total dissipation of the fractional type of the total energy of the system, is equal to the sum of the individual energy dissipations of all the energy dissipations of the Newton viscous fluid elements, of the fractional type, due to the axial velocities of the fractional type expansions of each of them.
For the dynamics of the Kelvin–Voigt RDD-KV-SFT-rheologic oscillator, the total potential energy and generalized function of energy dissipation of the fractional type, as shown in Figure 1, are as follows:
For the dynamics of the rheologic Maxwell fractional type discrete dynamic system-rheologic creeper, the kinetic energy, total potential energy, and generalized function of dissipation the fractional type of system energy are in the following form:
* For the first order of binding elements of the standard light rheologic complex model, as shown in the upper part of Figure 4,
*For the second reverse order of binding elements of the standard light and rheologic complex model, as shown in the lower part of Figure 4,
For the dynamics of rheologic Lethersich’s fractional type discrete dynamic system-rheologic creeper, the kinetic energy, total potential energy, and generalized function of the dissipation of the fractional type of system energy are in the following form:
* For the first order of binding elements of the standard light rheologic complex model, as shown in the upper part of Figure 5,
* For the second reverse order of binding elements of the standard light and rheologic complex model, as shown in the lower part of Figure 5,
For the dynamics of rheologic Jeffrys’ fractional type discrete dynamic system-rheologic creeper, the kinetic energy, total potential energy, and generalized function of dissipation of the fractional type of system energy are in the form:
*For the first order of binding elements of the standard light rheologic complex model, as shown in the upper part of the Figure 6,
* For the second reverse order of binding elements of the standard light and rheologic complex model, as shown in the lower part of the Figure 6,
For the dynamics of rheologic Jeffrys-H’s (Hooke) fractional type discrete dynamic system-rheologic oscillator, kinetic energy, total potential energy, and generalized function of dissipation of the fractional type of system energy are in the following form:
*For the first order of binding elements of the standard light rheologic complex model, as shown in the upper part of Figure 7,
* For the second reverse order of binding elements of the standard light and rheologic complex model, as shown in the lower part of Figure 6,
For the dynamics of rheologic Burgers’s fractional type discrete dynamic system-rheologic creeper, the kinetic energy, total potential energy, and generalized function of dissipation of the fractional type of system energy are in the following forms:
* For the first order of binding elements of the standard light rheologic complex model, as shown in the upper part of Figure 8,
* For the second reverse order of binding elements of the standard light and rheologic complex model, as shown in the lower part of Figure 8,
By comparing the expressions for the dynamic potential energies of rheologic discrete dynamic systems, the fractional type, bound by the same standard light rheologic complex models, fractional type, but with the opposite order of binding the model for a rigid body (material point), shown in the upper and lower parts of Figure 1, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, we determine the essential difference between those expressions. This indicates an important difference in the dynamics of those models of rheologic discrete dynamic systems.
We have confirmed this, in the previous sections, with different systems of differential equations of fractional order, which describe these dynamics, as well as differences in the expressions of Laplace transformations of independent generalized coordinates, which correspond to external and internal degrees of freedom of movement, rheologic creep, i.e., rheologic oscillations.
We come to the same conclusions by analyzing the expressions for the generalized functions of the dissipation fractional type, of the total energy of the system. By comparing the expressions for the generalized dissipation functions of the fractional type of the total mechanical energy of the dynamics of rheologic discrete dynamic systems, the fractional type, bound by the same standard light rheologic complex models, the fractional type, but with the opposite order of binding the model to a rigid body (material point), shown in the upper and lower parts Figure 1, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, we determine the essential difference in those expressions. This indicates an important difference in the dynamics of those models of discrete dynamic systems.
We have confirmed this, in the previous sections, with different systems of IDSFO, which describe these dynamics, as well as differences in the expressions of Laplace transformations of IGC, which correspond to external and internal degrees of freedom of movement, rheologic creep, i.e., rheologic oscillations.
6. Analytical Analysis of Laplace Surface of Eigen and Forced Modes of Independent Generalized Coordinates of Dynamics of Rheologic Discrete Dynamic Systems and Discussion
In beginning of the paper, we pointed out the basic elements of mathematical phenomenology in the study of the dynamics of each RDDSFT, which are the Laplace transformation of IGC of external and internal degrees of freedom of motion, which were determined for each RDDSFT studied in the previous chapter.
In this section, we will present the decomposition of analytical expressions of Laplace transforms of IGC, the external and internal degrees of freedom of dynamics of RDDSFT, into Laplace transforms
In this section, we will present the decomposition of analytical expressions of Laplace transforms of IGC, the external and internal degrees of freedom of dynamics of RDDSFT, into LT of rheologic natural-eigen and forced modes of motion. These are modes of natural and forced oscillations, that is, natural and forced creeping, the fractional type, “like sin”, or “like cosine” type.
The Kelvin–Voigt’s RDDSFT in Figure 1 is a rheologic oscillator. The order of binding of the structural elements in Kelvin–Voigt’s SLRBCJVFT, to a fixed wall or to main material particle (rigid body), does not influence the rheologic oscillatory dynamics of RDDSFT.
We will show these characteristic analytical expressions of the Laplace transform of IGC of the dynamics of RDDSFT, with space surfaces in coordinate systems with the following coordinate axes: the elongation of the Laplace transform, the exponent α of the differential operator of the fractional order of differentiation in the interval and the parameter .
So, let us form a series of sets of Laplace transforms of rheologic elastoviscous eigenmodes and forced modes of rheologic elastoviscous oscillation dynamics of a Kelvin–Voigt’s elastoviscous oscillation of RDDSFT.
The set of and of the elastoviscous eigenmodes of IGC of an external degree of freedom, of RDD-KV-FT Kelvin–Voigt’s elastoviscous oscillator, presented in Figure 1, is as follows:
The set of Laplace transforms and of forced modes of IGC of an external degree of freedom of dynamics of RDDSFT Kelvin–Voigt oscillator, under the action of a single frequency force or , presented in Figure 1, is as follows:
So, let us form series of sets of Laplace transforms of rheologic viscoelastic creeping eigenmodes and forced modes of dynamics of a RDDSMFT Maxwell’s viscoelastic creeper.
The set of and of the rheological viscoelastic eigenmodes of IGC of an external degree of freedom, of dynamics of RDDS-M-FT Maxwell’s viscoelastic creeper, model, presented in the upper part in Figure 5, is as follows:
The set of and of the forced viscoelastic creeper modes of IGC of an external degree of freedom of dynamics of RDDS-M-MFT Maxwell’s viscoelastic creeper, under the action of single frequency external force or , presented in the upper part of Figure 5, is as follows:
The set of and of the rheological viscoelastic eigenmodes of IGC of an internal degree of freedom, of the dynamics of RDDS-B-FT Maxwell’s viscoelastic creeper, presented in the upper part of Figure 5, is as follows:
The set of and of the rheologic viscoelastic forced modes of IGC of an internal degree of freedom, of the dynamics of RDDS-M-FT t Maxwell viscoelastic creeper, under the action of single frequency force or , presented in the upper part of Figure 5, is as follows:
So, let us form a series of sets of Laplace transforms of rheologic viscoelastic creeping eigenmodes and forced modes of dynamics of an RDDS-B-FT Burgers’ viscoelastic creeper.
The set of and of the rheologic viscoelastic eigenmodes of IGC of an external degree of freedom, of RDDC-B-FT Burgers’ viscoelastic creeper, model presented in the upper part of Figure 8, is as follows:
The set of and of the forced viscoelastic creeper modes of IGC of an external degree of freedom of dynamics of RDDS-B-FT Burgers’s viscoelastic creeper system, under the action of single frequency force or , presented in the upper part of Figure 8, is
The set of and of the rheological viscoelastic eigenmodes of IGC of an internal degree of freedom, of the dynamics of RDDS-B-FT Burgers’ viscoelastic creeper presented in the upper part Figure 8, is
The set of and of the rheological viscoelastic forced modes of IGC of an internal degree of freedom, of the dynamics of Burgers’ RDDS-B-FT viscoelastic creeper, under the action of single frequency force or , presented in the upper part of Figure 8, is
The set of and of the rheological viscoelastic eigenmodes of IGC of an internal degree of freedom, of the dynamics of RDDS-B-FT Burgers’ viscoelastic creeper, presented in the upper part of Figure 8, is
The set of and of the rheological viscoelastic forced modes of IFC of an internal degree of freedom, of the dynamics of RDDS-B-FT Burgers’ viscoelastic creeper, under the action of single frequency force or , presented in upper part of Figure 8 is
7. Numerical Analysis of Laplace Surface of Eigen and Forced Modes of Independent Generalized Coordinates of Dynamics of Rheologic Discrete Dynamic Systems
After conducting extensive numerical experiments on the obtained solutions of Laplace transforms , , and for all three IGCs, , , and , of RDDSFT (presented different models of RDDSFT presented in Figure 1, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8), for free and forced rheologic oscillatory or rheologic creeper dynamics, we selected only a few characteristic graphs, Laplace transform surfaces in coordinate systems with axes, elongation of Laplace transform of IGC, exponent of fractional order differentiation in the interval , and parameter , to present in this paper.
A series of characteristic surfaces of elongations of Laplace transformations of rheologic free and forced modes, of the fractional type of IGC of the dynamics of RDDSFT of the elastoviscous oscillator type, see Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 for Kelvin–Voigt oscillator, i.e., viscoelastic creeper type, see Figure 17, Figure 18, Figure 19 and Figure 20 for Maxwell viscoelastic creeper dynamics, Figure 21, Figure 22, Figure 23 and Figure 24 for Burgers viscoelastic creeper dynamics, as a function of fractional order differentiation exponent in the interval and Laplace transformation parameter , is shown.
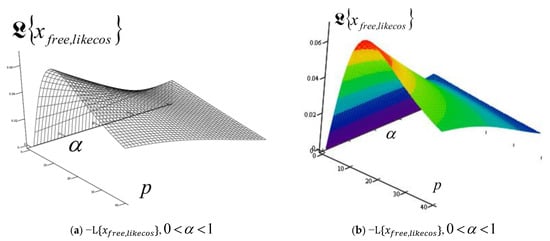
Figure 9.
The space surfaces of Laplace transforms of elastoviscous eigen modes -(a) in black–white and (b) in color of external IGC of Kelvin–Voigt RDDSFT-elastoviscous oscillator, depending on the exponent in the interval , and parameter , for the dynamics of Kelvin–Voigt RDDSFT model presented in the upper part of Figure 1, drawn using analytical expression (126).
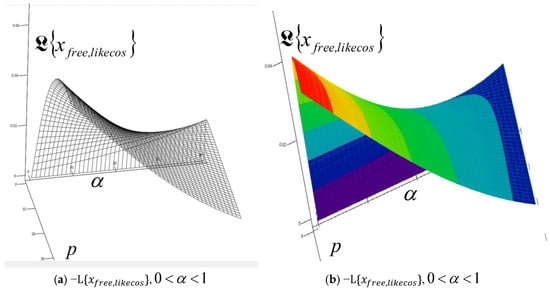
Figure 10.
The space surfaces of Laplace transforms of elastoviscous eigen modes -(a) in black–white and (b) in color of external IGC of the rheologic basic Kelvin–Voigt elastoviscous oscillator, depending on the exponent of in the interval , and parameter , for the dynamics of the rheological basic complex Kelvin–Voigt discrete dynamic system, presented in the upper part of Figure 1, drawn using analytical expression (136) and in different angles of view in comparison with previous Figure 1.
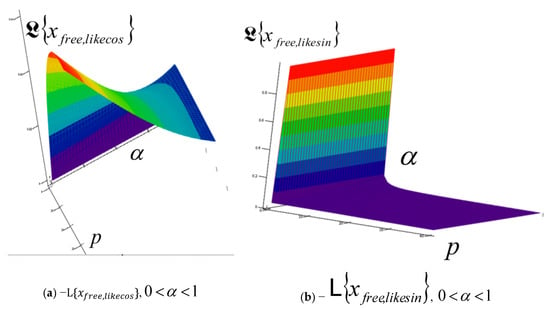
Figure 11.
The space surfaces of Laplace transforms of rheologic elastoviscous eigen oscillatory modes -(a) in in color and -(b) in color, of external IGC of the rheological basic Kelvin–Voigt elastoviscous oscillator, fractional-type depending on the exponent in the interval , and the Laplace transforms parameter , for the dynamics of the rheological basic complex Kelvin–Voigt discrete dynamic system, presented in upper part of Figure 4 drawn using analytical expressions (126) and (127) in comparison with rheological elastoviscous eigen oscillatory modes “like cos” determined by expression (136) and “like sin” determined by expression (127).
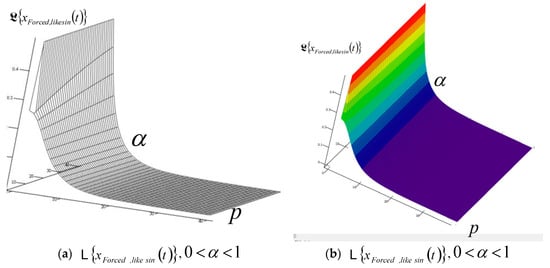
Figure 12.
The space surfaces of Laplace transforms of rheological elastoviscous forced mode
-(a) in black–white and (b) in color of IGC of the external degree of freedom of the rheological basic Kelvin–Voigt elasto-viscous oscillator, fractional-type depending on the exponent of the fractional order differentiation in the interval , and the Laplace transforms parameter , for the forced dynamics of Kelvin–Voigt RDDSFT, presented in the upper part of Figure 4, drawn using analytical expression (129), and in the case of single-frequency periodic force action for external forced frequency Ω = 2.
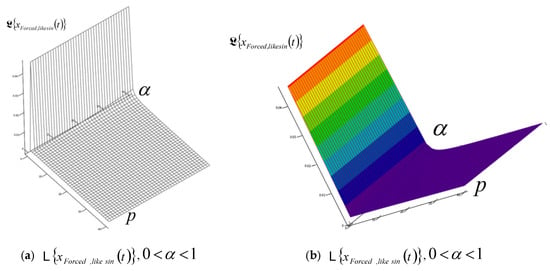
Figure 13.
The space surfaces of Laplace transforms of rheological elastoviscous forced mode
-(a) in black–white and (b) in color of IGC of the external degree of freedom, of the rheological basic Kelvin–Voigt oscillator, fractional-type depending on the exponent in the interval , and parameter , for the forced dynamics of Kelvin–Voigt RDDB-KV-MFT, presented in the upper part of Figure 4, drawn using analytical expression (139), and in the case of single-frequency periodic force action for external forced frequency Ω = 22.
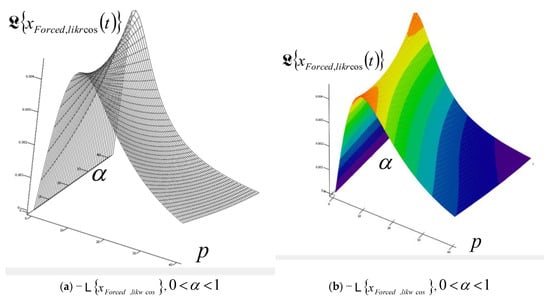
Figure 14.
The space surfaces of Laplace transforms of rheologic elastoviscous forced mode
-(a) in black–white and (b) in color of independent generalized coordinate , of an external degree of freedom, of the rheologic basic Kelvin–Voigt oscillator, fractional type depending on the exponent of the fractional order differentiation in the interval , and the Laplace transforms parameter , for the elastoviscous oscillatory forced dynamics of the rheologic basic complex Kelvin–Voigt discrete dynamic system, presented in upper part of from Figure 1, drawn using analytical expression (128), and in the case of external periodic force , forced frequency Ω = 2.
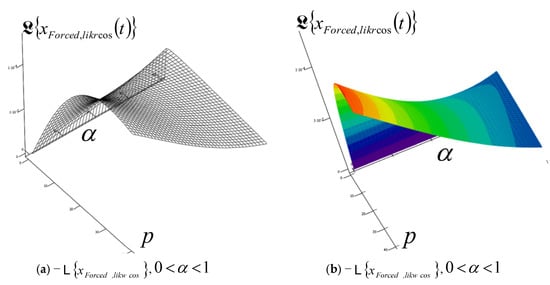
Figure 15.
The space surfaces of Laplace transforms of rheological elastoviscous forced mode
-(a) in black–white and (b) in color of , of an external degree of freedom, of Kelvin–Voigt RDDS-KV0FT-elastoviscous oscillator, depending on the exponent in the interval , and parameter , for the forced dynamics of Kelvin–Voigt RDDS-KC-FT, presented in the upper part of Figure 1, drawn using analytical expression (128), and in the case of external force action forced frequency Ω = 22.
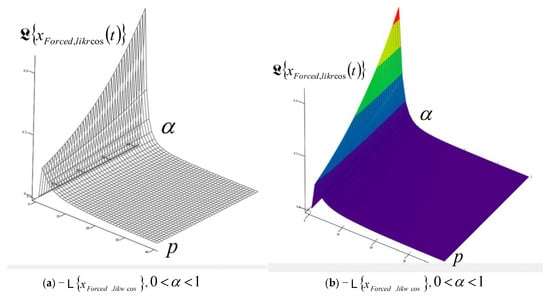
Figure 16.
The space surfaces of Laplace transforms of rheological elastoviscous forced mode
-(a) in black–white and (b) in color of IGC of an external degree of freedom motion, of Kelvin–Voigt RDDBCS-KV-FT-elastoviscous oscillator, depending on the exponent in interval , and parameter , for the forced dynamics of Kelvin–Voigt RDDBCS-KV-FT presented in the upper part of Figure 1, drawn using analytical expression (132), and in the case of periodic force action frequency Ω = 0.2.
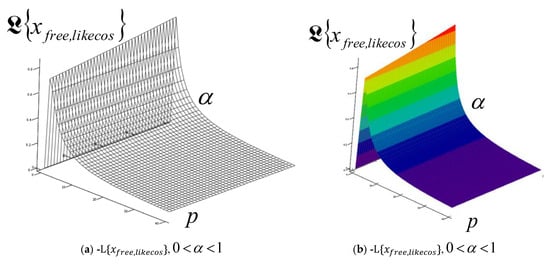
Figure 17.
The space surfaces of Laplace transforms of rheologic viscoelastic creeping eigen modes
-(a) in black–white and (b) in color of IGC , of an external degree of freedom, of RDDBC-M-FT Maxwell creeper, depending on the exponent in the interval , and parameter , for the dynamics of RDDBC-M-FT Maxwell, presented in the upper part of Figure 4, drawn using analytical expression (132).
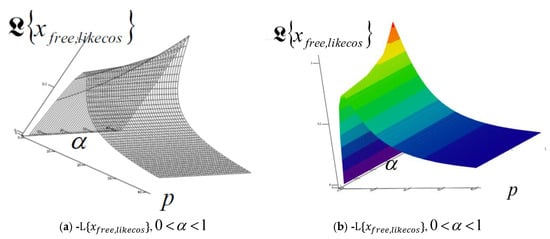
Figure 18.
The space surfaces of Laplace transforms of viscoelastic eigen modes -(a) in black–white and (b) in color of IGC of external degree of freedom dynamics of basic Maxwell viscoelastic creeper, fractional-type depending on the exponent in the interval , and the Laplace transforms parameter , for the dynamics of the rheological basic complex Maxwell discrete dynamic system, fractional type, presented in the upper part of Figure 4, drawn using analytical expression (132) and for different system parameters in comparison with previous Figure 17.
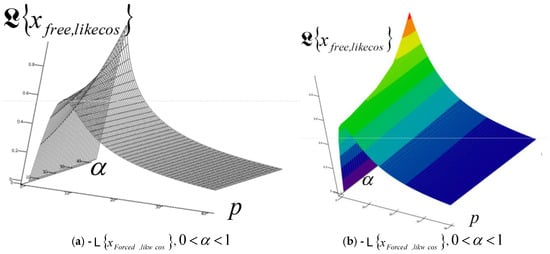
Figure 19.
The space surfaces of Laplace transforms of viscoelastic forced mode
- (a) in black–white and (b) in color of IGC , of external degree of freedom dynamics of the rheological basic complex Maxwell viscoelastic creeper, fractional-type depending on the exponent in the interval , and parameter , for the rheological forced dynamics of the rheological basic complex Maxwell viscoelastic creeper discrete dynamic system, presented in the upper part of Figure 4, drawn using analytical expression (132), and in the case of periodic force action frequency Ω = 0.2.
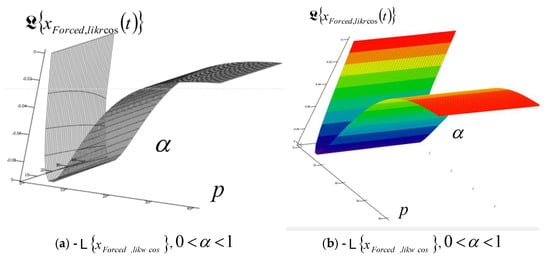
Figure 20.
The space surfaces of Laplace transforms of viscoelastic forced mode
-(a) in black–white and (b) in color of IGC , of external degree of freedom dynamics of the rheologic basic Maxwell viscoelastic creeper, fractional-type depending on the exponent in the interval , and parameter , for the forced dynamics of the rheologic basic complex Maxwell creeper discrete dynamic system, presented in the upper part of Figure 4, drawn using analytical expression (132), and in the case of periodic force action frequency Ω = 2 and a larger value of the coefficient of viscosity of the Newton fractional type fluid element in comparison with the model presented in previous Figure 19.
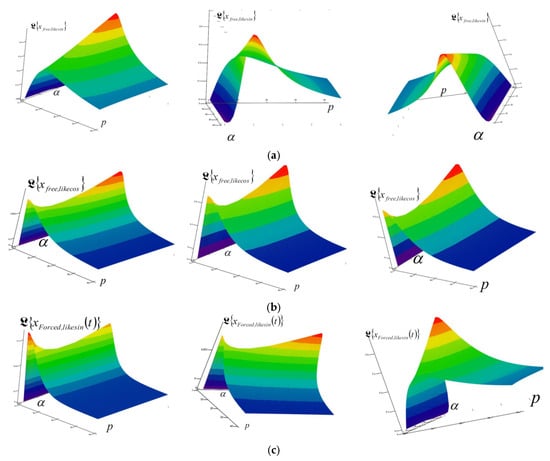
Figure 21.
The space surfaces of Laplace transforms
and of the viscoelastic free (eigen) creep (flow) modesand , of the viscoelastic forced creep (flow) mode of IGC , of external degree of freedom dynamics of RDD-B-FT Burgers creeper, depending on the exponent in the interval , and parameter , of RDD-B-FT Burgers creeper, and in the case of single-frequency periodic force action , presented in the Laplace transformation space and in coordinate system with coordinate axes: elongation of Laplace transformation, the exponent in the interval , and parameter , drawn using analytical expressions (130)–(132), for different system parameter values. (a) The space surfaces of Laplace transform , of the viscoelastic free (eigen) creep (flow) mode, “sine like” type, of IGC , of external degree of freedom dynamics of RDD-B-FT Burgers creeper, depending on the exponent in the interval , and parameter , for the dynamics of the RDD-B-FT Burgers creeper, presented in upper part of Figure 8, drawn using analytical expression (130) and for different system parameter values. (b) The space surfaces of Laplace transform , of the free (eigen) creep (flow) mode, “cosine-like” type, of external IGC e of RDD-B-FT Burgers creeper, depending on the exponent in the interval , and parameter , for RDD-B-FT Burgers creeper, presented in the upper part of Figure 8, drawn using analytical expression (131) and for different system parameter values. (c) The space surfaces of Laplace transform , of the forced creep (flow) mode, “sine-like” type, of the external IFC of RDD-B-FT Burgers creeper, depending on the exponent in the interval , and parameter , for the dynamics of RDD-B-FT Burgers creeper, presented in the upper part of Figure 8, drawn using analytical expression (132) and for different system parameter values, in the case of single-frequency periodic force action , for different system parameter values.
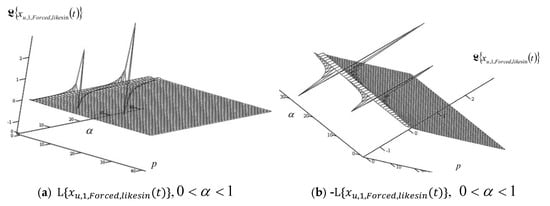
Figure 22.
The space surfaces of Laplace transforms of elastoviscous forced “sin like“ modes
-(a) in black–white and in comparison (b) in black–white and with different angles of view of the independent generalized coordinate of internal degree of freedom dynamics, of the rheologic complex Burgers-H discrete elastoviscous oscillator system, fractional type depending on the exponent of the fractional order differentiation in the interval , and the Laplace transforms parameter , for the rheologic forced dynamics of the rheologic complex Burgers-H discrete dynamic elastoviscous oscillatory system, drawn using the corresponding analytical expression and for different angles of view in comparison with Figure 22a,b and in the case of single-frequency periodic force action , for external forced frequency Ω = 30.
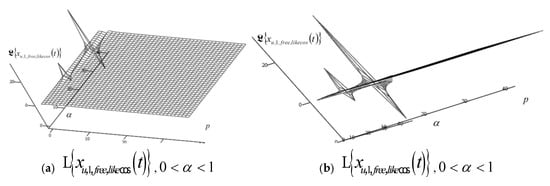
Figure 23.
The space surfaces of Laplace transforms of rheologic elastoviscous eigen modes
-(a) in black–white and in comparison (b) in black–white and with different angles of view of independent generalized coordinate of internal degree of freedom dynamics, of the rheological complex Burgers-H elastoviscous oscillator, fractional-type depending on the exponent of the fractional order differentiation in the interval , and the Laplace transforms parameter , for the dynamics of the rheological complex Burgers-H discrete dynamic oscillatory system, drawn using the corresponding analytical expression and for different angles of view in comparison with Figure 23a,b.
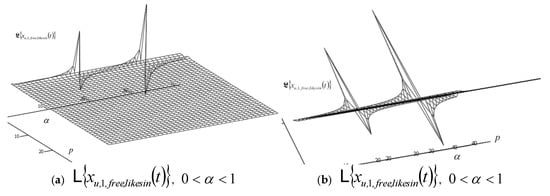
Figure 24.
The space surfaces of Laplace transforms of eigen “sin like”modes
-(a) in black–white and in comparison (b) in black–white and with different angles of view of internal independent generalized coordinate of the rheologic complex Burgers-H oscillator, fractional type depending on the exponent of the fractional order differentiation in the interval , and the Laplace transforms parameter , for the dynamics of the rheological complex Burgers-H discrete dynamic oscillatory system, drawn using the corresponding analytical expression and for different angles of view in comparison with Figure 24a,b.
By comparing the shapes of the Laplace transformation elongation surfaces of rheologic elastoviscous eigenmodes of the type “like sin” and type ’like cosine’‘ type, we conclude that the Laplace transformation elongation surfaces are round, see Figure 9, Figure 10 and Figure 11a, while the Laplace transformation elongation surfaces are very steep and drop sharply to zero, see Figure 11b.
For comparing the shapes of the Laplace transformation elastoviscous eigen cosine-“likecosie” modes , the Laplace transform elongation surface has elongation shapes that are rounded, while comparing the shapes of the Laplace transformation elastoviscous eigen sinusoidal--likesine” , Laplace transformation elongations are the largest for the fractional order differentiation exponent, and they are high and drop off sharply.
For changes with an increasing fractional order differentiation exponent from zero to unity, the Laplace transform elongations for the sinusoidal-“likesine” rheological elastoviscous eigen mode of the natural oscillations drop off sharply.
With increasing coefficients of Newton viscous fluid element of the fractional type, in parallel connection with Hooke’s ideally elastic element, a standard light rheologic base complex Kelvin–Voigt model of connection with a rigid body in a rheologic discrete dynamic system, elongations of the Laplace transform of eigenmodes of the Laplace transform -“likesine” and -“likecosinee” of IGC of system dynamics decrease.
From the series of surface elongations of Laplace transforms of elasto-phisto-viscous forced modes of IGC of the external degree of freedom of motion, of a rheological Kelvin–Voigt discrete dynamic system under the action of an external single-frequency force , we observe that with an increasing frequency of the external force, the peak on the graph of the surface elongation of the Laplace transform of the elastophisto-viscous forced mode of forced oscillation increases, under the action of a single-frequency sinusoidal force , and is smallest for the zero value of the exponent of fractional order differentiation and largest when the exponent of fractional order differentiation is equal to unity. See and compare the shapes of the surface elongations of Laplace transforms from Figure 12 and Figure 13.
From the series of surface elongations of Laplace transforms of elasto-viscous forced modes of IGC of the external degree of freedom of Kelvin–Voigt’s RDDBC-KV-FT under the action of an external force , we observe that with a decreasing force frequency, the peak on the graph of the surface Laplace transform of the forced mode of forced rheologic elastoviscous oscillation increases and is the smallest for a zero value of the exponent and the largest when the exponent s equal to unity. See and compare the shapes of the surface elongations of from Figure 14, Figure 16, and Figure 17.
The author believes that he has introduced the basic explanations in the captions under Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24 in the text, in accordance with the current research knowledge and conclusions on the spatial surfaces of Laplace transforms of eigen and forced rheologic modes of independent generalized coordinates of the dynamics of a number of studied dynamics of rheologic discrete dynamic systems.
Specifically, for a larger number of conclusions, in addition to those already written in the manuscript, and statements about the specificities and singularities of the spatial surfaces of Laplace transforms, on the critical values of the parameters of the Laplace transform, in the interval of the exponent of the derivative of the fractional order, from zero to one, as well as on the intervals of the circular frequency of the external single-frequency periodic force, the author is not able to formulate without additional and large mathematical and strong serious analytical research and serious analysis in accordance with analytical expressions (126)–(149) from Section 6. And this is a new serious analytical research task, which requires both new knowledge and evidence. This is not the subject of the content of this manuscript. In this paper, the space surfaces of the Laplace transforms of the eigen and forced modes of independent generalized coordinates of the dynamics of rheological discrete dynamic systems of the fractional type in the interval from zero to one, the exponent of differentiation of the fractional order, are shown for a number of eigen and forced modes and are just illustrations of different forms.
8. Concluding Considerations
We have shown that the generalized Newton’s element of an ideal viscous fluid, fractional type, has the ability to dissipate mechanical energy, of the fractional type.
For the basic generalized-modified Kelvin–Voigt and Maxwell models, of the fractional type, we have shown that they possess the properties of subsequent elasticity, the first, respectively, and relaxation of the normal stress, the second.
Then, we defined standard light rheologic complex and hybrid models, of the fractional type, and studied rheologic discrete dynamic systems, of the fractional type, in which these standard light models are in connection with rheologic models in the rheologic discrete dynamic system. We assumed that there are rheologic discrete dynamic systems, of the fractional type, rheologic elastoviscous oscillator type, or rheologic viscoelastic crawler type, depending on the properties of standard light rheological models, of the fractional type. It is shown that in addition to the “external” degrees of freedom of movement, the standard light, fractional order models also introduce some “internal” degrees of freedom of movement dynamics into the rheologic discrete dynamical system. Several theorems about it are also defined. It is shown that the change in the binding order of the basic elements of the structure of standard light complex models for objects of a rheological discrete dynamic system, of the fractional type, has a dominant influence on the dynamics of that rheologic dynamical system.
We also pointed out the differences between elastoviscous oscillators and the viscoelastic creeper (crawlers), as well as that this difference can also be seen from the structural scheme of a standard light rheologic complex model, which represents a connection within a rheologic discrete dynamic system, of the fractional type.
Theorem 2.
If at least one of Newton’s viscous fluid elements, of the fractional type, is regularly-serially connected in the structure on its own, and is not in a parallel relationship or not within a parallel relationship with any of Hooke’s ideally elastic elements, then it is also about the dynamics of the viscoelastic creeper and yield of elements of the rheological dynamic system. And if each of Newton’s fluid elements, of the fractional type, is connected in a parallel or intra-parallel connection with one of Hooke’s ideally elastic elements, then the rheological system is with elastoviscous damped oscillations.
Theorem 3.
Each regular connection of one of Newton’s fluid elements, of the fractional type, introduces one internal degree of freedom of movement of the rheological complex model, in addition to the external degrees of freedom of the rheological discrete dynamic system, which contains complex rheological light standard models as binding elements.
Figure 25 shows a tabular comparative overview of new class of complex rheological discrete dynamical systems of the fractional type. In the left vertical column are rheological discrete dynamic systems of the rheological oscillator type, bound by standard light elastoviscous complex binding elements. In the left column are rheological discrete dynamic systems of the creeper type, bound by standard light viscoelastic fluid binding elements.
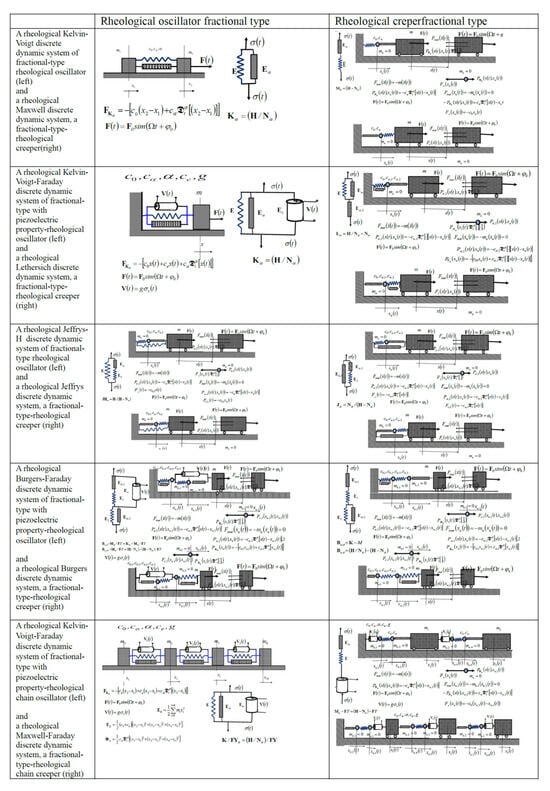
Figure 25.
Tabular comparative overview of new class of complex rheological discrete dynamical systems of the fractional type with one or a finite number of degrees of freedom.
At the end, we point out, that in the last horizontal row of Figure 25, images of rheologic discrete dynamic systems of the type of rheologic homogeneous chains, fractional type with piezoelectric properties, are shown. One is of the type of the rheological Kelvin–Voigt–Faraday chain with oscillatory dynamics (left column) and the other is of the type of the rheologic Maxwell–Faraday chain with creeper properties with a finite number of degrees of freedom of flow. These models await theoretical mathematical analytical and experimental research.
The main unsolved problems in the study of the dynamics of rheologic discrete dynamic systems, of the fractional type, are in determining the expression of inverse Laplace transformations of independent generalized coordinates, which are reached in the procedures of determining the solution of systems of differential equations of fractional order, based on external and internal independent generalized coordinates. It is easy to determine the Laplace transforms of all unknown external and internal independent generalized coordinates.
In this paper, we have presented a methodology for studying the dynamics. Figure 25 shows a tabular comparative overview of new class of complex rheological discrete dynamical systems of the fractional type. In the left vertical column are rheological discrete dynamic systems of the rheological oscillator type, bound by standard light elastoviscous complex binding elements. In the left column are rheological discrete dynamic systems of the creeper type, bound by standard light viscoelastic fluid binding elements.
There are oscillators in biomedical sciences, which we generally call biological oscillators. The basic property of such oscillators is to excite some vital functions of living organisms. The so-called “rheological fractional oscillator or peristaltic oscillator” also belongs to this group. We have not dealt with the study of the regime of special dynamics of such discrete dynamic systems here, because it is separate experimental research, although the complete theory presented here about rheological discrete dynamic systems is applicable as a basis for corresponding experimental research.
Also, in our work, we have implemented theoretical research scientific results and descriptions of the dynamics of rheological discrete models of dynamic systems, of the fractional type, oscillators and creepers under isothermal conditions. However, today, knowledge of the theory and applications of rheology as a science is rapidly expanding and increasing. This scientific field of rheology has experienced rapid progress, and for some specialized research, it is necessary to include relevant achievements. Here, we will only highlight the Zou rheological model, as presented in reference [58].
This model can offer additional perspectives on the rheological behavior of materials, in non-isothermal conditions of changing temperature fields. This opens a new direction for the study of the dynamics of rheological discrete systems in non-isothermal conditions. It is noted that this may be relevant for new studies of RDDSFT in non-isothermal conditions. Integrating such new knowledge into the directions of contemporary research can strengthen the relevance of the same and show awareness of the broader rheological landscape.
At the end, using the knowledge and suggestion of one of the Reviewers, the author inserts the following text into the text of the manuscript:
“In this part of the paper, we study the dynamics of a rheological discrete dynamic system of fractional type with the properties of a rheological oscillator of fractional type. At the suggestion of one of the reviewers, two terms “fractional oscillator” and “fractal oscillator” appear in the literature and that the text should distinguish between these two terms and the properties of mechanical discrete and continuous systems. The reviewer pointed out to the author that the concept of “a fractal oscillator” uses a fractal derivative on two scales to model vibrating continuous systems within fractal space”.
Also, the author, at the suggestion of one of the Reviewers, points out that the limitation of determining the inverse Laplace transformation, which we have not dealt with here, except in one case, could perhaps be overcome by the method of homotopic perturbations. This method represents a promising approach for overcoming this deficiency. This method has not been applied to the decomposition of complex systems of fractional order differential equations. In the case of its application to nonlinear differential equations, it has proven effective in some cases when it decomposes a nonlinear problem into a series of linear problems, thereby simplifying the process of solving nonlinear problems. For further details, it is suggested to consult the references [60,61].
Funding
This authors’ work on this paper was not funded.
Data Availability Statement
No data were created or used in preparing this paper.
Acknowledgments
The author has presented new ideas and new results in the field of dynamics of fractional-type rheological discrete dynamical systems. The author discussed some applications to biomaterials with Anđelka Hedrih. From these very inspiring conversations, she came to the conclusion that the new material rheological models, presented in this paper through rheological discrete dynamical systems, are of great importance for future applications in medicine. The author also expresses his great gratitude to Associate Editor, for very useful suggestions, with which the author initially improved the manuscript and brought it up to the standards of the important scientific journal “Fractal and Fractional” to be sent for review. The author also expresses his own special gratitude to the three competent and well-intentioned reviewers, not only for the time they spent reading the manuscript and writing extensive reviews, but also for the very useful and specific content of the reviews, which helped the author to improve the revised manuscript and better ‘illuminate’ the present and explain the scientific results contained in it. Also, at end, the author expresses his great gratitude to Associate Editor, for the professional support of this paper.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Hedrih, K.R. Generalized function of fractional order dissipation of system energy and extended Lagrange differential Lagrange equation in matrix form, Dedicated to 86th Anniversary of Radu MIRON’S Birth. Tensor 2014, 75, 35–51. [Google Scholar]
- Hedrih, K.R. New Class of Complex Models of Materials with Piezoelectric Properties with Differential Constitutive Relations of Fractional Order: An Overview. Fractal Fract. 2025, 9, 170. [Google Scholar] [CrossRef]
- Hedrih, K.R.; Machado, J.T. Discrete fractional order system vibrations. Int. J. Non-Linear Mech. 2015, 73, 2–11. [Google Scholar] [CrossRef]
- Goroško, O.A.; Hedrih, K. Analitička Dinamika (Mehanika) Diskretnih Naslednih Sistema, Analytical Dynamics (Mechanics) of Discrete Hereditary Systems; University of Niš: Niš, Serbia, 2001; p. 426. (In Serbian) [Google Scholar]
- Rabotnov, Y.N. Creep Problems in Structural Members. In Applied Mathematics and Mechanics; North-Holland: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Mechanics of Solids; Nauka: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Savin, G.N.; Ruschisky, Y.Y. Elements of Hereditary Media Mechanics; Vyscha shkola: Kyiv, Ukraine, 1976. (In Ukrainian) [Google Scholar]
- Katok, A.; Hasselblatt, B. Introduction to the Modern Theory of Dynamical Systems; Cambridge University Press: Cambridge, UK, 1995; ISBN 978-0-521-34187-5. [Google Scholar]
- Holmes, P. Poincaré, celestial mechanics, dynamical-systems theory and “chaos”. Phys. Rep. 1990, 193, 137–163. [Google Scholar] [CrossRef]
- Giunti, M.; Mazzola, C. Dynamical systems on monoids: Toward a general theory of deterministic systems and motion. In Methods, Models, Simulations and Approaches Towards a General Theory of Change; Minati, G., Abram, M., Pessa, E., Eds.; World Scientific: Singapore, 2012; pp. 173–185. ISBN 978-981-4383-32-5. [Google Scholar]
- Galor, O. Discrete Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Stojiljković, D.T.; Petrović, V.; Đurović-Petrović, M. Rheological modeling of yarn elongation. Tekstil 2007, 56, 554–561. [Google Scholar]
- Stoiljkoic, D.T. Dinamicko Ponasanje Sistema Mehanizam—Radni Objekat Tkackog Procesa. Ph.D. Thesis, Masinski fakultet u Nišu, Niš, Serbia, 1992. [Google Scholar]
- Miličić, I.M.; Vlajić, L.M. Models of civil engineering–classification and definition. In Proceedings of the 9th International Conference DQM-2006, Belgrade, Serbia, 14–15 June 2006; Available online: https://www.researchgate.net/publication/289098053 (accessed on 19 April 2025).
- Đurić, M. Teorija Spregnutih i Prethodno Napregnutih Konstrukcija; SANU: Beograd, Serbia, 1963. [Google Scholar]
- Mihailović, V.; Landović, A. The Relation Properties of Concrete and Their Characteristic in Rheological Models, ZBORNIK RADOVA 19; Univerzitet u Novom Sadu: Novi Sad, Serbia, 2010. [Google Scholar]
- Tomović, Z. Reološki model puzanja matriksa meke stijene (Rheologica model od of soft rocks of creep). Mater. I Konstr. 2007, 50, 1–2. [Google Scholar]
- Hedrih, K.R.; Hedrih, A.N. Rheological Burgers–Faraday Models and Rheological Dynamical Systems with Fractional Derivatives and Their Application in Biomechanics. Fractal Fract. 2024, 8, 742. [Google Scholar] [CrossRef]
- Verdier, C. Review: “Rheological properties of living materials. From cells to tissues”. J. Theor. Med. 2003, 5, 67–91. [Google Scholar]
- Yang, X. New rheological problems involving general fractional Derivatives with nonsingular power-law kernels. Proc. Rom. Acad. 2018, 19, 45–52. [Google Scholar]
- Yang, X.; Chen, W.; Xiao, R.; Ling, L. A Fractional Model for Time-Variant Non-Newtonian Flow. Therm. Sci. 2017, 21, 61–68. [Google Scholar] [CrossRef]
- Bonfanti, A.; Fouchard, J.; Khalilgharibi, N.; Charras, G.; Kabla, A. A unified rheological model for cells and cellularised materials. R. Soc. Open Sci. 2020, 7, 190920. [Google Scholar] [CrossRef]
- Bačlić, B.S.; Atanacković, T.M. Stability and creep of a fractional derivative order viscoelastic Rod. Bull. Cl. Sci. Math. Natturalles 2000, 25, 115–131. [Google Scholar]
- Atanacković, T.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; Wiley-ISTE: London, UK, 2014. [Google Scholar]
- Atanacković, T.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles; Wiley-ISTE: London, UK, 2014. [Google Scholar]
- Petrovitch, M. M’ecanismes Communs aux Phénomènes Disparates, Nouvelle Collection Scientifique; F’elix Alcan: Paris, French, 1921. [Google Scholar]
- Petrovi’c, M. Phenomenological Mapping; Serbian Royal Academy: Belgrade, Serbia, 1933. [Google Scholar]
- Mijajlovi’c, Ž.; Pilipovi’c, S.; Milovanovi’c, G.; Mateljevi’c, M.; Albijani’c, M.; Andri’c, V. Mihailo Petrovi’c Alas: Life, Work, Times–On the Occasion of the 150th Anniversary of His Birth; Serbian Academy of Sciences and Arts: Belgrade, Serbia, 2019. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Letnikov, A.V. Theory of differentiation with an arbitrary index. Mat. Sb. 1868, 3, 1–66. [Google Scholar]
- Letnikov, A.V. An explanation of the concepts of the theory of differentiation of arbitrary index. Mat. Sb. 1872, 6, 413–445. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives–Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Debnath, L. A brief historical introduction to fractional calculus. Int. J. Math. Educ. Sci. Technol. 2004, 35, 487–501. [Google Scholar] [CrossRef]
- Ross, B. A brief history and exposition of the fundamental theory of fractional calculus. In Fractional Calculus and Its Applications: Proceedings of the International Conference Held at the University of New Haven; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Kiryakova, V. A brief story about the operators of generalized fractional calculus. Fract. Calc. Appl. Anal. 2008, 11, 203–220. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity. An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar] [CrossRef]
- Kiryakova, V. Generalized Fractional Calculus and Applications, Pitman Research Notes I Mathematics Series; CRC Press: Boca Raton, FL, USA, 1994; p. 301. [Google Scholar]
- Mitrinović, D.S.; Djoković, D.Ž. Special Functions (Specijalne Funkcije); Gradjevinska Knjiga: Belgrade, Serbia, 1964; 267p. [Google Scholar]
- Rašković, D. Teorija Oscilacija (Theory of Oscillatins). 1965. Available online: http://elibrary.matf.bg.ac.rs/handle/123456789/3778 (accessed on 19 April 2025).
- Rašković, D. Analitička Mehanika (Analytical Mechanics); Mašinski Fakultet Kragujevac: Kragujevac, Serbia, 1974; Available online: http://elibrary.matf.bg.ac.rs/ (accessed on 19 April 2025).
- Rašković, D. Teorija Elastičnosti (Theory of Elasticity); Naučna Knjiga: Belgrade, Serbia, 1985. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012. [Google Scholar]
- Garrappa, R.; Popolizio, M. Evaluation of generalized Mittag-Leffler functions on the real line. Adv. Comput. Math. 2013, 39, 205–225. [Google Scholar] [CrossRef]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Luo, M.J.; Milovanovi’c, G.V.; Agarwal, P. Some results on the extended beta and extended hypergeometric functions. Appl. Math. Comput. 2014, 248, 631–651. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Sandev, T.; Tomovski, Ž. Fractional Equations and Models. In Theory and Applications; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus–An Introduction For Physicists; World Scientific: Singapore, 2014. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book; Wolfram Media. Inc.: Champaign, IL, USA, 2003. [Google Scholar]
- Hedrih, K.R.; Milovanovic, G.V. Elements of mathematical phenomenology and analogies of electrical and mechanical oscillators of the fractional type with finite number of degrees of freedom of oscillations: Linear and nonlinear modes. Commun. Anal. Mech. 2024, 16, 738–785. [Google Scholar] [CrossRef]
- Hedrih, K.R.; Hedrih, A.N. The Kelvin–Voigt visco-elastic model involving a fractional-order time derivative for modelling torsional oscillations of a complex discrete biodynamical system. Acta Mech. 2023, 234, 1923–1942. [Google Scholar] [CrossRef] [PubMed]
- Zuo, Y.T. Effect of sic particles on viscosity of 3-D print paste: A Fractal Rheological Model and Experimental Verification. Therm. Sci. 2021, 25, 2405–2409. [Google Scholar] [CrossRef]
- He, J. Beyond Laplace and Fourier Transforms: Challenges and Future Prospects; Soochow University: Suzhou, China. [CrossRef]
- Moussa, B.; Youssouf, M.; Abdoul Wassiha, N.; Youssouf, P. Homotopy perturbation method to solve Duffing-Van der Pol equation. Adv. Differ. Equ. Control. Process. 2024, 31, 299–315. [Google Scholar] [CrossRef]
- He, J.; He, C.; Alsolami, A.A. A good initial guess for approximating nonlinear oscillators by the homotopy perturbation method. Facta Univ. 2023, 21, 21–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).