Existence of Solutions to Fractional Differential Equations with Mixed Caputo–Riemann Derivative

Abstract

The study of fractional differential equations is gaining increasing significance due to their wide-ranging applications across various fields. Different methods, including fixed-point theory, variational approaches, and the lower and upper solutions method, are employed to analyze the existence and uniqueness of solutions to fractional differential equations. This paper investigates the existence and uniqueness of solutions to a class of nonlinear fractional differential equations involving mixed Caputo–Riemann fractional derivatives with integral initial conditions, set within a Banach space. Sufficient conditions are provided for the existence and uniqueness of solutions based on the problem’s parameters. The results are derived by constructing the Green’s function for the initial value problem. Schauder’s fixed-point theorem is used to prove existence, while Banach’s contraction mapping principle ensures uniqueness. Finally, an example is given to demonstrate the practical application of the results.

1. Introduction

Fractional differential equations have garnered considerable attention due to their broad applications across fields such as physics, mechanics, chemistry, biology, economics, and biophysics (see references [1,2]). These equations model physical phenomena, including fractional oscillator equations and fractional Euler–Lagrange equations with mixed fractional derivatives, as explored in references [3,4,5].

In particular, the study of mixed fractional derivatives has attracted significant interest in the applied sciences. Researchers have investigated their utility in modeling diverse systems, including mechanical systems, particle dynamics, field theory, and complex media. For example, Dumitru Baleanu et al. [6] examined numerical solutions to the Euler–Lagrange equations for the fractional Bateman–Feshbach–Tikochinsky system using a fractional Hamiltonian framework. Blaszczyk [7] addressed a fractional oscillator equation in a non-resisting medium, developing and numerically solving a discrete version. Klimek [8] introduced a symmetric fractional derivative and derived corresponding Euler–Lagrange and Hamiltonian equations, showing that these models, though nonconservative, align with classical mechanics in the appropriate limit.

The theoretical contributions of these studies are applicable to real-world problems characterized by memory effects and nonlocal dynamics. The proposed framework for nonlinear fractional differential equations, incorporating mixed Caputo–Riemann derivatives and integral initial conditions, is particularly suitable for modeling anomalous diffusion in physics such as sub- and super diffusion in heterogeneous media. Similar models effectively describe viscoelastic behavior in mechanics, charge transport in electrochemistry, and biological processes with intrinsic memory, like population dynamics and gene regulation. In economics, they capture long-memory behaviors such as asset price volatility, and in engineering, they enhance the modeling of thermal systems and control mechanisms. These diverse applications underscore the broad relevance of fractional modeling approaches (see references [9,10,11,12]). Despite their utility, finding exact solutions to such equations remains challenging. This has prompted extensive research into various analytical aspects, including the existence and uniqueness of solutions under different initial and boundary conditions [13,14,15,16], Ulam stability [17,18,19], and exact and numerical solution [20,21]. Studies have also addressed equations with integral boundary conditions [22,23,24] and, more recently, equations involving mixed fractional derivatives [25,26].

In the context of solution behavior and robustness, the concept of Ulam stability has gained prominence. Numerous works have examined its implications for fractional differential equations (see references [27,28,29]). For instance, Ibrahim [30] studied Ulam stability for the fractional Cauchy differential equation in the complex disk $\{z\in \mathbb{C};|z|\le 1\}$. Chen et al. [31] analyzed Ulam–Hyers stability for nabla fractional Caputo difference equations, particularly focusing on the case $0<\alpha \le 1$ on finite intervals.

The goal of this paper is to study the existence, uniqueness, and stability of the fractional differential equation in the following form.

$${}^{\mathrm{R}}D^b{(}^C{D}^{a}u\left(x\right)+h^C{D}^{a-1}u\left(x\right))=g(x,u\left(x\right)),x\in I=[0,1],h\ne 0$$

(1)

with the integral initial conditions

$$u\left(0\right)=0,u\prime \left(0\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-s)}^{\gamma -1}u\left(s\right)ds,$$

(2)

$$u″\left(0\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-s)}^{b-1}u\left(s\right)ds$$

where $a\in (1,2),b\in (0,1]$, $\gamma \in (0,1]$, $f:I\times \mathbb{R}\to \mathbb{R}$, ${}^{\mathrm{C}}D^a$ is the Caputo fractional derivative, and ${}^{\mathrm{R}}D^b$ is the Riemann fractional derivative. Lastly, an example is presented to illustrate the practical application of our main result.

2. Preliminaries

This section provides fundamental definitions and lemmas that are utilized in what follows.

Definition 1 

([32,33] (Riemann–Liouville fractional integral)). The Reimann–Liouville fractional integral of the order α of a function $g\left(t\right)$ with respect to x, with constant of integration c, is defined for a general $\alpha \in \mathbb{C}$ with a positive real part as

$${}_{\mathrm{c}}{}^{\mathrm{R}}I_x^{\alpha }g\left(x\right):={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_c^x{(x-s)}^{\alpha -1}g\left(s\right)ds,Re\left(\alpha \right)>0,$$

for any $x,c$ and function g such that this integral is well-defined.

Definition 2 

([32,33] (Riemann–Liouville fractional derivative)). The Riemann–Liouville fractional derivative of the order α of a function $g\left(x\right)$ with respect to x, with constant of integration c, is defined for a general $\alpha \in \mathbb{C}$ with a non-negative real part as

$${}_{\mathrm{c}}{}^{\mathrm{R}}D_t^{\alpha }g\left(x\right):={\displaystyle \frac{d^m}{d{t}^m}}\left({}_c{}^{\mathrm{R}}I_x^{m-\alpha }g\left(x\right)\right),m:=\lfloor Re\left(\alpha \right)\rfloor +1,Re\left(\alpha \right)⩾0$$

for any $x,c$ and function g such that this formula is well-defined.

Definition 3 

([2] (Caputo fractional derivative)). The Caputo-type fractional derivative of the order α of a function $g\left(x\right)$ with respect to x, with constant of integration c, is defined for a general $\alpha \in \mathbb{C}$ with a non-negative real part as

$${}_c{}^{\mathrm{C}}D_x^{\alpha }g\left(x\right){=}_c^R{I}_x^{m-\alpha }\left({\displaystyle \frac{d^m}{d{t}^m}}g\left(x\right)\right)m:=\lfloor Re\left(\alpha \right)\rfloor +1,Re\left(\alpha \right)⩾0,$$

for any $x,c$ and function g such that this formula is well-defined.

Lemma 1 

([2]). Let $\alpha \in [0,\infty )$, $\beta \in [0,\infty )$, and $g\left(x\right)$ in $L_1[a,b]$. Then,

$${}^{\mathrm{R}}I^{\alpha }{}^{\mathrm{R}}I^{\beta }g\left(x\right){=}^R{I}^{\alpha +\beta }g\left(x\right)\mathit{almost} \mathit{everywhere} \mathit{on} \mathit{the} \mathit{closed} \mathit{interval} [a,b].$$

Furthermore, if the function $g\left(x\right)$ is continuous in $[a,b]$, then the composition property above holds $\forall x\in [a,b]$

Lemma 2 

([34]). Let $\nu >0$, $m=\lceil \nu \rceil$ and let $g\left(s\right)\in L(a,b)$. If  ${}_c{}^{\mathrm{R}}D^{\nu -1}g$ exists and $g\in AC[a,b]$, then ${}_c{}^{\mathrm{R}}D^{\nu -i}g=k_i$ exists for $i=1,2,\dots ,m$;  ${}_c{}^{\mathrm{R}}D^{v}g$ exists almost everywhere on $[a,b]$ in $L(a,b)$, and

$${}_c{}^{\mathrm{R}}I^v{}_c{}^{\mathrm{R}}D^{v}g\left(s\right)=g\left(s\right)-\sum _{i=1}^m{\displaystyle \frac{k_i{(s-c)}^{\nu -i}}{\mathsf{\Gamma }(\nu -i+1)}}\mathit{everywhere} \mathit{on} s\in [a,b]$$

Moreover, if $g\left(s\right)$ is continuous on $(a,b]$, then the inequality is satisfied everywhere on $(a,b]$.

Lemma 3 

([35]). Let $\nu >0$. Assuming that $u\in C(0,1)\cap L_1(0,1)$, the Caputo fractional differential equation

$$D^{\nu }u\left(x\right)=0$$

has the solution

$$u\left(x\right)=b_0+b_{1}x+b_2{x}^2+\dots +b_{m-1}{x}^{m-1}$$

where $b_i\in \mathbb{R}, i=0,1,2,\dots ,m-1,$ and $m=\lfloor \nu \rfloor +1$.

Lemma 4 

([35]). Let $u\in C(0,1)\cap L_1(0,1)$, $\nu >0$ and ${}^{\mathrm{C}}D^{v}u\left(x\right)\in C(0,1)\cap L_1(0,1)$. Then,

$${}^{\mathrm{R}}I^v{}^{\mathrm{C}}D^{v}u\left(x\right)=u\left(x\right)+b_0+b_{1}x+b_2{x}^2+\dots +b_{m-1}{x}^{m-1},$$

for $b_i\in \mathbb{R},i=0,1,2,\dots ,m-1,$ where $m=\lceil \nu \rceil$.

Lemma 5 

([2,34]). Let $a,b,c\in \mathbb{R},b>-1$. Then, for all $x>c$,

$${}_{\mathrm{c}}{}^{\mathrm{R}}I^a{\displaystyle \frac{{(x-c)}^b}{\mathsf{\Gamma }(b+1)}}=\left\{\begin{array}{cc}{\displaystyle \frac{{(x-c)}^{a+b}}{\mathsf{\Gamma }(a+b+1)}}\hfill & a+b\ne \mathit{negative} \mathit{integers}\hfill \\ 0\hfill & a+b=\mathit{negative} \mathit{integers}\hfill \end{array}\right.$$

Definition 4 

([2]). The definition of the Mittag–Leffler function with two parameters is given by

$$E_{a,b}\left(x\right)=\sum _{m=0}^{\infty }{\displaystyle \frac{x^m}{\mathsf{\Gamma }(ma+b)}},a,b,x\in \mathbb{C},Re\left(a\right)>0, \mathrm{and} Re\left(b\right)>0$$

Theorem 1 

([36] (Ascoli-Arzela Theorem)). A subset $\mathcal{F}$ of $C\left(K\right)$ is totally bounded iff it is point-wise bounded and equicontinuous.

Theorem 2 

([36] (Schauder fixed-point theorem)). Let M be a convex, closed, and bounded subset of a Banach space A. If $U:M\to M$ is a continuous operator where $UM$ is a relatively compact subset of A, then U has at least one fixed point in M.

Theorem 3 

([36] (Banach contraction mapping principle)). Let $(A,d)$ be a complete metric space, and $U:M\to M$ a contraction mapping, if for all $a,b\in M$, and $c\in (0,1)$

$$d(Ua,Ub)\le cd(a,b).$$

Then, the operator U has a unique fixed point x in M, i.e., $UM=x.$

Definition 5 

([5]). Equation (1) is Ulam–Hyers stable. If there is $m_g\in {\mathbb{R}}^{+}$ s.t for all positive ϵ and solution $y\in C^1(I,\mathbb{R})$ to the inequality

$${|}^R{D}^b({}^{C}D^{a}y\left(x\right)+h^C{D}^{a-1}y\left(x\right))-g(x,y\left(x\right))|\le ϵx\in I,$$

there is a solution $v\in C^1(I,\mathbb{R})$ to Equation (1) with

$$|y\left(x\right)-v\left(x\right)|\le m_g·ϵ,x\in I.$$

Definition 6 

([23]). Equation (1) is Ulam–Hyers–Rassias stable with respect to nondecreasing $\varphi \in C(I,{\mathbb{R}}_{+})$. If ∃ a real number $m_g>0$ s.t for all positive ϵ and solution $y\in C^1(I,\mathbb{R})$ to the inequality

$${|}^R{D}^{\beta }{(}^C{D}^{\alpha }y\left(x\right)+h^C{D}^{\alpha -1}y\left(x\right))-g(x,y\left(x\right))|\le ϵ\varphi \left(x\right),x\in I,$$

there is a solution $v\in C^1(I,\mathbb{R})$ to Equation (1) with

$$|y\left(x\right)-v\left(x\right)|\le m_gϵ\varphi \left(x\right),x\in I.$$

Lemma 6. 

Let $g\in C[0,1],u\in C^1[0,1]$; then, the initial value problem of (1) and (2) has a solution

$$u\left(x\right)={\int }_0^{1}F(x,z)g(z,u\left(z\right))dz,$$

where $F(x,z)$ is the Green function described by

$$\begin{array}{c}F(x,z)=\left\{\begin{array}{c}{e}^{-h(x-z)}{\displaystyle \frac{1}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^z{(z-s)}^{a+b-2}ds+{\displaystyle \frac{1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h)}}\hfill \\ {\int }_{\tau }^1{\int }_r^z\left[{\displaystyle \frac{{\varpi }_2}{\mathsf{\Gamma }\left(\gamma \right)}}{(1-z)}^{\gamma -1}-{\displaystyle \frac{{\varpi }_1}{\mathsf{\Gamma }\left(b\right)}}{(1-z)}^{b-1}\right]{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{(\tau -r)}^{a+b-2}g(r,u\left(r\right))d\tau dz\hfill \\ x^{a+b-1}{E}_{1,a+b}(-hx)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)h{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h)}}\hfill \\ {\int }_{\tau }^1{\int }_r^z\left[{\displaystyle \frac{(E_{1,2b+a}(-h)-1)(1-z^{b-1})}{\gamma \left(b\right)}}-{\displaystyle \frac{(E_{1,2\gamma +a}(-h)+h){(1-z)}^{\gamma -1}}{\gamma \left(\gamma \right)}}\right]{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{(\tau -r)}^{a+b-2}\hfill \\ g(r,u\left(r\right))d\tau dz[1-e^{-hx}] \mathrm{if} 0\le z\le x,\hfill \\ {\displaystyle \frac{1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h)}}\hfill \\ {\int }_{\tau }^1{\int }_r^z\left[{\displaystyle \frac{{\varpi }_2}{\mathsf{\Gamma }\left(\gamma \right)}}{(1-z)}^{\gamma -1}-{\displaystyle \frac{{\varpi }_1}{\mathsf{\Gamma }\left(b\right)}}{(1-z)}^{b-1}\right]{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{(\tau -r)}^{a+b-2}g(r,u\left(r\right))d\tau dz\hfill \\ x^{a+b-1}{E}_{1,a+b}(-hx)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)h{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h)}}\hfill \\ {\int }_{\tau }^1{\int }_r^z\left[{\displaystyle \frac{(E_{1,2b+a}(-h)-1)(1-z^{b-1})}{\gamma \left(b\right)}}-{\displaystyle \frac{(E_{1,2\gamma +a}(-h)+h){(1-z)}^{\gamma -1}}{\gamma \left(\gamma \right)}}\right]{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{(\tau -r)}^{a+b-2}\hfill \\ g(r,u\left(r\right))d\tau dz[1-e^{-hx}] \mathit{if} x\le z\le 1,\hfill \end{array}\right.\end{array}$$

(3)

where

• ${\mathsf{\Psi }}_1={\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^{\tau }{(\tau -r)}^{a+b-2}g(r,u\left(r\right))drd\tau dz$
• ${\mathsf{\Psi }}_2={\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}{\tau }^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}d\tau dz=E_{1,2b+a}(-h)$
• ${\mathsf{\Psi }}_3={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^{\tau }{(\tau -r)}^{a+b-2}g(r,u\left(r\right))drd\tau dz$
• ${\mathsf{\Psi }}_4={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}{\tau }^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}d\tau dz=E_{1,2\gamma +a}(-h)$
• ${\varpi }_1={\displaystyle \frac{1}{h}}[{\displaystyle \frac{1}{\mathsf{\Gamma }(\gamma +1)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{e}^{-hz}dz={\displaystyle \frac{1}{h}}({\displaystyle \frac{1}{\mathsf{\Gamma }(\gamma +1)}}-E_{1,\gamma +1}(-h))$
• ${\varpi }_2={\displaystyle \frac{1}{h}}[{\displaystyle \frac{1}{\mathsf{\Gamma }(b+1)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{e}^{-hz}dz={\displaystyle \frac{1}{h}}({\displaystyle \frac{1}{\mathsf{\Gamma }(b+1)}}-E_{1,b+1}(-h))$

Proof. 

Given

$${}^{\mathrm{R}}D^{\mathrm{b}}({}^{\mathrm{C}}D^{\alpha }u\left(x\right)+h^C{D}^{a-1}u\left(x\right))=g(x,u\left(x\right)),$$

we apply the operator ${}^{\mathrm{R}}I^b$ on (1) to set

$${}^{\mathrm{C}}D^{a}u\left(x\right)+h^C{D}^{a-1}u\left(x\right)-\sum _{i=1}^1{\displaystyle \frac{k_i{x}^{b-i}}{\mathsf{\Gamma }(b-i+1)}}{=}^R{I}^{b}g(x,u\left(x\right))$$

Now, we apply ${}^{\mathrm{R}}I^a$ on both sides:

$${}^{\mathrm{R}}I^a({}^{\mathrm{C}}D^{a}u\left(x\right){+}^C{D}^{a-1}\left(hu\left(x\right)\right)-{\displaystyle \frac{k_1^R{I}^a{x}^{b-1}}{\mathsf{\Gamma }\left(b\right)}}{=}^R{I}^{a+b}g(x,u\left(x\right)).$$

Using Lemmas 2 and 4,

$$u\left(x\right)+h{\int }_0^{x}u\left(z\right)dz+c_0+c_{1}x-k_1{\displaystyle \frac{\mathsf{\Gamma }\left(b\right)x^{a+b-1}}{\mathsf{\Gamma }(a+b-1+1)\mathsf{\Gamma }\left(b\right)}}{=}^R{I}^{a+b}g(x,u\left(x\right))$$

$$u\left(x\right)+h{\int }_0^{x}u\left(z\right)dz{=}^R{I}^{a+b}g(x,u\left(x\right))+{\displaystyle \frac{k_1{x}^{a+b-1}}{\mathsf{\Gamma }(a+b)}}-c_0-c_{1}x$$

Differentiating both sides yields

$$Du\left(x\right)+hu\left(x\right)={}^{R}I^{a+b-1}g(x,u\left(x\right))+{\displaystyle \frac{k_1(a+b-1)x^{a+b-2}}{\mathsf{\Gamma }(a+b)}}-c_1$$

$$Du\left(x\right)+hu\left(x\right)={}^{R}I^{a+b-1}g(x,u\left(x\right))+{\displaystyle \frac{k_1{x}^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}-c_1$$

$$(D+h)u\left(x\right)={}^{R}I^{a+b-1}g(x,u\left(x\right))+{\displaystyle \frac{k_1(x^{a+b-2}}{\mathsf{\Gamma }(a+b)}}-c_1$$

$$D\left(e^{hx}u\left(x\right)\right)=[{}^{R}I^{a+b-1}g(x,u\left(x\right))+k_1{\displaystyle \frac{x^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}+c_1]e^{hx}.$$

(4)

Integrating both sides of Equation (4) from 0 to x yields

$$\begin{array}{c}{e}^{hx}u\left(x\right)-e^{0}u\left(0\right)={\int }_0^x[{}^{R}I^{a+b-1}g(z,u\left(z\right))+k_1{\displaystyle \frac{z^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}+c_1]e^{hz}dz\\ \\ u\left(x\right)=u\left(0\right)e^{-hx}+{\int }_0^x{e}^{-hx}{e}^{hz}{}^{R}I^{a+b-1}g(z,u\left(z\right))dz+k_1{\int }_0^x{e}^{-hx}{e}^{hz}{\displaystyle \frac{z^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}dz\\ +{\int }_0^x{c}_1{e}^{-hx}{e}^{hz}dz\\ \hfill ={\int }_0^x{e}^{-h(x-z)}{}^{R}I^{a+b-1}g(z,u\left(z\right))dz+k_1{\int }_0^x{\displaystyle \frac{e^{-h(x-z)}{z}^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}dz+{\displaystyle \frac{c_1}{h}}[1-e^{-hx}].\end{array}$$

Now, by applying the initial conditions given in (2), we get

$$y\prime \left(0\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^{\tau }{(\tau -r)}^{a-b-2}g(r,u\left(r\right))drd\tau dz$$

$$+c_1{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}{\tau }^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}d\tau dz+{\displaystyle \frac{k_1}{h}}\left[{\displaystyle \frac{1}{\mathsf{\Gamma }(\gamma +1)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{e}^{-hz}dz\right]$$

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^{\tau }{(\tau -r)}^{a+b-2}g(r,u\left(r\right))drd\tau dz$$

$$+c_1{\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}{\tau }^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}d\tau dz+{\displaystyle \frac{k_1}{h}}\left[{\displaystyle \frac{1}{\mathsf{\Gamma }(b+1)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}{e}^{-hz}dz\right]$$

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}}{\mathsf{\Gamma }(a+b-1)}}{\int }_0^{\tau }{(\tau -r)}^{a+b-2}g(r,u\left(r\right))drd\tau dz$$

$$\begin{array}{c}+c_1{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{\int }_0^z{\displaystyle \frac{e^{-h(z-\tau )}{\tau }^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}d\tau dz+\hfill \\ \hfill {\displaystyle \frac{k_1}{h}}\left[{\displaystyle \frac{1}{\mathsf{\Gamma }(\gamma +1)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}{e}^{-hz}dz\right]\end{array}$$

To find $c_1$ and $k_1$

$${\psi }_3+c_1{\psi }_4+k_1{\varpi }_1=c_1$$

(5)

$${\psi }_1+c_1{\psi }_2+k_1{\varpi }_2=-h{c}_1$$

(6)

$$k_1={\displaystyle \frac{{\psi }_1({\psi }_4-1)-{\psi }_3({\psi }_2+h)}{{\varpi }_1({\psi }_2+h)+{\varpi }_2(1-{\psi }_4)}}.$$

$$={\displaystyle \frac{{\psi }_1(E_{1,2\gamma +a}(-h)-1)-{\psi }_3(E_{1,2b+a}(-h)+h)}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}.$$

$$c_1={\displaystyle \frac{{\psi }_3{\varpi }_2-{\psi }_1{\varpi }_1}{{\varpi }_1({\psi }_2+h)+{\varpi }_2(1-{\psi }_4)}}$$

$$={\displaystyle \frac{{\psi }_3{\varpi }_2-{\psi }_1{\varpi }_1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}$$

Substituting $k_1$ and $c_1$, we reach

$$\begin{array}{cc}\hfill u\left(x\right)& ={\int }_0^x{e}^{-h(x-z)}{}^{R}I^{a+b-1}g(z,u\left(z\right))dz\hfill \\ & +\left({\displaystyle \frac{{\psi }_3{\varpi }_2-{\psi }_1{\varpi }_1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right)\hfill \\ & \times {\int }_0^x{\displaystyle \frac{e^{-h(x-z)}{z}^{a+b-2}}{\mathsf{\Gamma }(a+b-1)}}dz\hfill \\ & +\left({\displaystyle \frac{{\psi }_1(E_{1,2\gamma +a}(-h)-1)-{\psi }_3(E_{1,2b+a}(-h)+h)}{h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right)[1-e^{-hx}]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\int }_0^x{e}^{-h(x-z)}{}^{R}I^{a+b-1}g(z,u\left(z\right))dz\hfill \\ & +\left({\displaystyle \frac{{\psi }_3{\varpi }_2-{\psi }_1{\varpi }_1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right)x^{a+b-1}{E}_{1,a+b(-hx)}\hfill \\ & +\left({\displaystyle \frac{{\psi }_1(E_{1,2\gamma +a}(-h)-1)-{\psi }_3(E_{1,2b+a}(-h)+h)}{h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right)[1-e^{-hx}]\hfill \end{array}$$

That is, $u\left(x\right)={\int }_0^{1}F(x,z)g(z,u\left(z\right))dz.$  □

3. Main Result

In this part, the existence and uniqueness of the solution to the problem of (1) and (2) are studied in the Banach space C using the Banach contraction mapping principle and the Schauder fixed-point theorem. Let $C\left(\right[0,1],\mathbb{R})$ denote the set of all continuous functions in the Banach space of C from $[0,1]$ to $\mathbb{R}$ with the norm

$$\parallel u\parallel =sup\left\{\right|u\left(x\right)|;x\in I\}$$

The following assumptions are needed to interpret the main results:

• (A1) ∃ a positive constant ${\gamma }_1$,${\gamma }_2$ s.t
  $\left|g(x,u\left(x\right))\right|\le {\gamma }_1+{\gamma }_2\left|u\left(x\right)\right|,\forall x\in I$ and $u\in \mathbb{R}$.
• (A2) $\exists k\in {\mathbb{R}}^{+}$ s.t $\left|g\right(x,t\left(x\right))-g(x,u\left(x\right)\left)\right|\le k\left|t\right(x)-u(x\left)\right|,\forall x\in I$ and $t,u\in \mathbb{R}$.
• (A3) ∃ an increasing function $\phi \in C(I,{\mathbb{R}}_{+})$ and ${\zeta }_1>0$ s.t for any $x\in I$.

  $${\int }_0^x\left|F(x,z)dz\right|\le {\zeta }_1\phi \left(x\right)$$

  For simplicity, we introduce the following notations:

  $$\begin{array}{cc}\hfill {\eta }_1& =\left|{\displaystyle \frac{E_{1,a+2\gamma +1}(-h){\varpi }_2-E_{1,a+2b+1}(-h){\varpi }_1}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|\hfill \\ \hfill {\eta }_2& =\left|{\displaystyle \frac{E_{1,2b+1}(-h)(E_{1,2\gamma +a}(-h)-1)-E_{1,a+2\gamma +1}(-h)(E_{1,2b+a}(-h)+h)}{(h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|\hfill \\ \hfill {\zeta }_1& =|E_{1,a+b}(-hx)|+{\eta }_1{x}^{a+b-1}\left|E_{1,a+b}(-hx)\right|+{\eta }_2[1+e^{-hx}].\hfill \end{array}$$

  Applying the Schauder fixed-point theorem allows us to obtain the result of existence.

Theorem 4. 

Let $g:I\times \mathbb{R}\to \mathbb{R}$ be continuous and satisfy the condition (A1). Then, the problem of (1) and (2) has a solution.

Proof. 

Consider the operator $\mathcal{T}$ defined on $C\left(I\right)$ by

$$\left(\mathcal{T}u\right)\left(x\right)={\int }_0^{1}F(x,z)g(z,u\left(z\right))dz.$$

since $F(x,z)$ and $g(x,u(x\left)\right)$ are continuous functions, we have $\mathcal{T}u\in C\left(I\right)$$\forall u\in C\left(I\right)$. Define the set $B_r=\{u\left(x\right)\in C(I,\mathbb{R}):\parallel u\parallel \le r\}$ by choosing $r\ge {\displaystyle \frac{{\gamma }_{1{\zeta }_1}}{(1-{\gamma }_2{\zeta }_1)}}$. First, we need to show that $\mathcal{T}{B}_r\subseteq B_r$ for $u\in B_r$. To achieve this, consider

$$\parallel \left(\mathcal{T}u\right)\left(x\right)\parallel =\underset{x\in I}{sup}{\int }_0^1\left|F(x,z)g(z,u\left(z\right))\right|dz.$$

Applying (A1) yields

$$\parallel \left(\mathcal{T}u\right)\left(x\right)\parallel \le ({\gamma }_1+{\gamma }_{2}r)\underset{x\in I}{sup}{\int }_0^1\left|F(x,z)\right|dz.$$

Now, we can obtain the following inequality according to the definition of the Green function:

$$\begin{array}{cc}\hfill & \parallel \left(\mathcal{T}u\right)\left(x\right)\parallel \le ({\gamma }_1+{\gamma }_{2}r)\left(\right|E_{1,a+b+1}(-h)|+\hfill \\ & \left|{\displaystyle \frac{E_{1,a+2\gamma +1}(-h){\varpi }_2-E_{1,a+2b+1}(-h){\varpi }_2}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|+|E_{1,a+b}(-h)\hfill \\ & \left|{\displaystyle \frac{E_{1,a+2b+1}(-h)(E_{1,2\gamma +a}(-h)-1)-E_{1,a+2\gamma +1}(-h)(E_{1,2b+a}(-h)+h)}{h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|\hfill \\ & \times [1+e^{-hx}])\hfill \end{array}$$

implies that

$$\parallel \left(\mathcal{T}u\right)\left(x\right)\parallel \le ({\gamma }_1+{\gamma }_{2}r){\zeta }_1\le r.$$

• Therefore, $\mathcal{T}{B}_r\subseteq B_r$.
• By fixing $Q={sup}_{x\in I}\left|g(x,u\left(x\right))\right|$, where $u\in B_r$, and $x,\chi \in I$ with $x<\chi$, we can prove that the operator $\mathcal{T}$ is completely continuous.

  $$\parallel \mathcal{T}\left(u\right)\left(x\right)-\mathcal{T}\left(u\right)\left(\chi \right)\parallel \le Q\underset{x\in J}{sup}{\int }_0^1|F(x,z)-F(\chi ,z)|dz.$$

Therefore,

$$\begin{array}{cc}\hfill & \parallel \mathcal{T}\left(u\right)\left(x\right)-\mathcal{T}\left(u\right)\left(\chi \right)\parallel \le Q\left(\right|x^{a+b}{E}_{1,a+b+1}(-hx)-{\chi }^{a+b}{E}_{1,a+b+1}(-h\chi )|+\hfill \\ & |x^{a+b-1}{E}_{1,a+b}(-hx)-{\chi }^{a+b-1}{E}_{1,a+b}(-h\chi )|{\eta }_1+{\eta }_2|e^{-hx}-e^{-h\chi }\left|\right).\hfill \end{array}$$

We note that as x tends to $\chi$, the RHS of the above inequality approaches zero. Consequently, $\mathcal{T}$ is uniformly bounded and equicontinuous. According to the Ascoli-Arzelà theorem, $\mathcal{T}$ is completely continuous. Therefore, we can find a solution to the problem of (1) and (2) in $C(J,\mathbb{R})$ by applying Schauder’s fixed-point theorem. □

Theorem 5. 

Suppose the condition (A2) holds. If

$$\begin{array}{cc}\hfill & (|E_{1,a+b+1}(-h)|+\left|{\displaystyle \frac{E_{1,a+2\gamma +1}(-h){\varpi }_2-E_{1,a+2b+1}(-h){\varpi }_2}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|+\hfill \\ & |E_{1,a+b}(-h)\left|{\displaystyle \frac{E_{1,a+2b+1}(-h)(E_{1,2\gamma +a}(-h)-1)-E_{1,a+2\gamma +1}(-h)(E_{1,2b+a}(-h)+h)}{h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|\hfill \\ & \times [1+e^{-hx}])<1\hfill \end{array}$$

(7)

Proof. 

Assume that $t,v\in C(I,\mathbb{R})$. Then,

$$\parallel \mathcal{T}\left(t\right)\left(x\right)-\mathcal{T}\left(v\right)\left(x\right)\parallel \le \underset{x\in I}{sup}{\int }_0^1\left|F(x,z)\right||g(z,t\left(z\right))-g(z,v\left(z\right))|dz.$$

Using (A2) yields

$$\parallel \mathcal{T}\left(t\right)\left(x\right)-\mathcal{T}\left(v\right)\left(x\right)\parallel \le k\underset{x\in I}{sup}{\int }_0^1\left|F(x,z)\right||t\left(z\right)-v\left(z\right)|dz,$$

which can also be written as

$$\begin{array}{cc}\hfill & \parallel \mathcal{T}\left(t\right)\left(x\right)-\mathcal{T}\left(v\right)\left(x\right)\parallel \le k\parallel t\left(x\right)-v\left(x\right)\parallel |E_{1,a+b+1}(-h)|+\hfill \\ & \left|{\displaystyle \frac{E_{1,a+2\gamma +1}(-h){\varpi }_2-E_{1,a+2b+1}(-h){\varpi }_2}{{\varpi }_1(E_{1,2b+a}(-h)+h)+{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|+|E_{1,a+b}(-h)\hfill \\ & \left|{\displaystyle \frac{E_{1,a+2b+1}(-h)(E_{1,2\gamma +a}(-h)-1)-E_{1,a+2\gamma +1}(-h)(E_{1,2b+a}(-h)+h)}{h{\varpi }_1(E_{1,2b+a}(-h)+h)+h{\varpi }_2(1-E_{1,2\gamma +a}(-h))}}\right|\hfill \\ & \times [1+e^{-hx}])\hfill \end{array}$$

Hence,

$$\parallel \mathcal{T}\left(t\right)\left(x\right)-\mathcal{T}\left(v\right)\left(x\right)\parallel \le k{\zeta }_1\parallel t\left(x\right)-v\left(x\right)\parallel .$$

Utilizing condition (7), we establish that $\mathcal{T}$ satisfies the properties of a contraction mapping. Consequently, according to the Banach contraction mapping, it is ensured that $\mathcal{T}$ possesses a fixed point, which corresponds to the exclusive solution to the problem of (1) and (2). This concludes the proof. □

3.1. Stability Theorems

In this part of the study, we will investigate the Ulam–Hyers and Ulam–Hyers–Rassias stability of (1) and (2).

Theorem 6. 

If $g:I\times \mathbb{R}\to \mathbb{R}$ is a continuous function and (A2) is satisfied with $k{\zeta }_1<1$, then the problem of (1) and (2) is Ulam–Hyers stable.

Proof. 

Let $y\left(x\right)\in C(I,\mathbb{R})$ be a solution to the inequality in Definition 5 and let there be a solution $v\in C(I,\mathbb{R})$ to Equations (1) and (2). Then, we get

$$u\left(x\right)={\int }_0^{1}F(x,z)g(z,u\left(z\right))dz.$$

$$\underset{0\le x\le 1}{max}{\int }_0^{1}F(x,z)dz={\zeta }_1$$

From Definition 5 we get

$$\begin{array}{cc}\hfill |y\left(x\right)-{\int }_0^{1}F(x,z)g(z,y\left(z\right))dz|& \le {\int }_0^1\left|F(x,z)g(z,u\left(z\right))\psi \left(z\right)\right|dz\hfill \\ & \le {\int }_0^1\left|F(x,z)g(z,u\left(z\right))\right|\left|\psi \left(z\right)\right|dz\hfill \\ & \le ϵ{\int }_0^1\left|F(x,z)g(z,u\left(z\right))\right|\hfill \\ & \le ϵ{\zeta }_1.\hfill \end{array}$$

(8)

Using (A2), we have

$$|y\left(x\right)-u\left(x\right)|\le |y\left(x\right)-{\int }_0^{1}F(x,z)g(z,y\left(z\right))dz|+k{\int }_0^{1}F(x,z)|y\left(z\right)-u\left(z\right)|dz,\forall x\in I.$$

From Equation (8), we get

$$|y\left(x\right)-u\left(x\right)|\le {\displaystyle \frac{ϵ{\zeta }_1}{1-k{\zeta }_1}},1-k{\zeta }_1\ne 0$$

Assume that $C_g={\displaystyle \frac{{\zeta }_1}{1-k{\zeta }_1}}$. That is,

$$|y\left(x\right)-u\left(x\right)|\le C_gϵ,x\in I$$

So, the problem of (1) and (2) is Ulam–Hyres stable. □

Theorem 7. 

Suppose that $g:I\times R\to R$ is a continuous function and (A2)–(A3) hold with $k{\zeta }_1<1$. Then, the integral initial value of problems (1) and (2) is Ulam–Hyres–Rassias stable.

Proof. 

Let $y\left(x\right)\in C(I,\mathbb{R})$ be a solution to the inequality in Definition 6, and let ∃ a solution $v\in C(I,\mathbb{R})$ to Equations (1) and (2). Now, from the inequality in Definition 6 and $\forall x\in I$, we have

$$\begin{array}{cc}\hfill |y\left(x\right)-{\int }_0^{1}F(x,z)g(z,y\left(z\right))dz|& \le ϵ{\int }_0^1\left|F(x,z)g(z,y\left(z\right))\right|\phi \left(z\right)dz\hfill \\ & \le ϵ{\zeta }_1\phi \left(x\right).\hfill \end{array}$$

(9)

According to (A2), $\forall x\in I$, we have

$$|y\left(x\right)-u\left(x\right)|\le |y\left(x\right)-{\int }_0^{1}F(x,z)g(z,y\left(z\right))dz|+k{\int }_0^{1}F(x,z)|y\left(z\right)-u\left(z\right)|dz.$$

Using Equation (9), we get

$$|y\left(x\right)-u\left(x\right)|\le {\displaystyle \frac{ϵ{\zeta }_1\phi \left(x\right)}{1-k{\zeta }_1}},1-k{\zeta }_1\ne 0$$

Let $C_g={\displaystyle \frac{{\zeta }_1}{1-k{\zeta }_1}}$; then,

$$|y\left(x\right)-u\left(x\right)|\le C_gϵ\phi \left(x\right),x\in I$$

holds, and the integral initial value problem of (1) and (2) is Ulam–Hyres–Rassias stable. □

3.2. Example

Consider the following problem:

$$\left\{\begin{array}{l}{}^{R}D^{0.4}\left({}^{C}D^{1.2}u\left(x\right){+}^C{D}^{0.2}u\left(x\right)\right)={\displaystyle \frac{x}{5}}cosu\left(x\right),x,u\in I,\\ u\left(0\right)=0, u\prime \left(0\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_0^1{(1-z)}^{\gamma -1}u\left(z\right)dz,\\ u″\left(0\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(b\right)}}{\int }_0^1{(1-z)}^{b-1}u\left(z\right)dz\end{array}\right.$$

(10)

Taking $a=1.2,b=0.4,\gamma =0.4$ and $h=1$, and also abiding by the Lipschitz condition, we have $k=0.2$. Using Theorem 3, we get $k{\zeta }_1=0.351601312<1$, which proves that the problem of (10) has a unique solution.

Now, according to Theorem 6,

$$|y\left(x\right)-u\left(x\right)|\le {\displaystyle \frac{ϵ{\zeta }_1}{1-k{\zeta }_1}}, \mathrm{where} {\displaystyle \frac{{\zeta }_1}{1-k{\zeta }_1}}=2.711304931>0,$$

which proves that the problem of (10) is Ulam–Hyers stable, see Figure 1.

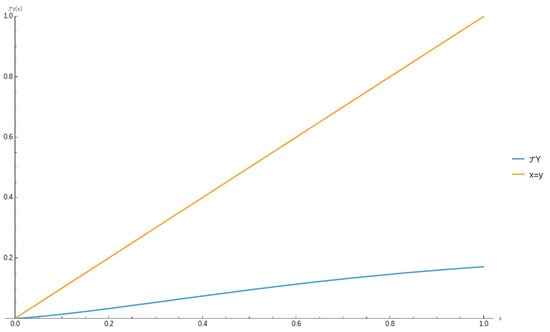
Figure 1. The response of the operator $\mathcal{T}$ for values of t in J.

Now, in order to examine the actions of the operator $\mathcal{T}$, it becomes apparent that $\left|g\right(x,u\left(x\right)|\le 0.1080604612$ and $\left|\mathcal{T}u\left(x\right)\right|\le 0.1080604612{\zeta }_1$.

4. Conclusions

This research aimed to analyze the solutions to nonlinear fractional equations with integral initial conditions. Using the Schauder fixed-point theorem and the contraction mapping principle, we demonstrated the existence and uniqueness of a solution to the nonlinear problem. Moreover, we examined the Hyers–Ulam and Hyers–Ulam–Rassias stability of Equations (1) and (2). To highlight the practical implications of our main results, we also provided an illustrative example.