Fractional Dynamics of Laser-Induced Heat Transfer in Metallic Thin Films: Analytical Approach
Abstract
1. Introduction
2. Mathematical Model
2.1. Formulation of the Problem
2.2. Analytical Solution
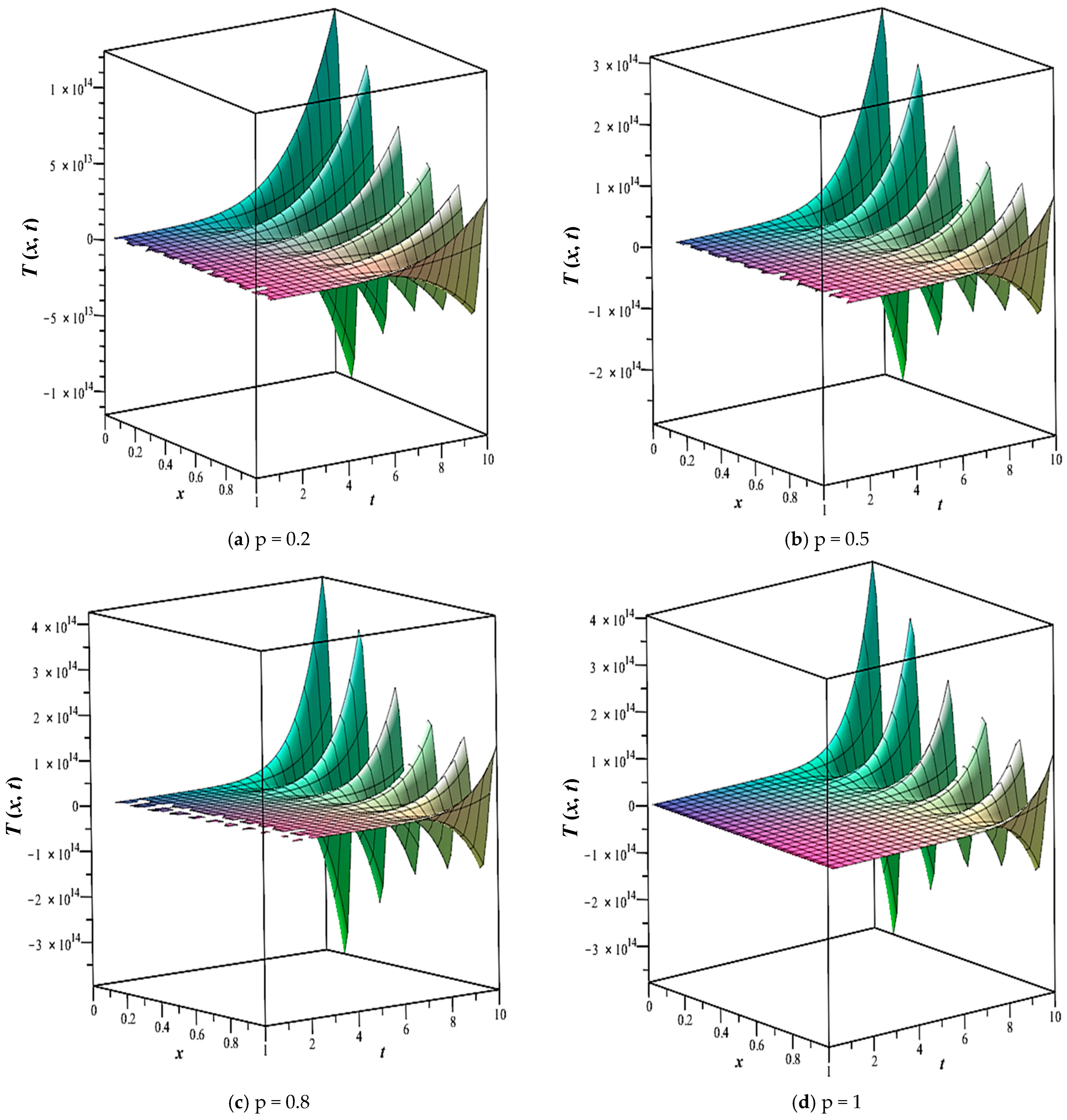
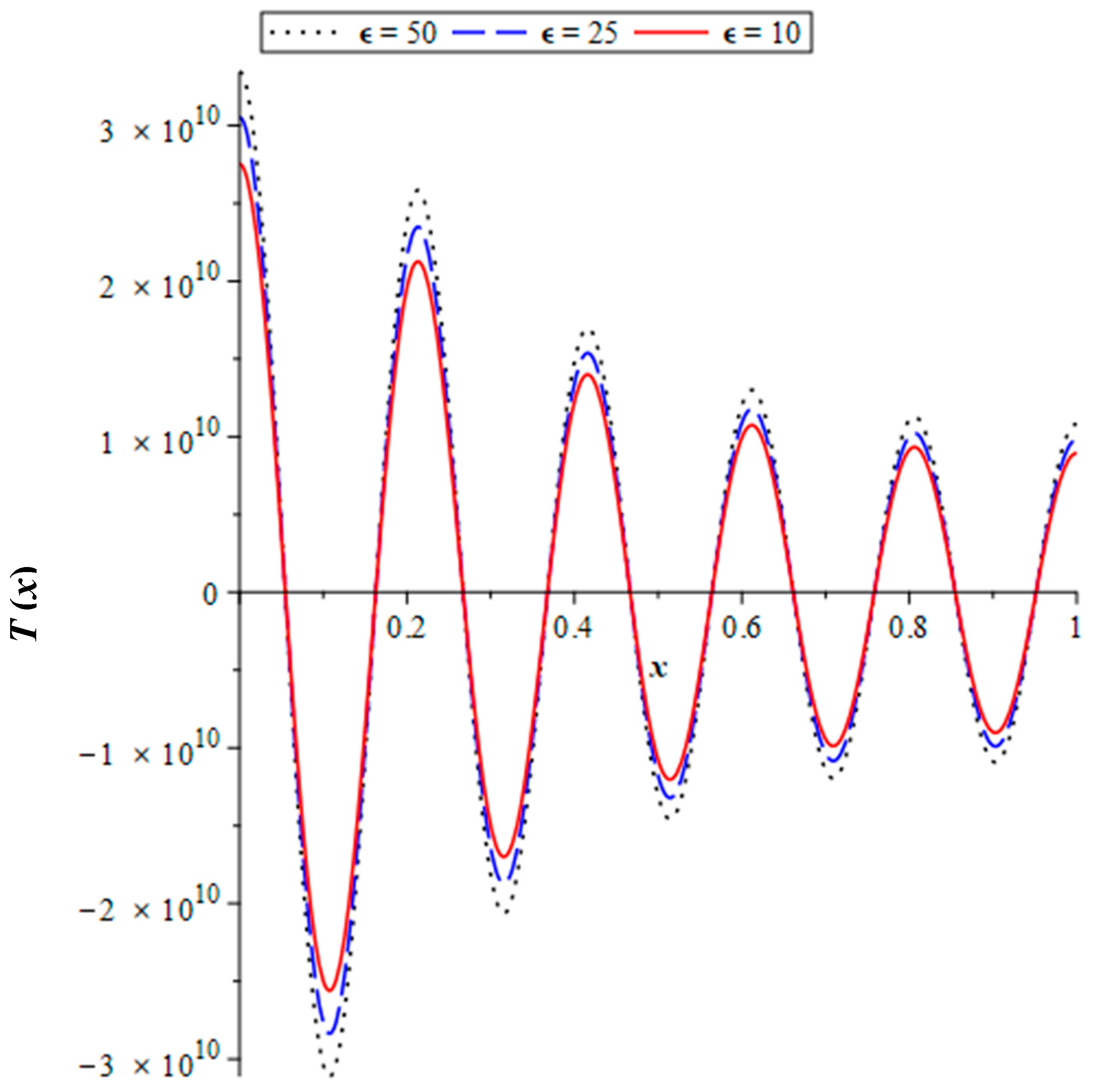
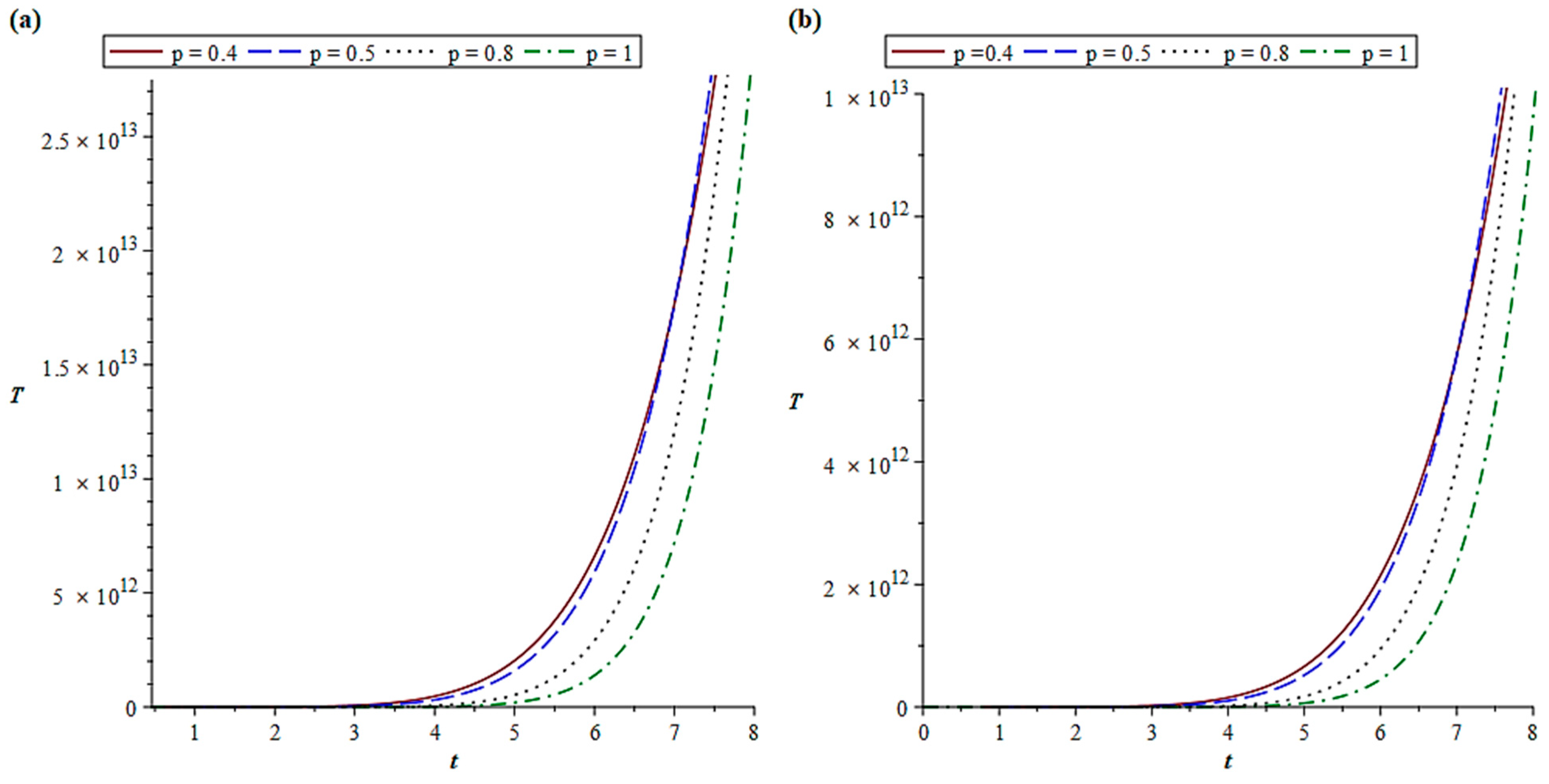
3. Results and Discussion
4. Validation and Physical Relevance
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Nomenclature
| fractional order of differentiation | |
| thickness of thin film | |
| unit step Heaviside function of time | |
| absorbed laser intensity | |
| surface reflectance | |
| laser incident intensity (W/m2) | |
| specific heat at constant pressure J/(Kg.K) | |
| thermal conductivity (W/Km) | |
| dimensionless space variable | |
| dimensionless time variable | |
| dimensionless temperature | |
| Greek symbols | |
| fractional differential operator with respect to time | |
| temperature of thin film | |
| initial temperature | |
| space variable | |
| time variable | |
| α | thermal diffusivity |
| ρ | density (Kg/m3) |
| ω | absorption coefficient |
| relaxation time | |
| dimensionless absorption parameter | |
| dimensionless relaxation time | |
| dimensionless rate of energy absorbed in the medium | |
Appendix A. Verification of the Analytical Solution
Appendix A.1. Substituted Solution
Appendix A.2. Analytical Solution Structure
- is the mean temperature component, representing the zero-mode of the Fourier cosine series:
- is the two-parameter Mittag–Leffler function:
- is the -th modal amplitude, involving source terms and fractional convolution integrals (as provided in Equation (16)).
Appendix A.3. Substitution into Governing Equation (Equation (7))
- First-order time derivative:
- Fractional derivative:
- •
- For (mean component)
- •
- For
Appendix A.4. Substitution into Initial Conditions (Equation (8))
- , because the integrals start from .
- All and their derivatives are also zero (Mittag–Leffler terms vanish at zero) and, hence, initial conditions are satisfied.
Appendix A.5. Substitution into Boundary Conditions
References
- Mishra, S.; Yadava, V. Modeling and optimization of laser beam percussion drilling of thin aluminum sheet. Opt. Laser Technol. 2013, 48, 461–474. [Google Scholar] [CrossRef]
- Kim, B.; Nam, H.-K.; Kim, Y.-J.; Kim, S.-W. Lift-Off Ablation of Metal Thin Films for Micropatterning Using Ultrashort Laser Pulses. Metals 2021, 11, 1586. [Google Scholar] [CrossRef]
- Craciun, F.; Lippert, T.; Dinescu, M. Pulsed laser deposition: Fundamentals, applications, and perspectives. In Handbook of Laser Micro- and Nano-Engineering; Springer International Publishing: Cham, Switzerland, 2021; pp. 1291–1323. [Google Scholar]
- Bauer, F.; Michalowski, A.; Kiedrowski, T.; Nolte, S. Heat accumulation in ultra-short pulsed scanning laser ablation of metals. Opt. Express 2015, 23, 1035–1043. [Google Scholar] [CrossRef]
- Zenji, A.; Pernot, G.; Lacroix, D.; Rampnoux, J.-M.; Bourgeois, O.; Grauby, S.; Dilhaire, S. Seeking non-Fourier heat transfer with ultrabroad band thermoreflectance spectroscopy. Commun. Mater. 2024, 5, 123. [Google Scholar] [CrossRef]
- Shomali, Z.; Kovács, R.; Ván, P.; Kudinov, I.V.; Ghazanfarian, J. Lagging heat models in thermodynamics and bioheat transfer: A critical review. Contin. Mech. Thermodyn. 2022, 34, 637–679. [Google Scholar] [CrossRef]
- Alvarez, F.X.; Jou, D. Memory and nonlocal effects in heat transport: From diffusive to ballistic regimes. Appl. Phys. Lett. 2007, 90, 083109. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Liu, F.; Shen, M. Review of the fractional Black-Scholes equations and their solution techniques. Fractal Fract. 2024, 8, 101. [Google Scholar] [CrossRef]
- El-Gazar, E.F.; Hassan, H.; Rabia, S.I.; Hu, C.; Zahra, W.K. A new fractional Cattaneo model for enhancing the thermal performance of photovoltaic panels using heat spreader: Energy, exergy, economic and enviroeconomic (4E) analysis. Environ. Sci. Pollut. Res. 2023, 30, 105840–105855. [Google Scholar] [CrossRef] [PubMed]
- Bonse, J.; Krüger, J. Structuring of thin films by ultrashort laser pulses. Appl. Phys. A 2023, 129, 14. [Google Scholar] [CrossRef]
- Ansari, A. Fundamental solution of a multi-dimensional distributed order fractional diffusion equation. Eur. Phys. J. Plus 2021, 136, 1–23. [Google Scholar] [CrossRef]
- Kiskinov, H.; Milev, M.; Petkova, M.; Zahariev, A. Variable-Order Fractional Linear Systems with Distributed Delays—Existence, Uniqueness and Integral Representation of the Solutions. Fractal Fract. 2024, 8, 156. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Jain, S.; Pindza, E.; Mare, E. Comprehensive Numerical Analysis of Time-Fractional Reaction–Diffusion Models with Applications to Chemical and Biological Phenomena. Mathematics 2024, 12, 3251. [Google Scholar] [CrossRef]
- Hamadneh, T.; Hioual, A.; Saadeh, R.; Abdoon, M.A.; Almutairi, D.K.; Khalid, T.A.; Ouannas, A. General methods to synchronize fractional discrete reaction–diffusion systems applied to the glycolysis model. Fractal Fract. 2023, 7, 828. [Google Scholar] [CrossRef]
- Sene, N. Fractional model for a class of diffusion-reaction equation represented by the fractional-order derivative. Fractal Fract. 2020, 4, 15. [Google Scholar] [CrossRef]
- Luchko, Y. On the 1st-level general fractional derivatives of arbitrary order. Fractal Fract. 2023, 7, 183. [Google Scholar] [CrossRef]
- Lee, H.G. A second-order operator splitting Fourier spectral method for fractional-in-space reaction–diffusion equations. J. Comput. Appl. Math. 2018, 333, 395–403. [Google Scholar] [CrossRef]
- Xu, G.; Wang, J. Analytical solution of time fractional Cattaneo heat equation for finite slab under pulse heat flux. Appl. Math. Mech. 2018, 39, 1465–1476. [Google Scholar] [CrossRef]
- Talaee, M.R.; Sarafrazi, V. Analytical solution for three-dimensional hyperbolic heat conduction equation with time-dependent and distributed heat source. J. Mech. 2017, 33, 65–75. [Google Scholar] [CrossRef]
- Al-Khairy, R.T.; Al-Ofey, Z.M. Analytical Solution of the Hyperbolic Heat Conduction Equation for Moving Semi-Infinite Medium under the Effect of Time-Dependent Laser Heat Source. J. Appl. Math. 2009, 2009, 604695. [Google Scholar] [CrossRef]
- Alkallas, F.H.; Mostafa, A.M.; Khater, M.A.; Elsharkawy, W.B.; Younes, A.A.O.; Rezk, R.A.; Trabelsi, A.B.G.; Essawy, M.A.I. Experimental and Mathematical Modeling of Thermal Diffusion in Steel Alloys via Finite Fourier Transform with In-Situ Analysis of Single and Double Pulses in Laser-Induced Breakdown Spectroscopy. Plasma Process. Polym. 2025, 22, e70011. [Google Scholar] [CrossRef]
- Maillet, D. A review of the models using the Cattaneo and Vernotte hyperbolic heat equation and their experimental validation. Int. J. Therm. Sci. 2019, 139, 424–432. [Google Scholar] [CrossRef]
- Akbarzadeh, A.H.; Cui, Y.; Chen, Z.T. Thermal wave: From nonlocal continuum to molecular dynamics. RSC Adv. 2017, 7, 13623–13636. [Google Scholar] [CrossRef]
- Ahmed, Y.; Zakria, A.; Osman, O.A.A.; Suhail, M.; Rabih, M.N.A. Fractional Moore–Gibson–Thompson Heat Conduction for Vibration Analysis of Non-Local Thermoelastic Micro-Beams on a Viscoelastic Pasternak Foundation. Fractal Fract. 2025, 9, 118. [Google Scholar] [CrossRef]
- Nuruddeen, R.I. Approximate analytical solution to the Cattaneo heat conduction model with various laser sources. J. Appl. Math. Comput. Mech. 2022, 21, 67–78. [Google Scholar] [CrossRef]
- Li, S.-N.; Cao, B.-Y. Generalized Boltzmann transport theory for relaxational heat conduction. Int. J. Heat Mass Transf. 2021, 173, 121225. [Google Scholar] [CrossRef]
- Ghazizadeh, H.; Maerefat, M.; Azimi, A. Explicit and implicit finite difference schemes for fractional Cattaneo equation. J. Comput. Phys. 2010, 229, 7042–7057. [Google Scholar] [CrossRef]
- Pradhan, S.; Bhattarai, J.S.; Murugavel, M.; Sharma, O.P. Machine Learning Approaches to Surpass the Limitations of the Beer–Lambert Law. ACS Omega 2025, 10, 16597–16601. [Google Scholar] [CrossRef]
- Qi, H.; Jiang, X. Solutions of the space-time fractional Cattaneo diffusion equation. Phys. A Stat. Mech. Its Appl. 2011, 390, 1876–1883. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D. Ordinary and Partial Differential Equations: With Special Functions, Fourier Series, and Boundary Value Problems; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Alrakathi, M.; Alodah, A. Assessing the Impact of Climate Change on Intensity-Duration-Frequency (IDF) Curves for the Qassim Region, Saudi Arabia. Atmosphere 2025, 16, 59. [Google Scholar] [CrossRef]
- Alqahtani, A.M.; Bilal, M.; Ali, A.; Khalifa, H.A.E.; Alqahtani, H. Numerical calculation of unsteady MHD nanofluid flow across two fluctuating discs with chemical reaction and zero mass flux. Zamm 2024, 104, e202300001. [Google Scholar] [CrossRef]
- Mostafa, D.M. Linear Stability of Magneto Viscoelastic Walter’s B′ Type with Heat and Mass Transfer. Adv. High. Energy Phys. 2022, 2022, 6577512. [Google Scholar] [CrossRef]
- Rafique, K.; Mahmood, Z.; Muhammad, T.; Taj, M.; Alballa, T.; Khalifa, H.A.E.-W. Analyzing the effects of variable fluid properties on radiative dissipative hybrid nanofluid over moving wedge with MHD and Joule heating. Mod. Phys. Lett. B 2025, 39, 2550055. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, X.; Qi, H.; Xu, H. Numerical simulation and parameters estimation of the time fractional dual-phase-lag heat conduction in femtosecond laser heating. Int. Commun. Heat Mass Transf. 2021, 125, 105355. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, P.; Li, C.; He, T. Fractional order and memory-dependent analysis to the dynamic response of a bi-layered structure due to laser pulse heating. Int. J. Heat Mass Transf. 2019, 144, 118664. [Google Scholar] [CrossRef]
- Dutta, J.; Biswas, R.; Kundu, B. Analytical solution of dual-phase-lag based heat transfer model in ultrashort pulse laser heating of A6061 and Cu3Zn2 nano film. Opt. Laser Technol. 2020, 128, 106207. [Google Scholar] [CrossRef]
- Karakas, A.; Tunc, M.; Camdali, Ü. Thermal analysis of thin multi-layer metal films during femtosecond laser heating. Heat Mass Transf. 2010, 46, 1287–1293. [Google Scholar] [CrossRef]
- Ji, C.-C.; Dai, W.; Sun, Z.-Z. Numerical schemes for solving the time-fractional dual-phase-lagging heat conduction model in a double-layered nanoscale thin film. J. Sci. Comput. 2019, 81, 1767–1800. [Google Scholar] [CrossRef]
- Mozafarifard, M.; Mortazavinejad, S.M.; Toghraie, D. Numerical simulation of fractional non-Fourier heat transfer in thin metal films under short-pulse laser. Int. Commun. Heat Mass Transf. 2020, 115, 104607. [Google Scholar] [CrossRef]
- Mozafarifard, M.; Toghraie, D. Time-fractional subdiffusion model for thin metal films under femtosecond laser pulses based on Caputo fractional derivative to examine anomalous diffusion process. Int. J. Heat Mass Transf. 2020, 153, 119592. [Google Scholar] [CrossRef]
- Amoruso, S.; Nedyalkov, N.; Wang, X.; Ausanio, G.; Bruzzese, R.; Atanasov, P. Ultrashort-pulse laser ablation of gold thin film targets: Theory and experiment. Thin Solid Film. 2014, 550, 190–198. [Google Scholar] [CrossRef]


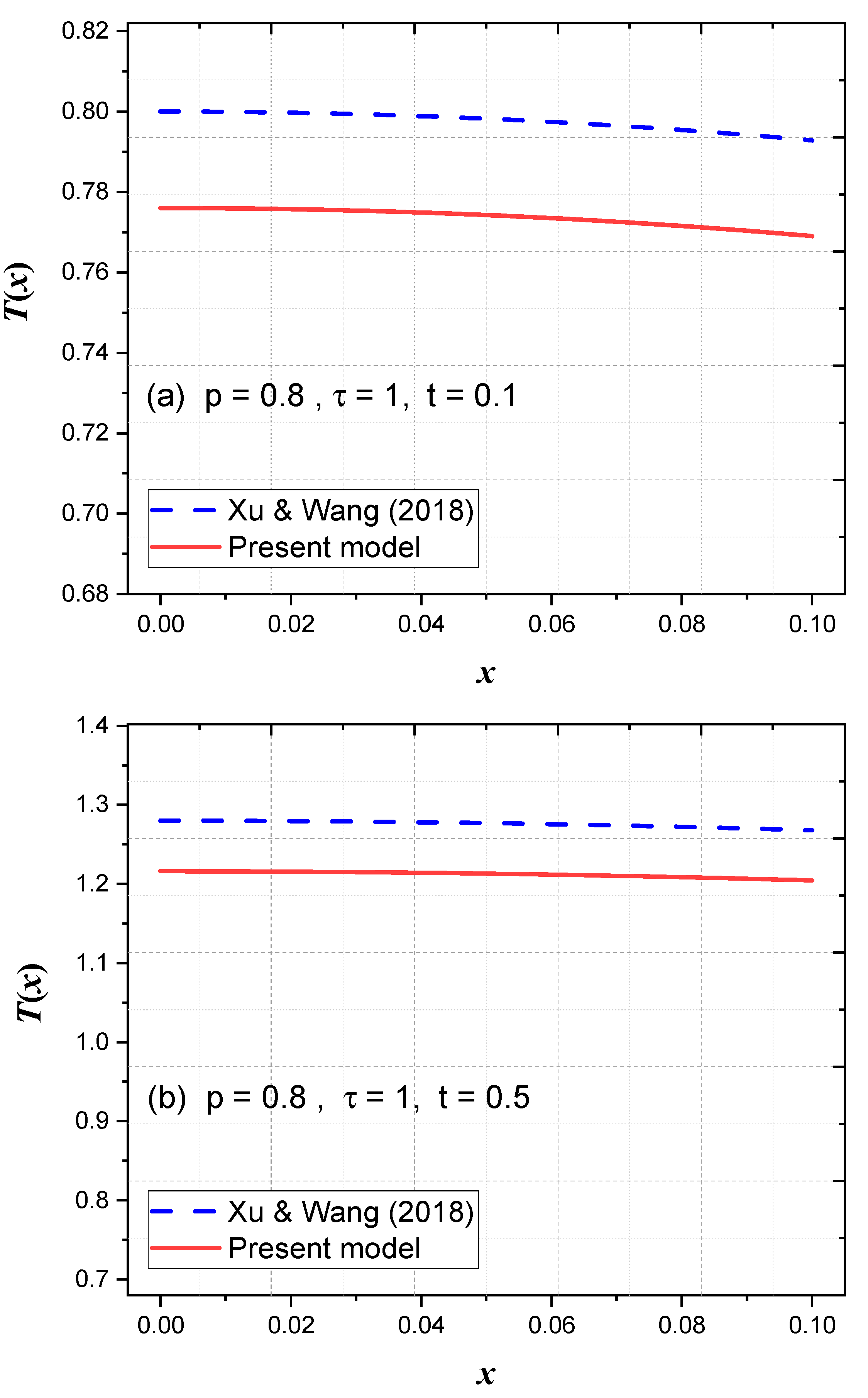
| t | T(x, t) | |||
|---|---|---|---|---|
| (a) x = 0 | (b) x = 1 | |||
| Present | Ref. [18] | Present | Ref. [18] | |
| 0.1 | 0.372708 | 0.380162 | 0.1007231 | 0.1248162 |
| 0.3 | 0.517713 | 0.524029 | 0.2116723 | 0.2398079 |
| 0.5 | 0.719142 | 0.725336 | 0.4071926 | 0.4258017 |
| 0.7 | 0.934299 | 0.962019 | 0.6020973 | 0.6270351 |
| 1.0 | 1.195604 | 1.211253 | 0.8093021 | 0.8230743 |
| 1.5 | 1.821032 | 1.839273 | 1.3542706 | 1.3711425 |
| 2.5 | 1.998765 | 2.000000 | 1.9684253 | 1.9999785 |
| Overlay Temperature Profiles | Peak Temperature | Time to Peak | Thermal Wave Speed | Fractional Order (p or α) | Relaxation Time (τ) | |
|---|---|---|---|---|---|---|
| Current Work (Essawy et al.) | Analytical via Mittag–Leffler; damped wavefronts depending on p and τ | Decreases with higher p and τ | Increases with p; delayed heat front | Slows down with increasing p and τ | p (0 < p ≤ 1); key modeling tool | Explicit τ; impacts damping and delay |
| Qiao et al. (2021) [36] | Numerical/semi-analytical; validated vs. experiments | Thickness-dependent; experimentally supported | Increases with film thickness | Inferred from simulations; thickness impact | Different α for heat flux and gradient | τ estimated via optimization |
| Li et al. (2019) [37] | Laplace-based for bi-layers; shows spatial delay | Affected by interface conditions | Memory and delay factor affect timing | Controlled by kernel function and delay | Fractional order affects thermoelastic coupling | Delay and memory functions involved |
| Dutta et al. (2020) [38] | Exact solutions for A6061/Cu3Zn2; deviates from Fourier | Material-specific; significantly lower in DPL vs. Fourier | Related to pulse duration; material impacts it | DPL gives finite speed vs. Fourier’s infinite | Not used explicitly; DPL model analog | τq and τT in DPL framework |
| Karakas et al. (2010) [39] | Two-temperature model; gold/chromium metal interactions | Influenced by multilayer dynamics | Two-step model shows delay | Hyperbolic wave propagation used | Not fractional | Electron-lattice relaxation time |
| Ji et al. (2019) [40] | FDM solutions; shows jump conditions | Lower than classical due to lagging terms | Delayed due to fractional operators | Defined via Knudsen number | α and α + 1 modeled via Caputo form | τq, τT in Caputo framework |
| Mozafarifard et al. (2020) [41] | Caputo-based numerical model; fits experimental profiles | Lower than classical; influenced by β and material | Slower rise for lower α | Wave-like front with non-Fourier features | β = 0.5–1 in Caputo model; fits data | Estimated from data; critical for model |
| Mozafarifard & Toghraie (2020) [42] | Subdiffusion profiles; validated; lower gradient | Lower than Fourier; matches experiments | Larger delays with smaller α | Slow subdiffusive waves | β ∈ (0.5, 1); Caputo subdiffusion | Parametrized with laser depth |
| Amoruso et al. (2014) [43] | MD simulation; thin film shows smoother, more uniform profile | Uniform for film; less variance than bulk material | Not directly given; inferred from heat propagation dynamics | Faster in bulk; slower, more confined in thin film | Not fractional; uses MD and thermodynamic simulations | τ not named but behavior inferred from two-step MD model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Essawy, M.A.I.; Rezk, R.A.; Mostafa, A.M. Fractional Dynamics of Laser-Induced Heat Transfer in Metallic Thin Films: Analytical Approach. Fractal Fract. 2025, 9, 373. https://doi.org/10.3390/fractalfract9060373
Essawy MAI, Rezk RA, Mostafa AM. Fractional Dynamics of Laser-Induced Heat Transfer in Metallic Thin Films: Analytical Approach. Fractal and Fractional. 2025; 9(6):373. https://doi.org/10.3390/fractalfract9060373
Chicago/Turabian StyleEssawy, M. A. I., Reham A. Rezk, and Ayman M. Mostafa. 2025. "Fractional Dynamics of Laser-Induced Heat Transfer in Metallic Thin Films: Analytical Approach" Fractal and Fractional 9, no. 6: 373. https://doi.org/10.3390/fractalfract9060373
APA StyleEssawy, M. A. I., Rezk, R. A., & Mostafa, A. M. (2025). Fractional Dynamics of Laser-Induced Heat Transfer in Metallic Thin Films: Analytical Approach. Fractal and Fractional, 9(6), 373. https://doi.org/10.3390/fractalfract9060373







