Entropies and Degree-Based Topological Indices of Generalized Sierpiński Graphs
Abstract
1. Introduction
- •
- for .
- •
- : For two vertices and in , if there exists such that
- (i)
- For all , ;
- (ii)
- and ;
- (iii)
- For all , and .
- •
- The first Zagreb entropyIf , . The first Zagreb entropy is defined as follows [34]:
- •
- The second Zagreb entropyIf , . The second Zagreb entropy is [34]
- •
- The forgotten entropyIf , . The forgotten entropy is [34]
- •
- The augmented Zagreb entropyIf , . The augmented Zagreb entropy is [34]
- •
- The Sombor entropyIf , . The Sombor entropy is
- •
- The elliptic Sombor entropyIf , . The elliptic Sombor entropy is
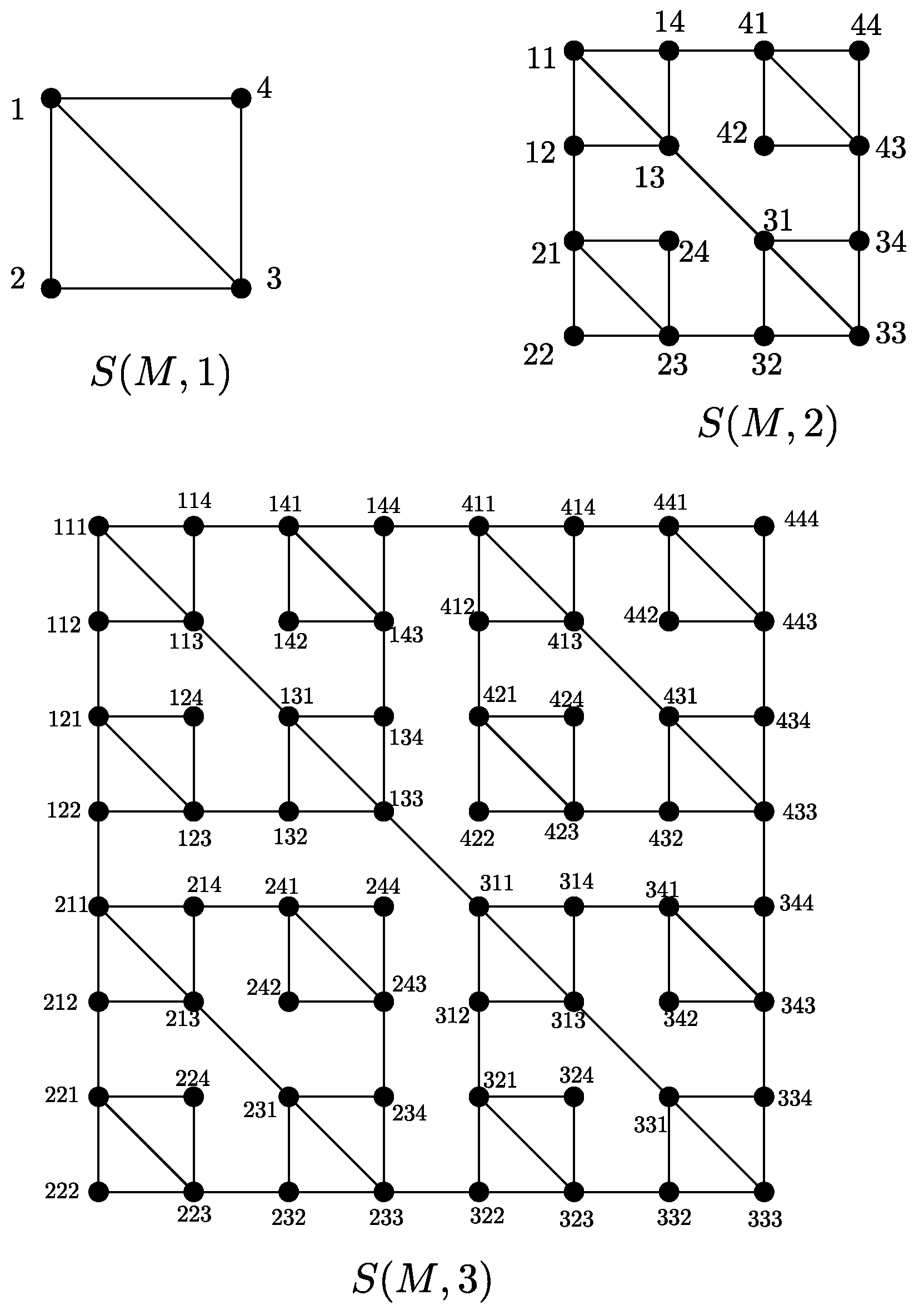
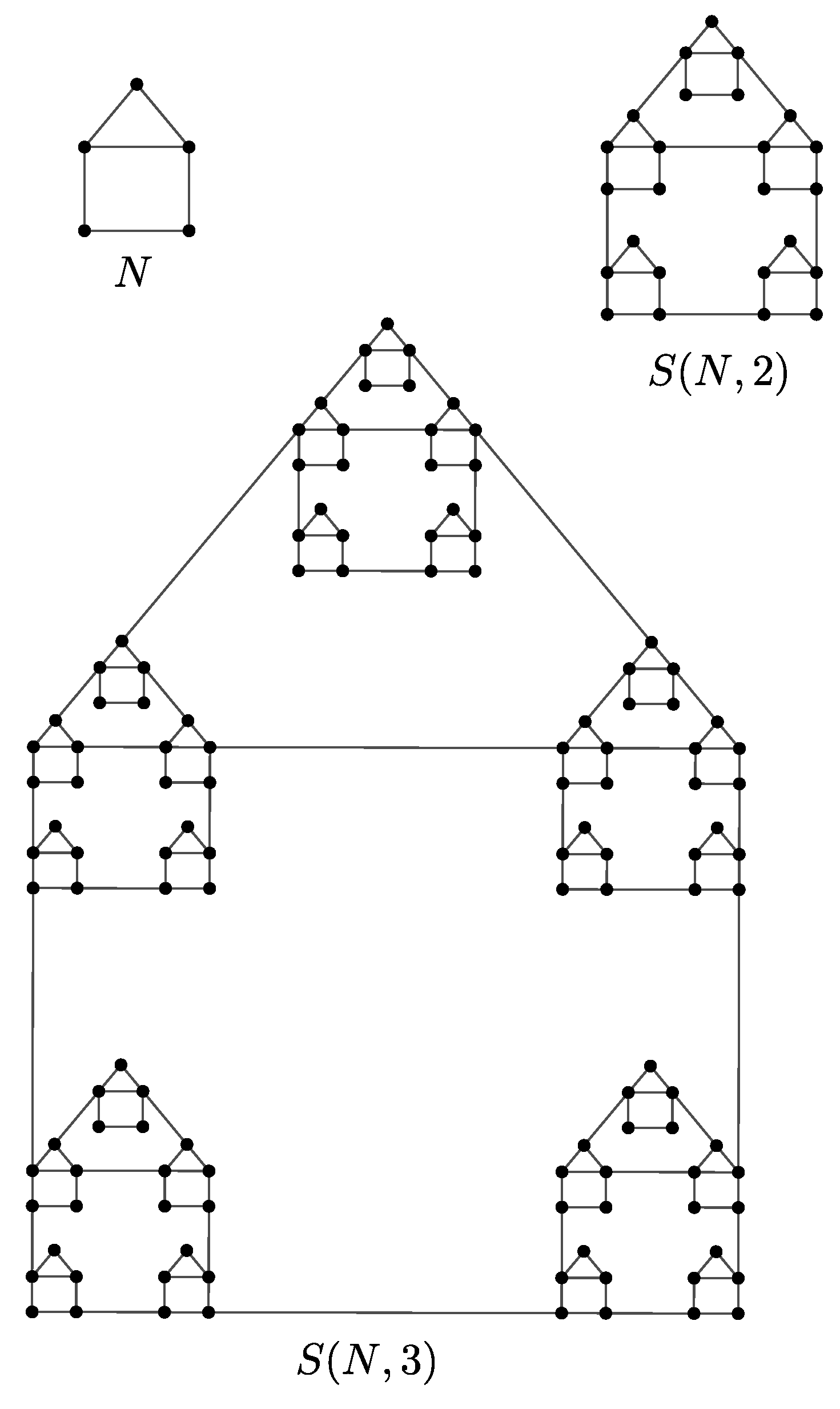
2. Topological Indices and Entropies of the Generalized Sierpiński Graphs
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- ;
- 6.
- .
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- 5.
- 6.
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- ;
- 5.
- .
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statements
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Shi, Y. A note on distance-based graph entropies. Entropy 2014, 16, 5416–5427. [Google Scholar] [CrossRef]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Emmert-Streib, F.; Shi, Y. Entropy of weighted graphs with Randić weights. Entropy 2015, 17, 3710–3723. [Google Scholar] [CrossRef]
- Chen, H.; Wu, R.; Deng, H. The extremal values of some topological indices in bipartite graphs with a given matching number. Appl. Math. Comput. 2016, 280, 103–109. [Google Scholar] [CrossRef]
- Deng, H.; Huang, G.; Jiang, X. A unified linear-programming modeling of some topological indices. J. Comb. Optim. 2015, 30, 826–837. [Google Scholar] [CrossRef]
- Liu, J.B.; Pan, X.F. Minimizing Kirchhoff index among graphs with a given vertex bipartiteness. Appl. Math. Comput. 2016, 291, 84–88. [Google Scholar] [CrossRef]
- Manzoor, S.; Siddiqui, M.K.; Ahmad, S. On entropy measures of molecular graphs using topological indices. Arab. J. Chem. 2020, 13, 6285–6298. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Jency, J.; Abraham, J.; Ruth Julie Kavitha, S.; Balasubramanian, K. Two-dimensional coronene fractal structures: Topological entropy measures, energetics, NMR and ESR spectroscopic patterns and existence of isentropic structures. Mol. Phys. 2022, 120, e2079568. [Google Scholar] [CrossRef]
- Ashraful Alam, M.; Ghani, M.U.; Kamran, M.; Shazib Hameed, M.; Hussain Khan, R.; Baig, A. Degree-based entropy for a non-Kekulean benzenoid graph. J. Math. 2022, 2022, 2288207. [Google Scholar] [CrossRef]
- Ghani, M.U.; Campena, F.J.H.; Ali, S.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Galal, A.M. Characterizations of chemical networks entropies by K-banhatii topological indices. Symmetry 2023, 15, 143. [Google Scholar] [CrossRef]
- Klein, D.; Cravey, M.; Hite, G. Fractal benzenoids. Polycycl. Aromat. Compd. 1991, 2, 163–182. [Google Scholar] [CrossRef]
- Klavžar, S.; Milutinović, U. Graphs S(n,k) and a variant of the tower of Hanoi problem. Czechoslov. Math. J. 1997, 47, 95–104. [Google Scholar] [CrossRef]
- Klavžar, S.; Milutinović, U.; Petr, C. 1-perfect codes in Sierpiński graphs. Bull. Austral. Math. Soc. 2002, 66, 369–384. [Google Scholar] [CrossRef]
- Gravier, S.; Klavžar, S.; Mollard, M. Codes and L(2,1)-labelings in Sierpiński graphs. Taiwan. J. Math. 2005, 9, 671–681. [Google Scholar] [CrossRef]
- Lipscomb, S.L.; Perry, J.C. Lipscomb’s L(A) space fractalized in Hilbert’s l2(A) space. Proc. Amer. Math. Soc. 1992, 115, 1157–1165. [Google Scholar]
- Milutinovic, U. Completeness of the Lipscomb space. Glas. Mat. Ser. III 1992, 27, 343–364. [Google Scholar]
- Klavžar, S. Coloring Sierpiński graphs and Sierpiński gasket graphs. Taiwan. J. Math. 2008, 12, 513–522. [Google Scholar] [CrossRef]
- Klavžar, S.; Mohar, B. Crossing numbers of Sierpiński-like graphs. J. Graph Theory 2005, 50, 186–198. [Google Scholar] [CrossRef]
- Parisse, D. On some metric properties of the Sierpiński graphs S(n,k). Ars Comb. 2009, 90, 145–160. [Google Scholar]
- Hinz, A.M.; Parisse, D. The average eccentricity of Sierpiński graphs. Graphs Combin. 2012, 28, 671–686. [Google Scholar] [CrossRef]
- Gravier, S.; Kovše, M.; Parreau, A. Generalized Sierpiński Graphs. In Posters at EuroComb’11, Budapest. Available online: http://www.renyi.hu/conferences/ec11/posters/parreau.pdf (accessed on 17 February 2025).
- Chanda, S.; Iyer, R. On the Sombor index of Sierpiński and Mycielskian Graphs. Commun. Comb. Optim. 2025, 10, 20–56. [Google Scholar]
- Javaid, I.; Benish, H.; Imran, M.; Khan, A.; Ullah, Z. On some bounds of the topological indices of generalized Sierpiński and extended Sierpiński graphs. J. Inequal. Appl. 2019, 2019, 37. [Google Scholar] [CrossRef]
- Alizadeh, Y.; Estaji, E.; Klavžar, S.; Petkovšek, M. Metric properties of generalized Sierpiński graphs over stars. Discret. Appl. Math. 2019, 266, 48–55. [Google Scholar] [CrossRef]
- Rodríguez-Velázquez, J.A.; Tomás-Andreu, J. On the Randić index of polymeric networks modelled by generalized Sierpiński graphs. MATCH Commun. Math. Comput. Chem 2015, 74, 145–160. [Google Scholar]
- Estrada-Moreno, A.; Rodríguez-Velázquez, J.A. On the general Randić index of polymeric networks modelled by generalized Sierpiński graphs. Discret. Appl. Math. 2019, 263, 140–151. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U. Graph Theory; Springer-Verlag: London, UK, 2008. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem 2021, 86, 11–16. [Google Scholar]
- Gutman, I.; Furtula, B.; Oz, M.S. Geometric approach to vertex-degree-based topological indices–elliptic Sombor index, theory and application. Int. J. Quantum Chem. 2024, 124, e27346. [Google Scholar] [CrossRef]
- Manzoor, S.; Chu, Y.M.; Siddiqui, M.K.; Ahmad, S. On topological aspects of degree based entropy for two carbon nanosheets. Main Group Met. Chem. 2020, 43, 205–218. [Google Scholar] [CrossRef]

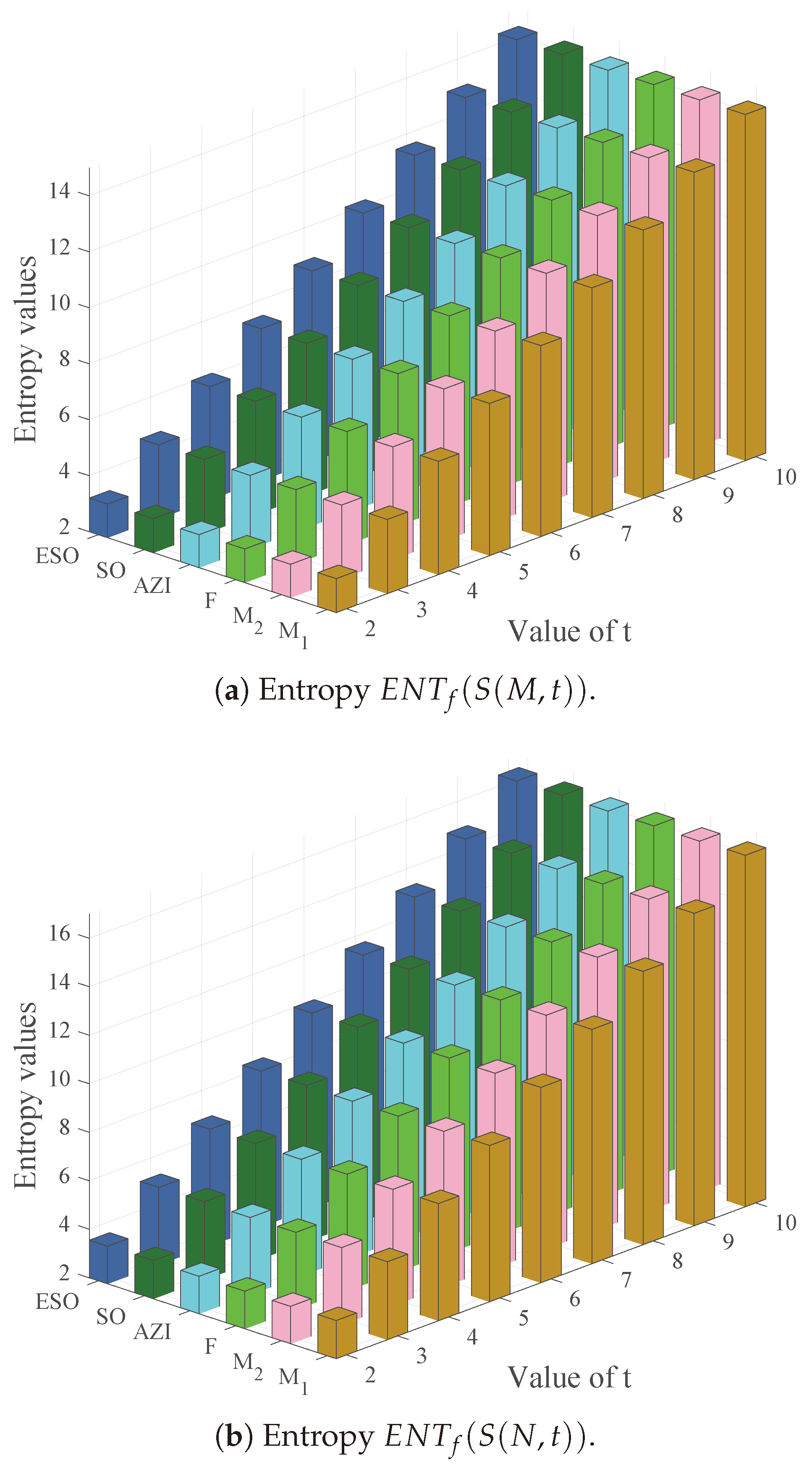
| (2,4) | (3,3) | (3,4) | (4,4) | |
|---|---|---|---|---|
| 4 |
| (2,2) | (2,3) | (2,4) | (3,3) | (3,4) | (4,4) | |
|---|---|---|---|---|---|---|
| f | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3.2136 | 4.6494 | 6.0479 | 7.4372 | 8.8242 | 10.2107 | 11.5971 | 12.9834 | 14.3697 | |
| 3.19 | 4.6288 | 6.0288 | 7.4185 | 8.8057 | 10.1922 | 11.5785 | 12.9648 | 14.3511 | |
| F | 3.2024 | 4.6408 | 6.0404 | 7.43 | 8.8171 | 10.2036 | 11.59 | 12.9763 | 14.3626 |
| 3.1777 | 4.6175 | 6.0177 | 7.4075 | 8.7947 | 10.1812 | 11.5676 | 12.9539 | 14.3402 | |
| 3.2148 | 4.6507 | 6.0492 | 7.4385 | 8.8256 | 10.212 | 11.5984 | 12.9847 | 14.371 | |
| 3.2001 | 4.6384 | 6.038 | 7.4276 | 8.8148 | 10.2013 | 11.5876 | 12.9739 | 14.3602 |
| f | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3.5735 | 5.2149 | 6.8308 | 8.4415 | 10.0512 | 11.6607 | 13.2701 | 14.8795 | 16.489 | |
| 3.5403 | 5.1798 | 6.7957 | 8.4064 | 10.0161 | 11.6256 | 13.2351 | 14.8445 | 16.454 | |
| F | 3.5482 | 5.189 | 6.805 | 8.4157 | 10.0254 | 11.6349 | 13.2443 | 14.8538 | 16.4632 |
| 3.5432 | 5.1829 | 6.7988 | 8.4096 | 10.0193 | 11.6287 | 13.2382 | 14.8476 | 16.4571 | |
| 3.574 | 5.2157 | 6.8316 | 8.4423 | 10.052 | 11.6615 | 13.2709 | 14.8804 | 16.4898 | |
| 3.547 | 5.1874 | 6.8033 | 8.414 | 10.0237 | 11.6332 | 13.2426 | 14.8521 | 16.4615 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.-A.; Si, J.-D.; Liu, J.-B. Entropies and Degree-Based Topological Indices of Generalized Sierpiński Graphs. Fractal Fract. 2025, 9, 190. https://doi.org/10.3390/fractalfract9030190
Xu S-A, Si J-D, Liu J-B. Entropies and Degree-Based Topological Indices of Generalized Sierpiński Graphs. Fractal and Fractional. 2025; 9(3):190. https://doi.org/10.3390/fractalfract9030190
Chicago/Turabian StyleXu, Si-Ao, Jia-Dong Si, and Jia-Bao Liu. 2025. "Entropies and Degree-Based Topological Indices of Generalized Sierpiński Graphs" Fractal and Fractional 9, no. 3: 190. https://doi.org/10.3390/fractalfract9030190
APA StyleXu, S.-A., Si, J.-D., & Liu, J.-B. (2025). Entropies and Degree-Based Topological Indices of Generalized Sierpiński Graphs. Fractal and Fractional, 9(3), 190. https://doi.org/10.3390/fractalfract9030190







