Investigation of Delay-Induced Hopf Bifurcation in a Fractional Neutral-Type Neural Network
Abstract
1. Introduction
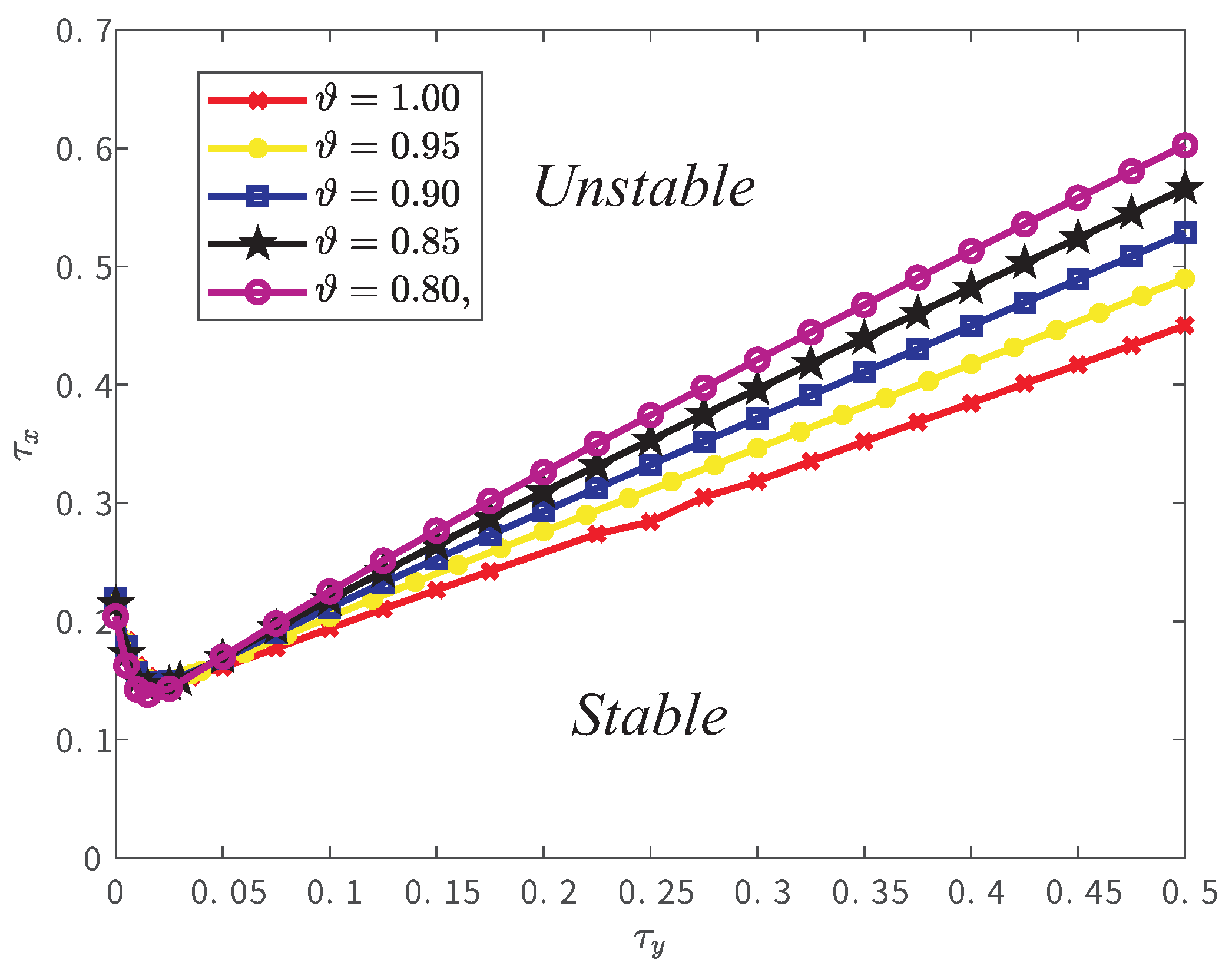
- Our numerical findings indicate that neutral delay and fractional order are the two most sensitive parameters affecting the bifurcation value. Notably, neutral delay can trigger multiple stability switches.
2. Main Results
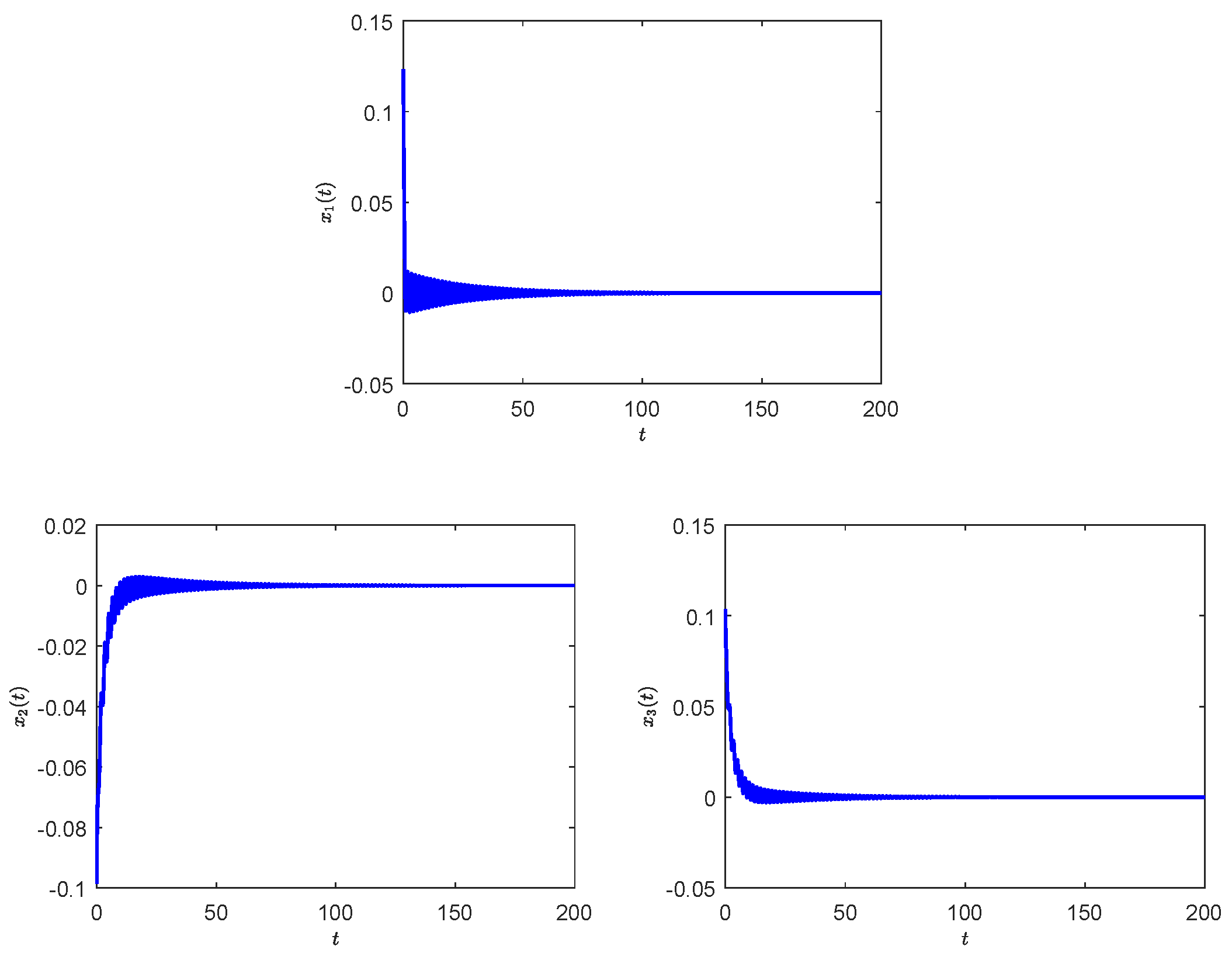
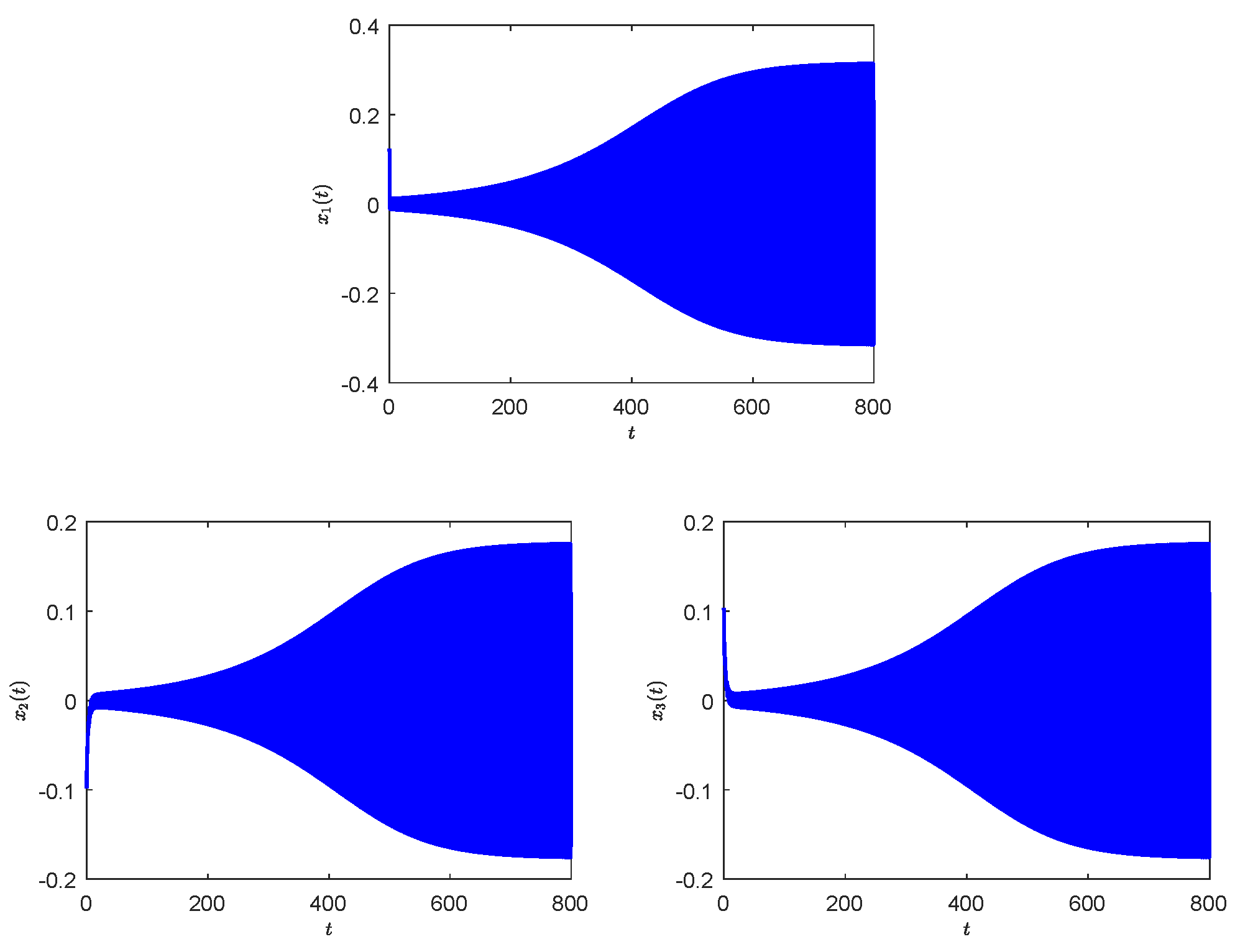
3. Illustrative Example
- Although, in general, the stability of the equilibrium improves as the fractional order decreases, opposite trends can be observed when the neutral delay is small, as shown in Table 1.
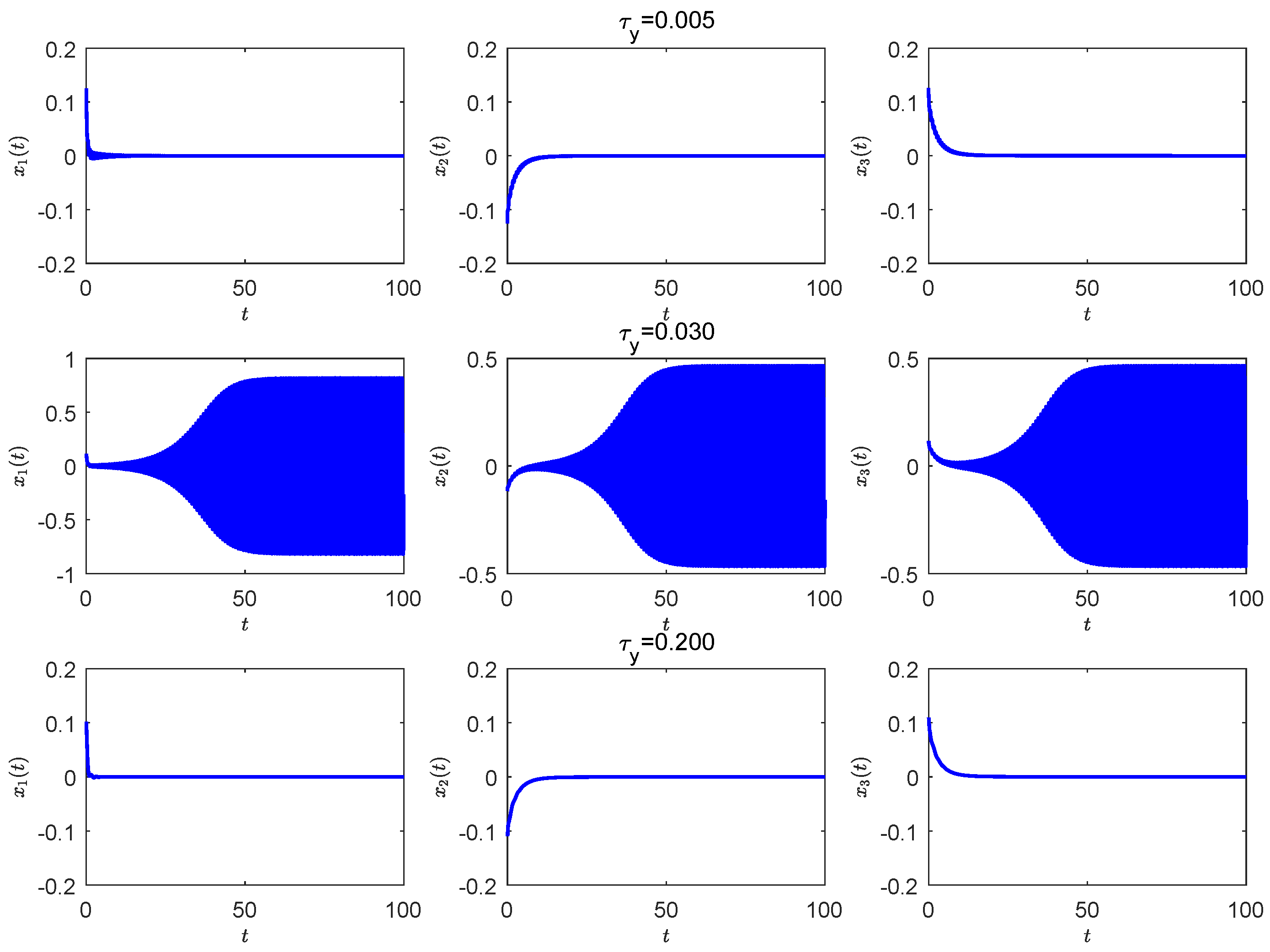
- In contrast to neural networks with only retarded delays, the Hopf bifurcation curve is non-monotonic. This indicates that system (24) with a fixed communication delay can exhibit stability switches and eventually stabilize as the neutral delay increases. We also plotted the time series for , , and , respectively, by fixing , as shown in Figure 4 which is in excellent agreement with our observation.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10. [Google Scholar]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef]
- Marcus, C.M.; Westervelt, R.M. Stability of analog neural networks with delay. Phys. Rev. A 1989, 39, 347. [Google Scholar] [CrossRef]
- Krstic, M. Delay Compensation for Nonlinear, Adaptive, and PDE Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Pahnehkolaei, S.M.A.; Alfi, A.; Machado, J.T. Delay-dependent stability analysis of the QUAD vector field fractional order quaternion-valued memristive uncertain neutral type leaky integrator echo state neural networks. Neural Netw. 2019, 117, 307–327. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.X.; Xiao, M.; Liang, J.L.; Chen, J.; Lin, J.X.; Wang, Z.X.; Cao, J.D. Spatiotemporal Evolution of Large-Scale Bidirectional Associative Memory Neural Networks With Diffusion and Delays. IEEE Trans. Syst. Man. Cybern. Syst. 2023, 54, 1388–1400. [Google Scholar] [CrossRef]
- Wei, J.J.; Ruan, S.G. Stability and bifurcation in a neural network model with two delays. Phys. D 1999, 130, 255–272. [Google Scholar] [CrossRef]
- Gupta, P.D.; Majee, N.; Roy, A. Stability, bifurcation and global existence of a Hopf-bifurcating periodic solution for a class of three-neuron delayed network models. Nonlinear Anal. Theory Methods Appl. 2007, 67, 2934–2954. [Google Scholar] [CrossRef]
- Lien, C.H.; Yu, K.W.; Lin, Y.F.; Chung, Y.J.; Chung, L.Y. Global exponential stability for uncertain delayed neural networks of neutral type with mixed time delays. IEEE Trans. Syst. Man. Cybern. B. 2008, 38, 709–720. [Google Scholar] [CrossRef]
- Song, Q.K.; Zhao, Z.J.; Liu, Y.R.; Alsaadi, F.E. Mean-square input-to-state stability for stochastic complex-valued neural networks with neutral delay. Neurocomputing 2022, 470, 269–277. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, W.B.; Zhou, D.M. Global asymptotic stability to a generalized Cohen–Grossberg BAM neural networks of neutral type delays. Neural Netw. 2012, 25, 94–105. [Google Scholar] [CrossRef]
- Fridman, E. New Lyapunov–Krasovskii functionals for stability of linear retarded and neutral type systems. Syst. Control. Lett. 2001, 43, 309–319. [Google Scholar] [CrossRef]
- Han, Q.L. Robust stability of uncertain delay-differential systems of neutral type. Automatica 2002, 38, 719–723. [Google Scholar] [CrossRef]
- Cheng, C.J.; Liao, T.L.; Yan, J.J.; Hwang, C.C. Globally asymptotic stability of a class of neutral-type neural networks with delays. IEEE Trans. Syst. Man. Cybern. B. 2006, 36, 1191–1195. [Google Scholar] [CrossRef]
- Zhang, H.G.; Liu, Z.W.; Huang, G.B. Novel delay-dependent robust stability analysis for switched neutral-type neural networks with time-varying delays via SC technique. IEEE Trans. Syst. Man. Cybern. B. 2010, 40, 1480–1491. [Google Scholar] [CrossRef]
- Faydasicok, O. New criteria for global stability of neutral-type Cohen–Grossberg neural networks with multiple delays. Neural Netw. 2020, 125, 330–337. [Google Scholar] [CrossRef] [PubMed]
- Arik, S. New criteria for stability of neutral-type neural networks with multiple time delays. IEEE Trans. Neural Networks Learn. Syst. 2019, 31, 1504–1513. [Google Scholar] [CrossRef]
- He, Y.; Liu, G.P.; Rees, D.; Wu, M. Stability analysis for neural networks with time-varying interval delay. IEEE Trans. Neural Netw. 2007, 18, 1850–1854. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; Xia, L.M. Stability and Hopf bifurcation of a reaction–diffusion neutral neuron system with time delay. Int. J. Bifurcat. Chaos 2017, 27, 1750214. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, O.M.; Lee, S.M. LMI optimization approach on stability for delayed neural networks of neutral-type. Appl. Math. Comput. 2008, 196, 236–244. [Google Scholar] [CrossRef]
- Feng, J.E.; Xu, S.Y.; Zou, Y. Delay-dependent stability of neutral type neural networks with distributed delays. Neurocomputing 2009, 72, 2576–2580. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Huang, J.; Gorbachev, S.; Aravind, R.V. Exploration on bifurcation for an incommensurate five-neuron fractional-order BAM neural network involving multiple delays. Phys. D 2024, 460, 134047. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J.; Liao, M.; Li, P.; Qin, Y. Bifurcation investigation and control scheme of fractional neural networks owning multiple delays. Comp. Appl. Math. 2024, 43, 1–33. [Google Scholar] [CrossRef]
- Li, S.; Cao, J.; Liu, H.; Huang, C. Delay-dependent parameters bifurcation in a fractional neural network via geometric methods. Appl. Math. Comput. 2024, 478, 128812. [Google Scholar] [CrossRef]
- Wu, Z.; Cai, Y.; Wang, Z.; Wang, W. Global stability of a fractional order SIS epidemic model. J. Differ. Equations 2023, 352, 221–248. [Google Scholar] [CrossRef]
- Khalighi, M.; Lahti, L.; Ndaïrou, F.; Rashkov, P.; Torres, D.F. Fractional modelling of COVID-19 transmission incorporating asymptomatic and super-spreader individuals. Math. Biosci. 2025, 380, 109373. [Google Scholar] [CrossRef]
- Lundstrom, B.N.; Higgs, M.H.; Spain, W.J.; Fairhall, A.L. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef]
- Anastasio, T.J. The fractional-order dynamics of brainstem vestibulo-oculomotor neurons. Biol. Cybern. 1994, 72, 69–79. [Google Scholar] [CrossRef]
- Pu, Y.F.; Yuan, X.; Yu, B. Analog circuit implementation of fractional-order memristor: Arbitrary-order lattice scaling fracmemristor. IEEE Trans. Circuits Syst. I: Regul. Pap. 2018, 65, 2903–2916. [Google Scholar] [CrossRef]
- Chen, J.J.; Zeng, Z.G.; Jiang, P. Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z. Control of the Bifurcation Behaviors of Delayed Fractional-Order Neural Networks with Cooperation–Competition Topology. Fractal Fract. 2024, 8, 689. [Google Scholar] [CrossRef]
- Ortigueira, M.D. A factory of fractional derivatives. Symmetry 2024, 16, 814. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.D.; Lopes, A.M. How many fractional derivatives are there? Mathematics 2022, 10, 737. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Huang, W.; Song, Q.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Robust stability for a class of fractional-order complex-valued projective neural networks with neutral-type delays and uncertain parameters. Neurocomputing 2021, 450, 399–410. [Google Scholar] [CrossRef]
- Popa, C.A. Neutral-type and mixed delays in fractional-order neural networks: Asymptotic stability analysis. Fractal Fract. 2022, 7, 36. [Google Scholar] [CrossRef]
- Huang, C.D.; Liu, H.; Huang, T.W.; Cao, J.D. Bifurcations Due to Different Neutral Delays in a Fractional-Order Neutral-Type Neural Network. IEEE Trans. Emerg. Top. Comput. 2024, 8, 563–575. [Google Scholar] [CrossRef]
- Kumar, P.; Lee, T.H.; Erturk, V.S. A novel fractional-order neutral-type two-delayed neural network: Stability, bifurcation, and numerical solution. Math. Comput. Simul. 2025, 232, 245–260. [Google Scholar] [CrossRef]
- Li, L.; Yuan, Y. Dynamics in three cells with multiple time delays. Nonlinear Anal. Real World Appl. 2008, 9, 725–746. [Google Scholar] [CrossRef]
- Wang, H.; Huang, C.; Liu, S.; Cao, J.; Liu, H. Bifurcation detection of a neutral-type fractional-order delayed neural network via stability switching curve. Nonlinear Dyn. 2025, 113, 3781–3790. [Google Scholar] [CrossRef]
- Gao, J.; Huang, C.D.; Liu, H. Hopf bifurcations in a fractional-order neural network introducing delays into neutral terms. Eur. Phys. J. Plus. 2024, 139, 1–11. [Google Scholar] [CrossRef]
- Deng, W.H.; Li, C.P.; Lü, J.H. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Pakzad, M.A.; Pakzad, S.; Nekoui, M.A. On the stability of fractional-order systems of neutral type. J. Comput. Nonlinear Dyn. 2015, 10, 051013. [Google Scholar] [CrossRef]
- Tuan, H.T.; Thai, H.D.; Garrappa, R. An analysis of solutions to fractional neutral differential equations with delay. Commun. Nonlinear Sci. Numer. Simul. 2021, 100, 105854. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Huang, C.D.; Yuan, S.L. Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays. Nonlinear Dyn. 2022, 108, 379–396. [Google Scholar] [CrossRef]
- Chen, C.; Min, F.; Cai, J.; Bao, H. Memristor synapse-driven simplified Hopfield neural network: Hidden dynamics, attractor control, and circuit implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 2308–2319. [Google Scholar] [CrossRef]
- Kong, X.; Yu, F.; Yao, W.; Cai, S.; Zhang, J.; Lin, H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Bounoua, M.D.; Yin, C. Hopf bifurcation in Caputo–Hadamard fractional-order differential system. Fractals 2022, 30, 2250015. [Google Scholar] [CrossRef]
| ine | ||||||
|---|---|---|---|---|---|---|
| ine | 0.2195 | 0.2206 | 0.2197 | 0.2147 | 0.2042 | |
| 0.1497 | 0.1501 | 0.1491 | 0.1467 | 0.1431 | ||
| 0.1610 | 0.1654 | 0.1681 | 0.1696 | 0.1701 | ||
| 0.1773 | 0.1845 | 0.1900 | 0.1944 | 0.1982 | ||
| 0.1940 | 0.2036 | 0.2115 | 0.2185 | 0.2252 | ||
| 0.2104 | 0.2222 | 0.2324 | 0.2419 | 0.2513 | ||
| 0.2265 | 0.2403 | 0.2529 | 0.2648 | 0.2767 | ||
| 0.2424 | 0.2583 | 0.2730 | 0.2873 | 0.3017 | ||
| 0.2484 | 0.2760 | 0.2929 | 0.3094 | 0.3261 | ||
| 0.2738 | 0.2936 | 0.3126 | 0.3314 | 0.3503 | ||
| 0.2841 | 0.3112 | 0.3323 | 0.3532 | 0.3742 | ||
| 0.3050 | 0.3287 | 0.3519 | 0.3749 | 0.3977 | ||
| 0.3185 | 0.3463 | 0.3715 | 0.3964 | 0.4212 | ||
| 0.3354 | 0.3640 | 0.3910 | 0.4179 | 0.4444 | ||
| 0.3520 | 0.3817 | 0.4107 | 0.4393 | 0.4675 | ||
| 0.3685 | 0.4000 | 0.4303 | 0.4606 | 0.4904 | ||
| 0.3844 | 0.4174 | 0.4499 | 0.4818 | 0.5131 | ||
| 0.4011 | 0.4354 | 0.4695 | 0.5030 | 0.5357 | ||
| 0.4170 | 0.4535 | 0.4892 | 0.5241 | 0.5581 | ||
| 0.4334 | 0.4716 | 0.5088 | 0.5451 | 0.5804 | ||
| 0.4502 | 0.4898 | 0.5284 | 0.5660 | 0.6025 | ||
| Parameters | for | Parameters | for |
|---|---|---|---|
| −1.1851 | 0.5117 | ||
| 0.0541 | 0.0097 | ||
| 0.0400 | −0.0428 | ||
| 0.0400 | −0.0428 | ||
| 0.0043 | −0.0872 | ||
| 0.1166 | −0.1726 | ||
| 0.1803 | −0.4168 | ||
| −0.0043 | −0.0872 | ||
| 0.1803 | −0.4168 | ||
| 0.1166 | −0.1726 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Song, X.; Huang, C. Investigation of Delay-Induced Hopf Bifurcation in a Fractional Neutral-Type Neural Network. Fractal Fract. 2025, 9, 189. https://doi.org/10.3390/fractalfract9030189
Li S, Song X, Huang C. Investigation of Delay-Induced Hopf Bifurcation in a Fractional Neutral-Type Neural Network. Fractal and Fractional. 2025; 9(3):189. https://doi.org/10.3390/fractalfract9030189
Chicago/Turabian StyleLi, Shuai, Xinyu Song, and Chengdai Huang. 2025. "Investigation of Delay-Induced Hopf Bifurcation in a Fractional Neutral-Type Neural Network" Fractal and Fractional 9, no. 3: 189. https://doi.org/10.3390/fractalfract9030189
APA StyleLi, S., Song, X., & Huang, C. (2025). Investigation of Delay-Induced Hopf Bifurcation in a Fractional Neutral-Type Neural Network. Fractal and Fractional, 9(3), 189. https://doi.org/10.3390/fractalfract9030189






