Abstract
The purpose of this paper is to propose a fractal–fractional-order for computer virus propagation dynamics, in accordance with the Atangana–Baleanu operator. We examine the existence of solutions, as well as the Hyers–Ulam stability, uniqueness, non-negativity, positivity, and boundedness based on the fractal–fractional sense. Hyers–Ulam stability is significant because it ensures that small deviations in the initial conditions of the system do not lead to large deviations in the solution. This implies that the proposed model is robust and reliable for predicting the behavior of virus propagation. By establishing this type of stability, we can confidently apply the model to real-world scenarios where exact initial conditions are often difficult to determine. Based on the equivalent integral of the model, a qualitative analysis is conducted by means of an iterative convergence sequence using fixed-point analysis. We then apply a numerical scheme to a case study that will allow the fractal–fractional model to be numerically described. Both analytical and simulation results appear to be in agreement. The numerical scheme not only validates the theoretical findings, but also provides a practical framework for predicting virus spread in digital networks. This approach enables researchers to assess the impact of different parameters on virus dynamics, offering insights into effective control strategies. Consequently, the model can be adapted to real-world scenarios, helping improve cybersecurity measures and mitigate the risks associated with computer virus outbreaks.
1. Introduction
In this study, the dynamics of computer virus propagation are examined within complex interconnected digital networks. The method utilizes advanced mathematical tools, such as fractal–fractional calculus and the Atangana–Baleanu derivative. Viruses, as they are discussed in this study, are malicious programs that are designed to replicate and spread across networked environments. By exploiting vulnerabilities, they disrupt operations, steal sensitive data, or damage systems. There are a number of factors that contribute to the propagation of these viruses, including the topology of the network, the degree of connectivity between nodes, and the inherent memory effects that are observed in digital systems. Memory effects play a crucial role in the propagation of computer viruses, as they influence how quickly and effectively a virus can spread through a network. These effects can cause certain nodes to retain information about past infections, potentially making them more susceptible to future attacks. Understanding these memory dynamics allows researchers to develop more effective strategies for predicting and controlling virus outbreaks within digital environments.
Fractional calculus has gained significant attention for its applications in engineering [], plant epidemiology [], mathematical biology [], medicine [], and psychological and life sciences []. Several types of fractional derivatives are used in this field, including the Riemann–Liouville, Caputo, Caputo–Fabrizio, and Atangana–Baleanu operators. These have applications in physics [,,,,,,,,], viscoelasticity [], electromagnetic wave propagation [], quantum dynamics [], Langevin systems [], diabetes [,,,,,,,,,,], pneumonia [,], engineering [], tobacco smoking [], COVID-19 [], influenza [], infectious diseases [], epidemics [], cancer [], coronavirus [], monkeypox [], zoonotic viral infections [], and alcohol-related models []. There are numerous interdisciplinary systems that can be adequately represented by fractional differential equations. In the field of fractional derivatives, one of the most highly regarded derivatives is the Atangana–Baleanu derivative. This derivative has gained popularity due to its non-local and non-singular kernel, providing a more realistic representation of dynamic processes in biological systems. Fractal–fractional models represent complex, real-world phenomena. As a result, FF models offer better predictive capabilities and insights into system dynamics. By studying these models, we can identify infection mechanisms and develop better treatments. By bridging the gap between fractional modeling and computer virus dynamics, this work advances the mathematical understanding of such diseases. It provides a foundation for future studies. The proposed model not only highlights the importance of integrating memory effects and spatial heterogeneity, but also underscores the potential of fractal–fractional approaches to inform effective public health interventions in regions with significant human–wildlife interactions [,]. Despite the growing body of literature on fractional calculus in biological modeling, the integration of Atangana–Baleanu fractal–fractional derivatives in computer virus transmission remains underexplored, particularly in the context of wildlife–people interactions. Existing studies have demonstrated the utility of fractional models for general epidemiological applications []. However, few have addressed the combined roles of fractal geometry and memory effects in zoonotic contexts. This gap is especially critical in regions like Al-Baha, where human–wildlife interactions create complex transmission dynamics.
In this study, a novel fractal–fractional model is developed to capture the intricate dynamics of virus spread. There is a combination of memory effects, which reflect the lingering effects of previous infections, as well as fractal geometry, which illustrates the complex and recursive nature of digital networks. Among the key objectives are gaining an understanding of the virus transmission mathematical behavior, validation of the model through numerical simulations, and the identification of effective mitigation measures. It examines interventions such as the deployment of antivirus measures at high-degree network hubs where viruses spread rapidly, for instance. Fractal–fractional calculus is used in this paper to provide insights into viral behavior from both a theoretical and practical perspective. Moreover, it contributes to the development of robust control strategies. It is apparent from these findings that advanced mathematical frameworks can be effectively applied for enhancing cybersecurity and safeguarding interconnected digital infrastructure against evolving threats.
This study aims to develop a comprehensive fractal–fractional model based on the Atangana–Baleanu derivative to analyze and understand computer virus propagation dynamics in complex networks. Through the integration of memory effects and fractal geometry, the goal of this research is to develop a mathematical model that incorporates fractal–fractional derivatives to capture virus dynamics in networked environments. It aims to establish an analytical framework for ensuring the existence and uniqueness of solutions using fixed-point theory and to conduct stability analyses to ensure robustness. The model will be validated by numerical simulations and the virus spread will be investigated across various topologies of networks. Furthermore, the study explores targeted interventions, such as the deployment of antivirus strategies at high-degree hubs, in an effort to mitigate virus transmission. Finally, the study emphasizes the potential of fractal–fractional calculus for optimizing control strategies for interconnected digital systems by providing examples of its application in the real world.
The remainder of this paper is structured as follows: Section 2 introduces the fractal–fractional computer virus propagation model based on the Atangana–Baleanu derivative, detailing the compartments, governing equations, and incorporation of memory effects and fractal geometry. Section 3 establishes the boundedness and non-negativity of the model solution, while Section 4 investigates the existence and uniqueness of solutions using fixed-point theory. Section 5 investigates Hyers–Ulam stability. Atangana–Baleanu is used to implement the numerical model in Section 7, followed by a numerical simulation in Section 8, which illustrates propagation dynamics. Section 9 discusses the implications of the findings for real-world virus mitigation strategies, and Section 10 concludes the paper by summarizing the key findings and suggesting directions for future research.
2. Preliminar Definitions
Definition 1
([,]). Consider the fractal differentiable on
of order
for
. The following is a fractal–fractional derivative operator for
in the Atangana–Baleanu setting:
where,
, and
.
Definition 2
([,]). The fractal–fractional integration operator are provided by
3. Model Formulation
According to the following model, a computer virus spreads within a population of computers under the protection of antivirus mechanisms. This model assumes no time-delay effects and divides the computer population into four compartments: susceptible (), latently infected (), breaking-out (), and antivirus-capable () computers. The model accounts for the virus’s transmission, progression, and mitigation. The governing system of nonlinear differential equations is []:
The fractional extension of this system incorporates memory effects and long-term influence on the computer population dynamics.
For the computer virus model (1), we use fractal–fractional differential and integral operators:
The authors remodeled the computer virus system using the fractal–fractional approach in the sense of the Atangana–Baleanu derivative to incorporate memory effects and non-local behavior, which are crucial for accurately modeling virus propagation in digital networks. Unlike classical integer-order models, which assume instantaneous interactions, the Atangana–Baleanu derivative accounts for the lingering effects of past infections, making the model more realistic. This approach improves our understanding of virus transmission dynamics and allows for better prediction and control strategies, as confirmed by theoretical stability analysis and numerical simulations.
4. Boundedness and Non-Negativity of the Solution
Following similar approaches as those in [], we state the following theorem:
Theorem 1.
For model (2), the solutions that start in
are uniformly bounded.
Proof.
Let
. Then, we have:
Adding a damping term
to ensure positivity:
For all
, choose
to ensure positivity. Thus:
Using the Laplace transform, we find:
Hence, the solutions starting in
are uniformly bounded in the region:
□
We now check the non-negativity of the model:
Thus, the solutions remain in
, ensuring that
is the biologically feasible region.
5. Existence and Uniqueness
In this section, the existence criterion is ensured by fixed-point theory. Here, for the qualitative analysis, we define the Banach space
, where
under the norm
for which
. We rewrite the right-hand side of the fractal–fractional SLBR model (2) as
As the integral is differentiable, we write the fractal–fractional SLBR model (2) in the following form:
Thus, the developed system is illustrated using the following IVP
where
, and
, and
To transform thiss into a fixed-point problem, we define
by
must satisfy these Lipschitz and growth conditions. Denote
Theorem 2.
For each
, ∃ a constant
satisfies
where
Proof.
For each
, one obtains
Therefore,
satisfies the Lipschitz condition. □
: Let us assume that
, and
are bounded and satisfy
,
,
,
.
Theorem 3.
Let (H1) hold. Then, the given fractal–fractional model (2) has a unique solution if
So, it has a unique solution.
Proof.
For
in
, we obtain
Because of this,
is a contraction and there is only one solution to the model. □
6. Hyers–Ulam Stability
The use of Hyers–Ulam stability was motivated by the work in [,].
Definition 3.
Model (2) is Hyers–Ulam stable, if and only if, a constant
,
fulfilling for any
,
exists,
there is an approximation
that satisfies the given model, so that
satisfies
Theorem 4.
Model (2) is Hyers–Ulam stable.
Proof.
Let us say the approximate solution to model (2) is
,
Let
,
. Then,
Next,
Let
,
. Then
Also
Let
,
. Then
Also
Let
,
. Then
Thus, the result follows. □
For system (2), Hyers–Ulam stability and Lyapunov stability describe different aspects of the system behavior:
- •
- Hyers–Ulam stability ensures that if the system is subject to small deviations from an approximate solution, there exists a true solution nearby. In other words, small perturbations in the initial conditions do not lead to large deviations in the overall system trajectory, making the model robust to minor errors.
- •
- Lyapunov stability, on the other hand, guarantees that solutions that start close to an equilibrium point remain close over time. It is more focused on maintaining system stability around equilibrium states rather than ensuring proximity to approximate solutions.
Simply put, Hyers–Ulam stability ensures that solutions do not drift too far from a nearby approximate solution, whereas Lyapunov stability ensures that solutions remain close to a given equilibrium over time.
7. Numerical Scheme
Following [], the Antangana–Baleanu integral gives us
Replacing
by
, we have
The application of the two-step Lagrange polynomial yields
By using the Lagrange polynomial to solve the given problem, we obtain
Now, solving the integral we obtain
Now, replacing the value of
, we obtain
Therefore, the above system’s numerical scheme is
8. Numerical Simulation
In the model, the parameters are calibrated to represent different infection scenarios, such as virus-free steady states or virus-persistent steady states. In order to model these scenarios, we used the parameter values presented in Table 1.

Table 1.
Parameter values for the computer virus model [].
Several important insights can be gained from the figures in this study concerning the dynamics of computer virus propagation and the impact of fractional orders in fractal–fractional systems. Figure 1 illustrates the approximate numerical solutions for the compartmental variables
(susceptible),
(latently infected),
(breaking-out), and
(antivirus-capable) under varying fractional orders () using the Atangana–Baleanu operator. These plots reveal how fractional-order parameters influence the evolution of each compartment, demonstrating, for instance, that higher fractional orders () correspond to more pronounced changes in the dynamics, while lower orders () exhibit slower transitions, capturing memory effects inherent in the system. Figure 2 provides time-series simulations of the same compartments, emphasizing the interplay between fractional orders and temporal behavior. As viruses spread, susceptible populations decrease, while latently infected and breaking-out populations rise before stabilizing. The antivirus-capable population grows steadily, reflecting effective mitigation strategies. In combination, these figures demonstrate the importance of fractional calculus in capturing the long-term, anomalous diffusion patterns of computer viruses in complex networks, offering practical insights for targeted interventions.
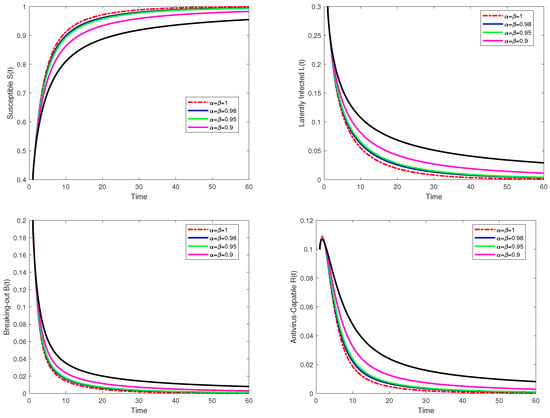
Figure 1.
An approximate numerical solution for
,
,
, and
is obtained using the fractal–fractional method in the sense of Atangana–Baleanu operators for different values, namely
, ,
,
,
,
,
. The parameter values used for these computations are given in Table 1.
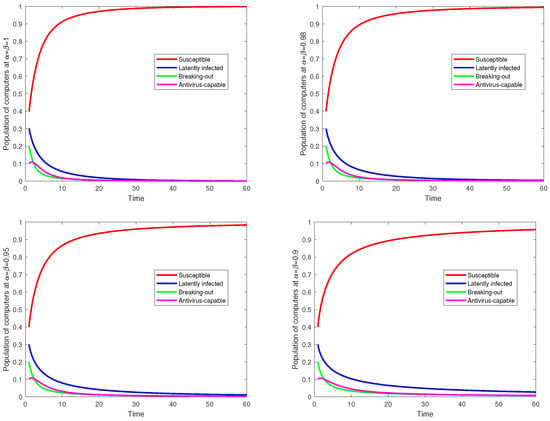
Figure 2.
Time series of
,
,
, and
using fractal–fractional methods using Atangana–Baleanu operators for different values of
,
,
.
9. Discussion
By using a fractal–fractional model, significant advances can be made in the understanding and control of virus propagation in complex networks. Using the Atangana–Baleanu derivative, the model incorporates memory effects that reflect the behavior of real-world digital systems in which past interactions have a significant influence on present states. The results of numerical simulations indicate that targeted interventions, such as the deployment of antivirus software in hubs or the isolation of high-risk nodes, can effectively mitigate the spread of viruses. As a result of the findings, it is clear that resources should be allocated first to regions that are densely connected, while baseline defenses should be maintained in areas that are sparsely connected. Moreover, the model’s ability to simulate anomalous diffusion and delayed responses provides a realistic representation of virus dynamics, thereby separating it from classical approaches. Incorporating a fractal–fractional calculus establishes a robust framework for future studies of networked systems, which extends beyond computer viruses to biological and ecological systems as well.
The numerical simulation results provide valuable insights into the effectiveness of the proposed fractal–fractional model in mitigating computer virus propagation. The application of the Atangana–Baleanu derivative allows for the incorporation of memory effects and non-local behavior, offering a more realistic representation of virus dynamics in digital networks. The analysis of Figure 1, which presents the approximate numerical solutions of the susceptible, latently infected, breaking-out, and antivirus-capable compartments, demonstrates the influence of fractional orders on virus transmission. It is observed that higher fractional orders (
) lead to more rapid changes in population dynamics, whereas lower fractional orders () introduce memory effects that slow the progression of the infection. This suggests that fractional models more accurately capture the persistent nature of virus outbreaks in interconnected networks. Figure 2 provides a comparative time-series analysis of the different compartments, illustrating the impact of antivirus interventions. The results indicate that as viruses spread, the susceptible population decreases while the latently infected and breaking-out populations initially rise before stabilizing. Notably, the antivirus-capable population grows steadily, signifying the effectiveness of mitigation measures. A key takeaway from these simulations is that targeted intervention strategies, such as deploying antivirus software at high-degree network hubs or isolating highly infected nodes, effectively reduce the spread of viruses. The simulations validate the theoretical stability analysis, confirming that the model remains bounded and maintains non-negativity in all compartments. Furthermore, the persistence of virus spread in the absence of control measures reinforces the necessity of proactive cybersecurity strategies. The model also demonstrates the influence of key parameters on virus dynamics. A comparative analysis of the virus-free steady state (VFSS) and virus-persistent steady state (VPSS) scenarios reveals that an increase in the transmission rate () significantly prolongs virus persistence, whereas higher recovery rates () and lower latency periods () accelerate virus containment. These findings support the model’s practical relevance in informing cybersecurity policies and optimizing response strategies against digital virus outbreaks.
10. Conclusions
This study presents a novel fractal–fractional model for analyzing and mitigating computer virus propagation in complex networks using the Atangana–Baleanu derivative. By incorporating memory effects and fractal network structures, the model provides an advanced representation of virus dynamics, surpassing classical integer-order models. Theoretical analyses confirm the existence, uniqueness, and Hyers–Ulam stability of the model, ensuring robustness in predicting the virus behavior. Numerical simulations further validate the model by illustrating the impact of fractional-order parameters and intervention strategies on virus spread. The results indicate that the proposed model effectively mitigates virus propagation by enabling targeted interventions, such as prioritizing antivirus deployment in high-risk network regions. Key findings include the observation that lower fractional orders capture long-term memory effects, leading to slower but more persistent infection patterns. Additionally, parameter sensitivity analysis highlights the role of transmission rates, latency periods, and recovery rates in controlling virus dynamics. These insights emphasize the necessity of timely and adaptive cybersecurity strategies to prevent large-scale digital infections. In conclusion, this fractal–fractional approach offers a comprehensive framework for understanding virus propagation in digital environments. Future research could extend the model by incorporating stochastic perturbations, time-delay effects, and adaptive network structures to further enhance its applicability in real-world cybersecurity scenarios.
Author Contributions
M.A. and S.S. contributed equally to this study. M.A. was primarily responsible for conceptualizing the research and developing the mathematical model, focusing on the integration of fractal–fractional calculus and the Atangana–Baleanu derivative. He also supervised the analytical and theoretical validation of the results. S.S. conducted the numerical simulations, performed the stability analysis, and prepared the sections on Hyers–Ulam stability and numerical methods. He managed correspondence with the journal and ensured the manuscript’s scientific accuracy and coherence. Both authors collaborated in drafting, reviewing, and finalizing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research, Development, and Innovation Authority (RDIA)—Kingdom of Saudi Arabia—with grant number 12803-baha-2023-BUR-3-1-EI.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This article is derived from a research grant funded by the Research, Development, 267 and Innovation Authority (RDIA)-Kingdom of Saudi Arabia-with grant number 12803-268 baha-2023-BU-R-3-1-EI.
Conflicts of Interest
Please add the corresponding content of this part.
References
- Arena, P.; Caponetto, R.; Fortuna, L.; Porto, D. Nonlinear Noninteger Order Circuits and Systems; World Scientific: Singapore, 2000. [Google Scholar]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Ravichandran, C. A review of fractional-order models for plant epidemiology. Prog. Fract. Differ. Appl. 2024, 10, 489–521. [Google Scholar]
- Ahmed, E.; Elgazzar, A.S. On fractional order differential equations model for nonlocal epidemics. Physica A 2007, 379, 607–614. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, Y.; Cao, J.; Abdel-Aty, M. Dynamics and backward bifurcations of SEI tuberculosis models in homogeneous and heterogeneous populations. J. Math. Anal. Appl. 2025, 543, 128924. [Google Scholar] [CrossRef]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Ravichandran, C. A review of fractional order epidemic models for life sciences problems: Past, present and future. Alex. Eng. J. 2024, 95, 283–305. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Saber, S. Control of chaos in the Burke-Shaw system of fractal-fractional order in the sense of Caputo-Fabrizio. J. Appl. Math. Comput. Mech. 2024, 23, 83–96. [Google Scholar] [CrossRef]
- Yan, T.; Alhazmi, M.; Youssif, M.Y.; Elhag, A.E.; Aljohani, A.F.; Saber, S. Analysis of a Lorenz Model Using Adomian Decomposition and Fractal-Fractional Operators. Thermal Sci. 2024, 8, 5001–5009. [Google Scholar] [CrossRef]
- Alsulami, A.; Alharb, R.A.; Albogami, T.M.; Eljaneid, N.H.; Adam, H.D.; Saber, S. Controlled chaos of a fractal–fractional Newton-Leipnik system. Thermal Sci. 2024, 28, 5153–5160. [Google Scholar] [CrossRef]
- Alhazmi, M.; Dawalbait, F.M.; Aljohani, A.; Taha, K.O.; Adam, H.D.; Saber, S. Numerical approximation method and Chaos for a chaotic system in sense of Caputo-Fabrizio operator. Thermal Sci. 2024, 28, 5161–5168. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Existence of chaos and the approximate solution of the Lorenz–Lü–Chen system with the Caputo fractional operator. AIP Adv. 2024, 14, 015112. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. On chaos control of nonlinear fractional Newton-Leipnik system via fractional Caputo-Fabrizio derivatives. Sci. Rep. 2023, 13, 22726. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Chaos control and numerical solution of time-varying fractional Newton-Leipnik system using fractional Atangana-Baleanu derivatives. AIMS Math. 2023, 8, 25863–25887. [Google Scholar] [CrossRef]
- Ahmed, K.I.; Adam, H.D.; Almutairi, N.; Saber, S. Analytical solutions for a class of variable-order fractional Liu system under time-dependent variable coefficients. Results Phys. 2024, 56, 107311. [Google Scholar] [CrossRef]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Heaviside, O. Electromagnetic Theory; Chelsea: New York, NY, USA, 1971. [Google Scholar]
- Kusnezov, D.; Bulgac, A.; Dang, G.D. Quantum Levy processes and fractional kinetics. Phys. Rev. Lett. 1999, 82, 1136. [Google Scholar] [CrossRef]
- Hammad, H.A.; Qasymeh, M.; Abdel-Aty, M. Existence and stability results for a Langevin system with Caputo–Hadamard fractional operators. Int. J. Geom. Methods Mod. Phys. 2024, 21, 2450218. [Google Scholar] [CrossRef]
- Tornheim, K. Are metabolic oscillations responsible for normal oscillatory insulin secretion? Diabetes 1997, 46, 1375–1380. [Google Scholar] [CrossRef]
- Derouich, M.; Boutayeb, A. The effect of physical exercise on the dynamics of glucose and insulin. J. Biomech. 2002, 35, 911–917. [Google Scholar] [CrossRef]
- Dalla Man, C.; Caumo, A.; Basu, R.; Rizza, R.; Toffolo, G.; Cobelli, C. Minimal model estimation of glucose absorption and insulin sensitivity from oral test: Validation with a tracer method. Am. J. Physiol.-Endocrinol. Metab. 2004, 287, E637–E643. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; DeGaetano, A.; Arino, O. Modeling the Intravenous Glucose Tolerance Test: A Global Study for a Single-Distributed-Delay Model. Discret. Contin. Dyn. Syst. Ser. B 2004, 4, 407–418. [Google Scholar]
- Saber, S.; Bashier, E.B.M.; Alzahrani, S.M.; Noaman, I.A. A Mathematical Model of Glucose-Insulin Interaction with Time Delay. J. Appl. Comput. Math. 2018, 7, 416. [Google Scholar]
- Alshehri, M.H.; Duraihem, F.Z.; Alalyani, A.; Saber, S. A Caputo (discretization) fractional-order model of glucose-insulin interaction: Numerical solution and comparisons with experimental data. J. Taibah Univ. Sci. 2021, 15, 26–36. [Google Scholar] [CrossRef]
- Saber, S.; Alalyani, A. Stability analysis and numerical simulations of IVGTT glucose-insulin interaction models with two time delays. Math. Model. Anal. 2022, 27, 383–407. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Saber, S.; Duraihem, F.Z. Dynamical analysis of fractional-order of IVGTT glucose–insulin interaction. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 1123–1140. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Saber, S. Different strategies for diabetes by mathematical modeling: Applications of fractal-fractional derivatives in the sense of Atangana-Baleanu. Results Phys. 2023, 26, 106892. [Google Scholar] [CrossRef]
- Ahmed, K.I.; Adam, H.D.; Youssif, M.Y.; Saber, S. Different strategies for diabetes by mathematical modeling: Modified Minimal Model. Alex. Eng. J. 2023, 80, 74–87. [Google Scholar] [CrossRef]
- Ahmed, K.I.; Mirgani, S.M.; Seadawy, A.; Saber, S. A comprehensive investigation of fractional glucose-insulin dynamics: Existence, stability, and numerical comparisons using residual power series and generalized Runge-Kutta methods. J. Taibah Univ. Sci. 2025, 19, 2460280. [Google Scholar] [CrossRef]
- Saber, S.; Alghamdi, A.M.; Ahmed, G.A.; Alshehri, K.M. Mathematical Modelling and optimal control of pneumonia disease in sheep and goats in Al-Baha region with cost-effective strategies. AIMS Math. 2022, 7, 12011–12049. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S.; Ahmad, H. The fractal-fractional Atangana-Baleanu operator for pneumonia disease: Stability, statistical and numerical analyses. AIMS Math. 2023, 8, 29382–29410. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex systems. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Shah, A.; Etemad, S.; Rezapour, S.; Park, C. A study on the fractal-fractional tobacco smoking model. AIMS Math. 2022, 7, 13887–13909. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Tunç, O.; Kaabar, M.K.A. A fractal–fractional COVID-19 model with a negative impact of quarantine on diabetic patients. Results Control Optim. 2023, 10, 100199. [Google Scholar] [CrossRef]
- Evirgen, F.; Uçar, E.; Uçar, S.; Özdemir, N. Modelling Influenza A disease dynamics under Caputo-Fabrizio fractional derivative with distinct contact rates. Math. Model. Numer. Simul. Appl. 2023, 3, 58–73. [Google Scholar] [CrossRef]
- Özdemir, N.; Uçar, E.; Avcı, D. Dynamic analysis of a fractional SVIR system modeling an infectious disease. Facta Univ. Ser. Math. Inform. 2022, 37, 605–619. [Google Scholar] [CrossRef]
- Olumide, O.O.; Othman, W.A.M.; Özdemir, N. Efficient solution of fractional-order SIR epidemic model of childhood diseases with optimal homotopy asymptotic method. IEEE Access 2022, 10, 9395–9405. [Google Scholar] [CrossRef]
- Özdemir, N.; Uçar, E. Investigating an immune system-cancer mathematical model with Mittag-Leffler kernel. AIMS Math. 2020, 5, 1519–1531. [Google Scholar] [CrossRef]
- Li, X.P.; Ullah, S.; Zahir, H.; Alshehri, A.; Riaz, M.B.; Al Alwan, B. Modeling the dynamics of coronavirus with super-spreader class: A fractal-fractional approach. Results Phys. 2022, 34, 105179. [Google Scholar] [CrossRef]
- Alzubaidi, A.M.; Othman, H.A.; Ullah, S.; Ahmad, N.; Alam, M.M. Analysis of Monkeypox viral infection with human-to-animal transmission via fractional and fractal-fractional operators with power law kernel. Math. Biosci. Eng. 2023, 20, 6666–6690. [Google Scholar] [CrossRef]
- Li, S.; Ullah, S.; Samreen; Khan, I.U.; Al Qahtani, S.A.; Riaz, M.B. A robust computational study for assessing the dynamics and control of emerging zoonotic viral infection with a case study: A novel epidemic modeling approach. AIP Adv. 2024, 14, 015051. [Google Scholar] [CrossRef]
- Li, S.; Samreen; Ullah, S.; Riaz, M.B.; Awwad, F.A.; Teklu, S.W. Global dynamics and computational modeling approach for analyzing and controlling alcohol addiction using a novel fractional and fractal–fractional modeling approach. Sci. Rep. 2024, 14, 5065. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A. On chaos and synchronization in fractional-order chaotic systems: A biological network perspective. J. Biol. Syst. 2019, 27, 633–647. [Google Scholar]
- Atangana, A.; Akgul, A. Analysis of fractal fractional differential equations. Alex. Eng. J. 2020, 59, 1117–1134. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Akgul, A. A fractional model for disease transmission in wildlife. J. Comput. Phys. 2020, 45, 230–240. [Google Scholar]
- Abro, K.A.; Atangana, A. A comparative study of convective fluid motion in rotating cavity via Atangana–Baleanu and Caputo–Fabrizio fractal–fractional differentiations. Eur. Phys. J. Plus 2020, 135, 226. [Google Scholar] [CrossRef]
- Raza, A.; Fatima, U.; Rafiq, M.; Ahmed, N.; Khan, I.; Nisar, K.S.; Iqbal, Z. Mathematical analysis and design of the nonstandard computational method for an epidemic model of computer virus with delay Effect: Application of mathematical biology in computer science. Results Phys. 2021, 21, 103750. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Hu, C.; Jiang, Y.; Teng, Z. Dynamical Analysis of a Fractional-Order Predator-Prey Model Incorporating a Prey Refuge. J. Appl. Math. Comput. 2016, 54, 435–449. [Google Scholar] [CrossRef]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publ.: New York, NY, USA, 1960. [Google Scholar]
- Ulam, S.M. Problems in Modern Mathematics; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic: Cambridge, UK, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).