Abstract
This paper introduces a novel framework for modeling nonlocal fractional system with a p-Laplacian operator under power nonlocal fractional derivatives (PFDs), a generalization encompassing established derivatives like Caputo–Fabrizio, Atangana–Baleanu, weighted Atangana–Baleanu, and weighted Hattaf. The core methodology involves employing a PFD with a tunable power parameter within a non-singular kernel, enabling a nuanced representation of memory effects not achievable with traditional fixed-kernel derivatives. This flexible framework is analyzed using fixed-point theory, rigorously establishing the existence and uniqueness of solutions for four symmetric cases under specific conditions. Furthermore, we demonstrate the Hyers–Ulam stability, confirming the robustness of these solutions against small perturbations. The versatility and generalizability of this framework is underscored by its application to an epidemiological model of transmission of Hepatitis B Virus (HBV) and numerical simulations for all four symmetric cases. This study presents findings in both theoretical and applied aspects of fractional calculus, introducing an alternative framework for modeling complex systems with memory processes, offering opportunities for more sophisticated and accurate models and new avenues for research in fractional calculus and its applications.
1. Introduction
The study of dynamical systems is fundamental to understanding a wide array of phenomena across diverse fields of science and engineering. These systems, characterized by their evolving states, are often modeled using differential Equations [1,2,3,4]. While traditional integer-order differential equations have served as the cornerstone for many of these models, they can sometimes fall short when dealing with complex phenomena that exhibit memory effects and nonlocal interactions. In recent years, it has become increasingly evident that many real-world processes do not adhere to the assumptions underpinning classical integer-order models. Instead, their past trajectories influence their present states, leading to what is known as nonlocal behavior. To address this limitation, fractional calculus has emerged as a powerful mathematical tool. By extending the concept of differentiation and integration to non-integer orders, fractional derivatives offer a more versatile way to capture the memory and nonlocal characteristics inherent in many complex systems [5,6]. These advancements have driven extensive research toward the development of rigorous mathematical frameworks for fractional differential equations, particularly focusing on the existence and uniqueness conditions of their solutions, as well as the analysis of complex operators [7,8,9,10,11].
Among the more intriguing areas of research in this domain is the study of hybrid fractional differential equations. These equations are of particular importance since they integrate different types of fractional derivatives and operators, leading to richer and more accurate representations of complex systems [12,13,14]. A notable operator that often appears in hybrid fractional differential equations is the p-Laplacian operator. With applications in non-Newtonian fluid mechanics, image processing, and porous media flow, the inclusion of the p-Laplacian operator adds a layer of complexity and practical relevance [15,16,17]. However, the combination of a p-Laplacian operator with recent advancements in fractional calculus, such as PFD, still remains largely unexplored in the literature.
A novel class of nonlocal fractional derivatives, known as power fractional derivative (PFD), has recently been introduced based on the generalized power Mittag–Leffler (PML) function [18]. This operator generalizes existing derivatives, including Caputo–Fabrizio [19], Atangana–Baleanu [20], weighted Atangana–Baleanu [21], and Hattaf derivatives [22]. The key feature of PFD is its incorporation of a tunable power parameter “p”, enhancing flexibility in modeling diverse memory effects. This represents a significant advance beyond traditional fractional derivatives with fixed kernels. Prior research on PFD has primarily focused on establishing their basic properties, deriving their Laplace transform, and applying them to linear FDEs [18]. Recently, Zitane et al. [23] have investigated the existence, uniqueness, and numerical approximations for a class of fractional differential equations employing power nonlocal and non-singular kernels, the analysis of nonlinear fractional differential equations using PFD still lacks thorough investigations.
This work introduces a novel framework for modeling nonlocal fractional systems by combining a p-Laplacian operator with PFD. While individual studies of p-Laplacian operators with different fractional derivatives are present in the literature, their combination in a nonlinear system with PFD remains unexplored. Our work is one of the first to address this gap, allowing the study of a new class of problems and opening new avenues for more precise models of complex systems. The core novelty of our methodology lies in the use of a PFD with a tunable power parameter within a non-singular kernel, which allows for a more nuanced representation of memory effects than traditional fixed-kernel derivatives. This framework offers the possibility of more precise and flexible modeling of phenomena that cannot be described with traditional derivatives.
The PFD used in this work is distinct from many traditional fractional derivatives, such as those of Riemann–Liouville or Caputo, in it incorporates a ’power’ parameter within a non-singular kernel. This parameter provides additional flexibility in the way memory effects are modeled. The PFD is also a unifying concept that encompasses well-known derivatives as specific cases, such as Caputo–Fabrizio, Atangana–Baleanu, weighted Atangana–Baleanu, and weighted Hattaf. This means that different specific behaviors can be analyzed from the same, general definition, showing the great power of this framework. This ability to adapt the derivative to different modeling needs is a significant advantage compared with other, fixed-kernel derivatives.
The importance of developing new mathematical frameworks in fractional calculus that can model complex phenomena exhibiting memory effects and nonlocal interactions is evident in numerous fields of science and engineering. Such systems are commonly present in disease transmission, porous media flow, non-Newtonian fluid mechanics, and more. Accurate modeling is fundamental for creating better predictive models and control strategies in those fields. The combination of a PFD with p-Laplacian operators in our system offers opportunities for a new understanding of those systems, potentially yielding new ways of modeling and analyzing them. This work makes a significant contribution by providing an alternative and versatile framework for modeling those complex systems.
Significant efforts have been made in the field of fractional calculus in recent years. However, those works have focused on p-Laplacian operators within different fractional derivatives [24,25,26,27]. Our work contributes to the field of fractional calculus by combining the flexibility of PFD with the complexity of the p-Laplacian operator, thus filling a significant gap in the literature. In particular, our study of nonlinear fractional differential equations within this framework provides a significant contribution to the field. The proposed framework also contributes to the literature by providing the theoretical basis for numerical simulations using PFD in nonlinear systems, showing that these derivatives can be used in a similar way as other fractional order derivatives.
Motivated by these advancements, this article introduces a system of FDEs that features a p-Laplacian operator within a power nonlocal kernel. The primary objective is to provide a rigorous theoretical framework and enable numerical simulations for the following system
where and are the PFD of order , in the Caputo sense, with respect to the non-decreasing weight function min and the function . The nonlinear functions are continuous satisfies some conditions described later. The nonlinear operator and The model (1) is generalized of many models depending on the parameters and weighted function The symmetric cases of model (1) are given as follows:
- If Then, the model (1) is reduced to the weighted generalized Hattaf fractional model.
- If and Then, the model (1) is reduced to the Atangana–Baleanu fractional model.
- If Then, the model (1) is reduced to the weighted Atangana–Baleanu fractional model.
- If and Then, the model (1) is reduced to the Caputo–Fabrizio fractional model.
In this work, we develop a general framework, allowing to incorporation of a tunable power parameter. This framework is analyzed using fixed point theory. We establish the existence, uniqueness, and Hyers–Ulam stability of solutions as well as the existence, uniqueness and stability of solutions for four symmetric cases under specified conditions. Furthermore, to highlight the versatility and generalizability of our results, we apply the model to an epidemiological problem modeling the transmission of the Hepatitis B Virus (HBV). Numerical simulations for four distinct symmetric cases arising from our novel framework are presented to illustrate the applicability of our approach. This research contributes to the field of fractional calculus by
- Presenting a rigorous analysis of the existence and uniqueness of solutions for nonlinear hybrid fractional differential equations using a novel PFD within a p-Laplacian context which has not been extensively studied.
- Offering a generalized model that encompasses several existing formulations by varying a tuning power parameter.
- Demonstrating the Hyers–Ulam stability of the proposed model, indicating the robustness of the solutions under small perturbations.
- Providing numerical simulations for a range of cases and showing the application of the model to a real-world application through a complex disease transmission model.
- Ultimately, our findings provide an alternative framework for modeling complex systems with memory processes, creating opportunities for more sophisticated and accurate modeling tools and new avenues for research into the applications of fractional calculus.
By addressing both the theoretical aspects and the practical need for numerical solutions, this research significantly advances the field of fractional calculus and paves the way for wider application of PFD in modeling and analyzing complex real-world phenomena. This contribution is particularly important given the increasing recognition of the PFD’s versatility and potential in capturing the intricate dynamics of systems with memory effects.
2. Basic Concepts
To establish a basis for our subsequent analysis, this section introduces essential concepts concerning fractional operators characterized by power nonlocal and non-singular kernels. In 2022, Lotfi et al. [18] explored and defined the power fractional derivative, a new development in fractional calculus.
Definition 1
([18]). Let with and where is Sobolev space. The PFD of order β, in the Caputo sense, of a function with respect to the weight function , is defined by
where
- represents the PML function given by
- represents a normalization positive function obeying
According to Theorem 1 of [18], the PML function is locally uniformly convergent for any see Theorem 1 of [18].
Remark 1.
The PFD in the Caputo sense, as defined by Definition 1, serves as a generalization encompassing several well-established fractional derivatives. Specific cases of the PFD, obtained by particular choices of parameters, include
(1) Caputo–Fabrizio Fractional Derivative: If , , and , then Definition 1 reduces to the Caputo–Fabrizio fractional derivative:
(2) Atangana–Baleanu Fractional Derivative: If , , and , then Definition 1 reduces to the Atangana–Baleanu fractional derivative:
(3) Weighted Atangana–Baleanu Fractional Derivative: If and , then Definition 1 reduces to the weighted Atangana–Baleanu fractional derivative:
(4) Weighted Generalized Hattaf Fractional Derivative: If , then Definition 1 reduces to the weighted generalized Hattaf fractional derivative:
Definition 2
([18]). The PFI of order β, of a function with respect to the weight function , is defined by
where
- denotes the standard weighted Riemann–Liouville fractional integral of order δ given by
Remark 2.
Theorem 1
(Theorem 1. [28]). Let with and Then, the PFD and PFI are commutative operators as follows:
- (i)
- (ii)
If we put , then we obtain the results of generalized Hattaf fractional operators [29].
Lemma 1.
The PFD and PFI satisfy the Newton–Leibniz formula
Lemma 2
([30,31]). Let be a Laplacian operator. Then, the following conditions hold true:
(1) For and we have
(2) For and we have
Lemma 3
([28]). Let be a continuous nonlinear function such that Then, the function is a solution of the following problem
if and only if satisfies the following integral equation
Definition 3.
Assume is a bounded and continuous operator. Then, the operator is Lipschitz with a Lipschitz constant Υ, provided
for all . Furthermore, the operator is classified as a strict contraction provided
Proposition 1.
The operator is satisfies the property of being Υ–Lipschitz with constants equal to 0 if is compact.
Hypothesis
We impose the following assumptions for our analysis of existence, uniqueness, and stability
For the continuous functions and , there exists constant number such that
and
The functions are continuous and there exist constants and such that
and
3. Qualitative Behavior of the Power Nonlocal Model (1) with p-Laplacian Operator
3.1. Equivalent Integral Equation
In the following theorem, we convert the power nonlocal model (1) with p-Laplacian operator into equivalent integral equations.
Theorem 2.
The solution of model (1) is given by
Proof.
Apply to the system (1), we have
By Def 2 and Theorem 1, we have
This implies that
By the p-Laplacian operator, we have
Apply again to above equation, we obtain
By conditions and we have
By Theorem 1, we have
To simplify our analysis, we rewrite the solution as follows
where
3.2. Notations
To prepare for our analysis, we establish the following notations.
By Theorem 2, we will define an operator by
The model given by Equation (1) possesses a solution precisely when the operator has fixed points.
3.3. Lipschitz Properties of Operator
Theorem 3.
Under assumptions (), the operator is Υ-Lipschitz, provided that
Proof.
Thus, is -Lipschitz. □
3.4. Compactness of Operator
Theorem 4.
The operator defined by is completely continuous.
Proof.
Let be a bounded set defined by with and let a sequences in such that as Due to and are continuous. Then, we have
Using , we have
Thus, the operator is continuous. Let . Then, we have
Thus, by (3), we have
where Therefore, is bounded. To show the equicontinuity property, let Then, we have
Thus, by (H1 − H2), we have
This implies that
The above argument demonstrates that is uniformly continuous. Therefore, from the Arzela–Ascoli theorem, we infer that the operator is relatively compact and hence, completely continuous. □
3.5. Existence of Solution
Theorem 5.
Given assumptions (), the power nonlocal model (1) admits a bounded set of solutions, which ensures the existence of at least one solution when
Proof.
As a consequence of Lemma 3, the operator is shown to be -Lipschitz with Lipschitz constant . A set of solutions to Equation (1) can be characterized as follows
which implies that
Thus, by (H2), we have
Thus by (5) in Theorem 4, we have
where Consider the set is unbounded. Now, we divide both sides of the above inequality by , then, we obtain:
This contradiction implies that must be bounded set. Consequently, the operator possesses at least one fixed point, which corresponds to a solution of power nonlocal model (1). □
3.6. Uniqueness of Solution
Theorem 6. (Uniqueness of solution) Given assumptions (H1, H3), the power nonlocal model (1) possesses a unique solution, provided that
3.7. Symmetric Cases of System (1)
In this subsection, we consider some symmetric cases of system (1):
- Case 1: If Then, the model (1) is reduced to the following the weighted generalized Hattaf fractional model
Corollary 1.
Assume that both (H1) and (H2) hold, let then system (6) has at least one solution , given by
- Case 2: If and Then, the model (1) is reduced to the following Atangana–Baleanu fractional model
Corollary 2.
Assume that both and hold, let then, system (7) has at least one solution given by
- Case 3: If Then, the model (1) is reduced to the following weighted Atangana–Baleanu fractional model
Corollary 3.
Assume that and hold, let then system (8) has at least one solution given by
- Case 4: If and Then, the model (1) is reduced to the following Caputo–Fabrizio fractional model
Corollary 4.
Under assumptions (). If , then, the Caputo–Fabrizio fractional model (9) possesses at least one solution given by
3.8. Hyers–Ulam Stability
Before analyzing the stability, we recall some definitions and lemmas. (see [32]).
Definition 4.
Remark 3.
Let Q be a mappingin ( Q dependent of , such that for any :
(i)
Lemma 4.
According to solution (13) and considering first part in Remark 3, we have
Theorem 7.
Under the condition that , the solution to power nonlocal model (1) is shown to possess both HU stability and generalized HU stability.
Proof.
Let be a solution of power nonlocal model (1), and let be a unique result. Then, we take
By Lemma 4 and Theorem 3, we have
which further yields
3.9. UH Stability of Symmetric Cases
According to Theorem 7, we can easily prove UH stable of symmetric systems as follows:
4. Numerical Scheme
In this part, by using the Lagrange interpolating polynomial method [23], we present approximate solutions of power nonlocal fractional differential equations with p-Laplacian operator (1).
Consider the power nonlocal model:
From Lemma 2, the solution of (16) is given by
Since, the q-Laplacian is a nonlinear operator. Therefore, we can define nonlinear function
Then, (17) obtains the following form:
Let with and h be the discretization steps. One has
Now, we approximate the functions on by using the Lagrange interpolation polynomial through the points and as follows
Replacing the approximation (19) in Equation (18), we find that
Furthermore, we have
and
Thus, by (21) and (22), Equation (20) becomes as follows
where
5. Application of the Numerical Scheme to an HBV Model
Controlling Hepatitis B Virus (HBV) requires a comprehensive understanding of its transmission dynamics, particularly the role of asymptomatic carriers. In this study, we extend a classical HBV model by incorporating asymptomatic carriers and analyzing its behavior using power nonlocal fractional derivatives. Our findings offer new insights that can inform improved prevention, treatment, and public health strategies.
This model tracks the dynamics of HBV across six population classes. Susceptible individuals enter the population at a birth rate of . The model incorporates an effective contact rate and a natural fatality rate . Upon exposure, individuals transition to an infected state at a rate of . A fraction of these individuals becomes acutely infected (class ), while a portion transitions to an asymptomatic carrier state (). Acute and asymptomatic individuals become carriers at rates and , respectively. The model also includes recovery rates for acute , asymptomatic , and carrier individuals . Disease-related death rates are denoted by for acute infections and for chronic infections. Finally, and represent the relative infectiousness of asymptomatic and chronic infections compared to acute infections, respectively. The total population, , is categorized into susceptible (), exposed (), acutely infected (), asymptomatic carrier (), chronically infected (), and recovered () such that , with initial conditions and
We will illustrate the behavior of the power nonlocal fractional HBV transmission model (24) and its symmetric cases (Caputo–Fabrizio, Atangana–Baleanu, weighted Atangana–Baleanu, and Hattaf derivatives) using graphical representations. These graphics will show how the model’s solutions change when varying the fractional order and other key biological parameters and . In addition, the initial values are selected as and The numerical approximate solution of power nonlocal fractional HBV transmission model (24) with different fractional order and with , and weight function is displayed in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.
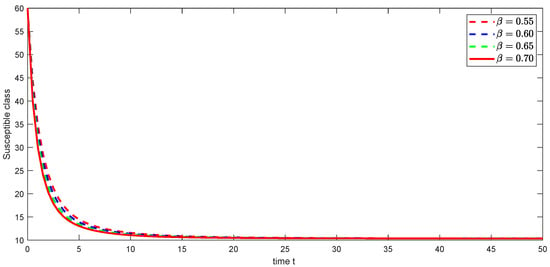
Figure 1.
Graphical illustration of approximate solution for susceptible class using different values of , and with power .
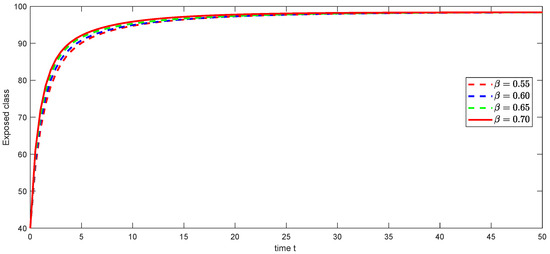
Figure 2.
Graphical illustration of approximate solution for exposed class using different values of , and with power .
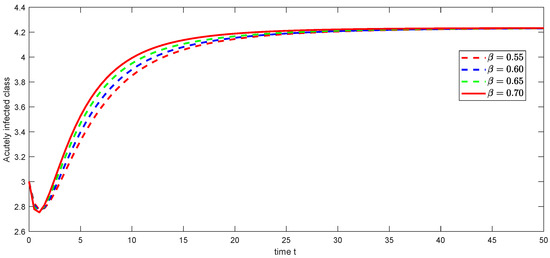
Figure 3.
Graphical illustration of approximate solution for acutely infected class using different values of , and with power .
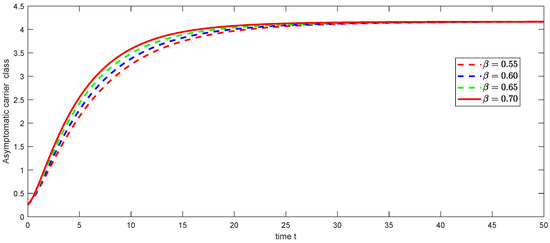
Figure 4.
Graphical illustration of approximate solution for asymptomatic carrier class using different values of , and with power .
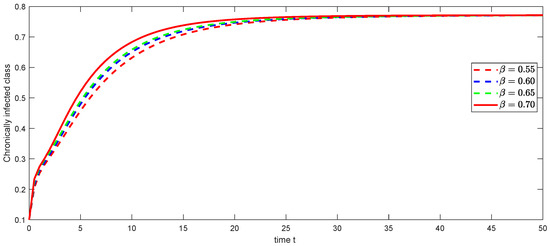
Figure 5.
Graphical illustration of approximate solution for chronically class using different values of , and with power .
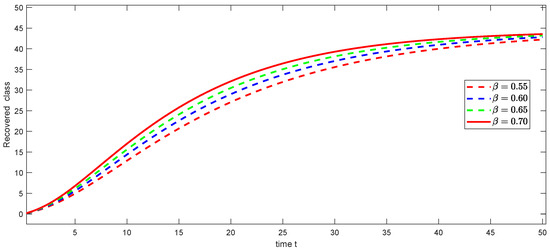
Figure 6.
Graphical illustration of approximate solution for recovered class using different values of , and with power .
6. Symmetric Cases
Here, we present the approximate numerical solutions of four symmetric cases of the model (24) as follows:
- Case 1: The numerical approximate solution of weighted generalized Hattaf fractional HBV transmission model (24) with different fractional order and with , and weight function is displayed in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, respectively.
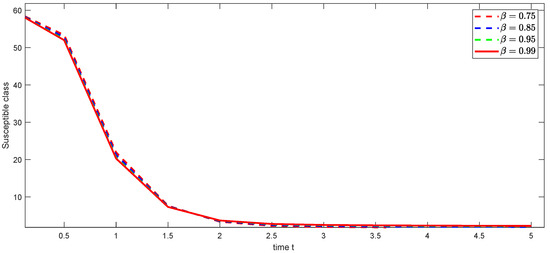 Figure 7. Graphical illustration of approximate solution for susceptible class using different values of , and with power .
Figure 7. Graphical illustration of approximate solution for susceptible class using different values of , and with power .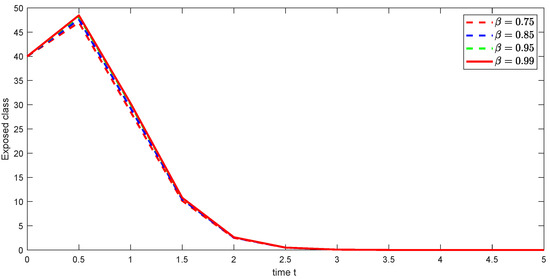 Figure 8. Graphical illustration of approximate solution for exposed class using different values of , and with power .
Figure 8. Graphical illustration of approximate solution for exposed class using different values of , and with power .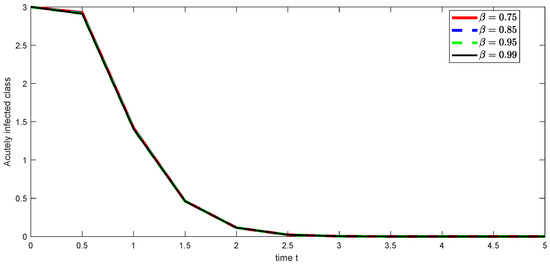 Figure 9. Graphical illustration of approximate solution for acutely infected class using different values of , and with power .
Figure 9. Graphical illustration of approximate solution for acutely infected class using different values of , and with power .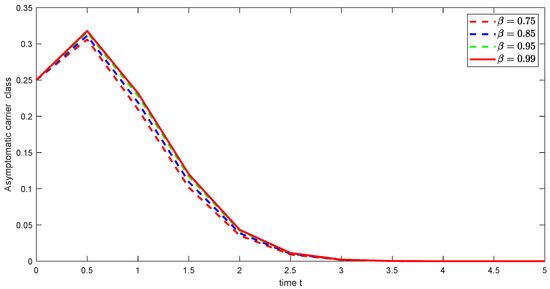 Figure 10. Graphical illustration of approximate solution for asymptomatic carrier class using different values of , and with power .
Figure 10. Graphical illustration of approximate solution for asymptomatic carrier class using different values of , and with power .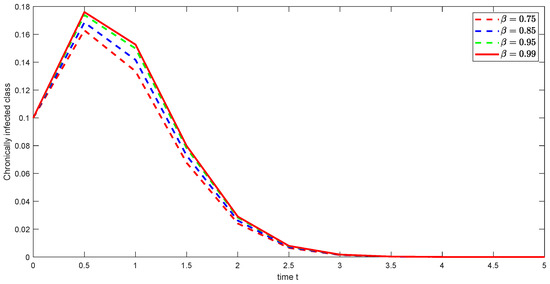 Figure 11. Graphical illustration of approximate solution for chronically class using different values of , and with power .
Figure 11. Graphical illustration of approximate solution for chronically class using different values of , and with power .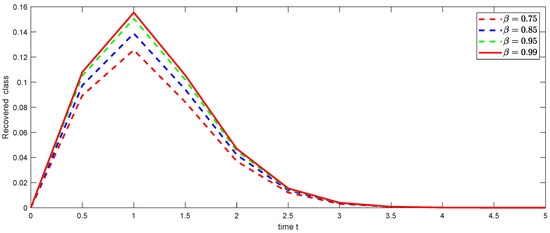 Figure 12. Graphical illustration of approximate solution for recovered class using different values of , and with power .
Figure 12. Graphical illustration of approximate solution for recovered class using different values of , and with power . - Case 2: The numerical approximate solution of Atangana–Baleanu fractional HBV transmission model (24) with different fractional order and with , and weight function is displayed in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, respectively.
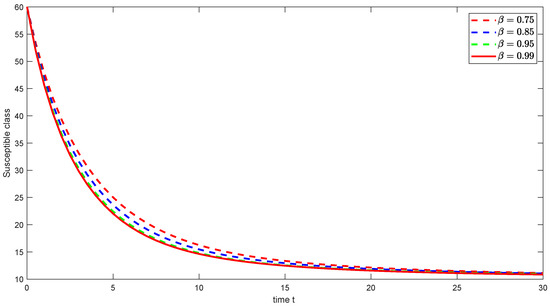 Figure 13. Graphical illustration of approximate solution for susceptible class using different values of with power .
Figure 13. Graphical illustration of approximate solution for susceptible class using different values of with power .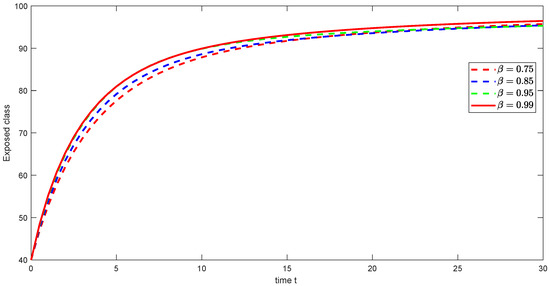 Figure 14. Graphical illustration of approximate solution for exposed class using different values of with power .
Figure 14. Graphical illustration of approximate solution for exposed class using different values of with power .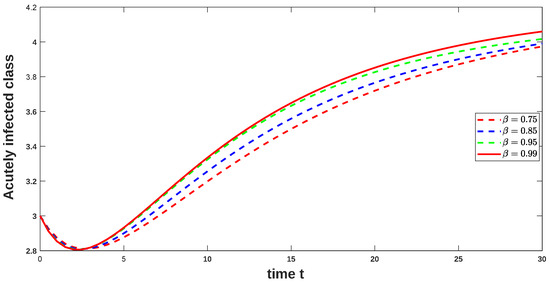 Figure 15. Graphical illustration of approximate solution for acutely infected class using different values of with power .
Figure 15. Graphical illustration of approximate solution for acutely infected class using different values of with power .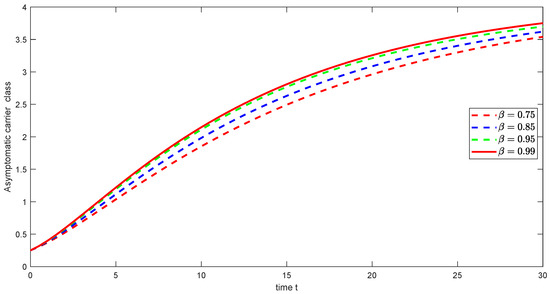 Figure 16. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .
Figure 16. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .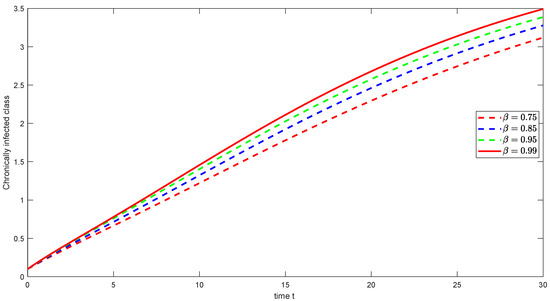 Figure 17. Graphical illustration of approximate solution for chronically class using different values of with power .
Figure 17. Graphical illustration of approximate solution for chronically class using different values of with power .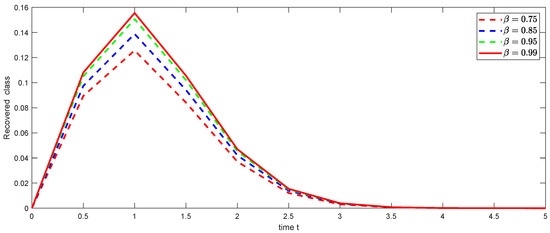 Figure 18. Graphical illustration of approximate solution for recovered class using different values of with power .[H]
Figure 18. Graphical illustration of approximate solution for recovered class using different values of with power .[H] - Case 3: The numerical approximate solution of weighted Atangana–Baleanu fractional HBV transmission model (24) with different fractional order and with , and weight function is displayed in Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24, respectively.
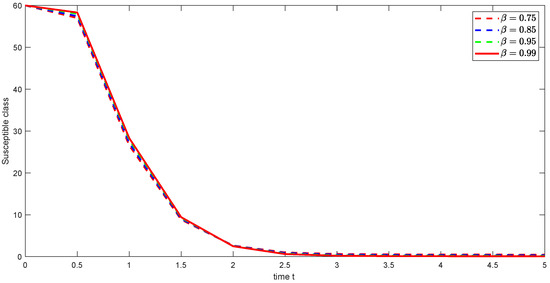 Figure 19. Graphical illustration of approximate solution for susceptible class using different values of with power .
Figure 19. Graphical illustration of approximate solution for susceptible class using different values of with power .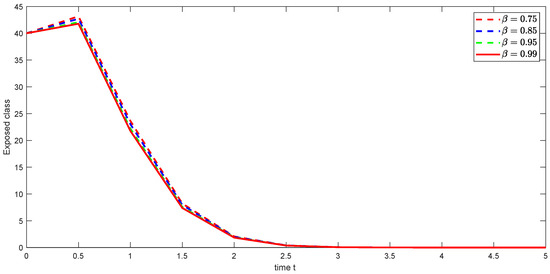 Figure 20. Graphical illustration of approximate solution for exposed class using different values of with power .
Figure 20. Graphical illustration of approximate solution for exposed class using different values of with power .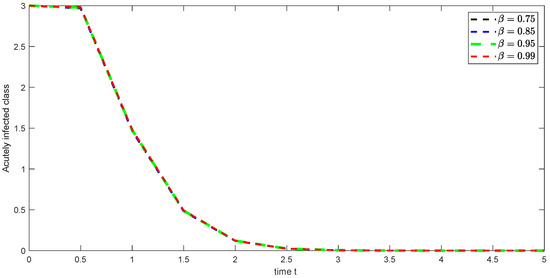 Figure 21. Graphical illustration of approximate solution for acutely infected class using different values of with power .
Figure 21. Graphical illustration of approximate solution for acutely infected class using different values of with power .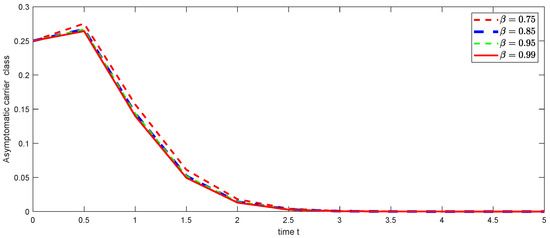 Figure 22. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .
Figure 22. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .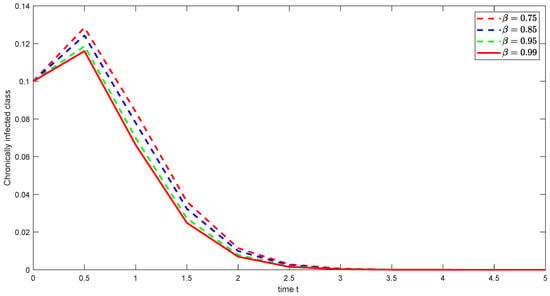 Figure 23. Graphical illustration of approximate solution for chronically class using different values of with power .
Figure 23. Graphical illustration of approximate solution for chronically class using different values of with power .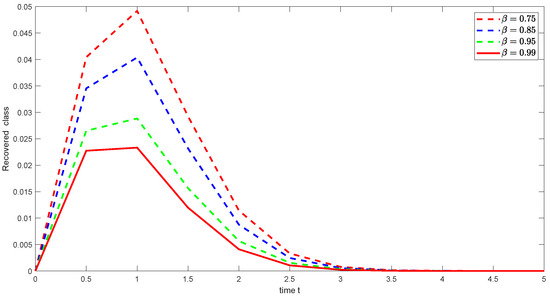 Figure 24. Graphical illustration of approximate solution for recovered class using different values of with power .
Figure 24. Graphical illustration of approximate solution for recovered class using different values of with power . - Case 4: The numerical approximate solution of Caputo–Fabrizio fractional HBV transmission model (24) with different fractional order and with , and weight function is displayed in Figure 25, Figure 26, Figure 27, Figure 28, Figure 29 and Figure 30, respectively.
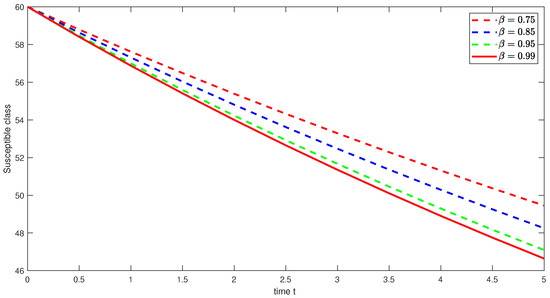 Figure 25. Graphical illustration of approximate solution for susceptible class using different values of with power .
Figure 25. Graphical illustration of approximate solution for susceptible class using different values of with power .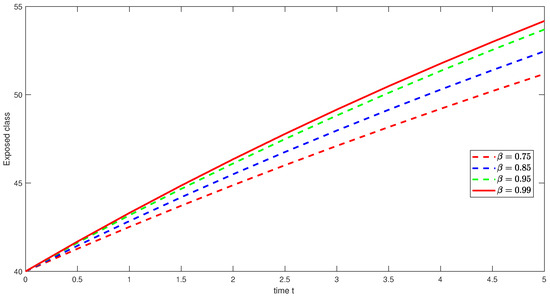 Figure 26. Graphical illustration of approximate solution for exposed class using different values of with power .
Figure 26. Graphical illustration of approximate solution for exposed class using different values of with power .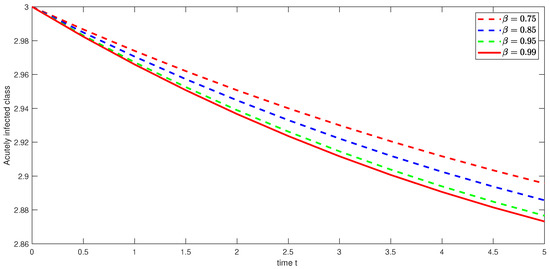 Figure 27. Graphical illustration of approximate solution for acutely infected class using different values of with power .
Figure 27. Graphical illustration of approximate solution for acutely infected class using different values of with power .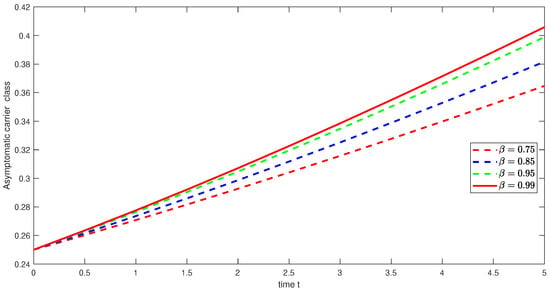 Figure 28. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .
Figure 28. Graphical illustration of approximate solution for asymptomatic carrier class using different values of with power .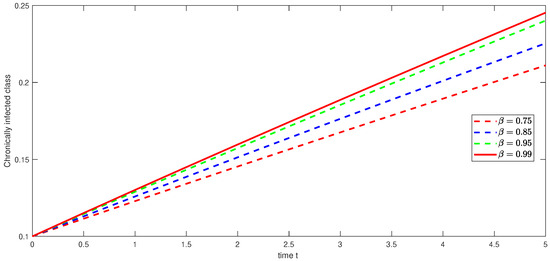 Figure 29. Graphical illustration of approximate solution for chronically class using different values of with power .
Figure 29. Graphical illustration of approximate solution for chronically class using different values of with power .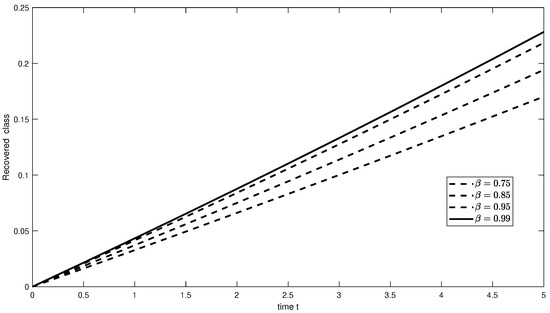 Figure 30. Graphical illustration of approximate solution for recovered class using different values of with power .
Figure 30. Graphical illustration of approximate solution for recovered class using different values of with power .
7. Discusion and Conclusions
While the p-Laplacian operator is a powerful tool for modeling certain systems, it also introduces some complexities in analysis. In particular, the analysis is more challenging than with a typical Laplacian operator, and the results concerning the existence and uniqueness of solutions for the model are only valid under certain conditions, or when using specific values of the parameter ’p’. Despite these limitations, the inclusion of the p-Laplacian operator is essential to capture the characteristics of the complex systems considered in this study, especially in applications of non-Newtonian fluids, porous media, and image processing. It is important to point out that this added complexity is an expected tradeoff for the flexibility offered by the p-Laplacian.
Across all the symmetric cases (Hattaf, Atangana–Baleanu, weighted Atangana–Baleanu, and Caputo–Fabrizio), similar qualitative trends are observed for all classes, demonstrating the unifying property of the PFD framework. The specific choices of parameters, including the fractional order and the kernel structure, lead to variations in the convergence rates and steady-state values, highlighting the versatility and tunable nature of nonlocal power fractional operators. The numerical simulations effectively capture the dynamic interactions among various population classes, underscoring the relevance of this approach to real-world public health modeling. This study employs graphical representations to analyze the dynamic behavior of an HBV transmission model using PFD. The graphs illustrate the evolution of six key epidemiological classes: susceptible, exposed, acutely infected, asymptomatic carrier, chronically infected, and recovered over time. By varying the fractional order parameter and considering four different derivative cases (Hattaf, Atangana–Baleanu, weighted Atangana–Baleanu, and Caputo–Fabrizio), these visualizations allow for comparative analysis of the influence of memory effects on disease dynamics. The PFD framework, encompassing Hattaf, Atangana–Baleanu, weighted Atangana–Baleanu, and Caputo–Fabrizio derivatives, provides a versatile approach to modeling HBV transmission, capturing diverse memory effects inherent in biological systems. Across the six aforementioned classes, the fractional order parameter modulates the temporal dynamics, with lower values reflecting a more gradual evolution of the population classes and a heightened influence of historical data and higher values indicating a faster transition and the dominance of recent events. Specifically, the choice of kernel structure (exponential for Caputo–Fabrizio and Mittag–Leffler for Atangana–Baleanu) provides different mechanisms for capturing the memory effects, thus leading to distinct patterns in the evolution of different stages of HBV infection. While all four cases produce similar qualitative trends, the weighted Atangana–Baleanu and Hattaf derivatives offer increased flexibility with their additional weighting parameters, thus adapting the model based on the system dynamics. Hence, a model using a higher parameter should be employed for systems with faster transitions, while a model with a lower parameter should be used when longer-term effects and gradual transitions are of interest.
The graphical representations illustrate the effect of different fractional order parameters on the time evolution of the different epidemiological classes. In particular, the fractional order ’’ modulates the convergence rate towards steady-states, as shown in the graphs for susceptible, exposed, infected, asymptomatic carriers and chronically infected and recovered individuals. The change in fractional orders shows significant differences in the behavior of the system, with a lower parameter associated with a more gradual evolution of the population classes, indicating that the past has more influence in the actual state, and a higher parameter associated with a faster transition, indicating that recent events dominate the dynamics. While the qualitative trend is similar for all cases, the different values of result in changes in the rate of convergence and the time when the steady state is achieved. This is very relevant to the modeling of real-world phenomena, allowing for a better fitting of the parameters to the system under analysis, in order to create more accurate models. These changes clearly show the tunable nature of the fractional derivatives used in this work. Future research should explore extending the proposed model to incorporate additional biological factors, such as immune response dynamics and antiviral therapy effects. Additionally, further numerical experiments could validate the theoretical results by comparing them with real-world epidemiological data.
Author Contributions
Conceptualization, M.S.A. and M.A.A.; methodology, M.A.A.; software, B.M.; formal analysis, M.S.; investigation, M.H. and S.I.; writing—original draft preparation, M.A.A.; writing—review and editing, M.S.A., K.A. and S.I.; visualization, M.H.; supervision, M.A.A. and K.A.; project administration, K.A.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data used in this work are contained within the article.
Acknowledgments
The Researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).
Conflicts of Interest
There are no conflicts of interest declared by the authors.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon & Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering. 2; Begell House: Redding, CA, USA, 2006. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus. In Series on Complexity, Nonlinearity and Chaos; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2012; Volume 3. [Google Scholar]
- Srivastava, H.M.; Saad, K.M. Some new models of the time-fractional gas dynamics equation. Adv. Math. Models Appl. 2018, 3, 5–17. [Google Scholar]
- Yadav, P.; Jahan, S.; Shah, K.; Peter, O.J.; Abdeljawad, T. Fractional-order modelling and analysis of diabetes mellitus: Utilizing the Atangana-Baleanu Caputo (ABC) operator. Alex. Eng. J. 2023, 81, 200–209. [Google Scholar] [CrossRef]
- Aldwoah, K.A.; Almalahi, M.A.; Shah, K. Theoretical and numerical simulations on the hepatitis B virus model through a piecewise fractional order. Fractal Fract. 2023, 7, 844. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Alfwzan, W.F.; Gulzar, H. Nonlinear dynamics of a piecewise modified ABC fractional-order leukemia model with symmetric numerical simulations. Symmetry 2023, 15, 1338. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Jang, B. A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications. Fractal Fract. 2024, 8, 65. [Google Scholar] [CrossRef]
- Azeem, M.; Farman, M.; Akgül, A.; De la Sen, M. Fractional order operator for symmetric analysis of cancer model on stem cells with chemotherapy. Symmetry 2023, 15, 533. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Aldowah, K.; Alqarni, F.; Hleili, M.; Shah, K.; Birkea, F.M. On modified Mittag–Leffler coupled hybrid fractional system constrained by Dhage hybrid fixed point in Banach algebra. Sci. Rep. 2024, 14, 30264. [Google Scholar] [CrossRef] [PubMed]
- Alraqad, T.; Almalahi, M.A.; Mohammed, N.; Alahmade, A.; Aldwoah, K.A.; Saber, H. Modeling Ebola Dynamics with a Φ-Piecewise Hybrid Fractional Derivative Approach. Fractal Fract. 2024, 8, 596. [Google Scholar] [CrossRef]
- Boutiara, A.; Abdo, M.S.; Almalahi, M.A.; Ahmad, H.; Ishan, A. Implicit hybrid fractional boundary value problem via generalized Hilfer derivative. Symmetry 2021, 13, 1937. [Google Scholar] [CrossRef]
- Rahman, S.U.; Palencia, J.L.D. Regularity and analysis of solutions for a MHD flow with a p-Laplacian operator and a generalized Darcy-Forchheimer term. Eur. Phys. J. Plus 2022, 137, 1328. [Google Scholar] [CrossRef]
- Alfwzan, W.F.; Khan, H.; Alzabut, J. Stability analysis for a fractional coupled Hybrid pantograph system with p-Laplacian operator. Results Control. Optim. 2024, 14, 100333. [Google Scholar] [CrossRef]
- Boutiara, A.; Abdo, M.S.; Almalahi, M.A.; Shah, K.; Abdalla, B.; Abdeljawad, T. Study of Sturm–Liouville boundary value problems with p-Laplacian by using generalized form of fractional order derivative. AIMS Math 2022, 7, 18360–18376. [Google Scholar] [CrossRef]
- Lotfi, E.M.; Zine, H.; Torres, D.F.M.; Yousfi, N. The power fractional calculus: First definitions and properties with applications to power fractional differential equations. Mathematics 2022, 10, 3594. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and nonsingular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Al-Refai, M. On weighted Atangana-Baleanu fractional operators. Adv. Difference Equ. 2020, 11, 3. [Google Scholar] [CrossRef]
- Hattaf, K. A new generalized definition of fractional derivative with non-singular kernel. Computation 2020, 8, 49. [Google Scholar] [CrossRef]
- Zitane, H.; Torres, D.F. A class of fractional differential equations via power non-local and non-singular kernels: Existence, uniqueness and numerical approximations. Phys. D Nonlinear Phenom. 2024, 457, 133951. [Google Scholar] [CrossRef]
- Cheng, L.; Guo, L. Positive Solution Pairs for Coupled p-Laplacian Hadamard Fractional Differential Model with Singular Source Item on Time Variable. Fractal Fract. 2024, 8, 682. [Google Scholar] [CrossRef]
- Zhou, J.; Gong, C.; Wang, W. The Sign-Changing Solution for Fractional (p, q)-Laplacian Problems Involving Supercritical Exponent. Fractal Fract. 2024, 8, 186. [Google Scholar] [CrossRef]
- Rahman, S.U.; Díaz Palencia, J.L. Analytical and Computational Approaches for Bi-Stable Reaction and p-Laplacian Diffusion Flame Dynamics in Porous Media. Mathematics 2024, 12, 216. [Google Scholar] [CrossRef]
- Yang, D.; Bai, Z.; Bai, C. Existence of Solutions for Nonlinear Choquard Equations with (p, q)-Laplacian on Finite Weighted Lattice Graphs. Axioms 2024, 13, 762. [Google Scholar] [CrossRef]
- Al-Refai, M.; Jarrah, A.M. Fundamental results on weighted Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2019, 126, 7–11. [Google Scholar] [CrossRef]
- Hattaf, K. On some properties of the new generalized fractional derivative with non-singular kernel. Math. Probl. Eng. 2021, 1, 1580396. [Google Scholar] [CrossRef]
- Khan, H.; Chen, W.; Sun, H.G. Analysis of positive solution and Hyers-Ulam stability for a class of singular fractional differential equations with p-Laplacian in Banach space. Math. Meth. Appl. Sci. 2018, 41, 3430–3440. [Google Scholar] [CrossRef]
- Khan, H.; Li, Y.; Suna, H.; Khan, A. Existence of solution and Hyers-Ulam stability for a coupled system of fractional differential equations with p-Laplacian operator. Bound. Value Probl. 2017, 2017, 157. [Google Scholar] [CrossRef]
- Ibrahim, R.W. Generalized Hyers-Ulam stability for fractional differential equations. Int. J. Math. 2012, 23, 1250056. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).