Representation of Special Functions by Multidimensional A- and J-Fractions with Independent Variables

Abstract

The paper deals with the problem of representing special functions by branched continued fractions, particularly multidimensional A- and J-fractions with independent variables, which are generalizations of associated continued fractions and Jacobi continued fractions, respectively. A generalized Gragg’s algorithm is constructed that enables us to compute, by the coefficients of the given formal multiple power series, the coefficients of the corresponding multidimensional A- and J-fractions with independent variables. Presented below are numerical experiments for approximating some special functions by these branched continued fractions, which are similar to fractals.

1. Introduction

The problem of representing special functions arises, in particular, when solving various functional equations. It contributes to the development and implementation of effective methods and algorithms that are implemented until the construction of special software [1,2,3,4,5]. Currently, various tools are used to represent these functions, including the multidimensional generalization of continued fractions—branched continued fractions—as a special family of functions (see, [6,7,8,9,10,11,12,13,14]). The construction of the rational approximations of a special function is based on the correspondence between the approximants of the branched continued fraction and the formal multiple power series, which represents this function (see, [15,16]). Furthermore, the problem of constructing the corresponding branched continued fractions contributes to the emergence of their various structures (see, [17,18,19,20,21,22,23]).

In [24], Dmytro Bodnar introduced the so-called “branched continued fractions with independent variables”, which, by their structure, are a multidimensional analogue of the multiple power series. The correspondence properties of these branched continued fractions with polynomial elements are closely connected to the degree and form of these polynomials. Their types are essential in the analytical continuation of special functions through branched continued fractions [16,25,26,27]. Based on the classical algorithm [15,28], algorithms have been constructed that enable us to compute, by the coefficients of the formal multiple power series, the coefficients of the corresponding multidimensional C-, g-, S-, A-, and J-fractions with independent variables [16,29,30].

The paper considers the problem of representing special functions by multidimensional A- and J-fractions with independent variables, which are generalizations of associated continued fractions (or A-fractions) and Jacobi continued fractions (or J-fractions) [31], respectively.

In the analytical theory of continued fractions, the use of Gragg’s algorithm [32], which is based on Theorem 7.14 [28], is efficient for the constructed corresponding A- and J-fractions.

Let the coefficients of the formal power series

$$\begin{array}{c}\hfill L\left(z\right)=1+c_{1}z+c_2{z}^2+c_3{z}^3+\dots \end{array}$$

satisfy the conditions $H_n^{\left(1\right)}\ne 0$, $n\ge 1,$ where $H_n^{\left(1\right)}$ and $n\ge 1,$ are Hankel determinants associated with $L\left(z\right).$ Then, the coefficients of the A-fraction

$$\begin{array}{c}\hfill 1+{\displaystyle \frac{p_{1}z}{{\displaystyle 1+q_{1}z-{\displaystyle \frac{p_2{z}^2}{{\displaystyle 1+q_{2}z-{\displaystyle \frac{p_3{z}^2}{{\displaystyle 1+q_{1}z{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}}\end{array}$$

corresponding to $L\left(z\right)$, can be computed as follows:

$$\begin{array}{c}\hfill p_{k+1}={\displaystyle \frac{{\sigma }_k}{{\sigma }_{k-1}}},q_{k+1}={\tau }_{k-1}-{\tau }_k,k\ge 0,\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_k=\sum _{r=0}^k{b}_{k,r}{c}_{2k+1-r},{\tau }_k={\displaystyle \frac{1}{{\sigma }_k}}\sum _{r=0}^k{b}_{k,r}{c}_{2k+2-r},\end{array}$$

and for $1\le r\le k+1,$

$$\begin{array}{c}\hfill b_{k+1,r}=b_{k,r}+q_{k+1}{b}_{k,r-1}-p_{k+1}{b}_{k-1,r-2},\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{-1}=b_{0,0}=b_{k+1,0}=1,{\tau }_{-1}=b_{k-1,-1}{b}_{k,k+1}=0.\end{array}$$

In this paper, we construct and study a generalization of the Gragg’s algorithm. First, in Section 2, we give the necessary definitions. Then, in Section 3, we construct a generalized Gregg’s algorithm and establish necessary and sufficient conditions for its existence (Theorems 1 and 2 for multidimensional A- and J-fractions with independent variables, respectively). Finally, in Section 4, we give examples of representing special functions by multidimensional A- and J-fractions with independent variables, which are similar to fractals.

2. Correspondence

2.1. Formal Multiple Power Series [15,16]

Formal multiple power series at $\mathbf{z}=\mathbf{0}$. Let N be a fixed natural number, ${\mathbb{Z}}_{\ge 0}$ be the set of non-negative integers, $\mathbb{C}$ be the set of complex numbers, ${\mathbb{Z}}_{\ge 0}^N={\mathbb{Z}}_{\ge 0}\times {\mathbb{Z}}_{\ge 0}\times \dots \times {\mathbb{Z}}_{\ge 0}$ be the Cartesian product of N copies of the ${\mathbb{Z}}_{\ge 0}$, ${\mathbb{C}}^N=\mathbb{C}\times \mathbb{C}\times \dots \times \mathbb{C}$ be the Cartesian product of N copies of the $\mathbb{C},$ $\mathbf{k}=(k_1,k_2,\dots ,k_N)$ be an element of ${\mathbb{Z}}_{\ge 0}^N$, and $\mathbf{z}=(z_1,z_2,\dots ,z_N)$ be an element of ${\mathbb{C}}^N.$ For $\mathbf{k}\in {\mathbb{Z}}_{\ge 0}^N$ and $\mathbf{z}\in {\mathbb{C}}^N$, put

$$\begin{array}{c}\hfill \mathbf{k}!=k_1!k_2!\dots k_N!,\left|\mathbf{k}\right|=k_1+k_2+\dots +k_N,{\mathbf{z}}^{\mathbf{k}}=z_1^{k_1}{z}_2^{k_2}\dots z_N^{k_N}.\end{array}$$

A series of the form

$$\begin{array}{c}\hfill L_{*}\left(\mathbf{z}\right)=\sum _{\left|\mathbf{k}\right|\ge 0}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}},\end{array}$$

where $c_{\mathbf{k}}\in \mathbb{C}$ for $\left|\mathbf{k}\right|\ge 0$ is called a formal multiple power series at $\mathbf{z}=\mathbf{0}.$ A set of formal multiple power series at $\mathbf{z}=\mathbf{0}$ is denoted by $\mathbb{L}.$

Let $R\left(\mathbf{z}\right)$ be a function holomorphic in a neighbourhood of the origin $(\mathbf{z}=\mathbf{0}).$ Let the mapping $\Lambda :R\left(\mathbf{z}\right)\to \Lambda \left(R\right)$ associate with $R\left(\mathbf{z}\right)$ its Taylor expansion in a neighbourhood of the origin. A sequence $\left\{R_n\left(\mathbf{z}\right)\right\}$ of functions holomorphic at the origin is said to correspond at $\mathbf{z}=\mathbf{0}$ to a formal multiple power series $L_{*}\left(\mathbf{z}\right)$ if

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\lambda (L_{*}-\Lambda \left(R_n\right))=\infty ,\end{array}$$

where $\lambda$ is the function defined as follows: $\lambda :\mathbb{L}\to {\mathbb{Z}}_{\ge 0}\cup \{\infty \}$; if $L_{*}\left(\mathbf{z}\right)\equiv 0$, then $\lambda \left(L_{*}\right)=\infty$; if $L_{*}\left(\mathbf{z}\right)\not\equiv 0$ then $\lambda \left(L_{*}\right)=m,$ where m is the smallest degree of homogeneous terms for which $c_{\mathbf{k}}\ne 0,$ that is $m=\left|\mathbf{k}\right|.$

If $\left\{R_n\left(\mathbf{z}\right)\right\}$ corresponds at $\mathbf{z}=\mathbf{0}$ to a formal multiple power series $L_{*}\left(\mathbf{z}\right),$ then the order of correspondence of $R_n\left(\mathbf{z}\right)$ is defined as

$$\begin{array}{c}\hfill {\nu }_n=\lambda (L_{*}-\Lambda \left(R_n\right)).\end{array}$$

By the definition of $\lambda ,$ the series $L_{*}\left(\mathbf{z}\right)$ and $\Lambda \left(R_n\right)$ agree for all homogeneous terms up to and including degree $({\nu }_n-1).$

Formal multiple power series at $\mathbf{z}=\mathbf{\infty }$. A sequence of rational functions $\left\{R_n\left(\mathbf{z}\right)\right\}$ is said to correspond at $\mathbf{z}=\mathbf{\infty }$ to a formal multiple power series

$$L^{*}\left(\mathbf{z}\right)=\sum _{\left|\mathbf{k}\right|\ge 0}{\displaystyle \frac{c_{\mathbf{k}}}{{\mathbf{z}}^{\mathbf{k}}}},$$

(1)

where $c_{\mathbf{k}}\in \mathbb{C}$, $\mathbf{k}\ge 0,$ if the sequence $\left\{R_n(1/w_1,1/w_2,\dots ,1/w_N)\right\}$ corresponds to a formal multiple power series at $\mathbf{w}=\mathbf{0}$ obtained from (1) by replacing $z_i$ with $1/w_i,$ $1\le i\le N.$

A formal multiple power series (1) is said to be an asymptotic expansion of a function $R\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{\infty },$ with respect to a region D in ${\mathbb{C}}^N,$ if for every $n\ge 0$ there exist ${\rho }_n>0$ and ${\eta }_n>0$ such that

$$\left|R\left(\mathbf{z}\right)-\sum _{\left|\mathbf{k}\right|=0}^n{\displaystyle \frac{c_{\mathbf{k}}}{{\mathbf{z}}^{\mathbf{k}}}}\right|\le {\eta }_n{\left(\sum _{k=1}^N{\displaystyle \frac{1}{|z_k|}}\right)}^{n+1},\left|z_k\right|>{\rho }_n,1\le k\le N,\mathbf{z}\in D.$$

We denote this by

$$R\left(\mathbf{z}\right)\approx \sum _{\left|\mathbf{k}\right|\ge 0}{\displaystyle \frac{c_{\mathbf{k}}}{{\mathbf{z}}^{\mathbf{k}}}},z_k\to \infty ,1\le k\le N.$$

2.2. Branched Continued Fractions [16,25]

Let $i\left(0\right)=0$, ${\mathfrak{I}}_0=\left\{0\right\},$ and, for $k\ge 1,$

$$\begin{array}{c}\hfill {\mathfrak{I}}_k=\{i\left(k\right):i\left(k\right)=(i_1,i_2,\dots ,i_k),1\le i_p\le i_{p-1},1\le p\le k,i_0=N\}.\end{array}$$

Let $⟨{\left\{a_{i\left(k\right)}\right\}}_{i\left(k\right)\in {\mathfrak{I}}_k,k\ge 1},{\left\{b_{i\left(k\right)}\right\}}_{i\left(k\right)\in {\mathfrak{I}}_k,k\ge 0}⟩$ denote the ordered pair of sequences of complex numbers with $a_{i\left(k\right)}\ne 0$ for all $i\left(k\right)\in {\mathfrak{I}}_k$, $k\ge 1,$ and if for $k\ge 1$ there exists a multi-index $i\left(k\right)\in {\mathfrak{I}}_k$ such that $b_{i\left(k\right)}=0,$ than $b_{i(k-1),j}\ne 0$ for $1\le j\le i_{k-1}$ and $j\ne i_k.$ Let the sequence $\left\{f_k\right\}$ is defined as follows:

$$\begin{array}{cc}\hfill f_0& =b_0,\hfill \\ \hfill f_1& =b_0+\sum _{i_1=1}^N{\displaystyle \frac{a_{i\left(1\right)}}{b_{i\left(1\right)}}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill f_2& =b_0+\sum _{i_1=1}^N{\displaystyle \frac{a_{i\left(1\right)}}{{\displaystyle ‘b_{i\left(1\right)}+\sum _{i_2=1}^{i_1}\frac{a_{i\left(2\right)}}{b_{i\left(2\right)}}}}},\hfill \\ & \dots ,\hfill \\ \hfill f_k& =b_0+\sum _{i_1=1}^N{\displaystyle \frac{a_{i\left(1\right)}}{{\displaystyle b_{i\left(1\right)}+\sum _{i_2=1}^{i_1}\frac{a_{i\left(2\right)}}{{\displaystyle b_{i\left(2\right)}{+}_{{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_k=1}^{i_{k-1}}\frac{a_{i\left(k\right)}}{b_{i\left(k\right)}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}},\hfill \\ \hfill & \dots .\hfill \end{array}$$

The ordered pair

$$⟨⟨{\left\{a_{i\left(k\right)}\right\}}_{i\left(k\right)\in {\mathfrak{I}}_k,k\ge 1},{\left\{b_{i\left(k\right)}\right\}}_{i\left(k\right)\in {\mathfrak{I}}_k,k\ge 0}⟩,{\left\{f_k\right\}}_{k\ge 0}⟩$$

is the branched continued fraction with independent variables denoted by the symbol

$$b_0+\sum _{i_1=1}^N{\displaystyle \frac{a_{i\left(1\right)}}{{\displaystyle b_{i\left(1\right)}+\sum _{i_2=1}^{i_1}\frac{a_{i\left(2\right)}}{{\displaystyle b_{i\left(2\right)}+\sum _{i_3=1}^{i_2}\frac{a_{i\left(3\right)}}{b_{i\left(3\right)}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}.$$

(2)

The numbers $a_{i\left(k\right)}$ and $b_{i\left(k\right)}$ are called the elements of the branched continued fraction with independent variables, the relation $a_{i\left(k\right)}/b_{i\left(k\right)}$ is called the kth partial quotient, and the value $f_k$ is called the kth approximant.

Let $(i_1,i_2,\dots ,i_k,\dots )$ be a fixed infinite multi-index, such that $1\le i_k\le i_{k-1}$ for $k\ge 1,$ where $i_0=N.$ The continued fraction

$$\begin{array}{c}\hfill {\displaystyle \frac{a_{i_1}}{{\displaystyle b_{i_1}+{\displaystyle \frac{a_{i_1,i_2}}{b_{i_1,i_2}+{\displaystyle \frac{a_{i_1,i_2,i_3}}{{\displaystyle b_{i_1,i_2,i_3}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}\end{array}$$

is called the $(i_1,i_2,\dots ,i_k,\dots )$-branch of the branched continued fraction with independent variables (2).

Next, let $e_0=(0,0,\dots ,0),$ $e_k=({\delta }_{k,1},{\delta }_{k,2},\dots ,{\delta }_{k,N})$ be a multi-index, where $1\le k\le N$, ${\delta }_{i,j}$ is a Kronecker symbol. Let us introduce the following sets of multi-indices for $k\ge 1$

$$\begin{array}{c}\hfill {\mathfrak{E}}_k=\{e_{i\left(k\right)}:e_{i\left(k\right)}=e_{i_1,i_2,\dots ,i_k}=e_{i_1}+e_{i_2}+\dots +e_{i_k},i\left(k\right)\in {\mathfrak{I}}_k\}\end{array}$$

and the mapping $\phi$: ${\mathfrak{I}}_k\to {\mathfrak{E}}_k,$ such that $\phi \left(i\left(k\right)\right)=e_{i\left(k\right)}$ for all $i\left(k\right)\in {\mathfrak{I}}_k,$ $k\ge 1.$ It can be shown that the mapping $\phi$ is bijective.

Multidimensional A-fraction with independent variables. A branched continued fraction with independent variables of the form

$$\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i\left(1\right)}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i\left(1\right)}}{z}_{i_1}+\sum _{i_2=1}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+\sum _{i_3=1}^{i_2}\frac{{(-1)}^{{\delta }_{i_2,i_3}}{p}_{e_{i\left(3\right)}}{z}_{i_2}{z}_{i_3}}{{\displaystyle 1+q_{e_{i\left(3\right)}}{z}_{i_3}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}},$$

(3)

where the $p_{e_{i\left(k\right)}}\in \mathbb{C}\setminus \left\{0\right\},$ $q_{e_{i\left(k\right)}}\in \mathbb{C}$, $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $k\ge 1,$ is called a multidimensional A-fraction with independent variables. For each $n\ge 1$ the nth approximant $f_n\left(\mathbf{z}\right)$ of (3) is expressed by

$$\begin{array}{c}\hfill f_n\left(\mathbf{z}\right)=\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i\left(1\right)}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i\left(1\right)}}{z}_{i_1}+\sum _{i_2=1}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}\frac{{(-1)}^{{\delta }_{i_{n-1},i_n}}{p}_{e_{i\left(n\right)}}{z}_{i_{n-1}}{z}_{i_n}}{1+q_{e_{i\left(n\right)}}{z}_{i_n}}}}}}}}}.\end{array}$$

(4)

A multidimensional A-fraction with independent variables (3) is said to correspond at $\mathbf{z}=\mathbf{0}$ to a formal multiple power series $L_{*}\left(\mathbf{z}\right)$ if its sequence of approximants $\left\{f_n\left(\mathbf{z}\right)\right\}$ corresponds to $L_{*}\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{0}.$

The following result was proved in ([16], Theorem 3.5), and for convenience, we present its proof.

Theorem 1.

Every multidimensional A-fraction with independent variables (3) with sequence of approximants $\left\{f_n\left(\mathbf{z}\right)\right\}$ corresponds at $\mathbf{z}=\mathbf{0}$ to a uniquely determined formal multiple power series

$$L\left(\mathbf{z}\right)=\sum _{\left|\mathbf{k}\right|\ge 1}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}},$$

(5)

where $c_{\mathbf{k}}\in \mathbb{C}$, $\left|\mathbf{k}\right|\ge 1.$ The order of correspondence of the nth approximant $f_n\left(\mathbf{z}\right)$ is $(2n+1)$, $n\ge 0,$ and hence the formal Taylor series at $\mathbf{z}=\mathbf{0}$ of $f_n\left(\mathbf{z}\right)$ has the form

$$\begin{array}{c}{f}_n\left(\mathbf{z}\right)=\sum _{\left|\mathbf{k}\right|=1}^{2n}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+\sum _{\left|\mathbf{k}\right|\ge 2n+1}{\gamma }_{\mathbf{k}}^{\left(n\right)}{\mathbf{z}}^{\mathbf{k}},n\ge 1,\end{array}$$

(6)

where ${\gamma }_{\mathbf{k}}^{\left(n\right)}\in \mathbb{C},$ $\left|\mathbf{k}\right|\ge 2n+1$, $n\ge 0.$

Proof. 

Let

$$\begin{array}{c}{Q}_{e_{i\left(n\right)}}^{\left(n\right)}\left(\mathbf{z}\right)=1+q_{e_{i\left(n\right)}}{z}_{i_n},e_{i\left(n\right)}\in {\mathfrak{E}}_n,n\ge 1,\end{array}$$

and

$$\begin{array}{c}{Q}_{e_{i\left(k\right)}}^{\left(n\right)}\left(\mathbf{z}\right)=1+q_{e_{i\left(k\right)}}{z}_{i_k}+\sum _{i_{k+1}=1}^{i_k}{\displaystyle \frac{{(-1)}^{{\delta }_{i_k,i_{k+1}}}{p}_{e_{i(k+1)}}{z}_{i_k}{z}_{i_{k+1}}}{{\displaystyle 1+q_{e_{i(k+1)}}{z}_{i_{k+1}}+\sum _{i_{k+2}=1}^{i_{k+1}}\frac{{(-1)}^{{\delta }_{i_{k+1},i_{k+2}}}{p}_{e_{i(k+2)}}{z}_{i_{k+1}}{z}_{i_{k+2}}}{{\displaystyle 1+q_{e_{i(k+2)}}{z}_{i_{k+2}}+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}\frac{{(-1)}^{{\delta }_{i_{n-1},i_n}}{p}_{e_{i\left(n\right)}}{z}_{i_{n-1}}{z}_{i_n}}{1+q_{e_{i\left(n\right)}}{z}_{i_n}}}}}}}}},\end{array}$$

where $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $0\le k\le n-1$, $n\ge 1$. Then

$$\begin{array}{c}{f}_n\left(\mathbf{z}\right)=\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i\left(1\right)}}{z}_{i_1}}{Q_{e_{i\left(1\right)}}^{\left(n\right)}\left(\mathbf{z}\right)}},n\ge 1.\end{array}$$

Since the equality $Q_{e_{i\left(k\right)}}^{\left(n\right)}\left(\mathbf{0}\right)=1$ holds for all $i\left(k\right)\in {\mathfrak{E}}_k$, $1\le k\le n$, $n\ge 1,$ then for each $i\left(k\right)\in {\mathfrak{E}}_k$, $1\le k\le n$, $n\ge 1,$ the finite branched continued fraction $1/Q_{e_{i\left(k\right)}}^{\left(n\right)}\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{0}$ has a formal multiple power series (5). Then, every nth approximant $f_n\left(\mathbf{z}\right),$ $n\ge 1$ is a function holomorphic in origin, and hence, for each $n\ge 1,$ let the formal multiple power series

$$\begin{array}{c}{f}_n\left(\mathbf{z}\right)=\sum _{\mathbf{k}\ge \mathbf{1}}{\gamma }_{\mathbf{k}}^{\left(n\right)}{\mathbf{z}}^{\mathbf{k}},\end{array}$$

be the expansion of the approximant $f_n\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{0}$.

Since

$$\begin{array}{c}{Q}_{e_{i\left(k\right)}}^{\left(n\right)}\left(\mathbf{z}\right)\not\equiv 0,i\left(k\right)\in {\mathfrak{E}}_k,1\le k\le n,n\ge 1,\end{array}$$

then, using the well-known formula for the difference between two approximants of (3) (see [16] and also [33]), for $n\ge 1$ and $k\ge 1$, we obtain

$$\begin{array}{c}{f}_{n+k}\left(\mathbf{z}\right)-f_n\left(\mathbf{z}\right)=\sum _{i_1=1}^N\sum _{i_2=1}^{i_1}\dots \sum _{i_{n+1}=1}^{i_n}{\displaystyle \frac{{\displaystyle {(-1)}^n{p}_{e_{i\left(1\right)}}{z}_{i_1}\prod _{r=2}^{n+1}{(-1)}^{{\delta }_{i_{k-1},i_k}}{p}_{e_{i\left(k\right)}}{z}_{i_{k-1}}{z}_{i_k}}}{{\displaystyle \prod _{r=1}^{n+1}{Q}_{e_{i\left(r\right)}}^{(n+k)}\left(\mathbf{z}\right)\prod _{r=1}^n{Q}_{e_{i\left(r\right)}}^{\left(n\right)}\left(\mathbf{z}\right)}}}\end{array}$$

in neighborhood of origin. Hence, for arbitrary $n\ge 1$ and $k\ge 1,$ we have

$$\begin{array}{c}\Lambda \left(f_{n+k}\right)-\Lambda \left(f_n\right)=\sum _{\left|\mathbf{k}\right|\ge 2n+1}({\gamma }_{\mathbf{k}}^{(n+k)}-{\gamma }_{\mathbf{k}}^{\left(n\right)}){\mathbf{z}}^{\mathbf{k}}\end{array}$$

in a neighborhood of $\mathbf{z}=\mathbf{0}$. So, for every $n\ge 1$ and $k\ge 1$

$$\begin{array}{c}{\nu }_n=\lambda (\Lambda \left(f_{n+k}\right)-\Lambda \left(f_n\right))=2n+1\end{array}$$

and it tends monotonically to ∞ as $n\to \infty$.

Thus, for each $n\ge 1$, $k\ge 1,$ the relation ${\gamma }_{\mathbf{k}}^{(n+k)}={\gamma }_{\mathbf{k}}^{\left(n\right)}$ holds for any $1\le \left|\mathbf{k}\right|\le 2n$. The multidimensional A-fraction with independent variables (3) corresponds to the formal multiple power series (5), where $c_{\mathbf{k}}={\gamma }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}$ (here, $[·]$ means the integer part of the number) for all $\mathbf{k}\ge \mathbf{0},$ since

$$\begin{array}{c}L\left(\mathbf{z}\right)-\Lambda \left(f_n\right)=\sum _{\left|\mathbf{k}\right|\ge 2n+1}({\gamma }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}-{\gamma }_{\mathbf{k}}^{\left(n\right)}){\mathbf{z}}^{\mathbf{k}}\end{array}$$

for each $n\ge 1$. Hence, the order of correspondence of the nth approximant $f_n\left(\mathbf{z}\right)$ is $(2n+1)$ and the formal multiple power series (6) is a formal Taylor series for $f_n\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{0}$.

Let us prove that this $L\left(\mathbf{z}\right)$ is unique. Assume that the multidimensional A-fraction with independent variables (3) also corresponds to

$$\begin{array}{c}P\left(\mathbf{z}\right)=\sum _{\mathbf{k}\ge \mathbf{1}}{\beta }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}{\mathbf{z}}^{\mathbf{k}}\end{array}$$

at $\mathbf{z}=\mathbf{0}$. Since for any $n\ge 1$

$$\begin{array}{c}P\left(\mathbf{z}\right)-\Lambda \left(f_n\right)=\sum _{\left|\mathbf{k}\right|\ge 2n+1}({\beta }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}-{\gamma }_{\mathbf{k}}^{\left(n\right)}){\mathbf{z}}^{\mathbf{k}},\end{array}$$

then ${\beta }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}={\gamma }_{\mathbf{k}}^{\left(\right[\left|\mathbf{k}\right|/2]+1)}$ for all $\mathbf{k}$ such that $1\le \left|\mathbf{k}\right|\le n$ and $n\ge 1$. That is, the $L\left(\mathbf{z}\right)$ is unique. □

The following results is true.

Theorem 2.

Let $\mathfrak{D}$ be a domain containing the origin ($\mathbf{z}=\mathbf{0}$). Assume that a multidimensional A-fraction with independent variables (3) corresponds at $\mathbf{z}=\mathbf{0}$ to a formal multiple power series (5) and converges uniformly on every compact subset of $\mathfrak{D}$ to a function $f\left(\mathbf{z}\right),$ holomorphic in the domain $\mathfrak{D}.$ Then, the formal multiple power series (5) is the formal Taylor series at $\mathbf{z}=\mathbf{0}$ of the function $f\left(\mathbf{z}\right).$

Proof. 

Since the sequence of approximants $\left\{f_n\left(\mathbf{z}\right)\right\}$ of (3) converges uniformly on every compact subset of the domain $\mathfrak{D}$ to a function $f\left(\mathbf{z}\right)$ holomorphic in $\mathfrak{D},$ then, by Weierstrass’ theorem (see [34]) for arbitrary $\mathbf{k}\ge \mathbf{0}$, we have

$$\begin{array}{c}{\displaystyle \frac{{\partial }^{\left|\mathbf{k}\right|}{f}_n\left(\mathbf{z}\right)}{\partial {\mathbf{z}}^{\mathbf{k}}}}\to {\displaystyle \frac{{\partial }^{\left|\mathbf{k}\right|}f\left(\mathbf{z}\right)}{\partial {\mathbf{z}}^{\mathbf{k}}}}\end{array}$$

on each compact subset of the domain $\mathfrak{D}$. In addition, by Theorem 1 for each $n\ge 1,$ the $\Lambda \left(f_n\right)$ and $L\left(\mathbf{z}\right)$ agree for all homogeneous terms up to and including degree $2n$.

Thus, for any $\mathbf{k}\ge \mathbf{0}$, we obtain

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\left({\displaystyle \frac{{\partial }^{\left|\mathbf{k}\right|}{f}_n}{\partial {\mathbf{z}}^{\mathbf{k}}}}\left(\mathbf{0}\right)\right)& ={\displaystyle \frac{{\partial }^{\left|\mathbf{k}\right|}f}{\partial {\mathbf{z}}^{\mathbf{k}}}}\left(\mathbf{0}\right)\hfill \\ & =\mathbf{k}!c_{\mathbf{k}},\hfill \end{array}$$

where $\mathbf{k}!=k_1!k_2!\dots k_N!$.

Hence,

$$\begin{array}{c}f\left(\mathbf{z}\right)=\sum _{\mathbf{k}\ge \mathbf{1}}\left({\displaystyle \frac{{\partial }^{\left|\mathbf{k}\right|}f}{\partial {\mathbf{z}}^{\mathbf{k}}}}\left(\mathbf{0}\right)\right){\displaystyle \frac{{\mathbf{z}}^{\mathbf{k}}}{\mathbf{k}!}}=\sum _{\mathbf{k}\ge \mathbf{1}}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}\end{array}$$

for all $\mathbf{z}\in \mathfrak{D}$. □

Note that the domain of convergence of the multidimensional A-fraction with independent variables (3) may be wider than the domain of convergence of the multiple power series (5). Then, the branched continued fraction (3) is the analytical continuation of the function represented by this series.

Multidimensional J-fraction with independent variables. A branched continued fraction with independent variables of the form

$$\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i\left(1\right)}}}{{\displaystyle q_{e_{i\left(1\right)}}+z_{i_1}+\sum _{i_2=1}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}}{{\displaystyle q_{e_{i\left(2\right)}}+z_{i_2}+\sum _{i_3=1}^{i_2}\frac{{(-1)}^{{\delta }_{i_2,i_3}}{p}_{e_{i\left(3\right)}}}{{\displaystyle q_{e_{i\left(3\right)}}+z_{i_3}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}},$$

(7)

where $p_{e_{i\left(k\right)}}$, $q_{e_{i\left(k\right)}}$, $e_{i\left(k\right)}\in {\mathfrak{E}}_k,$ $k\ge 1,$ are complex numbers and, in addition, $p_{e_{i\left(k\right)}}\ne 0,$ $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $k\ge 1,$ is called a multidimensional J-fraction with independent variables.

A multidimensional J-fraction with independent variables (7) is said to correspond at $\mathbf{z}=\mathbf{\infty }$ to the formal multiple power series (1) if its sequence of approximants $\left\{f_n^{*}\left(\mathbf{z}\right)\right\}$ corresponds to $L^{*}\left(\mathbf{z}\right)$ at $\mathbf{z}=\mathbf{\infty }.$

Note that multidimensional J-fractions with independent variables are closely related to multidimensional A-fractions with independent variables.

Indeed, if we set $z_i=1/w_i$, $1\le i\le N,$ in (3) and perform the equivalence transformation (see, [33]), setting ${\rho }_{e_{i\left(k\right)}}=w_{i_k},$ $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $k\ge 1,$ then, as a result, we will arrive at a multidimensional J-fraction with independent variables.

Finally, note that a multidimensional J-fraction with independent variables (7) does not always exist that corresponds to the formal multiple power series (1) at $z=\infty$. The necessary and sufficient conditions for the coefficients of the formal multiple power series will be given in the next section for multidimensional A-fractions with independent variables (3).

3. Branched Continued Fraction Construction

3.1. Generalized Gragg’s Algorithm

Let $N\ge 2.$ Let us consider the formal multiple power series (5) and show step by step the process of constructing the multidimensional A-fraction with independent variables (3).

Step 1.1: Let $c_{e_{i_1}}\ne 0$ for $2\le i_1\le N.$ Then, we can rewrite $L\left(\mathbf{z}\right)$ in the form

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)=P_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{c}_{e_{i_1}}{z}_{i_1}{R}_{e_{i_1}}\left(\mathbf{z}\right),\end{array}$$

where

$$\begin{array}{c}\hfill P_{e_0}\left(z_1\right)=\sum _{n=1}^{\infty }{c}_{n{e}_1}{z}_1^n,R_{e_{i_1}}\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\mathbf{k}\ge \mathbf{0}\\ mathbf{k}_j=0,i_1+1\le j\le N\end{array}}{\displaystyle \frac{c_{\mathbf{k}+e_{i_1}}}{c_{e_{i_1}}}}{\mathbf{z}}^{\mathbf{k}}.\end{array}$$

Step 1.2: Let $H_{e_1}\left(n\right)\ne 0$ for $n\ge 1,$ where

$$\begin{array}{c}\hfill H_{e_1}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_1}& c_{2e_1}& \dots & c_{n{e}_1}\\ c_{2e_1}& c_{3e_1}& \dots & c_{(n+1)e_1}\\ \cdots & \cdots & \cdots & \cdots \\ c_{n{e}_1}& c_{(n+1)e_1}& \dots & c_{(2n-1)e_1}\end{array}\right|\end{array}$$

(we note that here $H_{e_1}\left(n\right)$ comprises the Hankel determinants (of dimension n) associated with the formal power series $P_{e_0}\left(z_1\right)$). By Gragg’s algorithm, there exist numbers $p_{n{e}_1}$ and $q_{n{e}_1}$, $n\ge 1,$ such that $p_{n{e}_1}\ne 0,$ $n\ge 1,$ and

$$\begin{array}{c}\hfill P_{e_0}\left(z_1\right)=\sum _{n=1}^{\infty }{c}_{n{e}_1}{z}_1^n\sim {\displaystyle \frac{p_{e_1}{z}_1}{{\displaystyle 1+q_{e_1}{z}_1-\frac{p_{2e_1}{z}_1^2}{{\displaystyle 1+q_{2e_1}{z}_1-\frac{p_{3e_1}{z}_1^2}{1+q_{3e_1}{z}_1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}=F_{e_0}\left(z_1\right),\end{array}$$

where the symbol ‘∼’ means the correspondence between $P_{e_0}\left(z_1\right)$ and $F_{e_0}\left(z_1\right)$ (at the origin). The coefficients $p_{n{e}_1}$ and $q_{n{e}_1}$, $n\ge 1,$ are given by the formulas

$$\begin{array}{c}\hfill p_{(n+1)e_1}={\displaystyle \frac{{\sigma }_{n{e}_1}}{{\sigma }_{(n-1)e_1}}},q_{(n+1)e_1}={\tau }_{(n-1)e_1}-{\tau }_{n{e}_1},n\ge 0,\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_{n{e}_1}=\sum _{r=0}^n{c}_{(2n+1-r)e_1}{B}_{n{e}_1}\left(r\right),{\tau }_{n{e}_1}{\sigma }_{n{e}_1}=\sum _{r=0}^n{c}_{(2n+2-r)e_1}{B}_{n{e}_1}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{(n+1)e_1}\left(r\right)=B_{n{e}_1}\left(r\right)+q_{(n+1)e_1}{B}_{n{e}_1}(r-1)-p_{(n+1)e_1}{B}_{(n-1)e_1}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{-e_1}=B_{0e_1}\left(0\right)=B_{(n+1)e_1}\left(0\right)=1,{\tau }_{-e_1}=B_{(n-1)e_1}(-1)=B_{n{e}_1}(n+1)=0.\end{array}$$

Thus, we can write

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{c}_{e_{i_1}}{z}_{i_1}{R}_{e_{i_1}}\left(\mathbf{z}\right).\end{array}$$

Step 1.3: Let $H_{e_{i_1}}\left(n\right)\ne 0$ for $2\le i_1\le N$ and $n\ge 1,$ where

$$H_{e_{i_1}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_1}}& c_{2e_{i_1}}& \dots & c_{n{e}_{i_1}}\\ c_{e_{2e_{i_1}}}& c_{3e_{i_1}}& \dots & c_{(n+1)e_{i_1}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{n{e}_{i_1}}& c_{(n+1)e_{i_1}}& \dots & c_{(2n-1)e_{i_1}}\end{array}\right|.$$

(8)

By Gragg’s algorithm, for each $2\le i_1\le N$, there exists numbers $p_{n{e}_{i_1}}^{\prime }$ and $q_{n{e}_{i_1}}^{\prime }$, $n\ge 1,$ such that $p_{n{e}_{i_1}}^{\prime }\ne 0$, $n\ge 1,$ and

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{c}_{n{e}_{i_1}}{z}_{i_1}^n\sim {\displaystyle \frac{p_{e_{i_1}}^{\prime }{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}^{\prime }{z}_{i_1}-\frac{p_{2e_{i_1}}^{\prime }{z}_{i_1}^2}{{\displaystyle 1+q_{2e_{i_1}}^{\prime }{z}_{i_1}-\frac{p_{3e_{i_1}}^{\prime }{z}_{i_1}^2}{1+q_{3e_{i_1}}^{\prime }{z}_{i_1}{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}.\end{array}$$

The coefficients $p_{n{e}_{i_1}}^{\prime }$ and $q_{n{e}_{i_1}}^{\prime }$, $n\ge 1$ are given by the formulas

$$\begin{array}{c}\hfill p_{(n+1)e_{i_1}}^{\prime }={\displaystyle \frac{{\sigma }_{n{e}_{i_1}}}{{\sigma }_{(n-1)e_{i_1}}}},q_{(n+1)e_{i_1}}^{\prime }={\tau }_{(n-1)e_{i_1}}-{\tau }_{n{e}_{i_1}},n\ge 0,\end{array}$$

where

$${\sigma }_{n{e}_{i_1}}=\sum _{r=0}^n{c}_{(2n+1-r)e_{i_1}}{B}_{n{e}_{i_1}}\left(r\right),{\tau }_{n{e}_{i_1}}{\sigma }_{n{e}_{i_1}}=\sum _{r=0}^n{c}_{(2n+2-r)e_{i_1}}{B}_{n{e}_{i_1}}\left(r\right),$$

(9)

and for $1\le r\le n+1,$

$$B_{(n+1)e_{i_1}}\left(r\right)=B_{n{e}_{i_1}}\left(r\right)+q_{(n+1)e_{i_1}}{B}_{n{e}_{i_1}}(r-1)-p_{(n+1)e_{i_1}}{B}_{(n-1)e_{i_1}}(r-2)$$

(10)

with the initial conditions

$${\sigma }_{-e_{i_1}}=B_{0e_{i_1}}\left(0\right)=B_{(n+1)e_{i_1}}\left(0\right)=1,{\tau }_{-e_{i_1}}=B_{(n-1)e_{i_1}}(-1)=B_{n{e}_{i_1}}(n+1)=0.$$

(11)

Since

$$c_{e_{i_1}}=c_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)={\displaystyle \frac{{\sigma }_{0e_{i_1}}}{{\sigma }_{-e_{i_1}}}}=p_{e_{i_1}}^{\prime },2\le i_1\le N,$$

we set $p_{e_{i_1}}=p_{e_{i_1}}^{\prime },$ $2\le i_1\le N.$

Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{p}_{e_{i_1}}{z}_{i_1}{R}_{e_{i_1}}\left(\mathbf{z}\right).\end{array}$$

Step 1.4: For each $2\le i_1\le N$ by

$$R_{e_{i_1}}^{\prime }\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\left|\mathbf{k}\right|\ge 0\\ mathbf{k}_j=0,i_1+1\le j\le N\end{array}}{c}_{\mathbf{k}}^{e_{i_1}}{\mathbf{z}}^{\mathbf{k}}$$

(12)

we denote a formal multiple power series reciprocal to $R_{e_{i_1}}\left(\mathbf{z}\right).$ The coefficients of (12) are uniquely determined by the recurrence relations

$$c_{\mathbf{k}}^{e_{i_1}}=-\sum _{\left|\mathbf{r}\right|=1}^{\left|\mathbf{k}\right|}{c}_{\mathbf{k}-\mathbf{r}}^{e_{i_1}}{\displaystyle \frac{c_{\mathbf{r}+e_{i_1}}}{c_{e_{i_1}}}},$$

(13)

where $c_{\mathbf{0}}^{e_{i_1}}=1$; moreover, $c_{\mathbf{k}}^{e_{i_1}}=0,$ if there exists an index $j,$ $1\le j\le N,$ such that $k_j<0.$

Thus, we can write

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{R_{e_{i_1}}^{\prime }\left(\mathbf{z}\right)}}.\end{array}$$

The next construction of the multidimensional A-fraction with independent variables will be carried out using the ideas outlined in Steps 1.1–1.4.

Step 2.1: Let $c_{e_{i_2}}^{e_{i_1}}\ne 0$ for $2\le i_2\le i_1$ and $2\le i_1\le N.$ In addition, for the formation of partial denominators of the multidimensional A-fraction with independent variables, we set the following conditions $c_{n{e}_{i_2}}^{e_{i_1}}=0$ for $1\le i_2\le i_1-1,$ $2\le i_1\le N$ and $n\ge 1.$ Then, for each $2\le i_1\le N$, we can rewrite the formal multiple power series (12) in the form

$$\begin{array}{c}\hfill R_{e_{i_1}}^{\prime }\left(\mathbf{z}\right)=1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+z_{i_1}{P}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}{c}_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}{R}_{e_{i\left(2\right)}}\left(\mathbf{z}\right),\end{array}$$

where

$$\begin{array}{c}\hfill P_{e_{i_1}}\left(z_1\right)=\sum _{n=1}^{\infty }{c}_{e_{i_1}+n{e}_1}^{e_{i_1}}{z}_1^n,R_{e_{i\left(2\right)}}\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\left|\mathbf{k}\right|\ge 0\\ mathbf{k}_j=0,i_2+1\le j\le N\end{array}}{\displaystyle \frac{c_{\mathbf{k}+e_{i\left(2\right)}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}}{\mathbf{z}}^{\mathbf{k}}.\end{array}$$

Since

$$\begin{array}{c}\hfill c_{e_{i_1}}^{e_{i_1}}=-{\displaystyle \frac{c_{2e_{i_1}}}{c_{e_{i_1}}}}=-{\displaystyle \frac{c_{2e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}{{\sigma }_{0e_{i_1}}}}=-{\tau }_{0e_{i_1}}=q_{e_{i_1}}^{\prime },2\le i_1\le N,\end{array}$$

we set $q_{e_{i_1}}=q_{e_{i_1}}^{\prime }$, $2\le i_1\le N.$

Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{P}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}{c}_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}{R}_{e_{i\left(2\right)}}\left(\mathbf{z}\right)}}}.\end{array}$$

Step 2.2: Let $H_{e_{i_1}+e_1}^{e_{i_1}}\left(n\right)\ne 0$ for $2\le i_1\le N$ and $n\ge 1,$ where

$$H_{e_{i_1}+e_1}^{e_{i_1}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_1}+e_1}^{e_{i_1}}& c_{e_{i_1}+2e_1}^{e_{i_1}}& \dots & c_{e_{i_1}+n{e}_1}^{e_{i_1}}\\ c_{e_{i_1}+2e_1}^{e_{i_1}}& c_{e_{i_1}+3e_1}^{e_{i_1}}& \dots & c_{e_{i_1}+(n+1)e_1}^{e_{i_1}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{e_{i_1}+n{e}_1}^{e_{i_1}}& c_{e_{i_1}+(n+1)e_1}^{e_{i_1}}& \dots & c_{e_{i_1}+(2n-1)e_1}^{e_{i_1}}\end{array}\right|.$$

By Gragg’s algorithm, for each $2\le i_1\le N$ there exist numbers $p_{e_{i_1}+n{e}_1}$ and $q_{e_{i_1}+n{e}_1}$, $n\ge 1,$ such that $p_{e_{i_1}+n{e}_1}\ne 0$, $n\ge 1,$ and

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{c}_{e_{i_1}+n{e}_1}^{e_{i_1}}{z}_1^n\sim {\displaystyle \frac{p_{e_{i_1}+e_1}{z}_1}{{\displaystyle 1+q_{e_{i_1}+e_1}{z}_1-\frac{p_{e_{i_1}+2e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i_1}+2e_1}{z}_1-\frac{p_{e_{i_1}+3e_1}{z}_1^2}{1+q_{e_{i_1}+3e_1}{z}_1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}=F_{e_{i_1}}\left(z_1\right).\end{array}$$

The coefficients $p_{e_{i_1}+n{e}_1}$ and $q_{e_{i_1}+n{e}_1},$ $n\ge 1$ are given by the formulas

$$\begin{array}{c}\hfill p_{e_{i_1}+(n+1)e_1}={\displaystyle \frac{{\sigma }_{e_{i_1}+n{e}_1}^{e_{i_1}}}{{\sigma }_{e_{i_1}+(n-1)e_1}^{e_{i_1}}}},q_{e_{i_1}+(n+1)e_1}={\tau }_{e_{i_1}+(n-1)e_1}^{e_{i_1}}-{\tau }_{e_{i_1}+n{e}_1}^{e_{i_1}},n\ge 0,\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_{e_{i_1}+n{e}_1}^{e_{i_1}}=\sum _{r=0}^n{c}_{e_{i_1}+(2n+1-r)e_1}^{e_{i_1}}{B}_{e_{i_1}+n{e}_1}^{e_{i_1}}\left(r\right),{\tau }_{e_{i_1}+n{e}_1}^{e_{i_1}}{\sigma }_{e_{i_1}+n{e}_1}^{e_{i_1}}=\sum _{r=0}^n{c}_{e_{i_1}+(2n+2-r)e_1}^{e_{i_1}}{B}_{e_{i_1}+n{e}_1}^{e_{i_1}}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{e_{i_1}+(n+1)e_1}^{e_{i_1}}\left(r\right)=B_{e_{i_1}+n{e}_1}^{e_{i_1}}\left(r\right)+q_{e_{i_1}+(n+1)e_1}{B}_{e_{i_1}+n{e}_1}^{e_{i_1}}(r-1)-p_{e_{i_1}+(n+1)e_1}{B}_{e_{i_1}+(n-1)e_1}^{e_{i_1}}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{e_{i_1}-e_1}^{e_{i_1}}=B_{e_{i_1}+0e_1}^{e_{i_1}}\left(0\right)=B_{e_{i_1}+(n+1)e_1}^{e_{i_1}}\left(0\right)=1,{\tau }_{e_{i_1}-e_1}^{e_{i_1}}=B_{e_{i_1}+(n-1)e_1}^{e_{i_1}}(-1)=B_{e_{i_1}+n{e}_1}^{e_{i_1}}(n+1)=0.\end{array}$$

Thus, we can write

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}{c}_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}{R}_{e_{i\left(2\right)}}\left(\mathbf{z}\right)}}}.\end{array}$$

Step 2.3: Let $H_{e_{i_1}+e_{i_2}}^{e_{i_1}}\left(n\right)\ne 0$ for $2\le i_2\le i_1-1$, $2\le i_1\le N$ and $n\ge 1,$ where

$$\begin{array}{c}\hfill H_{e_{i_1}+e_{i_2}}^{e_{i_1}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_1}+e_{i_2}}^{e_{i_1}}& c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}& \dots & c_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}\\ c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}& c_{e_{i_1}+3e_{i_2}}^{e_{i_1}}& \dots & c_{e_{i_1}+(n+1)e_{i_2}}^{e_{i_1}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}& c_{e_{i_1}+(n+1)e_{i_2}}^{e_{i_1}}& \dots & c_{e_{i_1}+(2n-1)e_{i_2}}^{e_{i_1}}\end{array}\right|.\end{array}$$

Then, by Gragg’s algorithm, for each $2\le i_2\le i_1-1$ and $2\le i_1\le N$, there exist numbers $p_{e_{i_1}+n{e}_{i_2}}^{\prime }$ and $q_{e_{i_1}+n{e}_{i_2}}^{\prime }$, $n\ge 1,$ such that $p_{e_{i_1}+n{e}_{i_2}}^{\prime }\ne 0$, $n\ge 1,$ and

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{c}_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}{z}_{i_2}^n\sim {\displaystyle \frac{p_{e_{i_1}+e_{i_2}}^{\prime }{z}_{i_2}}{{\displaystyle 1+q_{e_{i_1}+e_{i_2}}^{\prime }{z}_{i_2}-\frac{p_{e_{i_1}+2e_{i_2}}^{\prime }{z}_{i_2}^2}{{\displaystyle 1+q_{e_{i_1}+2e_{i_2}}^{\prime }{z}_{i_2}-\frac{p_{e_{i_1}+3e_{i_2}}^{\prime }{z}_{i_2}^2}{1+q_{e_{i_1}+3e_{i_2}}^{\prime }{z}_{i_2}{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}.\end{array}$$

The coefficients $p_{e_{i_1}+n{e}_{i_2}}^{\prime }$ and $q_{e_{i_1}+n{e}_{i_2}}^{\prime }$, $n\ge 1$ are given by the formulas

$$\begin{array}{c}\hfill p_{e_{i_1}+(n+1)e_{i_2}}^{\prime }={\displaystyle \frac{{\sigma }_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}}{{\sigma }_{e_{i_1}+(n-1)e_{i_2}}^{e_{i_1}}}},q_{e_{i_1}+(n+1)e_{i_2}}^{\prime }={\tau }_{e_{i_1}+(n-1)e_{i_2}}^{e_{i_1}}-{\tau }_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}\mathrm{for}n\ge 0,\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}=\sum _{r=0}^n{c}_{e_{i_1}+(2n+1-r)e_{i_2}}^{e_{i_1}}{B}_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}\left(r\right),{\tau }_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}{\sigma }_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}=\sum _{r=0}^n{c}_{e_{i_1}+(2n+2-r)e_{i_2}}^{e_{i_1}}{B}_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{e_{i_1}+(n+1)e_{i_2}}^{e_{i_1}}\left(r\right)=B_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}\left(r\right)+q_{e_{i_1}+(n+1)e_{i_2}}{B}_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}(r-1)-p_{e_{i_1}+(n+1)e_{i_2}}{B}_{e_{i_1}+(n-1)e_{i_2}}^{e_{i_1}}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{e_{i_1}-e_{i_2}}^{e_{i_1}}=B_{e_{i_1}+0e_{i_2}}^{e_{i_1}}\left(0\right)=B_{e_{i_1}+(n+1)e_{i_2}}^{e_{i_1}}\left(0\right)=1,{\tau }_{e_{i_1}-e_{i_2}}^{e_{i_1}}=B_{e_{i_1}+(n-1)e_{i_2}}^{e_{i_1}}(-1)=B_{e_{i_1}+n{e}_{i_2}}^{e_{i_1}}(n+1)=0.\end{array}$$

Since for $2\le i_2\le i_1-1$, $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{e_{i\left(2\right)}}^{e_{i_1}}& =c_{e_{i\left(2\right)}}^{e_{i_1}}{B}_{e_{i_1}+0e_{i_2}}^{e_{i_1}}\left(0\right)\hfill \\ & ={\displaystyle \frac{{\sigma }_{e_{i_1}+0e_{i_2}}^{e_{i_1}}}{{\sigma }_{e_{i_1}-e_{i_2}}^{e_{i_1}}}}\hfill \\ & =p_{e_{i\left(2\right)}}^{\prime },\hfill \end{array}$$

and for $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{2e_{i_1}}^{e_{i_1}}& =-{\displaystyle \frac{c_{e_{i_1}}^{e_{i_1}}{c}_{2e_{i_1}}+c_{3e_{i_2}}}{c_{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{c_{3e_{i_1}}{c}_{e_{i_1}}-{\left(c_{2e_{i_1}}\right)}^2}{{\left(c_{e_{i_1}}\right)}^2}}\hfill \\ & =-{\displaystyle \frac{c_{3e_{i_1}}+c_{2e_{i_1}}{q}_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}{c_{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{c_{3e_{i_1}}{B}_{e_{i_1}}\left(0\right)+c_{2e_{i_1}}{B}_{e_{i_1}}\left(1\right)}{c_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}}\hfill \\ & =-{\displaystyle \frac{{\sigma }_{e_{i_1}}}{{\sigma }_{0e_{i_1}}}}\hfill \\ & =-p_{2e_{i_1}}^{\prime },\hfill \end{array}$$

we set $p_{e_{i\left(2\right)}}=p_{e_{i\left(2\right)}}^{\prime }$, $p_{2e_{i_1}}=p_{2e_{i_1}}^{\prime },$ $2\le i_2\le i_1-1$, $2\le i_1\le N.$ Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}{R}_{e_{i\left(2\right)}}\left(\mathbf{z}\right)}}}.\end{array}$$

Step 2.4: Let for each $2\le i_2\le i_1$ and $2\le i_1\le N$

$$\begin{array}{c}{R}_{e_{i\left(2\right)}}^{\prime }\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\left|\mathbf{k}\right|\ge 0\\ mathbf{k}_j=0,i_2+1\le j\le N\end{array}}{c}_{\mathbf{k}}^{e_{i\left(2\right)}}{\mathbf{z}}^{\mathbf{k}}\end{array}$$

(14)

be reciprocal to the formal multiple power series $R_{e_{i\left(2\right)}}\left(\mathbf{z}\right).$ It is known that the coefficients $c_{\mathbf{k}}^{e_{i\left(2\right)}}$, $\left|\mathbf{k}\right|\ge 1$, $k_j=0,$ $i_k+1\le j\le N$ of (14) are uniquely determined by a recurrence formula

$$\begin{array}{c}\hfill c_{\mathbf{k}}^{e_{i\left(2\right)}}=-\sum _{\left|\mathbf{r}\right|=1}^{\left|\mathbf{k}\right|}{c}_{\mathbf{k}-\mathbf{r}}^{e_{i\left(2\right)}}{\displaystyle \frac{c_{\mathbf{r}+e_{i\left(2\right)}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}},\end{array}$$

where $c_{\mathbf{0}}^{e_{i\left(2\right)}}=1$; moreover, $c_{\mathbf{k}}^{e_{i\left(2\right)}}=0,$ if there exists an index j such that $1\le j\le N$ and that $k_j<0.$ Then

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{R_{e_{i\left(2\right)}}^{\prime }\left(\mathbf{z}\right)}}}}.\end{array}$$

Let us continue the construction of the multidimensional A-fraction with independent variables.

Step 3.1: Let $c_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}\ne 0$ for $1\le i_3\le i_2,$ $2\le i_2\le i_1$, $2\le i_1\le N,$ and $c_{n{e}_{i_3}}^{e_{i\left(2\right)}}=0$ for $1\le i_3\le i_2-1,$ $2\le i_2\le i_1$, $2\le i_1\le N,$ and $n\ge 1.$ Then, for each $2\le i_2\le i_1$ and $2\le i_1\le N$, we have

$$\begin{array}{c}\hfill R_{e_{i\left(2\right)}}^{\prime }\left(\mathbf{z}\right)=1+c_{e_{i_2}}^{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{P}_{e_{i\left(2\right)}}\left(z_1\right)+\sum _{i_3=2}^{i_2}{c}_{e_{i_2,i_3}}^{e_{i\left(2\right)}}{z}_{i_2}{z}_{i_3}{R}_{e_{i\left(3\right)}}\left(\mathbf{z}\right),\end{array}$$

where

$$\begin{array}{c}\hfill P_{e_{i\left(2\right)}}\left(z_1\right)=\sum _{n=1}^{\infty }{c}_{e_{i_2}+n{e}_1}^{e_{i\left(2\right)}}{z}_1^n,R_{e_{i\left(3\right)}}\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\left|\mathbf{k}\right|\ge 0\\ {\mathbf{k}}_j=0,i_3+1\le j\le N\end{array}}{\displaystyle \frac{c_{\mathbf{k}+e_{i_2,i_3}}^{e_{i\left(2\right)}}}{c_{e_{i_2,i_3}}^{e_{i\left(2\right)}}}}{\mathbf{z}}^{\mathbf{k}}.\end{array}$$

Since for $2\le i_2\le i_1-1$, $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{e_{i_2}}^{e_{i\left(2\right)}}& =-{\displaystyle \frac{c_{e_{i_2}+e_{i\left(2\right)}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}{B}_{e_{i_1}+0e_{i_2}}\left(0\right)}{{\sigma }_{e_{i_1}+0e_{i_2}}^{e_{i_1}}}}\hfill \\ & =-{\tau }_{e_{i_1}+0e_{i_2}}^{e_{i_1}}\hfill \\ & =q_{e_{i\left(2\right)}}^{\prime },\hfill \end{array}$$

and for $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{e_{i_1}}^{2e_{i_1}}& =-{\displaystyle \frac{c_{3e_{i_1}}^{e_{i_1}}}{c_{2e_{i_1}}^{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{c_{2e_{i_1}}^{e_{i_1}}{c}_{2e_{i_1}}+c_{e_{i_1}}^{e_{i_1}}{c}_{3e_{i_1}}+c_{4e_{i_1}}}{c_{e_{i_1}}^{e_{i_1}}{c}_{2e_{i_1}}+c_{3e_{i_1}}}}\hfill \\ & ={\displaystyle \frac{c_{2e_{i_1}}}{c_{e_{i_1}}}}-{\displaystyle \frac{c_{4e_{i_1}}{c}_{e_{i_1}}-c_{3e_{i_1}}{c}_{2e_{i_1}}}{c_{3e_{i_1}}{c}_{e_{i_1}}-{\left(c_{2e_{i_1}}\right)}^2}}\hfill \\ & ={\displaystyle \frac{c_{2e_{i_1}}}{c_{e_{i_1}}}}-{\displaystyle \frac{c_{4e_{i_1}}+c_{3e_{i_1}}{q}_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}{c_{3e_{i_1}}{B}_{e_{i_1}}\left(0\right)+c_{2e_{i_1}}{q}_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}}\hfill \\ & ={\displaystyle \frac{c_{2e_{i_1}}}{c_{e_{i_1}}}}-{\displaystyle \frac{c_{4e_{i_1}}+c_{3e_{i_1}}{B}_{e_{i_1}}\left(1\right)}{c_{3e_{i_1}}{B}_{e_{i_1}}\left(0\right)+c_{2e_{i_1}}{B}_{e_{i_1}}\left(1\right)}}\hfill \\ & ={\displaystyle \frac{c_{2e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}{{\sigma }_{0e_{i_1}}}}-{\displaystyle \frac{c_{4e_{i_1}}{B}_{e_{i_1}}\left(0\right)+c_{3e_{i_1}}{B}_{e_{i_1}}\left(1\right)}{{\sigma }_{e_{i_1}}}}\hfill \\ \hfill & ={\tau }_{0e_{i_1}}-{\tau }_{e_{i_1}}\hfill \\ & =q_{2e_{i_1}}^{\prime },\hfill \end{array}$$

we set $q_{e_{i\left(2\right)}}=q_{e_{i\left(2\right)}}^{\prime }$, $q_{2e_{i_1}}=q_{2e_{i_1}}^{\prime },$ $2\le i_2\le i_1-1$, $2\le i_1\le N.$ Thus,

$$\begin{array}{cc}\hfill L\left(\mathbf{z}\right)& \sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{P}_{e_{i\left(2\right)}}\left(z_1\right)+\sum _{i_3=2}^{i_2}{c}_{e_{i_2,i_3}}^{e_{i\left(2\right)}}{z}_{i_2}{z}_{i_3}{R}_{e_{i\left(3\right)}}\left(\mathbf{z}\right)}}}}}.\hfill \end{array}$$

Step 3.2: Let $H_{e_{i_2}+e_1}^{e_{i\left(2\right)}}\left(n\right)\ne 0$ for $2\le i_2\le i_1,$ $2\le i_1\le N$ and $n\ge 1,$ where

$$\begin{array}{c}\hfill H_{e_{i_2}+e_1}^{e_{i\left(2\right)}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_2}+e_1}^{e_{i\left(2\right)}}& c_{e_{i_2}+2e_1}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+n{e}_1}^{e_{i\left(2\right)}}\\ c_{e_{i_2}+2e_1}^{e_{i\left(2\right)}}& c_{e_{i_2}+3e_1}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+(n+1)e_1}^{e_{i\left(2\right)}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{e_{i_2}+n{e}_1}^{e_{i\left(2\right)}}& c_{e_{i_2}+(n+1)e_1}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+(2n-1)e_1}^{e_{i\left(2\right)}}\end{array}\right|.\end{array}$$

Then, by Gragg’s algorithm, for each $2\le i_2\le i_1$ and $2\le i_1\le N$, there exist numbers $p_{e_{i\left(2\right)}+n{e}_1}$ and $q_{e_{i\left(2\right)}+n{e}_1}$, $n\ge 1,$ such that $p_{e_{i\left(2\right)}+n{e}_1}\ne 0$ for $n\ge 1$ and

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{c}_{e_{i_2}+n{e}_1}^{e_{i\left(2\right)}}{z}_1^n\sim {\displaystyle \frac{p_{e_{i\left(2\right)}+e_1}{z}_1}{{\displaystyle 1+q_{e_{i\left(2\right)}+e_1}{z}_1-\frac{p_{e_{i\left(2\right)}+2e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i\left(2\right)}+2e_1}{z}_1-\frac{p_{e_{i\left(2\right)}+3e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i\left(2\right)}+3e_1}{z}_1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}=F_{e_{i\left(2\right)}}\left(z_1\right).\end{array}$$

The coefficients $p_{e_{i\left(2\right)}+n{e}_1}$ and $q_{e_{i\left(2\right)}+n{e}_1},$ $n\ge 1$ are given by the formulas for $n\ge 0,$

$$\begin{array}{c}\hfill p_{e_{i\left(2\right)}+(n+1)e_1}={\displaystyle \frac{{\sigma }_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}}{{\sigma }_{e_{i\left(2\right)}+(n-1)e_1}^{e_{i\left(2\right)}}}},q_{e_{i\left(2\right)}+(n+1)e_1}={\tau }_{e_{i\left(2\right)}+(n-1)e_1}^{e_{i\left(2\right)}}-{\tau }_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}},\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}=\sum _{r=0}^n{c}_{e_{i\left(2\right)}+(2n+1-r)e_1}^{e_{i\left(2\right)}}{B}_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}\left(r\right),{\tau }_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}{\sigma }_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}=\sum _{r=0}^n{c}_{e_{i\left(2\right)}+(2n+2-r)e_1}^{e_{i\left(2\right)}}{B}_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{e_{i\left(2\right)}+(n+1)e_1}^{e_{i\left(2\right)}}\left(r\right)=B_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}\left(r\right)+q_{e_{i\left(2\right)}+(n+1)e_1}{B}_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}(r-1)-p_{e_{i\left(2\right)}+(n+1)e_1}{B}_{e_{i\left(2\right)}+(n-1)e_1}^{e_{i\left(2\right)}}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(2\right)}-e_1}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+0e_1}^{e_{i\left(2\right)}}\left(0\right)=B_{e_{i\left(2\right)}+(n+1)e_1}^{e_{i\left(2\right)}}\left(0\right)=1,{\tau }_{e_{i\left(2\right)}-e_1}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+(n-1)e_1}^{e_{i\left(2\right)}}(-1)=B_{e_{i\left(2\right)}+n{e}_1}^{e_{i\left(2\right)}}(n+1)=0.\end{array}$$

Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{F}_{e_{i\left(2\right)}}\left(z_1\right)+\sum _{i_3=2}^{i_2}{c}_{e_{i_2,i_3}}^{e_{i\left(2\right)}}{z}_{i_2}{z}_{i_3}{R}_{e_{i\left(3\right)}}\left(\mathbf{z}\right)}}}}}.\end{array}$$

Step 3.3: Let $H_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}\left(n\right)\ne 0$ for $2\le i_3\le i_2-1$, $2\le i_2\le i_1$, $2\le i_1\le N$ and $n\ge 1,$ where

$$\begin{array}{c}\hfill H_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}& c_{e_{i_2}+2e_{i_3}}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+n{e}_{i_3}}^{e_{i\left(2\right)}}\\ c_{e_{i_2}+2e_{i_3}}^{e_{i\left(2\right)}}& c_{e_{i_2}+3e_{i_3}}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+(n+1)e_{i_3}}^{e_{i\left(2\right)}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{e_{i_2}+n{e}_{i_3}}^{e_{i\left(2\right)}}& c_{e_{i_2}+(n+1)e_{i_3}}^{e_{i\left(2\right)}}& \dots & c_{e_{i_2}+(2n-1)e_{i_3}}^{e_{i\left(2\right)}}\end{array}\right|.\end{array}$$

Then, by Gragg’s algorithm, for each $2\le i_3\le i_2-1,$ $2\le i_2\le i_1$ and $2\le i_1\le N$ there exist numbers $p_{e_{i\left(2\right)}+n{e}_{i_3}}^{\prime }$ and $q_{e_{i\left(2\right)}+n{e}_{i_3}}^{\prime }$, $n\ge 1,$ such that $p_{e_{i\left(2\right)}+n{e}_{i_3}}^{\prime }\ne 0$, $n\ge 1,$ and

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{c}_{e_{i_2}+n{e}_{i_3}}^{e_{i\left(2\right)}}{z}_{i_3}^n\sim {\displaystyle \frac{p_{e_{i\left(3\right)}}^{\prime }{z}_{i_3}}{{\displaystyle 1+q_{e_{i\left(3\right)}}^{\prime }{z}_{i_3}-\frac{p_{e_{i\left(2\right)}+2e_{i_3}}^{\prime }{z}_{i_3}^2}{{\displaystyle 1+q_{e_{i\left(2\right)}+2e_{i_3}}^{\prime }{z}_{i_3}-\frac{p_{e_{i\left(2\right)}+3e_{i_3}}^{\prime }{z}_{i_3}^2}{{\displaystyle 1+q_{e_{i\left(2\right)}+3e_{i_3}}^{\prime }{z}_{i_3}{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}.\end{array}$$

The coefficients $p_{e_{i\left(2\right)}+n{e}_{i_3}}^{\prime }$ and $q_{e_{i\left(2\right)}+n{e}_{i_3}}^{\prime }$, $n\ge 1$ are given by the formulas for $n\ge 0,$

$$\begin{array}{c}\hfill p_{e_{i\left(2\right)}+(n+1)e_{i_3}}^{\prime }={\displaystyle \frac{{\sigma }_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}}{{\sigma }_{e_{i\left(2\right)}+(n-1)e_{i_3}}^{e_{i\left(2\right)}}}},q_{e_{i\left(2\right)}+(n+1)e_{i_3}}^{\prime }={\tau }_{e_{i\left(2\right)}+(n-1)e_{i_3}}^{e_{i\left(2\right)}}-{\tau }_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}},\end{array}$$

where

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}=\sum _{r=0}^n{c}_{e_{i\left(2\right)}+(2n+1-r)e_{i_3}}^{e_{i\left(2\right)}}{B}_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}\left(r\right),{\tau }_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}{\sigma }_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}=\sum _{r=0}^n{c}_{e_{i\left(2\right)}+(2n+2-r)e_{i_3}}^{e_{i\left(2\right)}}{B}_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{e_{i\left(2\right)}+(n+1)e_{i_3}}^{e_{i\left(2\right)}}\left(r\right)=B_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}\left(r\right)+q_{e_{i\left(2\right)}+(n+1)e_{i_3}}{B}_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}(r-1)-p_{e_{i\left(2\right)}+(n+1)e_{i_3}}{B}_{e_{i\left(2\right)}+(n-1)e_{i_3}}^{e_{i\left(2\right)}}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(2\right)}-e_{i_3}}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+0e_{i_3}}^{e_{i\left(2\right)}}\left(0\right)=B_{e_{i\left(2\right)}+(n+1)e_{i_3}}^{e_{i\left(2\right)}}\left(0\right)=1,{\tau }_{e_{i\left(2\right)}-e_{i_3}}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+(n-1)e_{i_3}}^{e_{i\left(2\right)}}(-1)=B_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}(n+1)=0.\end{array}$$

Since for $2\le i_3\le i_2-1$, $2\le i_2\le i_1,$ $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}& =c_{e_{i_2}+e_{i_3}}^{e_{i\left(2\right)}}{B}_{e_{i\left(2\right)}+0e_{i_3}}^{e_{i\left(2\right)}}\left(0\right)\hfill \\ & ={\displaystyle \frac{{\sigma }_{e_{i\left(2\right)}+0e_{i_3}}^{e_{i\left(2\right)}}}{{\sigma }_{e_{i\left(2\right)}-e_{i_3}}^{e_{i\left(2\right)}}}}\hfill \\ & =p_{e_{i\left(3\right)}}^{\prime },\hfill \end{array}$$

and for $2\le i_2\le i_1-1$, $3\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{2e_{i_2}}^{e_{i\left(2\right)}}& =-c_{e_{i_2}}^{e_{i\left(2\right)}}{\displaystyle \frac{c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}}-{\displaystyle \frac{c_{e_{i_1}+3e_{i_2}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{{\left(c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}\right)}^2-c_{e_{i\left(2\right)}}^{e_{i_1}}{c}_{e_{i_1}+3e_{i_2}}^{e_{i_1}}}{{\left(c_{e_{i\left(2\right)}}^{e_{i_1}}\right)}^2}}\hfill \\ \hfill & =-{\displaystyle \frac{c_{e_{i_1}+3e_{i_2}}^{e_{i_1}}+c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}{q}_{e_{i\left(2\right)}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}}\hfill \\ & =-{\displaystyle \frac{c_{e_{i_1}+3e_{i_2}}^{e_{i_1}}{B}_{e_{i\left(2\right)}}^{e_{i_1}}\left(0\right)+c_{e_{i_1}+2e_{i_2}}^{e_{i_1}}{B}_{e_{i\left(2\right)}}^{e_{i_1}}\left(1\right)}{c_{e_{i\left(2\right)}}^{e_{i_1}}{B}_{e_{i_1}+0e_{i_2}}^{e_{i_1}}\left(0\right)}}\hfill \\ & =-{\displaystyle \frac{{\sigma }_{e_{i\left(2\right)}}^{e_{i_1}}}{{\sigma }_{e_{i_1}+0e_{i_2}}^{e_{i_1}}}}\hfill \\ & =-p_{e_{i_1}+2e_{i_2}}^{\prime },\hfill \end{array}$$

(note that the coefficient $c_{2e_{i_2}}^{e_{i\left(2\right)}}$ is possible only if $N\ge 3$ and, of course, the appearance of this coefficient here and similar others in the following steps depends on the number N), and for $2\le i_1\le N,$

$$\begin{array}{cc}\hfill c_{2e_{i_1}}^{2e_{i_1}}& ={\displaystyle \frac{{\left(c_{3e_{i_1}}^{e_{i_1}}\right)}^2-c_{2e_{i_1}}^{e_{i_1}}{c}_{4e_{i_1}}^{e_{i_1}}}{{\left(c_{2e_{i_1}}^{e_{i_1}}\right)}^2}}\hfill \\ & =-{\displaystyle \frac{c_{e_{i_1}}(c_{e_{i_1}}{c}_{3e_{i_1}}{c}_{5e_{i_1}}+2c_{2e_{i_1}}{c}_{3e_{i_1}}{c}_{4e_{i_1}}-c_{3e_{i_1}}^3-c_{e_{i_1}}{c}_{4e_{i_1}}^2-c_{2e_{i_1}}^2{c}_{5e_{i_1}})}{{(c_{e_{i_1}}{c}_{3e_{i_1}}-c_{2e_{i_1}}^2)}^2}}\hfill \\ & =-{\displaystyle \frac{c_{5e_{i_1}}+c_{4e_{i_1}}(q_{e_{i_1}}+q_{2e_{i_1}})+c_{3e_{i_1}}(q_{e_{i_1}}{q}_{2e_{i_1}}-p_{2e_{i_1}})}{c_{3e_{i_1}}+c_{2e_{i_1}}{q}_{e_{i_1}}{B}_{0e_{i_1}}\left(0\right)}}\hfill \\ & =-{\displaystyle \frac{c_{5e_{i_1}}{B}_{2e_{i_1}}\left(0\right)+c_{4e_{i_1}}{B}_{2e_{i_1}}\left(1\right)+c_{3e_{i_1}}{B}_{2e_{i_1}}\left(2\right)}{c_{3e_{i_1}}{B}_{e_{i_1}}\left(0\right)+c_{2e_{i_1}}{B}_{e_{i_1}}\left(1\right)}}\hfill \\ & =-{\displaystyle \frac{{\sigma }_{2e_{i_1}}}{{\sigma }_{e_{i_1}}}}\hfill \\ & =-p_{3e_{i_1}}^{\prime },\hfill \end{array}$$

we put $p_{e_{i\left(3\right)}}=p_{e_{i\left(3\right)}}^{\prime }$, $2\le i_3\le i_2-1,$ $2\le i_2\le i_1$, $2\le i_1\le N;$ $p_{e_{i_1}+2e_{i_2}}=p_{e_{i_1}+2e_{i_2}}^{\prime },$ $2\le i_3\le i_2-1$, $3\le i_1\le N;$ $p_{3e_{i_1}}=p_{3e_{i_1}}^{\prime }$, $2\le i_1\le N.$

Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{F}_{e_{i\left(2\right)}}\left(z_1\right)+\sum _{i_3=2}^{i_2}{(-1)}^{{\delta }_{i_2,i_3}}{p}_{e_{i\left(3\right)}}{z}_{i_2}{z}_{i_3}{R}_{e_{i\left(3\right)}}\left(\mathbf{z}\right)}}}}}.\end{array}$$

Step 3.4: We obtain

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_{e_0}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+q_{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{F}_{e_{i\left(2\right)}}\left(z_1\right)+\sum _{i_3=2}^{i_2}\frac{{(-1)}^{{\delta }_{i_2,i_3}}{p}_{e_{i\left(3\right)}}{z}_{i_2}{z}_{i_3}}{R_{e_{i\left(3\right)}}^{\prime }\left(\mathbf{z}\right)}}}}}},\end{array}$$

where for each $2\le i_3\le i_2$, $2\le i_2\le i_1$, and $2\le i_1\le N,$

$$R_{e_{i\left(3\right)}}^{\prime }\left(\mathbf{z}\right)=\sum _{\begin{array}{c}\left|\mathbf{k}\right|\ge 0\\ {\mathbf{k}}_j=0,i_3+1\le j\le N\end{array}}{c}_{\mathbf{k}}^{e_{i\left(3\right)}}{\mathbf{z}}^{\mathbf{k}}$$

(15)

is reciprocal to the $R_{e_{i\left(3\right)}}\left(\mathbf{z}\right).$ The coefficients of (15) are calculated as follows

$$\begin{array}{c}\hfill c_{\mathbf{k}}^{e_{i\left(3\right)}}=-\sum _{\left|\mathbf{r}\right|=1}^{\left|\mathbf{k}\right|}{c}_{\mathbf{k}-\mathbf{r}}^{e_{i\left(3\right)}}{\displaystyle \frac{c_{\mathbf{r}+e_{i_2,i_3}}^{e_{i\left(2\right)}}}{c_{e_{i_2,i_3}}^{e_{i\left(2\right)}}}},\end{array}$$

where $c_{\mathbf{0}}^{e_{i\left(3\right)}}=1$; moreover, $c_{\mathbf{k}}^{e_{i\left(3\right)}}=0,$ if there exists an index j such that $1\le j\le N$ and $k_j<0.$

The further construction of the multidimensional A-fraction with independent variables (3) consists of gradually applying steps similar to Steps 2.1–2.4 to all formal multiple power series in the denominators of the ending partial quotients of the finite branches of the branched continued fraction.

As a result, computing the coefficients $c_{\mathbf{k}}^{e_{i_1}}$, $\left|\mathbf{k}\right|\ge 1,$ $k_j=0,i_1+1\le j\le N,$ and $2\le i_1\le N,$ using the recurrence Formula (13), and the coefficients $c_{\mathbf{k}}^{e_{i\left(k\right)}}$, $\left|\mathbf{k}\right|\ge 1,$ $k_j=0,i_k+1\le j\le N$, $k\ge 2$, $2\le i_p\le i_{p-1},$ and $1\le p\le k,$ using the recurrence formula

$$c_{\mathbf{k}}^{e_{i\left(k\right)}}=-\sum _{\left|\mathbf{r}\right|=1}^{\left|\mathbf{k}\right|}{c}_{\mathbf{k}-\mathbf{r}}^{e_{i\left(k\right)}}{\displaystyle \frac{c_{\mathbf{r}+e_{i_{k-1},i_k}}^{e_{i(k-1)}}}{c_{e_{i_{k-1},i_k}}^{e_{i(k-1)}}}},$$

(16)

where $c_{\mathbf{0}}^{e_{i\left(k\right)}}=1$; moreover, $c_{\mathbf{k}}^{e_{i\left(k\right)}}=0$ if there exists an index $j,$ $1\le j\le N,$ such that $k_j<0,$ provided that for $1\le i_1\le N$ and $n\ge 1$

$$H_{e_{i_1}}\left(n\right)\ne 0,$$

(17)

where $H_{e_{i_1}}\left(n\right)$ is as defined in (8), and provided that for each $1\le i_{k+1}\le i_k-1$, $2\le i_p\le i_{p-1}$, $1\le p\le k$, $k\ge 1$ and $n\ge 1$

$$c_{n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}=0,H_{e_{i_k,i_{k+1}}}^{e_{i\left(k\right)}}\left(n\right)\ne 0,$$

(18)

where $H_{e_{i_k,i_{k+1}}}^{e_{i\left(k\right)}}\left(n\right)$ is defined by

$$\begin{array}{c}\hfill H_{e_{i_k,i_{k+1}}}^{e_{i\left(k\right)}}\left(n\right)=\left|\begin{array}{cccc}{c}_{e_{i_k,i_{k+1}}}^{e_{i\left(k\right)}}& c_{e_{i_k}+2e_{i_{k+1}}}^{e_{i\left(k\right)}}& \dots & c_{e_{i_k}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}\\ c_{e_{i_k}+2e_{i_{k+1}}}^{e_{i\left(k\right)}}& c_{e_{i_k}+3e_{i_{k+1}}}^{e_{i\left(k\right)}}& \dots & c_{e_{i_k}+(n+1)e_{i_{k+1}}}^{e_{i\left(k\right)}}\\ \cdots & \cdots & \cdots & \cdots \\ c_{e_{i_k}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}& c_{e_{i_k}+(n+1)e_{i_{k+1}}}^{e_{i\left(k\right)}}& \dots & c_{e_{i_k}+(2n-1)e_{i_{k+1}}}^{e_{i\left(k\right)}}\end{array}\right|.\end{array}$$

For the formal multiple power series (5), we obtain the multidimensional A-fraction with independent variables (3), where the $p_{e_{i\left(k\right)}}$ and $q_{e_{i\left(k\right)}}$ for all $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $k\ge 1$ is defined by the following formulas:

$$\begin{array}{c}\hfill p_{(n+1)e_{i_1}}={\displaystyle \frac{{\sigma }_{n{e}_{i_1}}}{{\sigma }_{(n-1)e_{i_1}}}},q_{(n+1)e_{i_1}}={\tau }_{(n-1)e_{i_1}}-{\tau }_{n{e}_{i_1}},\end{array}$$

(19)

where $1\le i_1\le N$, $n\ge 0,$ and ${\sigma }_{n{e}_{i_1}},$ ${\tau }_{n{e}_{i_1}}$, $n\ge -1,$ are defined by (9)–(11),

$$\begin{array}{c}\hfill p_{e_{i\left(k\right)}+(n+1)e_{i_{k+1}}}={\displaystyle \frac{{\sigma }_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}}{{\sigma }_{e_{i\left(k\right)}+(n-1)e_{i_{k+1}}}^{e_{i\left(k\right)}}}},q_{e_{i\left(k\right)}+(n+1)e_{i_{k+1}}}={\tau }_{e_{i\left(k\right)}+(n-1)e_{i_{k+1}}}^{e_{i\left(k\right)}}-{\tau }_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}},\end{array}$$

(20)

where $2\le i_p\le i_{p-1}$, $1\le p\le k$, $1\le i_{k+1}\le i_k-1$, $k\ge 1$, $n\ge 0,$

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}=\sum _{r=0}^n{c}_{e_{i\left(k\right)}+(2n+1-r)e_{i_{k+1}}}^{e_{i\left(k\right)}}{B}_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}\left(r\right),{\tau }_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}{\sigma }_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}=\sum _{r=0}^n{c}_{e_{i\left(k\right)}+(2n+2-r)e_{i_{k+1}}}^{e_{i\left(k\right)}}{B}_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}\left(r\right),\end{array}$$

and for $1\le r\le n+1,$

$$\begin{array}{c}\hfill B_{e_{i\left(k\right)}+(n+1)e_{i_{k+1}}}^{e_{i\left(k\right)}}\left(r\right)=B_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}\left(r\right)+q_{e_{i\left(k\right)}+(n+1)e_{i_{k+1}}}{B}_{e_{i\left(k\right)}+n{e}_{i_{k+1}}}^{e_{i\left(k\right)}}(r-1)-p_{e_{i\left(k\right)}+(n+1)e_{i_{k+1}}}{B}_{e_{i\left(k\right)}+(n-1)e_{i_{k+1}}}^{e_{i\left(k\right)}}(r-2)\end{array}$$

with the initial conditions

$$\begin{array}{c}\hfill {\sigma }_{e_{i\left(2\right)}-e_{i_3}}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+0e_{i_3}}^{e_{i\left(2\right)}}\left(0\right)=B_{e_{i\left(2\right)}+(n+1)e_{i_3}}^{e_{i\left(2\right)}}\left(0\right)=1,{\tau }_{e_{i\left(2\right)}-e_{i_3}}^{e_{i\left(2\right)}}=B_{e_{i\left(2\right)}+(n-1)e_{i_3}}^{e_{i\left(2\right)}}(-1)=B_{e_{i\left(2\right)}+n{e}_{i_3}}^{e_{i\left(2\right)}}(n+1)=0.\end{array}$$

Thus, we have constructed the recurrence algorithm for computing the coefficients of the multidimensional A-fraction with independent variables (3) in terms of the formal multiple power series (5).

3.2. Multidimensional A-Fraction with Independent Variables

Let us show that the constructed in Section 3.1 the multidimensional A-fraction with independent variables (3) corresponds at $\mathbf{z}=\mathbf{0}$ to the formal multiple power series (5).

Using Formulas (13), (16), (19), and (20), we curtail (4) for $n\ge 1.$

Note that according to the described above algorithm for $e_0$ and for all $e_{i\left(k\right)}$ such that $2\le i_p\le i_{p-1}$, $1\le p\le k$, and $k\ge 1$, the continued fraction

$$\begin{array}{c}\hfill F_{e_{i\left(k\right)}}\left(z_1\right)={\displaystyle \frac{p_{e_{i\left(k\right)}+e_1}{z}_1}{{\displaystyle 1+q_{e_{i\left(k\right)}+e_1}{z}_1-\frac{p_{e_{i\left(k\right)}+2e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i\left(k\right)}+2e_1}{z}_1-\frac{p_{e_{i\left(k\right)}+3e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i\left(k\right)}+3e_1}{z}_1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}\end{array}$$

corresponds at the origin to the formal power series

$$\begin{array}{c}\hfill P_{e_{i\left(k\right)}}\left(z_1\right)=\sum _{r=1}^{\infty }{c}_{e_{i_k}+r{e}_1}^{e_{i\left(k\right)}}{z}_1^r\end{array}$$

and the order of correspondence is ${\nu }_n=2n+1.$ It follows that for $e_0$ and for each $e_{i\left(k\right)}$ such that $2\le i_p\le i_{p-1},$ $1\le p\le k$, $k\ge 1$ and for $n\ge 2$ the finite continued fraction

$$\begin{array}{c}\hfill F_{e_{i\left(k\right)}}^{\left(n\right)}\left(z_1\right)={\displaystyle \frac{p_{e_{i\left(k\right)}+e_1}{z}_1}{{\displaystyle 1+p_{e_{i\left(k\right)}+e_1}{z}_1-\frac{p_{e_{i\left(k\right)}+2e_1}{z}_1^2}{{\displaystyle 1+q_{e_{i\left(k\right)}+2e_1}{z}_1-{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle -\frac{p_{e_{i\left(k\right)}+n{e}_1}{z}_1^2}{1+q_{e_{i\left(k\right)}+n{e}_1}{z}_1}}}}}}}}\end{array}$$

has formal power series expansion

$$\begin{array}{c}\hfill P_{e_{i\left(k\right)}}^{\left(n\right)}\left(z_1\right)=\sum _{r=1}^{2n}{c}_{e_{i_k}+r{e}_1}^{e_{i\left(k\right)}}{z}_1^r+O\left(z_1^{2n+1}\right),\end{array}$$

where $c_{r{e}_1}^{e_0}=c_{r{e}_1}$ for $1\le r\le 2n$ and $n\ge 1,$ $O\left(z_1^p\right)$ is a symbolic mark for some formal power series, whose minimal degree of terms is not less than $p$, $p\ge 3.$

Now, for $n=1$, we have

$$\begin{array}{cc}\hfill f_1\left(\mathbf{z}\right)& =\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{1+q_{e_{i_1}}{z}_{i_1}}}\hfill \\ \hfill & =\sum _{i_1=1}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}}}\hfill \\ & =\sum _{i_1=1}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+\sum _{i_2=1}^{i_1}{c}_{e_{i_2}}^{e_{i_1}}{z}_{i_2}}}}\hfill \\ \hfill & =\sum _{i_1=1}^N{c}_{e_{i_1}}{z}_{i_1}\left(1+\sum _{i_2=1}^{i_1}{\displaystyle \frac{c_{e_{i\left(2\right)}}}{c_{e_{i_1}}}}{z}_{i_2}+O\left({\mathbf{z}}^2\right)\right)\hfill \\ \hfill & =\sum _{i_1=1}^N{c}_{e_{i_1}}{z}_{i_1}+\sum _{i_1=1}^N{z}_{i_1}\sum _{i_2=1}^{i_1}{c}_{e_{i\left(2\right)}}{z}_{i_2}+O\left({\mathbf{z}}^3\right)\hfill \\ & =\sum _{\left|\mathbf{k}\right|=1}^2{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^3\right),\hfill \end{array}$$

where $O\left({\mathbf{z}}^p\right)$ is a symbolic mark for some formal multiple power series, whose minimal degree of homogeneous terms is not less than $p$, $p\ge 2.$ Since

$$\begin{array}{c}\hfill \sum _{\left|\mathbf{k}\right|=1}^2{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^3\right)-\sum _{\left|\mathbf{k}\right|\ge 1}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}=O^{\prime }\left({\mathbf{z}}^3\right),\end{array}$$

where $O^{\prime }\left({\mathbf{z}}^p\right)$ is a symbolic mark for some formal multiple power series, whose minimal degree of homogeneous terms is not less than $p$, $p\ge 3,$ then $f_1\left(\mathbf{z}\right)\sim L\left(\mathbf{z}\right)$ and the order of correspondence is ${\nu }_1=3.$

For $n=2$ we can write

$$\begin{array}{cc}\hfill f_2\left(\mathbf{z}\right)& =F_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+\sum _{i_2=1}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}{z}_{i_1}{z}_{i_2}}{1+q_{e_{i\left(2\right)}}{z}_{i_2}}}}}\hfill \\ \hfill & =P_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+\sum _{i_2=1}^{i_1}\frac{c_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}}{1+c_{e_{i_2}}^{e_{i\left(2\right)}}{z}_{i_2}}}}}\hfill \\ \hfill & =P_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+\sum _{i_2=1}^{i_1}\frac{c_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+\sum _{i_3=1}^{i_2}{c}_{e_{i_3}}^{e_{i\left(2\right)}}{z}_{i_3}}}}}}\hfill \\ \hfill & =P_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+\sum _{i_2=1}^{i_1}{c}_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}\left(1+\sum _{i_3=1}^{i_2}\frac{c_{e_{i\left(2\right)}+e_{i_3}}^{e_{i_1}}}{c_{e_{i\left(2\right)}}^{e_{i_1}}}{z}_{i_3}+O\left({\mathbf{z}}^2\right)\right)}}}\hfill \\ & =P_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+\sum _{i_2=1}^{i_1}{c}_{e_{i_2}}^{e_{i_1}}{z}_{i_2}+\sum _{i_2=1}^{i_1}{z}_{i_2}\sum _{i_3=1}^{i_2}{c}_{e_{i_2,i_3}}^{e_{i_1}}{z}_{i_3}+\sum _{i_2=1}^{i_1}{z}_{i_2}\sum _{i_3=1}^{i_2}{z}_{i_3}\sum _{i_4=1}^{i_3}{c}_{e_{i\left(4\right)}-e_{i_1}}^{e_{i_1}}{z}_{i_4}+O\left({\mathbf{z}}^3\right)}}}\hfill \\ \hfill & =P_{e_0}^{\left(2\right)}\left(z_1\right)+\sum _{i_1=2}^N{c}_{e_{i_1}}{z}_{i_1}\left(1+\sum _{i_2=1}^{i_1}{\displaystyle \frac{c_{e_{i\left(2\right)}}}{c_{e_{i_1}}}}{z}_{i_2}+\sum _{i_2=1}^{i_1}{z}_{i_2}\sum _{i_3=1}^{i_2}{\displaystyle \frac{c_{e_{i\left(3\right)}}}{c_{e_{i_1}}}}{z}_{i_3}+\sum _{i_2=1}^{i_1}{z}_{i_2}\sum _{i_3=1}^{i_2}{z}_{i_3}\sum _{i_4=1}^{i_3}{\displaystyle \frac{c_{e_{i\left(4\right)}}}{c_{e_{i_1}}}}{z}_{i_4}+O\left({\mathbf{z}}^4\right)\right)\hfill \\ \hfill & =\sum _{\left|\mathbf{k}\right|=1}^4{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^5\right).\hfill \end{array}$$

Since

$$\begin{array}{c}\hfill \sum _{\left|\mathbf{k}\right|=1}^4{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^5\right)-\sum _{\left|\mathbf{k}\right|\ge 1}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}=O^{\prime }\left({\mathbf{z}}^5\right),\end{array}$$

then $f_2\left(\mathbf{z}\right)\sim L\left(\mathbf{z}\right)$ and ${\nu }_2=5.$

Next, let $n\ge 3$ be an arbitrary natural number. Then we obtain

$$\begin{array}{cc}\hfill f_n\left(\mathbf{z}\right)& =F_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{p_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+q_{e_{i_1}}{z}_{i_1}+z_{i_1}{F}_{e_{i_1}}^{(n-1)}\left(z_1\right)+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}{\displaystyle \frac{{(-1)}^{{\delta }_{i_{n-1},i_n}}{p}_{e_{i\left(n\right)}}{z}_{i_{n-1}}{z}_{i_n}}{1+q_{e_{i\left(n\right)}}{z}_{i_n}}}}}}}}\hfill \\ & =P_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+z_{i_1}{P}_{e_{i-1}}^{(n-1)}\left(z_1\right)+\sum _{i_2=2}^{i_1}\frac{c_{e_{i\left(2\right)}}^{e_{i_1}}{z}_{i_1}{z}_{i_2}}{{\displaystyle 1+c_{e_{i_2}}^{e_{i\left(2\right)}}{z}_{i_2}+z_{i_2}{P}_{e_{i\left(2\right)}}^{(n-2)}\left(z_1\right)+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}{\displaystyle \frac{c_{e_{i_{n-1},i_n}}^{e_{i(n-1)}}{z}_{i_{n-1}}{z}_{i_n}}{1+c_{e_{i_n}}^{e_{i\left(n\right)}}{z}_{i_n}}}}}}}}}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =P_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+z_{i_1}{P}_{e_{i_1}}^{(n-1)}\left(z_1\right)+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}{\displaystyle \frac{c_{e_{i_{n-1},i_n}}^{e_{i(n-1)}}{z}_{i_{n-1}}{z}_{i_n}}{{\displaystyle 1+\sum _{i_{n+1}=1}^{i_n}{c}_{e_{i_{n+1}}}^{e_{i\left(n\right)}}{z}_{i_{n+1}}}}}}}}}}\hfill \\ & =P_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+c_{e_{i_1}}^{e_{i_1}}{z}_{i_1}+z_{i_1}{P}_{e_{i_1}}^{(n-1)}\left(z_1\right)+{\genfrac{}{}{0pt}{}{}{\ddots }}_{{\displaystyle +\sum _{i_n=1}^{i_{n-1}}{c}_{e_{i_{n-1},i_n}}^{e_{i(n-1)}}{z}_{i_{n-1}}{z}_{i_n}\left(1+\sum _{i_{n+1}=1}^{i_n}\frac{c_{e_{i_{n-1},i_n,i_{n+1}}}^{e_{i(n-1)}}}{c_{e_{i_{n-1},i_n}}^{e_{i(n-1)}}}{z}_{i_{n+1}}+O\left({\mathbf{z}}^2\right)\right)}}}}}.\hfill \end{array}$$

Continuing this process on the final step, we obtain

$$\begin{array}{cc}\hfill f_n\left(\mathbf{z}\right)& =P_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{\displaystyle \frac{c_{e_{i_1}}{z}_{i_1}}{{\displaystyle 1+\sum _{i_2=1}^{i_1}{c}_{e_{i_2}}^{e_{i_1}}{z}_{i_2}+\dots +\sum _{i_2=1}^{i_1}{z}_{i_2}\dots \sum _{i_{2n-1}=1}^{i_{2n-2}}{z}_{i_{2n-1}}\sum _{i_{2n}=1}^{i_{2n-1}}{c}_{e_{i\left(2n\right)}-e_{i_1}}^{e_{i_1}}{z}_{i_{2n}}+O\left({\mathbf{z}}^{2n-1}\right)}}}.\hfill \end{array}$$

From this we have

$$\begin{array}{cc}\hfill f_n\left(\mathbf{z}\right)& =P_{e_0}^{\left(n\right)}\left(z_1\right)+\sum _{i_1=2}^N{c}_{e_{i_1}}{z}_{i_1}\left(1+\sum _{i_2=1}^{i_1}{\displaystyle \frac{c_{e_{i\left(2\right)}}}{c_{e_{i_1}}}}{z}_{i_2}+\dots +\sum _{i_2=1}^{i_1}{z}_{i_2}\dots \sum _{i_{2n-1}=1}^{i_{2n-2}}{z}_{i_{2n-1}}\sum _{i_{2n}=1}^{i_{2n-1}}{\displaystyle \frac{c_{e_{i\left(2n\right)}}}{c_{e_{i_1}}}}{z}_{i_{2n}}+O\left({\mathbf{z}}^{2n}\right)\right)\hfill \\ & =\sum _{\left|\mathbf{k}\right|=1}^{2n}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^{2n+1}\right).\hfill \end{array}$$

Since

$$\begin{array}{c}\hfill \sum _{\left|\mathbf{k}\right|=1}^{2n}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}+O\left({\mathbf{z}}^{2n+1}\right)-\sum _{\left|\mathbf{k}\right|\ge 1}{c}_{\mathbf{k}}{\mathbf{z}}^{\mathbf{k}}=O^{\prime }\left({\mathbf{z}}^{2n+1}\right),\end{array}$$

$f_n\left(\mathbf{z}\right)\sim L\left(\mathbf{z}\right)$ and ${\nu }_n=2n+1.$

At last, from the arbitrariness of n, it follows that $f_n\left(\mathbf{z}\right)\sim L\left(\mathbf{z}\right)$ for all $n\ge 1$ and that the order of correspondence is ${\nu }_n=2n+1.$ It follows that $\Lambda \left(f_n\right)$ and $L\left(\mathbf{z}\right)$ agree for all homogeneous terms up to and including degree $2n.$ Since

$$\begin{array}{c}\hfill \underset{n\to +\infty }{lim}{\nu }_n=\underset{n\to +\infty }{lim}2n+1=+\infty ,\end{array}$$

the multidimensional A-fraction with independent variables (3) corresponds at $\mathbf{z}=\mathbf{0}$ to the formal multiple power series (5).

Thus, the following theorem is true.

Theorem 3.

The multidimensional A-fraction with independent variables (3) corresponds at $\mathbf{z}=\mathbf{0}$ to the given formal multiple power series (5) if and only if the conditions (17) for $1\le i_1\le N$, $n\ge 1,$ and the conditions (18) for $1\le i_{k+1}\le i_k-1$, $2\le i_p\le i_{p-1}$, $1\le p\le k$, $k\ge 1$, $n\ge 1$ are satisfied.

It follows from Theorems 1 and 2 in [29] that the conditions for the existence of the generalized Gragg’s algorithm are the same as for the algorithm in [29]. However, this algorithm provides a more convenient numerical procedure for computing the coefficients of multidimensional A-fractions with independent variables corresponding to a formal multiple power series.

3.3. Multidimensional J-Fraction with Independent Variables

Let us consider the formal multiple power series

$$L^{*}\left(\mathbf{w}\right)=\sum _{\left|\mathbf{k}\right|\ge 1}{\displaystyle \frac{c_{\mathbf{k}}}{{\mathbf{w}}^{\mathbf{k}}}},$$

(21)

where $c_{\mathbf{k}}\in \mathbb{C}$, $\mathbf{k}\ge 1,$ and the multidimensional J-fraction with independent variables

$$\sum _{i_1=1}^N{\displaystyle \frac{p_{e_{i\left(1\right)}}}{{\displaystyle q_{e_{i\left(1\right)}}+w_{i_1}+\sum _{i_2=1}^{i_1}\frac{{(-1)}^{{\delta }_{i_1,i_2}}{p}_{e_{i\left(2\right)}}}{{\displaystyle q_{e_{i\left(2\right)}}+w_{i_2}+\sum _{i_3=1}^{i_2}\frac{{(-1)}^{{\delta }_{i_2,i_3}}{p}_{e_{i\left(3\right)}}}{{\displaystyle q_{e_{i\left(3\right)}}+w_{i_3}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}},$$

(22)

where $p_{e_{i\left(k\right)}}$, $q_{e_{i\left(k\right)}},$ and $e_{i\left(k\right)}\in {\mathfrak{E}}_k,$ $k\ge 1$ are complex numbers, herewith $p_{e_{i\left(k\right)}}\ne 0,$ $e_{i\left(k\right)}\in {\mathfrak{E}}_k$, $k\ge 1.$

The following theorem summarizes the connections between multidimensional A- and J-fractions with independent variables (see also [29], Theorem 3). Its proof is a simple application of Theorem 1.

Theorem 4.

Let $f_n\left(\mathbf{z}\right)$ ($f_n^{*}\left(\mathbf{w}\right)$) denote the nth approximants, respectively, of the multidimensional A-fraction with independent variables (3) (multidimensional J-fraction with independent variables (22)), where $z_i=1/w_i$ and $1\le i\le N.$ In addition, let the multidimensional A-fraction with independent variables (3) corresponds to the formal multiple power series (5) at $\mathbf{z}=\mathbf{0}.$ Then

(A) 

For any natural $n,$ the equality $f_n\left(\mathbf{z}\right)=f_n^{*}\left(\mathbf{w}\right)$ is true.

(B) 

The formal expansion of the nth approximant $f_n^{*}\left(\mathbf{w}\right)$ in the multiple power series at $\mathbf{w}=\infty$ has the form

$$\begin{array}{c}\hfill f_n^{*}\left(\mathbf{w}\right)=\sum _{\left|\mathbf{k}\right|=1}^{2n}{\displaystyle \frac{c_{\mathbf{k}}}{{\mathbf{w}}^{\mathbf{k}}}}+\sum _{\left|\mathbf{k}\right|\ge 2n+1}{\displaystyle \frac{c_{\mathbf{k}}^{\left(n\right)}}{{\mathbf{w}}^{\mathbf{k}}}},n\ge 1,\end{array}$$

where $c_{\mathbf{k}}^{\left(n\right)}\in \mathbb{C},$ $\left|\mathbf{k}\right|\ge 2n+1,$ and hence, the multidimensional J-fraction with independent variables (22) corresponds at $\mathbf{w}=\mathbf{\infty }$ to the formal multiple power series (21).

It follows from Theorem 3 that the generalized Gragg’s algorithm can also be used for computing the coefficients of multidimensional J-fractions with independent variables corresponding to a formal multiple power series.

4. Applications

In this section, we will give some applications of the above constructed algorithm.

The function of two variables

$$f\left(\mathbf{z}\right)=arctan\left(z_1\right)+arctan\left({\displaystyle \frac{z_2}{1+z_{2}arctan\left(z_1\right)}}\right)$$

(23)

has a formal double power series at origin given by

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)=\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^{k+1}}{2k-1}}{z}_1^{2k-1}+\sum _{r=1}^{\infty }{\displaystyle \frac{{(-1)}^{r+1}}{2r-1}}{\left(\sum _{s=0}^{\infty }{z}_2^{s+1}{\left(\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^k}{2k-1}}{z}_1^{2k-1}\right)}^s\right)}^{2r-1}.\end{array}$$

(24)

Applying the recurrence algorithm constructed in Section 3, we obtain the following.

Step 1.1: We have

$$\begin{array}{cc}\hfill L\left(\mathbf{z}\right)& =\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^{k+1}}{2k-1}}{z}_1^{2k-1}+z_2\left(1-z_1{z}_2-{\displaystyle \frac{1}{3}}{z}_2^2+{\displaystyle \frac{1}{3}}{z}_1^3{z}_2+z_1^2{z}_2^2+z_1{z}_2^3+{\displaystyle \frac{1}{5}}{z}_2^4\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{1}{5}}{z}_1^5{z}_2-{\displaystyle \frac{2}{3}}{z}_1^4{z}_2^2-{\displaystyle \frac{4}{3}}{z}_1^3{z}_2^3-2z_1^2{z}_2^4-z_1{z}_2^5-{\displaystyle \frac{1}{7}}{z}_2^6+\dots \right).\hfill \end{array}$$

Steps 1.2 and 1.3: By Formula (19), we obtain (see also Table 1)

$$\begin{array}{c}\hfill p_{1,0}=p_{0,1}=1,p_{k,0}=p_{0,k}=-{\displaystyle \frac{{(k-1)}^2}{(2k-3)(2k-1)}},k\ge 2,q_{k,0}=q_{0,k}=0,k\ge 0.\end{array}$$

Table 1. Results of algorithm applied to (23) on Steps 1.2 and 1.3 for $i_1=1,2$.

n	${\mathit{p}}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{q}}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{\sigma }}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{\tau }}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(0\right)$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(1\right)$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(2\right)$
$-1$			1	0
0			1	0	1
1	1	0	$-1/3$	0	1	0
2	$-1/3$	0	4/45	1/15	1	1/3	1/3
3	$-4/15$	0

Table 1. Results of algorithm applied to (23) on Steps 1.2 and 1.3 for $i_1=1,2$.

n	${\mathit{p}}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{q}}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{\sigma }}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{\tau }}_{{\mathit{ne}}_{{\mathit{i}}_1}}$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(0\right)$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(1\right)$	${\mathit{B}}_{{\mathit{ne}}_{{\mathit{i}}_1}}\left(2\right)$
$-1$			1	0
0			1	0	1
1	1	0	$-1/3$	0	1	0
2	$-1/3$	0	4/45	1/15	1	1/3	1/3
3	$-4/15$	0

Thus,

$$\begin{array}{cc}\hfill L\left(\mathbf{z}\right)& \sim F_0\left(z_1\right)+z_2\left(1-z_1{z}_2-{\displaystyle \frac{1}{3}}{z}_2^2+{\displaystyle \frac{1}{3}}{z}_1^3{z}_2+z_1^2{z}_2^2+z_1{z}_2^3+{\displaystyle \frac{1}{5}}{z}_2^4\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{1}{5}}{z}_1^5{z}_2-{\displaystyle \frac{2}{3}}{z}_1^4{z}_2^2-{\displaystyle \frac{4}{3}}{z}_1^3{z}_2^3-2z_1^2{z}_2^4-z_1{z}_2^5-{\displaystyle \frac{1}{7}}{z}_2^6+\dots \right),\hfill \end{array}$$

where

$$F_0\left(z_1\right)={\displaystyle \frac{p_{1,0}{z}_1}{{\displaystyle 1-{\displaystyle \frac{p_{2,0}{z}_1^2}{{\displaystyle 1-{\displaystyle \frac{p_{3,0}{z}_1^2}{{\displaystyle 1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}}.$$

Step 1.4: Through the recurrence Formula (13), we obtain

$$\begin{array}{cc}\hfill L\left(\mathbf{z}\right)& \sim F_0\left(z_1\right)+{\displaystyle \frac{z_2}{R_{0,1}^{\prime }\left(\mathbf{z}\right)}},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill R_{0,1}^{\prime }\left(\mathbf{z}\right)& =1+z_1{z}_2+{\displaystyle \frac{1}{3}}{z}_2^2-{\displaystyle \frac{1}{3}}{z}_1^3{z}_2-{\displaystyle \frac{1}{3}}{z}_1{z}_2^3-{\displaystyle \frac{4}{45}}{z}_2^4\hfill \\ & +{\displaystyle \frac{1}{5}}{z}_1^5{z}_2+{\displaystyle \frac{1}{9}}{z}_1^3{z}_2^3+{\displaystyle \frac{1}{3}}{z}_1^2{z}_2^4+{\displaystyle \frac{12}{45}}{z}_1{z}_2^5+{\displaystyle \frac{44}{945}}{z}_2^6+\dots .\hfill \end{array}$$

Step 2.1: We have

$$\begin{array}{cc}\hfill L(z_1& ,z_2)\sim F_0\left(z_1\right)+{\displaystyle \frac{z_2}{{\displaystyle 1+z_2\sum _{k=1}^{\infty }\frac{{(-1)}^{k+1}}{2k-1}{z}_1^{2k-1}+\frac{z_2^2}{3}{R}_{0,2}\left(\mathbf{z}\right)}}},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill R_{0,2}\left(\mathbf{z}\right)=1-z_1{z}_2-{\displaystyle \frac{4}{15}}{z}_2^2+{\displaystyle \frac{1}{3}}{z}_1^3{z}_2+z_1^2{z}_2^2+{\displaystyle \frac{12}{15}}{z}_1{z}_2^3+{\displaystyle \frac{44}{315}}{z}_2^4+\dots .\end{array}$$

Steps 2.2 and 2.3: By Formula (20), we obtain (see also Table 2)

$$\begin{array}{c}\hfill p_{1,1}=1,p_{n,1}=-{\displaystyle \frac{{(n-1)}^2}{(2n-3)(2n-1)}},n\ge 2,q_{n,1}=0,n\ge 0.\end{array}$$

Table 2. Results of algorithm applied to (23) on Steps 2.2 and 2.3.

n	${\mathit{p}}_{\mathit{n},1}$	${\mathit{q}}_{\mathit{n},1}$	${\mathit{\sigma }}_{\mathit{n},1}$	${\mathit{\tau }}_{\mathit{n},1}$	${\mathit{B}}_{\mathit{n},1}\left(0\right)$	${\mathit{B}}_{\mathit{n},1}\left(1\right)$	${\mathit{B}}_{\mathit{n},1}\left(2\right)$
$-1$			1	0
0			1	0	1
1	1	0	$-1/3$	0	1	0
2	$-1/3$	0	4/45	1/15	1	1/3	1/3
3	$-4/15$	0

Table 2. Results of algorithm applied to (23) on Steps 2.2 and 2.3.

n	${\mathit{p}}_{\mathit{n},1}$	${\mathit{q}}_{\mathit{n},1}$	${\mathit{\sigma }}_{\mathit{n},1}$	${\mathit{\tau }}_{\mathit{n},1}$	${\mathit{B}}_{\mathit{n},1}\left(0\right)$	${\mathit{B}}_{\mathit{n},1}\left(1\right)$	${\mathit{B}}_{\mathit{n},1}\left(2\right)$
$-1$			1	0
0			1	0	1
1	1	0	$-1/3$	0	1	0
2	$-1/3$	0	4/45	1/15	1	1/3	1/3
3	$-4/15$	0

Thus,

$$\begin{array}{c}\hfill L\left(\mathbf{z}\right)\sim F_0\left(z_1\right)+{\displaystyle \frac{z_2}{{\displaystyle 1+z_2{F}_1\left(z_1\right)+{\displaystyle \frac{z_2^2}{3}}{R}_{0,2}\left(\mathbf{z}\right)}}},\end{array}$$

where

$$F_1\left(z_1\right)={\displaystyle \frac{p_{1,1}{z}_1}{{\displaystyle 1-{\displaystyle \frac{p_{2,1}{z}_1^2}{{\displaystyle 1-{\displaystyle \frac{p_{3,1}{z}_1^2}{{\displaystyle 1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}}.$$

Step 2.4: Through the recurrence Formula (16), we obtain

$$\begin{array}{cc}\hfill L\left(\mathbf{z}\right)& \sim F_0\left(z_1\right)+{\displaystyle \frac{z_2}{1+z_2{F}_1\left(z_1\right)+{\displaystyle \frac{z_2^2/3}{R_{0,2}^{\prime }\left(\mathbf{z}\right)}}}},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill R_{0,2}^{\prime }\left(\mathbf{z}\right)=1+z_1{z}_2+{\displaystyle \frac{4}{15}}{z}_2^2-{\displaystyle \frac{1}{3}}{z}_1^3{z}_2-{\displaystyle \frac{4}{15}}{z}_1{z}_2^3-{\displaystyle \frac{44}{315}}{z}_2^4+\dots .\end{array}$$

And so on; at the end, we will obtain the corresponding two-dimensional A-fraction with independent variables of the form

$$\begin{array}{c}\hfill F_0\left(z_1\right)+{\displaystyle \frac{z_2}{1+z_2{F}_1\left(z_1\right)+{\displaystyle \frac{-p_{0,2}{z}_2^2}{1+z_2{F}_2\left(z_1\right)+{\displaystyle \frac{-p_{0,3}{z}_2^2}{1{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}},\end{array}$$

(25)

where for $k\ge 0$

$$\begin{array}{c}\hfill F_k\left(z_1\right)={\displaystyle \frac{z_1}{{\displaystyle 1-{\displaystyle \frac{p_{2,k}{z}_1^2}{{\displaystyle 1-{\displaystyle \frac{p_{3,k}{z}_1^2}{{\displaystyle 1{-}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}}}}},p_{n,k}=p_{0,n}=-{\displaystyle \frac{{(n-1)}^2}{(2n-3)(2n-1)}},n\ge 2.\end{array}$$

In addition, we note that (25) converges in the domains

$$\mathfrak{O}=\left\{\mathbf{z}\in {\mathbb{C}}^2:|z_1|<{\displaystyle \frac{\sqrt{3}}{2}},|z_2|<{\displaystyle \frac{\sqrt{6}}{4}},\left|z_1{z}_2\right|<{\displaystyle \frac{1}{8}}\right\}$$

and

$$\mathfrak{D}=\left\{\mathbf{z}\in {\mathbb{C}}^2:|arg\left(z_k\right)|<{\displaystyle \frac{\pi }{2}},k=1,2\right\},$$

which follows from [35] and [36] (Theorem 5), respectively. Hence, it represents a single-valued branch of the analytic function (23) in the domain $\mathfrak{O}\bigcup \mathfrak{D}.$

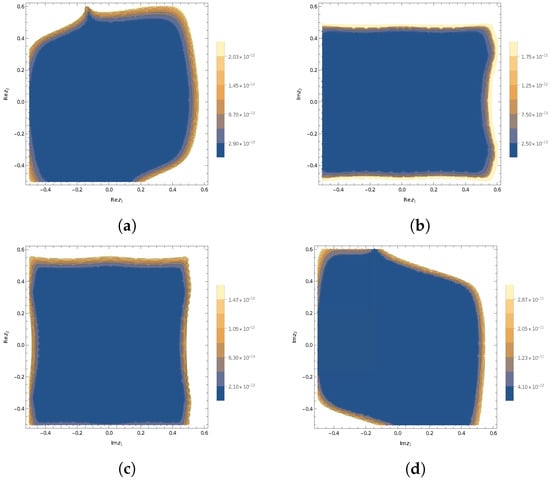
In Figure 1a,b, we can see the so-called “fork property” for a branched continued fraction with positive elements (see [33]). That is, the plots of the values of even (odd) approximations of (25) approach from below (above) the plot of the function (23). Figure 2a–d shows the plots, where the tenth approximant of (25) guarantees certain truncation error bounds for function (23).

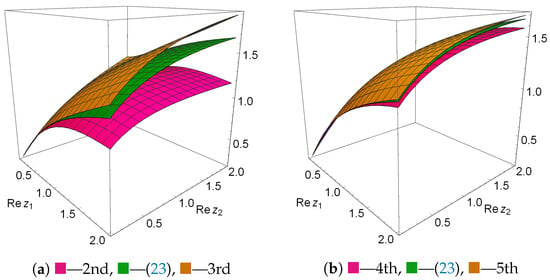
Figure 1. The plots of values of the nth approximants of (25).

Figure 2. The plots where the tenth approximant of (25) guarantees certain truncation error bounds for (23).

The numerical illustration of (24) and (25) is given in the Table 3. Here, we can see that the fifth approximant of (25) is eventually a better approximation to (23) than the fifth partial sum of (24) is.

Table 3. Relative error of fifth partial sum and fifth approximant.

z	(23)	(24)	(25)
$(-0.8,-0.7)$	$-1.1185$	$3.7401\times {10}^{-1}$	$1.0841\times {10}^{-4}$
$(-0.1,-0.1)$	$-0.1984$	$1.3790\times {10}^{-9}$	$1.7449\times {10}^{-12}$
$(0.5,-0.7)$	$-0.3396$	$2.0795\times {10}^{-3}$	$1.4715\times {10}^{-3}$
$(-0.9,0.1)$	$-0.6253$	$2.7472\times {10}^{-2}$	$1.3940\times {10}^{-4}$
$(0.2,0.3)$	$0.4734$	$2.2374\times {10}^{-5}$	$1.7797\times {10}^{-8}$
$(0.1,0.8)$	$0.7373$	$2.0631\times {10}^{-2}$	$3.5972\times {10}^{-5}$
$(0.9,0.9)$	$1.2297$	$2.4591$	$2.8455\times {10}^{-4}$
$(2,4)$	$1.7422$	$2.9054\times {10}^{+5}$	$2.3425\times {10}^{-2}$
$(5,10)$	$1.9697$	$1.0147\times {10}^{+9}$	$0.3417\times {10}^{-1}$
$(-8,10)$	$-2.0853$	$2.0193\times {10}^{+5}$	$0.9356\times {10}^{-1}$

Finally, consider the following function of two variables

$$\begin{array}{cc}\hfill {\psi }^{\prime }\left(\mathbf{z}\right)& ={\psi }^{\prime }\left(z_1\right)+{\psi }^{\prime }(z_2+{\psi }^{\prime }\left(z_1\right))\hfill \\ & \hfill ={\int }_0^{\infty }{\displaystyle \frac{t{e}^{-t{z}_1}}{1-e^{-t}}}dt+{\int }_0^{\infty }{\displaystyle \frac{s}{1-e^{-s}}}exp\left\{-s{z}_2-s{\int }_0^{\infty }{\displaystyle \frac{t{e}^{-t{z}_1}}{1-e^{-t}}}dt\right\}ds,\end{array}$$

(26)

where ${\psi }^{\prime }(.)$ is the trigamma function (see [37]).

Using the asymptotic expansion for ${\psi }^{\prime }(.)$ given in [37], we find the asymptotic representation for (26) as a formal double power series

$$\begin{array}{c}\hfill {\psi }^{\prime }\left(\mathbf{z}\right)\approx \sum _{k=0}^{\infty }{\displaystyle \frac{B_k^{+}}{z_1^{k+1}}}+\sum _{r=0}^{\infty }{\displaystyle \frac{B_r^{+}}{z_2^{r+1}}}{\left(\sum _{s=0}^{\infty }{\left(\sum _{k=0}^{\infty }{\displaystyle \frac{-B_k^{+}}{z_1^{k+1}{z}_2}}\right)}^s\right)}^{r+1},\mathbf{z}\to \mathbf{\infty },\end{array}$$

(27)

where $|arg(z_i\left)\right|<\pi$, $i=1,2,$ and

$$B_k^{+}=1-\sum _{r=0}^{k-1}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{r}}\right){\displaystyle \frac{B_r^{+}}{k-r+1}},k\ge 0,$$

are the Bernoulli numbers. Then, by Theorem 3, using the algorithm from Section 3, we obtain the corresponding two-dimensional J-fraction with independent variables

$$\sum _{i_1=1}^2{\displaystyle \frac{p_{e_{i\left(1\right)}}}{{\displaystyle q_{e_{i\left(1\right)}}+z_{i_1}+\sum _{i_2=1}^{i_1}\frac{p_{e_{i\left(2\right)}}}{{\displaystyle q_{e_{i\left(2\right)}}+z_{i_2}+\sum _{i_3=1}^{i_2}\frac{p_{e_{i\left(3\right)}}}{q_{e_{i\left(3\right)}}+z_{i_3}{+}_{\genfrac{}{}{0pt}{}{}{\ddots }}}}}}}},$$

(28)

where

$$\begin{array}{c}{p}_{e_1+r{e}_2}=p_{e_2}=1,r\ge 0,p_{k{e}_1+r{e}_2}=p_{k{e}_2}={\displaystyle \frac{{(k-1)}^4}{4(2k-3)(2k-1)}},k\ge 2,r\ge 0,\\ q_{k{e}_1+r{e}_2}=q_{k{e}_2}=-{\displaystyle \frac{1}{2}},k\ge 1,r\ge 0.\end{array}$$

In addition, in [38], it is shown that (28) converges and, hence, represents the analytic function (26) in the domain

$${\mathfrak{D}}_{\epsilon }=\left\{\mathbf{z}\in {\mathbb{C}}^2:\left|arg\left(z_k-{\displaystyle \frac{1}{2}}\right)\right|<{\displaystyle \frac{\pi }{2}}-\epsilon ,k=1,2\right\},$$

where $0<\epsilon <\pi /2.$

Plots of the values of the nth approximants of the two-dimensional J-fraction with independent variables (28) for function (26) are shown in Figure 3a,b. Figure 4a–d shows the plots, where the tenth approximant of (28) guarantees certain truncation error bounds for (26). The numerical illustration of (27) and (28) is given in the Table 4. Here, we have results similar to the results in the previous example.

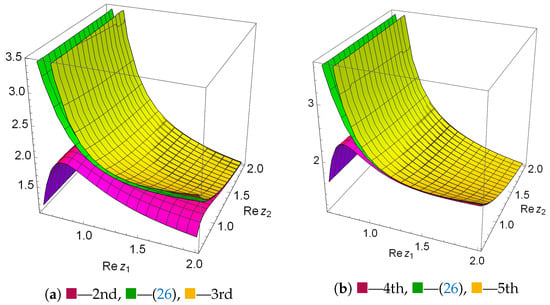
Figure 3. The plots of values of the nth approximants of (28).

Figure 4. The plots where the tenth approximant of (28) guarantees certain truncation error bounds for (26).

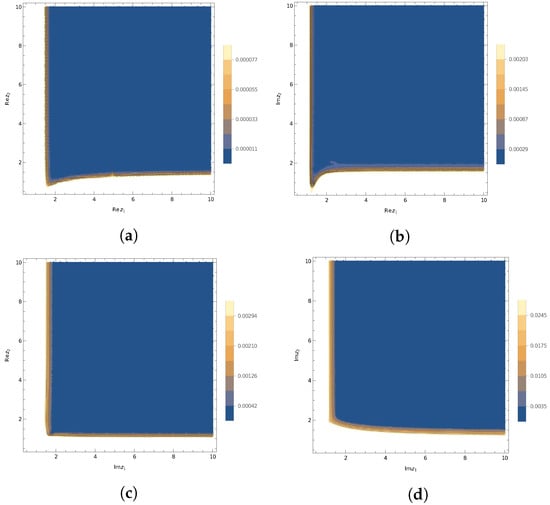
Table 4. Relative error of fifth partial sum and fifth approximant.

z	(26)	(27)	(28)
$(0.6,0.6)$	$3.9023$	$1.1536\times {10}^{+2}$	$9.1384\times {10}^{-1}$
$(0.9,0.8)$	$2.3654$	$8.0419$	$4.5692\times {10}^{-2}$
$(1.5,1.4)$	$1.4675$	$5.5267\times {10}^{-2}$	$7.2177\times {10}^{-4}$
$(2,3)$	$9.6031\times {10}^{-1}$	$1.1374\times {10}^{-4}$	$4.1428\times {10}^{-5}$
$\left(10.9\right)$	$2.2125\times {10}^{-1}$	$5.8012\times {10}^{-10}$	$1.0153\times {10}^{-11}$
$(20,40)$	$7.6553\times {10}^{-1}$	$7.1868\times {10}^{-14}$	$1.9746\times {10}^{-15}$
$(50,70)$	$3.4585\times {10}^{-2}$	$8.8000\times {10}^{-17}$	$1.8847\times {10}^{-19}$
$(100,110)$	$2.0099\times {10}^{-2}$	$7.8850\times {10}^{-19}$	$3.6751\times {10}^{-22}$
$(500,1000)$	$3.0025\times {10}^{-3}$	$2.1889\times {10}^{-26}$	$1.6536\times {10}^{-29}$

It should be noted that the two-dimensional A-fraction with independent variables (25) and two-dimensional J-fraction with independent variables (28) are similar to fractals.

The calculations and plots were performed using Wolfram Mathematica software 13.1.0.0 for Linux.

5. Conclusions

This paper concerns the representation of special functions by multidimensional A- and J-fractions with independent variables. The generalized Gragg’s algorithm is constructed and theorems are proved that provide necessary and sufficient conditions such that for a formal multiple power series there exist corresponding multidimensional A- and J-fractions with independent variables. Explicit formulas for the coefficients of these branched continued fraction are also given.

The obtained results can be used to construct approximate or exact analytical solutions to equations describing complex processes, for example, physics, chemistry, and engineering, thus providing a better and more meaningful understanding of the properties of processes and mechanisms.

The numerical experiments show, on the one hand, the efficiency of the proposed generalized Gragg’s algorithm and, on the other, the power and feasibility of the method in order to numerically approximate special functions from their formal multiple power series. In addition, they indicate the existence of wider domains of convergence multidimensional A- and J-fractions with independent variables, and hence, domains of analytical expansion of special functions. However, the problem of establishing them remains open. In [39,40], the truncation error bounds for these branched continued fractions were established; nevertheless, the problem of establishing them also remains open.