Fractional Mathieu Equation with Two Fractional Derivatives and Some Applications

Abstract

The importance of this research comes from the several applications of the Mathieu equation and its generalizations in many scientific fields. Two models of fractional Mathieu equations are provided using Katugampola fractional derivatives in the sense of Riemann-Liouville and Caputo. Each model contains two fractional derivatives with unique fractional orders, periodic forcing of the cosine stiffness coefficient, and many extensions and generalizations. The Banach contraction principle is used to prove that each model under consideration has a unique solution. Our results are applied to four real-life problems: the nonlinear Mathieu equation for parametric damping and the Duffing oscillator, the quadratically damped Mathieu equation, the fractional Mathieu equation’s transition curves, and the tempered fractional model of the linearly damped ion motion with an octopole.

1. Introduction

A linear differential equation with periodic coefficients, the famous Mathieu equation was first presented by Mathieu during his research on vibrating elliptical membranes [1,2]. Traditional applications of the classical Mathieu equation, a second-order linear differential equation, include the analysis of oscillatory systems like wave propagation in periodic media or mechanical vibrations in elastic materials [3,4]. Numerous mathematical and physical problems benefit from the equation, which frequently arises in nonlinear vibration problems. The Mathieu equation is frequently the result of the wave equation’s variables being separated in elliptical coordinates [5,6]. The standard form of it is

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+(k_1+k_{2}cos\left(\omega t\right))y\left(t\right)=0$$

(1)

where the generalized coordinate, y, represents the deflection angle, t is time, $k_1$ is the linear spring constant, $k_2$ is the driving amplitude, and $\omega$ is the excitation frequency. In the case of linear viscous damping, the Mathieu equation is known as the damped Mathieu equation and has the form

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+k{\displaystyle \frac{d}{dt}}y\left(t\right)+(k_1+k_{2}cos\left(\omega t\right))y\left(t\right)=0$$

(2)

where k is the linear damping rate.

The use of an external force and equations with parametric excitation are important when studying systems with oscillatory characteristics. The Mathieu equation is frequently employed for this purpose in a variety of domains because, despite its simplicity, it can effectively express significant aspects of this phenomenon. Nonlinear terms can be added to the Mathieu equation to produce a more realistic model [7]. A nonlinear Mathieu equation for parametric damping, also referred to as the Duffing oscillator, is defined as

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+2\mu {\displaystyle \frac{d}{dt}}y\left(t\right)+(a-2qcos\left(\omega t\right))y\left(t\right)+Q{y}^3\left(t\right)=0$$

(3)

where $\mu$ is the non-zero damping coefficient, a is the oscillator’s unforced natural frequency, q is the excitation amplitude, $\omega$ is the excitation frequency, and Q is the Duffing coefficient.

The quadratically damped Mathieu equation has the form

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+{\displaystyle \frac{d}{dt}}y\left(t\right)\left|{\displaystyle \frac{d}{dt}}y\left(t\right)\right|+(\delta +ϵcos\left(\omega t\right))y\left(t\right)=f\left(t\right).$$

(4)

The dynamics of a cable hauled by a submarine are governed by the equation of motion above, which is derived and has physical interpretations by Rand et al. [8]. More details and generalizations for the Mathieu equations can be found in the review article [9].

Fractional calculus arose around the same time as traditional integer-order calculus. Initially, the topic of modeling real-world situations with real or complex-order differential equations was unpopular among engineers and scientific researchers [10,11]. Even though numerous outstanding results have already been documented by researchers in a number of influential monographs and review articles, many non-local phenomena remain undiscovered and unexplored. We may thus learn new things about fractional modeling and applications every year. The study of fractional calculus has gained popularity since the creation of supercomputers and the development of technology that allows for more complex simulations. It is used in a variety of scientific disciplines, including biology, physics, chemistry, geology, sociology, and circuit theory [12,13]. The study of oscillatory behaviors in dynamical systems of fractional order has also drawn more interest in recent years. The fractional version makes it possible to describe systems that display cumulative or persistent behaviors more accurately by substituting fractional derivatives for integer-order derivatives [14,15].

Grace et al. [16] used the Caputo fractional derivative to examine the asymptotic behavior of non-oscillatory solutions to forced-perturbed fractional differential equations. To solve the time-fractional Navier-Stokes equations, Alqahtani et al. [17] developed analytical and approximation methods. According to [18], a nonlinear compact-polynomial computational scheme is used to explain a numerical approach for solving elliptic differential equations (on unstructured computational grids).

The memory characteristics of such materials must be described using a fractional-order model rather than an integer-order model because the vehicle’s spring and damper clearly exhibit fractional-order characteristics. The following fractional-order Mathieu equation’s transition curves that divide the zones of stability have been provided and examined by Rand et al. [19] as

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+c\left({\mathcal{D}}^{\alpha }y\right)\left(t\right)+(\delta +ϵcos\left(\omega t\right))y\left(t\right)=f\left(t\right).$$

(5)

where ${\mathcal{D}}^{\alpha }$ is the Riemann–Liouville (R–L) fractional derivative of order $\alpha \in (0,1)$, c is the damping coefficient, $\delta$ is the linear spring constant, and $ϵ$ is quantity of forcing amplitude. In reality, the fractional derivative term merges the effects of damping and stiffness into a single term as the parameter $\alpha$ fluctuates between 0 and 1. Also, by using a model of the pantograph-catenary system, Mu et al. [20] considered the fractional-order Mathieu equation under forced excitation

$${\displaystyle \frac{d^2}{d{t}^2}}y\left(t\right)+k\left({}_{}{}^c\mathcal{D}_{}^{\alpha }y\right)\left(t\right)+(k_1+k_{2}cos\left(\omega t\right))y\left(t\right)=f\left(t\right)$$

(6)

where ${}_{}{}^c\mathcal{D}_{}^{\alpha }$ is the Caputo fractional derivative of order $\alpha \in (0,1]$, $k\left({}_{}{}^c\mathcal{D}_{}^{\alpha }y\right)\left(t\right)$ is the air spring with fractional characteristics, and $f\left(t\right)$ is a function that depends on the excitation of the train on the pantograph.

Leung et al. [21] defined the general version of the fractional Mathieu equation as follows in a slightly modified version: by adding a fractional order time derivative of the damped Mathieu equation:

$$\left({}_{}{}^c\mathcal{D}_{}^{1+\alpha }y\right)\left(t\right)+k\left({}_{}{}^c\mathcal{D}_{}^{\alpha }y\right)\left(t\right)+(k_1+k_{2}cos\left(\omega t\right))y\left(t\right)=0$$

(7)

They replaced the derivative of second order with fractional order $1+\alpha ,0<\alpha \le 1$. An alternative approach would be to combine the effects of stiffness and damping in a single term.

Incorporating nonlinear factors, like cubic nonlinear stiffness, into the Mathieu equation yields a more realistic model. For this model, Leung et al. [21] produced a general version of the fractional Mathieu–Duffing equation in the form

$$\left({}_{}{}^c\mathcal{D}_{}^{1+\alpha }y\right)\left(t\right)+k\left({}_{}{}^c\mathcal{D}_{}^{\alpha }y\right)\left(t\right)+(k_1+k_{2}cos\left(\omega t\right))y\left(t\right)+Q{y}^3\left(t\right)=0.$$

(8)

Comprehending the motion of ions is crucial for a variety of reasons, including their use in processing quantum information and accelerating calculations. Researchers have recently become interested in controlling the oscillations of trapped ions. The tempered fractional differential model of the linearly damped ion motion with an octopole is examined by Alzabut et al. [12] due to the need for a better presentation of the physical properties of ion traps and their applications, as well as the fact that only flaws of the type

$${}_{}{}^c\mathcal{D}_{}^{r,\varrho }({}_{}{}^c\mathcal{D}_{}^{s,\varrho }+2\gamma )y\left(t\right)+2qcos\left(2t\right)y\left(t\right)=-4\ell qcos\left(2t\right)y^3\left(t\right),t\in [0,T]$$

(9)

where ${}_{}{}^c\mathcal{D}_{}^{r,\varrho }$ and ${}_{}{}^c\mathcal{D}_{}^{s,\varrho }$ are Caputo-type tempered fractional operators of order $r,s\in (0,1)$ with $1<r+s<2$ and $\varrho \ge 0$. In this case, q is a real parameter, ℓ is the fourth field harmonic relative to the quadrupole field, and $\gamma$ is the damping constant.

Numerous studies on the definition, use, and operation of fractional order derivatives have been carried out since the concept was first developed. The most important derivatives used to model real-life problems are Riemann–Liouville, Caputo, and Hadamard. However, many formulas appeared later that are considered generalizations of these formulas. The Katugampola formula of type $\varrho$ is considered a generalization of many of these formulas. The Katugampola fractional integral approaches the Riemann–Liouville fractional integral as $\varrho \to 1$ and approaches the Hadamard fractional integral as $\varrho \to 0$. There are two approaches for the Katugampola fractional derivative, one in the sense of Riemann-Liouville called R–L–Katugampola and other in the sense of Caputo called Caputo–Katugampola.

Motivated by the previous contributions and to generalize their fractional differential equations, we study the fractional Mathieu equation.

$$\left({\mathcal{D}}_a^{\beta ,\varrho }y\right)\left(t\right)+k\left({\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)+[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)=F(t,y\left(t\right),({\mathcal{D}}_a^{\upsilon ,\varrho }y)\left(t\right))$$

(10)

for all $t\in [a,b]$ with boundary conditions

$$\begin{array}{c}\hfill y\left(a\right)=0,y\left(b\right)=y_b,y_b\in \mathbb{R}\end{array}$$

using the R-L-Katugampola fractional derivatives ${\mathcal{D}}_a^{\beta ,\varrho }$ of order $1\le \beta <2$, ${\mathcal{D}}_a^{\alpha ,\varrho }$ of order $0\le \alpha <1$, and ${\mathcal{D}}_a^{\upsilon ,\varrho }$ of order $0\le \upsilon \le \beta -\alpha$ and type $\varrho >0$. Additionally, we study the fractional Mathieu equation

$$\left({}_{}{}^c\mathcal{D}_a^{\beta ,\varrho }y\right)\left(t\right)+k\left({}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)+[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)=F(t,y\left(t\right),({}_{}{}^c\mathcal{D}_a^{\upsilon ,\varrho }y)\left(t\right))$$

(11)

for all $t\in [a,b]$ with boundary conditions

$$\begin{array}{c}\hfill y\left(a\right)=y_a,y\left(b\right)=y_b,y_b\in \mathbb{R}\end{array}$$

using the Caputo–Katugampola fractional derivatives ${}_{}{}^c\mathcal{D}_a^{\beta ,\varrho }$ of order $1<\beta \le 2$, ${}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }$ of order $0<\alpha \le 1$, and ${}_{}{}^c\mathcal{D}_a^{\upsilon ,\varrho }$ of order $0<\upsilon \le \beta -\alpha$ and type $\varrho >0$.

Furthermore, our study stands out due to its numerous novelties, unique features, and innovative characteristics:

• It is worth noting that all preceding contributions are specialized cases of the two previous fractional Mathieu equations, including Equation (9), which will be explained later.
• Furthermore, our results can be used for a wide range of Mathieu equation applications, both fractional and ordinary, which are too many to discuss here.
• An efficient tool for the analysis of systems with nonlinear or cumulative characteristics is the R–L–Katugampola fractional derivative, which is especially helpful for controlling the boundary behavior of solutions at key places like zero and infinity.
• On the other hand, the Caputo–Katugampola fractional derivative offers flexibility and versatility by permitting more accurate modeling of systems with time-dependent behaviors and long memory effects.
• Also, the Caputo–Katugampola fractional derivative is more applicable for real-life problems due to its relation to the exact initial and boundary conditions, and it, with integer order, approaches the ordinary derivative.
• The fractional Mathieu equation, when paired with these advanced fractional operators, enables a better understanding of systems exhibiting oscillatory behavior, resonant phenomena, and stability under non-standard boundary conditions.
• With the use of these tools, we hope to provide novel insights, fresh perspectives, and answers to challenging problems in applied mathematics and physics.

We organize our paper as follows: The next section is devoted to providing some concepts, definitions, and properties for fractional calculus. Section 3 is concerned with the model of the fractional Mathieu equation with the Riemann–Liouville–Katugampola fractional derivative. The other model with the Caputo–Katugampola fractional derivative is offered in Section 4. Our results are applied to four real-life problems in Section 5: the nonlinear Mathieu equation for parametric damping and the Duffing oscillator, the quadratically damped Mathieu equation, the fractional Mathieu equation’s transition curves, and the tempered fractional model of the linearly damped ion motion with an octopole.

2. Preliminaries

To support the readers, we offer some fundamental definitions and lemmas that will be utilized throughout this investigation. Take $I=[a,b]$ and $\mathcal{M}$ is a Banach space on I. Let the Banach space $C(I,\mathcal{M})$ contain all continuous functions on I equipped with the norm ${\parallel y\parallel }_C={sup}_{t\in I}\left|y\left(t\right)\right|$. The weighted Banach space can be defined as

$$\begin{array}{c}\hfill C_{\upsilon ,\varrho }(I,\mathcal{M})=\left\{y:I\to \mathcal{M}:{\mathcal{T}}_{t,a}^{1-\upsilon }y\left(t\right)\in C(I,\mathcal{M})\right\},{\mathcal{T}}_{t,a}={\displaystyle \frac{t^{\varrho }-a^{\varrho }}{\varrho }}\end{array}$$

equipped with the norm

$${\parallel y\parallel }_{C_{\upsilon ,\varrho }}=\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }y\left(t\right)\right|.$$

Take into consideration the space $Y_r^p\left(I\right)$ (for $r\in \mathbb{R}$, $1\le p<\infty$, $-\infty \le a<b\le \infty$) that contains Lebesgue measurable functions y on $[a,b]$ with real-valued and ${\parallel y\parallel }_{Y_r^p}<\infty$, and

$${\parallel y\parallel }_{Y_r^p}={\left({\int }_a^b{\left|u^{r}y\left(u\right)\right|}^p{\displaystyle \frac{du}{u}}\right)}^{{\displaystyle \frac{1}{p}}},(1\le p<\infty ,r\in \mathbb{R}).$$

Furthermore, consider the spaces

$${\mathcal{W}}_{\upsilon ,\varrho }\left(I\right)=\left\{y\in C_{\upsilon ,\varrho }(I,\mathcal{M}),{\mathcal{D}}_a^{\nu ,\varrho }y\in C_{\upsilon ,\varrho }(I,\mathcal{M})\right\}$$

and

$${\mathcal{Q}}_{\upsilon ,\varrho }\left(I\right)=\left\{y\in C_{\upsilon ,\varrho }(I,\mathcal{M}){,}^c{\mathcal{D}}_a^{\upsilon ,\varrho }y\in C_{\upsilon ,\varrho }(I,\mathcal{M})\right\}.$$

It is clear that the spaces ${\mathcal{W}}_{\upsilon ,\varrho }\left(I\right)$ and ${\mathcal{Q}}_{\upsilon ,\varrho }\left(I\right)$ are Banach spaces equipped with the norms, respectively,

$${\parallel y\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}=\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }y\left(t\right)\right|+\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }\left({\mathcal{D}}_a^{\upsilon ,\varrho }y\right)\left(t\right)\right|,$$

and

$${\parallel y\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}=\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }y\left(t\right)\right|+\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }{(}^c{\mathcal{D}}_a^{\upsilon ,\varrho }y)\left(t\right)\right|.$$

Definition 1 

([22]). Let $0\le \xi <1$ and $AC\left(I\right)$ be the set of absolute continuous functions on I. Then, we define

$$\begin{array}{cc}\hfill A{C}_{\lambda }^m\left(I\right)& =\left\{y:I\to \mathbb{C}\mathit{and}{\lambda }^{m-1}y\in AC\left(I\right),\lambda =u^{1-\varrho }{\displaystyle \frac{d}{du}}\right\},\hfill \\ \hfill C_{\lambda ,\xi }^m\left(I\right)& =\left\{y:I\to \mathbb{C}\mathit{and}{\lambda }^{m-1}y\in C\left(I\right),{\lambda }^{m}y\in C_{\xi ,\varrho }\left(I\right),\lambda =u^{1-\varrho }{\displaystyle \frac{d}{du}}\right\}.\hfill \end{array}$$

Definition 2 

([23]). Let $0\le a<b\le \infty$, $y\in Y_r^p\left(I\right)$, and $\varrho ,r\in \mathbb{R}$. Then, the Katugampola fractional integral of order $\alpha >0$ and type $\varrho \ge r$ is defined by

$$\left({\mathcal{I}}_a^{\alpha ,\varrho }y\right)\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_a^t{\mathcal{T}}_{t,u}^{\alpha -1}y\left(u\right)u^{\varrho -1}dut>a.$$

Theorem 1 

([23]). Let $\alpha ,\beta >0$, $1\le p\le \infty$, $0<a<b<\infty$, and $\varrho ,r\in \mathbb{R}$ such that $\varrho \ge r$. Then, the semigroup property is valid for $y\in Y_r^p\left(I\right)$; we have

$$\left({\mathcal{I}}_a^{\alpha ,\varrho }{\mathcal{I}}_a^{\beta ,\varrho }y\right)\left(t\right)=\left({\mathcal{I}}_a^{\alpha +\beta ,\varrho }y\right)\left(t\right).$$

Definition 3 

([23]). Let $\varrho >0$, $m-1\le \alpha <m$, and $y\in Y_r^p\left(I\right)$. Then, the R–L–Katugampola fractional derivative is defined by

$$\left({\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)={\lambda }^m\left({\mathcal{I}}_a^{m-\alpha ,\varrho }y\right)\left(t\right)$$

where $m\in \mathbb{N}$, and $\lambda =u^{1-\varrho }{\displaystyle \frac{d}{du}}$.

Theorem 2 

([22]). Let $m\in \mathbb{N}$, $m-1\le \alpha <m$, $y\in C_{\lambda ,\xi }^m\left(I\right)$. Then,

$$\left({\mathcal{I}}_a^{\alpha ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)=y\left(t\right)-\sum _{i=1}^{m-1}{\displaystyle \frac{{\mathcal{D}}_a^{\alpha -i,\varrho }y\left(a\right)}{\Gamma (\alpha -i+1)}}{\mathcal{T}}_{t,a}^{\alpha -i}-{\displaystyle \frac{{\mathcal{I}}_a^{m-\alpha ,\varrho }y\left(a\right)}{\Gamma (\alpha -m+1)}}{\mathcal{T}}_{t,a}^{\alpha -m}.$$

Lemma 1 

([24]). Let $\alpha ,\beta >0$, $\varrho >0$, and $t>a$. Then,

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_a^{\alpha ,\varrho }{\left({\displaystyle \frac{u^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -1}\right)\left(t\right)& ={\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta +\alpha )}}{\left({\displaystyle \frac{t^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta +\alpha -1},\hfill \\ \hfill \left({\mathcal{D}}_a^{\alpha ,\varrho }{\left({\displaystyle \frac{u^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -1}\right)\left(t\right)& ={\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\alpha )}}{\left({\displaystyle \frac{t^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -\alpha -1},\alpha -\beta \notin {\mathbb{N}}_0,\hfill \\ \hfill \left({\mathcal{D}}_a^{\alpha ,\varrho }{\left({\displaystyle \frac{u^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -1}\right)\left(t\right)& =0,\alpha -\beta \in {\mathbb{N}}_0.\hfill \end{array}$$

Theorem 3 

([23]). Let $m\in \mathbb{N}$, $m-1<\alpha <m$, and $\beta >0$ such that $\alpha \le \beta$. Then, for $y\in Y_r^p\left(I\right)$ and ${\mathcal{I}}_a^{\beta ,\varrho }y\in C_{\lambda ,\xi }^m\left(I\right)$, we have

$$\left({\mathcal{D}}_a^{\alpha ,\varrho }{\mathcal{I}}_a^{\beta ,\varrho }y\right)\left(t\right)=\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right).$$

Lemma 2. 

Let $m\in \mathbb{N}$, $m-1<\alpha <m$, and $\beta >0$ such that $\alpha \le \beta$. Then, for $y\in C_{\lambda ,\xi }^m\left(I\right)$ and ${\mathcal{D}}_a^{\alpha ,\varrho }y\in Y_r^p\left(I\right)$, we have

$$\left({\mathcal{I}}_a^{\beta ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)=\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-\sum _{i=1}^{m-1}{\displaystyle \frac{{\mathcal{D}}_a^{\alpha -i,\varrho }y\left(a\right)}{\Gamma (\beta -i+1)}}{\mathcal{T}}_{t,a}^{\beta -i}-{\displaystyle \frac{{\mathcal{I}}_a^{m-\alpha ,\varrho }y\left(a\right)}{\Gamma (\beta -m+1)}}{\mathcal{T}}_{t,a}^{\beta -m}.$$

Proof. 

By using Theorem 2 and Lemma 1 while noting $\alpha \le \beta$, we have

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_a^{\beta ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)& =\left({\mathcal{I}}_a^{\beta -\alpha +\alpha ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }{\mathcal{I}}_a^{\alpha ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & ={\mathcal{I}}_a^{\beta -\alpha ,\varrho }\left(y\left(t\right)-\sum _{i=1}^{m-1}{\displaystyle \frac{{\mathcal{D}}_a^{\alpha -i,\varrho }y\left(a\right)}{\Gamma (\alpha -i+1)}}{\mathcal{T}}_{t,a}^{\alpha -i}-{\displaystyle \frac{{\mathcal{I}}_a^{m-\alpha ,\varrho }y\left(a\right)}{\Gamma (\alpha -m+1)}}{\mathcal{T}}_{t,a}^{\alpha -m}\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-\sum _{i=1}^{m-1}{\displaystyle \frac{{\mathcal{D}}_a^{\alpha -i,\varrho }y\left(a\right)}{\Gamma (\beta -i+1)}}{\mathcal{T}}_{t,a}^{\beta -i}-{\displaystyle \frac{{\mathcal{I}}_a^{m-\alpha ,\varrho }y\left(a\right)}{\Gamma (\beta -m+1)}}{\mathcal{T}}_{t,a}^{\beta -m}\hfill \end{array}$$

which ends the proof. □

Definition 4 

([22]). Let $m\in \mathbb{N}$, $m-1<\alpha \le m$, and $y\in A{C}_{\lambda ,\xi }^m\left(I\right)$. Then, the Caputo–Katugampola fractional derivative of order α is defined by

$$\begin{array}{cc}\hfill {(}^c{\mathcal{D}}_a^{\alpha ,\varrho }y)\left(t\right)& =\left({\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)-{\mathcal{D}}_a^{\alpha ,\varrho }\left(\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{j!}}{\mathcal{T}}_{t,a}^j\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{m-\alpha ,\varrho }{\lambda }^{m}y\right)\left(t\right).\hfill \end{array}$$

Theorem 4 

([22]). Let $m\in \mathbb{N}$, $m-1<\alpha \le m$ and $y\in A{C}_{\lambda }^m\left(I\right)$ or $C_{\lambda ,\xi }^m\left(I\right)$ and $\alpha \in \mathbb{C}$. Then, we have

$$\left({\mathcal{I}}_a^{\alpha ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)=y\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{j!}}{\mathcal{T}}_{t,a}^j.$$

Lemma 3.

Let $\alpha \le \beta$ and $m\in \mathbb{N}$ such that $m-1<\alpha <m$. Then, for $y\in A{C}_{\lambda }^m\left(I\right)$ or $C_{\lambda ,\xi }^m\left(I\right)$, we have

$$\left({\mathcal{I}}_a^{\beta ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)=\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{\Gamma (\beta -\alpha +j+1)}}{\mathcal{T}}_{t,a}^{\beta -\alpha +j}.$$

Proof. 

By using Theorem 4 and Lemma 1 while noting $\alpha <\beta$, we have

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_a^{\beta ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)& =\left({\mathcal{I}}_a^{\beta -\alpha +\alpha ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)=\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }{\mathcal{I}}_a^{\alpha ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & ={\mathcal{I}}_a^{\beta -\alpha ,\varrho }\left(y\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{j!}}{\mathcal{T}}_{t,a}^j\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{j!}}{\mathcal{I}}_a^{\beta -\alpha ,\varrho }{\mathcal{T}}_{t,a}^j\hfill \\ \hfill & =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{{\lambda }^{j}y\left(a\right)}{\Gamma (\beta -\alpha +j+1)}}{\mathcal{T}}_{t,a}^{\beta -\alpha +j}\hfill \end{array}$$

which is the desired result. □

Lemma 4 

([25]). Let $m\in \mathbb{N}$ such that $m-1<\alpha \le m$, $\beta >0$, $\varrho >0$, and $t>a$. Then,

$$\begin{array}{cc}\hfill \left({}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }{\left({\displaystyle \frac{u^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -1}\right)\left(t\right)& ={\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\alpha )}}{\left({\displaystyle \frac{t^{\varrho }-a^{\varrho }}{\varrho }}\right)}^{\beta -\alpha -1},\beta \ne 1,2,3,\dots ,m-1,\hfill \\ \hfill \left({}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }{\left({\displaystyle \frac{u^{\varrho }-a^{\varrho }}{\varrho }}\right)}^k\right)\left(t\right)& =0,k=0,1,2,3,\dots ,m-1.\hfill \end{array}$$

Lemma 5.

Let $m=1$ in Lemmas 2 and 3. Then, we get

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_a^{\beta ,\varrho }{\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)& =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-{\displaystyle \frac{{\mathcal{I}}_a^{1-\alpha ,\varrho }y\left(a\right)}{\Gamma \left(\beta \right)}}{\mathcal{T}}_{t,a}^{\beta -1},\hfill \\ \hfill \left({\mathcal{I}}_a^{\beta ,\varrho }{}_{}{}^c\mathcal{D}_a^{\alpha ,\varrho }y\right)\left(t\right)& =\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)-{\displaystyle \frac{y\left(a\right)}{\Gamma (\beta -\alpha +1)}}{\mathcal{T}}_{t,a}^{\beta -\alpha }.\hfill \end{array}$$

3. R–L–Katugampola Fractional Integral

Assume $1\le \beta <2$, $0\le \alpha <1$, and $\varrho >0$. Consider the linear fractional Mathieu equation

$$\left({\mathcal{D}}_a^{\beta ,\varrho }y\right)\left(t\right)+k\left({\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)+[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)=f\left(t\right),t\in I$$

(12)

with boundary conditions

$$\begin{array}{c}\hfill y\left(a\right)=0,y\left(b\right)=y_b,y_b\in \mathbb{R}\end{array}$$

where k is the linear damping rate, $k_1$ is the linear spring constant, $k_2$ is the driving amplitude, $\omega$ is excitation frequency, and $f\in Y_r^p\left(I\right)$.

Lemma 6.

Let $y\in {\mathcal{W}}_{\upsilon ,\varrho }\left(I\right)$, $1\le \beta <2$, $0\le \alpha <1$ and $\varrho >0$. Then, the problem (12) has a unique solution

$$\begin{array}{cc}\hfill y\left(t\right)& ={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{\beta -1}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[k_1+k_{2}cos\left(\omega b\right)\right]y\left(b\right)+y_b\right).\hfill \end{array}$$

(13)

Proof. 

By applying the fractional integral operator ${\mathcal{I}}_a^{\beta ,\varrho }$ to both sides of (12) while using Theorem 2 and Lemma 2, we get

$$y\left(t\right)={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)+C_1{\mathcal{T}}_{t,a}^{\beta -1}+C_2{\mathcal{T}}_{t,a}^{\beta -2}$$

where

$$C_1={\displaystyle \frac{{\mathcal{D}}_a^{\beta -1,\varrho }y\left(a\right)}{\Gamma \left(\beta \right)}}-k{\displaystyle \frac{{\mathcal{I}}_a^{1-\alpha ,\varrho }y\left(a\right)}{\Gamma \left(\beta \right)}}\mathrm{and}{C}_2={\displaystyle \frac{{\mathcal{I}}_a^{2-\beta ,\varrho }y\left(a\right)}{\Gamma (\beta -1)}}.$$

Since $\beta -2<0$ and $y\left(a\right)=0$, we must take $C_2=0$, which implies that

$$y\left(t\right)={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)+C_1{\mathcal{T}}_{t,a}^{\beta -1}.$$

Using the condition $y\left(b\right)=y_b$ gives

$$C_1={\mathcal{T}}_{b,a}^{1-\beta }\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b\right)$$

which leads to (13).

Conversely, let $y\in {\mathcal{W}}_{\upsilon ,\varrho }\left(I\right)$; by applying Theorem 3 and Lemma 1 on the solution (13), we get the fractional differential Equation (12). Also, it is easy to verify that (13) satisfies the conditions $y\left(a\right)=0$ and $y\left(b\right)=y_b$. □

Let $0<\upsilon \le \beta -\alpha$ and $\alpha \ge \upsilon$, which leads to $\beta \ge 2\upsilon$. Using Theorem 3 and Lemma 1 gives

$$\begin{array}{cc}\hfill \left({\mathcal{D}}_a^{\upsilon ,\varrho }y\right)\left(t\right)& ={\mathcal{I}}_a^{\beta -\upsilon ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha -\upsilon ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\upsilon )}}{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon -1}}{{\mathcal{T}}_{b,a}^{\beta -1}}}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b\right).\hfill \end{array}$$

(14)

Assume the following condition:

$\left(H_1\right)$

Let $f\left(t\right)=F(t,y\left(t\right),{\mathcal{D}}_a^{\upsilon ,\varrho })$ where $F:I\times C_{\upsilon ,\varrho }\times C_{\upsilon ,\varrho }\to C_{\upsilon ,\varrho }$ is continuous;

$\left(H_2\right)$

There exists a positive constant L such that

$$\left|F\right(t,y\left(t\right),h\left(t\right))-F(t,x\left(t\right),z\left(t\right)\left)\right|\le L\left(\right|y\left(t\right)-x\left(t\right)|+|h\left(t\right)-z\left(t\right)\left|\right)$$

where $t\in I$ and $y,x,h,z\in C_{\upsilon ,\varrho }$.

For appropriateness, we take

$$\begin{array}{cc}\hfill T_{\delta }^{\gamma }& =\left(1+{\displaystyle \frac{\Gamma \left(\beta \right)\Gamma (\beta -\gamma \alpha )}{\Gamma (\beta -\delta \upsilon )\Gamma (\beta -\gamma \alpha +\delta \upsilon )}}\right){\displaystyle \frac{[(1-\gamma )(L+\mathcal{G})+\gamma k]{\mathcal{T}}_{b,a}^{\beta -\gamma \alpha -\delta \upsilon }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\gamma \alpha +(1-\delta \left)\upsilon \right)}},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill R_{\delta }& =\left(1+{\displaystyle \frac{{\Gamma }^2\left(\beta \right)}{\Gamma (\beta -\delta \upsilon )\Gamma (\beta +\delta \upsilon )}}\right){\displaystyle \frac{\mathcal{N}{\mathcal{T}}_{b,a}^{\beta -\delta \upsilon }\Gamma \left(\upsilon \right)}{\Gamma (\beta +(1-\delta \left)\upsilon \right)}}+{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\delta \upsilon )}}{\mathcal{T}}_{b,a}^{1-(1+\delta )\upsilon }\left|y_b\right|\hfill \end{array}$$

(16)

where $\delta ,\gamma =0,1$,

$$\mathcal{N}=\underset{t\in I}{sup}|{\mathcal{T}}_{t,a}^{1-\upsilon }F(t,0,0)|,\mathrm{and}\mathcal{G}=\underset{t\in I}{sup}|k_1+k_{2}cos\left(\omega t\right)|.$$

It is easy to see that

$$\begin{array}{c}\hfill {\parallel f\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}\le L{\parallel y\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}+\mathcal{N}.\end{array}$$

Theorem 5.

The hypotheses $\left(H_1\right)$ and $\left(H_2\right)$ are satisfied. Then, the fractional Mathuie Equation (10) has a unique solution if $T_0^0+T_0^1+T_1^0+T_1^1<1$ where $T_{\delta }^{\gamma };\delta ,\gamma =0,1$ are defined in (15).

Proof. 

We define the mapping $\Psi :{\mathcal{W}}_{\upsilon ,\varrho }\to {\mathcal{W}}_{\upsilon ,\varrho }$

$$\begin{array}{cc}\hfill \Psi y\left(t\right)& ={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{\beta -1}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b\right)\hfill \end{array}$$

which has, from (14), the fractional derivative

$$\begin{array}{cc}\hfill ({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)& ={\mathcal{I}}_a^{\beta -\upsilon ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha -\upsilon ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\upsilon )}}{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon -1}}{{\mathcal{T}}_{b,a}^{\beta -1}}}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b\right).\hfill \end{array}$$

Now, we show that $\Psi \mathfrak{B}\subset \mathfrak{B}$ where $\mathfrak{B}$ is a closed ball defined as

$$\mathfrak{B}=\{y\in {\mathcal{W}}_{\upsilon ,\varrho }:\parallel y\parallel \le s\}$$

with radius

$$s>{\displaystyle \frac{R_0+R_1}{1-(T_0^0+T_0^1+T_1^0+T_1^1)}}.$$

From the assumptions, we have

$$\begin{array}{cc}\hfill |{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)|& \le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{1-\upsilon }}{\Gamma \left(\beta \right)}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -1}\left(\left|F(u,y\left(u\right),h\left(u\right))\right|+|k_1+k_{2}cos\left(\omega u\right)\left|\right|y\left(u\right)|\right){\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{1-\upsilon }}{\Gamma (\beta -\alpha )}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -\alpha -1}\left|y\left(u\right)\right|{\displaystyle \frac{du}{u^{1-\varrho }}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\upsilon }}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma (\beta -\alpha )}}{\int }_a^b{\mathcal{T}}_{b,u}^{\beta -\alpha -1}\left|y\left(u\right)\right|{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma \left(\beta \right)}}{\int }_a^b{\mathcal{T}}_{b,u}^{\beta -1}\left(\right|F(u,y\left(u\right),h\left(u\right))|+|k_1+k_{2}cos\left(\omega u\right)\left|\right|y\left(u\right)\left|\right){\displaystyle \frac{du}{u^{1-\varrho }}}+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }}{{\mathcal{T}}_{b,a}^{\beta -1}}}\left|y_b\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{1-\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)}{\Gamma \left(\beta \right)}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{1-\upsilon }s}{\Gamma (\beta -\alpha )}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -\alpha -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\upsilon }s}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma (\beta -\alpha )}}{\int }_a^b{\mathcal{T}}_{b,u}^{\beta -\alpha -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma \left(\beta \right)}}{\int }_a^b{\mathcal{T}}_{t,u}^{\beta -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }}{{\mathcal{T}}_{b,a}^{\beta -1}}}\left|y_b\right|\hfill \\ \hfill & ={\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\upsilon }s\Gamma \left(\upsilon \right)}{{\mathcal{T}}_{b,a}^{\alpha -\upsilon }\Gamma (\beta -\alpha +\upsilon )}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{{\mathcal{T}}_{b,a}^{-\upsilon }\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }}{{\mathcal{T}}_{b,a}^{\beta -1}}}\left|y_b\right|\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)\right|& \le {\displaystyle \frac{2{\mathcal{T}}_{b,a}^{\beta }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{2k{\mathcal{T}}_{b,a}^{\beta -\alpha }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}+{\mathcal{T}}_{b,a}^{1-\upsilon }\left|y_b\right|=(T_0^0+T_0^1)s+R_0.\hfill \end{array}$$

Similarly, we find that

$$\begin{array}{cc}\hfill |{\mathcal{T}}_{t,a}^{1-\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)|& \le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma \left(\beta \right)}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha -\upsilon }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha )}}\hfill \\ \hfill & +{\displaystyle \frac{\Gamma \left(\beta \right){\mathcal{T}}_{t,a}^{\beta -2\upsilon }}{\Gamma (\beta -\upsilon )}}\left({\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\upsilon -\alpha }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}+{\displaystyle \frac{\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{{\mathcal{T}}_{b,a}^{-\upsilon }\Gamma (\beta +\upsilon )}}+{\mathcal{T}}_{b,a}^{1-\beta }\left|y_b\right|\right)\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)\right|& \le \left(1+{\displaystyle \frac{{\Gamma }^2\left(\beta \right)}{\Gamma (\beta -\upsilon )\Gamma (\beta +\upsilon )}}\right){\displaystyle \frac{{\mathcal{T}}_{b,a}^{\beta -\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma \left(\beta \right)}}\hfill \\ \hfill & +\left(1+{\displaystyle \frac{\Gamma \left(\beta \right)\Gamma (\beta -\alpha )}{\Gamma (\beta -\upsilon )\Gamma (\beta -\alpha +\upsilon )}}\right){\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha -\upsilon }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha )}}\hfill \\ \hfill & +{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (\beta -\upsilon )}}{\mathcal{T}}_{b,a}^{1-2\upsilon }\left|y_b\right|=(T_1^0+T_1^1)s+R_1.\hfill \end{array}$$

These lead to

$$\begin{array}{cc}\hfill {\parallel \Psi y\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}& =\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)\right|+\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)\right|\hfill \\ \hfill & \le (T_0^0+T_0^1+T_1^0+T_1^1)s+R_0+R_1<s.\hfill \end{array}$$

which implies that the mapping $\Psi$ maps $\mathfrak{B}$ into itself.

Now, for $y_1,y_2\in {\mathcal{W}}_{\upsilon ,\varrho }$, while using the assumption $\left(H_2\right)$, we have

$$\begin{array}{cc}\hfill & |{\mathcal{T}}_{t,a}^{1-\upsilon }[(\Psi y_1)\left(t\right)-(\Psi y_2)\left(t\right)]|\le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{1-\upsilon }(L+\mathcal{G}){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}}{\Gamma \left(\beta \right)}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{1-\upsilon }{\parallel y_1-y_2\parallel }_{{\mathcal{C}}_{\upsilon ,\varrho }}}{\Gamma (\beta -\alpha )}}{\int }_a^t{\mathcal{T}}_{t,u}^{\beta -\alpha -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\upsilon }{\parallel y_1-y_2\parallel }_{{\mathcal{C}}_{\upsilon ,\varrho }}}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma (\beta -\alpha )}}{\int }_a^b{\mathcal{T}}_{b,u}^{\beta -\alpha -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\upsilon }(L+\mathcal{G}){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}}{{\mathcal{T}}_{b,a}^{\beta -1}\Gamma \left(\beta \right)}}{\int }_a^b{\mathcal{T}}_{t,u}^{\beta -1}{\mathcal{T}}_{u,a}^{\upsilon -1}{\displaystyle \frac{du}{u^{1-\varrho }}}\hfill \\ \hfill & \le \left[\left(1+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{-\upsilon }}{{\mathcal{T}}_{b,a}^{-\upsilon }}}\right){\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta }(L+\mathcal{G})\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+\left(1+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\alpha -\upsilon }}{{\mathcal{T}}_{b,a}^{\alpha -\upsilon }}}\right){\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}\right]{\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }[(\Psi y_1)\left(t\right)-(\Psi y_2)\left(t\right)]\right|& \le 2\left({\displaystyle \frac{{\mathcal{T}}_{b,a}^{\beta }(L+\mathcal{G})\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}\right){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}\hfill \\ \hfill & =(T_0^0+T_0^1){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}.\hfill \end{array}$$

Similarly, we find that

$$\begin{array}{c}\hfill \underset{t\in I}{sup}|{\mathcal{T}}_{t,a}^{\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_1)\left(t\right)-{\mathcal{T}}_{t,a}^{\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_2)\left(t\right)|=(T_1^0+T_1^1){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}.\end{array}$$

These lead to

$$\begin{array}{c}\hfill \parallel \Psi y_1-\Psi y_2{\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}\le (T_0^0+T_0^1+T_1^0+T_1^1){\parallel y_1-y_2\parallel }_{{\mathcal{W}}_{\upsilon ,\varrho }}.\end{array}$$

As $T_0^0+T_0^1+T_1^0+T_1^1<1$, the mapping $\Psi$ is a contraction and therefore there exists a unique fixed point $y^{*}\in \mathfrak{B}$ such that $\Psi y^{*}\left(t\right)=y^{*}\left(t\right)$. Any fixed point of $\Psi$ is the solution of Equation (10). □

4. Caputo–Katugampola Fractional Derivative

Assume $1<\beta \le 2$, $0<\alpha \le 1$ and $\varrho >0$. Consider the linear fractional Mathieu equation

$$\left({\mathcal{D}}_a^{\beta ,\varrho }y\right)\left(t\right)+k\left({\mathcal{D}}_a^{\alpha ,\varrho }y\right)\left(t\right)+[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)=f\left(t\right),t\in I$$

(17)

with boundary conditions

$$\begin{array}{c}\hfill y\left(a\right)=y_a,y\left(b\right)=y_b,y_a,y_b\in \mathbb{R}\end{array}$$

where k is the linear damping rate, $k_1$ is the linear spring constant, $k_2$ is the driving amplitude, $\omega$ is excitation frequency, and $f\in Y_r^p\left(I\right)$.

Lemma 7.

Let $y\in {\mathcal{Q}}_{\upsilon ,\varrho }\left(I\right)$, $1<\beta \le 2$, $0<\alpha \le 1$, and $\varrho >0$. Then, the problem (17) has a unique solution

$$\begin{array}{cc}\hfill y\left(t\right)& ={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b-y_a\right)\hfill \\ \hfill & +{\displaystyle \frac{k{y}_a}{\Gamma \left(\beta -\alpha +1\right)}}{\mathcal{T}}_{t,a}{\mathcal{T}}_{b,a}^{\beta -\alpha -1}\left({\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{\beta -\alpha -1}-1\right)+y_a.\hfill \end{array}$$

(18)

Proof. 

By applying the fractional integral operator ${\mathcal{I}}_a^{\beta ,\varrho }$ to both sides of (17) while using Theorem 4 and Lemma 3, we get

$$\begin{array}{c}\hfill y\left(t\right)={\mathcal{I}}_a^{\beta ,\varrho }[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)+C_1\left(1+{\displaystyle \frac{k}{\Gamma \left(\beta -\alpha +1\right)}}{\mathcal{T}}_{t,a}^{\beta -\alpha }\right)+C_2{\mathcal{T}}_{t,a}.\end{array}$$

Using the conditions $y\left(a\right)=y_a$ and $y\left(b\right)=y_b$ gives

$$\begin{array}{cc}\hfill C_1& =y\left(a\right)=y_a,\hfill \\ \hfill C_2& ={\left[t^{1-\varrho }{\displaystyle \frac{dy\left(t\right)}{dt}}\right]}_{t=a}\hfill \\ \hfill & ={\mathcal{T}}_{b,a}^{-1}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b-y_a-{\displaystyle \frac{k{y}_a}{\Gamma \left(\beta -\alpha +1\right)}}{\mathcal{T}}_{b,a}^{\beta -\alpha }\right)\hfill \end{array}$$

which lead to (18).

Conversely, let $y\in {\mathcal{Q}}_{\upsilon ,\varrho }\left(I\right)$; by applying Theorem 4 and Lemma 1 to the solution of (18), we get the fractional differential equation (17). Also, it is easy to verify that the (18) satisfies the conditions $y\left(a\right)=y_a$ and $y\left(b\right)=y_b$. □

Let $0<\upsilon \le \beta -\alpha$. Using Theorem 4 and Lemma 4, give

$$\begin{array}{cc}\hfill {(}^c{\mathcal{D}}_a^{\upsilon ,\varrho }y)\left(t\right)& ={\mathcal{I}}_a^{\beta -\upsilon ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha -\upsilon ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}^{1-\upsilon }{\mathcal{T}}_{b,a}^{-1}}{\Gamma (2-\upsilon )}}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b-y_a\right)\hfill \\ \hfill & -{\displaystyle \frac{{\mathcal{T}}_{t,a}^{1-\upsilon }}{\Gamma (2-\upsilon )}}{\displaystyle \frac{{\mathcal{T}}_{b,a}^{\beta -\alpha -1}k{y}_a}{\Gamma \left(\beta -\alpha +1\right)}}+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta -\alpha -\upsilon }k{y}_a}{\Gamma \left(\beta -\alpha -\upsilon +1\right)}}.\hfill \end{array}$$

(19)

For appropriateness, we take

$$\begin{array}{cc}\hfill {}_{}{}^{c}T_{\delta }^{\gamma }& =\left(1+{\displaystyle \frac{\Gamma (\beta -\gamma \alpha )}{\Gamma (2-\delta \upsilon )\Gamma (\beta -\gamma \alpha +\delta \upsilon )}}\right){\displaystyle \frac{[(1-\gamma )(L+\mathcal{G})+\gamma k]{\mathcal{T}}_{b,a}^{\beta -\gamma \alpha -\delta \upsilon }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\gamma \alpha +(1-\delta \left)\upsilon \right)}},\hfill \\ \hfill {}_{}{}^{c}R_{\delta }& =\left(1+{\displaystyle \frac{\Gamma (\beta -\alpha )}{\Gamma (2-\delta \upsilon )\Gamma (\beta -\alpha +\delta \upsilon )}}\right){\displaystyle \frac{\mathcal{N}{\mathcal{T}}_{b,a}^{\beta -\alpha -\delta \upsilon }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +(1-\delta \left)\upsilon \right)}}+{\displaystyle \frac{\delta k{\mathcal{T}}_{b,a}^{\beta -\alpha -2\upsilon +1}\left|y_a\right|}{\Gamma \left(\beta -\upsilon -\alpha +1\right)}}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{(2-\delta ){\mathcal{T}}_{b,a}^{1-(1+\delta )\upsilon }\left|y_a\right|}{\Gamma (2-\delta \upsilon )}}\left(1+{\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha }}{\Gamma \left(\beta -\alpha +1\right)}}\right)+{\displaystyle \frac{{\mathcal{T}}_{b,a}^{1-(1+\delta )\upsilon }\left|y_b\right|}{\Gamma (2-\delta \upsilon )}}\hfill \end{array}$$

(21)

where $\delta ,\gamma =0,1$.

Theorem 6.

The hypotheses $\left(H_1\right)$ and $\left(H_2\right)$ are satisfied. Then, the fractional Mathuie Equation (11) has a unique solution if ${}_{}{}^{c}T_0^0{+}^c{T}_0^1{+}^c{T}_1^0{+}^c{T}_1^1<1$ where $T_{\delta }^{\gamma };\delta ,\gamma =0,1$ are defined in (20).

Proof. 

We define the mapping $\Psi :{\mathcal{Q}}_{\upsilon ,\varrho }\to {\mathcal{Q}}_{\upsilon ,\varrho }$

$$\begin{array}{cc}\hfill \Psi y\left(t\right)& ={\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(t\right)-[k_1+k_{2}cos\left(\omega t\right)]y\left(t\right)\right]-k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\left(k\left({\mathcal{I}}_a^{\beta -\alpha ,\varrho }y\right)\left(b\right)-{\mathcal{I}}_a^{\beta ,\varrho }\left[f\left(b\right)-[k_1+k_{2}cos\left(\omega b\right)]y\left(b\right)\right]+y_b-y_a\right)\hfill \\ \hfill & +{\displaystyle \frac{k{y}_a}{\Gamma \left(\beta -\alpha +1\right)}}{\mathcal{T}}_{t,a}{\mathcal{T}}_{b,a}^{\beta -\alpha -1}\left({\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{\beta -\alpha -1}-1\right)+y_a.\hfill \end{array}$$

Now we can show that $\Psi \mathfrak{B}\subset \mathfrak{B}$, where $\mathfrak{B}$ is a closed ball defined as $\mathfrak{B}:=\{y\in {\mathcal{Q}}_{\upsilon ,\varrho }:\parallel y\parallel \le s\}$ with radius

$$s>{\displaystyle \frac{{}_{}{}^{c}R_0+{}_{}{}^{c}R_1}{1-({}_{}{}^{c}T_0+{}_{}{}^{c}T_1)}}.$$

From the assumptions, as in the previous section, we have

$$\begin{array}{cc}\hfill |{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)|& \le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}+{\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha +\upsilon -2}{\mathcal{T}}_{t,a}^{2-\upsilon }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{b,a}^{\beta +\upsilon -2}{\mathcal{T}}_{t,a}^{2-\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{{\mathcal{T}}_{t,a}^{2-\upsilon }}{{\mathcal{T}}_{b,a}}}|y_b-y_a|+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{2-\upsilon }\left|y_a\right|}{\Gamma \left(\beta -\alpha +1\right)}}{\mathcal{T}}_{b,a}^{\beta -\alpha -1}\hfill \\ \hfill & +{\mathcal{T}}_{t,a}^{1-\upsilon }\left|y_a\right|+{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha -\upsilon +1}\left|y_a\right|}{\Gamma \left(\beta -\alpha +1\right)}}\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)\right|& \le {\displaystyle \frac{2{\mathcal{T}}_{b,a}^{\beta }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}+{\displaystyle \frac{2k{\mathcal{T}}_{b,a}^{\beta -\alpha }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}+{\displaystyle \frac{2k{\mathcal{T}}_{b,a}^{\beta -\alpha -\upsilon +1}\left|y_a\right|}{\Gamma \left(\beta -\alpha +1\right)}}\hfill \\ \hfill & +2{\mathcal{T}}_{b,a}^{1-\upsilon }|y_a|+{\mathcal{T}}_{b,a}^{1-\upsilon }\left|y_b\right|=({}_{}{}^{c}T_0^0+{}_{}{}^{c}T_1^0)s+{}_{}{}^{c}R_0.\hfill \end{array}$$

Similarly, we find that

$$\begin{array}{cc}\hfill \underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }{(}^c{\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)\right|& \le \left(1+{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (2-\upsilon )\Gamma (\beta +\upsilon )}}\right){\displaystyle \frac{{\mathcal{T}}_{b,a}^{\beta -\upsilon }\left((L+\mathcal{G})s+\mathcal{N}\right)\Gamma \left(\upsilon \right)}{\Gamma \left(\beta \right)}}\hfill \\ \hfill & +\left(1+{\displaystyle \frac{\Gamma (\beta -\alpha )}{\Gamma (2-\upsilon )\Gamma (\beta -\alpha +\upsilon )}}\right){\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha -\upsilon }s\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha )}}\hfill \\ \hfill & +{\displaystyle \frac{{\mathcal{T}}_{b,a}^{1-2\upsilon }}{\Gamma (2-\upsilon )}}\left(|y_b|+|y_a|+{\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha }\left|y_a\right|}{\Gamma (\beta -\alpha +1)}}\right)+{\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha -2\upsilon +1}\left|y_a\right|}{\Gamma (\beta -\alpha -\upsilon +1)}}\hfill \\ \hfill & =({}_{}{}^{c}T_1^0+{}_{}{}^{c}T_1^1)s+{}_{}{}^{c}R_1.\hfill \end{array}$$

These lead to

$$\begin{array}{cc}\hfill {\parallel \Psi y\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}& =\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y)\left(t\right)\right|+\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }{(}^c{\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y)\left(t\right)\right|\hfill \\ \hfill & \le ({}_{}{}^{c}T_0^0+{}_{}{}^{c}T_0^1+{}_{}{}^{c}T_1^0+{}_{}{}^{c}T_1^1)s+{}_{}{}^{c}R_0+{}_{}{}^{c}R_1\le s\hfill \end{array}$$

which implies that the mapping $\Psi$ maps $\mathfrak{B}$ into itself. Now, for $y_1,y_2\in {\mathcal{W}}_{\upsilon ,\varrho }$, we have

$$\begin{array}{cc}\hfill & |{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y_1)\left(t\right)-{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y_2)\left(t\right)|\hfill \\ \hfill & \le {\displaystyle \frac{{\mathcal{T}}_{t,a}^{\beta }(L+\mathcal{G})\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}\left(1+{\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{-\upsilon }\right){\parallel y_1-y_2\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}\hfill \\ \hfill & +{\displaystyle \frac{k{\mathcal{T}}_{t,a}^{\beta -\alpha }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}\left(1+{\left({\displaystyle \frac{{\mathcal{T}}_{t,a}}{{\mathcal{T}}_{b,a}}}\right)}^{\alpha -\upsilon }\right){\parallel y_1-y_2\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill \underset{t\in I}{sup}|{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y_1)\left(t\right)-{\mathcal{T}}_{t,a}^{1-\upsilon }(\Psi y_2)\left(t\right)|\le ({}_{}{}^{c}T_0^0+{}_{}{}^{c}T_0^1){\parallel y_1-y_2\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}.\end{array}$$

Similarly, we find that

$$\begin{array}{c}\hfill \underset{t\in I}{sup}|{\mathcal{T}}_{t,a}^{1-\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_1)\left(t\right)-{\mathcal{T}}_{t,a}^{1-\upsilon }({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_2)\left(t\right)|\le ({}_{}{}^{c}T_1^0+{}_{}{}^{c}T_1^1){\parallel y_1-y_2\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}.\end{array}$$

These lead to

$$\begin{array}{cc}\hfill \parallel \Psi y_1-\Psi y_2{\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}& =\underset{t\in I}{sup}|{\mathcal{T}}_{t,a}^{1-\upsilon }[(\Psi y_1)\left(t\right)-(\Psi y_2)\left(t\right)]|+\underset{t\in I}{sup}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }[({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_1)\left(t\right)-({\mathcal{D}}_a^{\upsilon ,\varrho }\Psi y_2)\left(t\right)]\right|\hfill \\ \hfill & \le ({}_{}{}^{c}T_0^0+{}_{}{}^{c}T_0^1+{}_{}{}^{c}T_1^0+{}_{}{}^{c}T_1^1){\parallel y_1-y_2\parallel }_{{\mathcal{Q}}_{\upsilon ,\varrho }}.\hfill \end{array}$$

As ${}_{}{}^{c}T_0^0+{}_{}{}^{c}T_0^1+{}_{}{}^{c}T_1^0+{}_{}{}^{c}T_1^1<1$, the mapping $\Psi$ is a contraction; therefore, there exists a unique fixed point $y^{*}\in \mathfrak{B}$ such that $\Psi y^{*}\left(t\right)=y^{*}\left(t\right)$. □

5. Applications

The Mathieu equation represented by Equation (3) is considered a generalization of Equations (1) and (2), so we choose it as the first application. Also, we investigate Equation (4) due to it being slightly different. For the fractional Mathieu equation, we examine the Equations (5), (8), and (9). It is worth mentioning that it is preferable to obtain the ordinary differential equations from the fractional differential equations in the sense of Caputo. Therefore, we investigate all problems with Caputo–Katugamploa except for the fractional Mathieu Equation (5) because it contains an R–L fractional derivative.

5.1. The Mathieu Equation (3)

The parametric damping nonlinear Mathieu equation, also referred to as the Duffing oscillator, was introduced by El-Dib [7]. This is demonstrated in Equation (3) with $k=2\mu$, $k_1=a$, and $k_2=-2q$, where $\mu$ is a non-zero damping coefficient, a is an oscillator unforced natural frequency, and $q>0$ is an excitation amplitude. Our Equation (11) converts to Equations (3) if $\varrho =1$, $\beta =2$, $\alpha =\upsilon =1$, and the function $F=-Q{y}^3$. Let $I=[0,1]$ and $y_1,y_2,y_1^{\prime },y_2^{\prime }\in \mathfrak{B}$. Then,

$$|F(t,y_1,y_1^{\prime })-F(t,y_2,y_2^{\prime })|<3Q{s}^2|y_1-y_2|$$

which implies that $L=3Q{s}^2$, $\mathcal{G}=|a-2qcos(\omega \left)\right|$ for all $\omega \in [0,\pi /2]$ and hence

$$\begin{array}{cc}\hfill {}_{}{}^{c}T_0^0& ={\displaystyle \frac{2(L+\mathcal{G}){\mathcal{T}}_{b,a}^{\beta }\Gamma \left(\upsilon \right)}{\Gamma (\beta +\upsilon )}}=3Q{s}^2+|a-2qcos\left(\omega \right)|,\hfill \\ \hfill {}_{}{}^{c}T_0^1& ={\displaystyle \frac{2k{\mathcal{T}}_{b,a}^{\beta -\alpha }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha +\upsilon )}}=4\mu ,\hfill \\ \hfill {}_{}{}^{c}T_1^0& =\left(1+{\displaystyle \frac{\Gamma \left(\beta \right)}{\Gamma (2-\upsilon )\Gamma (\beta -\upsilon )}}\right){\displaystyle \frac{(L+\mathcal{G}){\mathcal{T}}_{b,a}^{\beta -\upsilon }\Gamma \left(\upsilon \right)}{\Gamma \left(\beta \right)}}=2(3Q{s}^2+|a-2qcos\left(\omega \right)|),\hfill \\ \hfill {}_{}{}^{c}T_1^1& =\left(1+{\displaystyle \frac{\Gamma (\beta -\alpha )}{\Gamma (2-\upsilon )\Gamma (\beta -\alpha +\upsilon )}}\right){\displaystyle \frac{k{\mathcal{T}}_{b,a}^{\beta -\alpha -\upsilon }\Gamma \left(\upsilon \right)}{\Gamma (\beta -\alpha )}}=4\mu .\hfill \end{array}$$

According to Theorem 6 and the radius of the ball, we get

$$9Q{s}^2+8\mu +3|a-2qcos\left(\omega \right)|<1$$

which implies that

$$s<\sqrt{{\displaystyle \frac{1-(8\mu +3|a-2qcos\left(\omega \right)\left|\right)}{9Q}}}\triangleq r.$$

In view of the above, we have to take $8\mu +3|a-2qcos(\omega \left)\right|<1$ for all $\omega \in [0,\pi /2]$. According to Theorem 6, there is a unique solution in the closed ball $\mathfrak{B}$ with the previous radius. In view of our equation, we note that $y=0\in \mathfrak{B}$ is a trivial solution if $y\left(0\right)=0$. Therefore, the unique solution of the problem (3) in the ball $\mathfrak{B}$ with radius $s<r$, is $y=0$ if $y\left(0\right)=0$.

The three graphs in Figure 1 show the region of the unique solution to Equation (3) under the plane $8\mu +3|a-2qcos(\omega \left)\right|=1$ at various values of the excitation frequency $\omega$ in $\mu qa$-space. While the three graphs in Figure 2 show the region of the unique solution at various values oscillator unforced natural frequency a and the excitation frequency $\omega$ in $q\mu$-plane. It is clear that the region of the existence increases with the value of $\omega$.

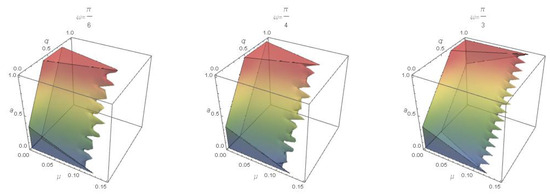
Figure 1. The region of the unique solution to Equation (3) at various values of $\omega$.

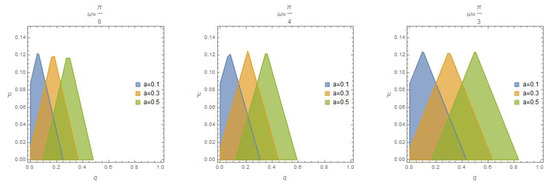
Figure 2. The region of the unique solution to Equation (3) at various values of $\omega$ and a.

5.2. The Quadratical Damped Mathieus Equation (4)

Rand et al. [8] introduced The quadratically damped Mathieus Equation (4), which is the simplest model of a towed mass, and analyzed it for linear stability and nonlinear dynamical effects. The mass is assumed to move exclusively in the horizontal direction y, which is perpendicular to the other two directions. This is demonstrated with $k=0$, $\omega =1$, $k_1=\delta >0$, which indicates the non-dimensional mean value of the towline tension; $k_2=ϵ>0$ reflects the amplitude of the towline tension’s oscillating portion, and $F=f\left(t\right)-y^{\prime }\left|y^{\prime }\right|$ for all $t\in I=[0,b]$ and $0<b\le \pi$, which satisfies

$$\begin{array}{cc}\hfill |F(t,y_1,y_1^{\prime })-F(t,y_2,y_2^{\prime })|& =\left|y_1|y_1^{\prime }|-y_2\left|y_2^{\prime }\right|\right|\hfill \\ \hfill & \le \left|y_1|y_1^{\prime }|-y_1\left|y_2^{\prime }\right|\right|+\left|y_1|y_2^{\prime }|-y_2\left|y_2^{\prime }\right|\right|\hfill \\ \hfill & \le |y_1|\left||y_1^{\prime }|-|y_2^{\prime }|\right|+\left|y_2^{\prime }\right|\left|y_1^{\prime }-y_2^{\prime }\right|\hfill \\ \hfill & \le 2s\left|y_1^{\prime }-y_2^{\prime }\right|\hfill \end{array}$$

for all $y_1,y_2,y_1^{\prime },y_2^{\prime }\in \mathfrak{B}$, with $L=2s$, $\mathcal{G}=\delta +ϵ$, and $\mathcal{N}={sup}_{t\in I}\left|{\mathcal{T}}_{t,a}^{1-\upsilon }f\left(t\right)\right|$. Here, we take $\beta =2$, and $\alpha =\upsilon =\varrho =1$ which lead to

$$\begin{array}{cc}\hfill {}_{}{}^{c}T_0^0& =b^2(2s+\delta +ϵ),{}_{}{}^{c}T_0^1=0,\hfill \\ \hfill {}_{}{}^{c}T_1^0& =2b(2s+\delta +ϵ),{}_{}{}^{c}T_1^1=0.\hfill \end{array}$$

These lead to

$$s<{\displaystyle \frac{1-b(b+2)(\delta +ϵ)}{2b(b+2)}}\triangleq r,0<b\le \pi .$$

which implies that $b(b+2)(\delta +ϵ)<1$. It is clear from this inequality that the area of the region containing $\delta$ and $ϵ$ expands as the length of the interval decreases and that the relationship between $\delta$ and $ϵ$ is linear. We also find that the domain of existence of the unique solution is the area under the line $b(b+2)(\delta +ϵ)=1$ in the $\delta ϵ$-plane, which appears in the second graph in Figure 3 under different values of b. Also, the first graph shows the region that contains all points $\delta ϵb$-space in which our problem has a unique non-zero solution. According to Theorem 6, there is a unique non-zero solution in the closed ball $\mathfrak{B}$ with radius $s<r$ for all points in $\delta ϵb$-plane shown in Figure 3.

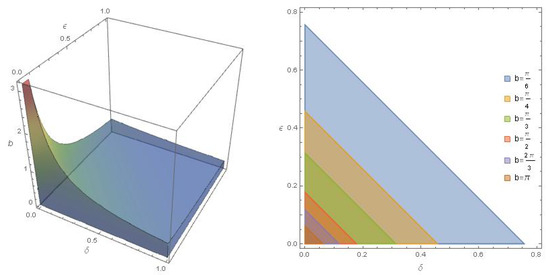
Figure 3. The region of the unique solution to Equation (4) in $\delta ϵb$-space and in $\delta ϵ$-plane at various values of b.

5.3. The Fractional Mathieu Equation (5)

Rand et al. [19] provided and examined the fractional-order Mathieu equation’s transition curves (5) that divide the zones of stability. This is demonstrated with $k=0$, $\omega =1$, $k_1=\delta >0$, indicating the non-dimensional mean value of the towline tension; $k_2=ϵ>0$ reflects the amplitude of the towline tension’s oscillating portion, and $F(t,y\left(t\right),\left({\mathcal{D}}_a^{\upsilon ,\varrho }y\right)\left(t\right))=f\left(t\right)-c\left({\mathcal{D}}_a^{\upsilon ,\varrho }y\right)\left(t\right)$ for all $t\in I=[0,1]$, $0<\upsilon <1$, and $c>0$, which satisfies

$$\begin{array}{c}\hfill |F(t,y_1,x_1)-F(t,y_2,x_2)|\le c\left|x_1-x_2\right|\end{array}$$

for all $y_1,y_2,x_1,x_2\in \mathfrak{B}$, with $L=c$, $\mathcal{G}=\delta +ϵ$, and $\mathcal{N}={sup}_{t\in I}\left|f\left(t\right)\right|$. Here, we take $\beta \to 2$, $0<\upsilon =\alpha <1$, and $\varrho =1$, which lead to

$$\begin{array}{cc}\hfill T_0^0& ={\displaystyle \frac{2(c+\delta +ϵ)\Gamma \left(\alpha \right)}{\Gamma (2+\alpha )}},T_0^1=0,\hfill \\ \hfill T_1^0& =\left(1+{\displaystyle \frac{1}{\Gamma (2-\alpha )\Gamma (2+\upsilon )}}\right)(c+\delta +ϵ)\Gamma \left(\alpha \right),T_1^1=0.\hfill \end{array}$$

These lead to $s>(R_0+R_1)/(1-T_0^0-T_1^0)>0$ if $T_0^0+T_1^0<1$ according to Theorem 5, which implies that $c+\delta +ϵ<1/F\left(\alpha \right)$ where

$$\begin{array}{c}\hfill F\left(\alpha \right)={\displaystyle \frac{\Gamma \left(\alpha \right)}{\Gamma (2+\alpha )}}\left(\Gamma (2+\alpha )+2+{\displaystyle \frac{1}{\Gamma (2-\alpha )}}\right),0<\alpha <1.\end{array}$$

It is easy to see that the function $F\left(\alpha \right)$ is increasing for all $0<\alpha <1$ and has a supremum value of $5/2$, so $0<c+\delta +ϵ<0.4$. The four graphs in Figure 4 show the region of the existence of the unique solution under the yellow plane $c+\delta +ϵ=1/F\left(\alpha \right)$ in $c\delta ϵ$-space with different values of b. They show that the larger the value of $\alpha$, the wider the region of existence. The second Figure 5 shows the region of existence at different values of the damping coefficient c at the supremum value of $\alpha$. It is obvious from this figure that the region of existence extends with decreasing value of the damping coefficient c.

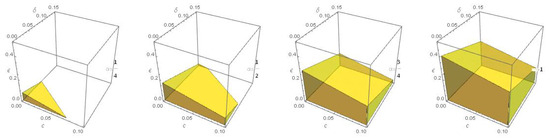
Figure 4. The region of the unique solution to Equation (5) at various values of fractional order $\alpha$.

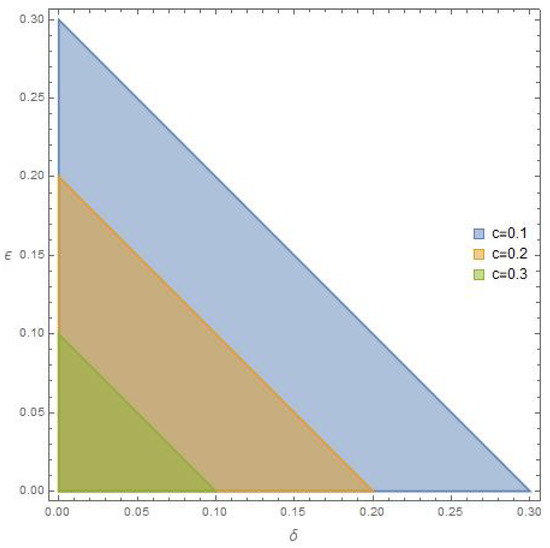
Figure 5. The region of the unique solution to Equation (5) at various values of c and supremum value of fractional order $\alpha \to 1$.

It is worth noting that if we take $F=f\left(t\right)$ for all $t\in I=[0,1]$ and $k=c$, then we obtain the same results. In the light of Theorem 5, there is a unique non-zero solution in the closed ball $\mathfrak{B}$ with the previous radius.

In light of (21), we get ${}_{}{}^{c}R_0+{}_{}{}^{c}R_1=4\mathcal{N}+3|y_0|+2|y_1|$. Also, Figure 5 shows that the existence of the unique solution is verified at any point in the region. Therefore, if we take $c=0.1$, then $\delta +ϵ<0.3$, which implies that $c+\delta +ϵ<0.4$. The last inequality holds if we take $c=0.2$ or $c=0.3$. These imply $T_0^0+T_1^0=5(c+\delta +ϵ)/2<5\left(0.4\right)/2=1$ for any point in the plane.

5.4. The Tempered Fractional Mathieu Equation (9)

First, we need to prove the relation between $\left({}_{}{}^c\mathcal{D}_a^{r,\varrho }\left({}_{}{}^c\mathcal{D}_a^{i,\varrho }y\right)\right)\left(t\right)$, and $\left({}_{}{}^c\mathcal{D}_a^{r+i,\varrho }y\right)\left(t\right)$ where $0<r,i\le 1$ and $\varrho \ge 0$. This can easily show by using Definition 4 and Lemma 1 as

$$\begin{array}{cc}\hfill \left({}_{}{}^c\mathcal{D}_a^{r,\varrho }\left({}_{}{}^c\mathcal{D}_a^{i,\varrho }y\right)\right)\left(t\right)& =\left({\mathcal{I}}_a^{1-r,\varrho }\lambda \left({\mathcal{I}}_a^{1-i,\varrho }\lambda y\right)\right)\left(t\right)=\left({\mathcal{I}}_a^{1-r,\varrho }\left({\mathcal{D}}_a^{i,\varrho }\lambda y\right)\right)\left(t\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{1-r,\varrho }[\left({}_{}{}^c\mathcal{D}_a^{i,\varrho }\lambda y\right)\left(t\right)+\left({\mathcal{D}}_a^{i,\varrho }\lambda y\right)\left(a\right)]\right)\left(t\right)\hfill \\ \hfill & =\left({\mathcal{I}}_a^{1-r,\varrho }\left({}_{}{}^c\mathcal{D}_a^{i,\varrho }\lambda y\right)\right)\left(t\right)+{\displaystyle \frac{\left({\mathcal{D}}_a^{i,\varrho }\lambda y\right)\left(a\right)}{\Gamma (2-r)}}{\mathcal{T}}_{t,a}^{1-r}\hfill \\ \hfill & =\left({\mathcal{I}}_a^{1-r,\varrho }\left({\mathcal{I}}_a^{1-i,\varrho }{\lambda }^{2}y\right)\right)\left(t\right)+{\displaystyle \frac{\left({\mathcal{D}}_a^{i,\varrho }\lambda y\right)\left(a\right)}{\Gamma (2-r)}}{\mathcal{T}}_{t,a}^{1-r}\hfill \\ \hfill & =\left({\mathcal{I}}_a^{2-(r+i),\varrho }{\lambda }^{2}y\right)\left(t\right)+{\displaystyle \frac{\left({\mathcal{D}}_a^{i,\varrho }\lambda y\right)\left(a\right)}{\Gamma (2-r)}}{\mathcal{T}}_{t,a}^{1-r}\hfill \\ \hfill & =\left({}_{}{}^c\mathcal{D}_a^{r+i,\varrho }y\right)\left(t\right)+C{\mathcal{T}}_{t,a}^{1-r}\hfill \end{array}$$

where C is a constant, provided that $1<r+i\le 2$. Hence, the tempered fractional Mathieu Equation (9) can be read as

$$\left({}_{}{}^c\mathcal{D}_{}^{r+i,\varrho }y\right)\left(t\right)+2\gamma \left({}_{}{}^c\mathcal{D}_{}^{r,\varrho }y\right)\left(t\right)+2qcos\left(2t\right)y\left(t\right)=-4\ell qcos\left(2t\right)y^3\left(t\right)-C{\mathcal{T}}_{t,a}^{1-r}.$$

The tempered fractional Mathieu Equation (9) can be demonstrated with $k=2\gamma$, $\omega =2$, $k_1=0$, $k_2=2q$, $\beta =2r$, $\alpha =r=i=\upsilon$, $1/2<r\le 1$, and $F=-4\ell qcos\left(2t\right)y^3\left(t\right)-C{\mathcal{T}}_{t,a}^{1-r}$ for all $t\in I=[0,1]$, which satisfies

$$\begin{array}{cc}\hfill |F(t,y_1,y_1^{\prime })-F(t,y_2,y_2^{\prime })|& =\left|4\ell qcos\left(2t\right)(y_1^3\left(t\right)-y_2^3\left(t\right)\right|\hfill \\ \hfill & \le 12\ell q{s}^2\left|y_1-y_2\right|\hfill \end{array}$$

for all $y_1,y_2,y_1^{\prime },y_2^{\prime }\in \mathfrak{B}$, with $L=12\ell q{s}^2$, $\mathcal{G}=2q$, and $\mathcal{N}=\left|C\right|{\mathcal{T}}_{b,0}^{2-2r}$, which lead to

$$\begin{array}{cc}\hfill {}_{}{}^{c}T_0^0& ={\displaystyle \frac{4q(1+6\ell s^2)\Gamma \left(r\right))}{{\varrho }^{2r}\Gamma \left(3r\right)}},{}_{}{}^{c}T_0^1={\displaystyle \frac{4\gamma \Gamma \left(r\right))}{{\varrho }^r\Gamma \left(2r\right)}},\hfill \\ \hfill {}_{}{}^{c}T_1^0& ={\displaystyle \frac{2q(1+6\ell s^2)\Gamma \left(r\right)}{{\varrho }^r\Gamma \left(3r\right)}}\left(1+{\displaystyle \frac{\Gamma \left(2r\right)}{\Gamma (2-r)\Gamma \left(3r\right)}}\right),{}_{}{}^{c}T_1^1=2\gamma \left(1+{\displaystyle \frac{\Gamma \left(r\right)}{\Gamma (2-r)\Gamma \left(2r\right)}}\right)\hfill \end{array}$$

These lead to

$$s<\sqrt{{\displaystyle \frac{1}{6\ell P_1}}\left({\displaystyle \frac{1}{2}}-P_1-P_2\right)}\triangleq R$$

where

$$\begin{array}{cc}\hfill P_1& ={\displaystyle \frac{q\Gamma \left(r\right)}{{\varrho }^{2r}\Gamma \left(3r\right)}}\left({\varrho }^r+2+{\displaystyle \frac{{\varrho }^r\Gamma \left(2r\right)}{\Gamma (2-r)\Gamma \left(3r\right)}}\right),\hfill \\ \hfill P_2& ={\displaystyle \frac{2\gamma \Gamma \left(r\right)}{{\varrho }^r\Gamma \left(2r\right)}}+\gamma \left(1+{\displaystyle \frac{\Gamma \left(r\right)}{\Gamma (2-r)\Gamma \left(2r\right)}}\right),\hfill \end{array}$$

which implies that $P_1+P_2<1/2$. According to Theorem 6, there is a unique non-zero solution in the closed ball $\mathfrak{B}$ with radius $s<R$. The three graphs in Figure 6 and the four graphs in Figure 7 show the region of the existence of the unique solution under the yellow plane $P_1+P_2=1/2$ in $qr\gamma$-space and $q\gamma \varrho$-space with various values of the fractional derivative type $\varrho$ and fractional order r, respectively. It is clear that the region expands with the increase in the value of the type and order. The three graphs in Figure 8 show the region of the unique solution to Equation (9) at various values of the fractional derivative type $\varrho$ and fractional order r. At $q=\gamma$, the first graph in Figure 9 shows the region of the unique solution to Equation (9) in $r\varrho q$-space, while the last two graphs show the region of the existence at various values of the fractional derivative type $\varrho$ and fractional order r and fractional order r.

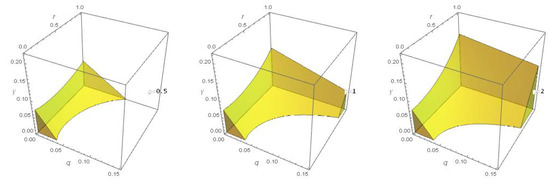
Figure 6. The region of the unique solution to Equation (9) at various values of the fractional derivative type $\varrho$.

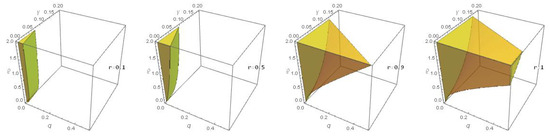
Figure 7. The region of the unique solution to Equation (9) at various values of the fractional order r.

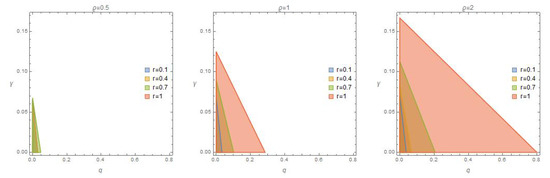
Figure 8. The region of the unique solution to Equation (9) at various values of the fractional derivative type $\varrho$ and fractional order r.

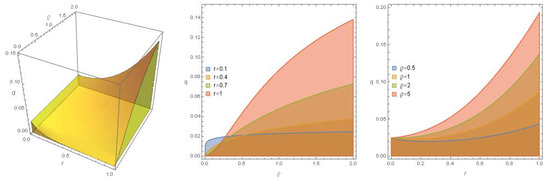
Figure 9. The region of the unique solution to Equation (9) at $q=\gamma$ and various values of the fractional derivative type $\varrho$ and fractional order r.

6. Conclusions

This paper concerned two models of the fractional Mathieu equation. The first was the Riemann–Liouville Katugampola fractional derivative, while the other model was the Caputo–Katugampola fractional derivative. It turned out that the Caputo–Katugampola fractional derivative is more applicable to real-life problems due to its relation to the exact initial and boundary conditions and ${}_{}{}^c\mathcal{D}_0^{n,1}={(t^{1-\varrho }d/dt)}^n;n\in \mathbb{N}$. Thus, we used the Caputo–Katugampola fractional derivative with the special cases containing the ordinary derivative. The Banach contraction principle is used to prove that each model under consideration has a unique solution. Our results were applied to four real-life problems: the nonlinear Mathieu equation for parametric damping and the Duffing oscillator (3), the quadratically damped Mathieu Equation (4), the fractional Mathieu equation’s transition curves (5), and the tempered fractional model of the linearly damped ion motion with an octopole (9). Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show the regions of the existence of the unique solution for several models of ordinary and fractional Mathieu equations in 3-dimensional space and 2-dimensional plane.