Abstract
This study employs the modified extended direct algebraic method (MEDAM) to investigate the generalized nonlinear fractional -dimensional wave equation with gas bubbles. This advanced analytical framework is used to construct a comprehensive class of exact wave solutions and explore the associated dynamical characteristics of diverse wave structures. The analysis yields several categories of soliton solutions, including rational, hyperbolic (sech, tanh), and trigonometric (sec, tan) function forms. To the best of our knowledge, these soliton solutions have not been previously documented in the existing literature. By selecting appropriate standards for the permitted constraints, the qualitative behaviors of the derived solutions are illustrated using polar, contour, and two- and three-dimensional surface graphs. Furthermore, a stability analysis is performed on the obtained soliton solutions to ascertain their robustness and dynamical stability. The suggested analytical approach not only deepens the theoretical understanding of nonlinear wave phenomena but also demonstrates substantial applicability in various fields of applied sciences, particularly in engineering systems, mathematical physics, and fluid mechanics, including complex gas–liquid interactions.
1. Introduction
Nonlinear partial differential equations (NLPDEs) play a vital role in describing diverse wave phenomena in physics, engineering, and applied mathematics. Higher-dimensional models, particularly in -dimensions, are increasingly relevant as they capture complex interactions among dispersion, nonlinearity, and external perturbations. Such models arise naturally in fluid mechanics, nonlinear optics, plasma dynamics, and gas–liquid interaction [1,2]. Analytical methods for obtaining exact solutions of NLPDEs have become a central research focus, as these solutions provide critical insights into the dynamics of nonlinear waves and benchmark results for analytical and numerical simulations. Over the past decade, numerous approaches have been developed to extract periodic, soliton, and singular solutions of nonlinear models. Techniques such as the Kudryashov method [3], the tanh-expansion method [4], the F-expansion scheme [5], the extended -expansion scheme [6], the -expansion scheme [7], the -expansion and extended sinh-Gordon equation expansion method [8], the exp -expansion method [9], the modified exponential rational function method [10], and the sub-equation method [11] have been successfully applied to different nonlinear equations. These methods have led to the discovery of bright and dark solitons, rogue waves, and periodic structures, enriching the theoretical understanding of nonlinear dynamics. Nevertheless, many generalized higher-dimensional models remain underexplored, with limited classifications of their solution spaces. Recent advances in analytical techniques have significantly enriched the study of nonlinear partial differential equations (NLPDEs), particularly through the development of the modified extended direct algebraic method (MEDAM) and its variants. This method has been effectively applied to a wide range of nonlinear models, yielding diverse classes of exact solutions that provide deeper insights into nonlinear wave dynamics. For instance, Bilal et al. [12] applied the MEDAM to nonlinear fractional diffusion–reaction equations with cubic nonlinearity, establishing exact soliton structures with practical implications in diffusion processes. Waqar et al. [13] employed the same approach to the -dimensional Zoomeron equation, deriving a spectrum of wave solutions that demonstrate the method’s robustness in handling multidimensional systems. Similarly, Yusuf et al. [14] explored propagation patterns of the modified complex KdV system via a new extended direct algebra method, showcasing rich dynamical behaviors. Further contributions include that of Shafique et al. [15], who reported abundant soliton solutions for the -dimensional Kadomtsev–Petviashvili-modified equal-width model, and Samir et al. [16], who examined traveling and soliton wave characteristics of the extended -dimensional KP equation in fluid contexts. Collectively, these studies highlight the growing importance of algebraic techniques in deriving exact solutions of nonlinear models, reinforcing their value in both theoretical analysis and applied mathematics.
Numerous nonlinear models, such as the Laksmanan–Porsezian–Daniel equation [17], the Korteweg–de Vries (KdV) equation [18], the Drinfeld Wilson Sokolov equation [19], the Schrödinger equation [20], the Biswas arshed equation [21], the Lonngren-wave equation [22], and the Boussinesq equation [23], have been extensively investigated to explore complex wave phenomena. These classical models have played a fundamental role in advancing the theoretical understanding of soliton dynamics, nonlinear dispersive effects, and wave interactions across various physical systems. However, with the growing complexity of modern physical and engineering problems, particularly those involving multidimensional wave propagation, there is an increasing need to study generalized nonlinear models that can capture richer and more diverse wave behaviors. In this study, we focus on the generalized nonlinear -dimensional wave equation with constant coefficients, expressed as
In the investigated system, the function denotes the smooth envelope function, where x, y, and z are spatial variables, and t represents time. The coefficients () are real constants that characterize the nonlinear, dispersive, and anisotropic effects of the system. Equation (1) is widely employed to describe the propagation of nonlinear acoustic waves in compressible liquids containing gas bubbles. The presence of bubbles modifies the compressibility and dispersion properties of the medium, thereby producing more complex wave dynamics compared to those in a pure liquid. In this formulation, represents the temporal evolution of the wave field; the nonlinear convective term captures nonlinear steepening effects; the dispersive contribution accounts for bubble-induced dispersion; the term models variable-coefficient diffusion/dispersion related to spatial heterogeneities of the bubble medium; and the transverse terms describe diffraction in the y- and z-directions, which is essential for modeling three-dimensional spreading in realistic bubble media. Recent studies on higher-dimensional nonlinear wave equations have highlighted their rich solution structures and practical significance in modeling shallow water and fluid dynamics systems. Gao [24] explored bilinear auto-Bäcklund transformations and similarity reductions for an extended time-dependent -dimensional shallow water wave equation, providing new insights into integrability properties in oceanic and riverine contexts. Similarly, Wang et al. [25] derived resonant Y-type soliton, interaction waves, and other exact solutions for the same equation, emphasizing nonlinear resonance and interaction mechanisms. Şenol [26] investigated abundant solitary wave solutions of an extended nonlinear evolution equation arising in fluid dynamics, further demonstrating the versatility of analytical approaches in constructing solitary profiles. Complementing these works, Gao and Tian [27] applied similarity-reduction techniques to extended shallow water wave models, offering compact reductions to lower-dimensional forms. In addition, Fenget al. [28] established bilinear Bäcklund transformations and constructed a diverse set of solutions including multi-soliton, breather, fission–fusion, and hybrid waveforms revealing the complexity and diversity of nonlinear structures in higher dimensions. Collectively, these contributions illustrate the growing interest in exact analytical solutions of -dimensional nonlinear wave models, underscoring their importance for advancing both the theory and applications of nonlinear dynamics in fluid systems. This article investigates a generalized nonlinear -dimensional wave equation [29] using the modified extended direct algebraic method. The study derives a variety of exact solutions, including dark, bright, singular, periodic, and singular periodic solitons. The obtained solutions are further analyzed through graphical illustrations such as contour diagrams, surface plots, and three-dimensional visualizations. These results contribute not only to the mathematical theory of nonlinear wave phenomena but also to practical applications in applied sciences, particularly in modeling fluid structure interactions, engineering processes, and gas–liquid systems. Further, we are applying the M-truncated fractional derivative on the considered model due to the significance role of the fractional derivative in the past couple of decades.
M-Truncated Fractional Derivative
The M-truncated fractional derivative, which is a standard generalization of the classical derivatives. They defined the fractional derivative of order for as follows [30]:
where
The generalized nonlinear fractional -dimensional wave equation form
This paper is structured as follows:
- Section 2 describes the conversion of the partial differential equation (PDE) into an ordinary differential equation (ODE) using a similarity transformation.
- Section 3 describes the main steps of the proposed analytical method in detail and presents the obtained exact solutions.
- Section 4 provides graphical visualizations, including two-dimensional, three-dimensional, and contour plots, to illustrate the different classes of soliton solutions and together with a comprehensive discussion of their associated dynamic wave profiles.
- Section 5 discusses the stability analysis of the obtained soliton solutions.
- Section 6 concludes the study by summarizing the key findings and highlighting the significance of the results.
2. Mathematical Analysis
In order to derive the soliton solutions of Equation (2), we employ the following wave transformation:
where
Substituting Equations (3) and (4) into Equation (2), we obtain
After performing two successive integrations of Equation (5) and setting the integration constant to zero, the resulting expression is
3. Modified Extended Direct Algebraic Method and Its Application
Some of the main steps are as follows:
Step 1: Assuming a nonlinear PDE,
where denotes a wave-function. Assume the following transformation:
Putting Equation (8) into Equation (7) yields
Step 2: Suppose the results of Equation (9) are
Here, are unknown. Function fulfills the given equation:
where , , and are constants and . Consider the solutions of Equation (11) in the following cases:
When and .
When and .
When and .
When and .
When and .
When and .
When .
When , and .
When , .
When , .
When and , .
When and .
where c and f are positive constants.
Step 3: Input Equations (10) and (11) into Equation (9). Collecting the coefficients equating to zero of each power of yields the algebraic system of equations. To obtain unknown values, solve the system.
Application
To determine form Equation (6), Equation (10) becomes
Putting Equation (49) with Equation (11) in Equation (6), we obtain these sets of solutions after some calculations:
- Set 1:
When and .
When and .
When and .
When and .
When and .
When .
When , .
When and , .
When and .
Set 2:
When and .
When and .
When and .
When and .
When and .
When and .
When .
When , .
When and , .
When and .
4. Graphs
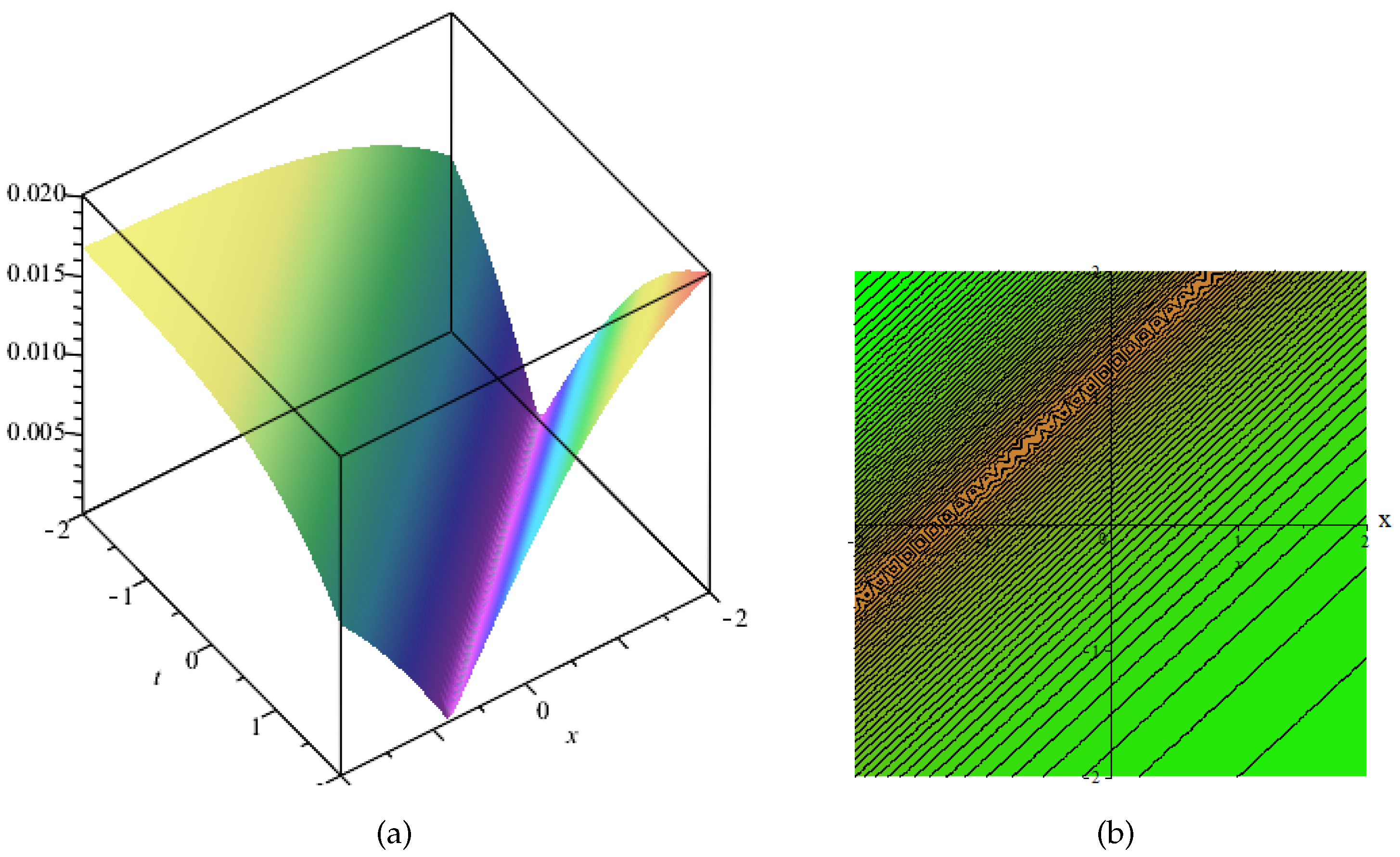
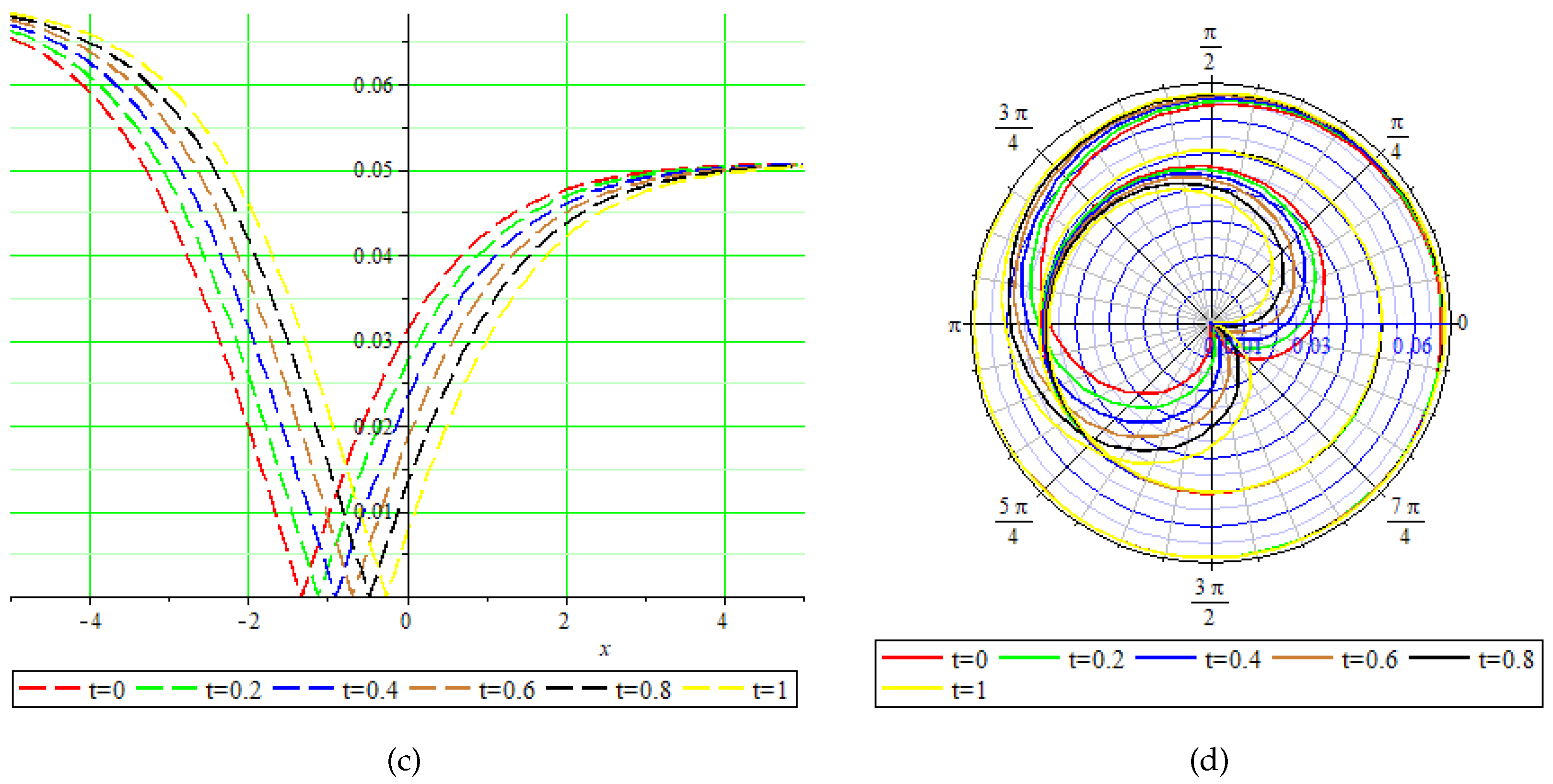
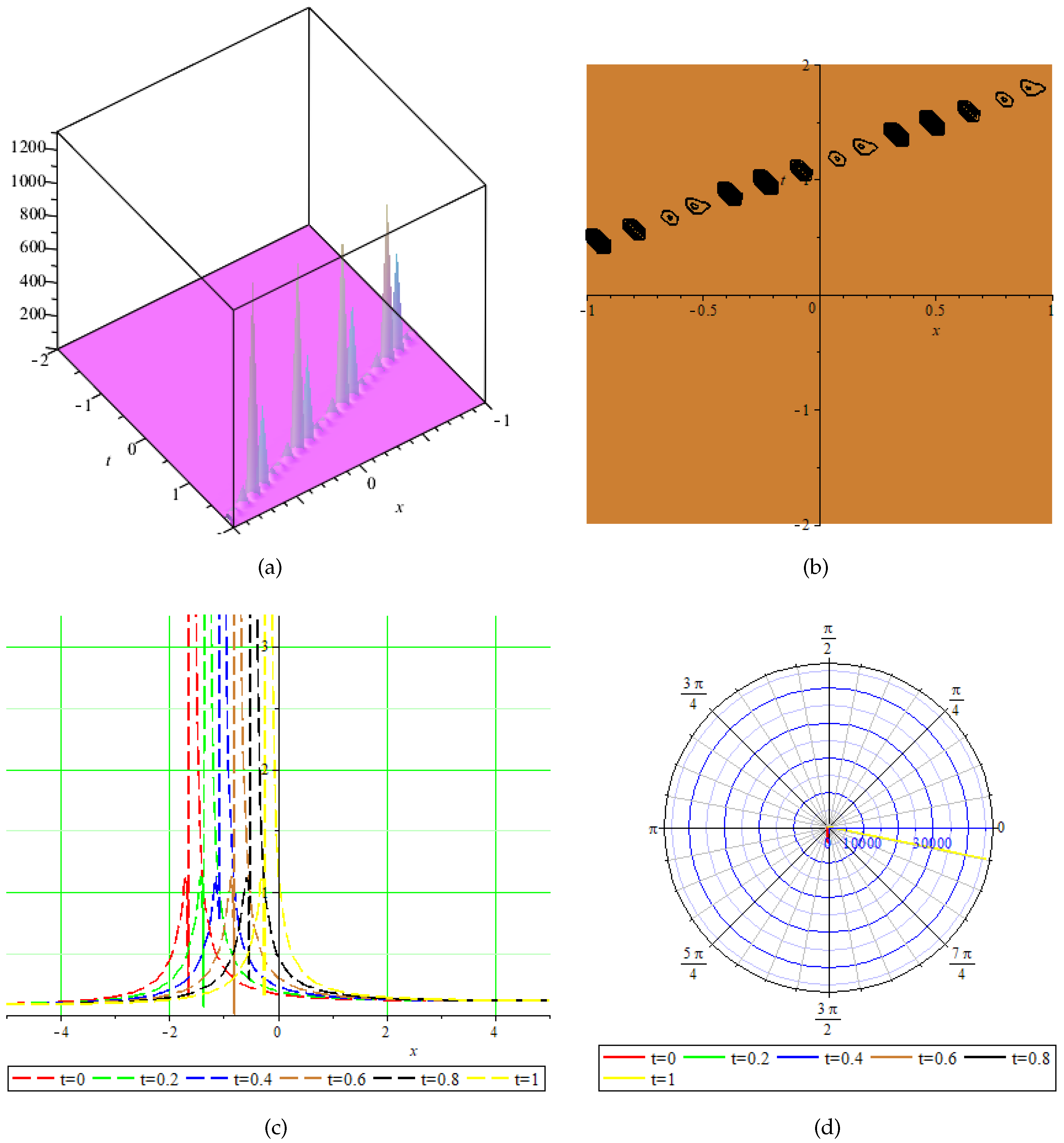
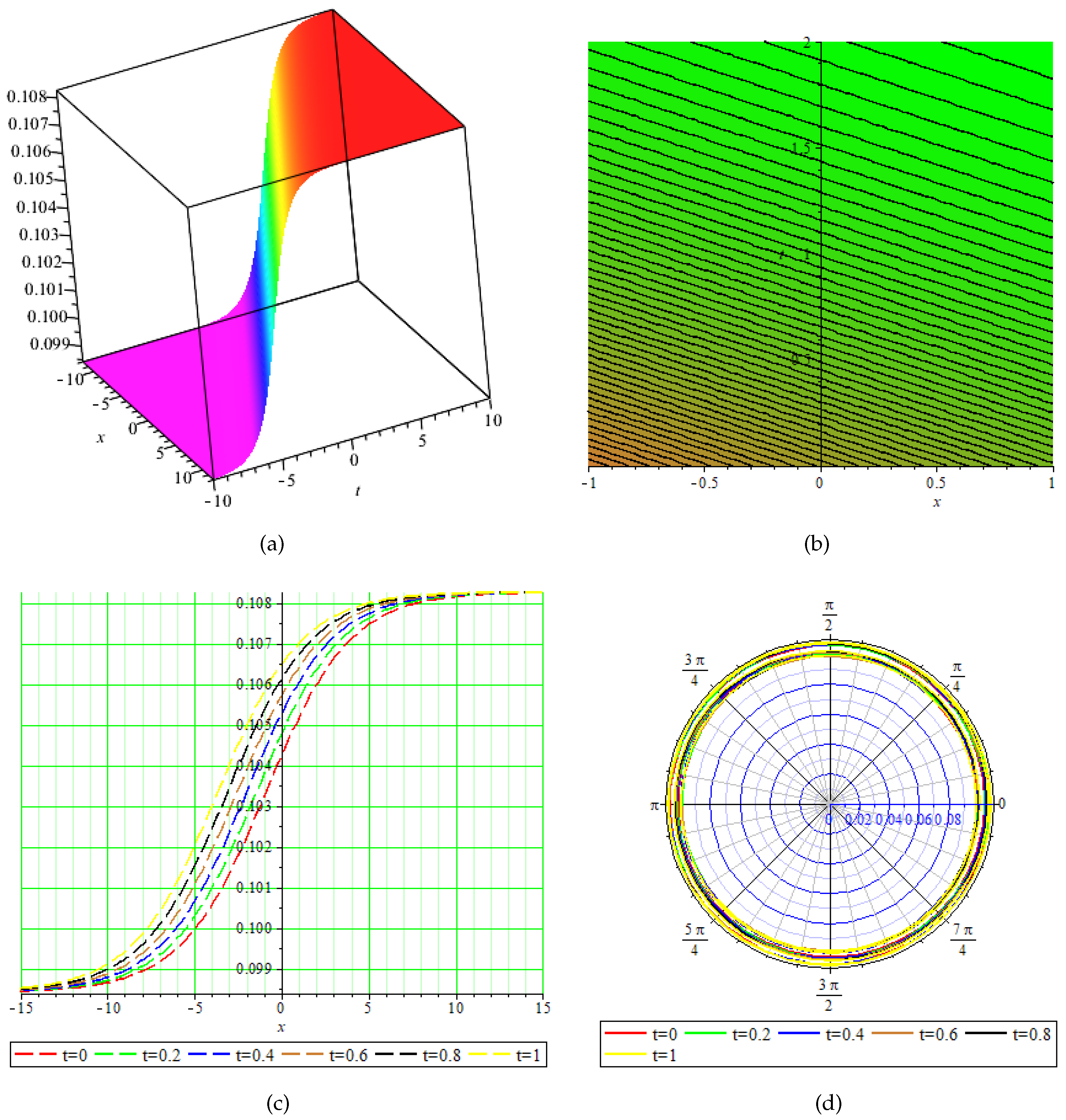
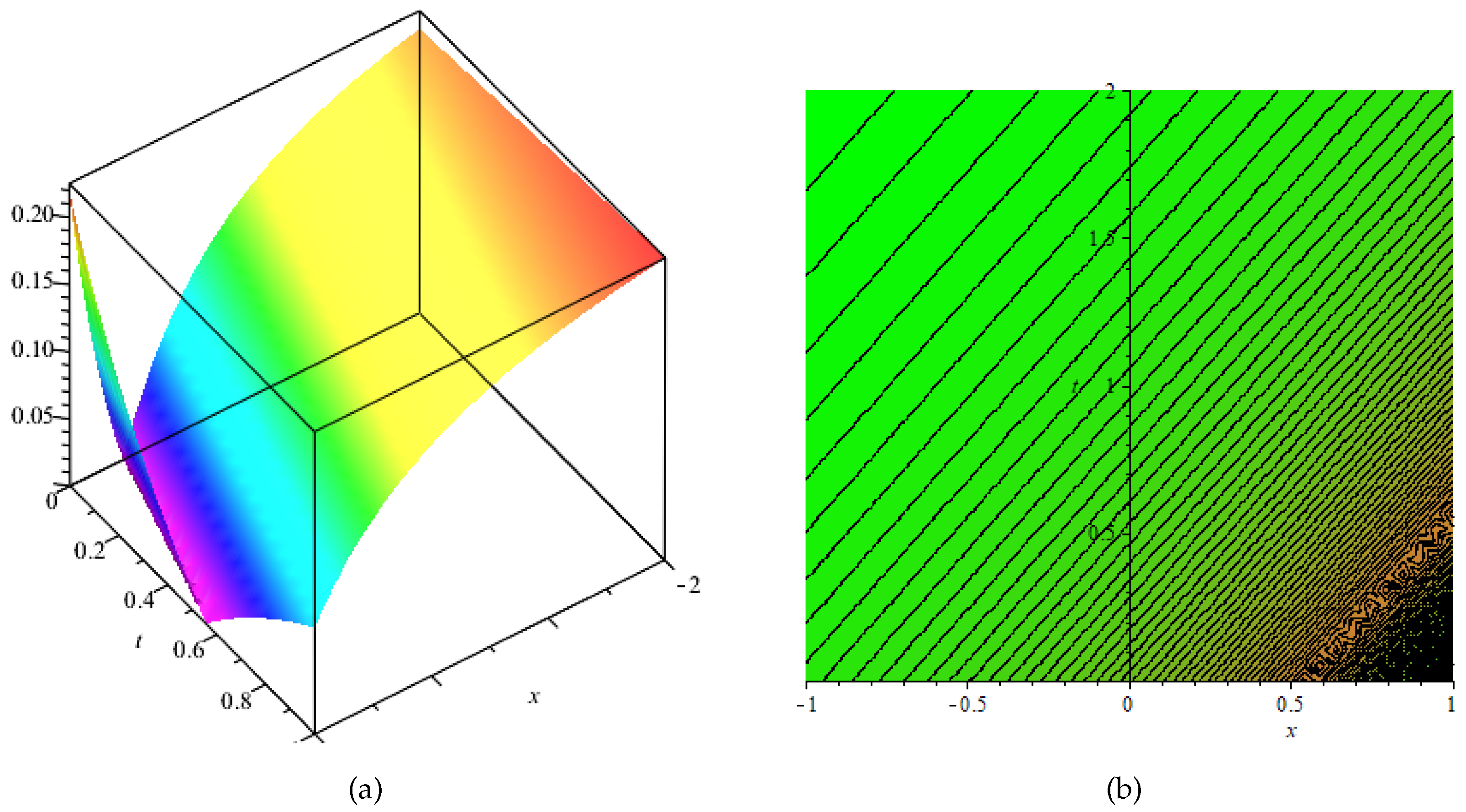
This section presents the physical behavior of the gain exact solution like rational, hyperbolic, and trigonometric function forms. Here, we discuss some exact solutions from the above by graphically presenting them in different forms (like in 3-dimensional, contour, 2-dimensional, and polar graphs) by choosing suitable values of the parameters present in the exact solutions in numerics, thus giving us the behavior of the wave form. Some graphs are shown in the following figures. Figure 1 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing , , , . Figure 2 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing , Figure 3 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing , , Figure 4 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing , , Figure 5 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing , , , , Figure 6 shows the (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs by choosing ,
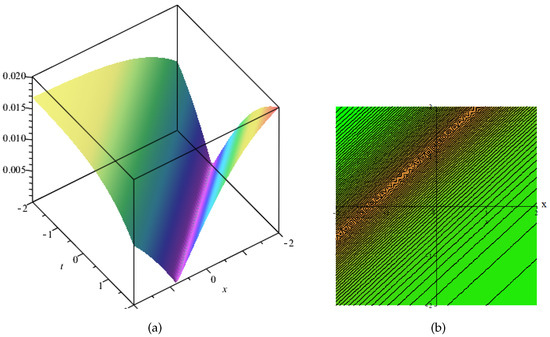
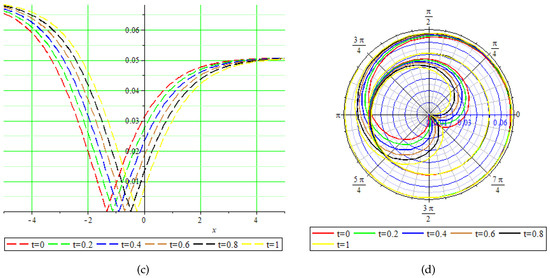
Figure 1.
Physical behavior of shown in Equation (50) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
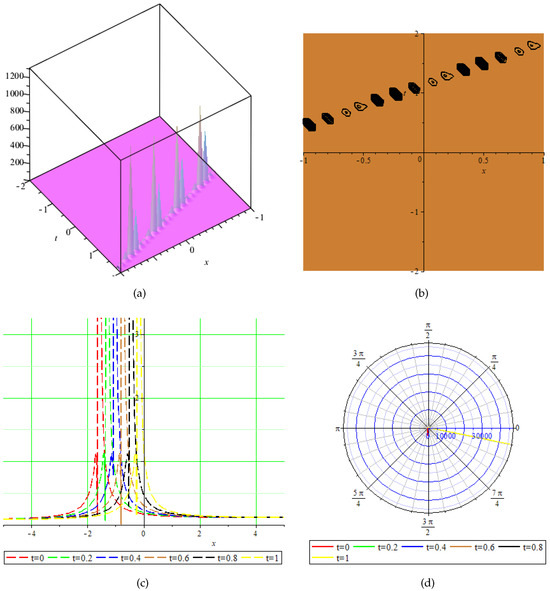
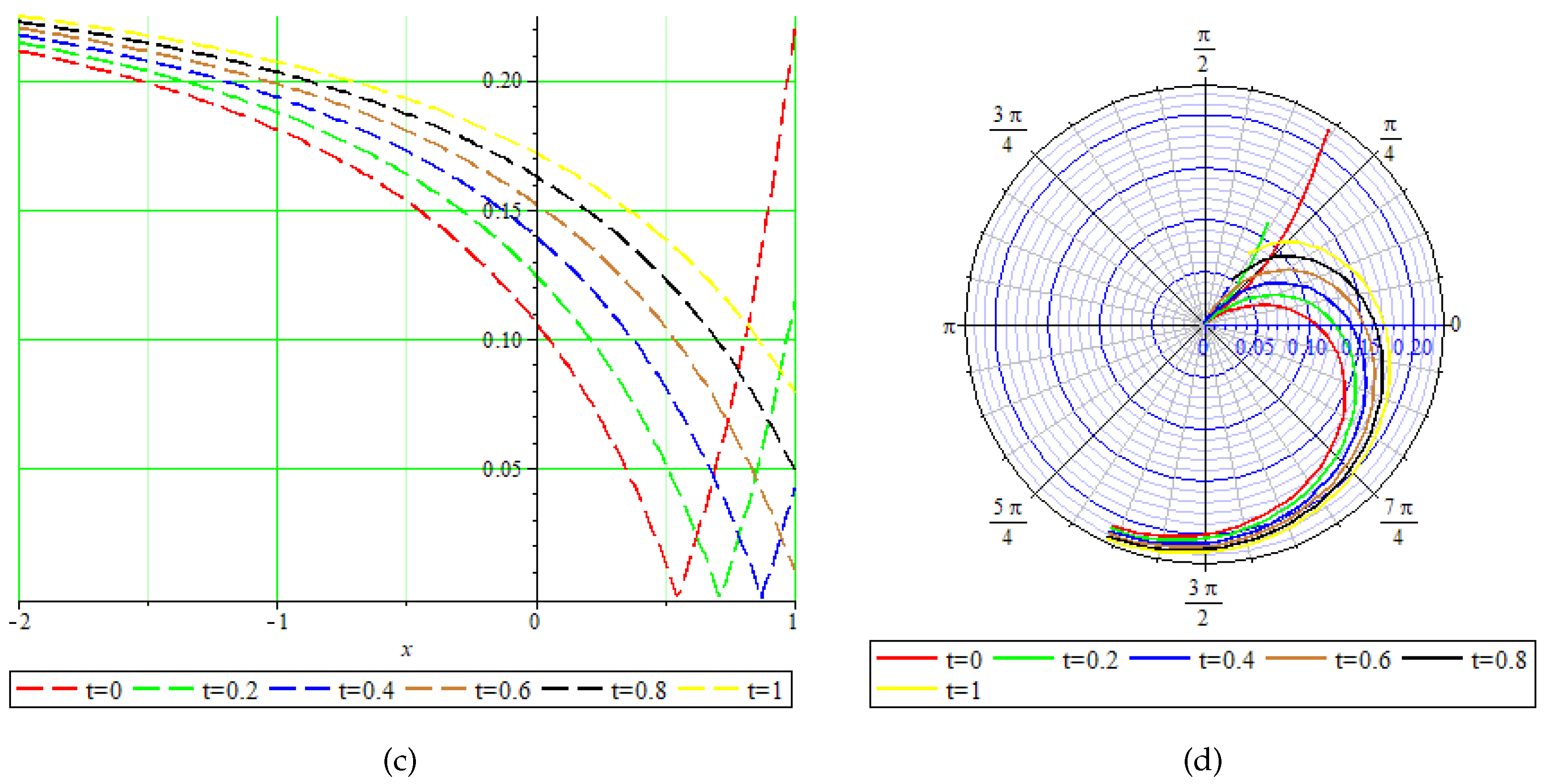
Figure 2.
Physical behavior of shown in Equation (51) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
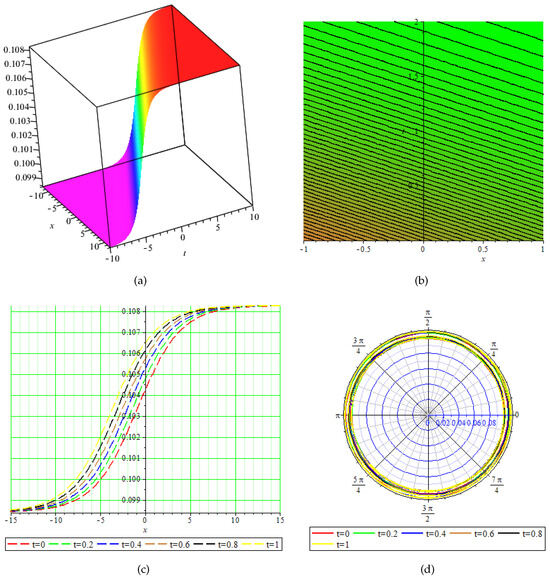
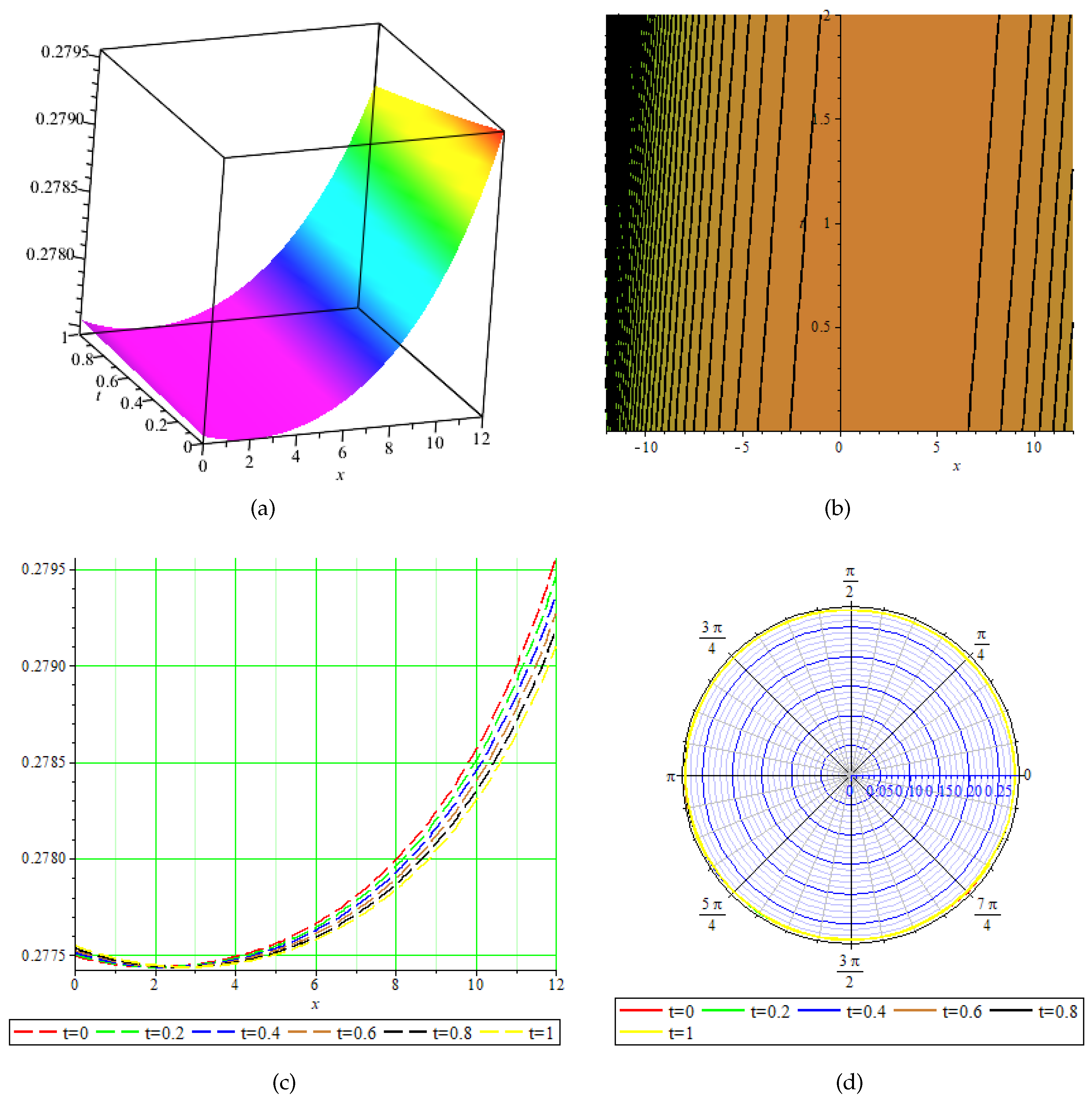
Figure 3.
Physical behavior of shown in Equation (55) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
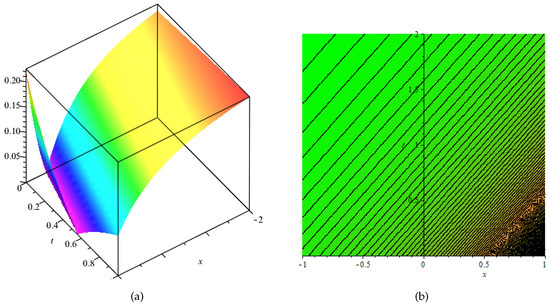
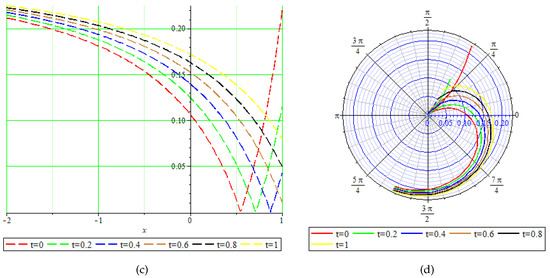
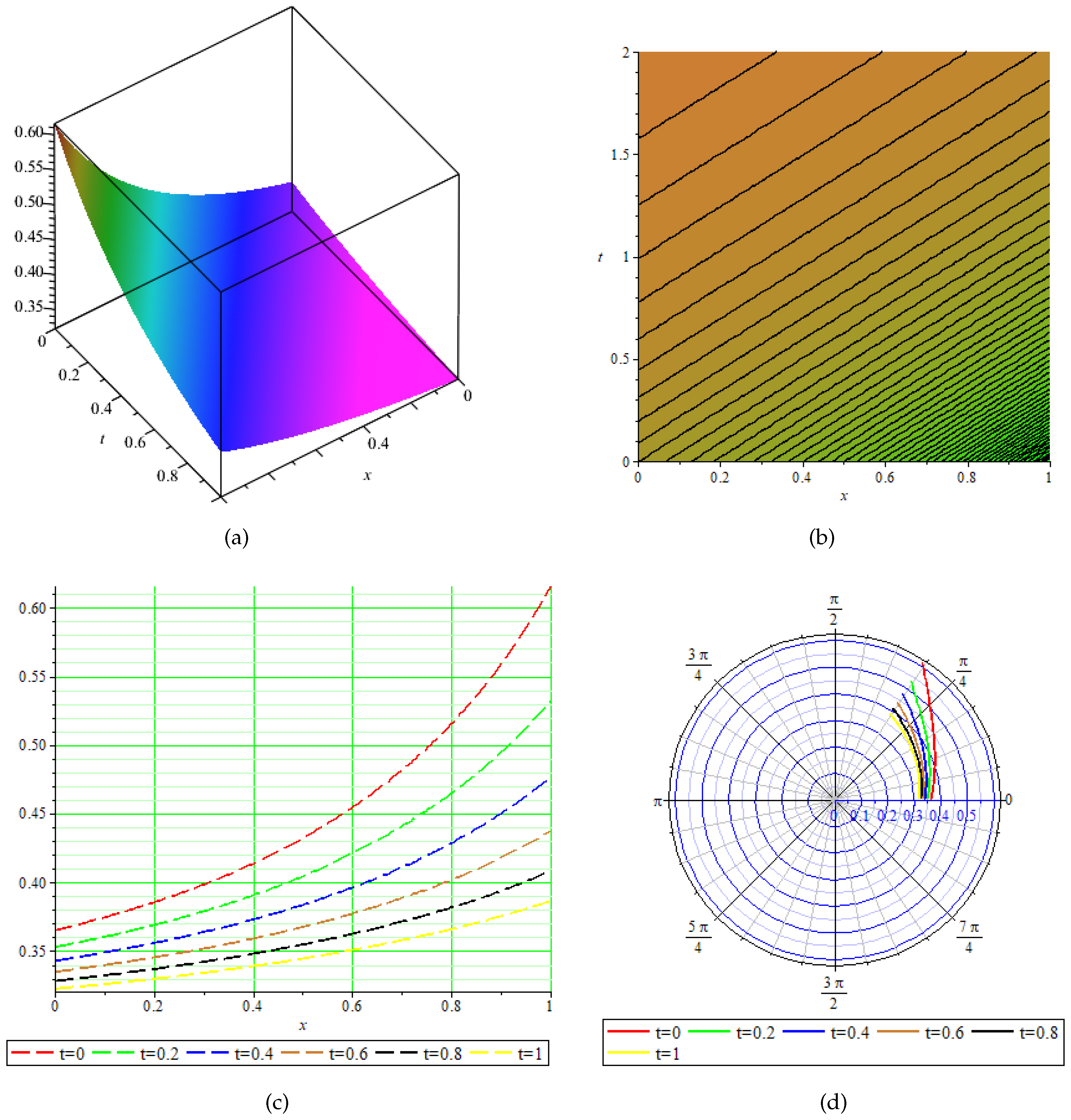
Figure 4.
Physical behavior of shown in Equation (56) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
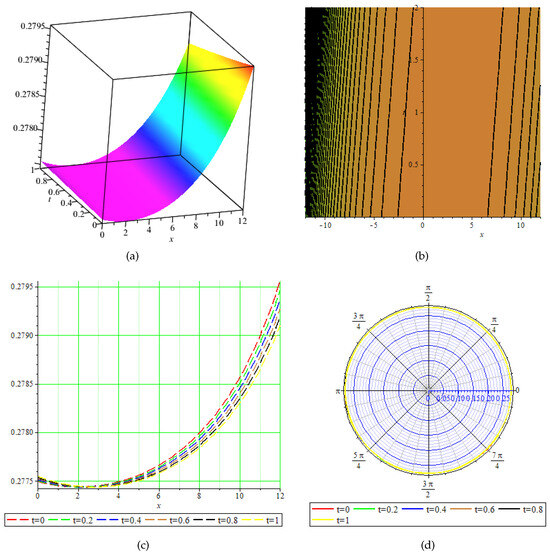
Figure 5.
Physical behavior of shown in Equation (60) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
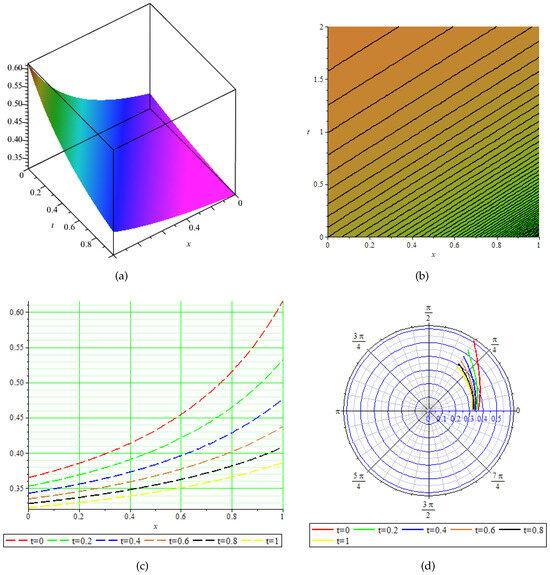
Figure 6.
Physical behavior of shown in Equation (61) in (a) 3-dimensional, (b) contour, (c) 2-dimensional, and (d) polar graphs.
5. Stability Analysis
Stability analysis plays a crucial role in numerous fields of science and engineering. It is employed to understand how a solution behaves under external perturbations and how it evolves over time. The analysis is typically carried out by utilizing the characteristics of a Hamiltonian system, and it is tested on several obtained results to determine the stability of the solution in practical applications. In this section, we analyze the stability of gained solutions. To accomplish this, the Hamiltonian transformation is defined as [8]
Here, the term denotes the momentum factor, while represents the power function. A necessary condition for the stability of soliton solutions is given by
which ensures the persistence of stable soliton profiles under small perturbations. In the equation, represents the wave speed. Substituting the solution given in Equation (50) into Equation (121) yields the following expression:
By applying the criterion defined in Equation (122), we obtain the corresponding stability condition with , .
Hence, this proves that our solution is stable. So, we can also check the remaining solution using this condition.
6. Conclusions
In conclusion, this work has employed the modified extended direct algebraic method to construct a diverse set of exact wave solutions for the generalized nonlinear fractional -dimensional wave equation. The obtained soliton families, including dark, bright, singular, periodic, and singular-periodic structures, represent new analytical forms not previously reported in the literature. By adjusting the free parameters, the qualitative dynamics of these solutions have been illustrated through two- and three-dimensional graphical depictions supported by contour plots. Corresponding stability analysis confirmed that certain soliton profiles exhibit stable behavior under small perturbations. These outcomes deepen the theoretical understanding of nonlinear wave propagation and demonstrate the applicability of the proposed framework to practical problems in fluid mechanics and gas–liquid interaction systems. Overall, the study provides a valuable analytical foundation for exploring complex wave dynamics in multidimensional nonlinear media, offering insights that can guide both theoretical investigations and experimental validations.
Author Contributions
Conceptualization, A.K.A. and M.Q.; Methodology, A.K.A. and M.Q.; Software, A.K.A. and M.Q.; Validation, A.K.A. and M.Q.; Formal analysis, A.K.A. and M.Q.; Investigation, A.K.A. and M.Q.; Writing—original draft, A.K.A. and M.Q.; writing—review and editing, A.K.A. and M.Q.; Visualization, A.K.A. and M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [KFU254310].
Data Availability Statement
All the data is available within the manuscript.
Conflicts of Interest
There is no conflict of interest.
References
- Murad, M.A.S.; Mustafa, M.A.; Younas, U.; Emadifar, H.; Khalifa, A.S.; Mohammed, W.W.; Ahmed, K.K. Soliton solutions to the generalized derivative nonlinear Schrödinger equation under the effect of multiplicative white noise and conformable derivative. Sci. Rep. 2025, 15, 19599. [Google Scholar] [CrossRef]
- Wang, K. New computational approaches to the fractional coupled nonlinear Helmholtz equation. Eng. Comput. 2024, 41, 1285–1300. [Google Scholar] [CrossRef]
- Aydın, Z.; Taşcan, F. Application of new Kudryashov method to Sawada-Kotera and Kaup-Kupershmidt equations. Comput. Methods Differ. Equ. 2025, 13, 608–617. [Google Scholar]
- Rahioui, M.; El Kinani, E.H.; Ouhadan, A. Bäcklund Transformations, Consistent Tanh Expansion Solvability, Interaction Solutions, and Some Exact Solitary Waves of a (3+1)-dimensional P-type Evolution Equation. Int. J. Theor. Phys. 2025, 64, 187. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A.; Nazir, A.; Ahmad, H.; Zaagan, A.A. Dark, bright and singular optical solitons for Biswas–Milovic equation with Kerr and dual power law nonlinearities. Mod. Phys. Lett. B 2025, 39, 2450443. [Google Scholar] [CrossRef]
- Li, Z. Optical Solutions of the Nonlinear Kodama Equation with the M-Truncated Derivative via the Extended (G′/G)-Expansion Method. Fractal Fract. 2025, 9, 300. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ali, M.Z.; Roshid, H.O. Stability analysis, model expansion method, and diverse chaos-detecting tools for the DSKP model. Sci. Rep. 2025, 15, 13658. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Alsharidi, A.K. Truncated M-Fractional Exact Solutions, Stability Analysis, and Modulation Instability of the Classical Lonngren Wave Model. Mathematics 2025, 13, 3107. [Google Scholar] [CrossRef]
- Hossain, S.; Rahman, M.M.; Bashar, M.H.; Biswas, S.; Roshid, M.M. Dynamical Structure of the Soliton Solution of M-Fractional (2+1)-Dimensional Heisenberg Ferromagnetic Spin Chain Model Through Advanced exp(Δ(ξ))-Expansion Schemes in Mathematical Physics. J. Appl. Math. 2025, 2025, 5535543. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A. Exploring new traveling and solitary wave solutions of conformable fractional (3+1)-D BLMP differential equations. In Advances in Computational Methods and Modeling for Science and Engineering; Elsevier: Amsterdam, The Netherlands, 2025; pp. 3–14. [Google Scholar]
- Khan, M.I.; Farooq, A.; Nisar, K.S.; Shah, N.A. Unveiling new exact solutions of the unstable nonlinear Schrödinger equation using the improved modified Sardar sub-equation method. Results Phys. 2024, 59, 107593. [Google Scholar] [CrossRef]
- Bilal, M.; Khan, A.; Ullah, I.; Khan, H.; Alzabut, J.; Alkhawar, H.M. Application of modified extended direct algebraic method to nonlinear fractional diffusion reaction equation with cubic nonlinearity. Bound. Value Probl. 2025, 2025, 16. [Google Scholar] [CrossRef]
- Waqar, M.; Saad, K.M.; Abbas, M.; Vivas-Cortez, M.; Hamanah, W.M. Diverse wave solutions for the (2+1)-dimensional Zoomeron equation using the modified extended direct algebraic approach. AIMS Math. 2025, 10, 12868–12887. [Google Scholar] [CrossRef]
- Yusuf, G.; Sabi’u, J.; Ibrahim, I.S.; Balili, A. Wave propagation patterns for the (2+1) dimensional modified complex KDV system via new extended direct algebra method. J. Basic Appl. Sci. Res. 2025, 3, 53–61. [Google Scholar] [CrossRef]
- Shafique, T.; Agarwal, R.P.; Mohammed, P.O.; Abbas, M.; Vivas-Cortez, M.; Nazir, T.; Djaouti, A.M. Abundant Solitons Solutions of the (2+1)-Dimensional Kadomtsev Petviashvili-Modified Equal width Model. Fractals 2025. [Google Scholar] [CrossRef]
- Samir, I.; Ahmed, H.M.; Emadifar, H.; Ahmed, K.K. Traveling and soliton waves and their characteristics in the extended (3+1)-dimensional Kadomtsev–Petviashvili equation in fluid. Partial Differ. Equ. Appl. Math. 2025, 14, 101146. [Google Scholar] [CrossRef]
- Raheel, M.; Zafar, A.; Razzaq, W.; Qousini, M.; Almusawa, M.Y. New analytical wave solitons and some other wave solutions of truncated M-fractional LPD equation along parabolic law of non-linearity. Opt. Quantum Electron. 2023, 55, 592. [Google Scholar] [CrossRef]
- Singh, K.; Kourakis, I. Generalized analytical solutions of a Korteweg–de Vries (KdV) equation with arbitrary real coefficients: Association with the plasma-fluid framework and physical interpretation. Wave Motion 2025, 132, 103443. [Google Scholar] [CrossRef]
- Liu, M.; Xiao, X. Topological properties, exact solutions and chaotic behaviors for coupled Drinfel’d–Sokolov–Wilson equation with conformal derivative. Eng. Comput. 2025, 42, 900–925. [Google Scholar] [CrossRef]
- Xu, L.; Yin, X.; Cao, N.; Bai, S. Multi-soliton solutions of a variable coefficient Schrödinger equation derived from vorticity equation. Nonlinear Dyn. 2024, 112, 2197–2208. [Google Scholar] [CrossRef]
- Zafar, A.; Razzaq, W.; Nazir, A.; Alomair, M.A.; Al Naim, A.S.; Alomair, A. Bifurcation Analysis and Solitons Dynamics of the Fractional Biswas–Arshed Equation via Analytical Method. Mathematics 2025, 13, 3147. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A. Machine learning-enhanced soliton solutions for the Lonngren-wave equation: An integration of Painlevé analysis and Hirota bilinear method. Rend. Lincei Sci. Fis. Nat. 2025, 1–16. [Google Scholar] [CrossRef]
- Kawser, M.A.; Akbar, M.A.; Khan, M.A.; Ghazwani, H.A. Exact soliton solutions and the significance of time-dependent coefficients in the Boussinesq equation: Theory and application in mathematical physics. Sci. Rep. 2024, 14, 762. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.Y. In an ocean or a river: Bilinear auto-Bäcklund transformations and similarity reductions on an extended time-dependent (3+1)-dimensional shallow water wave equation. China Ocean Eng. 2025, 39, 160–165. [Google Scholar] [CrossRef]
- Wang, K.J.; Shi, F.; Li, S.; Li, G.; Xu, P. Resonant Y-type soliton, interaction wave and other wave solutions to the (3+1)-dimensional shallow water wave equation. J. Math. Anal. Appl. 2025, 542, 128792. [Google Scholar] [CrossRef]
- Şenol, M. Abundant solitary wave solutions to the new extended (3+1)-dimensional nonlinear evolution equation arising in fluid dynamics. Mod. Phys. Lett. B 2025, 39, 2450475. [Google Scholar] [CrossRef]
- Gao, X.T.; Tian, B. In a river or an ocean: Similarity-reduction work on a (3+1)-dimensional extended shallow water wave equation. Appl. Math. Lett. 2025, 160, 109310. [Google Scholar] [CrossRef]
- Feng, C.H.; Tian, B.; Gao, X.T. Bilinear Bäcklund transformations, as well as n-soliton, breather, fission/fusion and hybrid solutions for a (3+1)-dimensional integrable wave equation in a fluid. Qual. Theory Dyn. Syst. 2025, 24, 1–19. [Google Scholar] [CrossRef]
- Khalifa, A.S.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B.; Emadifar, H.; Ahmed, K.K. Building novel solitary wave solutions for the generalized non-linear (3+1)-dimensional wave equation with gas bubbles in fluids using an analytic method. Partial Differ. Equ. Appl. Math. 2025, 101272. [Google Scholar] [CrossRef]
- Zafar, A.; Razzaq, W.; Rezazadeh, H.; Eslami, M. The complex hyperbolic Schrodinger dynamical equation with a truncated M-fractional by using simplest equation method. Comput. Methods Differ. Equ. 2024, 12, 44–55. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).