Adaptive Fuzzy Finite-Time Synchronization Control of Fractional-Order Chaotic Systems with Uncertain Dynamics, Unknown Parameters and Input Nonlinearities

Abstract

This work focuses on the finite-time synchronization control (FTSC) for fractional-order chaotic systems (FOCSs) subject to uncertain dynamics, unknown parameters and input nonlinearities. In the control law design, the uncertain dynamics of the FOCSs are addressed by using fuzzy logic systems (FLSs), while the unknown control direction caused by unknown input nonlinearity is handled through applying the Nussbaum gain function (NGF) method. Parameter adaptive laws are derived to estimate the unknown parameters of the given FOCSs, the parameter vectors of the FLSs, and unknown bounded constants, respectively. By integrating these parameter-adaptive laws with the FT backstepping control framework and FO Lyapunov direct method, an adaptive fuzzy FTSC strategy is developed. This strategy ensures that the synchronization error (SE) can converge to a small neighborhood of zero (SNoZ) within a FT and all signals of the closed-loop system (CLS) remain ultimately bounded. In the end, three simulation cases are utilized to demonstrate the efficiency of the proposed control method.

1. Introduction

Fractional calculus generalizes traditional integer-order calculus and is concerned with the study of derivatives and integrals for arbitrary real or complex orders. By overcoming the limitations of integer-order calculus, it provides a powerful tool for modeling various complex natural phenomena. In recent decades, its applications in engineering and physical systems have garnered significant attention from researchers [1,2,3]. Meanwhile, fractional calculus has enabled effective modeling of various practical systems, such as power chips [4,5], permanent magnet synchronous motors [6], hydraulic turbine regulating systems [7], financial systems [8] and DC-DC converters [9], paving the way for further investigation. It is worth noting, however, that many FO systems, including the FO Liu system, Lorenz system, Chen system and Chua system [10,11,12,13], can exhibit chaotic behavior under certain specific conditions.

The study of chaos can be traced back to the 1960s [14]. As a complex dynamical phenomenon, chaos exists in numerous nonlinear systems and has prompted extensive research. In [15], the problem of predicting chaotic time series was investigated within a fused framework incorporating both discrete-time and continuous-time models, and the neural network-based control strategy was proposed to significantly improve prediction length and accuracy. The authors of [16] studied a novel chaotic system that effectively reduces the implementation complexity associated with scroll chaotic attractors in circuit design. Furthermore, a disturbance-estimator-based reinforcement learning method for optimal stability control was proposed in [17], which can markedly enhance the stability and performance metrics of chaotic systems (CSs). By employing a model-free deep reinforcement learning approach, the authors of [18,19] successfully addressed the synchronization problem of CSs. Meanwhile, the problems of adaptive SC of CSs with unknown parameters were discussed in [20,21]. It should be noted that the aforementioned works represent only a small portion of a much broader body of literature.

Chaotic synchronization was first demonstrated to be achievable in [22] and has since evolved into a major research direction in control engineering, leading to the development of synchronization methods for integer-order CSs [23,24,25]. In recent years, the research focus has gradually shifted toward FOCSs. The stabilization and synchronization of these systems have prompted the development of various strategies. For instance, a robust controller was developed in [26] to achieve synchronization while improving transient performance. In [27], a control scheme based on the fuzzy control method and command filter was presented for the synchronization of uncertain FOCSs with disturbances. By utilizing the error compensation signal designed in [27], the filter error and the synchronization accuracy were effectively improved. For the FOCSs subject to model uncertainties, unknown dead-zone nonlinearity, input saturation and external disturbance, the adaptive control methods proposed in [28,29,30] can ensure asymptotic convergence of the SE. Furthermore, sliding mode control approaches have been widely applied in designing SC strategies for FOCSs [31,32,33]. Additional relevant results are found in [34,35,36,37] and the references therein.

It should be noted that a key weakness of the aforementioned control methods is that they only address asymptotic synchronization and stability [27,28,29,30,31,32,33], meaning the system states converge only when time approaches infinity. However, due to the sensitivity of CSs to initial values, convergence often needs to be achieved within a FT. To address this challenge, the FT control has gained increasing attention for the SC of FOCSs. For example, adaptive fuzzy FT sliding mode control schemes were developed in [38,39] to solve the FTSC problem. In [40], a FT convergent neural dynamics scheme was designed, which can guarantee superior convergence speed and robustness for a given FOCS. In [41], a robust control law utilizing quantized information was developed for the FTSC of nonlinear FOCSs under uncertain dynamics, actuator faults and time delays, successfully achieving the desired synchronization performance. Furthermore, FTSC methods have been applied to encryption and decryption of color images as well as secure communication [42,43], while significantly enhancing system security.

It is widely recognized that practical systems often involve various uncertainties, including unknown parameters, unmodeled dynamics, input nonlinearities, and external disturbances [44,45,46,47,48,49]. Although these factors pose considerable challenges for control design, the skillful integration of advanced techniques, such as neural networks, FLS, NGF technique, backstepping control, and dynamic surface control, has provided valuable insights for developing effective control strategies. Similarly, for FOCSs, the design of the SC strategy to achieve FTSC in the presence of the aforementioned uncertainties is obviously worthy of in-depth investigation. Unfortunately, many existing studies have not adequately addressed this issue.

Motivated by the above discussion, this work studies the FTSC issue for FOCSs in the presence of uncertain dynamics, unknown parameters, and input nonlinearities. To tackle this issue, an adaptive fuzzy FTSC strategy is developed by integrating the FLS, FT backstepping control framework, NGF technique and adaptive control method. In comparison with existing results, the main works are summarized as follows.

(1)

This work addresses a more general class of FOCSs, particularly incorporating unknown input nonlinearities, which distinguishes it significantly from the CSs discussed in [28,31,33,39,40].

(2)

FLSs are employed to approximate uncertain dynamics, while the NGF is applied to address unknown control directions arising from input nonlinearities. Furthermore, some parameter adaptive laws are designed to achieve bounded estimation of these unknown parameters. Compared with these methods in [26,29,30,32,35], this approach enables a more streamlined controller design.

(3)

An adaptive fuzzy FTSC scheme is designed, which guarantees that the SE converges to a SNoZ within a FT, and all signals of the CLS remain ultimately bounded.

(4)

Compared with the traditional PID controller and another FT control method, the proposed control method in this work can achieve better synchronization performance in a shorter FT.

The remainder of this work is structured as follows. Section 2 is devoted to the preliminaries and problem formulation. Section 3 covers the control strategy design and stability analysis. Section 4 presents the simulation results to validate the effectiveness of the proposed control method. The summary of the work can be found in Section 5.

2. Preliminaries and Problem Formulation

2.1. Preliminaries

Definition 1

([10]). The fractional integral of order $\eta$ for a function $\mathcal{H}(t)$ is defined as

$${\mathcal{I}}^{\eta }\mathcal{H}(t)={\displaystyle \frac{1}{\Gamma (\eta )}}{\displaystyle {\int }_0^T\frac{\mathcal{H}(t)}{{(t-\tau )}^{1-\eta }}}d\tau .$$

(1)

where $t\ge 0$, $\eta >0$ and $\Gamma (\eta )={\displaystyle {\int }_0^{+\infty }{\tau }^{\eta -1}}\exp (-\tau )d\tau$ stands for the Gamma function.

Definition 2

([11]). The $\eta \mathrm{th}$ order Caputo fractional derivative of function $\mathcal{H}(t)$ is described as

$${\mathcal{D}}^{\eta }\mathcal{H}(t)={\displaystyle \frac{1}{\Gamma (m-\eta )}}{\displaystyle {\int }_0^t\frac{{\mathcal{H}}^{(m)}(t)}{{(t-\tau )}^{\eta -m+1}}}d\tau .$$

(2)

where $m$ is the first integer, which is not less $\eta$, that is $m-1<\eta <m$. In this work, the case of $\eta \in (0,1)$ is considered.

Property 1.

If $\mathcal{Q}(t)\in R$ and $\mathcal{F}(t)\in R$ are continuous and differentiable functions, $d_1$, $d_2$ and $d_3$ are constants, then there exist

$$\left\{\begin{array}{l}{\mathcal{D}}^{\eta }{d}_1=0,\\ {\mathcal{D}}^{\eta }\left(d_2\mathcal{Q}(t)+d_3\mathcal{F}(t)\right)=d_2{\mathcal{D}}^{\eta }\mathcal{Q}(t)+d_3{\mathcal{D}}^{\eta }\mathcal{F}(t).\end{array}\right.$$

(3)

Property 2.

If a continuous function $\mathcal{K}(t)\in R$ is differentiable, one holds

$${\displaystyle \frac{1}{2}}{\mathcal{D}}^{\eta }\left({\left(\mathcal{K}(t)\right)}^T\mathcal{K}(t)\right)\le {\left(\mathcal{K}(t)\right)}^T\left({\mathcal{D}}^{\eta }\mathcal{K}(t)\right).$$

(4)

Definition 3

([29]). The two parameters Mittag-Leffler function is given as

$$E_{\eta ,\mu }(s)={\displaystyle \sum _{k=0}^{\infty }\frac{s^k}{\Gamma (k\eta +\mu )}}.$$

(5)

where $s$ is a complex term, $\eta >0$ and $\mu >0$. Noting $E_{\eta }(s)=E_{\eta ,1}(s)$ and $E_{1,1}(s)=\exp (s)$.

Definition 4

([50]). For the continuous function $\mathcal{N}(\chi )$, if there exist

$$\underset{\chi \to \infty }{\lim }\sup {\displaystyle \frac{1}{\chi }}{\displaystyle {\int }_0^{\chi }\mathcal{N}(s)ds}=+\infty , \mathrm{and} \underset{\chi \to \infty }{\lim }\inf {\displaystyle \frac{1}{\chi }}{\displaystyle {\int }_0^{\chi }\mathcal{N}(s)ds}=-\infty .$$

(6)

One can be called that $\mathcal{N}(\chi )$ is a NGF. There are some functions, including ${\chi }^2\sin (\chi )$, ${\chi }^2\cos (\chi )$, $\exp ({\chi }^2)\sin (\pi \chi /2)$ and $\exp ({\chi }^2)\cos (\pi \chi /2)$, that are often used as the NGF. In this work, the NGF is considered as $\exp ({\chi }^2)\cos (\pi \chi /2)$.

Remark 1.

Noting Definition 4, it can be seen that the NGF “explores” the correct control direction of an unknown system by oscillating between positive and negative. This effectively resolves the reliance on prior knowledge of the control direction in traditional adaptive control, eliminates the need for external persistent excitation, and has minimal impact on the system. As a result, it significantly enhances the robustness and adaptability of the controller when dealing with uncertain and time-varying systems.

Lemma 1

([29]). For $\forall \eta \in (0,2)$, $\mu \in R$, if there exists $ƛ\in \left(\pi \mu /2,\min (\pi ,\pi \eta )\right)$, then one has

$$\left|E_{\eta ,\mu }(s)\right|\le {\displaystyle \frac{\varsigma }{1+\left|s\right|}}.$$

(7)

where $\varsigma$ is any positive constant, and $ƛ\le \left|\arg (s)\right|\le \pi$.

Lemma 2

([51]). Let $\alpha \in R$ and $\mathcal{X}(t)\in {\mathcal{C}}^1\left([0,b],R\right)$, then for $\eta \in (0,1)$, one has

$${\mathcal{D}}^{\eta }{\left(\mathcal{X}(t)\right)}^{\alpha }={\displaystyle \frac{\Gamma (1+\alpha )}{\Gamma (1+\alpha -\eta )}}{\left(\mathcal{X}(t)\right)}^{\alpha -\eta }{\mathcal{D}}^{\eta }\mathcal{X}(t).$$

(8)

Lemma 3

([51]). Let the $\eta \mathrm{th}$ order fractional derivative of a smooth continuous function $V(t):\left[0,+\infty \right)\to R$ satisfy

$${\mathcal{D}}^{\eta }V(t)\le -q_{1}V(t)+q_2,\forall t\ge 0,$$

(9)

where $\eta \in (0,1)$, $q_1>0$ and $q_2>0$ represent constants, then one holds

$$V(t)\le V(0)E_{\eta }(-q_1{t}^{\eta })+{\displaystyle \frac{q_2\varsigma }{q_1}}.$$

(10)

where $\varsigma$ is defined in Lemma 1.

Lemma 4

([50]). Let $V(t)$ and ${\chi }_i(t)$ be smooth continuous functions defined on $[0,t_0)$ with $V(t)\ge 0$ for $\forall t\in [0,t_0)$ and all ${\lambda }_i(t)\ne 0$ be unknown but bounded time-varying parameters that have the same sign. If the following inequality holds

$${\mathcal{D}}^{\eta }V(t)\le -{\alpha }_{0}V(t)+{\displaystyle \sum _{i=1}^n\left({\lambda }_i(t)\mathcal{N}({\chi }_i)+1\right)}{\dot{\chi }}_i+C_0.$$

(11)

where ${\alpha }_0>0$ and $C_0>0$ stand for constants, then ${\displaystyle {\sum }_{i=1}^n\left({\lambda }_i(t)\mathcal{N}({\chi }_i)+1\right){\dot{\chi }}_i}$, ${\chi }_i(t)$ and $V(t)$ are bounded on $[0,t_0)$.

Lemma 5

([44]). For any positive constants ${\alpha }_1$, ${\alpha }_2$ and ${\alpha }_3$, ${\mathcal{S}}_1\in R$ and ${\mathcal{S}}_2\in R$, then there exists

$${\left|{\mathcal{S}}_1\right|}^{{\alpha }_1}{\left|{\mathcal{S}}_2\right|}^{{\alpha }_2}\le {\displaystyle \frac{{\alpha }_1}{{\alpha }_1+{\alpha }_2}}{\alpha }_3{\left|{\mathcal{S}}_1\right|}^{{\alpha }_1+{\alpha }_2}+{\displaystyle \frac{{\alpha }_2}{{\alpha }_1+{\alpha }_2}}{\alpha }_3^{-{\displaystyle \frac{{\alpha }_1}{{\alpha }_2}}}{\left|{\mathcal{S}}_2\right|}^{{\alpha }_1+{\alpha }_2}.$$

(12)

Lemma 6

([44]). For any constants $\mathcal{Q}$ and $\varpi >0$, the following inequality holds

$$0\le \left|\mathcal{Q}\right|-{\displaystyle \frac{{\mathcal{Q}}^2}{\sqrt{{\mathcal{Q}}^2+{\varpi }^2}}}\le \varpi .$$

(13)

Lemma 7

([44]). For $0<p\le 1$ and ${\mathcal{U}}_i\in R$, then there exists

$${\left({\displaystyle \sum _{i=1}^n\left|{\mathcal{U}}_i\right|}\right)}^p\le {\displaystyle \sum _{i=1}^n{\left|{\mathcal{U}}_i\right|}^p}\le n^{1-p}{\left({\displaystyle \sum _{i=1}^n\left|{\mathcal{U}}_i\right|}\right)}^p.$$

(14)

Lemma 8

([52]). Let $\nu \in (0,1)$ and $\tilde{\mathcal{M}}=\mathcal{M}-\mathcal{L}$, then one has

$$\tilde{\mathcal{M}}{(\mathcal{M}-\tilde{\mathcal{M}})}^{\nu }\le {\mathcal{l}}_1{\mathcal{M}}^{1+\nu }-{\mathcal{l}}_2{\tilde{\mathcal{M}}}^{1+\nu }.$$

(15)

where ${\mathcal{l}}_1=(1-2^{\nu -1})/(1+\nu )+(2^{-{(\nu -1)}^2}+\nu )/{(1+\nu )}^2$ and ${\mathcal{l}}_2=(2^{\nu -1}-2^{(1+\nu )(\nu -1)})/(1+\nu )>0$.

2.2. FLS

In this work, the FLS is utilized to deal with unknown nonlinear dynamics. An FLS is generally composed of a fuzzifier, fuzzy inference engine, knowledge base, and defuzzifier [27]. The following “If-Then” rules are used to build the knowledge base.

$${\mathcal{R}}_l: \mathrm{If} z_1 \mathrm{is} {\mathcal{F}}_1^l \mathrm{and} z_2 \mathrm{is} {\mathcal{F}}_2^l \mathrm{and} \dots \mathrm{and} z_n \mathrm{is} {\mathcal{F}}_n^l, \mathrm{Then} \mathcal{Y} \mathrm{is} {\mathcal{G}}_l, l=1,\dots ,M$$

where $z={\left[z_1,\dots ,z_n\right]}^T$ and $\mathcal{Y}$ represent the input and output of the FLS, respectively, and ${\mathcal{F}}_1^l,\dots ,{\mathcal{F}}_n^l$ and ${\mathcal{G}}_l$ represent fuzzy sets.

Applying product inference, singleton fuzzifier, and center average defuzzification, the FLS can be described as

$$\mathcal{Y}(z)={\displaystyle \frac{{\displaystyle {\sum }_{l=1}^M{w}_l{\prod }_{i=1}^n{\mu }_{{\mathcal{F}}_i^l}(z_i)}}{{\displaystyle {\sum }_{l=1}^M\left[{\prod }_{i=1}^n{\mu }_{{\mathcal{F}}_i^l}(z_i)\right]}}},$$

(16)

where ${\mu }_{{\mathcal{F}}_i^l}(z_i)$ stands for the membership function, and $w_l={\max }_{\mathcal{Y}\in R}{\mu }_{{\mathcal{G}}_l}(\mathcal{Y})$.

Assuming $W={\left[w_1,\dots ,w_M\right]}^T$, and $\psi (z)={\left[{\varphi }_1(z),\dots ,{\varphi }_M(z)\right]}^T$ with

$${\varphi }_l(z)={\displaystyle \frac{{\prod }_{i=1}^n{\mu }_{{\mathcal{F}}_i^l}(z_i)}{{\displaystyle {\sum }_{l=1}^M\left[{\prod }_{i=1}^n{\mu }_{{\mathcal{F}}_i^l}(z_i)\right]}}}, l=1,\dots ,M,$$

(17)

then the FLS (16) is transformed into $\mathcal{Y}(z)=W^T\psi (z)$.

Also, the membership function ${\mu }_{{\mathcal{F}}_i^l}(z_i)$ is usually considered as the Gaussian function, that is, ${\mu }_{{\mathcal{F}}_i^l}(z_i)=\exp \left(-{\left(z_i-{\mathcal{K}}_i\right)}^2/d_i^2\right)$, $i=1,\dots ,n$, where ${\mathcal{K}}_i$ and $d_i$ represent the center and width of the Gaussian function, respectively.

Lemma 9

([27]). For any continuous function $\mathcal{P}(x)$ defined on compact set ${\Omega }_x$, there exists an FLS $W^T\psi (x)$ such that

$${\sup }_{x\in {\Omega }_x}\left|\mathcal{P}(x)-W^T\psi (x)\right|\le \epsilon .$$

(18)

where $\epsilon$ represents the approximation error, and satisfies $\left|\epsilon \right|\le {\epsilon }_{\max }$ with ${\epsilon }_{\max }>0$.

2.3. Problem Formulation

In this work, the following $n-$ dimensional FOCSs as the drive system and response system are considered.

The drive system is described as

$${\mathcal{D}}^{\eta }{x}_i=a_i{x}_i+f_i\left(X,t\right)+F_i\left(X,t\right)+{\Delta }_{di}(t),$$

(19)

The response system is defined as

$${\mathcal{D}}^{\eta }{y}_i=a_i{y}_i+g_i\left(Y,t\right)+G_i\left(Y,t\right)+{\Delta }_{ri}(t)+\mathcal{U}\left(u_i(t)\right).$$

(20)

where $i=1,\dots ,n$, $0<\eta <1$ is the order of drive system and response system, $a_i$ stands for nonzero but unknown parameter, $X={\left[x_1,\dots ,x_n\right]}^T\in R^n$ and $Y={\left[y_1,\dots ,y_n\right]}^T\in R^n$ are the state vectors, $f_i\left(X,t\right):R^n\to R$ and $g_i\left(Y,t\right):R^n\to R$ represent known smooth nonlinear functions, $F_i\left(X,t\right):R^n\to R$ and $G_i\left(Y,t\right):R^n\to R$ denote the unknown uncertain dynamics, ${\Delta }_{di}(t)\in R$ and ${\Delta }_{ri}(t)\in R$ denote the external disturbances. In addition, $u_i(t)$ is the actual control signal and $\mathcal{U}\left(u_i(t)\right)$ is unknown nonlinearity which is given as

$$\mathcal{U}\left(u_i(t)\right)={\lambda }_i(t)u_i(t)+o_i(t).$$

(21)

where ${\lambda }_i(t)$ and $o_i(t)$ stand for unknown time-varying parameters.

Assumption 1.

There exist unknown constants ${\Delta }_{di,\max }>0$ and ${\Delta }_{ri,\max }>0$ ($i=1,\dots ,n$), such that $\left|{\Delta }_{di}(t)\right|\le {\Delta }_{di,\max }$ and $\left|{\Delta }_{ri}(t)\right|\le {\Delta }_{ri,\max }$.

Assumption 2.

The sign of ${\lambda }_i(t)$ ($i=1,\dots ,n$) is unknown, and $0<\left|{\lambda }_i(t)\right|\le {\lambda }_{i,\max }$ with ${\lambda }_{i,\max }>0$ being an unknown constant. Without loss of generality, let $0<{\lambda }_i(t)\le {\lambda }_{i,\max }$. In addition, $\left|o_i(t)\right|\le o_{i,\max }$ with $o_{i,\max }>0$.

According to the drive system (19) and response system (20), and the SE is defined as $e_i=y_i-x_i$($i=1,\dots ,n$), which is described as

$${\mathcal{D}}^{\eta }{e}_i=a_i{e}_i+\left(g_i\left(Y,t\right)-f_i\left(X,t\right)\right)+\left(G_i\left(Y,t\right)-F_i\left(X,t\right)\right)+{\Delta }_{ri}(t)-{\Delta }_{di}(t)+\mathcal{U}\left(u_i(t)\right).$$

(22)

Thus, the SC problem will be transformed into a stability problem regarding the SE. Therefore, the control goal is to develop an adaptive fuzzy FT control strategy $u_i(t)$ to ensure all signals of CLS are bounded, and the SE $e_i$ can converge to a SNoZ within a FT.

3. Control Strategy Design and Stability Analysis

3.1. Adaptive Fuzzy FT Control Strategy Design

In this subsection, an adaptive fuzzy FT control strategy is proposed for the response system (20) within the backstepping control framework. Moreover, both FLSs and the NGF technique are simultaneously considered during the control design. Without causing confusion, the time variable $t$ will be omitted in the subsequent analysis.

Step 1 ($i=1$). Let $V_{11}=e_1^2/2$ and considering (21) and (22), then the $\eta \mathrm{th}$ order derivative of $V_{11}$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{11}\le & e_1\left({\lambda }_1(t)u_1(t)\right)+a_1{e}_1^2+\left(g_1\left(Y\right)-f_1\left(X\right)\right)e_1+\left(G_1\left(Y\right)-F_1\left(X\right)\right)e_1\\ & +\left({\Delta }_{r1}-{\Delta }_{d1}+o_1\right)e_1.\end{array}$$

(23)

Due to $\left(G_1\left(Y\right)-F_1\left(X\right)\right)$ is unknown uncertain dynamic, an FLS is applied to approximate it, then we have

$$G_1\left(Y\right)-F_1\left(X\right)=W_1^T{\psi }_1(Z)+{\epsilon }_1(Z).$$

(24)

where $Z={\left[X^T,Y^T\right]}^T$, ${\epsilon }_1(Z)$ is an unknown constant and satisfies $\left|{\epsilon }_1(Z)\right|\le {\epsilon }_{1,\max }$ with ${\epsilon }_{1,\max }>0$.

According to Lemmas 5 and 6, we obtain

$$\left|e_1{W}_1^T{\psi }_1(Z)\right|\le c_1{\mathrm{H}}_1{\Psi }_1{e}_1^2+{\displaystyle \frac{1}{4c_1}},$$

(25)

$$\left|\left({\Delta }_{r1}-{\Delta }_{d1}+o_1+{\epsilon }_1(Z)\right)e_1\right|\le {\mathrm{M}}_1\left|e_1\right|\le {\displaystyle \frac{{\mathrm{M}}_1{e}_1^2}{\sqrt{e_1^2+{\varpi }^2}}}+{\mathrm{M}}_1\varpi ,$$

(26)

where ${\mathrm{H}}_1=W_1^T{W}_1$, ${\Psi }_1={\left({\psi }_1(Z)\right)}^T{\psi }_1(Z)$, ${\mathrm{M}}_1={\Delta }_{r1,\max }+{\Delta }_{d1,\max }+o_{1,\max }+{\epsilon }_{1,\max }$, and $c_1>0$ is design parameter.

Substituting (24)–(26) into (23) yields

$${\mathcal{D}}^{\eta }{V}_{11}\le e_1\left({\lambda }_1(t)u_1(t)\right)+a_1{e}_1^2+\left(g_1\left(Y\right)-f_1\left(X\right)\right)e_1+c_1{\mathrm{H}}_1{\Psi }_1{e}_1^2+{\displaystyle \frac{{\mathrm{M}}_1{e}_1^2}{\sqrt{e_1^2+{\varpi }^2}}}+{\displaystyle \frac{1}{4c_1}}+{\mathrm{M}}_1\varpi .$$

(27)

Choosing the candidate Lyapunov function $V_1$ as

$$V_1=V_{11}+{\displaystyle \frac{1}{2{\vartheta }_1}}{\tilde{a}}_1^2+{\displaystyle \frac{1}{2{\rho }_1}}{\tilde{\mathrm{H}}}_1^2+{\displaystyle \frac{1}{2{\theta }_1}}{\tilde{\mathrm{M}}}_1^2,$$

(28)

where ${\vartheta }_1>0$, ${\rho }_1>0$ and ${\theta }_1>0$ stand for design parameters, ${\tilde{a}}_1=a_1-{\widehat{a}}_1$, ${\tilde{\mathrm{H}}}_1={\mathrm{H}}_1-{\widehat{\mathrm{H}}}_1$, ${\tilde{\mathrm{M}}}_1={\mathrm{M}}_1-{\widehat{\mathrm{M}}}_1$, ${\widehat{a}}_1$, ${\widehat{\mathrm{H}}}_1$ and ${\widehat{\mathrm{M}}}_1$ are the estimate of $a_1$, ${\mathrm{H}}_1$ and ${\mathrm{M}}_1$, respectively.

Hence, considering (27), the $\eta \mathrm{th}$ order derivative of $V_1$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_1& \le e_1\left({\lambda }_1(t)u_1(t)\right)+a_1{e}_1^2+\left(g_1\left(Y\right)-f_1\left(X\right)\right)e_1+c_1{\mathrm{H}}_1{\Psi }_1{e}_1^2+{\displaystyle \frac{{\mathrm{M}}_1{e}_1^2}{\sqrt{e_1^2+{\varpi }^2}}}\\ & -{\displaystyle \frac{1}{{\vartheta }_1}}{\tilde{a}}_1{\mathcal{D}}^{\eta }{\widehat{a}}_1-{\displaystyle \frac{1}{{\rho }_1}}{\tilde{\mathrm{H}}}_1{\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_1-{\displaystyle \frac{1}{{\theta }_1}}{\tilde{\mathrm{M}}}_1{\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_1+{\displaystyle \frac{1}{4c_1}}+{\mathrm{M}}_1\varpi .\end{array}$$

(29)

Noting ${\lambda }_1(t)$ is nonzero but unknown parameter, and then the adaptive fuzzy FT control strategy $u_1(t)$ and parameter adaptive laws are proposed as

$$u_1(t)={\mathcal{N}}_1({\chi }_1)\left({\omega }_1{e}_1^{2\beta -1}+{\kappa }_1{e}_1+{\widehat{a}}_1{e}_1+\left(g_1\left(Y\right)-f_1\left(X\right)\right)+c_1{\widehat{\mathrm{H}}}_1{\Psi }_1{e}_1+{\displaystyle \frac{{\widehat{\mathrm{M}}}_1{e}_1}{\sqrt{e_1^2+{\varpi }^2}}}\right),$$

(30)

$${\dot{\chi }}_1={\omega }_1{e}_1^{2\beta }+{\kappa }_1{e}_1^2+{\widehat{a}}_1{e}_1^2+\left(g_1\left(Y\right)-f_1\left(X\right)\right)e_1+c_1{\widehat{\mathrm{H}}}_1{\Psi }_1{e}_1^2+{\displaystyle \frac{{\widehat{\mathrm{M}}}_1{e}_1^2}{\sqrt{e_1^2+{\varpi }^2}}},$$

(31)

$${\mathcal{D}}^{\eta }{\widehat{a}}_1={\vartheta }_1{e}_1^2-{\sigma }_{11}{\widehat{a}}_1-{\sigma }_{12}{\widehat{a}}_1^{2\beta -1},$$

(32)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_1={\rho }_1{c}_1{\Psi }_1{e}_1^2-{\varphi }_{11}{\widehat{\mathrm{H}}}_1-{\varphi }_{12}{\widehat{\mathrm{H}}}_1^{2\beta -1},$$

(33)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_1={\displaystyle \frac{{\theta }_1{e}_1^2}{\sqrt{e_1^2+{\varpi }^2}}}-{\phi }_{11}{\widehat{\mathrm{M}}}_1-{\phi }_{12}{\widehat{\mathrm{M}}}_1^{2\beta -1},$$

(34)

where $0<\beta <1$, ${\omega }_1$, ${\kappa }_1$, ${\sigma }_{11}$, ${\sigma }_{12}$, ${\varphi }_{11}$, ${\varphi }_{12}$, ${\phi }_{11}$ and ${\phi }_{12}$ are positive design parameters, ${\mathcal{N}}_1({\chi }_1)$ is given NGF.

Substituting (30)–(34) into (29), one has

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_1& \le -{\omega }_1{e}_1^{2\beta }-{\kappa }_1{e}_1^2+{\displaystyle \frac{{\sigma }_{11}}{{\vartheta }_1}}{\tilde{a}}_1{\widehat{a}}_1+{\displaystyle \frac{{\varphi }_{11}}{{\rho }_1}}{\tilde{\mathrm{H}}}_1{\widehat{\mathrm{H}}}_1+{\displaystyle \frac{{\phi }_{11}}{{\theta }_1}}{\tilde{\mathrm{M}}}_1{\widehat{\mathrm{M}}}_1+{\displaystyle \frac{{\sigma }_{12}}{{\vartheta }_1}}{\tilde{a}}_1{\widehat{a}}_1^{2\beta -1}+{\displaystyle \frac{{\varphi }_{12}}{{\rho }_1}}{\tilde{\mathrm{H}}}_1{\widehat{\mathrm{H}}}_1^{2\beta -1}\\ & \hspace{1em}+{\displaystyle \frac{{\phi }_{12}}{{\theta }_1}}{\tilde{\mathrm{M}}}_1{\widehat{\mathrm{M}}}_1^{2\beta -1}+\left({\lambda }_1(t){\mathcal{N}}_1({\chi }_1)+1\right){\dot{\chi }}_1+{\displaystyle \frac{1}{4c_1}}+{\mathrm{M}}_1\varpi .\end{array}$$

(35)

Step  $i$ ($i=2,\dots ,n-1$). Let $V_{i1}=e_i^2/2$ and considering (21) and (22), then the $\eta \mathrm{th}$ order derivative of $V_{i1}$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{i1}\le & e_i\left({\lambda }_i(t)u_i(t)\right)+a_i{e}_i^2+\left(g_i\left(Y\right)-f_i\left(X\right)\right)e_i+\left(G_i\left(Y\right)-F_i\left(X\right)\right)e_i\\ & +\left({\Delta }_{ri}-{\Delta }_{di}+o_i\right)e_i.\end{array}$$

(36)

Given that $\left(G_i\left(Y\right)-F_i\left(X\right)\right)$ is unknown uncertain dynamic, an FLS is applied to approximate it, then we have

$$G_i\left(Y\right)-F_i\left(X\right)=W_i^T{\psi }_i(Z)+{\epsilon }_i(Z).$$

(37)

where $Z={\left[X^T,Y^T\right]}^T$, ${\epsilon }_i(Z)$ is an unknown constant and satisfies $\left|{\epsilon }_i(Z)\right|\le {\epsilon }_{i,\max }$ with ${\epsilon }_{i,\max }>0$.

Likewise, using Lemmas 5 and 6, one has

$$\left|e_i{W}_i^T{\psi }_i(Z)\right|\le c_i{\mathrm{H}}_i{\Psi }_i{e}_i^2+{\displaystyle \frac{1}{4c_i}},$$

(38)

$$\left|\left({\Delta }_{ri}-{\Delta }_{di}+o_i+{\epsilon }_i(Z)\right)e_i\right|\le {\displaystyle \frac{{\mathrm{M}}_i{e}_i^2}{\sqrt{e_i^2+{\varpi }^2}}}+{\mathrm{M}}_i\varpi ,$$

(39)

where ${\mathrm{H}}_i=W_i^T{W}_i$, ${\Psi }_i={\left({\psi }_i(Z)\right)}^T{\psi }_i(Z)$, ${\mathrm{M}}_i={\Delta }_{ri,\max }+{\Delta }_{di,\max }+o_{i,\max }+{\epsilon }_{i,\max }$, and $c_i>0$ is design parameter.

Substituting (37)–(39) into (36) yields

$${\mathcal{D}}^{\eta }{V}_{i1}\le e_i\left({\lambda }_i(t)u_i(t)\right)+a_i{e}_i^2+\left(g_i\left(Y\right)-f_i\left(X\right)\right)e_i+c_i{\mathrm{H}}_i{\Psi }_i{e}_i^2+{\displaystyle \frac{{\mathrm{M}}_i{e}_i^2}{\sqrt{e_i^2+{\varpi }^2}}}+{\displaystyle \frac{1}{4c_i}}+{\mathrm{M}}_i\varpi .$$

(40)

Further, designing the candidate Lyapunov function $V_i$ as

$$V_i=V_{i-1}+V_{i1}+{\displaystyle \frac{1}{2{\vartheta }_i}}{\tilde{a}}_i^2+{\displaystyle \frac{1}{2{\rho }_i}}{\tilde{\mathrm{H}}}_i^2+{\displaystyle \frac{1}{2{\theta }_i}}{\tilde{\mathrm{M}}}_i^2,$$

(41)

where ${\vartheta }_i>0$, ${\rho }_i>0$ and ${\theta }_i>0$ represent design parameters, ${\tilde{a}}_i=a_i-{\widehat{a}}_i$, ${\tilde{\mathrm{H}}}_i={\mathrm{H}}_i-{\widehat{\mathrm{H}}}_i$, ${\tilde{\mathrm{M}}}_i={\mathrm{M}}_i-{\widehat{\mathrm{M}}}_i$, ${\widehat{a}}_i$, ${\widehat{\mathrm{H}}}_i$ and ${\widehat{\mathrm{M}}}_i$ are the estimate of $a_i$, ${\mathrm{H}}_i$ and ${\mathrm{M}}_i$, respectively.

Hence, considering (40), the $\eta \mathrm{th}$ order derivative of $V_i$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_i& \le {\mathcal{D}}^{\eta }{V}_{i-1}+e_i\left({\lambda }_i(t)u_i(t)\right)+a_i{e}_i^2+\left(g_i\left(Y\right)-f_i\left(X\right)\right)e_i+c_i{\mathrm{H}}_i{\Psi }_i{e}_i^2+{\displaystyle \frac{{\mathrm{M}}_i{e}_i^2}{\sqrt{e_i^2+{\varpi }^2}}}\\ & -{\displaystyle \frac{1}{{\vartheta }_i}}{\tilde{a}}_i{\mathcal{D}}^{\eta }{\widehat{a}}_i-{\displaystyle \frac{1}{{\rho }_i}}{\tilde{\mathrm{H}}}_i{\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_i-{\displaystyle \frac{1}{{\theta }_i}}{\tilde{\mathrm{M}}}_i{\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_i+{\displaystyle \frac{1}{4c_i}}+{\mathrm{M}}_i\varpi .\end{array}$$

(42)

According to the result of the $(i-1)\mathrm{th}$ step, one obtains

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{i-1}\le & -{\displaystyle \sum _{m=1}^{i-1}{\omega }_m{e}_m^{2\beta }}-{\displaystyle \sum _{m=1}^{i-1}{\kappa }_m{e}_m^2}+{\displaystyle \sum _{m=1}^{i-1}\left(\frac{{\sigma }_{m1}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m+\frac{{\varphi }_{m1}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m+\frac{{\phi }_{m1}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m\right)}\\ & +{\displaystyle \sum _{m=1}^{i-1}\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m^{2\beta -1}+\frac{{\varphi }_{m2}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m^{2\beta -1}+\frac{{\phi }_{m2}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m^{2\beta -1}\right)}\\ & +{\displaystyle \sum _{m=1}^{i-1}\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+{\displaystyle \sum _{m=1}^{i-1}\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right).}\end{array}$$

(43)

Noting ${\lambda }_i(t)$ is nonzero but unknown parameter, and then the adaptive fuzzy FT control strategy $u_i(t)$ and parameter adaptive laws are proposed as

$$u_i(t)={\mathcal{N}}_i({\chi }_i)\left({\omega }_i{e}_i^{2\beta -1}+{\kappa }_i{e}_i+{\widehat{a}}_i{e}_i+\left(g_i\left(Y\right)-f_i\left(X\right)\right)+c_i{\widehat{\mathrm{H}}}_i{\Psi }_i{e}_i+{\displaystyle \frac{{\widehat{\mathrm{M}}}_i{e}_i}{\sqrt{e_i^2+{\varpi }^2}}}\right),$$

(44)

$${\dot{\chi }}_i={\omega }_i{e}_i^{2\beta }+{\kappa }_i{e}_i^2+{\widehat{a}}_i{e}_i^2+\left(g_i\left(Y\right)-f_i\left(X\right)\right)e_i+c_i{\widehat{\mathrm{H}}}_i{\Psi }_i{e}_i^2+{\displaystyle \frac{{\widehat{\mathrm{M}}}_i{e}_i^2}{\sqrt{e_i^2+{\varpi }^2}}},$$

(45)

$${\mathcal{D}}^{\eta }{\widehat{a}}_i={\vartheta }_i{e}_i^2-{\sigma }_{i1}{\widehat{a}}_i-{\sigma }_{i2}{\widehat{a}}_i^{2\beta -1},$$

(46)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_i={\rho }_i{c}_i{\Psi }_i{e}_i^2-{\varphi }_{i1}{\widehat{\mathrm{H}}}_i-{\varphi }_{i2}{\widehat{\mathrm{H}}}_i^{2\beta -1},$$

(47)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_i={\displaystyle \frac{{\theta }_i{e}_i^2}{\sqrt{e_i^2+{\varpi }^2}}}-{\phi }_{i1}{\widehat{\mathrm{M}}}_i-{\phi }_{i2}{\widehat{\mathrm{M}}}_i^{2\beta -1},$$

(48)

where ${\omega }_i$, ${\kappa }_i$, ${\sigma }_{i1}$, ${\sigma }_{i2}$, ${\varphi }_{i1}$, ${\varphi }_{i2}$, ${\phi }_{i1}$ and ${\phi }_{i2}$ represent positive design parameters, ${\mathcal{N}}_i({\chi }_i)$ is given NGF.

Substituting (43)–(48) into (42), one has

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_i\le -& {\displaystyle \sum _{m=1}^i{\omega }_m{e}_m^{2\beta }}-{\displaystyle \sum _{m=1}^i{\kappa }_m{e}_m^2}+{\displaystyle \sum _{m=1}^i\left(\frac{{\sigma }_{m1}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m+\frac{{\varphi }_{m1}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m+\frac{{\phi }_{m1}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m\right)}\\ & +{\displaystyle \sum _{m=1}^i\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m^{2\beta -1}+\frac{{\varphi }_{m2}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m^{2\beta -1}+\frac{{\phi }_{m2}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m^{2\beta -1}\right)}\\ & +{\displaystyle \sum _{m=1}^i\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+{\displaystyle \sum _{m=1}^i\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right)}.\end{array}$$

(49)

Step $n$ ($i=n$). This is the last step. Let $V_{n1}=e_n^2/2$ and considering (21) and (22), then the $\eta \mathrm{th}$ order derivative of $V_{n1}$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{n1}& \le e_n\left({\lambda }_n(t)u_n(t)\right)+a_n{e}_n^2+\left(g_n\left(Y\right)-f_n\left(X\right)\right)e_n+\left(G_n\left(Y\right)-F_n\left(X\right)\right)e_n\\ & \hspace{1em}\hspace{1em}+\left({\Delta }_{rn}-{\Delta }_{dn}+o_n\right)e_n.\end{array}$$

(50)

Given that $\left(g_n\left(Y\right)-f_n\left(X\right)\right)$ is unknown uncertain dynamic, an FLS is applied to approximate it, then we have

$$G_n\left(Y\right)-F_n\left(X\right)=W_n^T{\psi }_n(Z)+{\epsilon }_n(Z).$$

(51)

where $Z={\left[X^T,Y^T\right]}^T$, ${\epsilon }_n(Z)$ is an unknown constant and satisfies $\left|{\epsilon }_n(Z)\right|\le {\epsilon }_{n,\max }$ with ${\epsilon }_{n,\max }>0$.

Further, taking into account Lemmas 5 and 6, one obtains

$$\left|e_n{W}_n^T{\psi }_n(Z)\right|\le c_n{\mathrm{H}}_n{\Psi }_n{e}_n^2+{\displaystyle \frac{1}{4c_n}},$$

(52)

$$\left|\left({\Delta }_{rn}-{\Delta }_{dn}+o_n+{\epsilon }_n(Z)\right)e_n\right|\le {\displaystyle \frac{{\mathrm{M}}_n{e}_n^2}{\sqrt{e_n^2+{\varpi }^2}}}+{\mathrm{M}}_n\varpi ,$$

(53)

where ${\mathrm{H}}_n=W_n^T{W}_n$, ${\Psi }_n={\left({\psi }_n(X)\right)}^T{\psi }_n(X)$, ${\mathrm{M}}_n={\Delta }_{rn,\max }+{\Delta }_{dn,\max }+o_{n,\max }+{\epsilon }_{n,\max }$, and $c_n>0$ is design parameter.

Substituting (51)–(53) into (50) yields

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{n1}& \le e_n\left({\lambda }_n(t)u_n(t)\right)+a_n{e}_n^2+\left(g_n\left(Y\right)-f_n\left(X\right)\right)e_n\\ & \hspace{1em}\hspace{1em}+c_n{\mathrm{H}}_n{\Psi }_n{e}_n^2+{\displaystyle \frac{{\mathrm{M}}_n{e}_n^2}{\sqrt{e_n^2+{\varpi }^2}}}+{\displaystyle \frac{1}{4c_n}}+{\mathrm{M}}_n\varpi .\end{array}$$

(54)

Further, choosing the candidate Lyapunov function $V_n$ as

$$V_n=V_{n-1}+V_{n1}+{\displaystyle \frac{1}{2{\vartheta }_n}}{\tilde{a}}_n^2+{\displaystyle \frac{1}{2{\rho }_n}}{\tilde{\mathrm{H}}}_n^2+{\displaystyle \frac{1}{2{\theta }_n}}{\tilde{\mathrm{M}}}_n^2,$$

(55)

where ${\vartheta }_n>0$, ${\rho }_n>0$ and ${\theta }_n>0$ stand for design parameters, ${\tilde{a}}_n=a_n-{\widehat{a}}_n$, ${\tilde{\mathrm{H}}}_n={\mathrm{H}}_n-{\widehat{\mathrm{H}}}_n$, ${\tilde{\mathrm{M}}}_n={\mathrm{M}}_n-{\widehat{\mathrm{M}}}_n$, ${\widehat{a}}_n$, ${\widehat{\mathrm{H}}}_n$ and ${\widehat{\mathrm{M}}}_n$ are the estimate of $a_n$, ${\mathrm{H}}_n$ and ${\mathrm{M}}_n$, respectively.

Hence, using (54), the $\eta \mathrm{th}$ order derivative of $V_n$ is

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_n& \le {\mathcal{D}}^{\eta }{V}_{n-1}+e_n\left({\lambda }_n(t)u_n(t)\right)+a_n{e}_n^2+\left(g_n\left(Y\right)-f_n\left(X\right)\right)e_n+c_n{\mathrm{H}}_n{\Psi }_n{e}_n^2+{\displaystyle \frac{{\mathrm{M}}_n{e}_n^2}{\sqrt{e_n^2+{\varpi }^2}}}\\ & -{\displaystyle \frac{1}{{\vartheta }_n}}{\tilde{a}}_n{\mathcal{D}}^{\eta }{\widehat{a}}_n-{\displaystyle \frac{1}{{\rho }_n}}{\tilde{\mathrm{H}}}_n{\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_n-{\displaystyle \frac{1}{{\theta }_n}}{\tilde{\mathrm{M}}}_n{\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_n+{\displaystyle \frac{1}{4c_n}}+{\mathrm{M}}_n\varpi .\end{array}$$

(56)

Similarly, using the result of the $(n-1)\mathrm{th}$ step, one obtains

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_{n-1}\le & -{\displaystyle \sum _{m=1}^{n-1}{\omega }_m{e}_m^{2\beta }}-{\displaystyle \sum _{m=1}^{n-1}{\kappa }_m{e}_m^2}+{\displaystyle \sum _{m=1}^{n-1}\left(\frac{{\sigma }_{m1}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m+\frac{{\varphi }_{m1}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m+\frac{{\phi }_{m1}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m\right)}\\ & +{\displaystyle \sum _{m=1}^{n-1}\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m^{2\beta -1}+\frac{{\varphi }_{m2}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m^{2\beta -1}+\frac{{\phi }_{m2}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m^{2\beta -1}\right)}\\ & +{\displaystyle \sum _{m=1}^{n-1}\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+{\displaystyle \sum _{m=1}^{n-1}\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right)}.\end{array}$$

(57)

Noting ${\lambda }_n(t)$ is nonzero but unknown parameter, and then the adaptive fuzzy FT control strategy $u_n(t)$ and parameter adaptive laws are proposed as

$$u_n(t)={\mathcal{N}}_n({\chi }_n)\left({\omega }_n{e}_n^{2\beta -1}+{\kappa }_n{e}_n+{\widehat{a}}_n{e}_n+\left(g_n\left(Y\right)-f_n\left(X\right)\right)+c_n{\widehat{\mathrm{H}}}_n{\Psi }_n{e}_n+{\displaystyle \frac{{\widehat{\mathrm{M}}}_n{e}_n}{\sqrt{e_n^2+{\varpi }^2}}}\right),$$

(58)

$${\dot{\chi }}_n={\omega }_n{e}_n^{2\beta }+{\kappa }_n{e}_n^2+{\widehat{a}}_n{e}_n^2+\left(g_n\left(Y\right)-f_n\left(X\right)\right)e_n+c_n{\widehat{\mathrm{H}}}_n{\Psi }_n{e}_n^2+{\displaystyle \frac{{\widehat{\mathrm{M}}}_n{e}_n^2}{\sqrt{e_n^2+{\varpi }^2}}},$$

(59)

$${\mathcal{D}}^{\eta }{\widehat{a}}_n={\vartheta }_n{e}_n^2-{\sigma }_{n1}{\widehat{a}}_n-{\sigma }_{n2}{\widehat{a}}_n^{2\beta -1},$$

(60)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{H}}}_n={\rho }_n{c}_n{\Psi }_n{e}_n^2-{\varphi }_{n1}{\widehat{\mathrm{H}}}_n-{\varphi }_{n2}{\widehat{\mathrm{H}}}_n^{2\beta -1},$$

(61)

$${\mathcal{D}}^{\eta }{\widehat{\mathrm{M}}}_n={\displaystyle \frac{{\theta }_n{e}_n^2}{\sqrt{e_n^2+{\varpi }^2}}}-{\phi }_{n1}{\widehat{\mathrm{M}}}_n-{\phi }_{n2}{\widehat{\mathrm{M}}}_n^{2\beta -1},$$

(62)

where ${\omega }_n$, ${\kappa }_n$, ${\sigma }_{n1}$, ${\sigma }_{n2}$, ${\varphi }_{n1}$, ${\varphi }_{n2}$, ${\phi }_{n1}$ and ${\phi }_{n2}$ represent positive design parameters, ${\mathcal{N}}_n({\chi }_n)$ is given NGF.

Substituting (57)–(62) into (56), one has

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_n\le -& {\displaystyle \sum _{m=1}^n{\omega }_m{e}_m^{2\beta }}-{\displaystyle \sum _{m=1}^n{\kappa }_m{e}_m^2}+{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m1}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m+\frac{{\varphi }_{m1}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m+\frac{{\phi }_{m1}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m\right)}\\ & +{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{\tilde{a}}_m{\widehat{a}}_m^{2\beta -1}+\frac{{\varphi }_{m2}}{{\rho }_m}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m^{2\beta -1}+\frac{{\phi }_{m2}}{{\theta }_m}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m^{2\beta -1}\right)}\\ & +{\displaystyle \sum _{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+{\displaystyle \sum _{m=1}^n\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right).}\end{array}$$

(63)

Remark 2.

Noting (30), (44) and (58), the control laws designed in this work employ various advanced techniques, such as FLS, NGF, and the FT adaptive control method, effectively addressing challenges posed by uncertain dynamics, unknown parameters, and unknown control gains. Evidently, this work introduces a novel approach for achieving synchronization control in FOCSs. It should be noted, however, that while numerous methods exist for realizing synchronization control, the approach proposed herein represents just one among many potential solutions.

3.2. Stability Analysis

The main results of this work can be summarized in the following theorem.

Theorem 1.

Consider the FOCSs, namely the drive system (19) and the response system (20). Under Assumptions 1 and 2, with parameter adaptive laws given by (31)–(34), (45)–(48) and (59)–(62), and the adaptive fuzzy FT control strategies designed as (30), (44) and (58), it can be guaranteed that the SE $e_i$ can converge to a SNoZ within a FT, and all signals of the CLS remain bounded.

Proof. 

From (63) and using Lemma 5, we have

$${\displaystyle \frac{{\sigma }_{m1}}{{\vartheta }_m}}{\tilde{a}}_m{\widehat{a}}_m\le -{\displaystyle \frac{{\sigma }_{m1}}{2{\vartheta }_m}}{\tilde{a}}_m^2+{\displaystyle \frac{{\sigma }_{m1}}{2{\vartheta }_m}}{a}_m^2,$$

(64)

$${\displaystyle \frac{{\varphi }_{m1}}{{\rho }_m}}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m\le -{\displaystyle \frac{{\varphi }_{m1}}{2{\rho }_m}}{\tilde{\mathrm{H}}}_m^2+{\displaystyle \frac{{\varphi }_{m1}}{2{\rho }_m}}{\mathrm{H}}_m^2,$$

(65)

$${\displaystyle \frac{{\phi }_{m1}}{{\theta }_m}}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m\le -{\displaystyle \frac{{\phi }_{m1}}{2{\theta }_m}}{\tilde{\mathrm{M}}}_m^2+{\displaystyle \frac{{\phi }_{m1}}{2{\theta }_m}}{\mathrm{M}}_m^2.$$

(66)

Considering Lemma 8, we obtain

$${\displaystyle \frac{{\sigma }_{m2}}{{\vartheta }_m}}{\tilde{a}}_m{\widehat{a}}_m^{2\beta -1}\le {\displaystyle \frac{{\mathcal{l}}_1{\sigma }_{m2}}{{\vartheta }_m}}{a}_m^{2\beta }-{\displaystyle \frac{{\mathcal{l}}_2{\sigma }_{m2}}{{\vartheta }_m}}{\tilde{a}}_m^{2\beta },$$

(67)

$${\displaystyle \frac{{\varphi }_{m2}}{{\rho }_m}}{\tilde{\mathrm{H}}}_m{\widehat{\mathrm{H}}}_m^{2\beta -1}\le {\displaystyle \frac{{\mathcal{l}}_1{\varphi }_{m2}}{{\rho }_m}}{\mathrm{H}}_m^{2\beta }-{\displaystyle \frac{{\mathcal{l}}_2{\varphi }_{m2}}{{\rho }_m}}{\tilde{\mathrm{H}}}_m^{2\beta },$$

(68)

$${\displaystyle \frac{{\phi }_{m2}}{{\theta }_m}}{\tilde{\mathrm{M}}}_m{\widehat{\mathrm{M}}}_m^{2\beta -1}\le {\displaystyle \frac{{\mathcal{l}}_1{\phi }_{m2}}{{\theta }_m}}{\mathrm{M}}_m^{2\beta }-{\displaystyle \frac{{\mathcal{l}}_2{\phi }_{m2}}{{\theta }_m}}{\tilde{\mathrm{M}}}_m^{2\beta }.$$

(69)

where ${\mathcal{l}}_1=(1-2^{2\beta -2})/(2\beta )+(2^{-4{(\beta -1)}^2}+2\beta -1)/{(2\beta )}^2$ and ${\mathcal{l}}_2=(2^{2\beta -2}-2^{(2\beta )(2\beta -2)})/(2\beta )$.

Substituting (64)–(69) into (63), one obtains

$$\begin{array}{ll}{\mathcal{D}}^{\eta }{V}_n& \le -{\displaystyle \sum _{m=1}^n{\omega }_m{e}_m^{2\beta }}-{\displaystyle \sum _{m=1}^n\frac{{\mathcal{l}}_2{\sigma }_{m2}}{{\vartheta }_m}{\tilde{a}}_m^{2\beta }}-{\displaystyle \sum _{m=1}^n\frac{{\mathcal{l}}_2{\varphi }_{m2}}{{\rho }_m}{\tilde{\mathrm{H}}}_m^{2\beta }}-{\displaystyle \sum _{m=1}^n\frac{{\mathcal{l}}_2{\phi }_{m2}}{{\theta }_m}{\tilde{\mathrm{M}}}_m^{2\beta }}-{\displaystyle \sum _{m=1}^n{\kappa }_m{e}_m^2}\\ & -{\displaystyle \sum _{m=1}^n\frac{{\sigma }_{m1}}{2{\vartheta }_m}{\tilde{a}}_m^2}-{\displaystyle \sum _{m=1}^n\frac{{\varphi }_{m1}}{2{\rho }_m}{\tilde{\mathrm{H}}}_m^2}-{\displaystyle \sum _{m=1}^n\frac{{\phi }_{m1}}{2{\theta }_m}{\tilde{\mathrm{M}}}_m^2}+{\displaystyle \sum _{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}\\ & +{\displaystyle \sum _{m=1}^n\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right)}+{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m1}}{2{\vartheta }_m}{a}_m^2+\frac{{\varphi }_{m1}}{2{\rho }_m}{\mathrm{H}}_m^2+\frac{{\phi }_{m1}}{2{\theta }_m}{\mathrm{M}}_m^2\right)}\\ & +{\mathcal{l}}_1{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{a}_m^{2\beta }+\frac{{\varphi }_{m2}}{{\rho }_m}{\mathrm{H}}_m^{2\beta }+\frac{{\phi }_{m2}}{{\theta }_m}{\mathrm{M}}_m^{2\beta }\right)},\end{array}$$

(70)

According to Lemma 7, it can be obtained from (70) that

$${\mathcal{D}}^{\eta }{V}_n(t)\le -{\hslash }_1{\left(V_n(t)\right)}^{\beta }-{\hslash }_2{V}_n(t)+{\displaystyle \sum _{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+D_0,$$

(71)

where

$${\hslash }_1=\min \left\{2^{\beta }{\omega }_m,2^{\beta }{\mathcal{l}}_2{\sigma }_{m2}{\vartheta }_m^{\beta -1},2^{\beta }{\mathcal{l}}_2{\varphi }_{m2}{\rho }_m^{\beta -1},2^{\beta }{\mathcal{l}}_2{\phi }_{m2}{\theta }_m^{\beta -1},m=1,\dots ,n\right\},$$

$${\hslash }_2=\min \left\{2{\kappa }_m,{\sigma }_{m1},{\varphi }_{m1},{\phi }_{m1},m=1,\dots ,n\right\},$$

$$D_0={\displaystyle \sum _{m=1}^n\left(\frac{1}{4c_m}+{\mathrm{M}}_m\varpi \right)}+{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m1}}{2{\vartheta }_m}{a}_m^2+\frac{{\varphi }_{m1}}{2{\rho }_m}{\mathrm{H}}_m^2+\frac{{\phi }_{m1}}{2{\theta }_m}{\mathrm{M}}_m^2\right)}+{\mathcal{l}}_1{\displaystyle \sum _{m=1}^n\left(\frac{{\sigma }_{m2}}{{\vartheta }_m}{a}_m^{2\beta }+\frac{{\varphi }_{m2}}{{\rho }_m}{\mathrm{H}}_m^{2\beta }+\frac{{\phi }_{m2}}{{\theta }_m}{\mathrm{M}}_m^{2\beta }\right)}.$$

Firstly, the boundedness of ${\displaystyle {\sum }_{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}$ will be proven. Considering the definitions of $V_n(t)$ and ${\hslash }_1$, it can be easily obtained from (71) that ${\hslash }_1{\left(V_n(t)\right)}^{\beta }>0$. Then, we obtain

$${\mathcal{D}}^{\eta }{V}_n(t)\le -{\hslash }_2{V}_n(t)+{\displaystyle \sum _{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}+D_0,$$

(72)

Using Lemma 4, the boundedness of ${\displaystyle {\sum }_{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}$ can be directly obtained. Let $E_0$ be the upper bound of ${\displaystyle {\sum }_{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}$, so there exists

$$\sup \left\{{\displaystyle {\sum }_{m=1}^n\left({\lambda }_m(t){\mathcal{N}}_m({\chi }_m)+1\right){\dot{\chi }}_m}\right\}\le E_0.$$

(73)

Secondly, the boundedness of all signals of the CLS will be shown. Considering ${\hslash }_1{\left(V_n(t)\right)}^{\beta }>0$, (71) and (73), we have

$${\mathcal{D}}^{\eta }{V}_n(t)\le -{\hslash }_2{V}_n(t)+C_0,$$

(74)

where $C_0=E_0+D_0$.

According to Lemmas 1 and 3, and noting (74), for any constant $\varsigma >0$, one has

$$V_n(t)\le V_n(0)E_{\eta }(-{\hslash }_2{t}^{\eta })+{\displaystyle \frac{\varsigma C_0}{{\hslash }_2}},$$

(75)

For all $t\ge 0$ and $0<\eta <1$, it holds $\left|-{\hslash }_2{t}^{\eta }\right|\ge 0$ and $\arg (-{\hslash }_2{t}^{\eta })=-\pi$. According to Lemma 1, one obtains

$$\left|E_{\eta }(-{\hslash }_2{t}^{\eta })\right|\le {\displaystyle \frac{\varsigma }{1+{\hslash }_2{t}^{\eta }}},$$

(76)

Further, from (76), it has

$$\left|V_n(0)E_{\eta }(-{\hslash }_2{t}^{\eta })\right|\le \left|V_n(0){\displaystyle \frac{\varsigma }{1+{\hslash }_2{t}^{\eta }}}\right|\le \varsigma V_n(0),$$

(77)

Substituting (77) into (75) yields

$$V_n(t)\le \varsigma V_n(0)+{\displaystyle \frac{\varsigma C_0}{{\hslash }_2}},$$

(78)

which indicates that $V_n(t)$ is bounded. Further, the boundedness of $e_i$, ${\tilde{a}}_i$, ${\tilde{\mathrm{H}}}_i$ and ${\tilde{\mathrm{M}}}_i$ can be obtained. From ${\tilde{a}}_i=a_i-{\widehat{a}}_i$, ${\tilde{\mathrm{H}}}_i={\mathrm{H}}_i-{\widehat{\mathrm{H}}}_i$ and ${\tilde{\mathrm{M}}}_i={\mathrm{M}}_i-{\widehat{\mathrm{M}}}_i$, it can be seen that ${\widehat{a}}_i$, ${\widehat{\mathrm{H}}}_i$ and ${\widehat{\mathrm{M}}}_i$ are also bounded. Hence, the SE $e_i$ satisfies

$$\left|e_i\right|\le \sqrt{2\varsigma V_n(0)+{\displaystyle \frac{2\varsigma C_0}{{\hslash }_2}}}, i=1,\dots ,n.$$

(79)

Finally, the FT convergence will be proven. From (71) and (73), and considering the definitions of ${\hslash }_2$ and $V_n(t)$, we have

$${\mathcal{D}}^{\eta }{V}_n(t)\le -{\hslash }_1{\left(V_n(t)\right)}^{\beta }+C_0,$$

(80)

There exists a constant $0<\iota <1$ such that

$${\mathcal{D}}^{\eta }{V}_n(t)\le -\left({\hslash }_1\iota \right){\left(V_n(t)\right)}^{\beta }-{\hslash }_1(1-\iota ){\left(V_n(t)\right)}^{\beta }+C_0.$$

(81)

Noting $V_n(t)$ is a positive continuous function, we shall proceed with the analysis by considering the following two cases.

Case 1.

If $V_n(t)>{\left(C_0/({\hslash }_1(1-\iota ))\right)}^{1/\beta }$, then one has

$${\mathcal{D}}^{\eta }{V}_n(t)\le -\left({\hslash }_1\iota \right){\left(V_n(t)\right)}^{\beta },$$

(82)

Selecting $\beta =2\upsilon -1$ and $\alpha =1+\eta$, the following inequality is obtained by using Lemma 2, that is

$$V_n(t){\mathcal{D}}^{\eta }{V}_n(t)={\displaystyle \frac{\Gamma (2)}{\Gamma (2+\eta )}}{\mathcal{D}}^{\eta }{\left(V_n(t)\right)}^{1+\eta }\le -\left({\hslash }_1\iota \right){\left(V_n(t)\right)}^{2\upsilon },$$

(83)

Let $\mathcal{V}(t)={\left(V_n(t)\right)}^{1+\eta }$, then we have ${\left(\mathcal{V}(t)\right)}^{(2\upsilon /(1+\eta ))}={\left(V_n(t)\right)}^{2\upsilon }$. Considering Lemma 2, and selecting $\alpha =\eta -\left(2\upsilon /(1+\eta )\right)$, then (83) leads to

$${\mathcal{D}}^{\eta }{\left(\mathcal{V}(t)\right)}^{\eta -\left(2\upsilon /(1+\eta )\right)}\le -{\displaystyle \frac{\left({\hslash }_1\iota \right)\Gamma (2+\eta )\Gamma \left(1+\eta -\left(2\upsilon /(1+\eta )\right)\right)}{\Gamma (2)\Gamma \left(1-\left(2\upsilon /(1+\eta )\right)\right)}},$$

(84)

Taking the fractional integral of (84) from 0 to $t$, one has

$${\left(\mathcal{V}(t)\right)}^{\eta -\left(2\upsilon /(1+\eta )\right)}-{\left(\mathcal{V}(0)\right)}^{\eta -\left(2\upsilon /(1+\eta )\right)}\le -\left[\frac{\left({\hslash }_1\iota \right)\Gamma (2+\eta )\Gamma \left(1+\eta -\left(2\upsilon /(1+\eta )\right)\right)}{\eta \Gamma (2)\Gamma \left(1-\left(2\upsilon /(1+\eta )\right)\right)\Gamma (\eta )}\right]t^{\eta },$$

(85)

Assuming $V_n(t)\equiv 0$ for any $t\ge T_f$, then the FT $T_f$ is calculated as

$$T_f={\left[\frac{{\eta \left(V_n(0)\right)}^{\eta (1+\eta )-2\upsilon }\Gamma (2)\Gamma \left(1-\left(2\upsilon /(1+\eta )\right)\right)\Gamma (\eta )}{\left({\hslash }_1\iota \right)\Gamma (2+\eta )\Gamma \left(1+\eta -\left(2\upsilon /(1+\eta )\right)\right)}\right]}^{1/\eta }.$$

(86)

Case 2.

If $V_n(t)\le {\left(C_0/({\hslash }_1(1-\iota ))\right)}^{1/\beta }$, given that the results of Case 1, it can be found that $V_n(t)$ will not exceed $V_n(t)\le {\left(C_0/({\hslash }_1(1-\iota ))\right)}^{1/\beta }$.

Based on the discussion of Cases 1 and 2, it is seen that $e_i$, ${\tilde{a}}_i$, ${\tilde{\mathrm{H}}}_i$ and ${\tilde{\mathrm{M}}}_i$ can converge to the SNoZ and remain there after the FT $T_f$. Hence, the proof is completed. □

Remark 3.

Noting (79), the SE $e_i$ can be made arbitrarily small by increasing the value of ${\hslash }_2$ or decreasing the values of $C_0$ and $\varsigma$. Furthermore, the regulation of ${\hslash }_2$ and $C_0$ can be achieved by adjusting ${\kappa }_m$, $c_m$, ${\vartheta }_m$, ${\rho }_m$, ${\theta }_m$, ${\sigma }_{m1}$, ${\sigma }_{m2}$, ${\varphi }_{m1}$, ${\varphi }_{m2}$, ${\phi }_{m1}$ and ${\phi }_{m2}$ ($m=1,\dots ,n$). However, the change in these parameters will further affect the amplitude of the control law $u_i(t)$. Therefore, a reasonable trade-off should be made for the SE $e_i$ and control law $u_i(t)$ in the selection of these parameters.

4. Simulation Analysis

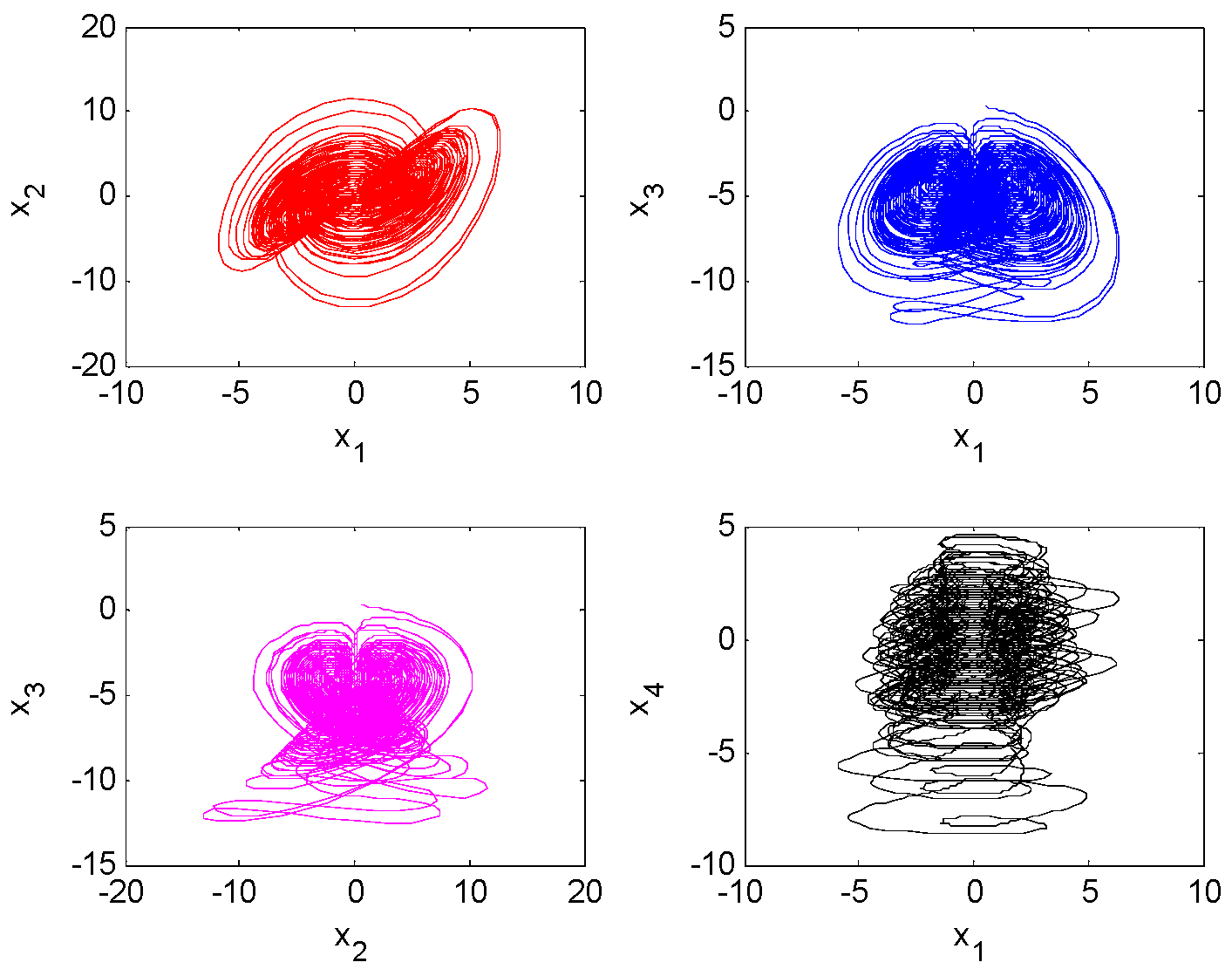
4.1. FTSC of FO Liu Hyperchaotic System

In this subsection, the FO Liu hyperchaotic system and the different structural FO Liu hyperchaotic system are considered as the drive system and response system [53], respectively.

The drive system (FO Liu hyperchaotic system) is described as

$$\left\{\begin{array}{l}{\mathcal{D}}^{\eta }{x}_1=-10x_1+10x_2+x_4+F_1\left(X,t\right)+{\Delta }_{d1}(t),\\ {\mathcal{D}}^{\eta }{x}_2=40x_1+10x_1{x}_3-x_4+F_2\left(X,t\right)+{\Delta }_{d2}(t),\\ {\mathcal{D}}^{\eta }{x}_3=-4x_1^2-2.5x_3-x_4+F_3\left(X,t\right)+{\Delta }_{d3}(t),\\ {\mathcal{D}}^{\eta }{x}_4=2.5x_1+F_4\left(X,t\right)+{\Delta }_{d4}(t).\end{array}\right.$$

(87)

The response system (different structural FO Liu hyperchaotic system) is described as

$$\left\{\begin{array}{l}{\mathcal{D}}^{\eta }{y}_1=-10y_1+10y_2+G_1\left(Y,t\right)+{\Delta }_{r1}(t)+\mathcal{U}\left(u_1(t)\right),\\ {\mathcal{D}}^{\eta }{y}_2=40y_1-10y_1{y}_3+y_4+G_2\left(Y,t\right)+{\Delta }_{r2}(t)+\mathcal{U}\left(u_2(t)\right),\\ {\mathcal{D}}^{\eta }{y}_3=4y_1^2-2.5y_3+y_4+G_3\left(Y,t\right)+{\Delta }_{r3}(t)+\mathcal{U}\left(u_3(t)\right),\\ {\mathcal{D}}^{\eta }{y}_4=-2.5y_2+G_4\left(Y,t\right)+{\Delta }_{r4}(t)+\mathcal{U}\left(u_4(t)\right).\end{array}\right.$$

(88)

For the systems (87) and (88), the uncertain dynamics and external disturbances are given as

$$\left\{\begin{array}{l}{F}_1\left(X,t\right)=0.3\cos (6t)x_1,{\Delta }_{d1}(t)=-0.1\sin (t),\\ F_2\left(X,t\right)=-0.2\cos (2t)x_2,{\Delta }_{d2}(t)=0.3\sin (3t),\\ F_3\left(X,t\right)=0.3\sin (3t)x_3,{\Delta }_{d3}(t)=0.1\cos (5t),\\ F_4\left(X,t\right)=0.1\sin (5t)x_4,{\Delta }_{d4}(t)=-0.2\cos (t),\\ G_1\left(Y,t\right)=-0.3\sin (4t)y_1,{\Delta }_{r1}(t)=0.2\sin (7t),\\ G_2\left(Y,t\right)=0.3\cos (6t)y_2,{\Delta }_{r2}(t)=0.1\cos (3t),\\ G_3\left(Y,t\right)=0.2\sin (t)y_3,{\Delta }_{r3}(t)=-0.2\sin (5t),\\ G_4\left(Y,t\right)=-0.2\sin (3t)y_4,{\Delta }_{r4}(t)=-0.1\cos (2t).\end{array}\right.$$

(89)

When the initial states of drive system and response system are set as $x_1(0)=0.6$, $x_2(0)=0.7$, $x_3(0)=0.3$, $x_4(0)=0.4$, $y_1(0)=0.5$, $y_2(0)=0.5$, $y_3(0)=0.2$ and $y_4(0)=0.5$, the FO for the two systems is chosen as $\eta =0.82$, the drive system (87) and response system (88) will show chaotic behavior, which are shown in Figure 1 and Figure 2.

Using the proposed adaptive fuzzy FT control strategy $u_i(t)$($i=1,2,3,4$), the conventional proportional-integral-derivative (PID) controller is considered for comparative study. In the simulation, the control strategy proposed in this work is represented by Scheme 1, and the PID controller is represented by Scheme 2. The PID controller is designed as

$$u_i(t)=-k_{Pi}{e}_i-k_{Ii}{\displaystyle {\int }_0^t{e}_i(\tau )}d\tau -k_{Di}{\displaystyle \frac{d{e}_i}{dt}}.$$

(90)

where $k_{Pi}$, $k_{Ii}$ and $k_{Di}$ are positive constants.

To tackle unknown uncertain dynamic $\left(G_i\left(Y,t\right)-F_i\left(X,t\right)\right)$($i=1,2,3,4$), the FLS is applied to approximate it, and the fuzzy membership functions of FLS are designed as

$${\mu }_{{\mathcal{F}}_i^1}(z_i)=\exp \left(-{\displaystyle \frac{{\left(z_i+\pi /6\right)}^2}{\pi /24}}\right), {\mu }_{{\mathcal{F}}_i^2}(z_i)=\exp \left(-{\displaystyle \frac{{\left(z_i+\pi /12\right)}^2}{\pi /24}}\right),$$

$${\mu }_{{\mathcal{F}}_i^3}(z_i)=\exp \left(-{\displaystyle \frac{{\left(z_i\right)}^2}{\pi /24}}\right)$$

where $z_i$ stands for input variable.

The parameters for unknown nonlinearities shown in (21) are given as ${\lambda }_1(t)=0.5+0.3\sin (t)$, ${\lambda }_2(t)=0.6+0.2\sin (t)$, ${\lambda }_3(t)=0.8+0.1\sin (t)$, ${\lambda }_4(t)=0.7+0.3\sin (t)$, $o_1(t)=0.4\sin (t)$, $o_2(t)=0.3\sin (t)$, $o_3(t)=0.5\sin (t)$ and $o_4(t)=0.2\sin (t)$.

The design parameters are set as $\beta =0.95$, $\varpi =1.0$, ${\omega }_i=2.0$, $k_i=400$, $c_i=80$, ${\vartheta }_i=3.0$, ${\sigma }_{i1}=6.5$, ${\sigma }_{i2}=3.5$, ${\rho }_i=1.5$, ${\varphi }_{i1}=5.0$, ${\varphi }_{i2}=2.5$, ${\theta }_i=4.5$, ${\phi }_{i1}=2.5$, ${\phi }_{i2}=1.5$, $k_{Pi}=1100$, $k_{Ii}=5.0$, $k_{Di}=0.5$ and $i=1,2,3,4$.

The initial conditions of parameter adaptive laws are considered as ${\chi }_i(0)=0.01$, ${\widehat{a}}_i(0)=0.01$, ${\widehat{\mathrm{H}}}_i(0)=0.01$ and ${\widehat{\mathrm{M}}}_i(0)=0.01$, where $i=1,2,3,4$. Simulation results are given in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.

As shown in Figure 3, it is easily seen that the state $y_i$ of the response system can track the state $x_i$ of the drive system within a FT under both control strategies. Meanwhile, the SE $e_i$ under the two control strategies is given in Figure 4. Clearly, the SE $e_i$ can converge to a SNoZ within a FT. Compared with the PID controller, the SE under the proposed control strategy exhibits smaller overshoot and shorter settling time. The results of Figure 3 and Figure 4 imply that the developed control scheme provides better synchronization performance than the PID controller, which further verifies its validity.

The curves of the two control strategies $u_i(t)$ are displayed in Figure 5. Although the curves of the two control laws are not smooth, both of them can be maintained in a very small region. Additionally, compared to the PID controller, the proposed method exhibits a larger overshoot during the initial transient stage but achieves significantly faster convergence within a bounded region.

Figure 6, Figure 7, Figure 8 and Figure 9 depict the adaptive parameters ${\widehat{a}}_i$, ${\widehat{\mathrm{H}}}_i$ and ${\widehat{\mathrm{M}}}_i$, adaptive law ${\chi }_i$, and NGF ${\mathcal{N}}_i({\chi }_i)$. It can be seen that these signals can converge to a SNoZ within a FT under the control designed strategy. Combined with the results in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, this fully demonstrates the correctness of the theoretical analysis.

4.2. FTSC Between FO Chen System and FO Lorenz System

In this subsection, the following simulation analysis will consider the FO Chen system and FO Lorenz system as the drive system and response system [54], respectively.

The drive system (FO Chen system) is described as

$$\left\{\begin{array}{l}{\mathcal{D}}^{\eta }{x}_1=-35x_1+35x_2+x_4+F_1\left(X,t\right)+{\Delta }_{d1}(t),\\ {\mathcal{D}}^{\eta }{x}_2=7x_1+12x_2-x_1{x}_3+F_2\left(X,t\right)+{\Delta }_{d2}(t),\\ {\mathcal{D}}^{\eta }{x}_3=x_1{x}_2-3x_3+F_3\left(X,t\right)+{\Delta }_{d3}(t),\\ {\mathcal{D}}^{\eta }{x}_4=x_2{x}_3+0.5x_4+F_4\left(X,t\right)+{\Delta }_{d4}(t).\end{array}\right.$$

(91)

The response system (FO Lorenz system) is described as

$$\left\{\begin{array}{l}{\mathcal{D}}^{\eta }{y}_1=-10y_1+10y_2+y_4+G_1\left(Y,t\right)+{\Delta }_{r1}(t)+\mathcal{U}\left(u_1(t)\right),\\ {\mathcal{D}}^{\eta }{y}_2=27y_1-y_2-y_1{y}_3+G_2\left(Y,t\right)+{\Delta }_{r2}(t)+\mathcal{U}\left(u_2(t)\right),\\ {\mathcal{D}}^{\eta }{y}_3=y_1{y}_2-8/3y_3+G_3\left(Y,t\right)+{\Delta }_{r3}(t)+\mathcal{U}\left(u_3(t)\right),\\ {\mathcal{D}}^{\eta }{y}_4=-y_2{y}_3-0.5y_4+G_4\left(Y,t\right)+{\Delta }_{r4}(t)+\mathcal{U}\left(u_4(t)\right).\end{array}\right.$$

(92)

For the systems (91) and (92), the uncertain dynamics and external disturbances are given as

$$\left\{\begin{array}{l}{F}_1\left(X,t\right)=0.2\cos (6t)x_1,{\Delta }_{d1}(t)=-0.2\sin (t),\\ F_2\left(X,t\right)=-0.3\cos (2t)x_2,{\Delta }_{d2}(t)=0.1\sin (3t),\\ F_3\left(X,t\right)=0.2\sin (3t)x_3,{\Delta }_{d3}(t)=0.2\cos (5t),\\ F_4\left(X,t\right)=0.3\sin (5t)x_4,{\Delta }_{d4}(t)=-0.1\cos (t),\\ G_1\left(Y,t\right)=-0.2\sin (4t)y_1,{\Delta }_{r1}(t)=0.2\sin (7t),\\ G_2\left(Y,t\right)=0.1\cos (4t)y_2,{\Delta }_{r2}(t)=0.3\cos (3t),\\ G_3\left(Y,t\right)=0.2\sin (4t)y_3,{\Delta }_{r3}(t)=-0.3\sin (5t),\\ G_4\left(Y,t\right)=-0.3\sin (t)y_4,{\Delta }_{r4}(t)=-0.2\cos (2t).\end{array}\right.$$

(93)

When the initial states of drive system and response system are set as $x_1(0)=2$, $x_2(0)=-2$, $x_3(0)=4$, $x_4(0)=1$, $y_1(0)=3$, $y_2(0)=-4$, $y_3(0)=2$ and $y_4(0)=2$, the FO for the two systems is chosen as $\eta =0.98$, the drive system (91) and response system (92) will show chaotic behavior, which are shown in Figure 10 and Figure 11.

Similarly, the PID controller is introduced to compare with the proposed control strategy, which is shown in (90). In the simulation, the control strategy proposed in this work is represented by Scheme 1, and the PID controller is represented by Scheme 2.

The design parameters are set as $\beta =0.95$, $\varpi =1.0$, ${\omega }_i=1.5$, $k_i=300$, $c_i=70$, ${\vartheta }_i=3.5$, ${\sigma }_{i1}=7.5$, ${\sigma }_{i2}=2.5$, ${\rho }_i=2.5$, ${\varphi }_{i1}=5.5$, ${\varphi }_{i2}=3.5$, ${\theta }_i=5.5$, ${\phi }_{i1}=3.0$, ${\phi }_{i2}=2.0$, $k_{Pi}=1000$, $k_{Ii}=20$, $k_{Di}=1.0$ and $i=1,2,3,4$.

Additionally, the membership functions of FLS, the parameters for the unknown nonlinearities shown in (21), and the initial values of adaptive control laws are kept the same as in Section 4.1. Simulation results are given in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.

The states $x_i$ and $y_i$ under both control strategies are given in Figure 12. Under the two control strategies, the states of the response system and drive system can be synchronized within a FT. Furthermore, the SE $e_i$ under the two control strategies is shown in Figure 13. Compared with the PID controller, the SE under the proposed control strategy exhibits shorter settling time and smaller convergence region. Obviously, the proposed strategy exhibits a much smaller steady-state SE than the PID controller.

The curves of the two control strategies $u_i(t)$ are provided in Figure 14. Similarly to Example 1, although the curves of the two control strategies are not smooth, both can remain within a very small region in the FT. In addition, the proposed method exhibits a larger overshoot during the initial transient stage but achieves significantly faster convergence within a bounded region.

Figure 15, Figure 16, Figure 17 and Figure 18 depict the adaptive parameters ${\widehat{a}}_i$, ${\widehat{\mathrm{H}}}_i$ and ${\widehat{\mathrm{M}}}_i$, adaptive law ${\chi }_i$, and Nussbaum function ${\mathcal{N}}_i({\chi }_i)$. It can be found that these signals can converge to a SNoZ within a FT under the designed control strategy. As evidenced by the bounded signals in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, the proposed control strategy demonstrates its effectiveness in ensuring system stability.

4.3. Comparative Analysis

In this subsection, a comparative analysis with another FT control method is provided to illustrate the availability of the designed control scheme. To highlight the comparative results, the FT control strategy presented in [55] is considered, where the control law designed in this work is referred to as Scheme 1, and the control strategy proposed in [55] is referred to as Scheme 3. To make the comparative results more convincing, the positive odd integer power in [55] is set to 1, and the settings of neural network parameters remain unchanged.

The other parameters of Scheme 3 are selected as: ${\gamma }_1=3.0$, ${\gamma }_2=2.0$, ${\gamma }_3=1.0$, ${\gamma }_4=0.5$, ${\xi }_1={\xi }_2={\xi }_3={\xi }_4=1.0$, ${\lambda }_1=4.5$, ${\lambda }_2=3.0$, ${\lambda }_3=3.5$, ${\lambda }_4=2.5$, $a_1=2.0$, $a_2=1.5$, $a_3=0.5$, $a_4=1.5$, ${\vartheta }_1={\vartheta }_2={\vartheta }_3={\vartheta }_4=1.0$, ${\chi }_1=8.0$, ${\chi }_2=3.5$, ${\chi }_3=1.5$, ${\chi }_4=2.5$, ${\kappa }_1={\kappa }_2={\kappa }_3={\kappa }_4=2.0$, $c_1=35$, $c_2=8.0$, $c_3=2.5$, $c_4=1.5$, $k_1=30$, $k_2=15$, $k_3=45$, $k_4=25$, $\eta =1.0$ and $\rho =0.95$. The initial states of all adaptive laws are set as 0.01.

Considering the drive system and response system provided in Section 4.1, the comparative results are shown in Figure 19, Figure 20 and Figure 21.

Considering the drive system and response system provided in Section 4.2, the comparative results are shown in Figure 22, Figure 23 and Figure 24.

Based on the application of the two control strategies, the comparative results of system states are shown in Figure 19 and Figure 22. Obviously, under both control strategies, the system states achieve synchronization within a FT. However, compared with the control strategy proposed in [55], the control strategy presented in this work achieves synchronization in a shorter time. Furthermore, the comparative results of SE under the two control strategies are depicted in Figure 20 and Figure 23. Although the SEs exhibit significant overshoot during the initial simulation stage, they are able to converge to a SNoZ within a FT. Notably, the SE curves under the proposed control strategy appear smoother. Figure 21 and Figure 24 display the curves of the two control strategies. Similarly, the control strategy curves exhibit large amplitudes in the initial simulation stage, then gradually decrease and eventually stabilize within a small region.

5. Conclusions

In this work, the FT synchronization issue for the FOCSs with uncertain dynamics, unknown parameters, and input nonlinearities is studied. Based on the FLSs, NGF method, adaptive FT backstepping technique, and FO Lyapunov method, the adaptive fuzzy FTSC strategy is proposed to guarantee that the SE can converge to a SNoZ within a FT, while ensuring the boundedness of all signals of the CLS. The validity of the developed control method is validated via three simulation cases. Furthermore, comparative results with the conventional PID controller and another FT control method highlight the superiority of the proposed approach.

However, it should be noted that the control laws presented in this work are only applicable to the systems without time delays and with fully measurable states. When nonlinear systems involve unknown time delays and immeasurable states, the control laws proposed in this work would become ineffective. Therefore, one of the future research directions is to design feasible control laws capable of realizing the FTSC of FOCSs with unknown time delays and partially immeasurable states.