A Fractional-Order SSIM-Based Gaussian Loss with Long-Range Memory for Dense VSLAM

Abstract

In dense visual simultaneous localization and mapping VSLAM (VSLAM), a fundamental challenge lies in the inability of existing loss functions to dynamically balance luminance, contrast, and structural fidelity under photometric variations, while their underlying mechanisms, particularly the conventional Gaussian kernel in SSIM, suffer from limited receptive fields due to rapid exponential decay, preventing the capture of long-range dependencies essential for global consistency. To address this, we propose a fractional Gaussian field (FGF) that synergizes Caputo derivatives with Gaussian weighting, creating a hybrid kernel that couples power-law decay for long-range memory with local smoothness. This foundational kernel serves as the core component of FGF-SSIM, a novel loss function that adaptively recalibrates luminance, contrast, and structure using fractional-order statistics. The proposed FGF-SSIM is further integrated into a complete 3D Gaussian Splatting (3DGS)-based SLAM system, named FGF-SLAM, where it is employed across both tracking and mapping modules to enhance performance. Extensive evaluations demonstrate state-of-the-art performance across multiple benchmarks. Comprehensive analysis confirms the superior long-range dependency of the fractional kernel, dedicated illumination robustness tests validate the enhanced invariance of FGF-SSIM, and quantitative results on TUM and Replica datasets show significant improvements in reconstruction quality and trajectory estimation. Ablation studies further substantiate the contribution of each proposed component.

1. Introduction

Visual simultaneous localization and mapping (VSLAM) constitutes a computational framework that performs simultaneous position estimation and environment mapping by primarily utilizing visual sensors to acquire photometric data and scene geometry [1]. Owing to its cost-effectiveness and compact form factor, VSLAM has emerged as a critical enabling technology for autonomous positioning and navigation systems [2]. The choice of map representation remains pivotal in VSLAM, yet prevailing loss functions present a fundamental bottleneck. Their static, local computations are unable to enforce global consistency and lack the adaptability to handle varying illumination.

In contrast to established scene representations (e.g., 2.5D elevation maps [3], Signed Distance Fields (SDF) [4], and Neural Radiance Fields (NeRF) [5]), 3D Gaussian Splatting (3DGS) [6] has recently demonstrated compelling performance in dense scene reconstruction. While adopting an explicit representation comprised of millions of 3D Gaussians, 3DGS achieves real-time differentiable rendering via splat-based rasterization, yet its optimization relies neither on direct geometric constraints nor on density field regularization as in prior methods. Each primitive is defined by its geometric parameters (e.g., 3D position, scale, and rotation) as well as view-dependent appearance attributes (e.g., color and opacity) [7]. The loss function of 3DGS is formulated as the color and depth information between the synthesized image and the actual observation, offering a straightforward and intuitive objective. Crucially, because the contribution of each Gaussian to the final rendered image is differentiable and locally confined, gradients can be efficiently propagated back to the corresponding geometric and appearance parameters [8]. This mechanism ensures a well-balanced optimization, simultaneously enhancing both the photometric accuracy of the rendered novel views and the geometric fidelity of the underlying 3D structure. Regarding the integration of loss functions with 3D Gaussians, numerous researchers have explored this area, yet comprehensive investigations remain limited. Existing efforts primarily revolve around variants of the L1 loss and the Structural Similarity Index (SSIM). The original 3DGS employs a composite “DSSIM + L1” loss function for rendering optimization, while derivative works such as SplaTAM [9] and RGBD GS-ICP SLAM [10] utilize a similar “SSIM + L1” formulation. Evidently, most methodologies adhere to the loss function framework established in the foundational 3DGS work. However, DSSIM was originally designed for meteorological floating-point data analysis, not robotic vision applications [11]. This metric neglects critical photometric differences inherent in SLAM environments, particularly dynamic illumination variations. Conversely, some studies omit SSIM for geometric consistency and pose estimation considerations: GS-SLAM [12] relies solely on L1 minimization for joint photometric-geometric optimization, whereas MonoGS [13] combines L1-based photometric loss with geometric error metrics and uniformity regularization. However, the window-based computation of SSIM renders it ineffective for global optimization, and relying solely on the L1 loss is inadequate for high-fidelity scene reconstruction. Meanwhile, fractional calculus aligns more closely with the physical essence of light transmission, facilitating adaptive regularization of Gaussian primitives and continuous-scale control of input imagery. However, its application in the construction and regulation of 3D Gaussian representations currently requires further development.

The mathematical modeling of anomalous diffusion and long-range dependence has been significantly advanced through the framework of fractional calculus. A unifying perspective is offered by combining spatial and temporal coordinate transformations within this framework. For instance, Soliman et al. [14] employ the improved modified extended tanh method (IMETM) to derive exact analytical solutions for a higher-order nonlinear Schrödinger (HNLS) equation incorporating fractional derivatives in both time and space. Similarly, Shao et al. [15] investigate approximate solutions for a two-dimensional space/multi-time fractional Bloch–Torrey model involving the Riesz fractional operator. Beyond these, fractional calculus has been extensively applied to telegraph equations [16], the dissipative Burgers equation [17], and the Korteweg–de Vries equation [18]. Despite these broad developments, the application of fractional calculus in image processing remains relatively underexplored. In this domain, Caputo fractional derivatives have shown particular promise. Building on the well-established Grünwald–Letnikov and Riemann–Liouville definitions, Pu et al. [19] introduced six fractional differential masks and analyzed their efficacy in multiscale texture enhancement. Further extending this line of work, Pu et al. [20] proposed a fractional-order variational framework for Retinex, formulated via fractional partial differential equations (FPDEs) to achieve multi-scale nonlocal contrast enhancement while preserving texture. Additional studies [21] have confirmed that fractional-order differential operators outperform integer-order models in enhancing high-frequency edge information while retaining low-frequency contour content in smooth regions [22]. In this context, fractional calculus not only more accurately captures the physical behavior of light transport but also provides a principled methodology for modeling multi-scale and long-memory visual phenomena [23]. Nevertheless, the potential of fractional operators in constructing and regulating advanced 3D Gaussian representations remains largely untapped, indicating a compelling direction for future methodological innovation.

To address the challenge of uncertainty propagation in visual loss functions induced by photometric variations, we introduce a fractional Gaussian field (FGF) grounded in fractal calculus and propose a novel FGF-SSIM loss function. The core innovation lies in replacing the conventional Gaussian kernel in SSIM with a fractional-order variant that combines power-law decay with Gaussian attenuation, enabling long-range dependency modeling while preserving local smoothness. Specifically, FGF-SSIM adaptively decomposes and recalibrates luminance, contrast, and structure components through fractional-order local statistics, achieving superior illumination robustness. Furthermore, we develop FGF-SLAM, a complete 3DGS-based SLAM framework that integrates FGF-SSIM into both tracking and mapping pipelines, demonstrating that the proposed loss improves both scene reconstruction quality and trajectory estimation accuracy. The main contributions of this work are as follows:

• To overcome the locality limitation of conventional operators that prevents them from capturing long-range dependencies essential for global consistency, we introduce a novel fractional Gaussian field formulation that integrates Caputo derivatives with Gaussian weighting kernels. This approach addresses the fundamental constraint of local receptive fields in existing methods by establishing a mathematical framework for long-range dependency modeling. The resulting kernel exhibits mathematically provable long-range memory properties while effectively mitigating boundary effects and relaxing isotropic constraints that arise in discrete image processing.
• To address the static nature of existing loss functions that renders them incapable of adaptively re-calibrating the balance between luminance, contrast, and structural fidelity under varying illumination conditions, we propose FGF-SSIM, a fractional-order loss function that dynamically recalibrates these three fundamental components. Building upon the SSIM framework, FGF-SSIM explicitly decouples and adaptively models luminance, contrast, and structure through fractional-order statistics, achieving superior performance in challenging illumination conditions while preserving structural fidelity for high-quality 3D scene reconstruction.
• To comprehensively validate the proposed framework and address the lack of global scene memory in conventional SLAM systems, we establish an extensive evaluation protocol that assesses both theoretical properties and practical effectiveness. We demonstrate the superiority of FGF-SSIM through rigorous comparisons under photometric variations and noise corruption, with detailed illumination invariance analysis highlighting its long-range dependency advantages. Furthermore, we integrate the loss into a complete 3DGS-based SLAM system, showing significant improvements in scene reconstruction quality, novel view synthesis fidelity, and trajectory estimation accuracy, particularly in recovering fine texture details and maintaining structural coherence under real-world operating conditions.

2. Preliminary

2.1. SSIM Loss Function

The design of loss functions is fundamentally constrained by the structural properties of the underlying scene representation. For example, the inherently unordered and permutation-invariant structure of point clouds necessitates the use of distribution-based metrics such as Chamfer distance, rather than direct point-to-point correspondences, in the loss formulation [24]. In VSLAM, modern scene representation methods effectively exploit the spatiotemporal coherence of sequential visual data through GPU-parallelized optimization frameworks. A widely adopted approach involves defining the loss function in image space, typically based on photometric or geometric discrepancies between observed and synthesized views. To prevent cancellation effects between positive and negative differences, the absolute value or square of pixel differences is typically adopted. Summing the absolute differences yields the L1 loss function [25], which is computationally simpler and exhibits enhanced robustness to outliers in regression tasks. Conversely, summing the squared differences produces the L2 loss function [26]. In early neural network research, L2 loss was frequently selected as the default due to its positive definiteness, chi-square properties, and encapsulation in standard frameworks (e.g., Caffe). However, both L1 and L2 losses assume ideal Gaussian white noise characteristics and presume statistical independence between noise and local image features, neglecting human visual system (HVS) perception. To address this limitation, SSIM-based loss functions [27] incorporate HVS characteristics by evaluating luminance, contrast, and structural similarities. Unlike pixel-wise methods, SSIM operates via sliding windows for computational efficiency. The Joint Video Team (JVT) formally integrated SSIM into the H.264/MPEG-4 Advanced Video Coding (AVC) standard in 2003, which is extensively deployed in video surveillance and digital broadcasting.

SSIM evaluates the similarity between two images x and y by comparing three components: luminance, contrast, and structure. The comparison is performed within local windows and the results are aggregated across the image. The functional expression of SSIM is:

$$S(x,y)=f(l(x,y),c(x,y),s(x,y))={\left(l(x,y)\right)}^{ϵ}·{\left(c(x,y)\right)}^{\epsilon }·{\left(s(x,y)\right)}^{\zeta },$$

(1)

$$l(x,y)={\displaystyle \frac{2{\mu }_x{\mu }_y+C_1}{{\mu }_x^2+{\mu }_y^2+C_1}},c(x,y)={\displaystyle \frac{2{\sigma }_x{\sigma }_y+C_2}{{\sigma }_x^2+{\sigma }_y^2+C_2}},s(x,y)={\displaystyle \frac{{\sigma }_{xy}+C_3}{{\sigma }_x{\sigma }_y+C_3}}.$$

(2)

where $l(x,y)$, $c(x,y)$, $s(x,y)$ represent the luminance, contrast, and structure comparison functions respectively; $ϵ$, $\epsilon$, $\zeta$ denote the proportional weights of each component; ${\mu }_x$ and ${\mu }_y$ are the local means of x and y; ${\sigma }_x$ and ${\sigma }_y$ represent the local standard deviations; and ${\sigma }_{xy}$ is the local covariance between x and y.

To ensure numerical stability when the comparison functions approach zero, constants ($C_1$, $C_2$, $C_3$) are added to both numerator and denominator. These constants are defined as $C_1={\left(k_{1}L\right)}^2$, $C_2={\left(k_{2}L\right)}^2$, where $k_1$ and $k_2$ are constants much smaller than 1, and L is the dynamic range of the image pixel values. For practical computation, the parameters are typically set to $ϵ=\epsilon =\zeta =1$, $C_3=0.5C_2$, $k_1=0.01$, $k_2=0.03$. Therefore, the simplified SSIM expression becomes:

$$S(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}}$$

(3)

For pixel-level computation, let p represent the pixel index within a local region P. Define $l\left(p\right)={\displaystyle \frac{2{\mu }_x{\mu }_y+C_1}{{\mu }_x^2+{\mu }_y^2+C_1}}$ and $cs\left(p\right)={\displaystyle \frac{2{\sigma }_{xy}+C_2}{{\sigma }_x^2+{\sigma }_y^2+C_2}}$. The pixel-wise SSIM can then be expressed as:

$$SSIM\left(p\right)=l\left(p\right)·cs\left(p\right)$$

(4)

In subsequent research, the MS-SSIM loss function [28] incorporates a multi-scale principle, effectively integrating resolution considerations into the loss function construction. Both G-SSIM [29] and MS-G-SSIM [30] enhance the robustness of the loss function for image processing under blur and noise degradation. IW-SSIM [31] focuses on the quality fusion stage within the full-reference image quality assessment (IQA) framework, proposing a multi-scale information-content-weighted quality evaluation method. However, existing improvements predominantly target structural distortions such as blurring and motion artifacts, while three critical issues remain understudied [32]. Firstly, the existing loss function for scene reconstruction using illumination-sensitive imagery remains insufficiently explored theoretically. Secondly, the existing loss function formulations are often highly scenario-specific, with limited research devoted to the development of generalizable formulations. Thirdly, the existing loss function fails to adequately account for long-range dependencies within the image and lacks a mechanistic analysis of its operation.

2.2. Fractional-Order Calculus

Let the function $f\left(t\right)$ be continuously differentiable on the interval $[a,t]$, then its $\alpha$-order Caputo definition can be presented as:

$${}^{C}D_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(n-\alpha )}}{\int }_a^t{\displaystyle \frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}}d\tau$$

(5)

where ${}^{C}D_t^{\alpha }$ represents the fractional operator in the Caputo definition, $n=⌈\alpha ⌉$, and $\mathrm{\Gamma }(·)$ is the gamma function. In image processing, we usually deal with spatial domains, and $\alpha \in (0,1)$, so n = 1.

The fractional derivative of the image at pixel p (with an order of $\alpha$) is denoted as:

$$D^{\alpha } f(p)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_0^p{\displaystyle \frac{f^{\prime }\left(t\right)}{{(p-t)}^{\alpha }}}dt$$

(6)

We adopt the Formula (6) to simplify the definition of Caputo fractional derivatives to better adapt to handling discrete two-dimensional pixels. Meanwhile, we did not directly use the function value difference, because in the local window P of image processing, the Caputo derivative does not require the pixel values outside the window, and the image boundary conditions can be handled more naturally through the integer order derivative.

2.3. Processing of Discrete Image Data

In the local window of image processing, we usually assume that the center of the window is the focus of attention, while the influence of the boundary is relatively small. When defining local statistics, to facilitate calculation, we use Gaussian weight kernels. We proposed expressing the Caputo derivative as an integer-order derivative convolution with a kernel function, and made this form compatible with the convolution operation of the Gaussian kernel, facilitating the unification of the framework:

$$D^{\alpha }x\left(p\right)=\sum _{k\in \mathrm{\Omega }}{\omega }_k^{\left(\alpha \right)}{G}_{\sigma }\left(k\right)·x(p-k)$$

(7)

where $\mathrm{\Omega }$ is the neighborhood of the convolution kernel, ${\omega }_k^{\left(\alpha \right)}={(-1)}^k\left(\genfrac{}{}{0pt}{}{\alpha }{k}\right)$ is the coefficient of the Grunwald-Letnikov fractional derivative. $G_{\sigma }\left(k\right)$ is the Gaussian weight kernel, and that is $G_{\sigma }\left(k\right)=exp\left(-{\displaystyle \frac{{\parallel k\parallel }^2}{2{\sigma }^2}}\right)$. It is worth noting that here we actually approximate the Caputo derivative on a discrete grid and add Gaussian weights to achieve localization.

However, in the local window P, directly using Caputo’s discrete approximation requires pixel values outside the window (historical or future values). At the image boundaries, these values do not exist, resulting in severe boundary effects. Meanwhile, image processing usually requires isotropic operations. The standard fractional difference is directionally dependent (for example, typically defined in the x or y direction), which does not meet the requirement of rotational invariance. Therefore, a novel form of Caputo derivative is needed to process discrete image data.

3. Methods

3.1. Fractional Gaussian Field

The SSIM framework and its derivatives (e.g., MS-SSIM [28], G-SSIM [29]) fundamentally rely on a conventional Gaussian kernel for computing local statistics. Specifically, the local mean ${\mu }_x$, standard deviation ${\sigma }_x$, and covariance ${\sigma }_{xy}$ defined in the SSIM formulation are computed using a Gaussian weighting function with a fixed spatial support, normalized to unit sum. This design provides rotational invariance and mitigates blocking artifacts. However, the kernel’s rapid exponential decay [33] is the source of its fundamental limitations. It strictly confines the effective receptive field, making it inherently a local operator that is myopic to long-range dependencies. Its static nature with a fixed scale prevents it from adapting to non-stationary statistics under varying illumination, and this sharp attenuation profile inherently amplifies boundary effects. These intrinsic properties of the conventional Gaussian kernel directly crystallize the three shortcomings outlined previously [34], including the inability to model global context, the infeasibility of adaptive re-balancing, and unreliable statistics under photometric variations. Therefore, the quest for a more robust loss function necessitates a fundamental evolution beyond the conventional Gaussian kernel.

To solve the above problems, we propose a novel fractional Gaussian field method. We combine the idea of Caputo derivatives with Gaussian weight kernels to overcome the boundary effects and isotropic requirements in discrete image processing. The fractional Gaussian field kernel function ${\mathcal{G}}^{\left(\alpha \right)}[m,n]$ can be obtained:

$${\mathcal{G}}^{\left(\alpha \right)}[m,n]={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\displaystyle \frac{1}{{(m^2+n^2)}^{\alpha /2}}}exp\left(-{\displaystyle \frac{m^2+n^2}{2{\sigma }^2}}\right)$$

(8)

where $\alpha$ represents the fractional order, controlling the degree of power-law attenuation. When $\alpha =0$, this kernel degenerates into a Gaussian kernel. $\mathrm{\Gamma }(1-\alpha )$ represents the Gamma function as the fractional-order normalization factor. $\sigma$ is the standard deviation of the Gaussian term, which controls the intensity of Gaussian attenuation. $(m,n)$ represents the integer displacement coordinates of pixel p relative to the central pixel $\tilde{p}$.

When calculating fractional-order local statistics, we normalize the convolution kernel in a discrete case to maintain numerical stability. We define the convolution kernel ${\omega }_{m,n}^{\left(\alpha \right)}$ used to compute fractional-order local statistics after normalization as follows:

$${\omega }_{m,n}^{\left(\alpha \right)}={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\displaystyle \frac{G_{\sigma }\left(\sqrt{m^2+n^2}\right)}{{\left(\sqrt{m^2+n^2}\right)}^{\alpha }}}={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\mathcal{G}}^{\left(\alpha \right)}[m,n]$$

(9)

The proposed fractional Gaussian field establishes a new computational paradigm for visual data analysis, wherein the presented fractional Gaussian kernel serves as the fundamental building block. This kernel’s hybrid structure, combining a power-law component for long-range dependence with a Gaussian term for local smoothness, makes significant contributions to addressing critical challenges in VSLAM. In practical image analysis, this translates to a superior ability to model global illumination changes and maintain structural coherence across the scene, overcoming the myopia of conventional local operators. For model-prediction assessment within SLAM systems, the kernel provides a more physically-grounded similarity metric that reflects the non-local interactions inherent in light transport, leading to more reliable evaluation of reconstruction quality under photometric variations. Beyond VSLAM, this kernel holds promise for a broader class of image processing tasks requiring multi-scale analysis and robustness to non-stationary statistics, such as medical image enhancement, remote sensing image fusion, and high dynamic range (HDR) imaging, where modeling complex, long-range pixel relationships is crucial. The foundational advancement of the fractional Gaussian field, operationalized through its kernel, thus creates a natural and powerful substrate for the subsequent development of our FGF-SSIM loss function, which leverages these properties to achieve a dynamic balance between photometric invariance and structural preservation.

3.2. FGF-SSIM

For the image window P centered on pixel $\tilde{p}$, we use the fractional Gaussian field convolution kernel to calculate the local statistics. In our formulation, the local statistics are computed within a sliding window P across the entire images x and y. The pixel coordinates $[i,j]$ specify the center of each local window, and the displacements $[m,n]$ are used to index relative positions within that window. This approach ensures that all statistical measures are derived from local neighborhoods, distinguishing them from global image properties. Also, since the weights ${\omega }_{m,n}^{\left(\alpha \right)}$ already include the normalization factor ${\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}$, there is no need to additionally divide by the window size. The fractional local mean at pixel location $[i,j]$ is defined as:

$${\mu }_x^{\left(\alpha \right)}[i,j]=\sum _{m=-M}^M\sum _{n=-N}^N{\omega }_{m,n}^{\left(\alpha \right)}·x[i-m,j-n]$$

(10)

Similarly, we can obtain that the fractional local variance is defined as:

$${\left({\sigma }_x^{\left(\alpha \right)}\right)}^2[i,j]=\sum _{m=-M}^M\sum _{n=-N}^N{\omega }_{m,n}^{\left(\alpha \right)}·{\left(x[i-m,j-n]-{\mu }_x^{\left(\alpha \right)}[i,j]\right)}^2$$

(11)

The fractional local covariances of the two images x and y are defined as:

$${\sigma }_{xy}^{\left(\alpha \right)}[i,j]=\sum _{m=-M}^M\sum _{n=-N}^N{\omega }_{m,n}^{\left(\alpha \right)}·\left(x[i-m,j-n]-{\mu }_x^{\left(\alpha \right)}[i,j]\right)\left(y[i-m,j-n]-{\mu }_y^{\left(\alpha \right)}[i,j]\right)$$

(12)

In the construction of the FGF-SSIM loss function, we retained the original formula of the SSIM loss function (Formula (2)). However, to simplify the calculation, we assume that $\epsilon =\zeta =1$, but $ϵ\ne 1$. Substitute the fractional statistics into the SSIM framework while retaining the luminance separation feature:

$${\mathcal{L}}^{\left(\alpha \right)}(x,y)={\displaystyle \frac{2{\mu }_x^{\left(\alpha \right)}{\mu }_y^{\left(\alpha \right)}+C_1}{{\left({\mu }_x^{\left(\alpha \right)}\right)}^2+{\left({\mu }_y^{\left(\alpha \right)}\right)}^2+C_1}}$$

(13)

Contrast-Structure function:

$${\mathcal{CS}}^{\left(\beta \right)}(x,y)={\displaystyle \frac{{\sigma }_{xy}^{\left(\beta \right)}+C_2}{{\sigma }_x^{\left(\beta \right)}{\sigma }_y^{\left(\beta \right)}+C_2}}$$

(14)

Therefore, we can obtain the expression of the core formula of FGF-SSIM:

$$\mathrm{FGF}\text{-}\mathrm{SSIM}(x,y)={\left[{\mathcal{L}}^{\left(\alpha \right)}(x,y)\right]}^{ϵ}·\left[{\mathcal{CS}}^{\left(\beta \right)}(x,y)\right]$$

(15)

3.3. Backpropagation Formula

In order to use FGF-SSIM as the loss function in the process of restoring the three-dimensional scene from the image, we need to derive its gradient. Let $L=1-\mathrm{FGF}\text{-}\mathrm{SSIM}$, total loss can be defined:

$${\mathcal{L}}_{\mathrm{total}}={\lambda }_1{\ell }_1+{\lambda }_{2}L$$

(16)

In backpropagation, we need to compute the gradient of the total loss to the input image x:

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{total}}}{\partial x}}={\lambda }_1{\displaystyle \frac{\partial {\ell }_1}{\partial x}}+{\lambda }_2{\displaystyle \frac{\partial L}{\partial x}}={\lambda }_1{\displaystyle \frac{\partial {\ell }_1}{\partial x}}-{\lambda }_2{\displaystyle \frac{\partial \mathrm{FGF}\text{-}\mathrm{SSIM}}{\partial x}}$$

(17)

We compute the L1 gradient term by ${\displaystyle \frac{\partial {\ell }_1}{\partial x}}=\mathrm{sign}(x-y)$. Compute the FGF-SSIM gradient term by decomposing into luminance components and contrast-structure components via the chain rule. Let $S=\mathrm{FGF}\text{-}\mathrm{SSIM}={\left[S_L\right]}^{\gamma }·{\left[S_C\right]}^{\delta }$, $S_L={\mathcal{L}}^{\left(\alpha \right)}$, $S_C={\mathcal{CS}}^{\left(\beta \right)}$. This can be obtained by applying the product rule and the chain rule:

$${\displaystyle \frac{\partial \mathrm{S}}{\partial x}}=\mathrm{S}\left\{{\displaystyle \frac{\gamma }{{\mathcal{L}}^{\left(\alpha \right)}}}{\displaystyle \frac{\partial {\mathcal{L}}^{\left(\alpha \right)}}{\partial x}}+{\displaystyle \frac{\delta }{{\mathcal{CS}}^{\left(\beta \right)}}}{\displaystyle \frac{\partial {\mathcal{CS}}^{\left(\beta \right)}}{\partial x}}\right\}$$

(18)

We then used the quotient rule and the fractional mean chain rule to solve for the luminance component gradient, and the quotient rule and the fractional covariance chain rule to solve for the contrast-structure component gradient.

$${\displaystyle \frac{\partial {\mathcal{L}}^{\left(\alpha \right)}}{\partial x}}=\sum _{m,n}{\omega }_{m,n}^{\left(\alpha \right)}·{\displaystyle \frac{2({\mu }_y^{\left(\alpha \right)}y-{\mu }_x^{\left(\alpha \right)}x)}{{({\mu }_x^{\left(\alpha \right)})}^2+{({\mu }_y^{\left(\alpha \right)})}^2+C_1}}$$

(19)

$${\displaystyle \frac{\partial {\mathcal{CS}}^{\left(\beta \right)}}{\partial x}}=\sum _{m,n}{\omega }_{m,n}^{\left(\beta \right)}·{\displaystyle \frac{(y-{\mu }_y^{\left(\beta \right)})-{\mathcal{CS}}^{\left(\beta \right)}\frac{{\sigma }_y^{\left(\beta \right)}}{{\sigma }_x^{\left(\beta \right)}}(x-{\mu }_x^{\left(\beta \right)})}{{\sigma }_x^{\left(\beta \right)}{\sigma }_y^{\left(\beta \right)}+C_2}}$$

(20)

Through the above derivation, the total gradient of FGF-SSIM can be expressed as:

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{total}}}{\partial x}}={\lambda }_1\mathrm{sign}(x-y)-{\lambda }_2·\mathrm{FGF}\text{-}\mathrm{SSIM}\left({\displaystyle \frac{\gamma }{{\mathcal{L}}^{\left(\alpha \right)}}}{\displaystyle \frac{\partial {\mathcal{L}}^{\left(\alpha \right)}}{\partial x}}+{\displaystyle \frac{\delta }{{\mathcal{CS}}^{\left(\beta \right)}}}{\displaystyle \frac{\partial {\mathcal{CS}}^{\left(\beta \right)}}{\partial x}}\right)$$

(21)

The gradient computation involves carefully tuned weighting parameters. Specifically, ${\lambda }_1$ and ${\lambda }_2$ balance the contributions of the L1 and FGF-SSIM components in the total loss, while $\gamma$ and $\delta$ control the relative importance of luminance versus contrast-structure preservation. These parameters were optimized through multi-objective optimization to ensure stable convergence and were fixed at ${\lambda }_{\mathrm{rgb}}=1.0$, ${\lambda }_{\mathrm{depth}}=0.8$, and ${\lambda }_{\mathrm{iso}}=0.2$ for all experiments.

4. 3D Gaussian SLAM with Fractional Gaussian Field Structural Similarity

4.1. FGF-SLAM

Figure 1 illustrates the comprehensive architecture of the proposed FGF-SLAM pipeline. Our framework aims to achieve simultaneous high-fidelity novel view synthesis and dense geometric reconstruction, enabling robust scene representation and real-time rendering capabilities. FGF-SLAM supports both RGB-D and monocular input data streams.

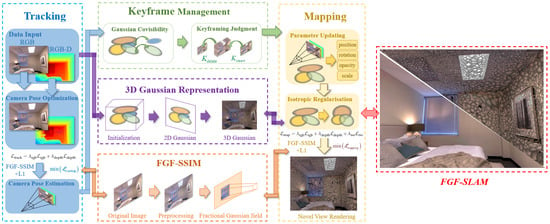
Figure 1. The comprehensive architecture of the proposed SLAM pipeline of FGF-SLAM.

The processing pipeline begins with the 3D Gaussian Scene Representation module, where input data undergoes scene initialization and is transformed into a collection of anisotropic 3D Gaussians through a structured parameterization process. Through differentiable projective transformation, each 3D Gaussian is projected to a 2D Gaussian on the image plane for efficient rasterization. These Gaussian primitives collectively encode both geometric and photometric properties of the environment. Simultaneously, the Camera Pose Tracking module coordinates the relationship between pose estimation and rendering optimization. This module employs a combined ‘L1+FGF-SSIM’ loss formulation for iterative camera pose refinement, enabling accurate online pose estimation for sequential frames. The Keyframe Management module subsequently performs keyframe retrieval, selection, and pruning based on pose constraints and Gaussian visibility metrics, significantly enhancing the computational efficiency and reconstruction quality of the SLAM system. In the Mapping and Optimization module, FGF-SLAM optimizes Gaussian insertion and parameter updates using refined pose information from preceding stages. The optimization incorporates isotropic regularization to prevent excessive anisotropic deformation in under-observed regions, while utilizing a ‘L1+FGF-SSIM’ strategy to construct an analogous loss function for mapping. The FGF-SSIM component employs adaptive fractional orders that are dynamically adjusted via ATE monitoring, ensuring robustness across varying illumination conditions while preserving structural consistency and contrast sensitivity.

4.2. 3D Gaussian Scene Representation

To establish a dense 3DGS-based VSLAM system capable of high-fidelity geometric reconstruction, we formulate the 3D scene representation as an adaptively controlled parametric model comprising anisotropic 3D Gaussian primitives:

$$\mathcal{G}=\left\{G_i({\mathit{\mu }}_i,{\mathbf{\Sigma }}_i,{\alpha }_i)|i=1,\dots ,N\right\}$$

(22)

where each 3D Gaussian primitive $G_i$ is defined by position ${\mathit{\mu }}_i\in {\mathbb{R}}^3$ in the world coordinate system, 3D covariance matrix ${\mathbf{\Sigma }}_i\in {\mathbb{R}}^{3\times 3}$ representing anisotropic geometry, and opacity ${\alpha }_i\in [0,1]$ controlling transparency. For numerical stability and optimization efficiency, the covariance matrix is factorized as ${\mathbf{\Sigma }}_i={\mathbf{R}}_i{\mathbf{S}}_i{\mathbf{S}}_i^{\top }{\mathbf{R}}_i^{\top }$ where ${\mathbf{R}}_i\in SO\left(3\right)$ represents the rotation matrix, ${\mathbf{S}}_i=\mathrm{diag}(s_x,s_y,s_z)$ represents the scaling matrix, and the factorization enables efficient gradient-based optimization through PyTorch (version 1.12.1) automatic differentiation framework.

When transforming from world coordinates to camera coordinates, the 3D Gaussian $G(\mathit{\mu },\mathbf{\Sigma })$ projects to a 2D Gaussian $G^{\prime }({\mathit{\mu }}^{\prime },{\mathbf{\Sigma }}^{\prime })$ on the image plane through differentiable projective transformation:

$${\mathbf{\Sigma }}^{\prime }=\mathbf{J}\mathbf{W}\mathbf{\Sigma }{\mathbf{W}}^{\top }{\mathbf{J}}^{\top }$$

(23)

where $\mathbf{J}$ denotes the Jacobian matrix of the projective transformation, $\mathbf{W}$ represents the view transformation matrix, $\mathbf{\Sigma }$ is the original 3D covariance matrix in world coordinates, and ${\mathbf{\Sigma }}^{\prime }$ is the projected 2D covariance matrix on the image plane. This formulation enables efficient rasterization by skipping blank regions while maintaining differentiability throughout the rendering pipeline.

In our experiments, Gaussian densification triggers every 100 iterations with gradient threshold 0.0002, and opacity resets occur at iterations 300 and 1500. The system maintains up to 100,000 Gaussians through visibility-based pruning using the occ_aware_visibility statistics.

4.3. Camera Pose Tracking

The tracking module estimates camera pose $\mathbf{T}\in SE\left(3\right)$ for each incoming frame while keeping the Gaussian parameters frozen. We formulate the optimization problem as a composite loss function that integrates FGF-SSIM for illumination-robust performance:

$${\mathcal{L}}_{\mathrm{track}}={\lambda }_{\mathrm{rgb}}{\mathcal{L}}_{\mathrm{rgb}}+{\lambda }_{\mathrm{depth}}{\mathcal{L}}_{\mathrm{depth}}$$

(24)

where ${\mathcal{L}}_{\mathrm{rgb}}$ represents the photometric loss component, ${\mathcal{L}}_{\mathrm{depth}}$ represents the geometric loss component when depth information is available, ${\lambda }_{\mathrm{rgb}}$ and ${\lambda }_{\mathrm{depth}}$ are weighting coefficients that balance the contributions of each loss term. This separation allows dedicated computational resources for camera motion estimation while avoiding environment model augmentation during tracking phases.

For monocular scenarios, we introduce the FGF-SSIM loss that combines traditional L1-norm with fractional-order structural similarity:

$${\mathcal{L}}_{\mathrm{rgb}}={\displaystyle \frac{1}{\left|\mathcal{M}\right|}}\sum _{\mathbf{p}\in \mathcal{M}}\left[{\lambda }_{\mathrm{L}1}{\parallel \widehat{I}\left(\mathbf{p}\right)-I\left(\mathbf{p}\right)\parallel }_1+{\lambda }_{\mathrm{FGF}\text{-}\mathrm{SSIM}}(1-\mathrm{FGF}\text{-}\mathrm{SSIM}(\widehat{I}\left(\mathbf{p}\right),I\left(\mathbf{p}\right)))\right]$$

(25)

where $\widehat{I}$ denotes the rendered image, I represents the ground truth image, $\mathcal{M}$ is the valid RGB mask region, $\mathbf{p}$ represents pixel coordinates, ${\lambda }_{\mathrm{L}1}$ and ${\lambda }_{\mathrm{FGF}\text{-}\mathrm{SSIM}}$ are weighting parameters for the L1 and FGF-SSIM components respectively. The FGF-SSIM metric provides superior edge preservation and multi-scale analysis capabilities critical for SLAM accuracy.

When depth information is available, we incorporate depth residuals to further constrain the camera pose optimization:

$${\mathcal{L}}_{\mathrm{depth}}={\displaystyle \frac{1}{|{\mathcal{M}}_d|}}\sum _{\mathbf{p}\in {\mathcal{M}}_d}{\parallel \widehat{D}\left(\mathbf{p}\right)-D\left(\mathbf{p}\right)\parallel }_1$$

(26)

where $\widehat{D}$ denotes the rendered depth map, D represents the ground truth depth map, ${\mathcal{M}}_d$ denotes the valid depth mask region, and $\mathbf{p}$ represents pixel coordinates. This combined approach leverages both photometric and geometric constraints for robust pose estimation.

In our experiments, the tracking optimization uses rotation learning rate $1\times {10}^{-3}$ and translation learning rate $2\times {10}^{-4}$, with early stopping at rotation delta < 0.001 rad and translation delta < 0.001 m. The loss combines RGB (${\lambda }_{\mathrm{rgb}}=1.0$) and depth (${\lambda }_{\mathrm{depth}}=0.8$) components, and FGF-SSIM weight starts at 0.1 with adaptive adjustment.

4.4. Keyframe Management

Keyframe selection employs strategic covisibility analysis of Gaussian distributions to maximize information diversity while minimizing computational overhead. The visibility of Gaussian $G_i$ during rasterization is quantitatively evaluated through:

$$\mathcal{V}\left(G_i\right)=\mathbb{I}\left({\int }_{\mathrm{ray}}{\alpha }_i\mathcal{N}(\mathbf{x};{\mathit{\mu }}_i,{\mathbf{\Sigma }}_i)d\mathbf{x}>{\tau }_v\right)$$

(27)

where $\mathbb{I}(·)$ denotes the indicator function, ${\alpha }_i$ represents the opacity of Gaussian $G_i$, $\mathcal{N}(\mathbf{x};{\mathit{\mu }}_i,{\mathbf{\Sigma }}_i)$ is the Gaussian probability density function, the integral represents ray accumulation through the Gaussian primitive, and ${\tau }_v$ is a visibility threshold. This visibility assessment serves as preprocessing step prior to keyframe management.

Keyframe selection employs rigorous covisibility analysis between current frame m and latest keyframe n:

$$\mathrm{IoU}({\mathcal{V}}_m,{\mathcal{V}}_n)={\displaystyle \frac{|{\mathcal{V}}_m\cap {\mathcal{V}}_n|}{|{\mathcal{V}}_m\cup {\mathcal{V}}_n|}}<{\tau }_{\mathrm{IoU}}$$

(28)

where ${\mathcal{V}}_m$ and ${\mathcal{V}}_n$ represent the visibility sets of frames m and n respectively, $|·|$ denotes set cardinality, and ${\tau }_{\mathrm{IoU}}$ is the intersection-over-union threshold. Additionally, relative motion constraints ensure sufficient baseline for triangulation:

$$\parallel {\mathbf{t}}_{mn}\parallel >max({\tau }_t,\eta ·\mathrm{median}\left(D_m\right))$$

(29)

where ${\mathbf{t}}_{mn}$ is the relative translation vector between frames m and n, ${\tau }_t$ is the absolute translation threshold, $\eta$ is a scaling factor, and $\mathrm{median}\left(D_m\right)$ represents the median depth value in frame m.

In our experiments, keyframe selection uses translation threshold 0.12× median depth, rotation threshold 0.1 rad, and overlap ratio cutoff 0.8. The system maintains 2 protected keyframes and a window size of 10, with covisibility cutoff 0.4 for pruning.

4.5. Mapping and Optimization

To prevent excessive anisotropic deformation of Gaussians in under-observed regions, we enforce isotropic constraints through a dedicated regularization term:

$${\mathcal{L}}_{\mathrm{iso}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{∥{\mathbf{s}}_i-{\overline{\mathbf{s}}}_i\mathbf{1}∥}_2^2$$

(30)

where ${\mathbf{s}}_i={[s_x,s_y,s_z]}^{\top }$ represents the scaling parameters of Gaussian $G_i$, ${\overline{\mathbf{s}}}_i={\displaystyle \frac{1}{3}}{\sum }_{j=1}^3{s}_{i,j}$ is the mean scaling value, $\mathbf{1}={[1,1,1]}^{\top }$ is the unit vector, and N is the total number of Gaussians. This regularization mechanism effectively constrains spatial expansion of Gaussian distributions.

The complete mapping objective integrates FGF-SSIM for superior structural preservation:

$${\mathcal{L}}_{\mathrm{map}}={\lambda }_{\mathrm{rgb}}{\mathcal{L}}_{\mathrm{rgb}}+{\lambda }_{\mathrm{depth}}{\mathcal{L}}_{\mathrm{depth}}+{\lambda }_{\mathrm{iso}}{\mathcal{L}}_{\mathrm{iso}}$$

(31)

where ${\lambda }_{\mathrm{rgb}}$, ${\lambda }_{\mathrm{depth}}$, ${\lambda }_{\mathrm{iso}}$, and ${\lambda }_{\mathrm{geom}}$ are weighting coefficients for the photometric, depth, and isotropic regularization respectively. The FGF-SSIM component employs adaptive fractional orders that are dynamically adjusted based on ATE monitoring.

For efficient optimization, we derive the gradients of the FGF-SSIM loss with respect to the rendered image. The fractional orders $\alpha$ and $\beta$ in FGF-SSIM are dynamically adjusted based on ATE monitoring to maintain robustness:

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{total}}}{\partial x}}={\lambda }_1\mathrm{sign}(x-y)-{\lambda }_2·\mathrm{FGF}\text{-}\mathrm{SSIM}\left({\displaystyle \frac{\gamma }{{\mathcal{L}}^{\left(\alpha \right)}}}{\displaystyle \frac{\partial {\mathcal{L}}^{\left(\alpha \right)}}{\partial x}}+{\displaystyle \frac{\delta }{{\mathcal{CS}}^{\left(\beta \right)}}}{\displaystyle \frac{\partial {\mathcal{CS}}^{\left(\beta \right)}}{\partial x}}\right)$$

(32)

where ${\lambda }_1$ and ${\lambda }_2$ are weighting parameters, $\mathrm{sign}(·)$ is the sign function, $\gamma$ and $\delta$ control the relative contributions of the luminance and contrast-structure components, and the partial derivatives are computed using the fractional Gaussian field kernel and chain rule differentiation. The ATE monitoring mechanism adjusts $\alpha$ and $\beta$ to optimize performance under varying conditions.

Gaussian parameters are optimized through gradient descent with type-specific learning rates:

$${\mathit{\theta }}^{(t+1)}={\mathit{\theta }}^{\left(t\right)}-\eta {\nabla }_{\mathit{\theta }}{\mathcal{L}}_{\mathrm{map}}$$

(33)

where $\mathit{\theta }$ represents the Gaussian parameters being optimized, t denotes the iteration step, $\eta$ is the learning rate, and ${\nabla }_{\mathit{\theta }}{\mathcal{L}}_{\mathrm{map}}$ is the gradient of the mapping loss with respect to the parameters. The learning rates are carefully tuned per parameter type to ensure stable convergence while preserving geometric fidelity.

In our experiments, initial mapping uses 2000 iterations and subsequent keyframes use 300 iterations. Isotropic regularization weight is 10.0, and the ATE monitor uses a 15-frame history with degradation threshold 1.15. Gaussian updates occur every 100 iterations (offset 50) with densification threshold 0.01 and opacity pruning threshold 0.005.

Through the synergistic integration of these components, FGF-SLAM achieves efficient and high-quality scene reconstruction and rendering performance in challenging illumination environments. This architectural framework provides beneficial insights for enhancing the robustness and practical deployment of VSLAM technology in real-world intelligent transportation systems.

5. Experimental Results

5.1. Experimental Setup

All experiments were conducted on a workstation equipped with an Intel^® Core™ i7-13700F processor (16-core, 8 performance-cores and 8 efficient-cores, 5.20 GHz) and an NVIDIA GeForce RTX 4090 GPU (16,384 CUDA cores, 24 GB GDDR6X). Algorithm validation was performed on three established benchmarks: the synthetic Replica dataset [35], real-world TUM RGB-D dataset [36], and M2UD benchmark [37]. For quantitative evaluation, we adopted three standardized metrics: Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS) for rendering quality assessment, complemented by Absolute Trajectory Error Root Mean Square (ATE RMSE) for pose estimation accuracy.

To ensure optimal performance across different experimental conditions, we implemented a systematic parameter optimization strategy for the fractal Gaussian kernel and FGF-SSIM framework. The key parameters were optimized through grid search and cross-validation on a held-out validation set. The fractional order parameters $\alpha$ and $\beta$, which control the long-range correlation and structure preservation respectively, were tuned over the ranges [0.2, 0.9] and [0.1, 0.8] with step sizes of 0.05. The optimal configuration was determined to be $\alpha =0.8$ and $\beta =0.4$, which balanced the trade-off between illumination robustness and structural detail preservation. For the Gaussian kernel parameters, we employed a kernel size of $3\times 3$ with adaptive standard deviation $\sigma$ computed using the scaling relation $\sigma =\mathrm{size}·(0.3+0.25\alpha +0.1\beta )$ that incorporates the fractional orders. For illumination robustness testing, we standardized the perturbation parameters to brightness change = 30, contrast change = 1.1, and gamma change = 1.6, representing challenging real-world lighting variations. All optimization procedures employed the Adam optimizer with an initial learning rate of $5\times {10}^{-4}$, decaying by a factor of 0.8 every 50 epochs, and convergence was determined when the relative improvement in validation loss fell below 0.1% for 5 consecutive epochs.

We incorporate the FGF-SSIM loss function into the MonoGS-SLAM baseline, resulting in an enhanced framework termed FGF-SLAM, to assess the practical efficacy of the fractal Gaussian field representation within a full SLAM framework. The 3D Gaussian Scene Representation module employs a composite loss with progressive FGF-SSIM weighting ($w_{\mathrm{fgf}}=min(0.7,0.1+0.6\times \mathrm{iteration}/3000)$), visibility-aware pruning (threshold = 3), and periodic opacity reset (every 1000 iterations). The Camera Pose Tracking module employs AdamW optimizer with weight decay $1\times {10}^{-6}$. Tracking iterations utilize conservative FGF-SSIM parameters ($\alpha =0.3$, kernel size = 5) with early stopping based on loss stagnation detection (patience=10 iterations, relative tolerance = 1%). The Keyframe Management module selects frames based on translation (>$0.12\times$ median depth), rotation (>0.1 rad), and overlap criteria (<0.8), while protecting two keyframes and pruning based on 0.4 covisibility cutoff. The Mapping and Optimization module utilizes aggressive FGF-SSIM parameters ($\alpha =0.5$, kernel size = 7) with ATE-aware adaptive control. The ATEMonitor employs a 15-frame sliding window and degradation threshold of 1.15, automatically reducing FGF-SSIM weight by 30% when performance decline is detected for two consecutive evaluations.

Through systematic optimization and ablation studies, we will demonstrate that the proposed loss function consistently enhances performance, confirming the advantages of incorporating fractal Gaussian priors in improving both robustness and accuracy in visual SLAM systems. Comparative analysis encompassed NeRF-based SLAM methods (e.g., NICE-SLAM [38], Vox-Fusion [39], Point-SLAM [40]) and 3DGS-based SLAM approaches (e.g., GS-SLAM [12], SplaTAM [9], MonoGS [13]) on their respective compatible datasets. Specifically, to evaluate performance under monocular RGB input constraints, we further compared against ORB-SLAM2 [41] (feature-based SLAM), MonoGS [13] (monocular Gaussian Splatting SLAM), and MotionGS [42] (explicit motion-guided deformation) on the TUM dataset. All comparisons were based on publicly reported performance metrics for these methods.

5.2. Gaussian vs. Fractional Kernels

Figure 2 presents a comparative analysis of the kernel functions employed in SSIM and FGF-SSIM, providing a visual illustration of the mathematical properties inherent to the fractional Gaussian field kernel. Figure 2a displays a two-dimensional heatmap visualization of the standard Gaussian kernel, which exhibits the characteristic profile of a high central weight with rapid exponential decay from the center. This indicates that during image processing, the kernel primarily incorporates information from immediately adjacent pixels, reflecting its limited receptive field. Figure 2b shows the corresponding heatmap of the fractional Gaussian field kernel. While high weights are also concentrated near the center, the kernel exhibits broader and more extensive weight distribution extending outward. It is worth noting that the redistribution of weight toward longer distances in the fractional kernel comes at the cost of slightly reduced emphasis on immediate neighbors compared to the conventional Gaussian kernel. Even at considerable distances from the center, the fractional kernel maintains non-negligible weight values—unlike the conventional Gaussian kernel, which attenuates rapidly to near-zero values. Figure 2c shows the difference map obtained by subtracting the Gaussian kernel from the FGF kernel, highlighting distinctions in their spatial weight distributions. A blue-toned central region suggests a weight advantage of the Gaussian kernel near the origin. This indicates that while the fractional kernel excels at capturing long-range dependencies, it exhibits a minor compromise in local sensitivity compared to the conventional Gaussian formulation. A neutral white intermediate ring indicates comparable magnitudes in this transitional region. Most notably, a pronounced red outer region reveals significantly higher weights in the FGF kernel at larger distances, providing direct visual evidence of its long-range memory characteristics.

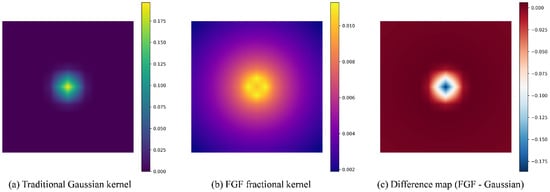
Figure 2. Comparative visualization of the standard Gaussian and fractional Gaussian field kernels.

Figure 3 presents a comparative analysis of the radial weight distribution between the Gaussian kernel and the FGF kernel, highlighting quantitative differences in their spatial weighting characteristics. Figure 3a shows one-dimensional profiles extracted from the center of each kernel, plotting weight value as a function of radial distance. The Gaussian kernel exhibits a steep exponential decay, with values declining rapidly from the center. In the immediate vicinity (0–2 pixels), the conventional Gaussian kernel maintains higher weight values, providing superior emphasis on local pixel relationships. In contrast, the FGF kernel demonstrates a more gradual attenuation, maintaining substantially higher weights at medium to large distances. This behavior confirms the stronger long-range memory characteristics of the FGF kernel. Figure 3b displays the same data with weight values converted to a logarithmic scale. In this representation, the Gaussian kernel closely follows an approximately straight line, consistent with its exponential nature. The FGF kernel, by contrast, exhibits a slowly curving trajectory indicative of power-law decay. This fundamental trade-off between local precision and global context capture represents a deliberate design choice in the fractional Gaussian formulation, where the benefits of extended receptive fields outweigh the minor reduction in local emphasis for VSLAM applications. This slower attenuation rate, a defining feature of heavy-tailed distributions, enables the FGF kernel to integrate information from longer distances, thereby facilitating enhanced structural preservation in image processing.

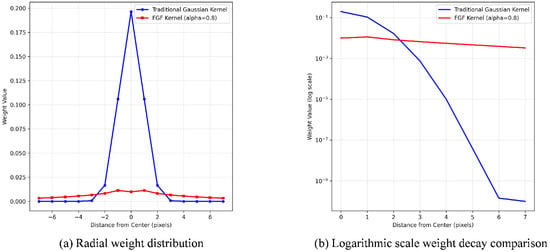
Figure 3. Comparative radial weight analysis of Gaussian and FGF kernels in linear and logarithmic scales.

The fundamental distinction between these kernels lies in their mathematical formulation and consequent performance characteristics. The standard Gaussian kernel exhibits exponential decay, inherently limiting its receptive field and making it susceptible to local illumination variations. In contrast, the fractional Gaussian kernel combines power-law decay with Gaussian attenuation, enabling capture of both local details and global context. This hybrid structure directly addresses core limitations of conventional SSIM in VSLAM applications. The power-law component provides long-range dependencies necessary for modeling global illumination changes, while the Gaussian term maintains local smoothness. The practical implication is that FGF-SSIM maintains structural consistency across larger spatial extents, making it particularly effective for SLAM applications with significant viewpoint changes and illumination variations.

More precisely, we use a Gaussian kernel in the luminance component, ${\sigma }_{\alpha }={\sigma }_0·\alpha$. In this way, when $\alpha$ increases, the variance of the Gaussian kernel increases, which means greater smoothing and greater robustness to changes in illumination. When $\alpha$ decreases, the variance of the Gaussian kernel decreases and it becomes more sensitive to changes in illumination. Within the local window, when the image satisfies stationarity (i.e., the local mean and variance remain constant), the variation of the fractional-order statistics is mainly affected by the order $\alpha$. We prove that when $\alpha$ approaches 1, the derivative of the fractional statistic with respect to $\alpha$ is approximately constant within the local window.

Consider the local mean of the luminance component:

$${\mu }_x^{\left(\alpha \right)}={\displaystyle \frac{\sum w_p^{\left(\alpha \right)}x\left(q\right)}{\sum w_p^{\left(\alpha \right)}}}$$

(34)

When $\alpha$ varies around 1, we can Taylor expand ${\mu }_x^{\left(\alpha \right)}$ at $\alpha =1$:

$${\mu }_x^{\left(\alpha \right)}\approx {\mu }_x^{\left(1\right)}+(\alpha -1)·{\left.{\displaystyle \frac{d{\mu }_x^{\left(\alpha \right)}}{d\alpha }}\right|}_{\alpha =1}$$

(35)

Among them, the derivative:

$${\displaystyle \frac{d{\mu }_x^{\left(\alpha \right)}}{d\alpha }}={\displaystyle \frac{\left(\sum \frac{d{w}_p^{\left(\alpha \right)}}{d\alpha }·x\left(p\right)\right)·\left(\sum w_p^{\left(\alpha \right)}\right)-\left(\sum w_p^{\left(\alpha \right)}x\left(p\right)\right)·\left(\sum \frac{d{w}_p^{\left(\alpha \right)}}{d\alpha }\right)}{{\left(\sum w_p^{\left(\alpha \right)}\right)}^2}}$$

(36)

In the local stationary region, $x\left(p\right)$ is approximately the constant c, then:

$${\displaystyle \frac{d{\mu }_x^{\left(\alpha \right)}}{d\alpha }}\approx {\displaystyle \frac{\left(\sum \frac{d{w}_p^{\left(\alpha \right)}}{d\alpha }·c\right)·\left(\sum w_p^{\left(\alpha \right)}\right)-\left(c·\sum w_p^{\left(\alpha \right)}\right)·\left(\sum \frac{d{w}_p^{\left(\alpha \right)}}{d\alpha }\right)}{{\left(\sum w_p^{\left(\alpha \right)}\right)}^2}}=0$$

(37)

Therefore, in the stationary region, the derivative of ${\mu }_x^{\left(\alpha \right)}$ with respect to $\alpha$ is 0 when $\alpha =1$. Similarly, variance and covariance also have similar properties. However, in non-stationary regions (such as edges), the derivative is not zero. However, in SLAM, the local areas between consecutive frames usually satisfy a gentle change in lighting, so we can consider that the derivative does not change much, that is, it can be approximately regarded as a constant. Therefore, in backpropagation, we can treat the fractional orders $\alpha$ and $\beta$ as constants (or through adaptive learning, but with a smaller learning rate set), which will not lead to unstable training.

5.3. Statistical Verification of FGF-SSIM

Figure 4 presents a normality assessment of Structural Similarity (SSIM) index distributions across five image denoising methodologies. The upper row displays quantile-quantile (Q–Q) plots, while the lower row shows corresponding histograms with fitted normal distributions, collectively characterizing the statistical distribution of each method. Although all Shapiro–Wilk test results (L2: $p=0.0002$; L1: $p=0.0004$; SSIM: $p=3.65\times {10}^{-10}$; MS-SSIM: $p=0.0002$; FGF-SSIM: $p=0.0134$) indicate significant deviations from normality ($\alpha =0.05$), the FGF-SSIM method exhibits notably superior distributional characteristics. Its Q–Q plot demonstrates the closest alignment with theoretical normality benchmarks, and the histogram confirms the most symmetric and well-shaped distribution profile among all evaluated methods. Although FGF-SSIM does not achieve complete normality, this distributional advantage provides critical justification for employing distribution-free statistical tests in subsequent analyses. Furthermore, these foundational distributional properties establish the necessary context for interpreting differential effect sizes in methodological comparisons, suggesting that FGF-SSIM’s enhanced distributional stability may contribute to more consistent performance advantages.

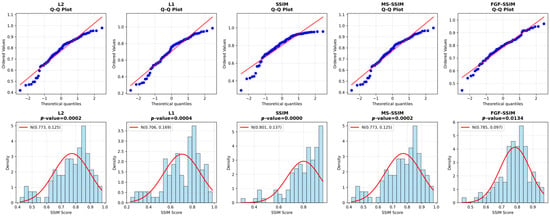
Figure 4. Assessment of Distribution Normality for SSIM Scores Across Loss Functions.

Figure 5a presents the results of Wilcoxon signed-rank tests comparing the proposed FGF-SSIM method against four established denoising approaches. The bar chart summarizes the statistical significance of pairwise comparisons, with all p-values for FGF-SSIM versus L2, L1, SSIM, and MS-SSIM falling below ${10}^{-10}$. This uniformly high level of statistical significance across all comparisons provides robust non-parametric evidence of systematic performance differences. The use of this distribution-free test is directly justified by the non-normal distribution characteristics established in Figure 4, ensuring valid statistical inference despite violations of parametric assumptions. The consistently minimal p-values anticipate the substantial effect sizes quantified later, particularly in comparisons against L1 and MS-SSIM, where the fractional Gaussian field kernel demonstrates superior structural preservation. These statistically significant outcomes are consistent with the methodological strengths of FGF-SSIM, which integrates fractional-order denoising, large-kernel filtering for long-range dependencies, and multi-feature fusion for illumination robustness. The agreement between the distributional characteristics established in Figure 4 and the non-parametric significance testing in Figure 5a provides strong evidence for the method’s consistent performance. This rigorous statistical foundation, which confirms a systematic advantage, is further complemented by an analysis of the practical effect magnitudes in the following section.

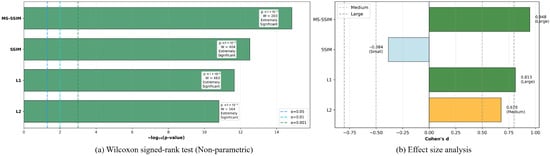
Figure 5. Wilcoxon Test Significance and Effect Size Analysis of Loss Functions.

Figure 5b quantifies the practical significance of performance differences through Cohen’s *d* effect size analysis, complementing the non-parametric statistical significance established in Figure 5a. The visualization presents effect sizes for all paired comparisons between FGF-SSIM and conventional methods, explicitly classified into small, medium, and large categories. The results indicate large effect sizes for FGF-SSIM compared to L1 and MS-SSIM, a medium effect compared to L2, and a small effect compared to SSIM. This small effect size indicates that while FGF-SSIM achieves statistically significant gains, its average performance advantage over SSIM in terms of the evaluated metrics is less pronounced than against other baselines. Nonetheless, FGF-SSIM demonstrates superior capabilities in specific aspects critical to SLAM, such as illumination robustness and geometric consistency, as detailed in Section 5.3 and Section 5.4. These differential effect sizes align with the theoretical advancements of FGF-SSIM, including the fractional Gaussian field kernel that couples power-law decay for long-range memory with local smoothness. In summary, this effect size analysis substantiates that FGF-SSIM provides consistent and meaningful improvements, with its most substantial gains realized in scenarios requiring robustness to photometric variations and the modeling of global context.

5.4. Loss Functions’ Comparison Results

Figure 6 compares the illumination robustness of FGF-SSIM with other loss functions on the urban01 scenario of the M2UD dataset [37]. Under consistent experimental conditions, we provide qualitative comparisons by presenting the resulting output images generated by each loss function. Additionally, we evaluated the proposed FGF-SSIM loss function against other loss functions using three standard image quality metrics: PSNR, SSIM, and MSE. After increasing the original image’s illumination intensity by 30%, the proposed FGF-SSIM loss preserves structural details more effectively than competing loss functions and achieves superior performance across multiple evaluation metrics.The results demonstrate that incorporating fractional-order calculus into SSIM significantly enhances algorithmic performance under real-world illumination variations. FGF-SSIM achieves the optimal performance, marginally surpassing the L2-based results and substantially outperforming conventional SSIM. Specifically, under a 30% luminance adjustment, FGF-SSIM attains peak metrics of 21.94 dB PSNR, 0.9639 SSIM, and 415.62 MSE, exceeding the L1 algorithm by 1.82 dB PSNR, 0.173 SSIM, and 216.21 MSE. This improvement stems from fractional-order local statistics in FGF-SSIM, which replaces first-order Gaussian convolution kernels in traditional SSIM with fractional-order counterparts for decoupled luminance-contrast-structure control. The power-law decaying weights ${(m^2+n^2)}^{-\alpha /2}$ confer long-range dependence to capture non-local illumination changes, while Gaussian attenuation preserves local details and smoothness, enabling robustness to global illumination variations without compromising structural fidelity.

Figure 6. Comparative results of robustness to illumination variations between FGF-SSIM and benchmark metrics using urban01 sequence on M2UD dataset.

As illustrated in Figure 7, We provide a more detailed analysis of FGF-SSIM and other loss functions in localized regions, with a specific focus on their denoising performance and illumination robustness of the M2UD dataset [37]. In terms of denoising efficacy, although SSIM and L2 achieve superior results, FGF-SSIM remains competitive, securing the third-best performance while preserving the desirable properties of conventional SSIM. More importantly, in assessing photometric robustness, FGF-SSIM outperforms all other methods across three key metrics: PSNR, SSIM, and MSE. This improvement can be attributed to the fractional-order gradient flow and the fractional Gaussian field, which enhance structural sensitivity and illumination invariance. By incorporating fractional calculus, FGF-SSIM more effectively captures fine-grained textures and edges while suppressing high-frequency noise, thereby increasing PSNR and SSIM while reducing MSE. Particularly in the highlighted scenario of direct sunlight exposure within an autonomous driving context, FGF-SSIM exhibits enhanced capability in capturing fine details and maintaining structural integrity. It demonstrates superior adaptability to challenging lighting conditions, such as in regions where sunlight interacts with complex textures like tree branches.

Figure 7. Comparative analysis of FGF-SSIM versus conventional loss functions in varying illumination conditions.

5.5. Illumination Invariance Performance Evaluation

Figure 8 presents the illumulation invariance performance evaluation between the SSIM and FGF-SSIM metrics applied to the urban03 scene from the M2UD dataset [37], alongside a comparative decomposition analysis. To underscore the advantages of incorporating fractal calculus into the SSIM framework, we provide a detailed examination of the principal loss components and error distributions of both methods. As illustrated in Figure 8a, both methods are evaluated under a 30% global illumination increase. The results demonstrate that FGF-SSIM exhibits significantly greater robustness to illumination variations. Images processed with FGF-SSIM appear more natural and sharper, with better preservation of structural details such as edges and textures. Figure 8b presents the Main Loss Component, which corresponds to the luminance computation segment of each loss function. The luminance error distribution of FGF-SSIM more effectively captures inter-object illumination variations, indicating its superior ability to maintain the global luminance structure of the scene. In Figure 8d, two localized regions are magnified for direct comparison. FGF-SSIM more accurately renders the brightness of fine structures such as background branches, thereby contributing to improved illumination invariance in the final output. Figure 8c compares the error distributions of both methods relative to the ground truth image. FGF-SSIM achieves lower and more uniformly distributed errors, confirming its higher reconstruction quality. This improvement is attributed to the long-range memory characteristics of FGF-SSIM, which enhance its capacity to preserve global structural information and fine details while effectively smoothing homogeneous regions. Figure 8e provides an additional zoomed-in comparison of two local patches. While SSIM fails to retain structural object details, FGF-SSIM clearly maintains the object’s structure, further corroborating its stability under illumination changes. Illumination variation constitutes a global monotonic transformation of pixel values. Although it significantly alters absolute intensity values, relative structural relationships within the image remain largely intact. FGF-SSIM leverages a fractional Gaussian field kernel endowed with long-range memory properties, enabling a wider receptive field. This allows the model to incorporate broader contextual information when estimating local luminance, emphasizing relational structural cues over absolute pixel values.

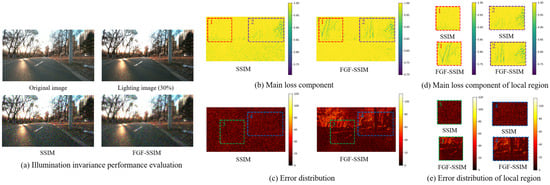
Figure 8. Illumination invariance performance evaluation and comparative decomposition analysis of SSIM and FGF-SSIM on the urban03 scene of the M2UD dataset.

Consequently, the Main Loss Component of FGF-SSIM remains substantially more stable under illumination shifts compared to that of conventional SSIM. This inherent stability of the core computational component directly translates to more consistent output quality, culminating in superior performance in illumination invariance evaluation. In summary, the illumination invariance exhibited by FGF-SSIM is not a product of post-processing techniques, but an intrinsic advantage rooted in its mathematical foundation based on fractional Gaussian fields.

5.6. Monocular Reconstruction Comparison Results

As shown in Table 1, we integrated the FGF-SSIM loss function into the SLAM framework and assessed its performance on the TUM monocular dataset [36], demonstrating consistent superiority across all evaluation measures. FGF-SLAM achieves a PSNR of 36.04 dB, SSIM of 0.95, and LPIPS of 0.07, exceeding the second-best method by margins of +12.11 dB, +0.15, and −0.18 respectively. The TUM Mono dataset presents considerable challenges including rapid motion-induced blur, underexposed and noisy images from legacy sensors, and textureless regions with repetitive patterns. These conditions impose stringent demands on monocular SLAM systems, where the absence of depth information amplifies sensitivity to photometric variations and structural inconsistencies. While MonoGS-SLAM employs a combination of L1 and conventional SSIM losses, and UDGS-SLAM utilizes an undisclosed loss formulation, both exhibit limitations in handling the complex illumination conditions and structural degradation inherent in monocular visual SLAM.

Table 1. Monocular reconstruction comparison results of SLAM methods.

Group	Method	Metric	Fr1	Fr2	Fr3	Avg.
3DGS-based SLAM	MonoGS	PSNR [dB] ↑	20.81	22.34	21.75	21.63
		SSIM ↑	0.71	0.73	0.75	0.73
		LPIPS ↓	0.36	0.28	0.37	0.34
		RMSE ATE ↓	3.78	4.60	3.50	3.96
	UDGS-SLAM	PSNR [dB] ↑	23.30	24.90	23.60	23.93
		SSIM ↑	0.79	0.80	0.81	0.80
		LPIPS ↓	0.26	0.22	0.26	0.25
		RMSE ATE ↓	3.00	2.20	11.30	5.50
	FGF-SLAM	PSNR [dB] ↑	34.27	35.32	38.54	36.04
		SSIM ↑	0.94	0.95	0.94	0.95
		LPIPS ↓	0.06	0.06	0.09	0.07
		RMSE ATE ↓	1.64	1.21	2.35	1.73

Best results are highlighted as first, second and third. The upward arrow (↑) indicates that higher values are better for that metric, while the downward arrow (↓) indicates that lower values are better. Our method surpasses all baseline approaches across a comprehensive set of evaluation metrics, underscoring the effectiveness of incorporating fractional calculus into the proposed framework.

The exceptional performance of FGF-SLAM in monocular settings stems from fundamental mechanistic advantages specifically designed for photometric robustness. MonoGS-SLAM’s L1+SSIM formulation, while providing basic structural awareness, suffers from the inherent limitations of conventional Gaussian kernels in SSIM—limited receptive fields and sensitivity to local illumination changes. This proves particularly problematic in monocular SLAM where depth ambiguity exacerbates the impact of photometric inconsistencies. UDGS-SLAM, while achieving competitive results, lacks the mathematical foundation to explicitly address long-range dependencies in illumination variations. In contrast, FGF-SSIM introduces a paradigm shift through its fractional Gaussian field formulation, which establishes extended spatial correlations via power-law decay while maintaining local structural fidelity. This is critically important in monocular SLAM, where the absence of geometric constraints from depth sensors places greater emphasis on photometric consistency for both tracking and mapping. The adaptive decomposition of luminance, contrast, and structural components allows FGF-SLAM to dynamically balance photometric invariance with structural preservation—a capability particularly valuable in monocular scenarios where illumination changes can easily mislead traditional photometric-based optimization.

5.7. New View Synthesis Results

Figure 9 presents a comparative analysis of novel view synthesis quality after 3D reconstruction among different 3DGS-based methods on the Replica dataset [35]. To evaluate the advantages of incorporating fractional Gaussian fields, we selected two state-of-the-art models from CVPR 2024 (SplaTAM [9], MonoGS [13]) for performance comparison. All three methods demonstrate competent scene reconstruction capabilities when provided with RGB-D input data. However, our proposed FGF-SLAM exhibits superior performance in detail preservation and long-range dependency modeling. In the Office1 scenario, for occluded regions in the input images (such as the rear corner of a pillow), SplaTAM employs blank Gaussian primitives for completion, resulting in visible artifacts. While MonoGS-SLAM attempts to reconstruct these areas, it introduces noticeable color discrepancies near boundaries, where whitish artifacts appear inconsistent with the original beige pillow and black sofa. In contrast, FGF-SLAM effectively handles these challenging regions by leveraging its long-range memory capacity during novel view synthesis, producing more natural and coherent scene reconstructions. This advantage becomes more pronounced in the sofa seam reconstruction of Office3. Given frontal views in the input sequence, SplaTAM generates blurred seam structures, MonoGS-SLAM produces moderately defined edges, whereas FGF-SLAM accurately reproduces sharp and geometrically consistent seams. Furthermore, FGF-SLAM demonstrates exceptional capability in fine detail reconstruction. In the Office4 scenario featuring wall graffiti, SplaTAM captures only coarse visual patterns while losing structural details of specific lines. MonoGS-SLAM achieves reasonable reconstruction but exhibits limitations in reproducing intricate patterns, particularly in complex shapes such as facial features and hat contours. FGF-SLAM successfully preserves all fine details with superior line accuracy and geometric fidelity. These results substantiate the effectiveness of fractional-order Gaussian fields in 3D reconstruction, directly attributable to the long-range dependency modeling enabled by fractional-order kernels, which enhances structural consistency across spatial domains.

Figure 9. Qualitative comparison of novel view synthesis between 3DGS-based SLAM methods on Replica dataset.

As shown in Table 2, we further assess the proposed FGF-SLAM on the Replica synthetic dataset [35], demonstrating its exceptional capability in novel view synthesis using RGB-D data. The results demonstrate that FGF-SLAM achieves notable improvements across both PSNR and LPIPS metrics, outperforming both NeRF-based SLAM systems (e.g., NICE-SLAM [38], Vox-Fusion [39], Point-SLAM [40]) and 3DGS-based approaches (such as GS-SLAM [12], SplaTAM [9], MonoGS [13]). Specifically, FGF-SLAM attains state-of-the-art average scores on Replica, reaching 38.70 dB in PSNR and 0.045 in LPIPS, exceed those of the second-best method by margins of +1.20 dB and −0.025, respectively. The Replica dataset consists of high-fidelity synthetic indoor scenes featuring noise-free, blur-free imagery and accurate geometric ground truth, thereby posing challenges such as reconstructing fine geometric details, handling highly reflective surfaces, and maintaining overall visual fidelity. These results indicate that FGF-SLAM, through the incorporation of fractional calculus, enhances the preservation of edge and texture details, effectively reducing pixel-level errors in detailed regions. This leads to superior global pixel fidelity, as reflected in the highest PSNR value. Moreover, by independently modulating the contrast-structure component, FGF-SLAM produces images with improved perceptual clarity, enriched textures, and more coherent structures. Even without exact pixel-wise alignment, the visual appearance and perceptual quality of the generated views are closest to the ground truth, accounting for its significant advantage in LPIPS, with a relative improvement of 35.71% over the second-best method. Although the SSIM score of 0.970 ranks second, it trails the top method by only 0.005. This minor gap can be attributed to an inherent trade-off between low-frequency luminance consistency and high-frequency detail enhancement, suggesting that FGF-SLAM prioritizes perceptually salient features over strict brightness uniformity, thereby achieving better overall perceptual and quantitative performance.

Table 2. New view synthesis results of SLAM methods.

	Method	Metric	Room 0	Room 1	Room 2	Office 0	Office 1	Office 2	Office 3	Office 4	Avg.
NeRF-based	Vox-Fusion	PSNR ↑	22.39	22.36	23.92	27.79	29.83	20.33	23.47	25.21	24.41
		SSIM ↑	0.683	0.751	0.798	0.857	0.876	0.794	0.803	0.847	0.801
		LPIPS ↓	0.303	0.269	0.234	0.241	0.184	0.243	0.213	0.199	0.236
	NICE-SLAM	PSNR ↑	22.12	22.47	24.52	29.07	30.34	19.66	22.23	24.92	24.42
		SSIM ↑	0.689	0.757	0.814	0.874	0.886	0.797	0.801	0.856	0.809
		LPIPS ↓	0.330	0.271	0.208	0.229	0.181	0.235	0.209	0.198	0.233
	Point-SLAM	PSNR ↑	32.40	34.08	35.50	38.26	39.16	33.99	33.48	33.49	35.17
		SSIM ↑	0.974	0.977	0.982	0.983	0.986	0.960	0.960	0.979	0.975
		LPIPS ↓	0.113	0.116	0.111	0.100	0.118	0.156	0.132	0.142	0.124
3DGS-based	SplaTAM	PSNR ↑	32.86	33.89	35.25	38.26	39.17	31.97	29.70	31.81	34.11
		SSIM ↑	0.98	0.97	0.98	0.98	0.98	0.97	0.95	0.95	0.97
		LPIPS ↓	0.07	0.10	0.08	0.09	0.09	0.10	0.12	0.15	0.10
	GS-SLAM	PSNR ↑	31.56	32.86	32.59	38.70	41.17	32.36	32.03	32.92	34.27
		SSIM ↑	0.968	0.973	0.971	0.986	0.993	0.978	0.970	0.968	0.975
		LPIPS ↓	0.094	0.075	0.093	0.050	0.033	0.094	0.110	0.112	0.082
	MonoGS	PSNR ↑	34.83	36.43	37.49	39.95	42.09	36.24	36.70	36.07	37.50
		SSIM ↑	0.954	0.959	0.965	0.971	0.977	0.964	0.963	0.957	0.960
		LPIPS ↓	0.068	0.076	0.075	0.072	0.055	0.078	0.065	0.099	0.070
	FGF-SLAM	PSNR ↑	35.48	38.50	38.33	43.04	43.71	37.18	36.72	36.62	38.70
		SSIM ↑	0.957	0.969	0.968	0.982	0.982	0.970	0.968	0.962	0.970
		LPIPS ↓	0.046	0.047	0.050	0.032	0.031	0.043	0.042	0.067	0.045

Best results are highlighted as first, second and third The upward arrow (↑) indicates that higher values are better for that metric, while the downward arrow (↓) indicates that lower values are better. Our method demonstrates superior performance over all baseline models in terms of PSNR and LPIPS, securing top-two rankings across quantitative evaluations.

5.8. Ablation Experiments Results

Table 3 presents a systematic ablation study of FGF-SSIM on the office1 scenario from the Replica dataset [35], analyzing the role of the proposed FGF-SSIM component within the SLAM system. Due to its low-light conditions, the Office 1 scenario in the Replica dataset is well-suited for assessing the efficacy of various loss terms in recovering scene luminosity and geometric structure. To evaluate their efficacy in low-light conditions, we ablated various loss function formulations (including L1, L2, SSIM, MS-SSIM, and our proposed FGF-SSIM) on the Office 1 scenario, assessing their impact on reconstruction quality. As shown in Table 3, the proposed FGF-SSIM achieves superior performance across all metrics compared to other loss functions. Notably, its ranking within the full VSLAM system (L2 < MS-SSIM < L1 < SSIM < FGF-SSIM) differs from its standalone evaluation (L1 < MS-SSIM < SSIM < L2 < FGF-SSIM). The limitations of L2 loss stem from its inherent rigidity, sensitivity to outliers, and instability in low-signal conditions. When integrated into a VSLAM framework, these shortcomings are magnified, propagating errors through the coupled pose estimation and mapping modules. In contrast, the SSIM loss assesses image fidelity through local luminance, contrast, and structure, prioritizing the preservation of edges, corners, and texture patterns over exact pixel-wise intensity. This makes it inherently more aligned with the requirements of robust SLAM. This discrepancy arises because a loss function’s efficacy in isolation does not fully predict its behavior in a complex, coupled system. Our proposed FGF-SSIM builds upon this principled foundation of SSIM, further enhancing the geometric clarity and structural coherence of the reconstructed map. FGF-SSIM demonstrates optimal synergy with the pose estimation and mapping modules, effectively balancing texture fidelity and geometric consistency, which is critical for overall VSLAM performance.

Table 3. Ablation experiments results of loss function formulations on the Replica dataset’s office1 scene.

Method	PSNR [dB] ↑	SSIM ↑	LPIPS ↓	RMSE ATE ↓
w/ L1	41.52	0.951	0.067	0.60
w/ L2	39.18	0.939	0.083	0.76
w/ SSIM	42.09	0.977	0.055	0.57
w/ MS-SSIM	40.66	0.945	0.070	0.68
FGF-SSIM	43.71	0.982	0.031	0.42

The upward arrow (↑) indicates that higher values are better for that metric, while the downward arrow (↓) indicates that lower values are better. Through ablations on the Replica dataset, the ablation study validates the efficacy of the proposed SLAM architecture in achieving high-fidelity scene reconstruction and precise trajectory estimation across different loss functions. Quantitative results establish a clear hierarchy of contributions (L2 < MS-SSIM < L1 < SSIM-SSIM < FGF-SSIM).

Table 4 presents a systematic loss function ablation study of FGF-SLAM conducted on the Replica dataset’s office1 scene [35]. We analyze three critical components: photometric loss, depth loss, and anisotropic regularization, quantifying their contributions to VSLAM performance. When disabling the photometric loss, the system retains functionality through depth alignment and anisotropic regularization. However, quantitative results indicate severe degradation in pose estimation accuracy (RMSE ATE error increases by 374% relative to the baseline scenario), confirming the essential role of photometric alignment in VSLAM. This component enables cross-frame pixel intensity alignment, serving as a primary visual feedback mechanism for camera localization. Furthermore, under photometric-deprived conditions, the ablation of photometric loss leads to a marked decline in reconstruction quality (PSNR decreases by 18.94%, SSIM decreases by 10.99%, PSNR increases by 393.81%). These results underscore the necessity of incorporating photometric processing via a fractional Gaussian field. Ablating the depth loss, by contrast, preserves reasonable reconstruction quality compared to photometric ablation (PSNR decreases by 10.89%, SSIM decreases by 8.25%, PSNR increases by 292.86%), suggesting RGB inputs alone can sustain mapping integrity. However, the pose estimation accuracy performance degrades substantially (RMSE ATE increases by 293%), indicating that depth constraints help curb error accumulation in pose estimation. This contrast underscores the secondary yet valuable role of depth loss: while not critical for scene representation, it supplies geometric priors that improve tracking accuracy. Notably, our FGF-SLAM framework was originally designed to perform 3D reconstruction without explicit depth input. When anisotropic regularization is disabled, performance degradation is the smallest among all ablations (PSNR decreases by 7.23%, SSIM decreases by 1.83%, PSNR increases by 122.58%, RMSE ATE increases by 52.38%), primarily manifesting as increased surface artifacts in reconstructed meshes. This confirms its auxiliary role in noise suppression rather than in core SLAM functionality. Nevertheless, such regularization aids in recovering finer luminance and structural details in VSLAM.

Table 4. Ablation experiments results of loss function components on the Replica dataset’s office1 scene.

Method	PSNR [dB] ↑	SSIM ↑	LPIPS ↓	RMSE ATE ↓
w/o Color Loss	35.43	0.874	0.188	4.74
w/o Depth Loss	38.95	0.901	0.112	3.35
w/o Isotropic Loss	40.55	0.964	0.069	0.64
FGF-SLAM	43.71	0.982	0.031	0.42

The upward arrow (↑) indicates that higher values are better for that metric, while the downward arrow (↓) indicates that lower values are better. The ablation study confirms the synergistic contributions of the individual loss functions in FGF-SLAM to reconstruction accuracy on the Replica dataset’s office1 scene. Quantitative results establish a clear hierarchy of contributions (Anisotropic regularization < Depth loss < Photometric loss).

6. Conclusions

This work presents a comprehensive solution to the fundamental challenge in dense visual SLAM where existing loss functions fail to properly balance luminance, contrast, and structural fidelity under varying illumination conditions. We introduce a fractional Gaussian field (FGF) that innovatively combines Caputo fractional derivatives with Gaussian weighting, creating a hybrid kernel coupling power-law decay for long-range memory with Gaussian attenuation for local smoothness. Kernel analysis confirms that the FGF maintains non-negligible weights at larger distances, retaining a weight of 0.01 even at 10-pixel distances while conventional Gaussian kernels attenuate rapidly to near-zero values, establishing superior long-range dependency while preserving local structural coherence. Building on this foundation, we develop FGF-SSIM, a novel loss function that adaptively recalibrates SSIM components through fractional-order statistics, and integrate it into a complete 3D Gaussian Splatting based SLAM framework (FGF-SLAM) where it serves as the primary photometric objective in both tracking and mapping modules. Rigorous validation confirms the effectiveness of our approach. Illumination robustness tests show FGF-SSIM achieves 21.94 dB PSNR under 30% luminance increase, outperforming L1 loss by 1.82 dB. Reconstruction accuracy on standard benchmarks reveals FGF-SLAM attains 36.04 dB PSNR on the TUM dataset, representing a 72% improvement with 1.73 cm ATE RMSE, and achieves 38.70 dB PSNR with 0.045 LPIPS on the Replica dataset. Ablation studies validate our design choices, showing that removing FGF-SSIM causes 18.9% PSNR degradation, confirming its critical role in achieving robust high-quality SLAM performance. While the proposed method demonstrates superior performance, the observed trade-off between long-range dependency modeling and local precision in the fractional Gaussian kernel warrants further investigation for optimal parameter adaptation across different visual conditions. Future work will focus on adaptive parameter optimization and explore broader applications in image processing domains such as medical image enhancement, remote sensing analysis, and high dynamic range imaging, where robust multi-scale feature preservation under varying acquisition conditions is equally crucial as in VSLAM systems.