Chaotic Dynamics, Complexity Analysis and Control Schemes in Fractional Discrete Market System

Abstract

The study of economic maps has consistently attracted researchers due to their rich dynamics and practical relevance. A deeper understanding of these systems enables the development of more effective control strategies. In this work, we examine the influence of the fractional order $\upsilon$ with the Caputo fractional difference on an economic market map. The primary contribution is the comprehensive analysis of how both commensurate and incommensurate fractional orders affect the stability and complexity of the map. Numerical investigations, including phase portraits, largest Lyapunov exponents, and bifurcation analysis, reveal that the system undergoes a cascade of period-doubling bifurcations before transitioning into chaos. To further characterize the dynamics, complexity is evaluated using the 0–1 test and $C_0$ complexity, both confirming chaotic behavior. Furthermore, two-dimensional control schemes are introduced and theoretically validated to both stabilize the chaotic economic market map and achieve synchronization with a combined response map. The theoretical and numerical results are validated through MATLAB 2016 simulations.

1. Introduction

Economic phenomena and practices are explained through the use of mathematically structured language in mathematical economics, which is one of the theoretical and practical disciplines [1,2]. The development of ideas and concepts in a form that is self-consistent and mathematically appropriate is an important objective of mathematical economics. Models of economic phenomena and processes are then built using these foundations. On the other hand, the market is a major issue in economic systems and is taken into consideration, and its consequences are thoroughly examined [3]. Economic models that depend on difference equations involving integer orders are unable to account for non-locality and memory processes. Thus, essential parts of economic processes and occurrences are not reflected by this mathematical language. When studying the suggested economic models in integer order, the underlying assumptions are based on standard macroeconomic linkages between output, demand, and investment [4,5]. In order to achieve a stable equilibrium, it is assumed that agents modify their economic choices in accordance with past market conditions. Supply and demand feedback mechanisms give rise to nonlinearities, which can produce intricate dynamics. It is essential to comprehend how the integer-order map represents the fundamental mechanics of market adjustment and stability in a memory-less context before moving on to the fractional-order scenario [4,5].

The discrete economic model with fractional order is relatively new in comparison to the continuous model. There are not many studies on discrete chaotic models in the economic domain [6,7]. In contrast, continuous economic models have been the topic of numerous recent publications [8,9,10,11]. Research has shown how to model systems in a variety of financial and economic domains, including macroeconomics and microeconomics.

Fractional calculus is considered a useful tool for representing nonlinear systems. Many real-world phenomena in a variety of fields, including neural networks [12], finance [13,14], biology [15], economics [16,17], and so on, can be more accurately described thanks to the unique properties of fractional-order systems. Therefore, it makes sense and supports arguments to use fractional calculus for presenting financial and economic models [18,19].

Recently, there has been a notable increase in the significance of chaos in economic systems. Additionally, an expansion of fractal concepts has been applied to the study of chaotic economic models [20,21]. One-parameter Mittag-Leffler as a basis of a mathematical system in [20] has been proposed to explain the Phillips curve and the relationship between inflation and unemployment rates, while Ming et al. [21] proposed a different application of fractional calculus in the economic growth systems of the Chinese economy. However, external disturbances and dynamic uncertainties always have an impact on economic systems. These features have been examined in numerous economic models, which have documented the chaotic behaviors that can result from various bifurcation types, including a period-doubling bifurcation. We explore how the complexity of market behavior can be altered by a single agent using both numerical computations and mathematical analysis. There are memory effects in many variables in economic systems, which can be described by discrete fractional calculus. Because of its captivating dynamics, the Caputo fractional derivative is also given more consideration and used in specific discrete models [22,23,24,25]. For example, a triopoly game involving bounded rationality using Caputo-like operator was proposed by Khennaoui et al. in [23]. Chu et al. [24] explored the dynamics of artificial macro-economics using fractional calculus. In [25], employing the Caputo difference discrete operator to present the fractional discrete Lotka–Volterra system. Further research into control procedures is necessary to achieve improved system synchronization and control performance in order to address these issues [26,27,28,29]. The current research is motivated by these issues. This paper delves deeply into the various nonlinear dynamical behaviors that economic maps with a market theme may exhibit, including chaos and a period-doubling bifurcation.

The essential discoveries and results obtained in this study are listed below:

1.

A new chaotic fractional economic market map is examined through mathematical methods.

2.

Fractional discrete calculus basics and an explanation of the new fractional form of an economic market map are provided.

3.

To validate the fractional map’s complexity, we provide chaos tests, such as the 0–1 test and $C_0$ complexity.

4.

The scheme of control for the present map stabilization and synchronization is achieved in accordance with the stability criterion for discrete nonlinear models.

The forthcoming sections are detailed as follows: certain notions and terms essential to the fractional discrete calculus are considered in Section 2. The goal of Section 3 is to create a new fractional map of the economic market while examining the chaotic dynamics concerning commensurate and incommensurate fractional-order values. After that, the $C_0$ complexity and 0–1 test of the chaotic map behaviors are examined in Section 4. Analytically and numerically establishing the convergence of the synchronization errors is conducted through the stabilization scheme, which is covered in Section 5. Finally, Section 6 offers a summary of this paper’s main concepts and suggests ideas for further research.

2. Fractional Discrete–Time Calculus

Let us first review some of the relevant notions of discrete fractional calculus before delving into the topic of a fractional economic market map under commensurate ${\upsilon }_1={\upsilon }_2=\upsilon$ and incommensurate ${\upsilon }_1\ne {\upsilon }_2$ fractional orders. It is important to understand that equations with the same order form a commensurate-order fractional model. The idea of incommensurate order, on the other hand, calls for using distinct fractional orders for each form equation.

Definition 1

([30]). The ν-th discrete fractional sum ${\mathrm{\Delta }}_r^{-\nu }$ for $\nu >0$ with the fractional order given by

$${\mathrm{\Delta }}_r^{-\nu }Y\left(s\right)={\displaystyle \frac{1}{\Gamma \left(\nu \right)}}\sum _{\varpi =r}^{s-\nu }{\left(s-1-\varpi \right)}^{\left(\nu -1\right)}Y\left(\varpi \right),s\in {\mathbb{N}}_{r+\nu },$$

(1)

where $Y:{\mathbb{N}}_r\to \mathbb{R}$, with ${\mathbb{N}}_r=\{r,r+1,r+2,\dots \}$, $r\in \mathbb{R}$ is the starting point.

Definition 2

([31]). For $\mathfrak{k}-1<\nu \le \mathfrak{k}$ and $\mathfrak{k}=⌈\nu ⌉+1$, the ν-th Caputo fractional delta operator for $Y\left(s\right)$ is expressed as

$$\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{\nu }Y\left(s\right)& ={\mathrm{\Delta }}_r^{-(\mathfrak{k}-\nu )}{\mathrm{\Delta }}^{\mathfrak{k}}Y\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma \left(\mathfrak{k}-\nu \right)}}\sum _{\varpi =r}^{s-\left(\mathfrak{k}-\nu \right)}{\left(s-1-\varpi \right)}^{\left(\mathfrak{k}-\nu -1\right)}{\mathrm{\Delta }}^{\mathfrak{k}}Y\left(\varpi \right),\hfill \end{array}$$

(2)

where $s\in {\mathbb{N}}_{r+\mathfrak{k}-\nu }$. Such as ${\left(s-1-\varpi \right)}^{\left(\mathfrak{k}-1-\nu \right)}$ can presented as

$$\begin{array}{cc}\hfill {\left(s-1-\varpi \right)}^{\left(\mathfrak{k}-1-\nu \right)}& ={\displaystyle \frac{\Gamma (s-\varpi )}{\Gamma \left(1+s-\varpi -\mathfrak{k}-\nu \right)}},\hfill \end{array}$$

(3)

and

$$\begin{array}{cc}\hfill {\mathrm{\Delta }}^{\mathfrak{k}}Y\left(s\right)& =\mathrm{\Delta }{\mathrm{\Delta }}^{\mathfrak{k}-1}Y\left(s\right)\hfill \\ \hfill & =\sum _{\eta =0}^{\mathfrak{k}}\left(\begin{array}{c}\mathfrak{k}\\ \eta \end{array}\right){\left(-1\right)}^{\mathfrak{k}-\eta }Y\left(s+\eta \right).\hfill \end{array}$$

(4)

For $\mathfrak{k}=1$, the ν-th Caputo discrete difference operator can expressed as

$$\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{\nu }Y\left(s\right)& ={\mathrm{\Delta }}_r^{-(1-\nu )}{\mathrm{\Delta }}^{n}Y\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma \left(1-\nu \right)}}\sum _{\varpi =r}^{s-\left(1-\nu \right)}{\left(s-1-\varpi \right)}^{-\nu }\mathrm{\Delta }Y\left(\varpi \right).\hfill \end{array}$$

(5)

Theorem 1

([32]). The equivalent discrete integral of

$$\left\{\begin{array}{c}{}^c\mathrm{\Delta }_r^{\nu }y\left(s\right)=Y(s+\nu -1,y(s+\nu -1)),\hfill \\ {\mathrm{\Delta }}^{\eta }y\left(r\right)=y_{\eta },\mathfrak{k}=\lceil \nu \rceil +1,\eta =0,1,\dots ,\mathfrak{k}-1,\hfill \end{array}\right.$$

(6)

can be obtained as

$$y\left(s\right)=y_0\left(r\right)+{\displaystyle \frac{1}{\Gamma \left(\nu \right)}}\sum _{\varpi =r+\mathfrak{k}-\nu }^{s-\nu }{(s+1-\varpi )}^{(\nu -1)}Y(\varpi -1+\nu ,y(\varpi -1+\nu )),$$

(7)

where

$$y_0\left(r\right)=\sum _{\eta =0}^{\mathfrak{k}-1}{\displaystyle \frac{{(s-t)}^{\eta }}{\Gamma (\eta +1)}}{\mathrm{\Delta }}^{\eta }y\left(r\right).$$

The following theorems must be established in order to determine the fractional map’s stability criteria using commensurate and incommensurate orders.

Theorem 2

([33]). The fixed point, ${\varpi }_p$, of a commensurate fractional discrete system ${}^c\mathrm{\Delta }^{\nu }g\left(s\right)=g\left(\mathfrak{A}(s-1+\nu )\right)$ where $\mathfrak{A}\left(s\right)={\left({\mathfrak{A}}_1\left(s\right),{\mathfrak{A}}_2\left(s\right),\dots ,{\mathfrak{A}}_n\left(s\right)\right)}^T$, $J_{\alpha }\left(\mathfrak{A}\right)={\left.{\displaystyle \frac{\partial g\left(y\right)}{\partial \mathfrak{A}}}\right|}_{\mathfrak{A}={\mathfrak{A}}_p}$ is the Jacobian matrix at ${\varpi }_p$ is asymptotically stable if all ${\lambda }_{\iota }$, $\iota =\overline{1,n}$, eigenvalues of $J_{\alpha }$ satisfy

$${\lambda }_{\iota }\in \left\{\varsigma \in \mathbb{C}:\left|\varsigma \right|<{\left(2cos{\displaystyle \frac{\left|arg\varsigma \right|-\pi }{2-\nu }}\right)}^{\nu }and\left|arg\varsigma \right|>{\displaystyle \frac{\nu \pi }{2}}\right\},$$

(8)

Theorem 3

([34]). Consider the system

$$\left\{\begin{array}{cc}\hfill & {}^c\mathrm{\Delta }_r^{{\nu }_1}{y}_1\left(\tau \right)={\beta }_1\left(y(s-1+{\nu }_1)\right),\hfill \\ \hfill & {}^c\mathrm{\Delta }_r^{{\nu }_2}{y}_2\left(\tau \right)={\beta }_2\left(y(s-1+{\nu }_2)\right),\hfill & \hfill s=0,1,\dots ,\\ & ⋮\hfill \\ \hfill & {}^c\mathrm{\Delta }_r^{{\nu }_{\mathfrak{m}}}{y}_{\mathfrak{m}}\left(s\right)={\beta }_{\mathfrak{m}}\left(y(s-1+{\nu }_{\mathfrak{m}})\right).\hfill \end{array}\right.$$

(9)

Set $y\left(s\right)={(y_1\left(s\right),...,y_{\mathfrak{m}}\left(s\right))}^T\in {\mathbb{R}}^{\mathfrak{m}}$, $\beta =({\beta }_1,{\beta }_2,...,{\beta }_{\mathfrak{m}}):{\mathbb{R}}^{\mathfrak{m}}\to {\mathbb{R}}^m$. Let ${\nu }_i\in (0,1]$, $i=\overline{1..\mathfrak{m}}$) be taken into consideration, and let C be the $\mathbf{LCM}$ of the denominators ${\overline{\mathfrak{b}}}_i$ of ${\upsilon }_i$ appended to ${\nu }_i={\displaystyle \frac{{\overline{\mathfrak{b}}}_i}{{\overline{a}}_i}}.$ Let $({\overline{\mathfrak{b}}}_i,{\overline{\mathfrak{a}}}_i)=1$, ${\overline{\mathfrak{b}}}_i,{\overline{\mathfrak{a}}}_i\in {\mathbb{Z}}_{+}$, $\forall \iota =\overline{1,m}$.

$$det(diag({\lambda }^{C{\nu }_1},\dots ,{\lambda }^{C{\nu }_m})-(1-{\lambda }^C)\mathfrak{B})=0,$$

(10)

where the Jacobin matrix of (9) is $\mathfrak{B}$. If every root of (10) is contained in $\mathbb{C}/K^{\delta }$ with $\delta ={\displaystyle \frac{1}{C}}$,

$$K^{\delta }=\left\{\alpha \in \mathbb{C}:\left|\alpha \right|\le {\left(2cos{\displaystyle \frac{\left|arg\alpha \right|}{\delta }}\right)}^{\delta }and\left|arg\alpha \right|\le {\displaystyle \frac{\delta \pi }{2}}\right\}.$$

(11)

The zero solution of (9) is asymptotically stable.

3. The Fractional Economic Market Map

The development of ideas and concepts into forms that are self-consistent and mathematically appropriate is the main objective of mathematical economics. Models of economic phenomena and processes are then built using these foundations. The variety of mathematical forms that economic models offer have made them one of the most interesting areas of study for scientists in recent years [35]. The suggested map is created using the fundamental interaction between supply and demand in a nonlinear economy [36]. In response to prior production levels, consumers alter their demand, while producers adjust their output based on past market pricing. Based on these presumptions, in our work, we introduce a new fractional-order economic market map using Caputo discrete difference operator ${}^C\mathrm{\Delta }_r^{{\upsilon }_i}$, $i=1,2,$ as given in

$$\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}x\left(\tau \right)& =-ax\left({\mu }_1\right)+{\displaystyle \frac{a}{{(bx\left({\mu }_1\right)+(1-b)y\left({\mu }_1\right))}^{\gamma }}},\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}y\left(\tau \right)& ={\displaystyle \frac{1}{{(bx\left({\mu }_2\right)+(1-b)y\left({\mu }_2\right))}^{\gamma }}}-y\left({\mu }_2\right),\hfill \end{array}$$

(12)

where ${\mu }_1=\tau -1+{\upsilon }_1$, ${\mu }_2=\tau -1+{\upsilon }_2$, $x\left(\tau \right)$ represents the supply, $y\left(\tau \right)$ denotes the demand, $a\in (0,0.3]$ is the supply adjustment rate to market changes, and $b\in [0,1]$ is the demand adjustment rate. Note that in the case where ${\upsilon }_1\ne {\upsilon }_2$, we obtain an incommensurate fractional economic market map, whereas in the other case, we obtain a commensurate fractional economic market map. An illustration of the main characteristics of a fractional economic map (12) is shown in Figure 1. The foundation of the model is the economic market map, which captures the interactions and standards that restrict economic dynamics. This core is impacted by two essential features: chaotic behavior, which emphasizes the dynamic sensitivity to initial conditions and the creation of intricate, irregular patterns, and fractional order, which represents the presence of long-memory and global interaction impacts in the economic map. The partial overlap of the circles highlights the relationship of the map properties.

Figure 1. The three main characteristics of the chaotic fractional economic market map (12).

3.1. Stability Analysis

Now, we assign the left0hand side of the fractional-order economic market map (12) to zero for calculating its equilibrium points $\left(EP\right)$ $P^{*}$ as follows:

$$\left\{\begin{array}{cc}\hfill & -a{x}^{*}+{\displaystyle \frac{a}{{((1-b)y^{*}+b{x}^{*})}^{\gamma }}}=0,\hfill \\ \hfill & {\displaystyle \frac{1}{{((1-b)y^{*}+b{x}^{*})}^{\gamma }}}-y^{*}=0.\hfill \end{array}\right.$$

(13)

Through algebraic calculation, the fractional map has a unique $\left(EP\right)$ $P^{*}=(1,1)$ independent of the controller’s parameters. The stability of the $\left(EP\right)$ is determined using the following conditions, which are adapted from the criteria presented in [33] to examine the stability of the $\left(EP\right)$ of map (12).

We apply the following proposition to examine the stability of the $\left(EP\right)$ of map (12).

Proposition 1

([33]). The fractional economic market map (12) may satisfy the following conditions:

$$det\left(J_{\alpha }\right)>0\mathit{\text{and}}{\displaystyle \frac{-\mathrm{tr}\left(J_{\alpha }\right)}{2}}\ge \sqrt{det\left(J_{\alpha }\right)},\upsilon >{log}_2{\displaystyle \frac{\sqrt{{\left(\mathrm{tr}\left(J_{\alpha }\right)\right)}^2-4det\left(J_{\alpha }\right)}-\mathrm{tr}\left(J_{\alpha }\right)}{2}},$$

(14)

or

$$det\left(J_{\alpha }\right)>0\mathit{\text{and}}{\displaystyle \frac{\left|\mathrm{tr}\right(J_{\alpha }\left)\right|}{2}}<\sqrt{det\left(J_{\alpha }\right)}<{\left(2cos\left({\displaystyle \frac{\rho -\pi }{2-\upsilon }}\right)\right)}^{\upsilon },\upsilon <{\displaystyle \frac{2\rho }{\pi }},$$

(15)

where

$$\rho ={\displaystyle \frac{\mathrm{tr}\left(J_{\alpha }\right)}{|{\left(\mathrm{tr}\left(J_{\alpha }\right)\right)}^2-4det\left(J_{\alpha }\right)|}}.$$

(16)

This means that the map is asymptotically stable locally.

Proof. 

The Jacobian matrix, $J_{\alpha }$, of the map evaluated at $P^{*}=(1,1)$ is simply calculated as

$$J_{\alpha }=\left(\begin{array}{cc}-a-a\gamma b& -a\gamma (1-b)\\ -\gamma b& -\gamma (1-b)-1\end{array}\right).$$

(17)

The trace, $tr\left(J_{\alpha }\right)$, is calculated as

$$tr\left(J_{\alpha }\right)=-a-a\gamma b-\gamma (1-b)-1.$$

(18)

The associated characteristic equation is

$$det\left(J_{\alpha }\right)={\lambda }^2+\lambda (a+a\gamma b-\gamma b+\gamma +1)+(a\gamma -ba\gamma +a{\gamma }^{2}b(1-b))>0,$$

(19)

for $a\in (0,0.3]$ and $b\in [0,1]$. The eigenvalues are

$${\lambda }_{\iota }={\displaystyle \frac{-f\pm \sqrt{f^2-4hd}}{2h}},\iota =1,2,$$

(20)

where

$$h=1,f=a+a\gamma b-\gamma b+\gamma +1,d=a\gamma -ba\gamma +a{\gamma }^{2}b(1-b).$$

If $tr\left(J_{\alpha }\right)>0$

$$2\sqrt{det\left(J_{\alpha }\right)}\le tr\left(J_{\alpha }\right)<2^{-\nu }det\left(J_{\alpha }\right)+2^{\nu },0<det\left(J_{\alpha }\right)<2^{2\nu },$$

(21)

or

$$2\sqrt{det\left(J_{\alpha }\right)}cos\left((2-\upsilon )arccos\left({\displaystyle \frac{det{\left(J_{\alpha }\right)}^{1/2\alpha }}{2}}\right)\right)<tr\left(J_{\alpha }\right)<2\sqrt{det\left(J_{\alpha }\right)}cos\left({\displaystyle \frac{\upsilon \pi }{2}}\right).$$

(22)

If $tr\left(J_{\alpha }\right)<0$

$$2\sqrt{-2det\left(J_{\alpha }\right)}<tr\left(J_{\alpha }\right)<-2^{1-\upsilon }det\left(J_{\alpha }\right)+2^{\upsilon },-2^{2\upsilon -1}<det\left(J_{\alpha }\right)<0,$$

(23)

or

$$2\sqrt{-2det\left(J_{\alpha }\right)}cos\left((2-\upsilon )arccos\left({\displaystyle \frac{{(-2det\left(J_{\alpha }\right))}^{1/2\nu }}{2}}\right)\right)<tr\left(J_{\alpha }\right)<2\sqrt{-2det\left(J_{\alpha }\right)}cos\left({\displaystyle \frac{\upsilon \pi }{2}}\right).$$

(24)

This means that $P^{*}=(1,1)$ is always asymptotically stable when the conditions meet (14) or (15). □

3.2. Lyapunov Exponents, Bifurcation and Chaos

This part will examine the behavior of the fractional economic market map (12) in light of two instances: incommensurate orders ${\upsilon }_1\ne {\upsilon }_2$ and the commensurate fractional orders ${\upsilon }_1={\upsilon }_2=\upsilon$. Numerous numerical techniques will be used in this investigation, including the plotting of bifurcation and maximum Lyapunov exponents ($L{E}_{max}$) and the presentation of phase portraits and time series of the suggested fractional map (12). To this aim, the numerical formula as per Theorem 1 is formulated as

$$\left\{\begin{array}{c}x\left(\mathfrak{k}\right)=x\left(0\right)+{\displaystyle \frac{1}{\Gamma \left({\upsilon }_1\right)}}{\displaystyle \sum _{\mathfrak{j}=0}^{\mathfrak{k}-1}}{\displaystyle \frac{\Gamma ({\upsilon }_1+\mathfrak{k}-\mathfrak{j}-1)}{\Gamma (\mathfrak{k}-\mathfrak{j})}}\left(-ax\left(\mathfrak{j}\right)+{\displaystyle \frac{a}{{(bx\left(\mathfrak{j}\right)+(1-b)y\left(\mathfrak{j}\right))}^{\gamma }}}\right),\hfill \\ y\left(\mathfrak{k}\right)=y\left(0\right)+{\displaystyle \frac{1}{\Gamma \left({\upsilon }_2\right)}}{\displaystyle \sum _{\mathfrak{j}=0}^{\mathfrak{k}-1}}{\displaystyle \frac{\Gamma ({\upsilon }_2+\mathfrak{k}-\mathfrak{j}-1)}{\Gamma (\mathfrak{k}-\mathfrak{j})}}\left({\displaystyle \frac{1}{{(bx\left(\mathfrak{j}\right)+(1-b)y\left(\mathfrak{j}\right))}^{\gamma }}}-y\left(\mathfrak{j}\right)\right).\hfill \end{array}\right.$$

(25)

Case 1: With the aim of analyzing in greater depth the influence of ${\upsilon }_1={\upsilon }_2=\upsilon$ commensurate derivatives on the dynamics of the fractional economic market map (12), once the two parameters, a and b, were determined to be bifurcation parameters, the bifurcation diagrams were drawn. In light of this, Figure 2 and Figure 3, respectively, present the maximum Lyapunov exponents assessed via the Jacobian Matrix method [37] and bifurcation versus a and b. First, we proposed a as the bifurcation parameter and set $b=0.8$, $\gamma =8$ as the system’s parameters, with the initial conditions $(x_0,y_0)=(1.5,3)$ (IN). When the parameter of bifurcation a was raised in $[0,0.3]$ for $\upsilon =0.9$ and $\upsilon =0.99$, it is evident that the fractional economic market map (12) began in periodic states and got into chaos via the reverse period-doubling route, with a few periodic windows shown as in Figure 2. Fractional economic market map (12) has been shown to generate complex dynamical behavior depending on different values of bifurcation parameters; these include a reverse period-doubling bifurcation, a period-doubling bifurcation, and chaos. According to these diagrams, fractional economic market map (12) started in a periodic state with a negative maximum Lyapunov exponent $L{E}_{max}$, the fractional economic market map (12) was in a chaotic state when a increased where $L{E}_{max}$ was positive, and it eventually entered reverse period-doubling bifurcation. In a similar manner with bifurcation parameter b in $[0,1]$, we chose $a=0.2$ and $\gamma =8$ for commensurate derivatives $\upsilon =0.9$ and $\upsilon =0.99$, as seen in Figure 3. It is clear to see that there are multiple chaotic regions in $[0,1]$, where chaos appears and disappears. It is evident that when b is close to 1, the states display reverse period-doubling. Next, we examine how $\upsilon$ influences fractional economic market map (12) behavior for $a=0.2$, $b=0.8$ and $\gamma =8$ in Figure 4 with $\mathrm{\Delta }\upsilon =0.0001$ step size and a time-series length of ${10}^5$ iterations. As one can note, the map is more chaotic when $\upsilon \in [0.1,0.2)\cup (0.94,1]$ where $L{E}_{max}$ has higher values, while when $\upsilon \in [0.35,0.62)$, chaos disappears and appears; otherwise, the states of the proposed map are stable on the rest of the intervals. For a more comprehensive understanding, Figure 5 portrays the phase plane and the corresponding time series for distinct commensurate fractional values. It is obvious that whenever the fractional values change, there is a resulting shift. The observable chaos of the fractional economic market model (12) behavior is suggested by the existence of the strange attractor when $\upsilon =0.99$. The 2D stability map of the system in the commensurate-order case is plotted in the $(a,\upsilon )$ plane, as shown in Figure 6. Parameter a is represented by the horizontal axis, while fractional order $\upsilon$ is represented by the vertical axis. The greatest Lyapunov exponent ($L{E}_{max}$) is represented by color, with yellow regions ($L{E}_{max}>0$) denoting chaotic behavior and the remaining regions ($L{E}_{max}<0$) denoting periodic dynamics. The black contour line at $L{E}_{max}=0$ in the illustration clearly delineates the threshold between stability and chaos. To further examine the characteristics of fractional economic market model (12), we present bifurcation charts for various values of $\upsilon$ by taking a as the bifurcation parameter and assuming $b=8$ and $\gamma =0.8$ for the remaining parameters, and the outcomes are shown in Figure 7. These analyses lead us to conclude that different fractional values produce different dynamical behaviors that influence the dynamics of fractional economic market map (12).

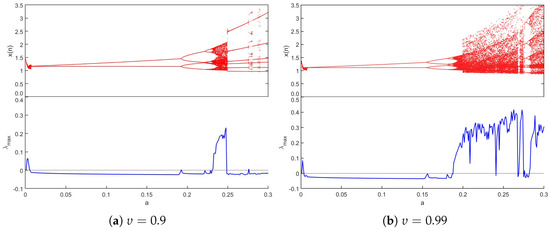
Figure 2. Bifurcation and $LE{m}_{ax}$ of (12) versus $a\in [0,0.3]$.

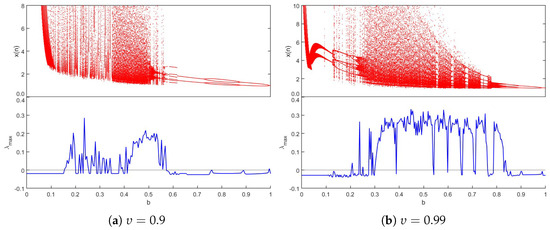
Figure 3. Bifurcation and $LE{m}_{ax}$ of (12) versus $b\in [0,1]$.

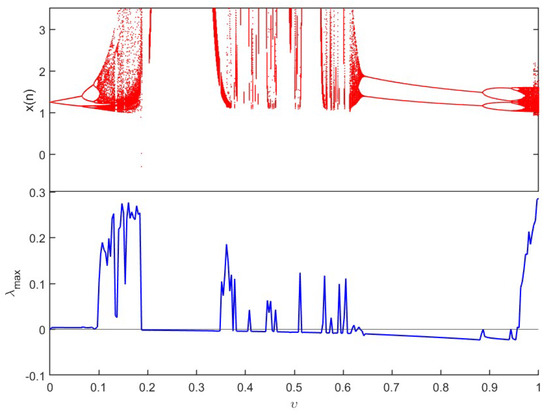
Figure 4. Bifurcation and $LE{m}_{ax}$ of (12) for $\upsilon \in (0,1]$.

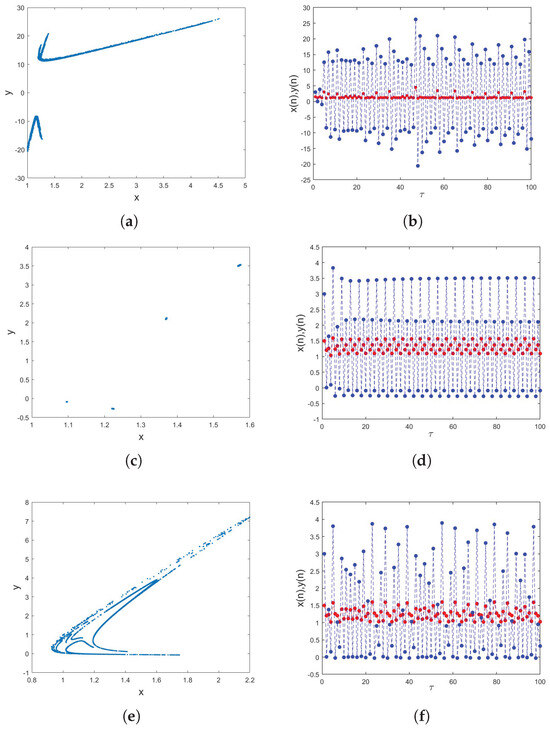
Figure 5. (a) Phase portrait for $\upsilon =0.15$. (b) Time series of $x\left(n\right)$ (red) and $y\left(n\right)$ (blue) associated with (a). (c) Phase portrait for $\upsilon =0.9$. (d) Time series associated with (c). (e) Phase portrait for $\upsilon =0.99$. (f) Time series associated with (e).

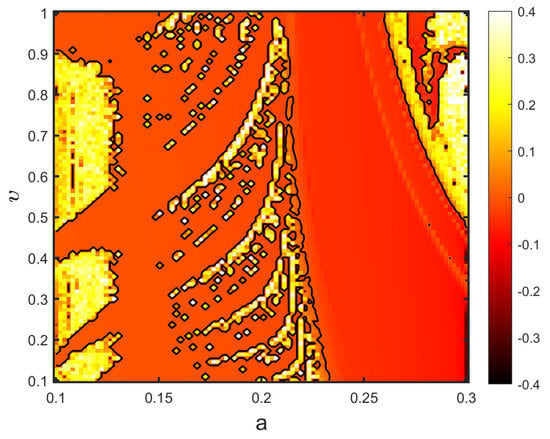
Figure 6. The $L{E}_{max}$ diagram of (12) for ${\upsilon }_1={\upsilon }_2=\upsilon$ in the $a\text{-}\upsilon$ plane.

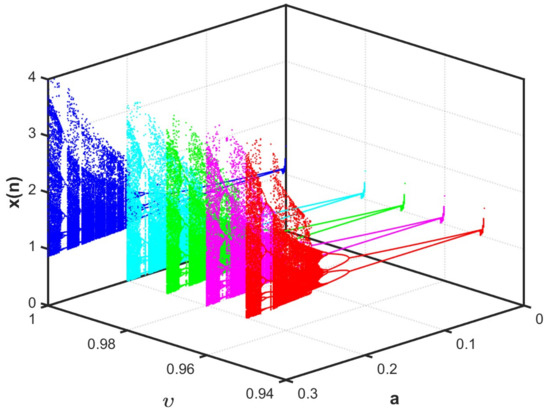
Figure 7. Bifurcation of (12) versus $a\in [0,0.3]$ for various fractional-order values $\upsilon$.

Case 2: This case is focused on investigating the dynamics of fractional economic market map (12) when ${\upsilon }_1\ne {\upsilon }_2$. Specifically, incommensurate fractional economic market map (12), where ${\upsilon }_1$ is the bifurcation parameter that varies in $(0,1]$ and ${\upsilon }_2=1$, is shown in Figure 8 along with its bifurcation and $L{E}_{max}$. We observe a transition in fractional economic market map (12) from stable to chaotic dynamics. Particularly, the chaotic behavior is shown when ${\upsilon }_1$ increases by means of a period-doubling bifurcation, as the $L{E}_{max}$ values change from negative to positive. Furthermore, Figure 9 displays the bifurcation and corresponding $L{E}_{max}$ for ${\upsilon }_2\in (0,1]$ and ${\upsilon }_1=1$, aiming to scrutinize the dynamics of (12) when ${\upsilon }_2$ varies. It seems that map (12) shows chaos when ${\upsilon }_2\in [0.3,0.33[\cup ]0.94,1]$ and regular states in the remainder of $(0,1]$. To gain a more thorough comprehension of the characteristics of fractional economic market map (12), bifurcation and $L{E}_{max}$ plots are carried out by taking into account a and b as bifurcation parameters. Figure 10 shows the period-doubling bifurcation when $a\in [0,0.3]$ varies for $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$ and $({\upsilon }_1,{\upsilon }_2)=(1,0.98)$ with $b=0.8$, $\gamma =8$ set as the system parameters. Similarly, b varies between $[0,0.1]$ for $({\upsilon }_1,{\upsilon }_2)=(1,0.32)$ and $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$ in Figure 11, and we see that the dynamics of fractional economic market map (12) gradually change. In particular, when the periodic motion shrinks, a chaotic region appears, whereas as b is increased, chaos disappears. Throughout the chaotic region, the $L{E}_{max}$ values are positive, evidently corresponding with the associated bifurcation. Since the incommensurate fractional values serve a crucial part in the dynamic behaviors of the suggested fractional economic market map (12), we can therefore confirm that it is a highly crucial parameter based on the previous findings. The 2D stability maps for the incommensurate-order case are shown in Figure 12 in planes $({\upsilon }_1,{\upsilon }_2)$, $(a,{\upsilon }_1)$, and $(a,{\upsilon }_2)$. The dynamics of the map are depicted in each subfigure as the fractional orders of the two state variables change. Stable (negative) and chaotic (positive) regimes are distinguished by the color distribution, which once more reflects $L{E}_{max}$. The diagram shows unequal regions of chaos in the $({\upsilon }_1,{\upsilon }_2)$ plane, suggesting that the two fractional orders do not equally contribute to system instability. As ${\upsilon }_2$ rises, chaos emerges more quickly, demonstrating its greater influence on behavior. Regardless of the fractional orders, the maps show that the dynamics remain largely chaotic in the $(a,{\upsilon }_1)$ and $(a,{\upsilon }_2)$ planes. The variation in the dynamical reactions is increased by the greater degrees of freedom introduced by the variations in the fractional orders. All things considered, these three maps verify that the system displays a richer and more intricate bifurcation structure in the incommensurate case compared to the commensurate one. Furthermore, Figure 13 shows the phase attractors and the time series according to various incommensurate fractional values. It is clear that fractional economic market map (12) exhibits a strange attractor when $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$. These findings suggest that, in comparison to fractional economic market map (12) with commensurate order, incommensurate fractional economic market map (12) has more complex dynamics.

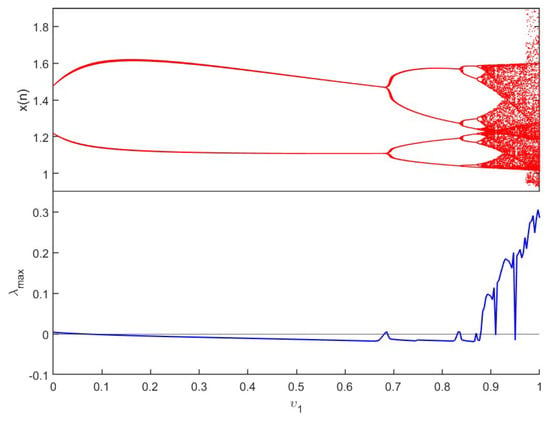
Figure 8. Bifurcation and $LE{m}_{ax}$ of (12) versus ${\upsilon }_1$ and ${\upsilon }_2=1$.

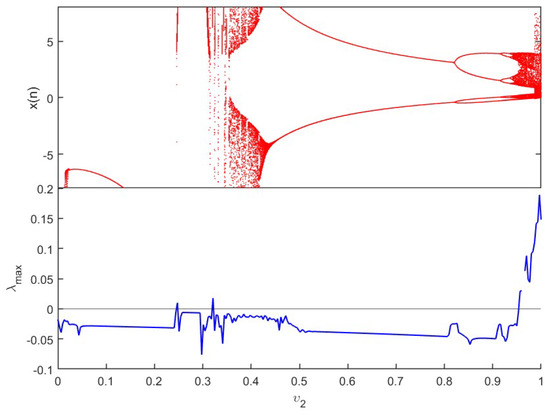
Figure 9. Bifurcation and $LE{m}_{ax}$ of (12) versus ${\upsilon }_2$ and ${\upsilon }_1=1$.

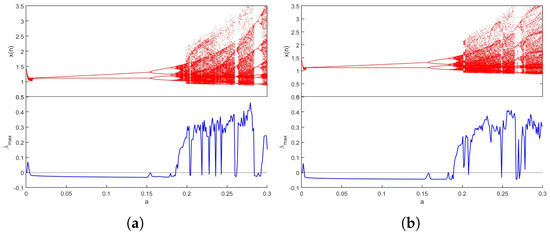
Figure 10. Bifurcation and $LE{m}_{ax}$ of (12) versus a for (a) $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$, (b) $({\upsilon }_1,{\upsilon }_2)=(1,0.98)$.

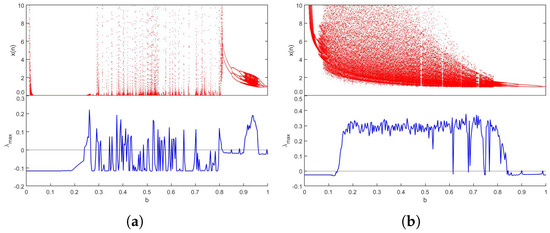
Figure 11. Bifurcation and $LE{m}_{ax}$ of (12) versus b for (a) $({\upsilon }_1,{\upsilon }_2)=(1,0.32)$, (b) $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$.

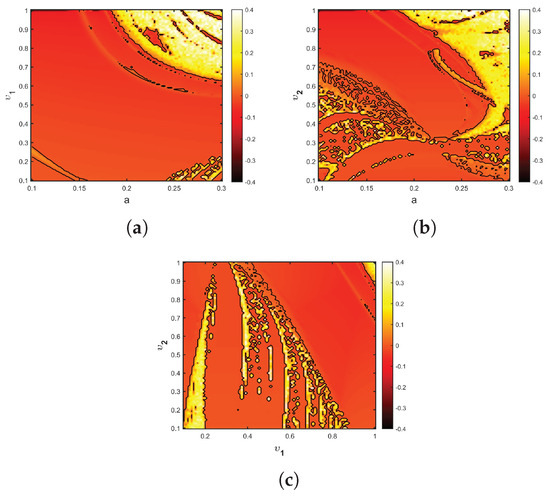
Figure 12. $L{E}_{max}$ diagram of (12) for ${\upsilon }_1\ne {\upsilon }_2$ (a) $a\text{-}{\upsilon }_1$ plane, (b) $a\text{-}{\upsilon }_2$ plane, (c) ${\upsilon }_1\text{-}{\upsilon }_2$ plane.

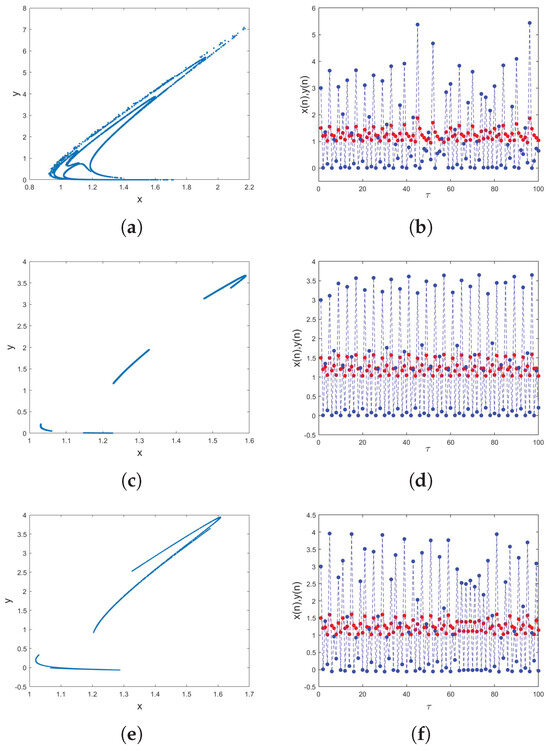
Figure 13. (a) Phase portrait for $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$. (b) Time series of $x\left(n\right)$ (red) and $y\left(n\right)$ (blue) associated with (a). (c) Phase portrait for $({\upsilon }_1,{\upsilon }_2)=(0.89,1)$. (d) Time series associated with (c). (e) Phase portrait for $({\upsilon }_1,{\upsilon }_2)=(1,0.98)$. (f) Time series associated with (e).

4. Complexity Analysis

This part evaluates the dynamic aspects of the suggested map by looking at the intricate nature of the chaotic behaviors. Specifically, in both incommensurate and commensurate cases, the complexity of the suggested economic market map (12) is estimated using $C_0$ complexity and the 0–1 test.

4.1. 0–1 Test

One more technique that can be used to study the fractional orders’ impact on the fractional map’s behaviors (12) is the ‘0–1 test’; this technique [38] is another method deployed for affirming the regular behavior and chaotic regions of chaotic economic market map (12). For $x\left(\overline{\mathfrak{h}}\right),\overline{\mathfrak{h}}=\overline{1,\mathfrak{Y}}$, $ϵ\in (0,\pi )$ is chosen at random, and the dynamics of the components

$$p_{ϵ}\left(\sigma \right)=\sum _{\overline{\mathfrak{h}}=1}^{\sigma }x\left(\overline{\mathfrak{h}}\right)cos\left(\overline{\mathfrak{h}}ϵ\right),q_{ϵ}\left(\sigma \right)=\sum _{\overline{\mathfrak{h}}=1}^{\sigma }x\left(\overline{\mathfrak{h}}\right)sin\left(\overline{\mathfrak{h}}ϵ\right),$$

(26)

provide a visual test, and the mean square displacement is defined by

$$M_{ϵ}\left(\sigma \right)=\underset{\mathfrak{Y}\to \infty }{lim}{\displaystyle \frac{1}{\mathfrak{Y}}}\sum _{\overline{\mathfrak{h}}=1}^{\mathfrak{Y}}\left[{\left(p_{ϵ}(\overline{\mathfrak{h}}+\sigma )-p_{ϵ}\left(\overline{\mathfrak{h}}\right)\right)}^2+{\left(q_{ϵ}(\overline{\mathfrak{h}}+\sigma )-q_{ϵ}\left(\overline{\mathfrak{h}}\right)\right)}^2\right],\sigma \le {\displaystyle \frac{\mathfrak{Y}}{10}}.$$

(27)

Furthermore, asymptotic growth rate $K_{ϵ}$ is represented as

$$K_{ϵ}=\underset{\overline{\mathfrak{h}}\to \infty }{lim}{\displaystyle \frac{log{M}_{ϵ}\left(\overline{\mathfrak{h}}\right)}{log\overline{\mathfrak{h}}}}.$$

(28)

Basically, if the plot of $p_{ϵ}$-$q_{ϵ}$ displays Brownian-like behavior, then output $K=median\left(K_{ϵ}\right)$ is close to 1, while if K is close to 0, then the $p_{ϵ}$-$q_{ϵ}$ plane exhibits bounded-like behavior.

Table 1 and Figure 14, show the findings of the 0–1 test of the chaotic fractional economic market map for ${\upsilon }_i$ fractional values. We see that when $\upsilon =0.15,\upsilon =0.99,({\upsilon }_1,{\upsilon }_2)=(0.98,1)$, K is close to 1, and p-q illustrates Brownian-like behavior, it suggests that the fractional economic market map is chaotic, as confirmed by the corresponding bifurcation diagram and $L{E}_{max}$. Additionally, Figure 14 shows bounded-like trajectories when $\upsilon =0.7,({\upsilon }_1,{\upsilon }_2)=(0.5,1),({\upsilon }_1,{\upsilon }_2)=(1,0.7)$, affirming that fractional economic market map (12) is periodic. This confirms the previous results of Section 3.

Table 1. The 0–1 test of chaotic fractional economic market map (12) for ${\upsilon }_i$.

${\mathit{\upsilon }}_1$	${\mathit{\upsilon }}_2$	K
0.15	0.15	0.9964
0.7	0.7	0.0018
0.99	0.99	0.9925
0.5	1	0.0023
1	0.7	0.0021
0.98	1	0.9923

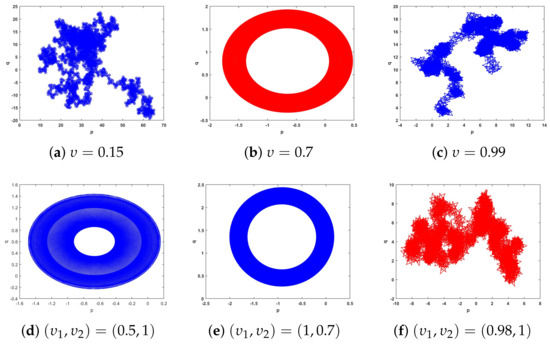
Figure 14. The 0–1 test of (12) for ${\upsilon }_i$ fractional values.

4.2. $C_0$ Complexity

This part calculates the complexity of fractional economic market map (12) using the $C_0$ complexity algorithm [39], which comes from the inverse Fourier transform. The $C_0$ algorithm for $\left\{\psi \right(\mathfrak{w}),\mathfrak{w}=1,...,\mathfrak{P}-1\}$ is given by

1

The Fourier transform of $\psi \left(\mathfrak{w}\right)$ is figured out by

$${\mathbf{X}}_{\mathfrak{P}}\left(\mathfrak{w}\right)={\displaystyle \frac{1}{\mathfrak{P}}}\sum _{\mathfrak{w}=0}^{\mathfrak{P}-1}\psi \left(s\right){exp}^{-2\pi i\left({\displaystyle \frac{Fj}{\mathfrak{P}}}\right)},s=0,1,..,\mathfrak{P}-1.$$

(29)

2

Our analysis of ${\mathbf{X}}_{\mathfrak{P}}\left(\mathfrak{w}\right)$ revealed the mean square as follows: $G_{\mathfrak{P}}={\displaystyle \frac{1}{\mathfrak{P}}}{\sum }_{\mathfrak{w}=0}^{N-1}{\left|{\mathbf{X}}_{\mathfrak{P}}\left(\mathfrak{w}\right)\right|}^2$ and set

$${\overline{\mathbf{X}}}_{\mathfrak{P}}\left(\mathfrak{w}\right)=\left\{\begin{array}{cc}{\mathbf{X}}_{\mathfrak{P}}\left(\mathfrak{w}\right)\hfill & \mathrm{if}\parallel {\mathbf{X}}_{\mathfrak{P}}{\left(\mathfrak{w}\right)\parallel }^2>{rG}_{\mathfrak{P}},\hfill \\ 0\hfill & \mathrm{if}\parallel {\mathbf{X}}_{\mathfrak{P}}{\left(\mathfrak{w}\right)\parallel }^2\le {rG}_{\mathfrak{P}}.\hfill \end{array}\right.$$

(30)

3

One can find the inverse Fourier transform as follows:

$$\mu (\mathit{ȷ})={\displaystyle \frac{1}{\mathfrak{P}}}\sum _{\mathfrak{w}=0}^{\mathfrak{P}-1}{\overline{\mathbf{X}}}_{\mathfrak{P}}\left(\mathfrak{w}\right){exp}^{2\pi i\left({\displaystyle \frac{\mathit{ȷ}\mathfrak{w}}{\mathfrak{P}}}\right)},\mathit{ȷ}=0,1,..,\mathfrak{P}-1.$$

(31)

4

Measure the $C_0$ complexity as

$$C_0={\displaystyle \frac{{\sum }_{\mathit{ȷ}=0}^{\mathfrak{P}-1}\parallel \mu (\mathit{ȷ})-\psi (\mathit{ȷ})\parallel }{{\sum }_{\mathit{ȷ}=0}^{\mathfrak{P}-1}{\parallel \psi (\mathit{ȷ})\parallel }^2}}.$$

(32)

We perform a numerical evaluation of the $C_0$ complexity for fractional economic market map (12), setting $a=0.2$, $b=0.8$, $\gamma =8$ and varying fractional orders $\upsilon$, ${\upsilon }_1$, and ${\upsilon }_3$ with $a\in (0,0.3]$, as shown in Figure 15. A higher $C_0$ complexity outcome indicates greater complexity in the fractional map (12). These outcomes are consistent with previous studies. Notably, the $C_0$ complexity is high for $\upsilon$, ${\upsilon }_1$, and ${\upsilon }_2$ values where $L{E}_{max}$ was positive and drops in the periodic windows with negative $L{E}_{max}$ values, confirming the bifurcation analysis. Thus, we are able to say that the $C_0$ complexity is a useful tool for precisely estimating the complexity of the map.

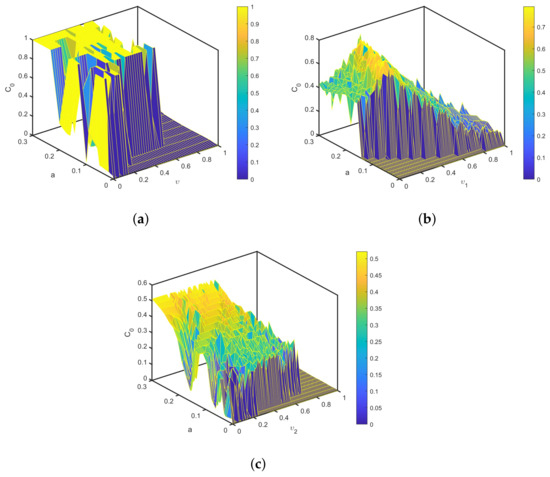
Figure 15. The $C_0$ complexity of (12) with $a\in [0,1]$ and (a) $\upsilon \in (0,1]$, (b) ${\upsilon }_1\in (0,1]$, ${\upsilon }_2=1$, (c) ${\upsilon }_2\in (0,1]$, ${\upsilon }_1=1$.

Remark 1.

Here, we compare the findings of Lyapunov exponents $L{E}_{max}$, the 0–1 test, and the $C_0$ complexity measure for representative parameter values compiled in Table 2 to facilitate a more thorough and detailed analysis of the various chaos detection techniques. The concordance between the three indications in detecting chaotic behavior in (12) under the same circumstances is highlighted in this comparative presentation, which validates and supports the earlier investigations.

Table 2. Comparison of $L{E}_{max}$, 0–1 test, and $C_0$ complexity results of (12) for ${\upsilon }_i$.

${\mathit{\upsilon }}_1$	${\mathit{\upsilon }}_2$	${\mathit{LE}}_{\mathit{max}}$	0–1 Test (K)	${\mathit{C}}_0$ Complexity
0.15	0.15	0.2361	0.9964	0.5104
0.7	0.7	−0.0463	0.0018	0.0367
0.99	0.99	0.1993	0.9925	0.680
0.5	1	−0.0349	0.0023	0.0183
1	0.7	−0.0413	0.0021	0.0265
0.98	1	0.3096	0.9923	0.7481

5. Chaos Control in the Fractional Economic Market Map

For the purpose of achieving stability and synchronizing the suggested fractional economic market map (12) to asymptotically drive all of its states toward zero, we propose the now adaptive laws in the next subsections.

5.1. Stabilization

We stabilize fractional economic market map (12) in two cases, ${\upsilon }_1\ne {\upsilon }_2$ and ${\upsilon }_1={\upsilon }_2=\upsilon$, by ensuring the stability conditions of Theorems 2 and 3 are met.

Firstly, the controlled map of fractional economic market map (12) can be described as

$$\left\{\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}x\left(\tau \right)& =-ax\left({\mu }_1\right)+{\displaystyle \frac{a}{{(bx\left({\mu }_1\right)+(1-b)y\left({\mu }_1\right))}^{\gamma }}}+{\mathbf{N}}_1\left({\mu }_1\right),\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}y\left(\tau \right)& ={\displaystyle \frac{1}{{(bx\left({\mu }_2\right)+(1-b)y\left({\mu }_2\right))}^{\gamma }}}-y\left({\mu }_2\right)+{\mathbf{N}}_2\left({\mu }_2\right),\hfill \end{array}\right.$$

(33)

where ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$ represent the adaptive controller representing the economic regulatory interventions.

Proposition 2.

The following two-dimensional control law stabilizes the fractional economic market map for the ${\upsilon }_1={\upsilon }_2=\upsilon$ commensurate order

$$\left\{\begin{array}{cc}\hfill {\mathit{N}}_1\left(\mu \right)& =-{\displaystyle \frac{a}{{(bx\left(\mu \right)+(1-b)y\left(\mu \right))}^{\gamma }}},\hfill \\ \hfill {\mathit{N}}_2\left(\mu \right)& =-{\displaystyle \frac{1}{{(bx\left({\mu }_1\right)+(1-b)y\left(\mu \right))}^{\gamma }}},\hfill \end{array}\right.$$

(34)

where $\mu =\tau -1+\upsilon$.

Proof. 

Substituting ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$ into (33) yields

$${}^C\mathrm{\Delta }_r^{\upsilon }\overline{V}=A\overline{V}\left(\mu \right),$$

(35)

where $\overline{V}={(x,y)}^T$ and

$$A=\left(\begin{array}{cc}-0.2& 0\\ 0& -1\end{array}\right).$$

(36)

It is simple to observe that eigenvalues ${\lambda }_1=-0.2$ and ${\lambda }_2=-1$ of A satisfy

$$\left|{\lambda }_{\mathit{ȷ}}\right|<{\left(2cos{\displaystyle \frac{\left|arg{\lambda }_{\mathit{ȷ}}\right|-\pi }{2-\upsilon }}\right)}^{\upsilon }\mathrm{and}\left|{\lambda }_{\mathit{ȷ}}\right|>{\displaystyle \frac{\upsilon \pi }{2}},\mathit{ȷ}=1,2.$$

Based on Theorem 2, the map’s (33) states converge to $(0,0)$; thus, map (12) is asymptotically stable. □

Proposition 3.

For the ${\upsilon }_1\ne {\upsilon }_2$ incommensurate order, the fractional economic market map is stabilized subject to the two-dimensional control law

$$\left\{\begin{array}{cc}\hfill {\mathit{N}}_1\left({\mu }_1\right)& =-{\displaystyle \frac{a}{{(bx\left({\mu }_1\right)+(1-b)y\left({\mu }_1\right))}^{\gamma }}},\hfill \\ \hfill {\mathit{N}}_2\left({\mu }_2\right)& =-{\displaystyle \frac{1}{{(bx\left({\mu }_2\right)+(1-b)y\left({\mu }_2\right))}^{\gamma }}}.\hfill \end{array}\right.$$

(37)

Proof. 

Substituting (37) into (33) yields

$$\left\{\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}x\left(\tau \right)& =-ax\left({\mu }_1\right),\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}y\left(\tau \right)& =-y\left({\mu }_2\right),\hfill \end{array}\right.$$

(38)

so

$$det(diag({\lambda }^{C{\upsilon }_1},{\lambda }^{C{\upsilon }_2}-(1-{\lambda }^C)M)=0,$$

where $C=50$,

$$M=\left(\begin{array}{ccc}-0.2& 0& \\ 0& -1& \end{array}\right).$$

(39)

For $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$

$$det\left(\left(\begin{array}{cc}{\lambda }^{49}& 0\\ 0& {\lambda }^{50}\end{array}\right)-\left(1-{\lambda }^{50}\right)M\right)=0,$$

⇔

$$\begin{array}{cc}\hfill & -0.2{\lambda }^{50}+{\lambda }^{49}+0.2=0.\hfill \end{array}$$

(40)

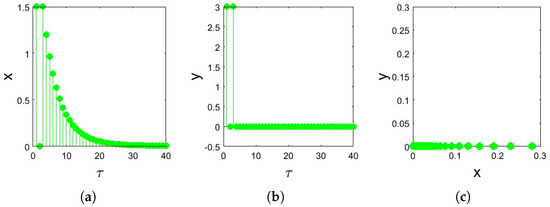
As an outcome of ${\lambda }_j\in \mathbb{C}/K^{{\displaystyle \frac{1}{50}}}(j=\overline{1,50})$ and Theorem 3, according to Theorem 3, the (33) map is asymptotically stable when it converges to $(0,0)$. To verify the results, we numerically implemented Propositions 2 and 3 using Matlab for 40 iterations. In Figure 16 and Figure 17, the stabilization states of fractional economic market map (12) are displayed. □

Figure 16. (a–c) The stabilized state of (33) when $({\upsilon }_1={\upsilon }_2=\upsilon )$ for $\upsilon =0.99$.

Figure 17. (a–c) The stabilized state of (33) when $({\upsilon }_1\ne {\upsilon }_2)$ for $({\upsilon }_1,{\upsilon }_2)=(0.98,1)$.

5.2. Synchronization

Now, let us look at another kind of control for fractional economic market map (12) that has been proposed. In this part, the goal of chaos synchronization is to regulate the states of the slave ‘Response’ fractional economic market map so that they precisely match the trajectories of a fractional economic market master ‘Drive’ map. We use the subscript ℓ to indicate the slave states. Therefore, we can define the slave map as

$$\left\{\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}{x}_{\ell }\left(\tau \right)& =-a{x}_{\ell }\left({\mu }_1\right)+{\displaystyle \frac{a}{{(b{x}_{\ell }\left({\mu }_1\right)+(1-b)y_{\ell }\left({\mu }_1\right))}^{\gamma }}}+{\mathbf{U}}_1\left({\mu }_1\right),\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}{y}_{\ell }\left(\tau \right)& ={\displaystyle \frac{1}{{(b{x}_{\ell }\left({\mu }_2\right)+(1-b)y_{\ell }\left({\mu }_2\right))}^{\gamma }}}-y_{\ell }\left({\mu }_2\right)+{\mathbf{U}}_2\left({\mu }_2\right).\hfill \end{array}\right.$$

(41)

The synchronization error conditions are described as

$$\left\{\begin{array}{cc}\hfill e_1\left(\mathit{\tau }\right)& =x_{\ell }-x,\hfill \\ \hfill e_2\left(\mathit{\tau }\right)& =y_{\ell }-y,\hfill \end{array}\right.$$

(42)

where ${lim}_{\tau \to \infty }\Vert e_{\mathfrak{j}}\left(\tau \right)\Vert =0$, $\forall \mathfrak{j}=1,2$. The fractional error map can be given by

$$\left\{\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}{e}_1\left(\tau \right)& =-a{e}_1\left({\mu }_1\right)+{\displaystyle \frac{a}{{(b{x}_{\ell }\left({\mu }_1\right)+(1-b)y_{\ell }\left({\mu }_1\right))}^{\gamma }}}-\hfill \\ \hfill & {\displaystyle \frac{a}{(bx\left({\mu }_1\right)+(1-b)y({\mu }_1){)}^{\gamma }}}+{\mathbf{U}}_1\left({\mu }_1\right),\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}{e}_2\left(\tau \right)& =-e_2\left({\mu }_2\right))+{\displaystyle \frac{1}{{(b{x}_{\ell }\left({\mu }_2\right)+(1-b)y_{\ell }\left({\mu }_2\right))}^{\gamma }}}-\hfill \\ \hfill & {\displaystyle \frac{1}{(bx\left({\mu }_2\right)+(1-b)y({\mu }_2){)}^{\gamma }}}+{\mathbf{U}}_2\left({\mu }_2\right)).\hfill \end{array}\right.$$

(43)

Proposition 4.

The drive–response fractional economic market maps (12)–(41) can be synchronized subject to

$$\left\{\begin{array}{cc}\hfill {\mathit{U}}_1\left({\mu }_1\right)& =-\left({\displaystyle \frac{a}{(bx\left({\mu }_1\right)+(1-b)y({\mu }_1){)}^{\gamma }}}-{\displaystyle \frac{a}{{(b{x}_{\ell }\left({\mu }_1\right)+(1-b)y_{\ell }\left({\mu }_1\right))}^{\gamma }}}\right),\hfill \\ \hfill {\mathit{U}}_2\left({\mu }_2\right)& =-\left({\displaystyle \frac{1}{(bx\left({\mu }_2\right)+(1-b)y({\mu }_2){)}^{\gamma }}}-{\displaystyle \frac{1}{{(b{x}_{\ell }\left({\mu }_2\right)+(1-b)y_{\ell }\left({\mu }_2\right))}^{\gamma }}}\right),\hfill \end{array}\right.$$

(44)

where $0\le a\le 2^{{\upsilon }_i},i=1,2$. The regulatory economic interventions denoted by ${\mathit{U}}_1$ and ${\mathit{U}}_2$ intend to achieve the synchronization.

Proof. 

Substituting (44) into error (45) yields

$$\left\{\begin{array}{cc}\hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_1}{e}_1\left(\mathit{\tau }\right)& =-a{e}_1\left({\mu }_1\right),\hfill \\ \hfill {}^c\mathrm{\Delta }_r^{{\upsilon }_2}{e}_2\left(\mathit{\tau }\right)& =-e_2\left({\mu }_2\right).\hfill \end{array}\right.$$

(45)

⟺

$${}^c\mathrm{\Delta }_r^{{\upsilon }_i}{(e_1\left(\mathit{\tau }\right),e_2\left(\mathit{\tau }\right))}^T=M{(e_1\left({\mu }_i\right),e_2\left({\mu }_i\right))}^T,i=1,2.,$$

(46)

where

$$M=\left(\begin{array}{cc}-a& 0\\ 0& -1\end{array}\right).$$

(47)

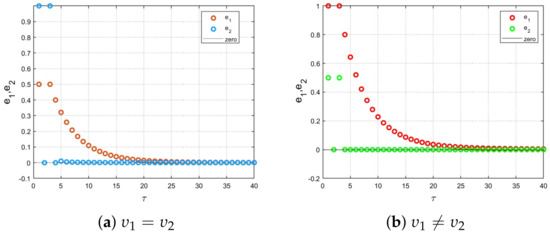
It is simple to observe that ${\lambda }_1=-a$ and ${\lambda }_2=-1$ of M for $0\le a\le 2^{{\upsilon }_i},i=1,2,$ satisfy the condition of Theorems 2 and 3. Consequently, drive–response fractional economic market maps (12)–(41) are synchronized. Matlab is used to illustrate this result. We set $(e_1\left(0\right),e_2\left(0\right)=(1.5,0.5)$. Figure 18 shows the states of error system (45). Thus, the errors that approach zero validate the results of the synchronization. □

Figure 18. Time series of the synchronization errors (45).

6. Conclusions

In this work, we considered a fractional economic market map in commensurate- and incommensurate-order versions; it is a simplified abstraction of a real market. Several methods were employed to analyze the dynamics of these maps: the estimate of Lyapunov exponents, bifurcation analysis, and phase portraits all reveal that the suggested fractional map displays chaotic behavior throughout a fractional-order area. Furthermore, we provided 2D stabilization laws for the suggested maps, which incorporate adaptive supplementary terms to asymptotically move the states of the maps towards zero by applying the stability theory, and the convergence and stability of these schemes were determined. Additionally, we suggested a synchronization schema with the fractional economic market map serving as the drive map. All these notes have been validated through numerical simulation studies. These findings imply that there are significant implications when fractional-order $\upsilon$ dynamics are utilized for the proposed economic map. The appearance of chaos in the fractional-order map specifically points to long-term memory effects, which can serve as a possible source of instability since the present market behavior is dependent on previous conditions over lengthy periods of time. This emphasizes how crucial it is to take memory-dependent mechanisms into account when simulating and controlling economic maps. As a future suggestion, a variable-order fractional derivative could be used to analyze the dynamics of the proposed economic market map. Complexity studies could also be applied to maps of other fractional chaotic phenomena. Moreover, to strengthen the link between the theoretical framework and empirical data, future research could concentrate on using fractional chaotic economic models to estimate their parameters and fractional order using actual economic data.