Fractional Optical Solitons in Metamaterial-Based Couplers with Strong Dispersion and Parabolic Nonlinearity

Abstract

The current study examines optical soliton solutions in a complicated system of metamaterial-based optical solutions coupled with extremely dispersive couplers. The conformable fractional derivative (CFD) influences the nonlinear refractive index, which is governed by a parabolic equation. Some soliton solutions are extracted, like bright, singular solitons, and singular periodic ones; also, Weierstrass elliptic doubly periodic, and several other exact solutions are systematically revealed by the study using the modified extended direct algebraic method. The findings shed important light on the many solitons in these intricate systems and the interactions between nonlinearity, dispersion, and metamaterial properties. The findings have significance beyond advancing our theoretical understanding of soliton behavior in metamaterial-based optical couplers; they might influence the advancement and development of optical communication technologies and systems. Complementary 2D and 3D representations show how stability parameters change throughout various dynamical regimes and confirm solution consistency. In order to comprehend the complex nonlinear phenomena of this system and its possible practical applications, this paper offers a comprehensive theoretical framework.

1. Introduction

The remarkable set of complex-valued evolution equations known as nonlinear Schr$\ddot{o}$dinger equations (NLSEs) [1] is attributed with several advantages in a wide range of modern scientific domains. Unquestionably, NLSEs are used extensively in several now very significant fields, including fluid flow in complex geometries [2], quantum physics [3], Bose–Einstein condensates [4], quantum mechanics [5], optics [6], opto-electronics, and contemporary communication, to mention a few [7,8]. It is essential to comprehend the equilibrium between nonlinearity and dispersion, which results in the formation of confined wave structures like solitons. In nonlinear optics, the NLSE simulates how strong laser beams and optical pulses travel through fibers, taking into consideration factors like self-phase modulation, group velocity dispersion, and nonlinear variations in refractive index [9,10,11]. The study of optical solitons, which are essential to high-speed fiber-optic communication systems, may be theoretically underpinned by them. The formula in fluid mechanics provides information on phenomena like rogue waves and nonlinear surface patterns by governing the dynamics of deep-water waves and internal solitary waves [12,13]. Similarly, it explains the evolution of Langmuir waves and nonlinear ion-acoustic waves in plasma physics, which are crucial for comprehending laboratory plasmas and space transfer of energy [14].

The NLSE is still a thriving field of study because of its many applications and depth of mathematics. In addition to expanding our knowledge of nonlinear wave dynamics, investigating novel forms of this equation and a variety of solution structures offers useful tools for the design and optimization of contemporary technological systems, including sophisticated optical devices and plasma-based communication systems [15].

Self-reinforcing wave packets known as optical solitons, which can keep their speed and form while traveling across a nonlinear medium, are essential to nonlinear optics and photonics [16]. These solitons are very important in both theoretical studies and real-world applications because of their special characteristics. Numerous scientific publications have been released, each exploring a distinct facet of solitons in optical systems and shedding light on their importance in diverse contexts across time.

Recent studies demonstrate the diverse applications and physical significance of solitons in modern science and engineering. Wang et al. [17] explored the phenomenon of launching by cavitation, highlighting nonlinear wave interactions that exhibit soliton-like stability and persistence in fluid systems, which have implications for energy transfer and control in fluid dynamics. Meanwhile, Mou et al. [18] investigated the formation and dynamic characteristics of optical solitons in photonic moiré lattices, revealing how nonlinear effects and lattice modulation can be harnessed to control light propagation and localization. Together, these works emphasize how soliton theory continues to bridge fields such as fluid mechanics and nonlinear optics, offering valuable insights into wave stability, energy confinement, and technological innovation.

The search for novel ways to improve functionality and performance is still crucial in the dynamic field of optical communication systems. Highly dispersive couplers that incorporate optical metamaterials have shown promise in enabling previously unheard-of control over the manipulation and propagation of light [19]. The dynamics of signal transmission are determined by the behavior of optical solitons, which are crucial in this complex field [20]. Solitons, which are fascinating phenomena in physics, are solitary waves that maintain their shape and speed while they travel across a medium. Solitons are essential to the development of optical metamaterial structures, which are synthetic materials with special optical characteristics not present in naturally occurring materials. These structures enable a range of applications, including nonlinear optics, pulse shaping, and signal transmission. In the setting of couplers with a parabolic law nonlinear refractive index, this work thoroughly investigates optical soliton solutions using a powerful mathematical method called the modified extended direct algebraic methodology. A rich and intricate interaction of dispersion, nonlinearity, and metamaterial features is introduced by the unique combination of optical metamaterials and extremely dispersive couplers. In addition to enhancing our theoretical knowledge, comprehending and describing the many soliton solutions that emerge in these systems is essential for revealing real-world applications in the development and enhancement of optical communication devices [21,22].

Highly dispersive optical solitons have been a significant topic of research in nonlinear optics, providing deep insights into light propagation in media with high dispersion and nonlinearities. Highly dispersive optical solitons retain their shape and stability even when high dispersion is present, making them absolutely essential for the research of ultrafast optical communication and pulse dynamics. Kudryashov [23] formulated a seminal analytical method for obtaining highly dispersive soliton solutions of optical nonlinear differential equations, to aid efficient modeling of complex optical systems. Similarly, Biswas et al. [24] studied such solitons within the quadratic–cubic law using the F-expansion method and found a broad spectrum of solution types and stability behaviors. Extending this effort, Jawad and Abu-AlShaeer [25] investigated highly dispersive solitons in the presence of cubic and higher-order nonlinearities, emphasizing the efficacy of analytical approaches in solving complex nonlinear problems. These efforts collectively showcase the growing importance of highly dispersive solitons in developing theoretical and applied photonics.

Since solitary wave solutions for nonlinear dynamical systems are used in many different fields, their retrieval has grown in importance. An intriguing subclass of nonlinear wave solutions, soliton waves preserve their energy and structure while moving across a medium. Many different fields frequently use these solitary waves, also known as solitons. Because of their special characteristics, they are the focus of much research, especially regarding how they react to noise. Given the importance of solitary waves in nonlinear dynamics, it is important to comprehend their behavior. Understanding the behavior of the system as a whole requires looking at how these waves interact and respond to perturbations. A variety of reactions to outside noise or disturbances can be displayed by nonlinear systems.

Numerous scientists have devised a range of methods to solve mathematical models. The extended F-expansion method [26], the Riccati–Bernoulli sub-ODE method [27], the improved $tan\left(\mathrm{\Phi }\right(\xi )/2)-$ expansion method [28], the $(\psi -\varphi )-$ expansion method [29], the generalized $(G^{\prime }/G)-$ expansion approach [30], and the improved Adomian decomposition method [31], the modified extended direct algebraic method [32] are a few of these.

1.1. Governing Model

A noteworthy development in this field is the creation of a dimensionless representation for extremely dispersive couplers using optical metamaterials with a parabolic power law and nonlinear refractive index, which can be stated as [33]

$$\begin{array}{cc}\hfill i{\mathcal{R}}_t& +i{\beta }_1{\mathcal{R}}_y+{\beta }_2{\mathcal{R}}_{yy}+i{\beta }_3{\mathcal{R}}_{yyy}+{\beta }_4{\mathcal{R}}_{yyyy}+i{\beta }_5{\mathcal{R}}_{yyyyy}+{\beta }_6{\mathcal{R}}_{yyyyyy}\hfill \\ \hfill & +\left({\mathbf{a}}_1{\left|\mathcal{R}\right|}^2+{\mathbf{b}}_1{\left|\mathcal{R}\right|}^4\right)\mathcal{R}-{\mathbf{e}}_1{\left({\mathcal{R}\left|\mathcal{R}\right|}^2\right)}_{yy}-{\mathbf{f}}_1{\mathcal{R}}_{yy}{\left|\mathcal{R}\right|}^2-{\mathbf{g}}_1{\mathcal{R}}^2{\left({\mathcal{R}}^{*}\right)}_{yy}\hfill \\ \hfill & -{\delta }_1\mathcal{Q}-i\left[{\lambda }_1{\left(\mathcal{R}\right|\mathcal{R}|}^2{)}_y+{\mu }_1{\mathcal{R}\left(\right|\mathcal{R}|}^2{)}_y+{\nu }_1{\mathcal{R}}_y{\left|\mathcal{R}\right|}^2\right]=0,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill i{\mathcal{Q}}_t& +i{\gamma }_1{\mathcal{Q}}_y+{\gamma }_2{\mathcal{Q}}_{yy}+i{\gamma }_3{\mathcal{Q}}_{yyy}+{\gamma }_4{\mathcal{Q}}_{yyyy}+i{\gamma }_5{\mathcal{Q}}_{yyyyy}+{\gamma }_6{\mathcal{Q}}_{yyyyyy}\hfill \\ \hfill & +\left({\mathbf{a}}_2{\left|\mathcal{Q}\right|}^2+{\mathbf{b}}_2{\left|\mathcal{Q}\right|}^4\right)\mathcal{Q}-{\mathbf{e}}_2{\left({\mathcal{Q}\left|\mathcal{Q}\right|}^2\right)}_{yy}-{\mathbf{f}}_2{\mathcal{Q}}_{yy}{\left|\mathcal{Q}\right|}^2-{\mathbf{g}}_2{\mathcal{Q}}^2{\left({\mathcal{Q}}^{*}\right)}_{yy}\hfill \\ \hfill & -{\delta }_2\mathcal{Q}-i\left[{\lambda }_2{\left(\mathcal{Q}\right|\mathcal{Q}|}^2{)}_y+{\mu }_2{\mathcal{Q}\left(\right|\mathcal{Q}|}^2{)}_y+{\nu }_2{\mathcal{Q}}_y{\left|\mathcal{Q}\right|}^2\right]=0.\hfill \end{array}$$

(2)

The above-mentioned model was previously investigated in [33] using the standard total derivative form. However, in the present study, we extend the analysis by incorporating a CFD on the temporal variable, reformulating the model into the following form:

$$\begin{array}{cc}\hfill i{\displaystyle \frac{{\partial }^{\alpha }\mathcal{R}}{\partial t^{\alpha }}}& +i{\beta }_1{\mathcal{R}}_y+{\beta }_2{\mathcal{R}}_{yy}+i{\beta }_3{\mathcal{R}}_{yyy}+{\beta }_4{\mathcal{R}}_{yyyy}+i{\beta }_5{\mathcal{R}}_{yyyyy}+{\beta }_6{\mathcal{R}}_{yyyyyy}\hfill \\ \hfill & +\left({\mathbf{a}}_1{\left|\mathcal{R}\right|}^2+{\mathbf{b}}_1{\left|\mathcal{R}\right|}^4\right)\mathcal{R}-{\mathbf{e}}_1{\left({\mathcal{R}\left|\mathcal{R}\right|}^2\right)}_{yy}-{\mathbf{f}}_1{\mathcal{R}}_{yy}{\left|\mathcal{R}\right|}^2-{\mathbf{g}}_1{\mathcal{R}}^2{\left({\mathcal{R}}^{*}\right)}_{yy}\hfill \\ \hfill & -{\delta }_1\mathcal{Q}-i\left[{\lambda }_1{\left(\mathcal{R}\right|\mathcal{R}|}^2{)}_y+{\mu }_1{\mathcal{R}\left(\right|\mathcal{R}|}^2{)}_y+{\nu }_1{\mathcal{R}}_y{\left|\mathcal{R}\right|}^2\right]=0,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill i{\displaystyle \frac{{\partial }^{\alpha }\mathcal{Q}}{\partial t^{\alpha }}}& +i{\gamma }_1{\mathcal{Q}}_y+{\gamma }_2{\mathcal{Q}}_{yy}+i{\gamma }_3{\mathcal{Q}}_{yyy}+{\gamma }_4{\mathcal{Q}}_{yyyy}+i{\gamma }_5{\mathcal{Q}}_{yyyyy}+{\gamma }_6{\mathcal{Q}}_{yyyyyy}\hfill \\ \hfill & +\left({\mathbf{a}}_2{\left|\mathcal{Q}\right|}^2+{\mathbf{b}}_2{\left|\mathcal{Q}\right|}^4\right)\mathcal{Q}-{\mathbf{e}}_2{\left({\mathcal{Q}\left|\mathcal{Q}\right|}^2\right)}_{yy}-{\mathbf{f}}_2{\mathcal{Q}}_{yy}{\left|\mathcal{Q}\right|}^2-{\mathbf{g}}_2{\mathcal{Q}}^2{\left({\mathcal{Q}}^{*}\right)}_{yy}\hfill \\ \hfill & -{\delta }_2\mathcal{Q}-i\left[{\lambda }_2{\left(\mathcal{Q}\right|\mathcal{Q}|}^2{)}_y+{\mu }_2{\mathcal{Q}\left(\right|\mathcal{Q}|}^2{)}_y+{\nu }_2{\mathcal{Q}}_y{\left|\mathcal{Q}\right|}^2\right]=0,\hfill \end{array}$$

(4)

where ${\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}$ is the CFD with order $0<\alpha \le 1$.

The wave profiles in this context are described by the complex-valued functions $\mathcal{R}(y,t)$ and $\mathcal{Q}(y,t)$, with $i=\sqrt{-1}$ representing their respective complex conjugates, ${\mathcal{R}}^{*}(y,t)$ and ${\mathcal{Q}}^{*}(z,t)$.

The governing equations, Equations (3) and (4), incorporate several physical effects through their coefficients:

• The linear-temporal evolution is governed by the coefficients ${\beta }_1$ and ${\gamma }_1$.
• Dispersion effects are represented by the parameters ${\beta }_j$ and ${\gamma }_j$ for $(j=2,\dots ,6)$, corresponding to chromatic dispersion (CD), third-order (3OD), fourth-order (4OD), fifth-order (5OD), and sixth-order dispersion (6OD), respectively. The dispersion properties of the considered medium play a crucial role in shaping the soliton dynamics. These parameters enable modeling of both normal and anomalous dispersion regimes, which determine whether bright or dark solitons can be sustained. The inclusion of higher-order dispersion makes the model suitable for analyzing highly dispersive and nonlinear photonic structures. Physically, the results are most applicable to single-mode optical fibers operating near the zero-dispersion wavelength, photonic crystal fibers with controllable dispersion through microstructural design, and highly nonlinear fibers that enhance the balance between dispersion and nonlinearity. Such engineered fiber systems and metamaterial-based couplers are capable of supporting the fractional-order soliton families reported in this study.
• The terms with coefficients ${\mathbf{a}}_j$ and ${\mathbf{b}}_j$ (where $j=1,2$) model the parabolic law nonlinearity.
• The constants ${\mathbf{e}}_j$, ${\mathbf{f}}_j$, and ${\mathbf{g}}_j$ (for $j=1,2$) are associated with the properties of the optical metamaterial.
• The coupling between the two components is quantified by the parameters ${\delta }_j$ ($j=1,2$).
• Furthermore, higher-order nonlinear dispersion is accounted for by the coefficients ${\mu }_j$ and ${\nu }_j$ ($j=1,2$), while the self-steepening (SS) effects are characterized by ${\lambda }_j$ ($j=1,2$).

The mathematical model established in this research, the time-fractional coupled nonlinear Schrödinger equation with parabolic nonlinearity, is particularly useful for applying to optical fibers as well as other dispersive media with non-integer order dispersion and nonlinearities. The parameters entering the equations are physical properties of the medium and laser radiation: the fractional order parameter $\alpha$ is a measure of temporal memory or non-local response of the medium, the dispersion coefficients relate to the group velocity dispersion, and the nonlinear parameters describe the parabolic nonlinearity, which is a simulation of a specific type of Kerr nonlinearity with the nonlinear response quadratically depending on the intensity. This model is founded on slowly varying envelope approximation (SVEA), hence being valid for narrow-band pulses relative to the carrier frequency. It is not, nevertheless, valid for ultrashort optical pulses (e.g., few-cycle pulses) where SVEA does not hold, as full-wave models are then required in such instances. Other limitations include the assumption of homogeneously mixed media and idealized parabolic nonlinearity, which may not be efficient in explaining more complex material responses or extreme nonlinear phenomena.

1.2. Main Novelty and Contribution

Characterizing and analyzing various types of soliton solutions, including dark solitons, bright solitons, singular solitons, Weierstrass elliptic doubly periodic, and several other precise solutions, is the primary objective and the main novelty of this study. Unlike conventional models, the inclusion of the time-fractional derivative introduces nonlocal dynamics, providing a more realistic framework for modeling wave propagation in nonlinear optical fibers and photonic media. The modified extended direct algebraic method is used to systematically reveal these solutions. We wish to use advanced mathematical methods to comprehend the complex dynamics of solitons in these intricate metamaterial-based optical couplers. The results of the investigation should yield valuable new information for the practical development of optical communication technologies, as well as a significant theoretical contribution to our understanding of soliton behavior in such systems. This paper addresses an understudied topic: optical solitons in highly dispersive couplers paired with optical metamaterials.

The following is the structure of our article: Section 1 delivers an introduction to the solitons and NLPDEs theory, and also provides an overview of the proposed model along with an explanation of its theoretical background. Section 2 provides some mathematical preliminaries of the applied scheme and the CFD and its properties. To obtain these few classes of exact solutions, a comprehensive symbolic computation is performed using the Wolfram Mathematica program, which summarizes all of the results in Section 3. The dynamic wave patterns of several different solutions are graphically shown in Section 4 using both 2D and 3D simulations. Some remarks are considered as a discussion about the results represented in Section 5. Section 6 concludes the study and offers some thoughts for the future.

2. Some Mathematical Preliminaries

In this section, we present the essential mathematical preliminaries required for the analysis, focusing on the specific type of fractional derivative employed, namely, the CFD. The fundamental definitions and key properties of the CFD are provided to establish a solid theoretical foundation for its application in modeling complex nonlinear dynamical systems. Furthermore, we discuss the modified extended direct algebraic method (MEDAM), which is utilized to construct exact analytical solutions of the proposed fractional model. A systematic outline of the method is provided, including its algorithmic steps and underlying mathematical framework, highlighting its capability to handle higher-order nonlinear terms and fractional operators efficiently. This combination of fractional calculus and advanced solution techniques allows for a deeper exploration of the model’s behavior and its physical interpretations.

2.1. Core Principles of Conformable Fractional Derivatives

Let $\psi :[0,\infty )\to \mathbb{R}$ be a real-valued function. The conformable fractional derivative of order $\alpha$ for the function $\psi$ is defined as [34]:

$${\mathcal{D}}^{\alpha }\psi \left(t\right)=\underset{\epsilon \to 0}{lim}{\displaystyle \frac{\psi (t+{\epsilon }^{1-\alpha })-\psi \left(t\right)}{\epsilon }},$$

(5)

where $t>0$, $\epsilon$ is a very small constant that approaches zero, and $0<\alpha \le 1$.

If $\psi$ is $\alpha -$ differentiable on an interval $(0,\alpha )$, with $\alpha >0$, and if the limit

$$\underset{t\to 0^{+}}{lim}{\mathcal{D}}^{\alpha }\psi \left(t\right)$$

exists, then the conformable derivative at the origin can be expressed as

$${\mathcal{D}}^{\alpha }\psi \left(0\right)=\underset{t\to 0^{+}}{lim}{\mathcal{D}}^{\alpha }\psi \left(t\right).$$

(6)

Theorem 1.

For $0<\alpha \le 1$, if $\psi \left(t\right)$ and ${\rm Y}\left(t\right)$ are both α-differentiable at $t>0$, the following properties hold [35]:

(1) 

Linearity:

$${\mathcal{D}}^{\alpha }[a\psi +b{\rm Y}]=a{\mathcal{D}}^{\alpha }\left[\psi \right]+b{\mathcal{D}}^{\alpha }\left[{\rm Y}\right],\forall a,b\in \mathbb{R}.$$

(2) 

Power rule:

$${\mathcal{D}}^{\alpha }\left[t^m\right]=m{t}^{m-\alpha },\forall m\in \mathbb{R}.$$

(3) 

Constant rule:

$${\mathcal{D}}^{\alpha }\left[C\right]=0,\mathit{for}\mathit{any}\mathit{constant}\mathit{function}\psi \left(t\right)=C.$$

(4) 

Product rule:

$${\mathcal{D}}^{\alpha }\left[\psi {\rm Y}\right]=\psi {\mathcal{D}}^{\alpha }\left[{\rm Y}\right]+{\rm Y}{\mathcal{D}}^{\alpha }\left[\psi \right].$$

(5) 

Quotient rule:

$${\mathcal{D}}^{\alpha }\left[{\displaystyle \frac{\psi }{{\rm Y}}}\right]={\displaystyle \frac{{\rm Y}{\mathcal{D}}^{\alpha }\left[\psi \right]-\psi {\mathcal{D}}^{\alpha }\left[{\rm Y}\right]}{{{\rm Y}}^2}}.$$

(6) 

Classical derivative relation:  If ψ is differentiable, then

$${\mathcal{D}}^{\alpha }\left[\psi \right]\left(t\right)=t^{1-\alpha }{\displaystyle \frac{d\psi }{dt}}\left(t\right).$$

The CFD is employed in this work due to its mathematical simplicity and its ability to preserve key rules of classical calculus, such as the product, quotient, and chain rules. In contrast, alternative definitions like Caputo and Riemann–Liouville derivatives introduce non-local memory kernels and require initial conditions expressed in integral form, which complicates both the analytical treatment and physical interpretation. For modeling nonlinear physical systems, like optical fibers, where precise closed-form solutions, including solitons, may be obtained while preserving a balance between mathematical precision and practical relevance, the conformable derivative is especially well-suited.

2.2. Mathematical Framework of the MEDAM

Several presumptions and analytical simplifications are necessary to make the issue mathematically tractable in order to apply the MEDAM to the current nonlinear coupled system. First, an appropriate wave transformation is introduced, assuming that the system accepts traveling wave solutions. Through this transformation, a single nonlinear ordinary differential equation (NLODE) replaces the initial collection of nonlinear partial differential equations (NLPDEs). This kind of change is possible if the wave keeps its shape during its journey, which is a basic feature of solitonic structures seen in a variety of physical systems, including plasma dynamics and nonlinear optics.

In this subsection, the core principles and operational framework of the MEDAM are introduced, providing the foundation for its application to the current nonlinear model [36,37,38].

Consider the general nonlinear partial differential equation (NLPDE) of the form:

$$\mathcal{F}\left(\mathrm{\Phi },{\displaystyle \frac{{\partial }^{\alpha }\mathrm{\Phi }}{\partial t^{\alpha }}},{\mathrm{\Phi }}_x,{\mathrm{\Phi }}_y,{\mathrm{\Phi }}_z,{\mathrm{\Phi }}_{xx},{\mathrm{\Phi }}_{yy},{\mathrm{\Phi }}_{zz},{\displaystyle \frac{{\partial }^{\alpha }{\mathrm{\Phi }}_x}{\partial t^{\alpha }}},{\displaystyle \frac{{\partial }^{\alpha }{\mathrm{\Phi }}_{xx}}{\partial t^{\alpha }}},\dots \right)=0,$$

(7)

where $\mathcal{F}$ is a functional expression involving the dependent variable $\mathrm{\Phi }$ and its various partial derivatives with respect to the independent variables $x,y,z,$ and t. The proposed MEDAM proceeds through the following sequential steps:

• Step 1: Traveling wave reduction

We assume that Equation (7) admits traveling wave solutions and introduce the transformation:

$$\mathrm{\Phi }=\chi \left(\xi \right),\xi =px+qy+rz-{\displaystyle \frac{\lambda t^{\alpha }}{\alpha }},0<\alpha \le 1,$$

(8)

where p, q, r, and $\lambda$ are unknown wave parameters that will be identified later. Substituting Equation (8) into Equation (7) reduces the original NLPDE to a NLODE:

$$\mathcal{G}\left(\chi ,{\chi }^{\prime },{\chi }^{\prime \prime },{\chi }^{\prime \prime \prime },\dots \right)=0,$$

(9)

where primes denote derivatives with respect to $\xi$.

• Step 2: Solution structure assumption

The general solution of Equation (9) is expressed as a finite series expansion in terms of a function $\chi \left(\xi \right)$:

$$\chi \left(\xi \right)=\sum _{k=-M}^M{\eta }_k{\mathrm{\Psi }}^k\left(\xi \right),$$

(10)

where ${\eta }_k$$(k=-M,\dots ,M)$ are real constants to be determined, and at least one of the coefficients ${\eta }_M$ or ${\eta }_{-M}$ must be non-zero. The function $\mathrm{\Psi }\left(\xi \right)$ satisfies the following first-order auxiliary equation:

$${\mathrm{\Psi }}^{\prime }\left(\xi \right)=\sqrt{{\zeta }_0+{\zeta }_1\mathrm{\Psi }\left(\xi \right)+{\zeta }_2{\mathrm{\Psi }}^2\left(\xi \right)+{\zeta }_3{\mathrm{\Psi }}^3\left(\xi \right)+{\zeta }_4{\mathrm{\Psi }}^4\left(\xi \right)+{\zeta }_6{\mathrm{\Psi }}^6\left(\xi \right)},$$

(11)

where ${\zeta }_i$$(i=0,1,2,3,4,6)$ are real parameters.

• Step 3: Determining M

By applying the homogeneous balance principle between the highest-order derivative and nonlinear terms in Equation (9), the integer M can be explicitly calculated, which defines the series truncation limit in Equation (10).

• Step 4: Parameter identification

Substituting Equations (10) and (11) into the reduced Equation (9) yields a polynomial in powers of $\mathrm{\Psi }\left(\xi \right)$. By equating the coefficients of like powers to zero, a nonlinear algebraic system for the unknown parameters ${\eta }_k$, ${\zeta }_i$, and the wave constants p, q, r, and $\lambda$ is obtained. This system is then solved using Wolfram Mathematica (v13.2) to derive exact closed-form solutions for the original fractional NLPDE.

3. Development of Novel Analytical Solutions via Conformable Fractional Derivatives

3.1. Mathematical Reduction via Traveling Wave Transformation

In pursuit of this goal, we assume that the formal solution adheres to the following specific structure, which enables the reduction and subsequent analysis of the governing equation.

Assume

$$\mathcal{R}(y,t)=\mathcal{G}\left(\xi \right)e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},$$

(12)

$$\mathcal{Q}(y,t)=\mathcal{H}\left(\xi \right)e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},$$

(13)

where $\mathcal{G}\left(\xi \right),\mathcal{H}\left(\xi \right)$ are real functions, with

$$\xi =y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}.$$

(14)

The pulse profiles are characterized by the real-valued parameters $\mathcal{V},\ell ,\omega ,\mathrm{\Delta }\in \mathbb{R}$, along with the functions $\mathcal{G}=\mathcal{G}\left(\xi \right)$ and $\mathcal{H}=\mathcal{H}\left(\xi \right)$. Here, $\mathcal{V}$, ℓ, and $\omega$ denote the soliton’s velocity, wave number, and frequency, respectively, while $\mathrm{\Delta }$ represents the phase constant.

By inserting Equations (12)–(14) in Equations (3) and (4), and separating the equations into their real and imaginary parts, yields the following outcomes:

Real parts:

$$\begin{array}{c}{\beta }_6{\mathcal{G}}^{\left(6\right)}+({\beta }_4-15{\beta }_6{\ell }^2+5{\beta }_5\ell ){\mathcal{G}}^{\left(4\right)}+({\beta }_2+15{\beta }_6{\ell }^4-10{\beta }_5{\ell }^3-6{\beta }_4{\ell }^2+3{\beta }_3\ell ){\mathcal{G}}^{\prime \prime }-(3{\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1){\mathcal{G}}^2{\mathcal{G}}^{\prime \prime }-6{\mathbf{e}}_1\mathcal{G}{\left({\mathcal{G}}^{\prime }\right)}^2\hfill \\ \hfill +(-\omega -{\beta }_6{\ell }^6+{\beta }_5{\ell }^5+{\beta }_4{\ell }^4-{\beta }_3{\ell }^3-{\beta }_2{\ell }^2+{\beta }_1\ell )\mathcal{G}-{\delta }_1\mathcal{H}+\left({\mathbf{a}}_1+{\ell }^2({\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1)-\ell ({\lambda }_1+{\nu }_1)\right){\mathcal{G}}^3+{\mathbf{b}}_1{\mathcal{G}}^5=0,\end{array}$$

(15)

$$\begin{array}{c}{\gamma }_6{\mathcal{H}}^{\left(6\right)}+\left({\gamma }_4-15{\gamma }_6{\ell }^2+5{\gamma }_5\ell \right){\mathcal{H}}^{\left(4\right)}+\left({\gamma }_2+15{\gamma }_6{\ell }^4-10{\gamma }_5{\ell }^3-6{\gamma }_4{\ell }^2+3{\gamma }_3\ell \right){\mathcal{H}}^{\prime \prime }-(3{\mathbf{e}}_2+{\mathbf{f}}_2+{\mathbf{g}}_2){\mathcal{H}}^2{\mathcal{H}}^{\prime \prime }-6{\mathbf{e}}_2\mathcal{H}{\left({\mathcal{H}}^{\prime }\right)}^2\hfill \\ \hfill +\left(-\omega -{\gamma }_6{\ell }^6+{\gamma }_5{\ell }^5+{\gamma }_4{\ell }^4-{\gamma }_3{\ell }^3-{\gamma }_2{\ell }^2+{\gamma }_1\ell \right)\mathcal{H}-{\delta }_2\mathcal{G}+\left({\mathbf{a}}_2+{\ell }^2({\mathbf{e}}_2+{\mathbf{f}}_2+{\mathbf{g}}_2)-\ell ({\lambda }_2+{\nu }_2)\right){\mathcal{H}}^3+{\mathbf{b}}_2{\mathcal{H}}^5=0,\end{array}$$

(16)

where the imaginary parts are:

$$\begin{array}{c}\left({\beta }_5-6{\beta }_6\ell \right){\mathcal{G}}^{\left(5\right)}+\left({\beta }_3+20{\beta }_6{\ell }^3-10{\beta }_5{\ell }^2-4{\beta }_4\ell \right){\mathcal{G}}^{\left(3\right)}+\left[2\ell \left(3{\mathbf{e}}_1+{\mathbf{f}}_1-{\mathbf{g}}_1\right)-\left(3{\lambda }_1+2{\mu }_1+{\nu }_1\right)\right]{\mathcal{G}}^2{\mathcal{G}}^{\prime }\hfill \\ \hfill +\left({\beta }_1-\mathcal{V}-6{\beta }_6{\ell }^5+5{\beta }_5{\ell }^4+4{\beta }_4{\ell }^3-3{\beta }_3{\ell }^2-2{\beta }_2\ell \right){\mathcal{G}}^{\prime }=0,\end{array}$$

(17)

$$\begin{array}{c}\left({\gamma }_5-6{\gamma }_6\ell \right){\mathcal{H}}^{\left(5\right)}+\left({\gamma }_3+20{\gamma }_6{\ell }^3-10{\gamma }_5{\ell }^2-4{\gamma }_4\ell \right){\mathcal{H}}^{\left(3\right)}+\left[2\ell \left(3{\mathbf{e}}_2+{\mathbf{f}}_2-{\mathbf{g}}_2\right)-\left(3{\lambda }_2+2{\mu }_2+{\nu }_2\right)\right]{\mathcal{H}}^2{\mathcal{H}}^{\prime }\hfill \\ \hfill +\left({\gamma }_1-\mathcal{V}-6{\gamma }_6{\ell }^5+5{\gamma }_5{\ell }^4+4{\gamma }_4{\ell }^3-3{\gamma }_3{\ell }^2-2{\gamma }_2\ell \right){\mathcal{H}}^{\prime }=0.\end{array}$$

(18)

Based on Equations (17) and (18), we obtain:

$$\ell ={\displaystyle \frac{{\gamma }_5}{6{\gamma }_6}}={\displaystyle \frac{{\beta }_5}{6{\beta }_6}}⟹{\gamma }_5{\beta }_6-{\beta }_5{\gamma }_6=0,$$

(19)

$$\begin{array}{cc}\hfill \mathcal{V}& ={\beta }_1-6{\beta }_6{\ell }^5+5{\beta }_5{\ell }^4+4{\beta }_4{\ell }^3-3{\beta }_3{\ell }^2-2{\beta }_2\ell ,\hfill \\ \hfill \mathcal{V}& ={\gamma }_1-6{\gamma }_6{\ell }^5+5{\gamma }_5{\ell }^4+4{\gamma }_4{\ell }^3-3{\gamma }_3{\ell }^2-2{\gamma }_2\ell ,\hfill \end{array}$$

(20)

with the following constraint conditions

$$\begin{array}{cc}\hfill & {\beta }_3+20{\beta }_6{\ell }^3-10{\beta }_5{\ell }^2-4{\beta }_4\ell =0,\hfill \\ \hfill & {\gamma }_3+20{\gamma }_6{\ell }^3-10{\gamma }_5{\ell }^2-4{\gamma }_4\ell =0,\hfill \\ \hfill & 2\ell \left(3{\mathbf{e}}_1+{\mathbf{f}}_1-{\mathbf{g}}_1\right)-\left(3{\lambda }_1+2{\mu }_1+{\nu }_1\right)=0,\hfill \\ \hfill & 2\ell \left(3{\mathbf{e}}_2+{\mathbf{f}}_2-{\mathbf{g}}_2\right)-\left(3{\lambda }_2+2{\mu }_2+{\nu }_2\right)=0.\hfill \end{array}$$

(21)

Using the following substitution

$$\mathcal{H}\left(\xi \right)=\varsigma ·\mathcal{G}\left(\xi \right),\varsigma \ne 0,1.$$

(22)

Consequently, Equations (15) and (16) transform into

$$\begin{array}{cc}\hfill & {\beta }_6{\mathcal{G}}^{\left(6\right)}+\left({\beta }_4-15{\beta }_6{\ell }^2+5{\beta }_5\ell \right){\mathcal{G}}^{\left(4\right)}+\left({\beta }_2+15{\beta }_6{\ell }^4-10{\beta }_5{\ell }^3-6{\beta }_4{\ell }^2+3{\beta }_3\ell \right){\mathcal{G}}^{\prime \prime }\hfill \\ \hfill & -\left(3{\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1\right){\mathcal{G}}^2{\mathcal{G}}^{\prime \prime }-6{\mathbf{e}}_1\mathcal{G}{\left({\mathcal{G}}^{\prime }\right)}^2+{\mathbf{b}}_1{\mathcal{G}}^5+\left({\mathbf{a}}_1+{\ell }^2({\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1)-\ell ({\lambda }_1+{\nu }_1)\right){\mathcal{G}}^3\hfill \\ \hfill & +\left(-{\delta }_1\varsigma -\omega -{\beta }_6{\ell }^6+{\beta }_5{\ell }^5+{\beta }_4{\ell }^4-{\beta }_3{\ell }^3-{\beta }_2{\ell }^2+{\beta }_1\ell \right)\mathcal{G}=0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {\gamma }_6\varsigma {\mathcal{G}}^{\left(6\right)}+\varsigma \left({\gamma }_4-15{\gamma }_6{\ell }^2+5{\gamma }_5\ell \right){\mathcal{G}}^{\left(4\right)}+\varsigma \left({\gamma }_2+15{\gamma }_6{\ell }^4-10{\gamma }_5{\ell }^3-6{\gamma }_4{\ell }^2+3{\gamma }_3\ell \right){\mathcal{G}}^{\prime \prime }\hfill \\ \hfill & -{\varsigma }^3\left(3{\mathbf{e}}_2+{\mathbf{f}}_2+{\mathbf{g}}_2\right){\mathcal{G}}^2{\mathcal{G}}^{\prime \prime }-6{\mathbf{e}}_2{\varsigma }^3\mathcal{G}{\left({\mathcal{G}}^{\prime }\right)}^2+{\mathbf{b}}_2{\varsigma }^5{\mathcal{G}}^5+{\varsigma }^3\left({\mathbf{a}}_2+{\ell }^2({\mathbf{e}}_2+{\mathbf{f}}_2+{\mathbf{g}}_2)-\ell ({\lambda }_2+{\nu }_2)\right){\mathcal{G}}^3\hfill \\ \hfill & +\left[\varsigma \left(-\omega -{\gamma }_6{\ell }^6+{\gamma }_5{\ell }^5+{\gamma }_4{\ell }^4-{\gamma }_3{\ell }^3-{\gamma }_2{\ell }^2+{\gamma }_1\ell \right)-{\delta }_2\right]\mathcal{G}=0.\hfill \end{array}$$

(24)

Equations (23) and (24) take on equivalent forms when the following constraint conditions are applied:

$$\begin{array}{cc}\hfill & {\gamma }_6={\displaystyle \frac{{\beta }_6}{\varsigma }},{\gamma }_5={\displaystyle \frac{{\beta }_5}{\varsigma }},{\gamma }_4={\displaystyle \frac{{\beta }_4+5\left({\beta }_6-{\beta }_5\right)\ell }{\varsigma }},{\gamma }_2={\displaystyle \frac{{\beta }_2+3\ell \left({\beta }_3-{\gamma }_3\varsigma +10\left({\beta }_6-{\beta }_5\right){\ell }^2\right)}{\varsigma }},\hfill \\ & {\mathbf{e}}_2={\displaystyle \frac{{\mathbf{e}}_1}{{\varsigma }^3}},{\mathbf{f}}_2={\displaystyle \frac{{\mathbf{f}}_1-{\mathbf{g}}_2{\varsigma }^3+{\mathbf{g}}_1}{{\varsigma }^3}},{\mathbf{a}}_2={\displaystyle \frac{{\mathbf{a}}_1-\ell \left(-\left({\varsigma }^3\left({\lambda }_2+{\nu }_2\right)\right)+{\lambda }_1+{\nu }_1\right)}{{\varsigma }^3}},\hfill \\ & {\mathbf{b}}_2={\displaystyle \frac{{\mathbf{b}}_1}{{\varsigma }^5}},\omega ={\displaystyle \frac{{\delta }_1\varsigma -{\delta }_2+25{\beta }_5{\ell }^5-25{\beta }_6{\ell }^5-2{\beta }_3{\ell }^3+2{\gamma }_3{\ell }^3\varsigma -{\beta }_1\ell +{\gamma }_1\ell \varsigma }{\varsigma -1}}.\hfill \end{array}$$

(25)

In this case, we can express Equation (23) as

$${\beta }_6{\mathcal{G}}^{\left(6\right)}+{\mathbf{b}}_1{\mathcal{G}}^5+{\mathcal{L}}_1{\mathcal{G}}^{\left(4\right)}+{\mathcal{L}}_2{\mathcal{G}}^{\prime \prime }+{\mathcal{L}}_3{\mathcal{G}}^2{\mathcal{G}}^{\prime \prime }+{\mathcal{L}}_4\mathcal{G}+{\mathcal{L}}_5{\mathcal{G}}^3-6{\mathbf{e}}_1\mathcal{G}{\left({\mathcal{G}}^{\prime }\right)}^2=0,$$

(26)

where ${\mathcal{L}}_i,(i=1,2,3,4,5)$ are some real constants which are expressed as

$$\begin{array}{cc}\hfill & {\mathcal{L}}_1={\beta }_4-15{\beta }_6{\ell }^2+5{\beta }_5\ell ,\hfill \\ \hfill & {\mathcal{L}}_2={\beta }_2+15{\beta }_6{\ell }^4-10{\beta }_5{\ell }^3-6{\beta }_4{\ell }^2+3{\beta }_3\ell ,\hfill \\ \hfill & {\mathcal{L}}_3=-\left(3{\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1\right),\hfill \\ \hfill & {\mathcal{L}}_4=-{\delta }_1\varsigma -\omega -{\beta }_6{\ell }^6+{\beta }_5{\ell }^5+{\beta }_4{\ell }^4-{\beta }_3{\ell }^3-{\beta }_2{\ell }^2+{\beta }_1\ell ,\hfill \\ \hfill & {\mathcal{L}}_5={\mathbf{a}}_1+{\ell }^2\left({\mathbf{e}}_1+{\mathbf{f}}_1+{\mathbf{g}}_1\right)-\ell \left({\lambda }_1+{\nu }_1\right).\hfill \end{array}$$

(27)

In order to facilitate the derivation of closed-form solutions, we employ the transformation given below:

$$\mathcal{G}\left(\xi \right)={\mathrm{\Theta }}^{3/2}\left(\xi \right).$$

(28)

Consider a transformation with $\mathrm{\Theta }=\mathrm{\Theta }\left(\xi \right)>0$. Substituting Equation (28) into Equation (26) yields the following NLODE:

$$\begin{array}{c}96{\mathrm{\Theta }}^{\left(6\right)}{\mathrm{\Theta }}^5+288{\beta }_6{\mathrm{\Theta }}^{\left(5\right)}{\mathrm{\Theta }}^4{\mathrm{\Theta }}^{\prime }+720{\beta }_6{\mathrm{\Theta }}^{\left(4\right)}{\mathrm{\Theta }}^4{\mathrm{\Theta }}^{\prime \prime }-360{\beta }_6{\mathrm{\Theta }}^{\left(4\right)}{\mathrm{\Theta }}^3{\left({\mathrm{\Theta }}^{\prime }\right)}^2+480{\beta }_6{\left({\mathrm{\Theta }}^{\left(3\right)}\right)}^2{\mathrm{\Theta }}^4\hfill \\ -1440{\beta }_6{\mathrm{\Theta }}^{\left(3\right)}{\mathrm{\Theta }}^3{\mathrm{\Theta }}^{\prime }{\mathrm{\Theta }}^{\prime \prime }+720{\beta }_6{\mathrm{\Theta }}^{\left(3\right)}{\mathrm{\Theta }}^2{\left({\mathrm{\Theta }}^{\prime }\right)}^3-360{\beta }_6{\mathrm{\Theta }}^3{\left({\mathrm{\Theta }}^{\prime \prime }\right)}^3+1620{\beta }_6{\mathrm{\Theta }}^2{\left({\mathrm{\Theta }}^{\prime }\right)}^2{\left({\mathrm{\Theta }}^{\prime \prime }\right)}^2\\ -1350{\beta }_6\mathrm{\Theta }{\left({\mathrm{\Theta }}^{\prime }\right)}^4{\mathrm{\Theta }}^{\prime \prime }+315{\beta }_6{\left({\mathrm{\Theta }}^{\prime }\right)}^6+64{\mathrm{\Theta }}^9{\mathcal{L}}_5+64{\mathrm{\Theta }}^6{\mathcal{L}}_4+48{\mathcal{L}}_3{\mathrm{\Theta }}^7{\mathcal{L}}_3\left(2\mathrm{\Theta }{\mathrm{\Theta }}^{\prime \prime }+{\left({\mathrm{\Theta }}^{\prime }\right)}^2\right)\\ +48{\mathcal{L}}_2{\mathrm{\Theta }}^4\left(2\mathrm{\Theta }{\mathrm{\Theta }}^{\prime \prime }+{\left({\mathrm{\Theta }}^{\prime }\right)}^2\right)+12{\mathrm{\Theta }}^2{\mathcal{L}}_1\left(12{\mathrm{\Theta }}^2{\left({\mathrm{\Theta }}^{\prime \prime }\right)}^2+3{\left({\mathrm{\Theta }}^{\prime }\right)}^4+8{\mathrm{\Theta }}^3{\mathrm{\Theta }}^{\left(4\right)}-12\mathrm{\Theta }{\left({\mathrm{\Theta }}^{\prime }\right)}^2{\mathrm{\Theta }}^{\prime \prime }+16{\mathrm{\Theta }}^2{\mathrm{\Theta }}^{\left(3\right)}{\mathrm{\Theta }}^{\prime }\right)\\ \hfill -864{\mathbf{e}}_1{\mathrm{\Theta }}^7{\left({\mathrm{\Theta }}^{\prime }\right)}^2+64{\mathbf{b}}_1{\mathrm{\Theta }}^{12}=0,\end{array}$$

(29)

In order to determine that $M=1.$, we first use the balancing principle to Equation (29) between ${\mathrm{\Theta }}^{12}$ and ${\mathrm{\Theta }}^{\left(6\right)}{\mathrm{\Theta }}^5$. The solution of Equation (29) may thus be expressed as follows:

$$\mathrm{\Theta }\left(\xi \right)={\eta }_0+{\eta }_1\mathrm{\Psi }\left(\xi \right)+{\displaystyle \frac{{\eta }_{-1}}{\mathrm{\Psi }\left(\xi \right)}},$$

(30)

assuming that ${\eta }_0,{\eta }_1$ and ${\eta }_{-1}$ are all unknown constants, they may be estimated by concurrently applying the restrictions ${\eta }_1$ and ${\eta }_{-1}\ne 0$ at the same time.

3.2. Extraction of Exact Solutions

The following outcomes can be achieved by solving the resulting system of nonlinear algebraic equations (NLAEs) using Wolfram Mathematica by grouping coefficients of like powers and setting them to zero after substituting Equations (30) and (11) into Equation (29).

Case-(1): If we set ${\eta }_0={\eta }_1={\eta }_3={\eta }_6=0$, then we have:

$\mathbf{Result}\mathbf{1}.\mathbf{1}:{\eta }_0={\eta }_{-1}=0,{\eta }_1=\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}\sqrt{{\displaystyle \frac{{\zeta }_4}{{\mathcal{L}}_5}}},{\beta }_6={\displaystyle \frac{8\left(-\frac{15{\mathcal{L}}_4{\mathcal{L}}_3^3}{{\mathcal{L}}_5^3}-1892\right)}{14509}},{\mathcal{L}}_1={\displaystyle \frac{4\left(4215{\mathcal{L}}_4{\mathcal{L}}_3^3+67364{\mathcal{L}}_5^3\right)}{130581{\mathcal{L}}_3{\mathcal{L}}_5^2}},{\mathcal{L}}_2=-{\displaystyle \frac{330702{\mathcal{L}}_4{\mathcal{L}}_3^3+530200{\mathcal{L}}_5^3}{391743{\mathcal{L}}_3^2{\mathcal{L}}_5}},{\mathbf{e}}_1={\displaystyle \frac{5{\mathcal{L}}_3}{18}},{\zeta }_2={\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}.$

We may get explicit solutions to the proposed equation as follows, based on the previous set of solutions:

(1.1) If ${\mathcal{L}}_3<0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5<0$, after that, we obtain bright soliton solutions, which are made as follows:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{1.1}(y,t)={\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}\mathrm{sech}\left(\sqrt{{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{3/2}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{1.1}(y,t)=\varsigma {\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}\mathrm{sech}\left(\sqrt{{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{3/2}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(32)

(1.2) If ${\mathcal{L}}_3<0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5>0$, consequently, we have singular periodic solutions, which are expressed as follows:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{1.2.1}(y,t)={\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}sec\left(\sqrt{-{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{1.2.1}(y,t)=\varsigma {\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}sec\left(\sqrt{-{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(34)

or

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{1.2.2}(y,t)={\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}csc\left(\sqrt{-{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{1.2.2}(y,t)=\varsigma {\left(\sqrt{-{\displaystyle \frac{1}{{\mathcal{L}}_3}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4-3388{\mathcal{L}}_5^3\right)}{14509{\mathbf{b}}_1}}}csc\left(\sqrt{-{\displaystyle \frac{2{\mathcal{L}}_5}{3{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}\hfill \\ & & \times e^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(36)

Case-(2): If ${\eta }_1={\eta }_3={\eta }_6=0$ and ${\eta }_0={\displaystyle \frac{{\eta }_2^2}{4{\eta }_4}}$, then we have

$\mathbf{Result}\mathbf{2}.\mathbf{1}:{\eta }_0=0,{\eta }_1=\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}}\pm {\displaystyle \frac{\sqrt{\frac{3{\zeta }_4}{2}}}{{\mathcal{L}}_5}},{\eta }_{-1}=\mp {\displaystyle \frac{\sqrt[6]{\frac{5}{14509}}\sqrt[6]{7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6}}{2\sqrt{6}\sqrt[6]{{\mathbf{b}}_1}\sqrt{{\zeta }_4}{\mathcal{L}}_3}},{\beta }_6={\displaystyle \frac{8\left(-\frac{15{\mathcal{L}}_4{\mathcal{L}}_3^3}{{\mathcal{L}}_5^3}-1892\right)}{14509}},{\mathcal{L}}_1={\displaystyle \frac{4\left(4215{\mathcal{L}}_4{\mathcal{L}}_3^3+67364{\mathcal{L}}_5^3\right)}{130581{\mathcal{L}}_3{\mathcal{L}}_5^2}},{\mathcal{L}}_2=-{\displaystyle \frac{330702{\mathcal{L}}_4{\mathcal{L}}_3^3+530200{\mathcal{L}}_5^3}{391743{\mathcal{L}}_3^2{\mathcal{L}}_5}},{\mathbf{e}}_1={\displaystyle \frac{5{\mathcal{L}}_3}{18}},{\zeta }_2=-{\displaystyle \frac{{\mathcal{L}}_5}{3{\mathcal{L}}_3}}.$

It is possible to identify the following solutions from the recovered solution set:

(2.1) If ${\mathcal{L}}_3>0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5>0$, afterwards, we obtain singular soliton solutions, which are expressed as:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{2.1}(y,t)=({\displaystyle \frac{1}{{\mathcal{L}}_5}}(\sqrt{{\displaystyle \frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}({\displaystyle \frac{\mp \sqrt{6}\sqrt[6]{\frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}coth\left(\sqrt{\frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)\right)}{2}}\hfill \\ & & \pm \sqrt{{\displaystyle \frac{3}{2}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}}tanh\left(\sqrt{{\displaystyle \frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right){\left)\right))}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{2.1}(y,t)=\varsigma ({\displaystyle \frac{1}{{\mathcal{L}}_5}}(\sqrt{{\displaystyle \frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}({\displaystyle \frac{\mp \sqrt{6}\sqrt[6]{\frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}coth\left(\sqrt{\frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)\right)}{2}}\hfill \\ & & \pm \sqrt{{\displaystyle \frac{3}{2}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}}tanh\left(\sqrt{{\displaystyle \frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right){\left)\right))}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(38)

(2.2) If ${\mathcal{L}}_3>0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5<0$, consequently, we have singular periodic solutions, which are expressed as follows:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{2.2}(y,t)=({\displaystyle \frac{1}{{\mathcal{L}}_5}}\left(\sqrt{{\displaystyle \frac{-{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\right({\displaystyle \frac{\mp \sqrt{6}\sqrt[6]{\frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}cot\left(\sqrt{\frac{-{\mathcal{L}}_5}{6{\mathcal{L}}_3}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)\right)}{2}}\hfill \\ & & \pm \sqrt{{\displaystyle \frac{3}{2}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}}tan\left(\sqrt{{\displaystyle \frac{-{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right){\left)\right))}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{2.2}(y,t)=\varsigma ({\displaystyle \frac{1}{{\mathcal{L}}_5}}\left(\sqrt{-{\displaystyle \frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\right({\displaystyle \frac{\mp \sqrt{6}\sqrt[6]{\frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}cot(-\sqrt{\frac{{\mathcal{L}}_5}{6{\mathcal{L}}_3}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right))}{2}}\hfill \\ & & \pm \sqrt{{\displaystyle \frac{3}{2}}}\sqrt[6]{{\displaystyle \frac{5\left(7335{\mathcal{L}}_3^3{\mathcal{L}}_4{\mathcal{L}}_5^3-3388{\mathcal{L}}_5^6\right)}{14509{\mathbf{b}}_1}}}tan\left(\sqrt{{\displaystyle \frac{-{\mathcal{L}}_5}{6{\mathcal{L}}_3}}}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right){\left)\right))}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(40)

Case-(3): If ${\zeta }_0={\zeta }_1={\zeta }_2={\zeta }_6=0$, then we obtain

$\mathbf{Result}\mathbf{3}.\mathbf{1}:{\eta }_0={\eta }_{-1}={\mathcal{L}}_4={\mathcal{L}}_5={\mathcal{L}}_1={\mathcal{L}}_2=0,{\beta }_6=-{\displaystyle \frac{3}{5}},{\mathcal{L}}_3=-{\displaystyle \frac{\sqrt[3]{-\frac{{\mathbf{b}}_1}{1093}}\left(798{\zeta }_3\right)}{{\eta }_1}},{\mathbf{e}}_1=-{\displaystyle \frac{154\sqrt[3]{-\frac{{\mathbf{b}}_1}{1093}}{\zeta }_3}{{\eta }_1}},{\zeta }_4={\displaystyle \frac{4}{3}}\sqrt[3]{-{\displaystyle \frac{{\mathbf{b}}_1}{1093}}}{\eta }_1^2$.

We may get the following explicit solutions to the proposed equations based on the previous set of solutions:

If ${\mathcal{L}}_3>0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5>0$, then we get a rational solutions are formulated as:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_3(y,t)={\left({\displaystyle \frac{16\sqrt[3]{-\frac{1}{1093}}\sqrt[3]{{\mathbf{b}}_1}{\eta }_1^3}{3\left({\zeta }_3^3{\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)}^2-\frac{16}{3}\sqrt[3]{-\frac{1}{1093}}\sqrt[3]{{\mathbf{b}}_1}{\eta }_1^2\right)}}\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_3(y,t)=\varsigma {\left({\displaystyle \frac{16\sqrt[3]{-\frac{1}{1093}}\sqrt[3]{{\mathbf{b}}_1}{\eta }_1^3}{3\left({\zeta }_3^3{\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)}^2-\frac{16}{3}\sqrt[3]{-\frac{1}{1093}}\sqrt[3]{{\mathbf{b}}_1}{\eta }_1^2\right)}}\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(42)

Case-(4): If ${\zeta }_2={\zeta }_4={\zeta }_6=0$, then we obtain

$\mathbf{Result}\mathbf{4}.\mathbf{1}:{\mathbf{e}}_1={\eta }_0={\eta }_1=0,{\beta }_6=-{\displaystyle \frac{353}{326}},{\mathcal{L}}_1=-{\displaystyle \frac{{260981}^{2/3}\sqrt[3]{{\mathcal{L}}_4}}{{489}^{2/3}\sqrt[3]{121090}}},{\mathcal{L}}_2={\displaystyle \frac{128\sqrt[3]{\frac{2609810}{489}}{\mathcal{L}}_4^{2/3}}{3{12109}^{2/3}}},{\mathcal{L}}_3=-{\displaystyle \frac{1038555{\left(\frac{3}{74566}\right)}^{2/3}\sqrt[3]{\frac{423815}{163}}{\zeta }_1^3}{163{\eta }_{-1}^3\sqrt[3]{{\mathcal{L}}_4}}},{\mathcal{L}}_5=-{\displaystyle \frac{1006691805{\zeta }_1^3}{97234064{\eta }_{-1}^3}},{\mathbf{b}}_1=-{\displaystyle \frac{166908529155375{\zeta }_1^6}{1812588804056{\eta }_{-1}^6{\mathcal{L}}_4}},{\zeta }_3={\displaystyle \frac{4{\left(\frac{163}{84763}\right)}^{2/3}\sqrt[3]{\frac{372830}{3}}{\mathcal{L}}_4^{2/3}}{27{\zeta }_1}},{\zeta }_0=-{\displaystyle \frac{42{\left(\frac{3}{37283}\right)}^{2/3}\sqrt[3]{\frac{847630}{163}}{\zeta }_1^2}{\sqrt[3]{{\mathcal{L}}_4}}}$.

The following are explicit solutions to the proposed equations that we may get using the previous set of solutions:

If ${\mathcal{L}}_3>0$, ${\mathbf{b}}_1\ne 0$ and ${\mathcal{L}}_5>0$, Weierstrass elliptic doubly periodic solutions are then obtained and expressed as follows:

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_4(y,t)={\left({\displaystyle \frac{{\eta }_{-1}}{\wp \left(\frac{\sqrt[3]{\frac{163}{84763}}\sqrt[6]{372830}\sqrt{\frac{{\mathcal{L}}_4^{2/3}}{{\zeta }_1}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)}{33^{2/3}}\right)}}\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_4(y,t)=\varsigma {\left({\displaystyle \frac{{\eta }_{-1}}{\wp \left(\frac{\sqrt[3]{\frac{163}{84763}}\sqrt[6]{372830}\sqrt{\frac{{\mathcal{L}}_4^{2/3}}{{\zeta }_1}}\left(y-\frac{\mathcal{V}{t}^{\alpha }}{\alpha }\right)}{33^{2/3}}\right)}}\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)}.\hfill \end{array}$$

(44)

Case-(5): If ${\zeta }_1={\zeta }_3={\zeta }_6=0$, then we obtain

$\mathbf{Result}\mathbf{5}.\mathbf{1}:{\mathcal{L}}_3={\mathcal{L}}_5={\mathbf{e}}_1={\eta }_0=0,{\eta }_{-1}=\pm {\displaystyle \frac{\sqrt{{\zeta }_0}{\eta }_1}{\sqrt{{\zeta }_4}}},{\beta }_6={\displaystyle \frac{-136224\pm \frac{5{\mathcal{L}}_4}{{\zeta }_0^{3/2}{\zeta }_4^{3/2}}}{130581}},{\mathcal{L}}_1={\displaystyle \frac{1405{\mathcal{L}}_4\mp 4850208{\zeta }_0^{3/2}{\zeta }_4^{3/2}}{391743{\zeta }_0{\zeta }_4}},{\mathcal{L}}_2=\pm {\displaystyle \frac{55117{\mathcal{L}}_4}{391743\sqrt{{\zeta }_0{\zeta }_4}}}-{\displaystyle \frac{192800{\zeta }_0{\zeta }_4}{3957}},{\mathbf{b}}_1={\displaystyle \frac{45\left(\mp \frac{815{\zeta }_4^{3/2}{\mathcal{L}}_4}{{\zeta }_0^{3/2}}-81312{\zeta }_4^3\right)}{928576{\eta }_1^6}},{\zeta }_2=\sqrt{{\zeta }_0{\zeta }_4}\pm 2$.

(5.1) When ${\zeta }_0{\zeta }_4>0$, one can uncover different solution types for the given system. Jacobi’s elliptic function solutions are observed when $m=0$.

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.1}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}sec\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+cos\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.1.1}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}sec\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+cos\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.2}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}csc\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+sin\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.1.2}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}csc\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+sin\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.3}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}sin\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+csc\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.1.3}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}sin\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+csc\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.4}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cos\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+sec\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.1.4}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cos\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+sec\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.5}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cot\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+tan\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.1.5}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cot\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+tan\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(54)

(5.2) When ${\zeta }_0{\zeta }_4>0$, one can uncover different solution types for the given system. Jacobi’s elliptic function solutions are observed when $m=1$.

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.1.1}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}coth\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+tanh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.2.1}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}coth\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+tanh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.2.2}(y,t)={\left({\eta }_1\left(coth\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}tanh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.2.2}(y,t)=\varsigma {\left({\eta }_1\left(coth\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}tanh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.2.3}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cosh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+\mathrm{sech}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.2.3}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}cosh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+\mathrm{sech}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{5.2.4}(y,t)={\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}\mathrm{sech}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+cosh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill & & {\mathcal{Q}}_{5.2.4}(y,t)=\varsigma {\left({\eta }_1\left(\pm \sqrt{{\displaystyle \frac{{\zeta }_0}{{\zeta }_4}}}\mathrm{sech}\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)+cosh\left(y-{\displaystyle \frac{\mathcal{V}{t}^{\alpha }}{\alpha }}\right)\right)\right)}^{{\displaystyle \frac{3}{2}}}{e}^{i\left(-\ell y+{\displaystyle \frac{\omega t^{\alpha }}{\alpha }}+\mathrm{\Delta }\right)},\hfill \end{array}$$

(62)

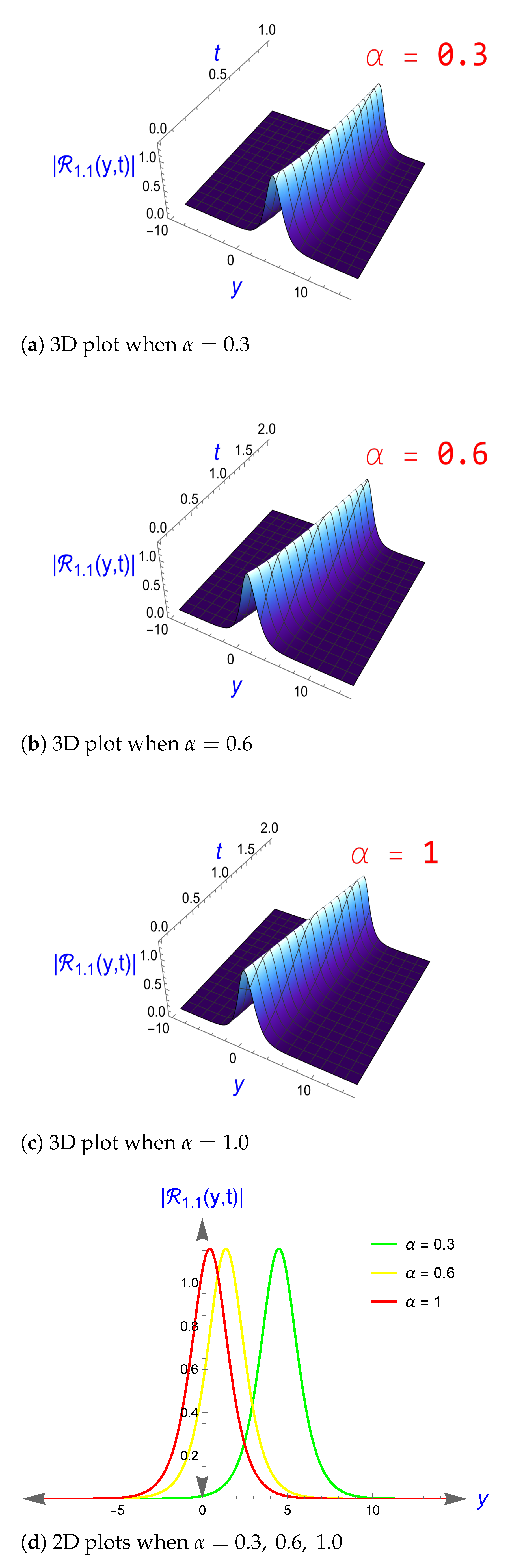
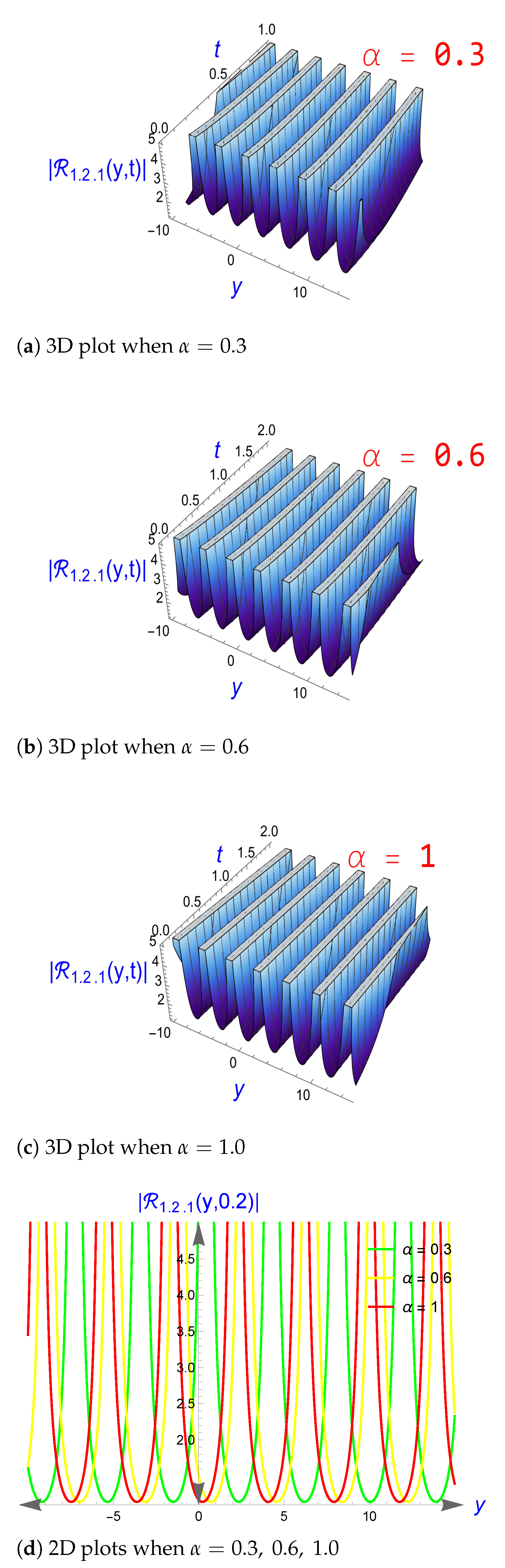
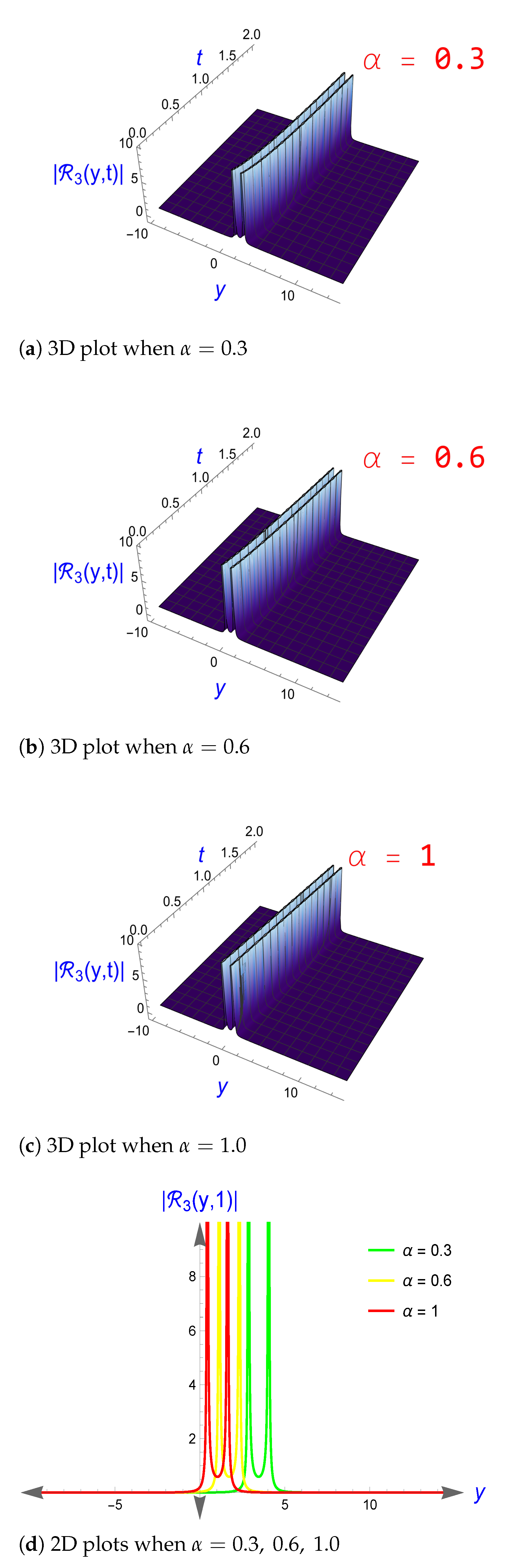
4. Graphical Representation for Some Retrieved Solutions

Different solution families for Equations (3) and (4) were generated by giving the parameters specific values. Consequently, this approach has produced several novel results that have never been published before. To illustrate the physical properties of the recovered solutions, two- and three-dimensional representations of some individual solutions are presented. With parameters ${\mathcal{L}}_4=1.6,{\mathcal{L}}_5=-0.9,{\mathcal{L}}_3=-0.9,{\mathbf{b}}_1=-1.6,\ell =0.7,$$\varsigma =3.8,{\gamma }_1=0.8,{\gamma }_3=0.8,{\delta }_1=0.7,{\delta }_2=0.6,{\beta }_1=0.8,{\beta }_2=0.7,{\beta }_3=0.9,$${\beta }_4=0.6,{\beta }_5=1.5,\mathrm{\Delta }=0.7,$ and $-10\le x\le 15$, Equation (31) shows a bright soliton solution in 3D and 2D plots as in Figure 1 but with different values of $\alpha$. These bright soliton profiles illustrate how the fractional-order parameter $\alpha$ affects the soliton dynamics. As $\alpha$ increases from 0.3 to 1, the soliton becomes narrower and its amplitude increases, indicating a stronger localization of the wave energy. This behavior reflects the role of the conformable fractional derivative in modulating the balance between dispersion and nonlinearity in the system. From the physics point of view, this implies that higher fractional orders correspond to more intense and localized optical pulses, which is a significant factor in controlling pulse propagation in nonlinear optical fibers and similar media. With parameters ${\mathcal{L}}_4=1.4,{\mathcal{L}}_5=-0.8,{\mathcal{L}}_3=-0.8,{\mathbf{b}}_1=-1.4,\ell =0.6,\varsigma =4,{\gamma }_1=0.7,$${\gamma }_3=0.8,{\delta }_1=0.6,{\delta }_2=0.7,{\beta }_1=0.9,{\beta }_2=0.8,{\beta }_3=0.8,{\beta }_4=0.7,{\beta }_5=1.5,$$\mathrm{\Delta }=0.8,$ $-10\le x\le 15$, and with different values of $\alpha$, Figure 2 elucidates 3D and 2D plots for the singular periodic solution of Equation (33). The singular periodic wave profiles depicted in Figure 2 demonstrate the effect of the fractional-order parameter $\alpha$ on the resulting solutions’ amplitude and periodic spacing. With the growth of $\alpha$ from 0.3 to 1, the amplitude of the singular periodic waves increases, and the oscillations become more localized and narrower. This phenomenon implies that higher fractional orders enhance the nonlinear-dominated phenomena in the system, which are related to stronger wave confinement and sharper singular structures. Physically, they are equivalent to regimes wherein periodic modulation and energy localization are significant phenomena responsible for plasma waves, nonlinear optics, and shallow-water systems describing complex dispersive and resonance interactions. For Equation (41), Figure 3 displays the rational solution with parameters ${\mathbf{b}}_1=-2.7,\ell =0.8,\varsigma =2,{\gamma }_1=0.6,{\gamma }_3=0.5,$${\delta }_1=0.7,{\delta }_2=0.9,{\beta }_1=0.4,{\beta }_2=0.9,{\beta }_3=0.6,{\beta }_4=0.5,{\beta }_5=0.5,\mathrm{\Delta }=0.9,{\zeta }_3=1,$ ${\eta }_1=0.7,$ and $-10\le x\le 15$, with different values of $\alpha$ in 3D and 2D plots. These plots illustrate how with growing fractional order from $\alpha =0.3$ to $\alpha =1$, the wave amplitude enhances and is further localized, and the peak width becomes significantly reduced. It indicates that a larger $\alpha$ enhances the nonlinearity of the system with increased wave focusing and energy concentration around the center region. The associated 2D profiles (Figure 3d) also confirm this tendency with a significant enhancement of the peak intensity for larger $\alpha$. Physically, such rational-type local structures resemble rogue or spike-like waves, where the fractional parameter controls dispersion vs. nonlinearity balance, a crucial aspect in optical fibers, fluid dynamics, and plasma systems with memory effects.

5. Discussion About Results

This section is divided into 2 parts. The first part is concerned with discussing the influence of the CFD on the retrieved solutions while the second part represents a comparison with some published literature.

5.1. The Influence of the CFD on the Retrieved Solutions

The influence of the CFD on the retrieved solutions clearly demonstrates how the fractional parameter governs the dynamical behavior of the system, modifying both the amplitude and localization of the obtained wave structures. This highlights the essential role of CFD in capturing memory and hereditary effects that are absent in classical integer-order models.

5.2. Comparison with Literature

Earlier works on optical solitons in the domain of dispersive media and metamaterial couplers have provided a rich variety of solution families and numerical results, but differ from the present work in several key aspects. Most of the earlier works considered integer-order models or single-component systems and standard nonlinear laws, which limited the available dynamical behaviors and the family of exact closed-form solutions. In contrast, our research is the first to integrate (i) a conformable fractional derivative description of nonlocality, (ii) a parabolic-law nonlinear refractive index applicable to certain metamaterial couplers, and (iii) the MEDAM in a view toward deriving a broader inventory of exact solutions, namely bright, dark, singular, and Weierstrass elliptic doubly periodic forms and parameter-dependent regimes of interaction.

This study can be considered as an extension of the study implemented in [33], where the authors studied the classical derivative and retrieved some special types of solutions. Conversely, this investigation implements a new approach to obtain exact solutions under the effect of CFD and produce a broad range of solutions, like bright, singular solitons, and singular periodic as well as Weierstrass elliptic doubly periodic, and many other exact solutions which have not been reported before in any published article. The dispersion characteristics in our model are governed by the time-fractional derivative in the coupled nonlinear Schrödinger equation, which generalizes standard dispersion models to include non-local interactions in the medium. The fractional model renders the description of dispersion more versatile, encompassing anomalous dispersion regimes that are required for the formation of bright solitons. The results have particular application to optical fibers with engineered dispersion properties, such as single-mode fibers that support propagation in the anomalous dispersion regime near the infrared wavelength, photonic crystal fibers that permit precise dispersion engineering through their microstructure, and highly nonlinear fibers that are designed to optimize nonlinearities. The parabolic nonlinearity assumed here is in agreement with the Kerr nonlinearity of such fibers, which support soliton propagation under appropriate conditions. However, the application of the model might be limited to fibers where the fractional dispersion parameters can be attained experimentally, i.e., in some microstructure or doped fibers.

5.3. Physical Interpretation and Applicability

This research on optical soliton solutions in metamaterial-based dispersive couplers carries significant physical interpretation and practical applicability, fundamentally studying how light pulses maintain their shape and energy over distances notwithstanding dispersion and nonlinear effects. The physics behind the work lies in the delicate balancing of how the conformable fractional derivative shapes the nonlinear refractive index against the unique properties of metamaterials, which allow control over light propagation in unprecedented ways. These extracted soliton solutions—bright, singular, and doubly periodic—represent self-reinforcing wave packets that behave like robust “light particles” resistant to distortions in much the same way quantum particles maintain coherence. The applicability ranges directly to the development of optical communication technologies, whereby such solitons might form the backbone of the next generation of information carriers, thus enabling higher data rates, minimal signal degradation, and compact photonic devices. In a systematic mapping of the evolution of stability parameters across dynamical regimes, the work outlines critical design principles for engineering practical optical systems where nonlinearity-dispersion trade-offs are very important to optimize performances in real-world telecommunication networks, optical computing, and signal processing applications.

6. Conclusions

This study has succeeded in deriving an array of optical soliton solutions to the time-fractional coupled nonlinear Schrödinger equation with parabolic nonlinearity through the powerful Modified Extended Direct Algebraic Method. The solutions, which include bright and singular solitons, singular periodic, and Weierstrass elliptic doubly periodic solutions, constitute a complete portfolio of probable wave behaviors in the modeled system.

The key physical relevance of these findings is the demonstrated subtle balance between the fractional dispersion supplied by the conformable derivative and the specific form of the parabolic nonlinearity. This balance is crucial for the existence and stability of the solitons found. The graphical plots not only verify the analytical solutions but also pictorially summarize the dynamical transitions between different wave regimes, giving an intuitive understanding of the nonlinear dynamics of the system. Furthermore, the model points out the crucial role of optical metamaterials in designing target dispersion and nonlinear properties to facilitate and manipulate such soliton propagation.

The results presented herein have direct applications in the design and optimization of new photonic devices, particularly in highly nonlinear or metamaterial-based systems such as soliton-based communication lines, all-optical switches, and sensitive optical sensors, where precise soliton control is essential.

As for future research, there are several promising directions in which this work can be extended. First, an investigation of the robustness of these solitons to perturbations would be essential for practical applications, possibly through numerical stability analysis. Second, extending the model to include higher-order effects like third-order dispersion and self-steepening would render it more applicable to ultra-short pulses. Finally, an exploration of other fractional operators beyond the CFD can lead to even more fruitful classes of soliton dynamics and a more generalized theory for wave propagation in complex media with strong memory effects. This work thus provides a solid theoretical foundation for future research in complex fractional nonlinear photonic systems.