Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative

Abstract

In this paper, we defined a new family of meromorphic functions whose analytic characterization was motivated by the definition of the multiplicative derivative. Replacing the ordinary derivative with a multiplicative derivative in the subclass of starlike meromorphic functions made the class redundant; thus, major deviation or adaptation was required in defining a class of meromorphic functions influenced by the multiplicative derivative. In addition, we redefined the subclass of meromorphic functions analogous to the class of the functions with respect to symmetric points. Initial coefficient estimates and Fekete–Szegö inequalities were obtained for the defined function classes. Some examples along with graphs have been used to establish the inclusion and closure properties.

1. Introduction and Definition

Let $\mathbb{U}$, $\mathbb{R}$, $\mathbb{C}$ and $\mathbb{N}$ denote the unit disc, set of real numbers, set of complex numbers and set of natural numbers, respectively. Also, ${\left(x\right)}_n$ will be used to denote the usual Pochhammer symbol, defined in terms of the Gamma function $\Gamma$, by

$${\left(x\right)}_n={\displaystyle \frac{\Gamma (x+n)}{\Gamma \left(x\right)}}=\left\{\begin{array}{cc}1\hfill & ifn=0\hfill \\ x(x+1)(x+2)\dots (x+n-1)\hfill & ifn\in \mathbb{N}=\{1,2,\dots \}.\hfill \end{array}\right.$$

For the functions f and g that are analytic in $\mathbb{U}$, we say that the function f is subordinate to g if there exits a function w, analytic in $\mathbb{U}$ with $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$, $z\in \mathbb{U}$ such that $f\left(z\right)=g\left(w\right(z\left)\right)$. We denote this subordination by $f\prec g$ or $f\left(z\right)\prec g\left(z\right)$. In particular, if the function g is univalent in $\mathbb{U}$, the above subordination is equivalent to $f\left(0\right)=g\left(0\right)$ and $f\left(\mathbb{U}\right)\subset g\left(\mathbb{U}\right)$.

Let

$${\mathcal{A}}_n=\{f\in \mathcal{H},f\left(z\right)=z+a_{n+1}{z}^{n+1}+a_{n+2}{z}^{n+2}+\cdots \}$$

and $\mathcal{A}={\mathcal{A}}_1$. Also, let $\mathcal{S}$ denote the collection of functions in $\mathcal{A}$ that are univalent in $\mathbb{U}$. Let $\Sigma$ denote the class of meromorphic functions of the form

$$f\left(z\right)={\displaystyle \frac{1}{z}}+\sum _{n=0}^{\infty }{a}_n{z}^n,$$

(1)

which are analytic in the open punctured unit disc ${\mathbb{U}}^{*}=\left\{z\in \mathbb{C}:0<\left|z\right|<1\right\}=\mathbb{U}\setminus \left\{0\right\}$.

The Mittag–Leffler function, is a well-known special function, known for its applications in definitions of the various fractional order derivatives. Explicitly, the Mittag–Leffler function, which involves several parameters introduced by Srivastava et al. [1], is given by

$$E_{{({\theta }_j,{\lambda }_j)}_m}^{\sigma ,k,\delta ,ϵ}\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\sigma \right)}_{kn}{\left(\delta \right)}_{ϵn}}{{\prod }_{j=1}^m\Gamma \left({\theta }_{j}n+{\lambda }_j\right)}}{\displaystyle \frac{z^n}{n!}},$$

(2)

$$\left({\theta }_j,{\lambda }_j,\sigma ,k,\delta ,ϵ\in \mathbb{C};Re\left({\theta }_j\right)>0,(j=1,\dots ,m);Re\left(\sum _{j=1}^m{\theta }_j\right)>Re(k+ϵ)-1\right).$$

Generalizing the operator introduced by Aouf and El-Emam [2], Horrigue and Madian in [3] introduced an operator ${\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right):\Sigma \to \Sigma$, explicitly defined as follows:

$${\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)={\displaystyle \frac{1}{z}}+\sum _{n=0}^{\infty }{\displaystyle \frac{\Gamma \left[\sigma +k(n+1)\right]\Gamma \left(\lambda \right)}{\Gamma \left(\sigma \right)\Gamma \left[\theta (n+1)+\lambda \right](n+1)!}}{\left[1+\tau (n+1)\right]}^m{a}_n{z}^n.$$

(3)

Remark 1.

The operator ${\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)$ is the meromorphic analogue of the operator recently studied by Umadevi and Karthikeyan [4]. We note that

1.

${\mathcal{L}}_k^0\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)=\Gamma \left(\lambda \right)z^{-1}{E}_{\theta ,\lambda }^{\sigma ,k}\left(z\right)$, where $E_{\theta ,\lambda }^{\sigma ,k}\left(z\right)={\sum }_{n=0}^{\infty }{\displaystyle \frac{{\left(\sigma \right)}_{nk}{z}^n}{\Gamma \left(\theta n+\lambda \right)n!}},z,\theta ,\lambda ,\sigma ,k\in \mathbb{C},Re\left(\theta \right)>0,Re\left(k\right)>0$ is the special case of (2). $E_{\theta ,\lambda }^{\sigma ,k}\left(z\right)$ was introduced and studied in [5] (also see [6,7]).

2.

${\mathcal{L}}_1^m\left(0,\lambda ,1;\tau \right)f\left(z\right)={\displaystyle \frac{1}{z}}+{\sum }_{n=0}^{\infty }{\left[1+\tau (n+1)\right]}^m{a}_n{z}^n$ is the operator that was introduced and studied by Aouf and El-Emam [2] (also see [8,9]).

3.

${\mathcal{L}}_1^0\left(0,\lambda ,1;\tau \right)f\left(z\right)=f\left(z\right)$, $(f\in \Sigma )$.

4.

${\mathcal{L}}_1^0\left(0,\lambda ,2;\tau \right)f\left(z\right)=2f\left(z\right)+z{f}^{\prime }\left(z\right)$, $(f\in \Sigma )$.

The geometrically defined subclass of $\mathcal{S}$, which had analytic characterizations, was redefined for the functions belonging to $\Sigma$. But the studies involving meromorphic functions did have their own challenges, as the results involving functions in $\mathcal{A}$ could not be easily translated to the functions belonging to $\Sigma$. A function $f\in \Sigma$ is said to be meromorphic starlike and meromorphic convex if it satisfies the condition

$$-Re\left\{{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right\}>0\mathrm{and}-Re\left\{1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\right\}>0,$$

respectively. Here, we will let meromorphic starlike and meromorphic convex function classes be denoted by ${\mathcal{MS}}^{*}$ and $\mathcal{MC}$.

Recently, Karthikeyan and Murugusundaramoorthy in [10] introduced and studied a class of analytic functions $\mathcal{R}\left(\psi \right)$, satisfying the subordination condition

$${\displaystyle \frac{z{e}^{\frac{z^2{f}^{\prime }\left(z\right)}{f\left(z\right)}}}{f\left(z\right)}}\prec \psi \left(z\right),(f\in \mathcal{A})$$

(4)

where $\psi \in \mathcal{P}$ is starlike symmetric with respect to the horizontal axis and is of the form

$$\psi \left(z\right)=1+{\mathfrak{M}}_{1}z+{\mathfrak{M}}_2{z}^2+{\mathfrak{M}}_3{z}^3+\cdots ,({\mathfrak{M}}_1\in \mathbb{C};z\in \mathbb{U}).$$

(5)

The class is non-empty and it does not reduce to the subclasses of $\mathcal{S}$. For the detailed analysis and closure properties of the class $\mathcal{R}\left(\psi \right)$, refer to [10].

The study of the class $\mathcal{R}\left(\psi \right)$ was motivated by the definition of Multiplicative calculus. Refer to [11,12] for a detailed definition and purpose of multiplicative derivative. The ∗-derivative of f at z belonging to a small neighbourhood of a domain in a complex plane, where f is a non-vanishing differentiable, is given by

$$f^{*}\left(z\right)=e^{f^{\prime }\left(z\right)/f\left(z\right)}$$

(6)

and $f^{*\left(n\right)}\left(z\right)=e^{{\left[f^{\prime }\left(z\right)/f\left(z\right)\right]}^{\left(n\right)}},n=1,2,\dots$. The existing architecture of the classes of univalent functions is built on a domain that admits zero, but the multiplicative derivative is defined only on a domain that omits zero. So when defining the class $\mathcal{R}\left(\psi \right)$, we were able to use only the idea and motivation behind the definition of a multiplicative calculus.

In this paper, we intend to study a class of functions in $\Sigma$, which would satisfy an analytic characterization analogous to the class $\mathcal{R}\left(\psi \right)$. The same analogous characterization of $\mathcal{R}\left(\psi \right)$ could not be adopted for functions belonging to $\Sigma$, and some major deviations were required in defining a class of meromorphic functions involving a multiplicative derivative.

Let $\mathcal{MR}\left(\psi \right)$ denote the functions in $f\in \Sigma$ satisfying the condition

$${\displaystyle \frac{e^{\frac{-z{f}^{\prime }\left(z\right)}{f\left(z\right)}}}{ezf\left(z\right)}}\prec \psi \left(z\right),$$

(7)

where $e=exp\left(1\right)$ and $\psi \in \mathcal{P}$ is defined as in (5).

Example 1.

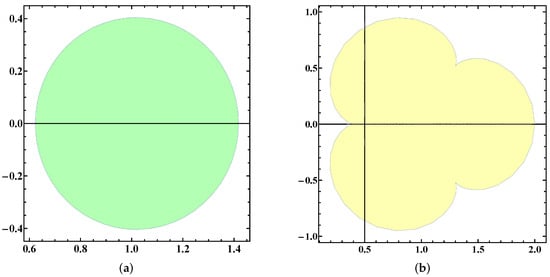
In this example, we will illustrate that the class $\mathcal{MR}\left(\psi \right)$ is non-empty. Let $f\left(z\right)={\displaystyle \frac{5}{z(5-z)}}$. Note that $f\left(z\right)={\displaystyle \frac{5}{z(5-z)}}$ is meromorphic of the form (1) and analytic in the open punctured unit disc ${\mathbb{U}}^{*}$. Then the differential characterization (18) is given by

$${\displaystyle \frac{e^{\frac{-z{f}^{\prime }\left(z\right)}{f\left(z\right)}}}{ezf\left(z\right)}}={\displaystyle \frac{(5-z)e^{\frac{2z-5}{(z-5)}-1}}{5}}:=\Omega \left(z\right).$$

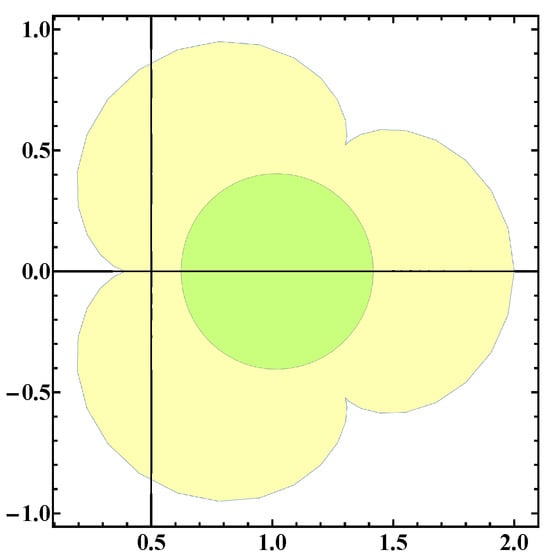
Figure 1a illustrates that $\Omega \left(z\right)$ maps $\mathbb{U}$ onto a circular region with center at $z=1$ in the right half-plane. The function $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$ is analytic with $\psi \left(z\right)=1$ and maps the unit disc onto a leaf-like region in the right half plane (see Figure 1b). Figure 2 illustrates that the image of $\Omega \left(z\right)$ lies inside the image of $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$. Therefore, the following relations hold if $f\left(z\right)={\displaystyle \frac{5}{z(5-z)}}$

$${\displaystyle \frac{e^{\frac{-z{f}^{\prime }\left(z\right)}{f\left(z\right)}}}{ezf\left(z\right)}}\prec 1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}.$$

Figure 1. (a) Image of $\left|z\right|<1$ under a mapping $\Omega \left(z\right):={\displaystyle \frac{(5-z)e^{\frac{2z-5}{(z-5)}-1}}{5}}$ (b) Image of $\left|z\right|<1$ under $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$.

Figure 2. 2D plots of $\Omega \left(z\right):={\displaystyle \frac{(5-z)e^{\frac{2z-5}{(z-5)}-1}}{5}}$ nested inside $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$.

Hence, $\mathcal{MR}\left(\psi \right)$ is non-empty.

Remark 2.

For $f\in \Sigma$ of the form (1), we will denote $\mathcal{MR}\left(\psi \right)$ as ${\mathcal{MR}}_{3L}$ if $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$.

Using the operator ${\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)$, we now define the following class analogous to the class $\mathcal{MR}\left(\psi \right)$.

Definition 1.

Let ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ denote the class of functions satisfying the conditions

$${\displaystyle \frac{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)F^{*}\left(z\right)}{ez\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)\right]}}\prec \psi \left(z\right),(f\in \Sigma ;z\in {\mathbb{U}}^{*}),$$

(8)

where ${\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)F^{*}\left(z\right)=e^{-{\displaystyle \frac{z{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f^{\prime }\left(z\right)}{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)}}}$, $\psi \in \mathcal{P}$ and $\psi \left(\mathbb{U}\right)$ is defined as in (5).

Remark 3.

Letting $m=\theta =0$ and $\sigma =k=1$ in Definition 1, the class ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ reduces to the class $\mathcal{MR}\left(\psi \right)$.

The following result is well-known, which we will be using to obtain the coefficient inequalities.

Lemma 1

([13]). If $\vartheta \left(z\right)=1+{\displaystyle \sum _{k=1}^{\infty }}{\vartheta }_k{z}^k\in \mathcal{P}$, and ρ is a complex number, then

$$\left|{\vartheta }_2-\rho {\vartheta }_1^2\right|\le 2max\left\{1;|2\rho -1|\right\},$$

and the result is sharp.

2. Main Results

We will start with the following.

Theorem 1.

If $f\left(z\right)\in {\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$, then we have

$$\left|a_0\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma \left(\theta +\lambda \right)\right|}{2{\left[1+\tau \right]}^m\left|\Gamma (\sigma +k)\Gamma \left(\lambda \right)\right|}}$$

(9)

$$\left|a_1\right|\le {\displaystyle \frac{2\left|{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )\right|}{3{\left[1+2\tau \right]}^m\left|\Gamma (\sigma +2k)\Gamma \left(\lambda \right)\right|}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right|\right\}$$

(10)

and for all $\rho \in \mathbb{C}$

$$\begin{array}{c}\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{2\left|{\mathfrak{M}}_1\right|\left|\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )\right|}{3{\left[1+2\tau \right]}^m\left|\Gamma (\sigma +2k)\Gamma \left(\lambda \right)\right|}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1{\mathcal{K}}_1\right|\right\},\end{array}$$

(11)

where ${\mathcal{K}}_1$ is given by

$$\begin{array}{c}{\mathcal{K}}_1=1-{\displaystyle \frac{3\rho {\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\sigma \right){\left(\Gamma \left[\theta +\lambda \right]\right)}^2}{7{\left[1+\tau \right]}^{2m}{\left(\Gamma (\sigma +k)\right)}^2\Gamma \left(\lambda \right)\Gamma (2\theta +\lambda )}}.\end{array}$$

(12)

The inequality is sharp for each $\rho \in \mathbb{C}$.

Proof. 

As $f\in {\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$, by (8), we have

$${\displaystyle \frac{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)F^{*}\left(z\right)}{ez\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)\right]}}=\psi \left[w\left(z\right)\right].$$

(13)

Thus, let $\vartheta \in \mathcal{P}$ be of the form $\vartheta \left(\xi \right)=1+{\sum }_{k=1}^{\infty }{\vartheta }_n{\xi }^n$ and defined by

$$\vartheta \left(\xi \right)={\displaystyle \frac{1+w\left(\xi \right)}{1-w\left(\xi \right)}},\xi \in \mathbb{U}.$$

On computation, the right-hand side of (13) is

$$\begin{array}{c}\psi \left[w\left(\xi \right)\right]=1+{\displaystyle \frac{{\vartheta }_1{\mathfrak{M}}_1}{2}}\xi +{\displaystyle \frac{{\mathfrak{M}}_1}{2}}\left[{\vartheta }_2-{\displaystyle \frac{{\vartheta }_1^2}{2}}\left(1-{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}\right)\right]{\xi }^2+\cdots .\end{array}$$

(14)

The left-hand side of (13) will be of the form

$$\begin{array}{c}{\displaystyle \frac{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)F^{*}\left(z\right)}{ez\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)\right]}}=1-2a_0{\displaystyle \frac{\Gamma \left[\sigma +k\right]\Gamma \left(\lambda \right)}{\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]}}{\left[1+\tau \right]}^{m}z+\\ {\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{7{\left[1+\tau \right]}^{2m}{\left(\Gamma \left[\sigma +k\right]\Gamma \left(\lambda \right)\right)}^2}{{\left(\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]\right)}^2}}{a}_0^2-{\displaystyle \frac{6{\left[1+2\tau \right]}^m\Gamma \left[\sigma +2k\right]\Gamma \left(\lambda \right)}{\Gamma \left(\sigma \right)\Gamma \left[2\theta +\lambda \right]2!}}{a}_1\right]z^2+\cdots .\end{array}$$

(15)

From (14) and (15), we obtain

$$a_0=-{\displaystyle \frac{\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]{\vartheta }_1{\mathfrak{M}}_1}{4{\left[1+\tau \right]}^m\Gamma (\sigma +k)\Gamma \left(\lambda \right)}}.$$

(16)

and

$$a_1=-{\displaystyle \frac{{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )}{3{\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\lambda \right)}}\left[{\vartheta }_2-{\displaystyle \frac{{\vartheta }_1^2}{2}}\left(1-{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}+{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right)\right].$$

(17)

Using the known inequality of $\left|{\vartheta }_1\right|\le 2$ in (16), we get (9). In view of Lemma 1, we get (10) from (17).

Now, to prove the Fekete–Szegö inequality for the class ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$, we consider

$$\begin{array}{c}\left|a_1-\rho a_0^2\right|=|-{\displaystyle \frac{{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )}{3{\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\lambda \right)}}\left[{\vartheta }_2-{\displaystyle \frac{{\vartheta }_1^2}{2}}\left(1-{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}+{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right)\right]\\ -{\displaystyle \frac{\rho {\left(\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]\right)}^2{\vartheta }_1^2{\mathfrak{M}}_1^2}{16{\left[1+\tau \right]}^{2m}{\left(\Gamma (\sigma +k)\Gamma \left(\lambda \right)\right)}^2}}|\end{array}$$

$$\begin{array}{c}=|-{\displaystyle \frac{{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )}{3{\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\lambda \right)}}\left[{\vartheta }_2-{\displaystyle \frac{{\vartheta }_1^2}{2}}\left(1-{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}+{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right.\right.\\ \left.\left.-{\displaystyle \frac{3\rho {\mathfrak{M}}_1{\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\sigma \right){\left(\Gamma \left[\theta +\lambda \right]\right)}^2}{8{\left[1+\tau \right]}^{2m}{\left(\Gamma (\sigma +k)\right)}^2\Gamma \left(\lambda \right)\Gamma (2\theta +\lambda )}}\right)\right]|\end{array}$$

Using the triangle inequality and Lemma 1 in the above equality, we can obtain (11). Following the steps as in [14] (Theorem 10), we can establish that inequality (11) would be sharp for the functions

$${\psi }_1\left(z\right)={\displaystyle \frac{1+z}{1-z}}\mathrm{and}{\psi }_2\left(z\right)={\displaystyle \frac{1+z^2}{1-z^2}}.$$

□

If we let $m=\theta =0$ and $\sigma =k=1$ in Theorem 1, we have

Corollary 1.

If $f\left(z\right)$ of the form (1) belongs to the class $\mathcal{MR}\left(\psi \right)$, then we have

$$\left|a_0\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{2}}\mathit{and}\left|a_1\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{3}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right|\right\}$$

and for all $\rho \in \mathbb{C}$

$$\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{3}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\left(1-{\displaystyle \frac{6\rho }{7}}\right)\right|\right\}.$$

If we let $m=\theta =0$, $\sigma =2$ and $k=1$ in Theorem 1, we have

Corollary 2.

If $f\left(z\right)$ of the form (1) satisfies the condition

$${\displaystyle \frac{e^{\frac{-z{\left[2f\left(z\right)+z{f}^{\prime }\left(z\right)\right]}^{\prime }}{2f\left(z\right)+z{f}^{\prime }\left(z\right)}}}{ez\left[2f\left(z\right)+z{f}^{\prime }\left(z\right)\right]}}\prec \psi \left(z\right)$$

then we have

$$\left|a_0\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{4}}\mathit{and}\left|a_1\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{9}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\right|\right\}$$

and for all $\rho \in \mathbb{C}$

$$\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\right|}{9}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{7}{8}}{\mathfrak{M}}_1\left(1-{\displaystyle \frac{9\rho }{14}}\right)\right|\right\}.$$

Letting $\psi \left(z\right)=1+{\displaystyle \frac{4z}{5}}+{\displaystyle \frac{z^4}{5}}$ (see [15] for detailed study pertaining to the three leaf-shaped region) in Corollary 1, we have the following result.

Corollary 3.

If $f\left(z\right)$ of the form (1) belongs to the class ${\mathcal{MR}}_{3L}$ (see Remark 2), then we have

$$\left|a_0\right|\le {\displaystyle \frac{2}{5}},\left|a_1\right|\le {\displaystyle \frac{4}{15}}$$

and for all $\rho \in \mathbb{C}$

$$\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{4}{15}}max\left\{1;\left|{\displaystyle \frac{28}{40}}\left(1-{\displaystyle \frac{6\rho }{7}}\right)\right|\right\}.$$

Letting $\psi \left(z\right)={\displaystyle \frac{2\sqrt{1+z}}{1+e^{-z}}}$ (considering only the principal branch cut) in Corollary 1, we have the following result.

Corollary 4.

If $f\left(z\right)$ of the form (1) satisfies the condition

$${\displaystyle \frac{e^{\frac{-z{f}^{\prime }\left(z\right)}{f\left(z\right)}}}{ezf\left(z\right)}}\prec {\displaystyle \frac{2\sqrt{1+z}}{1+e^{-z}}},$$

then we have

$$\left|a_0\right|\le {\displaystyle \frac{1}{2}},\left|a_1\right|\le {\displaystyle \frac{1}{3}}$$

and for all $\rho \in \mathbb{C}$,

$$\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{1}{3}}max\left\{1;{\displaystyle \frac{3}{4}}\left|1-\rho \right|\right\}.$$

Remark 4.

The principal branch of the function $\psi \left(z\right)={\displaystyle \frac{2\sqrt{1+z}}{1+e^{-z}}}$ is related to the analytic function associated with the Balloon-shaped region, recently introduced by Ahmad et al. [16].

Letting $\psi \left(z\right)=z+\sqrt{1+z^2}$ (considering only the principal branch cut) in Corollary 1, we have the following result.

Corollary 5.

If $f\left(z\right)$ of the form (1) belongs to the class ${\mathcal{MR}}_{3L}$, then we have

$$\left|a_0\right|\le {\displaystyle \frac{1}{4}},\left|a_1\right|\le {\displaystyle \frac{1}{3}}$$

and for all $\rho \in \mathbb{C}$,

$$\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{1}{3}}max\left\{1;\left|{\displaystyle \frac{3}{8}}-{\displaystyle \frac{3\rho }{4}}\right|\right\}.$$

Remark 5.

We note that several results can be presented by specializing the parameters and the superordinate function in the definition of the function class ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$.

3. Analytic Functions with Respect to Symmetric Points

The class $\mathcal{S}$ is not closed under most of the basic transformation. Motivated by the fact that the class $\mathcal{S}$ is preserved under k-root transformation, Sakaguchi [17] considered function $f\in \mathcal{A}$ starlike with respect to symmetrical points, which satisfies the inequality

$$Re\left({\displaystyle \frac{2z{f}^{\prime }\left(z\right)}{f\left(z\right)-f(-z)}}\right)>0\left(z\in \mathbb{U}\right).$$

Here, we will define and study the class of functions ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ with respect to symmetrical points.

Definition 2.

Let ${\mathcal{SR}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$, denote the class of functions satisfying the conditions

$${\displaystyle \frac{2e^{-\frac{z{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f^{\prime }\left(z\right)}{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)}-1}}{z\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)-{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f(-z)\right]}}\prec \psi \left(z\right),(f\in \Sigma ;z\in {\mathbb{U}}^{*}),$$

(18)

where $\psi \in \mathcal{P}$ and $\psi \left(\mathbb{U}\right)$ is defined as in (5).

Remark 6.

Letting $m=\theta =0$ and $\sigma =k=1$ in Definition 2, the class ${\mathcal{SR}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ reduces to the class

$${\mathcal{MR}}_s\left(\psi \right)=\left\{f\in \Sigma ;{\displaystyle \frac{2e^{-\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1}}{z\left[f\left(z\right)-f(-z)\right]}}\prec \psi \left(z\right),z\in {\mathcal{U}}^{*}\right\}.$$

Theorem 2.

If $f\left(z\right)\in {\mathcal{SR}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$, then we have

$$\left|a_0\right|\le {\displaystyle \frac{\left|{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma \left(\theta +\lambda \right)\right|}{{\left[1+\tau \right]}^m\left|\Gamma (\sigma +k)\Gamma \left(\lambda \right)\right|}}$$

(19)

$$\left|a_1\right|\le {\displaystyle \frac{2\left|{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )\right|}{3{\left[1+2\tau \right]}^m\left|\Gamma (\sigma +2k)\Gamma \left(\lambda \right)\right|}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{3}{2}}{\mathfrak{M}}_1\right|\right\}$$

(20)

and for all $\rho \in \mathbb{C}$

$$\begin{array}{c}\left|a_1-\rho a_0^2\right|\le {\displaystyle \frac{2\left|{\mathfrak{M}}_1\right|\left|\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )\right|}{3{\left[1+2\tau \right]}^m\left|\Gamma (\sigma +2k)\Gamma \left(\lambda \right)\right|}}max\left\{1;\left|{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}-{\displaystyle \frac{3}{2}}{\mathfrak{M}}_1{\mathcal{Q}}_1\right|\right\},\end{array}$$

(21)

where ${\mathcal{Q}}_1$ is given by

$$\begin{array}{c}{\mathcal{Q}}_1=1-{\displaystyle \frac{\rho {\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\sigma \right){\left(\Gamma \left[\theta +\lambda \right]\right)}^2}{{\left[1+\tau \right]}^{2m}{\left(\Gamma (\sigma +k)\right)}^2\Gamma \left(\lambda \right)\Gamma (2\theta +\lambda )}}.\end{array}$$

(22)

The inequality is sharp for each $\rho \in \mathbb{C}$.

Proof. 

The equations from (18) will be of the form

$$\begin{array}{c}{\displaystyle \frac{2e^{-\frac{z{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f^{\prime }\left(z\right)}{{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)}-1}}{z\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)-{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f(-z)\right]}}=1-a_0{\displaystyle \frac{\Gamma \left[\sigma +k\right]\Gamma \left(\lambda \right)}{\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]}}{\left[1+\tau \right]}^{m}z-\\ {\displaystyle \frac{3}{2}}\left[{\displaystyle \frac{2{\left[1+2\tau \right]}^m\Gamma \left[\sigma +2k\right]\Gamma \left(\lambda \right)}{\Gamma \left(\sigma \right)\Gamma \left[2\theta +\lambda \right]2!}}{a}_1-{\displaystyle \frac{{\left[1+\tau \right]}^{2m}{\left(\Gamma \left[\sigma +k\right]\Gamma \left(\lambda \right)\right)}^2}{{\left(\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]\right)}^2}}{a}_0^2\right]z^2+\cdots .\end{array}$$

(23)

From (14) and (23), we obtain

$$a_0=-{\displaystyle \frac{\Gamma \left(\sigma \right)\Gamma \left[\theta +\lambda \right]{\vartheta }_1{\mathfrak{M}}_1}{2{\left[1+\tau \right]}^m\Gamma (\sigma +k)\Gamma \left(\lambda \right)}}.$$

(24)

and

$$a_1=-{\displaystyle \frac{{\mathfrak{M}}_1\Gamma \left(\sigma \right)\Gamma (2\theta +\lambda )}{3{\left[1+2\tau \right]}^m\Gamma (\sigma +2k)\Gamma \left(\lambda \right)}}\left[{\vartheta }_2-{\displaystyle \frac{{\vartheta }_1^2}{2}}\left(1-{\displaystyle \frac{{\mathfrak{M}}_2}{{\mathfrak{M}}_1}}+{\displaystyle \frac{3}{2}}{\mathfrak{M}}_1\right)\right].$$

(25)

Following the steps as in Theorem 1, we can establish the assertion of the Theorem. □

4. Conclusions

In this paper, we defined a new family of meromorphic function whose differential characterization was motivated by the definition of the multiplicative derivative. Note that the class $\mathcal{MR}\left(\psi \right)$ was not defined by replacing the ordinary derivative with a multiplicative derivative in the meromorphic starlike function class. Rather, it is just a new class satisfying a new analytic characterization motivated by the multiplicative derivative. In addition, we redefined the subclass of meromorphic function analogous to the class of functions with respect to symmetric points. Now the question arises: Will the class be well-defined if the denominator $\left[{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f\left(z\right)-{\mathcal{L}}_k^m\left(\theta ,\lambda ,\sigma ;\tau \right)f(-z)\right]$ in ${\mathcal{SR}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ is replaced with $f_{\alpha }\left(z\right)={\displaystyle \frac{1}{\alpha }}{\sum }_{\nu =0}^{\alpha -1}{\displaystyle \frac{f\left({\epsilon }^{\nu }z\right)}{{\epsilon }^{\nu }}}$? In the analytic case, such a class was not well-defined and it required adaptation. Further, the question remains as to whether it is possible to obtain the sufficient condition for the star-likeness of ${\mathcal{R}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$ and ${\mathcal{SR}}_{k,\tau }^m(\theta ,\lambda ,\sigma ;\psi )$.