Crop and Weed Segmentation and Fractal Dimension Estimation Using Small Training Data in Heterogeneous Data Environment
Abstract
1. Introduction
- This is the first study that considers the segmentation of crops and weeds within a heterogeneous environmental setup utilizing one training data sample. We rigorously investigate the factors that cause performance degradation in heterogeneous datasets, including variations in illumination and contrast. To address this problem, we propose a method that applies the Reinhard (RH) transformation, leveraging the mean and standard deviation (std) adjustments.
- We address the issue of high data availability for real-world applications. For this purpose, we improved the performance using a small amount of training data. The small amount of additional training data significantly improves the segmentation performance while requiring fewer computational resources and less training time.
- We introduce the FD estimation approach in our framework, which is seamlessly combined as an end-to-end task to provide important information on the distributional features of crops and weeds.
- It is noteworthy that our proposed framework [28] is publicly accessible for a fair comparison with other studies.
2. Related Work
2.1. Homogenous Data-Based Methods
2.1.1. Handcrafted Feature-Based Methods
2.1.2. Deep Feature-Based Methods
2.2. Heterogeneous Data-Based Methods
3. Proposed Method
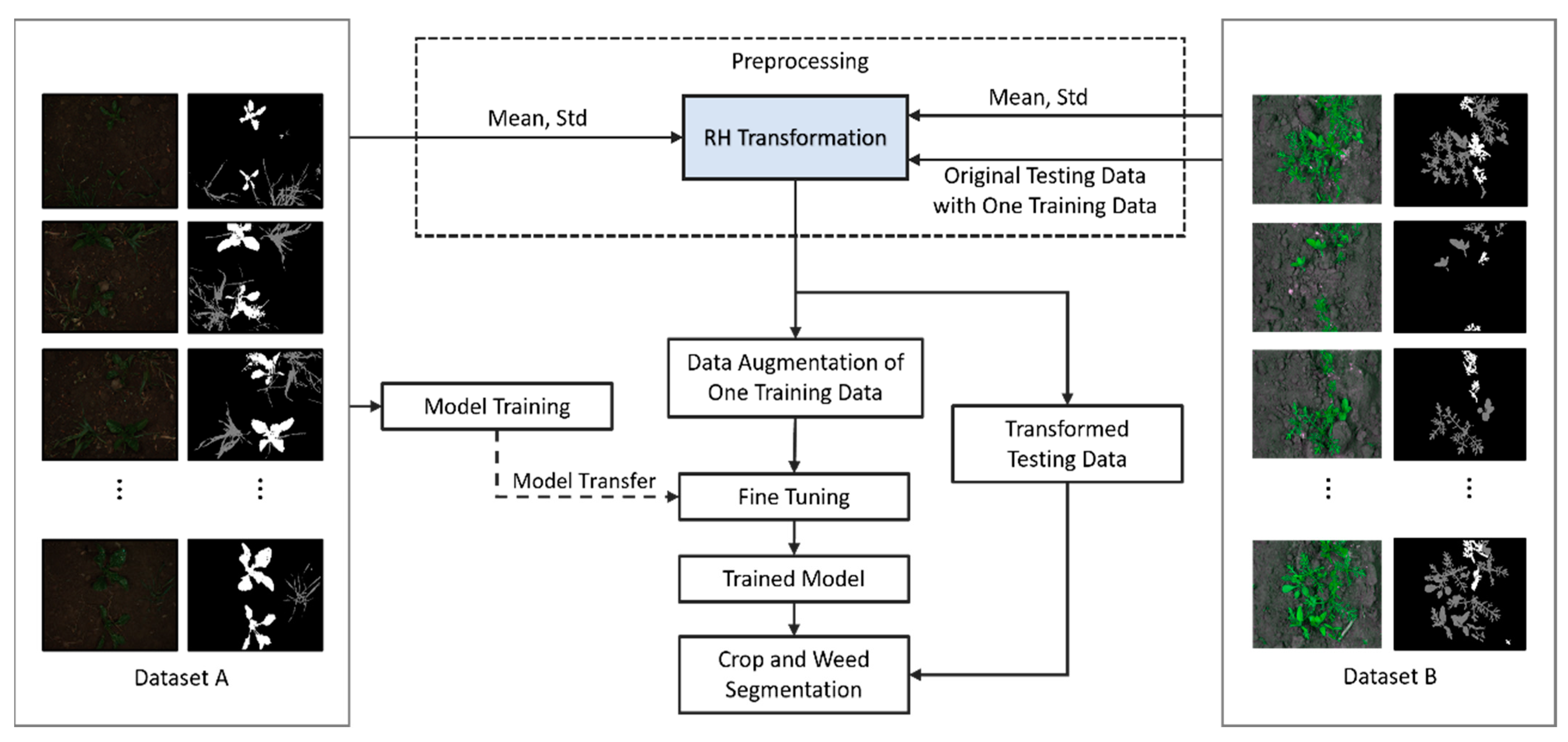
3.1. Overview of Proposed Method
3.2. Preprocessing
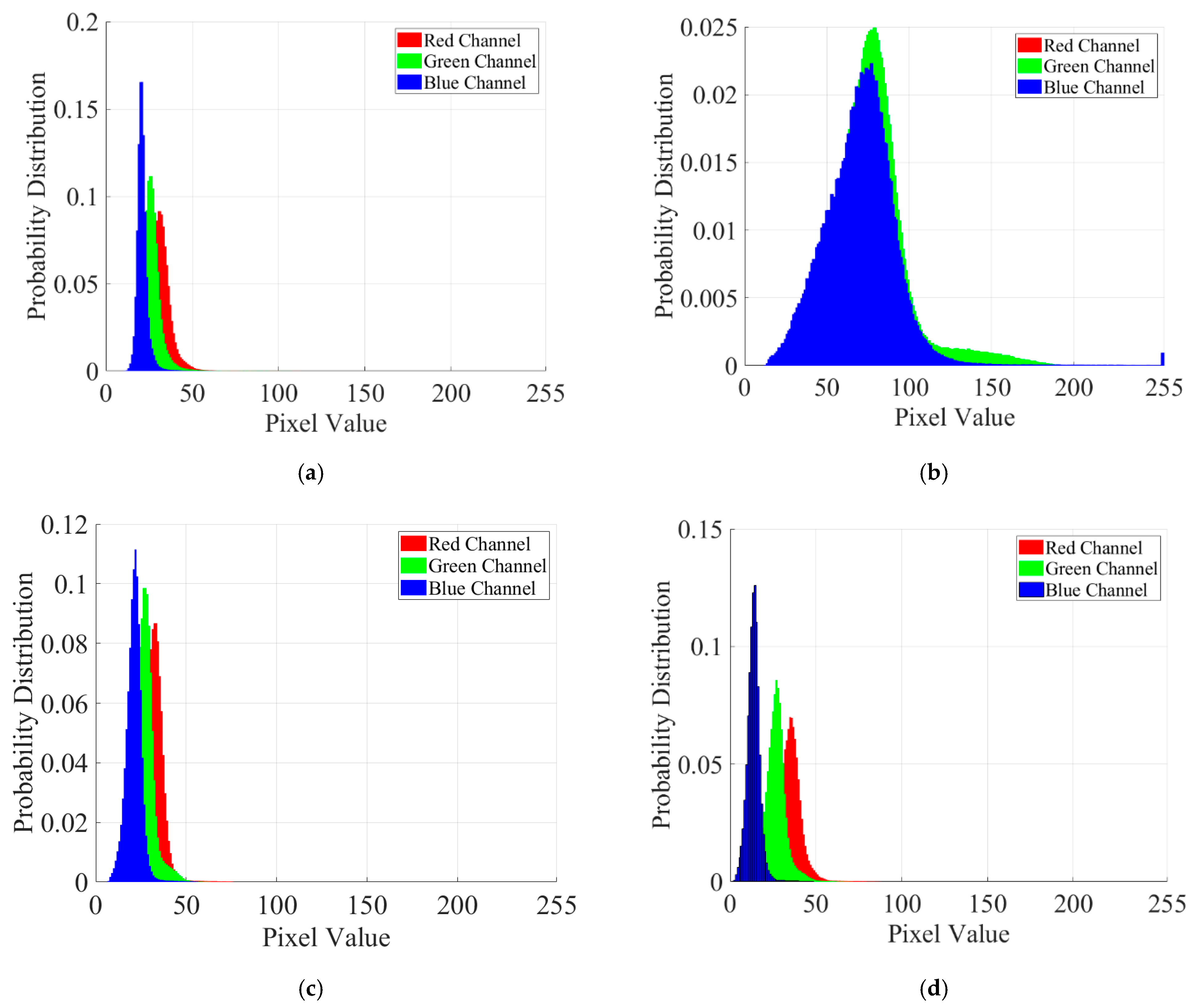
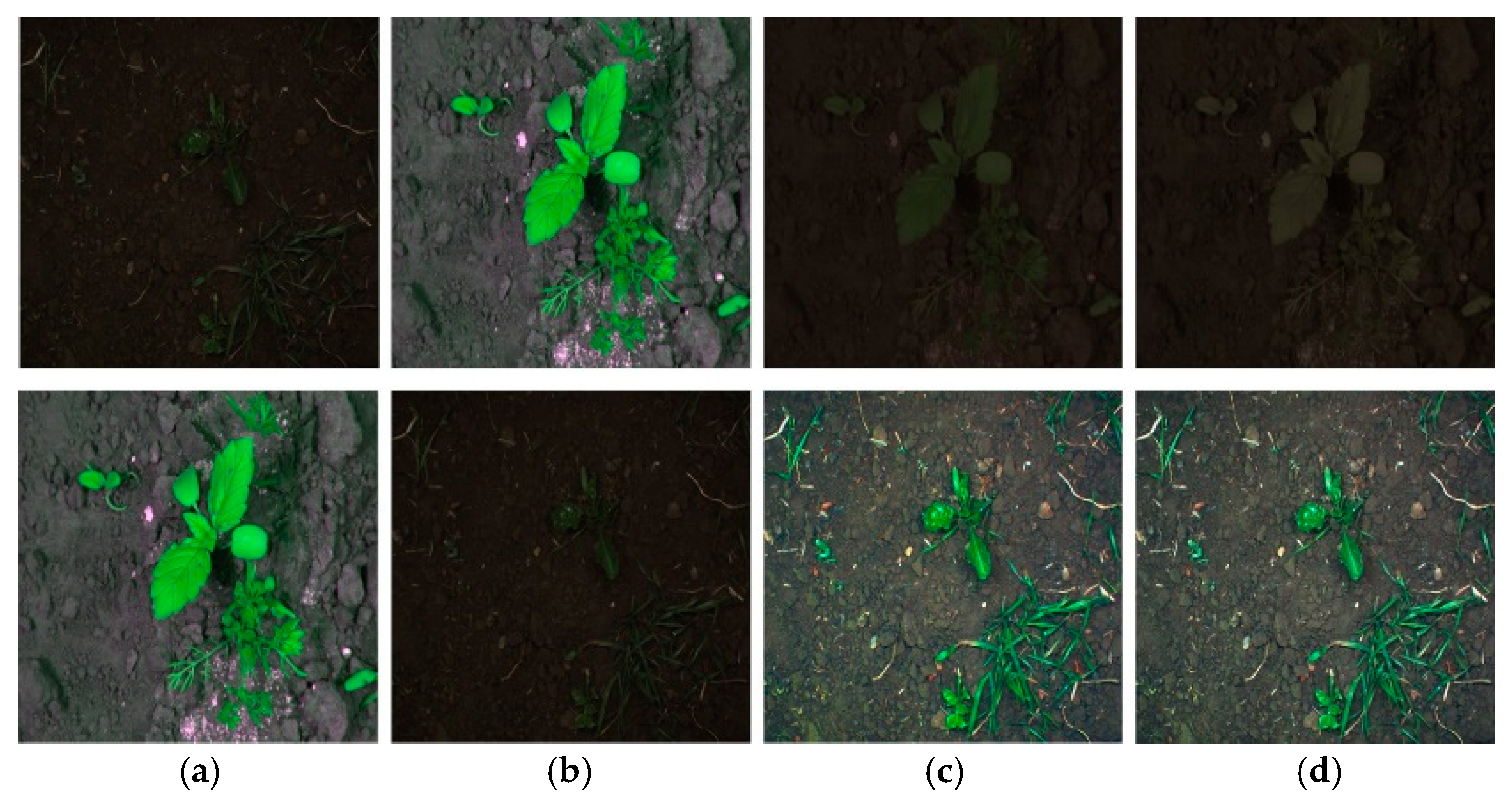
3.2.1. RH Transformation
| Algorithm 1: RH transformation with pseudo-code |
| Input: {dataB} tn; The total of t data samples, dataB: input dataset B images dataAm: training data from dataset A. |
| Output: (dataB’) the preprocessed sample |
| 1: Compute the std of the dataset B (input images) by dataB _std = std (dataB (:, :)) |
| 2: Compute the mean of the dataB dataB _mean = mean (dataB (:, :)) |
| 3: Compute the average std of the training data from dataset A using dataA_std = avg (std (dataAm (:, :)) |
| 4: Compute the average mean of the training data from dataset A using dataA_mean = avg (mean (dataAm (:, :)) |
| 5: Apply the RH transformation for m = 1: x for n = 1: y dataB’ (m, n) = [(dataB (m, n) − dataB_mean) × (dataA_std/dataB_std)] + dataA_mean end end return dataB’ |
3.2.2. RH Transformation with Additional Adjustments
3.3. Data Augmentation of One Training Data
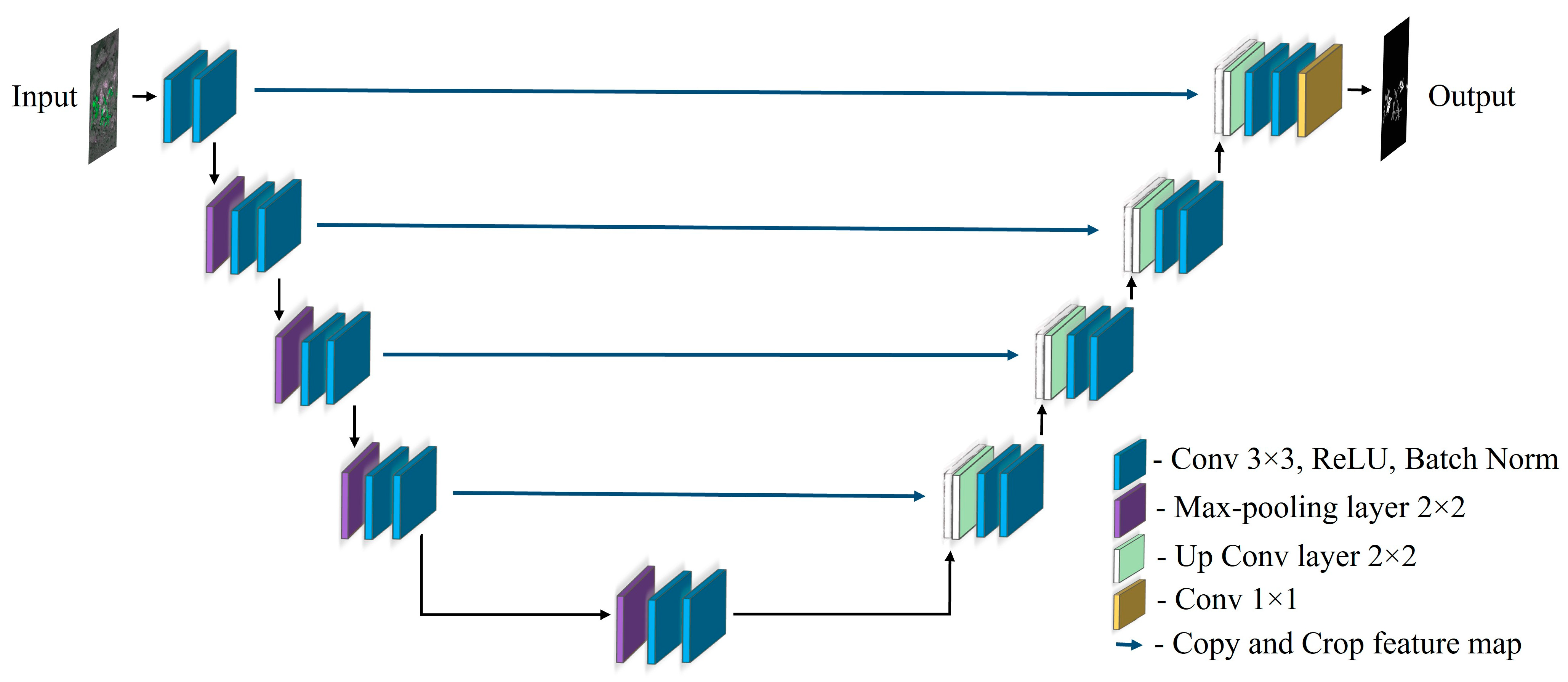
3.4. Semantic Segmentation Networks
3.4.1. U-Net
3.4.2. Modified U-Net
3.4.3. CED-Net

4. Experimental Results
4.1. Experimental Dataset and Setup
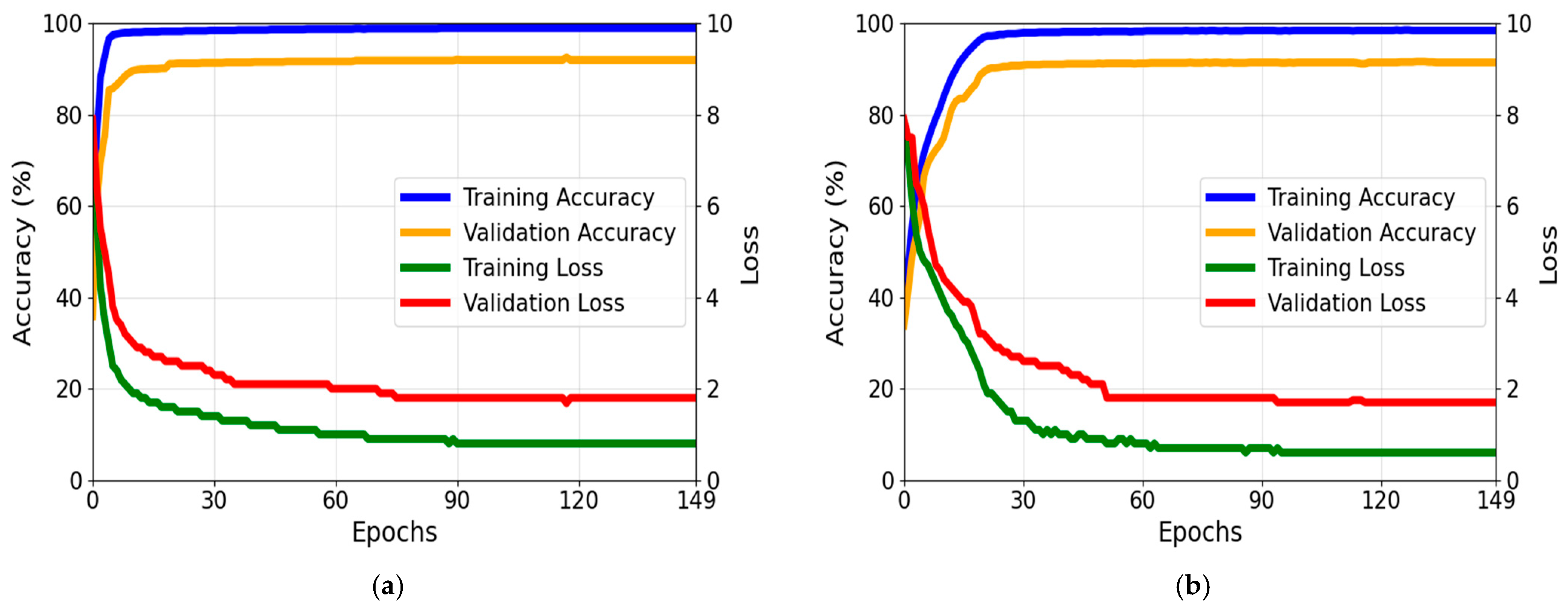
4.2. Training Setup
4.3. Evaluation Metrics
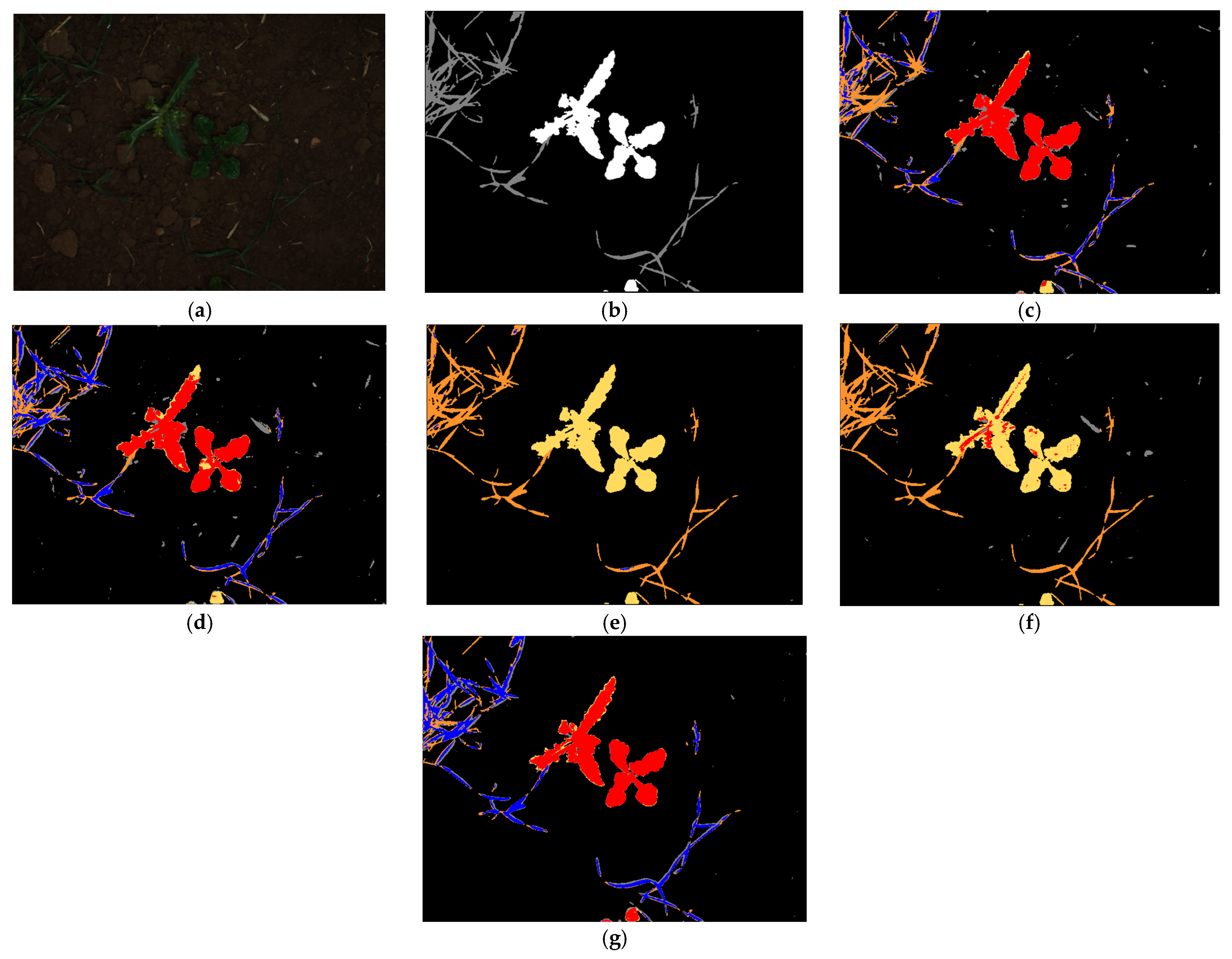
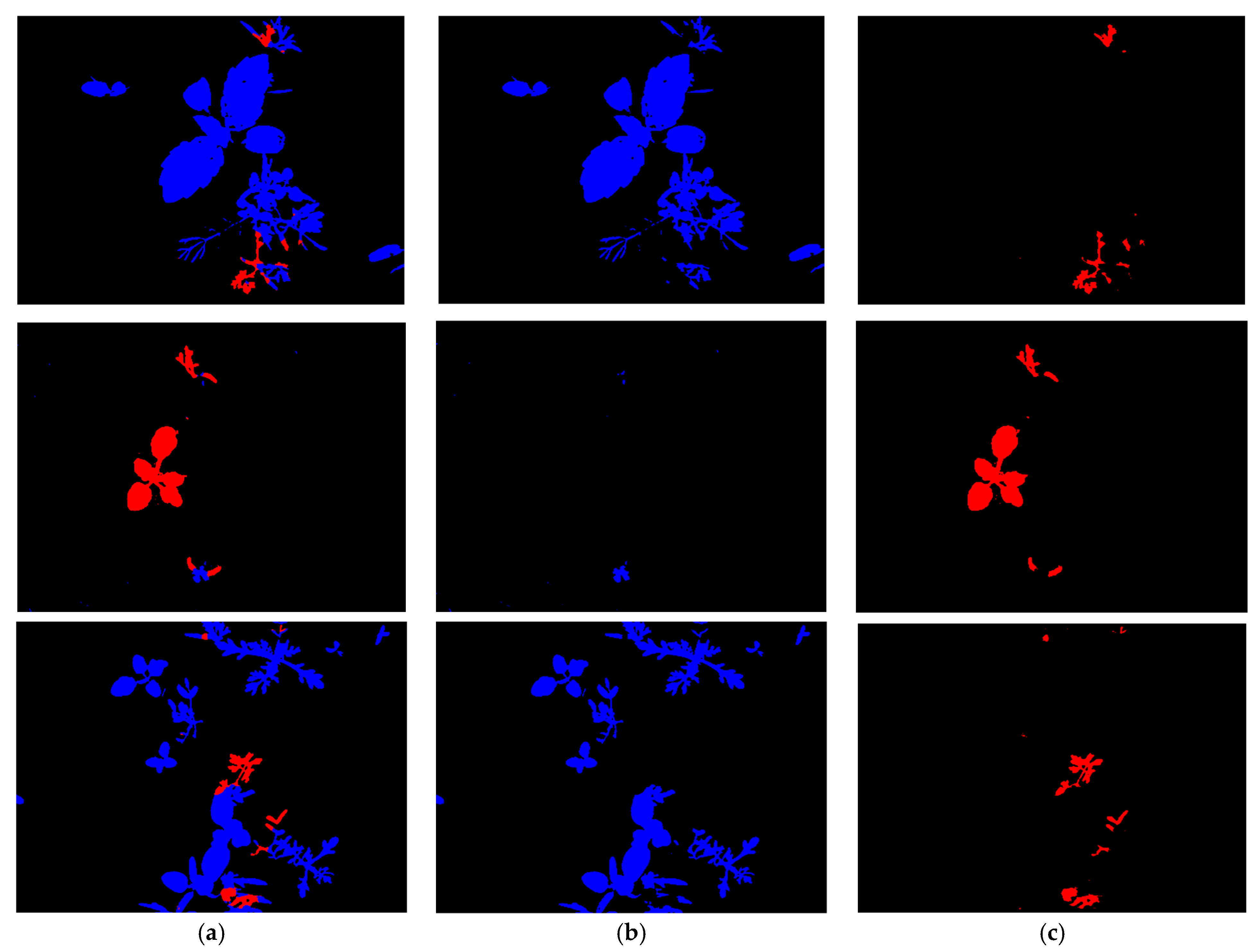
4.4. Testing for the Proposed Framework
4.4.1. Testing with CWFID after Training with BoniRob Dataset
Ablation Study
Performance Comparisons of the Proposed Framework with SOTA Transformations
4.4.2. Testing with BoniRob Dataset after Training with CWFID
Ablation Study
Performance Comparisons of the Proposed Framework with SOTA Transformations
4.5. Fractal Dimension Estimation
| Algorithm 2: Pseudo-code for measuring FD |
| Input: image (path to the input image) |
| Output: Fractal dimension (FD) value |
| 1: Read the input image and further convert it into grayscale 2: Set the maximum box-size with the power of 2 and ensure the dimensions s = 2^(log(max(size(image))/log2)] Add the padding if required to match the dimensions 3: Compute the number of boxes N(s) till minimum pixels 4: Reduce box size by 2 and recalculate N(s) iteratively while s > 1 5: Compute log(N(s)) and log(1/s) for each s 6: Draw a fitted line to the points (log(N(s)) and log(1/s)) |
| 7: FD value is the slope of the fitted line Return Fractal Dimension Value |
4.6. Comparisons of Processing Time
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.; Li, C. Convolutional Neural Networks for Image-Based High-Throughput Plant Phenotyping: A Review. Plant Phenomics 2020, 2020, 4152816. [Google Scholar] [CrossRef] [PubMed]
- Fathipoor, H.; Arefi, H.; Shah-Hosseini, R.; Moghadam, H. Corn Forage Yield Prediction Using Unmanned Aerial Vehicle Images at Mid-Season Growth Stage. J. Appl. Remote Sens 2019, 13, 034503. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, Y.; Liu, L.; Zhang, X. Adaptive Fractional-Order Multi-Scale Optimization TV-L1 Optical Flow Algorithm. Fractal Fract. 2024, 8, 8040179. [Google Scholar] [CrossRef]
- Huang, T.; Wang, X.; Xie, D.; Wang, C.; Liu, X. Depth Image Enhancement Algorithm Based on Fractional Differentiation. Fractal Fract. 2023, 7, 7050394. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, D.; Shi, S.; Yao, W.; Guo, Z.; Sun, J. A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise. Fractal Fract. 2023, 7, 7010064. [Google Scholar] [CrossRef]
- AlSheikh, M.H.; Al-Saidi, N.M.G.; Ibrahim, R.W. Dental X-ray Identification System Based on Association Rules Extracted by k-Symbol Fractional Haar Functions. Fractal Fract. 2022, 6, 6110669. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L.; Li, Y. A Novel Adaptive Fractional Differential Active Contour Image Segmentation Method. Fractal Fract. 2022, 6, 6100579. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Yang, F.; Yang, Q. A Study of Adaptive Fractional-Order Total Variational Medical Image Denoising. Fractal Fract. 2022, 6, 6090508. [Google Scholar] [CrossRef]
- Jiao, Q.; Liu, M.; Ning, B.; Zhao, F.; Dong, L.; Kong, L.; Hui, M.; Zhao, Y. Image Dehazing Based on Local and Non-Local Features. Fractal Fract. 2022, 6, 6050262. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, L. Image Enhancement Based on Rough Set and Fractional Order Differentiator. Fractal Fract. 2022, 6, 6040214. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, R.; Ren, J.; Gui, Q. Adaptive Fractional Image Enhancement Algorithm Based on Rough Set and Particle Swarm Optimization. Fractal Fract. 2022, 6, 6020100. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, Q.; Huang, X. An Algorithm for Crack Detection, Segmentation, and Fractal Dimension Estimation in Low-Light Environments by Fusing FFT and Convolutional Neural Network. Fractal Fract. 2023, 7, 7110820. [Google Scholar] [CrossRef]
- An, Q.; Chen, X.; Wang, H.; Yang, H.; Yang, Y.; Huang, W.; Wang, L. Segmentation of Concrete Cracks by Using Fractal Dimension and UHK-Net. Fractal Fract. 2022, 6, 6020095. [Google Scholar] [CrossRef]
- Sultan, H.; Owais, M.; Park, C.; Mahmood, T.; Haider, A.; Park, K.R. Artificial Intelligence-Based Recognition of Different Types of Shoulder Implants in X-Ray Scans Based on Dense Residual Ensemble-Network for Personalized Medicine. J. Pers. Med. 2021, 11, 11060482. [Google Scholar] [CrossRef] [PubMed]
- Arsalan, M.; Haider, A.; Hong, J.S.; Kim, J.S.; Park, K.R. Deep Learning-Based Detection of Human Blastocyst Compartments with Fractal Dimension Estimation. Fractal Fract. 2024, 8, 8050267. [Google Scholar] [CrossRef]
- González-Sabbagh, S.P.; Robles-Kelly, A. A Survey on Underwater Computer Vision. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Madokoro, H.; Takahashi, K.; Yamamoto, S.; Nix, S.; Chiyonobu, S.; Saruta, K.; Saito, T.K.; Nishimura, Y.; Sato, K. Semantic Segmentation of Agricultural Images Based on Style Transfer Using Conditional and Unconditional Generative Adversarial Networks. Appl. Sci. 2022, 12, 12157785. [Google Scholar] [CrossRef]
- Kim, Y.; Park, K.R. MTS-CNN: MTS-CNN: Multi-Task Semantic Segmentation-Convolutional Neural Network for Detecting Crops and Weeds. Comput. Electron. Agric. 2022, 199, 107146. [Google Scholar] [CrossRef]
- Wang, R.; Jiao, L.; Xie, C.; Chen, P.; Du, J.; Li, R. S-RPN: Sampling-Balanced Region Proposal Network for Small Crop Pest Detection. Comput. Electron. Agric. 2021, 187, 106290. [Google Scholar] [CrossRef]
- Huang, S.; Wu, S.; Sun, C.; Ma, X.; Jiang, Y.; Qi, L. Deep Localization Model for Intra-Row Crop Detection in Paddy Field. Comput. Electron. Agric. 2020, 169, 105203. [Google Scholar] [CrossRef]
- Kang, J.; Liu, L.; Zhang, F.; Shen, C.; Wang, N.; Shao, L. Semantic Segmentation Model of Cotton Roots In-Situ Image Based on Attention Mechanism. Comput. Electron. Agric. 2021, 189, 106370. [Google Scholar] [CrossRef]
- Le Louëdec, J.; Cielniak, G. 3D Shape Sensing and Deep Learning-Based Segmentation of Strawberries. Comput. Electron. Agric. 2021, 190, 106374. [Google Scholar] [CrossRef]
- Brilhador, A.; Gutoski, M.; Hattori, L.T.; de Souza Inácio, A.; Lazzaretti, A.E.; Lopes, H.S. Classification of Weeds and Crops at the Pixel-Level Using Convolutional Neural Networks and Data Augmentation. In Proceedings of the IEEE Latin American Conference on Computational Intelligence, Guayaquil, Ecuador, 11–15 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Chebrolu, N.; Lottes, P.; Schaefer, A.; Winterhalter, W.; Burgard, W.; Stachniss, C. Agricultural Robot Dataset for Plant Classification, Localization and Mapping on Sugar Beet Fields. Int. J. Robot. Res. 2017, 36, 1045–1052. [Google Scholar] [CrossRef]
- Haug, S.; Ostermann, J. A Crop/Weed Field Image Dataset for the Evaluation of Computer Vision Based Precision Agriculture Tasks. In Proceedings of the Computer Vision—ECCV 2014 Workshops, Zurich, Switzerland, 6–7 and 12 September 2014; pp. 105–116. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Nam, S.H.; Batchuluun, G.; Owais, M.; Park, K.R. An Ensemble Classification Method for Brain Tumor Images Using Small Training Data. Mathematics 2022, 10, 10234566. [Google Scholar] [CrossRef]
- Abdalla, A.; Cen, H.; Wan, L.; Rashid, R.; Weng, H.; Zhou, W.; He, Y. Fine-Tuning Convolutional Neural Network with Transfer Learning for Semantic Segmentation of Ground-Level Oilseed Rape Images in a Field with High Weed Pressure. Comput. Electron. Agric. 2019, 167, 105091. [Google Scholar] [CrossRef]
- Crops and Weeds Segmentation Method in Heterogeneous Environment. Available online: https://github.com/iamrehanch/crops_and_weeds_semantic_segmentation (accessed on 9 March 2023).
- Haug, S.; Michaels, A.; Biber, P.; Ostermann, J. Plant Classification System for Crop/Weed Discrimination without Segmentation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 1142–1149. [Google Scholar] [CrossRef]
- Lottes, P.; Hörferlin, M.; Sander, S.; Stachniss, C. Effective Vision-Based Classification for Separating Sugar Beets and Weeds for Precision Farming: Effective Vision-Based Classification. J. Field Robot. 2017, 34, 1160–1178. [Google Scholar] [CrossRef]
- Lottes, P.; Khanna, R.; Pfeifer, J.; Siegwart, R.; Stachniss, C. UAV-Based Crop and Weed Classification for Smart Farming. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, Singapore, 29 May–3 June 2017; pp. 3024–3031. [Google Scholar] [CrossRef]
- Yang, B.; Xu, Y. Applications of Deep-Learning Approaches in Horticultural Research: A Review. Hortic. Res. 2021, 8, 123. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2015, arXiv:1706.05587v3. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Zou, K.; Chen, X.; Wang, Y.; Zhang, C.; Zhang, F. A Modified U-Net with a Specific Data Argumentation Method for Semantic Segmentation of Weed Images in the Field. Comput. Electron. Agric. 2021, 187, 106242. [Google Scholar] [CrossRef]
- Milioto, A.; Lottes, P.; Stachniss, C. Real-Time Semantic Segmentation of Crop and Weed for Precision Agriculture Robots Leveraging Background Knowledge in CNNs. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 2235–2299. [Google Scholar] [CrossRef]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation. arXiv 2016, arXiv:1606.02147v1. [Google Scholar]
- Fathipoor, H.; Shah-Hosseini, R.; Arefi, H. Crop and Weed Segmentation on Ground_Based Images using Deep Convolutional Neural Network. In Proceedings of the ISPRS Annals of the Photogrammetry Remote Sensing and Spatial Information Sciences, Tehran, Iran, 13 January 2023; pp. 195–200. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 3–11. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556v6. [Google Scholar]
- Fawakherji, M.; Potena, C.; Bloisi, D.D.; Imperoli, M.; Pretto, A.; Nardi, D. UAV Image Based Crop and Weed Distribution Estimation on Embedded GPU Boards. In Proceedings of the Computer Analysis of Images and Patterns, Salerno, Italy, 6 September 2019; pp. 100–108. [Google Scholar] [CrossRef]
- Chakraborty, R.; Zhen, X.; Vogt, N.; Bendlin, B.; Singh, V. Dilated Convolutional Neural Networks for Sequential Manifold-Valued Data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, South Korea, 27 October—2 November 2019; pp. 10620–10630. [Google Scholar] [CrossRef]
- You, J.; Liu, W.; Lee, J. A DNN-Based Semantic Segmentation for Detecting Weed and Crop. Comput. Electron. Agric. 2020, 178, 10570. [Google Scholar] [CrossRef]
- Wang, H.; Song, H.; Wu, H.; Zhang, Z.; Deng, S.; Feng, X.; Chen, Y. Multilayer Feature Fusion and Attention-Based Network for Crops and Weeds Segmentation. J. Plant Dis. Prot. 2022, 129, 1475–1489. [Google Scholar] [CrossRef]
- Siddiqui, S.A.; Fatima, N.; Ahmad, A. Neural Network Based Smart Weed Detection System. In Proceedings of the International Conference on Communication, Control and Information Sciences, Idukki, India, 16–18 June 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Khan, A.; Ilyas, T.; Umraiz, M.; Mannan, Z.I.; Kim, H. CED-Net: Crops and Weeds Segmentation for Smart Farming Using a Small Cascaded Encoder-Decoder Architecture. Electronics 2020, 9, 9101602. [Google Scholar] [CrossRef]
- Reinhard, E.; Adhikhmin, M.; Gooch, B.; Shirley, P. Color Transfer between Images. IEEE Comput. Graph. Appl. 2001, 21, 34–41. [Google Scholar] [CrossRef]
- Ruderman, D.L.; Cronin, T.W.; Chiao, C.C. Statistics of Cone Responses to Natural Images: Implications for Visual Coding. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1998, 15, 2036–2045. [Google Scholar] [CrossRef]
- Mikołajczyk, A.; Grochowski, M. Data Augmentation for Improving Deep Learning in Image Classification Problem. In Proceedings of the International Interdisciplinary PhD Workshop, Świnouście, Poland, 9–12 May 2018; pp. 117–122. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep Learning Using Rectified Linear Units (ReLU). arXiv 2019, arXiv:1803.08375v2. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289v5. [Google Scholar]
- Intel Core i5-2320. Available online: https://www.intel.com/content/www/us/en/products/sku/53446/intel-core-i52320-processor-6m-cache-up_to-3-30-ghz/specifications.html (accessed on 5 October 2023).
- NVIDIA GeForce GTX 1070. Available online: https://www.nvidia.com/en-gb/geforce/10-series/ (accessed on 5 October 2023).
- PyTorch. Available online: https://pytorch.org/ (accessed on 5 October 2023).
- Python 3.8. Available online: https://www.python.org/downloads/release/python-380/ (accessed on 5 October 2023).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980v9. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2016, arXiv:1608.03983v5. Available online: https://arxiv.org/abs/1608.03983 (accessed on 5 October 2023).
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Cardoso, M.J. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Proceedings of the International Conference on Communication, Control and Information Sciences, Québec City, Canada, 9 September 2017; pp. 240–248. [Google Scholar] [CrossRef]
- Xiao, X.; Ma, L. Color Transfer in Correlated Color Space. In Proceedings of the ACM International Conference on Virtual Reality Continuum and Its Applications, Hong Kong, China, 14 June 2006; pp. 305–309. [Google Scholar] [CrossRef]
- Pitié, F.; Kokaram, A.C.; Dahyot, R. Automated Colour Grading Using Colour Distribution Transfer. Comput. Vis. Image Underst. 2007, 107, 123–137. [Google Scholar] [CrossRef]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image Style Transfer Using Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 23–27 June 2016; pp. 2414–2423. [Google Scholar] [CrossRef]
- Nguyen, R.M.H.; Kim, S.J.; Brown, M.S. Illuminant Aware Gamut-Based Color Transfer. Comput. Graph. Forum 2014, 33, 319–328. [Google Scholar] [CrossRef]
- Rezaie, A.; Mauron, A.J.; Beyer, K. Sensitivity Analysis of Fractal Dimensions of Crack Maps on Concrete and Masonry Walls. Autom.Constr. 2020, 117, 103258. [Google Scholar] [CrossRef]
- Wu, J.; Jin, X.; Mi, S.; Tang, J. An Effective Method to Compute the Box-counting Dimension Based on the Mathematical Definition and Intervals. Results Eng. 2020, 6, 100106. [Google Scholar] [CrossRef]
- Xie, Y. The Application of Fractal Theory in Real-life. In Proceedings of the International Conference on Computing Innovation and Applied Physics, Qingdao, Shandong, China, 30 November 2023; pp. 132–136. [Google Scholar] [CrossRef]
- Mishra, P.; Singh, U.; Pandey, C.M.; Mishra, P.; Pandey, G. Application of Student’s t-test, Analysis of Variance, and Covariance. Ann. Card. Anaesth. 2019, 22, 407–411. [Google Scholar] [CrossRef]
- Cohen, J. A Power Primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
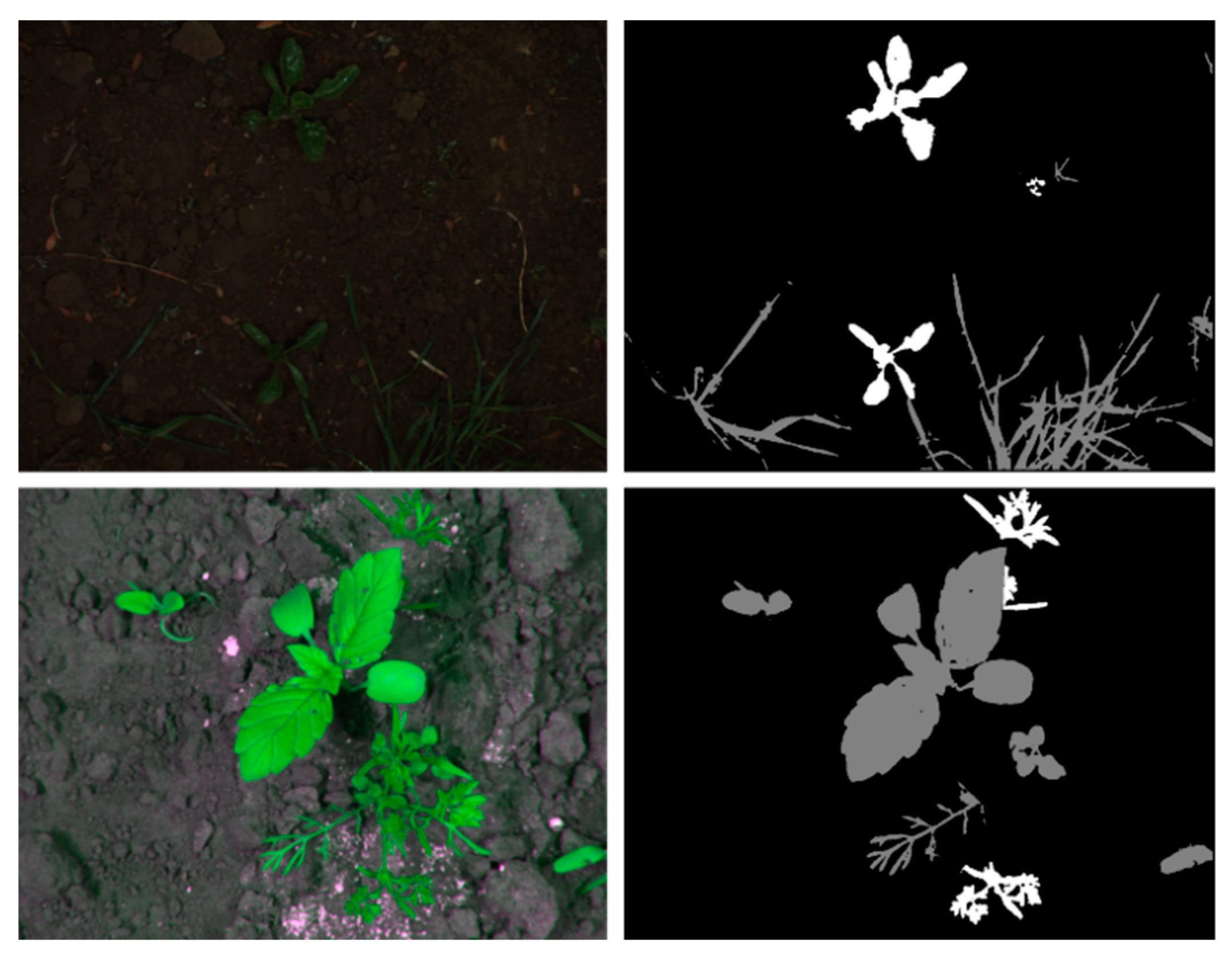








| Data | Type | Method | Strength/Motivation | Weakness |
|---|---|---|---|---|
| Homogeneous data-based | Handcrafted feature-based | RFC [29] | Handling overlapping of crops and weeds | Overlapping of multiple plants with the same class cannot be split |
| RFC + vegetation detection [30] | Detection of local and object-based features | Smoothing as post-processing on only local features | ||
| Plant-tailored feature extraction [31] | UAV intra-row-space-based weed detection in challenging conditions | The number of weeds is much smaller in the datasets used | ||
| Deep feature-based | MTS-CNN [18] | Separate object segmentation to avoid background-biased learning | Dependency of first stage network on second stage network | |
| Modified U-Net [37] | Effective two-stage training method with large applicability | Only weed-targeted segmentation | ||
| SegNet + Enet [38] | Fast and more accurate pixelwise predictions | Images contain very small portions of crops and weeds | ||
| U-Net and U-Net++ [40] | Detecting weeds in the early stages of growth | Uses a very small dataset and has no suitable real-time application | ||
| Modified U-Net + modified VGG-16 [43] | Effective result for distribution estimation problem with graphics processing unit (GPU)-based embedded board | Not focusing on the exact location of weeds in the images | ||
| UFAB [45] | Reducing redundancy by strengthening the model diversity | Unavailability of RGB and NIR input | ||
| DA-Net [46] | Expanding receptive field without affecting the computational cost | Hard and time-consuming mechanism to parallelize the system using attention modules | ||
| 4-layered CNN + data augmentation [47] | Good for the early detection of weeds, improving production, and is easy to deploy because of the cheap cost | Minimizing accuracy if weeds are not detected at the early stages | ||
| CED-Net [48] | Using a light model and achieving efficient results | Error at any level among the four levels affects the overall performance | ||
| Heterogeneous data-based | Proposed framework (proposed) | Use of small training images in a heterogeneous environment | Preprocessing steps are included |
| Cases | RH Transformation | Using One Training Data | Data Augmentation |
|---|---|---|---|
| Case I | |||
| Case II | ✔ | ||
| Case III | ✔ | ||
| Case IV | ✔ | ✔ | |
| Case V | ✔ | ✔ | |
| Case VI | ✔ | ✔ | ✔ |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| U-Net | Case I | 0.384 | 0.001 | 0.195 | 0.384 | 0.643 | 0.403 | 0.495 |
| Case II | 0.423 | 0.098 | 0.206 | 0.965 | 0.638 | 0.567 | 0.594 | |
| Case III | 0.493 | 0.322 | 0.175 | 0.982 | 0.621 | 0.605 | 0.611 | |
| Case IV | 0.589 | 0.472 | 0.309 | 0.985 | 0.732 | 0.721 | 0.724 | |
| Case V | 0.499 | 0.294 | 0.221 | 0.982 | 0.652 | 0.627 | 0.639 | |
| Case VI (proposed) | 0.620 | 0.524 | 0.349 | 0.986 | 0.762 | 0.749 | 0.752 |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| Modified U-Net | Case I | 0.380 | 0.006 | 0.195 | 0.941 | 0.645 | 0.406 | 0.497 |
| Case II | 0.427 | 0.104 | 0.209 | 0.968 | 0.657 | 0.563 | 0.601 | |
| Case III | 0.483 | 0.244 | 0.221 | 0.983 | 0.646 | 0.608 | 0.625 | |
| Case IV | 0.523 | 0.368 | 0.217 | 0.984 | 0.664 | 0.635 | 0.648 | |
| Case V | 0.471 | 0.195 | 0.234 | 0.983 | 0.656 | 0.615 | 0.634 | |
| Case VI (proposed) | 0.539 | 0.382 | 0.251 | 0.984 | 0.686 | 0.665 | 0.674 |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| CED-Net | Case I | 0.387 | 0.009 | 0.196 | 0.956 | 0.634 | 0.441 | 0.518 |
| Case II | 0.396 | 0.018 | 0.209 | 0.962 | 0.616 | 0.465 | 0.528 | |
| Case III | 0.461 | 0.234 | 0.175 | 0.974 | 0.603 | 0.559 | 0.579 | |
| Case IV | 0.516 | 0.409 | 0.168 | 0.971 | 0.640 | 0.592 | 0.614 | |
| Case V | 0.466 | 0.235 | 0.188 | 0.974 | 0.617 | 0.564 | 0.589 | |
| Case VI (proposed) | 0.521 | 0.472 | 0.120 | 0.972 | 0.637 | 0.613 | 0.624 |
| Experiment | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|
| RH transformation | 0.620 | 0.524 | 0.349 | 0.986 | 0.762 | 0.749 | 0.752 |
| RH transformation with additional adjustments | 0.468 | 0.199 | 0.229 | 0.975 | 0.631 | 0.615 | 0.621 |
| Segmentation Model | Transformation | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| U-Net | Xiao et al. [61] | 0.496 | 0.257 | 0.274 | 0.958 | 0.717 | 0.583 | 0.640 |
| Pitie et al. [62] | 0.548 | 0.378 | 0.312 | 0.953 | 0.776 | 0.601 | 0.675 | |
| Gatys et al. [63] | 0.457 | 0.313 | 0.101 | 0.958 | 0.558 | 0.575 | 0.563 | |
| Nguyen et al. [64] | 0.487 | 0.486 | 0.010 | 0.964 | 0.563 | 0.580 | 0.569 | |
| Proposed | 0.620 | 0.524 | 0.349 | 0.986 | 0.762 | 0.749 | 0.752 | |
| Modified U-Net | Xiao et al. [61] | 0.387 | 0.066 | 0.161 | 0.934 | 0.651 | 0.494 | 0.558 |
| Pitie et al. [62] | 0.462 | 0.200 | 0.221 | 0.966 | 0.716 | 0.569 | 0.630 | |
| Gatys et al. [63] | 0.396 | 0.157 | 0.083 | 0.948 | 0.452 | 0.544 | 0.490 | |
| Nguyen et al. [64] | 0.427 | 0.136 | 0.185 | 0.959 | 0.518 | 0.580 | 0.545 | |
| Proposed | 0.539 | 0.382 | 0.251 | 0.984 | 0.686 | 0.665 | 0.674 | |
| CED-Net | Xiao et al. [61] | 0.390 | 0.036 | 0.204 | 0.928 | 0.618 | 0.447 | 0.518 |
| Pitie et al. [62] | 0.394 | 0.109 | 0.180 | 0.894 | 0.673 | 0.472 | 0.553 | |
| Gatys et al. [63] | 0.360 | 0.000 | 0.143 | 0.938 | 0.605 | 0.378 | 0.465 | |
| Nguyen et al. [64] | 0.310 | 0.000 | 0.065 | 0.865 | 0.479 | 0.349 | 0.402 | |
| Proposed | 0.521 | 0.472 | 0.120 | 0.972 | 0.637 | 0.613 | 0.624 |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| U-Net | Case I | 0.316 | 0.000 | 0.000 | 0.948 | 0.333 | 0.329 | 0.330 |
| Case II | 0.570 | 0.230 | 0.508 | 0.971 | 0.704 | 0.679 | 0.688 | |
| Case III | 0.494 | 0.227 | 0.286 | 0.969 | 0.630 | 0.673 | 0.649 | |
| Case IV | 0.621 | 0.272 | 0.621 | 0.969 | 0.779 | 0.689 | 0.730 | |
| Case V | 0.507 | 0.232 | 0.322 | 0.968 | 0.645 | 0.679 | 0.659 | |
| Case VI (proposed) | 0.637 | 0.292 | 0.647 | 0.971 | 0.787 | 0.708 | 0.743 |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| Modified U-Net | Case I | 0.316 | 0.000 | 0.000 | 0.948 | 0.333 | 0.316 | 0.324 |
| Case II | 0.529 | 0.235 | 0.383 | 0.970 | 0.682 | 0.665 | 0.668 | |
| Case III | 0.448 | 0.212 | 0.163 | 0.968 | 0.588 | 0.596 | 0.589 | |
| Case IV | 0.605 | 0.266 | 0.593 | 0.955 | 0.833 | 0.651 | 0.728 | |
| Case V | 0.477 | 0.232 | 0.232 | 0.966 | 0.633 | 0.611 | 0.619 | |
| Case VI (proposed) | 0.622 | 0.294 | 0.610 | 0.962 | 0.837 | 0.667 | 0.739 |
| Model | Cases | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| CED-Net | Case I | 0.315 | 0.000 | 0.000 | 0.946 | 0.332 | 0.318 | 0.322 |
| Case II | 0.487 | 0.176 | 0.336 | 0.951 | 0.699 | 0.564 | 0.621 | |
| Case III | 0.488 | 0.013 | 0.572 | 0.879 | 0.624 | 0.537 | 0.575 | |
| Case IV | 0.552 | 0.218 | 0.504 | 0.935 | 0.838 | 0.592 | 0.691 | |
| Case V | 0.485 | 0.0143 | 0.581 | 0.860 | 0.623 | 0.539 | 0.576 | |
| Case VI (proposed) | 0.570 | 0.244 | 0.519 | 0.946 | 0.836 | 0.611 | 0.703 |
| Model | Transformation | mIoU | IoU (Cr) | IoU (Wd) | IoU (Bg) | Re | Pre | F1-Score |
|---|---|---|---|---|---|---|---|---|
| U-Net | Xiao et al. [61] | 0.530 | 0.505 | 0.124 | 0.962 | 0.696 | 0.589 | 0.635 |
| Pitie et al. [62] | 0.543 | 0.475 | 0.193 | 0.959 | 0.729 | 0.605 | 0.657 | |
| Gatys et al. [63] | 0.316 | 0.000 | 0.000 | 0.948 | 0.333 | 0.381 | 0.352 | |
| Nguyen et al. [64] | 0.332 | 0.049 | 0.000 | 0.946 | 0.352 | 0.417 | 0.379 | |
| Proposed | 0.637 | 0.647 | 0.292 | 0.971 | 0.787 | 0.708 | 0.743 | |
| Modified U-Net | Xiao et al. [61] | 0.526 | 0.521 | 0.145 | 0.911 | 0.787 | 0.573 | 0.661 |
| Pitie et al. [62] | 0.516 | 0.522 | 0.141 | 0.886 | 0.817 | 0.567 | 0.667 | |
| Gatys et al. [63] | 0.316 | 0.000 | 0.000 | 0.948 | 0.333 | 0.320 | 0.326 | |
| Nguyen et al. [64] | 0.187 | 0.014 | 0.031 | 0.516 | 0.387 | 0.368 | 0.375 | |
| Proposed | 0.622 | 0.610 | 0.294 | 0.962 | 0.837 | 0.667 | 0.739 | |
| CED-Net | Xiao et al. [61] | 0.423 | 0.339 | 0.067 | 0.862 | 0.709 | 0.475 | 0.566 |
| Pitie et al. [62] | 0.466 | 0.442 | 0.107 | 0.850 | 0.807 | 0.524 | 0.632 | |
| Gatys et al. [63] | 0.318 | 0.005 | 0.018 | 0.932 | 0.338 | 0.340 | 0.339 | |
| Nguyen et al. [64] | 0.316 | 0.000 | 0.001 | 0.948 | 0.333 | 0.375 | 0.349 | |
| Proposed | 0.570 | 0.519 | 0.244 | 0.946 | 0.836 | 0.611 | 0.703 |
| Dataset | Weed FD | Crop FD |
|---|---|---|
| CWFID | 1.61 | 1.26 |
| 0.76 | 1.43 | |
| 1.53 | 1.21 | |
| BoniRob dataset | 1.27 | 0.91 |
| 1.32 | 1.31 | |
| 0.97 | 1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, R.; Hong, J.S.; Kim, S.G.; Sultan, H.; Usman, M.; Gondal, H.A.H.; Tariq, M.H.; Ullah, N.; Park, K.R. Crop and Weed Segmentation and Fractal Dimension Estimation Using Small Training Data in Heterogeneous Data Environment. Fractal Fract. 2024, 8, 285. https://doi.org/10.3390/fractalfract8050285
Akram R, Hong JS, Kim SG, Sultan H, Usman M, Gondal HAH, Tariq MH, Ullah N, Park KR. Crop and Weed Segmentation and Fractal Dimension Estimation Using Small Training Data in Heterogeneous Data Environment. Fractal and Fractional. 2024; 8(5):285. https://doi.org/10.3390/fractalfract8050285
Chicago/Turabian StyleAkram, Rehan, Jin Seong Hong, Seung Gu Kim, Haseeb Sultan, Muhammad Usman, Hafiz Ali Hamza Gondal, Muhammad Hamza Tariq, Nadeem Ullah, and Kang Ryoung Park. 2024. "Crop and Weed Segmentation and Fractal Dimension Estimation Using Small Training Data in Heterogeneous Data Environment" Fractal and Fractional 8, no. 5: 285. https://doi.org/10.3390/fractalfract8050285
APA StyleAkram, R., Hong, J. S., Kim, S. G., Sultan, H., Usman, M., Gondal, H. A. H., Tariq, M. H., Ullah, N., & Park, K. R. (2024). Crop and Weed Segmentation and Fractal Dimension Estimation Using Small Training Data in Heterogeneous Data Environment. Fractal and Fractional, 8(5), 285. https://doi.org/10.3390/fractalfract8050285











