A Novel Technique for Solving the Nonlinear Fractional-Order Smoking Model
Abstract
1. Introduction
- Modeling complexity: Diseases often involve complex interactions between various biological, environmental, and social factors. NFDEs can represent these interactions more accurately than linear models, allowing for a more realistic portrayal of disease dynamics.
- Memory effects and long-range dependencies: Diseases may exhibit memory effects, where past events influence future outcomes, and long-range dependencies, where distant interactions impact disease spread. Nonlinear differential equations with fractional derivatives can capture these effects, providing a better understanding of disease behavior over time and space.
- Nonlinearity in biological processes: The biological processes underlying disease progression are often nonlinear, involving feedback loops, threshold effects, and complex interactions between different components of the system. NFDEs can model these nonlinearities more effectively, leading to more accurate predictions of disease outcomes.
- Personalized medicine: Nonlinear models can incorporate individual variability in disease susceptibility, response to treatment, and other factors, allowing for personalized predictions and treatment strategies tailored to specific patient characteristics.
- Assessment of intervention strategies: NFDEs can evaluate the effectiveness of various intervention strategies, such as vaccination campaigns, treatment protocols, and public health interventions. By simulating the impact of interventions on disease dynamics, these models can inform decision-making and resource allocation.
- Prediction of emergent phenomena: Diseases may exhibit emergent phenomena such as epidemics, outbreaks, and the emergence of drug resistance. NFDEs can predict these phenomena and identify critical factors driving their occurrence, helping to design proactive measures to mitigate their impact.
- Integration of data: NFDEs can integrate diverse sources of data, including epidemiological, clinical, genetic, and environmental data, to provide a comprehensive understanding of disease dynamics and inform evidence-based decision-making.
- Capturing complex dynamics: Smoking behavior is influenced by various factors such as addiction, psychological factors, social interactions, and environmental cues. NFDEs can capture the complex interactions between these factors and represent the dynamic nature of smoking behavior more accurately than traditional linear models.
- Memory effects and long-term dependencies: Individuals’ smoking behavior often exhibits memory effects, where past experiences influence current decisions, and long-term dependencies, where behavior is influenced by events far in the past. NFDEs with fractional derivatives can capture these memory effects and long-range dependencies, allowing for a more realistic representation of how past behavior influences current smoking habits.
- Modeling addiction dynamics: Smoking addiction involves nonlinear processes such as tolerance, withdrawal symptoms, and craving cycles. NFDE models can describe these nonlinear addiction dynamics and help understand the mechanisms underlying addiction development and persistence.
- Assessing intervention strategies: NFDE models can be used to evaluate the effectiveness of smoking cessation interventions, such as behavioral therapies, pharmacological treatments, and public health campaigns. By simulating the impact of interventions on smoking behavior dynamics, these models can help identify the most effective strategies for reducing smoking prevalence and improving public health outcomes.
- Predicting population-level trends: NFDE models can project population-level trends in smoking prevalence, cessation rates, and smoking-related morbidity and mortality. By incorporating demographic trends, socioeconomic factors, and policy changes, these models can help policymakers anticipate future challenges and develop targeted interventions to address them.
- Understanding heterogeneous responses: Individuals may respond differently to smoking cessation interventions due to factors such as genetics, socioeconomics, and cultural background. NFDE models can account for this heterogeneity and provide insights into how different subpopulations may respond to various interventions.
- For the first time in the literature, we have solved the smoking model using ERPSM, which offers the simplest method for determining series coefficients compared to the Adomian, homotopy, variational iteration, and residual methods.
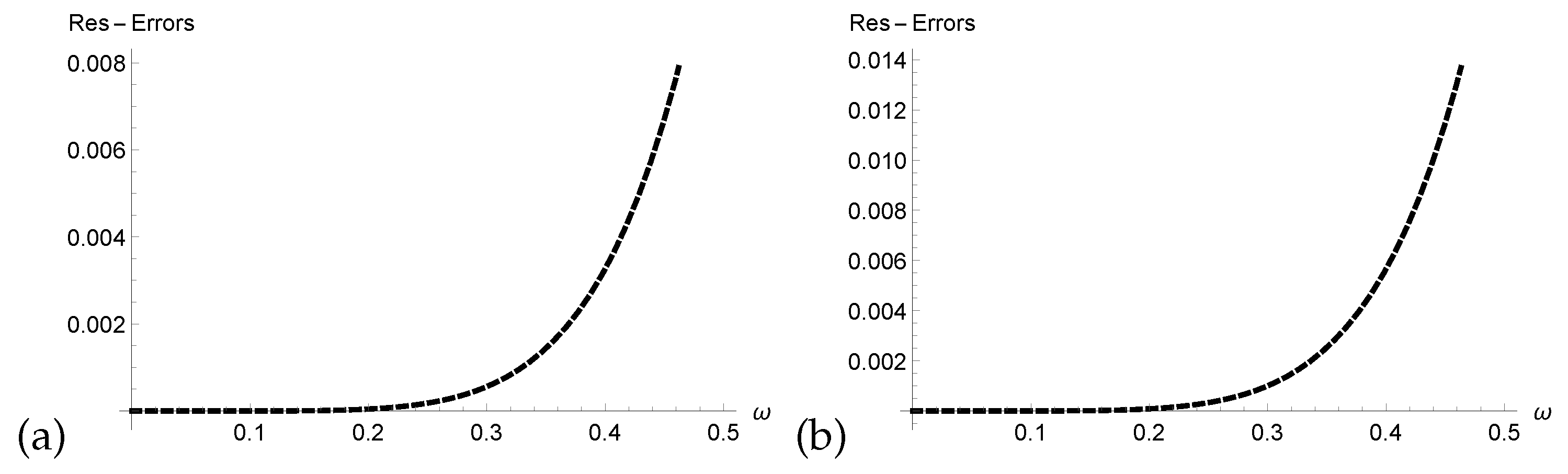
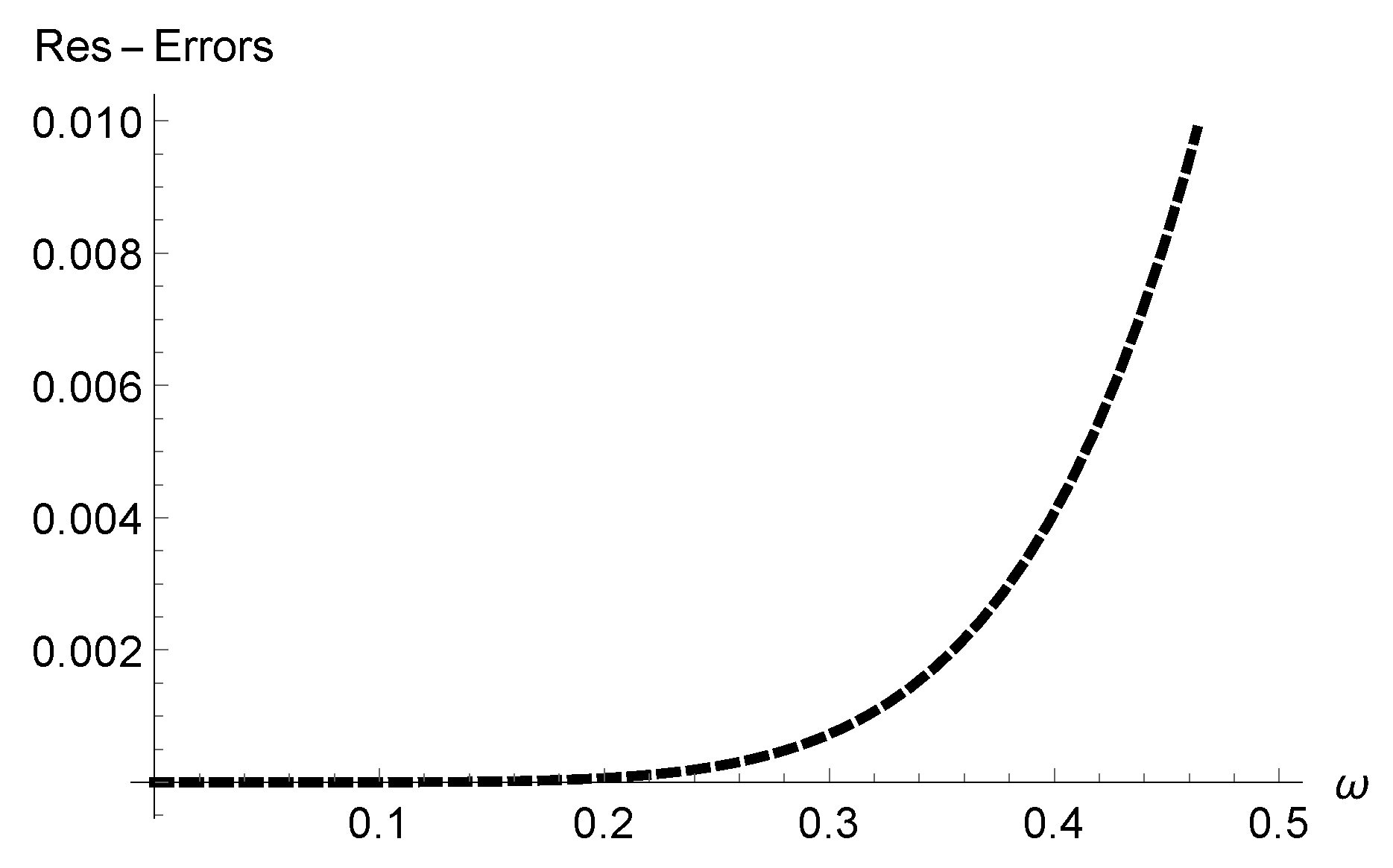
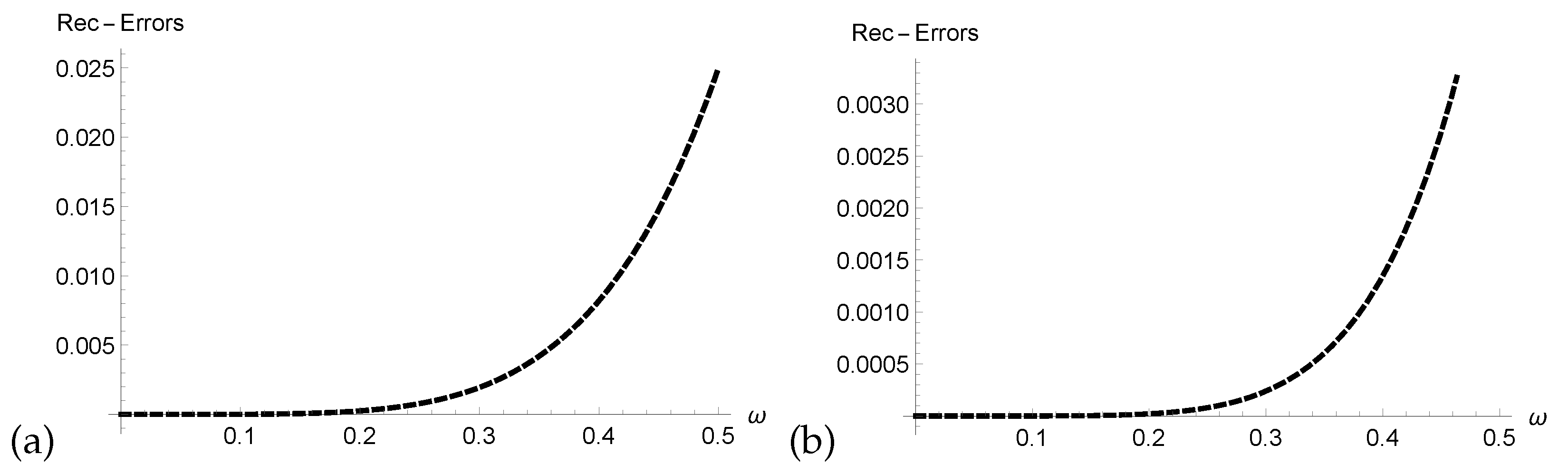
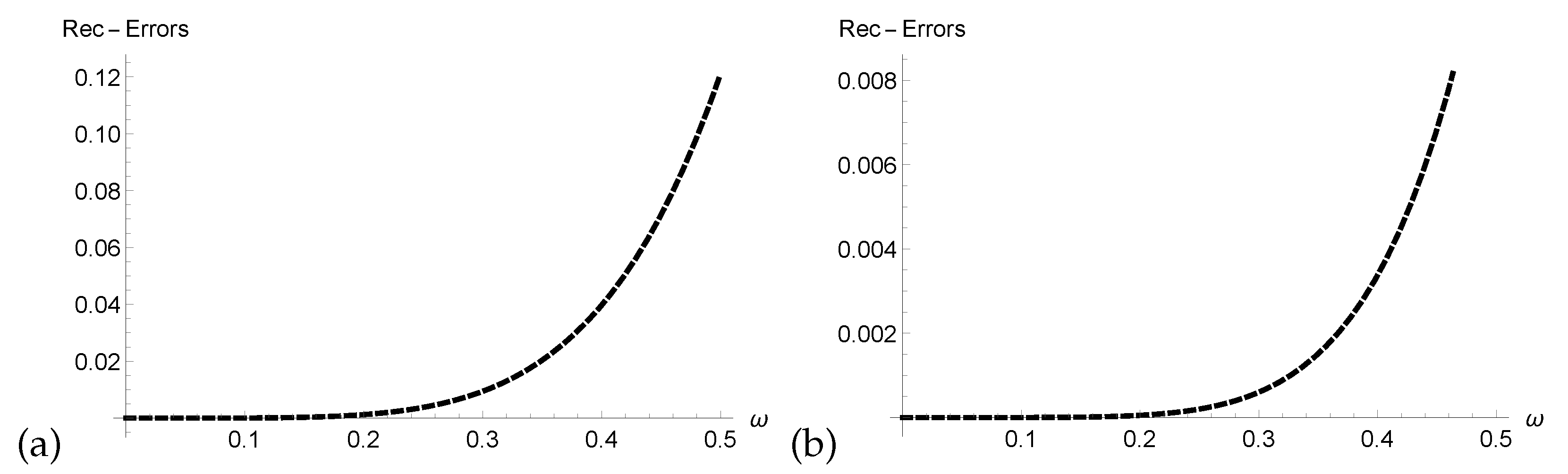
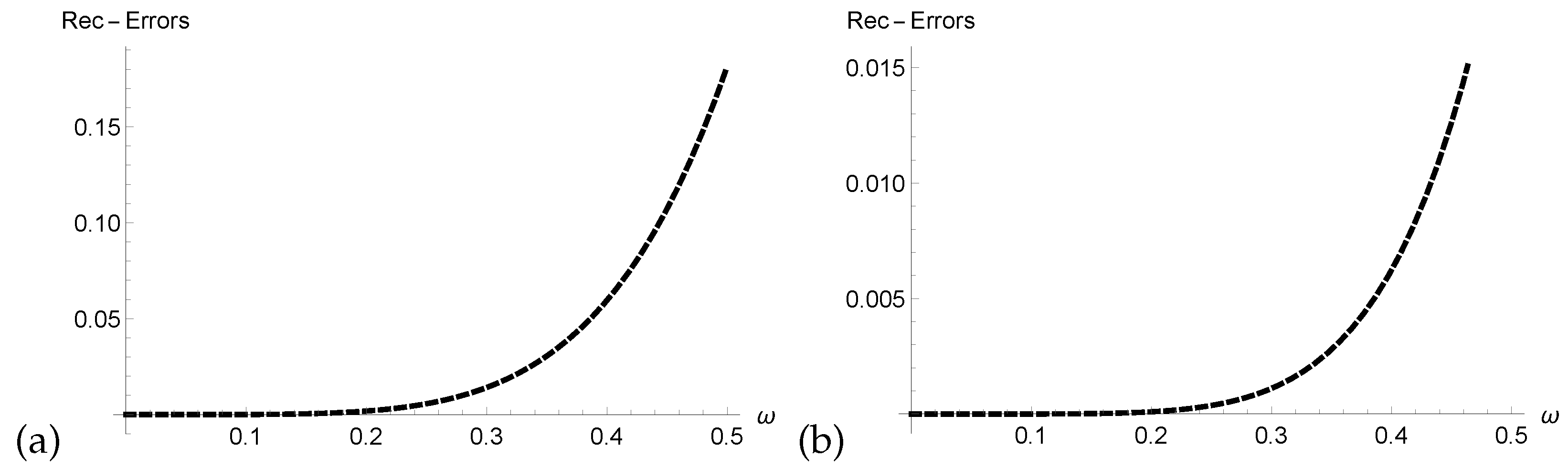
- We verified the correctness of our technique through analysis of Res-Errors and Rec-Errors.
- Moreover, we compared the solutions obtained by ERPSM with those obtained by LDM. Our results strongly agree with LDM, verifying that our approach is an alternative tool for solving NFDEs.
- To the best of our knowledge, in our research, we have solved the most modified model of smoking.
2. Preliminaries
- (i)
- .
- (ii)
- ,
- (iii)
- .
- (iv)
- .
- (v)
3. Stability Result and Algorithm of the ERPSM
3.1. The Stability Result for the Trivial Fixed Point
3.2. Algorithm of the ERPSM and Series Solutions of the Nonlinear Smoking Model
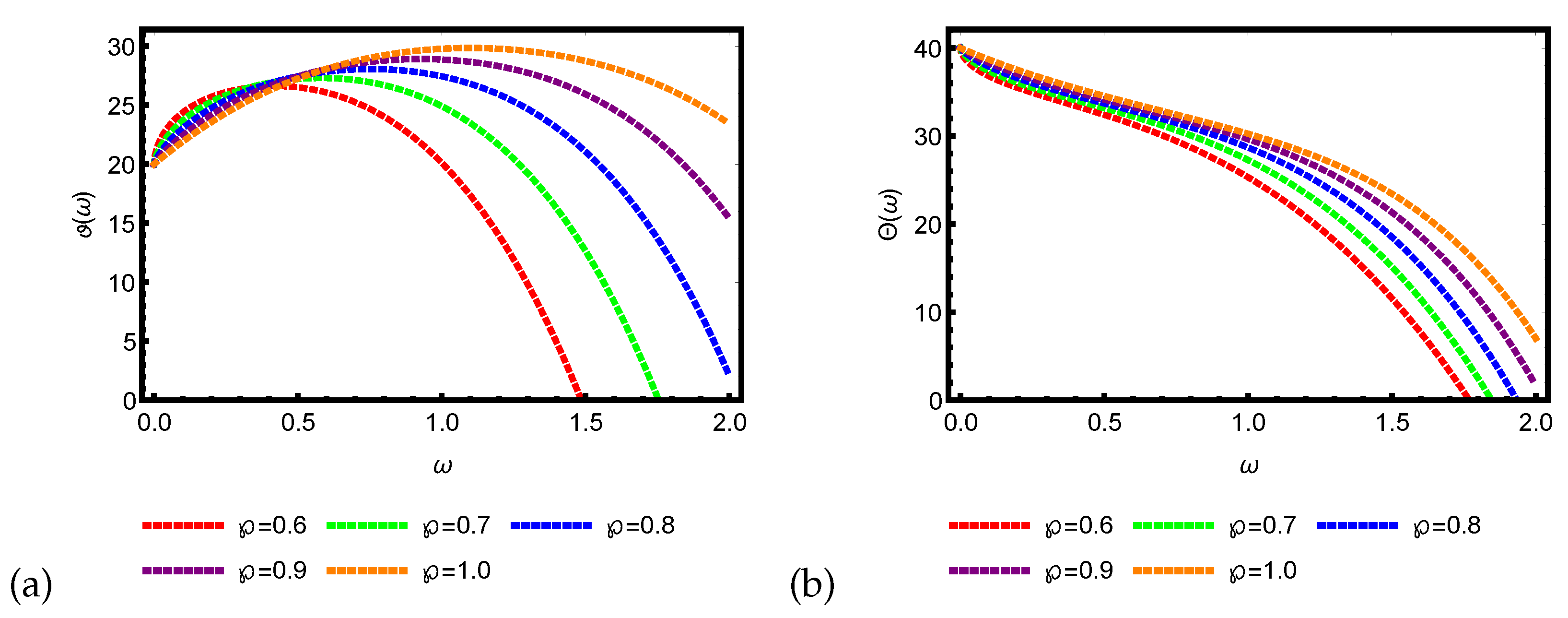
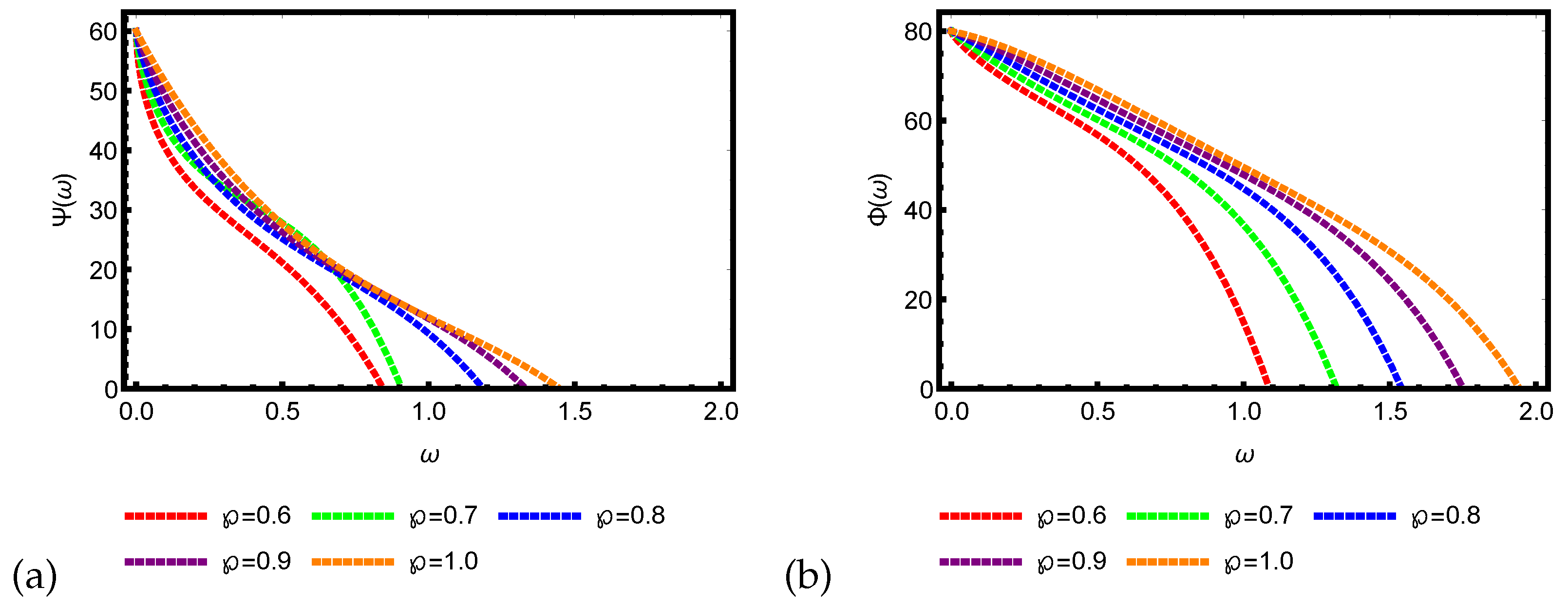
4. Graphical and Numerical Results of Approximate Solutions Attained by ERPSM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Samko, S. Fractional integration and differentiation of variable order: An overview. Nonlinear Dyn. 2013, 71, 653–662. [Google Scholar] [CrossRef]
- Abu-Ghuwaleh, M.; Saadeh, R. New definitions of fractional derivatives and integrals for complex analytic functions. Arab. J. Basic Appl. Sci. 2023, 30, 675–690. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, J.; Tang, J. Clarify the physical process for fractional dynamical systems. Nonlinear Dyn. 2020, 100, 2353–2364. [Google Scholar] [CrossRef]
- Arfan, M.; Lashin, M.M.; Sunthrayuth, P.; Shah, K.; Ullah, A.; Iskakova, K.; Abdeljawad, T. On nonlinear dynamics of COVID-19 disease model corresponding to nonsingular fractional order derivative. Med. Biol. Eng. Comput. 2022, 60, 3169–3185. [Google Scholar] [CrossRef] [PubMed]
- Mangal, S.; Misra, O.P.; Dhar, J. SIRS epidemic modeling using fractional-ordered differential equations: Role of fear effect. Int. J. Biomath. 2024, 17, 2350044. [Google Scholar] [CrossRef]
- Singh, H.; Baleanu, D.; Singh, J.; Dutta, H. Computational study of fractional order smoking model. Chaos Solit. Fract. 2021, 142, 110440. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Zeb, A.; Alzahrani, E.; Shah, K. Dynamical analysis of fractional-order tobacco smoking model containing snuffing class. Alex. Eng. J. 2021, 60, 3669–3678. [Google Scholar] [CrossRef]
- Hassani, H.; Machado, J.T.; Avazzadeh, Z.; Naraghirad, E.; Mehrabi, S. Optimal solution of the fractional-order smoking model and its public health implications. Nonlinear Dyn. 2022, 108, 2815–2831. [Google Scholar] [CrossRef]
- Liu, P.; Munir, T.; Cui, T.; Din, A.; Wu, P. Mathematical assessment of the dynamics of the tobacco smoking model: An application of fractional theory. AIMS Math. 2022, 7, 7143–7165. [Google Scholar] [CrossRef]
- Swartz, J.B. Use of a Multistage Model to Predict Time Trends in Smoking Induced Lung Cancer. J. Epidemiol. Community Health 1992, 46, 311–315. [Google Scholar] [CrossRef][Green Version]
- Brauer, F.; Castillo-Cha’vez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Zaman, G. Optimal campaign in the smoking dynamics. Comput. Math. Methods Med. 2011, 2011, 163834. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Yang, X. A New Nonlinear Compact Difference Scheme for a Fourth-Order Nonlinear Burgers Type Equation with a Weakly Singular Kernel. J. Appl. Math. Comput. 2024, 2024, 1–33. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, X. Pointwise error estimate of conservative difference scheme for supergeneralized viscous Burgers’ equation. Electron. Res. Arch. 2024, 32, 1471–1497. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Zhou, Z.; Yang, X. A Fast Compact Finite Difference Scheme for the Fourth-Order Diffusion-Wave Equation. Inter. J. Comput. Math. 2024, 101, 170–193. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, X. A time two-grid difference method for nonlinear generalized viscous Burgers’ equation. J. Math. Chem. 2024, 2014, 1–34. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Khan, A.; Akgül, A. Adaptation on power series method with conformable operator for solving fractional order systems of nonlinear partial differential equations. Chaos Solit. Fract. 2022, 157, 111984. [Google Scholar] [CrossRef]
- Zaky, M.A. An accurate spectral collocation method for nonlinear systems of fractional differential equations and related integral equations with nonsmooth solutions. Appl. Numer. Math. 2020, 154, 205–222. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. A new iterative method for the numerical solution of high-order non-linear fractional boundary value problems. Front. Phys. 2020, 8, 220. [Google Scholar] [CrossRef]
- Khalid, N.; Abbas, M.; Iqbal, M.K.; Singh, J.; Ismail, A.I.M. A computational approach for solving time fractional differential equation via spline functions. Alex. Eng. J. 2020, 59, 3061–3078. [Google Scholar] [CrossRef]
- Babaei, A.; Jafari, H.; Banihashemi, S. Numerical solution of variable order fractional nonlinear quadratic integro-differential equations based on the sixth-kind Chebyshev collocation method. J. Comput. Appl. Math. 2020, 377, 112908. [Google Scholar] [CrossRef]
- Li, D.; Sun, W.; Wu, C. A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions. Numer. Math. Theory Methods Appl. 2021, 14, 355–376. [Google Scholar]
- Haq, F.; Shah, K.; ur Rahman, G.; Shahzad, M. Numerical solution of fractional order smoking model via Laplace Adomian decomposition method. Alex. Eng. J. 2018, 57, 1061–1069. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Sweilam, N.H.; Higazy, M. Approximate solution for solving nonlinear fractional order smoking model. Alex. Eng. J. 2020, 59, 739–752. [Google Scholar] [CrossRef]
- Pavani, K.; Raghavendar, K. A novel technique to study the solutions of time fractional nonlinear smoking epidemic model. Sci. Rep. 2024, 14, 4159. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.A.; Shah, K.; Zaman, G.; Jarad, F. Existence Theory and Numerical Solutions to Smoking Model under Caputo-Fabrizio Fractional Derivative. Chaos: An Interdiscip. J. Nonlinear Sci. 2019, 29, 013128. [Google Scholar]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Gunerhan, H.; Rezazadeh, H.; Adel, W.; Hatami, M.; Sagayam, K.M.; Emadifar, H.; Hamoud, A.A. Analytical approximate solution of fractional order smoking epidemic model. Adv. Mech. Eng. 2022, 14, 1–11. [Google Scholar]
- Mohammed, O.H.; Salim, H.A. Computational methods based laplace decomposition for solving nonlinear system of fractional order differential equations. Alex. Eng. J. 2018, 57, 3549–3557. [Google Scholar] [CrossRef]
- He, W.; Chen, N.; Dassios, I.; Shah, N.A.; Chung, J.D. Fractional system of Korteweg-De Vries equations via Elzaki transform. Mathematics 2021, 9, 673. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgül, A.; Bayram, M. Series and Closed Form Solution of Caputo Time-Fractional Wave and Heat Problems with the Variable Coefficients by a Novel Approach. Opt. Quant. Electron. 2024, 56, 203. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Khan, A.; Akgül, A.; Ali, M.S. A Novel Numerical Technique for Fractional Ordinary Differential Equations with Proportional Delay. J. Funct. Spaces 2022, 2022, 1–21. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z. On conservative, positivity preserving, nonlinear FV scheme on distorted meshes for the multi-term nonlocal Nagumo-type equations. Appl. Math. Lett. 2024, 150, 108972. [Google Scholar] [CrossRef]
- Yang, X.; Qiu, W.; Chen, H.; Zhang, H. Second-order BDF ADI Galerkin finite element method for the evolutionary equation with a nonlocal term in three-dimensional space. Appl. Numer. Math. 2022, 172, 497–513. [Google Scholar] [CrossRef]




| - | - | - | - | - | - | |
|---|---|---|---|---|---|---|
| - | - | - | - | |
|---|---|---|---|---|
| - | - | - | - | - | - | |
|---|---|---|---|---|---|---|
| - | - | - | - | |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed Djaouti, A.; Khan, Z.A.; Imran Liaqat, M.; Al-Quran, A. A Novel Technique for Solving the Nonlinear Fractional-Order Smoking Model. Fractal Fract. 2024, 8, 286. https://doi.org/10.3390/fractalfract8050286
Mohammed Djaouti A, Khan ZA, Imran Liaqat M, Al-Quran A. A Novel Technique for Solving the Nonlinear Fractional-Order Smoking Model. Fractal and Fractional. 2024; 8(5):286. https://doi.org/10.3390/fractalfract8050286
Chicago/Turabian StyleMohammed Djaouti, Abdelhamid, Zareen A. Khan, Muhammad Imran Liaqat, and Ashraf Al-Quran. 2024. "A Novel Technique for Solving the Nonlinear Fractional-Order Smoking Model" Fractal and Fractional 8, no. 5: 286. https://doi.org/10.3390/fractalfract8050286
APA StyleMohammed Djaouti, A., Khan, Z. A., Imran Liaqat, M., & Al-Quran, A. (2024). A Novel Technique for Solving the Nonlinear Fractional-Order Smoking Model. Fractal and Fractional, 8(5), 286. https://doi.org/10.3390/fractalfract8050286






