Adaptive Output Synchronization of Coupled Fractional-Order Memristive Reaction-Diffusion Neural Networks

Abstract

This article discusses the adaptive output synchronization problem of coupled fractional-order memristive reaction-diffusion neural networks (CFOMRDNNs) with multiple output couplings or multiple output derivative couplings. Firstly, by using Lyapunov functional and inequality techniques, an adaptive output synchronization criterion for CFOMRDNNs with multiple output couplings is proposed. Then, an adaptive controller is designed for ensuring the output synchronization of CFOMRDNNs with multiple output derivative couplings. Finally, two numerical examples are given to verify the effectiveness of the theoretical results.

1. Introduction

In recent years, coupled neural networks (CNNs) have received significant attention because their dynamical behaviors have been applied in many fields such as chaos generators design, image processing and secure communication. As an important dynamical behavior of CNNs, synchronization has been widely discussed during the past decade [1,2,3,4,5]. With the help of convex combination technique and time-varying Lyapunov functions, Long et al. [3] investigated the synchronization of coupled switched neural networks affected by stochastic disturbances and impulses. The state synchronization of CNNs was studied in above works [1,2,3,4,5], however, state synchronization is often difficult to achieve. Actually, sometimes only partial state variables are needed to be synchronized. Hence, some scholars have considered the output synchronization of CNNs [6,7,8,9,10]. Wang et al. [6] solved the output synchronization problem of directed and undirected CNNs by employing matrix theory and inequality technique.

In practical situations, it is more appropriate to use multiple weighted complex networks to describe various real networks (e.g., communication networks, public transport networks, etc.). Since CNNs are a special type of complex networks, some authors have considered the dynamical behaviors of multiple weighted CNNs [11,12]. In [11], some synchronization criteria were established for CNNs with multistate couplings by designing suitable event-triggered controller. In [1,2,3,4,5,6,7,8,9,10,11,12], the authors discussed networks with state coupling. As a matter of fact, output coupling is also an important coupling form in CNNs. Recently, some investigations about the output synchronization of CNNs with multiple output couplings have been reported [13,14,15]. A class of CNNs with multiple output couplings was introduced by Liu et al. [14], and the output synchronization problem for the proposed networks was investigated by exploiting the Barbalat’s lemma and adaptive controller. On the other hand, different time derivatives of node states may lead to different changes of other nodes in some real networks. Thus, considering the dynamical behaviors for CNNs with derivative coupling is meaningful [16,17,18]. Tang et al. [16] designed an impulsive pinning control strategy to ensure that the derivative CNNs are synchronized.

It is worth pointing out that [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] only focused on integer-order coupled neural network models. In fact, compared with integer-order derivatives, fractional-order derivatives can better describe the memory and hereditary properties of diverse materials and processes. Furthermore, fractional calculus can also be applied to biological neurons. For example, fractional-order derivatives afford basic and universal computation for individual neuron that can facilitate stimulus anticipation and information processing in [19]. Hence, more and more authors have shown interest in the coupled fractional-order neural networks (CFONNs) and have obtained important results [20,21,22,23]. In [20], a kind of multi-weights CFONNs with and without uncertain parameters was introduced, and several output synchronization criteria for such networks were derived based on Mittag–Leffler functions and Laplace transforms. Additionally, considering the diffusion phenomenon is inevitable in CNNs when electrons are moving in a nonuniform electromagnetic field, some researchers investigated the dynamical behaviors of CFONNs with reaction-diffusion terms [24,25,26,27]. Wang et al. [26] presented a multiple weighted coupled fractional-order neural network model with reaction-diffusion terms and solved the synchronization problem for proposed model by using adaptive schemes and some inequality techniques. Regrettably, the output synchronization of CFONNs with reaction-diffusion terms has not been studied.

As is well known, in 2008, HP Labs first produced nanoscale memristor devices. In the implementation of neural network circuits, resistors can be replaced by memristors to simulate synaptic structures. Therefore, a memristive neural network model was established successfully [28,29]. Li et al. [29] presented a quaternion-valued fuzzy memristive neural network and derived several quasi-synchronization criteria for such a network. Moreover, due to the fractional-order systems having property of long-term memory, there has been growing attention about the dynamical behaviors of fractional-order memristive neural networks [30,31,32,33,34]. Ma et al. [30] introduced a delayed coupled fractional-order memristive neural network model with parameter mismatch and designed a discontinuous controller to ensure that the proposed model can achieve synchronization. On the basis of Lyapunov functionals and fractional-order derivative inequalities, Mao et al. [31] addressed the synchronization issue of fractional-order multidimensional memristive neural networks with time-varying delays. Unfortunately, the output synchronization of coupled fractional-order memristive reaction-diffusion neural networks (CFOMRDNNs) under adaptive controller has never been considered.

This article discusses the output synchronization of CFOMRDNNs with multiple output couplings or multiple output derivative couplings via adaptive control. The main contributions of this article are as follows.

(1) This article introduces a type of CFOMRDNNs with multi-output derivative couplings. Different from the existing coupled fractional-order reaction-diffusion neural network models [24,26], derivative coupling is considered in the network model of this article because the state change velocities of neighbor nodes have a great influence on each node.

(2) An output feedback controller and an adaptive scheme are designed to ensure the output synchronization of CFOMRDNNs with multi-output derivative couplings. Considering that in many cases only partial state variables are required to be synchronized, this article explores the output synchronization problem of CFOMRDNNs with multi-output derivative couplings, which is different from the synchronization of coupled fractional-order reaction-diffusion neural networks investigated in [26].

(3) Under the help of the Laplace transform and Lyapunov functional, an output synchronization criterion is presented for CFOMRDNNs with multi-output couplings. It is evident that tackling the output synchronization problem of CFOMRDNNs with multi-output couplings is very meaningful, as it has not been discussed before.

2. Preliminaries

Let ${\lambda }_M\left(Q\right)$ and ${\lambda }_m\left(Q\right)$ mean the maximum and the minimum eigenvalues of the real symmetric matrix Q, respectively. ⊗ represents the Kronecker product. * means the convolution operator. $\mathbb{R}$ and ${\mathbb{R}}^{+}$ denote the set of all real numbers and the set of all positive real numbers, respectively. ${\mathbb{R}}^n$ and ${\mathbb{R}}^{n\times \sigma }$ stand for the set of all n-dimensional real-valued vectors and the set of all $n\times \sigma$ real-valued matrices, respectively. $\mathsf{\Phi }=\{\varphi ={({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_N)}^T\in {\mathbb{R}}^N|\mid {\varphi }_l\mid <{\alpha }_l,l=1,2,\dots ,N\}$, $\partial \mathsf{\Phi }$ is the boundary of $\mathsf{\Phi }$ and $\overline{\mathsf{\Phi }}=\mathsf{\Phi }\cup \partial \mathsf{\Phi }$. For any $z(\varphi ,t)=(z_1(\varphi ,t),z_2(\varphi ,t),\dots ,z_{\sigma }(\varphi ,t))\in {\mathbb{R}}^{\sigma }$ with $(\varphi ,t)\in \mathsf{\Phi }\times \mathbb{R}$, ${\parallel z(·,t)\parallel }_2=\sqrt{{\int }_{\mathsf{\Phi }}{\sum }_i^{\sigma }{z}_i^2(\varphi ,t)d\varphi }$.

Definition 1

(See [26]). Letting $\gamma \left(t\right)\in C^1([0,+\infty ],\mathbb{R})$, the Caputo fractional derivative for $\gamma \left(t\right)$ is given by

$$\begin{array}{c}\hfill { }_0{D}_t^q\gamma \left(t\right)=\frac{1}{\mathsf{\Gamma }(1-q)}{\int }_0^t\frac{{\gamma }^{\prime }\left(\varsigma \right)}{{(t-\varsigma )}^q}d\varsigma ,t>0,\end{array}$$

where $0<q<1$.

Definition 2

(See [35]). The Mittag–Leffler function is defined by

$$\begin{array}{c}\hfill E_{\mu ,\nu }\left(\omega \right)={\displaystyle \sum _{\kappa =0}^{+\infty }}\frac{{\omega }^{\kappa }}{\mathsf{\Gamma }(\kappa \mu +\nu )},\end{array}$$

where μ, $\nu \in {\mathbb{R}}^{+},$$\omega \in \mathbb{C}$. When $\nu =1,E_{\mu }\left(\omega \right)=E_{\mu ,1}\left(\omega \right)={\sum }_{\kappa =0}^{+\infty }\frac{{\omega }^{\kappa }}{\mathsf{\Gamma }(\kappa \mu +1)}$.

Lemma 1

(See [36]). For any continuously differentiable function $\delta (\varphi ,t):{\mathbb{R}}^N\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{\sigma }$, one has

$$\begin{array}{c}\hfill { }_0{D}_t^q\left({\delta }^T(\varphi ,t)W\delta (\varphi ,t)\right)\le 2{\delta }^T(\varphi ,t)W_0{D}_t^q\delta (\varphi ,t),\end{array}$$

where $0\le W\in {\mathbb{R}}^{\sigma \times \sigma }$ and $0<q<1$.

Lemma 2

(See [37]). Set Φ be a cube $\mid {\chi }_l\mid <{\alpha }_l(l=1,2,\dots ,N)$ and set $\tau \left(\chi \right)$ be a real-valued function belonging to ${\mathcal{C}}^1\left(\mathsf{\Phi }\right)$ which vanishes on the boundary $\partial \mathsf{\Phi }$ of $\mathsf{\Phi },i.e,$${\tau \left(\chi \right)|}_{\partial \mathsf{\Phi }}=0$. We have

$$\begin{array}{c}\hfill {\int }_{\mathsf{\Phi }}{\tau }^2\left(\chi \right)d\chi \le {\alpha }_l^2{\int }_{\mathsf{\Phi }}{\left(\frac{\partial \tau }{\partial {\chi }_l}\right)}^{2}d\chi ,\end{array}$$

in which $\chi ={({\chi }_1,{\chi }_2,\dots ,{\chi }_N)}^T$.

3. Output Synchronization of CFOMRDNNs with Multiple Output Couplings

3.1. Network Model

The coupled fractional-order reaction-diffusion neural network model with multiple couplings considered in [26] is described by

$$\begin{array}{ccc}{ }_0{D}_t^q{u}_m(\varphi ,t)& =& G\mathsf{\Delta }{u}_m(\varphi ,t)-Y{u}_m(\varphi ,t)+Qf\left(u_m(\varphi ,t)\right)+C\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\breve{E}}_a{u}_n(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(1)

where $q\in (0,1)$; $u_m(\varphi ,t)={(u_{m1}(\varphi ,t),u_{m2}(\varphi ,t),\dots ,u_{mr}(\varphi ,t))}^T\in {\mathbb{R}}^r$ represents the state vector of the mth node; $G=\mathrm{diag}(g_1,g_2,\dots ,g_r)>0$; $\mathsf{\Delta }={\sum }_{l=1}^N\frac{{\partial }^2}{\partial {\varphi }_l^2}$ is the Laplace diffusion operator on $\mathsf{\Phi }$; $Y=\mathrm{diag}(y_1,y_2,\dots ,y_r)>0$; $f(·)$ denotes the activation function; $C={(c_1,c_2,\dots ,c_r)}^T\in {\mathbb{R}}^r$; ${\mathbb{R}}^{r\times r}\ni Q$ denotes a constant matrix; $b_a\in {\mathbb{R}}^{+}(a=1,2,\dots ,\xi )$ represents the coupling strength of the ath coupling form; $0<{\breve{E}}_a\in {\mathbb{R}}^{r\times r}$ is the inner coupling matrices; $H^a={\left(H_{mn}^a\right)}_{\varpi \times \varpi }\in {\mathbb{R}}^{\varpi \times \varpi }(a=1,2,\dots ,\xi )$ is the outer coupling matrix in the ath coupling form, in which $H_{mn}^a\in \mathbb{R}$ satisfies the following condition: if there is an edge between node m and node n, then $H_{mn}^a=H_{nm}^a>0(m\ne n)$; otherwise, $H_{mn}^a=H_{nm}^a=0(m\ne n)$; and $H_{mm}^a=-{\sum }_{\genfrac{}{}{0pt}{}{n=1}{n\ne m}}^{\varpi }{H}_{mn}^a$.

Based on model (1), in order to investigate the output synchronization, the CFOMRDNNs with multiple output couplings are presented in this section, which are given as

$$\begin{array}{ccc}{ }_0{D}_t^q{u}_m(\varphi ,t)& =& G\mathsf{\Delta }{u}_m(\varphi ,t)-Y{u}_m(\varphi ,t)+Qf\left(u_m(\varphi ,t)\right)+C\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\tilde{E}}_a{\epsilon }_n(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& X{u}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(2)

where $q,u_m(\varphi ,t),G,\mathsf{\Delta },Y,Q,f(·),b_a,C,H^a={\left(H_{mn}^a\right)}_{\varpi \times \varpi }\in {\mathbb{R}}^{\varpi \times \varpi }$ have similar meanings as these in network (1); ${\epsilon }_m(\varphi ,t)=({\epsilon }_{m1}(\varphi ,t),{\epsilon }_{m2}(\varphi ,t),\dots ,{\epsilon }_{m\sigma }(\varphi ,t))\in {\mathbb{R}}^{\sigma }(1\le \sigma \le r)$ denotes the output vector of the mth node;

$$\begin{array}{c}{\mathbb{R}}^{\sigma \times r}\ni X=\left(\begin{array}{cccccccc}{x}_1& 0& 0& \cdots & 0& 0& \cdots & 0\\ 0& x_2& 0& \cdots & 0& 0& \cdots & 0\\ 0& 0& x_3& \cdots & 0& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & x_{\sigma }& 0& \cdots & 0\end{array}\right),\end{array}$$

in which $x_{\vartheta }\in {\mathbb{R}}^{+},\vartheta =1,2,\dots ,\sigma$;

$$\begin{array}{c}{\mathbb{R}}^{r\times \sigma }\ni {\tilde{E}}_a=\left(\begin{array}{ccccc}{e}_1^a& 0& 0& \cdots & 0\\ 0& e_2^a& 0& \cdots & 0\\ 0& 0& e_3^a& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & e_{\sigma }^a\\ 0& 0& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\end{array}\right),\end{array}$$

where $e_{\vartheta }^k\in {\mathbb{R}}^{+},\vartheta =1,2,\dots ,\sigma$.

Consider the following CFOMRDNNs with multiple output couplings consisting of $\varpi$ identical fractional-order memristive reaction-diffusion neural networks with multiple output ouplings:

$$\begin{array}{ccc}{ }_0{D}_t^q{u}_m(\varphi ,t)& =& G\mathsf{\Delta }{u}_m(\varphi ,t)-Y{u}_m(\varphi ,t)+Q\left(u_m(\varphi ,t)\right)f\left(u_m(\varphi ,t)\right)+C\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\tilde{E}}_a{\epsilon }_n(\varphi ,t)+v_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& X{u}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(3)

where $u_m(\varphi ,t),{\epsilon }_m(\varphi ,t),G,\mathsf{\Delta },Y,f(·),b_a,C,H^a={\left(H_{mn}^a\right)}_{\varpi \times \varpi }\in {\mathbb{R}}^{\varpi \times \varpi },{\tilde{E}}_a,X$ have similar meanings as these in network (2); $Q\left(u_m(\varphi ,t)\right)$ is the memristor connection weight and $v_m(\varphi ,t)={(v_{m1}(\varphi ,t),v_{m2}(\varphi ,t),\dots ,v_{mr}(\varphi ,t))}^T\in {\mathbb{R}}^r$ represents the control input of the mth node.

The memristor connection weight $Q\left(u_m(\varphi ,t)\right)={\left(q_{ij}\left(u_{mi}(\varphi ,t)\right)\right)}_{r\times r}$ is defined as

$$\begin{array}{c}{q}_{ij}\left(u_{mi}(\varphi ,t)\right)=\left\{\begin{array}{c}{\widehat{q}}_{ij},\left|u_{mi}(\varphi ,t)\right|\ge {\Theta }_i,\hfill \\ {\check{q}}_{ij},\left|u_{mi}(\varphi ,t)\right|<{\Theta }_i,\hfill \end{array}\right.\end{array}$$

(4)

in which ${\Theta }_i$ denotes the switching jump, ${\widehat{q}}_{ij},{\check{q}}_{ij}$ are known constants, $i,j=1,2,\dots ,r.$

Define

$$\begin{array}{c}{\mathbb{R}}^{r\times r}\ni Q\left(u_m(\varphi ,t)\right)=\left(\begin{array}{cc}{Q}^{\left(1\right)}\left(u_m(\varphi ,t)\right)& Q^{\left(2\right)}\left(u_m(\varphi ,t)\right)\\ Q^{\left(3\right)}\left(u_m(\varphi ,t)\right)& Q^{\left(4\right)}\left(u_m(\varphi ,t)\right)\end{array}\right),\end{array}$$

in which $Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)\in {\mathbb{R}}^{\sigma \times \sigma },Q^{\left(2\right)}\left(u_m(\varphi ,t)\right)\in {\mathbb{R}}^{\sigma \times (r-\sigma )},Q^{\left(4\right)}\left(u_m(\varphi ,t)\right)\in {\mathbb{R}}^{(r-\sigma )\times (r-\sigma )},Q^{\left(3\right)}\left(u_m(\varphi ,t)\right)\in {\mathbb{R}}^{(r-\sigma )\times \sigma }$. The matrix $Q^{\left(2\right)}\left(u_m(\varphi ,t)\right)=0$ is considered in the following part of this article, then we can get

$$\begin{array}{c}{\mathbb{R}}^{r\times r}\ni Q\left(u_m(\varphi ,t)\right)=\left(\begin{array}{cc}{Q}^{\left(1\right)}\left(u_m(\varphi ,t)\right)& 0\\ Q^{\left(3\right)}\left(u_m(\varphi ,t)\right)& Q^{\left(4\right)}\left(u_m(\varphi ,t)\right)\end{array}\right).\end{array}$$

(5)

In many cases, only a fraction of state variables of the nodes are needed to reach synchronization. In the circumstances, these state variables may not be affected by the other state variables in the state of each node. Hence, the connection weight $Q\left(u_m(\varphi ,t)\right)$ is selected in the form of (5) throughout this article.

By taking ${\widehat{u}}_m(\varphi ,t)={(u_{m1}(\varphi ,t),u_{m2}(\varphi ,t),\dots ,u_{m\sigma }(\varphi ,t))}^T\in {\mathbb{R}}^{\sigma }$, ${\widehat{v}}_m(\varphi ,t)={(v_{m1}(\varphi ,t),v_{m2}(\varphi ,t),\dots ,v_{m\sigma }(\varphi ,t))}^T\in {\mathbb{R}}^{\sigma }$, ${\widehat{E}}_a=\mathrm{diag}(e_1^a,e_2^a,\dots ,e_{\sigma }^a)\in {\mathbb{R}}^{\sigma \times \sigma }$, $\widehat{G}=\mathrm{diag}(g_1,g_2,\dots ,g_{\sigma })$, $\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right)={(f_1\left(u_{m1}(\varphi ,t)\right),f_2\left(u_{m2}(\varphi ,t)\right),\dots ,f_{\sigma }\left(u_{m\sigma }(\varphi ,t)\right))}^T$, $\widehat{Y}=\mathrm{diag}(y_1,y_2,\dots y_{\sigma })$, $\widehat{C}={(C_1,C_2,\dots ,C_{\sigma })}^T$ and $\widehat{X}=\mathrm{diag}(x_1,x_2,\dots x_{\sigma })$, one gets from (3) and (5) that

$$\begin{array}{ccc}{ }_0{D}_t^q{\widehat{u}}_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\widehat{u}}_m(\varphi ,t)-\widehat{Y}{\widehat{u}}_m(\varphi ,t)+Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right)+\widehat{C}\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\widehat{E}}_a{\epsilon }_n(\varphi ,t)+{\widehat{v}}_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& \widehat{X}{\widehat{u}}_m(\varphi ,t),m=1,2,\dots ,\varpi .\end{array}$$

(6)

Base on the switch rules in (4), the state of $|u_{mi}(\varphi ,t)|$ can be $|u_{mi}(\varphi ,t)|\ge {\Theta }_i$ or $|u_{mi}(\varphi ,t)|<{\Theta }_i$ if the index i of ${\Theta }_i$ is fixed. Since the connection weight coefficient $q_{ij}\left(u_{mi}(\varphi ,t)\right)$ is determined according to the threshold value of $|u_{mi}(\varphi ,t)|$, there are two possible values for $q_{ij}\left(u_{mi}(\varphi ,t)\right)$. Hence, the number of possible forms of $Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)$ is $2^{{\sigma }^2}$. The characteristic function is defined as follows:

$$\begin{array}{c}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)=\left\{\begin{array}{c}1,Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)=Q_{\iota },\hfill \\ 0,otherwise,\hfill \end{array}\right.\end{array}$$

(7)

where $\iota \in \{1,2,\dots ,2^{{\sigma }^2}\}$. We can reach the conclusion that ${\sum }_{\iota =1}^{2^{{\sigma }^2}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)=1$. Based on (6) and (7), we have

$$\begin{array}{ccc}{ }_0{D}_t^q{\widehat{u}}_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\widehat{u}}_m(\varphi ,t)-\widehat{Y}{\widehat{u}}_m(\varphi ,t)+{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right)+\widehat{C}\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\widehat{E}}_a{\epsilon }_n(\varphi ,t)+{\widehat{v}}_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& \widehat{X}{\widehat{u}}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(8)

where ${\sum }_{\iota =1}^{2^{{\sigma }^2}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }=Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)$.

For simplicity, define ${\acute{q}}_{ij}=\max ({\widehat{q}}_{ij},{\check{q}}_{ij})$, $i,j=1,2,\dots ,\sigma .$$\acute{Q}=\mathrm{diag}({\sum }_{j=1}^{\sigma }{\acute{q}}_{1j}^2,{\sum }_{j=1}^{\sigma }{\acute{q}}_{2j}^2,\dots ,{\sum }_{j=1}^{\sigma }{\acute{q}}_{\sigma j}^2)$.

In this article, the network (3) is connected and function $f_{\vartheta }(·)(\vartheta =1,2,\dots ,\sigma )$ meets the Lipschitz condition, namely, there exists ${\mathbb{R}}^{+}\ni {\theta }_{\vartheta }$ which satisfies

$$|f_{\vartheta }\left({\psi }_1\right)-f_{\vartheta }\left({\psi }_2\right)|\le {\theta }_{\vartheta }|{\psi }_1-{\psi }_2|$$

for any ${\psi }_1,{\psi }_2\in \mathbb{R}$. Furthermore, define $\Theta =\mathrm{diag}({\theta }_1^2,{\theta }_2^2,\dots ,{\theta }_{\sigma }^2).$

The Dirichlet boundary condition and initial value of network (3) are given as

$$\begin{array}{ccc}& & u_m(\varphi ,0)={\varrho }_m\left(\varphi \right)\in {\mathbb{R}}^{\sigma },\varphi \in \mathsf{\Phi },\hfill \\ & & u_m(\varphi ,t)=0,(\varphi ,t)\in \partial \mathsf{\Phi }\times [0,+\infty ),\hfill \end{array}$$

where ${\varrho }_m\left(\varphi \right)(m=1,2,\dots ,\varpi )$ is continuous on $\overline{\mathsf{\Phi }}$.

Denote $\overrightarrow{f}\left(u(\varphi ,t)\right)=\widehat{f}\left({\widehat{X}}^{-1}u(\varphi ,t)\right)$, in which $u(\varphi ,t)\in {\mathbb{R}}^{\sigma }$. Then, it can be derived from (8) that

$$\begin{array}{ccc}{ }_0{D}_t^q{\epsilon }_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\epsilon }_m(\varphi ,t)-\widehat{Y}{\epsilon }_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)\\ & & +\widehat{X}\widehat{C}+{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{\epsilon }_n(\varphi ,t)+\widehat{X}{\widehat{v}}_m(\varphi ,t),\end{array}$$

(9)

where $m=1,2,\dots ,\varpi$.

By taking $\overline{\epsilon }(\varphi ,t)=\frac{1}{\varpi }{\sum }_{m=1}^{\varpi }{\epsilon }_m(\varphi ,t)$, we can acquire

$$\begin{array}{ccc}{ }_0{D}_t^q{\overline{\epsilon }}_m(\varphi ,t)\hfill & =\hfill & \widehat{G}\mathsf{\Delta }{\overline{\epsilon }}_m(\varphi ,t)-\widehat{Y}{\overline{\epsilon }}_m(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)\hfill \\ \hfill & \hfill & +\widehat{X}\widehat{C}+\frac{1}{\varpi }{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a\left({\displaystyle \sum _{m=1}^{\varpi }}{H}_{mn}^a\right)\widehat{X}{\widehat{E}}_a{\epsilon }_n(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\widehat{v}}_m(\varphi ,t)\hfill \\ \hfill & =\hfill & \widehat{G}\mathsf{\Delta }{\overline{\epsilon }}_m(\varphi ,t)-\widehat{Y}{\overline{\epsilon }}_m(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)+\widehat{X}\widehat{C}\hfill \\ \hfill & \hfill & +\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\widehat{v}}_m(\varphi ,t).\hfill \end{array}$$

(10)

Define $z_m(\varphi ,t)={(z_{m1}(\varphi ,t),z_{m2}(\varphi ,t),\dots ,z_{m\sigma }(\varphi ,t))}^T={\epsilon }_m(\varphi ,t)-\overline{\epsilon }(\varphi ,t)\in {\mathbb{R}}^{\sigma }$. By (9) and (10), we derive

$$\begin{array}{ccc}{ }_0{D}_t^q{z}_m(\varphi ,t)\hfill & =\hfill & \widehat{G}\mathsf{\Delta }{z}_m(\varphi ,t)-\widehat{Y}{z}_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)+\widehat{X}{\widehat{v}}_m(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_{\beta }(\varphi ,t)\right)+{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\widehat{v}}_{\beta }(\varphi ,t),\hfill \end{array}$$

(11)

where $m=1,2,\dots ,\varpi$.

In the following, the output synchronization is defined for the network (3).

Definition 3.

The network (3) can achieve output synchronization if

$$\begin{array}{ccc}& & \underset{t\to +\infty }{lim}{∥{\epsilon }_m(·,t)-\frac{1}{\varpi }{\displaystyle \sum _{n=1}^{\varpi }}{\epsilon }_n(·,t)∥}_2=0,p=1,2,\dots ,\varpi .\hfill \end{array}$$

3.2. Adaptive Control for Output Synchronization

Design following output feedback controller and adaptive scheme for the network (3)

$$\begin{array}{c}\left\{\begin{array}{c}{\widehat{v}}_m(\varphi ,t)=-{\sum }_{a=1}^{\xi }{b}_a{s}_m^a\left(t\right){\widehat{E}}_a{z}_m(\varphi ,t),\hfill \\ { }_0{D}_t^q{s}_m^a\left(t\right)=b_a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\widehat{X}P{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi -\frac{1}{2{\lambda }_M\left(P\right)}(s_m^a\left(t\right)-{\widehat{s}}_m^a),\hfill \end{array}\right.\end{array}$$

(12)

where $m=1,2,\dots ,\varpi ,{\mathbb{R}}^{\sigma \times \sigma }\ni P>0$, ${\widehat{s}}_m^a\in {\mathbb{R}}^{+}$, and $s_m^a\left(t\right)\in {\mathbb{R}}^{+}$.

Define

$$\begin{array}{c}\hfill z(\varphi ,t)={(z_1^T(\varphi ,t),z_2^T(\varphi ,t),\dots ,z_{\varpi }^T(\varphi ,t))}^T,\\ \hfill u(\varphi ,t)={(u_1^T(\varphi ,t),u_2^T(\varphi ,t),\dots ,u_{\varpi }^T(\varphi ,t))}^T.\end{array}$$

Theorem 1.

Under the adaptive controller (12), the network (3) can realize output synchronization.

Proof. 

Construct the Lyapunov functional for the network (3):

$$\begin{array}{ccc}{V}_1\left(t\right)\hfill & =\hfill & O_1\left(t\right)+K_1\left(t\right),\hfill \\ O_1\left(t\right)\hfill & =\hfill & {\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P{z}_m(\varphi ,t)d\varphi ,\hfill \\ K_1\left(t\right)\hfill & =\hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}^2,\hfill \end{array}$$

(13)

where $0<P=\mathrm{diag}(p_1,p_2,\dots ,p_{\sigma })\in {\mathbb{R}}^{\sigma \times \sigma }$.

By (11), (13) and Lemma 1, one has

$$\begin{array}{ccc}{ }_0{D}_t^q{O}_1\left(t\right)\hfill & \le \hfill & 2{\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P{ }_0{D}_t^q{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & =\hfill & 2{\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P[\widehat{G}\mathsf{\Delta }{z}_m(\varphi ,t)-\widehat{Y}{z}_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }(\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)\hfill \\ \hfill & \hfill & -\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)+\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right))-\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_{\beta }(\varphi ,t)\right)\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)-{\displaystyle \sum _{a=1}^{\xi }}{b}_a{s}_m^a\left(t\right)\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\widehat{v}}_{\beta }(\varphi ,t)]d\varphi .\hfill \end{array}$$

(14)

Because ${\overrightarrow{f}}_{\vartheta }(·)(\vartheta =1,2,\dots ,\sigma )$ satisfies the Lipschitz condition, one obtains

$$\begin{array}{ccc}\hfill & \hfill & 2{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\left[\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)-\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)\right]\hfill \\ \hfill & \le \hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)z_m^T(\varphi ,t)P\widehat{X}{Q}_{\iota }{\left({\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)z_m^T(\varphi ,t)P\widehat{X}{Q}_{\iota }\right)}^T\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{m=1}^{\varpi }}{\left[\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)-\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)\right]}^T\left[\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)-\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)\right]\hfill \\ \hfill & \le \hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{i=1}^{\sigma }}{\displaystyle \sum _{j=1}^{\sigma }}{p}_i^2{x}_i^2{\acute{q}}_{ij}^2{z}_{mi}^2(\varphi ,t)+{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{\vartheta =1}^{\sigma }}{\theta }_{\vartheta }^2{z}_{m\vartheta }^2(\varphi ,t)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)\left[P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t).\hfill \end{array}$$

(15)

Since

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=1}^{\varpi }}{z}_m(\varphi ,t)& =& {\displaystyle \sum _{m=1}^{\varpi }}({\epsilon }_m(\varphi ,t)-\overline{\epsilon }(\varphi ,t))\hfill \\ & =& {\displaystyle \sum _{m=1}^{\varpi }}\left({\epsilon }_m(\varphi ,t)-\frac{1}{\varpi }{\displaystyle \sum _{n=1}^{\varpi }}{\epsilon }_n(\varphi ,t)\right)\hfill \\ & =& {\displaystyle \sum _{m=1}^{\varpi }}{\epsilon }_m(\varphi ,t)-{\displaystyle \sum _{n=1}^{\varpi }}{\epsilon }_n(\varphi ,t)\hfill \\ & =& 0,\hfill \end{array}$$

then

$$\begin{array}{c}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)\widehat{X}\left({\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)-\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_{\beta }(\varphi ,t)\right)\right)=0,\hfill \end{array}$$

(16)

$$\begin{array}{cc}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)\widehat{X}\left(-\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}{\widehat{v}}_{\beta }(\varphi ,t)\right)=0.\hfill & \hfill \end{array}$$

(17)

Additionally,

$$\begin{array}{ccc}& & 2{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{G}\mathsf{\Delta }{z}_m(\varphi ,t)d\varphi \\ & =& 2{\displaystyle \sum _{\zeta =1}^{\sigma }}{p}_{\zeta }{g}_{\zeta }{\int }_{\mathsf{\Phi }}{z}_{m\zeta }(\varphi ,t)\mathsf{\Delta }{z}_{m\zeta }(\varphi ,t)d\varphi \\ & =& -2{\displaystyle \sum _{l=1}^N}{\displaystyle \sum _{\zeta =1}^{\sigma }}{p}_{\zeta }{g}_{\zeta }{\int }_{\mathsf{\Phi }}{\left(\frac{\partial z_{m\zeta }(\varphi ,t)}{\partial {\varphi }_l}\right)}^{2}d\varphi \\ & \le & -2{\displaystyle \sum _{l=1}^N}\frac{1}{{\alpha }_l^2}{\displaystyle \sum _{\zeta =1}^{\sigma }}{p}_{\zeta }{g}_{\zeta }{\int }_{\mathsf{\Phi }}{z}_{m\zeta }^2(\varphi ,t)d\varphi \\ & =& -2{\displaystyle \sum _{l=1}^N}\frac{1}{{\alpha }_l^2}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{G}{z}_m(\varphi ,t)d\varphi .\end{array}$$

(18)

From (14)–(18), we can derive

$$\begin{array}{ccc}{ }_0{D}_t^q{O}_1\left(t\right)& \le & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t)d\varphi \\ & & +2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)d\varphi \\ & & -2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi .\end{array}$$

(19)

By (12), (13) and Lemma 1, one has

$$\begin{array}{ccc}{ }_0{D}_t^q{K}_1\left(t\right)\hfill & \le \hfill & 2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}_0{D}_t^q{s}_m\left(t\right)\hfill \\ \hfill & \le \hfill & 2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}(s_m^a\left(t\right)-{\widehat{s}}_m^a)(b_a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\widehat{X}P{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -\frac{1}{2{\lambda }_M\left(P\right)}(s_m^a\left(t\right)-{\widehat{s}}_m^a)).\hfill \end{array}$$

(20)

In the light of (19) and (20), we have

$$\begin{array}{ccc}{ }_0{D}_t^q{V}_1\left(t\right)\hfill & \le \hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & +2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & +2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{s}}_m^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -\frac{1}{{\lambda }_M\left(P\right)}{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}^2\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & +2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{s}}_m^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi -\frac{1}{{\lambda }_M\left(P\right)}{K}_1\left(t\right)\hfill \\ \hfill & =\hfill & {\int }_{\mathsf{\Phi }}{z}^T(\varphi ,t)[I_{\varpi }\otimes \left(-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right)\hfill \\ \hfill & \hfill & +2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{H}^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)-2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{S}}^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)]z(\varphi ,t)-\frac{1}{{\lambda }_M\left(P\right)}{K}_1\left(t\right)\hfill \\ \hfill & \le \hfill & {\int }_{\mathsf{\Phi }}{z}^T(\varphi ,t)\left[\mathsf{\Lambda }-2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\lambda }_m\left({\widehat{S}}^a\right)\otimes \left(P\widehat{X}{\widehat{E}}_a\right)\right]z(\varphi ,t)-\frac{1}{{\lambda }_M\left(P\right)}{K}_1\left(t\right),\hfill \end{array}$$

(21)

where $\mathsf{\Lambda }=I_{\varpi }\otimes \left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]+2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{H}^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right), {\widehat{S}}^a=$$\mathrm{diag}({\widehat{s}}_1^a,{\widehat{s}}_2^a,\dots ,{\widehat{s}}_{\varpi }^a)(a=1,2,\dots ,\xi )$ and ${\widehat{s}}_m^a\in {\mathbb{R}}^{+}.$

Select sufficiently large ${\widehat{s}}_m^a$ such that

$$\begin{array}{c}{\lambda }_M\left(\mathsf{\Lambda }\right)-2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\lambda }_m\left({\widehat{S}}^a\right){\lambda }_m\left(P\widehat{X}{\widehat{E}}_a\right)\le -1.\end{array}$$

(22)

Furthermore, it follows from (21) and (22) that

$$\begin{array}{c}{ }_0{D}_t^q{V}_1\left(t\right)+{\Vert z(·,t)\Vert }_2^2\le -\frac{K_1\left(t\right)}{{\lambda }_M\left(P\right)}.\end{array}$$

(23)

By (13), one has

$$\begin{array}{c}{\lambda }_m{\left(P\right)\Vert z(·,t)\Vert }_2^2\le V_1\left(t\right)\le {\lambda }_M\left(P\right){\Vert z(·,t)\Vert }_2^2+K_1\left(t\right).\end{array}$$

(24)

Combining (23) and (24), one derives

$$\begin{array}{c}{ }_0{D}_t^q{V}_1\left(t\right){\lambda }_M\left(P\right)\le -V_1\left(t\right).\end{array}$$

(25)

Based on (24), there exists a $0\le \psi \left(t\right)\in \mathbb{R}$ such that

$$\begin{array}{c}{ }_0{D}_t^q{V}_1\left(t\right)+\psi \left(t\right)=-\frac{V_1\left(t\right)}{{\lambda }_M\left(P\right)}.\end{array}$$

(26)

Let $\mathsf{\Psi }\left(s\right)=\mathcal{L}\left[\psi \left(t\right)\right]$ and ${\mathcal{V}}_1\left(s\right)=\mathcal{L}\left[V_1\left(t\right)\right]$. According to (26), one acquires

$$\begin{array}{c}{s}^q{\mathcal{V}}_1\left(s\right)-s^{q-1}{V}_1\left(0\right)+\mathsf{\Psi }\left(s\right)=-\frac{{\mathcal{V}}_1\left(s\right)}{{\lambda }_M\left(P\right)}.\end{array}$$

(27)

From (27), we have

$$\begin{array}{c}{\mathcal{V}}_1\left(s\right)=\frac{s^{q-1}{V}_1\left(0\right)}{s^q+\frac{1}{{\lambda }_M\left(P\right)}}-\frac{\mathsf{\Psi }\left(s\right)}{s^q+\frac{1}{{\lambda }_M\left(P\right)}}.\end{array}$$

(28)

The inverse Laplace transform is used for (28), one has

$$\begin{array}{c}{V}_1\left(t\right)=V_1\left(0\right)E_q\left(-\frac{1}{{\lambda }_M\left(P\right)}{t}^q\right)-\psi \left(t\right)\ast t^{q-1}{E}_{q,q}\left(-\frac{1}{{\lambda }_M\left(P\right)}{t}^q\right).\end{array}$$

(29)

In consideration of the fact that $\psi \left(t\right)$ and $E_{q,q}\left(-\frac{1}{{\lambda }_M\left(P\right)}{t}^q\right)$ are nonnegative, it is derived from (24) and (29) that

$$\begin{array}{c}0\le {\lambda }_m\left(P\right){\Vert z(·,t)\Vert }_2^2\le V_1\left(t\right)\le V_1\left(0\right)E_q\left(-\frac{1}{{\lambda }_M\left(P\right)}{t}^q\right).\end{array}$$

(30)

Based on (30), we could gain

$$\begin{array}{c}\underset{t\to +\infty }{lim}{∥z(·,t)∥}_2=0.\end{array}$$

(31)

Thus, the network (3) under the adaptive controller (12) attains output synchronized. □

4. Output Synchronization of CFOMRDNNs with Multiple Output Derivative Couplings

4.1. Network Model

The CFORDMNNs with multiple output derivative couplings discussed are described as

$$\begin{array}{ccc}{ }_0{D}_t^q{u}_m(\varphi ,t)& =& G\mathsf{\Delta }{u}_m(\varphi ,t)-Y{u}_m(\varphi ,t)+Q\left(u_m(\varphi ,t)\right)f\left(u_m(\varphi ,t)\right)+C\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\tilde{E}}_a{ }_0{D}_t^q{\epsilon }_n(\varphi ,t)+v_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& X{u}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(32)

where $q,u_m(\varphi ,t),\mathsf{\Delta },{\epsilon }_m(\varphi ,t),G,Y,f(·),b_a,C,v_m(\varphi ,t),H^a={\left(H_{mn}^a\right)}_{\varpi \times \varpi }\in {\mathbb{R}}^{\varpi \times \varpi },{\tilde{E}}_a,X$ have the same meanings as these in network (3) and $Q\left(u_m(\varphi ,t)\right)={\left(q_{ij}\left(u_{mi}(\varphi ,t)\right)\right)}_{r\times r}$ have the same meanings as it in network (4).

The Dirichlet boundary condition and initial value of network (32) are given as

$$\begin{array}{ccc}\hfill u_m(\varphi ,0)& =& {\varrho }_m\left(\varphi \right)\in {\mathbb{R}}^{\sigma },\varphi \in \mathsf{\Phi },\hfill \\ \hfill u_m(\varphi ,t)& =& 0,(\varphi ,t)\in \partial \mathsf{\Phi }\times [0,+\infty ),\hfill \end{array}$$

where ${\varrho }_m\left(\varphi \right)(m=1,2,\dots ,\varpi )$ is continuous on $\overline{\mathsf{\Phi }}$.

According to (5) and (32), we have

$$\begin{array}{ccc}{ }_0{D}_t^q{\widehat{u}}_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\widehat{u}}_m(\varphi ,t)-\widehat{Y}{\widehat{u}}_m(\varphi ,t)+Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right)+\widehat{C}\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\widehat{E}}_a{ }_0{D}_t^q{\epsilon }_n(\varphi ,t)+{\widehat{v}}_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& \widehat{X}{\widehat{u}}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(33)

where $Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)$ has the same definition as it in (5); ${\widehat{u}}_m(\varphi ,t),{\widehat{v}}_m(\varphi ,t),\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right),{\widehat{E}}_a,\widehat{G},\widehat{Y},\widehat{C}$ and $\widehat{X}$ have the same definitions as these in (6).

By (7) and (33), one gets

$$\begin{array}{ccc}{ }_0{D}_t^q{\widehat{u}}_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\widehat{u}}_m(\varphi ,t)-\widehat{Y}{\widehat{u}}_m(\varphi ,t)+{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\widehat{f}\left({\widehat{u}}_m(\varphi ,t)\right)+\widehat{C}\\ & & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a{\widehat{E}}_a{ }_0{D}_t^q{\epsilon }_n(\varphi ,t)+{\widehat{v}}_m(\varphi ,t),\\ {\epsilon }_m(\varphi ,t)& =& \widehat{X}{\widehat{u}}_m(\varphi ,t),m=1,2,\dots ,\varpi ,\end{array}$$

(34)

in which ${\mathsf{\Gamma }}_{\iota }(\varphi ,t)$ and $Q_{\iota }$ have the same definitions as these in (7) and ${\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }=Q^{\left(1\right)}\left(u_m(\varphi ,t)\right)$.

On the basis of (34), we can obtain

$$\begin{array}{ccc}{ }_0{D}_t^q{\epsilon }_m(\varphi ,t)& =& \widehat{G}\mathsf{\Delta }{\epsilon }_m(\varphi ,t)-\widehat{Y}{\epsilon }_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)\\ & & +\widehat{X}\widehat{C}+{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{ }_0{D}_t^q{\epsilon }_n(\varphi ,t)+\widehat{X}{\widehat{v}}_m(\varphi ,t),\end{array}$$

(35)

in which $m=1,2,\dots ,\varpi ,\overrightarrow{f}(·)$ has the same definition as it in (9).

Letting $\overline{\epsilon }(\varphi ,t)=\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}{\epsilon }_m(\varphi ,t)$, one has

$$\begin{array}{ccc}{ }_0{D}_t^q{\overline{\epsilon }}_m(\varphi ,t)\hfill & =\hfill & \widehat{G}\mathsf{\Delta }{\overline{\epsilon }}_m(\varphi ,t)-\widehat{Y}{\overline{\epsilon }}_m(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)+\widehat{X}\widehat{C}\hfill \\ \hfill & \hfill & +\frac{1}{\varpi }{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a\left({\displaystyle \sum _{m=1}^{\varpi }}{H}_{mn}^a\right)\widehat{X}{\widehat{E}}_a{ }_0{D}_t^q{\epsilon }_n(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\widehat{v}}_m(\varphi ,t)\hfill \\ \hfill & =\hfill & \widehat{G}\mathsf{\Delta }{\overline{\epsilon }}_m(\varphi ,t)-\widehat{Y}{\overline{\epsilon }}_m(\varphi ,t)+\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)+\widehat{X}\widehat{C}\hfill \\ \hfill & \hfill & +\frac{1}{\varpi }{\displaystyle \sum _{m=1}^{\varpi }}\widehat{X}{\widehat{v}}_m(\varphi ,t).\hfill \end{array}$$

(36)

Denoting $z_m(\varphi ,t)={(z_{m1}(\varphi ,t),z_{m2}(\varphi ,t),\dots ,z_{m\sigma }(\varphi ,t))}^T={\epsilon }_m(\varphi ,t)-\overline{\epsilon }(\varphi ,t)\in {\mathbb{R}}^{\sigma }$, we derive

$$\begin{array}{ccc}{ }_0{D}_t^q{z}_m(\varphi ,t)\hfill & =\hfill & \widehat{G}\mathsf{\Delta }{z}_m(\varphi ,t)-\widehat{Y}{z}_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)+\widehat{X}{\widehat{v}}_m(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_{\beta }(\varphi ,t)\right)+{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{ }_0{D}_t^q{z}_n(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\widehat{v}}_{\beta }(\varphi ,t),\hfill \end{array}$$

(37)

where $m=1,2,\dots ,\varpi$.

4.2. Adaptive Control for Output Synchronization

An adaptive output feedback controller for the network (32) is devised as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\widehat{v}}_m(\varphi ,t)=-{\displaystyle \sum _{a=1}^{\xi }}{b}_a{s}_m^a\left(t\right){\widehat{E}}_a{z}_m(\varphi ,t),\hfill \\ { }_0{D}_t^q{s}_m^a\left(t\right)=b_a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\widehat{X}P{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi -\frac{1}{2{\lambda }_M\left(P\right)}(s_m^a\left(t\right)-{\widehat{s}}_m^a),\hfill \end{array}\right.\end{array}$$

(38)

where $m=1,2,\dots ,\varpi ,{\mathbb{R}}^{\sigma \times \sigma }\ni P>0,$${\widehat{s}}_m^a\in {\mathbb{R}}^{+}$ and $s_m^a\left(t\right)\in {\mathbb{R}}^{+}$.

Theorem 2.

The network (32) is output synchronized under the adaptive controller (38).

Proof. 

Take the following Lyapunov functional for the network (32):

$$\begin{array}{ccc}{V}_2\left(t\right)\hfill & =\hfill & O_2\left(t\right)+K_2\left(t\right)\hfill \\ O_2\left(t\right)\hfill & =\hfill & {\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\int }_{\mathsf{\Phi }}{z}^T(\varphi ,t)\left[H^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)\right]z(\varphi ,t)d\varphi ,\hfill \\ K_2\left(t\right)\hfill & =\hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}^2,\hfill \end{array}$$

(39)

in which $0<P=\mathrm{diag}(P_1,P_2,\dots ,P_{\sigma })\in {\mathbb{R}}^{\sigma \times \sigma }$.

From (37), (39) and Lemma 1, one obtains

$$\begin{array}{ccc}{ }_0{D}_t^q{O}_2\left(t\right)\hfill & \le \hfill & 2{\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P{ }_0{D}_t^q{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{z}^T(\varphi ,t){\left[H^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)\right]}_0{D}_t^{q}z(\varphi ,t)d\varphi \hfill \\ \hfill & =\hfill & 2{\int }_{\mathsf{\Phi }}{\displaystyle \sum _{m=1}^{\varpi }}{z}_m^T(\varphi ,t)P[\widehat{G}\mathsf{\Delta }{z}_m(\varphi ,t)-\widehat{Y}{z}_m(\varphi ,t)+\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }(\overrightarrow{f}\left({\epsilon }_m(\varphi ,t)\right)\hfill \\ \hfill \\ \hfill & \hfill & -\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right)+\overrightarrow{f}\left(\overline{\epsilon }(\varphi ,t)\right))-\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\displaystyle \sum _{\iota =1}^{2^{{\sigma }^2}}}{\mathsf{\Gamma }}_{\iota }(\varphi ,t)Q_{\iota }\overrightarrow{f}\left({\epsilon }_{\beta }(\varphi ,t)\right)\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{n=1}^{\varpi }}{b}_a{H}_{mn}^a\widehat{X}{\widehat{E}}_a{ }_0{D}_t^q{z}_n(\varphi ,t)-{\displaystyle \sum _{a=1}^{\xi }}{b}_a{s}_m^a\left(t\right)\widehat{X}{\widehat{E}}_a{z}_n(\varphi ,t)\hfill \\ \hfill & \hfill & -\frac{1}{\varpi }{\displaystyle \sum _{\beta =1}^{\varpi }}\widehat{X}{\widehat{v}}_{\beta }(\varphi ,t)]d\varphi -2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{z}^T(\varphi ,t){\left[H^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)\right]}_0{D}_t^{q}z(\varphi ,t)d\varphi .\hfill \end{array}$$

(40)

Using (15) to (18) and according to (40), we can derive

$$\begin{array}{ccc}{ }_0{D}_t^q{O}_2\left(t\right)\hfill & \le \hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t),\hfill \end{array}$$

(41)

where ${\acute{q}}_{ij}=\max ({\widehat{q}}_{ij},{\check{q}}_{ij})$, $i,j=1,2,\dots ,\sigma ,$$\acute{Q}=\mathrm{diag}\left({\displaystyle \sum _{j=1}^{\sigma }}{\acute{q}}_{1j}^2,{\displaystyle \sum _{j=1}^{\sigma }}{\acute{q}}_{2j}^2,\dots ,{\displaystyle \sum _{j=1}^{\sigma }}{\acute{q}}_{\sigma j}^2\right)$.

By (38), (39) and Lemma 1, one gets

$$\begin{array}{ccc}{ }_0{D}_t^q{K}_2\left(t\right)\hfill & \le \hfill & 2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}_0{D}_t^q{s}_m\left(t\right)\hfill \\ \hfill & \le \hfill & 2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}(s_m^a\left(t\right)-{\widehat{s}}_m^a)(b_a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\widehat{X}P{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -\frac{1}{2{\lambda }_M\left(P\right)}\left(s_m^a\left(t\right)-{\widehat{s}}_m^a\right)).\hfill \end{array}$$

(42)

In view of (41) and (42), we have

$$\begin{array}{ccc}{ }_0{D}_t^q{V}_2\left(t\right)\hfill & \le \hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]z_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{a=1}^{\xi }}{\displaystyle \sum _{m=1}^{\varpi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & +2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{s}_m^a\left(t\right){\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{s}}_m^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)P\widehat{X}{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -\frac{1}{{\lambda }_M\left(P\right)}{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{(s_m^a\left(t\right)-{\widehat{s}}_m^a)}^2\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{m=1}^{\varpi }}{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}P\widehat{X}+\Theta \right]z_m(\varphi ,t)d\varphi \hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{m=1}^{\varpi }}{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{s}}_m^a{\int }_{\mathsf{\Phi }}{z}_m^T(\varphi ,t)\widehat{X}P{\widehat{E}}_a{z}_m(\varphi ,t)d\varphi -\frac{1}{{\lambda }_M\left(P\right)}{K}_2\left(t\right)\hfill \\ \hfill & =\hfill & {\int }_{\mathsf{\Phi }}{z}^T(\varphi ,t)[I_{\varpi }\otimes \left(-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right)\hfill \\ \hfill & \hfill & -2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\widehat{S}}^a\otimes \left(P\widehat{X}{\widehat{E}}_a\right)]z(\varphi ,t)-\frac{1}{{\lambda }_M\left(P\right)}{K}_2\left(t\right)\hfill \\ \hfill & \le \hfill & {\int }_{\mathsf{\Phi }}{z}^T(\varphi ,t)\left[\Xi -2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\lambda }_m\left({\widehat{S}}^a\right)\otimes \left(P\widehat{X}{\widehat{E}}_a\right)\right]z(\varphi ,t)-\frac{1}{{\lambda }_M\left(P\right)}{K}_2\left(t\right),\hfill \end{array}$$

(43)

where $\Xi =I_{\varpi }\otimes \left[-2{\displaystyle \sum _{l=1}^N}\frac{P\widehat{G}}{{\alpha }_l^2}-2P\widehat{Y}+P\widehat{X}\acute{Q}\widehat{X}P+\Theta \right]$, ${\widehat{S}}^a=\mathrm{diag}({\widehat{s}}_1^a,{\widehat{s}}_2^a,\dots ,{\widehat{s}}_{\varpi }^a)$ and ${\widehat{s}}_m^a\in {\mathbb{R}}^{+}.$

Select sufficiently large ${\widehat{s}}_m^a$ such that

$$\begin{array}{c}{\lambda }_M(\Xi )-2{\displaystyle \sum _{a=1}^{\xi }}{b}_a{\lambda }_m\left({\widehat{S}}^a\right){\lambda }_m\left(P\widehat{X}{\widehat{E}}_a\right)\le -1.\end{array}$$

(44)

Moreover, we can obtain from (43) and (44) that

$$\begin{array}{c}{ }_0{D}_t^q{V}_2\left(t\right)+{\Vert z(·,t)\Vert }_2^2\le -\frac{K_2\left(t\right)}{{\lambda }_M\left(P\right)}.\end{array}$$

(45)

Similar to the proof from (24) to (30), we can obtain

$$\begin{array}{c}\underset{t\to +\infty }{lim}{∥z(·,t)∥}_2=0.\end{array}$$

(46)

Therefore, the network (32) can realize output synchronization under the adaptive controller (38). □

5. Numerical Examples

5.1. Example 1

Consider the following CFOMRDNNs with multiple output couplings:

$$\begin{array}{ccc}{ }_0{D}_t^{0.81}{u}_m(\varphi ,t)\hfill & =\hfill & G\frac{{\partial }^2{u}_m(\varphi ,t)}{\partial {\varphi }^2}-Y{u}_m(\varphi ,t)+Q\left(u_m(\varphi ,t)\right)f\left(u_m(\varphi ,t)\right)+C\hfill \\ \hfill & \hfill & +0.2{\displaystyle \sum _{n=1}^5}{H}_{mn}^1{\tilde{E}}_1{\epsilon }_n(\varphi ,t)+0.5{\displaystyle \sum _{n=1}^5}{H}_{mn}^2{\tilde{E}}_2{\epsilon }_n(\varphi ,t)\hfill \\ \hfill & \hfill & +0.3{\displaystyle \sum _{n=1}^5}{H}_{mn}^3{\tilde{E}}_3{\epsilon }_n(\varphi ,t)+v_m(\varphi ,t),\hfill \\ {\epsilon }_m(\varphi ,t)\hfill & =\hfill & X{u}_m(\varphi ,t),m=1,2,\dots ,5,\hfill \end{array}$$

(47)

where $\mathsf{\Phi }=\left\{\varphi \right|-0.5<\varphi <0.5\}$, $f_{\vartheta }\left(\eta \right)=\left(\right|\eta +1|-|\eta -1\left|\right)/8$, $\eta \in \mathbb{R},\vartheta =1,2,3,$$G=\mathrm{diag}(0.7,0.52,0.94,0.51),Y=\mathrm{diag}(0.27,0.42,0.16,0.38),C={(0.33,0.29,0.54,0.66)}^T$ and

$${\tilde{E}}_1=\left(\begin{array}{ccc}0.34& 0& 0\\ 0& 0.25& 0\\ 0& 0& 0.48\\ 0& 0& 0\end{array}\right),{\tilde{E}}_2=\left(\begin{array}{ccc}0.75& 0& 0\\ 0& 0.46& 0\\ 0& 0& 0.43\\ 0& 0& 0\end{array}\right),$$

$${\tilde{E}}_3=\left(\begin{array}{ccc}0.18& 0& 0\\ 0& 0.42& 0\\ 0& 0& 0.77\\ 0& 0& 0\end{array}\right),X=\left(\begin{array}{cccc}0.4& 0& 0& 0\\ 0& 0.55& 0& 0\\ 0& 0& 0.67& 0\end{array}\right),$$

$$\begin{array}{c}{H}^1=\left(\begin{array}{ccccc}-0.6& 0.1& 0& 0.5& 0\\ 0.1& -1.6& 0.8& 0.7& 0\\ 0& 0.8& -1.7& 0& 0.9\\ 0.5& 0.7& 0& -1.2& 0\\ 0& 0& 0.9& 0& -0.9\end{array}\right),\end{array}$$

$$\begin{array}{c}{H}^2=\left(\begin{array}{ccccc}-0.7& 0.2& 0& 0.5& 0\\ 0.2& -0.9& 0.5& 0.2& 0\\ 0& 0.5& -0.6& 0& 0.1\\ 0.5& 0.2& 0& -0.7& 0\\ 0& 0& 0.1& 0& -0.1\end{array}\right),\end{array}$$

$$\begin{array}{c}{H}^3=\left(\begin{array}{ccccc}-1.5& 0.4& 0& 1.1& 0\\ 0.4& -0.9& 0.3& 0.2& 0\\ 0& 0.3& -0.8& 0& 0.5\\ 1.1& 0.2& 0& -1.3& 0\\ 0& 0& 0.5& 0& -0.5\end{array}\right),\end{array}$$

$$\begin{array}{c}{\widehat{S}}^1=\left(\begin{array}{ccccc}0.26& 0& 0& 0& 0\\ 0& 0.26& 0& 0& 0\\ 0& 0& 0.27& 0& 0\\ 0& 0& 0& 0.22& 0\\ 0& 0& 0& 0& 0.19\end{array}\right),\end{array}$$

$$\begin{array}{c}{\widehat{S}}^2=\left(\begin{array}{ccccc}0.27& 0& 0& 0& 0\\ 0& 0.19& 0& 0& 0\\ 0& 0& 0.26& 0& 0\\ 0& 0& 0& 0.17& 0\\ 0& 0& 0& 0& 0.21\end{array}\right),\end{array}$$

$$\begin{array}{c}{\widehat{S}}^3=\left(\begin{array}{ccccc}0.23& 0& 0& 0& 0\\ 0& 0.22& 0& 0& 0\\ 0& 0& 0.21& 0& 0\\ 0& 0& 0& 0.25& 0\\ 0& 0& 0& 0& 0.15\end{array}\right),\end{array}$$

$$\begin{array}{ccc}\hfill q_{11}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.45,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill -0.3,|u_{m1}(\varphi ,t)|>1,\end{array}\right.& & q_{12}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.5,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill 0.46,|u_{m1}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{13}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.34,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill -0.18,|u_{m1}(\varphi ,t)|>1,\end{array}\right.& & q_{14}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.52,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill -0.38,|u_{m1}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{21}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.6,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill 0.38,|u_{m2}(\varphi ,t)|>1,\end{array}\right.& & q_{22}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.27,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill -0.33,|u_{m2}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{23}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.75,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill 0.66,|u_{m2}(\varphi ,t)|>1,\end{array}\right.& & q_{24}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.61,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill 0.67,|u_{m2}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{31}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.53,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill 0.39,|u_{m3}(\varphi ,t)|>1,\end{array}\right.& & q_{32}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.31,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill -0.44,|u_{m3}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{33}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.59,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill -0.74,|u_{m3}(\varphi ,t)|>1.\end{array}\right.& & q_{34}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.54,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill -0.47,|u_{m3}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{41}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.73,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill 0.46,|u_{m4}(\varphi ,t)|>1,\end{array}\right.& & q_{42}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.61,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill -0.28,|u_{m4}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{43}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.55,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill -0.38,|u_{m4}(\varphi ,t)|>1,\end{array}\right.& & q_{44}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.59,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill -0.74,|u_{m4}(\varphi ,t)|>1.\end{array}\right.\hfill \end{array}$$

Obviously, the function $f_{\vartheta }(·)(\vartheta =1,2,3)$ fulfills the Lipschitz condition with ${\theta }_{\vartheta }=0.25$. Based on Theorem 1, the network (47) attains output synchronization under the adaptive controller (12). Figure 1 displays the changing processes of norms of error vectors $z_m(·,t),m=1,2,\dots ,5$ in the networks (47). From Figure 1, it is clear that the norms of error vectors $z_m(·,t),m=1,2,\dots ,5$ can converge to 0, which reflects the effectiveness of the designed adaptive controller. Figure 2 depicts the change curves of the adaptive feedback gains $s_m^a\left(t\right)$ for the networks (47).

Figure 1. $\parallel z_m{(·,t)\parallel }_2,m=1,2,\dots ,5$.

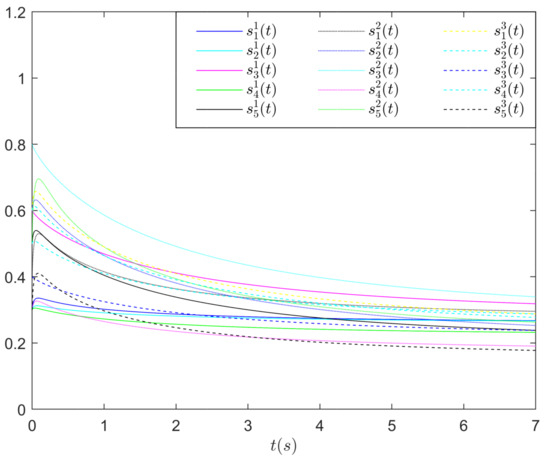
Figure 2. $s_m^a\left(t\right),m=1,2,\dots ,5,a=1,2,3$.

5.2. Example 2

Take into account the following CFOMRDNNs with multiple output derivative couplings:

$$\begin{array}{c}\begin{array}{cc}\hfill { }_0{D}_t^{0.95}{u}_m(\varphi ,t)=& G\frac{{\partial }^2{u}_m(\varphi ,t)}{\partial {\varphi }^2}-Y{u}_m(\varphi ,t)+Q\left(u_m(\varphi ,t)\right)f\left(u_m(\varphi ,t)\right)+C\hfill \\ \hfill & +0.4{\displaystyle \sum _{n=1}^5}{H}_{mn}^1{\tilde{E}}_1{ }_0{D}_t^{0.95}{\epsilon }_n(\varphi ,t)+0.5{\displaystyle \sum _{n=1}^5}{H}_{mn}^2{\tilde{E}}_2{ }_0{D}_t^{0.95}{\epsilon }_n(\varphi ,t)\hfill \\ \hfill & +0.6{\displaystyle \sum _{n=1}^5}{H}_{mn}^3{\tilde{E}}_3{ }_0{D}_t^{0.95}{\epsilon }_n(\varphi ,t)+v_m(\varphi ,t),\hfill \\ \hfill {\epsilon }_m(\varphi ,t)=& X{u}_m(\varphi ,t),m=1,2,\dots ,5,\hfill \end{array}\end{array}$$

(48)

where $\mathsf{\Phi }=\left\{\varphi \right|-0.5<\varphi <0.5\}$, $f_{\vartheta }\left(\eta \right)=\left(\right|\eta +1|-|\eta -1\left|\right)/8$, $\eta \in \mathbb{R},\vartheta =1,2,3,$$G=\mathrm{diag}(0.5,0.52,0.54,0.59),Y=\mathrm{diag}(0.47,0.42,0.46,0.38),C={(0.43,0.49,0.54,0.41)}^T$ and

$${\tilde{E}}_1=\left(\begin{array}{ccc}0.44& 0& 0\\ 0& 0.45& 0\\ 0& 0& 0.48\\ 0& 0& 0\end{array}\right),{\tilde{E}}_2=\left(\begin{array}{ccc}0.55& 0& 0\\ 0& 0.46& 0\\ 0& 0& 0.43\\ 0& 0& 0\end{array}\right),$$

$${\tilde{E}}_3=\left(\begin{array}{ccc}0.58& 0& 0\\ 0& 0.42& 0\\ 0& 0& 0.67\\ 0& 0& 0\end{array}\right),X=\left(\begin{array}{cccc}0.47& 0& 0& 0\\ 0& 0.55& 0& 0\\ 0& 0& 0.66& 0\end{array}\right),$$

$$H^1=\left(\begin{array}{ccccc}-0.53& 0& 0.23& 0.3& 0\\ 0& -0.55& 0& 0.23& 0.32\\ 0.23& 0& -0.44& 0& 0.21\\ 0.3& 0.23& 0& -0.63& 0.1\\ 0& 0.32& 0.21& 0.1& -0.63\end{array}\right),$$

$$H^2=\left(\begin{array}{ccccc}-0.5& 0.2& 0& 0.3& 0\\ 0.2& -0.75& 0.25& 0.3& 0\\ 0& 0.25& -0.55& 0& 0.3\\ 0.3& 0.3& 0& -0.6& 0\\ 0& 0& 0.3& 0& -0.3\end{array}\right),$$

$$H^3=\left(\begin{array}{ccccc}-0.4& 0.1& 0& 0.3& 0\\ 0.1& -0.45& 0.15& 0.2& 0\\ 0& 0.15& -0.55& 0& 0.4\\ 0.3& 0.2& 0& -0.5& 0\\ 0& 0& 0.4& 0& -0.4\end{array}\right),$$

$${\widehat{S}}^1=\left(\begin{array}{ccccc}0.5& 0& 0& 0& 0\\ 0& 0.6& 0& 0& 0\\ 0& 0& 0.6& 0& 0\\ 0& 0& 0& 0.6& 0\\ 0& 0& 0& 0& 0.7\end{array}\right),$$

$${\widehat{S}}^2=\left(\begin{array}{ccccc}0.4& 0& 0& 0& 0\\ 0& 0.7& 0& 0& 0\\ 0& 0& 0.6& 0& 0\\ 0& 0& 0& 0.5& 0\\ 0& 0& 0& 0& 0.5\end{array}\right),$$

$${\widehat{S}}^3=\left(\begin{array}{ccccc}0.5& 0& 0& 0& 0\\ 0& 0.6& 0& 0& 0\\ 0& 0& 0.4& 0& 0\\ 0& 0& 0& 0.7& 0\\ 0& 0& 0& 0& 0.5\end{array}\right),$$

$$\begin{array}{ccc}\hfill q_{11}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.55,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill -0.45,|u_{m1}(\varphi ,t)|>1,\end{array}\right.& & q_{12}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.46,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill -0.5,|u_{m1}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{13}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.48,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill 0.44,|u_{m1}(\varphi ,t)|>1,\end{array}\right.& & q_{14}\left(u_{m1}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.47,|u_{m1}(\varphi ,t)|\le 1,\\ \hfill 0.54,|u_{m1}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{21}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.48,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill -0.6,|u_{m2}(\varphi ,t)|>1,\end{array}\right.& & q_{22}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.53,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill 0.47,|u_{m2}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{23}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.66,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill -0.55,|u_{m2}(\varphi ,t)|>1,\end{array}\right.& & q_{24}\left(u_{m2}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.68,|u_{m2}(\varphi ,t)|\le 1,\\ \hfill -0.35,|u_{m2}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{31}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.49,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill 0.53,|u_{m3}(\varphi ,t)|>1,\end{array}\right.& & q_{32}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.44,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill -0.31,|u_{m3}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{33}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.51,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill 0.59,|u_{m3}(\varphi ,t)|>1.\end{array}\right.& & q_{34}\left(u_{m3}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.51,|u_{m3}(\varphi ,t)|\le 1,\\ \hfill -0.71,|u_{m3}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{41}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill 0.44,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill 0.63,|u_{m4}(\varphi ,t)|>1,\end{array}\right.& & q_{42}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.62,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill -0.53,|u_{m4}(\varphi ,t)|>1,\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q_{43}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.41,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill 0.58,|u_{m4}(\varphi ,t)|>1,\end{array}\right.& & q_{44}\left(u_{m4}(\varphi ,t)\right)=\left\{\begin{array}{c}\hfill -0.41,|u_{m4}(\varphi ,t)|\le 1,\\ \hfill -0.63,|u_{m4}(\varphi ,t)|>1.\end{array}\right.\hfill \end{array}$$

Evidently, the function $f_{\vartheta }(·)(\vartheta =1,2,3)$ satisfies the Lipschitz condition with ${\theta }_{\vartheta }=0.25$. From the Theorem 2, it is found that the network (48) is output synchronized under the adaptive controller (38). From Figure 3, we can see the norms of error vectors $z_m(·,t),m=1,2,\dots ,5$ can converge to 0, which reflects the designed adaptive output feedback controller in the networks (48) is effective. Figure 4 shows the change curves of the adaptive feedback gains $s_m^a\left(t\right)$ for the networks (48).

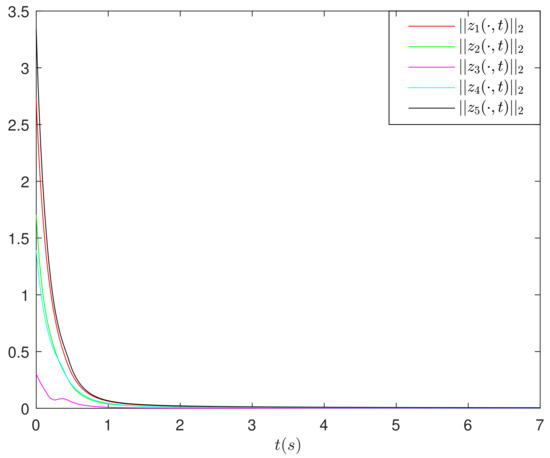
Figure 3. $\parallel z_m{(·,t)\parallel }_2,m=1,2,\dots ,5$.

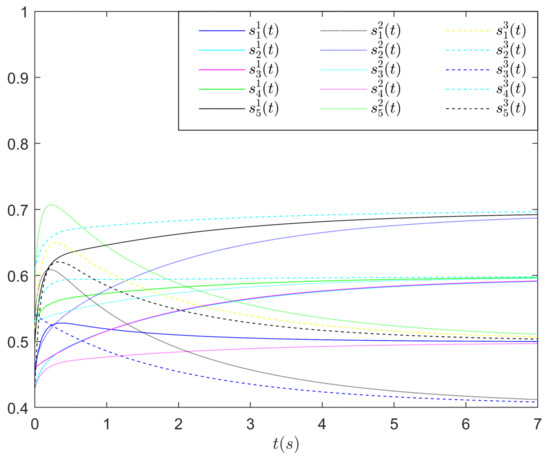
Figure 4. $s_m^a\left(t\right),m=1,2,\dots ,5,a=1,2,3$.

6. Conclusions

In this article, two types of CFOMRDNNs with multiple output couplings or multiple output derivative couplings have been presented. We have addressed the problem of output synchronization of CFOMRDNNs with multiple output couplings with the assistance of the inverse Laplace transform and the properties of Mittag–Leffler function. Taking into account the effect of derivative coupling, the output synchronization of CFOMRDNNs with multiple output derivative couplings has been further studied by employing adaptive control strategy. At last, two numerical examples have substantiated the effectiveness of the derived output synchronization criteria.