Positive Solution Pairs for Coupled p-Laplacian Hadamard Fractional Differential Model with Singular Source Item on Time Variable

Abstract

The mathematical theories and methods of fractional calculus are relatively mature, which have been widely used in signal processing, control systems, nonlinear dynamics, financial models, etc. The studies of some basic theories of fractional differential equations can provide more understanding of mechanisms for the applications. In this paper, the expression of the Green function as well as its special properties are acquired and presented through theoretical analyses. Subsequently, on the basis of these properties of the Green function, the existence and uniqueness of positive solutions are achieved for a singular p-Laplacian fractional-order differential equation with nonlocal integral and infinite-point boundary value systems by using the method of a nonlinear alternative of Leray–Schauder-type Guo–Krasnoselskii’s fixed point theorem in cone, and the Banach fixed point theorem, respectively. Some existence results are obtained for the case in which the nonlinearity is allowed to be singular with regard to the time variable. Several examples are correspondingly provided to show the correctness and applicability of the obtained results, where nonlinear terms are controlled by the integrable functions ${\displaystyle \frac{1}{\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}}$ and ${\displaystyle \frac{1}{\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}}$ in Example 1, and by the integrable functions $\theta ,\overline{\theta }$ and $\phi \left(v\right),\psi \left(u\right)$ in Example 2, respectively. The present work may contribute to the improvement and application of the coupled p-Laplacian Hadamard fractional differential model and further promote the development of fractional differential equations and fractional differential calculus.

1. Introduction

The p-Laplacian differential equation was first introduced by Leibenson [1] when he studied the turbulent flow in a porous medium. Later, differential equations containing p-Laplace operators have been widely used in many fields such as non-Newtonian mechanics, cosmic physics, plasma problems and elasticity theory [1,2,3,4,5,6]. The p-Laplacian operator $L_p$ is defined as $L_p\left(s\right)={\left|s\right|}^{p-2}s,p,q>1,{\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$. For recent developments in this regard, see [7,8,9,10,11].

Recently, more and more researchers have dedicated their research to the existence and number of solutions of fractional differential equations and the corresponding nonlinear deformation, flexural wave and vibration, and the coupled problem, which can be referred to in [2,4,12,13,14,15,16,17,18,19,20,21]. There are many approaches to studying fractional differential equations, such as the mixed monotone operator method [10], Banach’s fixed point theorem [22], Leray–Schauder’s alternative method [23,24], Hussein–Jassim’s method [25], the comparison principle method [26] and so on. In recent years, some scientists have devoted themselves to studying the Hadamard fractional differential equation as well as related nonlinear dynamical differential systems [6,22,26,27,28,29,30,31,32,33]. The Hadamard fractional derivative of $\nu$($\nu >0$) order of a continuous function $\mathsf{\Psi }:(0,\infty )\to {\mathbb{R}}_{+}^1$ is given by

$${}^H\mathcal{D}_{1^{+}}^{\nu }\hslash \left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(n-\nu )}}{\left(t{\displaystyle \frac{d}{dt}}\right)}^n{\int }_1^t{\displaystyle \frac{\mathsf{\Psi }\left(s\right)}{s{\left(ln\frac{t}{s}\right)}^{\nu -n+1}}}ds,$$

where $n=\left[\alpha \right]+1,\left[\alpha \right]$ denotes the integer part of the number $\alpha$, provided that the right-hand side is pointwise defined on $(0,\infty )$. The Hadamard fractional integral of $\nu$($\nu >0$) order of a function $\mathsf{\Psi }:(0,\infty )\to {\mathbb{R}}_{+}^1$ is given by

$${}^{H}I_{1^{+}}^{\nu }\hslash \left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}{\int }_1^t{(ln{\displaystyle \frac{t}{s}})}^{\nu -1}{\displaystyle \frac{\mathsf{\Psi }\left(s\right)}{s}}ds.$$

In order to better guide the practice, a large number of workers are devoted to the basic theoretical research of fractional differential equations, among which the structure of Hadamard fractional differential equations is one of them. It has been noticed that some of the structure of fractional differential equations is based on Hadamard fractional differential equations. In [18], the authors discussed the following Hadamard fractional equations:

$$\begin{array}{l}{}^{H}D_{1^{+}}^{q}u\left(t\right)+\mathcal{F}(t,u\left(t\right),v\left(t\right))=0,1<t<e,\\ {}^{H}D_{1^{+}}^{q}v\left(t\right)+\overline{\mathcal{F}}(t,u\left(t\right),v\left(t\right))=0,1<t<e,\end{array}$$

with the following multi-point boundary conditions:

$$\begin{array}{l}u\left(1\right)=\delta u\left(1\right)=0,u\left(e\right)={\displaystyle \sum _{j=1}^{m-1}}{a}_{j}u\left({\xi }_j\right),\\ v\left(1\right)=\delta v\left(1\right)=0,v\left(e\right)={\displaystyle \sum _{j=1}^{m-1}}{b}_{j}u\left({\eta }_j\right),\end{array}$$

where $q\in (2,3]$ is a real number, and ${}^{H}D_{1^{+}}^{q}u$ is the standard Hadamard fractional derivative. $a_i,b_j\ge 0,{\xi }_i,{\eta }_j\in (1,e)$ with ${\sum }_{i=1}^{m-1}{a}_i{(log{\xi }_i)}^{q-1}\in [0,1)$, and ${\sum }_{j=1}^{m-1}{b}_j{(log{\eta }_j)}^{q-1}\in [0,1)$; $\mathcal{F},\overline{\mathcal{F}}\in C([1,e]\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+},{\mathbb{R}}^{+})$$({\mathbb{R}}^{+}=[0,+\infty )).$ The authors obtained a triple positive solution and a nontrivial solution by a fixed point theorem and through the relationship between nonlinear and linear operators. Ardjouni [15] studied the following Hadamard fractional differential equations:

$${}^{H}D_{1^{+}}^{\alpha }u\left(t\right)+\varphi (t,u\left(t\right))={}^{H}D_{1^{+}}^{\beta }\phi (t,u\left(t\right)),1<t<e,$$

with integral boundary conditions:

$$u\left(1\right)=0,u\left(e\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(\alpha -\beta )}}{\int }_1^e{(log{\displaystyle \frac{e}{s}})}^{\alpha -\beta -1}g(s,x\left(s\right)){\displaystyle \frac{ds}{s}},$$

where $1<\alpha \le 2,0<\beta \le \alpha -1,$$\phi ,\varphi :[1,e]\times [0,\infty )\to [0,\infty )$ are given as continuous functions, $\varphi$ does not require any monotone assumption and $\phi$ is non-decreasing on x. The authors obtained the existence and uniqueness of the positive solution by the method of upper and lower solutions and Schauder and Banach fixed point theorems. In [34], we consider the following singular Hadamard fractional differential equation:

$${}^{H}D_{1^{+}}^{\alpha }\left({\phi }_p\left({}^{H}D_{1+}^{\gamma }u\right)\right)\left(t\right)+\hslash (t,u\left(t\right),{}^{H}D_{1^{+}}^{\mu }u\left(t\right))=0,1<t<e,$$

with the infinite-point boundary condition:

$$\begin{array}{l}{u}^{(j+\mu )}\left(1\right)=0,j=0,1,2,\dots ,n-2{;}^H{D}_{1^{+}}^{r_1}u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_j^H{D}_{1^{+}}^{r_2}u\left({\xi }_j\right),\\ {}^{H}D_{1^{+}}^{\gamma }u\left(1\right)=0;{\phi }_p\left({}^{H}D_{1^{+}}^{\gamma }u\left(e\right)\right)={\displaystyle \sum _{j=1}^{\infty }}{\zeta }_j{\phi }_p\left({}^{H}D_{1^{+}}^{\gamma }u\left({\xi }_j\right)\right),\end{array}$$

where $\alpha ,\gamma ,\mu \in {\mathbb{R}}^{+}=[0,+\infty )$; $1<\alpha \le 2$, $n<\gamma \le n+1(n\ge 3)$; $r_1,r_2\in [2,n-2]$; $r_2\le r_1$; the p-Laplacian operator ${\phi }_p$ is defined as ${\phi }_p\left(s\right)={\left|s\right|}^{p-2}s,p,q>1,{\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1, 0<\mu \le n-2$ and $0<{\eta }_i, {\zeta }_i<1, 1<{\xi }_i<e(i=1,2,\dots ,\infty )$; $\hslash \in C((1,e)\times {\mathbb{R}}_{+}^1\times {\mathbb{R}}_{+}^1)({\mathbb{R}}_{+}^1=[0,+\infty ))$ and may be singular at $t=1,e$; and ${}^{H}D_{1^{+}}^{\alpha }u,{}^{H}D_{1^{+}}^{\gamma }u,{}^{H}D_{1^{+}}^{\mu }u$, ${}^{H}D_{1^{+}}^{r_i}u(i=1,2)$ are the standard Hadamard fractional derivatives. The existence of positive solutions is investigated by spectral analysis by us. For the portion of the research results that include the fractional differential systems and the corresponding nonlinear deformation, flexural wave and vibration, please refer to [4,15,16,17,18,19,20,21,35].

Motivated by the excellent results above, we consider the following Hadamard fractional differential system (HFDS):

$$\begin{array}{l}{L}_{p_1}{(}^H{D}_{1^{+}}^{\nu }u\left(t\right))+\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(t\right))=0,1<t<e,\\ L_{p_2}{(}^H{D}_{1^{+}}^{\iota }v\left(t\right))+\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(t\right))=0,1<t<e,\end{array}$$

(1)

with nonlocal integral and infinite-point boundary conditions:

$$\begin{array}{l}{u}^{\left(i\right)}\left(1\right)=0,i=0,1,2,\dots ,n-2,u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_{j}u\left({\xi }_j\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\\ v^{\left(j\right)}\left(1\right)=0,i=0,1,2,\dots ,m-2,v\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\overline{\eta }}_{j}v\left({\overline{\xi }}_j\right)+{\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right),\end{array}$$

(2)

where $n-1<\nu \le n,m-1<\iota \le m,0<\varsigma <max\{\nu -1,\iota -1\}$; the p-Laplacian operator $L_{p_i}$ is defined as $L_{p_i}\left(s\right)={\left|s\right|}^{p_i-2}s,p_i,q_i>1,{\displaystyle \frac{1}{p_i}}+{\displaystyle \frac{1}{q_i}}=1(i=1,2)$; ${\eta }_j,{\overline{\eta }}_j\ge 0,$ $1<{\xi }_j<e, 1<{\overline{\xi }}_j<e(j=1,2\cdots )$ are parameters; $B,\overline{B}$ are functions of bounded variation; $h\left(t\right),\overline{h}\left(t\right)\in L^1(1,e)$${\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)$ and ${\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right)$ denote the Riemann–Stieltjes integral with respect to $B\left(t\right)$ and $\overline{B}\left(t\right)$; $\mathcal{F},\overline{\mathcal{F}}\in C((1,e)\times {(0,+\infty )}^2,{\mathbb{R}}_{+}^1))$ and $\mathcal{F}(t,x_1,x_2),$$\overline{\mathcal{F}}(t,x_1,x_2)$ have singularity at $t=1,e$; and ${}^{H}D_{1^{+}}^{\nu }u,$${}^{H}D_{1^{+}}^{\iota }u$ are the standard Hadamard fractional derivatives.

In this paper, we investigate the existence of positive solutions for a singular infinite-point coupled p-Laplacian boundary value system. Compared with [18,19], the nonlinear term is singular in regard to time variable in this study, fractional derivatives are involved in the nonlinear terms and infinite point is involved in boundary conditions for HFDS (1) and (2). However, the nonlinear term is continuous in the studies [18,19] and the nonlinear terms of reference [18,19] do not contain derivative terms. Compared with [19,36,37], the equation in this paper is a p-Laplacian boundary value system which is a great extension from the general fractional differential equation. Compared with the references, on the one hand, the equations we study are complex and the singular form of nonlinearity can simulate more complex systems; on the other hand, we obtain the existence and uniqueness of the solutions to the equations.

This paper is organized as follows: In Section 1, we explain the research background and necessity of studying such a fractional differential equation in the Introduction section. In Section 2, we introduce some definitions and lemmas which will be used later, and give the expression of the theorem of the Green function, provide the nature of the theorem of Green function, and prove the continuity and total continuity of operators. In Section 3, we obtain the main results by using the method of a nonlinear alternative of Leray–Schauder-type, Guo–Krasnoselskii’s fixed point theorem in cone and the Banach fixed point theorem, respectively. In Section 4, we list three examples to illustrate the validity of the proposed theories. Finally, we summarize some conclusions with the current shortcomings and future research plans in Section 5.

2. Preliminaries and Lemmas

With respect to some essential definitions and lemmas of fractional calculus of the Hadamard type, the reader may consult the recent bibliography such as those in [5,38,39]. Only the parts are listed here.

For convenience in terms of presentation, we list herein some conditions to be used throughout the paper.

$\left(H_0\right)$: $\mathcal{F},\overline{\mathcal{F}}:(1,e)\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, and there exists a function $\theta \left(t\right),\overline{\theta }\left(t\right):(1,e)\to {\mathbb{R}}^{+}$ such that $\mathcal{F}(t,x_0,x_1)\le \theta \left(t\right),\overline{\mathcal{F}}(t,x_0,x_1)\le \overline{\theta }\left(t\right)$ for $\forall (x_0,x_1)\in E\times E$, and

$${\int }_1^e{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}<+\infty ,{\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}<+\infty .$$

$\left(H_1\right)$

$${\int }_1^{e}h\left(t\right){(lnt)}^{\alpha -1}dB\left(t\right)<+\infty ,{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\beta -1}d\overline{B}\left(t\right)<+\infty .$$

Lemma 1 

([3,5]). If $\nu ,\iota >0$, then

$${}^{H}I_{1^{+}}^{\nu }{(lnx)}^{\iota -1}={\displaystyle \frac{\mathsf{\Gamma }\left(\iota \right)}{\mathsf{\Gamma }(\iota +\nu )}}{\left(lnx\right)}^{\iota +\nu -1},{}^H\mathcal{D}_{1^{+}}^{\nu }{(lnx)}^{\iota -1}={\displaystyle \frac{\mathsf{\Gamma }\left(\iota \right)}{\mathsf{\Gamma }(\iota -\nu )}}{\left(lnx\right)}^{\iota -\nu -1}.$$

Lemma 2 

([3]). Suppose that $\nu >0$ and $\mathsf{\Psi }\in C[0,\infty )\cap L^1[0,\infty )$, then the solution of Hadamard fractional differential equation ${}^H\mathcal{D}_{1^{+}}^{\nu }\mathsf{\Psi }\left(t\right)=0$ is

$$\mathsf{\Psi }\left(t\right)={\kappa }_1{(lnt)}^{\nu -1}+{\kappa }_2{(lnt)}^{\nu -2}+\cdots +{\kappa }_n{(lnt)}^{\nu -n},{\kappa }_i\in \mathbb{R}(i=0,1,\cdots ,n),n=\left[\nu \right]+1.$$

Lemma 3 

([3]). Suppose that $\nu >0,\nu$ is not a natural number, $\mathsf{\Psi }\in C[1,\infty )\cap L^1[1,\infty )$, then

$$\mathsf{\Psi }\left(t\right){=}^H{I}_{1^{+}}^{\nu }{}^H\mathcal{D}_{1^{+}}^{\nu }\hslash \left(t\right)+\sum _{k=1}^n{\kappa }_k{(lnt)}^{\nu -k},$$

for $t\in (1,e]$, where ${\kappa }_k\in \mathbb{R}(k=1,2,\cdots ,n),$ and $n=\left[\nu \right]+1$.

Lemma 4. 

Let E be a real Banach space, and $P\subset E$ be a cone. Let ${\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2$ be two bounded open subsets in E such that $\theta \in {\mathsf{\Omega }}_1$ and ${\overline{\mathsf{\Omega }}}_1\subset {\mathsf{\Omega }}_2$. Let the operator $T:({\overline{\mathsf{\Omega }}}_2\setminus {\mathsf{\Omega }}_1)\cap P\to P$ be completely continuous. Suppose that one of the conditions is as follows:

(i) 

If $\parallel Tx\parallel \le \parallel x\parallel ,\forall x\in P\cap \partial {\mathsf{\Omega }}_1$, $\parallel Tx\parallel \ge \parallel x\parallel$ for all $x\in P\cap \partial {\mathsf{\Omega }}_2$;

(ii) 

If $\parallel Tx\parallel \ge \parallel x\parallel ,\forall x\in P\cap \partial {\mathsf{\Omega }}_1$, $\parallel Tx\parallel \le \parallel x\parallel$ for all $x\in P\cap \partial {\mathsf{\Omega }}_2$ holds, then T has a fixed point in $({\overline{\mathsf{\Omega }}}_2\setminus {\mathsf{\Omega }}_1)\cap P.$

Lemma 5. 

Let E be a Banach space and $\mathsf{\Omega }\subset E$ be closed and convex. Assume U is a relatively open subset of Ω with $\theta \in U$, and let operator $A:\overline{U}\to \mathsf{\Omega }$ be a continuous compact map. Then, either one of the following occurs:

(1) 

A has a fixed point in U;

(2) 

There exists $u\in \partial U$ and $\phi \in (0,1)$ with $u=\phi Au.$

Lemma 6 

([40], Theorem 1.2.7). Let $\mathsf{\Theta }\subset C^1[J,E]$, then Θ is a relatively compact set if and only if the following are true:

(a) 

${\mathsf{\Theta }}^{\prime }$ is equicontinuous and ${\mathsf{\Theta }}^{\prime }\left(t\right)$ is a relatively compact set for any $t\in J$ on E;

(b) 

There exists $t_0\in J$ such that $\mathsf{\Theta }\left(t_0\right)$ is a relatively compact set on $E.$

Now, we consider the following linear fractional differential equations.

Theorem 1. 

Given $y,\overline{y}\in L^1(1,e)\cap C(1,e)$, then the liner HFDE problems

$$\left\{\begin{array}{l}{L}_{p_1}{(}^H{D}_{1^{+}}^{\nu }u\left(t\right))+y\left(t\right)=0,1<t<e,\\ u^{\left(j\right)}\left(1\right)=0,j=0,1,2,\cdots ,n-2;u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_{j}u\left({\xi }_j\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\end{array}\right.$$

(3)

$$\left\{\begin{array}{l}{L}_{p_2}\left(D_{1^{+}}^{\iota }v\left(t\right)\right)+\overline{y}\left(t\right)=0,1<t<e,\\ v^{\left(j\right)}\left(1\right)=0,j=0,1,2,\cdots ,m-2;v\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\overline{\eta }}_{j}v\left({\overline{\xi }}_j\right)+{\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right)\end{array}\right.$$

(4)

have integral representation

$$\begin{array}{l}u\left(t\right)={\int }_1^e\mathcal{G}(t,s){\displaystyle \frac{{\phi }_{q_1}\left(y\left(s\right)\right)}{s}}ds,\\ v\left(t\right)={\int }_1^e\mathcal{H}(t,s){\displaystyle \frac{{\phi }_{q_2}\left(\overline{y}\left(s\right)\right)}{s}}ds,\end{array}$$

(5)

where

$$\mathcal{G}(t,s)={\mathcal{G}}_1(t,s)+{\mathcal{G}}_2(t,s),$$

$$\mathcal{H}(t,s)={\mathcal{H}}_1(t,s)+{\mathcal{H}}_2(t,s),$$

in which

$${\mathcal{G}}_1(t,s)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\left\{\begin{array}{ll}\mathcal{P}\left(s\right)\mathsf{\Gamma }\left(\nu \right){(lnt)}^{\nu -1}{(ln{\displaystyle \frac{e}{s}})}^{\nu -1}-\mathsf{\Delta }{(ln{\displaystyle \frac{t}{s}})}^{\nu -1},& 1\le s\le t\le e,\\ \mathcal{P}\left(s\right)\mathsf{\Gamma }\left(\nu \right){(lnt)}^{\nu -1}{(ln{\displaystyle \frac{e}{s}})}^{\nu -1},& 1\le t\le s\le e,\end{array}\right.$$

(6)

$${\mathcal{G}}_2(t,s)={\displaystyle \frac{{(lnt)}^{\nu -1}}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){\mathcal{G}}_1(t,s)dB\left(t\right),$$

(7)

$${\mathsf{\Delta }}_1=\mathsf{\Delta }-{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right),\mathsf{\Delta }=1-\sum _{i=1}^{\infty }{\eta }_j{(ln{\xi }_j)}^{\nu -1},$$

$$\mathcal{P}\left(s\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\sum _{j=1}^{\infty }{\eta }_j{\left({\displaystyle \frac{ln{\xi }_j-lns}{lne-lns}}\right)}^{\nu -1},$$

$${\mathcal{H}}_1(t,s)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\left\{\begin{array}{ll}{(lnt)}^{\iota -1}{(ln{\displaystyle \frac{e}{s}})}^{\iota -1}-\overline{\mathsf{\Delta }}{(ln{\displaystyle \frac{t}{s}})}^{\iota -1},& 1\le s\le t\le e,\\ {(lnt)}^{\iota -1}{(ln{\displaystyle \frac{e}{s}})}^{\iota -1},& 1\le t\le s\le e,\end{array}\right.$$

(8)

$${\mathcal{H}}_2(t,s)={\displaystyle \frac{{(lnt)}^{\iota -1}}{{\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){{\mathcal{H}}_{\mathcal{1}}}_1(t,s)d\overline{B}\left(t\right),$$

(9)

$${\overline{\mathsf{\Delta }}}_1=\overline{\mathsf{\Delta }}-{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right),\overline{\mathsf{\Delta }}=1-\sum _{i=1}^{\infty }{\overline{\eta }}_j{(ln{\xi }_j)}^{\iota -1},$$

$$\overline{\mathcal{P}}\left(s\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\sum _{j=1}^{\infty }{\overline{\eta }}_j{\left({\displaystyle \frac{ln{\xi }_j-lns}{lne-lns}}\right)}^{\iota -1}.$$

Proof. 

By using Lemma 3, Equation (3) can be reduced to an equivalent integral equation:

$$u\left(t\right)={-}^H{I}_{1^{+}}^{\nu }{L}_{q_1}\left(y\left(t\right)\right)+{\kappa }_1{(lnt)}^{\nu -1}+{\kappa }_2{(lnt)}^{\nu -2}+\cdots +{\kappa }_n{(lnt)}^{\nu -n},$$

for some ${\kappa }_1,{\kappa }_2,\cdots ,{\kappa }_n\in {\mathbb{R}}^1.$ Via $u\left(1\right)=0$ of (2), one has ${\kappa }_n=0$, then

$$u^{\prime }\left(t\right)={-}^H{I}_{1^{+}}^{\nu -1}{L}_{q_1}\left(y\left(t\right)\right)+{\kappa }_1(\nu -1){(lnt)}^{\nu -2}{\displaystyle \frac{1}{t}}+{\kappa }_2(\nu -2){(lnt)}^{\nu -3}{\displaystyle \frac{1}{t}}+\dots ,$$

by means of $u^{\prime }\left(t\right)=0$, one obtains ${\kappa }_{n-1}=0$; by the same means, one arrives at ${\kappa }_2={\kappa }_3=\dots ={\kappa }_{n-2}=0$, and then

$$u\left(t\right)=-{\int }_1^t{\displaystyle \frac{{(ln\frac{t}{s})}^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)}}{\displaystyle \frac{L_{q_1}\left(y\left(s\right)\right)}{s}}ds+{\kappa }_1{(lnt)}^{\nu -1}.$$

(10)

By simple calculation, we have

$$u\left(e\right)={-}^H{I}_{1^{+}}^{\nu }{L}_{q_1}\left(y\left(e\right)\right)+{\kappa }_1.$$

(11)

Substituting (11) into $u\left(e\right)={\sum }_{j=1}^{\infty }{\eta }_{j}u\left({\xi }_j\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)$, we have

$$\begin{array}{ll}{\kappa }_1{-}^H{I}_{1^{+}}^{\nu }{L}_{q_1}\left(y\left(e\right)\right)=& {\displaystyle \sum _{i=1}^{\infty }}{\eta }_j\left(C_1{(ln{\xi }_j)}^{\nu -1}{-}^H{I}_{1^{+}}^{\nu }{L}_{q_1}\left(y\left({\xi }_j\right)\right)\right)\\ & +{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\end{array}$$

then

$$\begin{array}{l}{\kappa }_1={\int }_1^e{\displaystyle \frac{{(lne-lns)}^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)\mathsf{\Delta }}}{L}_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}-{\displaystyle \sum _{j=1}^{\infty }}{\eta }_j{\int }_1^{{\xi }_j}{\displaystyle \frac{{(ln{\xi }_j-lns)}^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)\mathsf{\Delta }}}{L}_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}\hspace{1em}+{\displaystyle \frac{1}{\mathsf{\Delta }}}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)\\ \hspace{1em}={\int }_1^e{\displaystyle \frac{{(lne-lns)}^{\nu -1}\mathcal{P}\left(s\right)}{\mathsf{\Delta }}}{L}_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}+{\displaystyle \frac{1}{\mathsf{\Delta }}}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right).\end{array}$$

(12)

Incorporating (12) into (10), one has

$$\begin{array}{l}u\left(t\right)=-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}{\int }_1^t{(ln{\displaystyle \frac{t}{s}})}^{\nu -1}{\displaystyle \frac{L_{q_1}\left(y\left(s\right)\right)}{s}}ds\\ \hspace{1em}\hspace{1em}+{(lnt)}^{\nu -1}{\displaystyle \frac{\frac{1}{\mathsf{\Gamma }\left(\nu \right)}{\int }_1^e{(ln\frac{e}{s})}^{\nu -1}\frac{L_{q_1}\left(y\left(s\right)\right)}{s}ds-{\sum }_{i=1}^{\infty }{\eta }_j\frac{1}{\mathsf{\Gamma }\left(\nu \right)}{\int }_1^{{\xi }_j}ln{\left(\frac{{\xi }_j}{s}\right)}^{\nu -1}\frac{L_{q_1}\left(y\left(s\right)\right)}{s}ds}{\mathsf{\Delta }}}\\ \hspace{1em}\hspace{1em}+{\displaystyle \frac{{(lnt)}^{\nu -1}}{\mathsf{\Delta }}}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)\\ \hspace{1em}={\int }_1^e\mathcal{G}(t,s){\displaystyle \frac{L_{q_1}\left(y\left(s\right)\right)}{s}}ds+{\displaystyle \frac{{(lnt)}^{\nu -1}}{\mathsf{\Delta }}}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right).\end{array}$$

(13)

Multiplying Equation (13) by $h\left(t\right)$ and the Riemann–Stieltjes integral from 1 to e, one arrives at

$$\begin{array}{ll}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)=& {\int }_1^{e}h\left(t\right)\left[{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}\right]dB\left(t\right)\\ & +{\displaystyle \frac{{\int }_1^{e}h\left(t\right){(lnt)}^{\alpha -1}dB\left(t\right)}{\mathsf{\Delta }}}{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right);\end{array}$$

hence,

$${\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right)={\displaystyle \frac{\mathsf{\Delta }}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right)\left[{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}\right]dB\left(t\right),$$

and then,

$$\begin{array}{ll}u\left(t\right)& ={\int }_1^e{\mathcal{G}}_1(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}+{\displaystyle \frac{{(lnt)}^{\nu -1}}{\mathsf{\Delta }}}{\displaystyle \frac{\mathsf{\Delta }}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right)\left[{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}\right]dB\left(t\right)\\ & ={\int }_1^e{\mathcal{G}}_1(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}+{\int }_1^e{\mathcal{G}}_2(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & ={\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(y\left(s\right)\right){\displaystyle \frac{ds}{s}},\end{array}$$

where $\mathcal{G}(t,s),{\mathcal{G}}_1(t,s),{\mathcal{G}}_2(t,s),\mathsf{\Delta },{\mathsf{\Delta }}_1$ are as (5)–(7). Moreover, by simple calculation, one arrives at

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s){=}^H{D}_{1^{+}}^{\varsigma }{\mathcal{G}}_1(t,s)+{\displaystyle \frac{\mathsf{\Gamma }\left(\nu \right)}{{\mathsf{\Delta }}_1\mathsf{\Gamma }(\nu -\varsigma )}}{(lnt)}^{\nu -1-\varsigma }{\int }_1^{e}h\left(t\right){\mathcal{G}}_1(t,s)dB\left(t\right),.$$

(14)

and

$${}^{H}D_{1^{+}}^{\mu }{\mathcal{G}}_1(t,s)={\displaystyle \frac{1}{\mathsf{\Delta }\mathsf{\Gamma }(\nu -\mu )}}\left\{\begin{array}{l}\mathcal{P}\left(s\right)\mathsf{\Gamma }\left(\nu \right){(lnt)}^{\nu -1-\varsigma }{(ln{\displaystyle \frac{e}{s}})}^{\nu -1}-\mathsf{\Delta }{(ln{\displaystyle \frac{t}{s}})}^{\nu -1-\varsigma },1\le s\le t\le e,\\ \mathcal{P}\left(s\right)\mathsf{\Gamma }\left(\nu \right){(lnt)}^{\nu -1-\varsigma }{(ln{\displaystyle \frac{e}{s}})}^{\nu -1},1\le t\le s\le e.\end{array}\right.$$

Similarly, when one has (8) and (9), we omit the detail here. Moreover, one arrives at

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s){=}^H{D}_{1^{+}}^{\varsigma }{\mathcal{H}}_1(t,s)+{\displaystyle \frac{\mathsf{\Gamma }\left(\iota \right)}{{\mathsf{\Delta }}_1\mathsf{\Gamma }(\iota -\varsigma )}}{(lnt)}^{\iota -1-\varsigma }{\int }_1^e\overline{h}\left(t\right){\mathcal{H}}_1(t,s)dB\left(t\right),$$

(15)

and

$${}^{H}D_{1^{+}}^{\varsigma }{\mathcal{H}}_1(t,s)={\displaystyle \frac{1}{\overline{\mathsf{\Delta }}\mathsf{\Gamma }(\iota -\varsigma )}}\left\{\begin{array}{l}{(lnt)}^{\iota -1-\varsigma }{(ln{\displaystyle \frac{e}{s}})}^{\iota -1}-\overline{\mathsf{\Delta }}{(ln{\displaystyle \frac{t}{s}})}^{\iota -1-\varsigma },\\ 1\le s\le t\le e,\\ {(lnt)}^{\iota -1-\varsigma }{(ln{\displaystyle \frac{e}{s}})}^{\iota -1},1\le t\le s\le e.\end{array}\right.$$

□

Theorem 2. 

The functions $\mathcal{G}(t,s)$, ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)$, $\mathcal{H}(t,s)$, and ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)$ given by (5) have the following properties:

(1) $\mathcal{G}(t,s)$, ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)$, $\mathcal{H}(t,s)$, and ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)$ are uniformly continuous on $[1,e]\times [1,e];$

(2)

$$\mathcal{G}(t,s)\le {\mathcal{G}}_1(e,s)\mathsf{{\rm Y}},\mathcal{G}(t,s)\ge {(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)\overline{\mathsf{{\rm Y}}},$$

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s){\le }^H{D}_{1^{+}}^{\varsigma }{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(t,s)\ge {(lnt)}^{\nu -\varsigma -1}{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{G}}_1(e,s)\overline{\mathsf{{\rm Y}}},$$

where

$$\mathsf{{\rm Y}}=1+{\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right)dB\left(t\right),\overline{\mathsf{{\rm Y}}}=1+{\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right);$$

(3)

$$\mathcal{H}(t,s)\le {\mathcal{H}}_1(e,s)\mathsf{\Xi },\mathcal{H}(t,s)\ge {(lnt)}^{\iota -1}{\mathcal{H}}_1(e,s)\overline{\mathsf{\Xi }},$$

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s){\le }^H{D}_{1^{+}}^{\varsigma }{\mathcal{H}}_1(e,s)\mathsf{{\rm Y}}{,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(t,s)\ge {(lnt)}^{\iota -\varsigma -1}{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{H}}_1(e,s)\overline{\mathsf{{\rm Y}}},$$

where

$$\mathsf{\Xi }=1+{\displaystyle \frac{{(lnt)}^{\iota -1}}{{\mathsf{\Delta }}_1}}{\int }_1^e\overline{h}\left(t\right)d\overline{B}\left(t\right),\overline{\mathsf{\Xi }}=1+{\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right).$$

Proof. 

(1) It is easy to check whether $\mathcal{G}(t,s)$, ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)$, $\mathcal{H}(t,s)$ and ${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)$ have uniformly continuous properties on $[1,e]\times [1,e].$

(2) By a similar method with [41], for $t,s\in [1,e]$, we obtain

$${(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)\le {\mathcal{G}}_1(t,s)\le {\mathcal{G}}_1(e,s);$$

hence, we have

$$\begin{array}{ll}\mathcal{G}(t,s)& ={\mathcal{G}}_1(t,s)+{\mathcal{G}}_2(t,s)\\ & \le {\mathcal{G}}_1(e,s)+{\displaystyle \frac{{(lnt)}^{\alpha -1}}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){\mathcal{G}}_1(e,s)dB\left(t\right)\\ & ={\mathcal{G}}_1(e,s)(1+{\displaystyle \frac{{(lnt)}^{\alpha -1}}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right)dB\left(t\right))={\mathcal{G}}_1(e,s)\mathsf{{\rm Y}},\end{array}$$

$$\begin{array}{ll}\mathcal{G}(t,s)& ={\mathcal{G}}_1(t,s)+{\mathcal{G}}_2(t,s)\\ & ={\mathcal{G}}_1(t,s)+{\displaystyle \frac{{(lnt)}^{\nu -1}}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){\mathcal{G}}_1(e,s)dB\left(t\right)\\ & \ge {(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)+{\displaystyle \frac{{(lnt)}^{\nu -1}}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)dB\left(t\right)\\ & \ge {(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)(1+{\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right))\\ & ={(lnt)}^{\nu -1}{\mathcal{G}}_1(e,s)\overline{\mathsf{{\rm Y}}}.\end{array}$$

By the same method, for $t,s\in [1,e]$, we have

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s){\le }^H{D}_{1^{+}}^{\varsigma }{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(t,s)\ge {(lnt)}^{\nu -\varsigma -1}{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{G}}_1(e,s)\overline{\mathsf{{\rm Y}}},$$

and

$${}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s){\le }^H{D}_{1^{+}}^{\varsigma }{\mathcal{H}}_1(e,s)\mathsf{\Xi }{,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(t,s)\ge {(lnt)}^{\nu -\varsigma -1}{{}^{H}D_{1^{+}}}^{\mu }{\mathcal{H}}_1(e,s)\overline{\mathsf{\Xi }}.$$

Let $E=C^{\varsigma }[1,e],$ and

$$\parallel u\parallel ={max\{\parallel u\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }{u\parallel }_0\},\parallel v\parallel ={max\{\parallel v\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }v{\parallel }_0\},$$

where

$${\parallel v\parallel }_0=\underset{t\in [1,e]}{max}{\left|v\left(t\right)\right|,\parallel }^H{D}_{1^{+}}^{\varsigma }{v\parallel }_0=\underset{t\in [1,e]}{max}{|}^H{D}_{1^{+}}^{\varsigma }v\left(t\right)|,$$

$${\parallel u\parallel }_0=\underset{t\in [1,e]}{max}{\left|u\left(t\right)\right|,\parallel }^H{D}_{1^{+}}^{\varsigma }{u\parallel }_0=\underset{t\in [1,e]}{max}{|}^H{D}_{1^{+}}^{\varsigma }u\left(t\right)|.$$

Then, $(E,\parallel ·\parallel )$ is a real Banach space, and $E\times E$ is a Banach space with the norm $\parallel (u,v)\parallel =max\{\parallel u\parallel ,\parallel v\parallel \}$. Define $P_0=\{u\in E:u\left(t\right)\ge 0{,}^H{D}_{1^{+}}^{\varsigma }u\left(t\right)\ge 0,\forall t\in (1,e)\}$, and let P be a cone on $E\times E$ and

$$P=\{(u,v)\in E\times E|u\in P_0,v\in P_0,t\in (1,e)\}.$$

The vector $(u,v)$ is a solution of system (1) and (2) if and only if $(u,v)\in C(1,e)\times C(1,e)$ is a solution of the following nonlinear integral equation system:

$$\left\{\begin{array}{l}u\left(t\right)\\ v\left(t\right)\end{array}\right\}=\left\{\begin{array}{l}{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ {\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\overline{\varsigma }}u\left(s\right)\right){\displaystyle \frac{ds}{s}},\end{array}\right\}=\left\{\begin{array}{l}{A}_1\left(v\right)\left(t\right)\\ A_2\left(u\right)\left(t\right)\end{array}\right\},$$

for $\forall u,v\in P,t\in (1,e).$

$$\left\{\begin{array}{l}{}^{H}D_{1^{+}}^{\varsigma }u\left(t\right)\\ {}^{H}D_{1^{+}}^{\overline{\mu }}v\left(t\right)\end{array}\right\}=\left\{\begin{array}{l}{\int }_1^e{}^{H}D_{1^{+}}{}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){}^{H}D_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ {\int }_1^e{}^{H}D_{1+}{}^{\overline{\varsigma }}\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right),{}^{H}D_{1^{+}}^{\overline{\varsigma }}u\left(s\right)\right){\displaystyle \frac{ds}{s}},\end{array}\right\}=\left\{\begin{array}{l}{}^{H}D_{1^{+}}^{\varsigma }{A}_1\left(v\right)\left(t\right)\\ {}^{H}D_{1^{+}}^{\overline{\varsigma }}{A}_2\left(u\right)\left(t\right).\end{array}\right\}$$

Now, an operator $A:P\to P$ is defined as follows:

$$A(u,v)\left(t\right)=(A_1\left(v\right)\left(t\right),A_2\left(u\right)\left(t\right)),(u,v)\in P,t\in (1,e).$$

Next, we show that the operators $A_i:P\to P(i=1,2)$ and $A:P\to P$ are three completely continuous operators. □

Theorem 3. 

Let $\left(H_0\right)$ and $\left(H_1\right)$ hold, then the operators $A_1$ and $A_2$ are continuous, that is, A is continuous.

Proof. 

At first, by the properties of $\mathcal{G}$, $\mathcal{H}$ and $\left(H_0\right)$, we have

$$\begin{array}{ll}{A}_1\left(v\right)\left(t\right)& ={\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le ({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)){\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le ({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)){\int }_1^e{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & <+\infty ,(v,u)\in P,t,s\in [1,e],\end{array}$$

(16)

$$\begin{array}{ll}{A}_2\left(u\right)\left(t\right)& ={\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le ({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)){\int }_1^e{L}_{q_2}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le ({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)){\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & <+\infty ,(v,u)\in P,t,s\in [1,e],\end{array}$$

(17)

so, we determine that $A(u,v)\left(t\right)=(A_1\left(v\right)\left(t\right),A_2\left(u\right)\left(t\right))$ is well defined on P.

Since $\mathcal{G}(t,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(t,s)$, $\mathcal{H}(t,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(t,s)$ are uniformly continuous, there exists a large $\mathsf{{\rm Y}}>0$ such that

$$max\{\mathcal{G}(t,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(t,s),\mathcal{H}(t,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(t,s)\}\le \mathsf{{\rm Y}},t,s\in [1,e].$$

(18)

Now, we show that $A:P\to P$ is continuous; let $(v_n,u_n)\to (v,u),{(}^H{D}_{1^{+}}^{\varsigma }{v}_n{,}^H{D}_{1^{+}}^{\varsigma }{u}_n)\to {(}^H{D}_{1^{+}}^{\varsigma }v{,}^H{D}_{1^{+}}^{\varsigma }u)$, which means that $v_n\to v{,}^H{D}_{1^{+}}^{\varsigma }{v}_n{\to }^H{D}_{1^{+}}^{\varsigma }v,u_n\to u{,}^H{D}_{1^{+}}^{\varsigma }{u}_n{\to }^H{D}_{1^{+}}^{\varsigma }u$ in $C^{\varsigma }[1,e]$. Since $v_n\to v{,}^H{D}_{1^{+}}^{\varsigma }{v}_n{\to }^H{D}_{1^{+}}^{\varsigma }v,u_n\to u{,}^H{D}_{1^{+}}^{\varsigma }{u}_n{\to }^H{D}_{1^{+}}^{\varsigma }u$, there exists a large enough $\mathsf{\Pi }>0$ such that $\parallel (v_n,u_n)\parallel \le \mathsf{\Pi },\parallel {(}^H{\mathcal{D}}_{1^{+}}^{\varsigma }{v}_n{,}^H{\mathcal{D}}_{1^{+}}^{\varsigma }{u}_n)\parallel \le \mathsf{\Pi }(n=1,2,\cdots ),$ and then $\parallel (v,u)\parallel \le \mathsf{\Pi },\parallel {(}^H{\mathcal{D}}_{1^{+}}^{\varsigma }v{,}^H{\mathcal{D}}_{1^{+}}^{\varsigma }u)\parallel \le \mathsf{\Pi },$ that is ${\parallel v\parallel <\mathsf{\Pi },\parallel }^H{\mathcal{D}}_{1^{+}}^{\varsigma }{v\parallel <\mathsf{\Pi },\parallel u\parallel <\mathsf{\Pi },\parallel }^H{\mathcal{D}}_{1^{+}}^{\varsigma }u\parallel <\mathsf{\Pi }$.

Furthermore, by $\left(H_0\right)$ and (18), we have

$$\left|{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_n\left(s\right))\right){\displaystyle \frac{ds}{s}}\right|<\mathsf{{\rm Y}}\left|{\int }_1^e{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\right|<+\infty ,$$

(19)

$$\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_n\left(s\right))\right){\displaystyle \frac{ds}{s}}\right|<\mathsf{{\rm Y}}\left|{\int }_1^e{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\right|<+\infty ,$$

(20)

$$\left|{\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right))\right){\displaystyle \frac{ds}{s}}\right|<\mathsf{{\rm Y}}\left|{\int }_1^e{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|<+\infty .$$

(21)

$$\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right))\right){\displaystyle \frac{ds}{s}}\right|<\mathsf{{\rm Y}}\left|{\int }_1^e{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|<+\infty .$$

(22)

By $\left(H_0\right)$, we know that $L_{q_1}\left(\theta \left(s\right)\right)$, and $L_{q_2}\left(\overline{\theta }\left(s\right)\right)$ is integrable. Hence, for any $t\in [1,e],$$n>N,$ by $\left(19\right)$–$\left(22\right)$ and the Lebesgue control convergence theorem, we obtain

$$\begin{array}{l}\hspace{1em}|\left(A_1{v}_n\right)\left(t\right)-\left(A_{1}v\right)\left(t\right)|\\ =\left|{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right.\\ \hspace{1em}\left.-{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ \le \epsilon ,\end{array}$$

$$\begin{array}{l}\hspace{1em}{|}^H{D}_{1^{+}}^{\varsigma }\left(A_1{v}_n\right)\left(t\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A_{1}v\right)\left(t\right)|\\ =\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right.\\ \hspace{1em}\left.-{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ \le \epsilon ,\end{array}$$

and

$$\begin{array}{l}\hspace{1em}|\left(A_2{u}_n\right)\left(t\right)-\left(A_{2}u\right)\left(t\right)|\\ =\left|{\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right.\\ \hspace{1em}\left.-{\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ =\left|{\int }_1^e\mathcal{H}(t,s)\left(L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right)\right.\right.\\ \hspace{1em}\left.-L_{q_2}\left(\mathcal{F}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ \le \epsilon ,\end{array}$$

$$\begin{array}{l}\hspace{1em}{|}^H{D}_{1^{+}}^{\varsigma }\left(A_2{u}_n\right)\left(t\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A_{2}u\right)\left(t\right)|\\ =\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right.\\ \hspace{1em}\left.-{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ =\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)\left(L_{q_2}\left(\overline{\mathcal{F}}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right)\right.\right.\\ \hspace{1em}\left.-L_{q_2}\left(\mathcal{F}(s,u_n\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_n\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ \le \epsilon ,\end{array}$$

and hence, we obtain $\parallel A_1{v}_n-A_1{v\parallel }_0\to 0,{{\parallel }^H{D}_{1^{+}}^{\varsigma }\left(A_1{v}_n\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A{v}_1\right)\parallel }_0\to 0,$$\parallel A_2{u}_n-A_2{u\parallel }_0\to 0,{{\parallel }^H{D}_{1^{+}}^{\varsigma }\left(A_2{u}_n\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A_{2}u\right)\parallel }_0\to 0(n\to \infty ).$ That is, $\parallel A_1{v}_n-A_{1}v\parallel \to 0,\parallel A_2{u}_n-A_{2}u\parallel \to 0,(n\to \infty )$, namely A is continuous in the space E. □

Theorem 4. 

Let $\left(H_0\right)$ and $\left(H_1\right)$ hold, then the operators $A_1$, $A_2$ and A are completely continuous.

Proof. 

From Theorem 2, we have $\left(Au\right)\left(t\right){,}^H{D}_{1^{+}}^{\mu }\left(Au\right)\left(t\right),\left(Av\right)\left(t\right){,}^H{D}_{1^{+}}^{\mu }\left(Av\right)\left(t\right)\ge 0$, $t\in [1,e]$, and thus, $A\left(P\right)\subset P$.

Now, we will prove that $AV$ is relatively compact for bounded $V\subset P$. Since V is bounded, there exists $D>0$ such that for any $(v,u)\in V$, $\parallel (v,u)\parallel \le D$. For $t\in [1,e],(v,u)\in V$, we have

$$\begin{array}{ll}{A}_1\left(v\right)\left(t\right)& ={\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)\right){\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)\right){\int }_1^e{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & =\left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right){\mathsf{\Delta }}_1}}\iota \right)𝚥<+\infty ,(v,u)\in P,t,s\in [1,e],\end{array}$$

(23)

$$\begin{array}{l}{}^{H}D_{1^{+}}^{\varsigma }{A}_1\left(v\right)\left(t\right)={\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right),{}^{H}D_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma ){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)\right){\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma ){\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right)\right){\int }_1^e{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ =\left({\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma ){\mathsf{\Delta }}_1}}\iota \right)𝚥<+\infty ,(u,v)\in P,t,s\in [1,e],\end{array}$$

(24)

where $\iota ={\int }_1^{e}h\left(t\right){(lnt)}^{\nu -1}dB\left(t\right),𝚥={\int }_1^e{\phi }_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}.$ Similarly, for $t\in [1,e],(v,u)\in V,$ we derive

$$\begin{array}{ll}{A}_2\left(u\right)\left(t\right)& ={\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)\right){\int }_1^e{L}_{q_2}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)\right){\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & =\left({\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right){\overline{\mathsf{\Delta }}}_1}}\overline{\iota }\right)\overline{𝚥}<+\infty ,(v,u)\in P,t,s\in [1,e],\end{array}$$

(25)

$$\begin{array}{l}{}^{H}D_{1^{+}}^{\mu }{A}_2\left(u\right)\left(t\right)={\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma ){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)\right){\int }_1^e{L}_{q_2}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left({\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma ){\overline{\mathsf{\Delta }}}_1}}{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right)\right){\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ =\left({\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma ){\overline{\mathsf{\Delta }}}_1}}\overline{\iota }\right)\overline{𝚥}<+\infty ,(u,v)\in P,t,s\in [1,e],\end{array}$$

(26)

where $\overline{\iota }={\int }_1^e\overline{h}\left(t\right){(lnt)}^{\iota -1}d\overline{B}\left(t\right),\overline{𝚥}={\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}},$ which shows that $AV$ is bounded. Next, we will verify that ${}^{H}D_{1^{+}}^{\varsigma }\left(AV\right)$ is equicontinuous. Let $t_1,t_2\in [1,e],t_1<t_2,(v,u)\in V$, we obtain

$$\begin{array}{l}\hspace{1em}{|}^H{D}_{1^{+}}^{\varsigma }\left(A_{1}v\right)\left(t_2\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A_{1}v\right)\left(t_1\right)|\\ =|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t_2,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}-{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t_1,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}|\\ =|{(ln{t}_2)}^{\nu -1-\varsigma }-{(ln{t}_1)}^{\nu -1-\varsigma }|{\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{s^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+|{(ln{t}_2)}^{\nu -1-\varsigma }-{(ln{t}_1)}^{\nu -1-\varsigma }|{\displaystyle \frac{\mathsf{\Gamma }\left(\nu \right){\int }_1^{e}h\left(t\right){\mathcal{G}}_{\mathcal{1}}(t,s)dB\left(t\right)}{{\mathsf{\Delta }}_1\mathsf{\Gamma }(\alpha -\mu )}}{\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\mu )}}{\int }_1^{t_1}\left|{(ln{t}_1-lns)}^{\nu -1-\varsigma }-{(ln{t}_2-lns)}^{\nu -1-\varsigma }\right|L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\int }_{t_1}^{t_2}{(ln{t}_1-lns)}^{\nu -1-\varsigma }{L}_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left|{(ln{t}_2)}^{\nu -1-\varsigma }-{(ln{t}_1)}^{\nu -1-\varsigma }\right|{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma )}}{\int }_1^e{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}+{\int }_{t_1}^{t_2}{(lnt-lns)}^{\nu -1-\varsigma }{L}_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\nu -\varsigma )}}{\int }_1^{t_1}|{(ln{t}_1-lns)}^{\nu -1-\varsigma }-{(ln{t}_2-lns)}^{\nu -1-\varsigma }|L_{q_1}\left(\vartheta \left(s\right)\right){\displaystyle \frac{ds}{s}},\end{array}$$

$$\begin{array}{l}\hspace{1em}\left|{}^{H}D_{1^{+}}^{\varsigma }\left(A_{2}u\right)\left(t_2\right){-}^H{D}_{1^{+}}^{\varsigma }\left(A_{2}u\right)\left(t_1\right)\right|\\ =\left|{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t_2,s)L_{q_2}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\right.\\ \hspace{1em}\left.-{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t_1,s)L_{q_2}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\right|\\ =|{(ln{t}_2)}^{\iota -1-\mu }-{(ln{t}_1)}^{\iota -1-\varsigma }|{\int }_1^e{L}_{q_1}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+|{(ln{t}_2)}^{\iota -1-\varsigma }-{(ln{t}_1)}^{\iota -1-\varsigma }|{\displaystyle \frac{\mathsf{\Gamma }\left(\iota \right){\int }_1^{e}h\left(t\right){\mathcal{H}}_{\mathcal{1}}(t,s)dB\left(t\right)}{{\mathsf{\Delta }}_1\mathsf{\Gamma }(\iota -\varsigma )}}{\int }_1^e{L}_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}{\int }_1^{t_1}|{(ln{t}_1-lns)}^{\iota -1-\varsigma }-{(ln{t}_2-lns)}^{\iota -1-\varsigma }|L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\int }_{t_1}^{t_2}{(ln{t}_1-lns)}^{\iota -1-\varsigma }{L}_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \le \left|{(ln{t}_2)}^{\iota -1-\varsigma }-{(ln{t}_1)}^{\iota -1-\varsigma }\right|{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}{\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}+{\int }_{t_1}^{t_2}{(lnt-lns)}^{\iota -1-\varsigma }{\phi }_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+{\displaystyle \frac{1}{\mathsf{\Gamma }(\iota -\varsigma )}}{\int }_1^{t_1}\left|{(ln{t}_1-lns)}^{\iota -1-\varsigma }-{(ln{t}_2-lns)}^{\iota -1-\varsigma }\right|L_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ \hspace{1em}+|{(ln{t}_2)}^{\iota -1-\varsigma }-{(ln{t}_1)}^{\iota -1-\varsigma }|{\displaystyle \frac{\mathsf{\Gamma }\left(\iota \right){\int }_1^{e}h\left(t\right){\mathcal{H}}_{\mathcal{1}}(t,s)dB\left(t\right)}{{\mathsf{\Delta }}_1\mathsf{\Gamma }(\iota -\varsigma )}}{\int }_1^e{L}_{q_2}\left(\overline{\vartheta }\left(s\right)\right){\displaystyle \frac{ds}{s}}.\end{array}$$

From the above and the uniform continuity of ${(lnt)}^{\nu -1-\varsigma },{(lnt-lns)}^{\nu -1-\varsigma }$,${(lnt)}^{\iota -1-\varsigma },{(lnt-lns)}^{\iota -1-\varsigma }$, and together with Lemma 6, we can derive that $AV$ is relatively compact in $C^{\left(\mu \right)}[1,e]$, and so, we determine that $A:P\to P$ is completely continuous. □

3. Main Results

Theorem 5. 

Suppose that $\left(H_0\right)$ and $\left(H_1\right)$ hold, and there exist $t_0\in (0,1)$ and two positive constants $\rho ,\xi$, $\rho >\xi$; further, suppose the following are true:

(i) For $\forall (t,x,y)\in [1,e]\times [0,\xi ]\times [0,\xi ],$

$$\begin{array}{ll}{L}_{q_1}\left(\mathcal{F}(t,v\left(t\right){,}^H{D}_{1+}^{\varsigma }v\left(t\right))\right)\ge & \xi max\left\{{\displaystyle \frac{1}{{(ln{t}_0)}^{\nu -1}\overline{\mathsf{{\rm Y}}}}}{\left({\int }_{t_0}^e{\mathcal{G}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1},\right.\\ & \left.{\displaystyle \frac{1}{{(ln{t}_0)}^{\nu -\varsigma -1}\overline{\mathsf{{\rm Y}}}}}{\left({\int }_{t_0}^e{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{G}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}\right\},\end{array}$$

$$\begin{array}{ll}{L}_{q_2}\left(\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1+}^{\varsigma }u\left(t\right))\right)\ge & \xi \left\{{\displaystyle \frac{1}{{(ln{t}_0)}^{\iota -1}\overline{\mathsf{\Xi }}}}{\left({\int }_{t_0}^e{\mathcal{H}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1},\right.\\ & \left.{\displaystyle \frac{1}{{(ln{t}_0)}^{\iota -\varsigma -1}\overline{\mathsf{\Xi }}}}{\left({\int }_{t_0}^e{{}^{H}D_{1+}}^{\mu }{\mathcal{H}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}\right\}.\end{array}$$

(ii) For $\forall (t,x,y)\in [1,e]\times [0,\rho ]\times [0,\rho ],$ we have

$$\begin{array}{l}\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right))\le \theta \left(s\right){\rho }^{{\displaystyle \frac{1}{q_1-1}}},\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right))\le \overline{\theta }\left(s\right){\rho }^{{\displaystyle \frac{1}{q_2-1}}},\\ \forall (t,x_0,x_1)\in [1,e]\times [0,+\infty )\times [0,+\infty ),\end{array}$$

and

$$\mathsf{{\rm Y}}{\int }_1^{e}max\left\{\mathcal{G}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(e,s)\right\}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}<1,$$

$$\mathsf{\Xi }{\int }_1^{e}max\left\{\mathcal{H}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(e,s)\right\}{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}<1.$$

Then, BVPs (1) and (2) have at least one positive solution.

Proof. 

Let ${\mathsf{\Omega }}_1=\{(u,v)\in P|\parallel u\parallel <\xi ,\parallel v\parallel <\xi \}$ such that $0<u\left(t\right),v\left(t\right)\le \xi$ for any $(u,v)\in P\cap \partial {\mathsf{\Omega }}_1$ and for all $t\in [1,e]$. By condition $\left(i\right)$ and Theorem 2, we have

$$\begin{array}{ll}{A}_{1}v\left(t_0\right)& ={\int }_1^e\mathcal{G}(t_0,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \ge {\int }_{t_0}^e{\mathcal{G}}_1(e,s){(ln{t}_0)}^{\nu -1}\overline{\mathsf{{\rm Y}}}{\displaystyle \frac{ds}{s}}{\displaystyle \frac{\xi }{{(ln{t}_0)}^{\nu -1}\overline{\mathsf{{\rm Y}}}}}{\left({\int }_{t_0}^e{\mathcal{G}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}\\ & =\xi ,\end{array}$$

$$\begin{array}{ll}{}^{H}D_{1^{+}}^{\varsigma }{A}_{1}v\left(t_0\right)& ={\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t_0,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \ge {\int }_{t_0}^e{(}^H{D}_{1^{+}}^{\varsigma }{\mathcal{G}}_1(e,s){(ln{t}_0)}^{\nu -\varsigma -1}\overline{\mathsf{{\rm Y}}}{\displaystyle \frac{ds}{s}}{\displaystyle \frac{\xi }{{(ln{t}_0)}^{\nu -\varsigma -1}\overline{\mathsf{{\rm Y}}}}}{\left({\int }_{t_0}^e\left({}^{H}D_{1^{+}}^{\varsigma }{\mathcal{G}}_1(t_0,s)\right){\displaystyle \frac{ds}{s}}\right)}^{-1}\\ & =\xi ,\end{array}$$

$$\begin{array}{ll}{A}_{2}u\left(t_0\right)& ={\int }_1^e\mathcal{H}(t_0,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \ge {\int }_{t_0}^e{\mathcal{H}}_1(e,s){(ln{t}_0)}^{\beta -1}\overline{\mathsf{\Xi }}{\displaystyle \frac{ds}{s}}{\displaystyle \frac{\xi }{{(ln{t}_0)}^{\beta -1}\overline{\mathsf{\Xi }}}}{\left({\int }_{t_0}^e{\mathcal{H}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}\\ & =\xi ,\end{array}$$

$$\begin{array}{ll}{}^{H}D_{1^{+}}^{\varsigma }{A}_{2}u\left(t_0\right)& ={\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{H}(t_0,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \ge {\int }_{t_0}^e{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{H}}_1(e,s){(ln{t}_0)}^{\iota -\varsigma -1}\overline{\mathsf{\Xi }}{\displaystyle \frac{ds}{s}}{\displaystyle \frac{\xi }{{(ln{t}_0)}^{\iota -\varsigma -1}\overline{\mathsf{\Xi }}}}{\left({\int }_{t_0}^e{{}^{H}D_{1^{+}}}^{\varsigma }{\mathcal{H}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}\\ & =\xi .\end{array}$$

Hence,

$$\parallel A_{1}v\parallel =max\{\parallel A_1{v\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }{A}_{1}v{\parallel }_0\}\ge \xi ,$$

$$\parallel A_{2}u\parallel =max\{\parallel A_2{v\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }{A}_{2}v{\parallel }_0\}\ge \xi ,\forall (u,v)\in P\cap \partial {\mathsf{\Omega }}_2.$$

So,

$$\parallel A(u,v)\parallel =max\{\parallel A_{1}v\parallel ,\parallel A_{2}u\parallel \}\ge \xi =\parallel (u,v)\parallel .$$

Let ${\mathsf{\Omega }}_1=\{(u,v)\in P|\parallel u\parallel <\rho ,\parallel v\parallel <\rho \}$, where $\rho >\xi$. For any $(u,v)\in P\cap \partial {\mathsf{\Omega }}_2,t\in [1,e]$, we have $0<u\left(t\right),v\left(t\right)\le \rho$. By condition $\left(ii\right)$ and Theorem 2, we have

$$\begin{array}{ll}{A}_{1}v\left(t\right)& ={\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le {\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}\rho L_{q_1}(\theta \left(s\right){\displaystyle \frac{ds}{s}}=\rho \mathsf{{\rm Y}}{\int }_1^e\mathcal{G}(e,s){\phi }_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \rho ,\end{array}$$

$$\begin{array}{ll}{}^{H}D_{1^{+}}^{\varsigma }{A}_{1}v\left(t\right)& ={\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le {\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }({\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}\rho L_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}=\rho \mathsf{{\rm Y}}{\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }\mathcal{G}(e,s)L_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \rho ,\end{array}$$

$$\begin{array}{ll}{A}_{2}u\left(t\right)& ={\int }_1^e\mathcal{H}(t,s)L_{q_1}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le {\int }_1^e{\mathcal{H}}_1(e,s)\rho \mathsf{\Xi }{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}=\mathsf{\Xi }\rho {\int }_1^e{\mathcal{H}}_1(e,s)L_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \rho ,\end{array}$$

$$\begin{array}{ll}{}^{H}D_{1^{+}}^{\varsigma }{A}_{2}u\left(t\right)& ={\int }_1^e{}^{H}D_{1^{+}}^{\mu }\mathcal{H}(t,s)L_{q_1}\left(\mathcal{F}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le {\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }{\mathcal{H}}_1(e,s)\rho L_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}=\mathsf{\Xi }\rho {\int }_1^e{}^{H}D_{1^{+}}^{\varsigma }{\mathcal{H}}_1(e,s)L_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \rho ,\end{array}$$

then we have

$$\parallel A_{1}v\parallel =max\{\parallel A_1{v\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }{A}_{1}v{\parallel }_0\}\le \rho ,$$

$$\parallel A_{2}u\parallel =max\{\parallel A_2{u\parallel }_0{,\parallel }^H{D}_{1^{+}}^{\varsigma }{A}_{2}u{\parallel }_0\}\le \rho ,\forall (u,v)\in P\cap \partial {\mathsf{\Omega }}_2.$$

Hence, $\parallel A(u,v)\parallel =max\{\parallel A_{1}v\parallel ,\parallel A_{2}u\parallel \}\le \rho =\parallel (u,v)\parallel$. According to Theorem 4, operator $A:P\to P$ is completely continuous; thus, by Lemma 4, the proof is finished. □

Theorem 6. 

Suppose that $\left(H_0\right)$ and $\left(H_1\right)$ hold, and there exist the functions $\theta \left(t\right),\overline{\theta }\left(t\right)$ and the non-decreasing functions $\phi ,\psi :[0,+\infty )\to (0,+\infty )$ such that

$\left(iii\right)$

$$\begin{array}{l}\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right))\le \theta \left(s\right){\phi }^{{\displaystyle \frac{1}{q_1-1}}}\left(v\right),\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right))\le \overline{\theta }\left(s\right){\psi }^{{\displaystyle \frac{1}{q_2-1}}}\left(u\right),\\ \forall (t,x_0,x_1)\in [1,e]\times [0,+\infty )\times [0,+\infty );\end{array}$$

$\left(iv\right)$ and there exists an $r>0$, such that

$${\displaystyle \frac{r}{max\left\{\phi \right(r\left)\right),\psi \left(\right(r\left)\right|\left)\right\}}}>max\left\{{\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}},{\int }_1^e{\mathcal{H}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\right\}.$$

Then, the BVPs (1) and (2) have a positive solution.

Proof. 

Let $U=\left\{\right(u,v)\in P|\parallel (u,v)\parallel <r\}$, then $U\subset P$. According to Theorems 3 and 4, we determine that operator $A:\overline{U}\to P$ is completely continuous. If there exists $(u,v)\in \partial U$ and $\tilde{\lambda }\in (0,1)$, we obtain $(u,v)=\tilde{\lambda }A(u,v)$, and then, by $\left(iii\right)$ for $t\in [1,e]$, we have

$$\begin{array}{ll}v\left(t\right)=\tilde{\lambda }{A}_{1}v\left(t\right)& =\tilde{\lambda }{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & <{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & <{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\theta \left(s\right)L^{{\displaystyle \frac{1}{q_1-1}}}\left(v\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \phi (\parallel v\parallel ){\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ & \le \phi (\parallel (u,v)\parallel ){\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}};\end{array}$$

hence,

$$\parallel v\parallel \le \phi (\parallel (u,v)\parallel ){\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}},$$

that is,

$${\displaystyle \frac{\parallel v\parallel }{\phi (\parallel (u,v)\parallel )}}\le {\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}.$$

Similarly,

$${\displaystyle \frac{\parallel u\parallel }{\psi (\parallel (u,v)\parallel )}}\le {\int }_1^e{\mathcal{H}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}.$$

Hence,

$$\begin{array}{l}{\displaystyle \frac{\parallel (u,v)\parallel }{max\left\{\phi \right(\parallel (u,v)\parallel ),\psi (\parallel (u,v)\parallel \left)\right\}}}\\ \le max\left\{{\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}},{\int }_1^e{\mathcal{H}}_1(e,s)\mathsf{\Xi }{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\right\}.\end{array}$$

By $\left(iv\right)$, we have $\parallel (u,v)\parallel \ne r$, which means $(u,v)\notin \partial U$. Then, by Lemma 5, a fixed point $(u,v)\in U$ is obtained. Hence, the BVPs (1) and (2) have a positive solution.

In this section, we consider the equation under the condition of $\mathcal{F}(s,x_1,y_1)$ and $\overline{\mathcal{F}}(s,x_1,y_1)$ being continuous. □

Theorem 7. 

Assume that functions $\mathcal{F}(s,x_1,y_1)$ and $\overline{\mathcal{F}}(s,x_1,y_1)$ are continuous, and there exist functions $\theta \left(t\right),\overline{\theta }\left(t\right)$ and non-decreasing functions $\phi ,\psi :[0,+\infty )\to (0,+\infty )$ such that

$$|L_{q_1}\left(\mathcal{F}(s,x_1,y_1)\right)-L_{q_1}\left(\mathcal{F}(s,x_2,y_2)\right)|\le L_1{\theta }_1\left(s\right)|x_1-x_2|+L_2{\theta }_2\left(s\right)|y_1-y_2|,$$

$$|L_{q_2}\left(\overline{\mathcal{F}}(s,x_1,y_1)\right)-L_{q_2}\left(\overline{\mathcal{F}}(s,x_2,y_2)\right)|\le {\overline{L}}_1{\overline{\theta }}_1\left(s\right)|x_1-x_2|+{\overline{L}}_2{\overline{\theta }}_2\left(s\right)|y_1-y_2|,$$

and

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\mathsf{{\rm Y}}\left(L_1{\theta }_1\left(s\right)+L_2{\theta }_1\left(s\right)\right)<1,$$

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\mathsf{\Xi }\left({\overline{L}}_1{\theta }_1\left(s\right)+{\overline{L}}_2{\overline{\theta }}_1\left(s\right)\right)<1.$$

Then, the BVPs (1) and (2) have a unique solution. In addition, we can obtain the unique solution by constructing an iterative sequence and error estimate.

Proof. 

In this section, we will use the Banach fixed point theorem. For $\forall t\in [1,e],v_1,v_2,u_1,u_2\in E$, we have

$$\begin{array}{l}\hspace{1em}|A_1{v}_2\left(t\right)-A_1{v}_1\left(t\right)|\\ =|{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_2\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_2\left(s\right)\right){\displaystyle \frac{ds}{s}}-{\int }_1^e\mathcal{G}(t,s)L_{q_1}\left(\mathcal{F}(s,v_1\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_1\left(s\right)\right){\displaystyle \frac{ds}{s}}|\\ ={\int }_1^e\mathcal{G}(t,s)|L_{q_1}\left(\mathcal{F}(s,v_2\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_2\left(s\right)\right)-L_{q_1}\left(\mathcal{F}(s,v_1\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{v}_1\left(s\right)\right)|{\displaystyle \frac{ds}{s}}\\ \le {\int }_1^e{\mathcal{G}}_1(t,s)\mathsf{{\rm Y}}(L_1{\theta }_1\left(s\right)|v_2\left(s\right)-v_1\left(s\right)|+L_2{\theta }_1{\left(s\right)|}^H{D}_{1^{+}}^{\varsigma }{v}_2\left(s\right){-}^H{D}_{1^{+}}^{\varsigma }{v}_1\left(s\right)\left|\right)\\ \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\parallel v_2-v_1\parallel \mathsf{{\rm Y}}\left(L_1{\theta }_1\left(s\right)+L_2{\theta }_1\left(s\right)\right),\end{array}$$

$$\begin{array}{l}\hspace{1em}|A_2{u}_2\left(t\right)-A_2{u}_1\left(t\right)|\\ =|{\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\overline{\mathcal{F}}(s,u_2\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_2\left(s\right)\right){\displaystyle \frac{ds}{s}}-{\int }_1^e\mathcal{H}(t,s)L_{q_2}\left(\mathcal{F}(s,u_1\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_1\left(s\right)\right){\displaystyle \frac{ds}{s}}|\\ ={\int }_1^e\mathcal{H}(t,s)|L_{q_1}\left(\mathcal{F}(s,u_2\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_2\left(s\right)\right)-L_{q_1}\left(\mathcal{F}(s,u_1\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }{u}_1\left(s\right)\right)|{\displaystyle \frac{ds}{s}}\\ \le {\int }_1^e{\mathcal{H}}_1(e,s)\mathsf{\Xi }({\overline{L}}_1{\overline{\theta }}_1\left(s\right)|u_2\left(s\right)-u_1\left(s\right)|+{\overline{L}}_2{\overline{\theta }}_2{\left(s\right)|}^H{D}_{1^{+}}^{\varsigma }{u}_2\left(s\right){-}^H{D}_{1^{+}}^{\varsigma }{u}_1\left(s\right)\left|\right)\\ \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}|u_2\left(s\right)-u_1\left(s\right)|\mathsf{\Xi }\left({\overline{L}}_1{\theta }_1\left(s\right)+{\overline{L}}_2{\overline{\theta }}_1\left(s\right)\right)\\ \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\parallel u_2-u_1\parallel \mathsf{\Xi }\left({\overline{L}}_1{\theta }_1\left(s\right)+{\overline{L}}_2{\overline{\theta }}_1\left(s\right)\right).\end{array}$$

Hence, we have

$$\begin{array}{l}\underset{t\in [1,e]}{max}|A(u_2,v_2)-A(u_1,v_1)|\\ =\parallel A(u_2,v_2)-A(u_1,v_1)\parallel =\parallel (A_1{v}_2,A_2{u}_2)-(A_1{v}_1,A_2{u}_1)\parallel \\ =\parallel (A_1{v}_2-A_1{v}_1,A_2{u}_2-A_2{u}_1)\parallel \le \tilde{L}\parallel (v_2-v_1,u_2-u_1)\parallel ,\end{array}$$

where

$$\tilde{L}=max\left\{{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\mathsf{{\rm Y}}\left(L_1{\theta }_1\left(s\right)+L_2{\theta }_1\left(s\right)|\right),{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\mathsf{\Xi }\left({\overline{L}}_1{\overline{\theta }}_1\left(s\right)+{\overline{L}}_2{\overline{\theta }}_1\left(s\right)|\right)\right\}<1.$$

BVPs (1) and (2) have a unique solution in E by the contraction mapping principle. □

4. Examples

Example 1. 

Consider the following boundary value problem:

$$\left\{\begin{array}{l}{L}_3\left({}^{H}D_{1^{+}}^{{\displaystyle \frac{5}{2}}}u\right)\left(t\right)+\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(t\right))=0,1<t<e,\\ L_2\left(D_{1^{+}}^{{\displaystyle \frac{5}{2}}}v\right)\left(t\right)+\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(t\right))=0,1<t<e,\\ u\left(1\right)=u^{\prime }\left(1\right)=0,u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_{j}u\left(e^{{\displaystyle \frac{1}{j^2}}}\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\\ v\left(1\right)=v^{\prime }\left(1\right)=0,v\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\overline{\eta }}_{j}v\left(e^{{\displaystyle \frac{1}{j^2}}}\right)+{\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right),\end{array}\right.$$

(27)

where $\alpha ={\displaystyle \frac{5}{2}},\beta ={\displaystyle \frac{5}{2}},$${\eta }_j={\overline{\eta }}_j={\displaystyle \frac{1}{2j^3}},$${\xi }_j={\overline{\xi }}_j=e^{{\displaystyle \frac{1}{j^2}}}$, $p_1=3,q_1={\displaystyle \frac{3}{2}},p_2=2,q_2={\displaystyle \frac{1}{2}},$$h\left(t\right)=\overline{h}\left(t\right)={(lnt)}^{{\displaystyle \frac{1}{2}}},$

$$B\left(t\right)=\overline{B}\left(t\right)=\left\{\begin{array}{l}0,t\in [0,{\displaystyle \frac{e}{2}}],\\ 4,t\in [{\displaystyle \frac{e}{2}},{\displaystyle \frac{3e}{4}}],\\ 1,t\in [{\displaystyle \frac{3e}{4}},e],\end{array}\right.$$

and

$$\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v\left(t\right))=\left\{\begin{array}{l}{\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}}{(v^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)}^2)}^2,\\ (t,v{,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)\in (1,e)\times [0,1]\times [0,1],\\ {\displaystyle \frac{{499}^2}{4\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}},\\ (t,v{,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)\in (1,e)\times (1,+\infty )\times (1,+\infty ),\end{array}\right.$$

$$\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u\left(t\right))=\left\{\begin{array}{l}{\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}}{(u^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)}^2)}^2,\\ (t,u{,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)\in (1,e)\times [0,1]\times [0,1],\\ {\displaystyle \frac{{499}^2}{4\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}},\\ (t,u{,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)\in (1,e)\times (1,+\infty )\times (1,+\infty ).\end{array}\right.$$

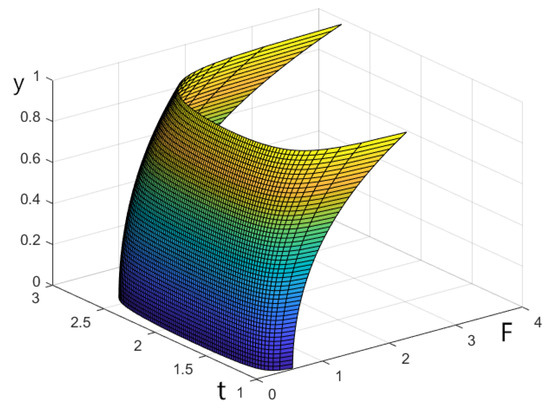
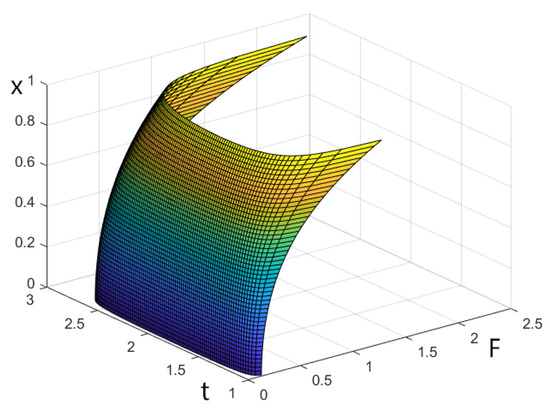
Now, let us simplify the expression of $\mathcal{F}$ to $\mathcal{F}(t,x,y)={\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}}(x^2+y^2)$ for $(t,x,y)\in (1,e)\times [0,1]\times [0,1]$, and draw Figure 1 and Figure 2 in order to reveal the influence of $\mathcal{F}$.

Figure 1. The first nonlinear function with singularity at points 1 and e (taking x = 1).

Figure 2. The first nonlinear function with singularity at points 1 and e (taking y = 0.5).

Figure 1 and Figure 2 show a visualization of singular nonlinear terms of $\mathcal{F}$; note that $\overline{\mathcal{F}}$ is similar with $\mathcal{F}$, hence we omit the impact of $\mathcal{F}$ here. It is found that the nonlinearity is singular at $t=1$ and e. Although the nonlinear term has significant singularity, it can be controlled by an integrable function, so the solutions of the equation are still stable and robust. By a simple calculation, we have

$$\mathsf{\Delta }=\overline{\mathsf{\Delta }}=1-\sum _{i=1}^{\infty }{\eta }_j{(ln{\xi }_j)}^{\alpha -1}=1-\sum _{i=1}^{\infty }{\displaystyle \frac{1}{2j^3}}{\displaystyle \frac{1}{j^3}}=1-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\pi }^6}{945}}\approx 0.4913,$$

$$\begin{array}{l}{\mathsf{\Delta }}_1={\overline{\mathsf{\Delta }}}_1=\overline{\mathsf{\Delta }}-{\int }_1^e\overline{h}\left(t\right){(lnt)}^{\beta -1}d\overline{B}\left(t\right)\\ =\mathsf{\Delta }-{\int }_1^{e}h\left(t\right){(lnt)}^{\alpha -1}dB\left(t\right)=\mathsf{\Delta }-{\int }_1^e{(lnt)}^{2}dB\left(t\right)\\ =0.4913-[4\times {(ln{\displaystyle \frac{e}{2}})}^2-3\times {(ln{\displaystyle \frac{3e}{4}})}^2]\approx 1.6369,\end{array}$$

$$\begin{array}{l}\mathsf{{\rm Y}}=1+{\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}{\int }_1^{e}h\left(t\right)dB\left(t\right)=1+{\displaystyle \frac{1}{1.6369}}{\int }_1^e{(lnt)}^{{\displaystyle \frac{1}{2}}}dB\left(t\right)\\ \hspace{1em}=1+{\displaystyle \frac{1}{1.6369}}(4\times {(ln{\displaystyle \frac{e}{2}})}^{{\displaystyle \frac{1}{2}}}-3\times {(ln{\displaystyle \frac{3e}{4}})}^{{\displaystyle \frac{1}{2}}})\approx 0.8067,\end{array}$$

and apparently,

$$\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v\left(t\right))\le {\displaystyle \frac{1}{\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}}=\theta \left(t\right),$$

$$\overline{\mathcal{F}}(t,v\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v\left(t\right))\le {\displaystyle \frac{1}{\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}}=\overline{\theta }\left(t\right).$$

Taking $\xi ={\displaystyle \frac{3}{4}},t_0={\displaystyle \frac{5}{4}},$ then for $(t,x,y)\in [1,e]\times [0,{\displaystyle \frac{3}{4}}]\times [0,{\displaystyle \frac{3}{4}}],$

$$L_3\left(\mathcal{F}(t,v\left(t\right){,}^H{D}_{1+}^{\mu }v\left(t\right))\right)\to +\infty \ge {\displaystyle \frac{\xi }{{(ln{t}_0)}^{\alpha -1}\overline{\mathsf{{\rm Y}}}}}{\left({\int }_{t_0}^e({\mathcal{G}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1},$$

$$L_2\left(\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1+}^{\varsigma }u\left(t\right))\right)\to +\infty \ge {\displaystyle \frac{\xi }{{(ln{t}_0)}^{\beta -1}\overline{\mathsf{\Xi }}}}{\left({\int }_{t_0}^e({\mathcal{H}}_1(t_0,s){\displaystyle \frac{ds}{s}}\right)}^{-1}.$$

Moreover, for $(t,x,y)\in [1,e]\times [0,\rho ]\times [0,\rho ](\rho >{\displaystyle \frac{3}{4}}),$

$$\begin{array}{l}\hspace{1em}\mathsf{{\rm Y}}{\int }_1^{e}max\left\{\mathcal{G}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(e,s)\right\}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}}\\ =\mathsf{{\rm Y}}{\int }_1^{e}max\left\{\mathcal{G}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{G}(e,s)\right\}{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}{(lns)}^{\frac{1}{4}}{(1-lns)}^{\frac{1}{4}}}}{\displaystyle \frac{ds}{s}}\\ \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\mathsf{{\rm Y}}{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}}}{\int }_1^e{\displaystyle \frac{1}{{(lns)}^{\frac{1}{4}}{(1-lns)}^{\frac{1}{4}}}}{\displaystyle \frac{ds}{s}}\\ ={\displaystyle \frac{0.8067}{\mathsf{\Gamma }\left(\nu \right)}}{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}}}B({\displaystyle \frac{5}{4}},{\displaystyle \frac{5}{4}})\approx 0.2116<1,\end{array}$$

$$\begin{array}{l}\hspace{1em}\mathsf{\Xi }{\int }_1^{e}max\left\{\mathcal{H}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(e,s)\right\}{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\\ =\mathsf{\Xi }{\int }_1^{e}max\left\{\mathcal{H}(e,s){,}^H{D}_{1^{+}}^{\varsigma }\mathcal{H}(e,s)\right\}{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}{(lns)}^{\frac{3}{8}}{(1-lns)}^{\frac{3}{8}}}}{\displaystyle \frac{ds}{s}}\\ \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\mathsf{\Xi }{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}}}{\int }_1^e{\displaystyle \frac{1}{{(lns)}^{\frac{3}{8}}{(1-lns)}^{\frac{3}{8}}}}{\displaystyle \frac{ds}{s}}\\ ={\displaystyle \frac{0.8067}{\mathsf{\Gamma }\left(\iota \right)}}{\displaystyle \frac{1}{{\pi }^{\frac{1}{2}}}}B({\displaystyle \frac{11}{8}},{\displaystyle \frac{11}{8}})\approx 0.1682<1.\end{array}$$

Hence, all the conditions of Theorem 5 are satisfied. Therefore, Equation (27) has at least one positive solution.

Example 2. 

Consider the following boundary value problem:

$$\left\{\begin{array}{l}{L}_3\left({}^{H}D_{1^{+}}^{{\displaystyle \frac{5}{2}}}u\right)\left(t\right)+\mathcal{F}(t,v\left(t\right){,}^H{D}_{1+}^{\varsigma }v\left(t\right))=0,1<t<e,\\ L_2\left(D_{1^{+}}^{{\displaystyle \frac{5}{2}}}v\right)\left(t\right)+\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1+}^{\varsigma }u\left(t\right))=0,1<t<e,\\ u\left(1\right)=u^{\prime }\left(1\right)=0,u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_{j}u\left({\xi }_j\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\\ v\left(1\right)=v^{\prime }\left(1\right)=0,v\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\overline{\eta }}_{j}v\left({\overline{\xi }}_j\right)+{\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right),\end{array}\right.$$

(28)

$$\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v\left(t\right))={\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}}{(v^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)}^2)}^2,$$

$$\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u\left(t\right))={\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}}{(u^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)}^2)}^2.$$

Apparently,

$$\begin{array}{l}\mathcal{F}(s,v\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }v\left(s\right))\le \theta \left(s\right){\phi }^{{\displaystyle \frac{1}{q_1-1}}}\left(v\right),\overline{\mathcal{F}}(s,u\left(s\right){,}^H{D}_{1^{+}}^{\varsigma }u\left(s\right))\le \overline{\theta }\left(s\right){\psi }^{{\displaystyle \frac{1}{q_2-1}}}\left(u\right),\\ \forall (t,x_0,x_1)\in [1,e]\times [0,+\infty )\times [0,+\infty ),\end{array}$$

where

$$\theta \left(t\right)={\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{1}{2}}{(1-lnt)}^{\frac{1}{2}}}},\overline{\theta }\left(t\right)={\displaystyle \frac{1}{4\pi {(lnt)}^{\frac{3}{4}}{(1-lnt)}^{\frac{3}{4}}}},$$

$$\phi \left(v\right)=v^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)}^2,\psi \left(u\right)=u^2+{{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)}^2;$$

hence, $\left(iii\right)$ holds. Taking $r=1>0$,

$$\begin{array}{l}{\displaystyle \frac{r}{max\left\{\phi \right(r\left)\right),\psi \left(\right(r\left)\right|\left)\right\}}}=1>max\left\{{\int }_1^e{\mathcal{G}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_1}\left(\theta \left(s\right)\right){\displaystyle \frac{ds}{s}},{\int }_1^e{\mathcal{H}}_1(e,s)\mathsf{{\rm Y}}{L}_{q_2}\left(\overline{\theta }\left(s\right)\right){\displaystyle \frac{ds}{s}}\right\}\\ =0.1682,\end{array}$$

so, $\left(iv\right)$ holds. Hence, all the conditions of Theorem 6 hold, which implies that Equation (28) has at least one positive solution.

Example 3. 

Consider the following boundary value problem:

$$\left\{\begin{array}{l}{L}_3\left({}^{H}D_{1^{+}}^{{\displaystyle \frac{5}{2}}}u\right)\left(t\right)+\mathcal{F}(t,v\left(t\right){,}^H{D}_{1+}^{\varsigma }v\left(t\right))=0,1<t<e,\\ L_2\left(D_{1^{+}}^{{\displaystyle \frac{5}{2}}}v\right)\left(t\right)+\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1+}^{\varsigma }u\left(t\right))=0,1<t<e,\\ u\left(1\right)=u^{\prime }\left(1\right)=0,u\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\eta }_{j}u\left({\xi }_j\right)+{\int }_1^{e}h\left(t\right)u\left(t\right)dB\left(t\right),\\ v\left(1\right)=v^{\prime }\left(1\right)=0,v\left(e\right)={\displaystyle \sum _{j=1}^{\infty }}{\overline{\eta }}_{j}v\left({\overline{\xi }}_j\right)+{\int }_1^e\overline{h}\left(t\right)v\left(t\right)d\overline{B}\left(t\right),\end{array}\right.$$

(29)

where

$$\mathcal{F}(t,v\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v\left(t\right))=4\pi {(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}{(v+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}v)+1)}^2,$$

$$\overline{\mathcal{F}}(t,u\left(t\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u\left(t\right))=4\pi {(lnt)}^{{\displaystyle \frac{3}{4}}}{(1-lnt)}^{{\displaystyle \frac{3}{4}}}{(u+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}u)+1)}^2.$$

By some calculations, we have

$$\begin{array}{l}\hspace{1em}|L_{q_1}(\mathcal{F}(s,v_1\left(s\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_1\left(s\right))-L_{q_1}(\mathcal{F}(s,v_2\left(s\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_2\left(s\right))|\\ {=|4\pi (lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}(v_1+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_1)+1)-8\pi {(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}(v_2+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_2)+1)|\\ \le 4\pi {\displaystyle \frac{1}{3}}{(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}|v_1-v_2|+8\pi {\displaystyle \frac{1}{3}}{(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}{|}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_1{-}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_2|\\ \le L_1{\theta }_1\left(s\right)|x_1-x_2|+L_2{\theta }_2\left(s\right)|y_1-y_2|,\end{array}$$

where $L_1=1,L_2=2,{\theta }_1\left(s\right)={\displaystyle \frac{1}{3}}4\pi {(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}},{\theta }_2\left(s\right)={\displaystyle \frac{8}{3}}\pi {(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}},$

$$\begin{array}{l}\hspace{1em}|L_{q_2}(\overline{\mathcal{F}}(s,u_1\left(s\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{u}_1\left(s\right))-L_{q_2}(\overline{\mathcal{F}}(s,u_2\left(s\right){,}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{u}_2\left(s\right))|\\ {=|4\pi (lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}(u_1+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{u}_1)+1)-8\pi {(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}(u_2+2{(}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{u}_2)+1)|\\ \le 4\pi {\displaystyle \frac{1}{3}}{(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}|v_1-v_2|+8\pi {\displaystyle \frac{1}{3}}{(lnt)}^{{\displaystyle \frac{1}{2}}}{(1-lnt)}^{{\displaystyle \frac{1}{2}}}{|}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_1{-}^H{D}_{1^{+}}^{{\displaystyle \frac{1}{2}}}{v}_2|\\ \le L_1{\theta }_1\left(s\right)|x_1-x_2|+L_2{\theta }_2\left(s\right)|y_1-y_2|\end{array},$$

$$|L_{q_2}\left(\overline{\mathcal{F}}(s,x_1,y_1)\right)-L_{q_2}\left(\overline{\mathcal{F}}(s,x_2,y_2)\right)|\le {\overline{L}}_1{\overline{\theta }}_1\left(s\right)|x_1-x_2|+{\overline{L}}_2{\overline{\theta }}_2\left(s\right)|y_1-y_2|,$$

where ${\overline{L}}_1=1,{\overline{L}}_2=2,{\overline{\theta }}_1\left(s\right)={\displaystyle \frac{1}{3}}4\pi {(lnt)}^{{\displaystyle \frac{3}{4}}}{(1-lnt)}^{{\displaystyle \frac{3}{4}}},{\overline{\theta }}_2\left(s\right)={\displaystyle \frac{8}{3}}\pi {(lnt)}^{{\displaystyle \frac{3}{4}}}{(1-lnt)}^{{\displaystyle \frac{3}{4}}},$ and

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\nu \right)}}\mathsf{{\rm Y}}\left(L_1{\theta }_1\left(s\right)+L_2{\theta }_1\left(s\right){\displaystyle \frac{1}{\mathsf{\Gamma }(\varsigma +1)}}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\frac{5}{2}\right)}}{\displaystyle \frac{1}{3}}\times 0.8067(1+2{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\frac{3}{2}\right)}})\approx 0.6588<1,$$

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\iota \right)}}\mathsf{\Xi }\left({\overline{L}}_1{\theta }_1\left(s\right)+{\overline{L}}_2{\overline{\theta }}_1\left(s\right){\displaystyle \frac{1}{\mathsf{\Gamma }(\varsigma +1)}}\right){\displaystyle \frac{1}{\mathsf{\Gamma }\left(\frac{5}{2}\right)}}{\displaystyle \frac{1}{3}}\times 0.8067(1+2{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\frac{3}{2}\right)}})\approx 0.6588<1.$$

Hence, all the conditions of Theorem 7 hold, which implies that Equation (29) has one unique solution.

It is worth mentioning that in this study, the nonlinear terms in the fractional-order differential equations exhibit a singularity that is one of the main innovations of the present research. Although singular nonlinear terms pose analytical difficulties, they can be controlled by an integrable function, which is why the solutions of the considered Hadamard fractional differential model are still stable and robust. Of course, in the future, we will strengthen the research on singular factors in practical engineering applications, especially in terms of solution stability or robustness.

5. Conclusions

The existence and uniqueness for positive solutions of a singular p-Laplacian Hadamard fractional-order differential equation with nonlocal integral and infinite-point boundary conditions are investigated. The methods used are a nonlinear alternative of Leray–Schauder-type Guo–Krasnoselskii’s fixed point theorem in cone and the Banach fixed point theorem, respectively. First, we derive the expression of the Green function, and then determine some properties of the developed Green function. Subsequently, we demonstrate the existence of solutions of Hadamard fractional differential equation with nonlinear singular conditions by Leray–Schauder-type Guo–Krasnoselskii’s fixed point theorem, respectively. Finally, we prove the uniqueness of the positive solution using Banach’s fixed point theorem. The existence results of Theorems 5 and 6 are obtained under the condition of singular nonlinearity, while the nonlinear term is continuous in much of the previous literature (e.g., see [15,18]), which is one of the main contributions of the present study. Of course, there are also some limitations to this study, such as the absence of complete numerical solutions. We plan to conduct further research on numerical solution examples on this type of equation. Additionally, we will explore more complex boundary conditions, such as extending the present interval from $(1,e)$ to $(1,+\infty )$ or extending the study to other types of fractional differential equations, including Caputo–Hadamard, Atangana–Baleanu Caputo, and so on.