Controllability of Fractional Complex Networks

Abstract

Controllability is a fundamental issue in the field of fractional complex network control, yet it has not received adequate attention in the past. This paper is dedicated to exploring the controllability of complex networks involving the Caputo fractional derivative. By utilizing the Cayley–Hamilton theorem and Laplace transformation, a concise proof is given to determine the controllability of linear fractional complex networks. Subsequently, leveraging the Schauder Fixed-Point theorem, controllability Gramian matrix, and fractional calculus theory, we derive controllability conditions for nonlinear fractional complex networks with a weighted adjacency matrix and Laplacian matrix, respectively. Finally, a numerical method for the controllability of fractional complex networks is obtained using Matlab (2021a)/Simulink (2021a). Three examples are provided to illustrate the theoretical results.

1. Introduction

In recent decades, due to the widespread existence of complex networks in nature and society, complex networks have been undergoing a period of rapid development in various interdisciplinary research fields, particularly in engineering [1], mathematics [2], physics [3], biology [4] and other related areas. The ultimate goal of researching complex networks is to control them to facilitate our lives. Despite significant efforts being dedicated to comprehending the interactions between complex networks and their dynamic behaviors, controlling these networks remains a prominent challenge [5].

In order to establish a framework for controlling complex networks, a fundamental and essential step is to study their controllability. Controllability ensures that by manipulating a subset of nodes with appropriate control inputs, every node within the network can be steered to the desired state [6,7]. Many scholars from the fields of control, physics, and mathematics [8,9,10,11] have been inspired by the pioneering paper on the controllability of complex networks [12]. Liu et al. [8] analyzed the controllability of discrete-time dynamic networks with both switching and fixed interaction topologies. Cai [9] utilized the condition number of a matrix as a metric to quantitatively assess controllability. Chen [10] incorporated pinning control strategies into the study of controllability in directed networks. Meanwhile, Whalen et al. [11] developed a group representational framework to tackle the controllability of nonlinear networks that exhibit explicit symmetries.

Due to its memory and hereditary properties, fractional calculus has garnered considerable attention across various scientific fields and is widely adopted in science and engineering [13,14,15,16,17,18,19,20]. Fractional operators have been integrated into traditional complex networks, significantly improving model accuracy. It is worth noting that while the controllability of integer-order complex networks is relatively mature, the controllability results of fractional networks are still in their infancy. Some papers have addressed the controllability of fractional systems [21,22,23,24,25], but only a few papers have delved into the controllability of fractional complex networks because of their inherent complexity and long memory characteristics. Zhang et al. [26] examined the controllability of linear fractional directed complex networks, and subsequently, they [27] extended this work to explore the controllability of linear fractional dynamical networks with specific topological structures. However, given the ubiquitous nature of nonlinearity, it is imperative to consider the control of fractional complex networks with nonlinear dynamics. As far as we know, no research has yet been explored on the controllability of nonlinear fractional complex networks.

Motivated by the above analysis, this manuscript aims to address the controllability issues for fractional complex networks through rigorous mathematical theory. The distinctive contributions are summarized as follows: (i) A concise technique is established to prove the controllability of fractional complex networks with linear dynamic behavior. This allows the controllability of similar networks to be easily determined. (ii) For the first time, nonlinear fractional complex networks with weighted adjacency matrices or Laplacian matrices are shown to be controllable, effectively making up for the deficiency left by existing methods. (iii) Matlab/Simulink is used to obtain a numerical implementation for the controllability of fractional complex networks. Three examples are presented to validate theoretical results.

The remainder of this paper is outlined as follows: Section 2 recalls necessary definitions and Lemmas, Section 3 provides a more concise proof, Section 4 contains the main results, Section 5 presents three corresponding examples, and finally, a brief conclusion is given.

2. Preliminaries

This section presents algebraic graph theory and some necessary theories since we will use them later.

A graph is defined by $\mathbb{G}=(\mathbb{V},\mathbb{E})$, where $\mathbb{V}=\{v_1,v_2,\dots ,v_N\}$ and $\mathbb{E}=\{(v_j,v_i),v_j,v_i\in \mathbb{V}\}\subset \mathbb{V}\times \mathbb{V}$ denote node sets and link sets, respectively. Additionally, $(v_j,v_i)\in \mathbb{E}$ represents a link from node $v_j$ to node $v_i$. The concepts of a directed graph, undirected graph, and adjacency matrix can be found in [28,29,30].

Definition 1

([31]). The Caputo fractional derivative of order p of a function f is defined by

$$\begin{array}{c}\hfill {}_C{\mathcal{D}}_{0,t}^{p}f(t)=\frac{1}{\Gamma (n-p)}{\int }_0^t{(t-\varsigma )}^{n-p-1}{f}^{(n)}(\varsigma )\mathrm{d}\varsigma ,\end{array}$$

(1)

where $n-1<p\le n\in \mathbb{N}$ and $\Gamma (·)$ is the Gamma function.

Definition 2

([6]). The two-parameter Mittag–Leffler matrix function for a matrix $A\in {\mathbb{R}}^{N\times N}$ is defined as

$$\begin{array}{cc}\hfill & E_{p,q}(A)={\displaystyle \sum _{k=0}^{\infty }}\frac{A^k}{\Gamma (pk+q)},p,q>0.\hfill \end{array}$$

Note that when $q=1$, $E_{p,1}(A)=E_p(A)$ becomes a one-parameter Mittag–Leffler matrix function. Additionally, the Laplace transform of $t^{q-1}{E}_{p,q}(\pm A{t}^p)$ is given by

$$\begin{array}{c}\hfill \mathcal{L}\left\{t^{q-1}{E}_{p,q}(\pm A{t}^p);s\right\}=\frac{s^{p-q}}{s^{p}I\mp A}.\end{array}$$

Lemma 1

([32]). For $n-1<p\le n\in \mathbb{N}$, the Laplace transform of Caputo fractional derivative is given by

$$\begin{array}{c}\hfill \mathcal{L}\left\{{}_C{\mathcal{D}}_{0,t}^{p}f(t);s\right\}=s^{p}F(s)-{\displaystyle \sum _{k=0}^{n-1}}{s}^{p-k-1}{f}^{(k)}(0).\end{array}$$

(2)

In particular, if $0<p\le 1$, then

$$\begin{array}{c}\hfill \mathcal{L}\left\{{}_C{\mathcal{D}}_{0,t}^{p}f(t);s\right\}=s^{p}F(s)-s^{p-1}f(0),\end{array}$$

(3)

where $F(s)=\mathcal{L}\left\{f(t);s\right\}$.

Lemma 2

(Schauder Fixed-Point theorem [33]). Let M be a non-empty, closed, bounded, convex subset of a Banach space X. Suppose $G:M\to M$ is a compact operator, then G has a fixed point.

3. Controllability Analysis of Linear Fractional Complex Networks

In this part, a fractional complex network with linear dynamic behavior is described as follows:

$$\begin{array}{cc}\hfill & {}_C{\mathcal{D}}_{0,t}^p{x}_i(t)=c_i{x}_i(t)+{\displaystyle \sum _{j=1}^N}{a}_{ij}{x}_j(t)+{\displaystyle \sum _{k=1}^m}{b}_{ik}{u}_k(t),i=1,2,\cdots ,N,\hfill \end{array}$$

(4)

in which $0<p\le 1$, $x_i(t)\in \mathbb{R}$ represents the state of the node i, $c_i{x}_i(t)$ denotes the intrinsic dynamics, and $a_{ij}\ge 0$ denotes the weight of the network. Here, m represents the number of controllers and $u_k(t)\in \mathbb{R}$ is the outer controller. For example, the $u_k(t)$ can stand for the command from a leader in a social network or the signal from equipment in a sensor network. $b_{ik}$ represents the signal strength of the outer controller.

Let $x(t)={[x_1(t),x_2(t),\cdots ,x_N(t)]}^T\in {\mathbb{R}}^N$ be the whole state of the network (4), and $u(t)={[u_1(t),u_2(t),\cdots ,u_m(t)]}^T\in {\mathbb{R}}^m$ be the total outer controller. The linear network (4) can be reformulated as

$$\begin{array}{c}\hfill {}_C{\mathcal{D}}_{0,t}^{p}x(t)=(A+C)x(t)+Bu(t),\end{array}$$

(5)

where A represents the weighted (unweighted) adjacency matrix, $C=diag\{c_1,c_2,\dots ,c_N\}$, and $B\in {\mathbb{R}}^{N\times m}$ stands for the control matrix.

Definition 3

([7]). For a finite time $t_f$, any initial state $x(0)=x_0\in {\mathbb{R}}^N$ and any final state $x(t_f)=x_{t_f}\in {\mathbb{R}}^N$, if there exists a controller $u(t),t\in I=[0,t_f]$ that satisfies $x(t_f,x_0,u(t))=x_{t_f}$, then the linear fractional complex network (4) is called controllable on I.

Lemma 3

([34]). The linear fractional complex network (4) is controllable if the controllability Gramian matrix

$$\begin{array}{cc}\hfill W_F=& {\int }_0^{t_f}{E}_{p,p}((A+C){(t_f-\varsigma )}^p)B{B}^{*}{E}_{p,p}({(A+C)}^{*}{(t_f-\varsigma )}^p)\mathrm{d}\varsigma \hfill \end{array}$$

(6)

is invertible.

For the linear fractional complex network (4), a controllability result is proposed in [26], but we give a more concise proof below.

Theorem 1.

The fractional complex network (4) is controllable if $N\times (Nm)$ controllability matrix

$$\begin{array}{c}\hfill Q_F=[B,(A+C)B,\cdots ,{(A+C)}^{N-1}B]\end{array}$$

(7)

is of full rank, which is $rank(Q_F)=N$.

Proof. 

Using the Cayley–Hamilton theorem [35], one gets

$$\begin{array}{c}\hfill {(A+C)}^s={\displaystyle \sum _{k=0}^{N-1}}{a}_k^s{(A+C)}^k,s=N,N+1,\dots ,\infty .\end{array}$$

(8)

It immediately follows from (8) that

$$\begin{array}{cc}\hfill t^{p-1}{E}_{p,p}\left((A+C)t^p\right)=& {\displaystyle \sum _{k=0}^{N-1}}\frac{t^{pk+p-1}}{\Gamma (pk+p)}{(A+C)}^k+{\displaystyle \sum _{k=N}^{\infty }}\frac{t^{pk+p-1}}{\Gamma (pk+p)}{(A+C)}^k\hfill \\ \hfill =& {\displaystyle \sum _{k=0}^{N-1}}{\phi }_k(t){(A+C)}^k,\hfill \end{array}$$

(9)

where ${\phi }_k(t)=\frac{t^{pk+p-1}}{\Gamma (pk+p)}+{\sum }_{s=N}^{\infty }\frac{t^{ps+p-1}}{\Gamma (ps+p)}{a}_k^s,k=0,1,\dots ,N-1$.

By virtue of Laplace transformation and inverse Laplace transformation, the solution of (5) can be derived as follows:

$$\begin{array}{cc}\hfill x(t)=& E_p\left((A+C)t^p\right)x_0+{\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}((A+C){(t-\varsigma )}^p)Bu(\varsigma )\mathrm{d}\varsigma .\hfill \end{array}$$

(10)

When $t=t_f$, from (9) and (10), one has

$$\begin{array}{cc}\hfill x(t_f)=& E_p((A+C)t_f^p)x_0+{\int }_0^{t_f}{(t_f-\varsigma )}^{p-1}{E}_{p,p}((A+C){(t_f-\varsigma )}^p)Bu(\varsigma )\mathrm{d}\varsigma \hfill \\ \hfill =& E_p((A+C)t_f^p)x_0+{\displaystyle \sum _{k=0}^{N-1}}{\int }_0^{t_f}{\phi }_k(t_f-\varsigma ){(A+C)}^{k}Bu(\varsigma )\mathrm{d}\varsigma .\hfill \end{array}$$

(11)

Let

$$\begin{array}{c}\hfill \Psi =E_p((A+C)t_f^p)x_0.\end{array}$$

(12)

Then, applying (11) and (12) leads to

$$\begin{array}{cc}\hfill x(t_f)-\Psi & ={\displaystyle \sum _{k=0}^{N-1}}{(A+C)}^{k}B{\int }_0^{t_f}{\phi }_k(t_f-\varsigma )u(\varsigma )\mathrm{d}\varsigma \hfill \\ \hfill & =\left[B,(A+C)B,\cdots ,{(A+C)}^{N-1}B\right]\left[\begin{array}{c}{\xi }_0\\ {\xi }_1\\ ⋮\\ {\xi }_{N-1}\end{array}\right],\hfill \end{array}$$

(13)

in which ${\xi }_k={\int }_0^{t_f}{\phi }_k(t_f-\varsigma )u(\varsigma )\mathrm{d}\varsigma ,k=0,1,\cdots ,N-1$. Note that for any $x_0$ and $x_{t_f}$ in ${\mathbb{R}}^N$, the adequacy and necessity condition with an external controller vector $u(t)$ satisfying (13) is that

$$\begin{array}{c}\hfill \mathrm{rank}\left[B,(A+C)B,\cdots ,{(A+C)}^{N-1}B\right]=N.\end{array}$$

(14)

The theorem is, thus, proved. □

Remark 1.

Noticeably, the linear fractional complex network (4) denoted by a pair of matrices $(A+C,B)$ is controllable if the rank of $Q_F$ equals N. In particular, Theorem 1 is also true for network (5) with matrix $C=0$, i.e., when it (5) degenerates into

$$\begin{array}{c}\hfill {}_C{\mathcal{D}}_{0,t}^{p}x(t)=Ax(t)+Bu(t),\end{array}$$

(15)

a pair of $(A,B)$ is controllable as well.

4. Controllability Analysis of Nonlinear Fractional Complex Networks

Complex networks with different topology structures can describe different connection relationships in complex worlds. This section mainly focuses on nonlinear fractional complex networks with a weighted adjacency matrix and Laplacian matrix.

4.1. Nonlinear Networks Represented by a Weighted Adjacency Matrix

Consider a nonlinear fractional complex network with a weighted adjacency matrix depicted by

$$\begin{array}{cc}\hfill {}_C{\mathcal{D}}_{0,t}^p{x}_i(t)=f_i(x(t))+{\displaystyle \sum _{j=1}^N}{a}_{ij}{x}_j(t)+& {\displaystyle \sum _{k=1}^m}{b}_{ik}{u}_k(t),i=1,2,\cdots ,N,\hfill \end{array}$$

(16)

where $0<p\le 1$, $x_i(t)\in \mathbb{R}$ expresses the state of node i. $a_{ij}\ge 0$ denotes the weight of a link $(j,i)$, m represents the number of controllers, $u_k(t)\in \mathbb{R}$ is the outer controller, and $f_i(x(t)):{\mathbb{R}}^N\to \mathbb{R}$ is the nonlinear continuous function.

The nonlinear fractional complex network (16) can be recast into the following vector form

$$\begin{array}{cc}\hfill {}_C{\mathcal{D}}_{0,t}^{p}x(t)& =f(x(t))+Ax(t)+Bu(t).\hfill \end{array}$$

(17)

Here, $x(t)={[x_1(t),x_2(t),\cdots ,x_N(t)]}^T\in {\mathbb{R}}^N$ expresses the state vector; $u(t)={[u_1(t),u_2(t),\cdots ,u_m(t)]}^T\in {\mathbb{R}}^m$ represents the total outer controller; $A={(a_{ij})}_{N\times N}$ stands for the weighted adjacency matrix; $B={(b_{ik})}_{N\times m}$ represents the control matrix; $f(x(t))={[f_1(x(t)),f_2(x(t)),\dots ,f_N(x(t))]}^T:{\mathbb{R}}^N\to {\mathbb{R}}^N$ is the nonlinear vector function.

Similar to Definition 3, the definition of controllability for network (16) can also be given.

Henceforth, let us make the following assumptions:

$({\mathcal{A}}_1)$ There is a positive constant M that satisfies

$$\begin{array}{cc}\hfill & \parallel f(x(t)\parallel \le M,\mathrm{for}t\in I.\hfill \end{array}$$

$({\mathcal{A}}_2)$ The vector function $f(x(t))$ that is nonlinear meets the Lipschitz condition in vector form as follows:

$$\begin{array}{cc}\hfill & \parallel f(x(t))-f(y(t))\parallel \le k\parallel x(t)-y(t)\parallel ,\hfill \end{array}$$

where $k>0$, $t\in I$, and $x(t),y(t)\in {\mathbb{R}}^N$ are any vectors.

$({\mathcal{A}}_3)$ Let

$$\begin{array}{cc}\hfill & a_1=\underset{t,\varsigma \in I}{sup}\{\parallel E_{p,p}(A{(t-\varsigma )}^p)\parallel \},\hfill \\ \hfill & a_2=\underset{t,\varsigma \in I}{sup}{\left\{\right|(t-\varsigma )}^{p-2}|\parallel E_{p,p-1}(A{(t-\varsigma )}^p)\parallel \},\hfill \\ \hfill & a_3=\underset{t\in I}{sup}\left\{\right|t^{p-1}|\parallel A{E}_{p,p}(A{t}^p)x_0\parallel \},\hfill \\ \hfill & b_1=\parallel B\parallel \parallel B^{*}\parallel \parallel W_F^{-1}\parallel ,b_2=\underset{t\in I}{max}\{\parallel E_p(A{t}^p)x_0\parallel \},\hfill \\ \hfill & b_3=\parallel y_1\parallel +b_2,c_1=a_1^3{b}_1{p}^{-1}{t}_f^{p+1}k,\hfill \\ \hfill & c_2=\frac{a_1^2{a}_2}{p(2-p)}{b}_1{t}_f^{2}k,r=max\{r_1,r_2,1\},\hfill \\ \hfill & r_1=b_2+a_1{p}^{-1}{t}_f^{p}M+a_1^2{t}_f{b}_1(b_3+a_1{p}^{-1}{t}_f^{p}M),\hfill \\ \hfill & r_2=\frac{t_f^{1-p}}{\Gamma (2-p)}(a_3+a_2{t}_{f}M+\frac{a_1{a}_2}{2-p}{b}_1{t}_f^{2-p}(b_3+a_1{p}^{-1}{t}_f^{p}M)).\hfill \end{array}$$

Theorem 2.

Assume that conditions $({\mathcal{A}}_1)$ – $({\mathcal{A}}_3)$ are satisfied and system (15) is controllable, then the nonlinear fractional complex network (16) with a weighted adjacency matrix is controllable on I.

Proof. 

Give a Banach space

$$\begin{array}{c}\hfill X=\left\{x(t):x^{\prime }(t)\in C(I,{\mathbb{R}}^N)\mathrm{and}{}_C{\mathcal{D}}_{0,t}^{p}x(t)\in C(I,{\mathbb{R}}^N)\right\},\end{array}$$

which is endowed with the norm

$$\begin{array}{c}\hfill {\parallel x(t)\parallel }_X=max\{\parallel x(t)\parallel ,\parallel {}_C{\mathcal{D}}_{0,t}^{p}x(t)\parallel \}.\end{array}$$

By utilizing (15), it is possible to construct a controller $u(t)$ that can regulate any $x(t)$. In this case, the controller $u(t)$ can be constructed as

$$\begin{array}{cc}\hfill u(t)=& {(t_f-t)}^{1-p}{B}^{*}{E}_{p,p}(A^{*}{(t_f-t)}^p)W_F^{-1}\left[y_1-E_p(A{t}_f^p)x_0\right.\hfill \\ \hfill & -{\int }_0^{t_f}{(t_f-\varsigma )}^{p-1}{E}_{p,p}(A{(t_f-\varsigma )}^p)f(x(\varsigma ))\mathrm{d}\varsigma ].\hfill \end{array}$$

(18)

Now, we will prove that the nonlinear operator $G:X\to X$ has a fixed point, which is also a solution of (17). The G is designed as

$$\begin{array}{cc}\hfill (Gx)(t)=& E_p(A{t}^p)x_0+{\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)f(x(\varsigma ))\mathrm{d}\varsigma \hfill \\ \hfill & +{\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)Bu(\varsigma )\mathrm{d}\varsigma .\hfill \end{array}$$

(19)

Substituting (18) into (19) yields

$$\begin{array}{cc}\hfill (Gx)(t)=& E_p(A{t}^p)x_0+{\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)f(x(\varsigma ))\mathrm{d}\varsigma \hfill \\ \hfill & +{\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)B{B}^{*}{(t_f-\varsigma )}^{1-p}\hfill \\ \hfill & \times E_{p,p}(A^{*}{(t_f-\varsigma )}^p)W_F^{-1}\left[y_1-E_p(A{t}_f^p)x_0\right.\hfill \\ \hfill & -{\int }_0^{t_f}{(t_f-\omega )}^{p-1}{E}_{p,p}(A{(t_f-\omega )}^p)f(x(\omega ))\mathrm{d}\omega ]\mathrm{d}\varsigma .\hfill \end{array}$$

(20)

If the nonlinear operator G satisfies $(Gx)(t)=x(t)$, then $(Gx)(t_f)=x(t_f)=y_1$ in view of Lemma 3; that is, the nonlinear fractional complex network (16) can be steered from initial state $x_0$ to desired final state $y_1$ by the controller $u(t)$ within a finite time $t_f$. By assuming $({\mathcal{A}}_3)$ and using Equation (20), it is true that

$$\begin{array}{c}\hfill \parallel (Gx)(t)\parallel \le r_1.\end{array}$$

(21)

Taking into account derivatives of $(Gx)(t)$, one gets

$$\begin{array}{c}\hfill {\parallel (Gx)}^{{}^{\prime }}(t)\parallel \le r_2{t}_f^{p-1}\Gamma (2-p).\end{array}$$

(22)

From (22), it follows that

$$\begin{array}{cc}\hfill \parallel {}_C{\mathcal{D}}_{0,t}^p(Gx)(t)\parallel \le & \frac{1}{\Gamma (1-p)}{\int }_0^t{\parallel (t-\varsigma )}^{-p}{\parallel \parallel (Gx)}^{{}^{\prime }}(\varsigma )\parallel \mathrm{d}\varsigma \hfill \\ \hfill =& r_2.\hfill \end{array}$$

(23)

Define the subspace of X as $B_r={\{x(t)\in X:\parallel x(t)\parallel }_X\le r\}$. It is easy to see that the set $B_r$ is closed, bounded and convex. Let $x(t)\in B_r$, from (21) and (23), one has

$$\begin{array}{c}\hfill {\parallel (Gx)(t)\parallel }_X=max\{\parallel (Gx)(t)\parallel ,\parallel {}_C{\mathcal{D}}_{0,t}^p(Gx)(t)\parallel \}\le r.\end{array}$$

Thus, we obtain that the G maps $B_r$ into itself.

In what follows, we will prove that the G is continuous on $B_r$. Let $\left\{x_n(t)\right\}$ be a sequence of functions in $B_r$ with

$$\begin{array}{c}\hfill \parallel x_n(t)-x(t)\parallel \to 0\mathrm{as}n\to \infty ,t\in I.\end{array}$$

It can be deduced directly that

$$\begin{array}{cc}\hfill & \parallel (G{x}_n)(t)-(Gx)(t)\parallel \hfill \\ \hfill \le & \parallel {\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)(f(x_n(\varsigma ))-f(x(\varsigma )))\mathrm{d}\varsigma \parallel \hfill \\ \hfill & +\parallel {\int }_0^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)B{B}^{*}{(t_f-\varsigma )}^{1-p}{E}_{p,p}(A^{*}{(t_f-\varsigma )}^p)\hfill \\ \hfill & \times W_F^{-1}\left[{\int }_0^{t_f}{(t_f-\omega )}^{p-1}{E}_{p,p}(A{(t_f-\omega )}^p)\right.(f(x_n(\omega ))-f(x(\omega )))\mathrm{d}\omega ]\mathrm{d}\varsigma \parallel \hfill \\ \hfill \le & a_1{p}^{-1}{t}_f^{p}k\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}+c_1\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}\hfill \\ \hfill =& (a_1{p}^{-1}{t}_f^{p}k+c_1)\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill & \parallel {(G{x}_n)}^{{}^{\prime }}(t)-{(Gx)}^{{}^{\prime }}(t)\parallel \hfill \\ \hfill \le & \parallel {\int }_0^t{(t-\varsigma )}^{p-2}{E}_{p,p-1}(A{(t-\varsigma )}^p)(f(x_n(\varsigma ))-f(x(\varsigma ))\mathrm{d}\varsigma \parallel \hfill \\ \hfill & +\parallel {\int }_0^t{(t-\varsigma )}^{p-2}{E}_{p,p-1}(A{(t-\varsigma )}^p)B{B}^{*}{(t_f-\varsigma )}^{1-p}{E}_{p,p}(A^{*}{(t_f-\varsigma )}^p)\hfill \\ \hfill & \times W_F^{-1}\left[{\int }_0^{t_f}{(t_f-\omega )}^{p-1}{E}_{p,p}(A{(t_f-\omega )}^p)\right.(f(x_n(\omega ))-f(x(\omega )))\mathrm{d}\omega ]\mathrm{d}\varsigma \parallel \hfill \\ \hfill \le & a_2{t}_{f}k\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}+c_2\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}\hfill \\ \hfill =& (a_2{t}_{f}k+c_2)\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}.\hfill \end{array}$$

(25)

From (25), one obtains

$$\begin{array}{cc}\hfill & \parallel {}_C{\mathcal{D}}_{0,t}^p(G{x}_n)(t)-{}_C{\mathcal{D}}_{0,t}^p(Gx)(t)\parallel \hfill \\ \hfill =& \parallel \frac{1}{\Gamma (1-p)}{\int }_0^t{(t-\varsigma )}^{-p}({(G{x}_n)}^{{}^{\prime }}(\varsigma )-{(Gx)}^{{}^{\prime }}(\varsigma ))\mathrm{d}\varsigma \parallel \hfill \\ \hfill \le & \frac{t_f^{1-p}}{\Gamma (2-p)}(a_2{t}_{f}k+c_2)\underset{t\in I}{max}\{\parallel x_n(t)-x(t)\parallel \}.\hfill \end{array}$$

(26)

Combining (24) and (26) yields

$$\begin{array}{cc}\hfill & \parallel (G{x}_n)(t)-(Gx)(t){\parallel }_X\hfill \\ \hfill =& max\{\parallel (G{x}_n)(t)-(Gx)(t)\parallel ,\parallel {}_C{\mathcal{D}}_{0,t}^p(G{x}_n)(t)-{}_C{\mathcal{D}}_{0,t}^p(Gx)(t)\parallel \}\to 0\mathrm{as}n\to \infty .\hfill \end{array}$$

Thus, the nonlinear operator G is continuous on $B_r$.

Furthermore, we will demonstrate that the set $G(B_r)$ is relatively compact. Given that $x(t)\in B_r,t,\tau \in I,0<t<\tau <t_f$, it is shown that

$$\begin{array}{cc}\hfill & \parallel (Gx)(t)-(Gx)(\tau )\parallel \hfill \\ \hfill \le & \parallel E_p(A{t}^p)-E_p(A{\tau }^p)\parallel \parallel x_0\parallel +\parallel {\int }_{\tau }^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)f(x(\varsigma ))\mathrm{d}\varsigma \parallel \hfill \\ \hfill & +\parallel {\int }_0^{\tau }[{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)-{(\tau -\varsigma )}^{p-1}{E}_{p,p}(A{(\tau -\varsigma )}^p)]f(x(\varsigma ))\mathrm{d}\varsigma \parallel \hfill \\ \hfill & +\parallel {\int }_{\tau }^t{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)B{B}^{*}{(t_f-\varsigma )}^{1-p}{E}_{p,p}(A^{*}{(t_f-\varsigma )}^p)\hfill \\ \hfill & \times W_F^{-1}\left[y_1-E_p(A{t}_f^p)x_0\right.-{\int }_0^{t_f}{(t_f-\omega )}^{p-1}{E}_{p,p}(A{(t_f-\omega )}^p)f(x(\omega ))\mathrm{d}\omega ]\mathrm{d}\varsigma \parallel \hfill \\ \hfill & +\parallel {\int }_0^{\tau }[{(t-\varsigma )}^{p-1}{E}_{p,p}(A{(t-\varsigma )}^p)-{(\tau -\varsigma )}^{p-1}{E}_{p,p}(A{(\tau -\varsigma )}^p)]B{B}^{*}\hfill \\ \hfill & \times {(t_f-\varsigma )}^{1-p}{E}_{p,p}(A^{*}{(t_f-\varsigma )}^p)W_F^{-1}\left[y_1-E_p(A{t}_f^p)x_0\right.\hfill \\ \hfill & -{\int }_0^{t_f}{(t_f-\omega )}^{p-1}{E}_{p,p}(A{(t_f-\omega )}^p)f(x(\omega ))\mathrm{d}\omega ]\mathrm{d}\varsigma \parallel \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \parallel {}_C{\mathcal{D}}_{0,t}^p(Gx)(t)-{}_C{\mathcal{D}}_{0,t}^p(Gx)(\tau )\parallel \hfill \\ \hfill \le & \frac{1}{\Gamma (1-p)}\left(\parallel {\int }_{\tau }^t{(t-\varsigma )}^{-p}{(Gx)}^{{}^{\prime }}(\varsigma )\mathrm{d}\varsigma \parallel \right.+\parallel {\int }_0^{\tau }[{(t-\varsigma )}^{-p}-{(\tau -\varsigma )}^{-p}]{(Gx)}^{{}^{\prime }}(\varsigma )\mathrm{d}\varsigma \parallel ).\hfill \end{array}$$

Clearly, one has

$$\begin{array}{cc}\hfill & {\parallel (Gx)(t)-(Gx)(\tau )\parallel }_X\hfill \\ \hfill =& max\{\parallel (Gx)(t)-(Gx)(\tau )\parallel ,\parallel {}_C{\mathcal{D}}_{0,t}^p(Gx)(t)-{}_C{\mathcal{D}}_{0,t}^p(Gx)(\tau )\parallel \}\to 0\mathrm{as}t\to \tau .\hfill \end{array}$$

As a result, $G(B_r)$ is equicontinuous, and it is not difficult to obtain that $G(B_r)$ is uniformly bounded. By applying the well-known Arzelà–Ascoli theorem [33], the set $G(B_r)$ is relatively compact. Moreover, since the nonlinear operator G is continuous on the bounded set $B_r$ in X and maps it into the relatively compact set $G(B_r)$ in X, it can be conluded that G is compact. According to Lemma 2, the nonlinear operator G exists at a fixed point, which means the nonlinear fractional complex network (16) is controllable. This concludes the demonstration of Theorem 2. □

Remark 2.

The nonlinear fractional complex network (16) represented by a pair $(A,B,f)$ is controllable if the system $(A,B)$ is controllable and conditions $({\mathcal{A}}_1)-({\mathcal{A}}_3)$ hold.

4.2. Nonlinear Networks Represented by a Laplacian Matrix

A nonlinear fractional complex network with a Laplacian matrix can be described as follows:

$$\begin{array}{cc}\hfill {}_C{\mathcal{D}}_{0,t}^p{x}_i(t)=f_i(x(t))+{\displaystyle \sum _{j=1}^N}{a}_{ij}(x_j(t)-x_i(t))+& {\displaystyle \sum _{k=1}^m}{b}_{ik}{u}_k(t),i=1,2,\cdots ,N,\hfill \end{array}$$

(27)

in which all parameters represent the same meaning as (16).

The nonlinear network (27) can be recast as follows:

$$\begin{array}{cc}\hfill {}_C{\mathcal{D}}_{0,t}^{p}x(t)& =f(x(t))-Lx(t)+Bu(t),\hfill \end{array}$$

(28)

in which $L=D-A$ is the Laplacian matrix of network (27), $D=diag\{d_1,d_2,\dots ,d_N\}$, and $d_i={\sum }_{j=1,j\ne i}^N{a}_{ij}$ is the out-degree of node i.

Theorem 3.

If A is replaced by $-L$, conditions $({\mathcal{A}}_1)-({\mathcal{A}}_3)$ are true and system (15) is controllable, then network (27) with the Laplacian matrix can be controlled over interval I.

Proof of Theorem 3.

Similar to Theorem 2, Theorem 3 can be proved. Therefore, the proof is omitted here. □

5. Numerical Implementation

In this part, a numerical algorithm is given to demonstrate the controllability of the networks mentioned above with the help of the FOTF Toolbox [36]. Based on the maximum matching method [12], the minimum of the driven nodes of fractional complex networks can be obtained. For convenience, we take fractional order $p=0.5$ and the final time $t_f=1$.

Before the simulation, we will state two facts that are used to build the Matlab/Simulink simulation model.

Firstly, the control function u in (18) can be written as $u(t)=g(t)·h(t)$, where

$$\begin{array}{c}\hfill g(t)={(t_f-t)}^{1-p}{B}^{*}{E}_{p,p}(A^{*}{(t_f-t)}^p)W_F^{-1}\end{array}$$

and

$$\begin{array}{c}\hfill h(t)=y_1-E_p(A{t}_f^p)x_0-{\int }_0^{t_f}{(t_f-\varsigma )}^{p-1}{E}_{p,p}(A{(t_f-\varsigma )}^p)f(x(\varsigma ))\mathrm{d}\varsigma .\end{array}$$

The Simulink simulation model corresponding to control u is shown in Figure 1. Here, the Interpreted Matlab Function 1 and Interpreted Matlab Function 2 blocks are Matlab functions of $g(t)$ and $h(t)$, respectively. The integral in $h(t)$ is computed using the trapezoidal formula.

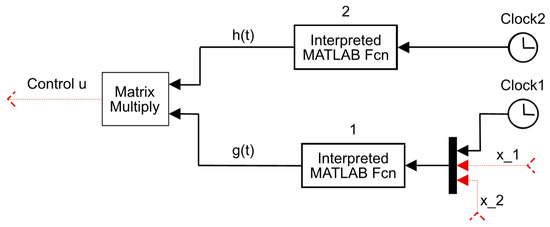
Figure 1. Simulink block diagram of the control u.

Secondly, the Caputo derivative Simulink block is constructed using the Riemann–Liouville block created by Professor Oustaloup with the combination of the classical integrator block. As we can see in Figure 2, by connecting a Riemann–Liouville differentiator of order $0.7$ to $y^{\prime }(t)$, the ${}_C{\mathcal{D}}_{0,t}^{0.3}y(t)$ signal can be defined.

Figure 2. The output $y(t)$ signal and its Caputo derivative of order $0.3$.

Example 1.

Consider a linear fractional complex network (4) comprising two nodes. The weighted adjacency matrix, control matrix, and diagonal matrix are presented as

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}0\hfill & \frac{1}{2}\hfill \\ 0\hfill & 0\hfill \end{array}\right],B=\left[\begin{array}{c}0\hfill \\ 2\hfill \end{array}\right],C=\left[\begin{array}{cc}0\hfill & 0\hfill \\ 0\hfill & \frac{1}{2}\hfill \end{array}\right],\end{array}$$

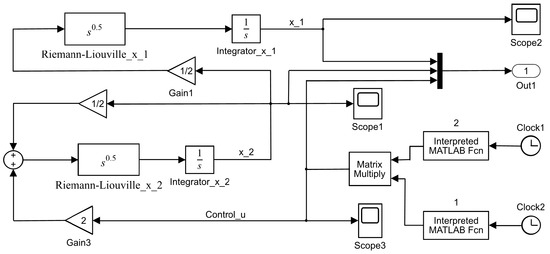
respectively. In the light of Theorem 1, the fractional complex network (4) with linear dynamic behavior can be controlled. Specifically, we used the Matlab/Simulink method. The block diagram of the simulation is depicted in Figure 3.

Figure 3. Matlab/Simulink block diagram for the network (4) in Example 1.

Here, the initial and final values of nodes $v_1$ and $v_2$ are taken as ${[x_1(0),x_2(0)]}^T={[0,-1]}^T$ and $y_1={[x_1(1),x_2(1)]}^T={[2+0.3k,2+0.3k]}^T,k=1,2,\dots ,5$, respectively. It is known that the Mittag–Leffler matrix function for matrix $A+C$ can be written as

$$\begin{array}{c}\hfill E_{0.5,0.5}((A+C)t^{0.5})=\left[\begin{array}{cc}{M}_1^2(t)& M_1(t)M_2(t)\\ M_1(t)M_2(t)& M_2^2(t)\end{array}\right],\end{array}$$

where $M_1(t)=E_{0.5,0.5}(0.5t^{0.5})-\frac{1}{\sqrt{\pi }}$ and $M_2(t)=E_{0.5,0.5}(0.5t^{0.5})$. The Gramian matrix of the network (4) is

$$\begin{array}{cc}\hfill W_F=& {\int }_0^1{E}_{0.5,0.5}((A+C){(1-\varsigma )}^{0.5})B{B}^{*}{E}_{0.5,0.5}({(A+C)}^{*}{(1-\varsigma )}^{0.5})\mathrm{d}\varsigma \hfill \\ \hfill =& 4{\int }_0^1\left[\begin{array}{cc}{M}_1^2(1-\varsigma )& M_1(1-\varsigma )M_2(1-\varsigma )\\ M_1(1-\varsigma )M_2(1-\varsigma )& M_2^2(1-\varsigma )\end{array}\right]\mathrm{d}\varsigma \hfill \\ \hfill =& \left[\begin{array}{cc}1.4507& 2.6830\\ 2.6830& 5.1886\end{array}\right].\hfill \end{array}$$

Using Matlab/Simulink, the controlled trajectories $x_1(t),x_2(t)$ and steering control

$$\begin{array}{cc}\hfill u(t)=& {(1-t)}^{0.5}{B}^{*}{E}_{0.5,0.5}(A^{*}{(1-t)}^{0.5})W_F^{-1}[y_1-E_{0.5}(A)x_0]\hfill \end{array}$$

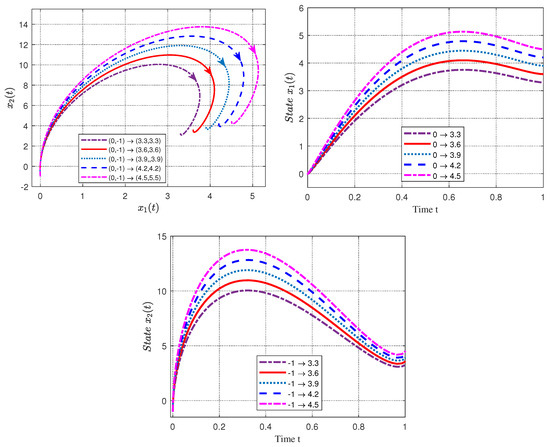
are computed and are depicted in Figure 4 and Figure 5. Then, we can see that a linear fractional complex network with two nodes can be steered from the initial value ${[0,-1]}^T$ to the desired value $y_1$.

Figure 4. The state trajectories of the linear fractional complex network in Example 1.

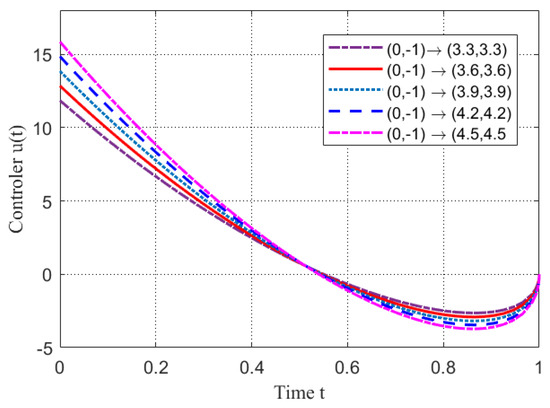
Figure 5. The trajectory of outer controller $u(t)$ imposed on node $v_2$ in Example 1.

Example 2.

Consider a nonlinear fractional complex network (16) comprising two nodes, where weighted adjacency matrix, control matrix, and nonlinear function $f(x(t))$ satisfying conditions $({\mathcal{A}}_1)-({\mathcal{A}}_3)$ are given as follows:

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}0\hfill & \frac{1}{2}\hfill \\ \frac{1}{2}\hfill & 0\hfill \end{array}\right],B=\left[\begin{array}{c}0\hfill \\ 2\hfill \end{array}\right],f(x(t))=\left[\begin{array}{c}0\hfill \\ \frac{1}{10}cos(x_2(t))\hfill \end{array}\right],\end{array}$$

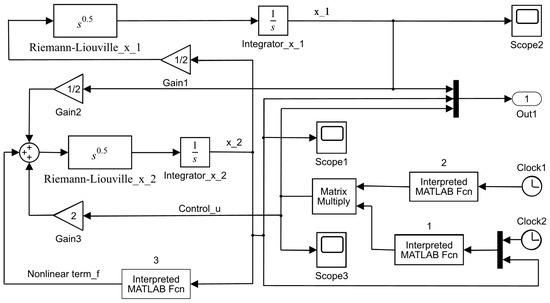
respectively. According to Remark 1, the system $(A,B)$ is controllable, which means that a nonlinear network (16) with a weighted adjacency matrix is controllable. To be specific, we used the Matlab/Simulink method. The block diagram of the simulation is depicted in Figure 6.

Figure 6. Matlab/Simulink block diagram for the network (16) in Example 2.

Here, the initial and final values of nodes $v_1$ and $v_2$ are taken as ${[x_1(0),x_2(0)]}^T={[1,-1]}^T$ and $z_1={[x_1(1),x_2(1)]}^T={[2+0.5k,1+0.5k]}^T,k=1,2,\dots ,5$, respectively. It is known that the Mittag–Leffler matrix function for a given matrix A can be written as

$$\begin{array}{c}\hfill E_{0.5,0.5}(A{t}^{0.5})=\left[\begin{array}{cc}{M}_2^2(t)& M_1(t)M_2(t)\\ M_1(t)M_2(t)& M_1^2(t)\end{array}\right],\end{array}$$

where

$$M_1(t)=\frac{1}{2}[E_{0.5,0.5}(0.5t^{0.5})+E_{0.5,0.5}(-0.5t^{0.5})]$$

and

$$M_2(t)=\frac{1}{2}[E_{0.5,0.5}(0.5t^{0.5})-E_{0.5,0.5}(-0.5t^{0.5})].$$

The corresponding Gramian matrix of network (16) is

$$\begin{array}{cc}\hfill W_F=& {\int }_0^1{E}_{0.5,0.5}(A{(1-\varsigma )}^{0.5})B{B}^{*}{E}_{0.5,0.5}(A^{*}{(1-\varsigma )}^{0.5})\mathrm{d}\varsigma \hfill \\ \hfill =& 4{\int }_0^1\left[\begin{array}{cc}{M}_2^2(1-\varsigma )& M_1(1-\varsigma )M_2(1-\varsigma )\\ M_1(1-\varsigma )M_2(1-\varsigma )& M_1^2(1-\varsigma )\end{array}\right]\mathrm{d}\varsigma \hfill \\ \hfill =& \left[\begin{array}{cc}0.7026\hfill & 1.1814\hfill \\ 1.1814\hfill & 2.1232\hfill \end{array}\right].\hfill \end{array}$$

Using Matlab/Simulink, the controlled trajectories $x_1(t),x_2(t)$ and steering control

$$\begin{array}{cc}\hfill u(t)=& {(1-t)}^{0.5}{B}^{*}{E}_{0.5,0.5}(A^{*}{(1-t)}^{0.5})W_F^{-1}\left[z_1-E_{0.5}(A)x_0\right.\hfill \\ \hfill & -{\int }_0^1{(1-\varsigma )}^{-0.5}{E}_{0.5,0.5}(A{(1-\varsigma )}^{0.5})f(x(\varsigma ))\mathrm{d}\varsigma ]\hfill \end{array}$$

are computed and are depicted in Figure 7 and Figure 8. Then, we can see that the nonlinear network with two nodes can be steered from the initial value ${[1,-1]}^T$ to the desired value $z_1$.

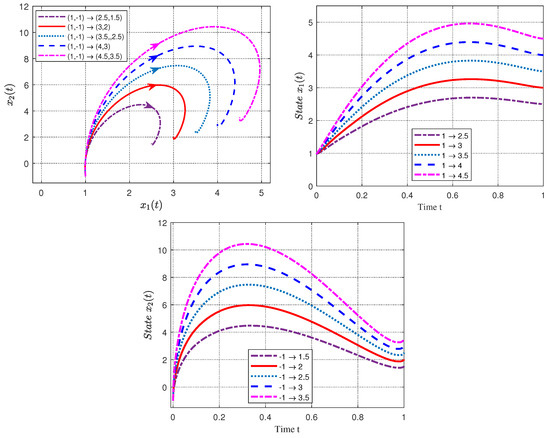
Figure 7. The state trajectories of a nonlinear fractional complex network with a weighted adjacency matrix in Example 2.

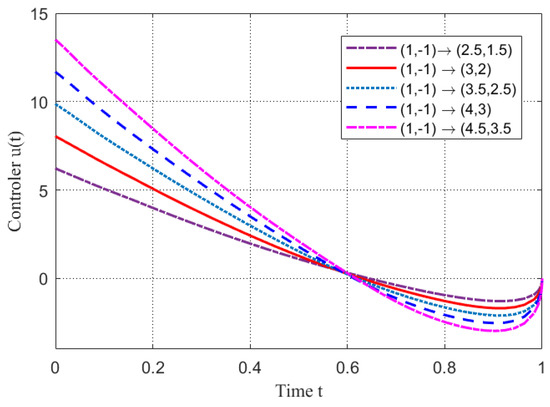
Figure 8. The trajectories of outer controller $u(t)$ imposed on node $v_2$ in Example 2.

Example 3.

Consider a nonlinear fractional directed network (27) with a Laplacian matrix. The Laplacian matrix, control matrix, and nonlinear function $f(x(t))$ satisfying conditions $({\mathcal{A}}_1)-({\mathcal{A}}_3)$ are given as

$$\begin{array}{c}\hfill L=\left[\begin{array}{cc}0.5& 0\\ -0.5& 0\end{array}\right],B=\left[\begin{array}{c}1\\ 0\end{array}\right],f(x(t))=\left[\begin{array}{c}\frac{1}{100}cos(x_2(t))\hfill \\ 0\hfill \end{array}\right],\end{array}$$

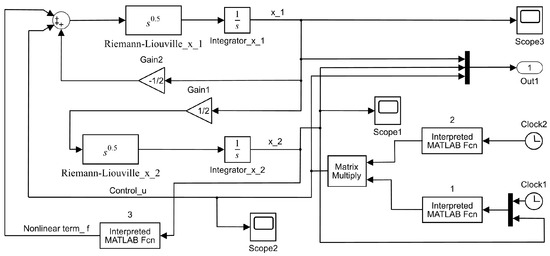
respectively. On the basis of Remark 1, the system $(-L,B)$ is controllable, which indicates that a nonlinear directed network (27) with a Laplacian matrix is controllable. Concretely, we used the Matlab/Simulink method. The block diagram of the simulation is depicted in Figure 9.

Figure 9. Matlab/Simulink block diagram for the network (27) in Example 3.

Here, the initial and final values of nodes $v_1$ and $v_2$ are taken as ${[x_1(0),x_2(0)]}^T={[-1,0]}^T$ and $w_1={[x_1(1),x_2(1)]}^T={[1+0.5k,3+0.5k]}^T,k=1,2,\dots ,5$, respectively. It is known that the Mittag–Leffler matrix function for a given matrix $-L$ can be written as

$$\begin{array}{c}\hfill E_{0.5,0.5}(-L{t}^{0.5})=\left[\begin{array}{cc}{M}_1^2(t)& M_1(t)M_2(t)\\ M_1(t)M_2(t)& M_2^2(t)\end{array}\right],\end{array}$$

where $M_1(t)=E_{0.5,0.5}(-0.5t^{0.5})$ and $M_2(t)=E_{0.5,0.5}(-0.5t^{0.5})+\frac{1}{\sqrt{\pi }}$. The corresponding Gramian matrix of the network (27) is

$$\begin{array}{cc}\hfill W_F=& {\int }_0^1{E}_{0.5,0.5}(-L{(1-\varsigma )}^{0.5})B{B}^{*}{E}_{0.5,0.5}(-L^{*}{(1-\varsigma )}^{0.5})\mathrm{d}\varsigma \hfill \\ \hfill =& {\int }_0^1\left[\begin{array}{cc}{M}_1^2(1-\varsigma )& M_1(1-\varsigma )M_2(1-\varsigma )\\ M_1(1-\varsigma )M_2(1-\varsigma )& M_2^2(1-\varsigma )\end{array}\right]\mathrm{d}\varsigma \hfill \\ \hfill =& \left[\begin{array}{cc}0.1157\hfill & 0.0727\hfill \\ 0.0727\hfill & 0.0571\hfill \end{array}\right].\hfill \end{array}$$

Using Matlab/Simulink, the controlled trajectories $x_1(t),x_2(t)$ and steering control

$$\begin{array}{cc}\hfill u(t)=& {(1-t)}^{0.5}{B}^{*}{E}_{0.5,0.5}(-L^{*}{(1-t)}^{0.5})W_F^{-1}\left[w_1-E_{0.5}(-L)x_0\right.\hfill \\ \hfill & -{\int }_0^1{(1-\varsigma )}^{-0.5}{E}_{0.5,0.5}(-L{(1-\varsigma )}^{0.5})f(x(\varsigma ))\mathrm{d}\varsigma ]\hfill \end{array}$$

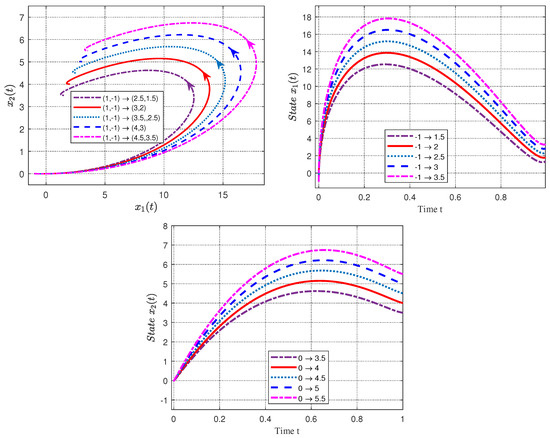
are computed and are depicted in Figure 10 and Figure 11. Then, we can see that a nonlinear fractional complex network with two nodes can be steered from the initial value ${[-1,0]}^T$ to the desired value $w_1$.

Figure 10. The state trajectories of a nonlinear fractional complex network with Laplacian matrix in Example 3.

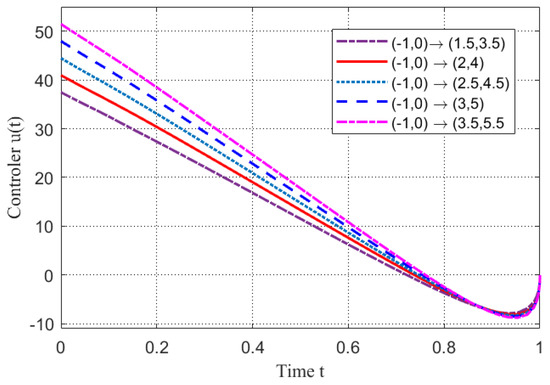
Figure 11. The trajectories of outer controller $u(t)$ imposed on node $v_1$ in Example 3.

6. Conclusions

Considering the fact that controllability is one of the most basic problems in the field of fractional complex network control and complex networks are typically nonlinear in real-world applications, this paper investigates the controllability problems of nonlinear fractional complex networks with a weighted adjacency matrix or Laplacian matrix. What is worth mentioning is that all controllability results obtained are proved by means of rigorous mathematical theory. Our findings indicate that the fractional complex networks with linear dynamic behavior can be controlled if the controllability matrix is of full rank. More importantly, the controllability criteria of nonlinear fractional complex networks are deduced, which provides a theoretical framework for the controllability analysis. Finally, three corresponding examples clearly show that it is convenient and efficient to obtain the controllability of given networks by using a newly developed technique. It is believed that this manuscript will play a crucial role in the controllability analysis and controller design of nonlinear fractional complex networks. In the future, we will continue to focus on the following interesting topics:

•

Solve the other control problems like optimal control, approximate controllability, etc.;

•

Develop the controllability and observability on complex fractional time-varying systems;

•

Implement controllability for complex time-varying systems numerically using the Matlab/Simulink method.