Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR
Abstract
1. Introduction
2. Experiments and Theory
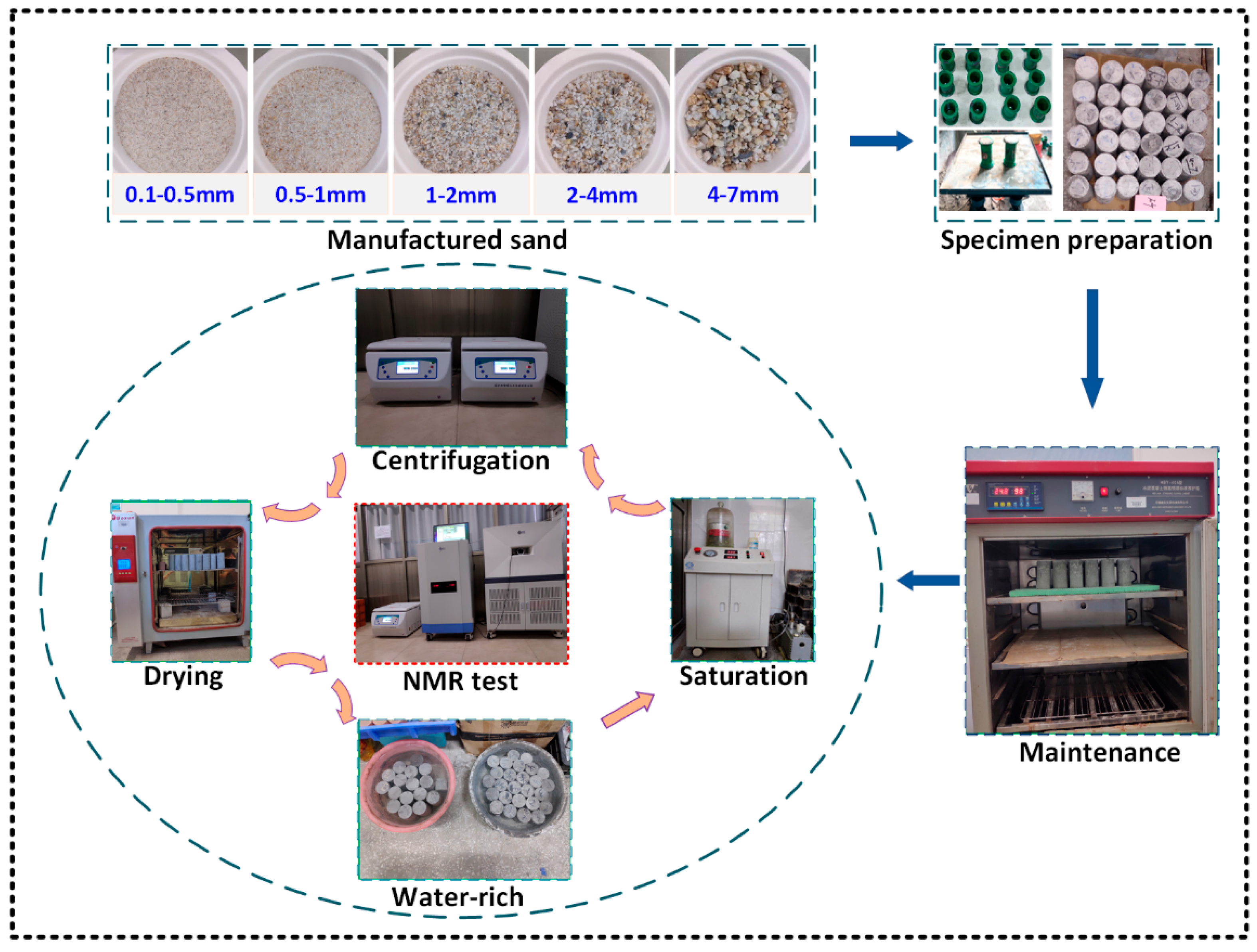
2.1. Materials and Experimental Procedures
- (1)
- Aggregate preparation. Manufactured sands were obtained by crushing limestone. To investigate the impact of aggregate particle size on the pore structure of mortar, five different graded manufactured sands were used: 0.1–0.5 mm, 0.5–1 mm, 1–2 mm, 2–4 mm, and 4–7 mm, the bulk densities of aggregates were 1334.76 kg/m3, 1346.48 kg/m3, 1358.70 kg/m3, 1362.88 kg/m3, and 1430.82 kg/m3, respectively. Particle size distribution followed a Gaussian distribution. Samples were prepared and marked as M1, M2, M3, M4, and M5 groups with three parallel samples. Additionally, to simulate realistic natural environments or conditions, the five types of aggregates were mixed to form a synthetic-graded aggregate that was used to create the M-syn group. The M-syn group encompassed the entire aggregate size range of the individual M groups (M1, M2, M3, M4, and M5).
- (2)
- Cement mortar was prepared by mixing pure water, P.O. 42.5 Portland cement, and manufactured sand in proportions of 0.28: 0.77: 1, respectively. The water–cement ratio was 0.36. The composition of the mortar is illustrated in Figure 2b. Specimens were shaped into cylinders with a diameter of 50 mm and a height of 100 mm according to the Rock Test Rules for Water Conservancy and Hydropower Projects (SL/T 264-2020). After filling, tamping, initial curing, and demoulding, mortars were placed in a curing chamber at 22 °C with a relative humidity of 98% for 28 days.
- (3)
- Water saturation treatment. Prior to conducting the NMR test, a vacuum saturation device operating at a pressure of 0.1 MPa was used to saturate the specimen’s pores with water for a duration of 48 h.
- (4)
- NMR test. The NMR tests on each specimen were conducted using the AiniMR-150 NMR system manufactured by Suzhou New-market Analytical Instruments Co., Ltd. [30]. The CPMG sequence was conducted with 0.1 ms echo time (TE = 0.1 ms), 3000 echos (NECH = 3000), 1000 ms waiting time (TW = 1000 ms), and 16 scans. NMR tests obtained the T2 distribution and porosity of the pores.
- (5)
- Centrifugation and drying. Saturated specimens were centrifuged at 4000 rpm for 90 min and then tested for NMR. Next, the specimens were dried at 50 °C for 20 h and tested again for NMR.
- (6)
- Water saturation curing. The mortars after 28 days of hydration were removed from the curing box and fully immersed in water within a container for 365 days.
2.2. Background Theory
2.2.1. NMR Theory
2.2.2. Fractal Theory Based on NMR
3. Results
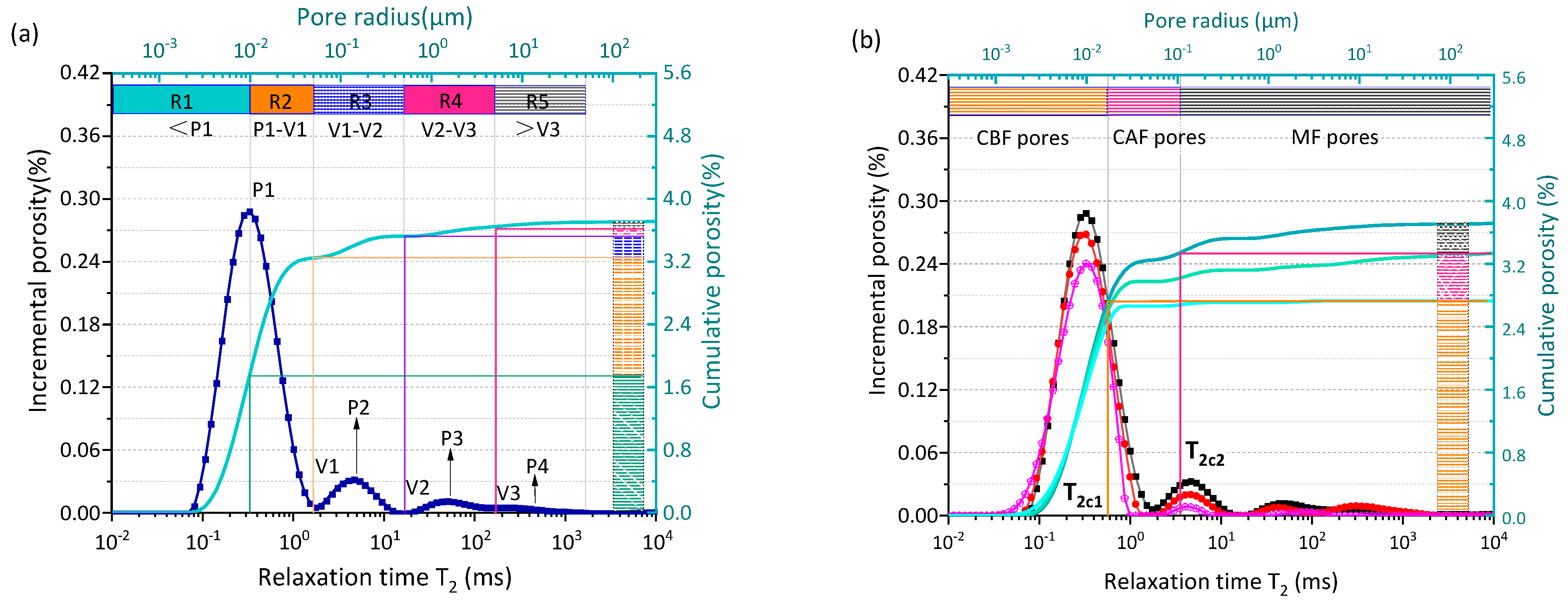
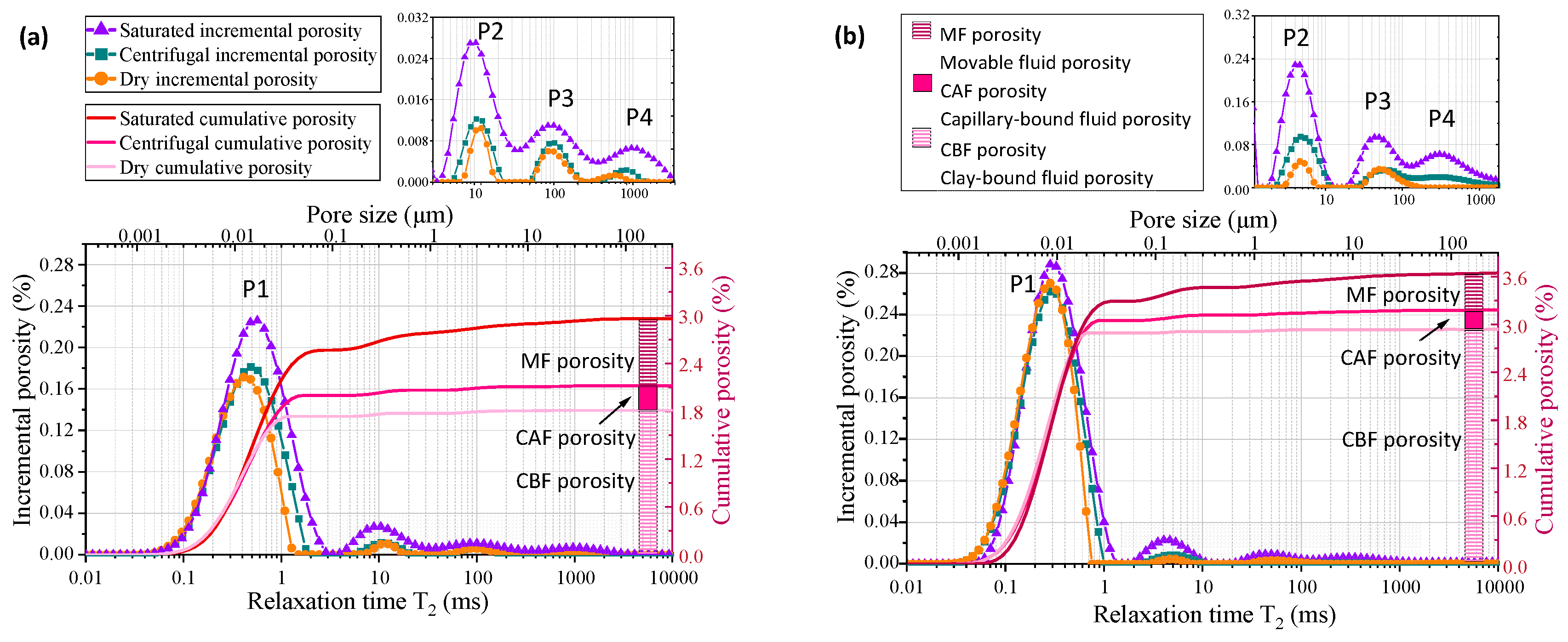
3.1. Evolution of T2 Spectr$um and Porosity
3.2. Evaluation of Pore Connectivity
3.3. The Permeability Variation
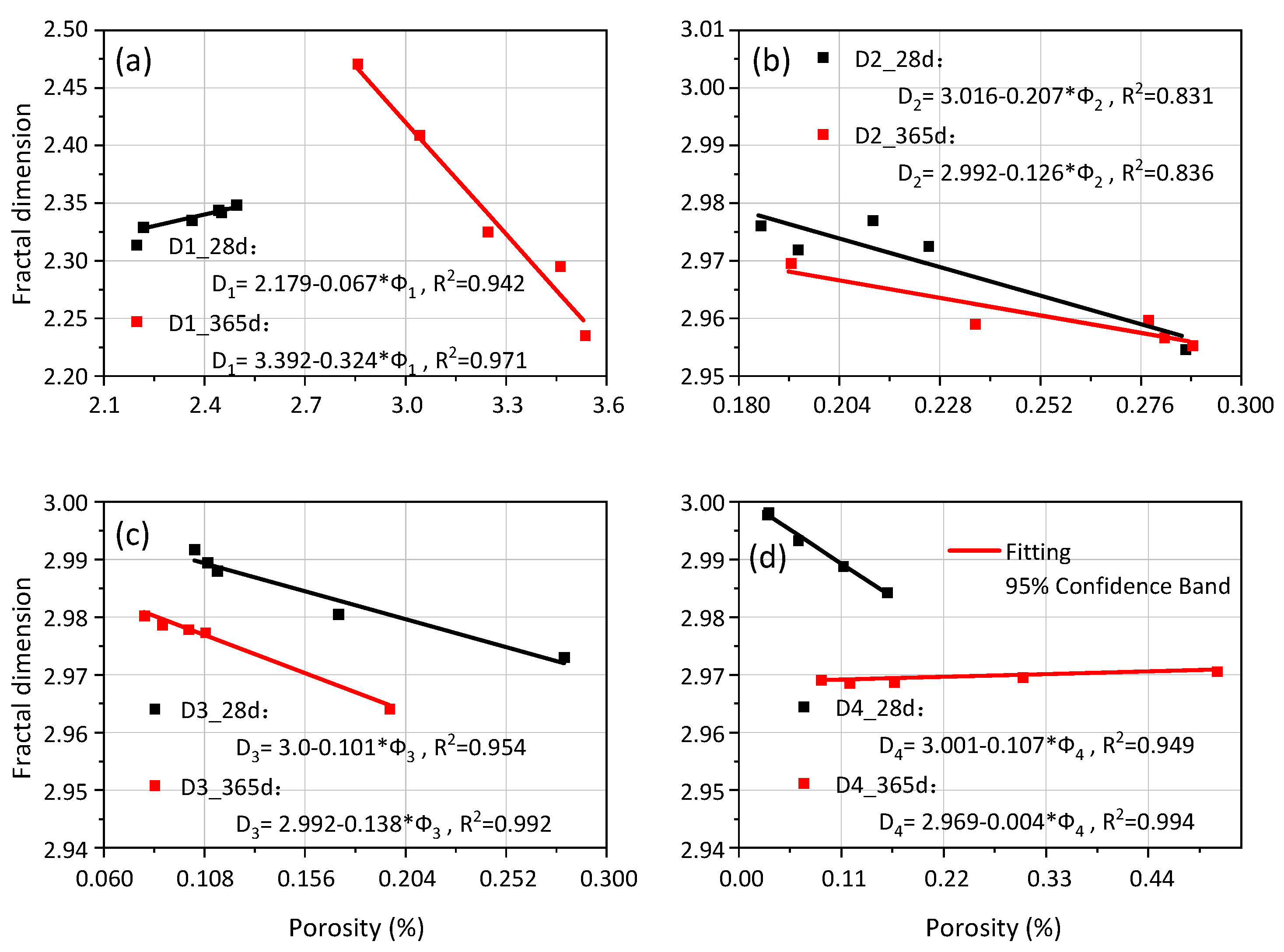
3.4. Fractal Characteristics of Pore Structure
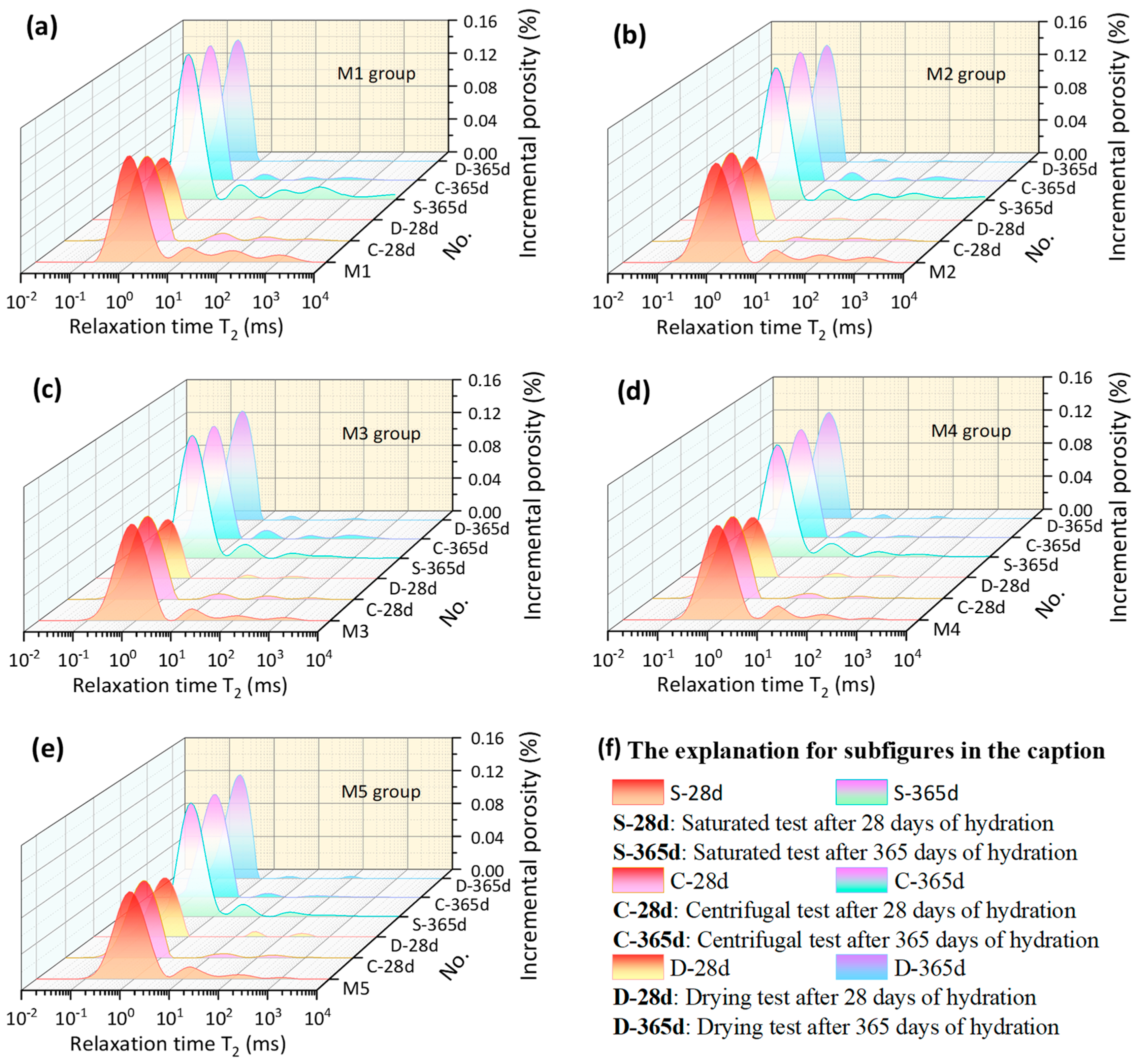
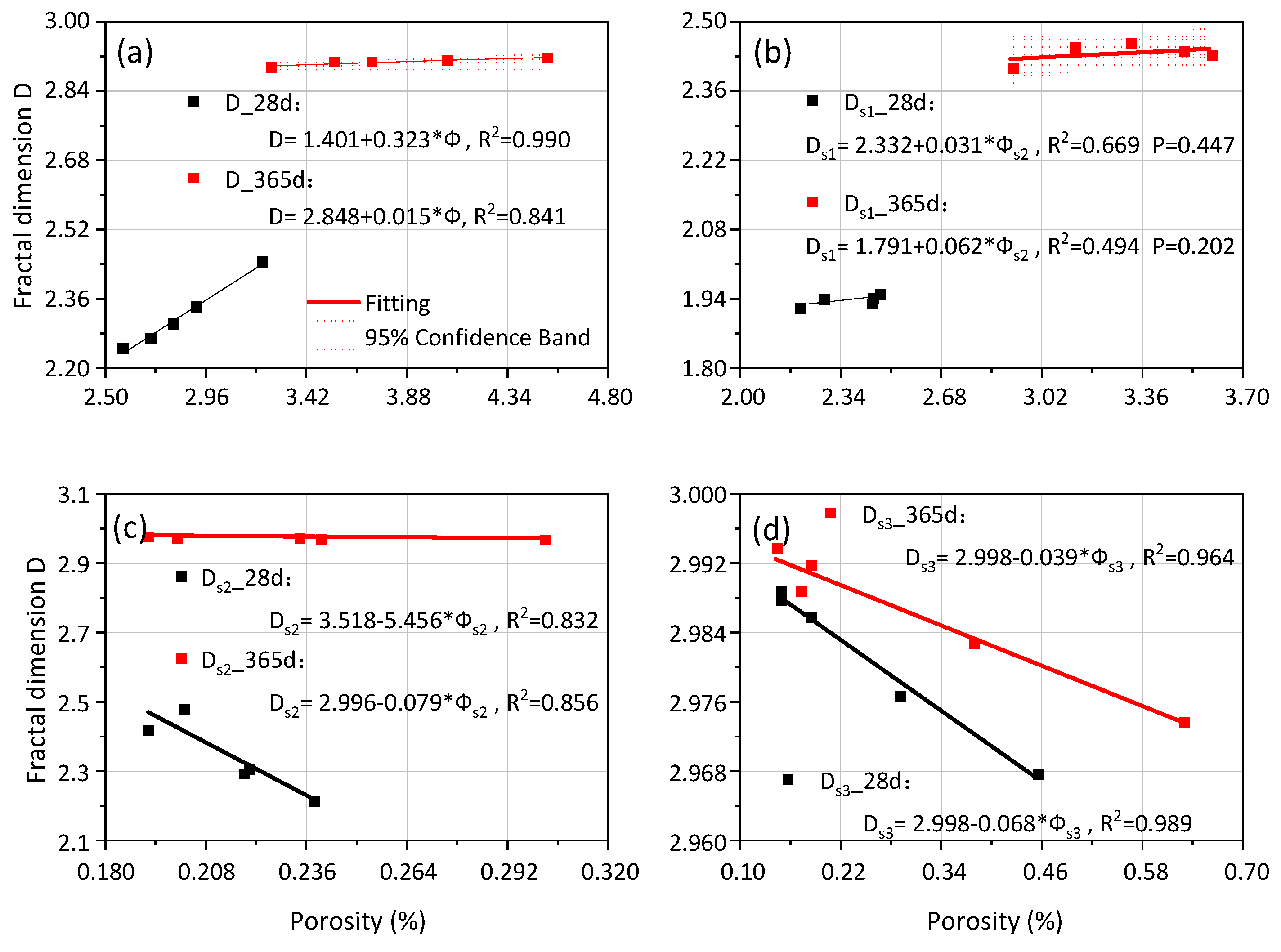
3.5. Pore evolution Characteristics of Synthetic-Graded Mortar
4. Discussion
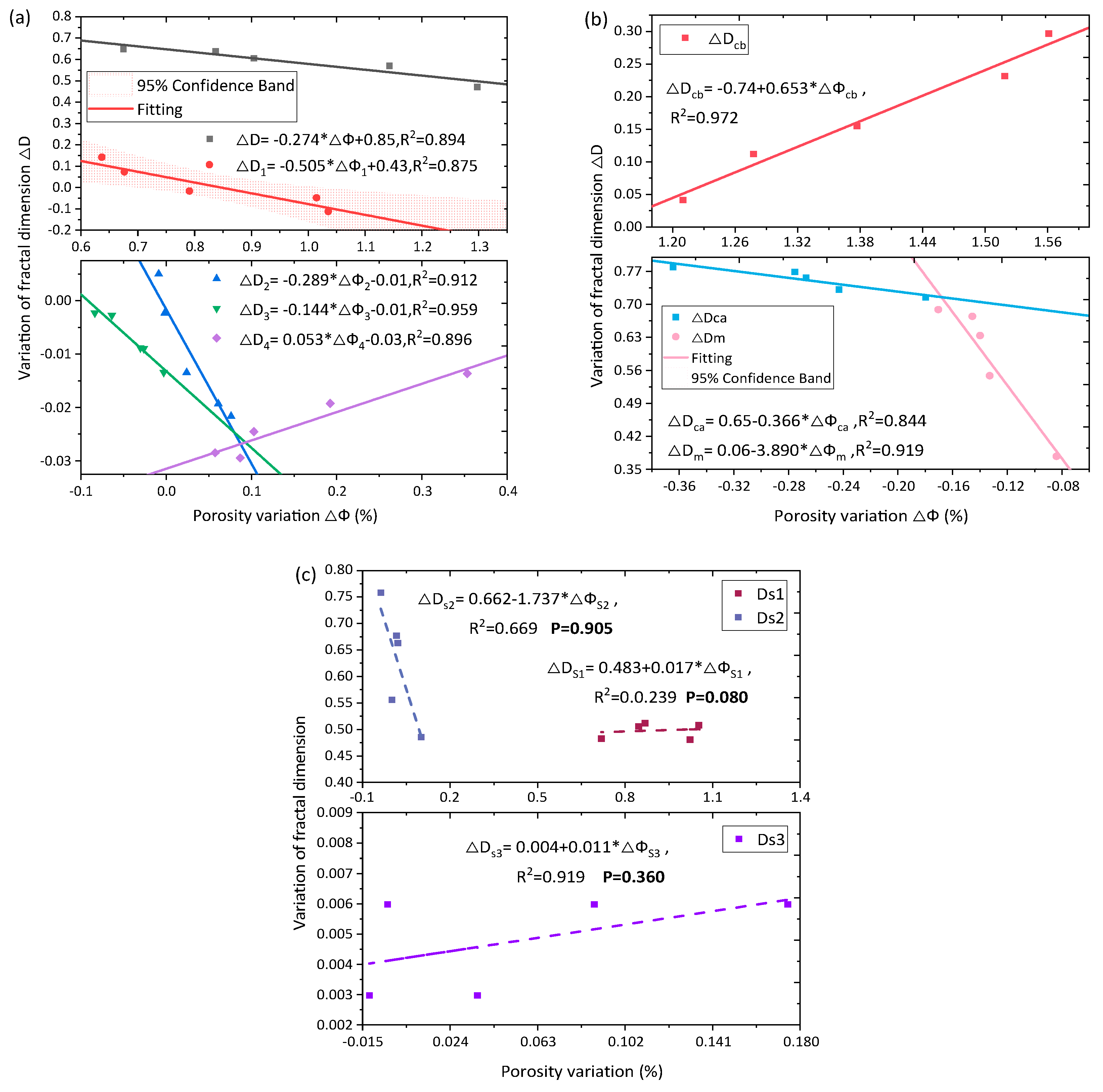
4.1. Porosity Variation Characteristics of Mortar
4.2. Fractal Correlation Model of Pore Evolution
5. Conclusions
- MSA has a fresh rock surface, which greatly reduces the number of pores in the mortar, especially the number of large pores. MSA mortar exhibits excellent compactness and small porosity.
- The particle size of MSA significantly affects the pore structure distribution in mortar. The SVR of the aggregate shows a positive power-exponential relationship with mortar porosity, and a strong correlation exists between varying gradations of pores and SVR.
- Long-term water saturation causes an increase in mortar porosity, primarily manifested by the growth of micropores, indicating further hydration reactions. Additionally, dissolution leads to an upward trend in both the maximum size and porosity of macropores.
- The permeability of single-graded mortar increases proportionally with SVR, and the permeability increases after 365 days of water saturation. However, synthetic-graded mortar exhibits a decrease in permeability, indicating enhanced impermeability and corrosion resistance.
- Mortar pores exhibit favorable fractal characteristics. Pore gradation in fractal analysis is determined using the F−sv method, F−T2c method, and F−ps method. All three methods establish a correlation model between porosity and fractal dimension, representing classification based on a variable pore size range, enabling the construction of a correlation model between porosity variable amplitude and fractal dimension variable amplitude.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Zhang, T.; Luo, T.; Zhou, M.; Zhang, K.; Ma, W. Study on the Deterioration of Concrete under Dry–Wet Cycle and Sulfate Attack. Materials 2020, 13, 4095. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.Z.; Yang, J.; Hu, S.G.; Zhang, Y.H.; Liu, Y.P. Research on the Fatigue Behavior of Cement Asphalt Mortar Exposed to Water. Adv. Mater. Res. 2013, 687, 274–281. [Google Scholar] [CrossRef]
- Xu, W.; Han, Z.; Tao, L.; Ding, Q.; Ma, H. Random non-convex particle model for the fraction of interfacial transition zones (ITZs) in fully-graded concrete. Powder Technol. 2018, 323, 301–309. [Google Scholar] [CrossRef]
- Ke, X.; Hou, H.; Zhou, M.; Wang, Y.; Zhou, X. Effect of particle gradation on properties of fresh and hardened cemented paste backfill. Constr. Build. Mater. 2015, 96, 378–382. [Google Scholar] [CrossRef]
- Li, T.; Nogueira, R.; de Brito, J.; Liu, J. Quantitative analysis of the influence of fine aggregate’s grading on mortar’s rheology. J. Mater. Res. Technol. 2023, 25, 310–318. [Google Scholar] [CrossRef]
- Wu, J.; Feng, M.; Ni, X.; Mao, X.; Chen, Z.; Han, G. Aggregate gradation effects on dilatancy behavior and acoustic characteristic of cemented rockfill. Ultrasonics 2019, 92, 79–92. [Google Scholar] [CrossRef]
- Liu, Q.; Shen, X.; Wei, L.; Dong, R.; Xue, H. Grey Model Research Based on the Pore Structure Fractal and Strength of NMR Aeolian Sand Lightweight Aggregate Concrete. JOM 2020, 72, 536–543. [Google Scholar] [CrossRef]
- Yang, C.C.; Su, J.K. Approximate migration coefficient of interfacial transition zone and the effect of aggregate content on the migration coefficient of mortar. Cem. Concr. Res. 2002, 32, 1559–1565. [Google Scholar] [CrossRef]
- Lin, J.; Zhao, Q.; Chen, H.; Li, M.; Yuan, L. A numerical framework for the ITZ percolation, effective fraction and diffusivity of concrete systems considering the nonuniform ITZ. J. Build. Eng. 2023, 77, 107429. [Google Scholar] [CrossRef]
- Wu, J.; Feng, M.; Han, G.; Ni, X.; Chen, Z. Experimental Investigation on Mechanical Properties of Cemented Paste Backfill under Different Gradations of Aggregate Particles and Types and Contents of Cementing Materials. Adv. Mater. Sci. Eng. 2019, 2019, 9456861. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Q.; Ma, Y.; Lai, M.; Ho, J.C.M. Mortar film thickness on the autogenous shrinkage of concrete: Test and simulation. J. Build. Eng. 2023, 66, 105833. [Google Scholar] [CrossRef]
- Feng, M.; Wu, J.; Ma, D.; Ni, X.; Yu, B.; Chen, Z. Experimental investigation on the seepage property of saturated broken red sandstone of continuous gradation. Bull. Eng. Geol. Environ. 2018, 77, 1167–1178. [Google Scholar] [CrossRef]
- Gao, Y.; De Schutter, G.; Ye, G. Micro- and meso-scale pore structure in mortar in relation to aggregate content. Cem. Concr. Res. 2013, 52, 149–160. [Google Scholar] [CrossRef]
- He, H.; Senetakis, K.; Coop, M.R. Stiffness of a recycled composite aggregate. Soil Dyn. Earthq. Eng. 2018, 110, 185–194. [Google Scholar] [CrossRef]
- He, H.; Senetakis, K. A study of wave velocities and poisson ratio of recycled concrete aggregate. Soils Found. 2016, 56, 593–607. [Google Scholar] [CrossRef]
- Zhang, Z.; Geng, O.; Ma, Z.; Ji, Y.; Xu, Z.; Gao, F.; Zhang, J. Study on the deterioration mechanism of alkali dissolution of concrete mixed with Na2SO4 in external water sources. Constr. Build. Mater. 2022, 356, 129283. [Google Scholar] [CrossRef]
- Ren, F.; Zhou, C.; Li, L.; Cui, H.; Chen, X. Modeling the dependence of capillary sorptivity on initial water content for cement-based materials in view of water sensitivity. Cem. Concr. Res. 2023, 168, 107158. [Google Scholar] [CrossRef]
- Muller, A.C.A.; Scrivener, K.L.; Gajewicz, A.M.; McDonald, P.J. Densification of C–S–H Measured by1 H NMR Relaxometry. J. Phys. Chem. C 2013, 117, 403–412. [Google Scholar] [CrossRef]
- Ning, L.; Zhao, Y.; Bi, J.; Wang, C.; Shen, M.; Li, Y. Effect of aggregate size on water distribution and pore fractal characteristics during hydration of cement mortar based on low-field NMR technology. Constr. Build. Mater. 2023, 389, 131670. [Google Scholar] [CrossRef]
- Sakai, Y. Relationship between water permeability and pore structure of cementitious materials. Mag. Concr. Res. 2020, 72, 1235–1242. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, S.; Wang, J.; Hu, Q.; Wang, M.; Chao, J. Applying Fractal Theory to Characterize the Pore Structure of Lacustrine Shale from the Zhanhua Depression in Bohai Bay Basin, Eastern China. Energy Fuels 2018, 32, 7539–7556. [Google Scholar] [CrossRef]
- Yuan, Y.; Rezaee, R. Fractal analysis of the pore structure for clay bound water and potential gas storage in shales based on NMR and N2 gas adsorption. J. Pet. Sci. Eng. 2019, 177, 756–765. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, J.; Yang, Y.; Xiao, H.; Ma, F. Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory. Minerals 2022, 12, 403. [Google Scholar] [CrossRef]
- Deng, H.; Tian, G.; Yu, S.; Jiang, Z.; Zhong, Z.; Zhang, Y. Research on Strength Prediction Model of Sand-like Material Based on Nuclear Magnetic Resonance and Fractal Theory. Appl. Sci. 2020, 10, 6601. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, F.; Kuang, Y.; Yang, D.; Zheng, M.; Zhao, L. Microscopic characteristics of the action of an air entraining agent on cemented paste backfill pores. Alex. Eng. J. 2020, 59, 1583–1593. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Cai, J. Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Fu, J.; Wang, K.; Wang, J. Internal pore evolution and early hydration characterization of fly ash cement backfill. J. Build. Eng. 2023, 72, 106716. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, H. Study on permeability performance of cemented tailings backfill based on fractal characteristics of pore structure. Constr. Build. Mater. 2023, 365, 130035. [Google Scholar] [CrossRef]
- Tian, G.; Deng, H.; Xiao, Y. Correlation Analysis between Microscopic Pore Parameters and Macroscopic Mechanical Properties of Rock-like Materials from the Perspective of Water-Cement Ratio and Sand-Cement Ratio. Materials 2022, 15, 2632. [Google Scholar] [CrossRef]
- Jiang, Z.; Cai, G.; Tian, G.; Liu, X. Effect of aggregate particle size on mortar pore structure. Constr. Build. Mater. 2022, 352, 128988. [Google Scholar] [CrossRef]
- Holthausen, R.S.; Raupach, M. Monitoring the internal swelling in cementitious mortars with single-sided 1H nuclear magnetic resonance. Cem. Concr. Res. 2018, 111, 138–146. [Google Scholar] [CrossRef]
- Korb, J.P.; Monteilhet, L.; McDonald, P.J.; Mitchell, J. Microstructure and texture of hydrated cement-based materials: A proton field cycling relaxometry approach. Cem. Concr. Res. 2007, 37, 295–302. [Google Scholar] [CrossRef]
- Fischer, N.; Haerdtl, R.; McDonald, P.J. Observation of the redistribution of nanoscale water filled porosity in cement based materials during wetting. Cem. Concr. Res. 2015, 68, 148–155. [Google Scholar] [CrossRef]
- Dalas, F.; Korb, J.; Pourchet, S.; Nonat, A.; Rinaldi, D.; Mosquet, M. Surface Relaxivity of Cement Hydrates. J. Phys. Chem. C 2014, 118, 8387–8396. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, Y.; Liu, D.; Zheng, S.; Sun, G.; Chang, Y. Shale pore size classification: An NMR fluid typing method. Mar. Pet. Geol. 2018, 96, 591–601. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, G.; Dong, Y.; Danesh, N.N.; Chen, Z.; Zhang, T. Comparison of low-field NMR and microfocus X-ray computed tomography in fractal characterization of pores in artificial cores. Fuel 2017, 210, 217–226. [Google Scholar] [CrossRef]
- Yang, X.; Li, L.; Dai, H.; Jia, M. Effect of fractal dimension in concrete meso-structure on its axial mechanical behavior: A numerical case study. Fractals 2021, 29, 2140011. [Google Scholar] [CrossRef]
- Zang, Q.; Liu, C.; Awan, R.S.; Yang, X.; Li, G.; Wu, Y.; Lu, Z.; Feng, D. Occurrence characteristics of the movable fluid in heterogeneous sandstone reservoir based on fractal analysis of NMR data: A case study of the Chang 7 Member of Ansai Block, Ordos Basin, China. J. Pet. Sci. Eng. 2022, 214, 110499. [Google Scholar] [CrossRef]
- Yue, J.; Sheng, J.; Wang, H.; Hu, Y.; Zhang, K.; Luo, Y.; Zhou, Q.; Zhan, M. Investigation on Pore Structure and Permeability of Concrete–Rock Interfacial Transition Zones Based on Fractal Theory. Fractal Fract. 2022, 6, 329. [Google Scholar] [CrossRef]
- Xiao, L.; Li, J.; Mao, Z.; Lu, J.; Yu, H.; Guo, H.; Li, G. A method to determine nuclear magnetic resonance (NMR) T2cutoff based on normal distribution simulation in tight sandstone reservoirs. Fuel 2018, 225, 472–482. [Google Scholar] [CrossRef]
- Valckenborg, R.; Pel, L.; Hazrati, K.; Kopinga, K.; Marchand, J. Pore water distribution in mortar during drying as determined by NMR. Mater. Struct. 2001, 34, 599–604. [Google Scholar] [CrossRef]
- Ramyar, K.; Topal, A.; Andiç, Ö. Effects of aggregate size and angularity on alkali–silica reaction. Cem. Concr. Res. 2005, 35, 2165–2169. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; An, M.; Yu, P.; Hou, X. The Influence of Rehydration on the Properties of Portland Cement-Based Materials with Low Water/Binder Ratios: A Review of Existing Research. Materials 2023, 16, 970. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, M.; Hou, D. Nanoscale insights into the anti-erosion performance of concrete: A molecular dynamics study. Appl. Surf. Sci. 2022, 593, 153403. [Google Scholar] [CrossRef]
- Yang, X.; Feng, Y.; Rong, H.; Liang, J.; Zhang, G.; Huang, Y. The leaching-deterioration properties and leaching mechanism of cement mortar under dry-wet cycles. Constr. Build. Mater. 2023, 400, 132672. [Google Scholar] [CrossRef]
- Bao, H.; Xu, G.; Yu, M.; Wang, Q.; Li, R.; Saafi, M.; Ye, J. Evolution of ITZ and its effect on the carbonation depth of concrete under supercritical CO2 condition. Cem. Concr. Comp. 2022, 126, 104336. [Google Scholar] [CrossRef]
- Wang, L.; Luo, R.; Zhang, W.; Jin, M.; Tang, S. Effects of fineness and content of phosphorus slag on cement hydration, permeability, pore structure and fractal dimension of concrete. Fractals 2021, 29, 2140004. [Google Scholar] [CrossRef]
- Korb, J.P. NMR and nuclear spin relaxation of cement and concrete materials. Curr. Opin. Colloid Interface Sci. 2009, 14, 192–202. [Google Scholar] [CrossRef]
- Li, J.; Guo, Y.; Zhang, T.; Gao, P.; Wu, J.; Ren, Q.; Wei, J.; Yu, Q. Clarifying the effects of volume proportion and surface area of aggregate on chloride diffusivity of concrete through microstructural design. Cem. Concr. Compos. 2023, 143, 105248. [Google Scholar] [CrossRef]
- Gao, Y.; Gu, Y.; Mu, S.; Jiang, J.; Liu, J. The multifractal property of heterogeneous microstructure in cement paste. Fractals 2021, 29, 2140006. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Li, S.F. Determination of the surface fractal dimension for porous-media by mercury porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
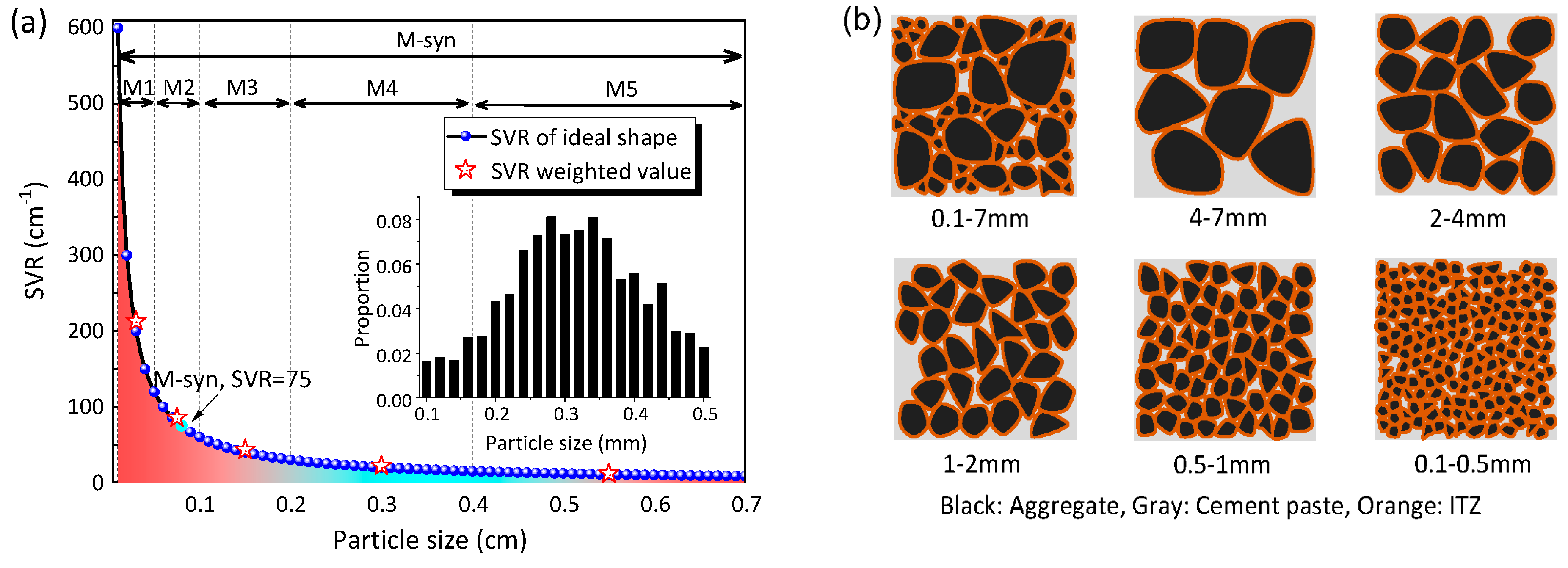


| Gradation of Aggregates | Aggregate Size/mm | SVR /cm−1 | No. | Solid Density ρ28d/kg·m−3 | Solid Density ρ365d/kg·m−3 | Density Loss ∆ρ/kg·m−3 | Φ28d/% | Φ365d/% |
|---|---|---|---|---|---|---|---|---|
| Synthetic gradation M-syn | 0.1–7.0 | 75.02 | M-syn-1 | 1395.33 | 1421.78 | 4.49 | 3.12 | 3.82 |
| M-syn-2 | 1407.87 | 1404.41 | 3.46 | 2.94 | 3.42 | |||
| M-syn-3 | 1389.71 | 1382.39 | 7.32 | 2.84 | 3.7 | |||
| M-syn-Ave | 1397.64 | 1402.86 | 5.09 | 2.96 | 3.64 | |||
| Single gradation M groups | 0.1–0.5 | 213.03 | M1-1 | 1423.03 | 1412.35 | 10.69 | 3.02 | 4.56 |
| M1-2 | 1396.31 | 1382.62 | 13.69 | 3.12 | 4.46 | |||
| M1-3 | 1383.24 | 1361.01 | 12.06 | 3.52 | 4.52 | |||
| M1-Ave | 1400.86 | 1385.33 | 12.15 | 3.22 | 4.52 | |||
| 0.5–1.0 | 85.41 | M2-1 | 1415.08 | 1403.65 | 11.43 | 2.64 | 4.12 | |
| M2-2 | 1396.16 | 1386.53 | 9.63 | 3.10 | 3.84 | |||
| M2-3 | 1406.21 | 1389.76 | 1.07 | 3.00 | 4.22 | |||
| M2-Ave | 1405.82 | 1393.32 | 7.38 | 2.92 | 4.06 | |||
| 1.0–2.0 | 43.12 | M3-1 | 1446.55 | 1436.61 | 9.93 | 2.46 | 3.64 | |
| M3-2 | 1412.85 | 1406.98 | 5.87 | 2.88 | 3.66 | |||
| M3-3 | 1383.40 | 1383.65 | −1.25 | 3.08 | 3.84 | |||
| M3-Ave | 1414.27 | 1409.08 | 4.85 | 2.82 | 3.72 | |||
| 2.0–4.0 | 21.68 | M4-1 | 1433.21 | 1423.19 | 10.02 | 2.58 | 3.58 | |
| M4-2 | 1426.27 | 1421.71 | 4.56 | 2.82 | 3.54 | |||
| M4-3 | 1407.31 | 1407.34 | −0.03 | 2.72 | 3.50 | |||
| M4-Ave | 1422.26 | 1417.42 | 4.85 | 2.7 | 3.54 | |||
| 4.0–7.0 | 11.77 | M5-1 | 1401.65 | 1400.82 | 0.83 | 2.64 | 3.22 | |
| M5-2 | 1417.75 | 1409.93 | 7.83 | 2.64 | 3.22 | |||
| M5-3 | 1427.52 | 1422.25 | 5.28 | 2.56 | 3.40 | |||
| M5-Ave | 1415.64 | 1411.00 | 4.64 | 2.62 | 3.28 |
| No. | Hydration Time | CBF Pores | CAF Pores | MF Pores | |||
|---|---|---|---|---|---|---|---|
| Φcb | Dcb | Φca | Dca | Φm | Dm | ||
| M-syn | 28 d | 2.120 | 1.497 | 0.432 | 2.724 | 0.408 | 2.976 |
| 365 d | 2.910 | 1.907 | 0.420 | 2.986 | 0.316 | 2.988 | |
| M1 | 28 d | 1.488 | 1.490 | 0.692 | 2.250 | 1.036 | 2.590 |
| 365 d | 3.048 | 1.787 | 0.512 | 2.966 | 0.952 | 2.967 | |
| M2 | 28 d | 1.528 | 1.603 | 0.688 | 2.229 | 0.702 | 2.432 |
| 365 d | 3.046 | 1.834 | 0.444 | 2.962 | 0.568 | 2.981 | |
| M3 | 28 d | 1.518 | 1.629 | 0.684 | 2.188 | 0.608 | 2.351 |
| 365 d | 2.894 | 1.784 | 0.418 | 2.945 | 0.404 | 2.985 | |
| M4 | 28 d | 1.474 | 1.670 | 0.676 | 2.176 | 0.506 | 2.309 |
| 365 d | 2.750 | 1.782 | 0.400 | 2.946 | 0.392 | 2.984 | |
| M5 | 28 d | 1.460 | 1.723 | 0.662 | 2.169 | 0.458 | 2.297 |
| 365 d | 2.670 | 1.765 | 0.298 | 2.949 | 0.288 | 2.986 | |
| Fractal Method | Type | 28 d | 365 d | ||
|---|---|---|---|---|---|
| Φ | D | Φ | D | ||
| F−sv method | Total | 2.957 | 2.886 | 3.646 | 2.898 |
| Φ1-D1 | 2.574 | 2.617 | 3.290 | 2.333 | |
| Φ2-D2 | 0.214 | 2.980 | 0.174 | 2.972 | |
| Φ3-D3 | 0.114 | 2.989 | 0.068 | 2.985 | |
| Φ4-D4 | 0.058 | 2.995 | 0.114 | 2.994 | |
| F−ps method | Φs1-Ds1 | 2.558 | 2.264 | 3.328 | 2.473 |
| Φs2-Ds2 | 0.218 | 2.956 | 0.153 | 2.986 | |
| Φs3-Ds3 | 0.181 | 2.987 | 0.165 | 2.993 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; He, H.; Tian, G.; Guo, W.; Li, Y.; Pan, Z. Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR. Fractal Fract. 2024, 8, 42. https://doi.org/10.3390/fractalfract8010042
Jiang Z, He H, Tian G, Guo W, Li Y, Pan Z. Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR. Fractal and Fractional. 2024; 8(1):42. https://doi.org/10.3390/fractalfract8010042
Chicago/Turabian StyleJiang, Zhen, Huan He, Guanglin Tian, Weizuo Guo, Yingzhen Li, and Zheng Pan. 2024. "Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR" Fractal and Fractional 8, no. 1: 42. https://doi.org/10.3390/fractalfract8010042
APA StyleJiang, Z., He, H., Tian, G., Guo, W., Li, Y., & Pan, Z. (2024). Pore Structure Quantification and Fractal Characterization of MSA Mortar Based on 1H Low-Field NMR. Fractal and Fractional, 8(1), 42. https://doi.org/10.3390/fractalfract8010042









