A Preconditioned Iterative Method for a Multi-State Time-Fractional Linear Complementary Problem in Option Pricing

Abstract

Fractional derivatives and regime-switching models are widely used in various fields of finance because they can describe the nonlocal properties of the solutions and the changes in the market status, respectively. The regime-switching time-fractional diffusion equations that combine both advantages are also used in European option pricing; however, to our knowledge, American option pricing based on such models and their numerical methods is yet to be studied. Hence, a fast algorithm for solving the multi-state time-fractional linear complementary problem arising from the regime-switching time-fractional American option pricing models is developed in this paper. To construct the solution strategy, the original problem has been converted into a Hamilton–Jacobi–Bellman equation, and a nonlinear finite difference scheme has been proposed to discretize the problem with stability analysis. A policy-Krylov subspace method is developed to solve the nonlinear scheme. Further, to accelerate the convergence rate of the Krylov method, a tri-diagonal preconditioner is proposed with condition number analysis. Numerical experiments are presented to demonstrate the validity of the proposed nonlinear scheme and the efficiency of the proposed preconditioned policy-Krylov subspace method.

1. Introduction

Option pricing has been a popular research topic in finance, as option instruments are important derivatives in financial markets. The Black–Scholes model [1] is the most famous model for option pricing problems and has been widely used; however, this model has suffered many shortcomings because it is based on geometric Brownian motion and cannot model jumps in the assets’ prices. New models have been proposed to deal with these problems, such as stochastic volatility models [2,3], jump diffusion models [4], variance gamma models [5], tempered stable models [6], self-exciting jump models [7], and Hawkes jump diffusion models [8]. With the Levy processes used in option pricing, new pricing models involving fractional derivatives have emerged.

Option valuation involving fractional derivatives is widely discussed. Cartea and del-Castillo-Negrete find that the barrier option price can be obtained by solving fractional partial differential equations for some particular Levy processes [9], such as finite moment log stable process [10], CGMY process [11], and KoBoL process [6]. Further, spatial fractional derivatives have been used in American options pricing [12], European options pricing [13], and double barrier options pricing [14]; however, these models cannot describe the long-term memory effects of the option value. Hence, the time-fractional derivative started to be used in the option pricing problem, which was introduced by Wyss [15]. After that, two new families of fractional derivatives based on fractional Taylor’s series and modified Riemann–Liouville derivatives were proposed to replace the standard time derivatives to price the options [16]. Additionally, a partial differential equation containing a Caputo fractional derivative was developed to price the European-style options [17]. Subsequently, an option pricing model containing both time and spatial fractional derivatives was proposed in [18].

Although the fractional derivative can describe the nonlocal properties of the assets’ prices and the time-independence properties of the option value, it cannot describe changes in market states, such as bull and bear market transitions. Hence, regime-switching models have been proposed and applied in options pricing [19], time series [20], and credit default swaps [21]. Additionally, the regime-switching option pricing involving fractional derivatives has been developed in [22,23,24], which combines the advantages of both regime-switching and fractional derivatives. For European option pricing, a system of space fractional diffusion equations coupled by Markov terms from the regime-switching finite moment log stable model has been developed in [23,25]. Furthermore, a coupled tempered fractional diffusion equation has been used to value the European options [26,27]. In [28], a system of linear complementary problems (LCPs) involving tempered fractional derivatives generated from the regime-switching CGMY model and KoBoL model has been utilized to price the American options. The above models belong to the regime-switching models with spatial fractional derivatives, and there are relatively few studies of option pricing based on the regime-switching model involving time-fractional derivatives. A regime-switching model containing time-fractional derivatives has been developed in [24] to price the European options, and a fast positivity preserving numerical method has been proposed in [22] to solve it. To the best of our knowledge, no numerical results exist for such a model for pricing the American options. Hence, developing a fast solution strategy for the multi-state time-fractional LCP arising from the regime-switching model with a time-fractional derivative is the main aim of this paper.

As noted above, no study in the literature considers the numerical method for the multi-state time-fractional LCP arising from American option pricing. The development of the fast solution strategy can only refer to the numerical methods for the general American options pricing. The methods for pricing American options can be broadly classified into four categories. The first type of approach focuses on solving the problems via estimating the optimal execution boundary, such as the method proposed in [29]. The second type of approach is mainly converting the problem into a linear problem via designing a semi-implicit scheme or implicit–explicit scheme to solve the problem, such as the L-stable method [19], the linearly implicit predictor–corrector scheme [30], or the IMEX-BDF method [31]. The third type of approach is mainly transforming the problem into a nonlinear equation to solve with iterative methods, such as the preconditioned penalty method [28], the fix-point method [32], the fitted finite volume iterative method [33], the modulus-based matrix splitting iteration method [34], and the modified modulus-based matrix splitting iteration method [35]. The fourth type of approach is designing a iterative method to solve the LCP directly, such as the projected SOR method [36] and the projected algebraic multigrid method [37]. In this paper, we design the fast numerical method following the third type of method because this kind of method can be extended easily to handle other related option pricing problems. However, it needs to solve a nonlinear equation, which requires quite a lot of computational cost. In [38], the authors compare several iterative procedures for solving the nonlinear scheme and find that the performance of the fix-point policy iteration with direct control formulation is a reliable general-purpose method. Inspired by [38], the fast numerical method designed in this paper is based on the policy iteration and Krylov subspace method, which can be expected to be reliable and efficient.

The rest of this article is as follows. In Section 2, a nonlinear finite difference scheme is proposed to discretize the considered problem with stability analysis. In Section 3, a preconditioned policy-Krylov subspace method has been developed with convergence analysis. Numerical experiments are given in Section 4, and conclusions are provided in Section 5.

2. Numerical Scheme and Theoretical Analysis

In this paper, the multi-state time-fractional LCP generated from a regime-switching modified Black–Scholes model with a time-fractional derivative [24,39] for the non-dividend American put option pricing problem is considered. The considered problem can be written as an optimization problem containing $N_s$ LCPs coupled with a Markov generator matrix. For $j=1,2,\dots ,N_s$, the j-th LCP can be written as follows:

$$\left\{\begin{array}{cc}\hfill & {\mathcal{L}}_j{V}_j(S,t)-\frac{{\partial }^{{\beta }_j}{V}_j(S,t)}{\partial t^{{\beta }_j}}\ge 0,V_j(S,t)\ge V^{*}\left(S\right),\hfill \\ \hfill & \left({\mathcal{L}}_j{V}_j(S,t)-\frac{{\partial }^{{\beta }_j}{V}_j(S,t)}{\partial t^{{\beta }_j}}\right)\left(V_j(S,t)-V^{*}\left(S\right)\right)=0,\hfill \\ \hfill & V_j(S_{min},t)=\max \{K-S_{min},0\},t\in [0,T),\hfill \\ \hfill & V_j(S_{max},t)=\max \{K-S_{max},0\},t\in [0,T),\hfill \\ \hfill & V_j(S,T)=\max \{K-S,0\},S\in (S_{min},S_{max}),\hfill \\ \hfill & V^{*}\left(S\right)=\max \{K-S,0\},S\in (S_{min},S_{max}),\hfill \end{array}\right.$$

(1)

where

$${\mathcal{L}}_j{V}_j(S,t):=-\frac{1}{2}{\sigma }_j^2{S}^2\frac{{\partial }^2{V}_j(S,t)}{\partial S^2}-rS\frac{\partial V_j(S,t)}{\partial S}+r{V}_j(S,t)-\sum _{i=1}^{N_s}{q}_{j,i}{V}_i(S,t),$$

and $\frac{{\partial }^{{\beta }_j}{V}_j(S,t)}{\partial t^{{\beta }_j}}$ is the modified right Riemann–Liouville fractional derivative [16] and defined by

$$\frac{{\partial }^{{\beta }_j}{V}_j(S,t)}{\partial t^{{\beta }_j}}=\frac{1}{\mathsf{\Gamma }(1-{\beta }_j)}\frac{\partial }{\partial t}{\int }_t^T\frac{V_j(S,\xi )-V_j(S,T)}{{(\xi -t)}^{{\beta }_j}}d\xi .$$

(2)

In the above model, K is the strike price of the options, and r is the risk-free interest rate. ${\beta }_j$ is the order of the time-fractional derivative of the j-th state and satisfies $0<{\beta }_j<1$. ${\sigma }_j$ denotes the volatility when the underlying price is in the j-th regime. S is the asset’s price, and its lower and upper truncated boundaries are $S_{min}$ and $S_{max}$, respectively. The entry $q_{j,i}$ is the transition rate of the Markov chain.

Inspired by [38], we attempted to devise a fast solution strategy based on policy iteration and direct control formulation. Therefore, the considered LCPs (1) are solved by transforming them into the Hamilton–Jacobi–Bellman (HJB) equations. By defining a new variable $U_j(S,t)=V_j(S,T-t)$, the considered LCP (1) can be converted into the following HJB equation:

$$min\{U_j(S,t)-V^{*}\left(S\right),{}_0^C{D}_t^{{\beta }_j}{U}_j(S,t)+{\mathcal{L}}_j{U}_j(S,t)\}=0,$$

(3)

where ${}_0^C{D}_t^{{\beta }_j}{U}_j(S,t)$ is the Caputo fractional derivative [40], which is defined by

$${}_0^C{D}_t^{{\beta }_j}{U}_j(S,t)=\frac{1}{\mathsf{\Gamma }(1-{\beta }_j)}{\int }_0^t\frac{U_j^{{}^{\prime }}(S,\xi )}{{(t-\xi )}^{{\beta }_j}}d\xi .$$

Remark that the transformation between the right-modified Riemann–Liouville fractional derivatives and the Caputo fractional derivatives has been given in [18]. The boundary conditions of HJB Equation (3) are listed by

$$\left\{\begin{array}{c}{U}_j(S_{min},t)=max\{K-S_{min},0\},\hfill \\ U_j(S_{max},t)=max\{K-S_{max},0\}.\hfill \end{array}\right.$$

2.1. Finite Difference Method

A nonlinear finite difference scheme is developed to solve the coupled HJB equation given in (3). As the time-fractional derivative has been transferred into the Caputo fractional derivative, we can use the $L_1$ approximate [41] to discretize it, which is given by

$$\begin{array}{c}\hfill {}_0^C{D}_t^{{\beta }_j}{U}_j(S,t_m)=\frac{{\tau }^{-{\beta }_j}}{\mathsf{\Gamma }(2-{\beta }_j)}[a_0^{\left({\beta }_j\right)}{U}_j(S,t_m)-\sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_j\right)}-a_{m-s}^{\left({\beta }_j\right)})U_k(S,t_s)\\ \hfill -a_{m-1}^{\left({\beta }_j\right)}{U}_j(S,t_0)]+\mathcal{O}\left({\tau }^{2-{\beta }_j}\right),\end{array}$$

(4)

where

$$a_l^{\left({\beta }_j\right)}={(l+1)}^{1-{\beta }_j}-l^{1-{\beta }_j},\mathrm{for}l\ge 0.$$

Furthermore, the central difference method and backward finite difference method are used to discretize the second-order derivative and first-order derivative, respectively, which can be written by

$$\frac{{\partial }^2{U}_j(S,t)}{\partial S^2}=\frac{U_j(S+h,t)-2U_j(S,t)+U_j(S-h,t)}{h^2}+O\left(h^2\right),$$

(5)

and

$$\frac{\partial U_j(S,t)}{\partial S}=\frac{U_j(S+h,t)-U_j(S,t)}{h}+O\left(h\right).$$

(6)

Let N and M be the positive integers. The intervals $[S_{min},S_{max}]$ and $[0,T]$ can be divided into $N+1$ and M sub-intervals, respectively. Then, the numerical mesh can be defined by

$$\begin{array}{ccc}\hfill S_i& =& S_{min}+ih,\mathrm{for}i=0,1,\dots ,N+1,\hfill \\ \hfill t_m& =& m\tau ,\mathrm{for}m=0,1,\dots ,M,\hfill \end{array}$$

where $h=\frac{S_{max}-S_{min}}{N+1}$, $\tau =T/M$.

With the finite difference approximate given in (4), (5), and (6), by denoting $u_{j,i}^{\left(m\right)}$ as the numerical solution of $U_j(S_i,t_m)$, the HJB equation can be discretized. For $U_j(S,t)\in C^{(4,2)}([S_{min},S_{max}]\times [0,T])$, and $j=1,2,\dots ,N_s$, the numerical scheme for HJB Equation (3) can be written by

$$min\left\{u_{j,i}^{\left(m\right)}-v_i^{*},\frac{{\tau }^{-{\beta }_j}}{\mathsf{\Gamma }(2-{\beta }_j)}[a_0^{\left({\beta }_j\right)}{u}_{j,i}^{\left(m\right)}-\sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_j\right)}-a_{m-s}^{\left({\beta }_j\right)})u_{j,i}^{\left(s\right)}-a_{m-1}^{\left({\beta }_j\right)}{u}_{j,i}^{\left(0\right)}]+\tilde{\mathcal{L}}{u}_{j,i}^{\left(m\right)}\right\}=0,$$

(7)

where

$$\tilde{\mathcal{L}}{u}_{j,i}^{\left(m\right)}=-\frac{1}{2}{\sigma }_j^2{S}_i^2\frac{u_{j,i+1}^{\left(m\right)}-2u_{j,i}^{\left(m\right)}+u_{j,i-1}^{\left(m\right)}}{h^2}-r{S}_i\frac{u_{j,i+1}^{\left(m\right)}-u_{j,i}^{\left(m\right)}}{h}+r{u}_{j,i}^{\left(m\right)}-\sum _{s=1}^{N_s}{q}_{j,s}{u}_{j,s}^{\left(m\right)},$$

and $v_i^{*}=V^{*}\left(S_i\right)$.

2.2. Matrix Form

To simplify the notation of the matrix form, we define $T_n(a,b,c)$ as an n-by-n tri-diagonal matrix, which is given by

$$T_n(a,b,c)=\left[\begin{array}{cccc}b& c& & \\ a& b& \ddots & \\ & \ddots & \ddots & c\\ & & a& b\end{array}\right].$$

Then, define the vectors $u^{\left(m\right)}={[u_{1,1}^{\left(m\right)},u_{1,2}^{\left(m\right)},\dots ,u_{1,N}^{\left(m\right)},u_{2,1}^{\left(m\right)},u_{2,2}^{\left(m\right)},\dots ,u_{N_s,N}^{\left(m\right)}]}^T$, ${\tilde{v}}^{*}=\widehat{L}\otimes v^{*}$, where $v^{*}={[v_1^{*},v_2^{*},\dots ,v_N^{*}]}^T$ and $\widehat{L}$ is an $N_s$-by-1 column vector with all entries of 1.

With the above notations, the finite difference scheme (7) can be written by the following matrix form:

$$min\{u^{\left(m\right)}-{\tilde{v}}^{*},W{u}^{\left(m\right)}-h^{\left(m\right)}+D_1\otimes I_{N}f\}=0,$$

(8)

where

$$\begin{array}{c}\hfill W=\tilde{W}-D_{1}Q\otimes I_N,\\ \hfill \tilde{W}=I_{N_{S}N}+r{D}_1\otimes I_N-\frac{r}{h}{D}_1\otimes D_{s_1}{A}_1+D_2\otimes D_{s_2}{A}_2.\end{array}$$

(9)

The entry of Q is $q_{j,i}$, which is the generator of the Markov chain. Satisfy (1) $q_{j,i}\ge 0$, if $i\ne j$ and (2) $q_{j,j}=-{\sum }_{j\ne i}{q}_{j,i}$ for each $j=1,2,\dots ,N_s$. The other matrices in (9) are listed by

$$\begin{array}{c}\hfill D_{s_1}=diag\{S_1,S_2,\dots ,S_N\},\\ \hfill D_{s_2}=diag\{S_1^2,S_2^2,\dots ,S_N^2\},\\ \hfill D_1=diag\{{\tau }^{{\beta }_1}\mathsf{\Gamma }(2-{\beta }_1),{\tau }^{{\beta }_2}\mathsf{\Gamma }(2-{\beta }_2),\dots ,{\tau }^{{\beta }_{N_s}}\mathsf{\Gamma }(2-{\beta }_{N_s})\},\\ \hfill D_2=diag\{\frac{-{\tau }^{{\beta }_1}{\sigma }_1^2\mathsf{\Gamma }(2-{\beta }_1)}{2h^2},\frac{-{\tau }^{{\beta }_2}{\sigma }_2^2\mathsf{\Gamma }(2-{\beta }_2)}{2h^2},\dots ,\frac{-{\tau }^{{\beta }_{N_s}}{\sigma }_{N_s}^2\mathsf{\Gamma }(2-{\beta }_{N_s})}{2h^2}\},\\ \hfill A_1=T_N(0,-1,1),\\ \hfill A_2=T_N(1,-2,1).\end{array}$$

Additionally, vectors $h^{\left(m\right)}$ and f in (8) are defined as follows. Vector $h^{\left(m\right)}=[h_{1,1}^{\left(m\right)},h_{1,2}^{\left(m\right)},\dots ,$$h_{1,N}^{\left(m\right)},$$h_{2,1}^{\left(m\right)},$$h_{2,2}^{\left(m\right)},$$\dots ,$$h_{N_s,N}^{\left(m\right)}{]}^T$, whose entries are given by

$$h_{j,i}^{\left(m\right)}=\sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_j\right)}-a_{m-s}^{\left({\beta }_j\right)})u_{j,i}^{\left(s\right)}+a_{m-1}^{\left({\beta }_j\right)}{u}_{j,i}^{\left(0\right)},$$

and $f={[f_{1,1},f_{1,2},\dots ,f_{1,N},f_{2,1},f_{2,2},\dots ,f_{N_s,N}]}^T$ with entries

$$f_{j,i}=\left\{\begin{array}{c}0,i\ne 1,N\hfill \\ -\frac{{\sigma }_j^2{S}_1^2}{2h^2}{U}_j(S_{min},t_m),i=1,\hfill \\ -\frac{{\sigma }_j^2{S}_N^2}{2h^2}{U}_j(S_{max},t_m)-\frac{r{S}_N}{h}{U}_j(S_{max},t_m),i=N.\hfill \end{array}\right.$$

2.3. Stability Analysis

Although the finite difference method has been developed, its stability property is necessary. With the matrix form of the discrete HJB equation in (8), one lemma can be derived first.

Lemma 1.

For $0<\tau <1$, the matrix $W=\left[w_{p,q}\right]$ in (9) is an M-matrix with

$$|w_{p,p}|\ge \sum _{s=1,s\ne p}^{N{N}_s}\left|w_{p,s}\right|+1+{\tau }^{{\beta }_{max}}\mathsf{\Gamma }(2-\widehat{\beta })r,$$

where $\widehat{\beta }=arg{min}_{{\beta }_j\in \{{\beta }_1,{\beta }_2,\dots ,{\beta }_{N_s}\}}\left\{\mathsf{\Gamma }(2-{\beta }_j)\right\}$.

Proof. 

By the definition of matrix Q, we know that the row sum of it equals to zero. With the definition of matrix W in (9), and the properties of the Kronnecker product, the matrix $-\frac{r}{h}{D}_1\otimes D_{s_1}{A}_1+D_2\otimes D_{s_2}{A}_2-D_{1}Q\otimes I_N$ is a weakly diagonal dominant matrix with the positive main diagonal and negative off diagonals. The remaining part of the coefficient matrix W is a positive diagonal matrix $I_{N{N}_s}+r{D}_1\otimes I_N$. Hence, the matrix W has the positive main diagonal and negative off diagonal with the following property: $|w_{p,p}|-{\sum }_{s=1,s\ne p}^{N{N}_s}\left|w_{p,s}\right|\ge 1+{\tau }^{{\beta }_{min}}\mathsf{\Gamma }(2-\widehat{\beta })r$, where $\widehat{\beta }=arg{min}_{{\beta }_j\in \{{\beta }_1,{\beta }_2,\dots ,{\beta }_{N_s}\}}\left\{\mathsf{\Gamma }(2-{\beta }_j)\right\}$.    □

With Lemma 1, we have the following theorem, which ensures the unconditional stability of the nonlinear numerical scheme (7).

Theorem 1.

The nonlinear scheme (7) is unconditionally stable, i.e.,

$$\parallel u^{\left(m\right)}{\parallel }_{\infty }\le \parallel u^{\left(0\right)}{\parallel }_{\infty }+T^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty },$$

where $\tilde{\beta }=arg{max}_{{\beta }_j\in \{{\beta }_1,{\beta }_2,\dots ,{\beta }_{N_s}\}}\left\{T^{{\beta }_j}\right\}$.

Proof. 

Let $u^{\left(m\right)}$ be the solution of the discrete HJB Equation (8) on the m-th time level. Assume that $u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}$ is an entry of the vector $u^{\left(m\right)}$ and satisfies

$$\left|u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}\right|=\underset{1\le j\le N_s,1\le i\le N}{max}|u_{j,i}^{\left(m\right)}|=\parallel u^{\left(m\right)}{\parallel }_{\infty }.$$

Then, we discuss $\parallel u^{\left(m\right)}{\parallel }_{\infty }$ in two cases when the solution of (7) exists.

Case i: For $u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}>v_{\widehat{i}\left(m\right)}^{*}$, we know that $u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}$ is determined by ${(W{u}^{\left(m\right)}-h^{\left(m\right)}+D_1\otimes I_{N}f)}_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)}=0$, where ${\left(\mathrm{v}\right)}_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right))}$ denotes the $\left((\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)\right)$-th entry of any given vector $\mathrm{v}$. Hence, with Lemma 1, we obtain the following inequalities:

$$\begin{array}{cc}\hfill \parallel u^{\left(m\right)}{\parallel }_{\infty }=& |u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}|\le \left|w_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right),(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)}{u}_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}\right|\hfill \\ \hfill & -\left|\sum _{s\ne (\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)}{w}_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right),s}{u}_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}\right|\hfill \\ \hfill \le & \left|w_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right),(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)}{u}_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}+\sum _{s\ne (\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right)}{w}_{(\widehat{j}\left(m\right)-1)N+\widehat{i}\left(m\right),s}{u}_s^{\left(m\right)}\right|\hfill \\ \hfill =& \left|h_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}-{\tau }^{{\beta }_{\widehat{j}\left(m\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(m\right)})f_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}\right|\hfill \\ \hfill \le & \sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}-a_{m-s}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)})\left|u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(s\right)}\right|+a_{m-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}\left|u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(0\right)}\right|+{\tau }^{{\beta }_{\widehat{j}\left(m\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(m\right)})\left|f_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}\right|\hfill \\ \hfill \le & \sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}-a_{m-s}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)})\parallel u^{\left(s\right)}{\parallel }_{\infty }+a_{m-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}\parallel u^{\left(0\right)}{\parallel }_{\infty }+{\tau }^{{\beta }_{\widehat{j}\left(m\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(m\right)}){\parallel f\parallel }_{\infty }.\hfill \end{array}$$

Case ii: For $u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}=v_{\widehat{i}\left(m\right)}^{*}$, it is straightforward to know that $\parallel u^{\left(m\right)}{\parallel }_{\infty }\le {\parallel {\tilde{v}}^{*}\parallel }_{\infty }$.

Combining two cases yields the following inequality:

$$\begin{array}{cc}\hfill \parallel u^{\left(m\right)}{\parallel }_{\infty }=|u_{\widehat{j}\left(m\right),\widehat{i}\left(m\right)}^{\left(m\right)}|\le max\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },& \sum _{s=1}^{m-1}(a_{m-s-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}-a_{m-s}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}){\parallel u^{\left(s\right)}\parallel }_{\infty }\hfill \\ \hfill & +a_{m-1}^{\left({\beta }_{\widehat{j}\left(m\right)}\right)}\parallel u^{\left(0\right)}{\parallel }_{\infty }+{\tau }^{{\beta }_{\widehat{j}\left(m\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(m\right)}){\parallel f\parallel }_{\infty }\}.\hfill \end{array}$$

(10)

When $m=1$, since $u^{\left(0\right)}={\tilde{v}}^{*}$, we have

$$\begin{array}{cc}\hfill \parallel u^{\left(1\right)}{\parallel }_{\infty }\le & max\left\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },a_0^{\left({\beta }_{\widehat{j}\left(1\right)}\right)}\parallel u^{\left(0\right)}{\parallel }_{\infty }+{\tau }^{{\beta }_{\widehat{j}\left(1\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(1\right)}){\parallel f\parallel }_{\infty }\right\}\hfill \\ \hfill \le & \parallel u^{\left(0\right)}{\parallel }_{\infty }+t_1^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }.\hfill \end{array}$$

When $m=2$, with (10), it holds that

$$\begin{array}{cc}\hfill \parallel u^{\left(2\right)}{\parallel }_{\infty }\le & max\left\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },(a_0^{\left({\beta }_{\widehat{j}\left(2\right)}\right)}-a_1^{\left({\beta }_{\widehat{j}\left(2\right)}\right)})\parallel u^{\left(1\right)}{\parallel }_{\infty }+a_1^{\left({\beta }_{\widehat{j}\left(2\right)}\right)}\parallel u^{\left(0\right)}{\parallel }_{\infty }+{\tau }^{{\beta }_{\widehat{j}\left(2\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(2\right)}){\parallel f\parallel }_{\infty }\right\}\hfill \\ \hfill \le & max\left\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },(a_0^{\left({\beta }_{\widehat{j}\left(2\right)}\right)}-a_1^{\left({\beta }_{\widehat{j}\left(2\right)}\right)}){\parallel u^{\left(1\right)}\parallel }_{\infty }+a_1^{\left({\beta }_{\widehat{j}\left(2\right)}\right)}\left(\parallel u^{\left(0\right)}{\parallel }_{\infty }+\frac{{\tau }^{{\beta }_{\widehat{j}\left(2\right)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}\left(2\right)})}{(1-{\beta }_{\widehat{j}\left(2\right)})2^{-{\beta }_{\widehat{j}\left(2\right)}}}{\parallel f\parallel }_{\infty }\right)\right\}\hfill \\ \hfill \le & \parallel u^{\left(0\right)}{\parallel }_{\infty }+t_2^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }\hfill \end{array}$$

Assume that the following formula holds when $m=1,2,\dots ,l$, which is given by

$$\parallel u^{\left(m\right)}{\parallel }_{\infty }\le \parallel u^{\left(0\right)}{\parallel }_{\infty }+t_m^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }.$$

Then, when $m=l+1$, with (10), it yields that

$$\begin{array}{cc}\hfill \parallel u^{(l+1)}{\parallel }_{\infty }\le & max\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },\sum _{s=1}^l(a_{l-s}^{\left({\beta }_{\widehat{j}(l+1)}\right)}-a_{l-s+1}^{\left({\beta }_{\widehat{j}(l+1)}\right)})\parallel u^{\left(s\right)}{\parallel }_{\infty }+a_l^{\left({\beta }_{\widehat{j}(l+1)}\right)}{\parallel u^{\left(0\right)}\parallel }_{\infty }\hfill \\ \hfill & +{\tau }^{{\beta }_{\widehat{j}(l+1)}}\mathsf{\Gamma }(2-{\beta }_{\widehat{j}(l+1)}){\parallel f\parallel }_{\infty }\}\hfill \\ \hfill \le & max\{\parallel {\tilde{v}}^{*}{\parallel }_{\infty },\sum _{s=1}^l(a_{l-s}^{\left({\beta }_{\widehat{j}(l+1)}\right)}-a_{l-s+1}^{\left({\beta }_{\widehat{j}(l+1)}\right)})\left(\parallel u^{\left(0\right)}{\parallel }_{\infty }+t_s^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }\right)\hfill \\ \hfill & +a_l^{\left({\beta }_{\widehat{j}(l+1)}\right)}\left(\parallel u^{\left(0\right)}{\parallel }_{\infty }+t_{l+1}^{{\beta }_{\widehat{j}(l+1)}}\mathsf{\Gamma }(1-{\beta }_{\widehat{j}(l+1)}){\parallel f\parallel }_{\infty }\right)\}\hfill \\ \hfill \le & \parallel u^{\left(0\right)}{\parallel }_{\infty }+t_{l+1}^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }.\hfill \end{array}$$

Hence, the nonlinear scheme (7) is unconditionally stable, i.e., 

$$\parallel u^{\left(m\right)}{\parallel }_{\infty }\le \parallel u^{\left(0\right)}{\parallel }_{\infty }+T^{\tilde{\beta }}\mathsf{\Gamma }(1-{\beta }_{max}){\parallel f\parallel }_{\infty }.$$

   □

3. Preconditioned Policy-Krylov Subspace Method

In order to solve the HJB Equation (8), the policy iteration method [42] is used as a component in constructing the fast algorithm.

3.1. Policy Iteration Method

The discrete HJB equation can be written by the following component-wise form [42]:

$${\theta }_i{(u^{\left(m\right)}-{\tilde{v}}^{*})}_i+(1-{\theta }_i){(W{u}^{\left(m\right)}-h^{\left(m\right)}+D_1\otimes I_{N}f)}_i=0.$$

(11)

where ${\left(\mathrm{v}\right)}_i$ denotes the i-th entry of any given vector $\mathrm{v}$ and $1\le i\le N{N}_s$. The vector $\theta$ contains the control parameters and its i-th entry is valued by ${\theta }_i=arg{min}_{\theta \in \{0,1\}}\{\theta {(u^{\left(m\right)}-{\tilde{v}}^{*})}_i+(1-\theta ){(W{u}^{\left(m\right)}-h^{\left(m\right)}+D_1\otimes I_{N}f)}_i\}$. Then, the policy iteration method can be used to solve (11). The framework of the policy iteration method is presented in Algorithm 1.

Algorithm 1 Framework of the policy iteration method

Let ${\left(u^{\left(m\right)}\right)}^k$ be the k-th iteration of the policy iteration method for computing the solution $u^{\left(m\right)}$. Let ${\theta }^k\in R^{N{N}_s}$, $M^k\in R^{N{N}_s\times N{N}_s}$, and $b^k\in R^{N{N}_s}$. For $1\le i\le N{N}_s$, we have $$\begin{array}{ccc}\hfill {\left({\theta }^{\left(m\right)}\right)}_i^k& =& arg\underset{\theta \in \{0,1\}}{min}\{\theta {({\left(u^{\left(m\right)}\right)}^k-{\tilde{v}}^{*})}_i+(1-\theta ){(W{u}^{\left(m\right)}-h^{\left(m\right)}+D_1\otimes I_{N}f)}_i\},\hfill \\ \hfill {\left(M^{\left(m\right)}\right)}_i^k& =& {\left({\theta }^{\left(m\right)}\right)}_i^k{\left(I_{N{N}_s}\right)}_i+(1-{\left({\theta }^{\left(m\right)}\right)}_i^k){\left(W\right)}_i,\hfill \\ \hfill {\left(b^{\left(m\right)}\right)}_i^k& =& {\left({\theta }^{\left(m\right)}\right)}_i^k{\left(v^{*}\right)}_i+(1-{\left({\theta }^{\left(m\right)}\right)}_i^k){(h^{\left(m\right)}-D_1\otimes I_{N}f)}_i.\hfill \end{array}$$ Find ${\left(u^{\left(m\right)}\right)}^{k+1}\in R^{N{N}_s}$, such that $${\left(M^{\left(m\right)}\right)}^k{\left(u^{\left(m\right)}\right)}^{k+1}={\left(b^{\left(m\right)}\right)}^k.$$ (12)

With Algorithm 1, it is known that a linear system needs to be solved in each policy iteration. To ensure the algorithm is reliable, the coefficient matrix ${\left(M^{\left(m\right)}\right)}^k$ in (12) should be invertible. Hence, we have the following lemma. Remark that the notation $M^{m,k}$ is used to stand for ${\left(M^{\left(m\right)}\right)}^k$ to simplify the statement in the subsequent theoretical analysis.

Lemma 2.

For $0<{\beta }_j<1$, the coefficient matrix $M^{m,k}$ is invertible and satisfies

$$\parallel {\left(M^{m,k}\right)}^{-1}{\parallel }_{\infty }\le 1.$$

Proof. 

With Lemma 1, we know that matrix W is an M-matrix. Coefficient matrix $M^{m,k}$ is constructed by selecting rows from W and the identity matrix $I_{N{N}_s}$, thus matrix $M^{m,k}$ is also an M-matrix and invertible. In addition, the entries $\left[i_{j,k}\right]$ of the identity matrix hold that $|i_{k,k}|-{\sum }_{j\ne k}\left|i_{j,k}\right|=1$. Refer to [43], $\parallel {\left(M^{m,k}\right)}^{-1}{\parallel }_{\infty }\le 1$ can be obtained. □

The matrix W is an M-matrix, then the properties of the LCP considered in this paper are similar to the case in [42]. Refer to the proof in [42], the following theorem can be obtained straightforwardly, which ensures that the policy iteration method converges to the solution in finite steps.

Theorem 2.

Let ${\left(u^k\right)}_{k=0}^{\infty }$ be the sequence generated by Algorithm 1. Then,

$$\begin{array}{cc}& u^{k+1}\ge u^k,n\in N\\ \hfill and& u^n=u_{*},n\ge K\end{array}$$

where $u_{*}$ is the solution of (11) and K is an integer independent of $u^0$.

3.2. Preconditioned Krylov Subspace Method

In each policy iteration, a linear system (12) is needed to be solved. Based on the structure of the matrix $M^{m,k}$, a fast Krylov subspace method is used as the linear solver. The matrix-vector product $M^{m,k}\mathrm{v}$ can be obtained by

$$M^{m,k}\mathrm{v}={\mathsf{\Theta }}^{m,k}\mathrm{v}+(I_{N{N}_s}-{\mathsf{\Theta }}^{m,k})(\tilde{W}\mathrm{v}-\mathrm{vec}\left({\left(D_{1}Q{\mathrm{V}}^T\right)}^T\right)),$$

(13)

where $\mathrm{v}$ is any given vector, and $\mathrm{V}$ is an N-by-$N_s$ matrix reshaped by $\mathrm{v}$ column by column. ${\mathsf{\Theta }}^{m,k}$ is the diagonal matrix, and its i-th diagonal entry equals the control parameter ${\left({\theta }^{\left(m\right)}\right)}_i^k$ in Algorithm 1. Since matrix $\tilde{W}$ is a block diagonal matrix with tri-diagonal blocks, with (13), the operation cost of $M^{m,k}\mathrm{v}$ is $\mathcal{O}\left(N{N}_s^2\right)$, and each iteration of the Krylov subspace method also costs $\mathcal{O}\left(N{N}_s^2\right)$.

Although the operation cost of each iteration of the Krylov subspace method is $\mathcal{O}\left(N{N}_s^2\right)$, the total cost for solving the linear system (12) depends on the iteration number. If the coefficient matrix $M^{m,k}$ is ill conditioned, the Krylov subspace method converges to the solution slowly. Hence, the preconditioning technique is considered to reduce the iteration number and avoid this situation. However, extra computational costs are needed for the preconditioning technique in each iteration. The preconditioner based on circulant matrices will not be considered because its extra computational cost usually is $\mathcal{O}(N{N}_{s}logN{N}_s)$ due to the fast Fourier transformation. In this section, we develop a simple preconditioner with the tri-diagonal structure, which is defined by

$$P^{m,k}={\mathsf{\Theta }}^{m,k}{I}_{N_{s}N}+(I_{N{N}_s}-{\mathsf{\Theta }}^{m,k})(\tilde{W}-D_1{Q}_d\otimes I_N),$$

(14)

where $Q_d=diag\{q_{1,1},q_{2,2},\dots ,q_{N_s,N_s}\}$. Because the preconditioner $P^{m,k}$ keeps the tri-diagonal structure, the matrix-vector product ${\left(P^{m,k}\right)}^{-1}\mathrm{v}$ costs $\mathcal{O}\left(N{N}_s\right)$ based on the Thomas algorithm, where $\mathrm{v}$ is any given vector. Although the operation cost for the preconditioned Krylov subspace method is still $\mathcal{O}\left(N{N}_s^2\right)$ per iteration, some theorems are needed to ensure the proposed preconditioning technique is useful. First, we need to ensure the preconditioner is invertible.

Theorem 3.

The preconditioner $P^{m,k}$ is invertible and satisfies

$$\parallel {\left(P^{m,k}\right)}^{-1}{\parallel }_{\infty }\le 1.$$

Proof. 

By the definition of the preconditioner $P^{m,k}$, we know that it is constructed by selecting the row between the matrices $\tilde{W}-D_1{Q}_d\otimes I_N$ and $I_{N{N}_s}$. Refer to the proof of Lemmas 1 and 2, it is easy to know that $P^{m,k}$ is an M-matrix and satisfies $\parallel {\left(P^{m,k}\right)}^{-1}{\parallel }_{\infty }\le 1$. □

Despite the invertibility of the proposed preconditioner, proved by Theorem 3, the convergence rate of the preconditioned Krylov subspace method is critical. It is well known that the convergence rate of the Krylov subspace method is influenced by the condition number of the coefficient matrix. Therefore, the following theorem is given to prove that the condition number of the coefficient matrix with the proposed preconditioner has an upper boundary.

Theorem 4.

For $0<{\beta }_j<1$ and $0<\tau <1$, the condition number of the preconditioned coefficient matrix ${\left(P^{m,k}\right)}^{-1}{M}^{m,k}$ is bounded, that is,

$$cond\left({\left(P^{m,k}\right)}^{-1}{M}^{m,k}\right)\le {\left({\tau }^{{\beta }_{min}}\underset{k\in N_s}{max}\left\{\right|q_{k,k}\left|\right\}+1\right)}^2.$$

(15)

Proof. 

With Theorem 3, it is straightforward that

$$\begin{array}{cc}\hfill \parallel {\left(P^{m,k}\right)}^{-1}{M}^{m,k}{\parallel }_{\infty }=& \parallel {\left(P^{m,k}\right)}^{-1}(M^{m,k}-P^{m,k})+I_{N{N}_s}{\parallel }_{\infty }\hfill \\ \hfill \le & \parallel {\left(P^{m,k}\right)}^{-1}(I_{N{N}_s}-\mathsf{\Theta })\left(D_1(Q_d-Q)\otimes I_N\right){\parallel }_{\infty }+1\hfill \\ \hfill \le & {\tau }^{{\beta }_{min}}\underset{k\in N_s}{max}\left\{\right|q_{k,k}\left|\right\}+1.\hfill \end{array}$$

Additionally, with Lemma 2, it yields

$$\begin{array}{cc}\hfill \parallel {\left({\left(P^{m,k}\right)}^{-1}{M}^{m,k}\right)}^{-1}{\parallel }_{\infty }=& \parallel {\left(M^{m,k}\right)}^{-1}{P}^{m,k}{\parallel }_{\infty }={\parallel {\left(M^{m,k}\right)}^{-1}(P^{m,k}-M^{m,k})+I_{N{N}_s}\parallel }_{\infty }\hfill \\ \hfill \le & \parallel {\left(M^{m,k}\right)}^{-1}(P^{m,k}-M^{m,k}){\parallel }_{\infty }+1\hfill \\ \hfill \le & \parallel {\left(M^{m,k}\right)}^{-1}{\parallel }_{\infty }{\parallel \left(D_1(Q-Q_d)\otimes I_N\right)\parallel }_{\infty }+1\hfill \\ \hfill \le & {\tau }^{{\beta }_{min}}\underset{k\in N_s}{max}\left\{\right|q_{k,k}\left|\right\}+1.\hfill \end{array}$$

Hence, the condition number of the preconditioned matrix ${\left(P^{m,k}\right)}^{-1}{M}^{m,k}$ is bounded, which can be written by

$$\begin{array}{cc}\hfill cond\left({\left(P^{m,k}\right)}^{-1}{M}^{m,k}\right)=& \parallel {\left(P^{m,k}\right)}^{-1}{M}^{m,k}{\parallel }_{\infty }{\parallel {\left({\left(P^{m,k}\right)}^{-1}{M}^{m,k}\right)}^{-1}\parallel }_{\infty }\hfill \\ \hfill \le & {\left({\tau }^{{\beta }_{min}}\underset{k\in N_s}{max}\left\{\right|q_{k,k}\left|\right\}+1\right)}^2.\hfill \end{array}$$

□

With Theorem 4, we know that the proposed preconditioner is able to ensure that the condition number of the preconditioned matrix is bounded. The upper bound is affected by Q, but ${\tau }^{{\beta }_{min}}$ usually being sufficiently small can help us to ensure that the upper bound is not too large. Hence, the proposed preconditioner can be expected to reduce the condition of the coefficient matrix and improve the convergence rate of the Krylov subspace method.

Remark 1.

Although Theorem 4 holds for the left preconditioner, this theorem still holds for the right preconditioner with similar proofs. The numerical tests with the right preconditioning technique are also given in Section 4.

4. Numerical Experiment

In this section, three American option pricing problems with time-fractional derivatives containing two states, four states, and eight states are considered as the numerical examples to test our proposed preconditioned policy-Krylov subspace method. All the numerical experiments were carried out in Matlab 2016a in the workstation with the following configuration: Intel(R) Core(TM) i9-10900K CPU 3.70 GHz and 64 GB RAM. The bi-conjugate gradient stabilized method and the GMRES method are used in this section, and their stopping criterion is ${10}^{-10}$. The stopping criterion of the policy iteration method is ${10}^{-7}$. The initial guesses of two iterative methods are both the numerical solution on the previous time step. The restart of the GMRES method is 20 in this section. In addition, to facilitate the calculation, in this section, we set a new symbol $\tilde{N}$ that satisfies $\tilde{N}=N+1$.

In the numerical experiment, we assume that the strike price $K=50$, the risk-free interest rate $r=0.05$, and the expiry moment $T=1$, i.e., one year. The truncation boundaries $[S_{min},S_{max}]=[0,100]$. The other parameters of the three cases are listed by

(a)

$N_s=2$, $\sigma =[0.2,0.4]$, $\beta =[0.8,0.95]$, $Q=\left[\begin{array}{cc}-2& 2\\ 3& -3\end{array}\right].$

(b)

$N_s=4$, $\sigma =[0.2,0.3,0.15,0.2]$, $\beta =[0.8,0.95,0.6,0.7]$,

$Q=\left[\begin{array}{cccc}-45& 20& 15& 10\\ 30& -80& 30& 20\\ 10& 10& -60& 40\\ 20& 10& 20& -50\end{array}\right].$

(c)

$N_s=8$, $\sigma =[0.2,0.3,0.15,0.2,0.5,0.2,0.4,0.3]$, $\beta =[0.8,0.95,0.6,0.7,0.8,0.3,0.2,0.6]$,

$Q=\left[\begin{array}{cccccccc}-192& 34& 16& 36& 31& 23& 25& 27\\ 32& -125& 3& 37& 15& 2& 29& 7\\ 17& 21& -144& 19& 9& 9& 25& 14\\ 36& 5& 4& -118& 16& 14& 18& 25\\ 7& 34& 7& 13& -145& 32& 21& 31\\ 10& 24& 9& 36& 5& -98& 11& 3\\ 5& 14& 16& 14& 37& 1& -124& 37\\ 5& 20& 1& 4& 38& 6& 7& -81\end{array}\right].$

The first part of the numerical experiment is to test the convergence rate of the nonlinear scheme (7) and the effectiveness of the proposed solution strategy. The performance of the Krylov subspace method without preconditioning technique is also presented in order to demonstrate the performance of the proposed preconditioner $P^{m,k}$. Since the exact solution is absent, the numerical solution from a fine grid where $\tilde{N}=2^{13}$ and $M=2^{11}$ is regarded as the exact solution to compute the truncation errors. Related numerical results from the bi-conjugate gradient stabilized method are presented in Table 1, while the numerical results from the GMRES method are given in Table 2.

Table 1. Numerical results from the bi-conjugate gradient stabilized methods.

					CG		PCG
N	M	Error	Rate	Ite-Out	Ite-In	Time	Ite-In	Time
Case (a)
$2^8$	$2^6$	$3.9728\times {10}^{-3}$	-	2.86	77.46	0.37 s	2.56	0.08 s
$2^9$	$2^7$	$1.9224\times {10}^{-3}$	1.0472	2.82	106.05	1.24 s	2.08	0.21 s
$2^{10}$	$2^8$	$9.1278\times {10}^{-4}$	1.0746	2.86	141.44	4.96 s	1.78	0.79 s
$2^{11}$	$2^9$	$3.9949\times {10}^{-4}$	1.1921	2.86	184.55	23.49 s	1.54	4.40 s
Case (b)
$2^8$	$2^6$	$8.9047\times {10}^{-3}$	-	2.73	62.25	0.38 s	7.92	0.19 s
$2^9$	$2^7$	$4.5215\times {10}^{-3}$	0.9778	2.77	91.38	1.59 s	5.79	0.51 s
$2^{10}$	$2^8$	$2.1635\times {10}^{-3}$	1.0634	2.71	138.52	8.79 s	4.61	2.26 s
$2^{11}$	$2^9$	$9.3962\times {10}^{-4}$	1.2032	2.69	208.57	44.75 s	3.70	9.30 s
Case (c)
$2^8$	$2^6$	$1.9890\times {10}^{-3}$	-	3.33	427.40	4.83 s	14.84	0.55 s
$2^9$	$2^7$	$9.8072\times {10}^{-4}$	1.0201	3.32	848.73	35.33 s	11.46	2.04 s
$2^{10}$	$2^8$	$4.8702\times {10}^{-4}$	1.0099	3.26	1705.16	242.65 s	9.43	7.15 s
$2^{11}$	$2^9$	$2.1722\times {10}^{-4}$	1.1648	3.24	-	-	7.41	30.50 s

Table 2. Numerical results from the GMRES methods.

					GMRES		PGMRES
N	M	Error	Rate	Ite-Out	Ite-In	Time	Ite-In	Time
Case (a)
$2^8$	$2^6$	$3.9724\times {10}^{-3}$	-	2.86	156.68	1.66 s	5.04	0.11 s
$2^9$	$2^7$	$1.9220\times {10}^{-3}$	1.0474	2.82	242.87	6.81 s	4.12	0.26 s
$2^{10}$	$2^8$	$9.1239\times {10}^{-4}$	1.0749	2.86	406.86	36.64 s	3.33	0.90 s
$2^{11}$	$2^9$	$3.9910\times {10}^{-4}$	1.1929	2.86	692.43	392.76 s	3.05	5.00 s
Case (b)
$2^8$	$2^6$	$8.9046\times {10}^{-3}$	-	2.73	113.89	1.58 s	13.86	0.30 s
$2^9$	$2^7$	$4.5214\times {10}^{-3}$	0.9778	2.77	191.73	8.20 s	10.59	0.72 s
$2^{10}$	$2^8$	$2.1634\times {10}^{-3}$	1.0635	2.71	372.04	99.65 s	8.29	3.07 s
$2^{11}$	$2^9$	$9.3955\times {10}^{-4}$	1.2032	2.69	760.57	637.37 s	6.55	11.78 s
Case (c)
$2^8$	$2^6$	$1.9890\times {10}^{-3}$	-	3.33	1411.11	36.60 s	24.77	0.98 s
$2^9$	$2^7$	$9.8069\times {10}^{-4}$	1.0202	3.32	8428.32	1409.52 s	18.56	4.21 s
$2^{10}$	$2^8$	$4.8698\times {10}^{-4}$	1.0099	3.26	32,658.12	17,206.00 s	14.56	10.57 s
$2^{11}$	$2^9$	$2.1718\times {10}^{-4}$	1.1650	3.24	-	-	11.55	39.96 s

In Table 1 and Table 2, the notation `Error’ denotes the infinity norm of the truncation error of the nonlinear scheme (7) solved by the preconditioned policy-Krylov subspace method, and `Rate’ means the convergence rate. The notations `CG’ and `PCG’ stand for the bi-conjugate gradient stabilized method without and with the proposed preconditioner, respectively. Similarly, `GMRES’ and `PGMRES’ denote the GMRES method and the GMRES method with the proposed preconditioner, respectively. The iteration numbers of the policy iteration method with different linear solvers are almost the same. Thus only the average number of policy iterations from the preconditioned Krylov subspace method is given and denoted by `Ite-Out’. The notations `Ite-In’ and `Time’ are the average iteration numbers of the linear solvers and CPU time, respectively. Remark that the left preconditioning technique is used for the preconditioned bi-conjugate gradient stabilized method, and the right preconditioning technique is used for the preconditioned GMRES method.

From Table 1 and Table 2, it can be seen that the convergence rate of the proposed nonlinear scheme is first-order. Note that the errors of the two tables are close because both of these linear solvers solve the same problem with the same stopping criterion. The policy iteration method converges to the solution rapidly, which can be found by `Ite-Out’. Compared with the bi-conjugate gradient stabilized method and GMRES method, we find that the GMRES method takes more iterations for the same problem in our numerical examples. Significantly, the proposed preconditioner can improve the convergence rate of the bi-conjugate gradient stabilized and GMRES methods. As analyzed in Theorem 4, the upper bound on the condition number of Case (c) is higher than Case (a) and (b) due to the number of states being larger. Hence, the bi-conjugate gradient stabilized method and the GMRES method with preconditioner needs more iterations to converge.

To further analyze the effect of the preconditioning technique and verify Theorem 4, the second part of the numerical experiment focuses on testing the eigenvalues and condition numbers of the preconditioned matrix ${\left(P^{m,k}\right)}^{-1}{M}^{m,k}$ and coefficient matrix $M^{m,k}$. It is difficult to choose a specific matrix to finish the test since the matrices $P^{m,k}$ and $M^{m,k}$ are determined by m and k. Given the existence of the American option free boundary, there is usually a point ${\theta }_{*}$ such that the matrix satisfies $\theta =1$ when $S<{\theta }_{*}$ and $\theta =0$ when $S\ge {\theta }_{*}$. To facilitate further analysis, we used Case (b) to finish the test and set a particular P and M that satisfied ${\theta }_{*}=\lfloor \frac{\tilde{N}}{2}\rfloor$. Then, the eigenvalue distributions of the coefficient matrix M and preconditioned matrix $P^{-1}M$ when $M=\tilde{N}=2^{10}$ are given in Figure 1. Additionally, the condition numbers of them when $M=\tilde{N}$ are given in Figure 2.

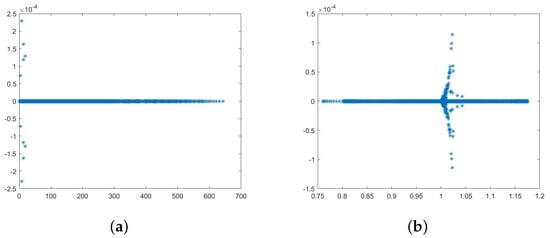
Figure 1. Eigenvalues distribution: (a) eigenvalue of coefficient matrix M; (b) eigenvalue of preconditioned matrix $P^{-1}M$.

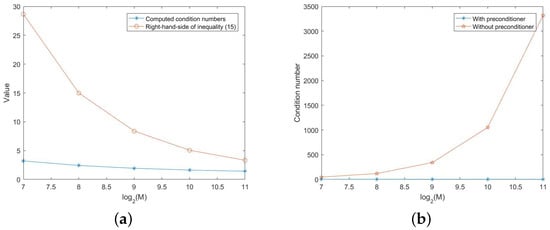
Figure 2. Condition number of the coefficient matrix: (a) condition number of preconditioned matrix $P^{-1}M$; (b) comparison of condition number of $P^{-1}M$ and M.

From Figure 1a, we know that the maximum of the real part of the eigenvalues of the coefficient matrix is more than 600, which may cause the slow convergence rate of the Krylov subspace method. Conversely, the eigenvalues in Figure 1b are clustered around one after preconditioning, although the gathering radius is close to $0.3$, which helps improve the convergence rate of the Krylov subspace method.

In Figure 2, the condition number of the coefficient matrix M, the condition number of the preconditioned matrix $P^{-1}M$, and the upper boundary of the condition number given by Theorem 4 are presented. From Figure 2a, the condition number is lower than 5 with the preconditioning technique. The theoretical upper boundary decreases from $28.65$ to $3.33$ as M increases. In Figure 2b, the condition number without the preconditioning technique is given to compare with the condition number of $P^{-1}M$. One can see that the condition number is increasing with M and the maximum value is 3318.69 when $M=2^{11}$. With the proposed preconditioning technique, the condition number is kept below 5, which demonstrates that the proposed preconditioner can reduce the condition number of the coefficient matrix M.

In the last part of the numerical experiment, the option values of three cases are presented in Figure 3 when $M=\tilde{N}=2^{12}$, respectively. In Figure 3, we can find that multi-regimes cause the option value differences between different regimes.

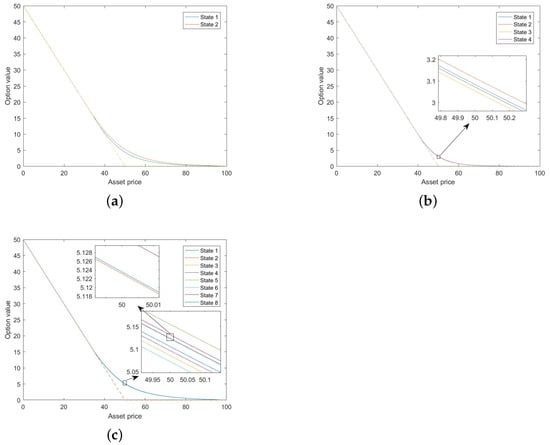
Figure 3. Option value of three examples: (a) option value of two regimes; (b) option value of four regimes; (c) option value of eight regimes.

5. Concluding Remark

This paper considers the multi-state time-fractional LCP for American options pricing and proposes a preconditioned policy-Krylov subspace method to handle this problem. The considered problem has been transformed into HJB equations coupled by the Markov generator matrix, then a nonlinear finite difference scheme is developed to discretize it with unconditional stability guarantees. A preconditioned policy-Krylov subspace method has been proposed to solve the discrete HJB equation with convergence guarantees. The condition number of the preconditioned coefficient matrix has been proven to have an upper boundary. The numerical experiments are presented to demonstrate the efficiency of the proposed nonlinear finite difference scheme and the preconditioned policy-Krylov subspace method.

In addition, the considered problem is based on a non-dividends option pricing model, and the dividend models are yet to be addressed. The problem of pricing American options with dividends, as well as the problem of pricing options with fractional order derivatives in space-time, will be addressed in our future work.