Fast and Accurate Numerical Algorithm with Performance Assessment for Nonlinear Functional Volterra Equations

Abstract

An efficient numerical algorithm is developed for solving nonlinear functional Volterra integral equations. The core idea is to define an appropriate operator, then combine the Krasnoselskij iterative scheme with collocation at discrete points and the Newton–Cotes quadrature rule. This results in an explicit scheme that does not require solving a nonlinear or linear algebraic system. For the convergence analysis, the discretization error is estimated and proved to converge via a recurrence relation. The discretization error is combined with the Krasnoselskij iteration error to estimate the total approximation error, hence establishing the convergence of the method. Then, numerical experiments are provided, first, to demonstrate the second order convergence of the proposed method, and secondly, to show the better performance of the scheme over the existing nonlinear-based approach.

1. Introduction

This study is devoted to analyzing and computing the solution of nonlinear functional Volterra integral equations. These equations have applications in several areas such as physical sciences [1,2,3], optimal control and economics [4,5,6,7], reformulation of more difficult mathematical problems [8,9], and epidemiology [10,11]. In [12], sufficient conditions for the existence of a principal solution were derived for nonlinear Volterra equations and an explicit method was also proposed.

Since closed-form analytical solutions, in general, do not exist, numerical techniques provide a means of approximating them. For example, numerical algorithms have been proposed based on triangular functions [13], collocation methods [14,15], CAS wavelets [16,17], the variational iteration methods [18,19,20,21], collocation–trapezoidal methods [22,23], linear programming [24], Picard–trapezoidal rule [9], and Taylor series [25]. Moreover, see [10,11,26,27,28,29] for other ideas. Most of these methods are based on directly discretizing the original nonlinear integral equations without using any fixed-point iteration (such as the Picard iteration). In this work, we shall refer to this type of methods as direct discretization (DD) algorithms. A typical example is the one proposed in [22].

It is well known that, under suitable conditions and with an arbitrary initial function in a suitable Banach space, the fixed point of an appropriate operator can be approximated using an applicable fixed-point iteration technique, such as the Picard, Krasnoselskijj, Mann, or Ishikawa schemes [30,31,32,33], see also [34]. These iterative methods can produce analytical expressions for the approximating functions, provided all the operations in the operator are analytically realizable. We shall refer to this type of approach as the Picard-type (PT) schemes. See [35] for an example.

The challenge with DD schemes is that they lead to nonlinear algebraic systems which require a lot of computational resources, time, and even high programming skills to solve. The PT schemes face the challenge of not being practically useful once the operations involved in the operator cannot be obtained analytically. This is usually the case in nonlinear problems. Micula [9] came up with the idea of combining PT schemes with DD using the Picard iteration and trapezoidal rule; see also [36] for Mann’s iteration.

It is known that the Mann iteration converges faster than the Picard’s [36]; however, it is also proved in Theorem 9.4 of [30] that for certain operators, given any Mann iteration that converges to the fixed point, there is always a Krasnoselskij iteration which converges faster. Therefore, the present paper develops the combined technique for functional integral equations using the Krasnoselkij iterative algorithm and a one-dimensional quadrature rule defined at collocation points. The advantages of the approach are as follows: First, unlike the DD schemes, it does not lead to a coupled nonlinear algebraic system, and not even linear systems are encountered. Hence, Newton or other nonlinear solvers are completely avoided and even linear iterative algorithms are also not needed. Second, unlike the PT schemes, every integral is explicitly approximated. A systematic analysis of the convergence of the approach is carried out and numerical examples are provided to show the second-order accuracy of the method. Moreover, the existence and uniqueness of the results in Micula [9,36] are obtained on the basis of a contraction assumption. In the current work, we prove the solvability of the problem without any contraction assumption by employing the generalized Banach contraction principle.

To be precise, the problem investigated in this work is the following nonlinear functional Volterra integral equation of the second kind:

$$\begin{array}{c}\hfill u\left(x\right)=g\left(x\right)+f\left(x,{\int }_{y=a}^{x}k(x,y,u\left(y\right))dy\right),x\in [a,b]\subset ,\end{array}$$

(1)

where $C[a,b]\ni g:\to ,f:\times \to ,k:\times \times \to$.

The solvability of the problem is proved in Section 2, whereas the numerical algorithm which begins with the Krasnoselskij iteration is derived in Section 3. The error and convergence of the method are analyzed in Section 4, whereas numerical examples are provided in Section 5 to demonstrate the accuracy. In Section 6 we assess the performance. Some concluding remarks are given in Section 7.

2. Solvability

We make the following assumptions:

• $g,k,f(x,{\int }_{y=a}^{x}k(x,y,u\left(y\right))dy)\in L^{\infty }$.
• The functional f is Lipschitz continuous with respect to the second argument, with a Lipschitz constant ${\alpha }_f\ge 0$:

  $$\begin{array}{c}\hfill \parallel f(x,u)-f(x,v)\parallel \le {\alpha }_f\parallel u-v\parallel ,\mathrm{for} \mathrm{all} u,v\in L^{\infty }.\end{array}$$

  (2)
• The kernel, k is Lipschitz continuous with respect to u with Lipschitz constant ${\alpha }_k\ge 0$:

  $$\begin{array}{c}\hfill \parallel k(x,y,u)-k(x,y,v)\parallel \le {\alpha }_k\parallel u-v\parallel \mathrm{for} \mathrm{all} u,v\in L^{\infty }.\end{array}$$

  (3)

We define an operator, T, by

$$\begin{array}{c}\hfill \left(Tu\right)\left(x\right):=g\left(x\right)+f\left(x,{\int }_{y=a}^{x}k(x,y,u\left(y\right))dy\right).\end{array}$$

(4)

Lemma 1.

The operator T defined in (4) satisfies the inequality:

$$\begin{array}{c}\hfill |T^{k}u\left(x\right)-T^{k}v\left(x\right)|\le \frac{{\left({\alpha }_f{\alpha }_k(x-a)\right)}^k}{k!}|u\left(x\right)-v\left(x\right)|,for k=1,2,\cdots .\end{array}$$

(5)

Proof. 

We prove this by induction. Setting $k=1$, we obtain:

$$\begin{array}{cc}\hfill \left|\right(Tu\left)\right(x)-(Tv\left)\right(x\left)\right|& =|f\left(x,{\int }_a^{x}k(x,y,u\left(y\right))dy\right)-f\left(x,{\int }_a^{x}k(x,y,v\left(y\right))dy\right)|\hfill \\ \hfill & \le {\alpha }_f{\alpha }_k{\int }_a^x|u\left(y\right)-v\left(y\right)|dy(\mathrm{by} \mathrm{Lipschitz} \mathrm{Continuity} \mathrm{of} f \mathrm{and} k)\hfill \\ \hfill & ={\alpha }_f{\alpha }_k|u\left(y\right)-v\left(y\right)|{\int }_a^{x}dy\hfill \\ \hfill & \le {\alpha }_f{\alpha }_k(x-a)|u\left(y\right)-v\left(y\right)|.\hfill \end{array}$$

(6)

This shows that (5) is true for $k=1$. Next, we let $k=2$, then we obtain:

$$\begin{array}{cc}\hfill |T^{2}u\left(x\right)-T^{2}v\left(x\right)|& \le {\alpha }_f{\alpha }_k{\int }_a^x|Tu\left(y\right)-Tv\left(y\right)|dy\hfill \\ \hfill & \le {\alpha }_f{\alpha }_k{\int }_a^x{\alpha }_f{\alpha }_k(y-a)|u\left(y\right)-v\left(y\right)|dy\hfill \\ \hfill & \le {\alpha }_f^2{\alpha }_k^2\frac{{(x-a)}^2}{2}|u\left(x\right)-v\left(x\right)|\hfill \end{array}$$

which is also true. Now we assume it is true for any k. Then

$$\begin{array}{cc}\hfill |T^{k+1}u\left(x\right)-T^{k+1}v\left(x\right)& |\le {\alpha }_f{\alpha }_k{\int }_a^x|T^{k}u\left(y\right)-T^{k}v\left(y\right)|dy\hfill \\ \hfill & \le {\alpha }_f{\alpha }_k{\int }_a^x\frac{{\left({\alpha }_f{\alpha }_k(y-a)\right)}^k}{k!}|u\left(y\right)-v\left(y\right)|dy\hfill \\ \hfill & =\frac{{\left({\alpha }_f{\alpha }_k(x-a)\right)}^{k+1}}{(k+1)!}|u\left(x\right)-v\left(x\right)|.\hfill \end{array}$$

Hence, it is true for all k. □

Theorem 1

(Solvability). If Assumptions 1–3 are true, then the nonlinear functional Volterra integral Equation (1) has a unique solution.

Proof. 

Assumption (1) above guarantees that $T:L^{\infty }\to L^{\infty }$. Now, Lemma 1 gives

$$\begin{array}{cc}\hfill |T^{k}u\left(x\right)-T^{k}v\left(x\right)|& \le \frac{{\left({\alpha }_f{\alpha }_k(x-a)\right)}^k}{k!}|u\left(x\right)-v\left(x\right)|,\mathrm{for} k=1,2,\cdots \hfill \\ \hfill & \le \frac{{\left({\alpha }_f{\alpha }_k(b-a)\right)}^k}{k!}|u\left(x\right)-v\left(x\right)|\to 0 \mathrm{as} k\to \infty .\hfill \end{array}$$

(7)

This shows that T is a contraction and it follows from the generalized Banach contraction principle that T has a unique fixed point which is the unique solution of problem (1). □

3. Numerical Algorithm

This section details the numerical approximation of problem (1). To this end, let $N\in {\mathbb{Z}}^{+}$ and define the mesh ${\Omega }_h=\{x_i=a+ih:i=0,1,\cdots ,N,h:=\frac{b-a}{N}\}$. We also define the grid functions

$$\begin{array}{c}\hfill u_i\approx u\left(x_i\right)\mathrm{for} \mathrm{each} i, \mathrm{and} {\xi }_i^N:=h\left\{\begin{array}{c}\frac{1}{2},\mathrm{if} i=0,N,\hfill \\ 1,\mathrm{otherwise},\hfill \end{array}\right..\end{array}$$

(8)

Since T is a contraction, the sequence ${\left\{u\left(x\right)\right\}}_{n=0}^{\infty }$ generated by

$$\begin{array}{c}\hfill u_{n+1}\left(x\right)=(1-\lambda )u_n\left(x\right)+\lambda T{u}_n\left(x\right),\lambda \in (0,1),\end{array}$$

(9)

converges to the fixed point of T [30] with the error estimate [31]:

$$\begin{array}{c}\hfill \parallel u_{n+1}\left(x\right)-u\left(x\right)\parallel \le {\alpha }^n\parallel u_1\left(x\right)-u\left(x\right)\parallel \mathrm{for} \mathrm{each} x\in [a,b],\end{array}$$

(10)

where

$$\begin{array}{c}\hfill \alpha =[1-(1-\widehat{\alpha })\lambda ]<1,\widehat{\alpha }={\alpha }_f{\alpha }_k(b-a)<1.\end{array}$$

(11)

Lemma 2

(See [37]). Let $x_i=a+ih,i=0,N,h=(b-a)/N$ be points in the interval $[a,b]$. Suppose that $f\in C^2[a,b]$. Then

$$\begin{array}{c}\hfill {\int }_a^{b}f\left(x\right)dx=\left(\sum _{j=0}^N\left({\xi }_j^{N}f\left(x_j\right)\right)\right)+R_f,\end{array}$$

(12)

and there exists $0\le R_m<\infty$ such that

$$\begin{array}{c}\hfill |R_f|\le R_m=\underset{\chi \in [a,b]}{max}\left\{\frac{h^2(b-a)}{12}{f}^{″}\left(\chi \right)\right\}=O\left(h^2\right).\end{array}$$

(13)

To derive the method, we first collocate problem (1) at $x_0=a\in {\Omega }_h$. This gives:

$$\begin{array}{c}\hfill u\left(x_0\right)=g\left(x_0\right)+f(x_0,0).\end{array}$$

(14)

Observe that this is exact as no approximation has been made. Hence, we can initialize the Krasnoselskij sequence (9) from (14) as follows:

$$\begin{array}{c}\hfill u_0\left(x\right)=g\left(x\right)+f(x,0),\mathrm{for} \mathrm{all} x\in [a,b].\end{array}$$

Therefore, the iteration becomes:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{n+1}\left(x\right)=(1-\lambda )u_n\left(x\right)+\lambda \left(T{u}_n\right)\left(x\right),n\ge 0,\hfill \\ u_0\left(x\right)=g\left(x\right)+f(x,0),0<\lambda <1.\hfill \end{array}\right.\end{array}$$

(15)

We now collocate (15) at $x_i\in {\Omega }_h\backslash \left\{x_0\right\}$:

$$\begin{array}{cc}\hfill & 0<\lambda <1,u_0\left(x_i\right)=g\left(x_i\right)+f(x_i,0),\hfill \\ \hfill & n\ge 0:\left\{\begin{array}{c}{I}_n\left(x_i\right)={\int }_{y=a}^{x_i}k(x_i,y,u_n\left(y\right))dy,\hfill \\ u_{n+1}\left(x_i\right)=(1-\lambda )u_n\left(x_i\right)+\lambda \left(g\left(x_i\right)+f(x_i,I_n\left(x_i\right))\right).\hfill \end{array}\right.\hfill \end{array}$$

(16)

Using the trapezoidal rule in Lemma 2 to approximate the integral on the iterative scheme (16), we have the algorithm:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & x_i\in {\Omega }_h\backslash \left\{x_0\right\},n=0,1,\cdots ,\hfill \\ {\widehat{u}}_{n+1}\left(x_i\right)\hfill & =(1-\lambda ){\widehat{u}}_n\left(x_i\right)+\lambda (g\left(x_i\right)+f(x_i,{\widehat{I}}_{h,n}\left(x_i\right))),\hfill \\ {\widehat{u}}_0\left(x_i\right)\hfill & =u_0\left(x_i\right),\mathrm{for} \mathrm{all} x_i\in {\Omega }_h,\hfill \\ {\widehat{I}}_{h,n}\left(x_i\right)\hfill & =\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,{\widehat{u}}_n\left(x_j\right)).\hfill \end{array}\right.\end{array}$$

(17)

The system (17) constitutes the numerical algorithm for approximating problem (1). We prove in the next section that a sequence of solutions computed with this scheme converges to the exact solution of problem (1).

4. Convergence Analysis

Definition 1

(Maximum Error). The numerical error, $e_h$, is the maximum error committed in approximating $u\left(x_i\right)$ by using the scheme (17) for all $x_i\in {\Omega }_h$ when $n\to \infty$. That is

$$\begin{array}{c}\hfill e_h=\underset{n\to \infty }{lim}\left(\underset{x_i\in {\Omega }_h}{max}{e}_n\left(x_i\right)\right)\end{array}$$

(18)

where

$$e_n\left(x_i\right)=|u\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|.$$

Remark 1.

The goal in this section is to show that the quantity $e_n\left(x_i\right)$ vanishes whenever $n\to \infty$, $h\to 0$, and assumption (11) holds.

Let us first prove the following lemma.

Lemma 3.

Let γ be a Lipschitz operator with constant ${\alpha }_g$. Then

$$\begin{array}{c}\hfill \gamma (u+v)\le \gamma \left(u\right)+{\alpha }_g\left|v\right|for all u,v\in Dom\left(\gamma \right).\end{array}$$

(19)

Proof. 

The result is trivial when $v=0$. It is also trivial if $v\ne 0$ and $\gamma (u+v)\le \gamma \left(u\right)$. We only prove the inequality for the case when $v\ne 0$ and

$$\begin{array}{c}\hfill \gamma (u+v)>\gamma \left(u\right).\end{array}$$

(20)

By the Lipschitz continuity of $\gamma$, we have

$$|\gamma (u+v)-\gamma \left(u\right)|\le {\alpha }_g\left|v\right|.$$

Because of (20), we can write the left side of the last inequality as:

$$\gamma (u+v)-\gamma \left(u\right)\le {\alpha }_g\left|v\right|.$$

Hence the result. □

Lemma 4

(Recurrence Relation). The error, ${\widehat{R}}_n\left(x_i\right)=|u_n\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|$, committed in using the scheme (17) to approximate the iterative process (16) satisfies the recurrence relation:

$$\begin{array}{c}\hfill {\widehat{R}}_{n+1}\left(x_i\right)\le \left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_n\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|.\end{array}$$

(21)

Proof. 

First, since ${\widehat{u}}_0\left(x_i\right)=u_0\left(x_i\right)$, it means that ${\widehat{R}}_0=0$.

Setting $n=0$ in (17), we have:

$$\begin{array}{cc}\hfill & u_1\left(x_i\right)=(1-\lambda )u_0\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,u_0\left(x_j\right))+{\tilde{R}}_1\right)\right)\hfill \\ \hfill & \le (1-\lambda )u_0\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,u_0\left(x_j\right))\right)+{\alpha }_f\left|{\tilde{R}}_1\right|\right)(\mathrm{see} \mathrm{Lemma} 3)\hfill \\ \hfill & \le (1-\lambda )u_0\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,u_0\left(x_j\right))\right)\right)+{\alpha }_f\lambda \left|R_m\right|\hfill \\ \hfill & ={\widehat{u}}_1\left(x_i\right)+{\alpha }_f\lambda \left|R_m\right|.\hfill \end{array}$$

(22)

Hence,

$$\begin{array}{cc}\hfill {\widehat{R}}_1& :=|u_1\left(x_i\right)-{\widehat{u}}_1\left(x_i\right)|\hfill \\ \hfill & \le {\alpha }_f\lambda |R_m|=\left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^{n-1}{\xi }_j^i\right){\widehat{R}}_0\left(x_i\right)+{\alpha }_f\lambda \left|R_m\right|.\hfill \end{array}$$

(23)

Similarly, setting $n=1$, we obtain:

$$\begin{array}{cc}\hfill & u_2\left(x_i\right)=(1-\lambda )u_1\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,u_1\left(x_j\right))+{\tilde{R}}_2\right)\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_1\left(x_i\right)+(1-\lambda ){\widehat{R}}_1\left(x_i\right)\hfill \\ \hfill & +\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k\left(x_i,x_j,{\widehat{u}}_1\left(x_j\right)+{\widehat{R}}_1\right)+R_m\right)\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_1\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,{\widehat{u}}_1\left(x_j\right))+{\alpha }_k\left|{\widehat{R}}_1\right|\sum _{j=0}^i{\xi }_j^i+R_m\right)\right)\hfill \\ \hfill & +(1-\lambda ){\widehat{R}}_1\left(x_i\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_1\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,{\widehat{u}}_1\left(x_j\right))\right)\right)\hfill \\ \hfill & +\left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_1\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|\hfill \\ \hfill & ={\widehat{u}}_2\left(x_i\right)+\left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_1\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|.\hfill \end{array}$$

(24)

Hence,

$$\begin{array}{cc}\hfill {\widehat{R}}_2\left(x_i\right)& =|u_2\left(x_i\right)-{\widehat{u}}_2\left(x_i\right)|\hfill \\ \hfill & \le \left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_1\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|.\hfill \end{array}$$

(25)

In general,

$$\begin{array}{cc}\hfill & u_{n+1}\left(x_i\right)=(1-\lambda )u_n\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,u_n\left(x_j\right))+{\tilde{R}}_{n+1}\right)\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_n\left(x_i\right)+(1-\lambda ){\widehat{R}}_n\left(x_i\right)\hfill \\ \hfill & +\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k\left(x_i,x_j,{\widehat{u}}_n\left(x_j\right)+{\widehat{R}}_n\right)+R_m\right)\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_n\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,{\widehat{u}}_n\left(x_j\right))+{\alpha }_k{\widehat{R}}_n\sum _{j=0}^i{\xi }_j^i+R_m\right)\right)\hfill \\ \hfill & +(1-\lambda ){\widehat{R}}_n\left(x_i\right)\hfill \\ \hfill & \le (1-\lambda ){\widehat{u}}_n\left(x_i\right)+\lambda \left(g\left(x_i\right)+f\left(x_i,\sum _{j=0}^i{\xi }_j^{i}k(x_i,x_j,{\widehat{u}}_n\left(x_j\right))\right)\right)\hfill \\ \hfill & +\left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_n\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|\hfill \\ \hfill & ={\widehat{u}}_{n+1}\left(x_i\right)+\left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_n\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|.\hfill \end{array}$$

(26)

Inequality (26) gives:

$$\begin{array}{cc}\hfill {\widehat{R}}_{n+1}& :=|u_{n+1}\left(x_i\right)-{\widehat{u}}_{n+1}\left(x_i\right)|\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & \le \left(1-\lambda +\lambda {\alpha }_f{\alpha }_k\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_n\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|.\hfill \end{array}$$

(28)

This proves the claim. □

Theorem 2

(Convergence). The error ${\widehat{R}}_n\left(x_i\right)=|u_n\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|$ committed in using the scheme (17) to approximate the iterative process (16) satisfies:

$$\begin{array}{c}\hfill {\widehat{R}}_n\left(x_i\right)\le c_2\sum _{j=0}^{n-1}{c}_1^j,\end{array}$$

(29)

hence

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\widehat{R}}_n\left(x_i\right)& \le \frac{{\alpha }_f}{1-{\alpha }_f{\alpha }_k{\sum }_{j=0}^i{\xi }_j^i}\left|R_m\right|=O\left(h^2\right),\hfill \end{array}$$

(30)

where $c_1=1-\lambda +\lambda {\alpha }_f{\alpha }_k{\sum }_{j=1}^{n-1}{\xi }_j^i$ and $c_2=\lambda {\alpha }_f\left|R_m\right|$.

Proof. 

From Lemma 21, we have

$$\begin{array}{cc}\hfill {\widehat{R}}_n\left(x_i\right)& \le \left(1-\lambda +\lambda {\alpha }_f{\alpha }_f\sum _{j=1}^i{\xi }_j^i\right){\widehat{R}}_{n-1}\left(x_i\right)+\lambda {\alpha }_f\left|R_m\right|\hfill \\ \hfill & =c_1{\widehat{R}}_{n-1}+c_2\le c_1\left(c_1{\widehat{R}}_{n-2}+c_2\right)+c_2\hfill \\ \hfill & \le c_1^2{\widehat{R}}_{n-2}+c_1{c}_2+c_2\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le c_1^n{\widehat{R}}_0+c_2\sum _{j=0}^{n-1}{c}_1^j\hfill \\ \hfill & =c_2\sum _{j=0}^{n-1}{c}_1^j.\hfill \end{array}$$

(31)

Taking limit:

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\widehat{R}}_n& \le \frac{c_2}{1-c_1}=\frac{{\alpha }_f}{1-{\alpha }_f{\alpha }_k{\sum }_{j=0}^i{\xi }_j^i}\left|R_m\right|=O\left(h^2\right).\hfill \end{array}$$

(32)

□

Theorem 3

(Convergence). The numerical solution, ${\widehat{u}}_n\left(x\right)$, computed using the scheme (17), converges to the exact solution, $u\left(x\right)$.

Proof. 

The error $e_n\left(x_i\right)$ between $u\left(x_i\right)$ and ${\widehat{u}}_n\left(x_i\right)$ is

$$\begin{array}{cc}\hfill e_n\left(x_i\right)& =|u\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|=|u\left(x_i\right)-u_n\left(x_i\right)+u_n\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|\hfill \\ \hfill & \le |u\left(x_i\right)-u_n\left(x_i\right)|+|u_n\left(x_i\right)-{\widehat{u}}_n\left(x_i\right)|\hfill \\ \hfill & \le {\alpha }^n|u\left(x_i\right)-u_n\left(x_i\right)|+\frac{{\alpha }_f}{1-{\alpha }_f{\alpha }_k{\sum }_{j=0}^i{\xi }_j^i}\left|R_m\right|\hfill \\ \hfill & ={\alpha }^n|u\left(x_i\right)-u_n\left(x_i\right)|+O\left(h^2\right).\hfill \end{array}$$

where $\alpha <1$ is defined in (11). Hence, the convergence result follows (see definition 1 and the remark that follows it). □

Remark 2.

Observe the appearance of $1-{\alpha }_f{\alpha }_k{\sum }_{j=0}^i{\xi }_j^i$ in (30). This implies that we require this quantity to be non-negative (since the left hand side of (30) is positive). Since ${\alpha }_f{\alpha }_k{\sum }_{j=0}^i{\xi }_j^i\le {\alpha }_f{\alpha }_k(b-a)$, it follows that the requirement is satisfied if

$$\begin{array}{c}\hfill {\alpha }_f{\alpha }_k(b-a)<1.\end{array}$$

(33)

This is a requirement for the scheme to be convergent.

Remark 3

(Implication of the analysis). As observed in the proof of Theorem 3, the numerical error consists of two parts—the fixed-point iteration error and the quadrature error. Hence, both errors must converge to zero for the proposed method to converge to the exact solution, and the solutions computed with the method would be obtained at minimal computational cost compared to methods which involve solving nonlinear systems. However, since the convergence of the fixed-point iteration is guaranteed whenever the operator is a contraction, it then implies that if an appropriate quadrature rule is in place, then the contractivity of the associated operator guarantees that numerical solutions can be computed accurately and efficiently.

5. Numerical Experiments

Numerical examples are now presented to assess the accuracy and efficiency of the scheme (17). The examples are derived through the method of manufacture solutions [38]. In each of the four problems, a sequence of solutions is computed with different meshes of varying sizes. In all the computations, we take $\lambda =0.5$ and terminate each Krasnoselskij iteration whenever $|u_{n+1}\left(x_i\right)-u_n\left(x_i\right)|\le 8\times {10}^{-11}$. The error (in maximum norm) is computed as in (18), whereas the experimental order of convergence is computed using:

$$\begin{array}{cc}\hfill EOC& =\frac{log\left(\frac{e_h}{e_{h/2}}\right)}{log\left(2\right)},\hfill \end{array}$$

(34)

see [39].

5.1. Example 1

The following problem is considered (see [22]):

$$\begin{array}{c}\hfill u\left(x\right)=g\left(x\right)+\frac{sin\left(x\right)}{1+{\left({\int }_0^{x}u\left(y\right)e^{x-y-u^2}dy\right)}^2},x\in [0,1].\end{array}$$

(35)

where

$$g\left(x\right)=e^{-x}-\frac{sin\left(x\right)}{{\left(-e^{-1}{e}^x/2+e^x{e}^{-e^{-2x}}/2\right)}^2+1}.$$

The exact solution of this problem is $u\left(x\right)=e^{-x}$. Table 1 tabulates the numerical results and shows that the computed solution converges to the exact solution with second order of accuracy. Figure 1 shows the plots of the numerical and exact solutions on grids with $2,3,6$ and 20 grid points. The convergence of the method is obviously ascertained.

Table 1. Numerical Results for Example 1. N = number of sub-intervals. Errors are computed with the infinity norm. EOC = Experimental order of convergence.

N	Error	EOC
1	0.01213743114921989	-
2	0.005090501313527285	1.2535834665481371
4	0.0013464449826251501	1.9186524594014347
8	0.00035011541689816683	1.943252785210336
16	8.790389104307295 $\times {10}^{-5}$	1.993831658033252
32	2.2059673406571445 $\times {10}^{-5}$	1.9945155953164302
64	5.515784523291156 $\times {10}^{-6}$	1.9997734284826107
128	1.3789984285583756 $\times {10}^{-6}$	1.9999452855688975
256	3.4476374671799093 $\times {10}^{-7}$	1.9999408304436097
512	8.619000313458969 $\times {10}^{-8}$	2.000015626096606
1024	2.1545896289332234 $\times {10}^{-8}$	2.000107431585809
2048	5.385888846021203 $\times {10}^{-9}$	2.000156753556326

Figure 1. Plot of solution of Example 1 for different grid sizes.

5.2. Example 2

In this example, we consider the problem (see also [22]):

$$\begin{array}{c}\hfill u\left(x\right)=-\frac{x^2}{9}-{\left(x^{6/27}+1\right)}^{1/3}+f\left(x,{\int }_0^{1}k(x,y,u\left(y\right))dy\right),\end{array}$$

(36)

where

$$f(x,I)={(I^2+1)}^{1/3},k(x,y,u)=\left\{\begin{array}{cc}u,\hfill & \mathrm{if} y\le x,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The exact solution to this problem is $u\left(x\right)=\frac{x^2}{9}$. The numerical results as tabulated in Table 2 show that the computed solution converges to the exact solution with second order of accuracy. To make the discussion easier to understand, the solutions computed on different grids are plotted in Figure 2, and the convergence of the method is obvious.

Table 2. Numerical results for Example 2.

N	Error	EOC
1	0.0005814856077918928	-
2	0.00012230339333171858	2.2492790520697135
4	2.91619860433856 $\times {10}^{-5}$	2.0683035510752483
8	7.202538943651415 $\times {10}^{-6}$	2.017511515015079
16	1.7951203420268902 $\times {10}^{-6}$	2.0044249926801028
32	4.4841246069071694 $\times {10}^{-7}$	2.001182289199546
64	1.1207335620655456 $\times {10}^{-7}$	2.000383029609112
128	2.80046026646108 $\times {10}^{-8}$	2.000707475089127
256	6.996875440146155 $\times {10}^{-9}$	2.0008812453274856
512	1.7429708232263863 $\times {10}^{-9}$	2.005162389306972
1024	4.336317416253621 $\times {10}^{-10}$	2.0070061491915854
2048	1.0526418625644851 $\times {10}^{-10}$	2.042455689416187
4096	2.525327169600189 $\times {10}^{-11}$	2.059472461771361

Figure 2. Plot of solution of Example 2 for different grid sizes.

5.3. Example 3

As a third example, we consider the problem:

$$\begin{array}{c}\hfill u\left(x\right)=g\left(x\right)+\frac{x^2}{1+{\left({\int }_0^x\frac{x^3{y}^5}{1+u^2}dy\right)}^2}x\in [0,1].\end{array}$$

(37)

where

$$g\left(x\right)=\frac{x^2(x(x^{6}log{(x^6+1)}^2+36)-36)}{x^{6}log{(x^6+1)}^2+36}.$$

The exact solution of this problem is $u\left(x\right)=x^3$. It can also be seen in Table 3 that the numerical solution converges to the exact solution with second order of convergence. Moreover, Figure 3 demonstrates the convergence of the method as the grid is refined from just two points to twenty points. The proposed numerical scheme is clearly convergent. The astonishing feature of the method is that very high accuracy is attained even with very coarse grids.

Table 3. Numerical results for Example 3. Results show second-order convergence.

N	Error	EOC
1	0.05163523545962034	-
2	0.006373161885883882	3.018274672426548
4	0.0012307613112914062	2.372458308685062
8	0.0002983915555665462	2.044272385454718
16	7.400954062197762 $\times {10}^{-5}$	2.0114235414553514
32	1.8465882868468064 $\times {10}^{-5}$	2.002849020979508
64	4.6142027866347135 $\times {10}^{-6}$	2.000708925979108
128	1.1534254369394148 $\times {10}^{-6}$	2.00015666531903
256	2.883532977948633 $\times {10}^{-7}$	2.0000153169770556
512	7.209643260175369 $\times {10}^{-8}$	1.9998377416249797
1024	1.802702365161224 $\times {10}^{-8}$	1.9997666548103157
2048	4.511132578599586 $\times {10}^{-9}$	1.9985996290821917
4096	1.129273896616212 $\times {10}^{-9}$	1.998094243306733
8192	2.8453139844231146 $\times {10}^{-10}$	1.9887356731658479

Figure 3. Plot of solution of Example 3 for different grid sizes.

5.4. Example 4

Finally, we consider the problem:

$$\begin{array}{cc}\hfill u\left(x\right)& =g\left(x\right)+x^3+\frac{1}{3}[\frac{1}{4}{\left({\int }_0^{x}k(x,y,u\left(y\right))dy\right)}^4\hfill \\ \hfill & -\frac{3}{2}{\left({\int }_0^{x}k(x,y,u\left(y\right))dy\right)}^2+{\int }_0^{x}k(x,y,u\left(y\right))dy]x\in [0,1],\hfill \end{array}$$

where

$$k(x,y,u\left(y\right))=x^4+y^2-\frac{1}{3}{u}^3\left(y\right)+u^2\left(y\right)$$

and

$$\begin{array}{cc}\hfill g\left(x\right)& =-0.333333333333333x^5-1.11111111111111x^3\hfill \\ \hfill & -0.166666666666667x-0.0833333333333333(x^5+x^3/3+x/2+\hfill \\ & sin{\left(x\right)}^3/9+sin\left(x\right)cos\left(x\right)/2-sin\left(x\right)/3{)}^4+0.5(x^5+x^3/3+x/2\hfill \\ & +sin{\left(x\right)}^3{/9+sin\left(x\right)cos\left(x\right)/2-sin\left(x\right)/3)}^2\hfill \\ & -0.037037037037037sin{\left(x\right)}^3-0.166666666666667sin\left(x\right)cos\left(x\right)\hfill \\ & +0.111111111111111sin\left(x\right)+cos\left(x\right).\hfill \end{array}$$

The exact solution to this problem is $u\left(x\right)=cos\left(x\right)$. Similar to the previous examples, one can see in Table 4 that the numerical solution converges to the exact solution with second order of convergence. Figure 4 displays the plots of the numerical and exact solutions on different grids. It is evident that the method converges.

Table 4. Numerical results for Example 4. Results show second-order convergence.

N	Error	EOC
1	0.12721182356988314	-
2	0.019477425482774535	2.707357866274032
4	0.004206018337715833	2.211275950082332
8	0.0010008191561557966	2.0712738313024626
16	0.0002468037760221531	2.019744936190632
32	6.148467592825835 $\times {10}^{-5}$	2.0050656757391567
64	1.5357610263277977 $\times {10}^{-5}$	2.0012731451169947
128	3.838580611259523 $\times {10}^{-6}$	2.000308890953441
256	9.596195429395493 $\times {10}^{-7}$	2.0000385014534188
512	2.3991099107334435 $\times {10}^{-7}$	1.999963285326972
1024	5.999148333657445 $\times {10}^{-8}$	1.9996696446899704
2048	1.5002635800343 $\times {10}^{-8}$	1.999541714861857

Figure 4. Plot of solution of Example 4 for different grid sizes.

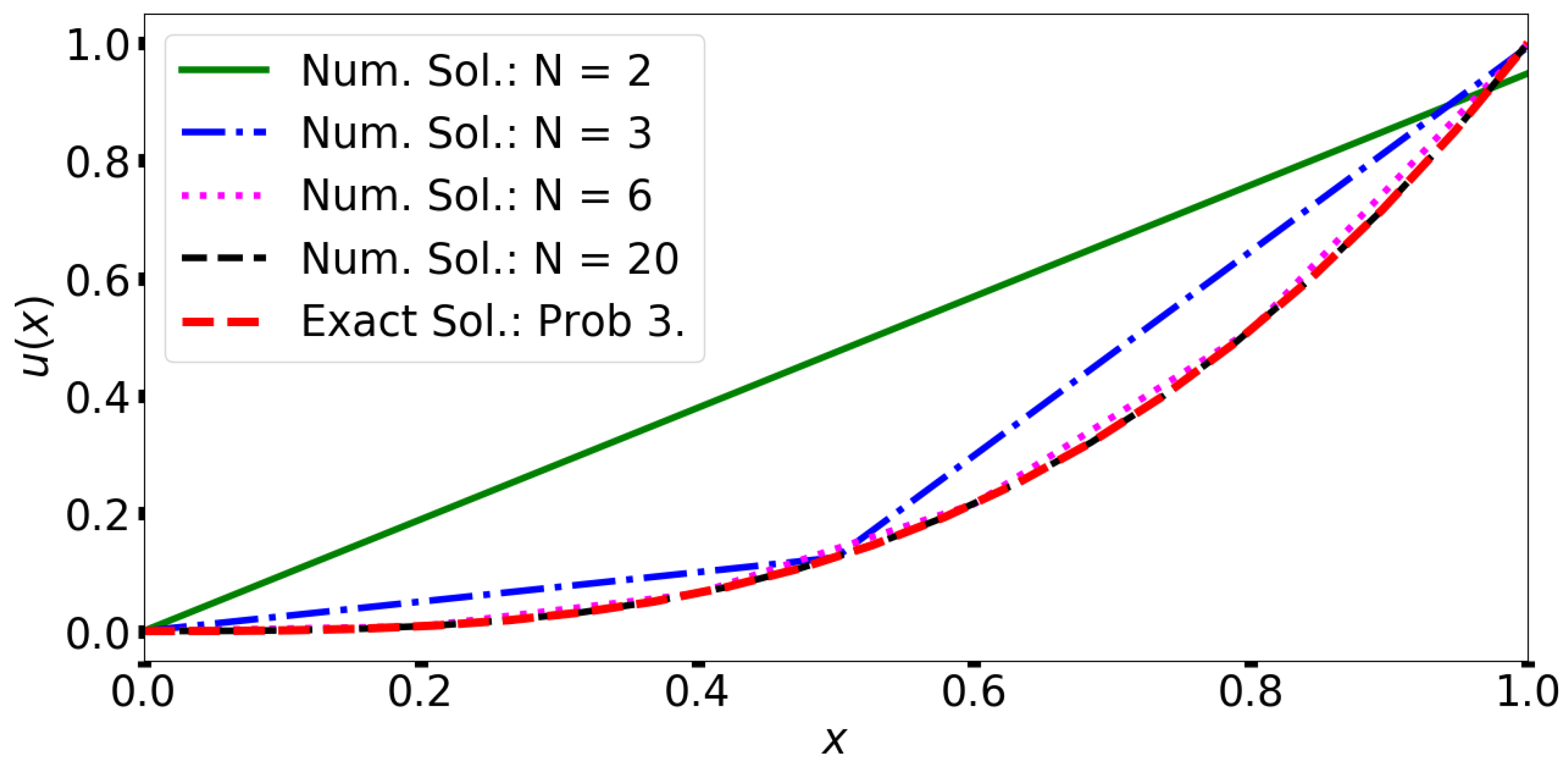
6. Performance Analysis

In this section, we reuse the examples in Section 5 to assess the computational efficiency of the proposed method in comparison with a nonlinear system based (DD) method as proposed in [22]. We achieve this by comparing CPU times used by each method. We will also briefly discuss the memory usage of the scheme. For example 1, we set $\lambda =0.9$; for example 2, we set $\lambda =0.8$; example 3 used $\lambda =0.9$; whereas example 4 used $\lambda =0.95$. Both algorithms (the proposed method and that of [22]) solve each of the four example problems on $N=4096$ equal sub-intervals in [$0,1$]. Table 5, Table 6, Table 7 and Table 8 display the results with the elapsed CPU time and error committed by each method in solving the problem. It is obvious that the proposed method highly outperforms the direct discretization (DD) method [22] as it has much better computational efficiency. It is important to notice that the error of the DD scheme is not better than that of the new scheme.

Table 5. Performance results from Example 1. (Proposed scheme used $\lambda =0.9$).

Scheme	CPU Time (s)	Error
Proposed Method	210.16	$1.347\times {10}^{-9}$
Direct Discretization	839.41	$1.347\times {10}^{-9}$

Table 6. Performance results from Example 2. (Proposed scheme used $\lambda =0.8$).

Scheme	CPU Time (s)	Error
Proposed Method	72.24	$2.714\times {10}^{-11}$
Direct Discretization	144.52	$2.738\times {10}^{-11}$

Table 7. Performance results from Example 3. (Proposed scheme used $\lambda =0.9$).

Scheme	CPU Time (s)	Error
Proposed Method	122.89	$1.127\times {10}^{-9}$
Direct Discretization	264.84	$1.127\times {10}^{-9}$

Table 8. Performance results from Example 4. (Proposed scheme used $\lambda =0.95$).

Scheme	CPU Time (s)	Error
Proposed Method	149.10	$3.75\times {10}^{-9}$
Direct Discretization	189.18	$3.75\times {10}^{-9}$

In addition to the above merits, the new scheme is also more memory efficient than the DD scheme since it does not require to solve linear or nonlinear systems. Yet, from the programming point of view, the new scheme is very easy to program or implement. All these advantages lead to the conclusion that the present method is highly competitive.

7. Conclusions

A fixed-point iteration—the Krasnoselskij scheme—is used to construct an efficient scheme for solving nonlinear functional Volterra equations without a need for nonlinear systems nor a concern for differentiability of the kernels or functionals. The convergence to the exact solution is thoroughly analyzed. Numerical experiments are provided and lead to the following conclusions:

• The scheme is very accurate and competitive;
• The scheme is less computationally expensive than the direct discretization methods, such as the one proposed in [22];
• It is also more memory efficient than that of [22];
• This approach should be adopted whenever possible.

The implication is that if the associated operator is a contraction (satisfying a condition similar to inequality (33)), then fixed-point methods can be formulated to approximate the solution accurately and efficiently. As a further study, we intend to investigate the convergence and performance of other iterative algorithms for related operator equations.