A Numerical Solution of Generalized Caputo Fractional Initial Value Problems
Abstract
1. Introduction
2. Basic Definitions
3. Algorithm of the Apc-ABM Method
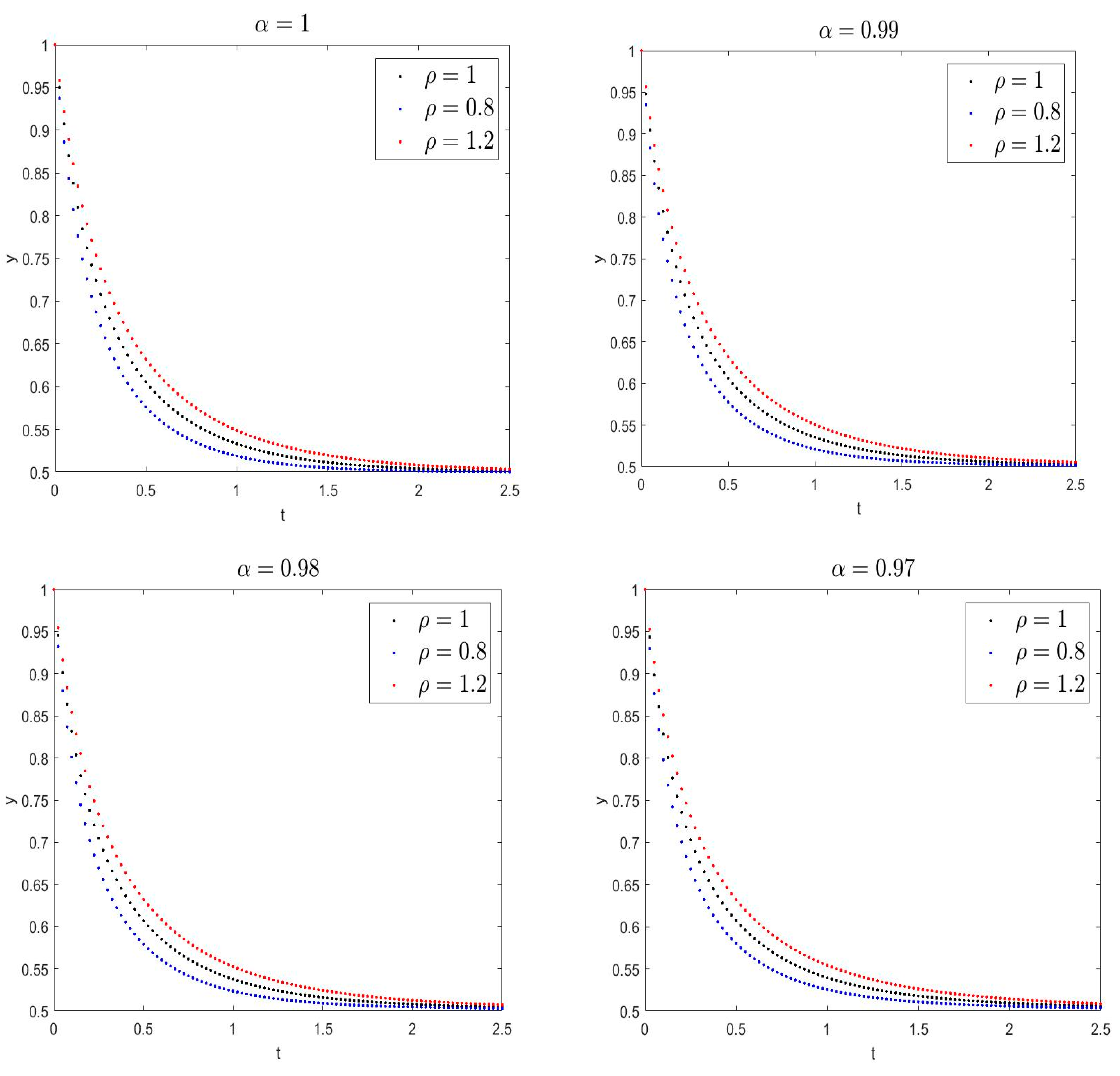
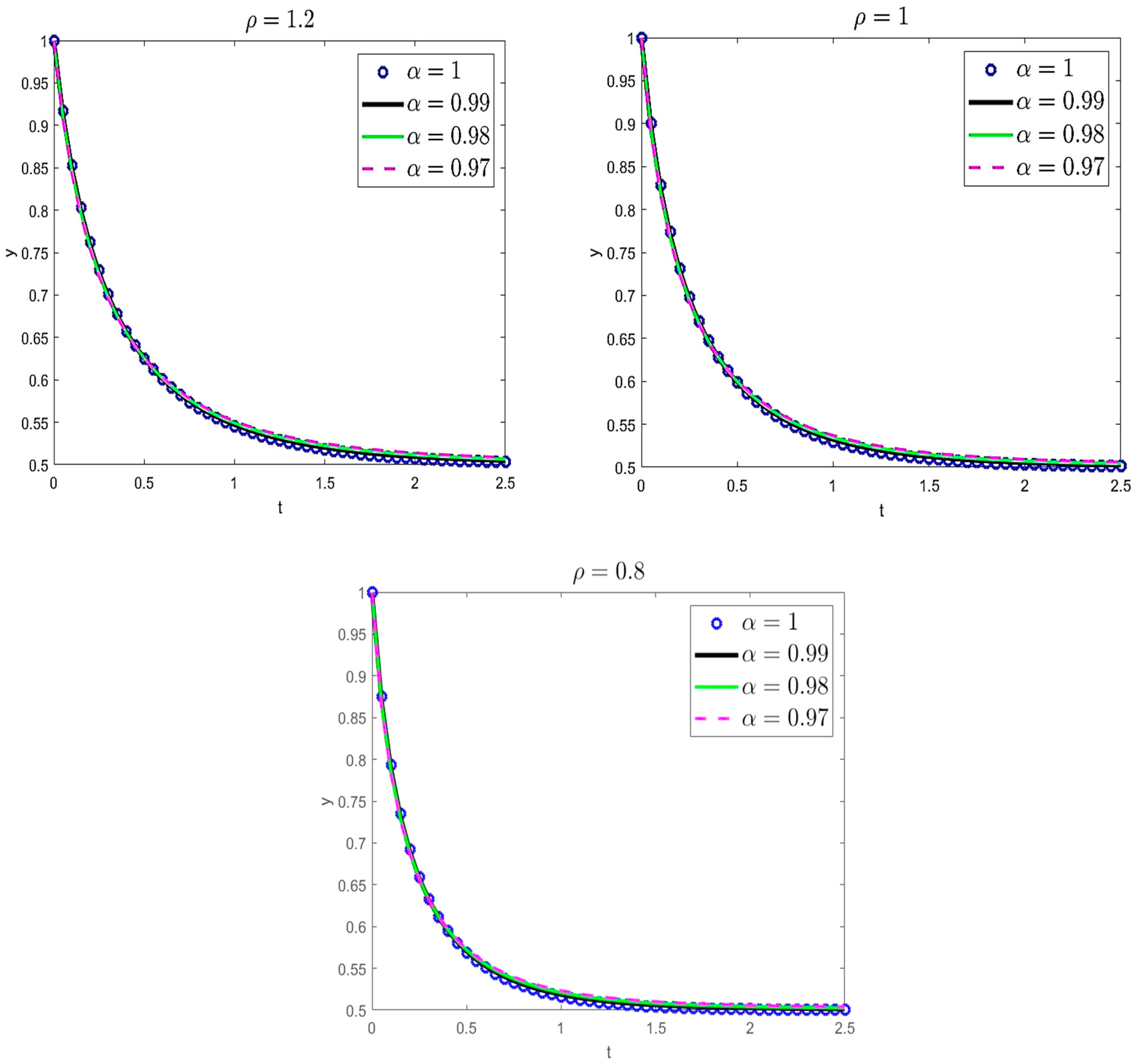
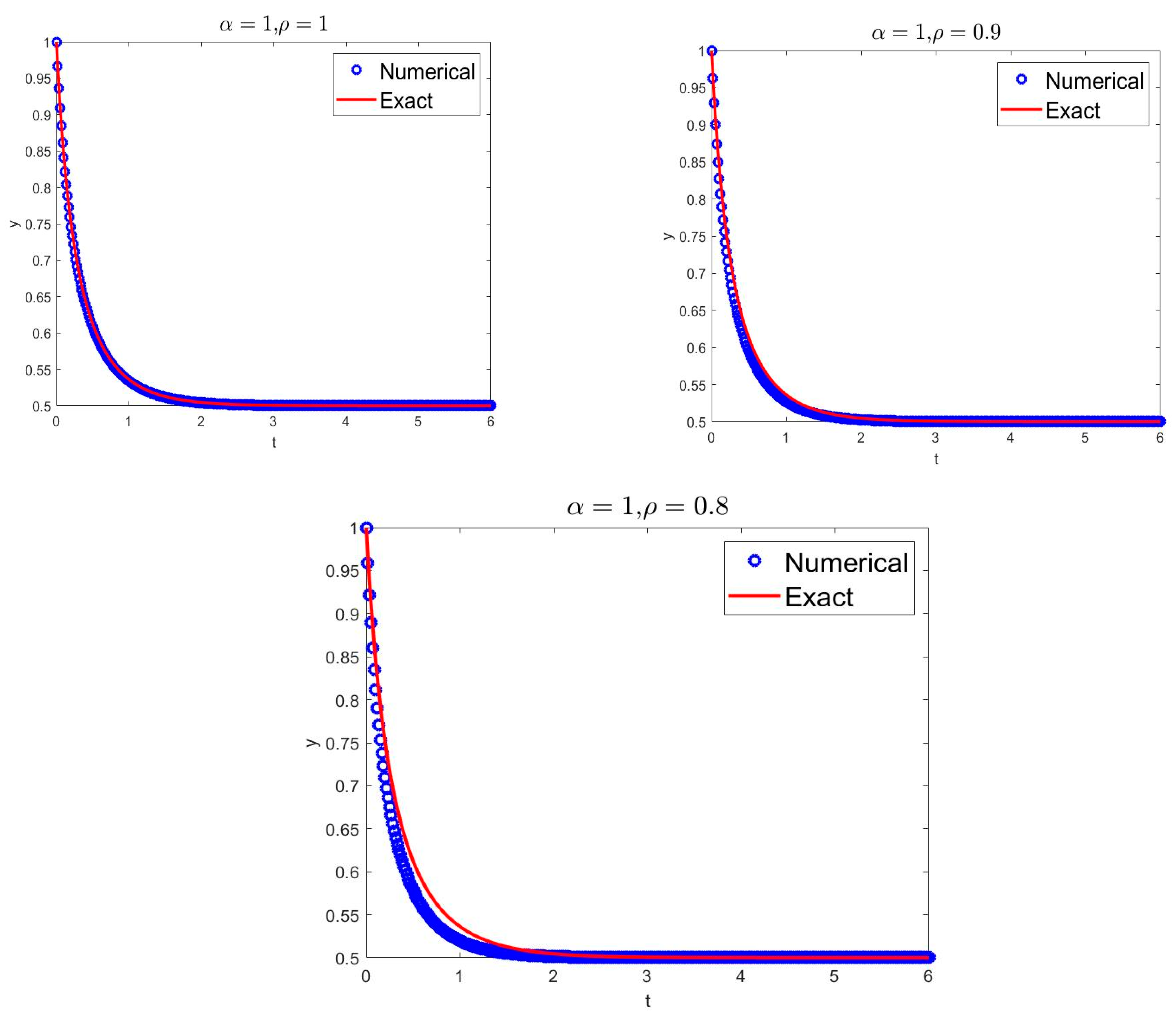
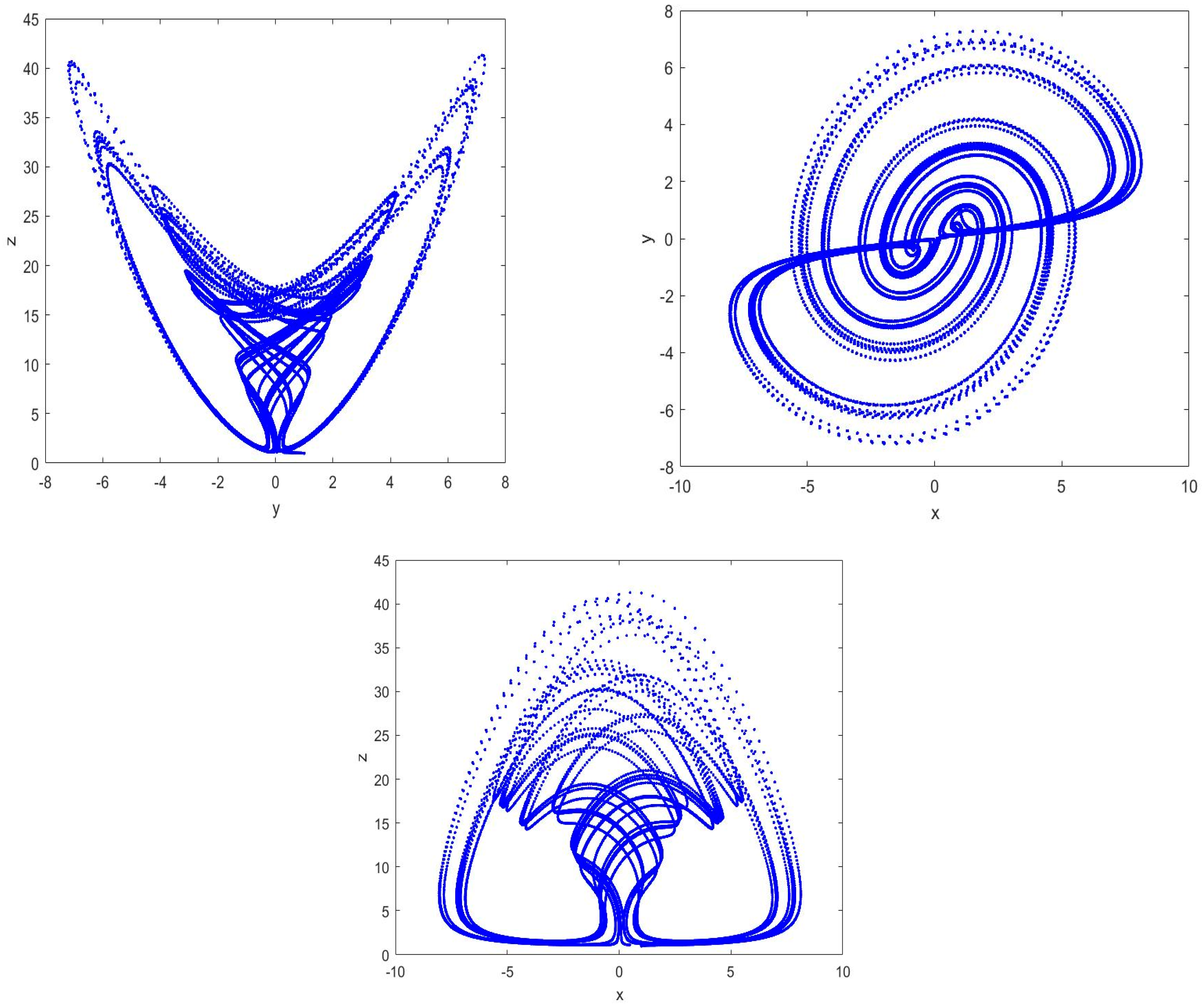
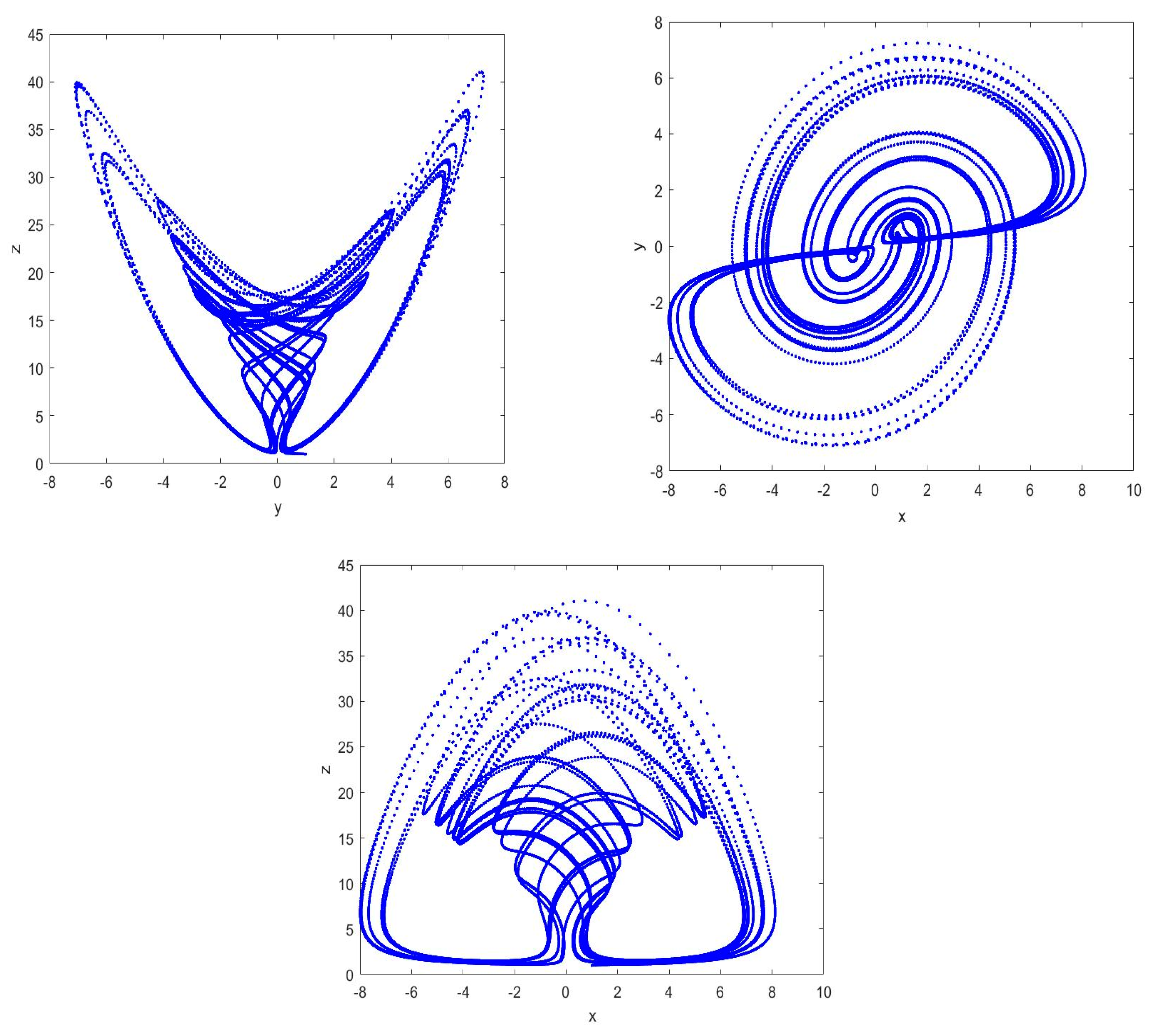
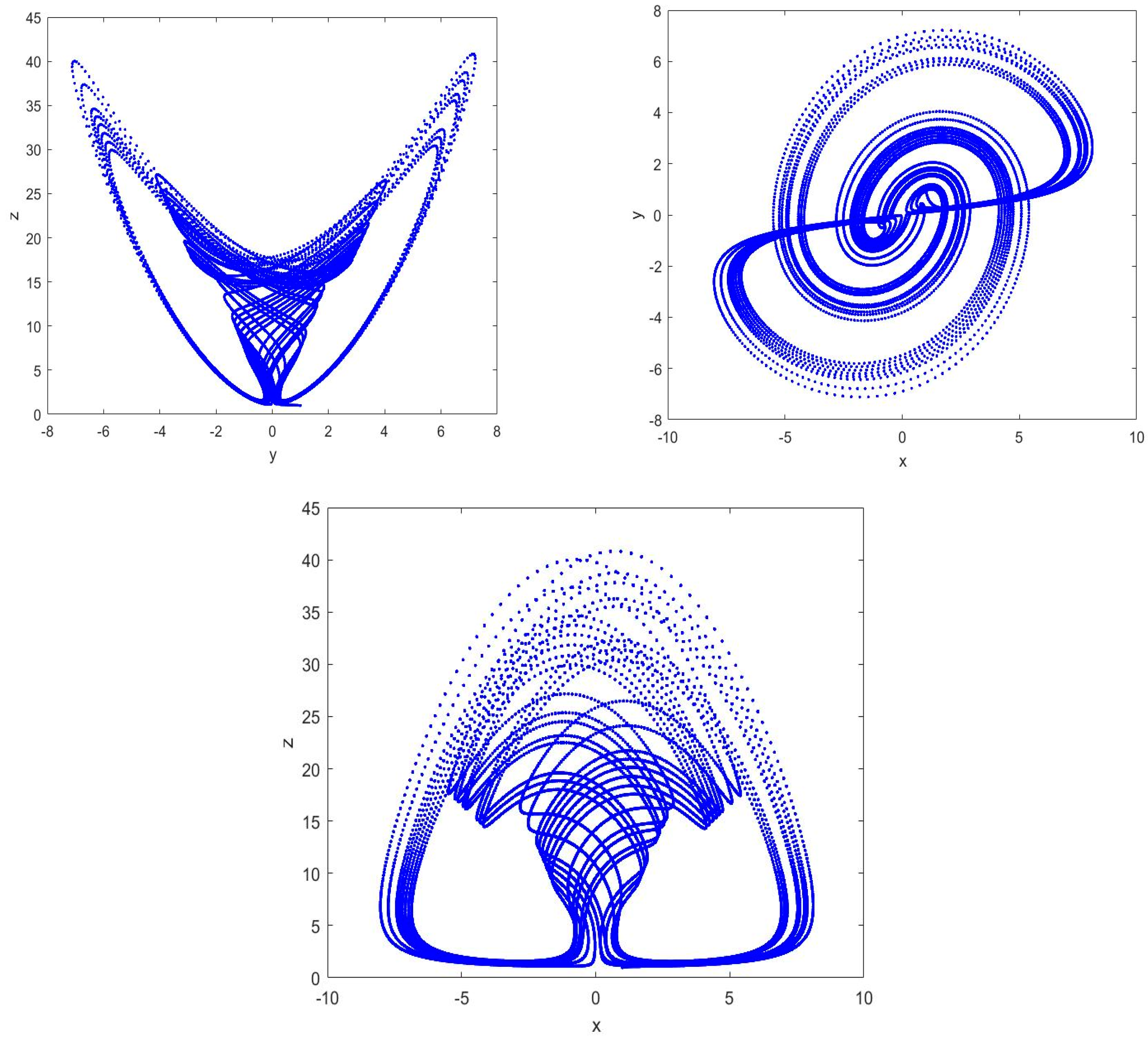
4. Applications
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, NY, USA, 1997; pp. 277–290. [Google Scholar]
- Samko, G.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Bagley, R.L.; Torvik, P.L. On the fractional calculus models of viscoelastic behaviour. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Al-Humedi, H.O.; Hasan, F.L. The Numerical Solutions of Nonlinear Time-Fractional Differential Equations by LMADM. Iraqi J. Sci. 2021, 17–26. [Google Scholar] [CrossRef]
- Abdoon, M.A. First Integral Method: A General Formula for Nonlinear Fractional Klein-Gordon Equation Using Advanced Computing Language. Am. J. Comput. Math. 2015, 5, 127–134. [Google Scholar] [CrossRef]
- Hasan, F.L.; Abdoon, M.A. The generalized (2 + 1) and (3 + 1)-dimensional with advanced analytical wave solutions via computational applications. Int. J. Nonlinear Anal. Appl. 2021, 12, 1213–1241. [Google Scholar]
- Abdoon, M.A.; Hasan, F.L.; Taha, N.E. Computational Technique to Study Analytical Solutions to the Fractional Modified KDV-Zakharov-Kuznetsov Equation. Abstr. Appl. Anal. 2022, 2022, 2162356. [Google Scholar] [CrossRef]
- Elbadri, M. Initial Value Problems with Generalized Fractional Derivatives and Their Solutions via Generalized Laplace Decomposition Method. Adv. Math. Phys. 2022, 2022, 3586802. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y.; Wei, L.; Guan, B. Exact solutions to fractional drinfel’d-sokolov-wilson equations. Chin. J. Phys. 2018, 56, 708–720. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, H. Soliton solutions for the space-time nonlinear partial differential equations with fractional-orders. Chin. J. Phys. 2017, 55, 556–565. [Google Scholar] [CrossRef]
- Sarwar, S.; Iqbal, S. Stability analysis, dynamical behavior and analytical solutions of nonlinear fractional differential system arising in chemical reaction. Chin. J. Phys. 2018, 56, 374–384. [Google Scholar] [CrossRef]
- Sadri, K.; Hosseini, K.; Hinçal, E.; Baleanu, D.; Salahshour, S. A pseudo-operational collocation method for variable-order time-space fractional KdV–Burgers–Kuramoto equation. In Mathematical Methods in the Applied Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2023. [Google Scholar]
- Hosseini, K.; Samadani, F.; Kumar, D.; Faridi, M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik 2017, 157, 1101–1105. [Google Scholar] [CrossRef]
- Hosseini, K.; Mayeli, P.; Ansari, R. Bright and singular soliton solutions of the conformable time-fractional Klein–Gordon equations with different nonlinearities. Waves Random Complex Media 2017, 28, 426–434. [Google Scholar] [CrossRef]
- Hosseini, K.; Mayeli, P.; Bekir, A.; Guner, O. Density-Dependent Conformable Space-time Fractional Diffusion-Reaction Equation and Its Exact Solutions. Commun. Theor. Phys. 2018, 69, 1. [Google Scholar] [CrossRef]
- Hosseini, K.; Kumar, D.; Kaplan, M.; Bejarbaneh, E.Y. New Exact Traveling Wave Solutions of the Unstable Nonlinear Schrödinger Equations. Commun. Theor. Phys. 2017, 68, 761. [Google Scholar] [CrossRef]
- Hosseini, K.; Bekir, A.; Kaplan, M.; Güner, Ö. On a new technique for solving the nonlinear conformable time-fractional differential equations. Opt. Quantum Electron. 2017, 49, 343. [Google Scholar] [CrossRef]
- Hosseini, K.; Manafian, J.; Samadani, F.; Foroutan, M.; Mirzazadeh, M.; Zhou, Q. Resonant optical solitons with perturbation terms and fractional temporal evolution using improved tan (ϕ(η)/2)-expansion method and exp function approach. Optik 2018, 158, 933–939. [Google Scholar] [CrossRef]
- Hosseini, K.; Xu, Y.J.; Mayeli, P.; Bekir, A.; Yao, P.; Zhou, Q.; Güner, O. A study on the conformable time-fractional Klein–Gordon equations with quadratic and cubic nonlinearities. Optoelectron. Adv. Mater. 2017, 11, 423–429. [Google Scholar]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Katugampola, U.N. Existence and uniqueness results for a class of generalized fractional differential equations. arXiv 2014, arXiv:1411.5229. [Google Scholar]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional Differential Equations with Dependence on the Caputo–Katugampola Derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Borah, M.; Singh, P.P.; Roy, B.K. Improved chaotic dynamics of a fractional order system, its chaos-suppressed synchronisation and circuit implementation. Circ. Syst. Signal Process. 2016, 35, 1871–1907. [Google Scholar] [CrossRef]
- Vincent, U.; Kareem, S.; Nbendjo, B.N.; Njah, A. Quasi-synchronization dynamics of coupled and driven plasma oscillators. Chaos, Solitons Fractals 2015, 70, 85–94. [Google Scholar] [CrossRef]
- Rashtchi, V.; Rahimpour, E.; Fotoohabadi, H. Parameter identification of transformer detailed model based on chaos optimisation algorithm. IET Electr. Power Appl. 2011, 5, 238–246. [Google Scholar] [CrossRef]
- Lin, C.-J.; Yang, S.-K.; Yau, H.-T. Chaos suppression control of a coronary artery system with uncertainties by using variable structure control. Comput. Math. Appl. 2012, 64, 988–995. [Google Scholar] [CrossRef]
- El-Gohary, A. Chaos and optimal control of cancer self-remission and tumor system steady states. Chaos Solitons Fractals 2008, 37, 1305–1316. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, W.; Sprott, J.C.; Ma, X. Application of Takagi–Sugeno fuzzy model to a class of chaotic synchronization and anti-synchronization. Nonlinear Dyn. 2013, 73, 1495–1505. [Google Scholar] [CrossRef]
- Borah, M.; Roy, B.K. Dynamics of the fractional-order chaotic PMSG, its stabilisation using predictive control and circuit validation. IET Electr. Power Appl. 2017, 11, 707–716. [Google Scholar] [CrossRef]
- Salah, E.; Saadeh, R.; Qazza, A.; Hatamleh, R. Direct Power Series Approach for Solving Nonlinear Initial Value Problems. Axioms 2023, 12, 111. [Google Scholar] [CrossRef]
- Qazza, A.; Saadeh, R.; Salah, E. Solving fractional partial differential equations via a new scheme. AIMS Math. 2022, 8, 5318–5337. [Google Scholar] [CrossRef]
- Salah, E.; Qazza, A.; Saadeh, R.; El-Ajou, A. A hybrid analytical technique for solving multi-dimensional time-fractional Navier-Stokes system. AIMS Math. 2023, 8, 1713–1736. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Amawi, K. A New Approach Using Integral Transform to Solve Cancer Models. Fractal Fract. 2022, 6, 490. [Google Scholar] [CrossRef]
- Saadeh, R.; Ala’Yed, O.; Qazza, A. Analytical Solution of Coupled Hirota–Satsuma and KdV Equations. Fractal Fract. 2022, 6, 694. [Google Scholar] [CrossRef]

| 0.5000007458 | 0.5000000179 | 0.5000000001 | |
| 0.5000010853 | 0.5000000179 | 0.5000000002 | |
| 0.5000012953 | 0.5000000225 | 0.5000000003 | |
| 0.5000014116 | 0.5000000252 | 0.5000000004 | |
| 0.5000014728 | 0.5000000266 | 0.5000000004 | |
| 0.5000015041 | 0.5000000273 | 0.5000000004 | |
| 0.5000015200 | 0.5000000277 | 0.5000000005 | |
| 0.5000015360 | 0.5000000281 | 0.5000000005 |
| 0.500000002050 | 0.500000024787 | 0.500000264437 | |
| 0.500000004467 | 0.500000044735 | 0.500000328657 | |
| 0.500000006389 | 0.500000058854 | 0.500000365178 | |
| 0.500000007587 | 0.500000067188 | 0.500000384626 | |
| 0.500000008255 | 0.500000071708 | 0.500000394658 | |
| 0.500000008607 | 0.500000074060 | 0.500000399752 | |
| 0.500000008788 | 0.500000075259 | 0.500000264437 |
| 0.500000000004 | 0.500000000118 | 0.500000002731 | |
| 0.500000000011 | 0.500000000256 | 0.500000003624 | |
| 0.500000000018 | 0.500000000366 | 0.500000004156 | |
| 0.500000000023 | 0.500000000435 | 0.500000004447 | |
| 0.500000000026 | 0.500000000473 | 0.500000004599 | |
| 0.500000000028 | 0.500000000494 | 0.500000004676 | |
| 0.500000000028 | 0.500000000504 | 0.500000002731 |
| h. | x | y | z |
|---|---|---|---|
| 1/160 | 0.5008215 | 0.8421048 | 0.5712066 |
| 1/320 | 0.5008442 | 0.8426022 | 0.5710918 |
| 1/640 | 0.5008554 | 0.8428494 | 0.5710347 |
| 1/1280 | 0.5008610 | 0.8429727 | 0.5710062 |
| 1/2560 | 0.5008639 | 0.8430342 | 0.5709920 |
| 1/5120 | 0.5008653 | 0.8430649 | 0.5709849 |
| 1/10240 | 0.5008660 | 0.8430803 | 0.5709813 |
| 1/20480 | 0.5008663 | 0.8430880 | 0.5709795 |
| 1/40960 | 0.5008665 | 0.8430918 | 0.5709786 |
| 1/81920 | 0.5008666 | 0.8430957 | 0.5709778 |
| R K4 | 0.5008666 | 0.8430937 | 0.5709782 |
| 1/160 | 0.5350965 | 0.4761896 | 0.7847857 |
| 1/320 | 0.5351654 | 0.4772751 | 0.7844803 |
| 1/640 | 0.5351998 | 0.4778157 | 0.7843281 |
| 1/1280 | 0.5352170 | 0.4780855 | 0.7842521 |
| 1/2560 | 0.5352256 | 0.4782202 | 0.7842141 |
| 1/5120 | 0.5352299 | 0.4782876 | 0.7841952 |
| 1/10240 | 0.5352320 | 0.4783212 | 0.7841857 |
| 1/20480 | 0.5352331 | 0.4783381 | 0.7841809 |
| 1/40960 | 0.5352336 | 0.4783465 | 0.7841786 |
| 1/81920 | 0.5352339 | 0.4783507 | 0.7841774 |
| R K4 | 0.5352342 | 0.4783549 | 0.7841762 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadeh, R.; A. Abdoon, M.; Qazza, A.; Berir, M. A Numerical Solution of Generalized Caputo Fractional Initial Value Problems. Fractal Fract. 2023, 7, 332. https://doi.org/10.3390/fractalfract7040332
Saadeh R, A. Abdoon M, Qazza A, Berir M. A Numerical Solution of Generalized Caputo Fractional Initial Value Problems. Fractal and Fractional. 2023; 7(4):332. https://doi.org/10.3390/fractalfract7040332
Chicago/Turabian StyleSaadeh, Rania, Mohamed A. Abdoon, Ahmad Qazza, and Mohammed Berir. 2023. "A Numerical Solution of Generalized Caputo Fractional Initial Value Problems" Fractal and Fractional 7, no. 4: 332. https://doi.org/10.3390/fractalfract7040332
APA StyleSaadeh, R., A. Abdoon, M., Qazza, A., & Berir, M. (2023). A Numerical Solution of Generalized Caputo Fractional Initial Value Problems. Fractal and Fractional, 7(4), 332. https://doi.org/10.3390/fractalfract7040332










