High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications

Abstract

We provide streamlined criteria for evaluating the oscillatory behavior of solutions to a class of higher-order functional differential equations in the non-canonical case. We use a comparison approach with first-order equations that have standard oscillation criteria. Normally, in the non-canonical situation, the oscillation test requires three independent conditions, but we provide criteria with two-conditions without checking the additional conditions. Lastly, we give examples to highlight the significance of the findings.

1. Introduction

Studying the properties of solutions of differential equations or finding their solutions (FDE) is crucial for understanding problems and events that arise in the actual world, or at the very least for recognizing the characteristics of the equations that result from modeling these occurrences. However, the equations resulting from the modeling of phenomena often cannot find solutions for them in a closed form. Therefore, studying the properties of their solutions is one way to understand these phenomena. The theory that deals with the properties of solutions of differential equations is called the qualitative theory. Existence, oscillation, periodicity, boundedness, and stability are examples of qualitative features of differential equations that have garnered a lot of attention, see [1,2].

Practically all fields of science and engineering now cover fractional calculus as a common topic. For the past twenty years, the oscillation of solutions for fractional FDEs has been studied because of the astounding interest in the theory of fractional calculus, see for example [3,4,5,6].

The oscillation theory has grown in importance as a numerical mathematical tool in a variety of disciplines and high-tech fields. Finding oscillation requirements for specific FDEs has been a hot topic in recent decades, and the books by Agarwal et al. [7,8] and Gyri and Ladas [9] offer a wealth of references and summaries of previously published results.

This study presents new conditions through which we test the oscillatory behavior of solutions of the FDE

$$\frac{\mathrm{d}}{\mathrm{ds}}\left(a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right)+h\left(\mathrm{s}\right)\left(G\circ \upsilon \circ \theta \right)\left(\mathrm{s}\right)=0,$$

(1)

where $\mathrm{s}\ge {\mathrm{s}}_0$, $n\ge 4$ is an even natural number, ℓ is a ratio of odd positive integers, and the following hypotheses are satisfied:

(H1)

$a\in C^1\left(\left[{\mathrm{s}}_0,\infty \right),{\mathbb{R}}^{+}\right),$$a^{\prime }\left(\mathrm{s}\right)\ge 0,$$h\in C\left(\left[{\mathrm{s}}_0,\infty \right),\left[0,\infty \right)\right)$, $\theta \in C^1\left(\left[{\mathrm{s}}_0,\infty \right),\mathbb{R}\right)$, ${\theta }^{\prime }\left(\mathrm{s}\right)\ge 0,$ and

$${\int }_{{\mathrm{s}}_0}^{\infty }{a}^{-1/\ell }\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}<\infty ,$$

(2)

which is called a non-canonical condition;

(H2)

$G\in C\left(\mathbb{R},\mathbb{R}\right)$, $G^{\prime }\left(\upsilon \right)\ge 0,$$\upsilon G\left(\upsilon \right)>0$ for $\upsilon \ne 0$, and $G\left(\upsilon y\right)\ge G\left(\upsilon \right)G\left(y\right)$ for $\upsilon y>0$.

A continuous function $\upsilon$ on $\left[{\mathrm{s}}_{\upsilon },\infty \right)$ for ${\mathrm{s}}_{\upsilon }\ge {\mathrm{s}}_0$ is called a proper solution of (1) if it is continuous on $\left[{\mathrm{s}}_{\upsilon },\infty \right)$ along with its derivatives up to the ${\left(n-1\right)}^{\mathrm{sh}}$ order, $a{\left({\upsilon }^{\left(n-1\right)}\right)}^{\ell }$ is differentiable on $\left[{\mathrm{s}}_{\upsilon },\infty \right)$, satisfies (1), and $sup\left\{\left|\upsilon \left(\mathrm{s}\right)\right|,\mathrm{s}\ge \mathrm{s}\right\}>0$ for all $\mathrm{s}\ge {\mathrm{s}}_{\upsilon }$. The oscillatory solution is a solution that has an infinite number of arbitrary zeros.

In 2012, Baculíková et al. [10] studied the oscillation of the solutions of (1) based on the development of comparison theorems between a higher order equation and one or more first-order delay FDE. They considered both the canonical case, that is

$${\int }_{{\mathrm{s}}_0}^{\infty }{a}^{-1/\ell }\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}=\infty ,$$

and non-canonical case (2). The most important results that they obtained, for the even-order equation in the non-canonical case, are summarized in the following theorem:

Theorem 1.

Assume that the first-order equations

$$z^{\prime }\left(\mathrm{s}\right)+h\left(\mathrm{s}\right)G\left(\frac{{ϵ}_0}{\left(n-1\right)!}\frac{{\theta }^{n-1}\left(\mathrm{s}\right)}{a^{1/\ell }\left(\mathrm{s}\right)}\right)G\left(z^{1/\ell }\left(\theta \left(\mathrm{s}\right)\right)\right)=0$$

and

$$z^{\prime }\left(\mathrm{s}\right)+{\left(\frac{1}{a\left(\mathrm{s}\right)}{\int }_{{\mathrm{s}}_0}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{{ϵ}_1{\theta }^{n-2}\left(\mathfrak{y}\right)}{\left(n-2\right)!}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left(z\left(\theta \left(\mathrm{s}\right)\right)\right)=0$$

are oscillatory for some ${ϵ}_0,$ ${ϵ}_1\in \left(0,1\right)$, and there is a $\rho \in C^1\left(\left[{\mathrm{s}}_0,\infty \right)\right)$ with

$$\rho \left(\mathrm{s}\right)>\mathrm{s},{\rho }^{\prime }\left(\mathrm{s}\right)\ge 0\mathit{and}\left({\rho }_{n-2}\circ h\right)\left(\mathrm{s}\right)<\mathrm{s},$$

(3)

such that

$$z^{\prime }\left(\mathrm{s}\right)+{\left(\frac{1}{a\left(\mathrm{s}\right)}{\int }_{{\mathrm{s}}_0}^{\mathrm{s}}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left({\varphi }_{n-2}\left(\theta \left(\mathrm{s}\right)\right)\right)G^{1/\ell }\left(z\left({\rho }_{n-2}\left(\theta \left(\mathrm{s}\right)\right)\right)\right)=0$$

is oscillatory, where

$${\rho }_1=\rho ,{\rho }_{i+1}={\rho }_i\circ \rho ,{\varphi }_1=\rho -\mathrm{s}\mathit{and}{\varphi }_{i+1}\left(\mathrm{s}\right)={\int }_{\mathrm{s}}^{\rho \left(\mathrm{s}\right)}{\varphi }_i\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y},$$

for $i=1,2,\cdots ,n-3$. Then, (1) is oscillatory.

Then, they used Theorem 2.4.1 [11] to provide oscillation criteria for the first-order equations in Theorem 1, as shown below:

Corollary 1.

Assume that

$$\frac{G\left({\upsilon }^{1/\ell }\right)}{\upsilon }\ge 1\mathit{for}\left|\upsilon \right|\in \left(0,1\right].$$

Then, (1) is oscillatory if

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{{ϵ}_0}{\left(n-1\right)!}\frac{{\theta }^{n-1}\left(\mathfrak{y}\right)}{a^{1/\ell }\left(\mathfrak{y}\right)}\right)\mathrm{d}\mathfrak{y}>\frac{1}{\mathrm{e}},$$

(4)

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}{\left(\frac{1}{a\left(v\right)}{\int }_{{\mathrm{s}}_0}^{v}h\left(\mathfrak{y}\right)G\left(\frac{{ϵ}_1{\theta }^{n-2}\left(\mathfrak{y}\right)}{\left(n-2\right)!}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }\mathrm{d}v>\frac{1}{\mathrm{e}},$$

(5)

and there is a $\rho \in C^1\left(\left[{\mathrm{s}}_0,\infty \right)\right)$ that satisfies (3) such that

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{{\rho }_{n-2}\left(\theta \left(\mathrm{s}\right)\right)}^{\mathrm{s}}{\left(\frac{1}{a\left(v\right)}{\int }_{{\mathrm{s}}_0}^{v}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left({\varphi }_{n-2}\left(\theta \left(v\right)\right)\right)\mathrm{d}v>\frac{1}{\mathrm{e}},$$

(6)

where ${\rho }_{n-2}$ and ${\varphi }_{n-2}$ are defined as in Theorem 1.

Moreover, they applied these results to the special case

$$\frac{\mathrm{d}}{\mathrm{ds}}\left({\mathrm{e}}^{\mathrm{s}}\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)+h_0{\mathrm{e}}^{\mathrm{s}}\upsilon \left(\mathrm{s}-1\right)=0,\mathrm{s}\ge 1,$$

(7)

and proved that (7) is oscillatory if $h_0>2^5/\mathrm{e}$. As another example, by choosing $\rho \left(\mathrm{s}\right)=c\mathrm{s}$, where $c=\left(1+{\kappa }^{-1/2}\right)/2$, we can apply Theorem 1 to the FDE of Euler type

$$\frac{\mathrm{d}}{\mathrm{ds}}\left({\mathrm{s}}^4\frac{{\mathrm{d}}^3}{{\mathrm{ds}}^3}\upsilon \left(\mathrm{s}\right)\right)+h_0\upsilon \left(\kappa \mathrm{s}\right)=0,$$

(8)

where $\kappa \in \left(0,1\right)$ and $h_0>0$. With some arithmetic procedures, we find that conditions (4)–(6) reduce to

$$\frac{1}{6\kappa }{h}_{0}ln\frac{1}{\kappa }>\frac{1}{\mathrm{e}},$$

$$\frac{1}{6}{h}_0{\kappa }^{2}ln\frac{1}{\kappa }>\frac{1}{\mathrm{e}},$$

and

$$\frac{1}{2}{h}_0{\kappa }^2\left(c-1\right)\left(c^2-1\right)ln\frac{1}{c^2\kappa }>\frac{1}{\mathrm{e}}.$$

Then, we conclude that (8) is oscillatory if

$$h_0>max\left\{\frac{6\kappa }{\mathrm{e}ln\frac{1}{\kappa }},\frac{6}{\mathrm{e}{\kappa }^{2}ln\frac{1}{\kappa }},\frac{2}{\mathrm{e}{\kappa }^2\left(c-1\right)\left(c^2-1\right)ln\frac{1}{c^2\kappa }}\right\}.$$

(9)

By using various substitutions Riccati, Zhang et al. [12,13,14] and Moaaz et al. [15,16,17] studied special cases of (1) either assuming $G\left(\upsilon \right)={\upsilon }^{\ell }$, or focusing on the fourth-order.

On the other hand, the odd-order equations have also attracted great interest in recent times. Articles [18,19,20,21,22,23,24,25,26] deal with the oscillation of third-order differential equations with different methods, approaches, and comparisons.

In this paper, we establish comparative theorems that compare the oscillation of (1) with two equations of the first-order, not three. We also use an approach that reduces constraints on the functions and does not need to assume unknown functions ${\rho }_i$ and ${\varphi }_i$ as in Theorem 1 because it is difficult to choose function $\rho$ that satisfies the conditions in (3) and also fulfill condition (6).

2. Preliminary Results

We need to define the following operators, which make it easier to display the results:

$${\pounds }_0\left(\mathrm{s}\right):={\int }_{\mathrm{s}}^{\infty }{a}^{-1/\ell }\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}$$

and

$${\pounds }_r\left(\mathrm{s}\right):={\int }_{\mathrm{s}}^{\infty }{\pounds }_{r-1}\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y},$$

for $r=1,2,\cdots ,n-2$.

As usual, the study of oscillatory behavior begins by classifying the positive solutions of the studied equation according to the signs of their derivatives, as follows.

Lemma 1.

Assume that υ is one of the eventually positive solutions of (1). Then,

$$\frac{\mathrm{d}}{\mathrm{ds}}\left(a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right)\le 0,$$

and positive solutions are classified eventually as follows:

(c₁)

$\frac{{\mathrm{d}}^r}{{\mathrm{ds}}^r}\upsilon \left(\mathrm{s}\right)>0$ for $r=0,1,n-1$ and $\frac{{\mathrm{d}}^n}{{\mathrm{ds}}^n}\upsilon \left(\mathrm{s}\right)<0;$

(c₂)

$\frac{{\mathrm{d}}^r}{{\mathrm{ds}}^r}\upsilon \left(\mathrm{s}\right)>0$ for $r=0,1,n-2$ and $\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}{\upsilon }^{\left(n-1\right)}\left(\mathrm{s}\right)<0;$

(c₃)

${\left(-1\right)}^r\frac{{\mathrm{d}}^r}{{\mathrm{ds}}^r}\upsilon \left(\mathrm{s}\right)>0$ for $r=0,1,\cdots ,n-1.$

Proof. 

The proof of this lemma comes directly from applying Lemma 2.2.1 in [7] so it has been omitted. □

Lemma 2.

Assume that υ is one of the eventually positive solutions of (1) and satisfies case $\left(c_2\right)$. Then, eventually,

$$\upsilon \left(\mathrm{s}\right)\ge \frac{ϵ}{\left(n-2\right)!}{\mathrm{s}}^{n-2}\frac{{\mathrm{d}}^{n-2}}{{\mathrm{ds}}^{n-2}}\upsilon \left(\mathrm{s}\right),$$

(10)

for all $ϵ\in \left(0,1\right)$.

Proof. 

The proof of this lemma comes directly from applying Lemma 2.2.3 in [7] so it has been omitted. □

Lemma 3.

Assume that υ is one of the eventually positive solutions of (1) and satisfies case $\left(c_2\right)$ of Lemma 1. Then, there is a positive solution of the FDE of the first-order

$$\frac{\mathrm{d}}{\mathrm{ds}}w\left(\mathrm{s}\right)+\frac{1}{a^{1/\ell }\left(\mathrm{s}\right)}{\left({\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left(w\left(\theta \left(\mathrm{s}\right)\right)\right)=0.$$

(11)

Proof. 

From the fact that $\upsilon$ is an eventually positive solution, we can assume that there is a ${\mathrm{s}}_1\ge {\mathrm{s}}_0$ such that $\upsilon \left(\mathrm{s}\right)$ and $\left(\upsilon \circ \theta \right)\left(\mathrm{s}\right)$ are positive for $\mathrm{s}\ge {\mathrm{s}}_1$. From Lemma 2, we have that (10) holds. Integrating (1) from ${\mathrm{s}}_1$ to $\mathrm{s}$, we arrive at

$$\begin{array}{ccc}\hfill a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }& =& a\left({\mathrm{s}}_1\right){\left.{\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right|}_{\mathrm{s}={\mathrm{s}}_1}-{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\upsilon \left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y},\hfill \\ & \le & -{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\upsilon \left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y},\hfill \end{array}$$

which with (10) gives

$$\begin{array}{ccc}\hfill a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }& \le & -{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right){\upsilon }^{\left(n-2\right)}\left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y}\hfill \\ & \le & -{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right)\right)G\left({\upsilon }^{\left(n-2\right)}\left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y}\hfill \\ & \le & -G\left({\upsilon }^{\left(n-2\right)}\left(\theta \left(\mathrm{s}\right)\right)\right){\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}.\hfill \end{array}$$

If, we set $w\left(\mathrm{s}\right):=\frac{{\mathrm{d}}^{n-2}}{{\mathrm{ds}}^{n-2}}\upsilon \left(\mathrm{s}\right)>0$, then w is a positive solution of the inequality

$$\frac{\mathrm{d}}{\mathrm{ds}}w\left(\mathrm{s}\right)+\frac{1}{a^{1/\ell }\left(\mathrm{s}\right)}{\left({\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left(w\left(\theta \left(\mathrm{s}\right)\right)\right)\le 0.$$

In view of Theorem 1 in [27], there is also a positive solution of the FDE (11). This completes the proof. □

Lemma 4.

Assume that υ is one of the eventually positive solutions of (1) and satisfies case $\left(c_3\right)$ of Lemma 1. Then

$${\left(-1\right)}^{r+1}\frac{{\mathrm{d}}^{n-r-2}}{{\mathrm{ds}}^{n-r-2}}\upsilon \left(\mathrm{s}\right)\le {\pounds }_r\left(\mathrm{s}\right)a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right),$$

(12)

for $r=0,1,\cdots ,n-2$, eventually.

Proof. 

From the fact that $\upsilon$ is an eventually positive solution, we can assume that there is a ${\mathrm{s}}_1\ge {\mathrm{s}}_0$ such that $\upsilon \left(\mathrm{s}\right)$ and $\left(\upsilon \circ \theta \right)\left(\mathrm{s}\right)$ are positive for $\mathrm{s}\ge {\mathrm{s}}_1$. From Lemma 1, we have that $a·{\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }$ is non-increasing, and then

$$\begin{array}{ccc}\hfill a^{1/\ell }\left(\mathrm{s}\right)\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right){\int }_{\mathrm{s}}^{\infty }\frac{1}{a^{1/\ell }\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}& \ge & {\int }_{\mathrm{s}}^{\infty }\frac{1}{a^{1/\ell }\left(\mathfrak{y}\right)}{a}^{1/\ell }\left(\mathfrak{y}\right)\left(\frac{{\mathrm{d}}^{n-1}}{\mathrm{d}{\mathfrak{y}}^{n-1}}\upsilon \left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}\hfill \\ & =& \underset{\mathrm{s}\to \infty }{lim}\left(\frac{{\mathrm{d}}^{n-2}}{{\mathrm{ds}}^{n-2}}{\upsilon }^{\left(n-2\right)}\left(\mathrm{s}\right)\right)-\frac{{\mathrm{d}}^{n-2}}{{\mathrm{ds}}^{n-2}}\upsilon \left(\mathrm{s}\right)\hfill \\ & \ge & -{\upsilon }^{\left(n-2\right)}\left(\mathrm{s}\right).\hfill \end{array}$$

Thus,

$$-\frac{{\mathrm{d}}^{n-2}}{{\mathrm{ds}}^{n-2}}\upsilon \left(\mathrm{s}\right)\le {\pounds }_0\left(\mathrm{s}\right)a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right).$$

(13)

We note that the solution and its derivatives in case $\left(c_3\right)$ are either decreasing positive functions or increasing negative functions. Using this property and and integrating (13) and the successive inequalities that result a total of $n-2$ times from $\mathrm{s}$ to ∞, we obtain

$${\left(-1\right)}^{r+1}\frac{{\mathrm{d}}^{n-r-2}}{{\mathrm{ds}}^{n-r-2}}\upsilon \left(\mathrm{s}\right)\le {\pounds }_r\left(\mathrm{s}\right)a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right),$$

for $r=1,\cdots ,n-2$. This completes the proof. □

Lemma 5.

Assume that υ is one of the eventually positive solutions of (1), ${\pounds }_{n-2}\left({\mathrm{s}}_0\right)<\infty$ and

$${\int }_{{\mathrm{s}}_0}^{\infty }{\pounds }_{n-3}\left(u\right){\left({\int }_{{\mathrm{s}}_0}^{u}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }\mathrm{d}u=\infty .$$

(14)

Then, υ cannot satisfy case $\left(c_1\right)$ of Lemma 1.

Proof. 

From the fact that $\upsilon$ is an eventually positive solution, we can assume that there is a ${\mathrm{s}}_1\ge {\mathrm{s}}_0$ such that $\upsilon \left(\mathrm{s}\right)$ and $\left(\upsilon \circ \theta \right)\left(\mathrm{s}\right)$ are positive for $\mathrm{s}\ge {\mathrm{s}}_1$. Using (14) and the fact that ${\pounds }_{n-2}\left({\mathrm{s}}_0\right)<\infty$, we have that

$${\int }_{{\mathrm{s}}_0}^{\infty }h\left(\mathfrak{y}\right)\mathrm{d}\eta =\infty .$$

(15)

Now, we assume the contrary that $\upsilon$ satisfies case $\left(c_1\right)$. By integrating (1) from ${\mathrm{s}}_1$ to $\mathrm{s}$, we arrive at

$$a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }=a\left({\mathrm{s}}_1\right){\left.{\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right|}_{\mathrm{s}={\mathrm{s}}_1}-{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\upsilon \left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y}.$$

Using the fact that $\theta ,$ $\upsilon$ and G are non-decreasing functions and (14), we obtain

$$a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\le a\left({\mathrm{s}}_1\right){\left.{\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right|}_{\mathrm{s}={\mathrm{s}}_1}-G\left(\upsilon \left(\theta \left({\mathrm{s}}_1\right)\right)\right){\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}$$

Taking $\mathrm{s}\to \infty$ and using (15), we obtain that

$$a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\to -\infty ,\mathrm{as}\mathrm{s}\to \infty ,$$

which contradicts to the positivity of $a·{\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \right)}^{\ell }$. This completes the proof. □

3. Oscillation Theorems

The following theorem provides a criterion for testing the oscillation of solutions of (1) by using conditions that guarantee the oscillation of the first-order equations.

Theorem 2.

Assume that ${\pounds }_{n-2}\left({\mathrm{s}}_0\right)<\infty$. If

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}{\pounds }_{n-3}\left(u\right){\left({\int }_{{\mathrm{s}}_1}^{u}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }\mathrm{d}u>\frac{1}{\mathrm{e}}$$

(16)

and

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}\frac{1}{a^{1/\ell }\left(u\right)}{\left({\int }_{{\mathrm{s}}_1}^{u}h\left(\mathfrak{y}\right)G\left(\frac{ϵ}{\left(n-2\right)!}{\theta }^{n-2}\left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }\mathrm{d}u>\frac{1}{\mathrm{e}},$$

(17)

for some $ϵ\in \left(0,1\right)$, then all solutions of (1) are oscillatory.

Proof. 

Assume, on the contrary, that Equation (1) has a positive solution $\upsilon$. In order for condition (16) to be fulfilled, it is necessary that condition (14) is satisfied. Using Lemma 5, we obtain that $\upsilon$ cannot satisfy case $\left(c_1\right)$ of Lemma 1. Then, from Lemma 1, $\upsilon$ satisfies $\left(c_2\right)$ or $\left(c_3\right)$.

Suppose that $\upsilon$ satisfies case $\left(c_2\right)$. From Lemma 3, there is a positive solution of the FDE (11). However, it follows from Theorem 2 in [28] that condition (17) implies oscillation of (11).

Suppose that $\upsilon$ satisfies case $\left(c_3\right)$. Integrating (1) from ${\mathrm{s}}_1$ to $\mathrm{s}$, we obtain

$$a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\le -{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)G\left(\upsilon \left(\theta \left(\mathfrak{y}\right)\right)\right)\mathrm{d}\mathfrak{y}.$$

Using the facts that $\theta$ and G are non-decreasing and $\upsilon$ is decreasing, we obtain

$$a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\le -G^{1/\ell }\left(\upsilon \left(\theta \left(\mathrm{s}\right)\right)\right){\left({\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }.$$

Using (12) at $r=n-3$, we arrive at

$$\frac{\mathrm{d}}{\mathrm{d}}\upsilon \left(\mathrm{s}\right)+{\pounds }_{n-3}\left(\mathrm{s}\right){\left({\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left(\upsilon \left(\theta \left(\mathrm{s}\right)\right)\right)\le 0.$$

(18)

Thus, $\upsilon$ is a positive solution of the inequality (18). In view of Theorem 1 in [27], there is also a positive solution of the FDE

$$\frac{\mathrm{d}}{\mathrm{d}}\upsilon \left(\mathrm{s}\right)+{\pounds }_{n-3}\left(\mathrm{s}\right){\left({\int }_{{\mathrm{s}}_1}^{\mathrm{s}}h\left(\mathfrak{y}\right)\mathrm{d}\mathfrak{y}\right)}^{1/\ell }{G}^{1/\ell }\left(\upsilon \left(\theta \left(\mathrm{s}\right)\right)\right)=0.$$

(19)

However, it follows from Theorem 2 in [28] that condition (16) implies the oscillation of (19). This completes the proof. □

Theorem 3.

Assume that $G\left(u\right):=u^{\ell }$, $\ell \ge 1$, and either (14) or

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}{\left(\frac{ϵ{\theta }^{n-1}\left(\mathfrak{y}\right)}{\left(n-1\right)!}\right)}^{\ell }\frac{h\left(\mathfrak{y}\right)}{a\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}>\frac{\ell }{\mathrm{e}}$$

(20)

holds. If (17) and

$$\underset{\mathrm{s}\to \infty }{liminf}{\int }_{\theta \left(\mathrm{s}\right)}^{\mathrm{s}}{\pounds }_{n-3}\left(u\right){\int }_{{\mathrm{s}}_1}^u\frac{h\left(\mathfrak{y}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}\mathrm{d}u>\frac{\ell }{\mathrm{e}},$$

(21)

hold, then all solutions of (1) are oscillatory.

Proof. 

Assume, on the contrary, that Equation (1) has a positive solution $\upsilon$. Using Lemma 1, we obtain that $\upsilon$ satisfies one of the cases $\left(c_1\right)-\left(c_3\right)$. From (1), we conclude that

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}}{\mathrm{ds}}\left(a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)& =& \frac{\mathrm{d}}{\mathrm{ds}}{\left(a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right)}^{1/\ell }\hfill \\ & =& \frac{1}{\ell }{\left(a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{1-\ell }\frac{\mathrm{d}}{\mathrm{ds}}\left(a\left(\mathrm{s}\right){\left(\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{\ell }\right)\hfill \\ & =& -\frac{1}{\ell }h\left(\mathrm{s}\right){\upsilon }^{\ell }\left(\theta \left(\mathrm{s}\right)\right){\left(a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)}^{1-\ell }.\hfill \end{array}$$

(22)

Suppose that $\upsilon$ satisfies case $\left(c_1\right)$. If (14) holds, then it follows from Lemma 5 that $\upsilon$ cannot satisfy case $\left(c_1\right)$. On the other hand, from Lemma 2.2.3 in [7], we obtain

$$\upsilon \left(\mathrm{s}\right)\ge \frac{ϵ}{\left(n-1\right)!}{\mathrm{s}}^{n-1}\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right),$$

or

$$\upsilon \left(\theta \left(\mathrm{s}\right)\right)\ge \frac{ϵ}{\left(n-1\right)!}{\theta }^{n-1}\left(\mathrm{s}\right){\upsilon }^{\left(n-1\right)}\left(\theta \left(\mathrm{s}\right)\right)$$

Hence, from (22), we obtain

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}}{\mathrm{ds}}\left(a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)& \le & -\frac{1}{\ell }h\left(\mathrm{s}\right){\upsilon }^{\ell }\left(\theta \left(\mathrm{s}\right)\right){\left(a^{1/\ell }\left(\mathrm{s}\right){\upsilon }^{\left(n-1\right)}\left(\theta \left(\mathrm{s}\right)\right)\right)}^{1-\ell }\hfill \\ & \le & -\frac{1}{\ell }h\left(\mathrm{s}\right){\left(\frac{ϵ{\theta }^{n-1}\left(\mathrm{s}\right)}{\left(n-1\right)!}\right)}^{\ell }{a}^{\left(1-\ell \right)/\ell }\left(\mathrm{s}\right){\upsilon }^{\left(n-1\right)}\left(\theta \left(\mathrm{s}\right)\right).\hfill \end{array}$$

If we set $\omega :=a^{1/\ell }\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon >0$, then

$$\frac{\mathrm{d}}{\mathrm{ds}}\omega \left(\mathrm{s}\right)+\frac{1}{\ell }h\left(\mathrm{s}\right){\left(\frac{ϵ{\theta }^{n-1}\left(\mathrm{s}\right)}{\left(n-1\right)!}\right)}^{\ell }\frac{a^{\left(1-\ell \right)/\ell }\left(\mathrm{s}\right)}{a^{1/\ell }\left(\theta \left(\mathrm{s}\right)\right)}\omega \left(\theta \left(\mathrm{s}\right)\right)\le 0.$$

Since $a^{\prime }\left(\mathrm{s}\right)\ge 0$, we arrive at

$$\frac{\mathrm{d}}{\mathrm{ds}}\omega \left(\mathrm{s}\right)+\frac{1}{\ell }{\left(\frac{ϵ{\theta }^{n-1}\left(\mathrm{s}\right)}{\left(n-1\right)!}\right)}^{\ell }\frac{h\left(\mathrm{s}\right)}{a\left(\mathrm{s}\right)}\omega \left(\theta \left(\mathrm{s}\right)\right)\le 0,$$

Thus, $\omega$ is a positive solution of this inequality. In view of Theorem 1 in [27], there is also a positive solution of the FDE

$$\frac{\mathrm{d}}{\mathrm{ds}}\omega \left(\mathrm{s}\right)+\frac{1}{\ell }{\left(\frac{ϵ{\theta }^{n-1}\left(\mathrm{s}\right)}{\left(n-1\right)!}\right)}^{\ell }\frac{h\left(\mathrm{s}\right)}{a\left(\mathrm{s}\right)}\omega \left(\theta \left(\mathrm{s}\right)\right)=0.$$

(23)

However, it follows from Theorem 2 in [28] that condition (20) implies oscillation of (23).

In the event that $\upsilon$ fulfills case $\left(c_2\right)$, the proof is exactly as in Theorem 2.

Suppose that $\upsilon$ satisfies case $\left(c_3\right)$. Using (12) at $r=n-2$, we obtain

$$-a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\le \frac{\upsilon \left(\mathrm{s}\right)}{{\pounds }_{n-2}\left(\mathrm{s}\right)}\le \frac{\upsilon \left(\theta \left(\mathrm{s}\right)\right)}{{\pounds }_{n-2}\left(\mathrm{s}\right)},$$

which with (22) yields

$$\frac{\mathrm{d}}{\mathrm{ds}}\left(a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)\right)\le -\frac{1}{\ell }\frac{h\left(\mathrm{s}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathrm{s}\right)}\upsilon \left(\theta \left(\mathrm{s}\right)\right).$$

(24)

Integrating this inequality from ${\mathrm{s}}_1$ to $\mathrm{s}$, we obtain

$$\begin{array}{ccc}\hfill a^{1/\ell }\left(\mathrm{s}\right)\frac{{\mathrm{d}}^{n-1}}{{\mathrm{ds}}^{n-1}}\upsilon \left(\mathrm{s}\right)& \le & -\frac{1}{\ell }{\int }_{{\mathrm{s}}_1}^{\mathrm{s}}\frac{h\left(\mathfrak{y}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathfrak{y}\right)}\upsilon \left(\theta \left(\mathfrak{y}\right)\right)\mathrm{d}\mathfrak{y}\hfill \\ & \le & -\frac{1}{\ell }\upsilon \left(\theta \left(\mathrm{s}\right)\right){\int }_{{\mathrm{s}}_1}^{\mathrm{s}}\frac{h\left(\mathfrak{y}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y},\hfill \end{array}$$

Using (12) at $r=n-3$, we arrive at

$$\frac{\mathrm{d}}{\mathrm{ds}}\upsilon \left(\mathrm{s}\right)+\frac{1}{\ell }\upsilon \left(\theta \left(\mathrm{s}\right)\right){\pounds }_{n-3}\left(\mathrm{s}\right){\int }_{{\mathrm{s}}_1}^{\mathrm{s}}\frac{h\left(\mathfrak{y}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}\le 0.$$

Thus $\upsilon$ is a positive solution of this inequality. In view of Theorem 1 in [27], there is also a positive solution of the FDE

$$\frac{\mathrm{d}}{\mathrm{ds}}\upsilon \left(\mathrm{s}\right)+\frac{1}{\ell }\upsilon \left(\theta \left(\mathrm{s}\right)\right){\pounds }_{n-3}\left(\mathrm{s}\right){\int }_{{\mathrm{s}}_1}^{\mathrm{s}}\frac{h\left(\mathfrak{y}\right)}{{\pounds }_{n-2}^{1-\ell }\left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}=0.$$

(25)

However, it follows from Theorem 2 in [28] that condition (21) implies oscillation of (25). This completes the proof. □

Example 1.

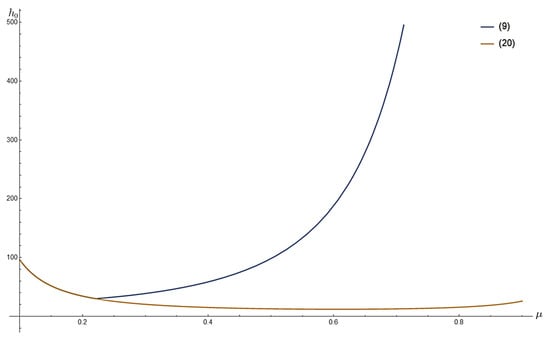
Referring to Equation (7), we see that ${\pounds }_r\left(\mathrm{s}\right)={\mathrm{e}}^{-\mathrm{s}}$ for every $r=0,1,\cdots ,n-2$. It is simple to verify whether condition (17) is met. From Theorem 2, we obtain that (7) is oscillatory if (16) is met, that is, $\mathrm{e}{h}_0>1$.

Example 2.

Referring to Equation (7), we see that ${\pounds }_0\left(\mathrm{s}\right)={\left(3{\mathrm{s}}^3\right)}^{-1},$ ${\pounds }_1\left(\mathrm{s}\right)={\left(6{\mathrm{s}}^2\right)}^{-1}$, and ${\pounds }_2\left(\mathrm{s}\right)={\left(6\mathrm{s}\right)}^{-1}$. Criteria (16) and (17) become, respectively,

$$\mathrm{e}{h}_{0}ln\left(1/\kappa \right)>6,$$

and

$$\mathrm{e}{\kappa }^2{h}_{0}ln\left(1/\kappa \right)>6,$$

From Theorem 2, Equation (8) is oscillatory if

$$h_0>\frac{6}{\mathrm{e}{\kappa }^{2}ln\left(1/\kappa \right)}.$$

(26)

Remark 1.

It is easy to note that our results provide an improved criterion $(h_0>1/\mathrm{e})$ for the oscillation of (7) compared to the results in [10], which ensures the oscillation of (7) when $h_0>2^5/\mathrm{e}$. On the other hand, Figure 1 compares the two criteria (9) and (26) to test the oscillation of (8).

Figure 1. The minimum values of $h_0$ for which conditions (9) and (26) are satisfied.

Remark 2.

It is obvious that, in comparison to the findings in cite [10] $(h_0>2^5/\mathrm{e})$, our results offer a more precise criterion $(h_0>1/\mathrm{e})$ for the oscillation of (7). Figure 1 illustrates how the two criteria (9) and (26) vary.

4. Conclusions

We first divided the positive solutions of the investigated equation into several categories based on the sign of their derivatives. Then, we presented certain properties for each of these categories. By verifying that all solutions to Equation (11) oscillate, we excluded positive solutions from class $\left(c_2\right)$. Moreover, we excluded positive solutions from class $\left(c_1\right)$ by utilizing condition (14). Then, we establish new standards to evaluate the oscillation of all solutions (1).

In this study, rather than three first-order equations, we established comparison theorems that compare the oscillation of (1) with two of them. Additionally, unlike Theorem 1, our method lowers limitations on the functions and does not need the assumption of the unknown functions ${\rho }_i$ and ${\varphi }_i$. It would be interesting to extend our results to fractional differential equations as well as to the neutral case of the studied equation.