On Novel Mathematical Modeling for Studying a Class of Nonlinear Caputo-Type Fractional-Order Boundary Value Problems Emerging in CGT

Abstract

Chemical graph theory (CGT) is a field of mathematical science that applies classical graph theory to chemical structures and processes. Chemical graphs are the principal data format used in cheminformatics to illustrate chemical interactions. Several researchers have addressed boundary-value problems using star graphs. Star graphs were used since their method requires a central point linked to other vertices but not to itself. Our objective is to expand the mechanism by introducing the idea of an isobutane graph that has the chemical formula $C_4{H}_{10}$ and CAS number 75-28-5. By using the appropriate fixed point theory findings, this paper investigates the existence of solutions to fractional boundary value problems of Caputo type on such graphs. Additionally, two examples are provided to strengthen our important conclusions.

1. Introduction and Preliminaries

The link between graph theory and chemistry has evolved significantly over time. Numerous investigations relating to both subjects have shown robust linkages between them, resulting in the formation of the research field known as chemical graph theory (shortly CGT) (for detail, see [1]). Chemical graphs were initially mentioned in the late eighteenth century, when Isaac Newton’s concepts influenced the way chemistry was seen (see [1]). Although research on the relationships of atoms accelerated over that century, the chemical bonds remained unknown. Thus, chemical graphs were first used to describe hypothetical forces between molecules and atoms.

CGT uses graph theory to describe molecules in order to explore their many physical characteristics. A graph $\mathfrak{G}=(\mathfrak{V},\mathfrak{E})$ is composed of a set $\mathfrak{V}$ of vertices (or nodes) and a set $\mathfrak{E}$ of unordered pairs of different components of $\mathfrak{V}$ that constitute the edges. The vertices denote the atoms in a molecule in chemistry, whereas the edges represent the chemical bonds.

John Dalton devised the initial atomic model in 1805 by associating various atom kinds with distinct rings that can only represent the chemical positions and quantities of atoms in a compound (for detail, see [2,3]). August Kékule, on the other hand, demonstrated both the physical and orientational locations of atoms inside a molecule. He categorized many organic compounds and showed the bonding arrangements between particles in his model related to the “Tetrahedral Carbon Atom (see Figure 1)”, which featured the benzene ring (see [4]).

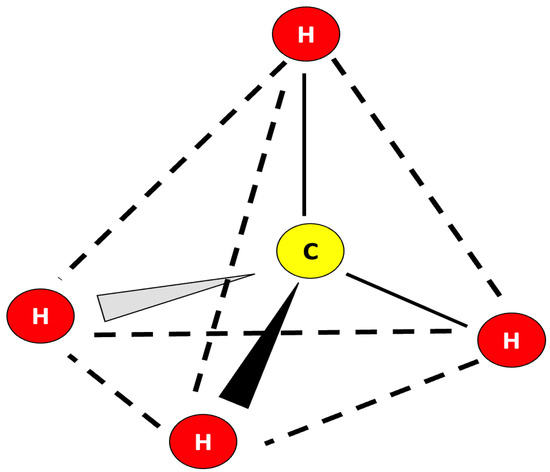
Figure 1. A sketch of a tetrahedral carbon atom model.

Alexander Butlerov coined the phrase “molecular structure” in 1861, implying that any compound should have a rigid molecular composition. This phrase referred to a number of the compounds’ chemical features (for detail, see [5]). The line depiction of atomic bonds was originally used in [6] as a different interpretation paradigm. However, since these lines represented merely interatomic forces and not individual bonds, Couper’s work is credited with being the first graphical depiction of a chemical bond (see [7]). The molecular formula for acetic acid was established and represented chemically as a framework with geometric shapes linking the atoms in a molecule to symbolize chemical bonds (Figure 2). To learn more, the reader can refer to [8,9,10] and the references therein.

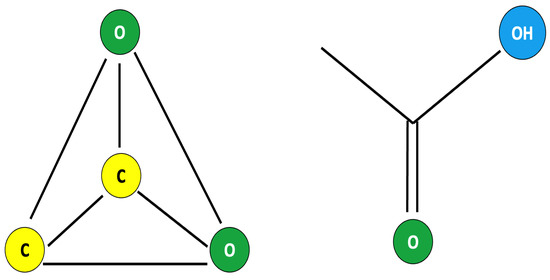
Figure 2. A chemical and structural representation of acetic acid.

On the other hand, there has been considerable conceptual and practical progress lately in the subject of differential equations (see [11,12,13,14]). Many fields, including engineering, physics, and ecology, make use of differential equations on graphs. A graph $\mathrm{G}$ is a pair $\left(\mathrm{A}\left(\mathrm{G}\right),\mathrm{B}\left(\mathrm{G}\right)\right)$ consisting of nodes $\mathrm{A}\left(\mathrm{G}\right):=\left\{{\upsilon }_{\ell }:\ell =0,1,2,\dots \right\}$ and the edges $\mathrm{B}\left(\mathrm{G}\right):=\left\{e_{ı}:ı=1,2,3,\dots \right\}$ that link them (see Figure 3), which may be either finite or countably infinite in dimension. Local coordinates are defined on each edge (of a certain length), with the origin located at a specific node.

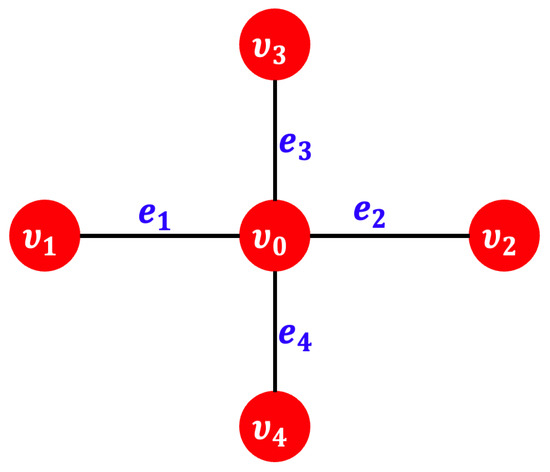
Figure 3. A sketch of a graph with three edges and four vertices.

The majority of studies on fractional calculus in the context of specific functions focus on the solution of differential equations (for detail, see [15,16,17,18,19]). A number of new papers have recently been published focusing on nonlinear fractional differential equations and their solutions, utilizing techniques including Leray–Schauder theorem, stability analysis, and fixed-point analysis (see [20,21,22,23]).

Lumer [24] pioneered the use of differential equation theory in graphs. He explored extended evolution equations by modifying specified operators on ramification spaces. In 1989, Zavgorodnij investigated the solution to the boundary value problem using a geometric structure defined at its inner nodes (see [25]). When finding computational solutions for the given differential equations, Gordeziani et al. used the double-sweep approach to obtain results (see [26]). In the literature, only a tiny amount of research has been carried out on star graphs (see Figure 4) linked with boundary value problems using specific fixed point methodologies (see [27,28]). We refer to [29,30,31,32,33,34,35,36] and the references therein for the current study in this area.

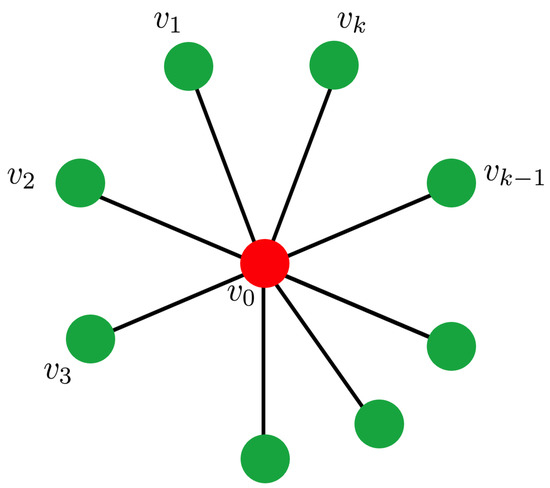
Figure 4. A sketch of a star graph with a junction node ${\upsilon }_0$ and k edges.

The techniques described in [27,28] for detecting the origin at vertices other than the junction node are unsuitable, as graphs typically have many junction points (for examples, see Figure 5 and Figure 6).

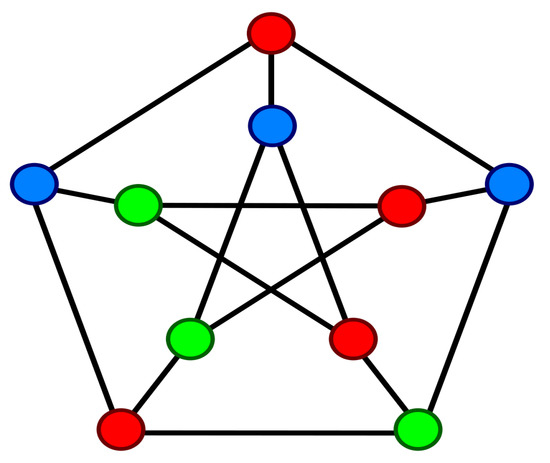
Figure 5. Example of a non-star graph with many junction nodes.

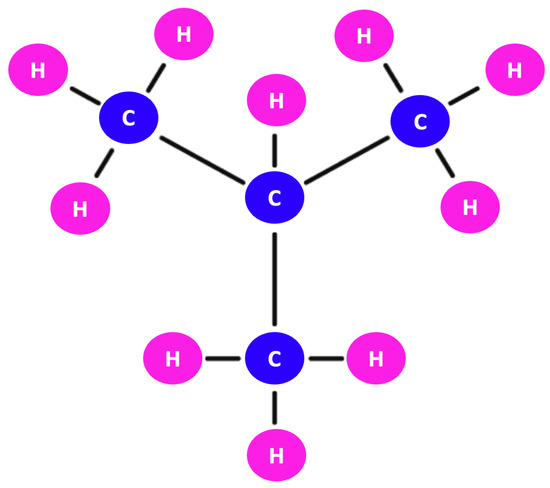
Figure 6. Chemical bond of an isobutane compound $C_4{H}_{10}$.

In [27,28], the authors framed the length of each edge as a parameter, but the size of all sides may be assumed constant from the initial stages of the computation. To solve this problem, we used a specific strategy in which we gave numerical values (0 or 1) to the vertices of the suggested graph $\mathfrak{G}$ with edge length $|{\tilde{p}}_{\tau }|=1$ (see Figure 7).

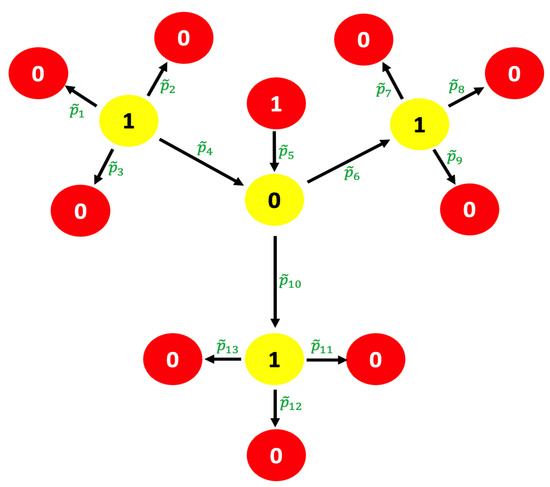
Figure 7. Isobutane compound graph with edge length $|{\tilde{p}}_{\tau }|=1$ and vertices 0 or 1.

Thus, the label for each vertex is determined by the direction of each associated edge. Consequently, some vertices can also be labeled by 0 or 1, while the length of every edge is not fixed. It changes based on the rotational path along the boundary. Standardizing the length of each edge with the given alteration is not required, as we can use comparable methods to choose one of the two vertices of the linked edge as the origin.

Contrarily, various sophisticated fractional modeling strategies are covered in the research, including (but not confined to) the well-known Riemann–Liouville and Caputo operators (for detail, see [37,38,39,40,41,42,43,44]). The Caputo–Hadamard, Hadamard, and Hilfer operators have undergone a number of notable changes this decade, and many modeling projects have used these new operators (for more detail, see [45,46,47,48,49]). Six years ago, Caputo and Fabrizio, in [50], proposed an updated version of a fractional paradigm without a singularity. Nieto and Losada focused on important mathematical facets in the immediate aftermath of this work. Numerous studies on fractional modeling were published after nonsingular operators were included (see [51,52,53,54] and references therein).

Using the study described above, we explored the existence of solutions to the system, for each $\tau =1,2,\dots ,13$, stated below:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^m{v}_{\tau }\left(s\right)& ={\mathcal{R}}_{\tau }(s,v_{\tau }\left(s\right),{\mathfrak{D}}^n{v}_{\tau }\left(s\right),v_{\tau }^{\prime }\left(s\right))(s\in [0,1]),\hfill \\ \hfill v_{\tau }\left(0\right)& ={\mathfrak{D}}^{m-1}{v}_{\tau }\left(1\right),{\eta }_1{\mathfrak{D}}^n{v}_{\tau }\left(1\right)+{\eta }_2{\mathcal{D}}^{2n}{v}_{\tau }\left(1\right)={\eta }_3{\int }_0^u{\mathfrak{D}}^{m-1}{v}_{\tau }\left(\theta \right)d\theta ,\hfill \end{array}\right.\end{array}$$

(1)

where $v_{\tau }:[0,1]\to \mathbb{R}$ is an unknown function, ${\mathfrak{D}}^m$ and ${\mathfrak{D}}^n$ are the Caputo fractional derivatives of $m\in \left(1,2\right]$, $m-1\in \left(0,1\right]$ and $n\in (0,1)$ orders, respectively, and ${\mathcal{D}}^{2n}$ is the sequential fractional derivative. Furthermore, ${\eta }_{\kappa }\in \mathbb{R}(\kappa =1,2,3)$ with ${\eta }_{\kappa }\ne 0$, $u\in (0,1)$, and ${\mathcal{R}}_{\tau }:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ is a given function that is continuously differentiable, where $\tau =13$ represents the total number of edges of the isobutane compound with length $|{\tilde{p}}_{\tau }|=1$.

This paper analyzes the link between the framework of fractional boundary value problems (1) and the isobutane graph (see Figure 6), as mentioned above. The rising popularity of CGT is the critical impetus for this study. This branch of mathematics examines how bond lines and inter-atomic interactions affect the results of chemical processes. These new applications can be seen in chemical kinetics and biomacromolecules.

The next sections will need the notable results stated below.

Definition 1 

([55]). The Caputo fractional derivative of order $\wp >0$ for a function $\mathcal{H}\in C^{\chi }([a,b],\mathbb{R})$ is given by

$${\mathfrak{D}}^{\wp }\mathcal{H}\left(s\right)=\frac{1}{\mathsf{\Gamma }(\chi -\wp )}{\int }_0^s{(s-\theta )}^{\chi -\wp -1}{\mathcal{H}}^{\left(\chi \right)}\left(\theta \right)d\theta (\chi -1<\wp <\chi ,\chi =[\wp ]+1),$$

where $[\wp ]$ represents the integer part of ℘.

For $\wp >0$, the general solution of ${\mathfrak{D}}^{\wp }v\left(s\right)=0$ is defined by

$$v\left(s\right)=d_0+d_{1}s+d_2{s}^2+\cdots +d_{n-1}{s}^{n-1},$$

where $d_k\in \mathbb{R},k=0,1,...,n-1$.

Definition 2 

([14]). The sequential fractional derivative for a sufficiently smooth function $\mathcal{H}\left(s\right)$ is defined as

$${\mathcal{D}}^{\varrho }\mathcal{H}\left(s\right)={\mathcal{D}}^{{\varrho }_1}{\mathcal{D}}^{{\varrho }_2}\cdots {\mathcal{D}}^{{\varrho }_{\ell }}\mathcal{H}\left(s\right),$$

(2)

where $\varrho =\left({\varrho }_1,\dots ,{\varrho }_{\ell }\right)$ is a multi-index.

Generally, ${\mathcal{D}}^{\varrho }$ as specified in (2) may typically be either a Caputo operator, a Riemann–Liouville operator, or another kind of integro–differential operator. For instance,

$${}^C{\mathcal{D}}^{\wp }\mathcal{H}\left(s\right)={\mathcal{D}}^{-(n-\wp )}{\left(\frac{d}{ds}\right)}^n\mathcal{H}\left(s\right),n-1<\wp <n,$$

whereas ${\mathcal{D}}^{-(n-\wp )}$ represents a fractional integral operator of order $n-\wp$.

Lemma 1. 

Suppose that ${\rm Y}\in C\left(\right[0,1],\mathbb{R})$. Then, $v^{🟉}:[0,1]\to \mathbb{R}$ is a solution of the subsequent problem:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^{m}v\left(s\right)& ={\rm Y}\left(t\right)(s\in [0,1\left]\right),\hfill \\ \hfill v\left(0\right)& ={\mathfrak{D}}^{m-1}v\left(1\right),{\eta }_1{\mathfrak{D}}^{n}v\left(1\right)+{\eta }_2{\mathcal{D}}^{2n}v\left(1\right)={\eta }_3{\int }_0^u{\mathfrak{D}}^{m-1}v\left(\theta \right)d\theta ,\hfill \end{array}\right.\end{array}$$

(3)

if $v^{🟉}$ is a solution of the integral equation given below:

$$\begin{array}{ccc}\hfill v\left(s\right)& =& {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\rm Y}\left(\theta \right)d\theta +{\int }_0^1{\rm Y}\left(\theta \right)d\theta \hfill \\ & & +\frac{1}{A_0}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\rm Y}\left(\zeta \right)d\zeta d\theta -{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\rm Y}\left(\theta \right)d\theta \right.\hfill \\ & & \left.-{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\rm Y}\left(\theta \right)d\theta \right],\hfill \end{array}$$

(4)

where $A_0=\left[\frac{{\eta }_1}{\mathsf{\Gamma }(2-n)}+\frac{{\eta }_2}{\mathsf{\Gamma }(2-2n)}-\frac{{\eta }_3{u}^{3-m}}{\mathsf{\Gamma }(4-m)}\right]$.

Proof. 

Assume that $v^{🟉}:[0,1]\to \mathbb{R}$ is a solution of (3). Thus, there exist constants $d_0,d_1\in \mathbb{R}$ such that

$$v^{🟉}\left(s\right)={\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\rm Y}\left(\theta \right)d\theta +d_0+d_{1}s.$$

(5)

From the above, we obtain

$${\mathfrak{D}}^{m-1}v\left(s\right)={\int }_0^s{\rm Y}\left(\theta \right)d\theta +\frac{s^{2-m}}{\mathsf{\Gamma }(3-m)}{d}_1,$$

and

$${\int }_0^u{\mathfrak{D}}^{m-1}v\left(\theta \right)d\theta ={\int }_0^u{\int }_0^{\theta }{\rm Y}\left(\zeta \right)d\zeta d\theta +\frac{u^{3-m}}{\mathsf{\Gamma }(4-m)}{d}_1.$$

Using the first boundary condition, we have

$$d_0={\int }_0^1{\rm Y}\left(\theta \right)d\theta +\frac{1}{\mathsf{\Gamma }(3-m)}{d}_1.$$

(6)

From the second boundary condition, we obtain

$$\begin{array}{ccc}\hfill d_1& =& \frac{1}{A_0}\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\rm Y}\left(\zeta \right)d\zeta d\theta -{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\rm Y}\left(\theta \right)d\theta \right.\hfill \\ & & \left.-{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\rm Y}\left(\theta \right)d\theta \right].\hfill \end{array}$$

Now, by substituting the value of $d_1$ into (6), we obtain

$$\begin{array}{ccc}\hfill d_0& =& {\int }_0^1{\rm Y}\left(\theta \right)d\theta +\left(\frac{1}{A_0\mathsf{\Gamma }(3-m)}\right)\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\rm Y}\left(\zeta \right)d\zeta d\theta \right.\hfill \\ & & \left.-{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\rm Y}\left(\theta \right)d\theta -{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\rm Y}\left(\theta \right)d\theta \right].\hfill \end{array}$$

Hence, substituting the values of $d_0,d_1$ into (5), we attain the solution (4). Conversely, it is obvious that $v^{🟉}$ satisfies (3) whenever it is a solution of (4). □

Our goal is to show that (1) has a solution using the following fixed point theory concepts.

Theorem 1 

([56]). Let $\mathcal{M}$ be a Banach space. If $\mathcal{T}:\mathcal{M}\to \mathcal{M}$ is a completely continuous operator, then either $\left\{v\in \mathcal{M}:v=b\mathcal{T}v\mathit{for}\mathit{some}0<b<1\right\}$ is unbounded or $\mathcal{T}$ has at least one fixed point in $\mathcal{M}$.

Theorem 2 

([56]). Let $\mathcal{V}$ be a closed, bounded, convex, and nonempty subset of Banach space $\mathcal{M}$ and ${\mathcal{T}}_1,{\mathcal{T}}_2:\mathcal{V}\to \mathcal{M}$ be two operators such that ${\mathcal{T}}_{1}k+{\mathcal{T}}_2{k}^{\prime }\in \mathcal{V}$ whenever $k,k^{\prime }\in \mathcal{V}$, where ${\mathcal{T}}_1$ is compact and continuous and ${\mathcal{T}}_2$ is a contraction mapping; that is, there is a ${\gamma }^{🟉}\in [0,1)$ such that

$$\parallel {\mathcal{T}}_{2}k-{\mathcal{T}}_2\tilde{k}\parallel \le {\gamma }^{🟉}\parallel k-\tilde{k}\parallel ,$$

for all $k,\tilde{k}\in \mathcal{V}$. Then, ${\mathcal{T}}_1+{\mathcal{T}}_2$ has a fixed point.

2. Main Results

Define $\tilde{\mathcal{M}}=\{v:[0,1]\to \mathbb{R}:v,{\mathfrak{D}}^{n}v,v^{\prime }\in C([0,1],\mathbb{R})\}$ as a Banach space with the norm

$${∥v∥}_{\tilde{\mathcal{M}}}=\underset{s\in [0,1]}{sup}\left|v\left(s\right)\right|+\underset{s\in [0,1]}{sup}\left|{\mathfrak{D}}^{n}v\left(s\right)\right|+\underset{s\in [0,1]}{sup}\left|v^{\prime }\left(s\right)\right|.$$

It is obvious that $\mathcal{M}={\tilde{\mathcal{M}}}_{13}$ is a Banach space equipped with the norm

$${∥v=(v_1,v_2,\dots ,v_{13})∥}_{\mathcal{M}}=\sum _{\tau =1}^{13}{∥v_{\tau }∥}_{{\tilde{\mathcal{M}}}_{\tau }}.$$

From Lemma 1, we can introduce an operator $\mathcal{T}:\mathcal{M}\to \mathcal{M}$ for each $(v_1,v_2,\dots ,v_{13})\in \mathcal{M}$ defined by

$$\mathcal{T}(v_1,v_2,\dots ,v_{13}):=\left({\mathcal{T}}_1(v_1,v_2,\dots ,v_{13}),{\mathcal{T}}_2(v_1,v_2,\dots ,v_{13}),\dots ,{\mathcal{T}}_{13}(v_1,v_2,\dots ,v_{13})\right),$$

(7)

for each $\tau =1,2,\dots ,13$, where ${\mathcal{T}}_{\tau }:\mathcal{M}\to \tilde{\mathcal{M}}$ is defined for each $(v_1,v_2,\dots ,v_{13})\in \mathcal{M}$ by

$$\begin{array}{ccc}\hfill {\mathcal{T}}_{\tau }(v_1,v_2,\dots ,v_{13})\left(s\right)& =& {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & +{\int }_0^1{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & +\frac{1}{A_0}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))d\zeta d\theta \right.\hfill \\ & & -{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & \left.-{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \right],\hfill \end{array}$$

(8)

for all $s\in [0,1]$.

We shall use the following notation to make computations easier:

$$\begin{array}{ccc}\hfill {\Delta }^{*}& =& \frac{{\eta }_1}{\mathsf{\Gamma }(2-n)}+\frac{{\eta }_2}{\mathsf{\Gamma }(2-2n)}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \widetilde{{\Delta }^{*}}& =& \frac{|{\eta }_3|}{2}+\frac{|{\eta }_2|}{\mathsf{\Gamma }(m-2n+1)}+\frac{|{\eta }_1|}{\mathsf{\Gamma }(m-n+1)}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill A_0& =& \left[{\Delta }^{*}-\frac{{\eta }_3{u}^{3-m}}{\mathsf{\Gamma }(4-m)}\right]\ne 0\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill A_1& =& \left[{\Delta }^{*}+\frac{{\eta }_3}{\mathsf{\Gamma }(4-m)}\right]\ne 0\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_0^{*}& =& 1+\frac{\widetilde{{\Delta }^{*}}}{|A_1|}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+1\right)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_1^{*}& =& \frac{1}{|A_1|\mathsf{\Gamma }(2-n)}\widetilde{{\Delta }^{*}}\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_2^{*}& =& \frac{1}{|A_1|}\widetilde{{\Delta }^{*}}.\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\mathcal{M}}_0^{*}& =& \frac{1}{\mathsf{\Gamma }(m+1)}+{\mathcal{V}}_0^{*}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{*}& =& \frac{1}{\mathsf{\Gamma }(m-n+1)}+{\mathcal{V}}_1^{*}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\mathcal{M}}_2^{*}& =& \frac{1}{\mathsf{\Gamma }\left(m\right)}+{\mathcal{V}}_2^{*}\hfill \end{array}$$

(18)

Theorem 3. 

Consider the problem (1). Assume that ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_{13}:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous functions and there are ${\mathsf{\Xi }}_{\tau }>0$$(\forall \tau =1,2,\dots ,13)$ such that $\left|{\mathcal{R}}_{\tau }(s,v,\tilde{v},\tilde{\tilde{v}})\right|\le {\mathsf{\Xi }}_{\tau }$, for all $s\in [0,1]$ and $v,\tilde{v},\tilde{\tilde{v}}\in \mathbb{R}$. Then, problem (1) has a solution.

Proof. 

The integral Equation (8) implies that the fixed points of $\mathcal{T}$ described by (7) exist if and only if (1) has a solution. To establish this, we must first demonstrate that $\mathcal{T}$ is completely continuous.

Since ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_{13}$ are continuous, $\mathcal{T}:\mathcal{M}\to \mathcal{M}$ is continuous too. Let $\mathcal{O}\in \mathcal{M}$ be a bounded set and $v=(v_1,v_2,\dots ,v_{13})\in \mathcal{M}$. For each $s\in [0,1]$, we have

$$\begin{array}{ccc}& & \left|\left({\mathcal{T}}_{\tau }v\right)\left(s\right)\right|\hfill \\ & \le & {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta +{\int }_0^1\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\mathsf{\Xi }}_{\tau }{\mathcal{M}}_0^{*},\hfill \end{array}$$

where ${\mathcal{M}}_0^{*}$ is given in (16). In addition,

$$\begin{array}{ccc}& & \left|\left({\mathfrak{D}}^n{\mathcal{T}}_{\tau }v\right)\left(s\right)\right|\hfill \\ & \le & {\int }_0^s\frac{{(s-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\left(\frac{s^{1-n}}{|A_0|\mathsf{\Gamma }(2-n)}\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \end{array}$$

$$\begin{array}{ccc}& & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\mathsf{\Xi }}_{\tau }{\mathcal{M}}_1^{*}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{T}}_{\tau }^{\prime }v\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{m-2}}{\mathsf{\Gamma }(m-1)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\left(\frac{1}{|A_0|}\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & =& {\mathsf{\Xi }}_{\tau }{\mathcal{M}}_2^{*},\hfill \end{array}$$

where ${\mathcal{M}}_1^{*},{\mathcal{M}}_2^{*}$ are given in (17) and (18), respectively, and for all $s\in [0,1]$. Therefore,

$${∥\left({\mathcal{T}}_{\tau }v\right)\left(s\right)∥}_{{\mathcal{M}}_{\tau }}\le {\mathsf{\Xi }}_{\tau }\left({\mathcal{M}}_0^{*}+{\mathcal{M}}_1^{*}+{\mathcal{M}}_2^{*}\right).$$

Hence,

$$\begin{array}{ccc}\hfill {∥\left(\mathcal{T}v\right)\left(s\right)∥}_{\mathcal{M}}& =& \sum _{\tau =1}^{13}{∥\left({\mathcal{T}}_{\tau }v\right)\left(s\right)∥}_{\tilde{\mathcal{M}}}\hfill \\ & \le & \sum _{\tau =1}^{13}{\mathsf{\Xi }}_{\tau }\left({\mathcal{M}}_0^{*}+{\mathcal{M}}_1^{*}+{\mathcal{M}}_2^{*}\right)\hfill \\ & <& \infty ,\hfill \end{array}$$

which demonstrates the uniform boundedness of the operator $\mathcal{T}$.

Now, we shall show that $\mathcal{T}$ is equicontinuous. For this, let $v=(v_1,v_2,\dots ,v_{13})\in \mathcal{O}$ and $s_1,s_2\in [0,1]$ with $s_1<s_2$. Then, we have

$$\begin{array}{ccc}& & \left|\left({\mathcal{T}}_{\tau }v\right)\left(s_2\right)-\left({\mathcal{T}}_{\tau }v\right)\left(s_1\right)\right|\hfill \\ & \le & {\int }_0^{s_1}\frac{{(s_2-\theta )}^{m-1}-{(s_1-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\left(\frac{s_2-s_1}{|A_1|}\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right].\hfill \end{array}$$

It is clear that, if $s_1\to s_2$ then the R.H.S of the above expression converges to zero independently. Thus,

$$\underset{s_1\to s_2}{lim}\left|\left({\mathfrak{D}}^n{\mathcal{T}}_{\tau }v\right)\left(s_2\right)-\left({\mathfrak{D}}^n{\mathcal{T}}_{\tau }v\right)\left(s_1\right)\right|=0,\underset{s_1\to s_2}{lim}\left|\left({\mathcal{T}}_{\tau }^{\prime }w\right)\left(s_2\right)-\left({\mathcal{T}}_{\tau }^{\prime }w\right)\left(s_1\right)\right|=0.$$

This reveals that ${∥\left(\mathcal{T}v\right)\left(s_2\right)-\left(\mathcal{T}v\right)\left(s_1\right)∥}_{\mathcal{M}}\to 0$ as $s_1\to s_2$. This proves that $\mathcal{T}$ is equicontinuous on $\mathcal{M}={\mathcal{M}}_1\times {\mathcal{M}}_2\times \cdots \times {\mathcal{M}}_{13}$. The Arzela–Ascoli theorem now entails the operator’s complete continuity.

Further, we have

$$\Theta :=\left\{(v_1,v_2,\dots ,v_{13})\in \mathcal{M}:(v_1,v_2,\dots ,v_{13})=b\mathcal{T}(v_1,v_2,\dots ,v_{13}),b\in (0,1)\right\}$$

of $\mathcal{M}$. We shall prove that $\Theta$ is bounded in this section. For this, let $(v_1,v_2,\dots ,v_{13})\in \Theta$. Then, we can write

$$(v_1,v_2,\dots ,v_{13})=b\mathcal{T}(v_1,v_2,\dots ,v_{13}),$$

and so

$$v_{\tau }\left(s\right)=b\left({\mathcal{T}}_{\tau }(v_1,v_2,\dots ,v_{13})\right),$$

for all $s\in [0,1]$ and $\tau =1,2,\dots ,13$. Thus,

$$\begin{array}{ccc}\hfill \left|v_{\tau }\left(s\right)\right|& \le & b\left[{\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta +{\int }_0^1\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right.\hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.\left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\right]\hfill \\ & \le & b{\mathsf{\Xi }}_{\tau }{\mathcal{M}}_0^{*},\hfill \end{array}$$

and by similar computations, we have

$$\begin{array}{ccc}\hfill \left|{\mathfrak{D}}^n{v}_{\tau }\left(s\right)\right|& \le & b{\mathsf{\Xi }}_{\tau }{\mathcal{M}}_1^{*},\hfill \\ \hfill \left|v_{\tau }^{\prime }\left(s\right)\right|& \le & b{\mathsf{\Xi }}_{\tau }{\mathcal{M}}_2^{*},\hfill \end{array}$$

where ${\mathcal{M}}_0^{*}-{\mathcal{M}}_2^{*}$ are given in (16)–(18). Hence,

$$\begin{array}{ccc}\hfill {∥v∥}_{\mathcal{M}}& =& \sum _{\tau =1}^{13}{∥v_{\tau }∥}_{\tilde{\mathcal{M}}}\hfill \\ & \le & b\sum _{\tau =1}^{13}{\mathsf{\Xi }}_{\tau }\left({\mathcal{M}}_0^{*}+{\mathcal{M}}_1^{*}+{\mathcal{M}}_2^{*}\right)\hfill \\ & <& \infty ,\hfill \end{array}$$

which shows that $\Theta$ is bounded. We can now verify that $\mathcal{T}$ has a fixed point in $\mathcal{M}$ and that (1) has a solution by using Lemma 1 and Theorem 1. □

We shall now look at the solution to problem (1) by putting different conditions.

Theorem 4. 

Consider the problem (1). Supposing that ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_{13}:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous functions and that there are bounded continuous functions ${\mathcal{Z}}_1,{\mathcal{Z}}_2,\dots ,{\mathcal{Z}}_{13}:[0,1]\to \mathbb{R}$, ${\mathcal{Q}}_1,{\mathcal{Q}}_2,\dots ,{\mathcal{Q}}_{13}:[0,1]\to [0,\infty )$ and nondecreasing continuous functions ${\mathcal{U}}_1,{\mathcal{U}}_2,\dots ,{\mathcal{U}}_{13}:[0,1]\to [0,\infty )$ such that $\left|{\mathcal{R}}_{\tau }(s,v,\tilde{v},\tilde{\tilde{v}})\right|\le {\mathcal{Q}}_{\tau }\left(s\right){\mathcal{U}}_{\tau }(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|)$ and $\forall s\in [0,1]$, $v_1,v_2,v_3$, ${\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3\in \mathbb{R}$ with $\tau =1,2,\dots ,13$, we have

$$\left|{\mathcal{R}}_{\tau }(s,v_1,v_2,v_3)-{\mathcal{R}}_{\tau }(s,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3)\right|\le {\mathcal{Z}}_{\tau }\left(s\right)(\left|v_1-{\tilde{v}}_1\right|+\left|v_2-{\tilde{v}}_2\right|+\left|v_3-{\tilde{v}}_3\right|).$$

If $\mathsf{\Lambda }:=\left({\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\right){\displaystyle \sum _{\tau =1}^{13}}∥{\mathcal{Z}}_{\tau }∥<1$, then (1) has a solution, where $∥{\mathcal{Z}}_{\tau }∥={sup}_{s\in [0,1]}\left|{\mathcal{Z}}_{\tau }\left(s\right)\right|$ and the constants ${\mathcal{V}}_0^{*}$–${\mathcal{V}}_2^{*}$ are given in (13)–(15), respectively.

Proof. 

We let $∥{\mathcal{Q}}_{\tau }∥={sup}_{s\in [0,1]}\left|{\mathcal{Q}}_{\tau }\left(s\right)\right|$. As for ${\kappa }_{\tau }$, we have

$${\kappa }_{\tau }\ge \sum _{\tau =1}^{13}{\mathcal{U}}_{\tau }\left({∥v_{\tau }∥}_{{\mathcal{M}}_{\tau }}\right)∥{\mathcal{Q}}_{\tau }∥\left\{{\mathcal{M}}_0^{*}+{\mathcal{M}}_1^{*}+{\mathcal{M}}_2^{*}\right\},$$

(19)

where ${\mathcal{M}}_0^{*}-{\mathcal{M}}_2^{*}$ are given in (16)–(18). We define a set

$${\mathcal{O}}_{{\kappa }_{\tau }}:=\left\{v=(v_1,v_2,\dots ,v_{13})\in \mathcal{M}:{∥v∥}_{\mathcal{M}}\le {\kappa }_{\tau }\right\},$$

where ${\kappa }_{\tau }$ is defined in (19). It is clear that ${\mathcal{O}}_{{\kappa }_{\tau }}$ is a nonempty, closed, bounded, and convex subset of $\mathcal{M}={\mathcal{M}}_1\times {\mathcal{M}}_2\times \cdots \times {\mathcal{M}}_{13}$. Now, we define ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ on ${\mathcal{O}}_{{\kappa }_{\tau }}$ by

$$\begin{array}{ccc}\hfill {\mathcal{T}}_1(v_1,v_2,\dots ,v_{13})\left(s\right)& :=& \left({\mathcal{T}}_1^{\left(1\right)}(v_1,v_2,\dots ,v_{13})\left(s\right),\dots ,{\mathcal{T}}_1^{\left(13\right)}(v_1,v_2,\dots ,v_{13})\left(s\right)\right),\hfill \\ \hfill {\mathcal{T}}_2(v_1,v_2,\dots ,v_{13})\left(s\right)& :=& \left({\mathcal{T}}_2^{\left(1\right)}(v_1,v_2,\dots ,v_{13})\left(s\right),\dots ,{\mathcal{T}}_2^{\left(13\right)}(v_1,v_2,\dots ,v_{13})\left(s\right)\right),\hfill \end{array}$$

where

$$\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s\right)={\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta$$

(20)

and

$$\begin{array}{ccc}\hfill \left({\mathcal{T}}_2^{\left(\tau \right)}v\right)\left(s\right)& =& {\int }_0^1{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & +\frac{1}{A_0}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))d\zeta d\theta \right.\hfill \\ & & -{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & \left.-{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))d\theta \right]\hfill \end{array}$$

(21)

for all $s\in [0,1]$ and $v=$$(v_1,v_2,\dots ,v_{13})\in {\mathcal{O}}_{{\kappa }_{\tau }}$.

Let ${\tilde{\mathcal{U}}}_{\tau }={sup}_{v_{\tau }\in {\mathcal{M}}_{\tau }}{\mathcal{U}}_{\tau }\left({∥v_{\tau }∥}_{{\mathcal{M}}_{\tau }}\right)$. For every $\tilde{v}=({\tilde{v}}_1,{\tilde{v}}_2,\dots ,{\tilde{v}}_{13})$, $v=(v_1,v_2,\dots ,v_{13})\in {\mathcal{O}}_{{\kappa }_{\tau }}$, we have

$$\begin{array}{ccc}& & \left|\left({\mathcal{T}}_1^{\left(\tau \right)}\tilde{v}+{\mathcal{T}}_2^{\left(\tau \right)}v\right)\left(s\right)\right|\hfill \\ & \le & {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,{\tilde{v}}_{\tau }\left(\theta \right),{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\theta \right),{\tilde{v}}_{\tau }^{\prime }\left(\theta \right))\right|d\theta +{\int }_0^1\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }\left|{\mathcal{R}}_{\tau }(\zeta ,v_{\tau }\left(\zeta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right),v_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{Q}}_{\tau }\left(\theta \right){\mathcal{U}}_{\tau }\left(\left|{\tilde{v}}_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\theta \right)\right|+\left|{\tilde{v}}_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +{\int }_0^1{\mathcal{Q}}_{\tau }\left(\theta \right){\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\times \left[|{\eta }_3|{\int }_0^u{\int }_0^{\theta }{\mathcal{Q}}_{\tau }\left(\zeta \right){\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\zeta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right)\right|+\left|v_{\tau }^{\prime }\left(\zeta \right)\right|\right)d\zeta d\theta \right.\hfill \\ & & +|{\eta }_2|{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\mathcal{Q}}_{\tau }\left(\theta \right){\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \end{array}$$

$$\begin{array}{ccc}& & \left.+|{\eta }_1|{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\mathcal{Q}}_{\tau }\left(\theta \right){\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \right]\hfill \\ & \le & ∥{\mathcal{Q}}_{\tau }∥{\tilde{\mathcal{U}}}_{\tau }{\mathcal{M}}_0^{*}.\hfill \end{array}$$

By similar computations, we have

$$\begin{array}{ccc}\hfill \left|{\mathfrak{D}}^n{\mathcal{T}}_1^{\left(\tau \right)}\tilde{v}\left(s\right)+{\mathfrak{D}}^n{\mathcal{T}}_2^{\left(\tau \right)}v\left(s\right)\right|& \le & ∥{\mathcal{Q}}_{\tau }∥{\tilde{\mathcal{U}}}_{\tau }{\mathcal{M}}_1^{*},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|{\left({\mathcal{T}}_1^{\left(\tau \right)}\tilde{v}\right)}^{\prime }\left(s\right)+{\left({\mathcal{T}}_2^{\left(\tau \right)}v\right)}^{\prime }\left(s\right)\right|& \le & ∥{\mathcal{Q}}_{\tau }∥{\tilde{\mathcal{U}}}_{\tau }{\mathcal{M}}_2^{*}.\hfill \end{array}$$

This yields that

$$\begin{array}{c}\hfill {∥{\mathcal{T}}_1\tilde{v}+{\mathcal{T}}_{2}v∥}_{\mathcal{M}}=\sum _{\tau =1}^{13}{∥{\mathcal{T}}_1^{\left(\tau \right)}\tilde{v}+{\mathcal{T}}_2^{\left(k\right)}v∥}_{\tilde{\mathcal{M}}}\le ∥{\mathcal{Q}}_{\tau }∥{\tilde{\mathcal{U}}}_{\tau }\left({\mathcal{M}}_0^{*}+{\mathcal{M}}_1^{*}+{\mathcal{M}}_2^{*}\right)\le {\kappa }_{\tau },\end{array}$$

and so ${\mathcal{T}}_1\tilde{v}+{\mathcal{T}}_{2}v\in {\mathcal{O}}_{{\kappa }_{\tau }}$. Furthermore, the continuity of ${\mathcal{R}}_{\tau }$ follows from the continuity of ${\mathcal{T}}_1$.

Now, we shall show that ${\mathcal{T}}_1$ is uniformly bounded. As for this purpose, we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & \le & \frac{1}{\mathsf{\Gamma }(m+1)}∥{\mathcal{Q}}_{\tau }∥{\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right).\hfill \end{array}$$

for all $v\in$${\mathcal{O}}_{{\kappa }_{\tau }}$. In addition,

$$\begin{array}{ccc}\hfill \left|\left({\mathfrak{D}}^n{\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}\left|{\mathcal{R}}_{\tau }(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & \le & \frac{1}{\mathsf{\Gamma }(m-n+1)}∥{\mathcal{Q}}_{\tau }∥{\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|{\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)}^{\prime }\left(s\right)\right|& \le & \frac{1}{\mathsf{\Gamma }\left(m\right)}∥{\mathcal{Q}}_{\tau }∥{\mathcal{U}}_{\tau }\left(\left|v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|v_{\tau }^{\prime }\left(\theta \right)\right|\right),\hfill \end{array}$$

for all $w\in$${\mathcal{O}}_{{\kappa }_{\tau }}$. Thus,

$$\begin{array}{ccc}\hfill {∥{\mathcal{T}}_{1}v∥}_{\mathcal{M}}& =& \sum _{\tau =1}^{13}{∥{\mathcal{T}}_1^{\left(\tau \right)}w∥}_{\tilde{\mathcal{M}}}\hfill \\ & \le & \left\{\frac{m+1}{\mathsf{\Gamma }(m+1)}+\frac{1}{\mathsf{\Gamma }(m-n+1)}\right\}\sum _{\tau =1}^{13}∥{\mathcal{Q}}_{\tau }∥{\mathcal{U}}_{\tau }\left({∥v_{\tau }∥}_{\tilde{\mathcal{M}}}\right),\hfill \end{array}$$

which shows that ${\mathcal{T}}_1$ is uniformly bounded on ${\mathcal{O}}_{{\kappa }_{\tau }}$.

Now, we shall demonstrate that ${\mathcal{T}}_1$ is compact on ${\mathcal{O}}_{{\kappa }_{\tau }}$. For this, let $s_1,s_2\in [0,1]$ with $s_1<s_2$. Then, we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s_2\right)-\left({\mathcal{T}}_1^{\left(k\right)}v\right)\left(s_1\right)\right|& \le & \left|{\int }_0^{s_2}\frac{{(s_2-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right.\hfill \\ & & \left.-{\int }_0^{s_1}\frac{{(s_1-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \left|{\int }_0^{s_1}\frac{{(s_2-\theta )}^{m-1}-{(s_1-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \\ & & +\left|{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \\ & \le & {\int }_0^{s_1}\frac{{(s_2-\theta )}^{m-1}-{(s_1-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)\right|d\theta \hfill \\ & & +{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{m-1}}{\mathsf{\Gamma }\left(m\right)}\left|{\mathcal{R}}_{\tau }\left(\theta ,v_{\tau }\left(\theta \right),{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right),v_{\tau }^{\prime }\left(\theta \right)\right)\right|d\theta \hfill \\ & \le & \left\{\frac{s_2^m-s_1^m-{\left(s_2-s_1\right)}^m}{\mathsf{\Gamma }(m+1)}+\frac{{\left(s_2-s_1\right)}^m}{\mathsf{\Gamma }(m+1)}\right\}∥{\mathcal{Q}}_{\tau }∥{\mathcal{U}}_{\tau }\left({∥v_{\tau }∥}_{{\mathcal{M}}_{\tau }}\right).\hfill \end{array}$$

Hence, $\left|\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s_2\right)-\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s_1\right)\right|\to 0$ as $s_1\to s_2$. In addition, we have

$$\begin{array}{c}\hfill \underset{s_1\to s_2}{lim}\left|\left({\mathfrak{D}}^n{\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s_2\right)-\left({\mathfrak{D}}^n{\mathcal{T}}_1^{\left(\tau \right)}v\right)\left(s_1\right)\right|=0,\underset{s_1\to s_2}{lim}\left|{\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)}^{\prime }\left(s_2\right)-{\left({\mathcal{T}}_1^{\left(\tau \right)}v\right)}^{\prime }\left(s_1\right)\right|=0.\end{array}$$

Hence, ${∥\left({\mathcal{T}}_{1}v\right)\left(s_2\right)-\left({\mathcal{T}}_{1}v\right)\left(s_1\right)∥}_{\mathcal{M}}$ tends to zero as $s_1\to s_2$. Thus, ${\mathcal{T}}_1$ is equicontinuous and therefore ${\mathcal{T}}_1$ is a relatively compact operator on ${\mathcal{O}}_{{\kappa }_{\tau }}$. Hence, T is compact on ${\mathcal{O}}_{{\kappa }_{\tau }}$ according to the Arzela–Ascoli theorem.

Lastly, it remains to prove that ${\mathcal{T}}_2$ is a contraction. To show this, let $\tilde{v},v\in {\mathcal{O}}_{{\kappa }_{\tau }}$; then,

$$\begin{array}{ccc}& & \left|\left({\mathcal{T}}_2^{\left(\tau \right)}\tilde{v}\right)\left(s\right)-\left({\mathcal{T}}_2^{\left(\tau \right)}v\right)\left(s\right)\right|\hfill \\ & \le & {\int }_0^1{\mathcal{Z}}_{\tau }\left(\theta \right)\left(\left|{\tilde{v}}_{\tau }\left(\theta \right)-v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\theta \right)-{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|{\tilde{v}}_{\tau }^{\prime }\left(\theta \right)-v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +\frac{1}{A_0}\left(\frac{1}{\mathsf{\Gamma }(3-m)}+s\right)\left[{\eta }_3{\int }_0^u{\int }_0^{\theta }{\mathcal{Z}}_{\tau }\left(\zeta \right)\left(\left|{\tilde{v}}_{\tau }\left(\zeta \right)-v_{\tau }\left(\zeta \right)\right|\right.\right.\hfill \\ & & \left.+\left|{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\zeta \right)-{\mathfrak{D}}^n{v}_{\tau }\left(\zeta \right)\right|+\left|{\tilde{v}}_{\tau }^{\prime }\left(\zeta \right)-v_{\tau }^{\prime }\left(\zeta \right)\right|\right)d\zeta d\theta \hfill \\ & & +{\eta }_2{\int }_0^1\frac{{(1-\theta )}^{m-2n-1}}{\mathsf{\Gamma }(m-2n)}{\mathcal{Z}}_{\tau }\left(\theta \right)\left(\left|{\tilde{v}}_{\tau }\left(\theta \right)-v_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\theta \right)-{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|\right.\hfill \\ & & \left.+\left|{\tilde{v}}_{\tau }^{\prime }\left(\theta \right)-v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta +{\eta }_1{\int }_0^1\frac{{(1-\theta )}^{m-n-1}}{\mathsf{\Gamma }(m-n)}{\mathcal{Z}}_{\tau }\left(\theta \right)\left(\left|{\tilde{v}}_{\tau }\left(\theta \right)-v_{\tau }\left(\theta \right)\right|\right.\hfill \\ & & \left.+\left|{\mathfrak{D}}^n{\tilde{v}}_{\tau }\left(\theta \right)-{\mathfrak{D}}^n{v}_{\tau }\left(\theta \right)\right|+\left|{\tilde{v}}_{\tau }^{\prime }\left(\theta \right)-v_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta ]\hfill \\ & \le & ∥{\mathcal{Z}}_{\tau }∥{\mathcal{V}}_0^{*}{∥{\tilde{v}}_{\tau }-v_{\tau }∥}_{\tilde{\mathcal{M}}}\hfill \end{array}$$

for each $\tau =1,2,\dots ,13,$, where ${\mathcal{V}}_0^{*}$ is given in (13). In addition, by similar computations, we have

$$\underset{s\in [0,1]}{sup}\left|\left({\mathfrak{D}}^n{\mathcal{T}}_2^{\left(\tau \right)}\tilde{v}\right)\left(s\right)-\left({\mathfrak{D}}^n{\mathcal{T}}_2^{\left(\tau \right)}v\right)\left(s\right)\right|\le ∥{\mathcal{Z}}_{\tau }∥{\mathcal{V}}_1^{*}{∥{\tilde{v}}_{\tau }-v_{\tau }∥}_{\tilde{\mathcal{M}}},$$

and

$$\underset{s\in [0,1]}{sup}\left|{\left({\mathcal{T}}_2^{\left(\tau \right)}\tilde{v}\right)}^{\prime }\left(s\right)-{\left({\mathcal{T}}_2^{\left(\tau \right)}v\right)}^{\prime }\left(s\right)\right|\le ∥{\mathcal{Z}}_{\tau }∥{\mathcal{V}}_2^{*}{∥{\tilde{v}}_{\tau }-v_{\tau }∥}_{\tilde{\mathcal{M}}},$$

where ${\mathcal{V}}_1^{*}$ and ${\mathcal{V}}_2^{*}$ are given in (14) and (15), respectively. Thus, we have

$$\begin{array}{c}\hfill {∥{\mathcal{T}}_2\tilde{v}-{\mathcal{T}}_{2}v∥}_{\mathcal{M}}=\sum _{\tau =1}^{13}{∥{\mathcal{T}}_2^{\left(\tau \right)}\tilde{v}-{\mathcal{T}}_2^{\left(\tau \right)}v∥}_{\tilde{\mathcal{M}}}\le \left({\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\right)\sum _{\tau =1}^{13}∥{\mathcal{Z}}_{\tau }∥{∥{\tilde{v}}_{\tau }-v_{\tau }∥}_{\tilde{\mathcal{M}}},\end{array}$$

and so

$${∥{\mathcal{T}}_2\tilde{v}-{\mathcal{T}}_{2}v∥}_{\mathcal{M}}\le \mathsf{\Lambda }{∥\tilde{v}-v∥}_{\tilde{\mathcal{M}}}.$$

Since $\Lambda <1,$${\mathcal{T}}_2$ is a contraction on ${\mathcal{O}}_{{\kappa }_{\tau }}$, we deduce that $\mathcal{T}$ has a fixed point that is a solution to problem (1) as a consequence of Theorem 2. □

3. Some Illustrative Examples

The conclusions of the proposed model (1) regarding the existence of solutions can be interpreted in several ways in relation to organic chemistry, which is the study’s underlying assumption. Any solution, say $v_{\tau }$, at any edge (${\tilde{p}}_{\tau }$) may thus represent the bond polarity, strength, energy, etc. Additionally, several chemical concepts can be interpreted in this way by the integer and fractional-order derivatives of the unknown functions, while ${\mathfrak{D}}^n$’s nonlocal character allows it to analyze the velocity of chemical interactions during a particular time interval $[0,1]$. Moreover, ${\mathcal{R}}_{\tau }$ is defined as functions of such quantities with respect to the time $t\in [0,1]$ on each edge ${\tilde{p}}_{\tau },\tau \in \left\{1,2,3,\dots ,13\right\}$.

Here, we provide two examples to demonstrate the relevance of our findings.

Example 1. 

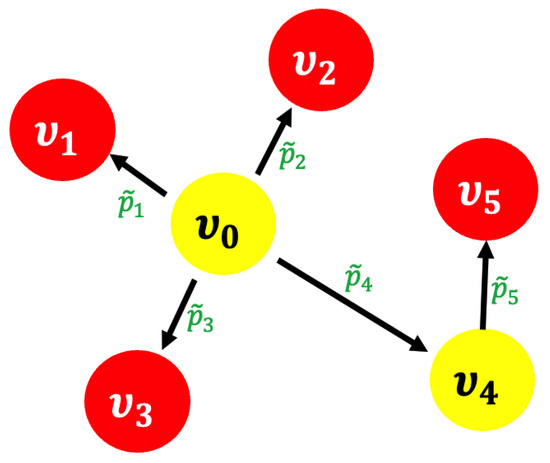
Consider the boundary value problem

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^{1.8}{v}_1\left(s\right)& =\frac{18e^s{\left[v_1\left(s\right)\right]}^2}{60000(1+{\left[v_1\left(s\right)\right]}^2)}+0.0003e^{s}sin\left({\mathfrak{D}}^{0.05}{v}_1\left(s\right)\right)+\frac{3e^s{sinh}^{-1}{v}_1^{\prime }\left(s\right)}{10000},\hfill \\ \hfill {\mathfrak{D}}^{1.8}{v}_2\left(s\right)& =\frac{s[arctan{v}_2\left(s\right)]}{10000}+0.0001s\left[sin\left({\mathfrak{D}}^{0.05}{v}_2\left(s\right)\right)\right]+\frac{8s{\left[v_2^{\prime }\left(s\right)\right]}^2}{10000\left(1+{\left[v_2^{\prime }\left(s\right)\right]}^2\right)},\hfill \\ \hfill {\mathfrak{D}}^{1.8}{v}_3\left(s\right)& =\frac{e^s{\left[v_3\left(s\right)\right]}^2}{25000(1+{\left[v_3\left(s\right)\right]}^2)}+\frac{4e^s{sinh}^{-1}\left({\mathfrak{D}}^{0.05}{v}_3\left(s\right)\right)}{100000}+\frac{12e^{s}arctan{v}_3^{\prime }\left(s\right)}{300000},\hfill \\ \hfill {\mathfrak{D}}^{1.8}{v}_4\left(s\right)& =0.0009s(sin{v}_4\left(s\right))+\frac{180s{\left[{\mathfrak{D}}^{0.05}{v}_4\left(s\right)\right]}^2}{200000+200000{\left[{\mathfrak{D}}^{0.05}{v}_4\left(s\right)\right]}^2}+\frac{36s(arctan{v}_4^{\prime }\left(s\right))}{40000},\hfill \\ \hfill {\mathfrak{D}}^{1.8}{z}_5\left(s\right)& =0.0001s\left({sinh}^{-1}{z}_5\left(s\right)\right)+\frac{60s{\left[{\mathfrak{D}}^{0.05}{z}_5\left(s\right)\right]}^2}{600000+600000{\left[{\mathfrak{D}}^{0.05}{z}_5\left(s\right)\right]}^2}+\frac{3s\left(arctan{z}_5^{\prime }\left(s\right)\right)}{30000},\hfill \\ \hfill {\mathfrak{D}}^{1.8}{z}_6\left(s\right)& =\frac{s\left(arctan{z}_6\left(s\right)\right)}{25000}+0.00004s\left(sin\left({\mathfrak{D}}^{0.05}{z}_6\left(s\right)\right)\right)+\frac{4s{\left[z_6^{\prime }\left(s\right)\right]}^2}{100000\left(1+{\left[z_6^{\prime }\left(s\right)\right]}^2\right)},\hfill \end{array}\right.\end{array}$$

(22)

with boundary conditions

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill v_1\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_1\left(\theta \right)d\theta \hfill \\ \hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_1\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_1\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_1\left(\theta \right)d\theta \hfill \\ \hfill v_2\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_2\left(\theta \right)d\theta \hfill \\ \hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_2\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_2\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_2\left(\theta \right)d\theta \hfill \\ \hfill v_3\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_3\left(\theta \right)d\theta \hfill \\ \hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_3\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_3\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_3\left(\theta \right)d\theta \hfill \\ \hfill v_4\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_4\left(\theta \right)d\theta \hfill \\ \hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_4\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_4\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_4\left(\theta \right)d\theta \hfill \\ \hfill v_5\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_5\left(\theta \right)d\theta \hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_5\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_5\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_5\left(\theta \right)d\theta \hfill \\ \hfill v_6\left(0\right)& ={\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_6\left(\theta \right)d\theta \hfill \\ \hfill \frac{7}{2}{\mathfrak{D}}^{0.05}{v}_6\left(1\right)+\frac{9}{4}{\mathcal{D}}^{0.1}{v}_6\left(1\right)& =\frac{23}{6}{\int }_0^{0.95}{\mathfrak{D}}^{0.8}{v}_6\left(\theta \right)d\theta \hfill \end{array}\right.\end{array}$$

(23)

where $m=1.8,n=0.05,{\eta }_1=\frac{7}{2},{\eta }_2=\frac{9}{4},{\eta }_3=\frac{23}{6}$ and ${\mathfrak{D}}^m$, ${\mathfrak{D}}^n$ are the Caputo derivatives of order m and n, respectively.

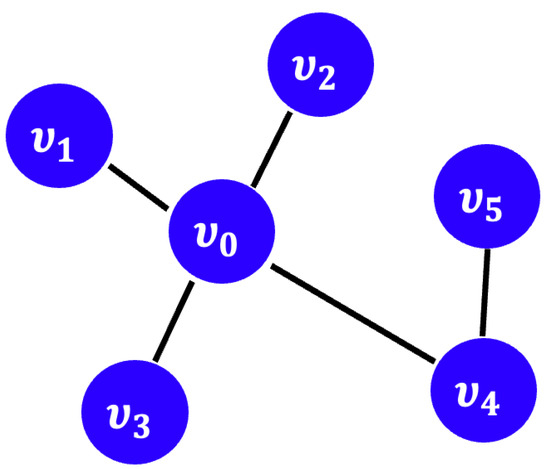
Here, we establish coordinate systems with ${\nu }_0,{\nu }_1,{\nu }_2,{\nu }_3,{\nu }_4$, and ${\nu }_5$ on the graphs with more than one junction nodes (see Figure 8 and Figure 9 below), where ${\tilde{p}}_1$ is the solution of the system (22) with (23) on $\overrightarrow{{\nu }_0{\nu }_1}$, $t\in [0,1]$. Similarly, ${\tilde{p}}_2,{\tilde{p}}_3,{\tilde{p}}_4,$ and ${\tilde{p}}_5$ are the solutions of the system (22) with (23) on $\overrightarrow{{\nu }_0{\nu }_2},\overrightarrow{{\nu }_0{\nu }_3},\overrightarrow{{\nu }_0{\nu }_4},$ and $\overrightarrow{{\nu }_4{\nu }_5}$, respectively, where $t\in [0,1]$.

Figure 8. A sketch of a graph.

Figure 9. A sketch of a directed graph.

Now, we shall prove that system (22) with (23) has a unique solution on each edge. For this, let ${\mathcal{R}}_1,{\mathcal{R}}_2,{\mathcal{R}}_3,{\mathcal{R}}_4,{\mathcal{R}}_5,{\mathcal{R}}_6:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be continuous functions defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{R}}_1\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{18e^s{\left[v\right]}^2}{60000(1+{\left[v\right]}^2)}+0.0003e^{s}sin\left({\mathfrak{D}}^{0.04}\tilde{v}\right)+\frac{3e^s{sinh}^{-1}\tilde{\tilde{v}}}{10000},\hfill \\ \hfill {\mathcal{R}}_2\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{s\left(arctanv\right)}{10000}+0.0001ssin\left({\mathfrak{D}}^{0.04}\tilde{v}\right)+\frac{8s{\left[\tilde{\tilde{v}}\right]}^2}{10000(1+{\left[\tilde{\tilde{v}}\right]}^2)},\hfill \\ \hfill {\mathcal{R}}_3\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{e^s{\left[v\right]}^2}{25000(1+{\left[v\right]}^2)}+\frac{4e^s{sinh}^{-1}\left({\mathfrak{D}}^{0.04}\tilde{v}\right)}{100000}+\frac{12e^{s}arctan\tilde{\tilde{v}}}{300000},\hfill \\ \hfill {\mathcal{R}}_4\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =0.0009s\left(sinv\right)+\frac{180s{\left[{\mathfrak{D}}^{0.04}\tilde{v}\right]}^2}{200000+200000{\left[{\mathfrak{D}}^{0.04}\tilde{v}\right]}^2}+\frac{36s(arctan\tilde{\tilde{v}})}{40000},\hfill \\ \hfill {\mathcal{R}}_5\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =0.0001s\left({sinh}^{-1}v\right)+\frac{60s{\left[{\mathfrak{D}}^{0.05}\tilde{v}\right]}^2}{600000+600000{\left[{\mathfrak{D}}^{0.05}\tilde{v}\right]}^2}+\frac{3s\left(arctan\tilde{\tilde{v}}\right)}{30000},\hfill \\ \hfill {\mathcal{R}}_6\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{s\left(arctanv\right)}{25000}+0.00004s\left(sin\left({\mathfrak{D}}^{0.05}\tilde{v}\right)\right)+\frac{4s{\left[\tilde{\tilde{v}}\right]}^2}{100000\left(1+{\left[\tilde{\tilde{v}}\right]}^2\right)}.\hfill \end{array}\right.\end{array}$$

Let $v_1,v_2,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{\tilde{v}}}_1,{\tilde{\tilde{v}}}_2\in \mathbb{R}$. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|{\mathcal{R}}_1\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_1\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{3e^s}{10000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_2\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_2\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{s}{10000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_3\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_3\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{e^s}{25000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_4\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_4\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{9s}{10000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_5\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_5\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{s}{10000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_6\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_6\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{s}{25000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right).\hfill \end{array}\end{array}$$

Here, ${\mathcal{Z}}_1\left(s\right)=\frac{3e^s}{10000},{\mathcal{Z}}_2\left(s\right)=\frac{s}{10000},{\mathcal{Z}}_3\left(s\right)=\frac{e^s}{25000},{\mathcal{Z}}_4\left(s\right)=\frac{9s}{10000},{\mathcal{Z}}_5\left(s\right)=\frac{s}{10000}$, and ${\mathcal{Z}}_6\left(s\right)=\frac{s}{25000}$, where $∥{\mathcal{Z}}_1∥=\frac{3}{10000},∥{\mathcal{Z}}_2∥=\frac{1}{10000},∥{\mathcal{Z}}_3∥=\frac{1}{25000},∥{\mathcal{Z}}_4∥=\frac{9}{10000},∥{\mathcal{Z}}_5∥=\frac{1}{10000}$, and $∥{\mathcal{Z}}_6∥=\frac{1}{25000}$. Let ${\mathcal{U}}_1,{\mathcal{U}}_2,\dots ,{\mathcal{U}}_6:[0,\infty )\to \mathbb{R}$ be identity functions. Thus, we obtain

$$\begin{array}{ccc}\hfill \left|{\mathcal{R}}_1(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{3e^s}{10000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_2(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{s}{10000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_3(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{e^s}{25000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_4(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{9s}{10000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_5(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{s}{10000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_6(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{s}{25000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \end{array}$$

for all $s\in [0,1]$ and $v,\tilde{v},\tilde{\tilde{v}}\in \mathbb{R}$. In addition, the continuous function ${\mathcal{Q}}_1,{\mathcal{Q}}_2,\dots ,{\mathcal{Q}}_6:[0,1]\to \mathbb{R}$ are defined by ${\mathcal{Q}}_1\left(s\right)=\frac{3e^s}{10000},{\mathcal{Q}}_2\left(s\right)=\frac{s}{10000},{\mathcal{Q}}_3\left(s\right)=\frac{e^s}{25000},{\mathcal{Q}}_4\left(s\right)=\frac{9s}{10000},{\mathcal{Q}}_5\left(s\right)=\frac{s}{10000},and{\mathcal{Q}}_6\left(s\right)=\frac{s}{25000}$. In addition,

$${\mathcal{V}}_0^{*}\simeq 2.2346,{\mathcal{V}}_1^{*}\simeq 0.6031\mathrm{and}{\mathcal{V}}_2^{*}\simeq 5.9096,$$

and so

$${\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\simeq 8.7473.$$

Furthermore,

$$\Lambda :=\left({\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\right)\left(∥{\mathcal{Z}}_1∥+∥{\mathcal{Z}}_2∥+∥{\mathcal{Z}}_3∥+∥{\mathcal{Z}}_4∥+∥{\mathcal{Z}}_5∥+∥{\mathcal{Z}}_6∥\right)\simeq 0.0136<1.$$

Hence, by Theorem 4, the problem (22)–(23) has a solution.

Example 2. 

Consider the problem stated below:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^{1.25}{v}_1\left(s\right)& =\frac{21s}{5000}arctan{v}_1\left(s\right)+\frac{63{\left[{\mathcal{D}}^{0.2}{v}_1\left(s\right)\right]}^{2}s}{15000+15000{\left[{\mathcal{D}}^{0.2}{v}_1\left(s\right)\right]}^2}+0.0042s(arctan{v}_1^{\prime }\left(s\right)),\hfill \\ \hfill {\mathcal{D}}^{1.25}{v}_2\left(s\right)& =\frac{106{[sin{v}_2\left(s\right)]}^2{e}^s}{16000\left(1+{[sin{v}_2\left(s\right)]}^2\right)}+\frac{371e^s}{56000}\left(sin\left({\mathcal{D}}^{0.2}{v}_2\left(s\right)\right)\right)\hfill \\ & +\frac{53{[arctan{v}_2^{\prime }\left(s\right)]}^2{e}^s}{8000+8000{[arctan{v}_2^{\prime }\left(s\right)]}^2},\hfill \\ \hfill {\mathcal{D}}^{1.25}{v}_3\left(s\right)& =0.005125s(arctan{v}_3\left(s\right))+\frac{41s{\left[{\mathcal{D}}^{0.2}{v}_3\left(s\right)\right]}^2}{8000\left(1+{\left[{\mathcal{D}}^{0.3}{v}_3\left(s\right)\right]}^2\right)}+\frac{205s}{40000}{sinh}^{-1}{v}_3^{\prime }\left(s\right),\hfill \end{array}\right.\end{array}$$

(24)

with boundary conditions

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill v_1\left(0\right)& ={\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_1\left(\theta \right)d\theta \hfill \\ \hfill \frac{11}{3}{\mathfrak{D}}^{0.2}{v}_1\left(1\right)+\frac{13}{7}{\mathcal{D}}^{0.4}{v}_1\left(1\right)& =\frac{21}{4}{\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_1\left(\theta \right)d\theta \hfill \\ \hfill v_2\left(0\right)& ={\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_2\left(\theta \right)d\theta \hfill \\ \hfill \frac{11}{3}{\mathfrak{D}}^{0.2}{v}_2\left(1\right)+\frac{13}{7}{\mathcal{D}}^{0.4}{v}_2\left(1\right)& =\frac{21}{4}{\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_2\left(\theta \right)d\theta \hfill \\ \hfill v_3\left(0\right)& ={\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_3\left(\theta \right)d\theta \hfill \\ \hfill \frac{11}{3}{\mathfrak{D}}^{0.2}{v}_3\left(1\right)+\frac{13}{7}{\mathcal{D}}^{0.4}{v}_3\left(1\right)& =\frac{21}{4}{\int }_0^{0.5}{\mathfrak{D}}^{0.25}{v}_3\left(\theta \right)d\theta \hfill \end{array}\right.\end{array}$$

(25)

where $m=1.25,n=0.2,{\eta }_1=\frac{11}{3},{\eta }_2=\frac{13}{7},{\eta }_3=\frac{21}{4}$, and ${\mathfrak{D}}^m$, ${\mathfrak{D}}^n$ are the Caputo derivatives of order m and n, respectively. Let ${\mathcal{R}}_1,{\mathcal{R}}_2,{\mathcal{R}}_3:[0,1]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be continuous functions defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{R}}_1\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{21s}{5000}arctanv+\frac{63{\left[{\mathcal{D}}^{0.2}\tilde{v}\right]}^{2}s}{15000+15000{\left[{\mathcal{D}}^{0.3}\tilde{v}\right]}^2}+0.0042s(arctan\tilde{\tilde{v}}),\hfill \\ \hfill {\mathcal{R}}_2\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =\frac{106{[sinv]}^2{e}^s}{16000\left(1+{[sinv]}^2\right)}+\frac{371e^s}{56000}sin\left({\mathcal{D}}^{0.2}\tilde{v}\right)+\frac{53{[arctan\tilde{\tilde{v}}]}^2{e}^s}{8000+8000{[arctan\tilde{\tilde{v}}]}^2},\hfill \\ \hfill {\mathcal{R}}_3\left(s,v,\tilde{v},\tilde{\tilde{v}}\right)& =0.005125s(arctanv)+\frac{41s{\left[{\mathcal{D}}^{0.2}\tilde{v}\right]}^2}{8000\left(1+{\left[{\mathcal{D}}^{0.3}\tilde{v}\right]}^2\right)}+\frac{205s}{40000}{sinh}^{-1}\tilde{\tilde{v}}.\hfill \end{array}\right.\end{array}$$

Let $v_1,v_2,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{\tilde{v}}}_1,{\tilde{\tilde{v}}}_2\in \mathbb{R}$. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|{\mathcal{R}}_1\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_1\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{21s}{5000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_2\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_2\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{53e^s}{8000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_3\left(s,v_1,{\tilde{v}}_1,{\tilde{\tilde{v}}}_1\right)-{\mathcal{R}}_3\left(s,v_2,{\tilde{v}}_2,{\tilde{\tilde{v}}}_2\right)\right|\le & \frac{41s}{8000}\left(\left|v_1-v_2\right|+\left|{\tilde{v}}_1-{\tilde{v}}_2\right|+\left|{\tilde{\tilde{v}}}_1-{\tilde{\tilde{v}}}_2\right|\right).\hfill \end{array}\end{array}$$

Here, ${\mathcal{Z}}_1\left(s\right)=\frac{21s}{5000},{\mathcal{Z}}_2\left(s\right)=\frac{53e^s}{8000},{\mathcal{Z}}_3\left(s\right)=\frac{41s}{8000}$, and ${\mathcal{Z}}_5\left(s\right)=\cdots ={\mathcal{Z}}_{13}\left(s\right)=0$, where $∥{\mathcal{Z}}_1∥=\frac{21}{5000},∥{\mathcal{Z}}_2∥=\frac{53}{8000},∥{\mathcal{Z}}_3∥=\frac{41}{8000}$, and $\parallel {\mathcal{Z}}_5\parallel =\cdots =\parallel {\mathcal{Z}}_{13}\parallel =0$. Let ${\mathcal{U}}_1,{\mathcal{U}}_2,\dots ,{\mathcal{U}}_{13}:[0,\infty )\to \mathbb{R}$ be identity functions. Then, we obtain

$$\begin{array}{ccc}\hfill \left|{\mathcal{R}}_1(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{21s}{5000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_2(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{53e^s}{8000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \\ \hfill \left|{\mathcal{R}}_3(s,v,\tilde{v},\tilde{\tilde{v}})\right|& \le & \frac{41s}{8000}\left(\left|v\right|+\left|\tilde{v}\right|+\left|\tilde{\tilde{v}}\right|\right),\hfill \end{array}$$

for all $s\in [0,1]$ and $v,\tilde{v},\tilde{\tilde{v}}\in \mathbb{R}$. In addition, the continuous function ${\mathcal{Q}}_1,{\mathcal{Q}}_2,\dots ,{\mathcal{Q}}_{13}:[0,1]\to \mathbb{R}$ is defined by ${\mathcal{Q}}_1\left(s\right)=\frac{21s}{5000},{\mathcal{Q}}_2\left(s\right)=\frac{53e^s}{8000},{\mathcal{Q}}_3\left(s\right)=\frac{41s}{8000},and{\mathcal{Q}}_5\left(s\right)=\cdots ={\mathcal{Q}}_{13}\left(s\right)=0.$

In addition,

$${\mathcal{V}}_0^{*}\simeq 2.840,{\mathcal{V}}_1^{*}\simeq 0.946\mathrm{and}{\mathcal{V}}_2^{*}\simeq 0.881,$$

and so

$${\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\simeq 4.667.$$

Furthermore,

$$\mathsf{\Lambda }:=\left({\mathcal{V}}_0^{*}+{\mathcal{V}}_1^{*}+{\mathcal{V}}_2^{*}\right)\left(∥{\mathcal{Z}}_1∥+∥{\mathcal{Z}}_2∥+∥{\mathcal{Z}}_3∥+∥{\mathcal{Z}}_4∥\right)\simeq 0.074<1.$$

Hence, by Theorem 4, the problem (24)–(25) has a solution.

4. Conclusions

CGT refers to a specific part of graph theory that has applications in chemistry. Mathematical tools from pure mathematics, graph theory, functional analysis, and trigonometry are used to tackle chemistry-based problems such as structure elucidation and isomer enumeration, with repercussions for both fields. The rapid expansion of this field over the last several decades has led to the introduction of a plethora of novel ideas and methods for pursuing this kind of study. This article defines the boundary-value problems for each edge within the context of an isobutane graph. Using the Krasnoselskii and Schaefer fixed point theorems, we investigated the existence of solutions to the suggested problem. Our proposed model may be used for various graph configurations, including digraphs, which are often used in medical technology in connection to protein networks. Future studies can investigate more challenges involving the graph characterization of various chemical structures using quantitative and computational approaches.